7

ALTERNATIVAS

Primer principio básico del pensamiento lateral: cualquier modo de valorar una situación es sólo uno de los muchos modos posibles de valorarla. El pensamiento lateral explora estas alternativas mediante la reordenación de la información disponible. La misma palabra «lateral» significa movimiento perpendicular a la dirección del pensamiento vertical o lógico; es decir, movimiento a un lado u otro en vez de seguir el cauce convencional del desarrollo de un modelo preestablecido. (Véase el diagrama correspondiente.)

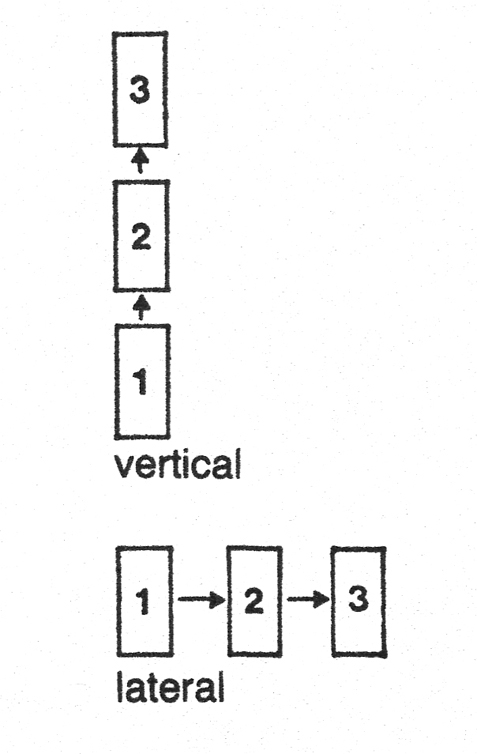
La búsqueda de alternativas y nuevos enfoques a una misma situación o problema parecerá quizás un proceso típico del pensamiento lógico. Muchas personas consideran que la búsqueda de dichas alternativas forma parte del pensamiento práctico diario. Hay indudablemente cierta analogía entre ambos procesos, pero la búsqueda lateral va mucho más lejos que la búsqueda lógica.

En la búsqueda lógica se aspira al mejor enfoque posible, mientras que en la búsqueda lateral se aspira al mayor número posible de enfoques, prescindiendo de su valor práctico real.

La búsqueda lógica se interrumpe cuando se llega a un enfoque satisfactorio. En el pensamiento lateral se reconoce también la calidad de un enfoque satisfactorio, pero se continúa la búsqueda de enfoques alternativos. Al final del proceso creador inicial se vuelve la mirada a dicho concepto prometedor para estudiarlo con más detalle.

En la búsqueda lógica de alternativas se consideran sólo aquellos conceptos que poseen cierto sentido común. En la búsqueda lateral se aceptan inicialmente alternativas exentas de todo sentido común.

La búsqueda lógica a menudo oculta una mera intención, que se abandona tan pronto como se encuentra una solución adecuada. La búsqueda lateral es una investigación consecuente y total, que no cesa ante un resultado, aunque el valor de éste sea obvio.

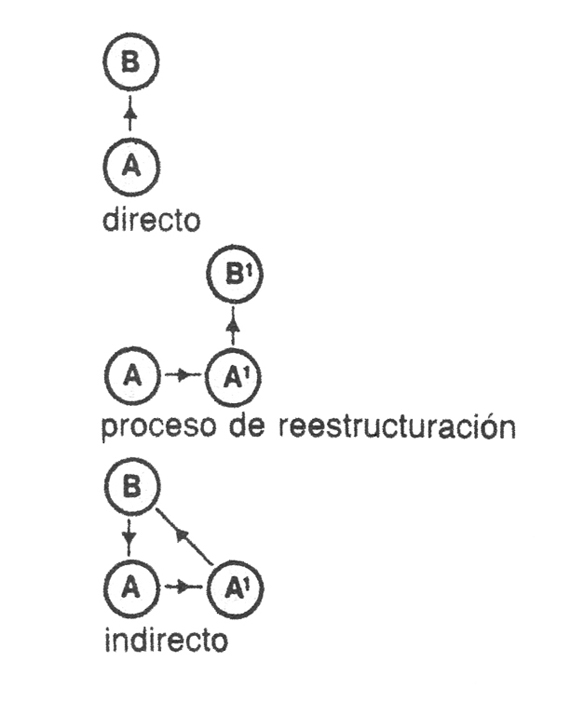
Por consiguiente, la principal diferencia reside en la finalidad de la búsqueda. La inclinación lógica es buscar alternativas para encontrar la mejor solución, mientras que el pensamiento lateral tiene como objetivo, no el hallazgo inmediato de una solución óptima, sino la superación de la rigidez de los modelos conceptuales, provocando su disgregación y subsiguiente reordenación en nuevos modelos. Este proceso puede derivar en diferentes situaciones:

• Pueden obtenerse varias alternativas, para luego volver al análisis de las más satisfactorias.

• Una de las alternativas encontradas puede convertirse en punto de partida hacia nuevas ideas.

• Una de las alternativas encontradas constituye en sí misma, sin mayor elaboración, una solución satisfactoria.

• Una de las alternativas provoca una reordenación de la información y el nuevo modelo constituye una solución perspicaz.

Aun en los casos en que la búsqueda lateral de alternativas no produzca resultados útiles, no se ha perdido el tiempo, ya que así se desarrolla la costumbre de buscar alternativas en vez de aceptar simplemente el enfoque más obvio y fácil.

La búsqueda de alternativas no impide que se acepte la solución más evidente obtenida por el pensamiento lógico si la misma se revela como la más efectiva. Al proceder en la búsqueda lateral lo único que se hace es aplazar la aceptación definitiva de dicha idea obvia, mientras se consiguen las alternativas, pero en ningún momento se niega su validez; antes al contrario, al final se habrá escogido no por ser la única solución, sino por ser la más eficaz.

Límite

Para que la búsqueda de alternativas no se limite a la mera intención de realizarla, sino que constituya una investigación a fondo y llegue a convertirse en una práctica accesible, conviene desde el principio fijar el número de alternativas que se han de alcanzar. La ventaja de establecer este tope mínimo es que permite buscar alternativas hasta cubrir el número requerido, en vez de cesar ante la primera alternativa que parece adecuada. Otra ventaja es el esfuerzo deliberado de buscar alternativas y no contentarse con un pequeño número de ellas, aunque parezcan las más obvias. Se incluyen, además, en la lista alternativas que pueden parecer artificiales o ridículas, pero que pueden tener validez con un examen más preciso o servir de eslabón para otras ideas. Como límite mínimo pueden fijarse 3, 4 o 5 alternativas.

Naturalmente, el fijar un límite mínimo no obliga a cesar la búsqueda de alternativas cuando se ha alcanzado el tope. Su objetivo es asegurar un número mínimo de esas alternativas.

Práctica

Figuras geométricas

La ventaja del uso de figuras geométricas y demás materiales visuales reside en su inequívoca presentación. Poseen un carácter único e inalterable, al contrario del material verbal, en el que el tono y el énfasis de la presentación pueden modificar la interpretación; además, ésta se presta a una mayor variedad de significados.

Las figuras geométricas son formas conocidas que pueden definirse claramente con una o dos palabras. Ello permite la descripción, sin lugar a dudas, de cambios y combinaciones en la explicación de procesos o en el planteamiento de problemas de solución lateral.

El enseñante debería recurrir al empleo de figuras geométricas en los primeros ejercicios de búsqueda de alternativas, aun cuando constituyan un medio artificial. Cuando los alumnos hayan comprendido perfectamente los procesos y actitudes implícitos en esta técnica, puede pasarse a la utilización de material verbal, con la presentación de situaciones más reales y complejas.

En el desarrollo de las clases el enseñante puede proceder de la siguiente manera:

1) Se representa la figura en la pizarra, o bien se distribuye a cada alumno en una hoja de papel.

2) Se pide a los alumnos que definan la figura de diferentes maneras.

3) El enseñante recoge los resultados o prescinde de ellos, según el número de alumnos y el tiempo de que disponga.

4-1) Sin recogida de los resultados.

El enseñante solicita de los alumnos que definan la figura. Si no aparece ningún voluntario, señala a un alumno para que dé la primera definición. Luego pide definiciones alternativas. Cada alternativa se relaciona en la pizarra.

4-2) Con recogida de los resultados.

El enseñante coge una o dos hojas y lee en voz alta las definiciones. Luego pide que se formulen definiciones alternativas o emplea otras hojas para leer variantes.

Si se dispone de tiempo entre una sesión y otra, el enseñante puede componer un diagrama estadístico de las alternativas obtenidas (como se muestra en el esquema de esta página). Este diagrama puede presentarse a la clase en la siguiente sesión.

5) El enseñante estimúlala creación de definiciones alternativas y las acepta sin valorarlas. Si una alternativa carece claramente de sentido no se critica, pero se solicita al que la compuso que la explique de modo más detallado. Si parece obvio que el sentido común impedirá a los alumnos aceptar dicha alternativa como válida, se relaciona al final de la lista, pero nunca ha de omitirse.

6) Cuando los alumnos no consiguen extraer definiciones alternativas, el enseñante puede citar algunas, previamente preparadas.

Ejercicios

1. ¿Cómo puede definirse la siguiente figura?

Alternativas

Dos círculos unidos por una recta.

Una recta con un círculo en cada extremo.

Dos pares de semicircunferencias unidas por una recta y dispuestas una sobre otra de forma que coincidan.

Dos canalones de desagüe superpuestos.

Comentario

Los estudiantes protestarán quizás aduciendo que «dos círculos unidos por una recta» es lo mismo que «una recta con un círculo en cada extremo»; sin embargo, no existe tal identidad, ya que en el primer caso se empieza con los círculos y en el segundo con la recta, y desde el punto de vista del proceso mental la secuencia de las ideas es de máxima importancia, ya que una diferencia en el punto de partida equivale a un enfoque diferente.

Algunas de las definiciones tienen carácter estático, ya que consisten en el simple dibujo o definición de la figura alternativa. Otras tienen carácter dinámico y precisan el empleo de diagramas adicionales; ello ocurre cuando la figura alternativa es el resultado de algún proceso en el que intervienen otras figuras.

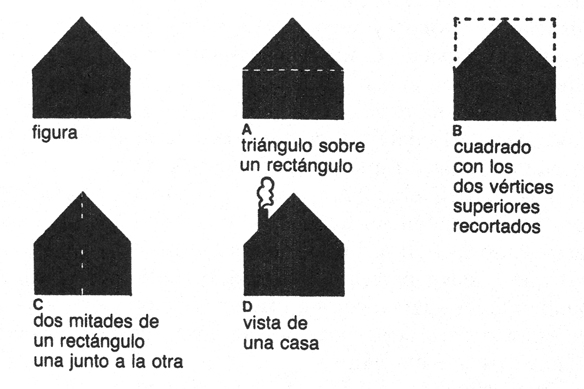
2. ¿Cómo puede definirse la siguiente figura?

Alternativas

Forma en L.

Una escuadra.

Una horca al revés.

Medio marco.

Dos rectángulos adosados uno al otro.

Un rectángulo grande del que se ha recortado un rectángulo pequeño.

Comentario

Se presentan a veces dificultades al describir una figura geométrica mediante un objeto físico; al decir «una escuadra» se incita a otras comparaciones, como por ejemplo «el perímetro de un edificio visto desde el aire». Hay que recordar entonces a los alumnos que se trata de buscar alternativas, no de lo que la figura podría ser ni de lo que sugiere su contemplación. La definición debe ser de tal tipo que permita dibujar la figura en cuestión, y la definición de que es «el perímetro de un edificio visto desde el aire» no es válida a menos que dicho perímetro se especifique como teniendo forma L, caso en el cual basta con decir «forma en L». Por otra parte, no es necesario insistir en que la definición sea muy precisa, ya que ello desviaría la atención hacia cuestiones de detalle, que nada tienen que ver con el pensamiento lateral.

A veces las definiciones constituyen el resultado de algún proceso. Por ejemplo, «dos rectángulos adosados» o «un rectángulo grande del que se ha recortado un rectángulo pequeño» exigen la combinación de otras figuras. Este método de definición es válido. La validez de las definiciones puede fundamentarse en los siguientes procesos:

• Combinación de unidades menores.

• Comparación con otra figura.

• Modificación de otra figura mediante la adición o sustracción de partes.

Como ya se ha dicho, en tales casos se requiere a veces el uso de diagramas complementarios. Cuando la exposición de la alternativa no sea comprensible puede solicitarse del alumno que la compuso que explique su significado.

3. ¿Cómo puede definirse la figura superior de las que vienen a continuación?

Alternativas

Dos cuadrados superpuestos.

Tres cuadrados.

Dos figuras en L rodeando un espacio hueco cuadrado.

Un rectángulo dividido en dos mitades con la línea que los corta descentrada.

Comentario

La definición «dos cuadrados superpuestos» parece tan precisa que cualquier otra definición se considera superflua. Esto ilustra el poder dominante que ejercen ciertos modelos. También en este caso pueden creer algunos alumnos que las definiciones «dos cuadrados superpuestos» y «tres cuadrados» tienen el mismo significado. Sin embargo, no existe tal equivalencia, a pesar de que la segunda definición esté ya implícita en la primera, y debe evitarse el considerar como idénticas ideas que posean cierta semejanza o que estén íntimamente asociadas entre sí, ya que una ligera desviación en el ángulo de enfoque puede conducir eventualmente a una gran divergencia de resultados. Otras definiciones son a veces tan extensas que cubren todas las posibles alternativas: «Dos cuadrados superpuestos en uno de sus ángulos, de modo que el área de superposición forma un tercer cuadrado cuyos lados son iguales a la mitad de los lados de los dos cuadrados originales». Estas extensas definiciones constituyen una reproducción verbal de la figura geométrica y, por consiguiente, incluyen varias definiciones. No obstante, estas definiciones han de aceptarse como válidas. En el pensamiento lógico una definición puede ser superflua por estar ya implícita en otra, pero desde el punto de vista de la percepción, la misma definición puede utilizar otros modelos. Por ejemplo, la idea de «tres cuadrados» es útil incluso cuando esté implícita en la descripción de «dos cuadrados superpuestos».

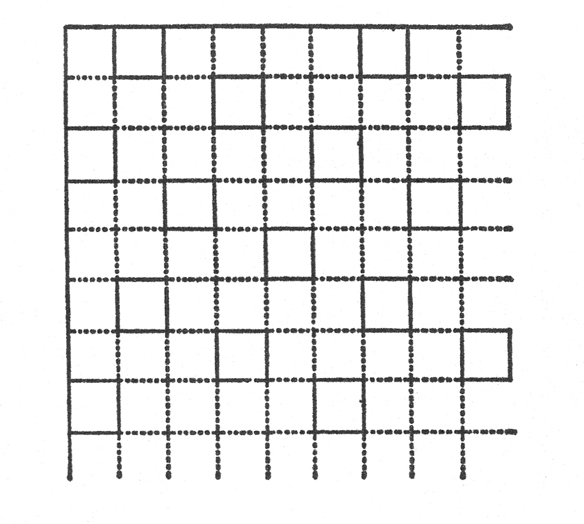
4. ¿Cómo puede definirse la figura que se ve a continuación?

Alternativas

Pequeños cuadrados rodeados de cuadrados grandes. Cuadrados grandes con cuadrados pequeños en sus ángulos.

Columnas de cuadrados grandes formando escalones. Un conjunto de cuadrados grandes y pequeños. Prolongación de los lados de un cuadrado pequeño con otros cuadrados pequeños en los extremos de estas prolongaciones.

Una serie de rectas, cada una con dos líneas perpendiculares.

Una cuadrícula en la que se suprimen algunas líneas formando entonces cuadrados mayores.

Cuadrados grandes colocados de modo que el lado de cada uno se superpone a la mitad del cuadrado adyacente. Dos modelos de líneas superpuestas en ángulo recto entre sí.

Comentario

Hay muchas otras definiciones alternativas posibles. Las definiciones han de ser suficientemente descriptivas para poder reproducir el original, e indicar claramente cómo se observa el modelo. Lo más importante es la variedad de enfoques: cuadrados grandes, cuadrados pequeños, una mezcla de ambos, líneas perpendiculares, espacios huecos, cuadrícula.

• Actividad

Los cuatro ejercicios anteriores consisten en la definición de alternativas.

Ahora pasamos a una segunda fase: en vez de las distintas formas de ver una misma cosa, trataremos de las diversas maneras de hacer una cosa. Esta fase es más difícil, ya que las definiciones constituían una visión de lo que estaba presente, mientras que el hacer algo representa poner en un sitio lo que no está allí.

5. ¿Cómo puede dividirse un cuadrado en cuatro partes iguales? (Conviene que cada alumno dibuje en una hoja de papel tantas versiones como pueda imaginar; no es conveniente hacer este ejercicio en la pizarra. Luego se recogen las hojas y se analizan los resultados o se dibujan las soluciones en la pizarra para que cada alumno vea las alternativas adicionales a las que ya ha descubierto.)

Alternativas

Cuatro secciones verticales u horizontales rectangulares.

Cuatro cuadrados pequeños.

Diagonales.

División del cuadrado en dieciséis pequeños cuadrados y luego trazar dos líneas en forma de cruz gamada. Otras formas, según la ilustración.

Comentario

La mayor parte de los alumnos suelen ver sólo la posibilidad de las secciones rectangulares y triangulares y los cuatro cuadrados pequeños. Luego, a alguien se le ocurre la idea de dividir la figura en dieciséis pequeños cuadrados y agruparlos de diversas maneras. El siguiente principio es que cualquier línea que se trace desde un punto de un lado de la figura al punto equivalente del lado opuesto y posea la misma forma por encima del punto central que por debajo, divide el cuadrado en dos mitades iguales; por consiguiente, la adición de una segunda línea en ángulo recto a la primera divide el cuadrado en cuatro partes iguales. Es obvio que estas líneas pueden tener una infinidad de variantes; a veces, algún alumno dibuja diversas versiones de esta solución sin descubrir el principio fundamental.

En tal caso, en vez de considerar cada variante como una alternativa, se incluyen todas ellas en el citado principio. Una variación de este principio es la división del cuadrado en dos mitades de igual área por una recta que pase por su centro, y la subsiguiente división de cada mitad en dos partes equivalentes mediante cualquier tipo de línea. Esta solución introduce una nueva serie de variantes, todas ellas comprendidas también en el mismo principio unitario.

Como no se trata de un ejercicio de geometría o de dibujo, no es necesario explorar todas las posibilidades de efectuar la mencionada división. Lo que se quiere conseguir es demostrar que hay normalmente otras formas de valorar una situación o un problema, aun cuando se crea lo contrario. El enseñante espera hasta que no se sugieren más alternativas descritas. (Naturalmente, puede ocurrir que todas las alternativas sean descubiertas por los alumnos.)

6. ¿Cómo puede dividirse una cartulina cuadrada sin efectuar más de dos cortes, de modo que tenga forma de L, y sin que se altere su área? (Pueden usarse cuadrados de cartulina o simplemente dibujar las soluciones en una hoja de papel.)

Alternativas

Dos secciones rectangulares (véase la figura en la página siguiente).

El recorte de un pequeño cuadrado.

Un corte diagonal.

Comentario

El requisito de no usar más de dos cortes introduce un factor de limitación; pero esta limitación no tiene sentido restrictivo, sino que estimula la búsqueda de alternativas difíciles, en vez de contentarse con las soluciones más obvias.

Puesto que tanto la figura original como el resultado exigido se basan en líneas horizontales y verticales, así como en ángulos rectos, el método diagonal no es fácil de encontrar. Quizá la mejor manera de hallarlo es «cortar el cuadrado diagonalmente y observar qué pasa». En realidad, con este ejercicio se empieza ya a recurrir a procedimientos de acertijo en lugar de simples técnicas analíticas.

Formas no geométricas

Después de haber usado las formas geométricas para ilustrar la búsqueda deliberada de alternativas (y la frecuente existencia de tales alternativas), puede pasarse a efectuar ejercicios más complejos. En los ejercicios que se presentan a continuación no se intenta descubrir alternativas fijadas ya en modelos establecidos, sino crear alternativas acoplando diversos elementos de modelos.

7. ¿Cómo puede definirse una botella de leche de un litro que contiene medio litro de agua?

Alternativas

Media botella de agua.

Una botella de leche medio llena de agua.

Medio litro de agua en una botella de leche de un litro vacía.

Comentario

El ejercicio es trivial, pero sirve para ilustrar cómo pueden coexistir dos modos completamente distintos de valorar una misma situación. También demuestra que cuando se ha elegido una de estas alternativas, las otras normalmente se ignoran. Es interesante constatar que cuando una botella está medio llena de leche se designa corrientemente como medio vacía, mientras que cuando está medio llena de agua se refiere como medio llena. La razón reside probablemente en el hecho de que, en el caso de la leche, se parte, en sentido descendente, de la botella llena, mientras que en el caso del agua el punto de partida es la botella vacía, con tendencia ascendente. El contexto de cualquier situación influye decisivamente en la manera de valorar.

• Imágenes

Las fotografías y otras imágenes recortadas de periódicos y revistas son la principal fuente de material visual; sin embargo, es difícil conseguir el suficiente número de imágenes para su uso en clases con muchos alumnos. Una solución consiste en adquirir varios ejemplares de un mismo periódico y utilizar el material para diversas clases. Es también posible dibujar las ilustraciones en la pizarra, pero este método es mucho menos eficaz. El tipo de material adecuado se describe en el capítulo «Uso de este libro». Las imágenes pueden utilizarse de dos modos:

• Para que los alumnos describan lo que creen que ocurre en la imagen.

• Para que describan tres alternativas de lo que ocurre en la imagen.

En el primer caso el enseñante utiliza una imagen ambigua, y pide a los alumnos que la interpreten a su manera. La diversidad de interpretaciones pone de manifiesto las diferentes alternativas de enfoque posibles. El enseñante no valorará las interpretaciones, evitando mencionar cuál es mejor o peor. Tampoco explicará el verdadero tema de la fotografía (puede haber olvidado su significado, si se solicitara su explicación).

En el segundo caso, si las interpretaciones de los alumnos son reducidas en número, a causa del bloqueo de las interpretaciones por otras alternativas más obvias, el maestro puede añadir otras posibles explicaciones de la imagen, en un orden de probabilidad. Para concluir, citará algunas interpretaciones menos plausibles, para demostrar que las alternativas no tienen que concordar necesariamente con el sentido común.

Ejemplo

Una fotografía con gente vadeando agua poco profunda. No llevan atuendo de baño. En el fondo se atisba una playa arenosa.

Se recibieron las siguientes interpretaciones:

Gente sorprendida por la pleamar.

Gente cruzando una depresión del terreno inundado por el agua de las lluvias.

Gente cruzando agua de poco nivel para alcanzar un islote o un trecho de arena.

Gente yendo hacia un transbordador que no puede arribar a la orilla.

Náufragos de un barco encallado.

Comentario

En realidad, la gente de la fotografía realizaba una manifestación de protesta contra el estado deficiente de la playa. No era importante adivinar el significado real de la imagen, pues no se trataba de un ejercicio de deducción lógica. Lo importante era obtener varias interpretaciones de una misma fotografía. Además de interpretaciones plausibles, es conveniente estimular la mención de alternativas más remotas (aun cuando las mismas hayan de ser rechazadas al proceder a su valoración crítica).

Ejemplo

La fotografía de un niño sentado en el banco de un parque.

Alternativas

Niño ocioso o perezoso.

Espacio libre en el banco de un parque.

Parte de un banco mantenida seca por un niño.

Comentario

Las interpretaciones de esta imagen son completamente diferentes de las del ejemplo anterior. Se pone en evidencia un menor intento de decir lo que ocurre (por ejemplo: un niño esperando a sus compañeros de juego, niño descansando, niño tomando el sol). En vez de ello, las interpretaciones se refieren a la escena en sí, no a su explicación (por ejemplo: niño en el banco de un parque, espacio libre en el banco de un parque). Hay también un intento de analizar la imagen desde un ángulo diferente, en la frase «parte de un banco mantenida seca por un niño», aunque la idea es quizá demasiado ajena a la fotografía. Pero aquí no se fijan límites.

En toda imagen hay varios niveles de interpretación: lo que representa gráficamente, lo que ocurre, lo que ha ocurrido y lo que va a suceder. Al pedir alternativas, el enseñante puede, al principio, dejar abiertos todos estos niveles para, en un estadio más avanzado, especificar en qué nivel han de formularse las interpretaciones.

• Imágenes alteradas

El inconveniente de las fotografías y dibujos es que a menudo el asunto a que se refieren es demasiado obvio y la interpretación correcta bloquea otras posibles interpretaciones. No sólo es difícil concebir alternativas, sino que las que se formulan parecen artificiales y ridículas. Para contrarrestar este efecto de bloqueo y conferir mayor aliciente al ejercicio, el enseñante puede alterar las fotografías cubriendo parte de ellas. Ello aumenta la dificultad de adivinar el tema real y se abre automáticamente la posibilidad de concebir un mayor número de interpretaciones. Hay también el incentivo adicional de adivinar el tema auténtico, que parecerá como evidente y natural al descubrir la totalidad de la imagen.

Ejemplo

La mitad de la fotografía está cubierta. La parte visible muestra un hombre manteniendo el equilibrio en la cornisa de un edificio.

Alternativas

Un hombre que amenaza con cometer suicidio.

Rescate de un gato bloqueado en una cornisa.

Escapando de un edificio en llamas.

El doble de un actor cinematográfico.

Hombre tratando de entrar en su habitación, que ha quedado cerrada con la llave dentro.

Comentario

El resto de la fotografía habría mostrado que el hombre estaba pegando un cartel mural. El uso de imágenes parcialmente cubiertas facilita la concepción de alternativas, pero cuando los alumnos han adquirido cierta práctica se precisa el efecto contrario, es decir, conseguir un considerable número de alternativas con imágenes de significado claro a pesar del efecto de bloqueo de este evidente significado. Sin embargo, puede utilizarse el método de imágenes alteradas para que los alumnos adquieran cierta práctica; ello comporta también la ventaja de ilustrar el hecho de que la interpretación de una situación puede encontrarse en lo que a primera vista no aparece. Este criterio de acción impulsa a los alumnos a buscar la solución de los problemas, no sólo en el contexto de los mismos, sino también fuera de ellos.

• Material escrito. Relatos

Los relatos pueden obtenerse de periódicos y revistas, e incluso de libros escolares.

Esos relatos pueden presentarse con diversos fines:

• Generar diferentes puntos de vista.

• Cambiar una descripción favorable en desfavorable, no modificando el material, sino el valor relativo de diferentes conceptos y el ángulo de visión o enfoque para el análisis.

• Extraer un significado de la información diferente al extraído por el autor.

Ejemplo

Relato periodístico sobre un águila que se ha escapado del parque zoológico y que resulta difícil de capturar. Se ha posado en las ramas más altas de un árbol y se resiste a los esfuerzos de los guardianes que tratan de atraerla a su jaula con señuelos.

Alternativas

Punto de vista del guardián: el ave puede alejarse volando y perderse, o ser abatida por algún cazador, a menos que se consiga su pronta captura. De poco valdría perseguirla trepando por los árboles, cuando puede levantar el vuelo. Alguien ha de responsabilizarse de que se haya escapado.

Punto de vista del periodista: cuanto más tiempo esté el águila fuera, mejor para el reportaje. Quizá sea posible acercarse y tomar una buena fotografía. Debo buscar algo que interese al público, además de exponer las diferentes maneras de cazar un águila.

Punto de vista del águila: pasmo ante tanta confusión; extraña sensación de no estar en la jaula; un poco de hambre; indecisión de hacia adonde volar.

Punto de vista de un espectador: esperanza de que el águila se aleje volando y quede libre por el resto de sus días. Sorpresa ante el denodado esfuerzo por cazarla. El ave parece más satisfecha en la copa del árbol que en la jaula. Quizás él mismo podría demostrar su habilidad y cazar el águila, cuando nadie parece capaz de ello.

Comentario

Cuando un relato comprende varias personas siempre es fácil exponer el punto de vista de todas ellas. Un mismo estudiante puede exponer los diferentes puntos de vista o bien puede señalársele que describa un punto de vista concreto. El ejercicio no estriba tanto en adivinar lo que cada personaje piensa como en mostrar que una misma situación puede estructurarse de diferentes maneras.

Ejemplo

Un relato sobre la vida incómoda de las comunidades primitivas en que se desconocía el leer y escribir y la subsistencia era posible sólo mediante el duro trabajo de la tierra.

Alternativas

La idea de la comodidad depende de las costumbres de cada uno.

Si se estaba acostumbrado a las cosas simples y era posible obtenerlas, ello resultaba mejor que el estado actual, en que se aspira a cosas complejas y se siente descontento por no poderlas alcanzar.

Quizás el leer y escribir sólo consigan entristecer a la gente, llevando a su conocimiento las desventuras que ocurren en el mundo.

La mayoría de la gente, ahora como antes, trabaja en un quehacer u otro; quizás el laboreo de la tierra causaba mayor satisfacción, al ver cómo nacía y crecía lo que se sembraba; además, cada uno cultivaba sus propios alimentos.

Comentario

El punto de vista alternativo no tiene que ser necesariamente el que el alumno crea como más acertado. El objetivo es demostrar que se pueden analizar las cosas de manera diferente, cambiando su enfoque, y desarrollar cierta práctica mediante ejercicios de este tipo. Tampoco es cuestión de demostrar que el propio punto de vista es mejor que el de otros. Se prescinde incluso del realismo lógico, como «las comunidades primitivas parecían idílicas, pero cuando un miembro enfermaba carecía de medios curativos». En la práctica es difícil evitar las actitudes polémicas. También es difícil presentar puntos de vista en los que no se cree; pero el hacerlo tiene la ventaja de su fácil reestructuración.

Ejemplo

Un relato hace referencia al cabello largo y las vestiduras llamativas de los jóvenes como signo de la pérdida de su masculinidad, que los hace difíciles de distinguir de las muchachas.

Alternativas

El dejarse crecer el cabello revela valor, el valor de desafiar las costumbres convencionales.

Hasta muy recientemente los hombres llevaban el cabello largo y no eran por ello afeminados, sino todo lo contrario. En cuanto al vestir llamativo, no es un atributo femenino, sino más bien signo de extravagancia. Refleja una búsqueda masculina del individualismo.

¡Qué hay de malo en que existan menos diferencias entre muchachos y muchachas! Quizás así las mujeres conseguirán tener los mismos derechos que los hombres.

Comentario

En este tipo de reestructuración no se requiere información adicional. No es el objetivo presentar el reverso de una situación, sino demostrar que el material ordenado para dar un punto de vista dado puede reordenarse de forma distinta para producir otro punto de vista.

Problemas

Los problemas pueden derivar de la vida cotidiana o de la lectura de periódicos. Las columnas de la prensa están saturadas de sucesos, disturbios, fracasos y protestas. Aun cuando todo ello no pueda presentarse en su forma original como problemas concretos, una simple modificación de su texto permite su planteamiento en clase. Basta con que se exponga el tema de un problema general; no es necesario que el problema sea específico ni descrito en detalle. Pueden utilizarse como problemas las situaciones reales en que se precisa alguna mejora o en las que existe alguna dificultad real o imaginaria.

En el uso del material de los problemas para estimular la concepción de alternativas, puede procederse de dos maneras diferentes:

1) Buscar alternativas al planteamiento del problema.

2) Buscar alternativas al enfoque del problema.

No se trata en estos ejercicios elementales de solucionar los problemas, sino de hallar enfoques diferentes a los mismos. Pueden formularse soluciones válidas, pero esto no es esencial.

Ejemplo

El problema de que los niños se separen de sus padres en el seno de una multitud.

1. Replanteamientos

Alternativas

Cómo evitar que los niños se separen de sus padres en el seno de la multitud.

Cómo evitar que los niños se pierdan.

Localización y retorno de niños extraviados.

Cómo evitar que los padres lleven niños pequeños a zonas de concentración de multitudes.

Comentario

Algunas de las alternativas del planteamiento del problema constituyen en sí mismas soluciones concretas. Cuanto más general es el planteamiento, menos tiende a señalar soluciones su reestructuración. Si se plantea un problema en términos muy generales, es difícil encontrar una alternativa de igual generalidad. Para evitarlo, puede recurrirse al uso de problemas más específicos. Por ejemplo, «el problema de los niños perdidos entre las multitudes» podría replantearse como «el problema de los padres descuidados en las multitudes» o, en un nivel más específico, como «el problema de devolver los niños perdidos a sus padres».

2. Enfoques alternativos

Alternativas

Sujetar los niños a los padres (¿con una correa?).

Mejor método de identificación de los niños (disco con la dirección).

Evitar llevar a los niños a zonas muy atestadas (uso de guarderías).

Centros oficiales donde puedan volverse a encontrar los niños perdidos y sus padres.

Exposición al público de una lista de niños perdidos.

Comentario

En este caso muchos de los enfoques parecen señalar soluciones. Sin embargo, en otros casos los enfoques alternativos indican sólo un nuevo punto de vista. Por ejemplo, en el problema de los niños extraviados, podría darse un enfoque como «recoger datos estadísticos acerca del número de padres que llevan a sus hijos a lugares atestados de gente: a) porque quieren que estén con ellos; b) porque no tienen dónde dejarlos».

• Tipos de problemas

El tipo de problema a seleccionar depende grandemente de la edad de los alumnos. A continuación se relacionan algunos problemas, divididos en dos grupos de edades.

Grupo más joven

Cómo simplificar o acelerar el lavado de la vajilla.

Cómo asistir puntual a la escuela.

Cómo hacer helados de mayor tamaño.

Cómo recuperar una pelota colgada en un árbol.

Cómo efectuar el cambio de turno de conductores y cobradores de autobuses.

Grupo de más edad

Embotellamientos de tráfico.

Espacio para aeropuertos.

Rentabilidad de los ferrocarriles.

Suficientes viviendas a bajo coste.

Problema alimentario mundial.

Ocupación de los jugadores de cricket profesionales en invierno.

Mejor diseño de una tienda de campaña.

Resumen

Este capítulo ha tratado de la búsqueda de alternativas. Su objetivo ha residido en conseguir el mayor número posible de alternativas, no de elegir la mejor alternativa. Durante el proceso de la búsqueda puede reconocerse alguna alternativa que constituye una solución satisfactoria al problema, pero éste no es el objetivo, ni por ello cesará la búsqueda. Lo que se pretende es aliviar la rigidez que caracteriza el enfoque de las situaciones y problemas, mostrar que siempre existen alternativas si se pone empeño en buscarlas y potenciar la costumbre de reestructurar modelos.

Es preferible fijar el número de alternativas que cada alumno ha de encontrar; el dejar los ejercicios exentos de dicho límite mínimo es adecuado cuando los mismos son fáciles, pero cuando hay dificultad en encontrar alternativas es preferible buscar un límite mínimo que sirva de estímulo a la búsqueda.