El fet que la llum vagi amb velocitat finita, encara que molt elevada, fou descobert per primera vegada el 1676 per l’astrònom danès Ole Christensen Roemer. Si observem les llunes de Júpiter, ens adonarem que de tant en tant desapareixen de la nostra vista perquè passen pel darrere del planeta gegant. Aquests eclipsis de les llunes de Júpiter s’haurien de produir a intervals regulars, però Roemer observà que no estaven espaiats amb la regularitat esperable. ¿S’acceleraven i frenaven les llunes en les seves òrbites? Roemer proposà una altra explicació.

Si la llum viatgés amb velocitat infinita, a la terra veuríem els eclipsis a intervals regulars, exactament en el moment mateix en què es produeixen, tal com els senyals d’un rellotge còsmic. Com que la llum travessaria instantàniament qualsevol distància, aquesta situació no canviaria si Júpiter s’allunyés o s’atansés a la terra.

Separació temporal dels eclipsis de les llunes de Júpiter.

Imaginem, en canvi, que la llum viatja amb velocitat finita. En aquest cas, veurem cada eclipsi un cert temps després que s’hagi produït. Aquest retard depèn de la velocitat de la llum i de la distància de Júpiter a la terra. Si aquesta distància no variés, el retard seria el mateix per a tots els eclipsis. Però de vegades Júpiter s’atansa a la terra, cas en què el «senyal» de cada eclipsi successiu hauria de recórrer cada vegada menys distància i arribaria a la terra progressivament abans que si Júpiter hagués restat a una distància constant. Per la mateixa raó, quan Júpiter s’està allunyant de la terra, veuríem que els eclipsis es van retardant progressivament respecte del que esperàvem. El grau d’anticipació o de retard d’aquesta arribada depèn de la velocitat de la llum i, per això, ens permet de mesurar-la. Això és el que féu Roemer: observà que els eclipsis de Júpiter s’avançaven en les èpoques de l’any en què la terra s’atansava a l’òrbita de Júpiter i es retardaven quan la terra se n’estava allunyant, i emprà aquesta diferència per calcular la velocitat de la llum. Les seves mesures de la distància de la terra a Júpiter, però, no eren gaire precises, de manera que el seu valor per a la velocitat de la llum fou de 225.000 quilòmetres per segon, en lloc dels 300.000 quilòmetres per segon acceptats actualment. Tanmateix, l’aportació reeixida de Roemer, no sols en demostrar que la llum viatja amb velocitat finita sinó també en mesurar aquesta velocitat, fou remarcable —tenint en compte que es va produir onze anys abans de la publicació dels Principia Mathematica de Newton!

Longitud d’ona.

Fins a 1865 no es va disposar d’una teoria satisfactòria de la velocitat de la llum, quan el físic britànic James Clerk Maxwell aconseguí unificar les teories parcials que havien estat emprades fins aleshores per descriure les forces de l’electricitat i el magnetisme. Les equacions de Maxwell predeien l’existència de pertorbacions de tipus ondulatori en el que anomenà camp electromagnètic, i que aquestes viatjarien amb una velocitat fixa, com ones en un estany. Quan en calculà la velocitat, trobà que coincidia exactament amb la velocitat de la llum! Actualment sabem que les ones de Maxwell resulten visibles a l’ull humà sempre que tinguin una longitud d’ona compresa entre quatre-centes i vuit-centes milionèsimes de mil·límetre (la longitud d’ona és la distància entre crestes successives de l’ona). Ones amb longituds d’ona menors que la llum visible són conegudes actualment com a ultraviolats, raigs X i raigs gamma. Ones amb longituds d’ona més grans són anomenades radioones (d’un metre o més), microones (uns pocs centímetres) o infraroigs (menys d’una deumil·lèsima de centímetre però més grans que el domini visible).

Les conseqüències de la teoria de Maxwell que les ones lluminoses o les ones de ràdio viatgen amb una velocitat fixada era difícil de conciliar amb la teoria de Newton, ja que, si no hi ha cap patró absolut de repòs, no hi pot haver un acord universal sobre la velocitat de cap objecte. Per entendre per què, imaginem altra vegada que juguem a ping-pong en el tren. Si llancem la pilota cap endavant amb una velocitat que, segons el nostre contrincant, val deu quilòmetres per hora, esperaríem que un observador quiet a l’andana veiés que la pilota es mou a 100 quilòmetres per hora —els 10 quilòmetres per hora de la velocitat respecte del tren més els 90 quilòmetres per hora amb què suposem que aquest es mou respecte de l’andana. Quina és la velocitat de la bola: 10 quilòmetres per hora o 100 quilòmetres per hora? Com la definim? Respecte al tren? Respecte a terra? Mancats d’un patró absolut de repòs, no li podem assignar una velocitat absoluta. Igualment podríem dir que la pilota té qualsevol velocitat, segons el sistema de referència respecte del qual aquesta sigui mesurada. Segons la teoria de Newton, el mateix hauria de passar amb la llum. De manera que, què significa en la teoria de Maxwell que les ones de llum viatgen amb una velocitat fixada?

Les diferents velocitats de la pilota de ping-pong.

Per reconciliar la teoria de Maxwell amb les lleis de Newton, es va suggerir l’existència d’una substància anomenada èter que estava present a tot arreu, fins i tot a les extensions de l’espai «buit». (La idea d’un èter tenia un cert atractiu addicional per als científics, que pensaven que de totes maneres, així com les ones d’aigua necessiten aigua o les ones del so necessiten aire, les ones de l’energia electromagnètica necessitarien algun medi on es poguessin propagar). Segons aquest punt de vista, les ones de la llum viatjaven per l’èter tal com les ones del so viatgen per l’aire, i la seva «velocitat» deduïda a partir de les equacions de Maxwell es referiria, doncs, a la mesurada respecte de l’èter. En aquesta perspectiva, diferents observadors veurien que la llum se’ls atansaria amb velocitats diferents, però la velocitat de la llum respecte de l’èter estaria fixada. Aquesta idea podria ser posada a prova. Imaginem la llum emesa per alguna font i que, segons la teoria de l’èter, viatja per l’èter amb la velocitat de la llum. Si ens desplacem vers ella per l’èter, la velocitat amb què ens hi atansem hauria de ser la suma de la seva velocitat respecte de l’èter més la nostra velocitat respecte de l’èter. La llum s’atansaria més ràpidament que si, diguem, no ens moguéssim, o que si ens moguéssim en alguna altra direcció. Tot i això, com que la velocitat de la llum és tan gran en comparació de les velocitats amb què ens podem moure, aquesta diferència de velocitat seria un efecte molt difícil de mesurar.

El 1887, Albert Michelson (que fou posteriorment el primer americà a rebre el premi Nobel de Física) i Edward Morley realitzaren un experiment molt acurat i difícil a l’escola Case de ciències aplicades de Cleveland. S’adonaren que, atès que la terra gira al voltant del sol amb una velocitat d’uns 40 quilòmetres per segon, el laboratori es movia amb una velocitat relativament elevada respecte de l’èter. Naturalment, ningú no sabia en quina direcció ni amb quina rapidesa, ja que l’èter es podria estar movent respecte del sol. Però repetint l’experiment en diverses èpoques de l’any, quan la terra es trobava en diferents posicions al llarg de la seva òrbita, podríem esperar descobrir aquest factor desconegut. Així, Michelson i Morley idearen un experiment per comparar la velocitat de la llum mesurada en la direcció del moviment de la terra respecte de l’èter (quan ens movem cap a la font) amb la velocitat de la llum perpendicularment a aquest moviment (quan no ens atansem ni ens allunyem de la font). Amb gran sorpresa, trobaren que la velocitat en les dues direccions és la mateixa!

Entre 1887 i 1905 hi hagué diversos intents de salvar la teoria de l’èter. El més remarcable fou el del físic holandès Hendrik Lorentz, que intentà explicar el resultat de l’experiment de Michelson-Morley en termes d’objectes que es contreien i rellotges que s’alentien en moure’s respecte de l’èter. Però en un cèlebre article de 1905, un empleat desconegut de l’oficina suïssa de patents, Albert Einstein, va fer notar que la idea mateixa d’un èter resultava innecessària, sempre que estiguéssim disposats a abandonar la idea d’un temps absolut (de seguida veurem per què). Poques setmanes després, un important matemàtic francès, Henri Poincaré, va fer una proposta similar. Els arguments d’Einstein eren més propers a la física que no pas els de Poincaré, que contemplava aquest problema com una qüestió merament matemàtica i (fins al dia de la seva mort) es negà a acceptar la interpretació d’Einstein de la teoria.

Moviment de la terra a l’èter.

El postulat fonamental d’Einstein de la teoria de la relativitat, com fou anomenada, estableix que les lleis de la ciència han de ser les mateixes per a tots els observadors que es mouen lliurement, sigui quina en sigui la velocitat. Això és veritat per a les lleis de Newton, però Einstein va ampliar la idea per incloure la teoria de Maxwell. En altres paraules, com que la teoria de Maxwell afirma que la velocitat de la llum té un valor donat, qualsevol observador en moviment lliure ha de mesurar el mateix valor, sigui quina sigui la velocitat amb què s’atansi o s’allunyi de la font. Aquesta idea tan senzilla certament explicava —sense emprar l’èter ni cap altre sistema de referència privilegiat— el significat de la velocitat de la llum en les equacions de Maxwell, però també tenia algunes conseqüències remarcables i sovint contraintuïtives.

Per exemple, l’exigència que tots els observadors hagin d’obtenir la mateixa velocitat de la llum ens obliga a canviar el concepte de temps. En relativitat, els observadors en el tren i a l’andana discreparien sobre la distància que la llum ha recorregut i, com que la velocitat és la distància dividida pel temps, l’única manera que puguin coincidir en el valor de la velocitat de la llum seria que discrepessin també sobre el temps transcorregut. Amb altres paraules, la teoria de la relativitat va posar fi a la idea d’un temps absolut! Sembla que cada observador hagi de tenir la seva pròpia mesura del temps, indicada per un rellotge que es mogués amb ell, i que rellotges idèntics portats per observadors diferents no haurien pas de coincidir!

En relativitat, no cal introduir la idea d’un èter, la presència del qual, de totes maneres, no es pot detectar, com ja demostrà l’experiment de Michelson-Morley. En lloc d’això, la teoria de la relativitat ens obliga a canviar fonamentalment les idees d’espai i de temps. Hem d’acceptar que el temps no està completament separat de l’espai, ni n’és independent, sinó que s’hi combina en una entitat anomenada espaitemps. Però aquestes idees no són fàcils d’assumir, ni tan sols a la comunitat dels físics, motiu pel qual van passar anys fins que la relativitat fou acceptada universalment. Aquesta acceptació és el millor homenatge a la imaginació d’Einstein, a la seva capacitat de concebre aquestes idees, i a la seva confiança en la lògica, que el dugué a examinar a fons totes les conseqüències, per estranyes que en semblessin les conclusions.

Coordenades espacials: podem descriure la posició d’un punt a l’espai mitjançant tres nombres.

Sabem per experiència que és possible descriure la posició d’un punt a l’espai mitjançant tres nombres, o coordenades. Per exemple, podem dir que un punt en una habitació és a 2 metres d’una paret, a 1 metre de l’altra i a 1,5 metres del terra. O bé, podem especificar que un punt és a una certa latitud, longitud i altura sobre el nivell del mar. Podem triar tres coordenades qualssevol que resultin adients, encara que només tinguin un domini de validesa limitat. No seria pràctic especificar la posició de la lluna en termes de quilòmetres al nord i a l’est de Piccadilly Circus, i en metres sobre el nivell del mar: és millor descriure-la en termes de la distància al sol, la distància al pla de les òrbites dels planetes, i l’angle format per la línia que la uneix amb el sol, i la línia que uneix el sol amb una estrella propera, com Proxima Centauri. Ni tan sols aquestes coordenades resultarien útils per descriure la posició del sol a la galàxia o la posició d’aquesta en el grup local de galàxies. De fet, és possible descriure tot l’univers en termes d’una col·lecció de pedaços espacials que s’encavalquin, en cadascun dels quals és possible utilitzar un conjunt diferent de tres coordenades per especificar la posició dels punts.

En l’espaitemps de la relativitat, qualsevol esdeveniment —és a dir, qualsevol cosa que passi en un punt particular de l’espai i en un instant particular del temps— pot ser especificat per quatre nombres o coordenades. També en aquest cas l’elecció de coordenades és arbitrària; podem emprar qualsevol conjunt ben definit de tres coordenades espacials i qualsevol mesura del temps. Però en la relativitat, no hi ha cap diferència real entre coordenades espacials i temporals, tal com no n’hi ha entre coordenades espacials qualssevol. Podríem escollir un nou conjunt de coordenades en què, diguem, la primera coordenada espacial fos una combinació de les dues primeres coordenades espacials del sistema antic. Així, en lloc de mesurar la posició d’un punt de la terra en quilòmetres al nord i a l’est de Piccadilly, podríem emprar quilòmetres al nordest i al nord-oest de Piccadilly. Anàlogament, podríem emprar una nova coordenada espacial que fos l’antiga (en segons) més la distància (en segons-llum) al nord de Piccadilly.

Una altra conseqüència cèlebre de la relativitat és l’equivalència entre massa i energia, resumida en la famosa equació d’Einstein E = mc2 (on E és l’energia, m la massa i c la velocitat de la llum). A causa de l’equivalència entre massa i energia, l’energia d’un objecte material deguda al seu moviment contribuirà a la seva massa; en altres paraules, farà més difícil incrementar-ne la velocitat. Aquest efecte només és realment significatiu per a objectes que es moguin amb velocitats properes a la de la llum. Per exemple, al 10 per cent de la velocitat de la llum, la massa dels objectes només és el 0,5 per cent més gran que en repòs, mentre que al 90 per cent de la velocitat de la llum, seria més del doble de la massa normal en repòs. A mesura que un objecte s’atansa a la velocitat de la llum, la seva massa augmenta més ràpidament, de manera que cada vegada costa més energia seguir-lo accelerant. Segons la teoria de la relativitat, un objecte, de fet, mai no pot atènyer la velocitat de la llum, perquè si fos així la seva massa esdevindria infinita i per l’equivalència entre massa i energia caldria una quantitat infinita d’energia per fer-li atènyer la velocitat esmentada. Aquesta és la raó per la qual, segons la relativitat, qualsevol objecte normal està confinat per sempre a moure’s amb velocitats inferiors a la de la llum. Només la llum, o altres ones que no tinguin una massa intrínseca, es poden moure amb la velocitat de la llum.

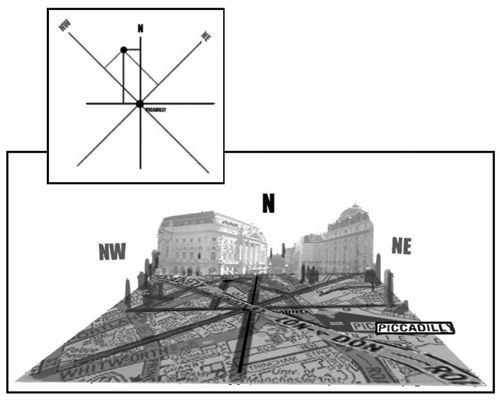
L’elecció de coordenades a l’espai o l’espaitemps és arbitrària.

La teoria d’Einstein de la relativitat de 1905 és anomenada «relativitat especial». En efecte, encara que resultava molt satisfactòria per explicar que la velocitat de la llum és la mateixa per tots els observadors i què passa quan les coses es mouen amb velocitats properes a la de la llum, resultava inconsistent amb la teoria newtoniana de la gravetat. La teoria de Newton estableix que, a cada instant, els objectes s’atrauen amb una força que depèn de la distància entre ells en aquell mateix instant. Això significa que si desplacéssim un dels objectes, la força sobre l’altre canviaria instantàniament. Si, diguem, el sol desaparegués sobtadament, la teoria de Maxwell ens diu que la terra no quedaria a les fosques fins a uns 8 minuts més tard (ja que aquest és el temps que tarda la llum del sol a arribar fins a nosaltres), però, segons la gravetat de Newton, la terra cessaria immediatament de notar l’atracció del sol, ja que ens arribaria amb velocitat infinita i no amb la velocitat de la llum o alguna velocitat inferior, com exigia la teoria especial de la relativitat. Entre 1908 i 1914, Einstein féu un cert nombre d’assaigs infructuosos per formular una teoria de la gravetat que resultés consistent amb la relativitat especial. Al final, el 1915, va proposar una teoria encara més revolucionària, que anomenem actualment la teoria general de la relativitat.