5. Distancia y tamaño

Sistemas binarios

Una vez que los astrónomos determinaron la distancia de las estrella, fue posible empezar a hablar de tamaños. Pudieron, por ejemplo, calcular las dimensiones de los sistemas binarios.

Si se observa un sistema binario a lo largo de años, se puede ir representando gráficamente el cambio de posición de las dos estrellas y trazar un pequeño diagrama de la forma en que se mueven. Se puede medir la separación de las dos estrellas en segundo de arco y, si la distancia es conocida, convertirla en kilómetros reales.

Por ejemplo, el magnífico sistema binario de Alpha Crucis está formado por dos estrellas separadas unos 80.000 millones de kilómetros. Una de ellas es 910 veces más brillante que el Sol, y la otra 570 veces más brillante.

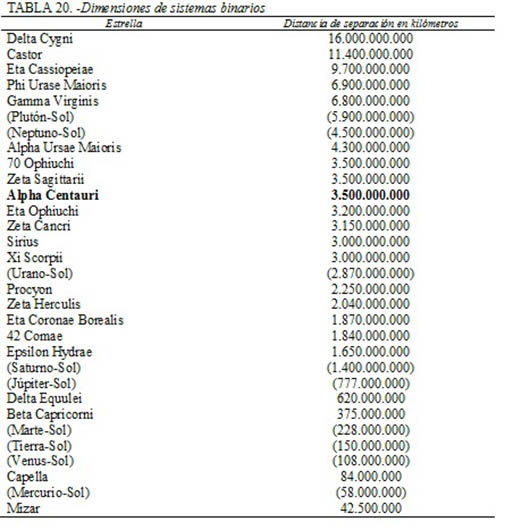
En la tabla 20 se da la distancia media entre las dos estrellas de cierto número de sistemas binarios. Para dar al lector una idea de la magnitud de estas separaciones en comparación con las más familiares de nuestro propio sistema solar, se dan los diversos planetas con sus distancias desde nuestro Sol, intercalándolos en los lugares apropiados de la tabla.

Las estrellas incluidas en la tabla 20 constituyen solamente una muestra, y las cifras que se dan para muchos de los sistemas tienen una exactitud solamente limitada.

La separación de las dos estrellas de Delta Cygni es casi tres veces mayor que la distancia de Plutón al Sol, pero hay también separaciones mayores que ésta. Después de todo, Alpha Centauri C está separada de Alpha Centauri A y B por aproximadamente 1.600 billones de kilómetros. Esta distancia es más de 250 veces mayor que la de Plutón al Sol, y aproximadamente 100 veces la que separa a las dos estrellas de Delta Cygni.

En el otro extremo de magnitud, las dos estrellas que forman el sistema binario de Mizar están más próximas entre sí que Mercurio con respecto al Sol, y sin embargo hay binarias en que las dos estrellas componentes están todavía mucho más cerca. Las parejas realmente próximas no se pueden distinguir visualmente una de otra ni siquiera con ayuda del telescopio. Afortunadamente, como veremos, hay otros instrumentos disponibles.

En el caso del sistema de Alpha Centauri, la separación media entre las dos estrellas Alpha Centauri A y Alpha Centauri B es mayor que la existente entre Urano y el Sol, y menor que la que hay entre Neptuno y el Sol. Sin embargo, si se superpusiera el sistema de Alpha Centauri sobre el sistema solar, con Alpha Centauri A en el lugar de nuestro Sol, Alpha Centauri B no ocuparía una órbita circular comprendida entre las de Urano y Neptuno. Las cosas serían un poco más complicadas.

Si la órbita de un objeto en movimiento alrededor de una estrella fuese un círculo exacto, la estrella permanecería en el centro preciso de la órbita, y ello representaría una situación muy sencilla. En realidad, la órbita es siempre una elipse, una especie de círculo aplanado (o aplastado). Una elipse tiene un eje mayor (su diámetro más largo) y un eje menor (su diámetro más corto). El centro de la elipse está en el punto en que se cruzan los dos ejes (véase la figura 1).

En la elipse hay dos puntos focales, o focos. Están situados en el eje mayor, cada uno a un lado del centro y a distancias iguales de éste. Cuanto más aplanada es la elipse, más alejados del centro están los dos focos, y más próximos a los extremos.

Estos focos están situados en tal forma que si se traza una línea recta desde uno de los focos a cualquier punto de la elipse, y luego se une este punto mediante una nueva recta al otro foco, la suma de las longitudes de las dos rectas es siempre igual, y tiene también siempre la misma longitud que el eje mayor.

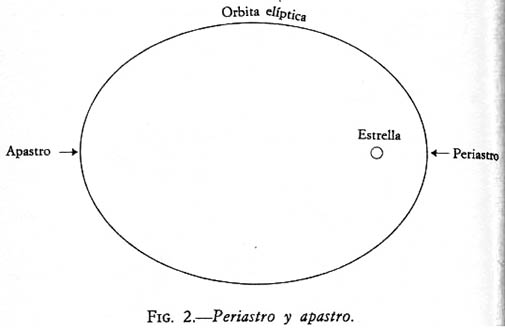
Casualmente, cuando un objeto se mueve alrededor de una estrella siguiendo una órbita elíptica, la estrella se encuentra siempre en uno de los focos, hallándose, por consiguiente, más próxima a un extremo de la órbita que al otro. El punto de mayor proximidad se llama el «periastro», de unas palabras griegas que significan «cerca de la estrella». El punto más lejano es el «apastro», nombre derivado de unas palabras griegas que significan «lejos de la estrella» (véase la figura 2).

En los sistemas binarios, las dos estrellas, bajo la atracción gravitatoria, se desplazan en una órbita alrededor de un punto situado entre ambas y llamado «centro de gravedad». Al moverse, ambas estrellas permanecen siempre en lados opuestos del centro de gravedad, y la estrella más grande está siempre más próxima a él. Esto significa que, aunque ambas estrellas tienen órbitas elípticas de la misma forma, la estrella más grande se desplaza siempre en la órbita más pequeña.

Cuando un objeto de un par binario es mucho más grande que el otro, forma una elipse tan pequeña alrededor del centro de gravedad que permanece prácticamente estacionario. Tal es el caso del Sol y la Tierra, por ejemplo, en el que el Sol apenas se mueve algo, mientras que la pequeña Tierra se desplaza trazando una gran elipse.

Siempre es posible, sin embargo, suponer que el más grande de los dos objetos de un sistema binario permanece inmóvil, y calcular la órbita del más pequeño alrededor de él. Esto distorsiona la situación con respecto a los observadores situados en otros sistemas planetarios (con respecto a nosotros, por ejemplo). Sin embargo, si pudiéramos imaginarnos a nosotros mismos observando el sistema binario desde la más grande de las dos estrellas, lo que veríamos sería la estrella más pequeña moviéndose alrededor de la mayor, que nos parecería inmóvil.

Cuando los astrónomos observan los sistemas binarios, es muy poco probable que lo vean exactamente «desde arriba», por decirlo así, de modo que puedan percibir las órbitas elípticas en la forma exacta que tienen. Generalmente ven las órbitas desde una posición inclinada según cierto ángulo, de modo que las elipses que perciben no son las descritas por las estrellas en sus órbitas. Lo que ven son elipses que aparecen más aplanadas, a veces aplanadísimas. Sin embargo, en estas elipses deformadas, la estrella más grande, que se supone estacionaria, no se encuentra en el foco de la órbita de la estrella más pequeña. Si los astrónomos tuercen o inclinan imaginariamente la órbita, hasta que la estrella se coloque en el foco, obtienen la elipse verdadera.

Excentricidad

El grado de achatamiento de una elipse se mide mediante su «excentricidad», puesto que cuanto mayor es la excentricidad, más alejados del centro se encuentran los focos. La excentricidad de un círculo, que no está aplanado en absoluto, es 0. Para una elipse, la excentricidad está siempre entre 0 y 1. Si una elipse tiene una excentricidad pequeña, por ejemplo, inferior a 0,1, está tan poco aplanada que, a simple vista, se parece muchísimo a un círculo. A medida que una elipse va siendo más y más achatada, se va acercando cada vez más a un valor de 1. Cuando se alcanza una excentricidad de 0,9, la órbita toma una forma bastante parecida a la de un cigarro puro.

Un ejemplo de alto grado de excentricidad en un sistema binario es el de Gamma Virginis, en el que la excentricidad es de 0,88. Esto significa que la distancia desde el centro de la elipse al foco es 0,88 veces la distancia desde el centro de la elipse al extremo de ésta. Con la estrella mayor situada en un foco, el extremo de la órbita de la otra estrella en la dirección de ese foco (el periastro) está a sólo 0,12 veces la distancia desde el centro, y a sólo 0,06 veces la longitud entera de la elipse desde un extremo a otro. El otro extremo de la elipse (el apastro) dista de la estrella mayor 0,94 veces la longitud entera de la elipse.

Así pues, en el caso de Gamma Virginis, aunque la distancia media que separa a las dos estrellas de la binaria es 6.800.000.000 de kilómetros, en el periastro la distancia de separación es solamente de 810.000.000 de kilómetros, mientras que en apastro es de 12.800.000.000 de kilómetros.

En otras palabras, las dos estrellas de Gamma Virginis, al girar cada una alrededor de la otra, se aproximan vertiginosamente hasta una separación igual a la existente entre Júpiter y el Sol, y luego se apartan de nuevo hasta una distancia más del doble de la que hay entre Plutón y el Sol. (El sistema estuvo en apastro en 1920, y las dos estrellas han venido acercándose cada vez más desde entonces. Estarán en periastro en el año 2006).

En general, las estrellas separadas por una distancia media bastante grande suelen tener excentricidades pronunciadas. Una binaria como Capella, con una separación media de sólo 84.000.000 de kilómetros, tiene una excentricidad muy pequeña, de sólo 0,0086. Esto significa que la distancia entre las estrellas del sistema Capella varía desde 83.300.000 kilómetros en el periastro a 84.700.000 kilómetros en el apastro.

Éste es un cambio tan pequeño que, desde el punto de vista de una de las estrellas del sistema Capella, la otra apenas parecería cambiar de brillo durante el período de revolución de 104 días. En el caso de Gamma Virginis, por otra parte, un observador situado cerca de una de las estrellas vería a la otra 250 veces más brillante en el periastro que en el apastro.

Digamos, de paso, que las excentricidades de las órbitas planetarias del sistema solar son mucho más parecidas a las de las estrellas de Capella que a las del sistema Gamma Virginis. Las excentricidades de las órbitas de Venus y Neptuno son aproximadamente iguales a las del sistema Capella, mientras que la de la Tierra (0,017) es sólo un poco mayor. Esto es bueno, también, porque una órbita muy excéntrica introduciría tales cambios de temperatura en el transcurso del año que un planeta cuya distancia media del Sol fuese la adecuada podría, a pesar de ello, resultar inhabitable.

Consideremos ahora el grupo de binarias de la tabla 20 cuyas separaciones medias son del orden de 3.000 a 3.500 millones de kilómetros, grupo en el que está incluida Alpha Centauri. En la tabla 21 se dan las excentricidades y las distancias de periastro y apastro correspondientes a este grupo.

Como puede verse, los apastros no difieren extraordinariamente, variando desde 4.100 a 6.080 millones de kilómetros, una diferencia de sólo un 50 por 100 aproximadamente. Los periastros, sin embargo, difieren desde 320 a 2.700 millones de kilómetros, una diferencia del 800 por 100.

El sistema de Alpha Centauri es más bien intermedio en lo que respecta a la excentricidad. Las órbitas de las dos estrellas Alpha Centauri A y B son más excéntricas que las de los planetas de nuestro sistema solar, pero menos que las de algunos de los cometas, asteroides y satélites de dicho sistema.

Si Alpha Centauri A estuviera en el lugar de nuestro Sol, Alpha Centauri B en su máximo alejamiento se hallaría a una distancia de 5.300.000.000 de kilómetros o, aproximadamente, la distancia media de Plutón a nuestro Sol. Desde la posición de la Tierra, próxima a Alpha Centauri A, Alpha Centauri B parecería una estrella puntual, pero sería mucho más brillante que cualquiera de las que vemos en nuestro cielo. Brillaría con un resplandor unas 100 veces mayor que el de nuestra Luna llena, aunque todavía sería sólo 1/4.500 del de Alpha Centauri A, si ésta se hallara en el lugar del Sol (o del de nuestro Sol ahora mismo).

Desde su punto de máximo alejamiento, sin embargo, Alpha Centauri B iría disminuyendo gradualmente su distancia a Alpha Centauri A (y a nosotros) al desplazarse a lo largo de su órbita (véase la figura 3) hasta que, al cabo de cuarenta años, estuviera en el periastro y a sólo 1.700.000.000 de kilómetros de Alpha Centauri A. En ese punto, se hallaría un poco más alejada de Alpha Centauri A que lo que Saturno lo está del Sol. Y cuando la Tierra estuviera en el lado de su órbita situada hacia Alpha Centauri B, la estrella compañera estaría sólo a 1.550.000.000 de kilómetros de nosotros.

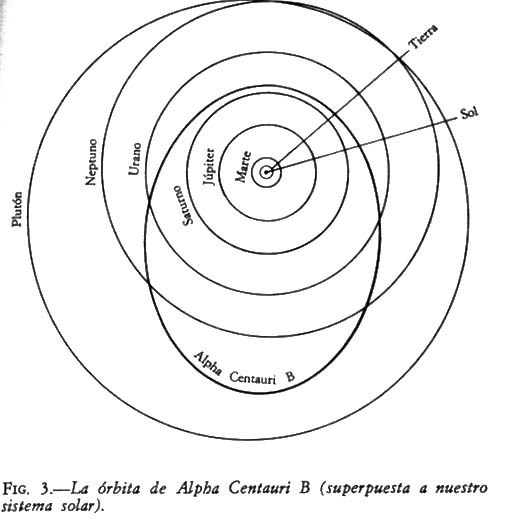
A esa distancia, el brillo de Alpha Centauri B sería algo más de 14 veces mayor que en el apastro. Sería 1.400 veces más brillante que la Luna llena, pero todavía sólo 1/326 del brillo de Alpha Centauri A.

Supongamos que fuera Alpha Centauri B la que se encontrara en el lugar de nuestro Sol, y que calculásemos la órbita de Alpha Centauri A, suponiendo que aquélla estuviese inmóvil. Entonces, Alpha Centauri A parecería moverse en la misma órbita en que Alpha Centauri B se había movido en el caso anterior^[1].

Alpha Centauri A pasaría por el mismo período de aumento de su brillo al ir desde el apastro al periastro, vista desde una Tierra que estaría girando alrededor de Alpha Centauri B en lugar de hacerlo alrededor de nuestro Sol, y por el mismo período de disminución del brillo al regresar al apastro. Sin embargo, y puesto que Alpha Centauri A es 3 1/4 veces más brillante que Alpha Centauri B, aparecería con un brillo proporcionalmente mayor en cualquier punto de su órbita. En su máximo brillo, luciría 5.000 veces más que lo que nuestra Luna llena lo hace ahora, y con sólo 1/100 del brillo con que vemos a nuestro Sol. Puesto que Alpha Centauri B aparecería con 1/30 del brillo de Alpha Centauri B.

Si estuviéramos dando vueltas alrededor de Alpha Centauri A en lugar de hacerlo alrededor del Sol, la presencia de Alpha Centauri B no nos produciría trastorno alguno. A pesar de la excentricidad de su órbita, que permite a Alpha Centauri B acercarse mucho y luego retirarse alternativamente en ciclos de cuarenta años, la estrella permanecería siempre tan alejada que su atracción gravitatoria nunca sería bastante fuerte para afectar seriamente a la órbita de la Tierra. Es más, la luz y el calor que sumase a los proporcionados por Alpha Centauri A nunca serían más de un tercio de 1 por 100. Y pensemos en el maravilloso espectáculo que nos proporcionaría en el cielo.

Si estuviésemos orbitando alrededor de Alpha Centauri B, el mayor brillo de Alpha Centauri A nos perturbaría más, pero si imaginásemos a la Tierra más aproximada a Alpha Centauri B, para recibir de este sol menor tanta luz y tanto calor como recibimos del nuestro, la interferencia de Alpha Centauri A no resultaría excesivamente molesta.

Bueno, ¿y qué pasaría con Alpha Centauri C, la Próxima Centauri? Aun cuando estaría mucho más cercana a nosotros —si la Tierra estuviese orbitando alrededor de Alpha Centauri A o de Alpha Centauri B- que lo está cualquier estrella en nuestro propio sistema solar, no llegaría a ser muy brillante. Sería una estrella bastante débil, de magnitud 3,7. Es más, su movimiento propio, como resultado de su revolución de 1.300.000. años alrededor del centro de gravedad de las dos estrellas mayores del sistema, sería casi exactamente de un segundo de arco por año.

Ni su brillo ni su movimiento propio atraerían mucho la atención, y los contempladores de estrellas podrían observar por siempre el firmamento sin sospechar que esta débil estrella perteneciese a su propio sistema. Lo único que podría desvelar su secreto sería que los astrónomos decidieran hacer una comprobación rutinaria de las paralajes de las diversas estrellas visibles en el cielo. Al cabo de un mes o cosa así, empezarían a sospechar una paralaje extraordinariamente grande y, finalmente, la medirían y verían que tenía 20 segundos de arco, un valor tan superior al de cualquier otra estrella que inmediatamente sospecharían que se trataba de un miembro de su propio sistema.

¿Puede haber allá fuera, en algún lugar, una débil estrella que pertenezca a nuestro propio sistema solar? ¿Podrá ocurrir que no nos hayamos dado cuenta de ello porque dé la casualidad de que los astrónomos no la hayan estudiado con el detenimiento suficiente para detectar una paralaje anormalmente grande? No es muy probable… pero es concebible.

Masa

Las estrellas binarias hacen posible el cálculo de las masas de al menos algunas estrellas; pero, en primer lugar, hemos de explicar lo que entendemos por «masa».

Una forma de definir la masa es considerar la intensidad o fuerza del campo gravitatorio producido por cualquier objeto. Si un objeto tiene el doble de masa que otro, produce un campo gravitatorio que, a una distancia determinada, es dos veces más intenso que el de éste. A la inversa, si podemos medir los campos gravitatorios de dos cuerpos y hallamos que el del primero es dos veces más intenso que el del segundo, sabemos que la masa del primero es el doble de la del segundo.

La atracción gravitatoria entre dos objetos depende del producto de sus dos masas. Si uno de los objetos permanece inalterado, y se mide su atracción gravitatoria hacia otros objetos diversos, la magnitud de tal atracción depende de la masa de cada uno de esos otros objetos.

Supongamos que consideramos todos los diferentes objetos que reposan sobre la superficie de la Tierra. Cada uno de ellos está sometido a una atracción gravitatoria entre él y la Tierra. Puesto que la masa de ésta es la misma en cada caso, la magnitud de la atracción gravitatoria ejercido sobre cada objeto depende de la masa de éste.

Para medir la atracción gravitatoria que se ejerce sobre un objeto situado en la superficie de la Tierra podemos pesar dicho objeto. Cuanto más fuerte tire de él la Tierra, más «pesado» decimos que es el objeto. Cuanto más débil sea la atracción ejercida por la Tierra, más «ligero» es el objeto. Cuanta más masa posee un objeto, más fuertemente es atraído por la Tierra, y más pesado es. Cuanto menos masa posee, más ligero es.

Mientras nos limitemos a la superficie de la Tierra, la masa y el peso están tan estrechamente relacionados que podemos utilizar cualquiera de las dos palabras. Sin embargo, la atracción gravitatoria decrece con la distancia. Dos objetos pueden tener la misma masa, pero si uno de ellos está a 2.630 kilómetros de altura sobre la superficie de la Tierra, ese objeto pesa sólo la mitad que su gemelo situado en la superficie. Repetimos que los cuerpos astronómicos distintos de la Tierra tienen diferentes intensidades de atracción gravitatoria. Un objeto situado en la superficie de la Luna pesa sólo un sexto de lo que un objeto de masa igual a la suya pesa en la superficie de la Tierra.

Por consiguiente, es mucho más seguro olvidarse del peso y de las palabras «pesado» y «ligero». En lugar de ello, hablamos de objetos de «mayor masa» y de «menor masa", o más y menos «masivo».

¿Podemos medir la masa de alguna otra forma que no sea la de pesar los objetos? Sí; recordemos que podemos comparar las intensidades gravitatorias.

En 1798, el científico inglés Henry Cavendish midió la atracción gravitatoria (verdaderamente diminuta) ejercida por una gran esfera de plomo sobre una esfera mucho más pequeña del mismo metal. Conocía la atracción gravitatoria de la Tierra sobre aquella pequeña bola de plomo. De la diferencia de estas atracciones, podía calcular la diferencia de masas entre la esfera grande de plomo y la Tierra, utilizando la «Ley Universal de la Gravitación» de Isaac Newton, que se dio a conocer por primera vez en 1687. Conociendo la masa de la esfera grande de plomo, pudo calcular la de la Tierra.

Resulta que la Tierra tiene una masa de 6.000.000.000.000.000.000.000.000 de kilogramos (6.000.000.000.000.000.000.000 toneladas).

Una vez conocida la masa de la Tierra, podemos calcular la de otros objetos del sistema solar.

El campo gravitatorio de la Tierra, por ejemplo, tira de la Luna desde una cierta distancia y, en respuesta a ello, la Luna se mueve en su órbita a una determinada velocidad y realiza su órbita a una determinada velocidad y realiza su órbita completa en cierto tiempo. Júpiter tiene algunos satélites a ciertas distancias de sí, y dichos satélites se mueven a determinadas velocidades y completan sus órbitas en tiempos igualmente determinados. Comparando la distancia de la Luna y su período de traslación alrededor de la Tierra con la distancia y el período de uno de los satélites que trazan sus órbitas alrededor de Júpiter, los astrónomos pueden calcular que el campo gravitatorio de Júpiter es 318 veces más intenso que el de la Tierra. Ello significa que Júpiter tiene una masa 318 veces mayor que la de nuestro planeta.

La Tierra se halla a cierta distancia del Sol; se desplaza alrededor de éste a cierta velocidad en respuesta a la gravedad solar y, por consiguiente, completa su órbita en un tiempo determinado. Comparando esto con la forma en que se mueve la Luna sometida a la gravedad de la Tierra, los astrónomos pueden calcular que la masa del Sol es 332.500 veces mayor que la de la Tierra. La masa del Sol es 2.000.000.000.000.000.000.000.000.000.000 kilogramos (2.000.000.000.000.000.000.000.000.000 toneladas).

La masa se calcula en esta forma utilizando la «Tercera Ley de Kepler», llamada así porque fue elaborada y expresada por el astrónomo alemán Johann Kepler en 1619. Para hacer uso de la Tercera Ley de Kepler, sin embargo, necesitamos un objeto que orbite alrededor de otro a una distancia determinada y en un tiempo definido, y poder medir ambas magnitudes.

Si una estrella se halla aislada en el espacio, sin la compañía de otros objetos que podamos detectar, la Tercera Ley de Kepler no nos puede servir. En el caso de las estrellas binarias, sin embargo, todo está perfectamente dispuesto. Si podemos medir la distancia media entre las estrellas y el tiempo que éstas necesitan para orbitar alrededor de su centro de gravedad, podremos calcular la masa total de las dos estrellas del sistema binario mediante la comparación de sus distancias y de sus tiempos con las distancias y los tiempos de nuestro propio sistema solar. En la tabla 22 se da la masa total de ciertos sistemas binarios.

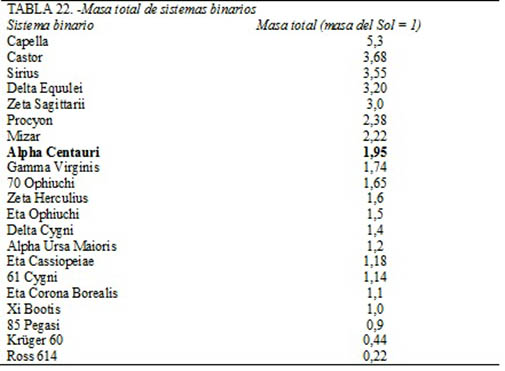
Si la masa total de un sistema binario es superior al doble de la del Sol, es posible que cada estrella del sistema binario tenga una masa mayor que la del Sol. Si la masa total está comprendida entre 1 y 2 veces la del Sol, entonces una de las estrellas ha de tener menos masa que él. Cuando la masa total es inferior a 1, las dos estrellas han de tener masas individuales menores que la del Sol.

En el caso de Alpha Centauri, una de las estrellas componentes ha de tener menos masa que el Sol. Es presumible que la menos brillante de las dos, Alpha Centauri B, sea también la de menor masa.

En realidad, se puede calcular la masa de cada componente de una binaria observando el tamaño de la órbita que cada una describe, tomando como referencia alguna estrella que esté próxima en el firmamento y que no forme parte del sistema. La estrella cuya masa es mayor, describe una órbita más pequeña. Se hace uso de este procedimiento, por ejemplo, para calcular la masa de nuestra Luna. La Luna y la Tierra giran alrededor del centro de gravedad del sistema Tierra-Luna, y la elipse descrita por el centro de la Tierra tiene una amplitud de sólo 1/81,3 de la descrita por el centro de la Luna. Esto significa que la masa de la Tierra es 81,3 veces mayor que la de la Luna.

En la tabla 23 se relacionan algunas binarias para las que se ha calculado la masa de cada estrella correspondiente.

Como puede verse en esta tabla, Alpha Centauri A tiene no sólo la misma luminosidad aproximada que el Sol, sino también casi la misma masa. Alpha Centauri B, que es menos luminosa que el Sol, tiene también menos masa que éste.

Efectivamente, a medida que los astrónomos fueron comprobando las masas de diferentes estrellas, fue resultando que las de mayor masa eran casi siempre más luminosas que las de masa menor. Esto parecía indicar la existencia de alguna relación entre luminosidad y masa.

Tal relación no podía ser muy simple, porque a medida que se determinaban las masas de más y más estrellas, se fue haciendo evidente que dichas masas no variaban en mucho. Algunas estrellas podían ser millones de veces más luminosas que otras y, sin embargo, su masa era sólo unos cientos de veces mayor. La variación de la masa era mucho menor que la de la luminosidad… pero, con la excepción de algunos casos especiales, siempre en la misma dirección.

El astrónomo inglés Arthur Stanley Eddington se dedicó a trabajar en este problema. Según él, una estrella ejerce una atracción gravitatoria sobre la materia que constituye sus propias capas más externas. Tal atracción determina en una estrella una tendencia a contraerse. Al contraerse la estrella, sus capas centrales se calientan. El calor tiende a producir la expansión de la estrella. Se precisan intensas temperaturas, del orden de millones de grados, en el núcleo de la estrella para que su tendencia a la expansión iguale a su tendencia a la contracción, y para que la estrella permanezca estable.

Cuanto mayor es la masa de una estrella, mayor es su campo gravitatorio y mayor su tendencia a contraerse. Cuanto más masiva es la estrella, más grande es la temperatura interna precisa para impedir que se contraiga. Finalmente, cuanta más masa tiene la estrella y más alta es su temperatura interna, más luz y más calor escapan hasta su superficie, y más luminosa es.

Eddington demostró que, desde este punto de vista, sería de esperar que la luminosidad creciese muy rápidamente al aumentar la masa. Su ley de «masa-luminosidad», anunciada en 1924, concordaba con lo que se conocía acerca de las estrellas binarias, y parecía razonable suponer que concordase también en el caso de las estrellas sencillas. Por consiguiente, cuando se conoce la luminosidad de una estrella y ésta no pertenece a una clase estelar excepcional (de estas clases excepcionales tendremos algo que decir más adelante en este libro), también nos será conocida su masa.

La ley de masa-luminosidad de Eddington establece unos límites superior e inferior para la masa. Si una estrella tiene una masa excesiva, la temperatura necesaria para impedir que la atracción gravitatoria provoque su colapso o hundimiento hacia el centro es tan alta que la estrella simplemente estalla en una gigantesca explosión. En realidad, aquellas estrellas que tienen una masa considerablemente mayor que la del Sol, pero no tan grande que impida que se mantengan enteras durante algún tiempo, corren el peligro de explotar en alguna etapa de su historia.

Por otra parte, si la masa de una estrella es inferior a cierto valor crucial, su temperatura en el centro nunca alcanza el valor necesario para que llegue a irradiar luz. En tal caso, no se trata realmente de una estrella, sino de un cuerpo oscuro, cuya superficie permanece fría.

La estrella de mayor masa observada hasta ahora parece que es HD 47129 (la que ocupa el puesto 47.129 en el catálogo de Henry Draper), que parece tener una masa unas 140 veces mayor que la del sol. En realidad, se trata de una binaria formada por dos estrellas, cada una de ellas con una masa unas 70 veces mayor que la del Sol. Su gran masa fue puesta de manifiesto por primera vez en 1922 por el astrónomo canadiense John Stanley Plaskett.

La estrella de menos masa que conocemos es Ross 614B, que aparece incluida en la tabla 23. Por lo menos, éste es el cuerpo de menor masa que se puede detectar gracias a su luz propia.

Dentro de nuestro sistema solar, conocemos muchos objetos con masas menores, que podemos observar gracias a la luz solar que reflejan, aun cuando no son suficientemente grandes para desarrollar una temperatura que les haga brillar con luz propia. Así, Júpiter, el planeta más grande de nuestro sistema, tiene aproximadamente 0,001 de la masa del Sol, 0 1/80 de la de Ross 614B. Brilla únicamente con luz reflejada, y si no estuviera cerca de una estrella sería imposible verlo.

Tanto nuestro Sol como las dos estrellas principales del sistema Alpha Centauri se hallan cómodamente situados entre estos límites. Alpha Centauri C se halla cerca del límite inferior.

Velocidad transversal

Una vez que se determinó la distancia de las estrellas más próximas, fue posible hacer algo más con el movimiento propio. Generalmente, estos movimientos se miden en segundos de arco por año; pero si se conoce la distancia de una estrella determinada, los astrónomos pueden calcular qué velocidad en kilómetros por segundo sería necesaria para producir a esa distancia el movimiento propio observado.

En realidad, todas las estrellas se mueven, incluido el Sol.

Las estrellas que nos rodean, incluido el Sol, forman todas parte de un gigantesco sistema de forma lenticular, que incluye a más de cien mil millones de estrellas. Lo que vemos en el firmamento como una banda débilmente luminosa, la Vía Láctea, es en realidad un conglomerado de estrellas muy distantes y débiles, que representa lo que vemos cuando miramos a través de la lente de estrellas en el sentido de mayor longitud. El sistema lenticular de estrellas recibe el nombre de «Galaxia», derivado de una palabra griega que significa «leche». Algunas veces se la llama galaxia de la Vía Láctea, para identificar de cuál se trata, ya que hay otras muchas galaxias además de la nuestra.

Tanto nuestro Sol como las demás estrellas de las que hemos venido hablando en este libro (con la excepción de S Doradus) se encuentran en una pequeña región de la Galaxia situada a 9.200 parsecs (30.000 años luz) del centro (véase la figura 4). Nuestro Sol y todas las demás estrellas de su vecindad se desplazan alrededor de dicho centro en una inmensa órbita en la que invierten 230 millones de años para dar una vuelta completa. Las estrellas próximas a nosotros giran alrededor del centro galáctico a una velocidad de unos 220 kilómetros por segundo.

Sin embargo, todas las estrellas próximas a nosotros no se mueven exactamente a la misma velocidad. Algunas se hallan un poco más próximas al centro, otras tienen órbitas más excéntricas que las de sus vecinas. Esto significa que una estrella determinada puede estar en el momento actual adquiriendo cierta ventaja sobre una segunda, y perdiendo terreno con respecto a una tercera.

Este adelantamiento o este retraso es lo que se pone de manifiesto como movimiento propio de las estrellas. La magnitud del movimiento propio depende de dos cosas. La primera es la velocidad real de la estrella perpendicularmente a nuestra línea de visión. Ésta es la «velocidad transversal». La segunda es la distancia de la estrella. Si dos estrellas se están moviendo con la misma velocidad transversal y una de ellas se encuentra mucho más lejana que la otra, la más alejada parece moverse mucho más lentamente y tener un movimiento propio mucho menor. Sin embargo, una vez que determinamos la distancia, la velocidad transversal es la única incógnita que queda, y se puede calcular fácilmente.

Para asignar un valor real a la velocidad transversal, lo lógico es suponer que nuestro Sol está inmóvil y entonces calcular la velocidad con respecto a nosotros. Podemos entonces ver con qué rapidez o lentitud nos está adelantando (o se está quedando detrás de nosotros) una estrella determinada, mientras ambos nos precipitamos en nuestra trayectoria alrededor del centro galáctico.

En la tabla 24 se dan las velocidades transversales de algunas estrellas. En todos los casos, tenemos una estrella determinada que se está moviendo en una dirección dada a través del firmamento. La dirección, sin embargo, sería difícil indicarla sin disponer de un mapa celeste, y podemos pasarnos sin ella. La tabla 24 da sólo las velocidades.

Como se puede ver, la estrella de Barnard, que es la que posee el mayor movimiento propio conocido, no es la estrella con velocidad transversal más grande. Hay por lo menos otras dos estrellas con velocidades transversales mayores.

Aquí es donde interviene el factor de la distancia. Parte de la razón por la que la estrella de Barnard tiene un movimiento propio tan elevado reside en el hecho de que se halla muy próxima a nosotros. La estrella de Barnard está a una distancia de menos de 6 años-luz, mientras que la estrella de Kapteyn, con un movimiento propio casi tan grande como el de aquélla, está a 13 años-luz.

Alpha Centauri, en lo que respecta a la velocidad transversal, como en tantas otras propiedades, se encuentra en una posición media, con un valor que no es ni muy alto ni muy bajo.

La velocidad transversal, sin embargo, no es todo lo que importa en cuanto al movimiento de una estrella, y no representa realmente la velocidad verdadera de la misma con respecto a nosotros. Si el cielo fuese una lejana cúpula sólida y las estrellas se arrastrasen por ella todas a la misma distancia de nosotros, entonces no habría nada más que la velocidad transversal…, pero la cosa no es así. Las estrellas están colocadas en un espacio tridimensional, y pueden estar acercándose o alejándose de nosotros, además de desplazarse transversalmente a nuestra línea de visión.

Una estrella puede hallarse más alejada del centro galáctico que nosotros, por ejemplo, pero puede tener una órbita más excéntrica y estar moviéndose en ángulo con nuestra trayectoria para precipitarse hacia un punto más próximo al centro, razón por la que puede estar acercándose a nosotros. O bien puede estar desplazándose hacia el exterior, hacia una distancia del centro galáctico mayor de la que nosotros podremos alcanzar jamás, y puede estar alejándose de nosotros por esa causa.

El movimiento de una estrella acercándose o alejándose de nosotros se llama «velocidad radial», nombre procedente de la palabra latina que designa el radio de una rueda. (Es como si nos imagináramos situados en el cubo de la rueda y la estrella se aproximase o se alejase a lo largo del radio).

Si queremos conocer la velocidad real de una estrella, hemos de conocer su velocidad radial.

Supongamos que dos estrellas se están moviendo a la misma velocidad, pero una lo está haciendo en forma completamente perpendicular a nuestra línea de visión, mientras que la otra se mueve radialmente (acercándose o alejándose directamente de nosotros). La estrella que se está moviendo completamente perpendicular a nuestra línea de visión está cambiando su posición en el cielo, y detectamos este cambio como movimiento propio. La otra estrella, a pesar de estar animada de la misma velocidad, se acerca o se aleja a lo largo de nuestra visual y no parece cambiar de posición en el cielo, de modo que no percibimos ningún movimiento propio.

La mayoría de las estrellas no se mueven completamente perpendiculares a nuestra línea de visión, ni tampoco en forma perfectamente radial, acercándose o alejándose. Se desplazan en alguna dirección intermedia, y percibimos parte de su movimiento como movimiento propio. Cuanto más se aproxime su dirección a la perpendicular a nuestra línea de visión, más grande es la fracción de su movimiento que percibimos como movimiento propio. Sin embargo, si no conocemos su velocidad radial además de la transversal, no podemos calcular qué grado de inclinación u oblicuidad hay en el movimiento de una estrella, ni a qué velocidad se desplaza realmente con respecto a nosotros.

¿Cómo podemos detectar el movimiento radial?

Una forma, tal vez, podría ser estudiar el brillo aparente de una estrella determinada. A medida que ésta se acerca a nosotros, iría haciéndose más brillante; a medida que se alejase, se haría más débil. Sin embargo, estos cambios serían extremadamente lentos, y podrían hacer falta muchos miles de años para que el movimiento radial fuese apreciable.

¿Hay alguna otra forma en que podamos detectar la velocidad radial?

Efectivamente, la hay. A mediados del siglo XIX se ideó y se perfeccionó un método para hacerlo, pero para explicar cómo funciona tendremos que volver atrás un poco.