The Milky Way, the galaxy in which we live, is but one of many galaxies. As a matter of fact, the Milky Way, also called the Galaxy, is a fairly average representative of the class of spiral galaxies. Two other examples of spiral galaxies are shown in Figs. 1.1 and 1.2, one of which we are viewing from above (face-on), the other from the side (edge-on). These are all stellar systems in which the majority of stars are confined to a relatively thin disk. In our own Galaxy, this disk can be seen as the band of stars stretched across the night sky, which led to it being named the Milky Way. Besides such disk galaxies, there is a second major class of luminous stellar systems, the elliptical galaxies. Their properties differ in many respects from those of the spirals.

It was less than a 100 years ago that astronomers first realized that objects exist outside our Milky Way and that our world is significantly larger than the size of the Milky Way. In fact, galaxies are mere islands in the Universe: the diameter of our Galaxy¹ (and other galaxies) is much smaller than the average separation between luminous galaxies. The discovery of the existence of other stellar systems and their variety of morphologies raised the question of the origin and evolution of these galaxies. Is there anything between the galaxies, or is it just empty space? Are there any other cosmic bodies besides galaxies? Questions like these motivated us to explore the Universe as a whole and its evolution. Is our Universe finite or infinite? Does it change over time? Does it have a beginning and an end? Mankind has long been fascinated by these questions about the origin and the history of our world. But for only a few decades have we been able to approach these questions in an empirical manner. As we shall discuss in this book, many of the questions have now been answered. However, each answer raises yet more questions, as we aim towards an ever increasing understanding of the physics of the Universe.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig1_HTML.jpg

Fig. 1.1

The spiral galaxy NGC 1232 may resemble our Milky Way if it would be observed from ‘above’ (face-on). This image, observed with the VLT, has a size of 6.^′8 × 6.^′8, corresponding to a linear size of 60 kpc at its distance of 30 Mpc. If this was our Galaxy, our Sun would be located at a distance of 8.0 kpc from the center, orbiting around it at a speed of ∼ 220 km∕s. A full revolution would take us about 230 × 10⁶ yr. The bright knots seen along the spiral arms of this galaxy are clusters of newly-formed stars, similar to bright young star clusters in our Milky Way. The different, more reddish, color of the inner part of this galaxy indicates that the average age of the stars there is higher than in the outer parts. The small galaxy at the lower left edge of the image is a companion galaxy that is distorted by the gravitational tidal forces caused by the spiral galaxy. Credit: European Southern Observatory

The stars in our Galaxy have very different ages. The oldest stars are about 12 billion years old, whereas in some regions stars are still being born today: for instance in the well-known Orion nebula. Obviously, the stellar content of our Galaxy has changed over time. To understand the formation and evolution of the Galaxy, a view of its (and thus our own) past would be useful. Unfortunately, this is physically impossible. However, due to the finite speed of light, we see objects at large distances in an earlier state, as they were in the past. One can now try to identify and analyze such distant galaxies, which may have been the progenitors of galaxies like our own Galaxy, in this way reconstructing the main aspects of the history of the Milky Way. We will never know the exact initial conditions that led to the evolution of the Milky Way, but we may be able to find some characteristic conditions. Emerging from such initial states, cosmic evolution should produce galaxies similar to our own, which we would then be able to observe from the outside. On the other hand, only within our own Galaxy can we study the physics of galaxy evolution in situ.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig2_HTML.jpg

Fig. 1.2

We see the spiral galaxy NGC 4565 from the side (edge-on); an observer looking at the Milky Way from a direction which lies in the plane of the stellar disk (‘from the side’) may have a view like this. The disk is clearly visible, with its central region partly obscured by a layer of dust. One also sees the central bulge of this galaxy. As will be discussed at length later on, spiral galaxies like this one are surrounded by a halo of matter which is observed only through its gravitational action, e.g., by affecting the velocity of stars and gas rotating around the center of the galaxy. Credit: European Southern Observatory

We are currently witnessing an epoch of tremendous discoveries in astronomy. The technical capabilities in observation and data reduction are currently evolving at an enormous pace. Two examples taken from ground-based optical astronomy should serve to illustrate this.

In 1993 the first 10-m class telescope, the Keck telescope, was commissioned, the first increase in light-collecting power of optical telescopes since the completion of the 5-m mirror on Mt. Palomar in 1948. Currently, 13 telescopes with diameter above 8 m are in use, and planning for telescopes with 30 m diameter or more has begun. In recent years, our capabilities to find very distant, and thus very dim, objects and to examine them in detail have improved immensely thanks to the capability of these large optical telescopes.

A second example is the technical evolution and size of optical detectors. Since the introduction of CCDs (charge-coupled devices) in astronomical observations at the end of the 1970s, which replaced photographic plates as optical detectors, the sensitivity, accuracy, and data rate of optical observations have increased enormously. At the end of the 1980s, a camera with 1000 × 1000 pixels (picture elements) was considered a wide-field instrument. In 2003 a camera called Megacam began operating; it has (18 000)² pixels and images a square degree of the sky at a sampling rate of 0.^″2 in a single exposure. Such a camera produces roughly 100 GB of data every night, the reduction of which requires fast computers and vast storage capacities. The largest astronomical CCD camera currently is that of the PanSTARRS-1 telescope, with more than 1.4 billion pixels, covering about 6 deg² on the sky. But it is not only optical astronomy that is in a phase of major development; there has also been huge progress in instrumentation in other wavebands, allowing us a multi-wavelength view of the Universe (Fig. 1.3). Space-based observing platforms are playing a crucial role in this. We will consider this topic in Sect. 1.3.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig3_HTML.jpg

Fig. 1.3

This image of the galaxy M82 illustrates very clearly that any given waveband provides a rather restricted—and biased—view of cosmic objects. Shown is a composite image, obtained from three different telescopes. Blue color shows the X-ray radiation of this galaxy, as recorded by the X-ray satellite Chandra. The infrared light is shown in red, and was observed with the Spitzer Space Telescope. The optical light from M82 was recorded with the Hubble Space Telescope and is shown in yellow-green. Finally, line emission from hydrogen gas is displayed in orange. The distributions of radiation from different wavelengths is obviously very different; only the joint set of observations can provide us with an understanding of this galaxy. In fact, M82 is a rather special object, a so-called starburst galaxy, named because this galaxy forms new stars at a rate much higher than this happens in the Milky Way and other ‘normal’ spiral galaxies. The stars of the galaxy are distributed in a disk, as seen from the optical light, and most of the newly formed stars are located close to the center. The most massive of the stars explode in a supernova; these gigantic explosions can heat, and drive substantial amounts of gas and dust out of the galactic plane. The hot gas radiates X-rays and is clearly seen on both sides of the stellar disk, as well as the dust which emits in the infrared light. The image size is 7.^′9, corresponding 8. 5 kpc for distance of 3. 7 Mpc. Credit: X-ray: NASA/CXC/JHU/D.Strickland; IR: NASA/JPL-Caltech/C. Engelbracht (University of Arizona); optical: NASA, ESA, and The Hubble Heritage Team

These technical advances have led to a vast increase in knowledge and insight in astronomy, especially in extragalactic astronomy and cosmology. Large telescopes and sensitive instruments have opened up a window to the distant Universe. Since any observation of distant objects is inevitably also a view into the past, due to the finite speed of light, studying objects in the early Universe has become possible. Today, we can study galaxies which emitted the light we observe at a time when the Universe was less than 10 % of its current age; these galaxies are therefore in a very early evolutionary stage. We are thus able to observe the evolution of galaxies throughout the past history of the Universe. We have the opportunity to study the history of galaxies and thus that of our own Milky Way. We can examine at which epoch most of the stars that we observe today in the local Universe have formed because the history of star formation can be traced back to early epochs. In fact, it was found that star formation is largely hidden from our eyes and only observable with space-based telescopes operating in the far-infrared waveband.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig4_HTML.jpg

Fig. 1.4

The radio galaxy Hercules A, an elliptical galaxy seen at the center of this image. Superposed on this optical image is an image taken at radio wavelength, which shows a very extended source indeed. Two streams of ionized matter, so-called jets, are ejected on opposite sides of the galaxy, which terminate in two extended regions, the radio lobes. The energy of the jets is produced by a supermassive black hole with a mass of $M_{\bullet } \sim 2.5 \times 10^{9}\,M_{\odot }$ . Credit: NASA, ESA, S. Baum and C. O’Dea (RIT), R. Perley and W. Cotton (NRAO/AUI/NSF), and the Hubble Heritage Team (STScI/AURA)

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig5_HTML.jpg

Fig. 1.5

The cluster of galaxies MACS J1206.2−0847, as seen in a multi-color image taken by the Hubble Space Telescope. The elliptical galaxy at the center of the image is the central galaxy of this massive galaxy cluster; many of the member galaxies of this clusters can be seen. They come in different shapes and colors, some being more reddish, which indicates stellar populations of large age, some being much bluer due to their ongoing star formation. In addition, this image shows some objects with rather peculiar shape. These are images of galaxies located behind the cluster whose observed shape is deformed by gravitational light deflection caused by the deep gravitational potential of the cluster. This image distortion can be used to determine the mass of this cluster, clearly showing that it contains far more mass than is seen in the visible cluster components. Credit: NASA, ESA, M. Postman (STScI), the CLASH Team, and the Hubble Heritage Team (STScI/AURA)

One of the most fascinating discoveries of recent years is that most galaxies harbor a black hole in their center, with a characteristic mass of millions or even billions of Solar masses—so-called supermassive black holes (see Fig. 1.4). Although as soon as the first quasars were found in 1963 it was proposed that only processes around a supermassive black hole would be able to produce the huge amount of energy emitted by these ultra-luminous objects, the idea that such black holes exist in normal galaxies is fairly recent. Even more surprising was the finding that the black hole mass is closely related to the other properties of its parent galaxy, thus providing a clear indication that the evolution of supermassive black holes is closely linked to that of their host galaxies.

Detailed studies of individual galaxies and of associations of galaxies, which are called galaxy groups or clusters of galaxies (see Fig. 1.5), led to the surprising result that these objects contain considerably more mass than is visible in the form of stars and gas. Analyses of the dynamics of galaxies and clusters show that only 10–20 % of their mass consists of stars, gas and dust that we are able to observe in emission or absorption. The largest fraction of their mass, however, is invisible. Hence, this hidden mass is called dark matter. We know of its presence only through its gravitational effects. The dominance of dark matter in galaxies and galaxy clusters was established in recent years from observations with radio, optical and X-ray telescopes, and it was also confirmed and quantified by other methods. However, we do not know what this dark matter consists of; the unambiguous evidence for its existence is called the ‘dark matter problem’.

The nature of dark matter is one of the central questions not only in astrophysics but also poses a challenge to fundamental physics, unless the ‘dark matter problem’ has an astronomical solution. Does dark matter consist of non-luminous celestial bodies, for instance burned-out stars? Or is it a new kind of matter? Have astronomers indirectly proven the existence of a new elementary particle which has thus far escaped detection in terrestrial laboratories? If dark matter indeed consists of a new kind of elementary particle, which is the common presumption today, it should exist in the Milky Way as well, in our immediate vicinity. Therefore, experiments which try to directly detect the constituents of dark matter with highly sensitive and sophisticated detectors have been set up in underground laboratories. Physicists and astronomers are eagerly waiting for results from the Large Hadron Collider (LHC), a particle accelerator at the European CERN research center which started regular operation in 2009, which produces particles at significantly higher energies than accessible before, and which in the first few years of operation already achieved a breakthrough with the discovery of the so-called Higgs particle. The hope is to find hints for new physics beyond the current Standard Model of particle physics, guiding us to extended models of particle physics which can accommodate an elementary particle that could serve as a constituent of dark matter.

Without doubt, the most important development in recent years is the establishment of a standard model of cosmology, i.e., the science of the Universe as a whole. The Universe is known to expand and it has a finite age; we now believe that we know its age with an uncertainty of as little as a few percent—it is t ₀ = 13. 8 Gyr. The Universe has evolved from a very dense and very hot state, the Big Bang, expanding and cooling over time. Even today, echoes of the Big Bang can be observed, for example in the form of the cosmic microwave background radiation. Accurate observations of this background radiation, emitted some 380 000 years after the Big Bang, i.e., at a time $\approx 2.7 \times 10^{-5}t_{0}$ , have made an important contribution to what we know today about the composition of the Universe. However, these results raise more questions than they answer: only ∼ 4 % of the energy content of the Universe can be accounted for by matter which is well-known from other fields of physics, the baryonic matter that consists mainly of atomic nuclei and electrons. About 25 % of the Universe consists of dark matter, as we already discussed in the context of galaxies and galaxy clusters. Recent observational results have shown that the mean density of dark matter dominates over that of baryonic matter also on cosmic scales.

Even more surprising than the existence of dark matter is the discovery that about 70 % of the Universe consists of something that today is called vacuum energy, or dark energy, and that is closely related to the cosmological constant introduced by Albert Einstein. The fact that various names do exist for it by no means implies that we have any idea what this dark energy is. It reveals its existence exclusively in its effect on the cosmic expansion, and it even dominates the expansion dynamics at the current epoch. Any efforts to estimate the density of dark energy from fundamental physics have failed hopelessly up to now. An estimate of the vacuum energy density using quantum mechanics results in a value that is roughly 120 orders of magnitude larger than the value derived from cosmology. For the foreseeable future observational cosmology will be the only empirical probe for dark energy, and an understanding of its physical nature probably has to wait for quite a number of years. The existence of dark energy may well pose the greatest challenge to fundamental physics today.

In this book we will present a discussion of the extragalactic objects found in astronomy, but we will start with describing the Milky Way which, being a typical spiral galaxy, is considered a prototype of this class of stellar systems. The other central topic in this book is a presentation of modern astrophysical cosmology, which has experienced tremendous advances in recent years. Methods and results will be discussed in parallel. Besides providing an impression of the fascination that arises from astronomical observations and cosmological insights, astronomical methods and physical considerations will be our prime focus. We will start in the next section with a concise overview of the fields of extragalactic astronomy and cosmology. This is, on the one hand, intended to whet the reader’s appetite and curiosity, and on the other hand to introduce some facts and technical terms that will be needed in what follows but which are discussed in detail only later in the book. In Sect. 1.3 we will describe some of the most important telescopes used in extragalactic astronomy today, and some of the most useful astronomical surveys having a broad range of applications are mentioned in Sect. 1.4.

1.2 Overview

1.2.1 Our Milky Way as a galaxy

The Milky Way is the only galaxy which we are able to examine in great detail. We can resolve individual stars and analyze them spectroscopically. We can perform detailed studies of the interstellar medium (ISM), such as the properties of molecular clouds and star forming regions. We can quantitatively examine extinction and reddening by dust. Furthermore, we can observe the local dynamics of stars and gas clouds as well as the properties of satellite galaxies (such the Magellanic Clouds). Finally, the Galactic center at a distance of only 8 kpc gives us the unique opportunity to examine the central region of a galaxy at very high resolution.² Only through a detailed understanding of our own Galaxy can we hope to understand the properties of other galaxies. Of course, we implicitly assume that the physical processes taking place in other galaxies obey the same laws of physics that apply to us. If this were not the case, we would barely have a chance to understand the physics of other objects in the Universe, let alone the Universe as a whole. We will return to this point shortly.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig6_HTML.jpg

Fig. 1.6

Schematic structure of the Milky Way consisting of the disk, the central bulge with the Galactic center, and the spherical halo in which most of the globular clusters are located. The Sun orbits around the Galactic center at a distance of about 8 kpc

We will first discuss the properties of our own Galaxy. One of the main problems here, and in astronomy in general, is the determination of the distance to an object. Thus we will start by considering this topic. From the analysis of the distribution of stars and gas in the Milky Way we will then derive its structure. It is found that the Galaxy consists of several distinct components:

a thin disk of stars and gas with a radius of about 20 kpc and a scale height of about 300 pc, which also hosts the Sun;
a ∼ 1 kpc thick disk, which contains a different, older stellar population compared to the thin disk;
a central bulge, as is also found in other spiral galaxies;
and a nearly spherical halo which contains most of the globular clusters, some old stars, and gas with different densities and temperatures.

Figure 1.6 shows a schematic view of our Milky Way and its various components. For a better visual impression, Figs. 1.1 and 1.2 show two spiral galaxies, the former viewed from ‘above’ (face-on) and the latter from the ‘side’ (edge-on). In the former case, the spiral structure, from which this kind of galaxy derives its name, is clearly visible. The bright knots in the spiral arms are regions where young, luminous stars have recently formed. The image shows an obvious color gradient: the galaxy is redder in the center and bluest in the spiral arms—while star formation is currently taking place in the spiral arms, we find mainly old stars towards the center, especially in the bulge.

The Galactic disk rotates, with rotational velocity V (R) depending on the distance R from the center. We can estimate the mass of the Galaxy from the distribution of the stellar light and the mean mass-to-light ratio of the stellar population, since gas and dust represent less than ∼ 10 % of the mass of the stars. From this mass estimate we can predict the rotational velocity as a function of radius simply from Newtonian mechanics. However, the observed rotational velocity of the Sun around the Galactic center is significantly higher than would be expected from the observed mass distribution. If M(R ₀) is the mass inside a sphere around the Galactic center with radius R ₀ ≈ 8 kpc, then the rotational velocity from Newtonian mechanics³ is

$\displaystyle{ V _{0} = \sqrt{\frac{G\,M(R_{0 } )} {R_{0}}} \;. }$

(1.1)

From the visible matter in stars we would expect a rotational velocity of ∼ 160 km∕s, but we observe V ₀ ∼ 220 km∕s (see Fig. 1.7). This discrepancy, and the shape of the rotation curve V (R) for larger distances R from the Galactic center, indicates that our Galaxy contains significantly more mass than is visible in the form of stars.⁴ This additional mass is called dark matter. Its physical nature is still unknown. The main candidates are weakly interacting elementary particles like those postulated by some elementary particle theories, but they have yet not been detected in the laboratory. Macroscopic objects (i.e., celestial bodies) are also in principle viable candidates if they emit very little light. We will discuss experiments which allow us to identify such macroscopic objects and come to the conclusion that the solution of the dark matter problem probably can not be found in astronomy, but rather most likely in particle physics.

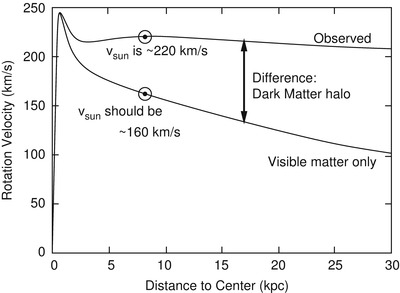
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig7_HTML.jpg

Fig. 1.7

The upper curve is the observed rotation curve V (R) of our Galaxy, i.e., the rotational velocity of stars and gas around the Galactic center as a function of their galacto-centric distance. The lower curve is the rotation curve that we would predict based solely on the observed stellar mass of the Galaxy. The difference between these two curves is ascribed to the presence of dark matter, in which the Milky Way disk is embedded. This image is adapted from Nick Strobel’s webpage at www.astronomynotes.com

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig8_HTML.jpg

Fig. 1.8

The Galactic disk observed in nine different wavebands. Its appearance differs strongly in the various images; for example, the distribution of atomic hydrogen and of molecular gas is much more concentrated towards the Galactic plane than the distribution of stars observed in the near-infrared, the latter clearly showing the presence of a central bulge. The absorption by dust at optical wavelengths is also clearly visible and can be compared to that in Fig. 1.2. Credit: NASA’s Goddard Space Flight Center

The stars in the various components of our Galaxy have different properties regarding their age and their chemical composition. By interpreting this fact one can infer some aspects of the evolution of the Galaxy. The relatively young age of the stars in the thin disk, compared to that of the older population in the bulge, suggests different phases in the formation and evolution of the Milky Way. Indeed, our Galaxy is a highly dynamic object that is still changing today. We see cold gas falling into the Galactic disk and hot gas outflowing. Currently the small neighboring Sagittarius dwarf galaxy is being torn apart in the tidal gravitational field of the Milky Way and will merge with it in the (cosmologically speaking) near future.

One cannot see far through the disk of the Galaxy at optical wavelengths due to extinction by dust. Therefore, the immediate vicinity of the Galactic center can be examined only in other wavebands, especially the infrared (IR) and the radio parts of the electromagnetic spectrum (see also Fig. 1.8). The Galactic center is a highly complex region but we have been able to study it in recent years thanks to various substantial improvements in IR observations regarding sensitivity and angular resolution. Proper motions, i.e., changes of the positions on the sky with time, of bright stars close to the center have been observed. They enable us to determine the mass M inside a volume of radius ∼ 0. 1 pc to be $M(0.1\,\mathrm{pc}) \sim 4 \times 10^{6}M_{\odot }$ . Although the data do not allow us to make a totally unambiguous interpretation of this mass concentration there is no plausible alternative to the conclusion that the center of the Milky Way harbors a supermassive black hole (SMBH) of roughly this mass. And yet this SMBH is far less massive than the ones that have been found in many other galaxies.

Unfortunately, we are unable to look at our Galaxy from the outside. This view from the inside renders it difficult to observe the global properties of the Milky Way. The structure and geometry of the Galaxy, e.g., its spiral arms, are hard to identify from our location. In addition, the extinction by dust hides large parts of the Galaxy from our view (see Fig. 1.9), so that the global parameters of the Milky Way (like its total luminosity) are difficult to measure. These parameters are estimated much better from outside, i.e., in other similar spiral galaxies. In order to understand the large-scale properties of our Galaxy, a comparison with similar galaxies which we can examine in their entirety is extremely helpful. Only by combining the study of the Milky Way with that of other galaxies can we hope to fully understand the physical nature of galaxies and their evolution.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig9_HTML.jpg

Fig. 1.9

The galaxy Dwingeloo 1 is only five times more distant than our closest large neighboring galaxy, Andromeda, yet it was not discovered until the 1990s because it hides behind the Galactic center. The absorption in this direction and numerous bright stars prevented it from being discovered earlier. The figure shows an image observed with the Isaac Newton Telescope in the V, R, and I bands. Credit: S. Hughes & S. Maddox; Isaac Newton Telescope

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig10_HTML.jpg

Fig. 1.10

NGC 2997 is a typical spiral galaxy, with its disk inclined by about 45^∘ with respect to the line-of-sight. Like most spiral galaxies it has two spiral arms; they are significantly bluer than other parts of the galaxy. This is caused by ongoing star formation in these regions so that young, hot and thus blue stars are present in the arms, whereas the center of the galaxy, especially the bulge, consists mainly of old stars. Credit: M. Altmann, Sternwarte der Universität Bonn

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig11_HTML.jpg

Fig. 1.11

M87 is a very luminous elliptical galaxy in the center of the Virgo cluster, at a distance of about 18 Mpc. The diameter of the visible part of this galaxy is about 40 kpc; it is significantly more massive than the Milky Way ( $M> 3 \times 10^{12}M_{\odot }$ ). We will frequently refer to this galaxy: it is not only an excellent example of a central cluster galaxy but also a representative of the family of ‘active galaxies’. It is a strong radio emitter (radio astronomers also know it as Virgo A), and it has an optical jet in its center. Credit: S. Frey & J.E. Gunn, Princeton University

1.2.2 The world of galaxies

Next we will discuss the properties of other galaxies. The two main types of galaxies are spirals (like the Milky Way, see also Fig. 1.10) and elliptical galaxies (Fig. 1.11). Besides these, there are additional classes such as irregular and dwarf galaxies, active galaxies, and starburst galaxies, where the latter have a very high star-formation rate in comparison to normal galaxies. These classes differ not only in their morphology, which forms the basis for their classification, but also in their physical properties such as color (indicating a different stellar content), internal reddening (depending on their dust content), amount of interstellar gas, star-formation rate, etc. Galaxies of different morphologies have evolved in different ways.

Spiral galaxies are stellar systems in which active star formation is still taking place today, whereas elliptical galaxies consist mainly of old stars—their star formation was terminated a long time ago. The S0 galaxies, an intermediate type, show a disk similar to that of spiral galaxies but like ellipticals they consist mainly of old stars, i.e., stars of low mass and low temperature. Ellipticals and S0 galaxies together are often called early-type galaxies, whereas spirals are termed late-type galaxies. These names do not imply any interpretation but exist only for historical reasons.

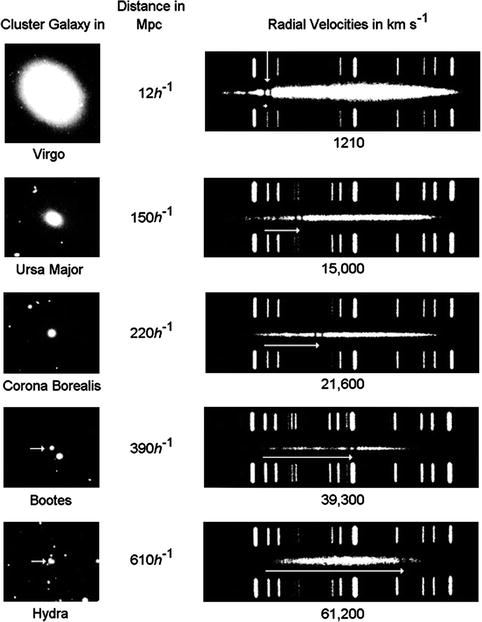
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig12_HTML.jpg

Fig. 1.12

The spectra of galaxies show characteristic spectral lines, e.g., the H+K lines of calcium. These lines, however, do not appear at the wavelengths measured in the laboratory but are in general shifted towards longer wavelengths. This is shown here for a set of sample galaxies, with distance increasing from top to bottom. The shift in the lines, interpreted as being due to the Doppler effect, allows us to determine the relative radial velocity—the larger it is, the more distant the galaxy is. The discrete lines above and below the spectra are for calibration purposes only. Credit: Hale Observatories; J. Silk, The Big Bang, 2nd Ed.

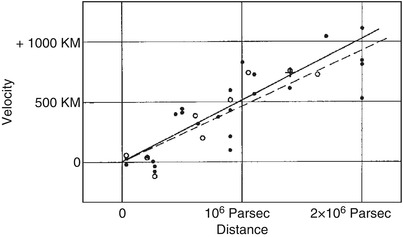
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig13_HTML.jpg

Fig. 1.13

The original 1929 version of the Hubble diagram shows the radial velocity of galaxies as a function of their distance. The reader may notice that the velocity axis is labeled with erroneous units—of course they should read km/s. While the radial (escape) velocity is easily measured by means of the Doppler shift in spectral lines, an accurate determination of distances is much more difficult; we will discuss methods of distance determination for galaxies in Sect. 3.9. Hubble has underestimated the distances considerably, resulting in too high a value for the Hubble constant. Only very few and very close galaxies show a blueshift, i.e., they move towards us; one of these is Andromeda ( = M31). Adapted from: E. Hubble 1929, A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae, Proc. Nat. Academy Sciences 15, No. 3, March 15, 1929, Fig. 1

The disks of spiral galaxies rotate differentially. As for the Milky Way, one can determine the mass from the rotational velocity using the Kepler law (1.1). One finds that, contrary to the expectation from the distribution of light, the rotation curve does not decline at larger distances from the center. Like our own Galaxy, spiral galaxies contain a large amount of dark matter; the visible matter is embedded in a halo of dark matter. We can only get rough estimates of the extent of this halo, but there are strong indications that it is substantially larger than the extent of the visual matter. For instance, the rotation curve is flat up to the largest radii where one still finds gas to measure the velocity. Studying dark matter in elliptical galaxies is more complicated, but the existence of dark halos has also been proven for ellipticals.

The Hertzsprung–Russell diagram of stars, or their color-magnitude diagram (see Appendix B), has turned out to be the most important diagram in stellar astrophysics. The fact that most stars are aligned along a one-dimensional sequence, the main sequence, led to the conclusion that, for main sequence stars, the luminosity and the surface temperature are not independent parameters. Instead, the properties of such stars are in principle characterized by only a single parameter: the stellar mass. We will also see that the various properties of galaxies are not independent parameters. Rather, dynamical properties (such as the rotational velocity of spirals) are closely related to the luminosity. These scaling relations are of similar importance to the study of galaxies as the Hertzsprung–Russell diagram is for stars. In addition, they turn out to be very convenient tools for the determination of galaxy distances.

Like our Milky Way, other galaxies also seem to harbor a SMBH in their center. We obtained the astonishing result that the mass of such a SMBH is closely related to the velocity distribution of stars in elliptical galaxies or in the bulge of spirals. The physical reason for this close correlation is as yet not known in detail, but it strongly suggests a joint evolution of galaxies and their SMBHs.

1.2.3 The Hubble expansion of the Universe

The radial velocity of galaxies, measured by means of the Doppler shift of spectral lines (Fig. 1.12), is positive for nearly all galaxies, i.e., they appear to be moving away from us. In 1928, Edwin Hubble discovered that this escape velocity v increases with the distance of the galaxy. He identified a linear relation between the radial velocity v and the distance D of galaxies, called the Hubble law,

$\displaystyle{ \fbox{$v = H_{0}D$}\;, }$

(1.2)

where H ₀ is a constant. If we plot the radial velocity of galaxies against their distance, as is done in the Hubble diagram of Fig. 1.13, the resulting points are approximated by a straight line, with the slope being determined by the constant of proportionality, H ₀, which is called the Hubble constant. The fact that all galaxies seem to move away from us with a velocity which increases linearly with their distance is interpreted such that the Universe is expanding. We will see later that this Hubble expansion of the Universe is a natural property of cosmological world models.

For a long time, the value of H ₀ was uncertain by almost a factor of two. However, in recent years the uncertainty was reduced to about 5 %, yielding

$\displaystyle{ H_{0} = (71 \pm 4)\,\mathrm{km}\,\mathrm{s}^{-1}\mathrm{Mpc}^{-1}\;, }$

(1.3)

obtained from several different methods which will be discussed later. The error margins vary for the different methods. The main problem in determining H ₀ is in measuring the absolute distance of galaxies (as will be discussed in Sect. 3.9), whereas Doppler shifts are easily measurable. If one assumes (1.2) to be valid, the radial velocity of a galaxy is a measure of its distance. One defines the redshift, z, of an object from the wavelength shift in spectral lines,

$\displaystyle{ z:= \frac{\lambda _{\mathrm{obs}} -\lambda _{0}} {\lambda _{0}} \;,\;\;\lambda _{\mathrm{obs}} = (1 + z)\lambda _{0}\;, }$

(1.4)

with λ ₀ denoting the wavelength of a spectral transition in the rest-frame of the emitter and λ _obs the observed wavelength. For instance, the Lyman-α transition, i.e., the transition from the first excited level to the ground state in the hydrogen atom is at λ ₀ = 1216 Å. For small redshifts,

$\displaystyle{ v \approx zc\;, }$

(1.5)

whereas this relation has to be modified for large redshifts, together with the interpretation of the redshift itself. ⁵ Combining (1.2) and (1.5), we obtain

$\displaystyle{ D \approx \frac{zc} {H_{0}} \approx 3000\,z\,h^{-1}\mathrm{Mpc}\;, }$

(1.6)

where the uncertainty in determining H ₀ is parametrized by the scaled Hubble constant h, defined as

$\displaystyle{ \fbox{$H_{0} = h\,100\,\mathrm{km}\,\mathrm{s}^{-1}\mathrm{Mpc}^{-1}$}\;. }$

(1.7)

Distance determinations based on redshift therefore always contain a factor of h ⁻¹, as seen in (1.6). With the recent determination of the Hubble constant (1.3), we have h = 0. 71 ± 0. 04. It needs to be emphasized once more that (1.5) and (1.6) are valid only for z ≪ 1; the generalization for larger redshifts will be discussed in Sect. 4.3. Nevertheless, z is also a measure of distance for large redshifts.

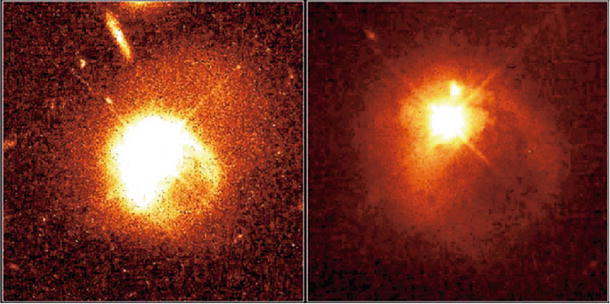
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig14_HTML.jpg

Fig. 1.14

The quasar PKS 2349 is located at the center of a galaxy, its host galaxy. The two images shown here differ only in their brightness contrast. The diffraction spikes (diffraction patterns caused by the suspension of the telescope’s secondary mirror) in the middle of the object show that the center of the galaxy contains a point source, the actual quasar, which is significantly brighter than its host galaxy. The galaxy shows clear signs of distortion, visible as large and thin tidal tails. The tails are caused by a neighboring galaxy that is visible in the right-hand image, just above the quasar; it is about the size of the Large Magellanic Cloud. Quasar host galaxies are often distorted or in the process of merging with other galaxies. Credit: J. Bahcall (IAS, Princeton), M. Disney (University of Wales), NASA

1.2.4 Active galaxies and starburst galaxies

A special class of galaxies are the so-called active galaxies which have a very strong energy source in their center (active galactic nucleus, AGN). The best-known representatives of these AGNs are the quasars, objects typically at high redshift and with quite exotic properties. Their spectrum shows strong emission lines which can be extremely broad, with a relative width of Δ λ∕λ ∼ 0. 03. The line width is caused by very high random velocities of the gas which emits these lines: if we interpret the line width as due to Doppler broadening resulting from the superposition of lines of emitting gas with a very broad velocity distribution, we obtain velocities of typically Δ v ∼ 10 000 km∕s. The central source in these objects is much brighter than the other parts of the galaxy, making these sources appear nearly point-like on optical images. Only with the Hubble Space Telescope (HST) did astronomers succeed in detecting structure in the optical emission for a large sample of quasars (Fig. 1.14).

Many properties of quasars resemble those of Seyfert type I galaxies, which are galaxies with a very luminous nucleus and very broad emission lines. For this reason, quasars are considered as particularly luminous members of this class. The total luminosity of quasars is extremely large, with some of them emitting more than a 1000 times the luminosity of our Galaxy. In addition, this radiation must originate from a very small spatial region whose size can be estimated, e.g., from the variability time-scale of the source. Due to these and other properties which will be discussed in Chap. 5, it is concluded that the nuclei of active galaxies must contain a supermassive black hole as the central powerhouse. The radiation is produced by matter falling towards this black hole, a process called accretion , thereby converting its gravitational potential energy into kinetic energy. If this kinetic energy is then transformed into internal energy (i.e., heat) as happens in the so-called accretion disk due to friction, it can get radiated away. This is in fact an extremely efficient process of energy production. For a given mass, the accretion onto a black hole is about ten times more efficient than the nuclear fusion of hydrogen into helium. AGNs often emit radiation across a very large portion of the electromagnetic spectrum, from radio up to X-ray and gamma radiation.

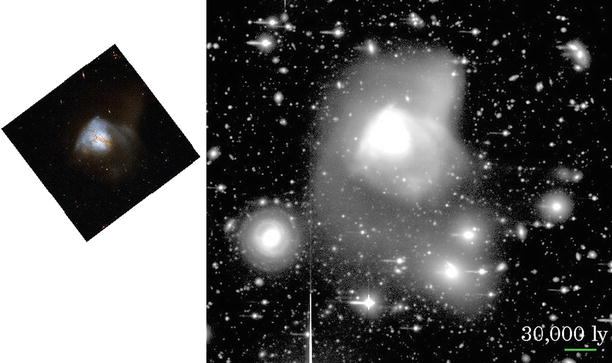
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig15_HTML.jpg

Fig. 1.15

Arp 220 is the most luminous object in the local Universe. Originally cataloged as a peculiar galaxy, the infrared satellite IRAS later discovered its enormous luminosity ( $L \sim 10^{12}L_{\odot }$ ) in the infrared (IR). Arp 220 is the prototype of ultra-luminous infrared galaxies (ULIRGs). The left panel shows a near-IR image taken with the Hubble Space Telescope (HST). The right panel shows a spectacular image taken with the Subaru telescope on Mauna Kea; it unveils the structure of this object. With two colliding spiral galaxies in the center of Arp 220, the disturbances in the interstellar medium caused by this collision trigger a starburst. Dust in the galaxy absorbs most of the ultra-violet (UV) radiation from the young hot stars and re-emits it in the IR. Credit: Left: Hubble Space Telescope/NASA. Right: Ehime University/NAOJ. ©National Astronomical Observatory of Japan, ©NAOJ, Courtesy of the National Astronomical Observatory of Japan, and Courtesy of NAOJ

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig16_HTML.jpg

Fig. 1.16

Two spiral galaxies interacting with each other. NGC 2207 (on the left) and IC 2163 are not only close neighbors in projection: the strong gravitational tidal interaction they are exerting on each other is clearly visible in the pronounced tidal arms, particularly visible to the right of the right-hand galaxy. Furthermore, a bridge of stars is seen to connect these two galaxies, also due to tidal gravitational forces. This image was taken with the Hubble Space Telescope. Credit: The Hubble Heritage Project, STScI, NASA

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig17_HTML.jpg

Fig. 1.17

The Coma cluster of galaxies, at a distance of roughly 90 Mpc from us, is the closest massive regular cluster of galaxies. Almost all brighter objects visible in this image of the central region of Coma are galaxies associated with the cluster—Coma contains more than a 1000 luminous galaxies. This images is a color composite made from optical data from the Sloan Digital Sky Survey (SDSS), shown in blue, and infrared data from the Spitzer Space Telescope, shown in red and green, for the longer and shorter wavelength, respectively. Credit: NASA/JPL-Caltech/GSFC/SDSS

Spiral galaxies still form stars today, indeed star formation is a common phenomenon in galaxies. In addition, there are galaxies with a considerably higher star-formation rate than ‘normal’ spirals. These galaxies are undergoing a burst of star formation and are thus known as starburst galaxies. Their star-formation rates are typically between 10 and $300M_{\odot }/\mathrm{yr}$ , whereas our Milky Way gives birth to about 2M _⊙∕yr of new stars. This vigorous star formation often takes place in localized regions, e.g., in the vicinity of the center of the respective galaxy. Starbursts are substantially affected, if not triggered, by disturbances in the gravitational field of the galaxy, such as those caused by galaxy interactions. Such starburst galaxies (see Fig. 1.15) can be extremely luminous in the far-infrared (FIR); they emit up to 98 % of their total luminosity in this part of the spectrum. This happens by dust emission: dust in these galaxies absorbs a large proportion of the energetic UV radiation produced by the massive stars in the star-formation region, thereby heats up, and then re-emits this energy in the form of thermal radiation in the FIR.

1.2.5 Voids, clusters of galaxies, and dark matter

The likelihood of galaxies to interact (Fig. 1.16) is enhanced by the fact that galaxies are not randomly distributed in space. The projection of galaxies on the celestial sphere, for instance, shows a distinct structure. In addition, measuring the distances of galaxies allows a determination of their three-dimensional distribution. One finds a strong correlation of the galaxy positions. There are regions in space that have a very high galaxy density, but also regions where nearly no galaxies are seen at all. The latter are called voids. Such voids can have diameters of up to 30h ⁻¹Mpc.

Clusters of galaxies are gravitationally bound systems of a hundred or more galaxies in a volume of diameter ∼ 2 h ⁻¹Mpc. Clusters predominantly contain early-type galaxies, so there is not much star formation taking place any more. Some clusters of galaxies seem to be rather circular in projection, others have a highly elliptical or irregular distribution of galaxies; some even have more than one center. The cluster of galaxies closest to us is the Virgo cluster, at a distance of ∼ 18 Mpc; it is a cluster with an irregular galaxy distribution. The closest regular cluster is Coma, at a distance of ∼ 90 Mpc.⁶ Coma (Fig. 1.17) contains about 1000 luminous galaxies, of which 85 % are early-type galaxies.

In 1933, Fritz Zwicky measured the radial velocities of the galaxies in Coma and found that their distribution around the mean has a dispersion of about 1000 km∕s. From the total luminosity of all its galaxies the mass of the cluster can be estimated. If the stars in the cluster galaxies have an average mass-to-light ratio (M∕L) similar to that of our Sun, we would conclude $M = (M_{\odot }/L_{\odot })L$ . However, stars in early-type galaxies are on average slightly less massive than the Sun and thus have a slightly higher M∕L.⁷ Thus, the above mass estimate needs to be increased by a factor of ∼ 10.

Zwicky then estimated the mass of the cluster by multiplying the luminosity of its member galaxies with the mass-to-light ratio. From this mass and the size of the cluster, he could then estimate the velocity that a galaxy needs to have in order to escape from the gravitational field of the cluster—the escape velocity. He found that the characteristic peculiar velocity of cluster galaxies (i.e., the velocity relative to the mean velocity) is substantially larger than this escape velocity. In this case, the galaxies of the cluster would fly apart on a time-scale of about 10⁹ yr—the time it takes a galaxy to cross through the cluster once—and, consequently, the cluster would dissolve. However, since Coma seems to be a relaxed cluster, i.e., it is in equilibrium and thus its age is definitely larger than the dynamical time scale of 10⁹ yr, Zwicky concluded that the Coma cluster contains significantly more mass than the sum of the masses of its galaxies. Using the virial theorem⁸ he was able to estimate the mass of the cluster from the velocity distribution of the galaxies. This was the first clear indicator of the existence of dark matter.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig18_HTML.jpg

Fig. 1.18

The Hydra A cluster of galaxies. The left-hand figure shows an optical image, the one on the right an image taken with the X-ray satellite Chandra. The cluster has a redshift of z ≈ 0. 054 and is thus located at a distance of about 250 Mpc. The X-ray emission originates from gas at a temperature of 40 × 10⁶K which fills the space between the cluster galaxies. In the center of the cluster, the gas is cooler by about 15 %. Credit: Optical: B. McNamara, La Palma; X-ray: NASA/CXC/SAO

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig19_HTML.jpg

Fig. 1.19

The cluster of galaxies Abell 383, as seen in optical light, superposed by an image taken at X-ray energies (purple) with the Chandra satellite observatory. The space between the galaxies is filled by a hot gas, with temperature of about 50 million degrees, which emits the energetic X-ray radiation. The cluster is at a redshift of z = 0. 19, corresponding to a distance of about 800 Mpc, and has an estimated mass of $\sim 3\, \times 10^{14}\,M_{\odot }$ . Credit: X-ray: NASA/CXC/Caltech/A. Newman et al./Tel Aviv/A. Morandi & M. Limousin; Optical: NASA/STScI, ESO/VLT, SDSS

X-ray satellites later revealed that clusters of galaxies are strong sources of X-ray radiation. They contain hot gas, with temperatures ranging from 10⁷ up to 10⁸ K (Fig. 1.18). This gas temperature is another measure for the depth of the cluster’s potential well, since the hotter the gas is, the deeper the potential well has to be to prevent the gas from escaping via evaporation. Mass estimates based on the X-ray temperature result in values that are comparable to those from the velocity dispersion of the cluster galaxies. Whereas the X-ray emitting gas provides a further mass component of ordinary, baryonic matter—in fact, the X-ray emitting gas contains more mass than the stars in the cluster galaxies—the total mass of clusters exceeds that of stars and gas by a factor of about five, thus clearly confirming the hypothesis of the existence of dark matter in clusters (Fig. 1.19). A third method for determining cluster masses, the so-called gravitational lensing effect, utilizes the fact that light is deflected in a gravitational field. The angle through which light rays are bent due to the presence of a massive object depends on the mass of that object. From observation and analysis of the gravitational lensing effect in clusters of galaxies, cluster masses are derived that are in agreement with those from the two other methods. Therefore, clusters of galaxies are a second class of cosmic objects whose mass is dominated by dark matter.

Clusters of galaxies are cosmologically young structures. Their dynamical time-scale, i.e., the time in which the mass distribution in a cluster settles into an equilibrium state, is estimated as the time it takes a member galaxy to fully cross the cluster once. With a characteristic velocity of v ∼ 1000 km∕s and a diameter of 2R ∼ 2 Mpc one thus finds

$\displaystyle{ t_{\mathrm{dyn}} \sim \frac{2R} {v} \sim 2 \times 10^{9}\,\mathrm{yr}\;. }$

(1.9)

As we will later see, the Universe is about 14 × 10⁹ yr old. During this time galaxies have not had a chance to cross the cluster many times. Therefore, clusters still contain, at least in principle, information about their initial state. Most clusters have not had the time to fully relax and evolve into a state of equilibrium that would be largely independent of their initial conditions. Comparing this with the time taken for the Sun to rotate around the center of the Milky Way—about 2 × 10⁸ yr—galaxies thus have had plenty of time to reach their state of equilibrium.

Besides massive clusters of galaxies there are also galaxy groups, which sometimes contain only a few luminous galaxies. In fact, the number density of groups is far larger than that of clusters. Our Milky Way is part of such a group, the Local Group, which also contains M31 ( Andromeda), a second luminous spiral galaxy besides the Milky Way, as well as some far less luminous galaxies such as the Magellanic Clouds. Some groups of galaxies are very compact, i.e., their galaxies are confined within a very small volume (Fig. 1.20). Interactions between these galaxies cause the lifetimes of many such groups to be much smaller than the age of the Universe, and the galaxies in such groups will merge.

1.2.6 World models and the thermal history of the Universe

Quasars, clusters of galaxies, and nowadays even single galaxies are also found at very high redshifts where the simple form of the Hubble law (1.2) is no longer valid. It is therefore necessary to generalize the distance-redshift relation. This requires considering world models as a whole, which are also called cosmological models. The dominant force in the Universe is gravitation. On the one hand, weak and strong interactions both have an extremely small (sub-atomic) range, and on the other hand, electromagnetic interactions do not play a role on large scales since the matter in the Universe is on average electrically neutral. Indeed, if it was not, currents would immediately flow to balance net charge densities. The accepted theory of gravitation is the theory of General Relativity (GR), formulated by Albert Einstein in 1915.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig20_HTML.jpg

Fig. 1.20

The galaxy group HCG87 belongs to the class of so-called compact groups. In this HST image we can see three massive galaxies belonging to this group: an edge-on spiral in the lower part of the image, an elliptical galaxy to the lower right, and another spiral in the upper part. The small spiral in the center is a background object and therefore does not belong to the group. The two lower galaxies have an active galactic nucleus, whereas the upper spiral seems to be undergoing a phase of star formation. The galaxies in this group are so close together that in projection they appear to touch. Between the galaxies, gas streams can be detected. The galaxies are disturbing each other, which could be the cause of the nuclear activity and star formation. The galaxies are bound in a common gravitational potential and will heavily interfere and presumably merge on a cosmologically small time scale, which means in only a few orbits, with an orbit taking about 10⁸ yr. Such merging processes are of utmost importance for the evolution of the galaxy population. Credit: STScI and the Hubble Heritage Project

Based on the two postulates that (1) our place in the Universe is not special, and thus not distinguished from other locations and that (2) the distribution of matter around us is isotropic, at least on large scales, one can construct homogeneous and isotropic world models (so-called Friedmann–Lemaître models) that obey the laws of General Relativity. Expanding world models that contain the Hubble expansion result from this theory naturally. Essentially, these models are characterized by three parameters:

the current expansion rate of the Universe, i.e., the Hubble constant H ₀;
the current mean matter density of the Universe ρ _m, often parametrized by the dimensionless density parameter of matter,

$\displaystyle{ \varOmega _{\mathrm{m}} = \frac{8\pi G} {3H_{0}^{2}}\rho _{\mathrm{m}}\;; }$

(1.10)
and the density of the so-called vacuum energy, described by the cosmological constant Λ or by the corresponding density parameter of the vacuum

$\displaystyle{ \varOmega _{\varLambda } = \frac{\varLambda } {3H_{0}^{2}}\;. }$

(1.11)

The cosmological constant was originally introduced by Einstein to allow stationary world models within GR. After the discovery of the Hubble expansion he is quoted to have called the introduction of Λ into his equations his greatest blunder. In quantum mechanics Λ attains a different interpretation, related to an energy density of the vacuum.

The values of the cosmological parameters are known quite accurately today (see Chap. 8), with values of Ω _m ≈ 0. 3 and Ω _Λ ≈ 0. 7. The discovery of a non-vanishing Ω _Λ came completely unexpectedly. To date, all attempts have failed to compute a reasonable value for Ω _Λ from quantum mechanics. By that we mean a value which has the same order-of-magnitude as the one we derive from cosmological observations. In fact, simple and plausible estimates lead to a value of Λ that is ∼ 10¹²⁰ times larger than that obtained from observation, a tremendously bad estimate indeed. This huge discrepancy is probably one of the biggest challenges in fundamental physics today.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig21_HTML.jpg

Fig. 1.21

Temperature distribution of the cosmic microwave background on the sky as measured by the COBE satellite. The top image shows a dipole distribution; it originates from the Earth’s motion relative to the restframe of the CMB. Our Solar System moves at a speed of 369 km∕s relative to that system, which leads to a dipole anisotropy with an amplitude of $\varDelta T/T \sim v/c \sim 1.2 \times 10^{-3}$ due to the Doppler effect. If this dipole contribution is subtracted, we get the map in the middle which clearly shows the emission from the Galactic disk. Since this emission has a different spectral energy distribution (it is not a blackbody of T ∼ 3 K), it can also be subtracted to get the temperature map at the bottom. These are the primordial fluctuations of the CMB, with an amplitude of about $\varDelta T/T \sim 2 \times 10^{-5}$ . Credit: COBE/DRM team, NASA

According to the Friedmann–Lemaître models, the Universe used to be smaller and hotter in the past, and it has continuously cooled down in the course of expansion. We are able to trace back the cosmic expansion under the assumption that the known laws of physics were also valid in the past. From that we get the Big Bang model of the Universe, according to which our Universe has evolved out of a very dense and very hot state, the so-called Big Bang. The Big Bang marks the beginning of the Universe, at least as far as physics can describe it, and is taken to be the origin of cosmic time. This world model makes a number of predictions that have been verified convincingly:

About 1/4 of the baryonic matter in the Universe should consist of helium which formed about 3 min after the Big Bang, while most of the rest consists of hydrogen. This is indeed the case: the mass fraction of helium in metal-poor objects, whose chemical composition has not been significantly modified by processes of stellar evolution, is about 24 %.

From the exact fraction of helium one can derive the number of neutrino families—the more neutrino species that exist, the larger the fraction of helium will be. From this, it was derived in 1981 that there are three kinds of neutrinos. This result was later confirmed by particle accelerator experiments.

Thermal radiation from the hot early phase of the Universe should still be measurable today. Predicted in 1946 by George Gamow, it was discovered by Arno Penzias and Robert Wilson in 1965. The corresponding photons have propagated freely after the Universe cooled down to about 3000 K and the plasma constituents—atomic nuclei and electrons—combined to neutral atoms, an epoch called recombination. As a result of cosmic expansion, this radiation has cooled down to about T ₀ ≈ 2. 73 K. This microwave radiation is observed to be nearly perfectly isotropic, once we subtract the radiation which is emitted locally by the Milky Way (see Fig. 1.21). Indeed, measurements from the COBE satellite showed that the cosmic microwave background (CMB) is the most accurate blackbody spectrum ever measured.

Today’s structures in the Universe have evolved out of very small density fluctuations in the early cosmos. The seeds of structure formation must have already been present in the very early phases of cosmic evolution. These density fluctuations should also be visible as small temperature fluctuations in the microwave background emitted about 380 000 years after the Big Bang at the epoch of recombination. In fact, COBE was the first to observe these predicted anisotropies (see Fig. 1.21). Later experiments, especially the WMAP and Planck satellites, observed the structure of the microwave background at much improved angular resolution and verified the theory of structure formation in the Universe in detail (see Sect. 8.6).

With these predictions so impressively confirmed, in this book we will exclusively consider this cosmological model; currently there is no competing model of the Universe that could explain these very basic cosmological observations in a natural way. In addition, this model does not seem to contradict any fundamental observation in cosmology. However, as the existence of a non-vanishing vacuum energy density shows, together with a matter density ρ _m that is about six times the mean baryon density in the Universe (which can be derived from the abundance of the chemical elements formed in the Big Bang), the physical nature of about 95 % of the content of our Universe is not yet understood.

Most of the CMB photons we receive today had their last physical interaction with matter when the Universe was about 3. 8 × 10⁵ yr old. Also, the most distant galaxies and quasars known today (at z ∼ 7) are strikingly young—we see them at a time when the Universe was less than a tenth of its current age . The exact relation between the age of the Universe at the time of the light emission and the redshift depends on the cosmological parameters H ₀, Ω _m, and Ω _Λ . In the special case that Ω _m = 1 and Ω _Λ = 0, called the Einstein–de Sitter model, one obtains

$\displaystyle{ t(z) = \frac{2} {3H_{0}} \frac{1} {(1 + z)^{3/2}}\;. }$

(1.12)

In particular, the age of the Universe today (i.e., at z = 0) in this model is

$\displaystyle{ t_{0} = \frac{2} {3H_{0}} \approx 6.5 \times 10^{9}\,h^{-1}\mathrm{yr}\;. }$

(1.13)

The Einstein–de Sitter (EdS) model is the simplest world model and we will sometimes use it as a reference, despite the fact the our Universe does not follow the EdS model, since Ω _m < 1 and Ω _Λ > 0. However, due to its mathematical simplicity, it is often convenient to obtain rough estimates within this model. The mean density of the Universe in the EdS model is

$\displaystyle{ \rho _{0} =\rho _{\mathrm{cr}} \equiv \frac{3H_{0}^{2}} {8\pi G} \approx 1.9 \times 10^{-29}h^{2}\,\mathrm{g}\,\mathrm{cm}^{-3}\;, }$

(1.14)

hence it is really, really small.

1.2.7 Structure formation and galaxy evolution

The low amplitude of the CMB anisotropies implies that the inhomogeneities must have been very small at the epoch of recombination, whereas today’s Universe features very large density fluctuations, at least on scales of clusters of galaxies. Hence, the density field of the cosmic matter must have evolved. This structure evolution occurs because of gravitational instability , in that an overdense region will expand more slowly than the mean Universe due to its self-gravity. Therefore, any relative overdensity becomes amplified in time. The growth of density fluctuations in time will then cause the formation of large-scale structures, and the gravitational instability is also responsible for the formation of galaxies and clusters. Our world model sketched above predicts the abundance of galaxy clusters as a function of redshift, which can be compared with the observed cluster counts. This comparison can then be used to determine cosmological parameters.

Another essential conclusion from the smallness of the CMB anisotropies is the existence of dark matter on cosmic scales. The major fraction of cosmic matter is dark matter. The baryonic contribution to the matter density is ≲ 20 % and to the total energy density ≲ 5 %. The energy density of the Universe is dominated by the vacuum energy.

Unfortunately, the spatial distribution of dark matter on large scales is not directly observable. We only observe galaxies or, more precisely, their stars and gas. One might expect that galaxies would be located preferentially where the dark matter density is high. However, it is by no means clear that local fluctuations of the galaxy number density are strictly proportional to the density fluctuations of dark matter. The relation between the dark and luminous matter distributions is currently only approximately understood.

Eventually, this relation has to result from a detailed understanding of galaxy formation and evolution. Locations with a high density of dark matter can support the formation of galaxies. Thus we will have to examine how galaxies form and why there are different kinds of galaxies. In other words, what decides whether a forming galaxy will become an elliptical or a spiral? This question has not been definitively answered yet, but it is supposed that ellipticals can form only by the merging of galaxies. Indeed, the standard model of the Universe predicts that small galaxies will form first; larger galaxies will be formed later through the ongoing merger of smaller ones.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig22_HTML.jpg

Fig. 1.22

Galaxy evolution caught in the act: The Tadpole galaxy (also called Arp 188) shows a ∼ 90 kpc long tail. Most likely, this spiral galaxy collided with a smaller galaxy some time in the past, which ripped part of its matter away from the main body of the galaxy. Inside the tail, clusters of newly formed stars are visible. Clearly, this galaxy will have changed from its earlier state after it becomes settled again. Credit: H. Ford (JHU), M. Clampin (STScI), G. Hartig (STScI), G. Illingworth (UCO/Lick), ACS Science Team, ESA, NASA

The evolution of galaxies can actually be observed directly. Galaxies at high redshift (i.e., cosmologically young galaxies) are in general smaller and bluer, and the star-formation rate was significantly higher at earlier times than it is today. The change in the mean color of galaxies as a function of redshift can be understood as a combination of changes in the star formation processes and an aging of the stellar population. Also, galaxy collisions which can be directly observed in the local Universe (Fig. 1.22; see also Fig. 1.16) have a strong impact on individual galaxies and need to be considered in models of galaxy evolution.

1.2.8 Cosmology as a triumph of the human mind

Cosmology, extragalactic astronomy, and astrophysics as a whole are a heroic undertaking of the human mind and a triumph of physics. To understand the Universe we apply physical laws that were found empirically under completely different circumstances. All the known laws of physics were derived ‘today’ and, except for General Relativity, are based on experiments on a laboratory scale or, at most, on observations in the Solar System, such as Kepler’s laws which formed the foundation for the Newtonian theory of gravitation. Is there any a priori reason to assume that these laws are also valid in other regions of the Universe or at completely different times? However, this is apparently indeed the case: nuclear reactions in the early Universe seem to obey the same laws of strong interaction that are measured today in our laboratories, since otherwise the agreement of the prediction of a 25 % helium mass fraction from nuclear reactions in the first minutes of our Universe with the observed helium abundance would be a pure coincidence. Quantum mechanics, describing the wavelengths of atomic transitions, also seems to be valid at very large distances—since even the most distant objects show emission lines in their spectra with frequency ratios (which are described by the laws of quantum mechanics) identical to those in nearby objects. In fact, cosmologists can put very tight upper limits on a possible variation of the ‘constants’ of nature with time, such as the fine-structure constant or the electron to proton mass ratio.

By far the greatest achievement is General Relativity. It was originally formulated by Albert Einstein since his special theory of relativity did not allow him to incorporate the laws of Newtonian gravity. No empirical findings were known at that time (1915) which would not have been explained by the Newtonian theory of gravity. Nevertheless, Einstein developed a totally new theory of gravitation for purely theoretical reasons. The first success of this theory was the correct description of the gravitational deflection of light by the Sun, measured in 1919, and of the perihelion rotation of Mercury.⁹ His theory permits a description of the expanding Universe, which became necessary after Hubble’s discovery in 1928. Only with the help of this theory can we reconstruct the history of the Universe back into the past. Today this history seems to be well understood up to the time when the Universe was about 10⁻⁶ s old and had a temperature of about 10¹³ K. Particle physics models allow an extrapolation to even earlier epochs.

The cosmological predictions discussed above are based on General Relativity describing an expanding Universe, therefore providing a test of Einstein’s theory. On the other hand, General Relativity also describes much smaller systems and with much stronger gravitational fields, such as neutron stars and black holes. With the discovery of a binary system consisting of two neutron stars, the binary pulsar PSR 1913+16, in the last ∼ 40 yr very accurate tests of General Relativity have become possible. For example, the observed perihelion rotation in this binary system and the shrinking of the binary orbit over time due to the radiation of energy by gravitational waves is extremely accurately described by General Relativity. Together, General Relativity has been successfully tested on length-scales from 10¹¹cm (the characteristic scale of the binary pulsar) to 10²⁸cm (the size of the visible Universe), that is over more than 10¹⁷ orders of magnitude—an impressive result indeed!

1.2.9 Astrophysics & Physics

Exploring the laws of gravity by astronomical observations in the Solar System and beyond is just one example for the close connection between physics and astronomy. As the word ‘astrophysics’ implies, the science of the Universe has become an integral part of physics. Astrophysics and cosmology not only apply the laws of physics to interpret and understand the cosmic objects like stars, galaxies and black holes, but also have led to discoveries concerning fundamental physics. A few examples should illustrate that point.

Measuring the flux of neutrinos from the Sun, which are produced by nuclear fusion in the Solar center to generate the Solar luminosity, it was found that the observed neutrino rate is only half of what was expected. The solution of this Solar neutrino problem led to the discovery of neutrino oscillations, disclosing a fundamental property of these weakly interacting particles, requiring them to have a finite rest mass (see Sect. 4.4.6), and providing clear evidence for the incompleteness of the Standard Model of elementary particles.
The fact that carbon has a large abundance in the Universe led Frey Hoyle in 1952 to suspect that there should be a particular excited state of this nucleus in resonance with energy levels of beryllium and helium, to enable the formation of carbon through nuclear fusion in stellar interiors. This previously unknown state, essential for the occurrence of the so-called triple-alpha process, was later on found in experiments.
Much of the development in the field of plasma physics was driven by astrophysicists in order to understand the behavior of plasmas in cosmic objects—ranging from the Sun (e.g., the occurrence of sunspots, the Solar corona) to the interplanetary space filled with the Solar wind and its interaction with the Earth’s magnetosphere, to the impact of magnetic fields on star-forming regions, to the formation of relativistic jets in active galactic nuclei.

Arguably the largest impact astrophysics has on other branches of physics today is related to the finding that the Universe is dominated by dark matter and dark energy—there is no evidence for the existence of these new forms of energy apart from astronomical observations. We will come back to that theme repeatedly in the course of this book.

However, there is one important difference between astrophysics and other branches of physics: we cannot do experiments with the subjects of interest, we cannot prepare the system is a way which allows a clean measurement under controlled external conditions, and repeat the measurement with changing conditions. We can only observe how our objects behave, how different objects of the same kind are similar—or different—in their behavior, and draw conclusions from it.

1.3 The tools of extragalactic astronomy

Extragalactic sources—galaxies, quasars, clusters of galaxies—are at large distances. This means that in general they appear to be faint even if they are intrinsically luminous. They are also seen to have a very small angular size despite their possibly large linear extent. In fact, just three extragalactic sources are visible to the naked eye: the Andromeda galaxy (M31) and the Large and Small Magellanic Clouds. Thus for extragalactic astronomy, telescopes are needed that have large apertures (photon collecting area) and a high angular resolution. This applies to all wavebands, from radio astronomy to gamma ray astronomy.

The properties of astronomical telescopes and their instruments can be judged by different criteria, and we will briefly describe the most important ones. The sensitivity specifies how dim a source can be and still be observable in a given integration time. The sensitivity depends on the aperture of the telescope as well as on the efficiency of the instrument and the sensitivity of the detector. The sensitivity of optical telescopes, for instance, was increased by a large factor when CCDs replaced photographic plates as detectors in the early 1980s. The sensitivity also depends on the sky background, i.e., the brightness of the sky caused by non-astronomical sources. Artificial light in inhabited regions has forced optical telescopes to retreat into more and more remote areas of the world where light pollution is minimized. Radio astronomers have similar problems caused by radio emission from the telecommunication infrastructure of modern civilization. The angular resolution of a telescope specifies down to which angular separation two sources in the sky can still be separated by the detector. For diffraction-limited observations like those made with radio telescopes or space-born telescopes, the angular resolution Δ θ is limited by the diameter D of the telescope. For a wavelength λ one has $\varDelta \theta =\lambda /D$ . For optical and near-infrared observations from the ground, the angular resolution is in general limited by turbulence in the atmosphere, which explains the choice of high mountain tops as sites for optical telescopes. These atmospheric turbulences cause, due to scintillation, the smearing of the images of astronomical sources, an effect that is called seeing . In interferometry, where one combines radiation detected by several telescopes, the angular resolution is limited by the spatial separation of the telescopes. The spectral resolution of an instrument specifies its capability to separate different wavelengths. The throughput of a telescope/instrument system is of particular importance in large sky surveys. For instance, the efficiency of spectroscopic surveys depends, in addition to the aperture of the telescope, on the number of spectra that can be observed simultaneously. Special multiplex spectrographs have been constructed for such tasks. Likewise, the efficiency of photometric surveys depends on the telescope’s diameter and the region of sky that can be observed simultaneously, i.e., the field-of-view of the camera. Finally, the efficiency of observations also depends on factors like the number of clear nights at an astronomical site, the fraction of an observing night in which actual science data is taken, the fraction of time an instrument cannot be used due to technical problems, the stability of the instrumental set-up (which determines the time required for calibration measurements), and many other such aspects.

In the rest of this section some telescopes will be presented that are of special relevance to extragalactic astronomy and to which we will frequently refer throughout the course of this book.

1.3.1 Radio telescopes

With the exception of optical wavelengths, the Earth’s atmosphere is transparent only for very large wavelengths—radio waves. The radio window of the atmosphere is cut off towards lower frequencies, at about ν ∼ 10 MHz, because radiation of a wavelength larger than λ ∼ 30 m is reflected by the Earth’s ionosphere and therefore cannot reach the ground. Below λ ∼ 5 mm radiation is increasingly absorbed by oxygen and water vapor in the atmosphere, and below about λ ∼ 0. 3 mm ground-based observations are no longer possible.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig23_HTML.jpg

Fig. 1.23

“Jansky’s Merry-Go-Round”. By turning the structure in an azimuthal direction, a rough estimate of the position of radio sources could be obtained. Credit: NRAO/AUI

Mankind became aware of cosmic radio radiation—in the early 1930s—only when noise in radio antennas was found that would not vanish, no matter how quiet the device was made. In order to identify the source of this noise the AT&T Bell Labs hired Karl Jansky, who constructed a movable antenna called “Jansky’s Merry-Go-Round” (Fig. 1.23). After some months Jansky had identified, besides thunderstorms, one source of interference that rose and set every day. However, it did not follow the course of the Sun which was originally suspected to be the source. Rather, it followed the stars. Jansky finally discovered that the signal originated from the direction of the center of the Milky Way. He published his result in 1933, but this publication also marked the end of his career as the world’s first radio astronomer.

Inspired by Jansky’s discovery, Grote Reber was the first to carry out real astronomy with radio waves. When AT&T refused to employ him, he built his own radio “dish” in his garden, with a diameter of nearly 10 m. Between 1938 and 1943, Reber compiled the first sky maps in the radio domain. Besides strong radiation from the center of the Milky Way he also identified sources in Cygnus and in Cassiopeia. Through Reber’s research and publications radio astronomy became an accepted field of science after World War II.

The largest single-dish radio telescope is the Arecibo telescope , shown in Fig. 1.24. Due to its enormous area, and thus high sensitivity, this telescope, among other achievements, detected the first pulsar in a binary system, which is used as an important test laboratory for General Relativity (see Sect. 7.9). Also, the first extra-solar planet, in orbit around a pulsar, was discovered with the Arecibo telescope. For extragalactic astronomy Arecibo plays an important role in measuring the redshifts and line widths of spiral galaxies, both determined from the 21 cm emission line of neutral hydrogen (see Sect. 3.4).

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig24_HTML.jpg

Fig. 1.24

With a diameter of 305 m, the Arecibo telescope in Puerto Rico is the largest single-dish telescope in the world; it may also be known from the James Bond movie “GoldenEye”. The disadvantage of its construction is its lack of steerability. Tracking of sources is only possible within narrow limits by moving the secondary mirror. Credit: Courtesy of the NAIC-Arecibo Observatory, a facility of the NSF

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig25_HTML.jpg

Fig. 1.25

The world’s two largest fully steerable radio telescopes. Left: The 100 m telescope in Effelsberg. It was commissioned in 1972 and is used in the wavelength range from 3.5 mm to 35 cm. Eighteen different detector systems are necessary for this. Right: The Green Bank Telescope. It does not have a rotationally symmetric mirror; one axis has a diameter of 100 m and the other 110 m. Credit: Left: Max-Planck-Institut für Radioastronomie. Right: NRAO/AUI

The Effelsberg 100 m radio telescope of the Max-Planck-Institut für Radioastronomie was, for many years, the world’s largest fully steerable radio telescope, but since 2000 this title has been claimed by the new Green Bank Telescope (see Fig. 1.25) after the old one collapsed in 1988. With Effelsberg, for example, star formation regions can be investigated. Using molecular line spectroscopy, one can measure their densities and temperatures. Magnetic fields also play a role in star formation, though many details still need to be clarified. By measuring the polarized radio flux, Effelsberg has mapped the magnetic fields of numerous spiral galaxies. It is also used to map the neutral hydrogen distribution in the Galaxy, its neighborhood and galaxies in the nearby Universe, as well as for pulsar research. In addition, due to its huge collecting area Effelsberg plays an important role in interferometry at very long baselines (see below).

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig26_HTML.jpg

Fig. 1.26

The Very Large Array (VLA) in New Mexico consists of 27 antennas with a diameter of 25 m each that can be moved on rails. It is used in four different configurations that vary in the separation of the telescopes; switching configurations takes about 2 weeks. Credit: NRAO/AUI

Because of the long wavelength, the angular resolution of even large radio telescopes is fairly low, compared to optical telescopes. For this reason, radio astronomers soon began utilizing interferometric methods, where the signals obtained by several telescopes are correlated to get an interference pattern. One can then reconstruct the structure of the source from this pattern using Fourier transformation. With this method one gets the same angular resolution (though, of course, not the same sensitivity) as one would achieve with a single telescope of a diameter corresponding to the maximum pair separation of the individual telescopes used.

Following the first interferometric measurements in England (around 1960) and the construction of the large Westerbork Synthesis Radio Telescope in the Netherlands (around 1970), at the end of the 1970s the Very Large Array (VLA) in New Mexico (see Fig. 1.26) began operating. With the VLA one achieved an angular resolution in the radio domain comparable to that of optical telescopes at that time. For the first time, this allowed the combination of radio and optical images with the same resolution and thus the study of cosmic sources over a range of several clearly separated wavelength regimes. With the advent of the VLA radio astronomy experienced an enormous breakthrough, particularly in the study of AGNs. It became possible to examine the large extended jets of quasars and radio galaxies in detail (see Sect. 5.1.2). Other radio interferometers must also be mentioned here, such as the British MERLIN (Multi-Element Radio Linked Interferometer Network), where seven telescopes with a maximum separation of 230 km are combined.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig27_HTML.jpg

Fig. 1.27

The 30 m telescope on Pico Veleta was designed for observations in the millimeter range of the spectrum. This telescope, like all millimeter telescopes, is located on a mountain to minimize the column density of water in the atmosphere. Credit: MPIfR, IRAM

The VLA recently underwent a major upgrade, in particular by installing new receivers. By increasing their bandwidth relative to the older ones, and installing state-of-the-art electronics, the sensitivity of the eVLA is about ten times higher than the ‘old’ VLA. Together with the introduction of two new frequency bands, the eVLA now covers the full frequency range from 1 to 50 GHz.

In the radio domain it is also possible to interconnect completely independent and diverse antennas to form an interferometer, since one can record the amplitude and phases of the electromagnetic radiation. For example, in Very Long Baseline Interferometry (VLBI) radio telescopes on different continents are used simultaneously. These frequently also include Effelsberg and the VLA. In 1995 a system of ten identical 25 m antennas was set up in the USA, exclusively to be used in VLBI, the Very Long Baseline Array (VLBA). Angular resolutions of better than a milliarcsecond (mas) can be achieved with VLBI. Therefore, in extragalactic astronomy VLBI is particularly used in the study of AGNs. With VLBI we have learned a great deal about the central regions of AGNs, such as the occurrence of apparent superluminal velocities in these sources. A further increase in angular resolution with VLBI will be obtained with the Russian RadioAstron mission, launched in 2011; it is a 10-m radio telescope on a highly eccentric orbit, reaching distances from the Earth up to almost 400 000 km.

Fig. 1.28

Left: The James Clerk Maxwell Telescope (JCMT) on Mauna Kea has a 15 m dish. It is protected by the largest single piece of Gore-Tex, which has a transmissivity of 97 % at sub-millimeter wavelengths. Right: The Atacama Pathfinder Experiment (APEX) 12-m sub-millimeter telescope has been in operation since 2005. It is located at ∼ 5000 m altitude on the Chajnantor plateau in the Atacama Desert in Chile, the same location as that of the ALMA observatory. APEX observes at wavelengths between 200 μm and 1. 5 mm. Credit: Left: Joint Astronomy Center. Right: ESO/H.H. Heyer

Some of the radio telescopes described above are also capable of observing in the millimeter regime. For shorter wavelengths the surfaces of the antennas are typically too coarse, so that special telescopes are needed for wavelengths of 1 mm and below. The 30 m telescope on Pico Veleta (Fig. 1.27), with its exact surface shape, allows observations in the millimeter range. It is particularly used for molecular spectroscopy at these frequencies. Furthermore, important observations of high-redshift galaxies at 1. 2 mm have been made with this telescope using the bolometer camera MAMBO (Max-Planck Millimeter Bolometer). Similar observations are also conducted with the SCUBA (Sub-millimeter Common-User Bolometer Array) camera at the James Clerk Maxwell Telescope (JCMT; Fig. 1.28) on Mauna Kea, Hawaii, which observes at wavelengths between 3 and 0.3 mm. With the SCUBA-camera, operating at 850 μm (0. 85 mm), we can observe star-formation regions in distant galaxies for which the optical emission is nearly completely absorbed by dust in these sources. These dusty star-forming galaxies can be observed in the (sub-)millimeter regime of the electromagnetic spectrum even out to large redshifts, as will be discussed in Sect. 9.3.3. Recently, the SCUBA-2 camera replaced the original one; its much larger field-of-view (10⁴ pixels vs. the 37 of SCUBA) enhances its survey capability by about a factor of 1000.

An even better site for (sub-)mm astronomy than Mauna Kea is the Cerro Chajnantor, a 5100 m altitude plateau in the Chilean Atacama desert, due to the smaller column of water vapor. Since 2005, the Atacama Pathfinder Experiment (APEX) operates there. It is a 12 m telescope (Fig. 1.28), equipped with several highly sensitive instruments. One of them is a bolometer array specifically designed to observe the Sunyaev–Zeldovich effect in galaxy clusters (see Sect. 6.4.4).

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig29_HTML.jpg

Fig. 1.29

The Atacama Large Millimeter/sub-millimeter Array (ALMA) on the Chajnantor Plateau, located at an altitude of 5000 m in the Chilean Andes. This photo was taken in December 2012, 4 months prior to the ALMA inauguration. ALMA consists of 50 12-m antennas which can be reconfigurated, to yield different baselines for interferometry, and an additional compact array of 16 antennas with diameter of 7 and 12 m. Credit: Clem & Adri Bacri-Normier (wingsforscience.com)/ESO

The site also hosts the ALMA (Atacama Large Millimeter/sub-millimeter Array) observatory, one of the most ambitious projects of ground-based astronomy yet (Fig. 1.29). ALMA consists of 50 antennas with 12 m diameter each, which can be moved around to change the separation between the telescopes (up to 16 km), i.e., the baselines for interferometry. In addition, it has a compact array consisting of twelve 7-m and four 12-m antennas. ALMA will provide a giant jump in the capabilities of sub-millimeter astronomy, due to the large collecting area, the large baselines, as well as the sensitivity and bandwidth of the receivers. The construction of ALMA, which observes at wavelength longer than 300 μm, was completed in 2013, but even with the incomplete array, observations were conducted, showing the impressive capabilities of this new observatory. ALMA is the result of a global cooperation between North America, Europe and East Asia, together with the host country Chile.

To measure the tiny temperature fluctuations of the cosmic microwave background radiation one needs extremely stable observing conditions and low-noise detectors. In order to avoid the thermal radiation of the atmosphere as much as possible, balloons and satellites were constructed to operate instruments at very high altitude or in space. The American COBE (Cosmic Background Explorer) satellite measured the anisotropies of the CMB for the first time, at wavelengths of a few millimeters. In addition, the frequency spectrum of the CMB was precisely measured with instruments on COBE. The WMAP (Wilkinson Microwave Anisotropy Probe) satellite obtained, like COBE, a map of the full sky in the microwave regime, but at a significantly improved angular resolution and sensitivity. The first results from WMAP, published in February 2003, were an enormously important milestone for cosmology, as will be discussed in Sect. 8.6.5. WMAP observed for a total of 9 years, with a final data release at the end of 2012. The new European Planck satellite was launched in May 2009, together with the Herschel satellite. It has a much larger frequency coverage than WMAP, from 30 to 850 GHz (thus covering both sides of the peak of the CMB spectrum), a higher sensitivity, and a better angular resolution. First cosmological results from Planck were released in March 2013 (see Sect. 8.6.6). Besides observing the CMB these missions (see Fig. 1.30) are also of great importance for millimeter astronomy; these satellites not only measure the cosmic background radiation but of course also the microwave radiation of the Milky Way and of other galaxies.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig30_HTML.jpg

Fig. 1.30

Left: Artist’s conception of the Cosmic Background Explorer (COBE) spacecraft, launched in 1989 into an Earth orbit, which discovered the temperature fluctuations in the cosmic microwave background. Middle: The Wilkinson Microwave Anisotropy Probe (WMAP) satellite was launched in 2001 and observed the microwave sky for 9 years. Right: The Planck satellite, launched in 2009 into an orbit at L2 (as for WMAP), has yielded the widest frequency range and highest angular resolution map of the full microwave sky yet. Results from these three satellite missions will be described in Sect. 8.6. Credit: Left: NASA/COBE Science Team. Middle: NASA/WMAP Science Team. Right: ESA (Image by AOES Medialab)

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig31_HTML.jpg

Fig. 1.31

The South Pole Telescope, a 10 m dish located at 2800 m altitude on the Antarctic Plateau. Its off-axis design and shielding minimize the effects from ground spill-over and scattering off the telescope optics. Credit: Glenn Grant, National Science Foundation

Beside space, the Antarctica offers excellent observing conditions in the millimeter regime; the very low temperatures and high altitude (the Antarctic Plateau lies at an altitude of 2800 m) yields a particularly low column density of water vapor. Together with the fact that the Sun does not rise and set every day, the atmospheric conditions are also very stable. Therefore, several astronomical projects are conducted, or are being planned, in the Antarctica. One of them is the South Pole Telescope (SPT, see Fig. 1.31), a 10 m telescope with a one square degree field-of-view. Its main scientific activity is a survey of clusters of galaxies through their Sunyaev–Zeldovich effect caused by the hot intracluster gas, as well as studying the CMB fluctuations at small angular scales.

1.3.2 Infrared telescopes

In the wavelength range 1 μm ≲ λ ≲ 300 μm, observations from the Earth’s surface are always subject to very difficult conditions, if they are possible at all. The atmosphere has some windows in the near-infrared (NIR, 1 μm ≲ λ ≲ 2. 4 μm) which render ground-based observations possible. In the mid-infrared (MIR, 2. 4 μm ≲ λ ≲ 20 μm) and far-infrared (FIR, 20 μm ≲ λ ≲ 300 μm) regimes, observations need to be carried out from outside the atmosphere, i.e., using balloons, high-flying airplanes, or satellites. The instruments have to be cooled to very low temperatures, otherwise their own thermal radiation would outshine any signal.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig32_HTML.jpg

Fig. 1.32

The left-hand picture shows an artist’s impression of IRAS in orbit. The project was a cooperation of the Netherlands, the USA, and Great Britain. IRAS was launched in 1983 and operated for 10 months; after that the supply of liquid helium, needed to cool the detectors, was exhausted. During this time IRAS scanned 96 % of the sky at four wavelengths. The ISO satellite, shown on the right, was an ESA project and observed between 1995 and 1998. Compared to IRAS it covered a larger wavelength range, had a better angular resolution and a thousand times higher sensitivity. Credit: NASA’s Infrared Astrophysics Data Center, Caltech/JPL; ESA

The first noteworthy observations in the far-infrared were made by the Kuiper Airborne Observatory (KAO), an airplane equipped with a 91 cm mirror which operated at altitudes up to 15 km. However, the breakthrough for IR astronomy had to wait until the launch of IRAS, the InfraRed Astronomical Satellite (Fig. 1.32). In 1983, with its 60 cm telescope, IRAS compiled the first IR map of the sky at 12, 25, 60, and 100 μm, at an angular resolution of 30″ (2′) at 12 μm (100 μm). It discovered about a quarter of a million point sources as well as about 20 000 extended sources. The positional accuracy for point sources of better than ∼ 20″ allowed an identification of these sources at optical wavelengths. Arguably the most important discovery by IRAS was the identification of galaxies which emit the major fraction of their energy in the FIR part of the spectrum. These sources, often called IRAS galaxies, have a very high star-formation rate where the UV light of the young stars is absorbed by dust and then re-emitted as thermal radiation in the FIR. IRAS discovered about 75 000 of these so-called ultra-luminous IR galaxies (ULIRGs) .

In contrast to the IRAS mission with its prime task of mapping the full sky, the Infrared Space Observatory ISO (Fig. 1.32) was dedicated to observations of selected objects and sky regions in a wavelength range of 2. 5–240 μm. Although the telescope had the same diameter as IRAS, its angular resolution at 12 μm was about a hundred times better than that of IRAS, since the latter was limited by the size of the detector elements. The sensitivity of ISO topped that of IRAS by a factor ∼ 1000. ISO carried four instruments: two cameras and two spectrographs. Among the most important results from ISO in the extragalactic domain are the spatially-resolved observations of the dust-enshrouded star formation regions of ULIRGs.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig33_HTML.jpg

Fig. 1.33

Left: The Spitzer Space Telescope, launched in 2003. Right: The Herschel Space Observatory, launched in 2009 together with the Planck satellite. Herschel is equipped with a 3.5-m mirror and three instruments, observing between 60 and 650 μm. Credit: Left: NASA/JPL-Caltech. Right: Max-Planck-Institut für Astronomie/European Space Agency

In 2003 a new infrared satellite was launched (the Spitzer Space Telescope , see Fig. 1.33) with capabilities that by far outperform those of ISO. With its 85 cm telescope, Spitzer observes at wavelengths between 3.6 and 160 μm. Its Infrared Array Camera (IRAC) takes images at 3.6, 4.5, 5.8 and 8.0 μm simultaneously, and has a field of view of 5.^′2 × 5.^′2 and 256 × 256 pixels, significantly more than the 32 × 32 pixels of ISOCAM on ISO that had a comparable wavelength coverage. The Multiband Imaging Photometer for Spitzer (MIPS) operated at 24, 70 and 160 μm, and the Infrared Spectrograph (IRS) was a spectrometer covering the wavelength regime between 5.3 and 40 μm, with a spectral resolution of about $R =\lambda /\varDelta \lambda \sim 100$ . In 2009, the helium of the cooler was exhausted, which rendered observations at longer wavelength impossible. Since then, the Spitzer Warm Mission continues to observe in the two short wavelengths of IRAC. Spitzer has made important contributions to all fields of astronomy, including the first direct detection of light from an extrasolar planet. Spitzer has provided information about the thermal dust emission of many nearby and distant galaxies, and thus of their star-formation activity.

In May 2009, the Herschel Space Observatory (Fig. 1.33) was launched, together with the Planck satellite, into an L2 orbit.¹⁰ With its 3. 5 m diameter, it was the largest astronomical telescope in space up to then. In total, the satellite had a diameter of 4 m, a height of 7.5 m, and weighs 3.4 tons. Herschel covered the spectral range from far-infrared to sub-millimeter wavelengths (55 μm to 670 μm), using three instruments: (1) the Photodetector Array Camera and Spectrometer (PACS), a camera and a low- to medium-resolution spectrometer for wavelengths up to about 205 μm, (2) the Spectral and Photometric Imaging REceiver (SPIRE) operated at three bands longward of λ = 200 μm, and (3) the Heterodyne Instrument for the Far Infrared (HIFI), a high-resolution spectrometer operating at λ ≥ 150 μm. The large aperture, the sensitivity of the instruments and the wide frequency coverage made Herschel the by far most powerful FIR observatory yet. Herschel observed until end of April 2013, when it ran out of coolant.

Following the IRAS satellite, two more recent missions conducted all-sky surveys in the infrared. The Japanese satellite AKARI, launched in February 2006, mapped the entire sky at six wavelengths between 9 and 160 μm, and thus produced the first all-sky survey in the infrared after that of IRAS. The source catalogs extracted from this survey were publicly released in March 2010 and contain more than 1.3 million sources. The AKARI survey is about ten times more sensitive than IRAS, and can locate the position of a point source with an accuracy of better than 2″ at the shorter wavelengths. Given the scientific impact of the IRAS survey, one can easily foresee that of the new all-sky results. In addition, AKARI carried out pointed observations. After its liquid helium ran out, only observations at shorter wavelengths could be conducted. The Wide-field Infrared Survey Explorer (WISE) was launched in December 2009 and mapped the full sky at four wavebands between 3 and 25 μm, with an angular resolution between 6″ and 12″, and a more than hundred times larger sensitivity than IRAS. The resulting catalog from WISE contains positional and photometric information for over 563 million objects.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig34_HTML.jpg

Fig. 1.34

Stratospheric Observatory for Infrared Astronomy (SOFIA), a 2.5-m telescope onboard a refurbished Boeing 747 aircraft, designed to fly at 12 km altitude. A huge door was installed which opens at the high cruising altitude to allow for astronomical observations—a substantial challenge for the structural stability of the aircraft. Regular observations with SOFIA started in 2010. Credit: NASA/Jim Ross

Another kind of infrared observatory is the Stratospheric Observatory for Infrared Astronomy (SOFIA), a 2. 5 m telescope mounted onboard a refurbished Boeing 747 (see Fig. 1.34). Flying at an altitude of 12 km, the observations happen above most of the Earth atmosphere. SOFIA, a US-German collaboration, has the advantage that technical developments in instrumentation can be implemented during the duration of the project.

1.3.3 Optical telescopes

The atmosphere is largely transparent in the optical part of the electromagnetic spectrum (0. 3 μm ≲ λ ≲ 1 μm), and thus we are able to conduct observations from the ground. Since for the atmospheric windows in the NIR one normally uses the same telescopes as for optical astronomy, we will not distinguish between these two ranges here. Despite the tremendous progress made in all wavelength regimes, the optical and NIR spectral region is arguably the single most informative for astronomy, for a combination of two reasons: first, most of the radiation emitted by galaxies is light from stars which has its maximum in the optical regime or, in case of star formation obscured by dust, in the FIR regime, and second, the efficiency of optical detectors is highest, much more than those of infrared detectors. Together, these two points cause the observable number density of sources on the sky to be highest for optical observations.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig35_HTML.jpg

Fig. 1.35

Telescopes at the summit of Mauna Kea, Hawaii, at an altitude of 4200 m. The cylindrical dome to the left and below the center of the image contains the Subaru 8-m telescope; just behind it are the two 10-m Keck telescopes. The two large domes at the back house the Canada-France-Hawaii telescope (CFHT, 3.6 m) and the 8-m Gemini North. The telescope at the lower right is the 15-m James Clerk Maxwell sub-millimeter telescope (JCMT). Credit: R. Wainscoat, University of Hawaii

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig36_HTML.jpg

Fig. 1.36

The La Silla Observatory of ESO in Chile. On the peak in the middle, one can see the New Technology Telescope (NTT), a 3.5-m prototype of the VLT. The silvery shining dome to its left is the MPG/ESO 2.2-m telescope whose Wide Field Imager, a 8096² pixel camera with a 0.5^∘ field-of-view, has been a very competitive instrument in the past decade. The picture was taken from the location of the 3.6-m telescope, the largest one on La Silla. Credit: European Southern Observatory

Although optical astronomy has been pursued for many decades, it has evolved very rapidly in recent years. This is linked to a large number of technical achievements. A good illustration of this is the 10-m Keck telescope which was put into operation in 1993; this was the first optical telescope with a mirror diameter of more than 6 m. Constructing telescopes of this size became possible by the development of active optics, a method to control the surface of the mirror. A mirror of this size no longer has a stable shape but is affected, e.g., by gravitational deformation as the telescope is steered. Such a large mirror, in order to have a stable shape, would need to have a thickness comparable with its diameter, and producing and operating such mirrors is infeasible. It was also realized that part of the air turbulence that generates the seeing is caused by the telescope and its dome itself. By improving the thermal condition of telescopes and dome structures a reduction of the seeing could be achieved. The aforementioned replacement of photographic plates by CCDs, together with improvements to the latter, resulted in a vastly enhanced quantum efficiency of ∼ 70 % (at maximum even more than 90 %), barely leaving room for further improvements.

The throughput of optical telescopes has been immensely increased by designing wide-field CCD cameras, the largest of which is currently that of PanSTARRS, with ∼ 1. 4 × 10⁹ pixels, covering ∼ 7 deg². Furthermore, multi-object spectrographs have been built which allow us to observe the spectra of a large number of objects simultaneously. The largest of them are able to get spectra for several hundred sources in one exposure. Finally, with the Hubble Space Telescope the angular resolution of optical observations was increased by a factor of ∼ 10 compared to the best sites on Earth. Further developments that will revolutionize the field even more, such as interferometry in the near IR/optical and adaptive optics, have recently been added to these achievements.

Currently, 13 optical telescopes of the 4-m class exist worldwide. They differ mainly in their location and their instrumentation. For example, the Canada-France-Hawaii Telescope (CFHT) on Mauna Kea (Fig. 1.35) has been a leader in wide-field photometry for many years, due to its extraordinarily good seeing. This is again emphasized by the installation of Megacam, a one square degree camera with 18 000 × 18 000 pixels. The Anglo-Australian Telescope (AAT) in Australia, in contrast, has distinctly worse seeing and has therefore specialized, among other things, in multi-object spectroscopy, for which the 2dF (two degree field) instrument was constructed. Most of these telescopes are also equipped with NIR instruments. The New Technology Telescope (NTT, see Fig. 1.36) made its largest contributions with its SOFI camera, a near-IR instrument with a large field-of-view of ∼ 5′ × 5′ and an excellent image quality.

Hubble Space Telescope. To avoid the greatest problem in ground-based optical astronomy, the rocket scientist Hermann Oberth speculated already in the 1920s about telescopes in space which would not be affected by the influence of the Earth’s atmosphere. In 1946 the astronomer Lyman Spitzer took up this issue again and discussed the possibilities for the realization of such a project.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig37_HTML.jpg

Fig. 1.37

Left: The HST mounted on the manipulator arm of the Space Shuttle during one of the servicing missions. Right: The Hubble Deep Field (North) was observed in December 1995 and the data released 1 month later. To compile this multicolor image, which at that time was the deepest image of the sky, images from four different filters were combined. The geometry of the field is due to the arrangement of the CCD detector arrays in the Wide Field and Planetary Camera 2, where one of the four chips is smaller than the other three and due to a smaller pixel scale. Credit: STScI, NASA

Shortly after NASA was founded in 1958, the construction of a large telescope in space was declared a long-term goal. After several feasibility studies and ESA’s agreement to join the project, the HST was finally built. However, the launch was delayed by the explosion of the space shuttle ‘Challenger’ in 1986, so that it did not take place until April 24, 1990. An unpleasant surprise came as soon as the first images were taken: it was found that the 2.4 m main mirror was ground into the wrong shape. This problem was remedied in December 1993 during the first “servicing mission” (a series of Space Shuttle missions to the HST; see Fig. 1.37), when a correction lens was installed. After this, the HST could observe at its diffraction limit, i.e., with an angular resolution of better than 0.^″1, and became one of the most successful and best-known scientific instruments. In fact, the HST was far more important for extragalactic astronomy than anticipated before its launch, due to the fact that distant galaxies turned out to be much more compact than their local counterparts, and thus have a higher surface brightness. A main contributor to the success (and cost) of HST was a series of five visits to the telescope, where not only parts that failed (e.g., gyroscopes) were replaced and thus the lifetime of the observatory extended to well over 20 years, but also new, increasingly more powerful instruments were installed.

After the final servicing mission SM-4 in 2009, the HST carries a powerful suite of scientific instruments. The ACS (Advanced Camera for Surveys) has a field-of-view of 3.^′4 × 3.^′4 and a pixel scale of 0.^″05. It was installed on Hubble in 2002, had to be shut down after a malfunction in 2007, but after the repair in 2009, it continues to be a powerful workhorse for high-resolution imaging in the optical wavebands. Several imaging surveys have been carried out with ACS, some of which will be considered in some detail in later chapters. Newly installed during SM-4 was the Wide Field Camera 3 (WFC3) , replacing the WFPC2 (Wide Field and Planetary Camera), which has been the most active instrument of HST since then. WFC3 covers a very broad range of wavebands, distributed over two different ‘channels’. The UVIS channel operates between 0. 2 and 1 μm with a 2.^′6 field of view, whereas the NIR channel operates between 0. 85 and 1. 7 μm and has a ∼ 2′ field. This field is considerably larger than that of the other NIR instrument on HST, the NICMOS (Near Infrared Camera and Multi Object Spectrograph) instrument. Already in its first months of operation, WFC3 led to great progress in the field of very high redshift galaxies, by increasing the number of known galaxies with redshifts z ≥ 6 by a large factor. The SM-4 mission also brought the Cosmic Origins Spectrograph (COS) to HST, operating in the UV region of the spectrum. The spectroscopic capability of HST in the UV-range, unavailable from the ground, was increased with COS by a large factor compared to the other UV instrument STIS (Space Telescope Imaging Spectrograph).

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig38_HTML.jpg

Fig. 1.38

The two Keck telescopes on Mauna Kea. With Keck I the era of large telescopes was heralded in 1993. Credit: R. Wainscoat, University of Hawaii

HST has provided important insights into our Solar System and the formation of stars, but it has achieved milestones in extragalactic astronomy. With HST observations of the nucleus of M87 (Fig. 1.11), one derived from the Doppler shift of the gas emission that the center of this galaxy contains a black hole of 2 billion Solar masses. HST has also proven that black holes exist in other galaxies and AGNs. The enormously improved angular resolution has allowed us to study galaxies to a hitherto unknown level of detail.

Arguably the most important contribution of the HST to extragalactic astronomy are the Hubble Deep Fields. Scientists managed to convince Robert Williams, then director of the Space Telescope Science Institute, to use the HST to take a very deep image in an empty region of the sky, a field with (nearly) no foreground stars and without any known clusters of galaxies. At that time it was not clear whether anything interesting at all would result from these observations. Using the observing time that is allocated to the Director, the ‘director discretionary time’, HST was pointed at such a field in the Big Dipper, taking data for 10 days December 1995. The outcome was the Hubble Deep Field North (HDFN), one of the most important astronomical data sets, displayed in Fig. 1.37. From the HDFN and its southern counterpart, the HDFS, one obtains information about the early states of galaxies and their evolution. One of the first conclusions was that most of the early galaxies are very small and classified as irregulars. In 2002, the Hubble Ultra Deep Field (HUDF) was observed with the then newly installed ACS camera. Not only did it cover about twice the area of the HDFN but it was even deeper, by about one magnitude, owing to the higher sensitivity of ACS compared to WFPC2. We will discuss some of the imaging surveys of HST in more detail in Sect. 9.2.1.

Large Telescopes. For more than 40 years the 5-m telescope on Mt. Palomar was the largest telescope in the western world—the Russian 6-m telescope suffered from major problems from the outset. 1993 saw the birth of a new class of telescopes, of which the two Keck telescopes (see Fig. 1.38) were the first, each with a mirror diameter of 10 m.¹¹

The site of the two Kecks at the summit of Mauna Kea (see Fig. 1.35) provides ideal observing conditions for many nights per year. This summit is now home to several large telescopes. The Japanese Subaru telescope and Gemini North are also located here, as well as the aforementioned CFHT and JCMT. The significant increase in sensitivity obtained by Keck, especially in spectroscopy, permitted completely new insights, for instance through absorption line spectroscopy of quasars. Keck was also essential for the spectroscopic verification of innumerable galaxies of redshift z ≳ 3, which are normally so dim that they cannot be examined with smaller telescopes.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig39_HTML.jpg

Fig. 1.39

The Paranal observatory after completion. The four large domes host one of the VLTs each. The smaller dome, seen to the left of the rightmost VLT, hosts the VLT Survey Telescope (VST), a dedicated 2.6 m telescope equipped with the wide-field optical camera OmegaCAM. The four much smaller domes host 1.5 m auxiliary telescopes, which are used in combination with the VLTs for optical interferometry. In the background, the VISTA (Visible and Infrared Survey Telescope for Astronomy) telescope is seen, equipped with a wide-field near-infrared camera. The buildings in front contain the control room for the telescopes and instruments, and a guest house for observers. Before the observatory was constructed, the top of the mountain was flattened to get a leveled surface of diameter ∼ 300 m, large enough to accommodate the telescopes and the facilities used for optical interferometry (VLTI). Credit: European Southern Observatory/G.Hüdepohl

The largest ground-based telescope project to date was the construction of the Very Large Telescope (VLT) of the European Southern Observatory (ESO), consisting of four telescopes each with a diameter of 8.2 m. ESO already operated the La Silla Observatory in Chile (see Fig. 1.36), but a better location was found for the VLT, the Cerro Paranal (at an altitude of 2600 m). This mountain is located in the Atacama desert, one of the driest regions on Earth. To build the telescopes on the mountain a substantial part of the mountain top first had to be cut off (Fig. 1.39).

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig40_HTML.jpg

Fig. 1.40

The segmented mirror of the Gran Telescopio Canarias (GTC) at the Roque de los Muchachos Observatory on La Palma, inside its support structure. The hexagonal elements can clearly be seen. At an altitude of 2400 m, this observatory is the best astronomical site in Europe. Credit: P. Schneider, Argelander-Institut für Astronomie, Universität Bonn

In contrast to the Keck telescopes and the Gran Telescopio Canarias (GTC; see Fig. 1.40), which have a primary mirror that is segmented into 36 hexagonal elements, the mirrors of the VLT are monolithic, i.e., they consist of a single piece. However, they are very thin compared to the 5-m mirror on Mt. Palomar, far too thin to be intrinsically stable against gravity and other effects such as thermal deformations. Therefore, as for the Kecks, the shape of the mirrors has to be controlled electronically (see Fig. 1.41). The monolithic structure of the VLT mirrors yields a better image quality than that of the Keck telescopes, resulting in an appreciably simpler point-spread function.¹²

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig41_HTML.jpg

Fig. 1.41

The active optics system at the VLT. Each mirror is supported at 150 points; at these points, the mirror is adjusted to correct for deformations. The primary mirror is always shaped such that the light is focused in an optimal way, with its form being corrected for the changing gravitational forces when the telescope changes the pointing direction. In adaptive optics, in contrast to active optics, the wave front is controlled: the mirrors are deformed with high frequencies in such a way that the wave front is as planar as possible after passing through the optical system. In this way one can correct for the permanently changing atmospheric conditions and achieve images at diffraction-limited resolution, though only across a fairly small region of the focal plane. Credit: European Southern Observatory

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig42_HTML.jpg

Fig. 1.42

One of the four Unit Telescopes of the VLT on the right, together with one of the auxiliary telescopes at the left. These auxiliary telescopes can be moved to allow for variable baseline configurations in optical interferometry. Credit: Iztok Boncina/European Southern Observatory

Each of the four telescopes has three accessible foci; this way, 12 different instruments can be installed at the VLT at any time. Switching between the three instruments is done with a deflection mirror. The permanent installation of the instruments allows their stable operation.

The VLT (Fig. 1.42) also marked the beginning of a new form of ground-based observation with large optical telescopes. Whereas until recently an astronomer proposing an observation was assigned a certain number and dates of nights in which she could observe with the telescope, the VLT is mainly operated in the so-called service mode. The observations are performed by local astronomers according to detailed specifications that must be provided by the principal investigator of the observing program, and the data are then transmitted to the astronomer at her home institution. A significant advantage of this procedure is that one can better account for special requirements for observing conditions. For example, observations that require very good seeing can be carried out during the appropriate atmospheric conditions. With service observing the chances of getting a useful data set are increased. More than half of the observations with the VLT are performed in service mode.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig43_HTML.jpg

Fig. 1.43

The principle of an integral field unit (IFU) based on image slicing is illustrated. In a first step, the image of an object is ‘sliced’, using an arrangement of mirrors. The light of each slice is then send through a long-slit spectrograph, so that a spectrum from each pixel of a slice is obtained. Hence, in this way one obtains a spectrum of each pixel element in the area of the extended object. Adding up the light from all wavelengths in a pixel then yields the original image of the object. By weighting the contributions from the various wavelengths by an appropriate filter function, images in different wavebands can be obtained. Using lines in the spectrum of each image element, the corresponding Doppler shift can be obtained and a two-dimensional velocity field of the object (such as a rotation curve) can be reconstructed. Credit: European Southern Observatory

Another aspect of service observing is that the astronomer does not have to make the long journey, at the expense of also missing out on the adventure and experience of observing. As mentioned before, the best astronomical sites are at quite remote places, and traveling to such an observatory is a physical experience. A trip from, e.g., Bonn to the Paranal starts with a train ride to Düsseldorf airport, a flight from there to Paris or Madrid, followed by a more than 12 h flight to Santiago de Chile. From there, another 2 h flight towards the Northern coast of Chile takes one to the city of Antofagasta. The final part of the journey is a 2 h car ride through the desert—literally, the last plant one sees in the outskirts of Antofagasta. And finally, from the distance, one can see the four majestic domes on the top of a mountain, the final destination of the journey.

Adaptive optics, integral field spectroscopy, and interferometry. New technical innovations in astronomy lead to improved data products; two examples should be mentioned here. One is adaptive optics, a technique to obtain an angular resolution approaching the diffraction limit of the telescope. This is usually not the case, as turbulence in the atmosphere leads to a blurring of an image. In adaptive optics, one accounts for this by deforming the mirror at a high frequency, as to counteract the changing image position on the sky due to the turbulence. The wavefront of the incoming light is controlled by observing a bright reference source located closely on the sky to the target of interest. The motion of the reference source on the CCD then yields the necessary information about the wavefront deformation, which thus can be corrected for. In many cases, the source to be observed does not have a bright source close-by. One way to use adaptive optics in this situation is to generate an artificial source on the sky, by pointing a laser upwards. By tuning the laser to a wavelength of 5892 Å, sodium atoms in the upper atmosphere at ∼ 90 km altitude are excited and re-emit the light. In this way, an artificial light source (called laser guide star) is created which is viewed through the same atmosphere as the source of interest.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig44_HTML.jpg

Fig. 1.44

The Large Binocular Telescope (LBT) on Mount Graham in Arizona. The two 8.4 m primary mirrors are mounted on a single structure, share one gigantic dome, and has been built specifically for optical interferometry. Credit: Large Binocular Telescope Observatory; courtesy NASA/JPL-Caltech

Another innovative technique, called integral field spectroscopy , allows one to obtain the spectral energy distribution for different regions of an extended source, pixel by pixel. Several different methods for this are used; a particular one, based on image slicing by an arrangement of mirrors, is explained in more detail in Fig. 1.43.

Optical interferometry is also reaching a state of maturity. Like in radio astronomy, the light received from several telescopes can be combined to obtain a higher-resolution image of a source. In contrast to VLBI techniques, the light at the different telescopes is not recorded and correlated afterwards; instead, the light beams from the different telescopes need to be combined directly. Below the plateau of the Paranal observatory is a large tunnel system where the light beams of the VLTs and/or the auxiliary telescopes are combined. The two Keck telescopes were built on a common structure to enable interferometry. The latest development in optical interferometry is the Large Binocular Telescope (LBT) , where the two mirrors are mounted on a single structure (see Fig. 1.44).

1.3.4 UV telescopes

Radiation with a wavelength shorter than λ ≲ 0. 3 μm = 3000 Å cannot penetrate the Earth’s atmosphere but is instead absorbed by the ozone layer, whereas radiation at wavelengths below 912 Å is absorbed by neutral hydrogen in the interstellar medium. The range between these two wave-lengths is the UV part of the spectrum, in which observation is only possible from space.

The Copernicus satellite (also known as the Orbiting Astronomical Observatory 3, OAO-3) was the first long-term orbital mission designed to observe high-resolution spectra at ultraviolet wavelengths. In addition, the satellite contained an X-ray detector. Launched on August 21, 1972, it obtained UV spectra of 551 sources until its decommissioning in 1981. Among the achievements of the Copernicus mission are the first detection of interstellar molecular hydrogen H₂ and of CO, and measurements of the composition of the interstellar medium as well as of the distribution of Ovi, i.e., five-time ionized oxygen.

The IUE (International Ultraviolet Explorer) operated between 1978 and 1996 and proved to be a remarkably productive observatory. During its 18 years of operation more than 10⁵ spectra of galactic and extragalactic sources were obtained. In particular, the IUE contributed substantially to our knowledge of AGN.

The HST, with its much larger aperture, marks the next substantial step in UV astronomy. Many new insights were gained with the HST, especially through spectroscopy of quasars in the UV, insights into both the quasars themselves and, through the absorption lines in their spectra, into the intergalactic medium along the line-of-sight towards the sources. In 1999 the FUSE (Far Ultraviolet Spectroscopic Explorer) satellite was launched. From UV spectroscopy of absorption lines in luminous quasars this satellite provided us with a plethora of information on the state and chemical composition of the intergalactic medium.

While the majority of observations with UV satellites were dedicated to high-resolution spectroscopy of stars and AGNs, the prime purpose of the Galaxy Evolution Explorer (GALEX) satellite mission (Fig. 1.45), launched in 2003, was to compile extended photometric surveys. GALEX observed at wavelengths 1350 Å ≲ λ ≲ 2830 Å and performed a variety of surveys. Amongst them are the All-Sky Imaging Survey, covering 26 000 square degrees of the extragalactic sky, the Medium Imaging survey, with considerably deeper imaging of 1000 square degrees in field where spectroscopic redshift surveys (like SDSS) were available, and the Deep Imaging Survey of 80 square degrees and an exposure time of about 8 h per field. Several more specialized surveys were carried out, including one on nearby galaxies and on the Milky Way. In addition, GALEX performed several spectroscopic surveys. The results from GALEX are of great importance, especially for the study of the star-formation rate in nearby and distant galaxies. In June 2013, the operation of GALEX was terminated.

1.3.5 X-ray telescopes

As mentioned before, interstellar gas absorbs radiation at wavelengths shortward of 912 Å, the so-called Lyman edge. This corresponds to the ionization energy of hydrogen in its ground state, which is 13. 6 eV. Only at energies about ten times this value does the ISM become transparent again¹³ and this denotes the low-energy limit of the domain of X-ray astronomy. Typically, X-ray astronomers do not measure the frequency of light in Hertz (or the wavelength in μm), but instead photons are characterized by their energy, measured in electron volts (eV).

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig45_HTML.jpg

Fig. 1.45

The Galaxy Evolution Explorer GALEX was launched in 2003, and decommissioned after 10 years of astronomical observations in June 2013. GALEX had a 50 cm mirror and operated in the UV spectral range. Credit: NASA/JPL-Caltech

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig46_HTML.jpg

Fig. 1.46

Principle of a Wolter telescope for X-ray astronomy. X-rays are reflected by a metal surface only if the angle of incidence is very small, i.e., if the photon direction is almost parallel (within ∼ 2^∘) to the metal surface. This principle can be employed for X-ray mirrors, by constructing a tube, consisting of a paraboloidal shaped surface combined with a hyperboloidal one in a way that X-ray photons are focussed. The effective area of such a mirror is very small, as only a small annular region of the photon beam hits this mirror, due to the small projected surface. The X-ray telescopes on XMM and Chandra are therefore composed of nested layers of such surfaces, each one acting like a focusing surface by itself, thereby multiplying the effective area. The figure illustrates the mirror of the Chandra observatory. Source: Wikipedia

The birth of X-ray astronomy was in the 1960s. Rocket and balloon-mounted telescopes which were originally only supposed to observe the Sun in X-rays also received signals from outside the Solar System. UHURU (the Swahili word for ‘freedom’) was the first satellite to observe exclusively the cosmic X-ray radiation and compiled the first X-ray map of the sky, discovering about 340 sources. This catalog of point sources was expanded in several follow-up missions, especially by NASA’s High Energy Astrophysical Observatory (HEAO-1) which also detected a diffuse X-ray background radiation. On HEAO-2, also known as the Einstein satellite, the first Wolter telescope (see Fig. 1.46) was used for imaging, increasing the sensitivity by a factor of nearly a thousand compared to earlier missions. The Einstein observatory also marked a revolution in X-ray astronomy because of its high angular resolution, about 2″ in the range of 0.1–4 keV. Among the great discoveries of the Einstein satellite is the X-ray emission of many clusters of galaxies that traces the presence of hot gas in the space between the cluster galaxies. The total mass of this gas significantly exceeds the mass of the stars in the cluster galaxies and therefore represents the main contribution to the baryonic content of clusters.

Fig. 1.47

Left: ROSAT, a German-US-British cooperation, observed from 1990 to 1999 in the energy range between 0.1 and 2.5 keV (soft X-ray). Upper right: Chandra was launched in July 1999. The energy range of its instruments lies between 0.1 and 10 keV. Its highly elliptical orbit permits long uninterrupted exposures. Lower right: XMM-Newton was launched in December 1999 and has since been in operation; it is the most successful ESA mission up to today, as measured from the number of publications resulting from its data. Observations are carried out with three telescopes at energies between 0.1 and 15 keV. Credit: Left: Max-Planck-Intitut für extraterrestrische Forschung (MPE) & DLR. Top right: NASA/CXC/SAO. Bottom right: European Space Agency

The next major step in X-ray astronomy was ROSAT (ROentgen SATellite; Fig. 1.47), launched in 1990. During the first 6 months of its 9-year mission ROSAT produced an all-sky map at far higher resolution than UHURU; this is called the ROSAT All Sky Survey. More than 10⁵ individual sources were detected in this survey, the majority of them being AGNs. In the subsequent period of pointed observations ROSAT examined, among other types of sources, clusters of galaxies and AGNs. One of its instruments (the Position Sensitive Proportional Counter PSPC) provided spectral information in the range between 0.1 and 2.4 keV at an angular resolution of ∼ 20″, while the other (High-Resolution Instrument HRI) instrument had a much better angular resolution ( ∼ 3″) but did not provide any spectral information. The Japanese X-ray satellite ASCA (Advanced Satellite for Cosmology and Astrophysics), launched in 1993, was able to observe in a significantly higher energy range of 0.5–12 keV and provided spectra of higher energy resolution, though at reduced angular resolution.

Since 1999 two new powerful satellites are in operation: NASA’s Chandra observatory and ESA’s XMM-Newton (X-ray Multi-Mirror Mission; see Fig. 1.47). Both have a large photon-collecting area and a high angular resolution, and they also set new standards in X-ray spectroscopy. Compared to ROSAT, the energy range accessible with these two satellites is larger, from 0.1 to ∼ 10 keV. The angular resolution of Chandra is about 0.^″5 and thus, for the first time, comparable to that of optical telescopes. This high angular resolution led to major discoveries in the early years of operation. For instance, well-defined sharp structures in the X-ray emission from gas in clusters of galaxies were discovered, as well as X-ray radiation from the jets of AGNs which had been previously observed in the radio. Furthermore, Chandra discovered a class of X-ray sources, termed Ultra-luminous Compact X-ray Sources (ULXs), in which we may be observing the formation of black holes (Sect. 9.3.1). XMM-Newton has a larger sensitivity compared to Chandra, however at a somewhat smaller angular resolution. Among the most important observations of XMM-Newton are the spectroscopy of AGNs and of clusters of galaxies.

Fig. 1.48

The left image shows the Compton Gamma Ray Observatory (CGRO) mounted on the Space Shuttle manipulator arm. This NASA satellite carried out observations between 1991 and 2000. It was finally shut down after a gyroscope failed, and it burned up in the Earth’s atmosphere in a controlled re-entry. ESA’s Integral observatory, in operation since 2002, is shown on the right. Credit: Left: NASA. Right: ESA

With Suzaku , a Japanese satellite launched in July 2005, a new X-ray observatory became available. One of its advantages compared to Chandra and XMM-Newton is its low orbit around the Earth, which keeps it inside the Earth magnetosphere and thus shields it from most of the Solar wind. Therefore, the radiation background of Suzaku is lower than for the other two X-ray observatories. This renders Suzaku particularly useful to study the low surface brightness outer regions of galaxy clusters.

1.3.6 Gamma-ray telescopes

The existence of gamma radiation was first postulated in the 1950s. This radiation is absorbed by the atmosphere, which is fortunate for the lifeforms on Earth. The first γ-ray telescopes were mounted on balloons, rockets, and satellites, and picked up fewer than 100 photons from cosmic sources. Those gamma photons had energies in the GeV range and above.

Detailed observations became possible with the satellites SAS-2 and COS-B. They compiled a map of the galaxy, confirmed the existence of a gamma background radiation, and for the first time observed pulsars in the gamma range. The first Gamma Ray Bursts (GRB), extremely bright and short-duration flashes on the gamma-ray sky, were detected from 1967 onwards by military satellites. Only the Italian-Dutch satellite Beppo-SAX (1996–2002) managed to localize a GRB with sufficient accuracy to allow an identification of the source in other wavebands, and thus to reveal its physical nature; we will come back to this subject in Sect. 9.7.

An enormous advance in high-energy astronomy was made with the launch of the Compton Gamma Ray Observatory (CGRO; Fig. 1.48) in 1991; the observatory was operational for 9 years. It carried four different instruments, among them the Burst And Transient Source Experiment (BATSE) and the Energetic Gamma Ray Experiment Telescope (EGRET). During its lifetime BATSE discovered about 3000 GRBs and contributed substantially to the understanding of the nature of these mysterious gamma-ray flashes. EGRET discovered many AGNs at very high energies above 20 MeV, which hints at extreme processes taking place in these objects.

One of the successors of the CGRO, the Integral satellite, was put into orbit as an ESA mission by a Russian Proton rocket at the end of 2002. At a weight of two tons, it was the heaviest ESA satellite that had been launched by then. It observes primarily at energies between 15 keV and 10 MeV in the gamma range, but has additional instruments for observation in the optical and X-ray regimes.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig49_HTML.jpg

Fig. 1.49

Artist’s drawing of the Fermi satellite, launched in 2008. Fermi observes at energies between 10 keV and 300 GeV. Credit: NASA E/PO, Sonoma State University, Aurore Simonnet

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig50_HTML.jpg

Fig. 1.50

The four 13 m-diameter telescopes, and the new 28-m telescope of the High Energy Stereoscopic System (H.E.S.S.) in Namibia, in South-West Africa. The optical quality of these mirrors is much lower than that of other optical telescopes. The angular resolution of the telescopes needs not to be better than a few arcminutes, as given by the width of the cone into which the Cherenkov light is emitted. Correspondingly, the pixel size is also adapted to this required angular resolution. Credit: H.E.S.S.-collaboration/Max-Planck-Institut für Kernphysik, Heidelberg

The other successor of the CGRO was launched in June 2008, the Fermi Gamma-ray Space telescope (Fig. 1.49). It carries two main instruments, the gamma-ray burst monitor (GBM) and the Large Area Telescope (LAT). With an energy range between 30 MeV and 300 GeV, comparable to, but wider than that of EGRET on CGRO, the LAT observes in a higher energy regime than Integral. Compared to EGRET, Fermi-LAT has higher sensitivity, a fourfold field-of-view (corresponding to 1/6 of the full sky), a better angular and energy resolution and a much better time resolution. Observations are conducted in the sky survey mode, mapping the whole sky every 3 h. Fermi-LAT made significant discoveries in its first years of operations in the field of pulsar, gamma-ray bursts, active galactic nuclei and the gamma-ray background radiation.

At energies above 100 GeV, the photon flux even from the brightest sources is too small to be detectable with space-based instruments—characteristic values are $\sim 10^{-11}\,\mathrm{photons}\,\mathrm{cm}^{-2}\,\mathrm{s}^{-1}$ above 1 TeV, or a few photons per m² per year. However, photons of these energies can be detected from the ground, using methods derived from cosmic ray physics. They make use of the fact that a high-energy photon hits an atom in the upper atmosphere, and in the interaction process, additional particles are generated, which by themselves are energetic enough to produce charged particles in further collisions. In this way, a number of particles are produced that are ultra-relativistic (meaning that their velocity is very close to that of the velocity of light) and all propagate in essentially the same direction as the incoming photon. Such a process is called an air shower. There are two different ways these air showers can be detected. First, some particles from the air shower propagate to the ground, and can there be detected in particle detectors.

The second method makes use of the fact that the propagation velocity of the particles in the air shower is higher than the local velocity of light in the atmosphere; in this case, charged particles emit Cherenkov radiation, and this radiation can be detected with optical telescopes. For TeV photons, the maximum of the air shower is found at altitudes around 10 km, and the minimum energy of an electron to emit Cherenkov radiation there is ∼ 40 MeV. About 100 such electrons need to be produced in the air shower in order to detect it unambiguously, which sets a threshold of the energy a photon must have to be detectable in this way. The typical energy threshold for current experiments is ∼ 100 GeV = 0. 1 TeV; one thus calls this the regime of TeV-astronomy. A major problem is the fact that charged particles from space—that is, cosmic rays (see Sect. 2.3.4)—also initiate air showers which have to be separated from the photon-induced ones. This is achieved by noting that air showers caused by charged particles are more complex, less collimated than the photon-induced ones. Another aspect of this technique is that one needs a dark and clear sky for the detection of the Cherenkov radiation, which limits the fraction of time in which such observations can be carried out.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig51_HTML.jpg

Fig. 1.51

One of the two MAGIC telescopes, located at the Roque de los Muchachos Observatory on La Palma. With their 17 m diameter, the MAGIC telescopes observe the Cherenkov radiation from air showers generated by TeV photons. The detector consists of > 450 photo-multipliers

Several such Cherenkov imaging telescopes are in operation, the most productive one up to now being H.E.S.S. (High Energy Stereoscopic System), shown in Fig. 1.50. Located in Namibia, H.E.S.S. consists of four telescopes each having a diameter of 13 m, recently complemented by a 28-m telescope. They observe the same region in the sky and detect the Cherenkov light from air showers, though under different viewing angles—they offer a stereoscopic view of the air shower. That permits the reconstruction of the geometry of the shower, in particular its direction and its intensity, resulting in an estimate of the direction of the incoming photon and its energy. In effect, the detector for the ultra-high energy photons is the atmosphere, and the effective area of the experiment is given by the field-of-view that the telescopes can cover, projected to an altitude of ∼ 10 km. In case of H.E.S.S., this is about 5 × 5 deg² yielding an effective area of ∼ 10⁵ m². The accuracy with which the direction and energy of an individual photon can be determined is about 5′ and ∼ 15 %, respectively. This direction accuracy allows one to determine the position of strong sources with an accuracy of ∼ 10″. Figure 1.51 shows one telescope of the MAGIC (Major Atmospheric Gamma-ray Imaging Cherenkov Telescopes) experiment on La Palma, another of the Cherenkov imaging telescopes.

Up to the present, more than 100 sources have been detected at energies > 100 GeV, most of them close to the Galactic plane. Many of them are as yet unidentified, but TeV radiation is observed from supernova remnants, pulsars and their immediate environment, and compact binary systems. Away from the Galactic plane, all of the (more than 50) detected TeV sources are active galactic nuclei, most of them blazars. Their very high energy emission provides insight into the processes that power these active objects.

1.4 Surveys

Modern astronomical research is partly based on large data sets, for example the spectra of a large number of objects used to investigate their spectral properties statistically. In some cases, these surveys are carried out for a single scientific objective, but frequently the same data are useful also for other branches of astronomy. Indeed, some of these data sets are very versatile and form an essential tool for a wide range of scientific applications. A few of these surveys which are of great relevance for several of the topics covered by this book are briefly described here, whereas more specialized ones will be discussed in connection with their (major) application in later chapters.

All-sky surveys. The most obvious example for versatile surveys are all-sky imaging surveys. If one finds a new source in a given waveband, then an obvious first step is to find out whether this source is also seen in other wavebands. For that, one initially uses all-sky surveys in these other wavebands and checks whether in them a source is seen at the same sky position. Optical all-sky surveys played an important role in the development of astronomy. The first optical Northern sky survey, the Bonner Durchmusterung, was carried out by Friedrich Wilhelm Argelander between 1852 and 1862 in Bonn, well before photographic plates became available for astronomical observations. It contains some 325 000 stars brighter than m ≈ 9. 5 and was later extended as Cordoba Survey to the Southern sky.

The Palomar Observatory Sky Survey (POSS) is a photographic atlas of the Northern (δ > −30^∘) sky. It consists of 879 pairs of photoplates observed in two color bands and was completed in 1960. The coverage of the Southern part of the sky was completed in 1980 in the ESO/SERC Southern Sky Surveys, where this survey is about two magnitudes deeper (B ≲ 23, R ≲ 22) than POSS. Later, the photoplates from both surveys were digitized, forming the Digitized Sky Survey (DSS) that covers the full sky. Sections from the DSS can be obtained directly via the Internet, with the full DSS having a data volume of some 600 GB. Using photographic plates with finer grain and higher sensitivity, the second Palomar Sky Survey (POSS-II) was carried out in the 1980s and 1990s. It is about one magnitude deeper compared to the first one and consists of images in three (instead of two) color filters. This will probably be the last photographic atlas of the sky because, with the development of large CCD mosaic cameras, we are now able to perform such surveys digitally.

The first digital optical survey which covers a substantial fraction of the sky is the Sloan Digital Sky Survey (SDSS). Its first phase was carried out between 2000 and 2008 with a dedicated 2.5 m telescope at Apache Point Observatory in New Mexico, equipped with two instruments. The first is a camera with 30 CCDs which scanned nearly a quarter of the sky in five photometric bands. The amount of data collected in this survey is enormous, and its storage and reduction required a tremendous effort. For this photometric part of the Sloan Survey, a new photometric system was developed, with its five filters (u, g, r, i, z) chosen such that their transmission curves overlap as little as possible (see Appendix A.4). The second instrument is a multi-object spectrograph, using optical fibers which have to be manually installed in holes that had been punched into a metal plate. With it, about 640 spectra could be recorded simultaneously. Within the SDSS, the spectra of more than a million objects (mostly galaxies and quasars) were recorded, and the data products of the SDSS were made publicly available in a sequence of seven data releases. The scientific yield of the SDSS has been enormous, well beyond the scientific purpose which formed the prime motivation for carrying out the survey in the first place, namely to measure the large-scale structure of the Universe (see Sect. 8.1.2). The telescope and its instruments are currently used for a number of additional surveys.

All-sky surveys have been carried out in other wavebands as well. We mentioned before the all-sky surveys carried out by several satellites, e.g., ROSAT in the X-ray regime, IRAS, AKARI and WISE in the infrared, and COBE, WMAP and Planck in the microwave regime. A ground-based survey in the near-IR was carried out in the 1990s and released to the public in 2002. This Two Micron All Sky Survey (2MASS) imaged the whole sky in three near-IR bands (J, H and K_s). More than half a billion stars were detected, as well as about 1.6 million resolved sources, of which more than 98 % are galaxies and which are published in the Extended Source Catalog (XSC). This catalog is more than 90 % complete at Galactic latitudes | b | > 20^∘ for sources with diameters ≳ 10″ and magnitudes K _s ≤ 13. 5. One of the prime science drivers was to penetrate the dust of the Milky Way—at near-IR wavelength, the opacity is only one tenth of that of visible radiation. Therefore, these near-IR images allow us to see galaxies much closer to the Galactic disk than possible in optical images (see Fig. 1.52). Hence, 2MASS has given us the first rather complete map of galaxies in the nearby (z ≲ 0. 1) Universe.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_1_Fig52_HTML.jpg

Fig. 1.52

A view of the full sky in near-IR light, as obtained from the 2MASS Extended Source Catalog (XSC). Color codes the distance of the galaxies, obtained from spectroscopic redshifts of ∼ 10⁵ galaxies, and estimated from their apparent brightness for the other > 10⁶ objects: blue indicates nearby galaxies (with z < 0. 01), green (0. 01 < z < 0. 04) and red (0. 04 < z < 0. 1) show increasingly more distant galaxies. In addition, the intensity is related to the brightness of objects to enhance the contrast. The map is shown in Galactic coordinates, such that the Galactic center is at the center of the image—there, the Milky Way is intransparent even to near-IR radiation, and thus the distribution of stars as observed in 2MASS is shown. Several of the most obvious structures are labeled. In particular one sees that the distribution of galaxies is highly structured. Credit: T. Jarrett, IPAC/Caltech

The Leiden-Argentine-Bonn (LAB) survey covers the whole sky in the 21-cm emission line of neutral hydrogen, within a velocity range of ± 400 km∕s. With its angular resolution of ∼ 36′ and velocity resolution of 1. 3 km∕s it maps the neutral hydrogen in and around our Milky Way. Other surveys at radio frequencies include the NRAO VLA Sky Survey (NVSS) , which covers the sky North of − 40^∘ declination at 1. 4 GHz, and the Bonn 408-MHz All-Sky Survey.

Deep multi-waveband Surveys. In order to understand the properties of galaxies and QSOs, data from a large range of wavelengths are required. Accounting for that, surveys are conducted on selected regions in the sky where several observatories make a coordinated effort to obtain a multi-wavelength data set. Perhaps the best-know example, and kind of a prototype, is the Hubble Deep Field, mentioned before and discussed in more detail in Sect. 9.2.1, where the deep HST data were soon supplemented by deep observations over all wavelengths, from the radio to the gamma-ray regime. Encouraged by the success of the scientific exploration of the HDF, several additional such surveys were carried out, including the Hubble Ultradeep Field (HUDF), the Great Observatories Origins Deep Survey (GOODS), the Galaxy Evolution from Morphology and Spectral Energy Distributions (GEMS) and the Cosmological Evolution Survey (COSMOS), with a sky coverage between that of the field-of-view of the ACS camera (HUDF) and nearly two square degrees (COSMOS). In all cases, a large number of other observatories acquired deep images in the same sky region to obtain the broadest waveband coverage possible, in addition to extended spectroscopic campaigns.

These deep multi-waveband surveys have yielded a large suite of results, mainly for distant objects. For each source in the survey field, the broad-band energy distribution is available and can be used to interpret the physical nature of the object—for example, normal galaxies can be distinguished from galaxies with weak nuclear activity which may show up in X-rays only. Unobscured star formation can be detected in the UV-part of the spectrum, whereas star formation hidden by dust shows up at infrared wavelengths. These surveys are also used for statistical properties of the galaxy population—for example, one can study the fraction of optically bright galaxies which show signs of nuclear activity in X-rays or in the radio. Using several optical and infrared bands, the redshift of an object can be estimated rather accurately, using the method of photometric redshifts (see Sect. 9.1.2). To end this highly incomplete list, one can search for rare objects in such surveys—for example those which are well detected in several near-IR bands, but show no sign of optical flux. As we will learn lateron (see Sect. 9.2.4), such an object is a very strong candidate for a galaxy with very high redshift.

Data bases and Virtual Observatories. Many of the surveys are designed to be of versatile use for many different research fields. In order for other astronomers to make use of the data, they have to be stored in well-organized data bases where the requested information can be readily searched for. But not only surveys are a valuable source of information for a wide range of applications; targeted observations of particular objects yield data sets which may be of interest to researchers other than the proposer of that observations. For space observatories, it has become standard for a long time that the data are stored in archives, and that every astronomer has access to the data in these archives, usually with a proprietary period of 1 year in which only the proposer has this access, to allow her to scientifically exploit the data and publish the results. Also several major ground-based facilities operate in this manner, where data (science plus calibration data) are made available to the community via dedicated archives.

In order to make the different data archives mutually compatible, new standards for data formats and storage systems are being developed. The goal of these virtual observatory initiatives is to develop a common platform in which astronomers can get with little effort a multi-wavelength image of selected regions in the sky, where the data at different wavelengths are stored in different archives spread around the world. The data included in a virtual observatory is not restricted only to observations, but can include simulation results as well. For example, results from cosmological simulations of the large-scale matter distribution in the Universe can be transformed into a mock sky map of the simulated sources, which can be analyzed in the same way as real data to allow for comparisons between observations and model predictions. In this way, one aims for making optimal use of valuable (and expensive) data.

1.5 Problems

1.1. Age of the Universe. Based on the Hubble law (1.2), we can get a simple first estimate of the age of the Universe. Consider a galaxy at distance D whose radial velocity is given by (1.2), and assume that this velocity was the same throughout cosmic time. In this case, at some time in the past the separation was zero, and we can identify that instant as the Big Bang. Under these assumptions, calculate the current age of the Universe using (1.7). Does it depend on the choice of the galaxy, i.e., the current distance D? Compare your result with the age of the oldest stars found in our Galaxy, which is about 12 × 10⁹ yr. Since no signal can propagate faster than the speed of light c, the age of the Universe times the speed of light is often called the ‘size of the visible Universe’. How large is that?

1.2. Sky fraction filled with nearby galaxies. The mean number density of luminous galaxies in the local Universe is about $2 \times 10^{-2}\,h^{3}\,\mathrm{Mpc}^{-3}$ . Assume that they are uniformly distributed, and that the diameter of their luminous region is about 20 kpc, comparable to that of the Milky Way. How many of these galaxies are contained in a sphere with radius $r_{0} = 1\,h^{-1}\,\mathrm{Gpc}$ around us? How many of these galaxies will be seen per square degree on the sky? What is the fraction of the sky which luminous galaxies within a distance of r ₀ subtend?

1.3. Density of the Universe. Our Universe has a mean matter density ρ _m given by (1.10), with Ω _m ≈ 0. 3. About 15 % of this mass density in contributed by baryonic matter, i.e., protons, neutrons and electrons, yielding a baryonic mass density of ρ _b ≈ 0. 15 ρ _m. Use h ≈ 0. 71, or h ² ≈ 1∕2 for this exercise.

The closest star to the Sun has a distance slightly larger than 1 pc, so that we can estimate the local mass density to be $\rho _{{\ast}\mathrm{local}} \approx 1M_{\odot }\,\mathrm{pc}^{-3}$ . Compare this value with ρ _b.

From the rotational velocity V ₀ ≈ 220 km∕s of the Sun around the center of the Milky Way, we obtain the mass M(R ₀) of the Milky Way contained in a sphere of radius R ₀ ≈ 8 kpc from the law (1.1) of Kepler rotation. By which factor is the mean density inside R ₀ larger than ρ _m?

If you place a cube of 1 m side-length at a random point in the Universe, how many baryons do you expect to find in it on average?

1.4. Free-fall time. Consider a sphere of mass M and initial radius r ₀. If there is no pressure acting against gravity, and if there is no outward-directed motion of the matter in the sphere, the sphere will reduce its radius, and in the idealized case considered here, collapse to a single point in a finite time. According to Newton’s law of gravity, the radius evolves in time obeying the equation of motion

$\displaystyle{\frac{\mathrm{d}^{2}r} {\mathrm{d}t^{2}} = -\frac{GM} {r^{2}} \;.}$

The solution of this equation depends on the initial velocity, as well the initial radius, and requires some algebra. However, a simple solution can be obtained by the ansatz $r(t) = r_{0}\left (1 - t/t_{\mathrm{f}}\right )^{\alpha }$ , where $r(t = 0) = r_{0}$ .

Show that this ansatz leads indeed to a solution of the equation of motion, and determine the two parameters α and t _f. Describe the qualitative behavior of the solution r(t).

Show that the time-scale t _f, i.e., the time it takes the sphere to collapse to a point, depends only on the mean initial density of the sphere. What is this time-scale for a density corresponding to the mean density inside the inner 8 kpc of our Galaxy? Hint: Make use of the fact that you know the orbital time of the Sun around the center of the Milky Way, t _orb ≈ 2. 3 × 10⁸ yr.

What is the time-scale t _f if the density is the mean density of the current Universe? How does this compare to the age of the Universe estimated in Problem 1.1? What is t _f for the Einstein–de Sitter model with density (1.14), and how does this compare to the current age of the Universe in the EdS model, given by (1.13)? Can you interpret your finding?

Footnotes

We shall use the terms ‘Milky Way’ and ‘Galaxy’ synonymously throughout.

1 parsec (1 pc) is the common unit of distance in astronomy, with 1 pc = 3. 086 × 10¹⁸ cm. Also used are 1 kpc = 10³ pc, 1 Mpc = 10⁶ pc, 1 Gpc = 10⁹ pc. Other commonly used units and constants are listed in Appendix C.

We use standard notation: G is the Newtonian gravitational constant, c the speed of light.

Strictly speaking, (1.1) is valid only for a spherically symmetric mass distribution. However, the rotational velocity for an oblate density distribution does not differ much, so we can use this relation as an approximation.

What is observed is the wavelength shift of spectral lines. Depending on the context, it is interpreted either as a radial velocity of a source moving away from us—for instance, if we measure the radial velocity of stars in the Milky Way—or as a cosmological escape velocity, as is the case for the Hubble law. It is in principle impossible to distinguish between these two interpretations, because a galaxy not only takes part in the cosmic expansion but it can, in addition, have a so-called peculiar velocity. We will therefore use the words ‘Doppler shift’ and ‘redshift’, respectively, and ‘radial velocity’ depending on the context, but always keeping in mind that both are measured by the shift of spectral lines. Only when observing the distant Universe where the Doppler shift is fully dominated by the cosmic expansion will we exclusively call it ‘redshift’.

The distances of these two clusters are not determined from redshift measurements, but by direct methods that will be discussed in Sect. 3.9; such direct measurements are one of the most successful methods of determining the Hubble constant.

In Chap. 3 we will see that for stars in spiral galaxies $M/L \sim 3M_{\odot }/L_{\odot }$ on average, while for those in elliptical galaxies a larger value of $M/L \sim 10M_{\odot }/L_{\odot }$ applies. Here and throughout this book, mass-to-light ratios are quoted in Solar units.

The virial theorem in its simplest form says that, for an isolated dynamical system in a stationary state of equilibrium, the kinetic energy is just half the potential energy,

$\displaystyle{ E_{\mathrm{kin}} = \frac{1} {2}\left \vert E_{\mathrm{pot}}\right \vert \;. }$

(1.8)

In particular, the system’s total energy is $E_{\mathrm{tot}} = E_{\mathrm{kin}} + E_{\mathrm{pot}} = E_{\mathrm{pot}}/2 = -E_{\mathrm{kin}}$ .

This was already known in 1915, but it was not clear whether it might not have any other explanation, e.g., a quadrupole moment of the mass distribution of the Sun.

In the Earth-Sun system, there are five points—called Lagrange points, where the total force, i.e., the sum of the gravitational forces of Sun plus Earth and the centrifugal force all balance to zero. Objects located at these Lagrangian point will thus orbit at the same angular velocity around the Sun as the Earth. The Lagrange point L2 is located on the line connecting Sun and Earth, about 1. 5 × 10⁶ km outside the Earth orbit. A satellite located there always sees Sun and Earth in the same direction and can thus be shielded from their radiation. The L2 point is therefore a preferred location for astronomical satellites.

The 13 telescopes with diameter > 8 m are: The two Keck telescopes, the four VLTs, Gemini-North (Mauna Kea) and Gemini-South (Chile), Subaru (Mauna Kea), the Hobby–Eberly Telescope (McDonald Observatory, Texas), the Large Binocular Telescope in Arizona consisting of two telescopes (see Fig. 1.44 below), and the Gran Telescopio Canarias at the Roque de los Muchachos Observatory on La Palma, Spain.

The point-spread function (PSF) $P({\boldsymbol \theta })$ describes the shape of the brightness profile of a point source as seen in the detector. Owing to seeing and diffraction effects, it has a finite width. The images of extended sources are also affected by the PSF: each small part of an extended sources can be considered as a point source, whose brightness in the detector is smeared by the PSF. Thus, if $I({\boldsymbol \theta })$ is the true brightness profile, the observed one is given by

$\displaystyle{I^{\mathrm{obs}}({\boldsymbol \theta }) =\int \mathrm{d}^{2}\theta '\;I({\boldsymbol \theta }')\,P({\boldsymbol \theta }-{\boldsymbol \theta }')\;,}$

where P is normalized to unity, $\int \mathrm{d}^{2}\theta \,P({\boldsymbol \theta }) = 1$ .

This is due to the fact that the ionization cross section behaves approximately as ∝ ν ⁻³, where ν is the photon frequency; hence, the probability that a photon will be absorbed through photo-ionization of neutral hydrogen is ∼ 1000 times smaller at 0. 1 keV than at the Lyman limit.

Prev Next