A collection of interacting and peculiar galaxies, as obtained by the Hubble Space Telescope. Such interactions and mergers are partly responsible for the formation of the current population of galaxies. Top row: Arp 148, UGC 9618, Arp 256, NGC 6670. Middle row: NGC 6240, ESO 593-8, NGC 454, UGC 8335. Bottom row: NGC 6786, NGC 17, ESO 77-14, NGC 6050. Credit: NASA, ESA, the Hubble Heritage (STScI/AURA)-ESA/Hubble Collaboration, and A. Evans (University of Virginia, Charlottesville/NRAO/Stony Brook University)

After having described the cosmological model in great detail, as well as the objects that inhabit our Universe at low and high redshifts, we will now try to understand how these objects can be formed and how they evolve in cosmic time.

The extensive results from observations of galaxies at high redshift which were presented earlier might suggest that the formation and evolution of galaxies is quite well understood today. We are able to examine galaxies at redshifts up to z ∼ 7 (and find plausible candidates at even higher redshifts) and therefore observe galaxies at nearly all epochs of cosmic evolution. This seems to imply that we can study the evolution of galaxies directly. However, this is true only to a certain degree. Although we observe the galaxy population throughout 90 % of the cosmic history, the relation between galaxies at different redshifts is not easily understood. We cannot suppose that galaxies seen at different redshifts represent various subsequent stages of evolution of the same kind of galaxy. The main reason for this difficulty is that different selection criteria need to be applied to find galaxies at different redshifts.

We shall explain this point with an example. Actively star-forming galaxies with z ≳ 2. 5 are efficiently detected by applying the Lyman-break criterion, but only those which do not experience much reddening by dust. Actively star-forming galaxies at z ∼ 1 are discovered as extremely red objects (EROs) if they are sufficiently reddened by dust, and at z ∼ 2. 5 as sub-millimeter galaxies. The relation between these galaxy populations depends, of course, on how large the fraction of galaxies is whose star-formation regions are enshrouded by dense dust. To determine this fraction, one would need to find Lyman-break galaxies (LBGs) at z ∼ 1, or EROs at z ∼ 3. Both observations are very difficult today, however. For the former, this is because the Lyman break is then located in the UV domain of the spectrum and thus can not be observed with ground-based telescopes. For the latter it is because the rest wavelength corresponding to the observed R-band lies in the UV where the emission of EROs is very small, so that virtually no optical radiation from such objects would be visible, rendering spectroscopy of these objects impossible. In addition to this, there is the problem that galaxies with 1. 3 ≲ z ≲ 2. 5 are difficult to discover because, for objects at those redshifts, hardly any spectroscopic indicators are visible in the optical range of the spectrum—both the 4000 Å-break and the λ = 3727 Å line of [Oii] are redshifted into the NIR, as are the Balmer lines of hydrogen, whereas the Lyman lines of hydrogen are located in the UV part of the spectrum. For these reasons, this range in redshift is also called the ‘redshift desert’.¹ Thus, it is difficult to trace the individual galaxy populations as they evolve into each other at the different redshifts. Do the LBGs at z ∼ 3 possibly represent an early stage of today’s ellipticals (and the passive EROs at z ∼ 1), or are they an early stage of spiral galaxies? Or do some galaxies form the bulk of their stellar population at z ∼ 3, whereas others do it at some later epoch?

The difficulties just mentioned are the reasons why our understanding of the evolution of the galaxy population is only possible within the framework of models, with the help of which the different observational facts are being interpreted. We will discuss some aspects of such models in this chapter.

Another challenge for galaxy evolution models are the observed scaling relations of galaxy properties. We expect that a successful theory of galaxy evolution can predict the Tully–Fisher relation for spiral galaxies, the fundamental plane for ellipticals, as well as the tight correlation between galaxy properties and the central black hole mass. This latter point also implies that the evolution of AGNs and galaxies must be considered in parallel, since the growth of black holes with time is expected to occur via accretion, i.e., during phases of activity in the corresponding galaxies. The hierarchical model of structure formation implies that high-mass galaxies form by the merging of smaller ones (Fig. 10.1); if the aforementioned scaling relations apply at high redshifts (and there are indications for this to be true, although with redshift-dependent pre-factors that reflect the evolution of the stellar population in galaxies), then the merging process must preserve the scaling laws, at least on average.

10.1 Introduction and overview

Key questions. In this final chapter we shall outline some of the current ideas on the formation and evolution of galaxies, their large-scale environment and their central black holes. We start with a list of questions a successful model is expected to provide answers for:

Why are galaxies the dominant objects in the Universe? We have seen that most of the stars live in galaxies with a luminosity which lies within a factor of ∼ 10 of the characteristic luminosity L ^∗ of the Schechter function [(3.52); see also (3.59)]; what defines this characteristic luminosity (and mass) scale?

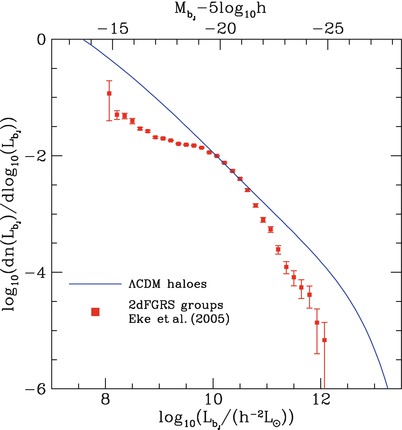Fig. 10.2
The red points with error bars show the luminosity function of galaxies and groups of galaxies as measured from the two-degree field galaxy redshift survey. In comparison, the solid curve shows the abundance of dark matter halos as predicted in a ΛCDM model, assuming a fixed mass-to-light ratio. This mass-to-light ratio is chosen such that the curves touch at one point, yielding $M/L \sim 80hM_{\odot }/L_{\odot }$ . The corresponding halo mass is M ∼ 10¹² h ⁻¹ M _⊙. There is an obvious discrepancy between the shape of the observed luminosity function and that expected if all halos had the same mass-to-light ratio. This implies that halos of different mass have different efficiency with which baryons are converted into stars. In other words, the mass-to-light ratio is smallest for halos of mass ∼ 10¹² h ⁻¹ M _⊙, and the efficiency of turning baryons into stars is suppressed for higher and lower mass halos. Source: C.M. Baugh 2006, A primer on hierarchical galaxy formation: the semi-analytical approach, arXiv:astro-ph/0610031, Fig. 6. Reproduced by permission of the author
Can the model of structure evolution in the Universe, which is based on gravitational instability and mainly driven by dark matter inhomogeneities, explain the formation of galaxies?
What is the reason for the existence of two main galaxy populations, the early-types or ellipticals, and the late-type or spirals? Do they have a different evolutionary history? Can we actually understand the relative abundance of these two populations, and even their distribution in luminosity or stellar mass?
Why is the shape of the galaxy luminosity function different from the shape of the dark matter halo mass function (see Fig. 10.2)? In other words, what causes the different mass-to-light ratios, or stellar-to-total mass ratios, of halos?
The properties of the galaxy population and its relative abundance depend on the environment. Why are red galaxies the dominant population in high-density regions such as clusters, whereas blue galaxies dominate the field population?
Can we understand the dependence of the star-formation rate on redshift, such as is displayed in the Madau diagram (see Sect. 9.6.2)? Why has the star-formation activity declined so strongly over the past five billion years?
Why is the mass of the supermassive black hole in the center of galaxies so tightly linked to the stellar properties of the galaxies? Which mechanism yields the co-evolution of the mass of the central black hole and the growth of the stellar mass? Do the stellar properties determine the mass of the black hole, or reversely, does the black hole affect the evolution of the stellar population—or are both of them jointly affected by the processes of galaxy growth?
What is the role of active galactic nuclei in the evolution of the galaxy population? Why are some galaxies very active, some are not, and why is the fraction of active galaxies such a strong function of redshift?
How are the special kinds of galaxies seen at high redshift related to the local galaxy population? What is the fate of an object which we can see as sub-millimeter galaxy at z ∼ 2, or a Lyman-break galaxy at z ∼ 3—into what kind of object have they developed?
Why are galaxies at high redshift significantly different from local ones, in terms of size and morphology?

As we shall see, for most of these question plausible answers can be given in the framework of the cosmological model. The panchromatic view of cosmic sources, provided to us by a suite of superb telescopes and instruments, allows us to link together the evidence about the physical nature of objects obtained from very different wavelengths. These observational results are used to build models of the evolution of galaxies which attempt to account for as many of them as possible. These models differ in detail, but we currently have a rather coherent picture of the key features that govern the formation and evolution of galaxies, although many important issues are still to be clarified.

Overview. The evolution of structure in the Universe is seeded by density fluctuations which at the epoch of recombination can be observed through the CMB anisotropy. Hence, we have direct observational evidence about the fluctuation spectrum at z ∼ 1100. Cosmological N-body simulations predict the evolution of the dark matter distribution as a function of redshift, in particular the formation of halos and their merger processes. Before recombination, baryons were coupled tightly to the photons and thus subject to a strong pressure which prevented them to fall into the potential wells formed by dark matter inhomogeneities (see Sect. 7.4.3). After recombination the baryonic matter decoupled from radiation, became essentially pressure free, and soon followed the same spatial distribution as the dark matter. However, baryonic matter is subject to physical processes like dissipation, friction, heating and cooling, and star formation. Since dark matter is not susceptible to these processes, the behavior of baryons and the dark matter is expected to differ in the ongoing evolution of the density field.

In the cold dark matter universe, small density structures formed first, which means that low-mass dark matter halos preceded those of higher mass. This ‘bottom-up’ scenario of structure formation follows from the shape of the power spectrum of density fluctuations, which itself is determined by the nature of dark matter—namely cold dark matter. The gas in these halos is compressed and heated, the source of heat being the potential energy. If the gas is able to cool by radiative processes, i.e., to get rid of some of its thermal energy and thus pressure, it can collapse into denser structures, and eventually form stars. In order for this to happen, the potential wells have to have a minimum depth, so the resulting kinetic energy of atoms is sufficient to excite the lowest-lying energy levels whose de-excitation then leads to the emission of a photon which yields the radiative cooling. We shall see that this latter aspect is particularly relevant for the first stars to form, since they have to be made of gas of primordial composition, i.e., only of hydrogen and helium.

Once the first stars form in the Universe, the baryons in their cosmic neighborhood get ionized. This reionization at first happens locally around the most massive dark matter halos that were formed; lateron, the individual ionized regions begin to overlap, the remaining neutral regions become increasingly small, until the process of reionization is completed, and the Universe becomes largely transparent to radiation, i.e., photons can propagate over large distances in the Universe. The gas in dark matter halos is denser than that in intergalactic space; therefore, the recombination rate is higher there and the gas in these halos is more difficult to ionize. Probably, the ionizing intergalactic radiation has a small influence on the gas in halos hosting a massive galaxy. However, for lower-mass halos, the gas not only maintains a higher ionization fraction, but the heating due to ionization can be appreciable. As a result, the gas in these low-mass halos finds it more difficult to cool and to form stars. Thus, the star-formation efficiency—or the fraction of baryons that is turned into stars—is expected to be smaller in low-mass galaxies.

The mass of halos grows, either by merging processes of smaller-mass halos or by accreting surrounding matter through the filaments of the large-scale density field. The behavior of the baryonic matter in these halos depends on the interplay of various processes. If the gas in a halo can cool, it will sink towards the center. One expects that the gas, having a finite amount of angular momentum like the dark matter halo itself, will initially accumulate in a disk perpendicular to the angular momentum of the gas, as a consequence of gas friction—provided a sufficiently long time of quiescent evolution for this to happen. The gas in the disk then reaches densities at which efficient star formation can set in. In this way, the formation of disk galaxies, thus of spirals, can be understood qualitatively.

As soon as star formation sets in, it has a feedback on the gas: the most massive stars very quickly explode as supernovae, putting energy into the gas and thereby heating it. This feedback then prevents that all the gas turns into stars on a very short time-scale, providing a self-regulation mechanism of the star-formation rate. In the accretion of additional material from the surrounding of a dark matter halo, also additional gas is accreted as raw material for further star formation.

When two dark matter halos with their embedded galaxies merge, the outcome depends mainly on the mass ratio of the halos: if one of them is much lighter than the other, its mass is simply added to the more massive halo; the same is true for their stars. More specific, the small-mass galaxy is disrupted by tidal forces, in the same way as the Sagittarius dwarf galaxy is currently destroyed in our Milky Way, with the stars being added to the Galactic halo. If, on the other hand, the masses of the two objects are similar, the kinematically cold disks of the two galaxies are expected to be disrupted, the stars in both objects obtain a large random velocity component, and the resulting object will be kinematically hot, resembling an elliptical galaxy. In addition, the merging of gas-rich galaxies can yield strong compression of the gas, triggering a burst of star formation, such as we have seen in the Antennae galaxies (see Fig. 9.25). Merging should be particularly frequent in regions where the galaxy density is high, in galaxy groups for instance. From the example shown in Fig. 6.68, a large number of such merging and collision processes are detected in galaxy clusters at high redshift.

In parallel, the supermassive black holes in the center of galaxies must evolve, as clearly shown by the tight scaling relations between black hole mass and the properties of the stellar component of galaxies (Sect. 3.8.3). The same gas that triggers star formation, say in galaxy mergers, can be used to ‘feed’ the central black hole. If, for example, a certain fraction of infalling gas is accreted onto the black hole, with the rest being transformed into stars, the parallel evolution of black hole mass and stellar mass could be explained. In those phases where the black hole accretes, the galaxy turns into an active galaxy; energy from the active galactic nucleus, e.g., in the form of kinetic energy carried by the jets, can be transmitted to the gas of the galaxy, thereby heating it. This provides another kind of feedback regulating the cooling of gas and star formation.

When two halos merge, both hosting a galaxy with a central black hole, the fate of the black holes needs to be considered. At first they will be orbiting in the resulting merged galaxy. In this process, they will scatter off stars, transmitting a small fraction of their kinetic energy to these stars. As a result, the velocity of the stars on average increases and many of them will be ‘kicked out’ of the galaxy. Through these scattering events, the black holes lose orbital energy and sink towards the center of the potential. Finally, they form a tight binary black hole system which loses energy through the emission of gravitational waves (see Sect. 7.9), until they merge. With the planned space-based laser interferometer LISA, one expects to detect these coalescing black hole events almost throughout the observable Universe.

The more massive halos corresponding to groups and clusters only form in the more recent cosmic epoch. In those regions of space where at a later cosmic epoch a cluster will form, the galaxy-mass halos form first—the larger-scale overdensity corresponding to the proto-cluster promotes the formation of galaxy-mass halos, compared to the average density region in the Universe; this is the physical origin of galaxy bias. Therefore, one expects the oldest massive galaxies to be located in clusters nowadays, explaining why most massive cluster galaxies are red. In addition, the large-scale environment provided by the cluster affects the evolution of galaxies, e.g., through tidal stripping of material.

In the rest of this chapter, we will elaborate on the various processes which are essential for our understanding of galaxy formation and evolution. In Sect. 10.2 we study the behavior of gas in a dark matter halo, in particular consider its heating and cooling properties; the latter obviously is most relevant for its ability to form stars. We then turn in Sect. 10.3 to the first generation of stars and consider their ability to reionize the Universe; we will also briefly discuss observational evidence for approaching the reionization epoch for the highest redshift objects known.

The formation of disk and elliptical galaxies is studied in Sects. 10.4 and 10.5, respectively. Here we will stress the importance of cooling processes on the one hand, and feedback processes that leads to gas heating on the other hand. We will also discuss the impact of mergers on the evolution of galaxies, the evolution of supermassive black holes, and the fate of these black holes in the aftermath of mergers. The final two sections are dedicated to modeling the formation and evolution of galaxies, both in the framework of numerical simulations which include the properties of the baryons (Sect. 10.6), and with somewhat simplified ‘semi-analytic’ models (Sect. 10.7) which, due to their great flexibility, have guided much of our understanding of galaxy evolution over the past two decades.

10.2 Gas in dark matter halos

We have seen in Sect. 7.5.1 how density fluctuations in the dark matter distribution evolve into gravitationally bound and virialized systems, the dark matter halos, through the process of gravitationally instability. In order to understand the formation of galaxies, we need to study the behavior of the baryons in these dark matter halos—the baryons out of which stars form.

10.2.1 The infall of gas during halo collapse

Gas heating. As long as the fractional overdensities are small, the spatial distribution of baryons and dark matter are expected to be very similar. In the language of the spherical collapse model, initially the radial distribution of an overdense sphere is the same for dark matter and baryons, scaled by their different mean cosmic density. However, when the sphere collapses, the behavior of both components must be very different: dark matter is collisionless, and the dark matter particles can freely propagate through the density distribution, crossing the orbits of other particles. Baryons, on the other hand, are collisional, which means that friction prevents gas from crossing through a gas distribution. Thus, as the halo collapses, the potential energy of the gas is transformed into heat through the frictional processes. Furthermore, the pressure of the gas can prevent it from falling into the dark matter potential well, depending on the gas temperature and the depth of the potential well, i.e., the halo mass. As we shall see below, this pressure effect is important for low-mass halos at high redshifts. But first, we assume that the gas initially is sufficiently cold such that this effect can be neglected in the halo collapse.

In the case of (approximate) spherical symmetry, one can picture this as follows: In the inner part of the halo, gas has already settled down into a quasi-hydrostatic state, where gas pressure balances the gravitational force. As the outer part of the halo collapses, gas falls onto this gas distribution. The infall speed is much higher than the sound velocity of the (cold) infalling gas, i.e., the gas falls in supersonically. This is the situation in which a shock front develops, i.e., a zone in which gas density, pressure, and velocity varies rapidly with position and in which the dissipation of kinetic energy (given by the infall velocity) into heat occurs. Inside this shock front, the gas is hot, and (almost) all of its kinetic energy gets converted into heat.

Virial temperature. We can now calculate the temperature of the gas inside a halo of (total) mass M. For that, we assume that the gas temperature T _g is uniform. According to the virial theorem, half of the potential energy of the infalling gas is converted into kinetic energy, which in turn is transformed into heat. We can therefore equate the thermal energy per unit volume to one half of the potential energy of the gas per unit volume,

$\displaystyle{ \frac{3} {2}nk_{\mathrm{B}}T_{\mathrm{g}} = \frac{3} {2}\,\frac{\rho _{\mathrm{g}}\,k_{\mathrm{B}}T_{\mathrm{g}}} {\mu m_{\mathrm{p}}} = \frac{\nu } {2}\rho _{\mathrm{g}}\,\frac{GM} {r} \;, }$

(10.1)

where μ m _p is the mean mass per particle in the gas, and the factor ν ∼ 1 depends on the assumed density profile of the halo of mass M and radius r. Note that the final term in (10.1) is just the square of the circular velocity, V _c ². Ignoring factors of order unity, the gas temperature will thus be similar to the virial temperature T _vir, defined as

$\displaystyle{ T_{\mathrm{vir}}:= \frac{\mu m_{\mathrm{p}}} {2k_{\mathrm{B}}}\,V _{\mathrm{c}}^{2} \approx 3.6 \times 10^{5}\mathrm{K}\left ( \frac{V _{\mathrm{c}}} {100\,\mathrm{km/s}}\right )^{2}\;. }$

(10.2)

Thus, a collapsed halo contains hot gas, with a temperature depending on the halo radius and mass. Such a hot gas is seen in galaxy groups and clusters though its X-ray emission (see Sect. 6.4). For galaxy-mass halos, this hot gas is much more difficult to observe: (10.2) predicts a characteristic gas temperature for galaxy-mass halos of ∼ 10⁶ K. At these temperatures, gas is very difficult to observe. The temperature is too low for being observable in X-rays—the corresponding X-ray energies are ∼ 0. 1 keV, for which the interstellar medium of the Milky Way is essentially opaque. Furthermore, at these temperatures most atoms are fully ionized, so there is little diagnostics of this gas from optical or UV line radiation. Nevertheless, some highly (but not fully) ionized species (such as five times ionized oxygen) exist, and their presence can be seen through absorption lines, e.g., in the spectrum of quasars. In this way, the presence of hot gas surrounding our Milky Way has been established. Nevertheless, some significant fraction the hot gas in galaxy-mass halos does not stay hot, but must cool, otherwise stars can not form. We shall turn to cooling processes next.

10.2.2 Cooling of gas

In order to form stars in a halo, the gas needs to compress to form dense clouds in which star formation occurs. The pressure of the hot gas prevents gas from condensing further, unless the gas can cool and thereby, at fixed pressure, increases its density.

Cooling processes. Optically thin gas can cool by emitting radiation—i.e., it gets rid of some of its energy in form of photons. There are several relevant processes by which internal energy can be transformed into radiation. In an ionized gas, the scattering between electrons and nuclei causes the emission of bremsstrahlung (free-free emission), as we discussed in Sect. 6.4.1. Collisions between atoms and electrons can lead to a transition of an atom into an excited state (collisional excitation). When the excited state decays radiatively, the energy difference between the ground level and the excited state is radiated away. Collisions can also lead to (partial) ionization of atoms, and subsequent recombination is again related to the emission of photons.

Cooling function. Common to all these processes is that they depend on the square of the gas density: they all are two-body processes due to collisions of particles. If we define the cooling rate C as the energy radiated away per unit volume and unit time, then C ∝ n _H ², with n _H being the number density of hydrogen nuclei (i.e., the sum of neutral and ionized hydrogen atoms). The constant of proportionality is called the cooling function, defined as

$\displaystyle{ \varLambda (T):= \frac{C} {n_{\mathrm{H}}^{2}}\;, }$

(10.3)

which depends on the gas temperature and its chemical composition. Figure 10.3 shows the cooling function for three different values of the gas metallicity.

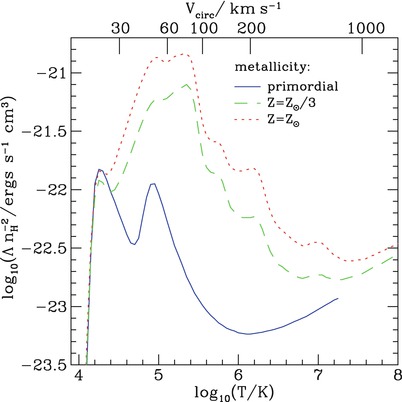
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig3_HTML.jpg

Fig. 10.3

The cooling function for gas with primordial composition (blue solid curve), 1/3 of the Solar metallicity (green dashed curve) and Solar metallicity (red dotted curve). On the top axis, the temperature is converted into a circular velocity, according to (10.2). To obtain such a cooling function, one needs to assume an equilibrium state of the gas. Here it is assumed that the gas is in thermodynamical equilibrium, where the fraction of ionization states of any atom depends just on T. The total cooling function shown here is a superposition of different gas cooling processes, including atomic processes and bremsstrahlung, the latter of which dominating at high T where the gas is fully ionized. Source: C.M. Baugh 2006, A primer on hierarchical galaxy formation: the semi-analytical approach, arXiv:astro-ph/0610031, Fig. 9. Reproduced by permission of the author

The relative importance and efficiency of the various cooling processes depend on the density and temperature of the gas, as well as on its chemical composition. At very high temperatures, all atoms are fully ionized, and thus the processes of collisional excitation and ionization are no longer of relevance. Then, bremsstrahlung becomes the dominant effect, with Λ(T) ∝ T ^1∕2 [see also (6.32)]. This behavior is seen in Fig. 10.3 for a pure hydrogen plus helium gas at T ≳ 10⁶ K; for gas with non-zero metallicity, bremsstrahlung starts to dominate the cooling at somewhat higher temperatures.

For gas with primordial abundance, we see two clear peaks in the cooling function in Fig. 10.3, one at T ∼ 2 × 10⁴ K, the other at T ∼ 10⁵ K. The former one is due to the fact that for gas at this temperature, hydrogen is mostly neutral, and many particles in the gas have an energy sufficient for the excitation of higher energy levels in hydrogen atoms; note that the lowest lying excited state of hydrogen has an energy corresponding to the Lyman-α transition, i.e., 10. 2 eV, corresponding to a temperature of T ∼ 10⁵ K. Thus, collisional excitation is efficient. At slightly higher temperatures, also collisional ionization (and subsequent recombination) is very effective, but with increasing T, the cooling function drops, because then hydrogen becomes mostly ionized. The second peak has the same origin, except that now the helium atom is the main coolant. Since the lowest energy level and the ionization energy in helium is higher than for hydrogen, the helium peak is simply shifted. Once helium is fully ionized, atomic cooling shuts off, and only at higher temperatures the bremsstrahlung effect takes over.

Although elements heavier than helium have a small abundance in number, they can dominate the gas cooling, due to the rich energy spectrum of many-electron atoms. The cooling function for gas with Solar metallicity is larger by more than an order of magnitude than that of primordial gas, over a broad range of temperatures. Hence, more enriched gas finds it easier to cool.

Atomic gas cannot cool efficiently for temperatures T ≲ 10⁴ K, due to the lack of charged particles (electrons and ions) in the gas. However, in chemically enriched gas, the few free electrons present at T ≲ 10⁴ K can excite low-energy states (the so-called fine-structure levels) of ions like that of oxygen or carbon. Molecules, on the other hand, have a rich spectrum of energy levels at considerably smaller energies, and can therefore lead to efficient cooling towards lower temperatures. This is the reason why star formation occurs in molecular clouds, where gas can efficiently cool and thereby compress to high densities.

Cooling time. Once we know the rate at which gas loses its energy, we can calculate the cooling time, the time it takes the gas (at constant cooling rate) to lose all of its energy:

$\displaystyle{ t_{\mathrm{cool}} = \frac{3nk_{\mathrm{B}}T} {2C} = \frac{3nk_{\mathrm{B}}T} {2n_{\mathrm{H}}^{2}\varLambda (T)}\;. }$

(10.4)

If this cooling time is longer than the age of the Universe, then the gas essentially stays at the same temperature and is unable to collapse towards the halo center. We have seen in Sect. 6.4.3 that for most regions in clusters, this is indeed the case; only in the central regions of clusters cooling can be effective.

Free-fall time. On the other hand, if the cooling time is sufficiently short, gas can compress towards the halo center. What ‘sufficiently short’ means can be seen if we compare the cooling time with the free-fall time, i.e., the time it takes a freely falling particle at some radius r in the halo to reach the center. The free-fall time depends only on the mean total mass density (i.e., dark matter plus baryons) inside r (see problem 4.7) and is given by

$\displaystyle{ t_{\mathrm{ff}} = \sqrt{ \frac{3\pi } {32G\rho }} = \sqrt{ \frac{3\pi f_{\mathrm{g} } } {32Gn\mu m_{\mathrm{p}}}}\;, }$

(10.5)

where we used the gas-mass fraction $f_{\mathrm{g}} =\rho _{\mathrm{g}}/\rho$ to convert the total density to the gas density, which was then expressed in terms of the particle number density n by ρ _g = n μ m _p.

Conditions for efficient cooling. If the cooling time is shorter than the free-fall time, then gas falls freely towards the center, essentially unaffected by gas pressure. If, on the other hand, the cooling time is much longer than the free-fall time, the gas at best sinks to the center at a rate given by the cooling rate—this is similar to the cooling flows discussed in Sect. 6.4.3. Hence, in this case, cooling is rather inefficient.

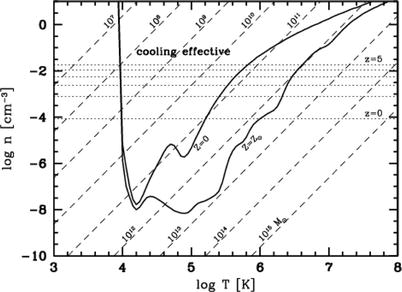
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig4_HTML.jpg

Fig. 10.4

The solid curves in this cooling diagram show the density as a function of temperature, for which t _cool = t _ff, both for gas with primordial abundance (Z = 0) and with Solar abundance (Z = Z _⊙). Note that this condition yields $n \propto f_{\mathrm{g}}^{-1}\left [T/\varLambda (T)\right ]^{2}$ , and so these curves are similar to the inverse of the cooling function in Fig. 10.3. Here, the gas fraction was chosen to correspond to its cosmic mean f _g = 0. 15. Dotted horizontal lines indicate the density of halos which form at the indicated redshifts, which is determined by the fact that the mean density of a halo is ∼ 200 times the critical density of the Universe at this epoch. The diagonal dashed lines show the n-T relation for fixed gas mass M _g, which is obtained from (10.2), r ∝ M∕T and the fact that M _g ∝ r ³ n. Eliminating r from these two relations yields $n \propto f_{\mathrm{g}}^{-1}M_{\mathrm{g}}^{-2}T^{3}$ . Source: H. Mo, F. van den Bosch & S. White 2010, Galaxy Formation and Evolution, Cambridge University Press, p. 386. Reproduced by permission of the author

Thus, the condition t _cool = t _ff separates situations in which gas can easily fall inside the halo and form denser gas concentrations from those where gas compression is prevented. In Fig. 10.4, this condition is shown as solid curves, both for primordial gas and gas with Solar abundance. For gas densities and temperature above the curves, cooling is efficient, whereas the cooling time is longer than the free-fall time below the curves.

The dotted horizontal lines in Fig. 10.4 indicate the mean gas density of halos collapsed at the redshift indicated, assuming a halos gas-mass fraction of f _g = 0. 15, i.e., about the cosmic average (recall that a halo has about 200 times the critical density of the Universe at the epoch of halo formation). Thus, for the cooling of gas in halos, only the region above the dotted lines is relevant. For each redshift, there is a range in temperatures for which gas can cool efficiently.

Finally, the dashed diagonal lines indicate the density n as a function of temperature, for a fixed mass M _g as indicated. For $M_{\mathrm{g}} \gtrsim 10^{13}M_{\odot }$ , the dashed line lies below the solid curves for all T; hence, gas in halos with mass $M \gtrsim 10^{13}/f_{\mathrm{g}}\,M_{\odot }$ cannot cool. Even for $M_{\mathrm{g}} \sim 10^{12}M_{\odot }$ , the dashed curve lies mostly outside the region where cooling is efficient, even for Solar abundance, except below the dotted lines, i.e., at densities which are smaller than the mean densities of halos. But if gas cannot cool, gas condensation and star formation is inefficient.

The difference between galaxies and groups/clusters. From Fig. 10.4, we can thus draw a first important conclusion: In sufficiently massive halos with $M_{\mathrm{g}} \gtrsim 10^{12}M_{\odot }$ , the small efficiency of gas cooling prevents gas from collapsing to the center and forming stars there. At smaller masses, cooling is effective to enable rapid gas collapse. This dividing line in mass is about the mass which distinguishes galaxies from groups and clusters. In the latter, only a small fraction of the baryons is turned into stars, and these are contained in the galaxies within the group; the group halo itself does not contain stars, with the exception of the intracluster light. But as we discussed in Sect. 6.3.4, these stars most likely have been stripped from galaxies in groups through interactions. In contrast, a large fraction of baryons in galaxies is concentrated towards the center, as visible in their stellar distribution. Thus, the difference between galaxies and groups/clusters is their efficiency to turn baryons into stars, and this difference is explained with the different cooling efficiency shown in Fig. 10.4.

This effect partly answers one of the questions posed at the start of this chapter. The mass-to-light ratio of very massive halos is much larger than that of galaxies (see Fig. 10.2) because of the much longer cooling time of the gas. In groups and clusters, most of the gas is present in the form of a hot gaseous halo.

Low-mass halos. Another conclusion we might want to draw from this cooling diagram is the behavior of halos at the low-mass end. A halo with gas mass $\sim 10^{7.5}M_{\odot }$ lies inside the cooling curve only at very high redshift, i.e., when the corresponding density in a halo is very high. Therefore, gas can cool, and stars form, in halos of this mass only if they formed early enough. We therefore expect that the stars in such low-mass halos are very old. We will soon find that there are additional effects which further strengthen this conclusion. Combined, these effects provide a natural explanation for the ‘missing satellite’ problem discussed in Sect. 7.8.

Cold accretion vs. hot accretion. The cooling diagram in Fig. 10.4 is very useful to discuss such properties qualitatively. Of course, the assumptions made to derive it are quite simple and idealized, such as the consideration of just the mean gas density, instead of a density profile, and the neglect of further effects, such as merging of halos.

A more realistic consideration needs to account for the fact that the gas is not homogeneous. The quasi-hydrostatic density profile implies that the gas density increases towards the center. In the inner part, it may be dense enough for cooling to be effective. In such halos, we therefore expect to have a central concentration of cold gas, surrounded by a hot gaseous halo with a temperature close to the virial temperature.

Furthermore, the implicit assumption of spherical symmetry made above may be misleading. From simulations of structure formation (see Sect. 7.5.3) we have seen that dark matter halos are embedded in a network of sheets and filaments, with massive halos forming at the intersection of filaments. Once formed, such halos accrete further matter, both dark and baryonic matter. In case of spherical symmetry, the gas would fall in and be heated through an accretion shock, as described before. However, the infall of matter occurs predominantly along the directions of the filaments connected to the halo, forming streams of gas which can reach the central regions of the halo without being strongly heated. Hydrodynamic simulations have identified this mode of accretion as an important route for halos to attain or replenish their gas.

10.3 Reionization of the Universe

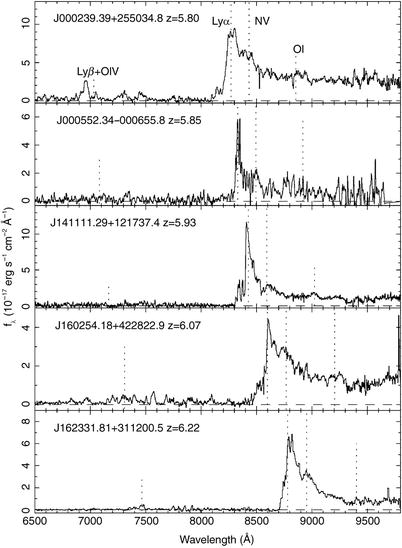
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig5_HTML.jpg

Fig. 10.5

Spectra of five QSOs at redshifts z > 5. 7, discovered in multi-color data from the Sloan Digital Sky Survey. The positions of the most important emission lines are marked. Particularly remarkable is the almost complete lack of flux bluewards of the Lyα emission line in some of the QSOs, indicating a strong Gunn–Peterson effect. However, this absorption is not complete in all QSOs, which points at strong variations in the density of neutral hydrogen in the intergalactic medium at these high redshifts. Either the hydrogen density varies strongly for different lines-of-sight, or the degree of ionization is very inhomogeneous. Source: X. Fan et al. 2004, A Survey of z > 5.7 Quasars in the Sloan Digital Sky Survey. III. Discovery of Five Additional Quasars, AJ 128, 515, p. 517, Fig. 1. ©AAS. Reproduced with permission

After recombination at z ∼ 1100, the intergalactic gas became neutral, with a residual ionization fraction of only ∼ 10⁻⁴. Had the Universe remained neutral we would not be able to receive any photons that were emitted bluewards of the Lyα line of a source, because the absorption cross section for Lyα photons is too large [see (8.27)]. Since such photons are observed from QSOs, as can be seen for instance in the spectra of the z > 5. 7 QSOs in Fig. 10.5, and since an appreciable fraction of homogeneously distributed neutral gas in the intergalactic medium can be excluded for z ≲ 5, from the tight upper bounds on the strength of the Gunn–Peterson effect (Sect. 8.5.1), the Universe must have been reionized between the recombination epoch and the redshift z ∼ 7 of the most distant known QSOs. As we have seen in Sect. 8.6.6, the anisotropies of the CMB led us to conclude that reionization occurred at z ∼ 10.

This raises the question of how this reionization proceeded, in particular which process was responsible for it. The latter question is easy to answer—reionization must have happened by photoionization. Collisional ionization can be ruled out because for it to be efficient the intergalactic medium (IGM) would need to be very hot, a scenario which can be excluded due to the perfect Planck spectrum of the CMB—the argument here is the same as in Sect. 9.5.3, where we excluded the idea of a hot IGM as the source of the cosmic X-ray background. Hence, the next question is what produced the energetic photons that caused the photoionization of the IGM.

Two kinds of sources may in principle account for them—hot stars or AGNs. Currently, it is not unambiguously clear which of these is the predominant source of energetic photons causing reionization since our current understanding of the formation of supermassive black holes is still insufficient. However, it is currently thought that the main source of photoionization photons is the first generation of hot stars.

10.3.1 The first stars

Following on from the above arguments, understanding reionization is thus directly linked to studying the first generation of stars. In the present Universe star formation occurs in galaxies; thus, one needs to examine when the first galaxies could have formed. From the theory of structure formation, the mass spectrum of dark matter halos at a given redshift can be computed by means of, e.g., the Press–Schechter model (see Sect. 7.5.2). Two conditions need to be fulfilled for stars to form in these halos. First, gas needs to be able to fall into the dark halos. Since the gas has a finite temperature, pressure forces may impede the infall into the potential well. Second, this gas also needs to be able to cool, condensing into clouds in which stars can then be formed, a process that we considered in the preceding section.

The Jeans mass. By means of a simple argument, we can estimate under which conditions pressure forces are unable to prevent the infall of gas into a potential well. To do this, we consider a slightly overdense spherical region of radius R whose density is only a little larger than the mean cosmic matter density $\bar{\rho }$ . If this sphere is homogeneously filled with baryons, the gravitational binding energy of the gas is about

$\displaystyle{\vert E_{\mathrm{grav}}\vert \sim \frac{GMM_{\mathrm{g}}} {R} \;,}$

where M and M _g denote the total mass and the gas mass of the sphere, respectively. The thermal energy of the gas can be computed from the kinetic energy per particle, multiplied by the number of particles in the gas, or

$\displaystyle{E_{\mathrm{th}} \sim c_{\mathrm{s}}^{2}\,M_{\mathrm{ g}}\;,\mbox{ where}\quad c_{\mathrm{s}} \approx \sqrt{\frac{k_{\mathrm{B} } T_{\mathrm{g} } } {\mu m_{\mathrm{p}}}} }$

is the speed of sound in the gas, which is about the average velocity of the gas particles, and μ m _p denotes, as before, the average particle mass in the gas. For the gas to be bound in the gravitational field, its gravitational binding energy needs to be larger than its thermal energy, | E _grav | > E _th, which yields the condition GM > c _s ² R. Since we have assumed an only slightly overdense region, the relation $M \sim \bar{\rho }\, R^{3}$ between mass and radius of the sphere applies. From the two latter equations, the radius can be eliminated, yielding the condition

$\displaystyle{ M > M_{\mathrm{J}} \equiv \frac{\pi ^{5/2}} {6} \left (\frac{c_{\mathrm{s}}^{2}} {G} \right )^{3/2} \frac{1} {\sqrt{\bar{\rho }}}\;, }$

(10.6)

where the numerical coefficient is obtained from a more accurate treatment. Thus, as a result of our simple argument we find that the mass of the halo needs to exceed a certain threshold for gas to be able to fall in. The expression on the right-hand side of (10.6) defines the Jeans mass M _J, which describes the minimum mass of a halo required for the gravitational infall of gas. The Jeans mass depends on the temperature of the gas, expressed through the sound speed c _s, and on the mean cosmic matter density $\bar{\rho }$ . The latter can easily be expressed as a function of redshift, $\bar{\rho }(z) =\bar{\rho } _{0}(1 + z)^{3}$ .

The baryon temperature T _b has a more complicated dependence on redshift. For sufficiently high redshifts, the small fraction of free electrons that remains after recombination provides a thermal coupling of the baryons to the cosmic background radiation, by means of Compton scattering. This is the case for redshifts z ≳ z _t, where

$\displaystyle{z_{\mathrm{t}} \approx 140\left ( \frac{\varOmega _{\mathrm{b}}h^{2}} {0.022}\right )^{2/5}\;;}$

hence, $T_{\mathrm{b}}(z) \approx T(z) = T_{0}(1 + z)$ for z ≳ z _t. For smaller redshifts, the density of photons gets too small to maintain this coupling, and baryons start to adiabatically cool down by the expansion, so that for z ≲ z _t we obtain approximately $T_{\mathrm{b}} \propto \rho _{\mathrm{b}}^{2/3} \propto (1 + z)^{2}$ (see problem 4.9).

From these temperature dependences, the Jeans mass can then be calculated as a function of redshift. For $z_{\mathrm{t}} \lesssim z \lesssim 1000$ , M _J is independent of z because $c_{\mathrm{s}} \propto T^{1/2} \propto (1 + z)^{1/2}$ and $\bar{\rho }\propto (1 + z)^{3}$ , and its value is

$\displaystyle{ M_{\mathrm{J}} = 1.35 \times 10^{5}\left (\frac{\varOmega _{\mathrm{m}}h^{2}} {0.15}\right )^{-1/2}M_{ \odot }\;, }$

(10.7)

whereas for $z \lesssim z_{\mathrm{t}}$ we obtain, with $T_{\mathrm{b}} \simeq 1.7 \times 10^{-2}(1 + z)^{2}\,\mathrm{K}$ ,

$\displaystyle\begin{array}{rcl} M_{\mathrm{J}}& =& 5.7 \times 10^{3}\left (\frac{\varOmega _{\mathrm{m}}h^{2}} {0.15}\right )^{-1/2} \\ & \times & \left ( \frac{\varOmega _{\mathrm{b}}h^{2}} {0.022}\right )^{-3/5}\left (\frac{1 + z} {10} \right )^{3/2}\ M_{ \odot }\;.{}\end{array}$

(10.8)

Hence, gas can not fall into halos with mass lower than these values.

Cooling of the gas. The Jeans criterion is a necessary condition for the formation of proto-galaxies, i.e., dark matter halos which contain baryons. In order to form stars, the gas in the halos needs to be able to cool further. Here, we are dealing with the particular situation of the first galaxies, whose gas is metal-free, so metal lines cannot contribute to the cooling. As we have seen in Fig. 10.3, the cooling function of primordial gas is much smaller than that of enriched material; in particular, the absence of metals means that even slow cooling though excitation of fine-structure lines cannot occur, as there are no atoms with such transitions present. Thus, cooling by the primordial gas is efficient only above $T \gtrsim 2 \times 10^{4}\,\mathrm{K}$ . However, the halos formed at high redshift have low mass. We have seen in Sect. 7.5.2 that the abundance of dark matter halos depends on the parameter ν in (7.51), given by the product of the density fluctuations on a given mass scale and the growth factor. At high redshift, the growth factor D ₊(a) is small, and thus to have a noticeable abundance of halos of mass M, σ(M) must be correspondingly large. At redshift z ∼ 10, the parameter ν is about unity for halos of mass $\sim 10^{3}M_{\odot }$ . Hence, at that time, substantially more massive halos than that were (exponentially) rare—i.e., only low-mass halos were around, and their virial temperature

$\displaystyle{ T_{\mathrm{vir}} \approx 2 \times 10^{2}\left ( \frac{M} {10^{5}h^{-1}M_{\odot }}\right )^{2/3}\left (\frac{1 + z} {10} \right )\,\mathrm{K} }$

(10.9)

is considerably below the energy scale where atomic hydrogen can efficiently cool. To derive (10.9), we have replaced V _c in (10.2) in favor of halo mass and radius, and used the fact that the mean matter density of a halo inside its virial radius is ∼ 200 times the critical density at a given redshift. Therefore, atomic hydrogen is a very inefficient coolant for these first halos, insufficient to initiate the formation of stars. Furthermore, helium is of no help in this context, since its excitation temperature is even higher than that of hydrogen.

The importance of molecular hydrogen. Besides atomic hydrogen and helium, the primordial gas contains a small fraction of molecular hydrogen which represents an extremely important component in cooling processes. Whereas in enriched gas, molecular hydrogen is formed on dust particles, the primordial gas had no dust, and so H₂ must form in the gas phase itself, rendering its abundance very small. However, despite its very small density and transition probability, H₂ dominates the cooling rate of primordial gas at temperatures below T ∼ 10⁴ K—see Fig. 10.6—where the precise value of this temperature depends on the abundance of H₂.

By means of H₂, the gas can cool in halos with a temperature exceeding about $T_{\mathrm{vir}} \gtrsim 1000\,\mathrm{K}$ , corresponding to a halo mass of $M \gtrsim 5 \times 10^{4}M_{\odot }$ at z ∼ 20. In these halos, stars may then be able to form. These stars will certainly be different from those known to us, because they do not contain any metals. Therefore, the opacity of the stellar plasma is much lower. Such stars, which at the same mass presumably have a much higher temperature and luminosity (and thus a shorter lifetime), are called population III stars. Due to their high temperature they are much more efficient sources of ionizing photons than stars with ‘normal’ metallicity.

10.3.2 The reionization process

Dissociation of molecular hydrogen. The energetic photons from these population III stars are now capable of ionizing hydrogen in their vicinity. More important still is another effect: photons with energy above 11.26 eV can destroy H₂. Since the Universe is transparent for photons with energies below 13.6 eV, photons with $11.26\,\mathrm{eV} \leq E_{\gamma } \leq 13.6\,\mathrm{eV}$ can propagate very long distances and dissociate molecular hydrogen. This means that as soon as the first stars have formed in a region of the Universe, molecular hydrogen in their vicinities will be destroyed and further gas cooling and star formation will then be prevented.² At this point, the Universe contains a low number density of isolated bubbles of ionized hydrogen, centered on those halos in which population III stars were able to form early, but this constitutes only a tiny fraction of the volume; most of the baryons remain neutral.

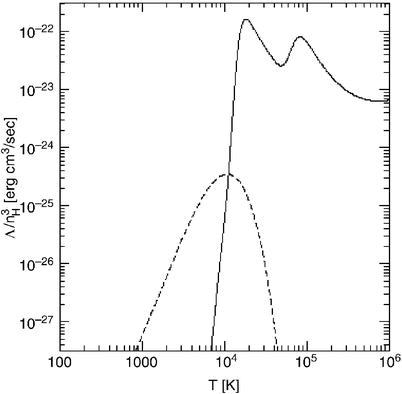
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig6_HTML.jpg

Fig. 10.6

Cooling rate as a function of the temperature for a gas consisting of atomic and molecular hydrogen (with 0.1 % abundance) and of helium. The solid curve describes the cooling by atomic gas, the dashed curve that by molecular hydrogen; thus, the latter is extremely important at temperatures below ∼ 10⁴ K. At considerably lower temperatures the gas cannot cool, hence no star formation can take place. Source: R. Barkana & A. Loeb 2000, In the Beginning: The First Sources of Light and the Reionization of the Universe, astro-ph/0010468, Fig. 12. Reproduced by permission of the author

Metal enrichment of the intergalactic medium. Soon after population III stars have formed, they will explode as supernovae. Through this process, the metals produced by them are ejected into the intergalactic medium, by which the initial metal enrichment of the IGM occurs. The kinetic energy transferred by SNe to the gas within the halo can exceed its binding energy, so that the baryons of the halo can be blown away and further star formation is prevented. Whether this effect may indeed lead to gas-free halos, or whether the released energy can instead be radiated away, depends on the geometry of the star-formation regions. In any case, it can be assumed that in those halos where the first generation of stars was born, further star formation was considerably suppressed, particularly since all molecular hydrogen was destroyed.

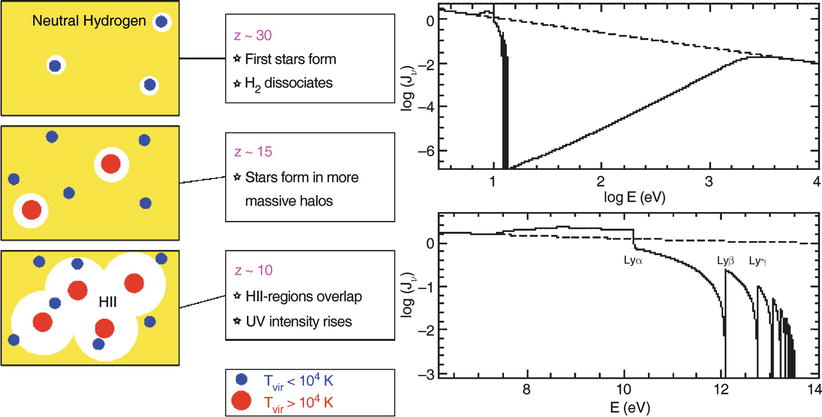
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig7_HTML.jpg

Fig. 10.7

On the left, a sketch of the geometry of reionization is shown: initially, relatively low-mass halos collapse, a first generation of stars ionizes and heats the gas in and around these halos. By heating, the temperature increases so strongly (to about T ∼ 10⁴ K) that gas can escape from the potential wells; these halos may never again form stars efficiently. Only when more massive halos have collapsed will continuous star formation set in. Ionizing photons from this first generation of hot stars produce Hii-regions around their halos, which is the onset of reionization. The regions in which hydrogen is ionized will grow until they start to overlap; at that time, the flux of ionizing photons will strongly increase. On the right, the average spectrum of photons at the beginning of the reionization epoch is shown; here, it has been assumed that the flux from the radiation source follows a power law (dashed curve). Photons with an energy higher than that of the Lyα transition are strongly suppressed because they are efficiently absorbed. The spectrum near the Lyman limit shows features which are produced by the combination of breaks corresponding to the various Lyman lines, and the redshifting of the photons. Source: R. Barkana & A. Loeb 2000, In the Beginning: The First Sources of Light and the Reionization of the Universe, astro-ph/0010468, Figs. 4, 11. Reproduced by permission of the author

We can assume that the metals produced in these first SN explosions are, at least partially, ejected from the halos into the intergalactic medium, thus enriching the latter. The existence of metal formation in the very early Universe is concluded from the fact that even sources at very high redshift (like QSOs at z ∼ 6) have a metallicity of about one tenth the Solar value. Furthermore, the Lyα forest also contains gas with non-vanishing metallicity. Since the Lyα forest is produced by the intergalactic medium, this therefore must have been enriched.

The final step to reionization. For gas to cool in halos without molecular hydrogen, their virial temperature needs to exceed about 10⁴ K (see Fig. 10.6). Halos of this virial temperature form with appreciable abundance at redshifts of z ∼ 10, corresponding to a halo mass of $\sim 10^{7}M_{\odot }$ , as can be estimated from the Press–Schechter model (see Sect. 7.5.2). In these halos, efficient star formation can then take place and the first proto-galaxies form. These then ionize the surrounding IGM in the form of Hii-regions, as sketched in Fig. 10.7. The corresponding Hii-regions expand because increasingly more photons are produced. If the halo density is sufficiently high, these Hii-regions start to overlap and soon after, to fill the whole volume. Once this occurs, the IGM is ionized, and reionization is completed.

We therefore conclude that reionization is a two-stage process. In a first phase, population III stars form through cooling of gas by molecular hydrogen, which is then destroyed by these very stars. Only in a later epoch and in more massive halos cooling is provided by atomic hydrogen, leading to reionization.

Escape fraction of ionizing photons. We note that only a small fraction of the baryons needs to undergo nuclear fusion in hot stars to ionize all hydrogen, as we can easily estimate: by fusing four H-nuclei (protons) to He, an energy of about 7 MeV per nucleon is released. However, only 13.6 eV per hydrogen atom is required for ionization. Hence, from a purely energetic point of view, reionization is not particularly demanding.

The number density of hot stars required to reionize the Universe is uncertain due to the unknown escape fraction f _esc of ionizing photons from the first galaxies, i.e., the ratio of the number of ionizing photons which can propagate out of the galaxy to the total number of ionizing photons produced by hot stars. Photons with energy E _γ ≥ 13. 6 eV are easily absorbed by the neutral fraction of the gas. For local star-forming galaxies, the escape fraction can be estimated to be between a few percent up to ∼ 0. 5. However, the first galaxies that formed were denser. Furthermore, the escape fraction depends on the geometrical arrangement of the hot stars relative to the interstellar medium, as well as the clumpiness of the latter. If the stars are located in the inner part of the galaxy, surrounded by a smooth interstellar medium, the escape fraction will be very small. If, however, the ISM is clumpy such that it only occupies a small fraction of the volume, photons can escape ‘between the clumps’, and the escape fraction can be appreciable. There is also the possibility that the star formation and subsequent supernovae drive much of the gas out of the galaxy halos, increasing the escape fraction for later stellar generations.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig8_HTML.jpg

Fig. 10.8

The volume of an expanding Hii region from an instantaneous starburst, normalized to the maximally possible volume V _max (which is given by equating the number of hydrogen atoms $N_{\mathrm{H}} =\bar{ n}_{\mathrm{H}}V _{\mathrm{max}}$ with the total number of ionizing photons generated by the starburst). The upper solid curve assumes that no recombination takes place. The two other solid curves assume that the starburst occurs at redshift z = 10, and that the intergalactic medium is uniform (middle solid curve) or strongly clumped (lower solid curve). The two dashed curves show the same, except that for them, z = 15 is assumed; since the density is higher at larger redshift, the recombination rate is accordingly higher. Source: R. Barkana & A. Loeb 2000, In the Beginning: The First Sources of Light and the Reionization of the Universe, astro-ph/0010468, Fig. 21. Reproduced by permission of the author

Clumpiness of the intergalactic medium. A further uncertainty in the quantitative understanding of reionization lies in the clumpiness of the intergalactic medium. An ionized hydrogen atom may become neutral again due to recombination. Hence, one may need more than one ionizing photon per atom for complete reionization. Since recombination is a two-body process (i.e., its rate depends quadratically on the gas density), its relative importance depends on the redshift of reionization and the clumpiness of the gas distribution: The higher the redshift, the larger the density of the intergalactic medium, and the higher the recombination rate. Clumpiness also increases the mean of the squared gas density, yielding a higher mean recombination rate (see Fig. 10.8).

Once reionization is completed, the intergalactic medium has a temperature of about 10⁴ K, due to the heating of the gas by photoionization: the typical energy of a photon which ionizes a hydrogen atom is somewhat larger than 13. 6 eV, and the energy difference is transferred to the electron, which is tightly coupled by Coulomb interactions with the other gas particles. Thus, this surplus energy causes a heating of the gas. The resulting temperature depends on the spectrum of the ionizing radiation; the harder the spectrum, the higher the temperature.

Suppression of low-mass galaxies. The increase of temperature causes an increase of the Jeans mass (10.6), due to its dependence on the sound velocity. Once the intergalactic medium is heated to ∼ 10⁴ K by intergalactic UV radiation, the gas pressure prevents gas inflow into low-mass halos, corresponding³ to circular velocities ≲ 30 km∕s. For this reason, one expects that halos of lower mass have a lower baryon fraction than that of the cosmic mixture, $f_{\mathrm{b}} =\varOmega _{\mathrm{b}}/\varOmega _{\mathrm{m}}$ . The actual value of the baryon fraction depends on the details of the merger history of a halo. Quantitative studies yield an average baryon mass of

$\displaystyle{ \bar{M}_{\mathrm{b}} = \frac{f_{\mathrm{b}}\,M} {\left [1 + (2^{\alpha /3} - 1)(M_{\mathrm{C}}/M)^{\alpha }\right ]^{(3/\alpha )}}\;, }$

(10.10)

where $M_{\mathrm{C}} \sim 10^{9}M_{\odot }$ is a characteristic mass, defined such that for a halo with mass M _C, $\bar{M}_{\mathrm{b}}/M = f_{\mathrm{b}}/2$ . For halos of mass smaller than M _C, the baryon fraction is suppressed, decreasing as (M∕M _C)³ for small masses, whereas for halo masses ≫ M _C, the baryon fraction corresponds to the cosmic average. The index α ∼ 2 determines the sharpness of the transition between these two cases. The characteristic mass M _C depends on redshift, being much smaller at high z due to the stronger ionizing background.

The ionizing flux has two additional effects on the gas that resides in halos: it provides a source of heating, due to photoionization, and it leads to a higher degree of ionization in the gas, reducing the number density of atoms which can be excited by collisions and cool through de-excitation. Both effects act in the same direction, by impeding an efficient cooling of the gas and hence the formation of stars. For halos of larger mass, intergalactic radiation is of fairly little importance because the corresponding heating rate is substantially smaller than that occurring by the dissipation of the gas which is needed to concentrate the baryons towards the halo center. For low-mass halos, however, this effect is important. Together, these two effects reduce the cooling rate of the gas, which is a dominant effect for low-mass halos. Thus, the gas in low-mass halos cannot cool efficiently, suppressing star formation—unless star formation occurred before the reionization was completed. We hence found one of the elements for the second part of the answer to the question about the different mass-to-light ratios in halos, illustrated in Fig. 10.2: star formation in low mass halos is strongly suppressed due to the ionizing background radiation. As already discussed in Sect. 7.8, this also provides an explanation of the ‘missing satellite problem’.

Helium reionization. Our discussion was confined to the ionization of hydrogen and we ignored helium. To singly ionize helium, photons of energy ≥ 24. 6 eV are required, and the ionization energy of He ii is four times that of hydrogen. In addition, the recombination rate of fully ionized helium is about five times higher than that of hydrogen. Therefore, the reionization of helium is expected to be completed at a later epoch when the density of photons with λ < 304 Å was high enough. Since even massive stars do not generate photons exceeding this energy in large quantities, the photons leading to helium reionization presumably are emitted by quasars; therefore, the ionization of helium has to wait for the ‘quasar epoch’ of the Universe, at z ≲ 4. From the statistical analysis of the Lyα forest and from the analysis of helium absorption lines and the helium Gunn–Peterson effect in high-redshift QSOs, a reionization redshift of z ∼ 3 for helium is obtained.

10.3.3 Observational probes of reionization

One of the challenges of current observational cosmology is to link the history of reionization, as outlined above, to the observation of the highest redshift sources, i.e., to see whether we can observe the sources which are responsible for cosmic reionization. Are the galaxy populations that we can find at very high redshifts sufficient to understand the reionization process? Here we shall mention some of the major obstacles for a direct observation probe of these ionizing sources.

The stellar mass at high redshifts. If reionization was caused by the energetic photons emitted during star formation, the remnants of this first generation of stars must be present in the post-reionization Universe, and thus be observable. As we discussed in some detail in Chap. 9, galaxies at redshift > 6 are observed, either as Lyman-break galaxies (LBGs), Lyman-alpha emitters (LAEs) or as sub-millimeter galaxies (SMGs). Their stellar masses can be estimated from observed light. However, most of the LBGs are observed only in the near-IR, which means that we see their restframe UV-emission. Converting the UV-light into a stellar mass is highly uncertain, since it depends strongly on the instantaneous star-formation rate. For LAEs, it is even more challenging to determine a stellar mass, since they are typically fainter in their broad-band (continuum) emission, which renders the determination of the stellar mass even more challenging.

Nevertheless, galaxies at very high redshift were found which appear to have high stellar masses, including a LAE at z = 6. 60 with an estimated stellar mass $M_{{\ast}}\gtrsim 10^{11}M_{\odot }$ . The high-redshift QSOs require a SMBH with $M_{\bullet } \gtrsim 10^{9}M_{\odot }$ to power their energy output, and these must be hosted is galaxies with very large stellar mass. Therefore, massive galaxies have formed very early on, delivering ionizing photons.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig9_HTML.jpg

Fig. 10.9

The spectra of three high-redshift QSOs (SDSS J1148+5251 at z = 6. 42, SDSS J1030+0524 at z = 6. 31, and the z = 7. 085 QSO ULAS J1120+0641) at the Lyman-α emission line. For this figure, the wavelength difference to the Lyman-α transition is expressed in proper distance away from the QSOs. The spectra are normalized, dividing them by the extrapolation of the continuum on the red side of the emission line, yielding the transmission. Source: D.J. Mortlock et al. 2011, A luminous quasar at a redshift of z = 7.085, Nature 474, 616, Fig. 3. Reprinted by permission of Macmillan Publishers Ltd: Nature, ©2011

However, these highest mass objects are very rare and, by themselves, by far not able to explain reionization. This fact can be clearly seen by considering the spectral shape of the Lyα emission line of high-redshift QSOs. Figure 10.9 shows the spectrum of three very high redshift QSOs near to the Lyman-α emission line. Whereas all three QSO show essentially no flux shortward of Lyman-α, once the wavelength difference exceeds ∼ 20 Å in the restframe, there is some transmitted flux very close to the Lyman-α transition. This near-zone transmission is understood as a region around the QSO where the intergalactic gas is fully ionized by the QSO, so it becomes transparent. The figure shows a clear trend that the size of this near zone decreases for higher redshifts, as would be expected due to the higher gas density and probably larger mean neutral fraction in the Universe. Thus, these very luminous objects are able to reionize the intergalactic medium in their immediate surroundings, but their effect is constrained to a rather limited volume. Most of the ionizing photons must come from the far more numerous lower-mass galaxies, i.e., far less luminous sources.

The UV-luminosity function at high redshifts. The large number of LBG candidates at redshifts z ≳ 7 recently obtained yields constraints on the luminosity function of galaxies in the rest-frame ultraviolet regime of the spectrum. As pointed out in Sect. 9.2.4, for most of them no spectroscopic confirmation is available, so that each individual case is burdened with uncertainty. We have an idea of what the UV-luminosity function looks like for z ≲ 8, as shown in Fig. 9.41, but the star-formation rate density beyond z ∼ 8 is still very uncertain, as shown in Fig. 9.57.

Since at such high redshifts, high-mass dark matter halos were extremely rare, we actually expect that most star formation at z ∼ 10 occurs in very low-mass systems which will be very difficult to detect. Thus, in order to translate the observed luminosity function into a star-formation rate, large extrapolations towards very low-luminosity sources are required, burdened with substantial uncertainties.

The UV-slope. The radiation we observe from high-redshift galaxies corresponds to wavelengths longward of the Lyα transition, i.e., at wavelengths considerably larger than that of ionizing photons. Therefore, to relate the observed properties to the ionizing power, the spectral shape needs to be extrapolated to shorter wavelengths.

This extrapolation is done using a power law for the UV-continuum which is conventionally parametrized as S _λ ∝ λ ^β . A source with slope $\beta = -2$ corresponds to a flat spectrum in S _ν , for which the AB-magnitudes (see Sect. A.4) would be independent of the chosen filter. Hence, in order to relate the observed flux of sources to their emission of ionizing photons, the slope β must be known. In principle, a very young, low-metallicity stellar population can have a hard spectrum with β ∼ −3, but as soon as the metallicity increases above $\sim 10^{-2}Z_{\odot }$ or the age of the stellar population is larger than ∼ 10⁷ yr, the spectrum will get flatter; of course, any extinction (and related reddening) leads to an increase of β as well.

In principle, the slope β can be obtained from observing galaxies in at least two wavebands. For the highest-redshift sources, that corresponds to bands in the observed near-IR regime. Unfortunately, even relatively small photometric uncertainties translate into rather large error bars on β. At present, observations seem to indicate that the mean value of β is between − 2 and − 2. 5 for z ∼ 7 galaxies.

The escape fraction. Even if the extrapolation from the observed rest-frame UV at λ ∼ 1500 Å to the ionizing region of λ < 912 Å were accurate, we still would not know the emission of ionizing photons from these galaxies. The interstellar medium in these objects is expected to absorb many of the ionizing photons, before they can escape the galaxy. The escape fraction f _esc is very uncertain, and any theoretical estimate of it is highly model dependent.

We thus conclude that, using reasonable guesses (within the current observational constraints) regarding the UV-luminosity function at high-z, the UV-slope β, and the escape fraction (f _esc ∼ 0. 2, as is suggested from the properties of z ∼ 3 LBGs), the number density of ionizing photons emitted from the early galaxies may be sufficient to explain the reionization of the Universe at z ∼ 10, as suggested by the results from the CMB anisotropies.

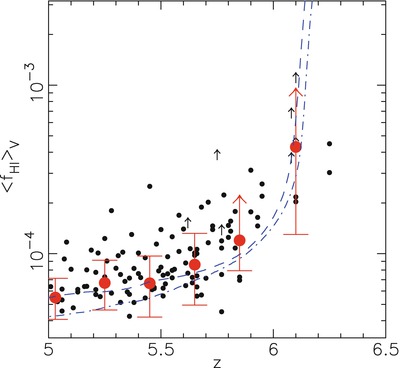
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig10_HTML.jpg

Fig. 10.10

Redshift evolution of the mean neutral fraction of hydrogen in the intergalactic medium, as obtained from the absorption of ionizing radiation from high-redshift QSOs (Gunn–Peterson effect). Individual measurements are shown as small dots, whereas the large circles with error bars represent averages over redshift bins. The two curves show results from numerical simulations. Source: X. Fan et al. 2006, Constraining the Evolution of the Ionizing Background and the Epoch of Reionization with z ∼ 6 Quasars. II. A Sample of 19 Quasars, AJ 132, 117, p. 126, Fig. 7. ©AAS. Reproduced with permission

Towards a larger neutral hydrogen fraction.

The observed spectrum of high-redshift QSOs shortwards of the Lyα emission line shows that an increasing fraction of the radiation is absorbed by neutral hydrogen on the line-of-sight. We have seen that the density of the Lyα forest increases with redshift (cf. Fig. 10.5) in such a way that only a tiny fraction of ionizing photons manage to escape absorption. This observation may be seen as an indication that we approach the epoch of reionization as the QSO redshift increases beyond z ∼ 6. However, as shown in Fig. 10.10, the mean neutral fraction of intergalactic hydrogen needed to cause this strong absorption of ionizing photons is still very small—a neutral fraction of much less than 1 % is sufficient to entirely block the light of QSOs shortward of the Lyα emission. Hence, the strong absorption implied by QSO spectra cannot be taken as evidence for z ∼ 6 signalling the end of the reionization epoch. Nevertheless, the trend of the data shown in Fig. 10.10 may suggest that beyond z ∼ 6, we may approach a phase where the neutral hydrogen fraction indeed starts to increase significantly.

Observing reionization directly may in principle be possible if a very high-redshift QSO could be identified whose absorption spectrum could reveal a tomographic view through the ionized ‘bubbles’ of the intergalactic medium, as sketched in Fig. 10.11. But we point out again that the very dense Lyα forest seen towards QSOs at high redshift, is no unambiguous sign for approaching the redshift of reionization, because a very small fraction of neutral atoms (about 1 %) is already sufficient to produce a large optical depth for Lyα photons.

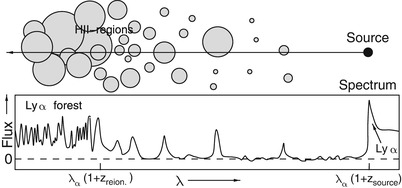
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig11_HTML.jpg

Fig. 10.11

Sketch of a potential observation of reionization: light from a very distant QSO propagates through a partially ionized Universe; at locations where it passes through Hii-regions, radiation will get through—flux will be visible at the corresponding wavelengths. When the Hii-regions start to overlap, the normal Lyα forest will be produced. Adapted from: R. Barkana & A. Loeb 2000, In the Beginning: The First Sources of Light and the Reionization of the Universe, astro-ph/0010468

With the upcoming Next Generation Space Telescope, the James Webb Space Telescope (JWST), one hopes to observe the epoch of reionization directly and to discover the first light sources in the Universe; this space telescope, with a diameter of 6.5 m, will be optimized for operation at wavelengths between 1 and 5 μm.

10.4 The formation of disk galaxies

We now turn to describe in somewhat more detail the fate of the cooling gas inside halos. The most important aspect in addition to the cooling processes described before is the fact that dark matter halos, and the gas inside of them, contain angular momentum. As we shall see, this naturally leads to the formation of galactic disks.

10.4.1 The contraction of gas in halos

We described in Sect. 7.6.2 that a non-spherical overdensity can attain an angular momentum, due to a torque caused by the tidal gravitational field in which the overdensity is located. Therefore, dark matter halos are born with a finite angular momentum, which we quantified by the spin parameter λ [see (7.65)]. Analytical estimates and numerical simulations show that the typical value is λ ∼ 0. 05, however with a rather broad distribution.

In the initial stages of the evolution of the overdensity, we expect that baryons and dark matter have the same spatial distribution, thus the specific angular momentum of the baryons and dark matter are the same. When the halo collapses, the gas distribution may become different from that of the dark matter, but the torque on the halo is strongest at maximum radius (i.e., at turnaround), and thus during collapse, little angular momentum is obtained.

When the gas in a halo cools, it collapses toward the center, thereby conserving its angular momentum. The gas can therefore not collapse to an arbitrarily small region; the angular momentum barrier prevents this. Frictional forces in the gas drive the gas onto approximately circular orbits, depending on the symmetries of the halo, in a plane perpendicular to the angular momentum vector—it forms a flat disk. The gas in the disk is much denser than it would be if the gas retained on almost spherical distribution; hence, gas in the disk finds it easier to cool and form stars—in accordance with observations: most of the quiescent star formation in the current Universe occurs in galactic disks.

The necessity for dark matter. Understanding the formation of disk galaxies requires the presence of dark matter, as we shall see now. Let us assume the contrary, namely that the density concentration which formed through gravitational instability consists solely of baryons. In this case, the baryons are also the only source of gravity. The characteristic spin parameter of the forming halo is about 0.05. The spin parameter of a self-gravitating, thin exponential disk can be calculated to be λ _d ≈ 0. 425. As the gas cloud collapses into a disk, it conserves its mass and its angular momentum, whereas it can get rid of energy by radiation emitted in the cooling processes. The binding energy scales like r ⁻¹. Therefore, the spin parameter scales like $r^{-1/2}$ , as follows from (7.65). The final spin parameter is thus related to the initial spin parameter λ _i by

$\displaystyle{ \lambda =\lambda _{\mathrm{i}}\sqrt{\frac{r_{\mathrm{i} } } {r}} \;, }$

(10.11)

where r _i is the radius of the virialized gas cloud before cooling. In order to get a spin parameter of ∼ 0. 42 for the exponential disk from a spin parameter λ _i obtained from tidal torques, the gas must collapse by a factor ∼ (0. 42∕0. 05)² ≈ 70.

We can take our Milky Way as an example for this process. The radius of the visible disk is of the order of 10 kpc, which, according to the previous assumptions, would have collapsed from an initial radius of ∼ 700 kpc. With a baryonic mass of $\sim 5 \times 10^{10}M_{\odot }$ for the Milky Way, the free-fall time from radius 700 kpc is ∼ 4 × 10¹⁰ yr, i.e., about three times the current age of the Universe. Therefore, the Milky Way disk could not have formed until today if it consisted only of baryonic matter. In fact, given that the Milky Way contains old stars, we have good reasons to assume that it has formed quite a bit before today, so that the discrepancy of time scales becomes even stronger.

Gas collapse in a dark matter halo. If, however, the gas contracts in a dark matter halo, the situation is quite different. Assume, for simplicity, that the density profile of the dark matter halo behaves like ρ ∝ r ⁻², up to the virial radius; this corresponds to the isothermal sphere which we discussed in Sect. 3.11.2 yielding a radius-independent rotational velocity V _c. If the halo has a spin parameter of λ = 0. 05, then the rotational velocity of the halo, and the gas inside of it, is about V _c∕7. If the gas sinks to the center, thereby conserving its specific angular momentum ∝ r v, it needs to reduce its radius by a mere factor of 7 to form a rotationally supported disk—an order of magnitude less than in the hypothetical case of baryon-only halos.⁴ The time-scale for the formation of a Milky Way-like disk is then reduced to ∼ 10⁹ yr, thus such disks can form sufficiently early in the cosmic evolution.

10.4.2 The formation of galactic disks

Empirically, it is found that the light distribution of disk galaxies follows an exponential law. Assuming a fixed mass-to-light ratio, this implies that the surface mass density Σ(R) behaves like

$\displaystyle{ \varSigma (R) =\varSigma _{0}\,\exp \left (-\frac{R} {R_{\mathrm{d}}}\right )\;, }$

(10.12)

where Σ ₀ is the central surface mass density, and R _d the scale-length of the disk. For the considerations that follow, we shall assume that the dark matter in the halo follows an isothermal density profile, and that the self-gravity of the disk is negligible. The former assumption is motivated by the observed flat rotation curves of disk galaxies; we point out that the rotational velocity predicted by NFW density profiles (see Sect. 7.6.1) is fairly constant over a broad range of radius.

Estimating the disk scale length. Starting from a dark matter halo, its virial mass M, virial radius r ₂₀₀ and virial velocity V ₂₀₀ are related through (7.58). The assumption of an isothermal profile then implies that the rotational velocity V _rot(r) = V ₂₀₀, independent of radius, and that the density profile is $\rho (r) = V _{200}^{2}/(4\pi Gr^{2})$ . If we assume that a fraction m _d of the halo mass is contained in the disk, we find for the disk mass

$\displaystyle\begin{array}{rcl} M_{\mathrm{d}}& =& m_{\mathrm{d}}\,M = m_{\mathrm{d}}\, \frac{V _{200}^{3}} {10\,G\,H(z)} \\ & \approx & 9 \times 10^{10}h^{-1}M_{ \odot }\left ( \frac{m_{\mathrm{d}}} {0.05}\right )\,\left ( \frac{V _{200}} {200\,\mathrm{km/s}}\right )^{3} \frac{1} {E(z)}\;,{}\end{array}$

(10.13)

where $E(z) = H(z)/H_{0}$ is the scaled Hubble function. On the other hand, the disk mass follows from (10.12),

$\displaystyle\begin{array}{rcl} M_{\mathrm{d}}& =& 2\pi \int _{0}^{\infty }\mathrm{d}R\;R\,\varSigma (R) = 2\pi R_{\mathrm{ d}}^{2}\varSigma _{ 0}\int _{0}^{\infty }\mathrm{d}x\;x\,\mathrm{e}^{-x} \\ & =& 2\pi R_{\mathrm{d}}^{2}\varSigma _{ 0}\; {}\end{array}$

(10.14)

where we set $x = R/R_{\mathrm{d}}$ in the last step. In the isothermal density profile of the dark matter halo, the rotational velocity of the disk is constant, and so its angular momentum is

$\displaystyle\begin{array}{rcl} J_{\mathrm{d}}& \,=\,& 2\pi \!\int _{0}^{\infty }\!\mathrm{d}R\,R^{2}\,V _{ 200}\,\varSigma (R)\,=\,2\pi V _{200}\varSigma _{0}R_{\mathrm{d}}^{3}\int _{ 0}^{\infty }\!\mathrm{d}x\,x^{2}\,\mathrm{e}^{-x} \\ & =& 4\pi V _{200}\varSigma _{0}R_{\mathrm{d}}^{3}\,=\,2M_{\mathrm{ d}}R_{\mathrm{d}}V _{200}\;, {}\end{array}$

(10.15)

where in the last step we used (10.14). We assume that the angular momentum of the disk is a fraction j _d of the total angular momentum of the halo, J _d = j _d J _h. The latter can be related to the spin parameter λ in (7.65), which in addition contains the total energy of the halo and the halo mass. The total energy follows from the virial theorem and the simple properties of an isothermal sphere, $\vert E\vert = MV _{200}^{2}/2$ . We then find

$\displaystyle{ \lambda = \frac{J_{\mathrm{h}}\vert E\vert ^{1/2}} {GM^{5/2}} = \left (\frac{m_{\mathrm{d}}} {j_{\mathrm{d}}} \right )\,\frac{2R_{\mathrm{d}}V _{200}\vert E\vert ^{1/2}} {GM^{3/2}} \;, }$

(10.16)

where we used (10.15) in the last step. Solving for R _d, this yields

$\displaystyle{ R_{\mathrm{d}} = \frac{\lambda GM} {\sqrt{2}V _{200}^{2}}\left ( \frac{j_{\mathrm{d}}} {m_{\mathrm{d}}}\right )\;, }$

(10.17)

where we inserted the expression for the binding energy. Finally, using (7.58) again, this can be written in the form

$\displaystyle\begin{array}{rcl} R_{\mathrm{d}}& =& \frac{1} {\sqrt{2}}\left ( \frac{j_{\mathrm{d}}} {m_{\mathrm{d}}}\right )\lambda \,r_{200} \\ & =& \frac{1} {\sqrt{2}}\left ( \frac{j_{\mathrm{d}}} {m_{\mathrm{d}}}\right )\lambda \left ( \frac{V _{200}} {10H(z)}\right ) \\ & \approx & 7h^{-1}\,\mathrm{kpc}\left ( \frac{j_{\mathrm{d}}} {m_{\mathrm{d}}}\right )\left ( \frac{\lambda } {0.05}\right )\left ( \frac{V _{200}} {200\,\mathrm{km/s}}\right ) \frac{1} {E(z)}\;.{}\end{array}$

(10.18)

Interpretation. This equation contains a number of interesting aspects. The first expression relates the virial radius of the halo to the scale-length of the disk. If we assume that the average specific angular momentum of the gas in the disk is the same as the average specific angular momentum of the halo, then j _d = m _d, and we simply get $R_{\mathrm{d}} = r_{200}\lambda /\sqrt{2}$ ; using the characteristic value of λ ∼ 0. 05, we obtain r ₂₀₀ ∼ 30R _d. For the Milky Way, R _d ≈ 3. 5 kpc, so that its virial radius is predicted by this consideration to be about 100 kpc.

The final expression in (10.18) relates the virial velocity—for the assumed isothermal distribution, this is the same as the rotational velocity—to the scale-length of the disk. Again using the Milky Way as an example, for which V _rot ≈ 220 km∕s, we see that the predicted scale length is about a factor of two larger than the observed one, for the same parameters. Thus, although this simple model provides a result which is within a factor ∼ 2 of the observed properties of the Milky Way disk, it fails to yield an accurate quantitative agreement. Of course it is possible that our Galaxy formed inside a halo where the spin parameter has a rather low value, or that the disk fraction of angular momentum is different from its mass fraction. For example, if we keep the assumption j _d = m _d, a spin parameter of λ ∼ 0. 02 would predict roughly the correct scale length, but such low values of λ have a rather small probability to occur. Furthermore, it would also lead to a large virial radius of ∼ 250 kpc, predicting a very massive halo for the Milky Way.

However, there is another issue of (10.18) which does not really fit the observations. The function E(z) at redshift z = 1 is $E(1) = \sqrt{8\varOmega _{\mathrm{m} } +\varOmega _{\varLambda }} \sim 1.7$ , implying that galactic disks at that epoch are considerably smaller than those today. Such a strong size evolution of disks is not consistent with the observations.

A third issue with this simple consideration is the mass fraction of baryons that end up in the disk. With a disk mass of $M_{\mathrm{d}} \sim 5 \times 10^{10}M_{\odot }$ for the Milky Way, (10.13) predicts about m _d ∼ 0. 02. If we assume that the halo contained the same baryon fraction as the cosmic mean at halo formation, then only about 10 % of the baryons end up in the disk. As we shall see later, there are processes which prevent gas from settling down is a disk, but it is difficult to find such processes efficient enough to hold back 90 % of the baryons.

Refinements of the model. The simplified model made a number of assumption which we know can not be correct in detail: Real dark matter halos do not have an isothermal profile, but follow approximately an NFW profile in which the rotational velocity is a slow function of galactocentric radius. In addition, the contraction of gas changes the overall gravitational potential of the halo, which also affects the dark matter distribution; the dark matter also gets somewhat more concentrated towards the halo center. This halo contraction will change the rotational velocity further.

The rotation curves of spiral galaxies show that the neglect of the disk self-gravity is an oversimplification. Within the optical radius of a disk, the baryons in the disk contribute substantially to the gravitational field. This is in accord with what we have learned from gravitational lensing studies of galaxies which show that within the Einstein radius, about half the mass is contributed by the baryonic component. Numerical simulations of disk galaxy formation which take the gas cooling and halo contraction into account indicate that the rotational velocity of disks is closely approximated by the maximum rotational velocity of an NFW profile (see Fig. 7.19) instead of the virial circular velocity.

Both, inclusion of self-gravity and the halo contraction lead to larger rotational velocities in the inner part of the halo compared to the simple model. As a consequence, the size and mass of the halo is smaller than obtained from the simple model, so that the corresponding estimate of m _d is increased. The proper inclusion of these two effects also yields a much smaller redshift-dependence of the scale-length than predicted by (10.18), i.e., considerably closer to the observational situation.

We thus conclude that the model described here, once accounting for the effects of disk self-gravity and halo contraction, provides a good quantitative model for understanding the formation of disk galaxies.

10.4.3 Dynamical effects in disks

Once the disk has formed, the gas is sufficiently dense so that star formation can proceed; we have seen in Sect. 3.3.3 before that the Schmidt-Kennicutt law describes the star-formation rate (per unit disk area) as a function of surface mass density. Hence, after some time a thin stellar disk is formed, with some fraction of the baryons left over in the form of gas.

Such a thin disk is subject to dynamical instabilities. Whereas in an axi-symmetric gravitational potential, stars move on circular orbits, perturbations of the gravitational field can perturb these orbits, which in turn can amplify the deviation from axial symmetry. The formation of spiral arms is one example of such perturbations. Another important aspect is the formation of bars in the center of a large fraction of spiral galaxies. The asymmetry of the bars can yield significant perturbations of the potential with corresponding changes of orbits, leading to a redistribution of mass and angular momentum. In particular, bars can cause stars and gas to migrate inwards, towards the center.

Pseudo-bulges. The corresponding accumulation of gas can trigger increased star formation in the center of galaxies. These stars then form a concentration at the galactic center. It is generally believed that this is the mechanism for the formation of pseudo-bulges in spiral galaxies—we recall that bulges are divided into classical bulges and pseudo-bulges, the latter being characterized by a Sérsic-index close to unity and fast rotation, whereas the former ones have a Sérsic-index close to that of ellipticals and considerably slower rotation. The formation of classical bulges is thus suspected to be related to the formation of elliptical galaxies, which will be discussed below.

Heating of the stellar distribution. We have seen in Sect. 2.3.1 that the velocity dispersion of stars in the Milky Way disk depends on their age—the older the stars, the higher their random velocities. Stars are formed by the molecular gas which is observed to have the thinnest distribution. Over their lifetime, the stars can gain a random velocity component, by scattering on the perturbations of the gravitational potential, such as caused by giant molecular clouds, spiral arms, or the subhalo population that we discussed in Sect. 7.8. Whatever the main source of heating, the trend with stellar age is expected in all these cases.

10.4.4 Feedback processes

Although the story as told above naturally leads to the formation of disk galaxies, early studies have shown that some ingredients are missing. In fact, hydrodynamical simulations of disk formation show that star formation in the gas disks is far too efficient, consuming the available gas in too short a time, so that most of the stars would be formed at high redshift, with little current star formation left. Furthermore, the resulting disks are too concentrated and too small, leading to rotation curves which are declining outwards beyond the (small) half-light radius of the disk, in marked contrast with observed rotation curves. This together is known as the overcooling problem in galaxy evolution. Real disk galaxies have a slower conversion of gas into stars and their disks remain larger. And finally, the efficient conversion of gas into stars in our simple model would predict that the stellar mass density in the Universe is much higher than observed—whereas Ω _b ∼ 0. 04, the density parameter in stars is less than 1 %. Hence, most baryons in the Universe habe not been converted to stars.

Feedback by supernovae. In order to balance the efficient gas cooling, heating sources need to be considered. An unavoidable source of heating is the energy injected into the interstellar medium by supernovae. Very shortly after star formation sets in, the most massive stars of the stellar population undergo a core-collapse supernova. The mechanical energy of the explosion is partly transferred to the gas surrounding the exploding star. Thereby the gas is heated, causing it to expand, thus to decrease its density, which in turn reduces its cooling efficiency. Note that this is a feedback process—the higher the star formation rate, the more energy is injected into the interstellar gas to prevent, or at least delay, further star formation. Depending on the efficiency of this feedback, the local gas of the disk may be blown out of the disk into the halo (and produce a hot gas corona outside the disk—see Sect. 3.3.7), or, in particular for low-mass halos, be removed from the halo through outflowing gas.

In fact, there is direct observational evidence of the occurrence of outflows from star-forming galaxies. For example, we have seen in Sect. 9.1.1 that the spectra of Lyman-break galaxies reveal substantial mass outflows, at a similar rate as their star-formation rate and with velocities of several hundreds of km/s.

The details of this feedback process are somewhat uncertain—how much of the supernova energy is converted into heat, and how much is transferred to the interstellar medium in form of bulk kinetic energy, is not well determined. Furthermore, the feedback by supernovae depends on the assumed initial mass function (IMF; see Sect. 3.5.1) of stars, which yields the fraction of newly formed stars which explode as core-collapse supernova. The flatter the IMF at the high-mass end, the more supernova energy per unit mass of newly formed stars is injected.

Assuming a universal IMF, the energy released by supernovae per unit mass of newly-formed stars is η _SN E _SN, where η _SN denotes the expected number of supernovae per unit mass of formed stars, and E _SN is the energy released per supernova. If we assume that this energy reheats some of the cold gas back to virial temperature of the halo, the amount of gas that is reheated after formation of a group of stars with mass Δ m _∗ is

$\displaystyle{ \varDelta m_{\mathrm{reheat}} \sim \epsilon \, \frac{\eta _{\mathrm{SN}}\ E_{\mathrm{SN}}} {V _{200}^{2}} \varDelta m_{{\ast}}\, }$

(10.19)

where ε parametrizes the efficiency of the reheating process. The reheated gas may be transferred back to the hot gaseous halo, whereas other models assume that the reheated gas is first ejected from the halo, and only later reincorporated into the hot halo on the dynamical time-scale of the halo. This ejection scenario effectively delays the time at which the reheated gas can cool and becomes available for star formation again.

As can be seen from (10.19), supernova feedback is more efficient at suppressing star formation in low-mass galaxies—which is due to the fact that the binding energy per unit mass is an increasing function of halo mass. This simply expresses the fact that for low-mass halos it is easier to drive the gas outwards.

AGN feedback. Whereas supernova feedback explains a decreasing conversion of gas into stars with decreasing halo mass, and thus can account for the difference of the slopes between the galaxy luminosity function and the halo mass function at the low mass/luminosity end (see Fig. 10.2), it is less efficient for higher-mass halos, due to the larger V ₂₀₀ in (10.19). The increase of the cooling time for higher-mass halos (see Fig. 10.4) by itself cannot account for the abrupt exponential decrease of the galaxy luminosity function beyond L ^∗. One requires another process which delays the cooling of gas in high-mass halos.

For very massive halos, we have already encountered such a process: The suppression of cooling flows in galaxy clusters is due to AGN activity of the central galaxy in the cluster. Since (almost) all massive galaxies contain a supermassive black hole (see Sect. 3.8), this kind of feedback may be operational not only in groups and clusters, but actually in individual massive galaxies as well. In particular, there is a great deal of evidence for a relation between nuclear starbursts in galaxies and AGN activity. The gas needed for a starburst in the center of a galaxy is also potential fuel for the central black hole. Again, the details of this process are quite uncertain, but with plausible prescriptions, the cut-off of the luminosity function at L ≳ L ^∗ can be successfully modeled.

Feedback by an AGN can occur in several ways. In the case of galaxy clusters, the major effect of the AGN is the insertion of hot bubbles into the intracluster medium through radio jets. The AGNs in most central cluster galaxies are not very luminous, and seem to be in the ‘radio mode’ (see Sect. 5.5.5) of low accretion rate. Thus, for low accretion rates, the main channel of feedback is the injection of mechanical energy into the surrounding gas. At high accretion rates, in the ‘quasar mode’, the main source of feedback is presumably heating of the gas. Furthermore, the strong radiation field from quasars changes the ionization structure of the surrounding gas, which affects its cooling curve compared to the one shown in Fig. 10.3 and at low temperatures actually leads to radiative heating. These various effects should be included in realistic models of the evolution of galaxies, at least in an approximate way; we shall come back to this below.

10.4.5 The formation and evolution of supermassive black holes

Black holes grow in mass by accreting material, a process we witness through the radiation from accreting black holes in AGNs (Chap. 5). Hence, once a population of supermassive black holes (SMBHs) is present, their evolution can be studied observationally, as well as through modeling. But how did the first generation of SMBH form? There is no firm conclusion on this question, but three plausible formation processes have been studied in detail. What we do know, however, is that the first SMBHs must have formed very early in the Universe, as indicated by the presence of very luminous QSOs at z > 6.

Remnants of population III stars. The first stars in the Universe form out of primordial gas, i.e., gas with zero metallicity. The cooling properties of this gas are quite different from those of enriched material, since no metal lines are available for radiating energy away. From simulations of star formation in primordial gas, it is suggested that many stars can form with very high masses, well above $100M_{\odot }$ . These stars burn their nuclear fuel very quickly, in a few million years, before they end their lives explosively. If the mass of a star is above $\sim 250M_{\odot }$ , its supernova will leave a black hole behind with a mass of $\gtrsim 100M_{\odot }$ . Since the first stars are expected to form at $z \gtrsim 20$ , this formation mechanism would yield a very early population of seed black holes. However, it is still unknown whether such very massive population III stars indeed formed.

Gas-dynamical processes. Another route for the formation of supermassive black holes arises if the primordial gas in a high-redshift dark matter halo manages to concentrate in its center, through global dynamical instabilities (e.g., related to the formation of bar-like structures) that are able to transport angular momentum outwards. This angular momentum transport is needed since otherwise, the central concentration of gas would be prevented by the angular momentum barrier. Subsequent cooling by molecular hydrogen may then lead to the formation of a rapidly rotating supermassive star with up to $10^{6}M_{\odot }$ , provided the accumulation of the gas occurs rapidly enough. Once the inner core of this supermassive star has burned its hydrogen, the core will collapse and form a black hole with a few tens of $M_{\odot }$ , where this mass depends on the initial angular velocity of the star. This black hole subsequently accretes material from the outer layers of the star, and this quasi-spherical accretion has a very low radiative efficiency ε. Therefore, the black hole can grow in mass quickly, until finally its exceeds the Eddington luminosity and the remaining gas is expelled, leaving behind a SMBH with $\sim 10^{5}M_{\odot }$ .

Stellar-dynamical processes. In the inner part of a forming galaxy, dense nuclear star clusters may form. Because of the high density, star-star collisions can occur which can lead to the formation of very massive stars with mass exceeding $10^{3}M_{\odot }$ . This has to happen very quickly, before the first stars explode as supernovae, since otherwise the massive star would be polluted with metals, its opacity increased, and it would no longer be stable. The fate of this supermassive star is then similar to the scenario described above, resulting in a black hole remnant of several hundred Solar masses.

These three possibilities are not mutually exclusive. At present, our theoretical understanding of these processes is not sufficient to establish their likelihood of occurrence. Whereas one may be able to distinguish between these scenarios, e.g., from the statistics of black hole masses in present day low-mass galaxies, the current observational situation does not conclusively support or reject any of these three routes.

Mass growth. Once the seed black holes have formed, they can grow in mass by accreting material. We saw in Sect. 5.3.5 that the characteristic time-scale for mass growth, i.e., the time on which the black hole mass can double, is $\epsilon t_{\mathrm{gr}} = \epsilon M_{\bullet }c^{2}/L_{\mathrm{edd}} \approx 5\epsilon \times 10^{8}\mathrm{yr}$ . With ε ∼ 0. 1, a $10^{4}M_{\odot }$ seed black hole formed at z ∼ 20 could grow to a $\mathrm{few} \times 10^{8}M_{\odot }$ by redshift 7 if it accreted continuously at the Eddington rate. The situation is more difficult for seed black holes formed from population III stars; they probably require super-Eddington accretion rates to be able to power the luminous QSOs at z > 6. As mentioned in Sect. 5.3.5, the accretion rate may exceed the Eddington rate though probably not by a large factor.

10.4.6 Cosmic downsizing

The hierarchical model of structure formation predicts that smaller-mass objects are formed first, with more massive systems forming later in the cosmic evolution. As discussed before, there is ample evidence for this to be the case; e.g., galaxies are in place early in the cosmic history, whereas clusters are abundant only at redshifts z ≲ 1. However, looking more closely into the issue, apparent puzzles are discovered. For example, the most massive galaxies in the local Universe, the massive ellipticals, contain the oldest population of stars, although at first sight, their formation should have occurred later than those of less massive galaxies. In turn, most of the star formation in the local Universe seems to be associated with low- or intermediate-mass galaxies, whereas the most massive ones are passively evolving. Now turning to high redshift: for z ∼ 3, the bulk of star formation seems to occur in LBGs and SMGs, which, according to their clustering properties (see Sect. 9.1.1), are associated with high-mass halos. The study of passively evolving EROs indicates that massive old galaxies were in place as early as z ∼ 2, hence they must have formed very early in the cosmic history. The phenomenon that massive galaxies form their stars in the high-redshift Universe, whereas most of the current star formation occurs in galaxies of lower mass, has been termed ‘downsizing’. We saw in Sect. 5.6.2 that a similar phenomenon also is observed for AGNs.

This downsizing can be studied in more detail using redshift surveys of galaxies. The observed profile of the absorption lines in the spectra of galaxies yields a measure of the characteristic velocity and thus the mass of the galaxies (and their halos). Studies carried out in the local Universe showed that local galaxies have a bimodal distribution in color (see Sect. 3.1.3), which in turn is related to a bimodal distribution in the specific star-formation rate. Extending such studies to higher redshifts, by spectroscopic surveys at fainter magnitudes, we can study whether this bimodal distribution changes over time. In fact, such studies reveal that the characteristic mass separating the star-forming galaxies from the passive ones evolves with redshift, such that this dividing mass increases with z. For example, this characteristic mass decreased by a factor of ∼ 5 between z = 1. 4 and z = 0. 4. Hence, the mass scale above which most galaxies are passively evolving decreases over time, restricting star formation to increasingly lower-mass galaxies.

Studies of the fundamental plane for field ellipticals at higher redshift also point to a similar conclusion. Whereas the massive ellipticals at z ∼ 0. 7 lie on the fundamental plane of local galaxies when passive evolution of their stellar population is taken into account, normal ellipticals of lower mass at these redshifts have a smaller mass-to-light ratio, indicating a younger stellar population. Also here, the more massive galaxies seem to be older than less massive ones. To reproduce these evolutionary effect requires to account for AGN feedback in models of galaxy evolution.

10.5 Formation of elliptical galaxies

Properties of ellipticals. Whereas the formation of disk galaxies can be explained qualitatively in a relatively straightforward way, the question of the formation of ellipticals is considerably more difficult to answer. Stars in ellipticals feature a high velocity dispersion, indicating that they were not formed inside a cool gas disk, or that the stellar distribution was subsequently heated very strongly. On the other hand, it is hard to comprehend how star formation may proceed without gas compression induced by dissipation and cooling.

In Sect. 3.4.3 we saw that the properties of ellipticals are very well described by the fundamental plane. It is also found that the evolution of the fundamental plane with redshift can almost completely be explained by passive evolution of the stellar population in ellipticals. In the same way, we stated in Sect. 6.8 that the ellipticals in a cluster follow a very well-defined color-magnitude relation (the red cluster sequence), which suggests that the stellar populations of ellipticals at a given redshift all have a similar age. By comparing the colors of stellar populations in ellipticals with models of population synthesis, an old age for the stars in ellipticals is obtained, as shown in Fig. 3.35

Monolithic collapse. A simple model is capable of coherently describing these observational facts, namely the monolithic collapse. According to this description, the gas in a halo is nearly instantaneously transformed into stars. In this process, most of the gas is consumed, so that no further generations of stars can form later. For all ellipticals with the same redshift to have nearly identical colors, this formation must have taken place at relatively high redshift, say z ≳ 2, so that the current ellipticals are all of essentially the same age. This scenario thus requires the formation of stars to happen quickly enough, before the gas can accumulate in a disk. The process of star formation remains unexplained in this picture, however, and most likely this model does not describe the processes that are responsible for the formation of ellipticals.

Instead, we have very good reasons to believe that elliptical galaxies form as a consequence of galaxy transformations. For example, we have seen that most ellipticals are found in dense environments, like groups and clusters, and within these high-mass structures, they are concentrated towards their center. In other words, elliptical galaxies are located in regions where, due to the enhanced density, interactions of galaxies happen preferentially. Furthermore, elliptical galaxies have rather complicated kinematics, often exhibiting small disks (sometimes counter-rotating) around their center, shells and ripples, which indicate a lively history of these objects. From a theoretical view, hierarchical structure formation predicts that high-mass halos are formed by merging of smaller ones, and so the collision of halos and their embedded galaxies must play a role in the distribution of galaxy properties. We shall therefore take a closer look at such halo mergers.

10.5.1 Merging of halos and their galaxies.

When two halos merge to form one with larger mass, their baryonic components will be affected as well. We have seen spectacular examples of this process in the form of colliding galaxies (e.g., Fig. 1.16). Clearly, after the two spiral galaxies collided, the resulting stellar distribution does not resemble that of a spiral anymore. Mergers of halos, and associated collision of galaxies, lead to morphological transformation of galaxies. Furthermore, such galaxy collisions are generally accompanied by massive star bursts. Hence, also the stellar population of the resulting object is affected by collisions.

In the Antennae (see Fig. 9.25), the mass of the two galaxies which collide is about equal. However, one expects that the collision of galaxies with very different masses is more frequent, and such mergers will have different consequences for the respective galaxies. One thus distinguishes between minor mergers, where the mass ratios of halos is large (typically in excess of 3:1), and major mergers where the two masses are similar.

Conditions for merging. Not every (near) collision of two halos leads to a merger. For example, we have seen in the bullet cluster (Sect. 6.6.2) that the two clusters simply move through each other, since their dark matter and stellar components are collisionless. Only the (collisional) gas components of the two clusters are strongly affected by this collision, but no merging will take place. The reason is that the relative velocity of these two clusters at collision is much larger than their internal velocity dispersion, or expressed differently, that the collision speed is much higher than the escape velocity of each cluster component.⁵ In order for a merger to happen, the collisional speed has to be of the same order, or smaller, than the intrinsic velocity dispersion. This implies that effective mergers of galaxies do not occur in massive clusters, where the velocity dispersion of the galaxies of the cluster—which is also the characteristic collision velocity—is considerably higher than the stellar velocity dispersion of the individual galaxies. In contrast, groups of galaxies have both, a high density of galaxies making collisions probable, and a sufficiently low velocity dispersion to enable the merging of galaxies. Hence we expect that the most efficient merging of galaxies happens in groups.

Minor mergers. Consider what may happen in the merging of two halos with their embedded galaxies. The outcome of a merger depends on several parameters, like the relative velocity, the impact parameter, the angular momenta, the orientation of their rotation, and particularly the mass ratio of the two merging halos. If a smaller galaxy merges with a massive one, the properties of the dominating galaxy are expected to change only marginally: the small galaxy will be embedded into the bigger halo, and survive as a satellite galaxy for a long while. Examples of this are the Magellanic Clouds, which orbit around the center of the Milky Way in its dark matter halo. Depending on the orbit of the satellite galaxy, it will not survive forever. Tidal forces strips matter from the outer parts of the satellite’s dark halo, which is thus expected to lose mass—the closer it orbits near the center, the stronger the tidal forces, and thus the higher the mass-loss rate.

Dynamical friction (see Sect. 6.3.3) acts on the satellite, causing it to lose orbital energy and angular momentum, which is transferred (mostly) to the dark matter halo of the massive collision partner. The satellite slowly migrates towards the center, and gets disrupted due to the stronger tidal forces there. The stars of the satellite galaxy are simply added to the stellar population of the massive galaxy, since the stars of the satellite have a small velocity dispersion, they are added as coherent ‘streams’ to the main galaxy (see Fig. 3.17). Such a ‘minor merger’ is currently taking place in the Milky Way, where the Sagittarius dwarf galaxy is being torn apart by the tidal field of the Galaxy, and its stars are being incorporated into the Milky Way as an additional population. This population has, by itself, a relatively small velocity dispersion, forming a cold stream of stars that can also be identified as such by its kinematic properties. However, the large-scale structure of the Galaxy is nearly unaffected by a minor merger like this.

The thick disk and the stellar halo. Spiral galaxies have, beside the thin stellar and gas disk, also a thick disk with distinct properties: it has a substantially larger scale-height (by a factor of ∼ 3) and a stellar population with lower metallicity and old age. Thick disks have been explained by a number of different models. For example, they could consist of stars formed in the thin disk, and being heated so strongly that their vertical velocity dispersion causes this population to thicken substantially. However, the clearly different age distribution of thick-disk stars provides an obstacle for this explanation which rather predicts a continuous transition from thin to thick-disk stars. Nevertheless, the satellite galaxies and their associated subhalos may well be a substantial source of heating.

Minor mergers provide an alternative explanation for the origin of thick disks. Due to dynamical friction, satellite galaxies are dragged into the plane of the disk of the parent galaxy, and their subsequent disruption leaves their stars in the plane of the disk. As the minor merger partner is of low mass, the age of the thick disk is expected to be old—we have seen that low-mass halos preferentially form their stars very early in cosmic history, before heating by an ionizing background radiation prevents efficient star formation. It is thus conceivable that the stars of the thick disk, and also those of the stellar halo, are relics of earlier minor mergers. The fact that an increasing number of stellar streams are found in the Milky Way and other neighboring galaxies, as well as numerical simulations, support this picture.

Thus, in summary, minor mergers do not alter the properties of the major collision partner strongly. The dark matter halo increases its mass, in the form of subhalos (which later on may be disrupted), the stellar population of the low-mass galaxy first forms a satellite galaxy, which later can be disrupted and added to the stellar population of the parent galaxy, probably with somewhat different kinematical properties.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig12_HTML.jpg

Fig. 10.12

The galaxy Centaurus A. The optical image is displayed in grayscales, the contours show the radio emission, and in red, an infrared image is presented, taken by the ISO satellite. The ISO map indicates the distribution of dust, which is apparently that of a barred spiral. It seems that this elliptical galaxy features a spiral that is stabilized by the gravitational field of the elliptical. Presumably, this galaxy was formed in a merger process; this may also be the reason for the AGN activity. Credit: ESA/ISO, ISOCAM Team, I.F. Mirabel and O. Laurent (CEA/DSM/DAPNIA), et al. 1998, astro-ph/9810419

Major mergers and morphological transformations of galaxies. The situation is different in a merger process where both partners have a comparable mass. In such ‘major mergers’ the galaxies will change completely. The disks will be destroyed, i.e., the disk population attains a high velocity dispersion and can transform into a spheroidal component. Furthermore, the gas orbits are perturbed, which may trigger massive starbursts like, e.g., in the Antenna galaxies. By means of this perturbation of gas orbits, the SMBH in the centers of the galaxies can be fed, initiating AGN activity, as it is presumably seen in the galaxy Centaurus A shown in Fig. 10.12. Due to the violence of the interaction, part of the matter is ejected from the galaxies. These stars and the respective gas are observable as tidal tails in optical images or by the 21 cm emission of neutral hydrogen. From these arguments, which are also confirmed by numerical simulations, one expects that in a ‘major merger’ an elliptical galaxy may form. In the violent interaction, the gas is either ejected, or heated so strongly that any further star formation is suppressed.

Dry vs. wet mergers. However, the situation is slightly more complicated than this. The violent starbursts, associated with the collision of gas-rich galaxies, generate a population of newly-born stars. If such mergers happen at redshifts z ≲ 2, the stellar population of the resulting galaxy may not resemble the ‘dead and red’ properties of observed ellipticals. Therefore, if ellipticals are formed through major mergers of gas-rich galaxies, that had to happen at an early epoch. One often calls the mergers where the two progenitor galaxies are gas-rich ‘wet’ mergers, and contrasts them to ‘dry’ mergers where gas plays only a small role.

Besides the issue of star formation, wet mergers are characterized by the dissipational properties of the gas. The associated friction can lead to higher spatial densities than it is possible for collisionless matter only. The gas can be driven towards the center of the merger remnant, condense there and form new stars. This process increases the matter density relative to the case of dry mergers.

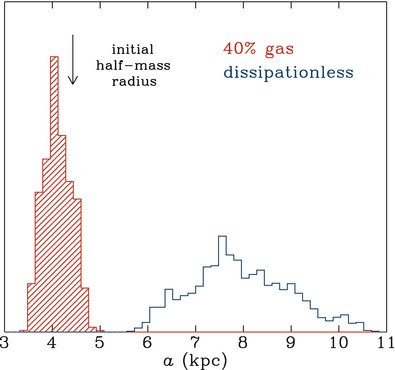
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig13_HTML.jpg

Fig. 10.13

Resulting distribution of the (half-light) semi-major axis a of merger remnants. The merging of identical disk galaxies was simulated, using a distribution of initial conditions, concerning orbital parameter and orientation of the disks. The merger remnants have fairly elliptical isophotes. Two families of simulations were considered: in the first one, the stellar disk of the progenitor galaxies consisted only of stars (dissipationless), whereas for the second family, a gas fraction of 40 % was assumed. The figure shows that the stellar distributions from dissipationless merger remnants have a rather large size, considerably larger than elliptical galaxies (the arrow indicates the half-mass radius of the progenitor disks). The inclusion of gas and corresponding cooling and star formation drastically changes this distribution towards considerably smaller sizes, in agreement with observations. Source: T.J. Cox et al. 2006, The Kinematic Structure of Merger Remnants, ApJ 650, 791, p. 795, Fig. 3. ©AAS. Reproduced with permission

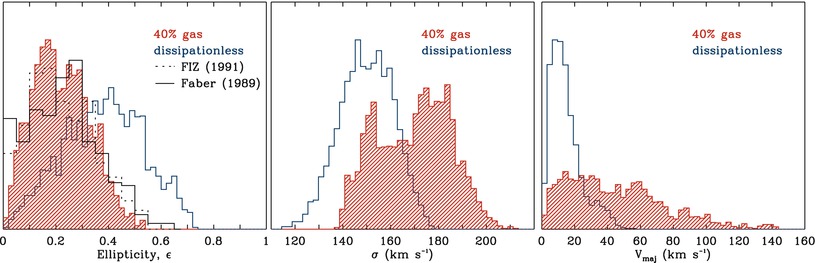
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig14_HTML.jpg

Fig. 10.14

From the same simulations as those described in Fig. 10.13, the distribution of ellipticity (left panel), central velocity dispersion (middle) and maximum velocity along the major axis (right) are shown. In each panel, the blue curves are from the dissipationless simulations, whereas for the red hatched histograms, gas physics was taken into account. The black curve in the left panel depicts the observed distribution of galaxy ellipticities. Source: T.J. Cox et al. 2006, The Kinematic Structure of Merger Remnants, ApJ 650, 791, p. 795, Fig. 3. ©AAS. Reproduced with permission

Early numerical simulations of galaxy mergers considered just the collisionless matter. Although the merger remnants resembled elliptical galaxies in many respects, in detail they differed from real ellipticals. For example, the resulting sizes were considerably larger than those of ellipticals (see Fig. 10.13). However, when merger simulations including gas physics became possible, the situation changed drastically. As we can see from Fig. 10.13, the inclusion of gas leads to considerably more concentrated merger remnants, in accord with observed properties of ellipticals. This is because the gas condenses in the central region of the merger remnant and forms stars there, yielding a higher mass (and stellar) concentration. Furthermore, as illustrated in Fig. 10.14, the distribution of the ellipticities of the stellar distribution in the remnant is changed significantly and much better resembles that found in observations. Wet mergers lead to considerably larger rotational velocities and central velocity dispersions than dry mergers, again in agreement with observations.

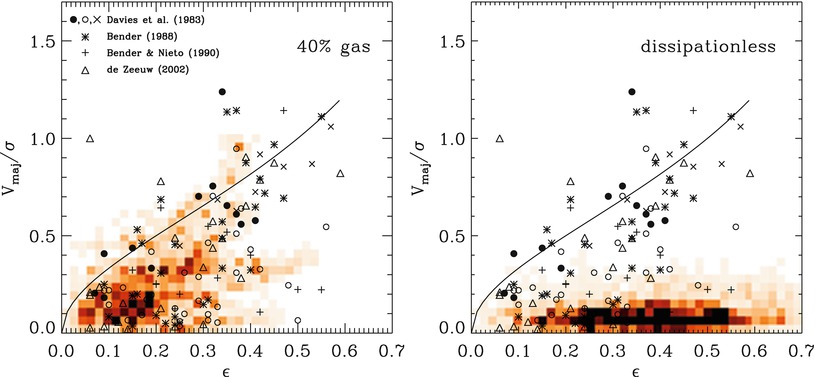
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig15_HTML.jpg

Fig. 10.15

Based on the same simulations as in Fig. 10.13, the distribution of the merger remnants in the parameter plane spanned by the ratio of the maximum rotational velocity along the major axis and the mean velocity dispersion within the half-light radius, and the ellipticity of the half-light ellipse of the stellar distribution of the merger remnant is shown as shaded areas. The left panel includes gas physics, whereas the right panel shows the dissipationless mergers. The curves in each panel shows the velocity ratio that would be needed to cause the flattening of ellipticals due to rotational support. Overplotted are the corresponding quantities of several samples of elliptical galaxies. Source: T.J. Cox et al. 2006, The Kinematic Structure of Merger Remnants, ApJ 650, 791, p. 797, Fig. 5. ©AAS. Reproduced with permission

A further strong difference between dry and wet mergers is the distribution of merger remnants with regards to their ratio of rotational velocity and velocity dispersion, and the projected ellipticity of the stellar light. We infer from Fig. 10.15 that dry mergers of disk galaxies predict far too small rotation of ellipticals when compared to observations, whereas wet mergers astonishingly well reproduce the observed distribution. Simulations like these therefore yield strong support for the merger hypothesis as the origin of elliptical galaxies. The required high gas fraction of the disk is a natural consequence of the requirement that these wet mergers have to happen early in cosmic history, to reproduce the old stellar population of current ellipticals. At high redshift, a smaller fraction of the gas has yet been converted into stars; thus, high-redshift disks are expected to be more gas rich than current spiral galaxies. Indeed, we saw in Sect. 9.4.4 that the gas-mass fraction of high-redshift galaxies is considerably higher than that of local ones.

Still, this is not the full story. Whereas the properties of ‘normal’ elliptical galaxies are well reproduced by the aforementioned gas-rich merger simulations, they fail to account for some of the characteristics of massive ellipticals, namely that these are slowly rotating and have boxy isophotes. Such objects, on the other hand, are produced by (dry) mergers of ellipticals.

The resulting scenario for the formation of ellipticals. Therefore, the following picture emerges: lower-mass normal ellipticals (i.e., not including dwarfs) are formed by wet major mergers of gas-rich (disk) galaxies at high redshift. Such mergers preferentially occur in overdense regions, i.e., in galaxy groups, which explains why ellipticals are preferentially found in groups and galaxy clusters (clusters are mainly formed by merging and accretion of groups, together with the galaxies they contain). In these dense environments, some of the ellipticals merge with other ellipticals, and these dry mergers lead to the formation of more massive galaxies with the characteristics of observed massive ellipticals.⁶

Numerical simulations have shown that gas-free mergers preserve the fundamental plane, in the sense that the merging of two ellipticals that live on the fundamental plane will lead to a merger remnant that lies on the plane as well.

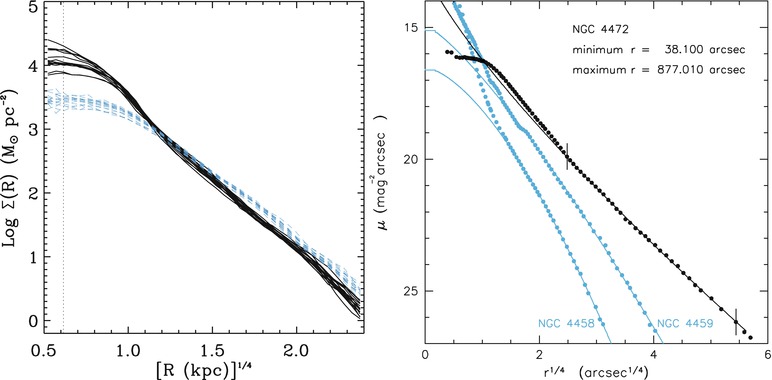
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig16_HTML.jpg

Fig. 10.16

The left panel shows the radial density profile of merger remnants, obtained from the gas-rich (black) and dissipationless (blue) merger simulations that were also considered in the previous figures. The right panel shows the corresponding radial surface brightness distribution of three elliptical galaxies in the Virgo cluster. The black points correspond to NGC 4472, a core elliptical, with the best fitting Sérsic profile shown as black curve. The angular region over which this fit was obtained is indicated by the short vertical lines. The two sets of blue points and curves show the brightness profiles of NGC 4458 and NGC 4459 and the best Sérsic profile fits at large radii, respectively. Source: Left: T.J. Cox et al. 2006, The Kinematic Structure of Merger Remnants, ApJ 650, 791, p. 796, Fig. 4. ©AAS. Reproduced with permission. Right: J. Kormendy et al. 2009, Structure and Formation of Elliptical and Spheroidal Galaxies, ApJS 182, 216, p. 274, Fig. 49. ©AAS. Reproduced with permission

Brightness profiles of merger remnants. Support for this picture comes from the brightness profiles of elliptical galaxies. The left panel in Fig. 10.16 shows the surface density profile of stars in the merger remnants. At large radii, they seem to be well described by a de Vaucouleurs profile (or, more generally, by a Sérsic profile), but there are significant differences closer to the center. The profiles of the dissipationless merger remnants near the center lie significantly below the extrapolation of the de Vaucouleurs profile from larger radii—these profiles have developed a finite core. On the other hand, the density of gas-rich merger remnants is higher in their center than the de Vaucouleurs extrapolation, which can be accounted for by the increased density through the star formation in wet mergers.

Interestingly enough, these two kinds of behavior are also found in elliptical galaxies. In a complete census of all known elliptical galaxies in the Virgo cluster, it was found that all the ten brightest galaxies have a core; one example is NGC 4472 shown in the right panel of Fig. 10.16. All of the 17 least luminous normal ellipticals have an excess of light above the extrapolation of the fitted Sérsic profile; two such examples are also shown in Fig. 10.16. The excess light can be explained by the gas dissipation and star formation in wet mergers, whereas dry mergers are not expected to develop such a light excess.

This picture is also supported further by the strong size evolution of elliptical galaxies with redshift (see Fig. 9.47). An elliptical which formed at high redshift by a wet merger is more compact than one which is the result of a dry merger at lower redshift (see Fig. 10.13). Additionally, the fact that the total stellar mass in massive elliptical galaxies is smaller by a factor ∼ 3 at z ∼ 1 than today implies that most of the current ellipticals have formed rather recently—however, not their stellar population which is required to be old. Such an evolution of the population of ellipticals can at least be qualitatively understood with the hypothesis of dry mergers.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig17_HTML.jpg

Fig. 10.17

An HST image of NGC 4650A, one out of about 100 known polar-ring galaxies. Spectroscopy shows that the inner disk-like part of the galaxy rotates around its minor axis. This part of the galaxy is surrounded by a rotating ring of stars and gas which is intersected by the polar axis of the disk. Hence, the inner disk and the polar ring have angular momentum vectors that are pretty much perpendicular to each other; such a configuration cannot form from the ‘collapse’ of the baryons in a dark matter halo. Instead, the most probable explanation for the formation of such special galaxies is a huge collision of two galaxies in the past. Originally the disk may have been the disk of the more massive of the two collision partners, whereas the less massive galaxy has been torn apart and its material has been forced into a polar orbit around the more massive galaxy. New stars have then formed in the disk, visible here in the bluish knots of bright emission. Since the polar ring is deep inside the halo of the other galaxy, the halo mass distribution can be mapped out to large radii using the kinematics of the ring. Credit: J. Gallagher & the Hubble Heritage Team (AURA/STScI/NASA)

Evidence for the importance of mergers for ellipticals is also provided by their small-scale brightness structure. We have seen in Sect. 3.2.5 that many ellipticals show signs of complex evolution which can be interpreted as the consequence of mergers. This is in accord with the picture where the formation of ellipticals in galaxy groups happens by violent merger processes, and that these then contribute to the cluster populations by the merging of groups into clusters.

The rate of mergers can be roughly estimated from the number of close pairs of galaxies with the same redshift. An example of this is found in Fig. 6.68, where several gravitationally bound pairs of early-type galaxies are seen in the outskirts of a cluster at z = 0. 83. These pairs will merge on a time-scale of ≲ 1 Gyr.

Whereas the impact of a major merger on the fate of a galaxy is dramatic, these events are not the primary process by which galaxies obtain their mass. Most of the mass growth of dark matter halos occurs through minor mergers and accretion of surrounding material, with major mergers contributing at the ∼ 20 % level. Indeed, from the large population of disk galaxies in the current Universe one concludes that at least for them, major mergers have played no role in the more recent cosmic history.

Polar ring galaxies. Another class of particular galaxies may provide the clearest indication of a merging process for their formation: polar ring galaxies (see Fig. 10.17). The kinematics of their stellar population cannot be explained by the collapse of gas in a halo, but must be due to an encounter of two galaxies.

The impact of AGN feedback in mergers. The black holes in the center of galaxies can be switched to an active mode if gas can be channeled into the center and subsequently accreted. Due to the angular momentum of gas, this is possible only if the gravitational field is substantially perturbed, either by internal processes in a galaxy (e.g., the presence of a bar), or external perturbations. Indeed, observations of low-redshift QSOs show that they are preferentially found in host galaxies which show signs of tidal interactions. It is therefore natural to expect that AGN activity is promoted by galaxy interactions, in particular by mergers.

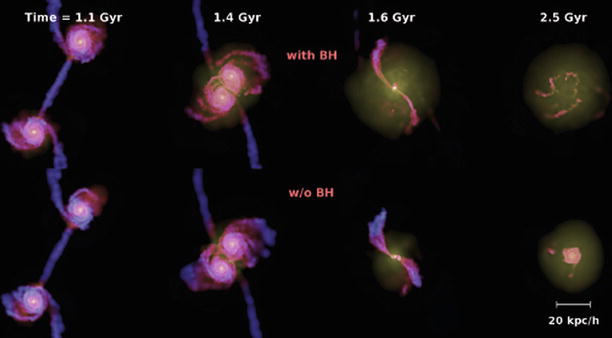
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig18_HTML.jpg

Fig. 10.18

Four different stages of a simulated merging event of two spiral galaxies whose dark matter halos have a virial velocity of 160 km∕s. The galaxies also have a stellar bulge and a gas-mass fraction in the disk of 20 %. The top panel shows the case that both galaxies contain a supermassive black hole with an initial mass of $2 \times 10^{5}M_{\odot }$ , whereas no SMBHs are included in the lower panel. A radiative efficiency of 10 % is assumed for the black hole accretion, and that 5 % of this energy can be transferred to heating the gas. In both cases, the gas distribution is shown, and color indicates gas temperature, increasing from blue to red to yellow. After their first mutual passage (the first time step shown), the two galaxies show strong signs of interactions, as seen in the tidal tails they develop. Shortly before they merge (second time step), the gas is considerably hotter in the case where SMBHs are included—it is heated by the energy from the AGN. The difference becomes even larger in the later stages of the merging: in the simulation with SMBHs, the gas density is low and heated to a high temperature, so that further star formation in the merger remnant is strongly suppressed: it resembles an early-type galaxy. During the merger, the accretion of gas is very efficient, and the final black hole mass of the merger remnant is $4 \times 10^{7}M_{\odot }$ . In the simulation without SMBHs, a substantial amount of cool gas remains to enable ongoing star formation. Source: T. di Matteo et al. 2005, Energy input from quasars regulates the growth and activity of black holes and their host galaxies, Nature 433, 604, Fig. 1. Reprinted by permission of Macmillan Publishers Ltd: Nature, ©2005

The feedback from an AGN, triggered by a merger event, has a substantial impact on the nature of the merger remnant. It can heat and expel the gas from the galaxy, shutting off subsequent star formation, whereas without this feedback mechanism, the merger remnant could still keep a substantial fraction of its gas to support further star formation. This consideration is strongly supported by numerical simulations of such merging events (Fig. 10.18).

Bulge formation. Depending on the masses of the progenitors, the resulting ellipses can have a fairly low mass. If the merger occurred in a region where the galaxy number density is rather small, the resulting small elliptical galaxy can survive for a long time without an additional (major) merger. In that time, together with its dark matter halo, it can accrete additional matter whose baryonic part may be able to cool. In this case, the baryons will undergo the same evolution as we have discussed in the context of disk galaxies before—a gas disk is built up which can then form stars. In this way, a disk galaxy is formed in the center of which one finds a small elliptical ‘galaxy’: this is the preferred explanation for (classical) bulges in disk galaxies. The bulge-to-disk ratio of these galaxies then depends on the mass of the merger remnant, the time available for accreting mass onto the halo, and the cooling time-scale of the gas.

10.5.2 Black hole binaries

The fate of the central black holes. Elliptical galaxies, or more generally, the spheroidal component of galaxies (i.e., the ellipticals, and the bulge of spirals) are observed to have a central supermassive black hole whose mass scales with the velocity dispersion of the stellar population (see Sect. 3.8). When two such galaxies merge, the behavior of their corresponding black holes is of interest. At first, they will follow the orbit of the progenitor galaxies; later, when the merging is in a later stage, they will orbit around the center of gravity in the merger remnant. One therefore expects to have a supermassive binary black hole orbiting within the newly formed galaxy.

The orbital radius of the binary black hole decreases in time. Owing to the high initial orbital angular momentum, the two SMBHs are, at the beginning of a merger, on an orbit with rather large mutual separation. By dynamical friction (see Sect. 6.3.3), caused by the matter distribution in the newly formed galaxy, the pair of SMBHs will lose orbital energy after the merger of the galaxies, and the two black holes will approach each other. Since this process takes a relatively long time, and since a massive galaxy will, besides a few major mergers, undergo numerous minor mergers, it is conceivable that many of the black holes that were originally the nuclei of low-mass satellite galaxies are today still on orbits at relatively large distances from the center of galaxies. This phase of orbit shrinking is estimated to bring the two black holes within a few parsecs of each other.

The subsequent evolution is less certain. The black hole binary orbit can further shrink through a number of processes. One of them is the interaction with stars. On average, due to the large mass ratio between stars and black holes, energy is transferred from the black holes to the stars, which can obtain enough energy to become gravitationally unbound to the galaxy (which may then lead to the occurrence of hypervelocity stars). This means that they carry away orbital energy which is thus lost from the black holes. In this way, the orbit of the binary black hole becomes tighter, at the expense of evaporating stars from the center of the galaxy. One can estimate that the total mass of ejected stars is of the same order as the black hole masses, and this estimate is further supported by numerical simulations. Hence, there is missing stellar light at the center of massive galaxies (i.e., a core) as found for all the most luminous ellipticals in the Virgo cluster (see the right panel of Fig. 10.16 for an example).

It is also possible that the black hole binary accretes matter from the merged host galaxy and forms a gas disk outside the orbital radius. Due to the strong tidal gravitational field, density waves are generated in this disk, at the expense of orbital momentum of the binary.

These processes can yield a hardening of the binary orbit down to ∼ 10⁻³ pc. When this separation is achieved, the black hole binary orbit will continue to shrink efficiently via the emission of gravitational waves (see Sect. 7.9), which then finally will lead to a black hole merger.

Black hole recoil. According to the theory of black holes, there is a closest binary separation at which an orbit still is stable. Once the separation has shrunk to that size, the merging occurs, accompanied by a burst of gravitational wave emission. If the two SMBHs have the same mass, each of them will emit the same amount of gravitational wave energy, but in opposite directions, so that the net amount of momentum carried away by the gravitational waves is zero. However, if the masses are not equal, this cancellation no longer occurs, and the waves carry away a net linear momentum. According to momentum conservation, this will yield a recoil to the merged SMBH, and it will therefore move out of the galactic nucleus. With numerical methods, the recoil velocity can be calculated.⁷ It depends on the mass ratio of the two black holes, as well as on their angular momentum and the rotational directions relative to the orbital plane. For two non-rotating black holes, the maximum recoil velocity is ∼ 175 km∕s, obtained for a mass ratio of ∼ 0. 36. For rotating black holes, the recoil velocity can be much larger, and in extreme cases (when the black holes have maximum spin and they are anti-aligned) can exceed 4000 km∕s.

The recoil will displace the merged black hole from the center of its host galaxy. Depending on the recoil velocity, it may return to the center in a few dynamical time-scales. However, if the recoil velocity is larger than the escape velocity from the galaxy, it may actually escape from the gravitational potential and become an intergalactic black hole. The likelihood of this effect is not quantitatively known, since we know too little about the spin of SMBHs, and these spins can be severely affected during the initial stages of the merging process. The black hole may carry away with it its accretion disk, and remain an active galactic nucleus for some time (say, ∼ 10⁶ yr).

Consequences. The merging of binary SMBHs has a number of consequences. First, it qualitatively predicts that the central supermassive black hole in galaxies should grow in proportion to the mass growth of galaxies due to mergers. This cannot be the full story, since at least some of the mass growth must occur due to accretion of gas in case of wet mergers; however, in wet mergers the galaxies are dominated by (gas rich) disks, and so the corresponding black hole masses are rather small if they follow the M _•-σ relation. A second consequence is the existence of binary black holes in at least some galaxy merger remnants, when they are caught in the initial stages of binary hardening. If the two individual SMBHs can retain (or regain) a gas reservoir around them and accrete, they can become active. If only one of them accretes, one might expect an AGN off-center in the merger remnant. Similarly, if the recoil displaces the merged SMBH away from the center of the galaxy, an off-center AGN may become visible.

How frequent such situations occur in mergers is difficult to predict. The occurrence rate depends on the gas content and distribution in the center of the two merging galaxies, and on the time-scale the two black holes orbit in the merger remnant before final coalescence—the longer it takes, the higher the probability to detect a binary AGN.

Observational evidence for binary SMBHs. According to the above expectations, there are a number of possible observational probes for binary SMBHs and their remnants: (1) Two AGNs in the same galaxy. (2) One AGN which is not located in the center of its host galaxy, either because only one of the two black holes is accreting at the time of observations, or because the merged SMBH has been displaced by the recoil effect. (3) One AGN which shows signs of orbital motion, either through a periodicity (with the period being the orbital period), or through double-peaked broad emission lines, which could be formed if both black holes in a close (unresolved) pair are associated with their own broad line region.

Binary AGNs have indeed been found. The radio source 3C 75 shown in Fig. 6.30 has two radio nuclei, both of which launch a pair of jets. These jets are strongly bent, which is interpreted as being due to the motion of the host galaxy through the cluster Abell 400 in which it is embedded. The interaction of the jet plasma with the intracluster medium then deforms the jets in this wide angle tail source. The large projected separation between the two radio nuclei implies that the black hole merging process has not advanced very much in this system.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig19_HTML.jpg

Fig. 10.19

On the left, a composite image of the galaxy NGC 6240 (z = 0. 0245) is shown. The X-ray emission is shown in red, orange and yellow, superposed on an optical image of this galaxy. A pair of two compact X-ray sources in the center, zoomed in on the right (at different orientation), shows the presence of two AGNs in this galaxy; their projected separation is ∼ 1. 4 kpc. With K-band integral field spectroscopy, the black hole mass of the more luminous of the two AGNs has been estimated to be $M_{\bullet } \sim 9 \times 10^{8}M_{\odot }$ . Credit: Left: X-ray (NASA/CXC/MIT/C. Canizares, M. Nowak); Optical (NASA/STScI). Right: NASA/CXC/MPE/S. Komossa et al.

The galaxy NGC 6240 shown in Fig. 10.19 is a recent merger, as seen from the disturbed morphology. Its large infrared luminosity of $L_{\mathrm{IR}} \sim 7 \times 10^{11}L_{\odot }$ indicates that the merger induced a strong burst of star formation. In the center of the galaxy, two AGNs are seen, revealed by their X-ray emission. The projected separation is ∼ 1. 4 kpc in this case.

Several more such binary AGNs have been found, with separation of ∼ 1 kpc or larger. In most of these systems, the host galaxy shows signs of a recent merger, such as strongly distorted morphology and/or intense star formation. However, one system was found where the separation is much smaller. In the radio galaxy 0402+379 (z = 0. 055), there are two compact radio sources with a projected separation of 7. 3 pc, suggesting that we are witnessing a more advanced merging stage.

Binary black holes candidates have also been claimed from spectral studies of AGNs, where a large velocity shift between the broad and the narrow emission lines was found. One interpretation of these observations is that the shift is due to the active SMBH orbiting in the host galaxy, carrying the broad line region along its orbit, whereas the gas emitting the narrow emission line is at rest in the host galaxy. The active SMBH can either be a member of a binary black hole with the other one inactive, or the merged SMBH which obtained its velocity through recoil. AGNs with double peaked emission lines may also be interpreted as a pair of spatially unresolved active nuclei, where the two peaks of the emission lines reflect the line-of-sight velocity of the two SMBHs. However, there are alternative explanations for the nature of these sources, and the evidence for a binary black hole is not unchallenged.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig20_HTML.jpg

Fig. 10.20

The big multi-color optical image shows a 1 ^′ × 1 ^′ part of the COSMOS field. The galaxy at the center is CID-42 (at z = 0. 36), of which three zoomed images are shown on the right, with a side length of 3. ^{′ ′} 7. The tidal tail seen in the optical suggests that this galaxy underwent a merger in the more recent past. The optical images displays two bright compact sources; only one of them has an X-ray counterpart. Credit: X-ray: NASA/CXC/SAO/F. Civano et al; Optical: NASA/STScI; Optical (wide field): CFHT, NASA/STScI

The galaxy CID-42 (Fig. 10.20) has two bright optical nuclei; one of them is point-like and appears as an AGN, whereas the other is slightly extended and most likely is a nuclear star cluster. The AGN is also seen in X-rays, whereas the other compact optical source has no detectable X-ray emission. The AGN is off-center; in addition, it has broad emission lines which have a velocity offset from the narrow emission lines of ∼ 1300 km∕s; note that this velocity is much larger than the orbital velocity of a binary black hole at the separation between these two compact source components. Thus, in this system one has both kinematical as well as positional indications for a SMBH which has been ejected from the center of the galaxy through recoil; it is the best candidate observed so far for this effect.

Another class of sources may indicate the occurrence of binary SMBH mergers, the so-called X-shaped radio sources (see Fig. 10.21). These sources are characterized by their radio morphology, containing two pairs of jets in different directions. The more luminous, inner pair of jets is connected to the central source, whereas the outer jets with lower brightness appears to consist of plasma that was ejected from the core some time in the past. One likely possibility to explain these sources is a change of orientation of the accretion disk, which may be due to a change of the black hole angular momentum vector. During the hardening of the black hole binary, the interaction of the black holes with the gas inside the host galaxy may cause such spin flips.

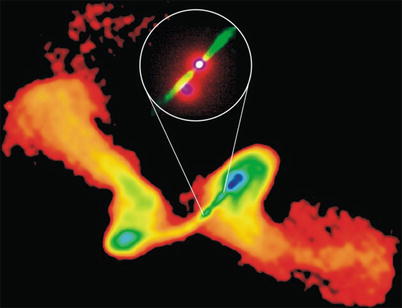
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig21_HTML.jpg

Fig. 10.21

The X-shaped radio galaxy 3C326, observed with the VLA. The inset shows an optical HST image of the innermost jets. The pair of radio jets at different directions may have its origin by a change of the black hole’s spin direction, as may occur in the process of binary black hole mergers. Credit: Image courtesy of NRAO/AUI and Inset: STScI

An accreting SMBH in orbit around the center of the host galaxy can produce periodicity in its emission. The best example yet found is the blazar OJ 287 at z = 0. 306. Variability of this object has been traced back to 1890, using archived photographic plates, and it shows a periodicity of 11. 86 yr. Merger models of the source that explain the periodicity involve a second SMBH with about 10 times lower mass. If the period of variability is identified with the orbital period, then this binary will merge over the next ∼ 10⁵ yr. However, the periodicity can have a different origin, like a precessing accretion disk, in which case the variability could be due to changes of the jet direction.

Overall, there are quite a number of observational indications for binary black holes and merger candidates. However, the best way to track down the SMBH merger will be by observing the gravitational wave emission. The planned space-based gravitational wave observatory LISA is expected to detect virtually all such supermassive black hole mergers throughout the visible Universe, and thus provide exquisite demographics of the cosmic merger history.

10.5.3 Environmental effects on galaxy properties

Major merger events between galaxies change the morphology and physical properties of galaxies dramatically. We have seen that this is the probable road to the formation of normal elliptical galaxies. However, this is not the only process in which the properties of a galaxy can be altered; it is merely the strongest one. Merging preferentially occurs in groups, which combine an environment of a high number density of galaxies with a relatively small velocity dispersion needed for mergers.

Harassment. In clusters of galaxies, the characteristic collision speed between galaxies is considerably higher than their internal velocity dispersion; as we argued before, in such a case no merging can take place. However, a high-speed collision between galaxies affect their internal properties in a different way. If we consider such a collision in the rest frame of one of the galaxies, then its components experience a rapid change of the gravitational potential as the other galaxies fly by. As a consequence, the matter in the galaxy increases its internal energy—it is impulsively heated. This causes the matter in the galaxy to expand, i.e., it is less gravitationally bound than before, and therefore is more easily affected by tidal gravitational forces. Furthermore, the heating of the stellar component changes the distribution function (i.e., the phase-space density f discussed in Sect. 2.3.1) of the stars—dynamically cold stellar disks are heated and may get destroyed, with the stars evolving into a spheroidal distribution. The cumulative effect of such high-speed collisions is often called galaxy harassment.

Ram-pressure stripping and strangulation. As a galaxy orbits in a cluster, it moves relative to the hot intracluster medium. In the rest frame of a galaxy, the ICM acts like a wind, with the wind speed equal to the orbital velocity of the galaxy. This wind causes a pressure force on the interstellar medium of the galaxy; it is proportional to the density of the ICM and the square of the velocity. If this force is stronger than the gravitational force of the galaxy which hosts the interstellar gas, this gas can be removed from the galaxy. This ram-pressure stripping can thus over time turn a gas-rich disk galaxy into a disk galaxy without gas, i.e., a spiral galaxy into an S0 galaxy. This effect may be the origin of the larger abundance of S0 galaxies in clusters than in the field population. It also provides a natural explanation for the Butcher–Oemler effect (see Sect. 6.8), which states that clusters of galaxies at higher redshift contain a larger fraction of blue galaxies. The blue (spiral) galaxies that have existed at higher redshift may have turned into S0 galaxies in the meantime. The fact that the fraction of ellipticals in a cluster remains rather constant as a function of redshift, whereas the abundance of S0 galaxies increases with decreasing z, indicates the importance of the latter process as an explanation of the Butcher–Oemler effect.

Gas which is removed from the galaxies is chemically enriched. The metallicity of the ICM is believed to be due to the mixing of this enriched gas with the intracluster medium. Hence, the metals of the ICM have been generated by earlier stellar populations in cluster galaxies.

The efficiency of this effect, as well as that of harassment, depends on the orbit of the galaxy. If the orbit comes close to the inner part of the cluster where the gas and galaxy number density are large, all the gas may be removed, whereas otherwise, only the outer, more loosely bound gas is lost. In this case, the galaxy retains its gas in the inner part and may continue to form stars for a while; only when this gas supply is exhausted, it then turns into a red galaxy, since no new gas can be gained from cooling or accretion. This effect is called strangulation.

Cannibalism. The orbit of a galaxy in a cluster is affected by dynamical friction (see Sect. 6.3.3); it loses energy and angular momentum, and so its orbit will shrink in time. The efficiency of this effect again depends on the galaxy orbit; the closer it comes to the inner parts of the cluster, the stronger are the gravitational friction forces. Furthermore, as seen from (6.30), it depends on the galaxy mass, with more massive galaxies being affected more strongly. Depending on the orbital parameters, a cluster galaxy can lose most of its angular momentum in a Hubble time, sink to the center, and there merge with the central galaxy. By this process, the central galaxy becomes more massive, as it ‘cannibalized’ other cluster members. The aforementioned mass dependence may lead to an increase of the mass and luminosity difference between the brightest cluster galaxy and the second-brightest one.

10.6 Evolution of the galaxy population: Numerical simulations

In the preceding sections, the formation of disk and elliptical galaxies were described; it is generally believed that the collapse of gas, together with its angular momentum, leads to the formation of disk galaxies, whereas mergers and interactions are the prime cause for the occurrence of early-type galaxies. Our understanding of these formation processes can now in principle be used to predict the evolution of the galaxy population in the cold dark matter universe. The cosmological model predicts the abundance of halos as a function of mass and redshift, the distribution of their spin parameter, as well as the frequency of major and minor mergers. One thus might expect that from these ingredients, the galaxy population can well be predicted.

However, there are some major difficulties which hamper easy progress in this direction. The evolution of galaxies (in contrast to their dark matter halos) is strongly governed by baryonic processes, many of which are not fully understood. For example, we have no quantitative understanding about star formation. The way how the explosion of a supernova feeds back energy into the interstellar medium is subject to considerable uncertainties; this is even more true for the feedback processes related to AGN activity in galaxies.

A further serious problem is related to the enormous dynamic range in length scales which are involved in galaxy evolution in the cosmological context. We have seen that galaxy evolution depends on the local environment; galaxies evolve differently in groups and clusters than in the field. Hence, one needs to consider a sufficiently large volume of the Universe such that it contains a representative population of cluster-mass halos. As we argued in Sect. 7.5.3, the cosmological box should not be much smaller than 200h ⁻¹ Mpc on the side. On the other hand, the Galactic disk has a scale-height of ∼ 100 pc, and star formation occurs in molecular clouds with a typical size of ∼ 1 pc. Hence, an ab initio simulation of galaxy evolution would have to have a dynamic range of at least 10⁸ in length—too ambitious to be carried out.

Nevertheless, enormous progress in our understanding of the galaxy population has been achieved in recent years. Essentially, two different methods are used to overcome the aforementioned problems: Historically the first was semi-analytic modelling of the evolution of galaxies; we will discuss these models in Sect. 10.7. But more recently, hydrodynamical cosmological simulations have been employed to study the formation and evolution of galaxies, which we describe in this section.

10.6.1 Numerical methods

The increase in computer power, as well as the evolution of efficient numerical codes have allowed cosmological simulations which include baryonic physics: heating and cooling of gas, hydrodynamical effects etc. Simulating these processes is much more difficult and time consuming than pure N-body simulations which solely contain gravity—correspondingly, either their box size and/or their spatial (and mass) resolution are smaller.

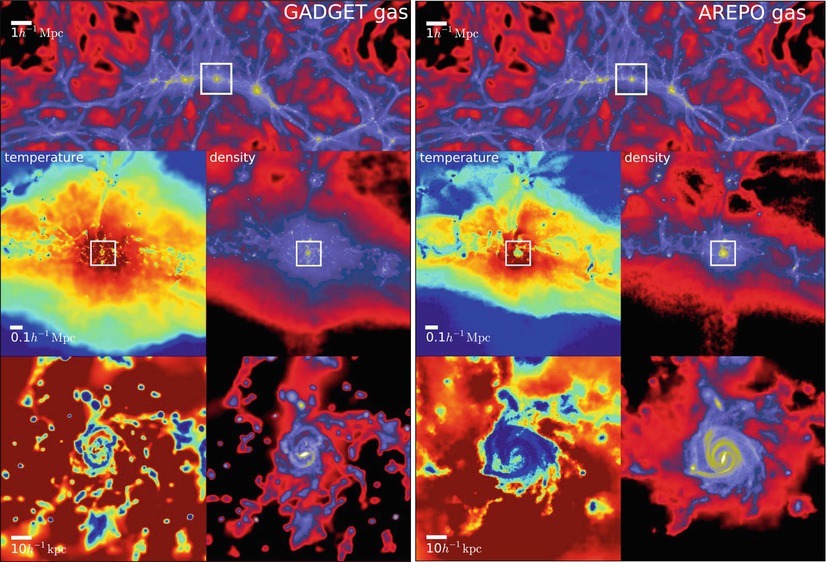
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig22_HTML.jpg

Fig. 10.22

The projected gas density from two hydrodynamical simulations of a galaxy. Both simulations use the same initial conditions, as well as the same prescriptions for star formation and feedback; the only difference is the numerical method with which the equations of hydrodynamics are treated. In the left panel, a smooth particle hydrodynamics (SPH) scheme was used, whereas in the right panel the new AREPO method was employed. The upper panels show the gas density at redshift z = 2 in a large fraction of the full numerical box, whereas the smaller panels show subsequent zooms (indicated by a white square in the previous step) of the gas temperature and density, centered on a disk galaxy. This galaxy has significantly different properties in both simulations. Whereas AREPO yields an extended disk with spiral arms and a bar, the corresponding galaxy is much smaller in the SPH simulation. Differences in the clumpiness of the medium are also visible. Source: M. Vogelsberger et al. 2012, Moving mesh cosmology: numerical techniques and global statistics, MNRAS 425, 3024, p. 3031, Fig. 1. Reproduced by permission of Oxford University Press on behalf of the Royal Astronomical Society

There are two widely spread methods for the numerical treatment of hydrodynamics. In the first case, a stationary grid is set up, and the differential equations of hydrodynamics (such as the continuity and Euler equations) are discretized on the grid.⁸ In the second case, the fluid is represented by fluid particles, which are considered representative of a mass element of gas. The interaction between these fluid particles are prescribed such that the transport of mass, momentum, and energy follows the laws contained in the equations of hydrodynamics; this approach is termed smooth particle hydrodynamics (SPH) . Different variations of these two basic schemes have been developed. For example, in the grid-based approach, one wants to have a higher spatial resolution in regions of large gas density; for this purpose, one can generate sub-grids with a smaller mesh size which yield higher spatial resolution. Such a numerical scheme is called adaptive mesh refinement (AMR). Lately, a new method has been developed, which is also based on a grid; however, the grid is not stationary but moves with the fluid, and the density of grid points adapts to the fluid density. First tests indicate that this new scheme (called AREPO) overcomes some of the problems of the two former schemes and yields considerably more reliable results (see Fig. 10.22).

The necessity for sub-grid physics. In order to overcome the resolution issues, several small-scale physical effects can be treated only approximately. Since these simulations are several orders of magnitude away from being able to resolve the formation of molecular clouds, one needs a recipe for star formation. For example, if the gas density exceeds a threshold value in one region (or for one SPH particle), one assumes that a fraction of this gas is turned into stars. In the simulation one keeps track of this newly formed stellar population, i.e., its mass, formation time and metallicity.

Since massive stars very quickly after formation explode as core-collapse supernovae, for each massive star formed (given by the total newly formed stellar mass and the assumed initial mass function) an energy of ∼ 10⁵¹ erg is transferred back to the surrounding gas distribution. Also this feedback process occurs on scales below the numerical resolution, so it is assumed that this energy is used to heat the local gas. Also refinements have been successfully implemented, where each gas cell or particle is split into a hot, diffuse part and a cold and dense part. Gas can be exchanged between these two phases due to heating and cooling processes. It turns out that the outcome of simulations depend on the detailed prescription of this feedback mechanism. If it is assumed that the supernova energy is transferred mainly to the cold and dense gas, then it can be radiated away rather quickly without affecting the dynamics of the gas appreciably. On the other hand, if the feedback energy heats the diffuse gas, radiative cooling is much less efficient, the gas increases its pressure and expands, driving gas out of the dense region (or, in physical terms, out of the disk where star formation is located).

Fig. 10.23

Results from the Aquila Comparison Project, in which, starting from the same initial conditions, the evolution of a disk galaxy was followed with 13 different simulations. The halo mass of the galaxy is similar to the one of the Milky Way, $\sim 1.6 \times 10^{12}M_{\odot }$ . The left-hand panel shows the rotation curves of the galaxy as obtained by the different simulations, with the rotation curve of the Milky Way shown in light grey for comparison. The solid black curve in each of the four subpanels is the rotation curve as obtained from a dark matter-only simulation of the same initial conditions. In most cases, the rotation curve has a peak at low radius, after which is strongly declines outwards—in contrast to observed rotation curves of spiral galaxies which are almost flat. The reason for this behavior is the too effective cooling of gas, yielding a far too concentrated baryonic distribution in the inner part of the galaxy. The right panel shows, for each of the 13 simulations, the total stellar mass as a function of the halo mass M ₂₀₀, as the galaxy evolved from redshift z = 2 (beginning of the curve) to today (symbol). The predicted stellar mass varies by about a factor 10 between the simulations. The dotted curve shows the expected stellar-to-dark matter relation, as expected from matching the abundance of dark matter halos to that of the observed galaxy abundance [essentially by defining a function M _∗(M ₂₀₀) which brings the two curves in Fig. 10.2 into agreement], the dashed curve shows the maximally possible stellar mass, given by the halo mass times the mean cosmic ratio of baryons to total matter. The two black curves (and stars) show the model predictions of two semi-analytic models of the same halo. Source: C. Scannapieco et al. 2012, The Aquila comparison project: the effects of feedback and numerical methods on simulations of galaxy formation, MNRAS 423, 1726, p. 1734, 1735, Figs. 5, 6. Reproduced by permission of Oxford University Press on behalf of the Royal Astronomical Society

Similarly, the accretion of gas onto a central supermassive black hole and the corresponding feedback can be treated only approximately. The accretion disk (or more generally, the accretion region) can not be resolved, but the accretion rate, and the corresponding energy output, depends mainly on the rate at which gas can be driven into the central region of the galaxy. The accretion rate can then be estimated from the physical conditions on scales much larger than the accretion disk size, and is often approximated by the Bondy–Hoyle rate [see (5.16)], bounded above by the Eddington rate or a small multiple of it. The resulting luminosity of the supermassive black hole is assumed to be a fraction ε of the rest-mass energy rate accreted, i.e., $L = \epsilon \dot{m}c^{2}$ , with ε ∼ 0. 1 (see Sect. 5.3.5). Some fraction of this energy output is assumed to be fed back into the surrounding gas. This gas, being suddenly heated, will greatly expand and drive a shock wave, by which it is blown out of the central region. This expanding blast wave can then be followed by the hydrodynamic solver.

The gravitational force is calculated in a very similar way as done for pure N-body simulations, except that the source of gravity is the sum of the densities of dark matter, gas, stars and the central black holes. Changes to the dark matter profile of halos due to the contraction of cooling gas is thus included in such simulations.

Comparison of numerical methods. We have reported some results of such simulations above, namely simulations of the merging of two disk galaxies (see Sect. 10.5.1). At present, the results from such simulations need to be analyzed with care; there are still considerable uncertainties regarding the small-scale physics (star formation and feedback), as well as the accuracy with which the hydrodynamical behavior of the gas can be followed. In the recent Aquila Comparison Project, a comparison of 13 different hydrodynamical simulations of one galaxy (where all simulations used the same initial conditions) was performed and significant differences were found. For example, the morphology of the galaxies shows strong variations between the different simulations. This can be traced back to the star-formation history: the earlier most of the stars are formed, the less pronounced is the disk today. Obviously, the amount of star formation in the early history of the galaxy depends on the amount of cooling gas and, in particular, the efficiency of feedback processes. The tendency of turning too much gas into stars is often called the ‘overcooling problem’ in galaxy evolution. On the other hand, the feedback must not prevent the later accretion of gas, to build up the disk at lower redshift.

The left hand panel of Fig. 10.23 shows the predicted rotation curves of the galaxy, as obtained from these 13 simulations. Most of them exhibit a pronounced peak at small radii, after which they decline outwards. Again, this is due to the concentration of stars in the inner part of the galaxy, which not only acts as a source of gravity by itself, but the corresponding efficient cooling of baryons led to the contraction of the dark matter halo. Only simulations with a very strong feedback lead to approximately flat rotation curves; unfortunately, these models usually do not have a well-developed disk. The compactness of the baryonic distribution yields corresponding circular velocities which are well above the observed Tully–Fisher relation for spirals. The stellar mass as predicted by the models in shown in the right-hand panel of Fig. 10.23; also here the variations between the simulations are large, again mainly due to the different feedback prescriptions. In some simulations, nearly all available baryons inside the halo were turned into stars, whereas other simulations have ∼ 10 times lower stellar mass.

Lessons. We present this comparison here for a number of reasons. First, this exercise shows which of the various differences between codes matter most for the predictions and thus gives insight on how the assumptions must be modified in order to obtain results closer to the observed properties of galaxies. That may seem like cheating at first sight: one turns the knobs in such a way that the results are in agreement with observations—what about the predictive power of such simulations then? However, one must keep in mind that some of the key processes (to repeat: star formation and feedback) cannot be followed from first principles, but are included in the form of recipes. In a sense, we parametrize our ignorance, and try to calibrate the set of parameters with a small number of key observational facts (such as the normalization of the Tully–Fisher relation, or the luminosity function of galaxies). The number of different predictions from such simulations is much larger than the number of parameters chosen; thus, once appropriate prescriptions for the ‘sub-grid’ physics are found, these models have predictive power.

A second, very important reason for this discussion here is to caution the reader about the reliability of some predictions of our cosmological model. We first note that a similar comparison was carried out for N-body simulations, with a very satisfactory overall agreement on scales larger than the resolution limit (of course, on scales below the numerical resolution, the results are even expected to be different). Thus, the predictions concerning dark matter-only are very robust. However, the inclusion of baryons, and the complex physical processes they are subject to, render predictions much less reliable. The smaller the scales and the denser the baryons, the more non-linear are the physical processes, and the harder it is to reliably trace them. In particular, processes on small scales have a strong effect on large scale—e.g., feedback.

This must be taken into account when arguments are made concerning the incompatibility of some observational results with ΛCDM. In most cases, these arguments concern the smallest scales or the least massive objects, for example properties of dwarf galaxies. From what was just stated, it is clear that currently we are not able to make detailed predictions about observational properties of small galaxies – when we cannot even predict the stellar mass of a massive galaxy halo to within a factor of 3! The fact that current simulations fail to reproduce spirals which fit the Tully–Fisher relation is most likely not a failure of the underlying cosmological model, but a lack of understanding of the complex small-scale physical processes involved.⁹

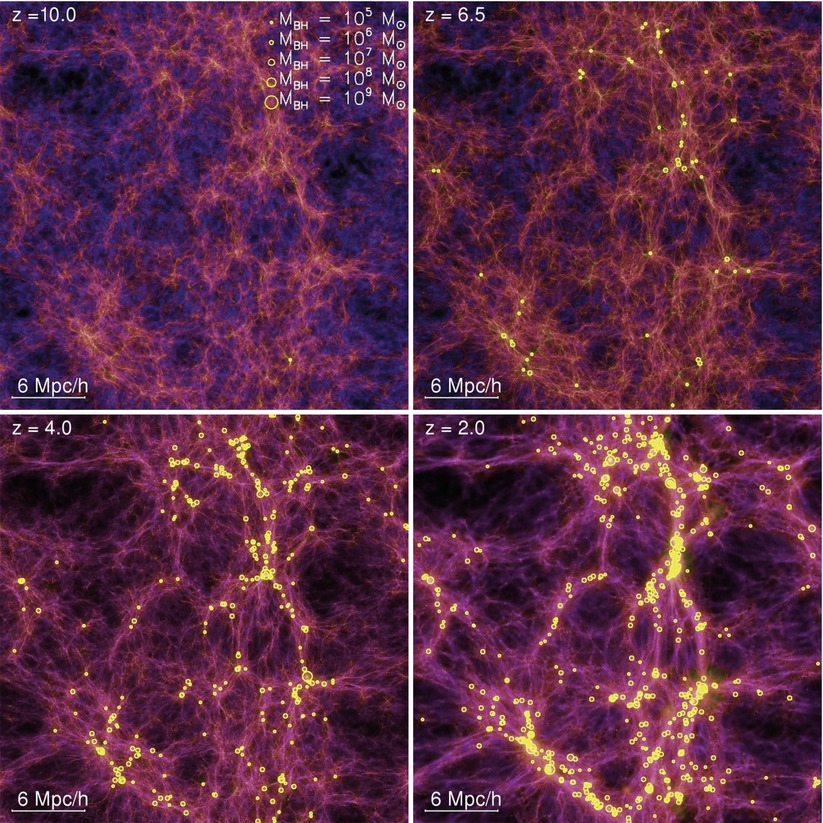
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig24_HTML.jpg

Fig. 10.24

The density of baryons from a hydrodynamical simulation, projected over a 5h ⁻¹ Mpc thick slice. Intensity and color indicate gas surface density and temperature, respectively. Four snapshots at different redshifts are shown. Yellow circles indicate the location of supermassive black holes, with the symbol size indicating the black hole mass. In this simulation, for which a box of size $L = 33.75h^{-1}\,\mathrm{Mpc}$ was chosen, it was assumed that 5 % of the AGN luminosity is fed back to the interstellar medium; this choice was made in order to reproduce the observed relation between black hole mass and velocity dispersion of the spheroidal stellar component. Source: T. di Matteo et al. 2008, Direct Cosmological Simulations of the Growth of Black Holes and Galaxies, ApJ 676, 33, p. 38, Fig. 1. ©AAS. Reproduced with permission

10.6.2 Results

The challenge for models of galaxy evolution is to explain the observational results of the galaxy population at low and high redshift. In this section, we will illustrate the current status of gas-dynamical cosmological simulations and their ability to reproduce key observations.

Growth of black holes and galaxies. The tight correlation between central black hole mass and properties of the spheroidal stellar component in galaxies suggest a close connection of the evolution of both components. Furthermore, feedback processes from AGN activity are essential for understanding the evolution of galaxies. We next present some results of a gas-dynamical cosmological simulation which includes the evolution of the supermassive black holes in galactic centers. For this simulation, the Bondi–Hoyle accretion rate was assumed, as described above. All halos, once they exceed a mass threshold, were artificially provided with a seed black hole of $10^{5}M_{\odot }$ at the location of the densest gas particle, thereby circumventing our lack of understanding on how the first massive black holes were formed. The mass of the seed black hole is rather unimportant as long as it is much smaller than the mass at later times. In particular, the total mass in these seed black holes is a minute fraction of the total mass of black holes at later epochs which is totally dominated by accretion processes.

Figure 10.24 shows the gas density and temperature in the simulation box, together with the location of black holes. As expected, these are located in the center of density maxima. The black hole distribution traces the overall density distribution, although with considerable scatter. The number density of black holes varies strongly between filaments of gas which apparently have very similar density. Already at redshift z = 6. 5, quite a number of black holes have formed, some with masses close to $10^{7}M_{\odot }$ , although no SMBH has formed with masses needed to explain the luminous quasars seen at $z \gtrsim 6$ (i.e., $M_{\bullet } \gtrsim 10^{8}M_{\odot }$ ). However, these quasars have a very low space density, and one cannot expect to find such massive black holes in a simulation box of the size considered here.

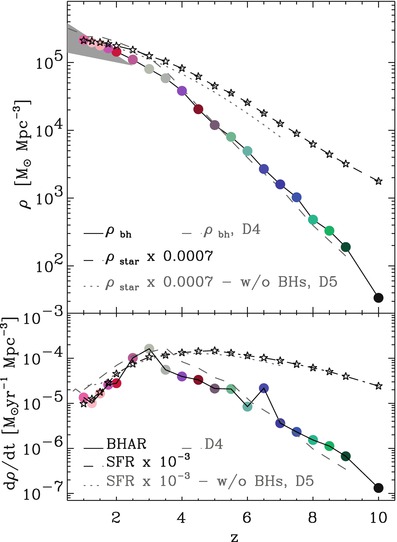
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig25_HTML.jpg

Fig. 10.25

The upper panel shows the mass density of black holes as a function of redshift (colored points and solid curve), for the simulation shown in Fig. 10.24. The lower dashed curve shows the same quantity for a simulation with the same initial conditions and physical assumptions, but lower mass resolution, indicating that this prediction of the model is not strongly affected by resolution effects. The dashed curve and the star symbols show the mean density of stars, scaled by a factor 7 × 10⁻⁴, whereas the dotted curve shows the stellar mass density from the same simulation, but where the feedback from the accreting black holes was absent. The shaded grey triangle at low redshifts shows estimates of the black hole mass density from observations. The lower panel displays the growth rate of the black hole mass density and stellar mass density, with the same line styles as in the upper panel. Source: T. di Matteo et al. 2008, Direct Cosmological Simulations of the Growth of Black Holes and Galaxies, ApJ 676, 33, p. 41, Fig. 4. ©AAS. Reproduced with permission

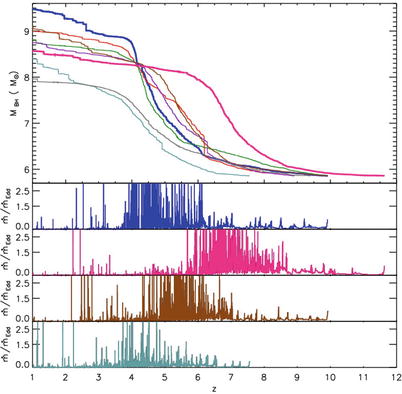
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig26_HTML.jpg

Fig. 10.26

The upper panel shows the mass of the six most massive black holes at z = 1, as well as that of two intermediate mass black holes, as a function of redshift. The two thicker lines highlight the most massive SMBHs in this simulation at z = 6 and at z = 1. The lower panels display the accretion rate in units of the Eddington rate as a function of redshift, with the same color coding as in the upper panel. Source: T. di Matteo et al. 2008, Direct Cosmological Simulations of the Growth of Black Holes and Galaxies, ApJ 676, 33, p. 48, Fig. 13. ©AAS. Reproduced with permission

The total mass density of the SMBHs in the simulation as a function of redshift is shown in the upper panel of Fig. 10.25 where it is compared to the mean mass density of stars. We see that the SMBH density increases faster with cosmic time than the stellar mass density, which shows that the evolution of the stellar density precedes that of the SMBH. This is shown more clearly in the lower panel, where the growth rate of these densities are displayed (i.e., the time derivative of the curves in the upper left panel). Both growth rates exhibit a peak at intermediate redshifts; however, whereas the peak in the stellar mass density is fairly broad (as observed in the Madau diagram—see Fig. 9.55), it is much more peaked for the black holes. Comparing the mass density of the SMBH population with observational estimates, one finds broad agreement.

It is instructive to consider the mass history of individual black holes in the simulation, which is displayed in the upper panel of Fig. 10.26 for the six most massive (at z = 1) black holes and two less massive ones. The growth of the SMBH mass is quite rapid at the beginning, and apparently episodic. The mass accretion rate in units of the Eddington rate (5.27) for four of the SMBHs is plotted in the lower panels (note that for this simulation, the maximum accretion rate was chosen to be three times the Eddington rate). The most massive black holes undergo extended periods where the accretion rate is very high, limited only by the Eddington ratio. Hence, these holes grow as fast as possible in these periods, since there is enough supply of fuel—presumably in the aftermath of a major merger. The most massive SMBH at z = 6 (pink curves) undergoes a very extended period of accretion between redshifts 5 and 7, after which it turns to become very inactive, with the exception of a few short episodes of accretion during which its mass is only slightly increased. The blue curve shows the most massive SMBH at z = 1, which started massive accretion only at redshift z ≲ 6, but then rapidly grew in mass. Hence we infer from the figure that the fates of individual SMBHs, and their corresponding AGN activity, are quite diverse.

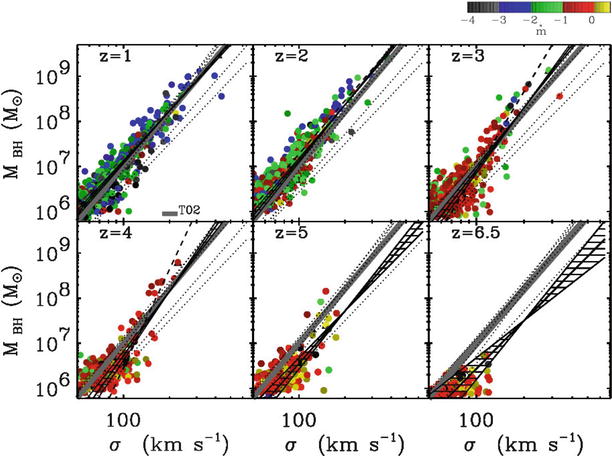
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig27_HTML.jpg

Fig. 10.27

From the same simulations as in Fig. 10.24, the black hole mass is plotted as a function of the velocity dispersion σ of the stellar mass particles within the half-mass radius, for six different redshifts as indicated. The thick grey line in all panels is the best fit to the local M _•-σ relation. For each redshift, a power-law relation was fitted to the points, which is shown as solid line, together with its 1-σ uncertainty (as hatched region; for the low redshifts, this uncertainty is so small that the hatched region is essentially invisible). The dotted lines in each panel show the power-law fits obtained at the other redshifts, increasing from top to bottom. The color of each point codes the accretion rate of the SMBH at the snapshot, in units of the Eddington accretion rate, with the corresponding color bar at the top of the figure. Source: T. di Matteo et al. 2008, Direct Cosmological Simulations of the Growth of Black Holes and Galaxies, ApJ 676, 33, p. 44, Fig. 8. ©AAS. Reproduced with permission

One of the most promising results of the simulation is the strong correlation between black hole mass and the velocity dispersion of the stellar component, as shown for six different redshifts in Fig. 10.27. There we see that beginning with z ∼ 4, the best-fit relation from the simulation agrees with the locally observed one (see Fig. 3.45). The normalization of the power-law fits depends on the assumed fraction of AGN luminosity that is available for feedback, chosen to be 5 % here. However, more exciting than the precise normalization of this relation is the fact that hierarchical galaxy evolution is able to explain the observed tight correlation without additional ad-hoc assumptions. Also seen is that the tight relation is satisfied by black holes independent of their accretion state—i.e., active and inactive SMBH lie on the same relation.

However, it must be pointed out that the resolution of these simulations do not allow statements about the morphology of galaxies; therefore, the velocity dispersion plotted in Fig. 10.27 is that of the total stellar population, not that of the spheroidal component only, for which the M _•-σ relation is observed.

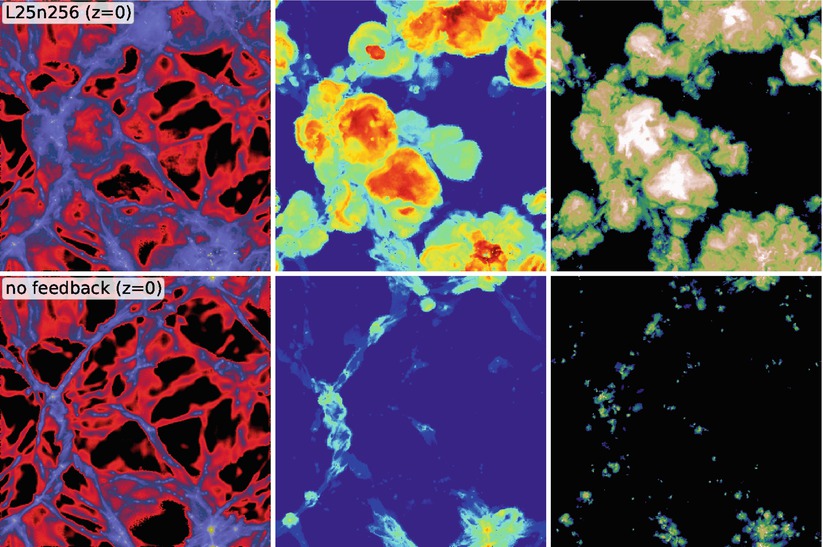
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig28_HTML.jpg

Fig. 10.28

Gas-dynamical simulations of structure formation, with (top) and without (bottom) the inclusion of feedback processes. Shown is the distribution of gas density (left), temperature (middle) and metallicity (right) at z = 0, over an area 25h ⁻¹Mpc on the side and projected over a slab of thickness 1h ⁻¹Mpc. Source: M. Vogelsberger et al. 2013, A model for cosmological simulations of galaxy formation physics, arXiv:1305.2913, Fig. 3. Reproduced by permission of the author

Impact of feedback on the gas. The foregoing discussion has shown the challenges of hydrodynamic cosmological simulations, in particular concerning numerical resolution and the implementation of sub-grid physics. We present next some recent results from simulations carried out with the AREPO code (see Fig. 10.22). Several runs were produced in which the parameters of the description for sub-grid physics were varied. The properties of the feedback by supernovae, which result in an outflow (‘wind’), were varied, both concerning the mass rate of the outflow as well as its velocity. Furthermore, several feedback descriptions of AGNs were employed.

Figure 10.28 illustrates the importance of the feedback on the properties of the gas. As seen in the left-hand panels, the distribution of the gas density is more extended when feedback processes are included, as the outflows generated by supernovae and AGN feedback distributes the gas over a larger volume, whereas in a model with no feedback, the high-density gas is more confined to dark matter halos and the denser regions of the dark matter filaments. The impact of feedback is more dramatic on the distribution of gas temperature, as seen in the middle panels; without feedback, hot gas is confined to the densest regions, whereas the action of strong radio-mode AGN activity distributes hot gas over large regions of space. The feedback-driven outflows also lead to a wide-spread enrichment of the intergalactic gas with metals (right-hand panels), which otherwise would stay close to their source of origin, i.e., the inner regions of halos in which stellar evolution takes place, in sharp contrast to observations of QSO absorption which show that the IGM is metal enriched.

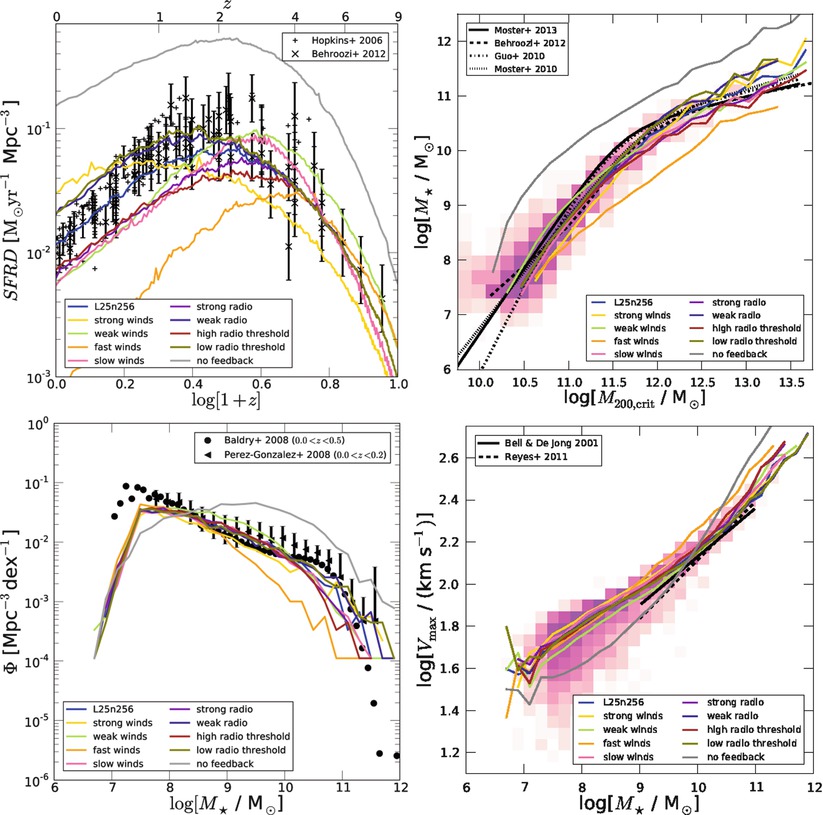
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig29_HTML.jpg

Fig. 10.29

Several results from the hydrodynamical simulations shown in Fig. 10.28 are displayed here. In all cases, the blue curve shows the simulation where all the free parameters of the model were set to their fiducial values. The other curves show variations of this model, which differ from the fiducial model by changing the prescription of various feedback processes by supernovae (these relate to the strong/weak/fast/slow wind models) and AGN. The grey curve corresponds to a model with no feedback. Top left: The star formation rate density as a function of redshift (i.e., the ‘Madau plot’). Black symbols with error bars show estimates from observations, as described in Sect. 9.6.2, whereas the curves show the results from the simulation. Top right: The stellar mass vs. halo mass. The shading indicates the probability density for the fiducial model, with the blue curve showing the median of M _∗ at fixed halo mass. The black curves show estimates of the M _∗(M ₂₀₀)-relation as obtained from abundance matching of galaxies with dark matter halos, the other curves correspond to variants of the numerical model. Bottom left: The stellar mass function at z = 0, compared to observational results (symbols with error bars). Bottom right: The maximum rotational velocity V _max of galaxies as a function of their stellar mass, i.e., the Tully–Fisher relation, for z = 0. The shading shows the probability density for the fiducial model, with the blue curve showing the median of V _max at fixed M _∗. The two black lines show the observed Tully–Fisher relation, the other curves variations of the fiducial model. Source: M. Vogelsberger et al. 2013, A model for cosmological simulations of galaxy formation physics, arXiv:1305.2913, Figs. 6, 7, 8, 10. Reproduced by permission of the author

The star-formation rate density. Every successful model of galaxy evolution must be able to reproduce the observed star-formation history in the Universe. We have seen in Sect. 9.6.2 that the star-formation rate density evolves strongly with redshift, showing a broad peak at redshifts between 2 and 4. The top left panel of Fig. 10.29 shows a recent version of the Madau-diagram, and predictions from the numerical simulations. Here and in the other panels of the figure, the blue curve corresponds to the fiducial set of feedback parameters, and the other colored curves show variations of the model. Whereas the fiducial model provides a satisfactory fit to the observational results, some of the other models fail dramatically. Foremost, the model with no feedback overproduces stars by a large factor, and can safely be ruled out also for this reason. Changing the feedback from SNe can also alter the model prediction substantially; for example, the model termed ‘fast winds’ blows the gas out of halos and thus prevents the formation of stars at later epochs. Strong winds remove the gas from halos at early times, thus reducing the star-formation rate, but later gas is reaccreted and results in star formation rates at low redshifts which are larger than those estimated from observations. Other parameter variations are seen to have a smaller impact on the predictions.

The stellar mass-halo mass relation. We saw in Sect. 7.7.4 that the ratio of M _∗∕M ₂₀₀ varies substantially with M ₂₀₀, which is the origin for the mismatch between the halo mass function and the stellar mass function, shown in Fig. 10.2. In particular, this ratio attains a maximum at a characteristic mass scale which corresponds to a massive galaxy in the current Universe. The top right panel of Fig. 10.29 shows the predictions of the $M_{{\ast}}(M_{200})$ -relation from the simulations, compared to the observed relation (shown as black curves). The fiducial model appears to reproduce the observed relation quite well, though the turnover at $M_{200} \sim 10^{12.2}\,M_{\odot }$ is less pronounced than that obtained from observations. The ‘fast wind’ model fails in a similar way as for the star-formation rate density—too much gas is blown out of halos. In general, variations of AGN feedback affect the upper mass end of the relation more strongly than for lower masses, and is essential for the suppression of star formation in high-mass halos, as argued several times before. Conversely, the low-mass end of the relation is more sensitive to feedback from supernovae.

The stellar mass function of galaxies. Successful galaxy evolution models should be able to reproduce the observed luminosity function of galaxies, as a function of redshift. Since the prediction of the luminosity in a specific spectral band depends not only on the properties of the stellar population, but also on the dust content and distribution, the calculated luminosity function is affected by an additional uncertainty. For that reason, a comparison of the stellar mass function between simulations and observations is slightly more straightforward. This is shown in the bottom left panel of Fig. 10.29, where the stellar mass function from the simulations is compared to observational results at low redshifts. The cut-off below M _∗ ∼ 10^7. 5 is due to the finite resolution of the simulations which implies a minimum halo mass that can be resolved. Models with fast or strong winds from supernovae severely underpredict the mass function over a broad mass range. The impact of AGN feedback is most clearly seen at and beyond the mass scale where the mass function starts to bend over; in particular, reducing the strength of AGN feedback overpredicts the stellar mass function at the high-M _∗ end.

The Tully–Fisher relation. Finally, the lower right panel of Fig. 10.29 compares the observed Tully-Fisher relation with the model prediction. The fiducial model reproduces the observed relation fairly well, but the changes that occur by altering the feedback model parameters are modest in this case. However, the model without AGN feedback fails also this comparison, yielding a much steeper relation than observed.

Conclusion. The example just presented shows that modern hydrodynamic simulations of galaxy evolution can reproduce some key observables. By comparing the predictions from the model to observations, the various free parameters describing the sub-grid physics can be adjusted. Whereas the ‘fiducial model’ fares quite well in the comparison shown, there remain several shortcomings. For example, the observed mass-metallicity relation (see Fig. 3.40) is not well matched by the simulation, whereas the stellar mass-black hole mass relation can be reproduced fairly well. Without doubt, this field will see further strong developments in the future.

10.7 Evolution of the galaxy population: Semi-analytic models

Hydrodynamic simulations are difficult and computationally expensive. This means that one cannot carry out large numbers of such simulations, for example, to test a large number of different parameter sets for the sub-grid physics (like feedback efficiency). Furthermore, their spatial resolution and/or the total volume covered by these simulations are typically inferior to those of pure N-body simulations. Hence, it is a larger challenge to include both the large-scale density perturbations in the matter field (on scales larger than ∼ L∕2), and the high resolution necessary to resolve the smaller-mass galaxies.

Instead, one can follow a different approach, in which the behavior of the dark matter distribution is obtained from N-body simulations, and simplified descriptions of the behavior of baryons in this matter distribution are employed. The formation of galaxies happens in dark matter halos, and so each dark matter halo is a potential site for the formation of stars—i.e., a galaxy. At the moment a halo forms, one expects that it contains a baryon fraction equal to the cosmic mean, and that the baryons have approximately the same spatial distribution and the same specific angular momentum as the dark matter (which is obtained from the N-body simulation). The fate of the baryons then depends on various physical processes which we have already discussed above: cooling, star formation, supernova feedback, accretion of gas onto a central black hole, etc. Furthermore, the N-body simulation yield the merging history of all dark matter halos, and so the processes which occur in minor and major mergers can be treated as well.

Some of these processes are rather well understood, such as cooling, whereas for those physical processes which we are unable to describe with a quantitative physical model, a parametrized, approximate description is chosen. To give one example, the star-formation rate in a galactic disk is expected (and observed) to depend on the local surface mass density Σ _g of gas in the disk. Therefore, the star-formation rate is parametrized in the form $\dot{\varSigma }_{\mathrm{SFR}} = A\varSigma _{\mathrm{g}}^{\beta }$ [see (3.16)], and the parameters A and β adjusted by comparison of the model predictions with observations. Such semi-analytic models of galaxy formation and evolution have contributed substantially to our understanding and interpretation of observations. We will discuss some of the properties and predictions of these models in the following.

10.7.1 Method for semi-analytic modeling

Merger trees. The distribution of particles resulting from an N-body simulation at a given output time can be used to identify dark matter halos. Several methods for that can be applied as described in Sect. 7.5.3, e.g., the friends-of-friends method, the spherical overdensity criterion, or a combination of these. Similarly, sub-halos within each halo can be identified as well. Comparing the lists of (sub-)halos and their particle contents at consecutive output times, one can identify whether a halo present at the earlier time has merged with another halo before the later output time. Over the course of time, more and more smaller halos have merged to more massive ones. Thus, for each halo at redshift z = 0, one can follow its complete merging history back in time, thereby obtaining its ‘merger tree’ (see Fig. 10.30).¹⁰

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig30_HTML.jpg

Fig. 10.30

A typical merger tree, as expected in a hierarchical CDM model of structure formation. The time axis runs from top to bottom. A massive halo at the present time t ₀ has formed by mergers of numerous halos of lower mass, as indicated in the figure. One defines the time of halo formation as the time t _f at which one of the sub-halos had reached half the mass of the current halo. Source: C. Lacey & S. Cole 1993, Merger rates in hierarchical models of galaxy formation, MNRAS 262, 627, p. 636, Fig. 6. Reproduced by permission of Oxford University Press on behalf of the Royal Astronomical Society

Gas cooling and star formation. In a halo where no merger process occurs at a given time, gas can cool. The cooling rate is determined by the chemical composition and the density of the gas as we described above. Besides the cooling processes, one can also account for the heating of the gas by the ionizing background radiation. Furthermore, one can account for the fact that low-mass halos are expected to have a smaller baryon fraction than the cosmic mean, if the gas is heated by the ionizing background to temperatures higher than the virial temperature of the halo, as described by (10.10).

Cool gas is assumed to settle down in a rotationally-supported thin disk. If the density of the gas is sufficiently high, it can form stars, where the star-formation rate is assumed to follow the Schmidt–Kennicutt law (3.16), averaged over the disk. A simpler prescription for star formation is $\dot{M}_{{\ast}}\propto M_{\mathrm{cool}}/\tau$ , where M _cool is the mass of cold gas in the halo, and τ a characteristic time, such as the dynamical time-scale of the disk. The newly formed stars are associated with a ‘disk component’.

Supernova feedback. Shortly after the formation of stars, the more massive of them will explode in the form of supernovae. This will re-heat the gas, since the radiation from the SN explosions and, in particular, the kinetic energy of the expanding shell, transfers energy to the gas. By this heating process, some of the cool gas can be heated again and be driven out into the halo, i.e., the hot gas mass of the halo is increased in this way. Furthermore, if the energy input by supernova feedback is large enough, the heated gas can actually be expelled from the halo altogether (and at some later time reaccreted onto the halo). The suppression of the formation of low-mass galaxies by the effects mentioned here is a possible explanation for the apparent problem of CDM substructure in halos of galaxies discussed in Sect. 7.8. In this model, CDM sub-halos would be present, but they would be unable to have experienced an efficient star-formation history—hence, they would be dark.

In any case, feedback reduces the amount of cold gas available for star formation. This leads to a self-regulation of star formation, which prevents all the gas in a halo from being transformed into stars. This kind of self-regulation by the feedback from supernovae (and, to some extent, also by the winds from the most massive stars) is also the reason why the star formation in our Milky Way is moderate, i.e., not all the gas in the disk is involved in the formation of stars.

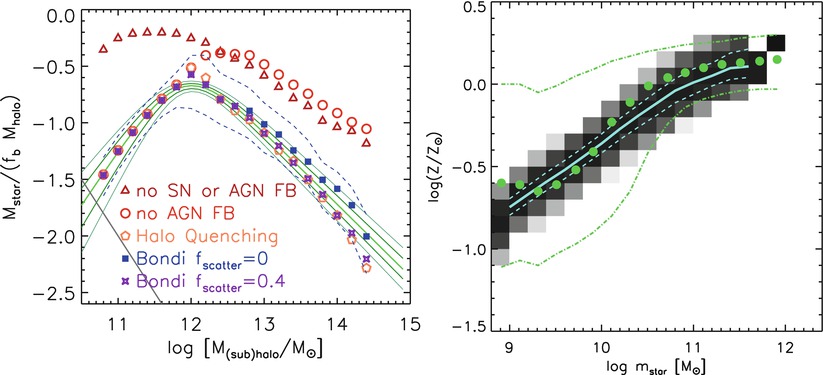
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig31_HTML.jpg

Fig. 10.31

Left panel: The fraction of baryons in the form of stars, as a function of halo mass, as predicted by a semi-analytic model. The brown triangles show the stellar mass fraction for a model run where no feedback was included. In this case, for galaxy-mass halos ( $\sim 10^{12}M_{\odot }$ ) most of the baryons have been converted into stars. For larger halos masses, the fraction decreases, since cooling becomes less efficient in these halos. The green curves show the range of stellar mass fractions that is obtained from observations. Obviously, the no-feedback assumption violates observational constraints on all mass scales. The red circles show results from a model in which supernova feedback was included, but no feedback from AGN. Here, the stellar mass fraction is very substantially reduced at the low-mass end, bringing it into the observed range; however, supernovae are inefficient at high halo masses. The other three types of symbols correspond to different assumptions about AGN feedback; clearly, AGN feedback is needed to account for the small star-formation efficiency in high-mass halos, such as groups and clusters. Right panel: The metallicity as a function of stellar mass. Grey shades indicate the probability distribution that a galaxy of stellar mass m _star has a metallicity Z (in Solar units), with the solid curve showing the median and the dashed curve the 1-σ range, as obtained from a semi-analytic model. The green points show the observed metallicity of galaxies. The median of the two distributions agree very well, though the spread is considerably larger in the observed galaxies. Source: R. Somerville et al. 2008, A semi-analytic model for the co-evolution of galaxies, black holes and active galactic nuclei, MNRAS 391, 481, p. 492, 494, Figs. 3, 6. Reproduced by permission of Oxford University Press on behalf of the Royal Astronomical Society

The left panel of Fig. 10.31 shows the importance of supernova feedback. Plotted here is the stellar mass fraction of baryons as a function of halo mass. A semi-analytic model without the inclusion of feedback yields the result that for halo masses below $\sim 10^{12}M_{\odot }$ , more than half of the baryons are contained in stars. This is in sharp contradiction to observations which show that star formation is a rather inefficient process. This is just one of several arguments—in the absence of feedback, a Milky Way-like galaxy would have consumed all its gas early in its history, leaving no gas reservoir for current star formation. Including supernova feedback, the stellar mass fraction of the model can be made to agree with observations, for galaxy-mass halos. For more massive halos, feedback by supernovae is no longer efficient, and a different feedback mechanism is required (see below).

Minor mergers. The merger trees obtained from the N-body simulations describe for each halo at which time it merges with another one. As we discussed above, the outcome of a merger will depend to a large degree on the mass ratio of the two merging halos (and galaxies): If the mass ratio is substantially different from unity (e.g., smaller than 1:3; minor merger), the merger will cause little damage to the galaxy of the more massive component, whereas for almost equal mass mergers, one expects that both galaxies will be destroyed and the stellar distribution be changed drastically.

If the masses of the two components in a merger are very different, the merging process of the two components does not occur instantaneously, but since the smaller galaxy will have, in general, a finite orbital angular momentum, it will first enter into an orbit around the more massive component. The smaller mass halo and galaxy can survive as a satellite galaxy. This satellite galaxy is subject to several processes, though. By moving through the hot gas of the larger halo, ram-pressure stripping can remove gas, at a rate depending on the gas density in the halo, the orbit of the satellite (as determined by the N-body simulation), and the gas density of the satellite (which has been recorded by the earlier evolution of that galaxy before the merger event). The stripped gas is added to the gas distribution of the main halo. The stripping of the gas reduced the reservoir from which the satellite can form stars, a process which explains that satellite galaxies in groups and clusters are usually redder than their central galaxy.

Furthermore, dynamical friction (see Sect. 6.3.3) changes the orbit of the satellite in time, bringing it closer to the halo center. Once that happens, the cold gas and the stars of the satellite galaxy are added to the disk component of the central galaxy of the halo.

It may also be that the orbit of a satellite galaxy comes close to the center of the main halo where the tidal forces are strong. In such a case, the galaxy may be tidally disrupted. Since the satellite in this case has a large velocity relative to the central galaxy, its stars are then assumed to be dispersed in the halo, contributing to the intracluster stellar population which has been found in individual clusters, as well as in the cluster population as a whole (see Sect. 6.3.4). Since the cold gas and the stars are more concentrated than the dark matter subhalo of the satellite, the galaxy (i.e., stars + gas) may survive tidal effects, even after the dark matter subhalo has been tidally disrupted. Hence, there may be orphan galaxies—satellite galaxies without a corresponding dark matter subhalo.

Major mergers. If the two merging galaxies have a mass ratio close to unity (i.e., larger than ∼ 1: 3), it is assumed that their disks are completely destroyed and their stars being rearranged into a spheroidal distribution. Furthermore, a fraction of the sum of the cold gas in both components is assumed to undergo a starburst. The newly formed stars are added to the spheroidal stellar component. For minor mergers, a corresponding collisional starburst can be added as well, where the newly formed stars are added to the disk component. The resulting strong supernova feedback can then expel most of the remaining gas from the remnant of a major merger, leaving a (gas-poor) elliptical galaxy.

After the formation, an elliptical can attain new cold gas from the cooling of hot gas in the halo, accretion of surrounding material, or subsequent minor merger events. By these processes, a new disk population may form. In this model, a spiral galaxy is created by forming a bulge in a ‘major merger’ at early times, with the disk of stars and gas being formed later in minor mergers and by accretion of gas. Hence the bulge of a spiral is, in this picture, nothing but a small elliptical galaxy, which is also suggested by the very similar characteristics of bulges and ellipticals, including the fact that both types of objects seem to follow the same relation between the black hole mass and the stellar velocity dispersion, as explained in Sect. 3.8.3.

Black hole growth, and feedback from AGN. When they form, galaxies are implanted a central black hole of small seed mass, as described above for the hydrodynamical simulations. The mass of the black holes then grows as a result of mergers and accretion of gas. The former process drives gas into the center of the galaxies, where a star-formation episode sets in; this process also feeds gas onto the supermassive black hole. The two SMBHs in a merger event are assumed to also merge. In this mode of accretion, star formation and AGN activity happen in parallel, and so do the corresponding feedback processes. Hence, only their sum is relevant.

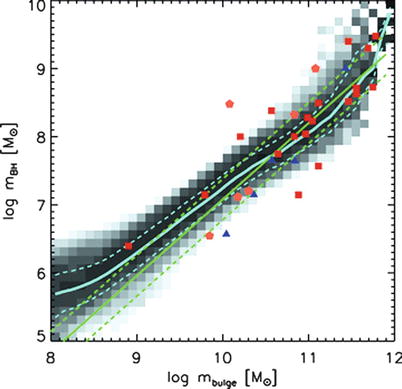
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig32_HTML.jpg

Fig. 10.32

The black hole mass vs. bulge mass relation, as predicted from a semi-analytic model. Grey shading indicates the probability distribution of the black hole mass for a given bulge mass, the blue solid and dashed curves yield the median of the black hole mass and its 1-σ range. The green lines show the corresponding results from observations, whereas symbols show individual observed galaxies. Source: R. Somerville et al. 2008, A semi-analytic model for the co-evolution of galaxies, black holes and active galactic nuclei, MNRAS 391, 481, p. 495, Figs. 7. Reproduced by permission of Oxford University Press on behalf of the Royal Astronomical Society

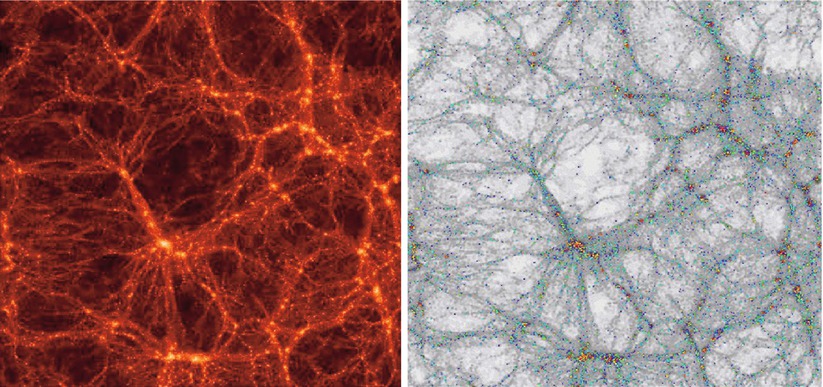
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig33_HTML.jpg

Fig. 10.33

On the left, the distribution of dark matter resulting from an N-body simulation is shown. The dark matter halos identified in this mass distribution were then modeled as the location of galaxy formation—the formation of halos and their merger history can be followed explicitly in the simulations. Semi-analytic models describe the processes which are most important for the gas and the formation of stars in halos, from which a model for the distribution of galaxies is built. In the panel on the right, the resulting distribution of model galaxies is represented by colored dots, where the color indicates the spectral energy distribution of the respective galaxy: galaxies with active star formation are shown in blue, while galaxies which are presently not forming any new stars are marked in red. The latter are particularly abundant in clusters of galaxies—in agreement with observations. Credit: G. Kauffmann, J. Colberg, A. Diaferio & S.D.M. White, and the GIF-Collaboration

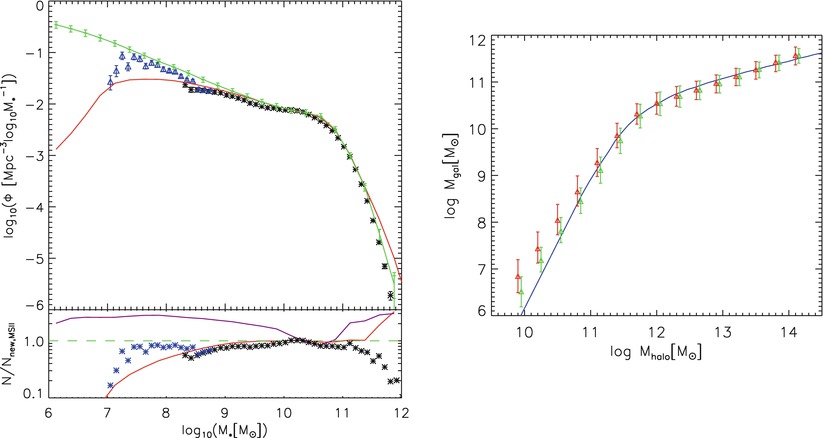
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig34_HTML.jpg

Fig. 10.34

Upper left panel: The stellar mass function of galaxies as obtained from a semi-analytic model for which the Millennium Simulation (MS) and the Millennium II (MS-II) simulations have been used for describing the dark matter evolution (see Sect. 7.5.3). The red and green curves show the model predictions from the MS and the MS-II, respectively. Owing to the better spatial and mass resolution of the MS-II, the stellar mass function can be followed to considerably smaller masses. Black and blue points show observational results as obtained from the SDSS; at the lowest mass end, the observed galaxies come from a very small local volume, and are therefore subject to a substantial ‘cosmic variance’. The lower left panel shows the ratio of the mass functions relative to the predictions from the MS-II. Clearly, the semi-analytic model can reproduce the observed mass function accurately over some 4 orders of magnitude (the purple curve in the lower panel shows the corresponding results from an earlier incarnation of semi-analytic modelling, where in particular the feedback was assumed to be weaker). The right panel shows the mean stellar mass and its dispersion as a function of the halo mass, as obtained from the simulations. Green symbols are for central galaxies of halos, whereas the red symbols correspond to satellite galaxies (where the corresponding halo mass is the mass of their subhalos at the time the satellite has merged with the main halo). The blue curve is obtained if the dark matter halo abundance is directly matched to the stellar mass function, assuming a monotonic dependence between these two quantities. Note that the slope of the relation is considerably steeper than unity at the low-mass end, and much flatter at the high-mass end. This relation therefore explains the different shapes of the halo mass and stellar mass functions shown in Fig. 10.2. Source: Q. Guo et al. 2011, From dwarf spheroidals to cD galaxies: simulating the galaxy population in a ΛCDM cosmology, MNRAS 413, 101, p. 115, 117, Figs. 7, 9. Reproduced by permission of Oxford University Press on behalf of the Royal Astronomical Society

However, we have seen in clusters that feedback must be highly efficient in suppressing cooling flows, and found clear direct evidence for the AGN feedback on the intracluster medium, in the form of extended radio emission (e.g., jets), and the corresponding cavities in the X-ray emitting gas. The corresponding AGN activity is rather moderate in terms of overall luminosity—the center of cool-core clusters usually do not contain a bright QSO, despite the large mass of the central galaxy and the corresponding large mass of the SMBH. Hence, these AGNs must accrete at a rate substantially lower than the Eddington rate. In this mode, a large fraction of the energy is released in form of radio jets, i.e., kinetic energy of a relativistic plasma. This ‘radio-mode’ accretion is highly inefficient in generating optical and UV-radiation. It is assumed that this low-rate accretion is related to a cooling flow from the intracluster medium. A simple picture would be that of a self-regulating feedback which quenches the cooling once it becomes too effective, thus leading to a large accretion rate, and subsequently a larger energy output from the central SMBH. Suppressing the cooling then reduces the accretion flow, leading to a decreased accretion rate, less feedback, and consequently, higher cooling rate after some time.¹¹ In semi-analytic models, the accretion rate can then be calculated from the cooling rate of the hot gas in the halo, and a certain fraction of the resulting energy release is assumed to be used for heating the gas in the halo.

The importance of this AGN feedback can be seen in the left panel of Fig. 10.31, where the stellar mass fraction of baryons is shown as a function of halo mass. AGN feedback is essential to suppress star formation in high-mass halos, i.e., to explain the small ratio of stellar-to-hot gas mass in galaxy clusters. Supernova feedback by itself is not efficient in high-mass halos. Furthermore, these models are successful in reproducing the relation between the SMBH mass and the properties of the stellar population, such as the bulge mass (see Fig. 10.32), luminosity, or velocity dispersion of the spheroidal component.

Stellar populations and chemical evolution. For each galaxy formed, the models keep track of their star-formation history. Hence, one can assign to each galaxy the stellar populations formed in time, once an initial mass function is selected. Using stellar population synthesis models, one can then obtain the stellar luminosity and spectral energy distribution for each galaxy [using (3.37)], and turn these parameters into ‘observables’, like magnitude and colors. In order to compare these predictions to observations, the effects of dust need to be accounted for. The amount of dust depends on the amount of gas and the metallicity of the gas which in turn is determined by the history of chemical enrichment. This is followed for each galaxy by the amount of metals ejected into the gas by supernovae and stellar winds. These metals are then mixed with the other gas, the newly forming stars are assigned the corresponding metallicity of the cool gas. In this way, the models can make predictions of observable properties of galaxies and their statistical distribution.

10.7.2 Results from semi-analytic models

The free parameters in semi-analytic models—such as the star-formation efficiency or the fraction of energy from SNe that is transferred into the gas—are fixed by comparison with some key observational results. For example, one requires that the models reproduce the correct normalization of the Tully–Fisher relation and that the number counts of galaxies match those observed. Although these models are too simplistic to trace the processes of galaxy evolution in detail, they are highly successful in describing the basic aspects of the galaxy population, and they are continually being refined. These refinements make use of empirical results (such as the Schmidt-Kennicutt law for star formation) and theoretical progress, such as detailed simulations of the merger process between pairs of galaxies. The outcome from such simulations are summarized in analytic expressions which are then applied to the semi-analytic models. In this section, we want to show some of the results from these models.

Red versus blue galaxies. For instance, all semi-analytic models predict that galaxies in clusters basically consist of old stellar populations, because here the interaction processes concluded already quite early in cosmic history. Therefore, at later times cold gas is no longer available for the formation of stars. Fig. 10.33 shows the outcome of such a model in which the merger history of the individual halos has been taken straight from the numerical N-body simulation, hence the spatial locations of the individual galaxies are also described by these simulations.

By comparison of the results from such semi-analytic models with the observed properties of galaxies and their spatial distribution, the models can be increasingly refined. In this way, we obtain more realistic descriptions of those processes which are included in the models in a parametrized form. This comparison is of central importance for achieving further progress in our understanding of the complex processes that are occurring in galaxy evolution, which can not be studied in detail by observations.

Stellar mass function and stellar-to-total mass ratio. Combining two dark matter simulations with the same cosmological parameters but different box size and spatial resolution (namely the Millennium and Millennium-II simulations; see Sect. 7.5.3), the properties of galaxies can be predicted over a very wide range of masses. For example, the left-hand side of Fig. 10.34 shows the predicted stellar mass function of galaxies at redshift z = 0, compared to results from observations. We see that the model can reproduce the observations over a range of several orders of magnitude in stellar mass. Key to this achievement are the feedback processes, as already discussed in connection with Fig. 10.31; together with the temperature- (and mass-)dependent cooling function of gas, they determine the overall efficiency of turning gas into stars, and thus lead to a preferred mass scale where the stellar-to-total mass of halos is maximized (see Fig. 10.2). This can also be seen in the right panel of Fig. 10.34 which plots the mean stellar mass as a function of halo mass. There, one can also see the characteristic mass scale where the slope of this relation changes sharply.

Tully–Fischer relation. Traditionally, galaxy evolution models had problems of reproducing the Tully–Fisher relation for disk galaxies (see Sect. 3.4.1). The implementation of the aforementioned result from numerical simulations, namely that the rotational velocity of a disk is well approximated by the maximum velocity of the corresponding NFW halo, largely solves this problem, as can be seen in Fig. 10.35 which shows the predicted relation between luminosity and rotational velocity for disk-dominated galaxies, compared to the observed Tully–Fisher relation. The agreement between these two distributions is fairly good, in particular concerning the overall amplitude. Whereas the shape of the Tully–Fisher relation in the model is not truly a power law, this may be related to a slightly too efficient feedback in massive galaxies, which decreases their luminosity.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig35_HTML.jpg

Fig. 10.35

The Tully–Fisher relation in the r-band. Green points show the absolute r-band magnitude of disk-dominated galaxies as a function of maximum rotational velocity of their host halos, as obtained from the same semi-analytic model as shown in Fig. 10.34. This is compared to observational results indicated by the blue crosses. Semi-analytic models are thus able to reproduce the zero point and approximate shape of the Tully–Fisher relation over a range of about 8 magnitudes. Source: Q. Guo et al. 2011, From dwarf spheroidals to cD galaxies: simulating the galaxy population in a ΛCDM cosmology, MNRAS 413, 101, p. 119, Fig. 13. Reproduced by permission of Oxford University Press on behalf of the Royal Astronomical Society

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig36_HTML.jpg

Fig. 10.36

Large-scale distribution of galaxies as obtained from redshift surveys (in blue) and from semi-analytic models of galaxies in the Millennium simulation (in red). On the left, one hemisphere of the 2dFGRS is shown (cf. Fig. 7.1), whereas on the top the small wedge diagram shows the CfA2 redshift survey (Fig. 7.2) with the Coma cluster at its center, and the large wedge is part of the SDSS. In much the same way as the observed distributions are obtained, the galaxy distribution from the Millennium simulation has been transformed into wedge diagrams shown in red. They are very similar to the observed ones—they show great walls, fingers of god (since the model galaxies are plotted in redshift space, as their peculiar velocity is given by the simulation), as well as the cellular structure of filaments and voids. Source: V. Springel et al. 2006, The large-scale structure of the Universe, Nature 440, 1137, Fig. 1. Reprinted by permission of Macmillan Publishers Ltd: Nature, ©2006

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig37_HTML.jpg

Fig. 10.37

The correlation function of galaxies (left) and dark matter (right) in the Millennium simulation, for different redshifts. The dashed curve in the left panel shows the z = 0 dark matter correlation, for easier comparison. The galaxies are selected above a given I-band luminosity. There are striking differences between these two correlations. As expected from structure growth, the dark matter correlation function decreases with increasing redshift (remember, on large scales where structure evolution follows linear perturbation theory, $\xi (r,z) \propto D_{+}^{2}(z)$ . In contrast to that, the evolution of the galaxy correlation function is much smaller, and it is not monotonic with redshift: the correlation at the highest redshift is almost the same as the one at z = 0. Source: V. Springel et al. 2006, The large-scale structure of the Universe, Nature 440, 1137, Fig. 5. Reprinted by permission of Macmillan Publishers Ltd: Nature, ©2006

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_10_Fig38_HTML.jpg

Fig. 10.38

In the top panels, one of the most massive halos at z = 6. 2 from the Millennium simulation (see Fig. 7.13) is shown, whereas in the bottom panels, the corresponding distribution in this spatial region at z = 0 is shown. Thus, this early massive halo is now located in the center of a very massive galaxy cluster. In the panels on the left, the mass distribution is displayed. The corresponding distribution of galaxies as determined from a semi-analytic model is shown in the right-hand panels. Galaxies at z = 6. 2 are all blue since their stellar population must be young, whereas at z = 0, most galaxies contain an old stellar population, here indicated by the red color. Each of the panels shows the projected distribution of a cube with a comoving side length of 10 h ⁻¹ Mpc. Source: V. Springel et al. 2005, Simulating the joint evolution of quasars, galaxies and their large-scale distribution, Nature 435, 629, Fig. 3. Reprinted by permission of Macmillan Publishers Ltd: Nature, ©2005

Spatial distribution and correlation function. Since the spatial location of the galaxies is known from such simulations, one can compare their spatial distribution with that of the galaxies from redshift surveys. This is illustrated in Fig. 10.36, which shows a comparison of wedge diagrams from redshift surveys with those obtained from the semi-analytic models applied to the dark matter distribution of the Millennium simulation. At least at first sight, the statistical properties of the ‘red’ and ‘blue’ wedge diagrams are the same. The model predicts the occurrence of ‘Great Walls’, as well as the system of voids and filaments in the overall galaxy distribution. This comparison can be made more quantitative, for example by comparing the two-point correlation function of model galaxies with that obtained from observations. Also here, good qualitative agreement is found, though the simulation slightly overpredicts the amplitude of the correlation function. This, however, may be due to the fact that the normalization of the power spectrum was chosen to be σ ₈ = 0. 9, slightly larger than the current best estimates for our Universe (see Sect. 8.7).

The correlation function of galaxies has a rather different behavior as a function of scale and redshift than that of the dark matter. In Fig. 10.37, the correlation function of luminous galaxies and that of the overall matter distribution is shown for four different redshifts. Several issues are remarkable. First, the dark matter correlation function ξ _m(r) is not well approximated by a power law, whereas the galaxy correlation function ξ _g(r) shows a power-law behavior over many decades of spatial scale, in agreement with observed galaxy correlation functions. At z = 0 (red curve), ξ _g(r) almost traces the correlation function of matter on scales r ≳ 1h ⁻¹ Mpc, but they disagree substantially on smaller scales. This implies that the bias of galaxies is strongly scale-dependent, at least on small scales. In fact, the question arises as to which processes in the evolution of galaxies may produce such a perfect power law: why does the bias factor behave just such that ξ _g attains this simple shape. The answer is found by analyzing galaxies with and without active star formation separately; for each of these sub-populations of galaxies, ξ _g is not a power law. Therefore, the simple shape of the correlation function shown in Fig. 10.37 is probably a mere coincidence (‘cosmic conspiracy’).

Second, the matter correlation function strongly decreases with increasing redshift, whereas ξ _g evolves much slower with z. This implies that the bias of galaxies is redshift dependent; for a given galaxy luminosity (or stellar mass), the bias increases with redshift. In fact, we see that ξ _g at z = 8. 55 is almost identical with the one at zero redshift—the dependence of ξ _g on redshift is not monotonic.

Early QSOs. Another result from such models is presented in Fig. 10.38, also from the Millennium simulation . Here, one of the most massive dark matter halos in the simulation box at redshift z = 6. 2 is shown, together with the mass distribution in this spatial region at redshift z = 0. In both cases, besides the distribution of dark matter, the galaxy distribution is also displayed, obtained from semi-analytic models. Massive halos which have formed early in cosmic history are currently found predominantly in the centers of very massive galaxy clusters. Assuming that the luminous QSOs at z ∼ 6 are harbored in the most massive halos of that epoch, we might suppose that these may today be identified as the central galaxies in clusters.¹² This may provide an explanation as to why so many central, dominating cluster galaxies show AGN activity, though with a smaller luminosity due to small accretion rates.

From what we presented in this section, we can summarize that semi-analytic modelling of galaxies is a very useful method to make the link between the dark matter distribution on the one hand, and the properties of the galaxy population on the other. Since semi-analytic models are computational inexpensive, compared to gas-dynamical simulations, one can experiment with them and study in detail the dependence of galaxy properties on certain assumptions and parameter choices. Furthermore, these models allow us to include our best knowledge and understanding of the various complex baryonic processes in a unified way which yields quantitative results. We also have a fairly good understanding of the mean properties of galaxies and their central black holes. Much of this knowledge has been obtained only in recent years, and there is no doubt that future observational results will lead to further refinements, and perhaps qualitative modifications, of our understanding.

Footnotes

Spectroscopy in the NIR is possible in principle, but the high level of night-sky brightness and, in particular, the large number of atmospheric transition lines renders spectroscopic observations in the NIR much more time consuming than optical spectroscopy.

To destroy all the H₂ in the Universe one needs less than 1 % of the photon flux that is required for the reionization.

We remind the reader about the connection between halo masses and circular velocities; cf. Sect. 7.6.1; see also (10.2).

Note that in this case, the baryons are embedded in a dark matter halo, so the consideration of the spin parameter, which applies for the total energy and angular momentum, no longer applies to the baryons only. Therefore, in this case (10.11) does not hold for the baryons alone.

In this case of high collision velocity, the time it takes a galaxy from one of the two clusters to cross the gravitational potential of the other cluster is shorter than the time it takes the matter of the second cluster to react to the changing conditions caused by the merger; therefore, the gravitational potential of the second cluster can be considered almost stationary during the collision process. Thus, the galaxy leaves the potential of the second cluster with almost the same velocity it had on entering, i.e., it is not gravitationally bound to the second cluster.

The fact that spectacular images of merging galaxies show mainly gas-rich mergers (such as in Fig. 9.25 or 1.16) can be attributed to selection effects. On the one hand, gas-rich mergers lead to massive star formation, yielding a statistically increased luminosity of the systems, whereas dry mergers basically preserve the luminosity. On the other hand, gas-rich mergers can be recognized as such for a longer period of time than dry ones, owing to the clearly visible tidal tails traced by luminous newly formed stars.

Calculating the behavior of a binary black, using the equations of General Relativity, turns out to be very difficult endeavor. Only since 2005 it has become possible to find numerical solutions of this problem.

The equations of hydrodynamics describe the behavior—or transport—of the mass, momentum and energy in a fluid. Mass conservation is expressed by the continuity equation (7.2). The evolution of the fluid momentum is given, in the simplest case, by the Euler equation (7.3); however, since gas is dissipative, frictional terms need to be included (the resulting equation for the fluid velocity is then called Navier–Stokes equation). Finally, the transport of energy is described by an energy equation, which contains sources and sinks of energy, as they can be caused by absorption and emission of radiation and the local generation of heat by frictional forces.

The situation is rather similar in meteorology, where we believe to know all the essential physical processes that affect the Earth atmosphere; nevertheless, we all know that weather predictions can be terribly wrong, even on short time-scales. The reason is that, although the relevant physical laws are known, their consequences cannot be calculated with sufficient accuracy due to the complexity of the underlying equations. Also in this case, small-scale, highly non-linear processes (convection, turbulence) have an impact on the large-scale properties of the atmosphere.

In fact, one can obtain a statistical ensemble of such merger trees also analytically from an extension of the Press–Schechter theory (see Sect. 7.5.2), but referring to N-body simulations also yields a prescription of the spatial distribution of the resulting galaxy distribution.

Of course, this simple picture ignores all the difficulties in understanding the transport of gas from large distances to the immediate vicinity of the black hole where it can be accreted.

This will not be true in every single case; as can be seen from Fig. 10.26, the most massive SMBHs at high redshifts are not necessarily the mass record holder at later epochs.

Prev Next