5

LAS CONSTANTES DE LA NATURALEZA

MARQUÉS DE MONTROSE

La importancia de ser constante

A menudo me pregunto, al leer las descripciones del proceso científico hechas por sociólogos, si es así como un átomo se sentiría si pudiera leer un libro de texto de mecánica cuántica.

JAMES TREFIL

La permanencia tiene algo que resulta atractivo. Sentimos de forma instintiva que las cosas que han permanecido invariables durante siglos deben poseer algún atributo que es intrínsecamente bueno. Han superado la prueba del tiempo. Nuestras creencias religiosas han descansado tradicionalmente en la confianza que podemos depositar en un Ser Supremo inmutable, cuya invariancia «ayer, hoy y siempre» es por consiguiente una garantía para el futuro. Y, a pesar del flujo constante de sucesos cambiantes, creemos que el mundo posee alguna trama invariante cuyo aspecto general permanece siempre igual. También a los físicos les gusta creer esto. Las ecuaciones que ellos utilizan para encapsular las leyes de la naturaleza contienen ciertos números invariantes que han llegado a conocerse como «constantes de la naturaleza». Adjudicar a una cantidad la calificación de «constante de la naturaleza» le confiere un estatus particularmente elevado en el sistema de las cosas.

Una de las ventajas más notables de las ecuaciones que animan la investigación científica de la naturaleza es que se puede hacer uso de ellas para predecir el futuro, aun cuando no se entienda por qué estos números constantes poseen precisamente los valores particulares que presentan. Nosotros tan sólo podemos medirlos. Si dichos valores se ven ligeramente modificados por medidas más precisas, la forma general de las soluciones a las ecuaciones no sufrirá ningún cambio notable. Tampoco se encuentran vinculadas a la naturaleza de las condiciones iniciales. Claro está, debemos mantener cierta reserva ante este afortunado estado de cosas. Si las constantes de la naturaleza aparecen como parámetros de proporcionalidad en una forma particular, aunque útil, de representar el mundo sobre el papel, entonces estas constantes podrían ser un mero resultado del tipo de representación elegida. Quizá existan formas alternativas de representar el mundo físico que lleven a cantidades invariantes diferentes. Ciertamente, la historia de la ciencia ha presenciado un continuo progreso en lograr que lo que una vez fue arbitrario y complicado en nuestra descripción de las cosas parezca cada vez más simple y necesario. Con frecuencia, esta simplificación se produce al hallarse que cantidades anteriormente consideradas constantes independientes de la naturaleza, o bien están relacionadas entre sí, o están formadas por combinaciones de otras constantes más básicas de la naturaleza. Todo avance realmente significativo de la ciencia física se da paralelamente a la revisión o extensión del conocimiento que poseemos de alguna constante de la naturaleza. El descubrimiento por Newton de una ley universal de la gravedad, hace ya más de trescientos años, contempló la introducción de una constante que ahora lleva su nombre y que especifica la intensidad intrínseca de la fuerza de la gravedad en el universo. La gran novedad de esta cantidad para Newton y sus seguidores fue el hecho de que la medida de la intensidad intrínseca de la gravedad debía ser efectivamente una constante en todo lugar y en todo tiempo. Esta relacionaba fenómenos tan diversos en apariencia como la caída de las manzanas y el movimiento de los planetas.

La constante de la gravitación de Newton fue la primera de las constantes modernas de la naturaleza en ser identificada. Su descubrimiento tuvo derivaciones en otras ramas de la filosofía y la teología. Algunos de los contemporáneos de Newton señalaron su misma universalidad como evidencia de una sola Autoría del universo físico. Fueron a menudo los que profesaban una creencia religiosa en la unidad, como el propio Newton, quienes hicieron un mayor hincapié en esta conexión.

A medida que la ciencia ha evolucionado y se ha vuelto más inquisitiva respecto a las cuestiones concernientes al mundo de la realidad, ya no se ha contentado con considerar a estas constantes de la naturaleza como estándares que sólo podemos conocer mediante la medida. Ni siquiera aquellos negativistas que en el cambio de siglo pensaron que el trabajo de la física estaba terminado, si no fuera por la medida cada vez más precisa de las constantes de la naturaleza, imaginaron que podría existir la posibilidad de calcular sus valores. No contaban con semejante programa en su agenda. Los buscadores modernos de una Teoría del Todo creen que en último término algún profundo principio de consistencia lógica permitirá que estas constantes de la naturaleza sean determinadas por simples procedimientos de contar. Para estos buscadores y sus predecesores, a quienes se puede encontrar en cualquier estadio del desarrollo de la física del siglo XIX, la capacidad para predecir estos números puros es el verdadero sello de distinción de una Teoría del Todo. Una teoría capaz de predecir o de explicar con éxito el valor de cualquier constante de la naturaleza atraería la atención de cualquier físico contemporáneo. La verdad de esta afirmación es comprendida de inmediato por aquellos científicos que reciben una gran cantidad de cartas procedentes de individuos desorientados entre el público anunciando el descubrimiento de su nueva «Teoría del universo» (el autor ha recibido dos sólo durante la última semana). Dichas propuestas presentan dos factores comunes (aparte del hecho curioso de que, según mi experiencia, proceden sin excepción de hombres antes que de mujeres): pretenden mostrar que Einstein estaba de alguna manera equivocado, y se centran por completo en la deducción de los valores numéricos de las constantes de la naturaleza por medio de una serie de misteriosos malabarismos combinatorios que de vez en cuando incluyen consideraciones tan abstrusas como las dimensiones de la Gran Pirámide o la interpretación de la cábala judía. El primero de estos factores tiene una motivación obviamente psicológica. A Einstein se le considera el científico por excelencia del siglo XX y, por tanto, uno imagina inocentemente que, sorprendiéndole en algún desliz, el novel autor será saludado como el nuevo mesías científico, mucho más sobresaliente que Einstein. Pero el segundo factor es el más revelador. La forma en que el trabajo de estos excéntricos se centra en el cálculo de las constantes de la naturaleza es una medida del grado al que esta búsqueda se considera un objetivo fundamental de la física moderna. Se trata de algo bien definido con una respuesta de fácil enunciación. Pero ¿de dónde procede esta percepción popular de la explicación de las constantes de la naturaleza como un Santo Grial para el físico? Yo creo que la respuesta debe buscarse en una parte del trabajo realizado por los científicos en la primera mitad del siglo XX, que alcanzó una gran popularidad en su época.

Fundamentalismo

El eminente Arthur Eddington dio una conferencia sobre su supuesta derivación de la constante de estructura fina a partir de la teoría fundamental. Goudsmit y Kramers se encontraban entre el público asistente. Goudsmit no entendió mucho, pero no vio en ello más que un dislate muy atractivo. Al terminar la discusión Goudsmit se acercó a su amigo y mentor Kramers y le confesó: «¿Es que todos los físicos deliran cuando envejecen?». Kramers respondió: «No, Sam, no tienes por qué preocuparte. Puede que quizá un genio como Eddington desvaríe, pero cualquier otro colega, como tú, sólo se vuelve más y más tonto».

M. DRESDEN

Para valorar plenamente la importancia de la física en la primera mitad del siglo XX, debería tenerse presente que al final del siglo XIX el centro de gravedad de la física se encontraba en Alemania. Pero los físicos alemanes habían heredado el legado filosófico de Kant y esto influyó en muchas de sus expectativas respecto a la posibilidad última de la investigación científica humana. Las conocidas leyes de la física eran vistas como creaciones de la mente humana y tenían que ser distinguidas de la verdadera naturaleza de las cosas. La mayoría de los libros de texto ofrecían una exposición preliminar sobre la filosofía de la ciencia que subrayaba la perspectiva del idealismo kantiano. Sobre esta atmósfera de fondo surgieron una diversidad de concepciones acerca de la finalidad de explicar la totalidad del mundo físico y las constantes de la naturaleza que definían su forma general. Por un lado estaban quienes, como Einstein, creían que el proceso de descripción de la naturaleza por medio de las leyes de la física era un proceso convergente. Siempre habría elementos de la descripción ordinaria que resultarían inadecuados, fragmentos de la verdadera historia que habrían sido omitidos. Este proceso gradual de revisión que llamamos «descubrimiento científico» podría sin embargo no tener fin, pues Einstein concibió la teoría general de la relatividad sólo como un paso más hacia la verdad fundamental, situada en una asíntota inalcanzable, pues

por mucho que seleccionemos mediante el criterio de simplicidad un complejo [de fenómenos] de la naturaleza, en ningún caso su tratamiento teórico resultará válido indefinidamente… Pero no dudo de que llegará el día en que, por razones que en el momento actual no alcanzamos a imaginar, esa descripción [la teoría general de la relatividad] tendrá asimismo que conducir a otra. Yo creo que este proceso de ahondamiento en la teoría no tiene límites.

Poco después de que estas palabras fueran escritas, Einstein comenzó a trabajar en su nefasta «teoría del campo unificado», su concepción de una Teoría del Todo que unificase su teoría de la gravitación con las leyes del electromagnetismo. Si «estas dos realidades, totalmente separadas una de otra conceptualmente», pudieran ser reunidas en «una configuración unificada», «toda la física se convertiría en un sistema acabado de pensamiento». Más tarde, todas sus energías intelectuales se centraron en la búsqueda de «teorías cuyo objeto es la totalidad de todas las manifestaciones físicas». Además de lograr una descripción más profunda del mundo en una forma unificada, Einstein creía también que una teoría de esta categoría resolvería las incertidumbres de la teoría cuántica que tanto le preocupaban, así como la incómoda predicción de que existe un principio del universo derivado de la teoría general de la relatividad. Según esta creencia en la unidad de la naturaleza, la postura de Einstein respecto a las constantes de la naturaleza era que no debía quedar ninguna cuyos valores no fueran explicados con precisión por la consistencia interna de cualquier Teoría del Todo unificada, pues

no puedo imaginar una teoría unificada y razonable que contenga explícitamente un número que el Creador pudiera haber elegido por capricho de otra forma, de lo que habría resultado una legalidad del mundo cualitativamente diferente… Una teoría que en sus ecuaciones fundamentales contiene explícitamente una constante [de la naturaleza] tendría que construirse en alguna forma a partir de pequeñas partes y trozos que son independientes lógicamente entre sí; pero confío en que este mundo no sea tal que se requiera una construcción tan fea para su comprensión teórica.

Para Einstein, los valores de cualquier constante de la naturaleza no especificada son inputs divinos que se requieren para especificar el universo unívocamente sobre y por encima de todas las leyes de la naturaleza y de sus condiciones de partida. No es fácil imaginar cómo podría ser esto cierto. Mientras que uno puede imaginar la reducción de todas las constantes de la naturaleza a un conjunto irreducible de uno o dos números puros que caractericen de alguna forma, por un lado, el tamaño del universo y, por otro, la tensión de la cuerda que nos habla de una simetría que gobierna todas las fuerzas de la naturaleza, todavía no se tiene idea alguna de cómo podría reducirse este número a cero. Para que esto fuera posible sería necesario que las constantes de la naturaleza estuviesen unívoca y completamente prescritas por la forma de las propias leyes de la naturaleza.

No todos los contemporáneos de Einstein compartieron su visión de un modelo fundamental de la naturaleza desprovisto de constantes. Algunos, como Max Planck, veían la ciencia física como una empresa esencialmente inductiva que nunca podría ceder el paso a una Teoría fundamental del Todo a la que se hubiera llegado por deducción pura. Para él no podía existir por consiguiente una teoría global accesible que explicase los valores de todas las constantes de la naturaleza. Planck distaba mucho de ser un idealista kantiano y vio de hecho el sello distintivo del avance de la ciencia en el progreso sistemático «hacia una separación tan drástica como sea posible entre los fenómenos en el mundo externo y aquellos de la conciencia humana». Caracterizó la búsqueda en pos de una Teoría del Todo como la búsqueda de una «única fórmula universal». Otros, como los instrumentalistas Pierre Duhem y Percy Bridgman, consideraron la anunciada separación planckiana de la descripción científica respecto a las convenciones humanas como inalcanzable en principio, ya que ellos consideraban que las constantes de la naturaleza se seguían por completo de imponer un modelo particular de explicación humana sobre una realidad desconocida.

Sir Arthur Eddington fue el astrofísico más relevante de la era anterior a la segunda guerra mundial. Eddington había iniciado el estudio sistemático de la estructura de las estrellas, había hecho avanzar significativamente nuestro entendimiento de los movimientos de las estrellas en la Vía Láctea, y había proporcionado a sus contemporáneos la exposición más lúcida de la nueva teoría de la gravitación por Einstein, al mismo tiempo que desempeñó un papel fundamental en su verificación experimental. Eddington fue también un cuáquero de hondas convicciones y es interesante preguntarse de qué manera pudo haber influido en su pensamiento científico la noción cuáquera de la «luz interna». Pese a ser un hombre tímido, que hablaba en público con reticencia y vacilación, Eddington utilizaba la pluma con gran habilidad. Sus escritos sobre ciencia, dirigidos al científico y al gran público en general, se cuentan entre los más selectos que jamás se hayan escrito y todavía se leen ampliamente hoy en día. Su habilidad para escribir con una vehemencia y una elegancia sin parangón hizo que sus obras populares se leyeran mucho más que ninguna de las otras exposiciones de la ciencia contemporánea. Sus escritos, pues, ejercieron una influencia formidable sobre filósofos y otras personas, que por primera vez pudieron acercarse a los desarrollos de la ciencia física. Y lo que los lectores de Eddington hallaron, entrelazada a su elocuente exposición de los hechos, fue una filosofía subyacente de la ciencia que difería dramáticamente de la ofrecida por cualquier otro científico eminente de su tiempo (y más si cabe por cualquier científico inglés de cualquier época). Eddington se hallaba muy cerca de ser un kantiano. Consideraba que la parte jugada por la mente humana en la construcción de nuestra imagen del mundo físico era esencialmente irreducible. Pero mientras que algunos idealistas habrían utilizado esto como una excusa para no ahondar más en la naturaleza de las cosas, Eddington consideró el origen de las leyes de la naturaleza en la mente humana como una garantía de su racionalidad fundamental. Se pregunta si no «podría ser que aquellas leyes cuyo origen no se encuentra en la mente son irracionales» en la medida en que «nunca podremos llegar a formularlas». Estimulado por la monumental reducción de la matemática a las proposiciones más básicas de la lógica llevada a cabo por Russell y Whitehead, Eddington quiso reducir la física a sus términos más sencillos y descubrir de esta manera si el éxito de nuestros sistemas para explicar el funcionamiento del mundo se debe en suma a alguna simplicidad intrínseca de la naturaleza o al hecho de que son creaciones de nuestras mentes. Durante la última parte de su vida, y hasta su muerte en 1944, Eddington trabajó en lo que él mismo llamó su Teoría fundamental. Sólo algunas partes de la misma se publicaron durante su vida. Se trataba de un intento de llegar a una Teoría del Todo que tuviera como objetivo primordial la explicación de los valores numéricos de todas las constantes de la naturaleza por medio de elaborados argumentos enumerativos. La filosofía subyacente a este trabajo ha sido descrita por Whittaker (uno de sus biógrafos científicos) como la creencia en que

todas las proposiciones cuantitativas de la física, esto es, los valores exactos de los números puros que son constantes de la ciencia, pueden ser deducidas por razonamiento lógico a partir de afirmaciones cualitativas, sin hacer uso alguno de datos cuantitativos derivados de la observación.

Esto, hay que reconocerlo, es el completo reverso de la concepción de la materia por Planck. Eddington cree que la contribución humana parcial, que Kant habría considerado como total, nos permite contemplar una descripción del mundo completamente autoconsistente en la que no quede por determinar cantidad alguna a través de la observación únicamente.

Las tentativas de Eddington para explicar los valores de las constantes fundamentales de la naturaleza fracasaron por completo en opinión de otros físicos, que consideraron que su trabajo se divorciaba de la física real, no siendo más que un ilusorio juego malabar de números para conseguir las respuestas que él quería. Es justo decir que, a la vista de cuarenta años durante los que ha sido posible examinar el manuscrito póstumo de Eddington sobre esta cuestión, no se ha encontrado en él nada de valor para la ciencia salvo la clara llamada de atención a explicar los valores de las constantes de la naturaleza. Su obra, y muy especialmente el relato de los curiosos resultados provisionales de su investigación contenido en sus libros, es la responsable del gran número de científicos amateurs que intentan seguir sus pasos poco afortunados y explicar los valores de las constantes de la naturaleza mediante una gimnasia aritmética. Pero lo que al físico moderno le resulta más llamativo al leer las tentativas de derivar las constantes de la naturaleza llevadas a cabo por Eddington es que la lógica empleada no presenta ningún punto de contacto con otras áreas de la ciencia. De hecho, incluso en su tiempo, Eddington halló serias dificultades en convencer a otros científicos de la seriedad de su trabajo. Se escribieron muchos artículos que parodiaban mordazmente sus puntos de vista y con mucha frecuencia se le acusó de ser oscuro e ininteligible. Esto le llegó a exasperar, especialmente cuando se concedía tanta importancia al trabajo de otros de sus colegas de Cambridge como Dirac. Acerca de sus nuevas tentativas de explicar las constantes de la naturaleza, escribió a un amigo:

Intento incesantemente descubrir por qué la gente encuentra oscuro el procedimiento… desde luego me resulta difícil creer que yo llegue a alcanzar alguna vez el oscurantismo de Dirac.

El programa de investigación de Eddington fracasó. Como el de Einstein, era un programa prematuro. Sencillamente, no conocíamos lo suficiente sobre esos ingredientes que deben incluirse en una Teoría del Todo para emprender la tarea de su construcción. Pero éste, más que ningún otro, planteó abiertamente el reto de explicar las constantes de la naturaleza. De forma similar a como los Argumentos del Designio del siglo XIX pusieron los hechos en el disparadero para que Darwin los explicara por el proceso de selección natural, así Eddington colocó el problema de los valores de las constantes de la naturaleza en el punto de mira de los tiradores de primera del futuro.

¿Qué nos dicen las constantes?

Estas cosas matemáticas poseen una asombrosa neutralidad y comparten algo de las cosas sobrenaturales, inmortales, intelectuales, simples e indivisibles y de las cosas naturales, mortales, apreciables, compuestas y divisibles.

JOHN DEE

Hemos venido considerando la importancia que los físicos han asignado tradicionalmente a los valores de las constantes de la naturaleza, pero ¿qué papel han jugado estas constantes en el universo? ¿Por qué se consideran tan importantes? Podemos lograr alguna perspectiva considerando primero el mundo de los átomos y las moléculas. Estas entidades no son partículas elementales, sino agregados de muchas partículas que se mantienen en equilibrio por fuerzas contrarias. Los tamaños de estas estructuras determinan la densidad de la materia, y las distribuciones de electrones en los átomos generan toda la gama de propiedades químicas de la materia. Sin embargo, a pesar de la inmensa complejidad de todo aquello compuesto por átomos y moléculas, junto a la gran variedad de propiedades compartidas por dos o más estados de la materia, desde los gases a los líquidos y a los sólidos, las características generales de todo este mundo de materiales están determinadas por los valores de sólo dos números. Los números en cuestión son: la masa del protón (que es el núcleo del átomo de hidrógeno) dividida por la masa del electrón,

y una cantidad que se conoce como la «constante de estructura fina». Ésta es el cuadrado de la carga eléctrica de un solo electrón dividida por el producto de la velocidad de la luz y de la constante de Planck de la teoría cuántica. Esta abstrusa combinación se toma en particular porque produce un número puro. Su valor peculiar de 1/137,036… se obtiene combinando los valores medidos de las tres constantes que lo comprenden. No sabemos por qué estos dos números toman estos valores precisos. Si fueran diferentes, nuestro universo sería diferente, quizás inimaginablemente diferente.

Si miramos allende la Tierra, a la estructura del sistema solar, las fuerzas químicas intervendrán junto a la fuerza de la gravedad en la determinación de las características generales de las cosas. La intensidad de la gravedad está determinada por la constante gravitatoria de Newton, y a partir de esta cantidad podemos determinar otro número puro similar a la constante de estructura fina, pero en la que el cuadrado de la carga del electrón se ha sustituido por el producto de la constante de Newton por el cuadrado de la masa del protón. Este número, la constante de estructura gravitatoria, tiene un valor ínfimo igual a 5,9041183… × 10⁻³⁹. Su pequeñez comparada con 1/137 nos dice que las fuerzas químicas de origen electromagnético son mucho más fuertes que las de la gravedad. De hecho, la gravedad es completamente irrelevante para la estructura de los átomos. Está presente, pero sus efectos, comparados con las fuerzas eléctricas entre los protones y los electrones, son tan pequeños que pueden ser completamente ignorados en todas las consideraciones prácticas de la química y de la física nuclear. Los tamaños de todos los cuerpos astronómicos en la escala que se extiende desde los asteroides hasta las estrellas están determinados esencialmente en relación únicamente a las constantes de estructura fina y gravitatoria. Esto se muestra en la figura 5.1, donde pueden verse los efectos de un cambio en los valores de las constantes de estructura fina y gravitatoria. Los tamaños de los planetas y estrellas no son accidentes fortuitos o el resultado preprogramado de condiciones iniciales particulares en el big bang. Antes bien, surgen como estados de equilibrio entre fuerzas opuestas de la naturaleza. Estas llegan a compensarse sólo cuando el agregado de partículas implicado alcanza un cierto tamaño. En los cuerpos fríos, como la Tierra, la fuerza compresora de la gravedad, que tiende a comprimir todas las cosas a un tamaño menor de mayor densidad, es compensada por un efecto mecánico-cuántico conocido como el principio de exclusión. Las partículas como los protones o los electrones ocupan nichos microscópicos en los que sólo se permite que haya una sola partícula. Cualquier intento de comprimir la materia de forma que se compela a más de una partícula a ocupar por la fuerza un mismo nicho se encuentra con una fuerza de resistencia. El equilibrio entre esta fuerza y el empuje hacia dentro de la gravedad produce los cuerpos grandes, estables y fríos que vemos en el sistema solar.

Las estrellas son diferentes. Una estrella es un cuerpo lo suficientemente masivo para que la compresión gravitatoria en su centro produzca una temperatura lo suficientemente alta para que se generen reacciones nucleares espontáneamente. Cuando se alcanza esta temperatura de combustión, las reacciones nucleares en la región central producirán un flujo de energía hacia fuera que en algún momento será radiado desde su superficie hacia el exterior en forma de luz y calor. La estrella se mantiene en equilibrio por la compensación de su presión interna por la gravedad. Se trata de un equilibrio estable, pues si la fuerza gravitatoria aumentase, el centro de la estrella se vería comprimido aún más, produciéndose así reacciones nucleares más rápidas y, en consecuencia, una presión adicional correspondiente empujando hacia fuera. De esta manera se restablecería rápidamente el equilibrio.

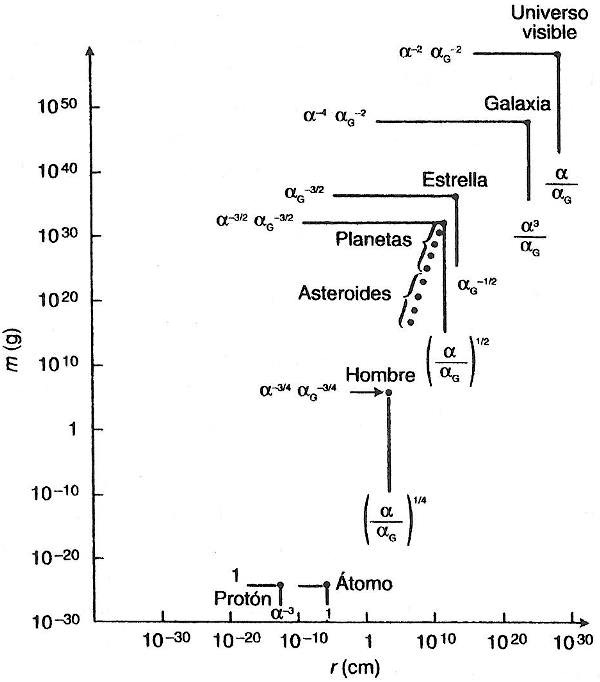
Figura 5.1 Las masas (en gramos) y los tamaños medios (en centímetros) de una amplia selección de los principales objetos que conocemos en el universo. Las estructuras compuestas son estados de equilibrio entre diferentes fuerzas de la naturaleza, y sus tamaños aproximados están determinados por la constante de estructura fina α = 1/137 y la constante de estructura gravitatoria α_G = 5,9 × 10⁻³⁹, la cual hemos introducido en el texto; la dependencia de la masa y del tamaño respecto a estas dos cantidades se indica para cada objeto.

El hecho de que un número tan notable de las creaciones más relevantes de la naturaleza deban sus tamaños y sus estructuras a los misteriosos valores de las constantes de la naturaleza coloca a nuestra propia existencia bajo una nueva e iluminadora perspectiva. Podemos ver cómo las condiciones necesarias para nuestra propia existencia están supeditadas a los valores que toman las constantes. En principio, uno podría pensar que un cambio en el valor de una constante modificaría ligeramente el tamaño de todas las cosas, pero que aún existirían estrellas y átomos. Sin embargo, esto resulta ser una visión demasiado ingenua de las cosas. Es evidente que se da una serie de coincidencias muy poco corrientes en relación a los valores que toman ciertas combinaciones particulares de esas constantes de la naturaleza que son condiciones necesarias para nuestra propia existencia. Si la constante de estructura fina se desviase tan sólo un 1 por 100 de su valor actual, la estructura de las estrellas sería dramáticamente diferente. De hecho, disponemos de sobradas razones para sospechar que no estaríamos aquí para discutir la materia. Pues los elementos biológicos como el carbono, el nitrógeno, el oxígeno y el fósforo se producen durante los estertores finales de la muerte explosiva de las estrellas. Son expelidos al espacio donde terminarán siendo incorporados por los planetas y, finalmente, por la gente. Pero el carbono, ese crucial elemento biológico que creemos esencial para la evolución espontánea de la vida, debería existir sólo como un remanente más, el más insignificante de hecho, en el universo, y no en la saludable abundancia en que lo encontramos. Esto se debe a que las reacciones nucleares explosivas que crean carbono en los estadios finales de la evolución estelar son claramente muy lentas en producirlo. No obstante, existe una notable coincidencia en la naturaleza que permite que se produzca carbono en cantidades insospechadas.

El carbono se origina en el universo mediante un proceso en dos etapas a partir de núcleos de helio o partículas alfa, como habitualmente los llamamos. Dos partículas alfa se combinan bajo condiciones estelares para crear un núcleo del elemento berilio. La adición de una partícula alfa más es necesaria para transformar este núcleo en un núcleo de carbono. Uno habría esperado que este proceso en dos etapas sería en extremo improbable, pero sorprendentemente la última etapa resulta poseer una rara propiedad llamada «resonancia» que permite que se produzca a una velocidad muy superior a la supuesta ingenuamente. En efecto, las energías de las partículas participantes más la energía del calor ambiente en la estrella suman un valor que se sitúa justo por encima de un nivel natural de energía del núcleo de carbono y así el producto de la reacción nuclear encuentra un estado natural en el que caer. Viene a ser algo así como el equivalente astronómico del «hoyo en uno». Pero esto no es todo. Mientras que ya es sorprendente por partida doble que exista, no ya un nivel de resonancia del carbono, sino uno situado justamente por encima del total de energía producido en el interior de la estrella, es casi milagroso descubrir que existe otro nivel de resonancia en el núcleo de oxígeno que se alcanzaría en el siguiente eslabón de la cadena de reacción nuclear cuando un núcleo de carbono interaccionase con otra partícula alfa. Pero este nivel de resonancia yace justo por encima de la energía total de la partícula alfa, el núcleo de carbono, y el medio ambiente de la estrella. En consecuencia, el apreciado carbono es destruido totalmente por una reacción nuclear resonante adicional. Esta coincidencia múltiple de los niveles de resonancia es una condición necesaria para nuestra existencia. Los átomos de carbono en nuestro cuerpo, responsables de la maravillosa flexibilidad de las moléculas de ADN que encontramos en la raíz de nuestra complejidad, se han originado en las estrellas como resultado de estas coincidencias. El emplazamiento de los niveles de resonancia queda determinado de una manera compleja por los valores numéricos precisos de las constantes de la física.

Hay otros muchos ejemplos de la misma índole. Casi a cada paso, las condiciones necesarias para la evolución de cualquier forma de complejidad en el universo explotan la existencia de coincidencias cruciales entre los valores de las constantes de la naturaleza. Hay quienes han atribuido a esto una gran importancia teológica, considerándolo como una suerte de sutil afinado divino del universo para asegurar la evolución de la vida. Este tipo de pruebas son reminiscencias de los Argumentos del Designio de los teólogos naturales del pasado. Pero lo único que podemos vindicar es que dichas coincidencias, sustentadoras de la vida, son necesarias para la evolución de ésta en la forma que la conocemos.

La evolución de la vida y de la mente se encuentra amenazada por callejones sin salida en cada estadio evolutivo. Hay tantas formas en que la vida puede cesar de evolucionar en un entorno complejo y hostil que sería pura arrogancia suponer que, simplemente contando con carbono suficiente y tiempo suficiente, todo es posible. Es más, suponer que la vida debe derivarse de la mezcla requerida de elementos químicos es justamente la clase de actitud teológica que los biólogos censuran acertadamente. No hay razón alguna por la que la vida tenga que evolucionar en el universo. Los complejos procesos graduales de este tipo no pueden predecirse debido a su dependencia extremadamente sensible de las condiciones de partida y de las sutiles interacciones entre el estado evolvente y su medio ambiente. Todo lo que podemos afirmar con seguridad es una negación: si las constantes de la naturaleza no se encontrasen entre el 1 por 100, o así, de sus valores observados, los ladrillos básicos de construcción de la vida no existirían en abundancia suficiente en el universo. Es más, cambios como éste perturbarían la propia estabilidad de los elementos e impedirían la existencia de los elementos requeridos en lugar de sencillamente limitar su abundancia^[6].

No es fácil interpretar este estado de cosas. Admitamos que existen coincidencias vitales entre los valores de aquellas constantes de la naturaleza cuya existencia es necesaria para la nuestra. Vayamos ahora más lejos y supongamos, como hipótesis, que estas coincidencias son necesarias para la evolución de cualquier forma de complejidad autoconsciente del tipo que llamamos «vida consciente». ¿Cuál sería el impacto —podría uno preguntarse— de una Teoría del Todo que explicase con éxito los valores de todas las constantes de la naturaleza? Si esa teoría fuese única, permitiendo sólo un reparto posible de las constantes, todo lo que podemos decir es que seríamos bastante afortunados. Cualesquiera conclusiones más profundas de naturaleza metafísica deben necesariamente ser especulativas y, con toda probabilidad, imposibles de excluir. Pero, si la Teoría del Todo muestra que los valores de las constantes (o al menos algunos de ellos) poseen algún elemento aleatorio que depende de sucesos particulares que acontecen localmente, o que las cantidades que tomamos por constantes pueden todas en principio (y quizá también en la práctica) variar aleatoriamente en el espacio, entonces en un universo infinito surgirán necesariamente regiones de todos los tamaños que poseerán combinaciones de las constantes adecuadas a la subsiguiente evolución de la complejidad. Nosotros debemos, claro está, habitar uno de estos oasis cósmicos de vida.

Consideraciones de este tipo nos muestran por qué los científicos anhelan tanto poder explicar los valores de las constantes de la naturaleza. Éstas explican por qué casi todo lo que existe puede existir. Y podemos ver una vez más por qué la noción de constante de la naturaleza ha resultado tan fructífera. Nuestra incapacidad para explicar por qué la constante de estructura fina tiene un valor próximo a 1/137 en lugar de, digamos, a 1/145, no nos impide hacer uso de la noción de constante de estructura fina y lograr una comprensión de cómo su valor determina otras cosas. Esto es una manifestación de una propiedad general del universo que hace que éste sea relativamente inteligible para nosotros. Existe un cierto tipo de estructura jerárquica en la naturaleza que nos permite entender la forma en que se comportan los agregados de materia sin necesidad de conocer la microestructura básica de la materia en sus dimensiones más ínfimas. Sería muy molesto que la lógica profunda de lo que determina el valor de la constante de estructura fina hubiera jugado también un papel significativo en nuestro entendimiento de todos los procesos físicos en los que entra dicha constante. Afortunadamente, no es necesario que conozcamos todo para poder llegar a entender algo.

Pero no tenemos que apelar a los mundos esotéricos de las partículas elementales o de la astronomía para reconocer el significado de las constantes de la naturaleza. Para el funcionamiento de la tecnología moderna y las comunicaciones es vital que existan patrones exactos de la medida del tiempo. En consecuencia, en la mayoría de los países desarrollados hay «laboratorios nacionales» especiales que dedican una parte de su trabajo a mantener medidas rigurosas del tiempo, la longitud y la masa, junto con otras medidas estándar. En el Reino Unido, esta tarea corresponde al Laboratorio Físico Nacional, mientras que en los Estados Unidos es realizada por la Oficina Nacional de Patrones y Medidas en Washington. Lo que estas instituciones precisan con vistas a preservar la medida del tiempo es un patrón de tiempo que se pueda fijar de manera absoluta. Dicho patrón puede entonces ser utilizado como una base a partir de la que calibrar otras medidas secundarias del tiempo. Supongamos, como los antiguos, que uno pensase que un reloj de arena (un cronometrador para cocer huevos, por ejemplo) pudiera servir para tal fin. Este dispositivo utiliza la fuerza de la gravedad para medir el tiempo. Explota el hecho de que todas las cosas caen con la misma aceleración bajo la fuerza del campo gravitatorio local de la Tierra. Pero es obvio que dicho ingenio es un patrón terrestre imposible, y mucho menos uno universal. El tamaño del agujero por el que pasa la arena será siempre ligeramente distinto de un aparato a otro; la granulosidad de la tierra diferirá de una muestra a otra; la textura de la superficie sobre la que se desliza la arena y el ángulo de su inclinación variarán: todos estos factores hacen que cada reloj de arena sea diferente de sus contendientes. No hay una única relación entre la variación de la caída de la arena y el paso del tiempo. Uno podría intentar resolver estos inconvenientes utilizando un reloj de péndulo. Este mecanismo hace asimismo uso de la fuerza de gravedad local para fijar el período de cada oscilación del péndulo. Pero el período de cada ida y venida depende también de la longitud del péndulo. Cada péndulo será por consiguiente ligeramente diferente. Es más, el empuje efectivo de la gravedad en la superficie de la Tierra varía, según uno se desplaza del ecuador hacia los polos, debido a la rotación de la Tierra en torno a su eje y al leve achatamiento en su forma que esto acarrea. Si uno se llevase el reloj a otro planeta, la intensidad de la gravedad en su superficie diferiría de la que existe sobre la Tierra y el reloj funcionaría a un régimen completamente diferente comparado con el de su réplica exacta en nuestro planeta. Cuanto mayor sea el planeta, más rápidamente oscilará un péndulo de la misma longitud bajo su gravedad (aumentando de hecho aproximadamente como la raíz cuadrada del radio del planeta). Si tuviésemos que elegir un reloj algo más sofisticado, nos iríamos al reloj eléctrico del tipo que encontramos en la mayoría de las casas. Este es mucho más preciso que un reloj de péndulo y alcanza una periodicidad exacta en relación al ciclo alternante de la red doméstica de corriente alterna. Sin embargo, aunque esta red mantiene una frecuencia relativamente estable, próxima a los cincuenta ciclos por segundo, está sujeta a variaciones impredecibles que difieren de un lugar a otro y de un instante de tiempo a otro. Un patrón semejante no podrá nunca ser verdaderamente universal, aunque es perfectamente apropiado para casi todas las tareas cotidianas. Un verdadero patrón nos exige encontrar algún modo de definir lo que entendemos por una unidad de tiempo que sea igual para todos, sin importar cuándo o dónde se esté observando. Este deseo de universalidad naturalmente nos empuja a buscar un patrón temporal que esté determinado sólo por las constantes de la naturaleza. Y así es, de hecho, cómo se definen los patrones modernos de tiempo absoluto. Estos evitan el uso de cualquier característica de la Tierra o de su campo gravitatorio y se centran en lugar de ello en las frecuencias naturales de oscilación de ciertas transiciones atómicas entre estados de diferente energía. El tiempo necesario para que una de estas transiciones tenga lugar en un átomo de cesio está determinado por la velocidad de la luz en el vacío, las masas del electrón y del protón, la constante de Planck y la carga de un solo electrón. Todas estas cantidades se toman como constantes de la naturaleza. Un intervalo de tiempo de un segundo se define entonces como un cierto número de estas oscilaciones. A pesar de su naturaleza esotérica, esta definición de tiempo es muy potente. Nos debería permitir comunicar con toda exactitud la longitud de tiempo de la que estamos hablando a los habitantes de una lejana galaxia. Si bien los andromedianos desconocerían probablemente lo que es un año o un día, pues se trata de unidades de tiempo que son propiedades de los movimientos de nuestro sistema solar particular (el día es el tiempo necesario para una revolución completa de la Tierra, y el año, el tiempo necesario para que la Tierra complete una órbita en torno al Sol, y ninguna de estas unidades es en realidad verdaderamente constante), tendrían que estar familiarizados, en caso de estar hablando con nosotros por medio de señales de radio, con los conceptos implicados en la definición de las constantes de la naturaleza. La inevitabilidad de su conocimiento de estas cantidades, podríamos argüir, garantiza que tendremos mucho en común. ¿Es esto cierto?

Constantes que varían

No hay nada constante en este mundo, salvo la inconstancia.

JONATHAN SWIFT

Aquí hay dos «síes» condicionales. ¿Habrían descubierto las civilizaciones extraterrestres las mismas constantes de la naturaleza? Y ¿son las así denominadas «constantes» realmente constantes en todo caso? La primera es una cuestión a un tiempo filosófica y sociológica. Si se adopta un punto de vista realista de la ciencia, se mantendrá que hay una estructura única y verdadera subyacente al universo físico que es descubierta, antes que inventada, por los científicos. Las constantes de la naturaleza tienen una existencia independiente de la mente. No son conceptos creados por la mente humana con el simple objeto de comprender el sentido de los hechos. A partir de este punto de vista podría argüirse que cualquier civilización científica o tecnológica habría de descubrir la misma realidad y los mismos conceptos básicos. Podrían usar diferentes símbolos o utilizar constantes que estuvieran definidas de manera ligeramente diferente por razones de conveniencia, pero reconocerían a pesar de ello nuestras constantes como fundamentales y podrían traducir de inmediato las suyas a las nuestras. Este punto de vista, más bien optimista, subyace en realidad a diversas propuestas dirigidas a la búsqueda de vida extraterrestre. Tanto los mensajes para extraterrestres que nuestras naves espaciales transportan cuando abandonan el sistema solar una vez concluida su misión, como las frecuencias en las que se emiten al espacio las señales de radio por si alguien estuviera escuchando, descansan en patrones fundamentales dictados por las constantes de la física. Se supone implícitamente que éstos serán reconocidos por cualquier sociedad tecnológica. Pero quizá esta línea de pensamiento esté equivocada. Si nuestra matemática y nuestra física han sido en gran medida inventadas para poder describir alguna realidad verdadera mucho más profunda, entonces no esperaríamos en ningún caso que los extraterrestres hubieran seguido el mismo camino. Nuestros conceptos científicos podrían haberse desarrollado en respuesta a los problemas sociales y prácticos que necesitaban ser resueltos en el planeta Tierra. Las nociones matemáticas aparentemente fundamentales, que forman la trama sobre la que se edifica nuestra ciencia, podrían deber mucho a los conceptos primarios que nuestras mentes parecen asimilar con mayor facilidad. Estos atributos mentales son, al menos en parte, el resultado de un proceso evolutivo que está guiado por las características ambientales de la Tierra. En otras palabras, este desarrollo habría sido diferente. Los resultados habrían sido diferentes. Podríamos confiar en que hubiera un único factor común básico. Debería existir una estrecha correspondencia entre la imagen de la realidad gestada por una afortunada criatura y la verdadera naturaleza de aquellos aspectos de la realidad necesarios para la supervivencia. Un mal aparejamiento entre imagen y realidad en este dominio inhibiría la posibilidad del progreso evolutivo. Sin embargo, esto deja todavía un amplio margen a la divergencia. Por ejemplo, nuestro planeta tiene una atmósfera bastante transparente que nos permite ver un gran número de estrellas por la noche. Si un planeta fuese opaco y estuviese oscurecido por densas nubes, el sonido habría sido un medio primario de comunicación más efectivo que la luz. Una diferencia de esta índole podría muy bien condicionar el desarrollo futuro de cualquier civilización avanzada al énfasis en el estudio de los fenómenos acústicos sobre el de los electromagnéticos. Un aspecto universal de toda esta cuestión lo constituye el estatus del lenguaje matemático en el que se encuentran expresadas todas nuestras deducciones sobre las constantes de la naturaleza. ¿Es ésta una faceta inventada o una faceta descubierta del universo? Este es un tema tan amplio que volveremos a discutirlo con más detalle en el último capítulo.

¿Qué podemos decir sobre nuestra segunda pregunta? ¿Son las constantes realmente constantes? Hasta ahora hemos supuesto, como hacen la mayoría de los físicos, que cantidades como la constante gravitatoria de Newton, la carga de un electrón o la constante de estructura fina son verdaderamente constantes. Esto no es meramente una esperanza piadosa. Uno puede probar esta suposición de diversas maneras. Cuando observamos objetos astronómicos distantes, como los quásares, los estamos viendo tal y como eran hace miles de millones de años debido al enorme período de tiempo que ha tenido que transcurrir antes de que las señales de luz por ellos emitidas alcanzaran nuestros telescopios en la Tierra. Este intervalo de tiempo nos permite probar si las constantes de la física que determinan las propiedades relativas de los diferentes tipos de luz emitidos por la fuente distante son idénticas a sus correlatos en la Tierra actualmente. Si el valor de ciertas constantes de la física ha sido distinto en un pasado lejano, entonces las diferencias se habrían puesto de manifiesto a no ser que sean menores de una parte en cien mil millones. También sabemos que si cantidades como la constante de estructura fina o la constante de estructura gravitatoria variaron en el pasado, el curso de los acontecimientos en los primeros estadios del universo habría sido muy diferente. En particular, la maravillosa concordancia entre las abundancias observadas de hidrógeno, helio, deuterio y litio en el universo, y aquellas predichas como resultado del big bang cuando el universo tenía sólo unos pocos minutos de edad, se vería destruida. Las consecuencias de las variaciones en las constantes de la naturaleza que juegan un papel en estos procesos se encuentran claramente restringidas a valores más pequeños que entre una parte en diez mil millones y una parte en un billón para que las abundancias observadas no cambien significativamente.

Hay circunstancias en las que podríamos esperar que esas cantidades que llamamos constantes de la naturaleza presentasen una variación en el tiempo o en el espacio. Nosotros observamos que existen tres dimensiones del espacio, pero los físicos de partículas han descubierto que las más elegantes y acabadas teorías de los procesos entre partículas elementales, en particular la teoría de cuerdas de la que hemos hablado en el capítulo anterior, predicen un número de dimensiones espaciales mucho mayor que tres (quizá otras seis más, o incluso otras veintidós en algunos casos). Para adecuar dicho estado de cosas a lo que vemos, se requiere que todas las dimensiones espaciales, salvo tres, sean pequeñas a escala microscópica. Supongamos que éste sea efectivamente el caso. Entonces las verdaderas constantes de la física son aquellas que determinan la naturaleza de todo el espacio, no sólo de nuestra sección tridimensional del mismo. Más aún, esto tiene como consecuencia que si examinamos esas cantidades que en nuestro subconjunto tridimensional del mundo hemos dado en llamar las constantes de la naturaleza, encontraremos que varían al mismo ritmo que la media de cualesquiera dimensiones adicionales del espacio. Las observaciones de constantes invariables nos dicen que si existen otras dimensiones extraordinarias del espacio, se encuentran hoy en día inertes en una altísima medida.

Este razonamiento en torno a las dimensiones extraordinarias del espacio es algo más que una mera especulación extravagante, pues las teorías de cuerdas de las que hemos hablado en los últimos capítulos poseen en efecto muchas dimensiones adicionales. De hecho, las milagrosas propiedades matemáticas que permiten a estas teorías poner remedio a los infinitos de las teorías de partículas puntuales parecen exigir la existencia de nueve o veinticinco dimensiones espaciales. En un marco cosmológico, requieren que nos imaginemos los primeros estadios del universo, cuando el estado cordal de las cosas era dominante, como estadios en los que todas estas dimensiones existen en pie de igualdad. Entonces, por alguna razón desconocida, debe haberse presentado una bifurcación de caminos. Tres de las dimensiones del espacio deben haberse expandido para convertirse en el universo visible actual con una extensión de quince mil millones de años luz. Las restantes deben haberse mantenido estáticas en una escala microscópica. Cómo sucedió esto y por qué tres y sólo tres dimensiones han escapado de este sempiterno apresamiento sigue siendo un misterio.

Una interesante cuestión de principio surge aquí. Si hay dimensiones adicionales del espacio, las verdaderas constantes de la naturaleza estarán definidas sobre la totalidad de las dimensiones del espacio. Aquellas que vemos en tres dimensiones pueden no ser por consiguiente verdaderamente fundamentales. Puede que no sean las constantes que nos daría la Teoría del Todo fundamental. Si esto fuera así, tendríamos que desembrollar por completo el proceso por el que tres de las dimensiones no sólo son grandes, sino que se hacen cada vez más grandes, según indican nuestras observaciones de la expansión cósmica, mientras que las otras permanecen pequeñas y estáticas. Este proceso podría no estar determinado por las leyes de la naturaleza. Puede que posea elementos intrínsecamente aleatorios a un nivel cuántico gravitatorio que podrían incluso hacerlo variar de un lugar a otro del universo. Si éste fuese el caso, las constantes que se conservan en las tres dimensiones extendidas del espacio toman valores que en principio son, al menos parcialmente, aleatorios.

En el interior de los agujeros de gusano

NADA. Nada es un concepto asombroso, aunque esencialmente mal asimilado; altamente apreciado por escritores de tendencias místicas o existencialistas, pero considerado por casi todos los demás con aprehensión, náusea o pánico.

The Encyclopaedia of Philosophy

Como era de esperar, los candidatos modernos a una Teoría del Todo aspiran a decir algo sobre las constantes de la naturaleza y sus valores. El primer candidato, el modelo de cuerdas de las partículas elementales con su nueva idea sobre cuáles son las entidades más elementales de la naturaleza y su descubrimiento del poder de la consistencia matemática para reducir el número de candidatos a la gran simetría que gobierna todas las cosas, mantiene que los valores de las constantes de la naturaleza están contenidos en la propia teoría. Deben de hallarse enterrados profundamente en el seno de la matemática de algún modo intrincado. Por desgracia, todavía no se ha encontrado la forma de extraer esta información de la teoría. De hecho, como acabamos de ver, puede que esta extracción sea sólo el primer estadio de un viaje problemático, porque una cosa es descubrir lo que la teoría tiene que decir acerca de constantes que viven en nueve o en veinticinco dimensiones del espacio, y otra muy distinta es descubrir de qué manera se procesa esta información para determinar los valores de las constantes en nuestro espacio tridimensional. Otro problema que debemos tener presente es el hecho de que aquello que emerja como una constante fundamental de una Teoría del Todo podría no ser exactamente lo mismo que una de las cantidades que acostumbramos a llamar una constante de la naturaleza. Puede que nos hallemos algo lejos de las constantes fundamentales de la naturaleza dada la forma en que nuestro entendimiento del mundo físico ha sido obtenido en el entorno de energía relativamente baja que se precisa para la evolución y la supervivencia de las cosas vivas. Pero la física moderna apunta siempre hacia energías más y más altas y hacia entornos que se hallan lo más lejos posible de nuestra propia intuición y experiencia, para dar respuesta a nuestros interrogantes más profundos. En la teoría de cuerdas, por ejemplo, la cantidad más fundamental resulta ser la tensión de la cuerda en lugar de una de las constantes de la naturaleza convencionales. En un principio, uno podría pensar que esta situación no es excesivamente incómoda. Supongamos que fuésemos capaces de desembrollar el proceso por el que un número de dimensiones se dividen en tres, que se expanden para hacerse grandes, y el resto, que permanece pequeño, y que pudiéramos al mismo tiempo calcular los valores numéricos de las constantes subyacentes de la Teoría del Todo. ¿Qué obstáculos podríamos encontrar? Para responder a esto, hemos de reconocer que hay constantes de la naturaleza y constantes de la naturaleza. Mientras que nosotros tendemos a reunirías a todas bajo una misma categoría para facilitar la discusión, parece ser que hay algunas que son más fundamentales que las otras. De aquellas que son más fundamentales esperaríamos que estuvieran completamente determinadas por alguna lógica interna de la Teoría del Todo, pero hay otras que parecen incorporar contribuciones de procesos particulares que tienen lugar en el universo y que alteran sus valores en formas impredecibles. La Teoría del Todo puede que nos deje lejos de predecir los valores de las constantes observadas de la naturaleza.

A pesar de este posible inconveniente, uno se sentiría contento sólo con que una de las Teorías del Todo candidatas pudiera predecir una sola constante de la naturaleza correctamente. Hasta muy recientemente, se esperaba que la teoría de cuerdas fuese capaz con el tiempo de aportar este resultado, de manera que sólo necesitaríamos comparar la predicción con la observación para probar la teoría. Pero, en los últimos años, ha aparecido una Teoría del (cuasi) Todo rival que ha puesto en tela de juicio hasta qué punto existe alguna constante verdaderamente fundamental que permanezca igual por siempre, sin verse afectada por los sucesos en el espacio y en el tiempo. Es a esta teoría rival a la que ahora nos vamos a referir.

Hay un tipo de constante que se explica más fácilmente que las demás. Es una cuyo valor es cero. En 1916, cuando Einstein aplicó por vez primera su nueva teoría de la gravitación al universo como un todo, se hallaba muy influido por los prejuicios filosóficos del pasado, según los cuales existía un espacio absoluto estático en el que tenían lugar todos los movimientos locales observados. La idea misma de la expansión del universo como un todo habría sido sumamente peculiar e inaceptable. Einstein descubrió que esta expansión era una consecuencia directa de su teoría, y estudió la manera de modificar la teoría para poder suprimir la presencia de universos en expansión (o a este respecto en contracción). Observó que esto podía lograrse simplemente con incluir en la teoría una nueva constante de la naturaleza que era permitida, pero no requerida, por su desarrollo matemático. Esta nueva constante, denominada la constante cosmológica, actuaba como una fuerza de largo alcance que contrarrestaba la fuerza de la gravedad. El equilibrio entre las dos fuerzas podía lograrse, resultando de ello un universo estático, sin cambio, que devenía imposible cuando en la teoría se omitía la constante cosmológica. No obstante, a continuación se mostró que si bien dicho universo estático podría existir en teoría, nunca podría mantenerse en la práctica, ya que el equilibrio entre el tirón de la gravedad y el empuje de la constante cosmológica es inestable. Al igual que cuando intentamos mantener un lápiz en equilibrio sobre su punta, el más ligero temblor en una u otra dirección producirá un cambio unidireccional. Si el universo estático de Einstein no estuviese perfectamente equilibrado (y en el mundo real nunca podría estarlo, debido a fluctuaciones variables y a inhomogeneidades, como nosotros mismos, que sabemos que existen en el universo), entonces pronto comenzaría a contraerse, o a expandirse. Cuando esta situación se hizo clara, el interés se dirigió hacia el estudio de un universo en expansión, el cual se vio especialmente impulsado por el monumental descubrimiento de Hubble en 1929 de que el universo está efectivamente en expansión.

El universo estático de Einstein era un subterfugio y su inventor lamentó más tarde el haber introducido una constante cosmológica para mantener un universo estático, refiriéndose a ello como «el mayor desacierto de mi vida», porque perdió la oportunidad de hacer la predicción científica más extraordinaria de todos los tiempos: la expansión del universo. Pero la constante cosmológica se negó a salir gentilmente del escenario. Estaba muy bien decir que ya no era necesaria, pero en realidad no había una razón de peso por la que debiera excluirse de las ecuaciones de Einstein. Muchos la consideraron sólo como un aditamento a la nueva teoría de la gravedad de Einstein, pudiendo así ser eliminada por carecer de contrapartida en la teoría clásica de la gravedad de Newton. Pues si se retuviese, la teoría de Newton, a la cual se reduce la de Einstein cuando la intensidad de todos los campos de gravedad es muy débil y todos los movimientos tienen lugar a velocidades mucho más pequeñas que la de la luz, no se recuperaría nunca más. En lugar de la famosa ley del inverso del cuadrado de Newton, que dice que la fuerza gravitatoria entre dos masas cuyos centros están separados a una distancia d es

(*)Fuerza ∝ 1/d²,

se encuentra que la ley de fuerza tiene la forma

(**)Fuerza ∝ 1/d² + Λd,

donde Λ es la constante cosmológica.

Resulta muy curioso que Newton pudo, de hecho, haber llegado a esta ley de fuerza hace trescientos años. Uno de los problemas que le preocuparon intensamente, y que retrasó durante muchos años la publicación de su opus magnum, los Principia, fue hallar una justificación a su suposición habitual, según la cual el tirón gravitatorio ejercido por una masa esférica es idéntico al ejercido por una «masa puntual» equivalente, de extensión cero, localizada en su centro. Esto se conoce como la «propiedad esférica». Newton llegó a demostrar que esta suposición es verdadera para la ley de fuerza del inverso del cuadrado (*), que constituye su ley de la gravedad, pero no para otras hipotéticas leyes de fuerza, como pudiera ser una ley del inverso del cubo o de las cuartas potencias de la distancia.

Pero, si Newton hubiese formulado la pregunta «¿Cuál es la ley de fuerza general bajo la que se cumple la propiedad esférica?», como el matemático francés Simón de Laplace llegaría más tarde a plantear, habría encontrado la ley (**) como respuesta. Así pues, si la gravedad newtoniana se hubiera formulado según el principio fundamental de la propiedad esférica, la constante cosmológica habría sido autorizada, pero no requerida; exactamente como Einstein halló que debía suceder en la fundamentación de la teoría general de la relatividad.

¿Y qué decir de la constante cosmológica hoy en día? Sabemos por los efectos que tendría sobre la velocidad de expansión de galaxias distantes que, si existe, su valor numérico debe ser infinitesimal, menor que 10⁻⁵⁵ por cm. Dichas unidades no son muy ilustrativas. Es más esclarecedor comparar su tamaño con el de la unidad básica de longitud en los mundos gravitatorios y de partículas elementales. Esta «longitud de Planck» es la única cantidad con las dimensiones de una longitud que puede formarse a partir de las tres constantes más fundamentales de la naturaleza: la velocidad de la luz c, la constante de Planck h y la constante gravitatoria de Newton G. Viene dada por

l_p = (Gh/c³)^1/2 = 4 × 10⁻³³ cm.

Esta pequeñísima dimensión resume los atributos de un mundo que es al mismo tiempo relativista (c), mecánico-cuántico (h) y gravitatorio (G). Es un patrón de longitud que no hace referencia a ningún artefacto del hombre, ni siquiera de las fuerzas nucleares y químicas de la naturaleza. En relación a esta unidad de longitud, el tamaño de todo el universo visible hoy en día abarca aproximadamente 10⁶⁰ longitudes de Planck, pero la constante cosmológica debe ser menor que 10⁻¹¹⁸ si se refiere a estas unidades de longitud de Planck en lugar de a centímetros. La consideración de semejante grado de pequeñez no tiene precedente en toda la historia de la ciencia. Cualquier cantidad de la que se requiera un valor tan próximo a cero por observación, es probable que sea en realidad cero exactamente. Esto es lo que muchos cosmólogos creen. Pero ¿por qué?

Durante muchos años los cosmólogos han buscado, con poca fortuna, algún principio fundamental capaz de revelar por qué la constante cosmológica debe ser cero. Los físicos de partículas elementales también han hecho sus indagaciones pero, lejos de hallar una respuesta al problema, lo han remedado mostrando sencillamente que, aun cuando exista un principio semejante por el que el universo hubiese comenzado su andadura en el big bang con un valor cero de la constante cosmológica, surgen complicados procesos de partículas elementales que producen tensiones que simulan la presencia de una constante cosmológica con un valor inaceptablemente grande, miles y miles de millones de veces mayor que lo permitido por la observación.

Lo que necesitamos a todas luces es, o bien un principio de «quita y pon» que establezca un valor inicialmente pequeño de la constante cosmológica en una forma que garantice el que permanezca pequeño, o bien algún otro tipo de principio que asegure que la constante cosmológica se haga infinitamente pequeña cuando el universo se haya expandido a un tamaño comparable al de sus dimensiones actuales de quince mil millones de años luz. Una fascinante posibilidad ha sido rescatada por investigaciones recientes en la forma de una teoría cuántica que describe el universo entero. Esta dirección de investigación ya la introdujimos al encontrarnos con las condiciones iniciales en un capítulo anterior. Se ha hallado que si el procedimiento para calcular la función de onda del universo se extiende de manera que incluya una nueva posibilidad especulativa, entonces tiene algo muy definitivo que decir sobre el valor de la constante cosmológica, al igual que sobre el origen de todas las otras constantes de la naturaleza.

Las trayectorias seguidas por partículas u ondas que se mueven de acuerdo con alguna ley del movimiento pueden ser halladas por otro principio, más elegante, que fue descubierto en primer lugar por el científico francés Moreau de Maupertuis en 1748. Considérense todos los caminos posibles que, en ausencia de una «ley» que constriña el movimiento, podría tomar un cuerpo que se mueve entre los puntos A y B. Maupertuis mostró que existe una cierta cantidad, denominada la «acción», que siempre toma su valor mínimo a lo largo de aquel camino que está determinado por las leyes del movimiento de Newton. Este principio puede por consiguiente utilizarse para descubrir cuáles son las leyes del movimiento. De hecho, su aplicación no se circunscribe a las leyes del movimiento de Newton; se pueden construir acciones de acuerdo con una determinada receta general y utilizarlas para derivar todas las otras leyes del movimiento que se obtienen bajo la influencia de otras fuerzas de la naturaleza^[7].

Cuando la mecánica cuántica se formula de esta manera, uno considera que un sistema (en este caso el universo entero) sigue todos los caminos evolutivos posibles desde su estado inicial a un estado futuro. Todos estos caminos se sopesan juntos en una forma determinada para dar la probabilidad de que se siga una historia particular. Esta representación la introdujimos en el capítulo 3 al discutir las condiciones iniciales y la función de onda del universo. Ahora bien, el físico norteamericano Sidney Coleman ha sugerido que la clase de caminos incluidos en este haz de historias posibles debería ser ampliado con el fin de dar cabida a una clase bastante inusual que es probablemente más familiar a los lectores de relatos de ciencia ficción que a los físicos. Se trata de esos caminos que involucran cosas llamadas «agujeros de gusano espacio-temporales».

Los agujeros de gusano pueden ser vistos como tubos que conectan partes del espacio y tiempo de otro modo distantes. Algunas de las derivaciones de una estructura de esta índole se ilustran en la figura 5.2. Éstos proporcionan nuevos tipos de conexidad no local en el espacio y el tiempo que podrían tener consecuencias impredecibles. Si aparecen partículas de un agujero de gusano en un entorno local, los observadores presenciarían lo que interpretarían como la violación de ciertas leyes de conservación de la física. La masa y la energía podrían surgir de la nada aparentemente. La carga eléctrica podría aparecer y desaparecer. No parece que tengamos que preocuparnos por caer en una de estas simas porque se supone que tienen un tamaño próximo al de la longitud fundamental de Planck que introdujimos más arriba. El tamaño de sus gargantas sería, pues, tan pequeño que sencillamente se asemejarían a la aparición o desaparición anómalas de algunas partículas elementales de tipo puntual o «cordal» en un experimento de física de partículas. Las leyes de conservación parecerían ser violadas en un lugar aunque en la realidad más completa, integrada por todos los universos conectados, podrían ser respetadas.

Figura 5.2 Un agujero de gusano conectando dos regiones planas de espacio-tiempo que no se encuentran distorsionadas por la presencia de masa-energía.

La posible existencia de agujeros de gusano emanando del espacio-tiempo nos mueve a imaginar la clase más general de estructura que nuestro universo pudo poseer durante sus primeros estadios como una complicada bola con muchas asas y ramas emanando de ella. Algunas de estas ramas se replegarían y se unirían nuevamente al universo madre, mientras que otras podrían acabar en otros «universos bebé» más pequeños o, incluso, en regiones tan grandes como nuestro universo. Nuestro universo madre^[8], otros universos madre y los universos bebé pueden interaccionar entre sí mediante las interconexiones de agujero de gusano. Algunas de estas posibilidades se ilustran en la figura 5.3.

Este es un gran salto especulativo en nuestra imagen de la estructura global del espacio y el tiempo. En lugar de representarlo como una bola suave conexa, debemos imaginarlo como una superficie con asas arrastrando almenajes y ramas que lo conectan a otros minimundos de corta y larga vida en sí mismos. Sin embargo, no conocemos ningún principio fundamental que nos diga por qué, a las pequeñas dimensiones de Planck, el universo no es así. Y de hecho, algo de esta borrosa incertidumbre en la estructura del espacio y el tiempo parece inevitable cuando la indeterminación de la teoría cuántica está entrelazada con el espacio y el tiempo dinámicos de la relatividad general. Pero la razón real que se ha venido barajando es que merece claramente la pena.

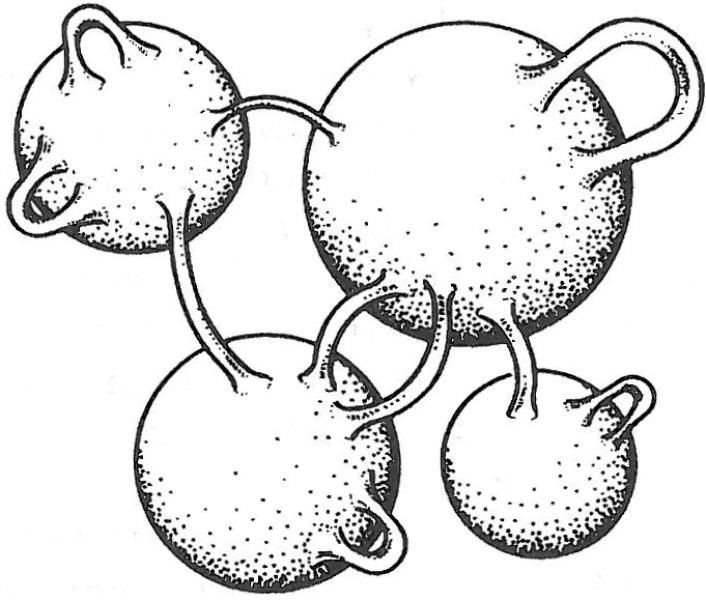
Figura 5.3 Agujeros de gusano conectando diferentes «universos» a sí mismos mediante asas, y a otros universos mediante «gargantas» de agujero de gusano.

Si se supone que la colección de caminos, a partir de la cual se ha de seleccionar el camino de acción óptimo desde el estado inicial del universo hasta un futuro estado, incluye los posibles caminos de agujero de gusano, dos cosas notables parecen suceder. La primera es que estos últimos parecen conspirar para suprimir la constante cosmológica cuando el universo es grande. Más específicamente, si uno imagina que existe para empezar una constante cosmológica, ésta inducirá interacciones vía los agujeros de gusano cuyo efecto es casi exactamente igual y opuesto a la constante cosmológica original. El resultado neto es su cancelamiento a un valor cero con una probabilidad extremadamente alta. En un universo que devenga grande como el nuestro, se predice un valor residual de la constante cosmológica que se encuentra concentrado en un pico agudo en torno al valor cero (según se ilustra en la figura 5.4).

La respuesta se da como una probabilidad, antes que como una proposición definida, debido al carácter intrínsecamente probabilístico de los aspectos cuánticos de la realidad. Pero la probabilidad de que aparezca un valor muy próximo a cero es esencialmente igual a uno. Si vivimos en un universo «probable», esperaríamos encontrar un valor de la constante cosmológica indistinguible de cero. La cuestión de si vivimos efectivamente en un universo «típico» la exploraremos más adelante ya que influye de forma más drástica sobre la segunda consecuencia derivada de considerar los caminos de agujero de gusano en nuestra imagen del espacio-tiempo.

Figura 5.4 Probabilidad de que se encuentre un valor Λ de la constante cosmológica, medida en un mundo de baja energía como el nuestro, como resultado de interacciones de agujeros de gusano con los universos bebé vecinos. Ésta forma un pico muy agudo en torno al valor cero.

Curiosamente se ha observado que el efecto de una amplia variedad de acoplamientos de agujeros de gusano con nuestro universo madre es dejar invariables sus leyes de la física pero producir una desviación aleatoria en los valores de sus constantes de la naturaleza respecto a los que hubieran tenido en ausencia de agujeros de gusano. Esto induce un profundo cambio en nuestra perspectiva sobre las capacidades de las Teorías del Todo. Nos previene de que, aun cuando exista alguna Teoría del Todo única de la variedad de cuerdas, por ejemplo, que determine los valores de las constantes de la naturaleza unívoca y completamente, estas predicciones especificarán la situación en el estado inicial del universo. Por consiguiente, estos prístinos valores se verán perturbados aleatoriamente por los efectos de agujeros de gusano que conectan nuestro universo a otros universos bebé o tienden puentes entre regiones distantes de nuestro universo. Cada universo madre o bebé estará dotado de un conjunto de constantes determinado por los efectos cuasi aleatorios de su red de conexiones de agujeros de gusano. No parece que nosotros podamos predecir los valores que se dan en nuestro universo madre, pues no podemos saber cómo serán estas minuciosas interconexiones de agujeros de gusano a las escalas de longitudes de Planck en las que la estructura del espacio y el tiempo se parece a una hormigueante espuma de incertidumbre. Un factor principal en la determinación de la estructura observada de nuestro universo se ha perdido para nosotros para siempre en el interior de los agujeros de gusano de espacio y tiempo. Todo lo que podemos esperar es que existan algunos casos como el de la constante cosmológica, en los que, aun cuando los agujeros de gusano produzcan cambios en su valor inicial de manera que el final tenga un aspecto aleatorio, el pico de la probabilidad resultante se encuentre tan concentrado en torno a un solo valor (cero en este caso), que las perturbaciones aleatorias no den lugar a una seria indeterminación si realmente habitamos uno de los universos más probables que pueden emerger de la era cuántica.

¿Qué vamos a hacer ante estos espectaculares desarrollos que han saltado a las páginas de las revistas de física recientemente? Son en extremo especulativos y pueden, por supuesto, ser incorrectos, tanto en su detalle técnico como en su gran diseño. Han sido predichos sobre la imagen euclidiana del comportamiento del tiempo y asumen como cierta la «condición de no contorno» que esbozamos en nuestro análisis del papel de las condiciones iniciales en el capítulo 3.^[9]

Si uno tuviese que adoptar una prescripción diferente del estado cuántico inicial del universo, entonces, aunque sería posible obtener una predicción diferente para el valor esperado de la constante cosmológica, que se concentraría esta vez en un pico en torno a un valor distinto a cero, hay una amplia variedad de opciones que siguen concentrándose en un pico en torno a cero. Por supuesto es fácil admitir que al incluir los agujeros de gusano damos un paso demasiado radical en la extensión de la imagen que poseemos del espacio y el tiempo, pero es asimismo posible que este paso no sea lo suficientemente radical. Uno podría imaginar otras posibilidades más exóticas, hasta ahora ignoradas, que arrasen por completo con los efectos de los agujeros de gusano y produzcan… quién sabe qué.

Hasta ahora, los cálculos de los efectos de los agujeros de gusano han sido realizados a partir de una serie de suposiciones simplificadoras que nos permiten tratarlos matemáticamente. Una de éstas es llamada la «aproximación del agujero de gusano diluido». Es un análogo de una suposición denominada «aproximación de gas diluido», la cual se emplea en el estudio de sistemas físicos, como los gases, que constan de muchos constituyentes sometidos a interacciones ocasionales con los otros. Si un gas está «diluido», cada interacción afectará de manera significativa sólo a las dos moléculas colisionantes en el momento de su colisión. Este es un factor que simplifica notablemente el problema bajo estudio en el caso del gas. Pero, en algunas situaciones, llamadas «críticas», cuando un gas está pasando, por ejemplo, del estado gaseoso al estado líquido, esta suposición pierde validez y muchos componentes del gas entran en interacción simultáneamente, con efectos que pueden ser percibidos en una gran parte del sistema. Este es un estado de cosas complicado que resulta muy difícil de analizar. En efecto, la distancia media recorrida por una de las moléculas en el gas antes de que interaccione de nuevo es menor que la distancia típica entre moléculas en el gas. Cuando el gas está «diluido», una molécula recorrerá varias distancias intermoleculares antes de interaccionar de nuevo. Un gas diluido es como un paseo por una villa escasamente poblada, con paradas ocasionales para pasar las horas del día; un gas no diluido es parecido a un viaje en hora punta en el metro de Londres (la interacción es continua, inevitable, y muy fuerte). La aproximación de agujero de gusano diluido supone que los agujeros de gusano se encuentran ampliamente distanciados entre sí, de manera que podemos considerar el efecto de un agujero de gusano sobre su universo paterno aislándolo respecto a los efectos de todos los demás. Es más, se supone que los agujeros de gusano sólo unen universos a universos bebé, o universos a sí mismos; no hay agujeros de gusano que unan diferentes universos bebé en esta aproximación, ni se permite que haya agujeros de gusano que se dividan en dos o más agujeros de gusano (véase la figura 5.5).

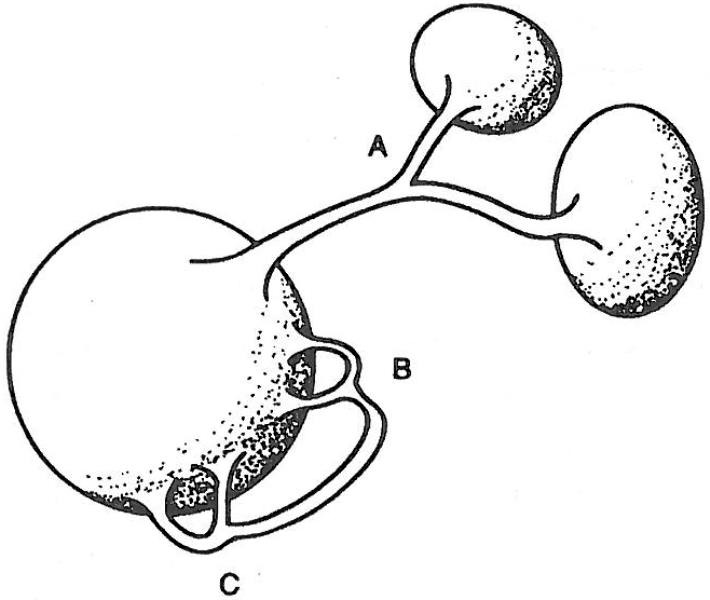
Figura 5.5 Algunas de las interconexiones concebibles —involucrando agujeros de gusano y universos bebé— no permitidas por la aproximación de «agujero de gusano diluido», necesaria para poder calcular las constantes de la naturaleza, inducidas por los agujeros de gusano, tratables actualmente. En A, B y C vemos agujeros de gusano dividiendo extensas regiones planas, y en B y C agujeros que no las conectan. Por el contrario, las configuraciones mostradas en las figuras 5.2 y 5.3 se adaptaban perfectamente a la aproximación de agujero de gusano diluido.

Figura 5.6 En la aproximación de agujero de gusano diluido, los efectos de las conexiones de agujero de gusano pueden representarse como una suma de aquellos efectos de las partes conectadas que se obtienen después de que las conexiones de agujero de gusano hayan sido cortadas.

La aproximación de agujero de gusano diluido nos permite mostrar que la situación de un universo, que está conectado en esta forma a varios universos bebé y a sí mismo, se parece a largo plazo a una colección de universos separados con otros valores de las constantes de la naturaleza (véase la figura 5.6). Aunque el uso de esta aproximación es absolutamente razonable —uno resuelve primero los problemas más sencillos—, no será una suposición realista en los primeros instantes transcurridos después del comienzo del universo. En este estado, esperaríamos que las interacciones fuesen tan complicadas y generales como pudieran probablemente serlo. Uno podría defender asimismo que la aproximación de agujero de gusano diluido no es válida, al igual que la aproximación de gas diluido pierde sentido para el contenido material del universo durante sus primeros instantes. No obstante, conociendo la ingenuidad de los físicos matemáticos, junto a su experiencia en el tratamiento de otros gases no diluidos, tenemos todas las razones para suponer que con el tiempo se encontrará una técnica que permita barrer algunas, si no todas, de las inhibiciones ocasionadas por la aproximación de gas diluido. Sin embargo, en este caso, el resultado de la variación de los valores de las constantes de la naturaleza no parece que sea un suceso tan bien definido: dependerá en alguna forma de la configuración de agujero de gusano inicial. Probablemente, esto no permitirá que se hagan simples predicciones, pero tendrá la consecuencia adicional de que establecerá un nexo entre los conceptos, previamente separados, de constantes de la naturaleza y condiciones iniciales. En el marco ampliado de la condición de «no contorno» para la función de ondas del universo, aparecería entonces una unión triple, muy interesante, entre leyes, condiciones iniciales y constantes. Sin embargo, todavía se puede ir más lejos con la especulación. Del mismo modo que nuestra experiencia en otras áreas de la física nos muestra que existen gases diluidos que son simples, así como sólidos y líquidos y complejas estructuras autoorganizadas de gran tamaño, donde la aproximación de gas diluido está lejos de ser verdadera, ¿no debería ser esto también cierto respecto a los universos? Quizás existan complicados agregados de universos fuertemente acoplados y universos bebé análogos a «líquidos universales» o a «sólidos universales» con sus exóticos efectos de orden de largo alcance, que no son una consecuencia inmediata de las leyes de la física o de los estados iniciales, sino la manifestación de haberse alcanzado un nivel crítico de complejidad. Si esto es así, ¿no podría ser que la complejidad potencial de las posibles estructuras espacio-temporales fuera insondable y que los valores correspondientes de las constantes de la naturaleza estuviesen envueltos en la incertidumbre?

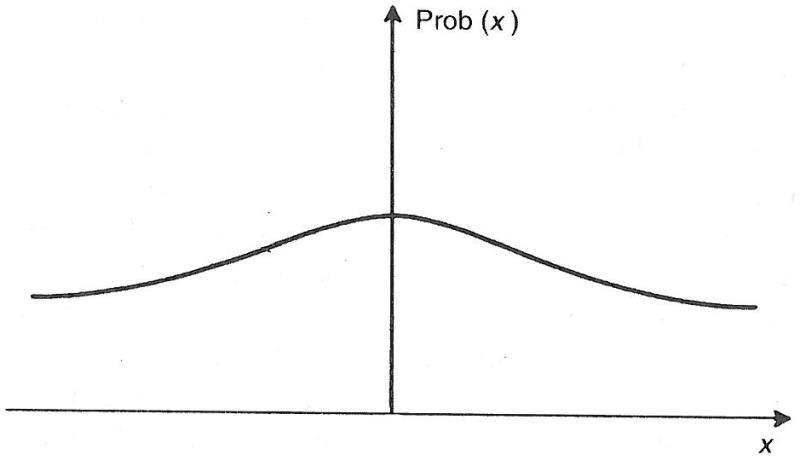
Figura 5.7 Distribución de probabilidad en la que ésta no se encuentra concentrada en un pico agudo en torno a un valor particular. Si las interacciones de agujero de gusano predijesen que la probabilidad de una constante de la naturaleza, x, en nuestro universo visible debía tener una forma similar a ésta, sería difícil decidir si deberíamos tomar el valor más probable (cero, en este caso) como el correspondiente a la realidad. Si los valores posibles de x en algún intervalo dieran lugar a universos que no pudieran evolucionar, ni dar cabida a seres inteligentes, no podrían ser observados. Nosotros hemos de comparar la observación con la probabilidad de que la constante tome el valor x condicionado a que dicho valor permita la evolución de vida, y ésta podría ser una cantidad muy diferente a la probabilidad, no sujeta a condiciones, de que tome simplemente el valor x.

El último detalle al que debemos hacer frente es la aplicación de cualesquiera resultados consistentes que puedan derivarse algún día de esta aproximación a la estructura del universo observado. Las investigaciones que se han realizado están basadas en la creencia de que vivimos en un universo «probable». Esto es, si la cosmología cuántica nos dice que las interacciones de agujero de gusano predicen que una constante de la naturaleza tome ciertos valores particulares con ciertas probabilidades, deberíamos comparar el más probable con el que observamos. En el caso de la constante cosmológica, el valor más probable tiene una probabilidad abrumadoramente mayor que la de todas las otras alternativas, de manera que uno se siente bastante contento de considerar nuestro universo como uno de esos que tienen valores despreciablemente pequeños de dicha constante. Pero ¿qué sucedería si se encontrase que el valor de otra de las constantes, como puede ser la de gravitación newtoniana, tuviera una distribución de probabilidad extendida suavemente a lo largo de todo el espectro de posibilidades numéricas, según se ilustra en la figura 5.7? ¿Qué concluiríamos de ello? En dicha situación, debemos inevitablemente traer a colación la consideración vital de que no hay razón alguna para pensar que nuestro universo es el «más probable» en relación a los valores de sus constantes de la naturaleza. Por el contrario, hemos visto ya cómo nuestra propia existencia, y la de cualquier observador que podamos imaginar, es posible sólo por el hecho de que los valores de muchas de estas constantes se encuentran muy próximos a los valores observados. Modificadlos un poco y no habrá observadores. Por lo tanto, vemos que debemos comparar los valores observados de las constantes de la naturaleza, no con el conjunto más probable de valores derivados de las interacciones de agujero de gusano, sino con los valores más probables obtenidos bajo condición de que permitan la evolución futura de observadores. Y este último conjunto de valores podría ser muy diferente al de los valores más probables en ausencia de dicho condicionamiento. El hecho de nuestra propia existencia, ni que decir del formidable problema de desentrañar todas las formas en que estas constantes de la naturaleza influyen en las condiciones cosmológicas y bioquímicas necesarias para nuestra propia existencia o para la de otros observadores, es un ingrediente vital en la interpretación y evaluación de las predicciones de los valores de las constantes de la naturaleza en cualquier espacio-tiempo infestado de agujeros de gusano. Necesitamos conocer todas esas constantes de la naturaleza de cuyos valores dependen las condiciones necesarias para la existencia de observadores. Esto origina un molesto dilema, pues muchas (si no todas) de estas constantes estarán vinculadas con cada una de las demás a través del andamiaje de alguna Teoría del Todo. Necesitamos conocer completamente dicha teoría antes de que podamos asegurar con certeza cuáles serán las probabilidades condicionales para la evolución de observadores complejos. Las predicciones de cualquier Teoría del Todo podrían, pues, estar a dos pasos de distancia de una explicación del universo visible. Los resultados de su unicidad lógica están tamizados por las impredecibles interacciones de agujero de gusano y, después, filtrados por la condición de que con el tiempo deben dar cabida a la evolución de complejos organismos bioquímicos. La determinación de las constantes de la naturaleza parece ahora plantear a las Teorías del Todo un reto mucho mayor que el planteado antes de que la búsqueda en pos de dichas teorías diese comienzo.