3
LAS CONDICIONES INICIALES
Érase una vez, y todos fueron felices y comieron perdices.
JAMES JOYCE
En el borde de las cosas
La ciencia es una ecuación diferencial. La religión es una condición de contorno.
ALAN TURING
Las leyes de la naturaleza nos dicen cómo cambian las cosas; pero creemos que tras ellas se ocultan ciertas invariancias que actúan como una camisa de fuerza sobre la realidad. Así, la naturaleza puede hacer lo que le plazca siempre y cuando estas encantadoras cantidades no se modifiquen durante el cambio. La Teoría del Todo trata de facilitarnos el directorio fundamental de todos los posibles cambios. El principio director en la búsqueda de esta fórmula, capaz de controlarlo todo, es que debe tratarse de una única ley y no de una colección de piezas diferentes. La unidad lógica del universo requiere una única invariancia que permanezca invariable frente a toda la complejidad y transitoriedad que observamos en nuestro derredor, desde las escalas subatómicas más pequeñas a los confines más lejanos del espacio exterior. Puede que la identificación de esta simetría global, si efectivamente existe y se manifiesta en una forma que nos sea inteligible, sea lo que más nos aproxime al descubrimiento del «secreto del universo».
Pero esto no es suficiente todavía. Aun cuando conociéramos las reglas que gobiernan el cambio de las cosas, solamente podríamos entender su estructura actual si supiéramos cómo comenzaron. Ésta es la herencia que hemos recibido de nuestra creencia en la ley de la causa y el efecto en el universo y de nuestra representación de las leyes de la naturaleza como ecuaciones diferenciales o algoritmos en los que el output está determinado de manera unívoca por el input. Las ecuaciones diferenciales son «máquinas» matemáticas que nos permiten predecir el futuro a partir del presente; así como nos permiten igualmente utilizar el presente para reconstruir el pasado.
Axiomas
La teoría de conjuntos puede ser considerada como una forma de teología exacta.
RUDY RUCKER
En las matemáticas el papel de las condiciones iniciales es desempeñado por los axiomas. Éstos son los postulados iniciales que se dan antes de comenzar a aplicar el razonamiento deductivo. El ejemplo clásico de sistema axiomático es el de la geometría plana, formulado por Euclides en torno al año 300 a. C. Éste constituye el modelo de todos los esquemas matemáticos rigurosos. Los axiomas son suposiciones iniciales, que se toman como verdades evidentes en sí mismas, a partir de las cuales puede procederse a las deducciones lógicas de acuerdo a las reglas del razonamiento estipuladas. Estas reglas del razonamiento lógico son análogas a las leyes de la naturaleza del científico, mientras que los axiomas desempeñan el papel de condiciones iniciales.
No somos libres de elegir los axiomas que queramos. Éstos deben ser lógicamente consistentes. Sin embargo, no hay ninguna limitación a su número, aunque la cantidad de axiomas que introduzcamos determinará la magnitud y la riqueza de las deducciones lógicas que puedan seguirse de ellos. Si bien Euclides y otros matemáticos de los siglos anteriores al XIX sabían que la consistencia lógica era esencial en toda elección de axiomas, eran también fuertemente partidarios de elegir axiomas que reflejasen la forma en la que observaban al mundo funcionar. Así, los axiomas de Euclides —por ejemplo, el axioma según el cual las rectas paralelas nunca se encuentran, o el que dice que sólo hay una línea recta que una dos puntos arbitrarios sobre una superficie plana— son el fruto evidente de la experiencia derivada de trazar líneas sobre una superficie plana. Los matemáticos posteriores no se sintieron tan conminados y sólo han exigido que su lista de axiomas sea consistente. Éstos no necesitan corresponderse con aquellas cosas que podemos ver o abstraer de la experiencia. Está por ver si las condiciones iniciales apropiadas a los problemas físicos más profundos, como el problema cosmológico que discutiremos más adelante, están directamente relacionadas a cosas físicas visualizadas, o si serán nociones lógicas o matemáticas abstractas que requieren sólo autoconsistencia. Aun en el caso en que prevalezca esto último, podría suceder que la condición de autoconsistencia en un sistema tan manifiestamente complejo como el universo físico sea apropiada para fijar esas condiciones iniciales unívoca y completamente.
Otra importante lección que hemos aprendido del estudio de los sistemas axiomáticos por los matemáticos es que se puede cuantificar la cantidad de información contenida en una colección de axiomas. Ninguna de las hipotéticas deducciones, que puedan probarse a partir de estos axiomas por medio de las leyes del razonamiento permitidas, puede poseer más información de la contenida inicialmente en los axiomas. Ésta es, en esencia, la razón de los famosos límites al poder de la deducción lógica revelados en el teorema de incompletitud de Gödel. Los axiomas de la aritmética ordinaria (y de cualquier sistema axiomático lo suficientemente rico como para abarcar la totalidad de la aritmética) contienen menos información que algunas proposiciones aritméticas y, por tanto, dichos axiomas y las reglas de razonamiento a ellos asociadas no pueden determinar si estas proposiciones son verdaderas o falsas. Observemos, no obstante, que un sistema axiomático que no sea tan amplio como la totalidad de la aritmética no se encuentra afectado por la incompletitud de Gödel. Por ejemplo, la denominada aritmética de Presburger, la cual consiste en la operación de adición (pero no de sustracción) sobre cero y todos los números enteros positivos, tiene la propiedad de que todas sus proposiciones son decidibles. Su reducido conjunto de axiomas contiene información suficiente para averiguar la verdad o falsedad de todas las proposiciones que puedan construirse utilizando su vocabulario.
En el capítulo anterior introdujimos la noción de compresibilidad algorítmica como un criterio para determinar el grado de aleatoriedad de las expresiones matemáticas. Ahora podemos utilizar una vez más este concepto para sacar punta a nuestra discusión. Si ante una secuencia particular no podemos probar que es aleatoria, podremos al menos probar que es no aleatoria hallando simplemente una compresión. La compresión mínima que admite un sistema lógico equivale a los axiomas del sistema. Vemos, pues, por qué no puede existir un teorema del sistema con un contenido de información mayor que el de los axiomas del sistema.
Los axiomas no son, por consiguiente, tan inmediatos como cabría esperarse. A menudo es una cuestión muy sutil decidir si los diferentes axiomas propuestos son verdaderamente independientes unos de otros. Existe un caso clásico de este tipo que encierra uno de los problemas no resueltos más difíciles de la matemática. Se conoce como la hipótesis del continuo. Antes del trabajo de Georg Cantor a mediados del siglo XIX, los matemáticos habían negado la existencia de verdaderos infinitos. De hecho, los infinitos eran una «abominación», en palabras de un matemático famoso. La postura de Gauss respecto a esta cuestión era que:
protestaré contra la utilización de las cantidades infinitas como algo consumado; dicha utilización no es admisible bajo ningún concepto en las matemáticas. El infinito es sólo una façon de parler: uno sabe que hay límites a los que ciertas razones se aproximan tanto como se quiera, mientras que otras razones pueden crecer indefinidamente.
Aquí encontramos expresada la idea de que el infinito nunca puede tener una existencia real; es meramente una forma abreviada de decir que algo puede ser tan grande como se quiera. Pero Cantor puso al mundo del revés al tratar a los infinitos como a otras cantidades matemáticas y al crear toda una secuencia de infinitos de diferente «tamaño». El más pequeño era el conjunto de los números naturales {1,2,3,4,5…} que fue designado ℵ0 (alef-cero). Se dice que un conjunto infinito tiene el mismo tamaño (o cardinalidad) que ℵ0 si sus elementos pueden ponerse en correspondencia biunívoca directa con los números naturales; esto es, si pueden ser enumerados sistemáticamente. Por ejemplo, el conjunto infinito de todos los números pares {2,4,6,8,10…} puede ser enumerado de esta manera mediante las correspondencias mostradas por las secuencias de flechas en la figura 3.1 (a). El camino indicado con flechas en la figura 3.1 (b) muestra entonces cómo podemos «contar» una por una todas las fracciones racionales dispuestas en una hilera infinita sin que ninguna sea omitida. Esto muestra que existe una correspondencia biunívoca directa entre ℵ0 y todas las fracciones racionales a través de la secuencia 1/1, 2/1, 1/2, 1/3, 2/2, 3/1, 4/1, 3/2, 2/3, 1/4, 1/5, 2/4, 3/3, 4/2, 5/1, 6/1, 5/2, 4/3…, y así ad infinitum. Así pues, en este sentido preciso, las fracciones racionales son un conjunto infinito del mismo tamaño que el de los números naturales. A primera vista, se trata de un resultado sorprendente ya que, mientras los números naturales se encuentran distribuidos muy espaciadamente, parece haber fracciones racionales densamente empacadas «entre ellos» por doquier, de manera que un proceso de enumeración debería encontrar muchas más fracciones que enteros. Pero esta intuición se fija demasiado en el orden en que aparecen los números, mientras que la correspondencia biunívoca que hemos establecido no necesita seguir el orden de magnitud con que aparecen las fracciones entre los enteros. Una fracción queda determinada precisamente por un par de números y hay tantos infinitos pares de números como números.
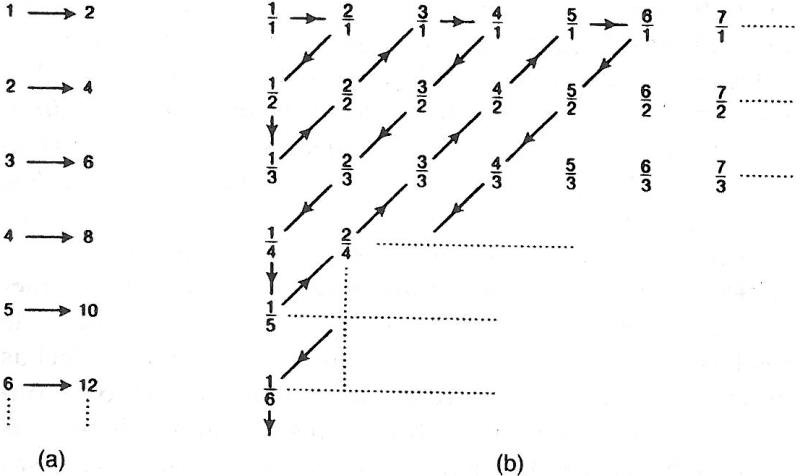
Figura 3.1 (a) Los números pares positivos forman un conjunto infinito del mismo «tamaño» que el de todos los enteros, porque los dos conjuntos pueden ponerse en la relación biunívoca aquí mostrada. Esto significa que pueden enumerarse sistemáticamente. (b) El conjunto de todas las fracciones racionales puede ponerse en una relación biunívoca con los enteros positivos y, por consiguiente, enumerarse sistemáticamente, si se listan según el modelo que mostramos y se cuentan a continuación en el orden marcado por la secuencia de flechas, ad infinitum.
Si ahora probamos a contar, no sólo todas las fracciones, sino también los decimales, sucede algo cualitativamente diferente debido a que hay muchos más decimales que fracciones. El salto en tamaño que significa el paso de los números naturales a los decimales es comparable al salto que uno tendría que dar para pasar de los números cero y uno a los más grandes. Para dar dicho paso se requiere más información, pues la única forma en que podemos formar un 2 a partir de 0 y 1 es sumando dos 1; pero una acción de esta índole requiere que poseamos previamente el concepto de «dos».
Cantor mostró que si intentamos contar los números con infinitos decimales (los denominados «números reales»), fracasaremos. Estos son de una cardinalidad superior a la de los números naturales y no pueden, por consiguiente, ponerse en correspondencia biunívoca con ellos. Cantor demostró esto mediante una nueva forma, ingeniosa y muy poderosa, de razonamiento que implica la noción de número diagonal. A modo de ilustración, supongamos que tenemos cuatro números de una longitud de cuatro dígitos:
1234
5678
9012
3456
El número diagonal 1616 no es entonces ninguno de los cuatro números dados. Lo que Cantor mostró fue que, si extendemos indefinidamente esta hilera de números, siempre habrá una forma de fabricar un número diagonal que no sea uno de la lista infinita de números dispuestos en hilera. Supongamos que consideramos sólo los números reales entre 0 y 1 (el argumento básico no varía significativamente si añadimos también los demás números reales) y supongamos que podemos contar todos los decimales infinitos. Esto conduce, según demostró Cantor, a una contradicción. Supongamos que fuéramos capaces de escribir sobre el papel todos los posibles decimales infinitos y de alinearlos, uno a uno, con los números naturales. Supongamos que la lista comienza como sigue:
| 1 | 0,234566789… |
| 2 | 0,575603737… |
| 3 | 0,463214516… |
| 4 | 0,846216388… |
| 5 | 0,562194632… |
| 6 | 0,466732271… |
y así hasta el infinito. Tomemos ahora el número diagonal con parte decimal compuesto por los dígitos resaltados:
0,273292…
A continuación, alteremos cada dígito añadiéndole la unidad para obtener el nuevo decimal:
0,384303…
Este nuevo número no podrá entonces aparecer en ningún lugar de la lista original porque difiere en un dígito de cada una de las entradas horizontales. Debe diferir de la primera entrada por lo menos en el primer dígito, de la segunda entrada en el segundo dígito, y así en adelante. Así pues, contrariamente a nuestra suposición inicial, la lista no habría podido contener todos los decimales posibles. Por consiguiente, nuestra suposición inicial, según la cual todos los decimales infinitos pueden ser enumerados sistemáticamente, era falsa. Los números reales poseen una cardinalidad superior a la de los números naturales, la cual se designa por el símbolo ℵ1 (alef-uno).
Cantor formuló la intrigante cuestión de saber si existen infinitos conjuntos de tamaño intermedio entre el de los números naturales y el de los números reales. El creía que no podían existir, pero no fue capaz de probarlo. Ésta es la denominada hipótesis del continuo. De hecho, parece ser que Cantor sufrió una depresión mental como consecuencia del esfuerzo intelectual que hizo estudiando esta cuestión. El problema permanece todavía sin resolver. No obstante, Kurt Gödel y su joven ayudante norteamericano Paul Cohen demostraron algunas cosas profundas e insólitas al respecto. Gödel mostró que, si tratamos la hipótesis del continuo simplemente como un axioma más y lo añadimos a los axiomas convencionales de la teoría de conjuntos[3], no puede darse ninguna contradicción lógica. Pero entonces, en 1963, Cohen demostró que la hipótesis del continuo es independiente de los otros axiomas de la teoría de conjuntos (al igual que se demostró finalmente que el postulado de las paralelas de Euclides era independiente de los otros axiomas de la geometría plana) y, por tanto, nunca podría ser probado o refutado a partir de estos axiomas.
La enseñanza que se desprende de lo anterior es que los axiomas matemáticos se parecen más de lo que podríamos haber sospechado a las condiciones iniciales de las leyes naturales. De hecho, hay quienes confían en que resulten ser la misma cosa: que las suposiciones básicas que uno debiera hacer sobre las hipótesis de partida de una Teoría del Todo sean aquellas requeridas por la consistencia lógica. Pero también hemos aprendido que su naturaleza e interrelación son extremadamente sutiles. Somos, de hecho, libres de elegir cualquier colección de axiomas que satisfaga nuestro propósito; pero, si no contamos con una obvia guía intuitiva sobre la conveniencia de axiomas sumamente abstrusos (como, por ejemplo, la hipótesis del continuo), ¿cómo sabremos si hemos de incluirlos o no? Movido por esta experiencia con el problema de la hipótesis del continuo, Alonso Church subrayó que:
… si ha de elegirse de alguna manera entre las teorías de conjuntos rivales, en lugar de desarrollar simple y neutralmente las consecuencias matemáticas de teorías alternativas, parece que el único fundamento para ello sea el mismo criterio informal de sencillez que determina la elección entre teorías físicas rivales, cuando ambas, o todas ellas, explican igualmente los hechos experimentales.
La demostración por Cohen de que la hipótesis del continuo es independiente del resto de los axiomas de la teoría de conjuntos significa que gozamos de completa libertad, tanto para añadir esta hipótesis, como su negación, a los axiomas existentes de la teoría de conjuntos. En cada caso obtendríamos una extensión diferente de la teoría de conjuntos, de forma similar a como podemos retener el postulado de las paralelas de Euclides, o sustituirlo por su negación, para crear geometrías no euclidianas formalmente consistentes. Si uno es un platonista, para quien las entidades matemáticas existen realmente, entonces sólo una de las dos teorías de conjuntos, mutuamente excluyentes, existe en la realidad; pero si se es un constructivista o un formalista, entonces ambas teorías son creaciones intelectuales igualmente válidas.
Existe un área de interacción entre la física fundamental y estas cuestiones fundacionales concernientes al infinito que está relacionada con la cuestión de saber si existe o no un verdadero continuo en la realidad. La mayoría de las imágenes fundamentales del mundo físico presuponen que las nociones básicas —campo, espacio, tiempo— son entidades continuas en lugar de discretas. La contraposición discontinuidad versus continuidad es un viejo dilema de la filosofía natural que resurge en cada época bajo un nuevo disfraz. Lo más importante a este respecto para la estructura de cualquier teoría del infinito es la enorme diferencia en complejidad que existiría entre una Teoría del Todo continua y otra discreta. Esto es debido a que el número de transformaciones continuas que podrían darse entre dos conjuntos de números reales es de un orden de infinitud menor que el número total de posibles transformaciones no continuas. Así pues, el requisito de continuidad produce una vasta y sorprendente reducción del alcance del problema. Las transformaciones continuas incluyen el catálogo de las posibles relaciones del que extrajimos la clase de transformaciones (o «ecuaciones») denominadas leyes de la física, de manera que un mundo discontinuo sería en potencia infinitamente más complejo. No posee tantas restricciones sobre lo que está o no permitido hacer. Actualmente, los físicos están enamorados de la simetría y buscan sólo imágenes continuas de la física fundamental; pero quizás algún día se sientan motivados a prestar atención a posibles estructuras de un mundo básicamente discreto. En el capítulo 9 veremos algunas de las ideas que pueden empujarles a ello.
Del contenido de información de los axiomas con los que contamos depende de manera crucial el tipo de afirmaciones que pueden demostrarse o refutarse. Algunos filósofos de la ciencia han utilizado los teoremas de Gödel concernientes a la incompletitud de la aritmética (y, por tanto, de cualquier sistema lógico que abarque a la aritmética) para defender que nunca podremos conocer todo sobre el universo físico en términos de leyes matemáticas de la naturaleza, porque no podemos construir todas las proposiciones verdaderas, y solamente las verdaderas, de la aritmética, ni tampoco podemos probar la veracidad o falsedad de todas las proposiciones aritméticas. Según Stanley Jaki, galardonado con el Premio Templeton:
Parece, según se desprende del teorema de Gödel, que las bases fundamentales de las audaces construcciones simbólicas de la física matemática permanecerán para siempre sumergidas en ese nivel de pensamiento más profundo caracterizado tanto por la sabiduría como por la vaguedad de las analogías e intuiciones. Para el físico especulativo esto implica que hay límites a la precisión de la certidumbre, que hay un límite incluso al pensamiento puro de la física teórica, como al de todos los otros campos de la especulación.
Pero podría suceder que la realidad física, aun cuando sea fundamentalmente matemática, no utilice la totalidad de la aritmética y pueda así ser completa. Podría, de hecho, formar parte de una de esas ramas decidibles de la matemática que no son tan ricas como la aritmética. Aunque pueda parecer que el universo hace uso de toda la parafernalia de la aritmética, al hacerlo nuestras versiones de sus leyes matemáticas de la naturaleza, es posible que solamente se deba a que estas versiones no son la representación más elegante y económica de las verdades que contienen.
Condiciones iniciales y simetría temporal
El historiador es un profeta que mira hacia atrás.
AUGUST VON SCHLEGEL
Algunas veces las condiciones iniciales pueden ejercer una influencia tan penetradora que crean la impresión de que está actuando un nuevo tipo de ley. El caso más conocido es el de la denominada «segunda ley de la termodinámica», la cual especifica que la entropía o nivel de desorden de un sistema físico cerrado no puede disminuir con el paso del tiempo. Vemos tazas de café que se rompen accidentalmente en trozos, pero nunca vemos recomponerse una taza a partir de los fragmentos. Nuestros escritorios degeneran naturalmente de un estado de orden a uno de desorden, pero nunca al contrario. Sin embargo, las leyes de la mecánica que gobiernan la forma en que los cambios tienen lugar permiten la inversión temporal de cada uno de estos movimientos comunes. Así pues, un mundo en el que los pedazos de porcelana china se recompongan en tazas de Staffordshire y el desorden de los escritorios se transforme constantemente en orden, no viola ninguna ley de la naturaleza. El que veamos cómo las cosas evolucionan de mal a peor en los sistemas cerrados es debido a que las condiciones de partida necesarias para producir un aumento del orden son fantásticamente raras y la probabilidad de que se den en la práctica es ridícula. Cada uno de los pedazos de porcelana china tendría que moverse precisamente a la velocidad correcta y justamente en la dirección correcta para que todos juntos lograsen formar una taza. Por otro lado, existe en la práctica un número infinitamente mayor de formas en las que un escritorio puede pasar de orden a desorden que de desorden a orden. En consecuencia, es la alta probabilidad de que se den las condiciones «típicas», de las que se sigue el desorden con más facilidad, la responsable de crear la ilusión de una ley de la naturaleza que produce desorden.
El ejemplo de la segunda ley de la termodinámica nos alerta de la importancia de entender las condiciones iniciales, especialmente en aquellas situaciones que no nos son familiares. Pues sin este entendimiento podríamos extraviarnos, tratando de hallar en una Teoría del Todo explicaciones a cosas que no merece la pena explicar. Es más, vemos cómo la elección (o accidente) de condiciones iniciales crea un sentido de direccionalidad temporal en un entorno físico. La «flecha» de crecimiento de la entropía es un reflejo de la improbabilidad de que en un sistema cerrado se den las condiciones iniciales que implican una disminución de la entropía.
Allá donde dirijamos nuestra mirada en el universo, observamos que los sistemas físicos cerrados evolucionan en el mismo sentido, desde estados ordenados hasta un estado de completo desorden llamado equilibrio térmico. Esto no puede ser una consecuencia de leyes conocidas de cambio, pues en su nivel más fundamental estas leyes poseen simetría temporal, esto es, admiten la inversión temporal de cualquier secuencia de acontecimientos permitida. Las condiciones iniciales desempeñan un papel decisivo en dotar al mundo de su sentido de dirección temporal. En nuestra discusión posterior de la cosmología cuántica exploraremos algunas de las dramáticas consecuencias derivadas de las condiciones iniciales para el universo entero. Se hará evidente entonces que una prescripción de las condiciones iniciales es crucial si queremos entender el universo observado. Una Teoría del Todo necesita complementarse con alguna de esas prescripciones independientes, que apelan a la sencillez, la naturalidad, la economía y a algunas otras nociones igualmente metafísicas, para apuntalar su credibilidad. La única alternativa radicalmente diferente debería apoyarse en la creencia de que el tipo de descripción matemática de la naturaleza que hemos llegado a conocer y a amar —el de las ecuaciones causales con condiciones de partida— es sólo un artilugio de nuestras propias categorías de pensamiento preferidas y una mera aproximación a la verdadera naturaleza de las cosas. Es posible que a un nivel más profundo sencillamente no exista una estricta división entre aquellos aspectos de la realidad que habitualmente llamamos «leyes» y aquellos que hemos llegado a conocer como «condiciones iniciales».
Tiempo sin tiempo
No hay nada nuevo bajo el sol.
Eclesiastés
Tanto Leibniz como Laplace se percataron de una enigmática consecuencia del determinismo absoluto. Si todas nuestras leyes del movimiento vienen dadas en la forma de ecuaciones que determinan unívoca y completamente el futuro a partir del presente, entonces, mediante un conocimiento absoluto del estado inicial, un superser podría predecir toda la historia futura del universo a partir de esta materia prima. Aunque a menudo se citan las tesis de Laplace a este respecto y el concepto de determinismo en la física clásica ha adoptado el calificativo de «determinismo laplaciano», existe una enunciación anterior y más explícita de esta idea en el notable libro de Boscovich de 1758, del que ya hablamos en el capítulo anterior. Sobre la cuestión del determinismo y la continuidad del movimiento, Boscovich escribe:
Cualquier punto material, dejando a un lado los movimientos libres producidos por la acción arbitraria de la voluntad, debe describir una línea curva continua, cuya determinación puede ser reducida al siguiente problema general: sea dado un número de puntos materiales y sea dado, para cada uno de ellos, el punto del espacio que ocupa en cualquier instante dado de tiempo; sean dadas también la dirección y la velocidad del movimiento inicial si éstos fueran proyectados, o del movimiento tangencial si estuvieran ya en movimiento; y sea dada la ley de fuerzas expresada por alguna curva continua [como la ley de fuerzas mostrada en la figura 2.1 del capítulo anterior]…, se pide encontrar el camino recorrido por cada uno de los puntos… Ahora bien, aun cuando un problema de esta índole sobrepasa todas las capacidades del intelecto humano, cualquier geómetra puede, sin embargo, ver fácilmente que el problema es determinado… una mente que tuviera la capacidad necesaria para tratar dicho problema en una forma adecuada, y fuera lo suficientemente perspicaz para percibir sus soluciones (y dicha mente podría ser incluso finita, siempre que el número de puntos fuera finito y la curva que representa la ley de fuerzas estuviera dada por una representación finita), dicha mente, digo, podría derivar la propia ley de fuerzas a partir de un arco continuo descrito en un intervalo de tiempo, sin importar cuán pequeño sea éste, por todos los puntos de materia… Ahora bien, si se conociera la ley de fuerzas, junto a la posición, velocidad y dirección de todos los puntos en cualquier instante de tiempo dado, sería posible para una mente de este tipo ver todos los movimientos y estados subsiguientes necesarios y predecir todos los fenómenos que se seguirían necesariamente de ellos.
Posteriormente, los científicos defenderían la factibilidad de obtener dicho conocimiento absoluto, y luego, en el siglo XX, la teoría cuántica cuestionaría el principio de que dicho conocimiento puede ser adquirido por cualquier observador e incluso de si tiene siquiera sentido su existencia. Pero dejemos a un lado estos importantes desarrollos y examinemos una de las sorprendentes consecuencias del rígido mundo determinista de Boscovich, Laplace y Leibniz, que subyace a la mayoría de los problemas cotidianos de los que se ocupan los físicos cuyo trabajo no se ve afectado directamente por las ambigüedades de la mecánica cuántica.
En un mundo completamente determinista toda la información sobre su estructura se encuentra implícita en las condiciones iniciales. La existencia del tiempo es un misterio. No se precisa para nada. No hay nada que necesite realmente «suceder», pues todo se encuentra ya latente en las leyes y condiciones iniciales. Una primera reacción ante esta tesis es hacer hincapié en las leyes de la naturaleza como algoritmos que predicen el futuro a partir del pasado, pero hemos visto que las leyes son equivalentes a principios de invariancia, es decir, a afirmaciones sobre el hecho de que alguna entidad no cambia. El corsé determinista hace que el tiempo parezca superfluo. Todo lo que vaya a suceder en algún momento se encuentra implícito en el estado inicial. Nuestro estado presente contiene toda la información necesaria para reconstruir el pasado y predecir el futuro. En las inquietantes palabras de Joseph Conrad en El corazón de las tinieblas: «La mente humana es capaz de cualquier cosa, porque todo está en ella, todo el pasado y todo el futuro».
Esta situación planteó siempre un dilema a los científicos de la era precuántica. Durante los debates del siglo XIX sobre la posibilidad de la evolución darwiniana frente a una creación especial del mundo vivo en su forma presente, increíblemente adaptada, varios comentaristas científicos insistieron en la convergencia esencial de estas dos concepciones, ya que el estado presente del mundo evolucionado no puede ser ni más ni menos que un espejo fiel de condiciones iniciales particulares. Otros se sintieron preocupados por el problema de la voluntad libre en un mundo gobernado por un rígido determinismo. Un examen de este problema condujo a James Clerk Maxwell a apreciar la enorme diferencia que existía entre el determinismo en teoría y el determinismo en la práctica.
Existe un vasto número de situaciones físicas, desde el clima hasta un latido de corazón, donde la más leve incertidumbre en nuestro conocimiento del estado del sistema en un instante dado trae consigo la pérdida total de información sobre su estado exacto después de un período muy breve de tiempo. Presentes casi idénticos conducen a futuros muy diferentes. Tales sistemas son llamados «caóticos». Su predominio es responsable de muchas de las complejidades de la vida: la economía, las fluctuaciones del mercado monetario o las variaciones climáticas. En estas situaciones no importa cuán exactamente conozcamos las reglas que determinan cómo deben producirse los cambios, porque no podemos comprobar con toda precisión el estado presente de las cosas. Nuestra capacidad de predicción desaparece velozmente. Resulta curioso lo mucho que tardaron los científicos en reconocer la abrumadora influencia de dicha sensibilidad a las condiciones iniciales en el mundo real. Tan cegados estaban por el trabajo de relojería determinista de la visión newtoniana del mundo y por los avances tecnológicos que se derivaron de ello, que las «leyes que nunca serán violadas» se impusieron como el aspecto dominante del carácter del mundo. Solamente los pensadores más profundos del siglo XIX, como Maxwell y Poincaré, reconocieron la verdadera naturaleza de las cosas, que tan a menudo nos deja sin poder predecir el futuro real, aun cuando tengamos en nuestras manos las leyes de la naturaleza apropiadas. Maxwell se vio llevado por sus reflexiones sobre el problema de la voluntad libre en la práctica a reconocer que muchas secuencias de sucesos naturales presentan una dependencia extremadamente sensible de sus particulares condiciones de partida. Posteriormente, las tentativas de comprender la sensible dinámica de los movimientos planetarios en nuestro sistema solar fue lo que condujo a Henri Poincaré a darse cuenta asimismo de que
cuando una causa muy pequeña que escapa a nuestra atención determina un efecto considerable que no podemos dejar de ver, decimos que el efecto se debe al azar. Si conociéramos con exactitud las leyes de la naturaleza y la situación del universo en el momento inicial, podríamos predecir exactamente la situación de dicho universo en un instante posterior. Pero, aun en el caso de que las leyes de la naturaleza no escondan ningún secreto para nosotros, sólo podremos conocer la situación inicial aproximadamente. Si eso nos permitiera predecir la situación posterior con la misma aproximación, y eso es todo lo que pedimos, deberíamos decir que el fenómeno ha sido predicho, que está regido por leyes. Pero no siempre es así; puede suceder que pequeñas diferencias en las condiciones iniciales produzcan diferencias muy grandes en el fenómeno final. Un pequeño error en los primeros producirá un error enorme en el último. La predicción se hace imposible, y tenemos el fenómeno fortuito.
Aquí Poincaré señala cómo la sensibilidad extrema de la evolución al estado de movimiento actual conduce a un comportamiento muy complicado y errático que no puede ser reconstruido a través de sus antecedentes en la práctica. De aquí que sea considerado un fenómeno «aleatorio» por quienes lo observan. No hay nada intrínsecamente indeterminado en los movimientos implicados. Si poseyésemos un conocimiento absolutamente exacto de las condiciones de partida, podríamos predecir con toda perfección el comportamiento futuro. Pero lo que nosotros sabemos ahora, y Poincaré no sabía, es que los aspectos cuánticos de la realidad prohíben por principio, y no solamente en la práctica, la adquisición de dicho conocimiento, libre de errores, de las condiciones iniciales. Estas restricciones cuánticas tampoco se hallan muy alejadas de la experiencia. Si golpeásemos una bola de billar con la precisión que permite la incertidumbre cuántica de la naturaleza, se necesitarían únicamente una docena de choques con las bandas de la mesa y con las otras bolas para que esta incertidumbre se viera amplificada al punto de abarcar la extensión de la mesa de billar entera. Las leyes del movimiento no nos dirían, por tanto, nada sobre la trayectoria individual de la bola.
Antes de abandonar estas visionarias observaciones de Maxwell y Poincaré no deja de ser fascinante buscar en la obra de Boscovich cuáles son sus pensamientos sobre la factibilidad de alguna «mente» capaz de comprender el contenido de todos los movimientos. Boscovich parece reconocer la inevitabilidad de influencias perturbadoras en la realidad, pero no su carácter inestable. Y, ante cualquier aspiración a explotar el determinismo para obtener un conocimiento completo, advierte:
No podemos aspirar a ello, no ya porque nuestro intelecto humano no alcance a realizar la tarea, sino también porque no conocemos el número, ni la posición o el movimiento de cada uno de estos puntos… y hay otra razón, a saber, que los movimientos libres producidos por sustancias espirituales afectan a estas curvas…
La ubicuidad de los fenómenos caóticos presenta otro problema más a nuestros sueños de omnisciencia a través de una Teoría del Todo. Aun cuando podamos superar el problema de las condiciones iniciales mediante una determinación del estado de partida más natural o unívocamente consistente, puede que tengamos que afrontar el hecho real de que existe una incertidumbre inevitable en torno a la determinación del estado inicial, que hace imposible la predicción exacta del estado futuro del universo. Solamente serán posibles afirmaciones de carácter estadístico.
Axiomas caóticos
«En las matemáticas —dijo David Hilbert— no hay un ignorabimus… Debemos saber, sabremos». Como muchas de las afirmaciones hechas por científicos de inmaculada reputación ya entrados en años, ésta estaba completamente equivocada.
IAN STEWART
La analogía entre las condiciones iniciales para las leyes deterministas de la naturaleza y los axiomas para las estructuras lógicas puede llevarse un poco más lejos, para revelar un inesperado paralelismo entre caos y aleatoriedad en los sistemas axiomáticos que impide a éstos dar respuestas a ciertas cuestiones: que hay un número infinito de hechos matemáticos que no pueden vincularse deductivamente a los axiomas. De nuevo, las nociones de complejidad y de compresibilidad algorítmica introducidas en el primer capítulo son el vehículo más apropiado para lograr un entendimiento. Podemos asociar una cierta cantidad de información con los axiomas y reglas del razonamiento que definen un sistema axiomático particular, y definir como su contenido de información el tamaño del programa de ordenador capaz de rastrear por todas las posibles cadenas de deducción y de probar todos los teoremas posibles. Este enfoque conduce a la conclusión de que no se puede demostrar la aleatoriedad de ningún número cuya complejidad sea mayor que la del sistema axiomático. Si se intenta atajar esta deficiencia añadiendo axiomas o reglas de inferencia adicionales, con el fin de aumentar el contenido de información del sistema, existirán siempre números todavía mayores cuya aleatoriedad no puede ser demostrada. Existe un límite real al poder de las matemáticas.
Más sorprendentemente, el matemático americano Gregory Chaitin ha explorado las consecuencias de esta línea de pensamiento en el contexto de un famoso problema matemático. Si escribimos una ecuación que relacione dos (o más) cantidades x e y, como
x + y2 = 1,
y si no restringimos los valores de x e y a los números enteros, entonces hay una infinidad de pares (x, y) que son soluciones de la ecuación (por ejemplo, x = 3/4 e y = 1/2). Pero supongamos que estemos interesados en determinar las soluciones en las que tanto x como y son números enteros positivos. Tenemos entonces un problema denominado «diofántico» en honor a Diofantes de Alejandría, el más grande algebrista de la antigüedad. En nuestro ejemplo elemental, (x, y) = (1, 0) o (0, 1) son las únicas soluciones. Un problema diofántico menos trivial es el planteado por el último teorema de Fermat. Mientras estudiaba la famosa obra Arithmetica de Diofantes, el abogado Pierre de Fermat, anotó al margen:
Es imposible descomponer un cubo en la suma de dos cubos, una potencia a la cuarta en dos potencias a la cuarta y, en general, cualquier potencia mayor que la segunda en dos de la misma especie, de lo cual he hallado una prueba notable. El margen es muy pequeño para anotarla.
Actualmente nadie cree que Fermat encontrara dicha prueba. En notación moderna, Fermat afirma tener una prueba de que no existe ninguna solución con enteros positivos x, y, z a la ecuación
xn + yn = zn,
donde n es un número entero mayor que 2. Todas las otras conjeturas matemáticas de Fermat han sido demostradas o refutadas, por lo que a este teorema, el más notable, se le denomina su «último teorema».
Más generalmente, podríamos escribir una ecuación diofántica que contenga un parámetro etiquetador q, el cual podría tomar cualquier valor entero 1,2,3,4… y así indefinidamente; por ejemplo,
x + y2 = q
se reduce al problema anterior cuando q = 1. Supongamos ahora que tenemos una cierta ecuación diofántica que contiene m variables diferentes x2, x3,…, xm, en lugar de sólo dos (x e y), así como una cantidad q. Representamos esquemáticamente esta ecuación en m variables por:
P(q, x1, x2, x3, …, xm) = 0.
Chaitin preguntó si una ecuación de esta forma tiene característicamente un número finito o infinito de soluciones para q = 1, 2, 3… A primera vista parece que se trata de una variación menor de la cuestión tradicional de si esta ecuación tiene una solución en el campo de los enteros para cada q = 1,2, 3… Sin embargo, es una cuestión infinitamente más difícil de responder. Sucede que no hay manera de determinar la respuesta. La respuesta es aleatoria en el sentido de que, para resolver el problema, se necesita más información de la que éste contiene en realidad, y no puede ser calculado reduciéndolo a otros hechos y axiomas matemáticos. Hasta la aritmética contiene aleatoriedad; algunas de sus verdades sólo pueden ser determinadas mediante investigación experimental. Vista de esta forma comienza a parecerse algo a la ciencia.
Tiempo cosmológico
El tiempo es la forma en que Dios evita que las cosas sucedan todas de una vez.
Graffiti tejano anónimo
Las condiciones iniciales que aparecen en la mayoría de los problemas científicos son muy mundanas. Las preparamos de manera especial con el objeto de poder observar mejor un cierto tipo de efecto que esperamos que se produzca. Pero en cosmología —el estudio de la estructura y evolución del universo como un todo— la situación es mucho más interesante. Pues sin ningún conocimiento de esas condiciones iniciales cósmicas, nuestro conocimiento del universo permanecería seriamente incompleto. Parece que incluso el conocimiento de la Teoría del Todo nos impediría entender por qué el universo comenzó de una forma determinada. Dada una secuencia de números, podría suceder que adivinásemos el modelo seguido, el cual permite predecir el siguiente número y comprimir algorítmicamente toda la secuencia, pero que no pudiésemos decir por qué comienza en el punto particular en que lo hace. Sin embargo, lo que realmente singulariza al problema de las condiciones iniciales cosmológicas es que posee implicaciones metafísicas. Si existen condiciones iniciales especiales, capaces de encauzar la evolución del universo en el curso que conduce al presente, ¿qué es lo que selecciona éstas y no otras condiciones de partida?
Las condiciones iniciales determinan la estructura de grano grueso del universo a gran escala. Desempeñan un papel en la determinación del tamaño del universo, de su forma, su temperatura y su composición. Por lo que ya hemos dicho, la situación está bien definida. Habrá condiciones iniciales especiales que conducen al estado que observamos en el momento actual, y a lo máximo que podemos aspirar es a descubrir cuáles son esas condiciones. Pero veremos que la situación reviste mucho más interés, pues durante más de veinticinco años la postura de los cosmólogos ante el tema de las condiciones iniciales ha alimentado casi todas nuestras ideas sobre la estructura del universo. Y, como esas condiciones iniciales se dieron hace más de diez mil millones de años, cuando el universo se asemejaba a un vasto experimento de física de altas energías, su consideración hace que la cosmología colisione con nuestras especulaciones sobre la estructura fundamental de las partículas elementales de la materia. La cuestión de por qué el universo es como es se encuentra ligada inextricablemente a la de por qué la física fundamental es de la forma que es.
Comencemos explorando las ramificaciones y opciones de las imágenes cosmológicas tradicionales en las que se hace una distinción fundamental entre leyes de la naturaleza y condiciones iniciales.
Después de que Hubble descubriese a finales de la década de 1920 que el universo se encuentra en un estado de expansión global, se estimó que esto implicaba que el universo debió tener un «principio» en el sentido de que su estado actual de expansión no podría prolongarse indefinidamente en el pasado. Creemos que encontraremos un instante en nuestro pasado finito en el que la densidad era infinita y toda la materia estaba comprimida a un tamaño nulo. Posteriormente, a mediados de la década de 1970, esta imagen del big bang se vio reforzada por el descubrimiento de un campo cósmico de radiación térmica, enormemente enfriada por la expansión, del cual se había predicho su existencia como un remanente del estado caliente inicial. Más tarde, el estudio minucioso de los modelos de universo en expansión, aportados por la teoría de la relatividad general de Einstein, ha confirmado otras predicciones detalladas que se basan en cómo debió haber sido el universo cuando contaba sólo un segundo de edad. Los cosmólogos modernos coinciden generalmente en que hemos establecido la estructura general del comportamiento del universo desde que tenía un segundo de edad hasta el presente, unos quince mil millones de años más tarde. Esto no significa afirmar que hemos entendido todo lo que sucedió. Así, no entendemos los pormenores de los procesos que dieron forma a las galaxias, si bien dichos procesos ejercen una influencia despreciable sobre el curso de la expansión global. Antes de un segundo después del aparente comienzo, nos encontramos en un terreno del todo resbaladizo. No disponemos de más restos fósiles directos del universo temprano con los que probar la exactitud de nuestra reconstrucción de su historia. Para reconstruir la historia del universo en estos primeros instantes necesitamos conocer cuál es el comportamiento de la materia a energías mucho más altas de las que podemos alcanzar mediante los experimentos terrestres. De hecho, puede que el estudio de los primerísimos estadios de la historia del universo sea el único medio de probar nuestras teorías sobre el comportamiento de la materia a muy altas temperaturas. Pues podría suceder que hallásemos que, si una posible partícula elemental existió realmente, habría sobrevivido al big bang en tal abundancia que la intensidad de su atracción gravitatoria hoy en día habría producido una desaceleración en la expansión del universo a un ritmo mucho mayor de la que se observa.
Nos encontramos, pues, atrapados en un círculo vicioso. Necesitamos conocer el comportamiento de las partículas elementales de la materia para poder entender los comienzos del universo, y necesitamos conocer cómo fueron esos primeros comienzos del universo para poder descubrir el comportamiento de las partículas elementales.
Una vez anotada esta advertencia, continuamos a pesar de todo con la extrapolación de nuestra afortunada imagen del universo al primer segundo de su historia, utilizando las ideas más recientes de la física de partículas elementales como una guía de lo que fue posible o probable en el pasado remoto y distante.
Tradicionalmente (y actualmente) se dan tres actitudes diferentes frente al problema de las condiciones iniciales cosmológicas:
- Mostrar que no existe ninguna.
- Mostrar que su influencia es mínima.
- Mostrar que tienen una forma especial.
La primera opción arranca de la creencia de que el universo no tuvo un principio —que no hubo ningún estado inicial. Esta postura fue adoptada con todo rigor por Hermann Bondi, Fred Hoyle y Thomas Gold, quienes en 1948 propusieron la teoría del «estado estacionario» del universo. La teoría específica que ellos presentaron entró hace ya tiempo en conflicto con la observación y sus detalles concretos no son importantes en nuestra presente discusión. Lo que resulta más interesante es su voluntad de evitar la aparición de tiempos especiales en la historia del universo, de la misma forma que Copérnico nos advirtió contra el dotar de significado especial a algunos lugares del universo. Obviamente, si el universo comienza a expandirse (o a existir) en algún instante finito del pasado o cesa su expansión (o deja de existir) en algún instante futuro, estos instantes son tiempos especiales para cualquier observador. Los «hombres del estado estacionario» denominaron a la extensión del principio copernicano de la localización espacial a la localización espacial y temporal, el principio cosmológico perfecto (un nombre que incitó a Herbert Dingle a comentar que esto era como «llamar al arado un instrumento agrícola perfecto» y a algunos americanos a insinuar que la estipulación de que el universo es el mismo en todo momento era meramente un artilugio con el que sus autores pretendían asegurar que siempre habría una Inglaterra). Aunque el universo estacionario se expande, mantiene en todo momento una densidad constante gracias a la suposición de que la materia se crea continuamente a un ritmo que contrarresta exactamente la rarefacción procedente por otro lado de la expansión. Esta creación continua contrasta con la creación en un instante dado y de una vez por todas defendida por los modelos cosmológicos del big bang de aquel entonces. El hecho de que la tasa de creación equilibrase exactamente los efectos de la expansión quedaba automáticamente asegurado, pues la tasa de creación es tan ínfima, menos de un átomo en un metro cúbico cada diez mil millones de años, que no se podría detectar directamente.
No obstante, a pesar de que el universo no tiene un principio real en esta teoría —en promedio siempre tendrá, y siempre se expandirá a la misma velocidad constante—, se requiere todavía especificar los parámetros que lo definen: no hay un universo estacionario único. El valor de su densidad de materia universal constante o, lo que es equivalente, su tasa constante de creación o la velocidad universal de expansión, necesita una explicación. Para definir este modelo debemos especificar ciertas condiciones en algún instante de tiempo. Una Teoría del Todo podría decirnos que el universo no tiene un origen en el tiempo y que se expande de una forma similar al universo estacionario (al menos desde hace unos diez mil millones de años), pero esto dejaría muchas cosas sin aclarar: la velocidad de expansión del universo, el origen de las galaxias, el contenido térmico del universo, el desequilibrio entre materia y antimateria.
Esta incompletitud lógica es característica de todo modelo cosmológico que descanse en la hipótesis de haber existido desde un tiempo pasado infinito. Aun cuando no exista estrictamente un instante «inicial» en sentido temporal, se requerirán todavía especificaciones extra que desempeñan el papel de condiciones «iniciales». Así, en el caso de un universo de edad infinita, se requieren condiciones iniciales en el pasado temporal infinito.
Es interesante observar que durante siglos los filósofos y los teólogos han intentado dirimir mediante el pensamiento puro la cuestión de si el universo podría o no ser infinitamente viejo. Esto es, hay quienes han intentado mostrar que existe una contradicción lógica inherente a la noción de un pasado temporal infinito. Y hay quienes todavía lo intentan. Dichas ideas presentan un vínculo con argumentos cosmológicos a favor de la existencia de Dios que no sólo buscan demostrar que ha debido de existir un origen en el tiempo del universo, sino que van más lejos al mostrar (o asumir en la práctica) que esto requiere que haya habido un creador. Éste es un argumento muy resbaladizo, a pesar de nuestra ignorancia básica sobre esas cuestiones tan irresistibles. Una forma habitual de este argumento señala el hecho de que todas las cosas que vemos tienen una causa y, por tanto, el universo debe tener una causa. Pero este razonamiento tiene una curva peligrosa hacia su mitad. El universo no es una «cosa» en el sentido en que lo son los otros ejemplos que se citan. Es una colección de cosas o, como Wittgenstein decía, «el mundo es la totalidad de los hechos». Nuestro argumento equivale entonces a sostener que todos los miembros de clubs tienen madres y, por tanto, todos los clubs tienen madres. También podría ponerse en entredicho la afirmación de que todos los sucesos tienen causa. En el sombrío mundo de la teoría cuántica ya no se precisa más que éste sea el caso. De acuerdo con algunas interpretaciones de la teoría cuántica, no podemos vincular las observaciones individuales a causas específicas y, de hecho, ésta es una de las razones por las que una descripción cuántica de la totalidad del universo puede aportar en principio una descripción de la creación del universo material sin necesidad de apelar a alguna causa inicial directa.
Cuando discutimos las características del universo estacionario que habría que especificar para complementar lo que nos dicen las leyes de la naturaleza, mencionamos la velocidad de expansión, pero no la forma del universo. Una de las características insólitas del modelo del estado estacionario era que permanecía estable frente a cualquier influencia que pudiera apartarle de poseer la misma velocidad de expansión en todas las direcciones del firmamento. Si tuviera lugar repentinamente un suceso violento en algún lugar del universo, o la Divinidad interviniese transitoriamente en un momento dado para hacer que se expandiera más rápidamente en una dirección que en otra, con el paso del tiempo estas desviaciones del estado requerido por el principio cosmológico perfecto desaparecerían y la expansión sería restablecida a un estado perfectamente simétrico. Una propiedad de este tipo es una característica muy atractiva para cualquier modelo cosmológico, porque se ha observado que nuestro universo se expande a la misma velocidad en cualquier dirección salvo error del uno por diez mil. La búsqueda más amplia en pos de una explicación natural a este hecho sorprendente nos lleva al segundo de los tres planteamientos generales que se han hecho para abordar el entendimiento de las condiciones iniciales del universo.
Es evidente que el rasgo más embarazoso en torno a la influencia de las condiciones iniciales en cosmología es el hecho de que representan el aspecto más incierto de nuestro conocimiento. Podría bien suceder que nunca podamos conocer cómo (y si) comenzó el universo. En consecuencia, siempre ha existido un lobby de opinión cosmológica que ha considerado oportuno buscar una explicación de la estructura actual del universo que delegue un mínimo de responsabilidades sobre la misma en condiciones iniciales inaccesibles a nuestro conocimiento. Pero ¿cómo podría lograrse esto?
Hay muchos sistemas físicos que pierden rápidamente la memoria de sus condiciones iniciales. Con esto queremos decir que sus estados futuros serán a un alto grado de precisión muy parecidos con independencia de cuál fue su punto de partida. Removed con fuerza una marmita grande de melaza y ésta recuperará rápidamente el mismo estado de reposo sin importar cómo la removisteis. Dejad caer una piedra en el vacío desde una altura suficientemente grande y tocará el suelo esencialmente a la misma velocidad con independencia de la fuerza con la que en un principio la lanzasteis, porque los efectos contrarios de la gravedad acelerando la piedra y de la resistencia del aire frenándola siempre actúan creando en todo momento una situación en la que tienen un efecto igual y opuesto, de manera que la piedra no siente ninguna fuerza neta y cae en consecuencia a velocidad constante. El universo podría comportarse de una manera similar. Los cosmólogos dedicaron la mayor parte de la década de 1970 a buscar procesos físicos naturales que pudieron haber emergido durante los primeros estadios del universo, forzando de manera inevitable su estado actual con independencia de los pormenores de cómo empezó. Confiaban, en particular, en poder explicar por qué el universo visible posee la notable propiedad de expandirse en todas las direcciones a la misma velocidad salvo error del uno por diez mil. Si se pudiera probar que, por muy dispares que hubieran podido ser las velocidades de expansión en las diferentes direcciones en el principio del universo, si esperásemos un tiempo suficientemente largo (y la vida necesita de un tiempo largo para evolucionar) encontraríamos siempre velocidades de expansión casi idénticas en direcciones diferentes, pues siempre surgen procesos físicos para transportar energía de un lugar a otro y barrer las disparidades en la energía de expansión entre unas direcciones y otras.
Esto parece un escenario atractivo. Desgraciadamente, las primeras tentativas de ponerlo en práctica fracasaron en su mayoría. El problema principal es que la desaparición de irregularidades es uno de esos procesos que se encuentran gobernados por la segunda ley de la termodinámica. La irregularidad en la expansión sólo puede reducirse si dicha disminución parcial del desorden (o «entropía», tal y como se denomina) se compensa con una producción aún mayor de entropía en otra forma. En la práctica, esta energía compensadora aparece en la forma de radiación térmica. Así, si construimos una silla con algunos trozos de madera desordenados, no violamos la segunda ley, porque ponemos en ello un gran esfuerzo físico y mental que se manifiesta mediante la producción de calor y sonido por nuestros cuerpos. Sin embargo, encontramos que el universo no contiene mucha radiación térmica en la actualidad por lo que la desaparición de irregularidades en el pasado debió de ser escasa. Es más, aun cuando se produjera dicha desaparición, existe una clase enorme de modelos cosmológicos en los que las irregularidades no podrían haber desaparecido completamente en el momento actual. Los efectos de la desaparición no son lo bastante fuertes como para contrarrestar la tendencia hacia una deformación cada vez mayor que encontramos latente en las condiciones de partida de algunos universos posibles.
A consecuencia de estos descubrimientos negativos, los cosmólogos se vieron algo desencantados hacia finales de la década de 1970 con este modo de explicar la regularidad a gran escala del universo. Pero entonces surgió una nueva idea. Alan Guth indicó que si la velocidad de expansión del universo hubiera alcanzado grandes valores durante un breve lapso de tiempo en sus primeros estadios, entonces la estructura actual del universo podría ser explicada haciendo sólo una referencia mínima a las condiciones iniciales, y sin tener que preocuparse por producir un calor excesivo.
El universo inflacionario es una receta para hacer justamente esto. Se basa en la expectativa de que existen ciertos tipos de materia en el reino de las partículas elementales que se comportan, en realidad, como si ejercieran repulsión en lugar de atracción gravitatoria. Esto es posible porque poseen una presión, o tensión, negativa, y en la teoría de la relatividad todas las formas de energía —y la presión es una de ellas— sienten la fuerza de la gravedad ya que todas ellas son equivalentes a una masa (por la famosa fórmula de Einstein E = mc2 que relaciona la energía E con la masa m y con la velocidad de la luz c). Si dicha tensión pudiera aparecer durante los primeros instantes de la expansión del universo, la gravedad dejaría entonces de tirar de la materia hacia atrás y de frenar la expansión del universo. En lugar de ello, actuaría para acelerar la expansión. El período de aceleración es lo que se denomina inflación del universo. Ésta provoca en un principio todo tipo de influencias distorsionantes para disminuir a continuación a gran velocidad, de manera que el universo adopta rápidamente un estado de expansión altamente simétrico capaz de explicar el estado residual, en extremo regular, que todavía observamos hoy en día. Aunque el período de inflación hubiera durado sólo un lapso de tiempo muy breve, habría sido suficiente para reducir todas las irregularidades que pudieron haber existido al inicio a un nivel infinitamente pequeño. Limpia la pista de patinaje. Así, Guth dice poder explicar la expansión regular que observamos actualmente con independencia de las condiciones iniciales. Esto no es, de hecho, del todo cierto. Siempre se pueden elegir perversamente ciertas condiciones iniciales que no serán suficientemente mitigadas por un período de inflación preespecificado, pero, a la inversa, si las condiciones iniciales se eligen en primer lugar, siempre existirá una cantidad de inflación que será suficiente para ello. Se parece al problema de la gallina y el huevo. Si puedes elegir el período de inflación después de haber elegido las condiciones iniciales, podrás siempre explicar lo que ves; pero si se fija primero el período de inflación mediante las leyes y constantes de la naturaleza, siempre existirán condiciones iniciales cuya influencia no puede ser eliminada en el presente. La respuesta a la cuestión, «¿qué debería elegirse primero?», depende en un sentido profundo de la concepción que uno tenga de las condiciones iniciales y de su relación con las leyes de la naturaleza. Si adoptamos el punto de vista clásico tradicional, según el cual las condiciones iniciales son independientes de las leyes de la física, entonces, en ausencia de otra información que diga lo contrario, deberíamos considerar que las condiciones iniciales del universo han de especificarse libremente, pero entonces ocuparían un lugar secundario en relación a las leyes y constantes de la física. Nosotros podemos imaginar sin ningún problema condiciones iniciales diferentes, y estamos acostumbrados a especificarlas a conveniencia siempre que utilizamos las leyes de la física en el laboratorio, pero alterar una ley de la física o el valor de una constante fundamental es algo mucho más drástico. Por consiguiente, parece más razonable considerar que las constantes y las leyes de la física y, en consecuencia, la duración de cualquier período de inflación, han sido determinadas antes de la especificación de las condiciones iniciales. Con esta elección, la inflación nunca puede darnos el universo observado con independencia de las condiciones iniciales. Podría todavía suceder que los estados iniciales condenados al fracaso fueran en algún sentido los «poco probables», pero la cuestión de qué es lo que distingue un estado inicial probable de uno improbable todavía sigue abierta.
En la imagen tradicional del big bang, del universo en expansión, la semejanza relativa del universo observado desde cualquier lugar es algo misterioso. Para entender este misterio debemos primero distinguir entre el universo entero, que podría tener una extensión infinita, y el «universo visible», esto es, aquella parte del universo que la luz ha tenido tiempo de recorrer desde que la expansión comenzó. Podemos imaginarnos el universo visible como una esfera de radio aproximadamente igual a quince mil millones de años luz centrada en nosotros. Quince mil millones de años luz es la distancia que la luz puede haber recorrido en los quince mil millones de años que utilizaremos como una buena estimación del tiempo transcurrido desde que la expansión comenzó aparentemente. (Es una media razonable de los diferentes retazos de evidencia observacional que indican una variación de edad de entre trece y dieciocho mil millones para la expansión universal). No sabemos nada sobre el universo que no provenga de lo que observamos en la porción finita visible del mismo. Por ejemplo, ninguna observación del universo visible nos podrá decir nunca si el universo entero es finito o infinito.
Es nuestro universo visible el que muestra una notable uniformidad a gran escala. Ahora bien, si extrapolamos esta región visible hacia atrás en el tiempo, podemos determinar cuánto más pequeño hubo de ser en épocas anteriores de la historia del universo. Por ejemplo, cuando el universo tenía un segundo de edad, nuestro actual universo visible habría estado comprimido en una región de un tamaño de sólo un año y medio de luz. Y cuando el universo tenía 10−35 segundos de edad, habría estado metido en una región de unos pocos centímetros de diámetro. Esto parece exageradamente pequeño, pero para el cosmólogo es excesivamente grande. Es 3 × 1025 veces mayor que el tamaño de las regiones cuyo contenido se hallaba en contacto causal en aquellos tiempos tempranos: pues en aquel tiempo la última distancia es simplemente el producto de 10−35 segundos por la velocidad de la luz (3 × 1010 centímetros por segundo), lo cual da 3 × 10−25 centímetros. El resultado de este estado de cosas es que la región que crece hasta convertirse en el universo visible en la actualidad está compuesta de un enorme número de regiones totalmente independientes que no pueden siquiera «saber» de la existencia de las otras en tiempos muy tempranos (véase la figura 3.2).

Figura 3.2 Las señales emitidas desde dos puntos separados A y B, cuando el universo comienza a expandirse, no pueden alcanzarse una a otra hasta el tiempo D. El interior de los ángulos CAD y DBE representan las zonas del espacio y el tiempo que pueden ser contactadas por señales que emanan de A y B, respectivamente. Esta restricción en la comunicación se da porque las señales no pueden viajar a una velocidad mayor que la de la luz; esto significa que la comunicación se encuentra confinada al interior de los ángulos. Obsérvese que A no puede predecir el futuro. Las condiciones en D no están determinadas únicamente por la señal transmitida por A, sino también por la transmitida desde B.
El origen de este «problema horizontal», como se denomina, es evidente por nuestra descripción. El universo se expande demasiado lentamente al principio, de manera que esa parte del mismo que abarca en la actualidad nuestro universo visible necesita haber crecido desde una región relativamente grande en los comienzos, una región mucho más grande que cualquiera que en aquel entonces pudiera conservarse suave y regular mediante procesos físicos cuya área de influencia está limitada por la velocidad de la luz. No obstante, el período de expansión acelerada que caracteriza la evolución temprana de los modelos de universo inflacionarios permite que todo nuestro universo visible haya evolucionado desde una región mucho más pequeña en un tiempo anterior del orden de 10−35 segundos. De hecho, si la inflación duró solamente un instante efímero —desde 10−35 a 10−33 segundos—, todo nuestro universo visible puede haber emergido de una región que se encontraba al alcance de las señales de luz en estos primeros comienzos. La vasta uniformidad del universo que observamos tiene ahora una explicación plausible. Es la imagen expandida de una región minúscula que era lo suficientemente pequeña como para haber sido alisada por procesos físicos cuyo alcance se encuentra limitado por las restricciones que impone la relatividad.
En la teoría estándar del big bang, en la que no hay inflación, el universo observado no puede haber surgido de ninguna de dichas regiones coherentes, causalmente correlacionadas. Por el contrario, es la conjunción de una miríada de regiones independientes de las que se esperaría que fueran muy diferentes unas de otras y, por tanto, que resultaran en un universo visible que sería disparatadamente diferente de un lugar a otro.
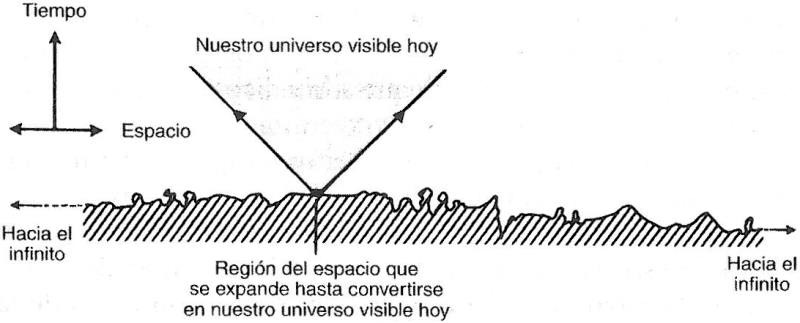
Figura 3.3 La estructura del universo visible sólo está determinada por las condiciones sobre una parte ínfima de las condiciones «iniciales» del universo. Si el universo tiene un tamaño infinito, tanto la parte visible del mismo como la parte de las condiciones iniciales que lo determinan son únicamente partes infinitesimales de la totalidad.
Esta nueva imagen de la evolución temprana del universo minimiza radicalmente el papel de las condiciones iniciales pues, aunque el universo visible entero refleja parcialmente la estructura de algunas condiciones «iniciales» que definen la estructura del universo antes del comienzo de la inflación, las condiciones iniciales particulares que realizan ese papel son sólo una parte ínfima del mapa global de condiciones iniciales para la totalidad del universo (probablemente finito) (véase la figura 3.3).
Esto es preocupante para el científico. Significa que nuestras observaciones de la estructura del universo visible pueden a lo sumo darnos información de sólo una parte ínfima de las condiciones iniciales que caracterizan los primeros instantes del universo en expansión. Nunca podremos conocer la estructura de la totalidad de las condiciones iniciales del universo mediante la ciencia observacional. Se encuentran en parte condenadas a permanecer siempre en el reino de la filosofía y la teología. También hace extraordinariamente difícil cualquier prueba de esta teoría. Aun cuando algunas variedades de condición inicial no permiten que se produzca ninguna o la suficiente inflación, siempre habrá alguna parte del universo total donde se den condiciones iniciales aceptables, y esto es todo lo que necesitamos. Como veremos en un capítulo posterior, es preciso que exploremos con algún detalle cómo nuestra propia experiencia desempeña un papel en la evaluación de dichas teorías.
La imagen de las condiciones iniciales que nos brinda la inflación es, por tanto, la de un estado original probablemente caótico o aleatorio según miramos de un lugar a otro del universo —algo así como la superficie del mar. Cada minúscula región local inflacionará, independientemente de las demás, en una cantidad determinada por sus condiciones locales. Nosotros nos encontraríamos viviendo dentro de una de estas regiones después de que se haya expandido de forma considerable. El interior de esta región debería parecer muy liso y expandirse uniformemente, pero fuera de sus fronteras hay regiones cuyos rayos de luz todavía no han tenido tiempo de llegar hasta nosotros. Y estas regiones fuera de nuestro alcance tendrán con toda probabilidad una estructura absolutamente diferente. Tenemos así una imagen que puede explicar por qué nuestra parte visible del universo es lisa aun cuando no se espere lo mismo del universo entero.
El período inflacionario de expansión no alisa las irregularidades a través de procesos generadores de entropía como los investigados por los cosmólogos de la década de 1970. Antes bien, barre la irregularidad fuera del horizonte de nuestro universo visible, donde no la podamos ver. Todo el universo de estrellas y galaxias que alcanzamos a ver no es, bajo esta hipótesis, más que el reflejo de una porción ínfima, quizás infinitesimal, de las condiciones iniciales del universo, cuya estructura y alcance fundamentales nunca podremos conocer. Una Teoría del Todo no nos es de ninguna ayuda aquí. La información contenida en la parte observable del universo deriva de la evolución de una parte ínfima de las condiciones iniciales para el universo entero. La suma total de todas las observaciones que supuestamente pudiéramos hacer sólo nos habla sobre una porción ínfima de la totalidad.
Es posible que la estricta línea divisoria que hemos trazado entre leyes y condiciones iniciales no exista; que algunas leyes solamente admitan un tipo de condiciones iniciales. Ésta es una posibilidad que exploraremos ahora algo más.
La última de nuestras opciones respecto a las condiciones iniciales del universo que queda por considerar es que existe un tipo especial de condición inicial —en realidad, una «metaley» que gobierne las condiciones iniciales. La filosofía inflacionaria prefiere considerar que las condiciones iniciales pueden especificarse libremente y que la inflación es un medio por el que podemos mostrar que su forma precisa es de poca relevancia para lo que vemos hoy en día, siempre y cuando las leyes de la física, la naturaleza de las partículas elementales y las constantes de la naturaleza permitan que se dé este fenómeno mágico de la inflación. Por el contrario, el lobby a favor de condiciones iniciales especiales busca un nexo fundamental entre la noción de ley y la de condiciones iniciales que trascienda nuestra experiencia ordinaria en física clásica. Tradicionalmente, las condiciones iniciales no están constreñidas por la forma de las leyes de cambio salvo de una manera muy débil. Si una solución de una ecuación de cambio fija asimismo las condiciones de partida de manera unívoca, significa invariablemente que la solución en cuestión es extremadamente especial y, por consiguiente, es improbable que se dé en la práctica. Así pues, para encontrar una conexión profunda entre la forma de las leyes de la naturaleza y sus condiciones de partida permitidas es preciso que tomemos en consideración una situación donde exista algún elemento probabilístico respecto a la posible forma de comportamiento evolutivo. Esto es algo que puede encontrarse en cualquier descripción cuántica de las cosas. En su mayor parte, estas tentativas de vincular las leyes a las condiciones iniciales se han centrado en la disciplina embrionaria, y en rápido crecimiento, de la cosmología cuántica. Al hacerlo así se ven enredados en otros problemas profundos, de una naturaleza fundamental, concernientes a la interpretación de la teoría cuántica, sobre la que se ha escrito mucho en otros lugares, y al problema del tiempo, mucho menos discutido.
El problema del tiempo
El pueblo inglés no es muy espiritual. Por ello inventaron el criquet, para que les diera alguna idea de eternidad.
GEORGE BERNARD SHAW
Existe un viejo rompecabezas filosófico respecto a la naturaleza del tiempo que ha aflorado en las obras de diferentes pensadores a lo largo de milenios. Se reduce a la cuestión de saber si el tiempo es un telón de fondo absoluto sobre el que se representan los sucesos, pero sin verse perturbado por ellos, o si es un concepto secundario que puede derivarse en su totalidad de los procesos físicos y, por tanto, verse afectado por ellos. Si adoptásemos la primera imagen, podríamos hablar sobre la creación del universo físico de materia en el tiempo. Tendría pleno sentido discutir sobre lo que ocurrió antes de la creación del universo material y sobre lo que pasará después de que haya terminado. Aquí el tiempo es una parte trascendente de la realidad sin un comienzo o un final concebibles. Esta idea se presta fácilmente a una interpretación platónica según la cual existen ciertas verdades o improntas eternas de las que las realidades temporales derivan sus cualidades. De hecho, el tiempo asume muchas de las cualidades tradicionalmente asociadas con una deidad. La alternativa, una idea que aflora en las obras de Aristóteles y de los primeros filósofos de la naturaleza islámicos, antes de ser recogida de manera memorable por san Agustín y Filón de Alejandría, es que el tiempo es algo que nace con el universo. Antes de que el universo fuera, no había tiempo, no había ningún concepto del «antes». Semejante artificio permitió a los escolásticos medievales soslayar difíciles adivinanzas sobre lo que tuvo lugar antes de la creación del mundo y lo que la deidad estaba haciendo en ese período. En esencia, el tiempo se ve como un fenómeno derivado, ligado inextricablemente a los contenidos del universo. El comienzo del tiempo es el instante en el que las constantes y las leyes de la naturaleza han de aparecer, ya formadas y dispuestas a actuar. San Agustín escribe en La ciudad de Dios:
Así pues, el mundo fue hecho con toda seguridad, no en el tiempo, sino simultáneamente con el tiempo. Pues lo que es hecho en el tiempo es hecho tanto después como antes de algún tiempo —después de lo que es pasado y antes de lo que es futuro. Pero no había nada que pudiera ser pasado en aquel entonces, pues no había criatura alguna cuyos movimientos pudieran servir para medir su duración. Así pues, el mundo se hizo simultáneamente con el tiempo.
Esto se aproxima a nuestra experiencia común del tiempo. Medimos el tiempo por medio de relojes que están hechos de materia y que obedecen las leyes de la naturaleza. Explotamos la existencia de movimientos periódicos, ya sean las revoluciones de la Tierra, las oscilaciones de un péndulo o las vibraciones de un cristal de cesio, de manera que los tics de estos relojes definen el paso del tiempo para nosotros. No contamos con un significado cotidiano que dar a la noción de tiempo aparte del proceso por el que se mide. Podríamos, pues, defender un punto de vista operacionalista en el que el tiempo está definido sólo por la forma en que se mide.
Mientras que un enfoque trascendental del tiempo nos permitiría hablar de cuerpos que se mueven en el tiempo, el enfoque anterior hace hincapié en la definición del tiempo por el movimiento de las cosas. Una de las ventajas del primer punto de vista es que uno sabe cuál es el lugar que ocupa y cómo va a verse el tiempo en todo momento: es el mismo ayer, hoy y siempre. Por el contrario, la segunda imagen promete producir nuevos conceptos de tiempo y puede que acabe incluso con el concepto mismo a medida que se altera la naturaleza del contenido material del universo bajo condiciones variables. Deberíamos tener especialmente presente dicha posibilidad cuando nos retrotraemos a esos instantes extremis en la vecindad del big bang. Pues cualquier instante que parezca ser el comienzo del tiempo existe inevitablemente ahí donde la misma noción de tiempo es probablemente más frágil. En un universo en expansión y en constante cambio, es probable que de la concepción operacionalista del tiempo se siga una idea sutil y variable del lugar que ocupa y del significado del tiempo.
Espacio y tiempo absolutos
Yo no defino el tiempo, el espacio, el lugar y el movimiento como algo por todos conocido. Únicamente debo señalar que la gente común no concibe estas magnitudes más que bajo la relación que presentan con los objetos sensibles. Y así surgen ciertos prejuicios…
ISAAC NEWTON
La imagen de un tiempo trascendental absoluto ensombreciendo la marcha de los acontecimientos sobre una tabla de billar cósmica de espacio infinito e invariable fue el fundamento de la monumental descripción del mundo por Newton. Una vez que se han dado las ecuaciones que gobiernan el cambio del mundo en el espacio y el tiempo, el curso futuro de los sucesos queda completamente determinado por las condiciones de partida[4]. El tiempo parece superfluo. Todo lo que ha de suceder está programado en el estado inicial.
Las leyes newtonianas del movimiento podrían ser aplicadas a la descripción del mundo y su curso seguirse hacia atrás en el tiempo. Observamos que nuestro universo se expande, por lo que una descripción newtoniana conduce a la afirmación de que debe haber existido un instante de tiempo pasado en el que todo estaba comprimido a un tamaño nulo y a una densidad infinita, el big bang, tal y como fue llamado por vez primera por Fred Hoyle. Sin embargo, dada la naturaleza absoluta del espacio y del tiempo en la imagen newtoniana del mundo, no podemos extraer ninguna conclusión sobre el big bang newtoniano como constitutivo de un origen en el tiempo, y menos aún de un origen del universo. Es simplemente un tiempo pasado en el que las leyes conocidas predicen que algunas cantidades físicas alcanzaron valores ilimitadamente grandes; decimos que se hicieron infinitas allí. Pero el espacio y el tiempo continúan con independencia de ello.
Los primeros en prestar atención a la relevancia de aquellos lugares donde las cosas cesan aparentemente de existir o se hacen infinitamente grandes («singularidades», como ahora las llamaríamos) en la teoría de Newton fueron los científicos del siglo XVIII, Leonhard Euler y Roger Boscovich. Ambos consideraron las implicaciones físicas de adoptar leyes de fuerza para la gravitación distintas de la famosa ley de Newton del inverso del cuadrado. Encontraron que algunas de las alternativas presentaban la incómoda característica de que las soluciones dejan sencillamente de existir después de un tiempo determinado en el futuro cuando se estudiaba el comportamiento de objetos en órbita en torno a un sol central. No pueden ser prolongadas más allá en un mundo gobernado por una de estas leyes de fuerza alternativas. Boscovich considera absurdo que un cuerpo deba desaparecer en el centro del universo si la ley de fuerzas fuera del inverso del cubo en lugar del inverso del cuadrado, y llama la atención sobre el estudio anterior de Euler en torno al movimiento bajo la influencia de la gravedad, donde el maestro de los matemáticos «asegura que el cuerpo en movimiento es aniquilado al aproximarse al centro de fuerzas. ¿No será más razonable inferir que esta ley de fuerzas es imposible?». Estas parecen ser las primeras consideraciones sobre dichas cuestiones en el contexto de la mecánica newtoniana.
De hecho, al intentar aplicar la teoría de la gravedad y del movimiento de Newton al universo como un todo surgen graves problemas. Esta teoría no tolerará la consideración de un espacio infinito en el que se distribuye la materia: esto conduce a un agregado infinito de influencias gravitatorias en cualquier punto, debido al número infinito de atracciones gravitatorias ejercidas por los demás. Por lo tanto, un universo newtoniano debe tener un tamaño finito y poseer en consecuencia un límite espacial. Si nos imaginamos el universo newtoniano estirado hacia fuera en cada dirección, este límite debe ser un borde definido. Por ejemplo, si el espacio es esférico en torno a nosotros, situados en el centro, la superficie del espacio es la superficie de la esfera. Por otro lado, el universo espacial podría ser un cubo cuyo límite estuviera compuesto por las seis caras del cubo. La perspectiva de un universo con límites es una imagen muy poco atractiva porque debemos especificar cuál es el comportamiento de todas las cantidades físicas en estos límites cuando el universo arranca de algún instante del pasado. Así, el mundo newtoniano requiere que el universo material sea una isla finita de materia en un océano de espacio absoluto infinito.
Peor aún, la teoría de Newton es incompleta. No contiene suficientes ecuaciones para decirnos cómo suceden de hecho todos los cambios permitidos al universo. Si el universo se expande o contrae exactamente a la misma velocidad en todas las direcciones, todas las cosas estarán efectivamente determinadas; pero cuando se permite cualquier desviación de la expansión esférica perfecta en el comienzo, el determinismo se quiebra, al no existir leyes newtonianas que dictaminen cómo cambiará en el tiempo la forma del mundo. Obviamente, la teoría de Newton del espacio y el tiempo absolutos es defectuosa. El siguiente paso a dar es considerar algún acoplamiento de las nociones de espacio y tiempo con el contenido material del mundo.
La especulación más temprana y más curiosa a este respecto fue hecha por William Clifford, un matemático inglés que consideró justamente el tipo de situación que Einstein construiría en la teoría general de la relatividad. Clifford se vio estimulado por las investigaciones matemáticas de Riemann, quien había formalizado el estudio geométrico de las superficies y los espacios curvos que poseen de una geometría no euclidiana (esto es, los tres ángulos interiores de un triángulo, cuyos vértices quedan determinados al trazar sobre la superficie curva las líneas más cortas que los unen formando sus lados, no suman ya 180 grados). Clifford tuvo en cuenta que el espacio tradicional de Euclides es, pues, uno de muchos, y que no podemos presuponer por más tiempo que la geometría del mundo real posee la simple forma euclidiana. El hecho de que parezca localmente plano no es convincente, porque la mayoría de las superficies curvas parecen planas cuando se consideran pequeñas áreas sobre ellas. Después de estudiar las ideas de Riemann, Clifford propuso la siguiente hipótesis radical en su artículo de 1876:
Quiero indicar aquí una de las formas en la que estas especulaciones pueden ser aplicadas a la investigación de los fenómenos físicos. Mantengo, de hecho:
1. Que las porciones pequeñas de espacio son efectivamente de una naturaleza análoga a la de pequeñas colinas sobre una superficie que es plana en promedio; es decir, que las leyes ordinarias de la geometría no tienen validez en ellas.
2. Que la propiedad de ser curvas o de estar deformadas se transfiere continuamente de una porción a otra del espacio al modo de una ola.
3. Que la variación de la curvatura del espacio es lo que realmente sucede en ese fenómeno que llamamos el movimiento de la materia, ya sea ponderable o etérea.
4. Que en el mundo físico únicamente se da esta variación, sujeta (probablemente) a la ley de continuidad.
Esta presciencia es muy notable. Aunque no parece que Einstein tuviera noticia de estas observaciones, la idea intuitiva de Clifford se convirtió en la idea central de la teoría general de la relatividad. La geometría del espacio y la razón del paso del tiempo ya no se encuentran absolutamente fijos ni son independientes del contenido material del espacio y tiempo. El contenido de materia y su movimiento determinan tanto la geometría como la razón del paso del tiempo y, simbióticamente, esta geometría dictamina cómo ha de moverse la materia. La elegante teoría de la gravitación formulada por Einstein posee un conjunto de ecuaciones que determinan el nexo entre el contenido de materia del universo y su geometría espacio-temporal. Estas se denominan ecuaciones de campo y son una generalización de la ecuación de campo newtoniana de Poisson, la cual comprende la ley de la gravitación del inverso del cuadrado de Newton. Además de esta estructura existen ecuaciones de movimiento que definen el equivalente de línea recta en la geometría curva. Estas generalizan las leyes del movimiento de Newton.
El estatus absoluto del tiempo newtoniano se ve erosionado aún más en la teoría de Einstein. Ésta se construyó sobre la premisa de que en el universo no hay observadores privilegiados, esto es, que no existe un conjunto de observadores para quienes las leyes de la naturaleza parezcan más simples. Las leyes de la física deben tener la misma forma para todos los observadores sin importar cuál sea su estado de movimiento. En otras palabras, cualquiera que sea el movimiento de tu laboratorio —ya sea de aceleración o de rotación respecto al de tu vecino—, las leyes de la física halladas como válidas deberían ser las mismas para ambos. Puede que cada uno midáis diferentes valores de los observables, pero éstos se hallarán ligados a las mismas relaciones invariantes.
En el universo de Einstein no hay una clase especial de observadores para quienes las leyes de la naturaleza parezcan particularmente simples en virtud de su movimiento y de disposiciones sobre la medida del tiempo. Esto no es cierto en la formulación del movimiento por Newton. Sus famosas leyes del movimiento son válidas únicamente para experimentadores ubicados en laboratorios que se mueven de manera uniforme y sin rotación unos respecto a otros y en relación a las estrellas más distantes, que Newton eligió para fijar un estado de reposo absoluto. Para aquellos otros observadores que rotan o aceleran en formas inusuales, las leyes del movimiento tendrán una forma diferente, más complicada. En particular, y en contra de la famosa primera ley del movimiento enunciada por Newton, estos observadores verán acelerarse cuerpos sobre los que no actúa ninguna fuerza.
Esta democracia de observadores que Einstein incorporó a la formulación de su teoría general de la relatividad significa que no hay un tiempo cósmico privilegiado. Mientras que en su teoría especial de la relatividad no podía existir un estándar absoluto del tiempo —todas las medidas de tiempo se efectúan en relación al estado de movimiento del observador—, en la teoría general de la relatividad las cosas son diferentes. En la relatividad general hay muchos tiempos absolutos. De hecho, parece haber un número infinito de candidatos posibles. Por ejemplo, los observadores en torno al universo podrían utilizar la densidad media local o la velocidad de expansión del universo para coordinar sus medidas del tiempo. Desafortunadamente, todavía no se ha hallado que alguno de estos tiempos absolutos posea un estatus más fundamental que los otros.
Una buena forma de concebir un universo entero de espacio y tiempo (un «espacio-tiempo») en la teoría de Einstein es como una pila de espacios (imaginad que sólo hay dos dimensiones espaciales en lugar de tres para poderlo visualizar), de manera que cada lámina en la pila representa el universo espacial total en tiempos diferentes. El tiempo es una etiqueta con la que identificamos cada lámina de la pila. La exposición del párrafo anterior significa que en realidad podemos cortar de muchas maneras diferentes todo el bloque espacio-tiempo en una pila de «láminas temporales». Podríamos seccionar de parte a parte la pila sólida bajo diversos ángulos diferentes. Ésta es la razón por la que siempre es más apropiado hablar del espacio-tiempo antes que de la pareja algo ambigua de espacio y tiempo. No obstante, el nexo entre la materia y la geometría espacio-temporal significa que el «tiempo» puede ser definido internamente por alguna propiedad geométrica, como la curvatura, de cada lámina y, por tanto, en términos del campo gravitatorio de la materia en la lámina que ha distorsionado su planaridad (la figura 3.4 muestra una sencilla ilustración). Así pues, comenzamos a ver el resquicio de una posibilidad de asociar el tiempo, incluyendo su principio y su fin, con alguna propiedad del contenido del universo y las leyes que gobiernan su cambio.
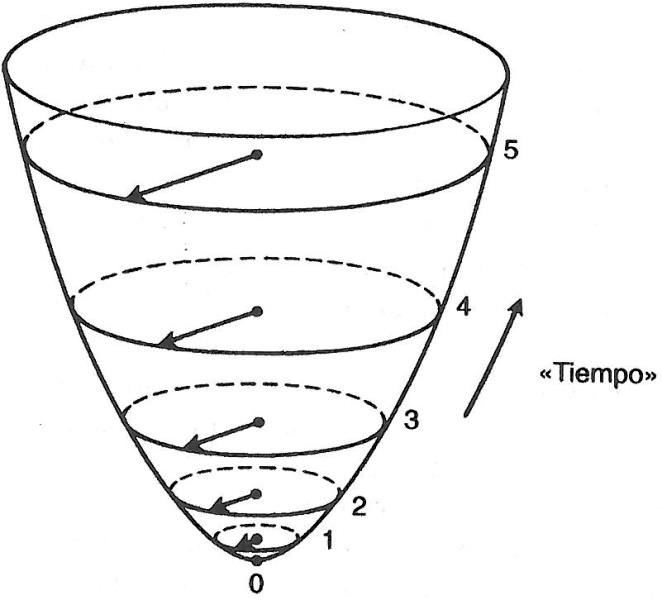
Figura 3.4 A cada una de las láminas 1, 2, 3, 4 y 5 tomadas a través del espacio puede asignársele una etiqueta de «tiempo», que es calibrado por el radio de la circunferencia (señalado por las flechas). Cuando avanzamos hacia arriba sobre la superficie curva, el aumento del tiempo se calibra por el aumento de los radios de las circunferencias que limitan las láminas.
La nueva imagen del espacio-tiempo, en lugar de espacio y tiempo, cambia considerablemente nuestra actitud hacia las condiciones iniciales y el comienzo probable del universo. Debido al acoplamiento que existe entre la estructura del espacio-tiempo y la materia, cualquier singularidad en el contenido material del espacio-tiempo (por ejemplo, el infinito en la densidad de materia que aparece en la imagen tradicional del big bang) indica que el espacio-tiempo ha llegado también a un final. Ahora tenemos singularidades de espacio y tiempo, no meramente singularidades en el espacio y el tiempo. Más aún, cualquier espacio-tiempo dado por la teoría general de la relatividad de Einstein es un universo entero. A diferencia de lo que sucede en la teoría de Newton, una singularidad no puede nunca describir meramente un objeto situado en un lugar externo del espacio fijo. Por lo tanto, las singularidades de la relatividad general son características del universo entero, y no de un lugar en él o de un instante de su historia. Estas singularidades señalan los límites del espacio y el tiempo.
Si estudiamos el universo en expansión de acuerdo con esta imagen y trazamos su historia hacia atrás, entonces es posible que haya comenzado en una singularidad de dicho tipo. Esta predicción ha sido utilizada por muchos como prueba de que el universo tiene un comienzo en el tiempo. Sin embargo, como toda deducción lógica, esta conclusión se sigue de ciertas suposiciones, cuya veracidad necesita ser examinada de cerca.
La más dudosa de estas suposiciones es aquella que dice que la gravedad es siempre atractiva. Nuestras teorías modernas de partículas elementales contienen muchos tipos de partículas, y formas de materia, para las que esta suposición no es cierta. De hecho, la concepción del universo inflacionario que introdujimos más arriba descansa toda ella sobre el requisito de que no sea cierta, pues sólo así puede surgir el breve período de expansión «inflacionaria» acelerada. No obstante, aunque el evitar una singularidad podría obviar un comienzo del tiempo, no nos libraría de tener que prescribir condiciones «iniciales» en algún momento pasado, para poder seleccionar nuestro universo actual entre la infinidad de otros mundos posibles que comienzan en singularidades. Incluso en el caso de haber existido una singularidad, uno debe hacerse cargo del hecho de que existen diferentes tipos de singularidad. La especificación de las propiedades de esta singularidad es una condición «inicial» a especificar en la frontera de nuestro espacio y tiempo. Pero todavía necesitamos hallar algún ingrediente extra que pueda darnos esa especificación.
¿Cuán lejos es suficientemente lejos?
Había una Puerta para la que no encontré ninguna llave.
Había un Velo a través del cual no pude ver.
Rubaiyat de OMAR KHAYYAM
La relatividad general (y cualquier otra teoría relativista de la gravedad que no posea un espacio o un tiempo fijos de manera absoluta) provoca otra propiedad sutil que no se encuentra presente en las simples concepciones newtonianas del espacio y el tiempo. Hay en realidad muchos espacio-tiempos distintos que pueden surgir de las mismas condiciones iniciales.
Supongamos que un espacio-tiempo S tiene unas condiciones iniciales establecidas en algún tiempo inicial cero, que designaremos t0. Podemos entonces construir otro espacio-tiempo eliminando toda la parte del primer espacio-tiempo situada en el futuro de algún tiempo t1 (posterior a t0), así como el propio tiempo t1. El nuevo espacio-tiempo S’ coincide con S en el pasado del instante t1 pero no contiene espacio o tiempo alguno en el futuro de t1, tal y como se ilustra en la figura 3.5. Pero tanto S como S’ surgen del mismo estado inicial; de hecho, podríamos haber cortado trozos de S de una infinidad de maneras diferentes para crear otros espacio-tiempos que parten de las mismas condiciones iniciales. No obstante, hay algo sospechoso en torno a S’ y sus universos compañeros truncados, a saber, que llega a su fin en el tiempo asignado t1 sin razón física aparente. No existe ninguna singularidad de ninguna cantidad física. De hecho, no hemos tenido que hacer mención alguna del contenido material del universo, y las ecuaciones que gobiernan el comportamiento de la materia alcanzarían todavía a predecir el futuro más allá de t1 sólo con que se permitiera la existencia de dicho futuro.

Figura 3.5 Dos espacio-tiempos S y S’ determinados por conjuntos idénticos de condiciones iniciales, prescritas sobre la superficie del tiempo inicial t0. En el caso (a), el espacio-tiempo S está máximamente extendido, mientras en (b) se le supone un final arbitrario en un tiempo futuro t1, pero sin surgir en él ningún infinito físico u otro defecto en la estructura del espacio-tiempo; el espacio-tiempo S’ es, por consiguiente, idéntico a S hasta el tiempo t1, pero no existe en el futuro de dicho momento. En la práctica se supone siempre que un conjunto dado de condiciones iniciales conduce a un espacio-tiempo máximamente extendido, y no a una de las infinitas alternativas artificiales que son idénticas hasta algún momento finito, tras el cual dejan de existir sin razón física aparente.
Este truncamiento arbitrario del futuro se considera irrazonablemente artificial, y los cosmólogos prefieren obviar su posibilidad y especificar la evolución futura de manera unívoca. Para hacer esto es necesario introducir una condición más en la prescripción de espacio-tiempos, o universos, posibles en teorías como la relatividad general, además de la especificación de condiciones iniciales y leyes de la naturaleza. Uno exige que el universo continúe existiendo hasta que las leyes de la naturaleza que rigen el comportamiento de la masa y la energía indiquen que el tiempo mismo ha llegado a su fin en una singularidad física real. En condiciones razonables, sucede que hay un único espacio-tiempo «máximo» capaz de abarcar a todos los otros espacio-tiempos que parten de las mismas condiciones iniciales, y que se obtiene dejando avanzar el tiempo hasta que las ecuaciones predicen una singularidad. Este universo máximamente extendido es el candidato natural a ocupar el puesto del espacio-tiempo que surge efectivamente de un conjunto particular de condiciones iniciales, aunque no deberíamos olvidar que, en principio, cualquiera de las otras realidades truncadas podría ser la que existe según las condiciones iniciales de nuestro universo. Si el universo máximamente extendido no es el existente, el final del universo de espacio y tiempo podría, de hecho, llegar en cualquier momento, «cual ladrón en la noche», sin ningún aviso o causa observable.
A pesar de todas estas sutilezas respecto a la naturaleza del tiempo, la relatividad general no ha conseguido acabar con la división tradicional entre leyes y condiciones iniciales. Aún existe una lámina inicial de nuestra pila de espacio-tiempos que determina en todo momento cómo se verán las demás en el futuro.
El misterio cuántico del tiempo
Era un libro para matar el tiempo destinado a aquellos que lo preferían muerto.
ROSE MACAULEY
El estatus del tiempo en la teoría cuántica es un misterio aún mayor de lo que les pareció a Newton y a Einstein. Si existe en una forma trascendente, no es una de esas cantidades sometidas al famoso principio de incertidumbre de Heisenberg; pero si se define operacionalmente, mediante otros aspectos intrínsecos de un sistema físico, se ve entonces afectado indirectamente por las restricciones impuestas por la incertidumbre cuántica. En consecuencia, cuando uno intenta fabricar una descripción cuántica del universo entero, puede anticipar algunas consecuencias insólitas para el tiempo. La más insólita ha sido la afirmación de que una cosmología cuántica nos permite interpretarlo como una descripción de un universo que ha sido creado a partir de la nada.
Los modelos cosmológicos no cuánticos de la relatividad general pueden comenzar en un instante pasado particular de tiempo, que se define utilizando ciertos tipos de relojes. Las condiciones iniciales, que determinan todo el comportamiento futuro de ese universo, deben ser establecidas en esa singularidad. Pero en la cosmología cuántica, la noción de tiempo no aparece explícitamente. El tiempo es un constructo de los campos de materia y sus configuraciones. Como tenemos ecuaciones que nos dicen algo sobre cómo cambian esas configuraciones según miramos de una lámina de espacio a otra, sería superfluo disponer también de un «tiempo». Esto no es del todo diferente a la forma en que un reloj de péndulo te da el tiempo. Las manecillas del reloj guardan sólo un registro del número de oscilaciones que realiza el péndulo. No hay necesidad de apelar a nada que se llame «tiempo». Asimismo, en el marco cosmológico, estamos etiquetando las láminas de nuestra pila de «espacio-tiempo» según la configuración de materia que crea la geometría intrínseca de cada lámina. Esta información sobre la geometría y la configuración material sólo nos es accesible probabilísticamente en la teoría cuántica, y se encuentra codificada en algo que ha pasado a conocerse como la función de onda del universo, y que nosotros designaremos en consecuencia por W.
La generalización de las ecuaciones de Einstein con vistas a incluir la teoría cuántica es uno de los grandes problemas de la física moderna. Una de las vías propuestas utiliza una ecuación que fue hallada primero por los físicos norteamericanos John A. Wheeler y Bryce De Witt. La ecuación de Wheeler-De Witt describe la evolución de W. Es una adaptación de la famosa ecuación de Schrödinger que rige a la función de onda de la mecánica cuántica ordinaria, si bien incorpora los atributos del espacio curvo de la relatividad general. Si conociéramos la forma actual de W, ésta nos diría cuál es la probabilidad de que el universo observado poseyera ciertas características a gran escala. Se espera que estas probabilidades se encuentren estrechamente concentradas en torno a valores particulares, de manera análoga a como las cosas grandes cotidianas tienen propiedades definidas, a pesar de las incertidumbres macroscópicas de la mecánica cuántica. Si los valores más favorecidos fueran similares a los valores observados, esto explicaría esas características como una consecuencia del hecho de que nuestro universo era uno de los más «probables» entre todos los universos posibles. Sin embargo, para hacer esto se requieren todavía algunas condiciones iniciales para la ecuación de Wheeler-De Witt —una forma inicial para la función de onda del universo.
La cantidad más útil implicada en la manipulación y estudio de W es la función de transición T[x1, t1; x2, t2]. Ésta da la probabilidad de encontrar el universo en un estado etiquetado por x2 en un tiempo t2, si estaba en un estado x1 en un tiempo anterior t1 donde los «tiempos» pueden ser prescritos por algún otro atributo del estado del universo, por ejemplo su densidad media (véase la figura 3.6).

Figura 3.6 Algunos caminos para espacio-tiempos, cuyos contornos están formados por dos espacios tridimensionales con curvaturas g1 y g2, en los que los campos de materia están en las configuraciones m1 y m2, respectivamente.
Por supuesto, en la física no cuántica, las leyes de la naturaleza predicen que un determinado estado futuro se seguirá de un estado pasado particular, de manera que no necesitaríamos utilizar semejantes nociones probabilísticas. Pero en la física cuántica un estado futuro está determinado sólo como una suma, con los pesos debidos, sobre todos los caminos lógicamente posibles a través del espacio y del tiempo que el sistema pudiera haber seguido. Uno de estos caminos ha de ser el único que una descripción no cuántica seguiría. Le llamamos el camino clásico. En aquellos casos en los que se tiene una situación determinista convencional, la descripción cuántica correspondiente posee una función de transición que está determinada principalmente por el camino clásico, dejando que los otros se combinen de forma tal que se cancelen unos a otros, algo así como los picos y los valles de ondas que se encuentran fuera de fase. De hecho, es una cuestión profunda saber si todas las posibles condiciones de partida permitidas en un universo cuántico pueden dar lugar a un universo «clásico» cuando se expanden a un tamaño mayor. Esto puede que resulte ser un requisito muy restrictivo, uno necesario también para la existencia de observadores vivos, que distingue a nuestro universo como algo extraordinario en el conjunto de todas las posibilidades. Si esto es cierto, entonces tendría también la interesante consecuencia de que sólo mediante un estudio de sus implicaciones cosmológicas podría lograrse una valoración completa de la mecánica cuántica.
En la práctica, W depende de la configuración material en el universo en una lámina particular de la pila de espacios y de alguna propiedad geométrica interna de la lámina (como su curvatura), que entonces etiqueta efectivamente su «tiempo» de manera unívoca. Una vez más, no hay una elección especial de una magnitud geométrica que prevalezca sobre todas las demás al etiquetar las láminas de esta forma. Hay muchas que bastarán, y con la ecuación de Wheeler-De Witt sabremos entonces cómo la función de onda en un valor de este tiempo internamente definido está relacionada con su forma en otro valor del mismo. Cuando nos hallamos cerca del camino clásico, estos desarrollos de la función de onda en función del tiempo interno se interpretan directamente como pequeñas «correcciones cuánticas» a la física clásica ordinaria. Pero éste no siempre es el caso y cuando el camino más probable se encuentra alejado del clásico, se hace más difícil interpretar la evolución cuántica como sucediendo en el tiempo en algún sentido. Es decir, la colección de láminas espaciales que la ecuación de Wheeler-De Witt nos da no se amontona naturalmente para parecerse a un espacio-tiempo. A pesar de ello, todavía pueden encontrarse las funciones de transición. La cuestión de las condiciones iniciales para la función de onda se convierte ahora en el equivalente cuántico de la búsqueda en pos de condiciones iniciales. Es en el corte de la función de transición dado por x1 y t1 donde podríamos insertar a nuestros candidatos.
Condiciones iniciales cuánticas
No hay error más común que suponer que porque se hayan realizado precisos y prolongados cálculos matemáticos, la aplicación del resultado a algún hecho de la naturaleza es absolutamente cierta.
A. N. WHITEHEAD
Hemos visto que la función de transición T nos habla sobre la transición de una configuración de la geometría espacial, en la que la materia tiene una distribución particular, a otra. Pensemos en esta función como T[m1, g1; m2, g2], donde m etiqueta la configuración de materia y g es alguna característica geométrica del espacio, como la curvatura, que estamos usando como un tiempo definido internamente en dos valores «1» y «2». Podemos imaginar universos que comienzan en un único punto, en lugar de hacerlo en un espacio inicial, de manera que su desarrollo es cónico en lugar de cilíndrico (como era el caso en la figura 3.6). Esto se ilustra esquemáticamente en la figura 3.7. Pero con ello no hemos avanzado apreciablemente en nuestro intento de metamorfosear la noción de condiciones iniciales, porque la singularidad de los modelos cosmológicos no cuánticos siempre aparece como una característica del camino cuántico clásico; y, en cualquier caso, parece que únicamente estemos eligiendo una condición inicial particular, capaz de describir la creación a partir de un punto inicial preexistente, sin ninguna razón aparente. No hemos acabado con el dualismo entre las leyes (representadas aquí por la ecuación de Wheeler-De Witt) y las condiciones iniciales.
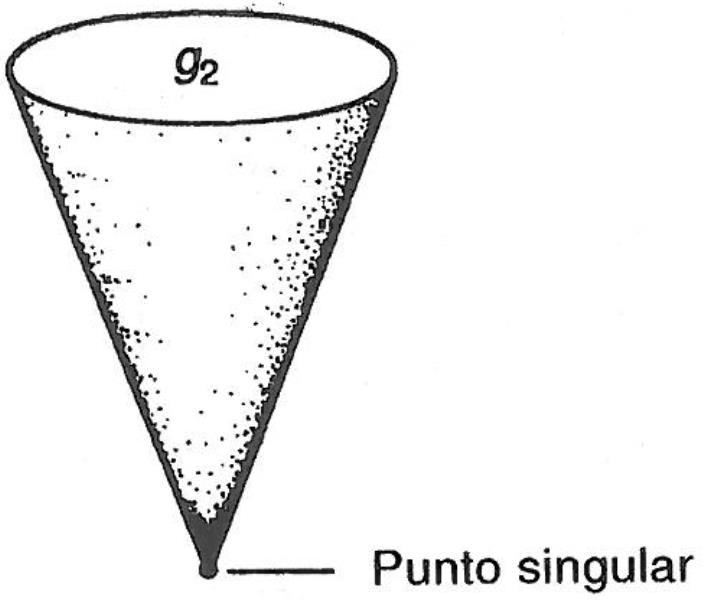
Figura 3.7 Un camino espacio-temporal, cuyo contorno está formado por un espacio curvo tridimensional, de curvatura g2, y un punto inicial singular en lugar de otro espacio tridimensional. Si existe una singularidad en la curvatura o en la configuración de materia en el punto, no podremos calcular la probabilidad de transición T desde este punto hasta el estado con la curvatura g2. Si esto fuera posible, obtendríamos la probabilidad de un tipo particular de universo que surge de un «punto» en lugar de hacerlo de «la nada».
Existe un camino radical que ahora se podría seguir. Si bien debería subrayarse que podría resultar vacío de cualquier significado físico. Es un artículo de fe. Si examinamos las figuras 3.6 y 3.7, podemos ver cómo la estipulación de una condición inicial g1, está relacionada con el estado del espacio más arriba del tubo o del cono, en g2. ¿Podrían combinarse en alguna forma los contornos de las configuraciones en g1, y g2 de manera que describieran un único espacio liso, libre de insidiosas singularidades?
Sabemos de algunas posibilidades sencillas en dos dimensiones, como en el caso de la superficie de una esfera, que son lisas y están libres de puntos singulares. Así pues, podríamos intentar imaginar todo el contorno de nuestro espacio-tiempo tetradimensional, no ya como g1 y g2, sino como una única superficie lisa en tres dimensiones. Esta podría ser la superficie de una esfera ubicada en cuatro dimensiones espaciales. Una de las curiosas y atractivas características de estas superficies lisas, habitualmente consideradas por los matemáticos con independencia de su dimensión, que nosotros podemos visualizar mejor regresando a la superficie bidimensional de una esfera ordinaria, es que tienen un tamaño finito y, sin embargo, no poseen bordes: la superficie de la esfera tiene un área finita (sólo se necesitaría un cantidad finita de pintura para pintarla), pero, muévase uno como se quiera, nunca caeremos en un punto excepcional como el vértice de un cono. Podríamos describir la esfera como una superficie sin límites desde el punto de vista de los habitantes de un mundo plano (bidimensional) que viven sobre su superficie. No deja de ser interesante que semejante configuración pueda ser considerada para el estado inicial del universo (véase la figura 3.8). No obstante —y ahora viene el paso radical— la esfera que estamos usando como ejemplo es un espacio de tres dimensiones con una superficie bidimensional como contorno. Pero, para nuestro límite cuántico, necesitamos un espacio tridimensional como contorno. Sin embargo, éste requiere que esa cosa tetradimensional de la que es contorno sea un espacio tetradimensional, y no un espacio-tiempo tetradimensional, que es lo que siempre se ha admitido como universo real. En consecuencia, se sugiere que en este marco cosmológico cuántico se trasciende nuestro concepto ordinario del tiempo, que pasa a ser como otra dimensión del espacio, convirtiendo así tres-más-una dimensiones de espacio y tiempo en un espacio tetradimensional. Esto no es tan místico como puede parecer, pues los físicos a menudo han utilizado este procedimiento de «cambiar tiempo en espacio» como un truco útil para resolver ciertos problemas de la mecánica cuántica ordinaria, aunque nunca llegaron a imaginar que el tiempo era realmente como el espacio. Al final del cálculo, regresaban sencillamente a la interpretación usual de una dimensión de tiempo y otras tres dimensiones, cualitativamente diferentes, de lo que llamamos espacio.

Figura 3.8 Un camino bastante atractivo es uno cuyo contorno está suavemente redondeado, de manera que consiste en un único espacio tridimensional sin ningún «punto» cónico en su base, como era el caso en la figura 3.7. Éste admite una interpretación de la probabilidad de transición como una creación a partir de «la nada», porque no existe un estado inicial: sólo hay un contorno. Esta posibilidad puede emplearse como la imagen del contorno tridimensional de un espacio-tiempo tetradimensional, solamente si suponemos que el tiempo se comporta como otra dimensión de espacio.
El carácter radical de este enfoque consiste en que considera al tiempo como verdaderamente igual al espacio en el entorno gravitatorio cuántico fundamental del big bang. Conforme uno se aleja del principio del universo, los efectos cuánticos empiezan a interferir de manera destructiva y se espera que el universo siga el camino clásico con una precisión cada vez mayor. Cuando esto sucede, comienza a cuajar la noción convencional de tiempo como un concepto distinto al de espacio. Y a la inversa, conforme uno se aproxima al comienzo, la imagen convencional del tiempo se desvanece y éste pasa a ser indistinguible del espacio en la medida en que se sienten los efectos de la condición de contorno.
Esta condición de «no contorno» fue propuesta por James Hartle y Stephen Hawking por razones estéticas. Soslaya las singularidades del estado inicial y elimina el dualismo convencional entre leyes y condiciones iniciales. Esto puede lograrlo rechazando la distinción entre espacio y tiempo. Más precisamente, la propuesta de «no contorno» estipula que, con el fin de hallar la función de ondas del universo, la calculamos como un agregado de caminos con pesos que están restringidos a aquellos espacios tetradimensionales que poseen un único contorno finito y suave como el esférico que acabamos de analizar. La probabilidad de transición que esta prescripción proporciona para la producción de una función de onda con algún otro contenido material m2 en una configuración geométrica g2 tiene justamente la forma T[m2, g2]. Por lo tanto, no hay cortes correspondientes a ningún estado «inicial» caracterizado por m1 y g1. Así, a menudo se dice que esto aporta una imagen de la «creación a partir de la nada», en la que T da la probabilidad de un cierto tipo de universo que ha sido creado partiendo de la nada. El efecto de la propuesta del «tiempo devenido espacio» es que no hay un instante o punto definido de creación. En términos mecánico-cuánticos más convencionales diríamos que el universo es el resultado de un proceso mecánico-cuántico de túnel, en el que aquél debe interpretarse como creado de la nada por efecto túnel. Los procesos cuánticos de túnel, con los que los físicos se hallan familiarizados y que se observan rutinariamente, corresponden a transiciones que no tienen un camino clásico.
La gran línea divisoria
Algunas veces me pregunto cómo sucedió que fuera yo quien desarrollara la teoría de la relatividad. La razón, pienso, es que un adulto normal nunca se para a pensar en problemas del espacio y el tiempo. Estas son cosas sobre las que reflexioné de niño. Pero mi desarrollo intelectual fue retardado, a consecuencia de lo cual sólo comencé a preguntarme sobre el espacio y el tiempo cuando ya había crecido.
ALBERT EINSTEIN
La imagen general que se desprende de este tipo de comienzo cuántico es que la ecuación de Wheeler-De Witt aporta la ley de la naturaleza que describe el cambio de la función de ondas W. La geometría del espacio puede ser utilizada como una medida del tiempo que coincide esencialmente con el tiempo ordinario de la relatividad general cuando uno se halla lejos del big bang. Pero cuando se mira atrás, hacia ese instante que habríamos llamado el cero del tiempo, la noción de tiempo se desvanece y finalmente deja de existir. Este tipo de universo cuántico no siempre ha existido; nace como lo haría en las cosmologías clásicas, pero no comienza en un big bang donde las cantidades físicas son infinitas y donde se necesita especificar otras condiciones iniciales. En ninguno de los dos casos tenemos información sobre a partir de qué pudo haber nacido.
Deberíamos subrayar de nuevo que ésta es una propuesta radical (que, como descubriremos en el capítulo 5, puede llegar a ser aún más radical). Tiene dos ingredientes: el primero es la propuesta de que el «tiempo deviene espacio»; el segundo es la propuesta añadida de «no contorno», una única prescripción para el estado del universo, que reúne los papeles de las ecuaciones iniciales y de las leyes de la naturaleza en la imagen tradicional. Aun cuando uno apruebe el primer ingrediente, hay muchas opciones que se podrían haber utilizado en lugar del segundo para especificar el estado de un universo que llega a existir por efecto túnel a partir de la nada. Todas ellas habrían requerido una especificación adicional de información.
El estudio de la función de onda del universo está en su infancia. Esta sufrirá sin duda muchos cambios antes de ser resuelta. La condición de «no contorno» deja mucho que desear. Probablemente contiene demasiada poca información para describir todas las características observables de un universo real que contiene irregularidades tipo galaxias. Debe complementarse con información adicional sobre los campos de materia en el universo y la distribución de los mismos. Claro que también puede completarse de manera absurda. La importante lección que queremos obtener de ello aquí es hasta qué punto nuestro tradicional dualismo respecto a las leyes y condiciones iniciales puede estar confundido. Puede que sea un resultado de nuestra experiencia en un dominio de la naturaleza en el que los efectos cuánticos son pequeños. Si una teoría de la naturaleza estuviera verdaderamente unificada, podríamos esperar que explotara la posibilidad de conservar el tiempo en términos del contenido material del universo, con el fin de casar los constituyentes de la naturaleza con las leyes que gobiernan su cambio y la naturaleza misma del tiempo. No obstante, todavía quedaría por elegir la condición de contorno que debería ser impuesta sobre una entidad como la función de ondas del universo. Por muy económica que sea su prescripción, es un hecho indiscutible que la condición de «no contorno» y sus diversos rivales son elegidos sólo por razones estéticas. No son requeridos por la consistencia lógica interna del universo cuántico.
La concepción dualista, según la cual las condiciones iniciales son independientes de las leyes de la naturaleza, deber ser reexaminada en el caso de las condiciones iniciales para el universo como un todo. Si el universo es único —la única posibilidad lógicamente consistente—, entonces las condiciones iniciales son únicas y se convierten a todos los efectos en una ley de la naturaleza. Esta es la motivación de quienes buscan principios básicos que puedan servir para delinear las condiciones iniciales del universo. Si éste es verdaderamente el caso, entonces introduce otro nuevo ingrediente en nuestras especulaciones sobre el universo, porque apunta a una asimetría fundamental entre el pasado y el futuro en la confección de las leyes de la naturaleza. Por otro lado, si creemos que hay muchos universos posibles —de hecho, puede que realmente existan muchos universos posibles «en algún lugar»—, las condiciones iniciales no necesitan poseer un estatus especial. Podrían ser sencillamente como en problemas físicos más mundanos, aquellas características definidoras que especifican una realidad particular de entre una clase general de posibilidades.
La concepción tradicional, según la cual las condiciones iniciales son incumbencia de los teólogos, y las ecuaciones de evolución, de los físicos, parece haber sido derrocada —al menos temporalmente. Los cosmólogos están ahora embarcados en el estudio de las condiciones iniciales para descubrir si existe una «ley» de condiciones iniciales, de la que la propuesta de «no contorno» sería sólo un posible ejemplo. Esto es algo claramente radical, pero quizás no sea lo suficientemente radical. No deja de ser inquietante que tantos conceptos e ideas utilizados en la descripción matemática moderna —«creación a partir de la nada», «tiempo que nace con el universo»— no sean más que imágenes refinadas de intuiciones y categorías del pensamiento humano más bien tradicionales. Seguramente son estas nociones tradicionales las que motivan muchos de los conceptos buscados, e incluso hallados, en el contexto de teorías modernas que son moldeadas en forma matemática. La propuesta del «tiempo que deviene espacio» es el único elemento verdaderamente radical que no podemos atribuir al legado de pasadas generaciones de pensamiento humano en teología filosófica. Uno sospecha que probablemente sea todavía necesario transformar muchos más de los conceptos más habituales antes de que la verdadera imagen comience a despuntar.