XI. LA VERDAD DEL PLANO

Hay veces en que el sumergirme en estos ensayos científicos que escribo me crea ciertos problemas. Por ejemplo, el otro día vi cómo la persona con la que estaba almorzando espolvoreaba sal sobre su plato después de haber tomado un bocado insatisfactorio, probaba luego otro y decía con satisfacción: «Así está mucho mejor».

Rebullí desasosegadamente en mi asiento y dije: «Lo que quieres decir en realidad es “así me gusta mucho más”. Al decir simplemente “así está mucho mejor” estás formulando la injustificada presunción de que la comida puede ser objetivamente mejor o peor por su gusto y la presunción subsiguiente de que tu propia sensación subjetiva de gusto constituye una guía segura con respecto a la situación objetiva».

Creo que estuve en un tris de encontrarme estrellado en la cara aquel plato, sazonado ya a la perfección; y lo habría tenido bien merecido además. Lo que pasaba era que yo acababa de escribir el ensayo anterior y estaba rebosante de presunciones.

De modo que volvamos a eso. El tema sujeto a consideración es el «quinto postulado» de Euclides, que repetiré aquí para que no tenga usted que consultarlo:

Si una línea recta que incide sobre dos líneas rectas forma los ángulos interiores del mismo lado menores de dos ángulos rectos, las dos líneas rectas, si se prolongan indefinidamente, se encuentran en el lado en que están los ángulos menores que dos ángulos rectos.

Todos los demás axiomas de Euclides son extremadamente sencillos, pero él pareció comprender que este quinto postulado, aunque complicado en apariencia, no podía ser demostrado a partir de los otros axiomas y debía, por consiguiente, ser incluido como un axioma también.

Durante dos mil años después de Euclides, otros geómetras siguieron intentando demostrar que Euclides se había precipitado al renunciar y esforzándose por encontrar algún ingenioso método de demostrar el quinto postulado a partir de los otros axiomas, de tal modo que pudiera, en consecuencia, ser excluido de la lista…, aunque sólo fuese porque era demasiado largo, demasiado complicado y demasiado carente de evidencia inmediata como para parecer un buen axioma.

Un sistema de abordar el problema era considerar el siguiente cuadrilátero:

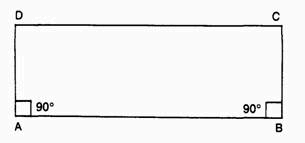
Dos de los ángulos, DAB y ABC, vienen dados como ángulos rectos en este cuadrilátero, y el lado AD tiene igual longitud que el lado BC. Dados estos datos, es posible demostrar que el lado DC es igual al lado AB y que los ángulos ADC y DCB son también ángulos rectos (por lo que el cuadrilátero es en realidad un rectángulo) si se utiliza el quinto postulado de Euclides.

Si no se utiliza el quinto postulado de Euclides y se recurre solamente a los otros axiomas, todo lo que uno puede hacer es demostrar que los ángulos ADC y DCB son iguales, pero no que son realmente ángulos rectos.

Se plantea entonces el problema de si es posible demostrar que a partir del hecho de que los ángulos ADC y DCB son iguales es posible demostrar que son también ángulos rectos. Si se pudiera hacer eso, se desprendería entonces de ello que el cuadrilátero ABCD es un rectángulo y que el quinto postulado es verdadero. Éste habría sido demostrado a partir de los otros axiomas solamente y ya no sería necesario incluir el quinto de Euclides entre ellos.

Este intento fue realizado primeramente por los árabes medievales, que continuaron las tradiciones de la geometría griega mientras la Europa Occidental permanecía sumida en las tinieblas. El primero en trazar este cuadrilátero y afanarse sobre sus ángulos rectos no fue otro que Omar Khayyam (1050-1123^[12]).

Omar señaló que, si los ángulos ADC y DCB eran iguales, había entonces tres posibilidades:

1) era cada uno de ellos un ángulo recto,

2) era cada uno de ellos menor que un ángulo recto, o sea, eran «agudos»,

3) era cada uno de ellos mayor que un ángulo recto, o sea, «obtusos».

Continuó esta línea de argumentación para mostrar que las hipótesis de ángulos agudos y obtusos eran absurdas, sobre la base de que dos líneas convergentes deben cortarse necesariamente.

Desde luego, es de perfecto sentido común suponer que dos líneas convergentes deben cortarse, pero, infortunadamente, sea o no de sentido común, esa presunción es matemáticamente equivalente al quinto postulado de Euclides. Omar Khayyam terminaba, por lo tanto, «demostrando» el quinto postulado mediante la presunción de que es verdadero como una de las condiciones de la prueba. Esto se llama «argumentación en círculo» o «petición de principio», pero, se llame como se llame, no está permitido en matemáticas.

Otro matemático árabe, Nasir Eddin al-Tus (1201-1274), realizó un intento similar sobre el cuadrilátero, utilizando una presunción diferente y más complicada para excluir las hipótesis de ángulos agudos y obtusos. Pero su presunción era también matemáticamente equivalente al quinto de Euclides.

Lo cual nos lleva al italiano Girolamo Saccheri (1667-1733), al que aludía al final del ensayo anterior y que fue profesor de matemáticas en la Universidad de Pisa y sacerdote jesuita.

Conocía el trabajo de Nasir Eddin y él también se enfrentó al cuadrilátero. Pero Saccheri introdujo algo completamente nuevo, algo que a lo largo de dos mil años nadie había pensado hacer en relación con el quinto de Euclides.

Hasta entonces, la gente había omitido el quinto de Euclides para ver qué pasaba, o había formulado presunciones que resultaban equivalentes al quinto de Euclides. Lo que Saccheri hizo fue comenzar dando por supuesto que el quinto de Euclides era falso y sustituyéndolo por algún otro postulado que fuese contradictorio con él. Proyectó luego tratar de construir una geometría basada en otros axiomas de Euclides más el «quinto alternativo» hasta que llegara a una contradicción (demostrar que un teorema concreto era falso y verdadero a la vez, por ejemplo).

Cuando se llegara a la contradicción, el «quinto alternativo» tendría que ser desechado. Si todo posible «quinto alternativo» es eliminado de esta manera, entonces el quinto de Euclides tiene que ser verdadero. Este método de demostrar un teorema demostrando que todas las demás posibilidades son absurdas constituye una técnica matemática perfectamente aceptable^[13], y Saccheri estaba en el buen camino.

Trabajando sobre este sistema, por consiguiente, Saccheri empezó presumiendo que los ángulos ADC y DCB eran ambos mayores que un ángulo recto. Con esta presunción, y con todos los axiomas de Euclides distintos del quinto, empezó a abrirse paso a través de lo que podríamos denominar «geometría obtusa». No tardó en tropezar con una contradicción. Eso significaba que la geometría obtusa no podía ser verdadera y que cada uno de los ángulos ADC y DCB no podían ser mayor que un ángulo recto.

Este logro era tan importante que el cuadrilátero que Omar Khayyam había sido el primero en utilizar en relación con el quinto de Euclides recibe ahora el nombre de «cuadrilátero de Saccheri».

Enormemente animado por esto, Saccheri abordó entonces la «geometría aguda», partiendo de la presunción de que cada uno de los ángulos ADC y DCB era menor de un ángulo recto. Debió de comenzar la tarea con optimismo, seguro de que, como en el caso de la geometría obtusa, no tardaría en encontrar una contradicción en la geometría aguda. En ese caso, quedaría demostrado el quinto de Euclides, y su «geometría de ángulo recto» no necesitaría ya aquella proposición incómodamente larga enunciada como axioma.

A medida que Saccheri iba pasando de proposición en proposición en su geometría aguda, su sentimiento de satisfacción empezó a ser sustituido por una creciente inquietud, ya que no tropezaba con ninguna contradicción. Se iba encontrando cada vez más enfrentado a la posibilidad de que se pudiera construir una geometría plenamente autoconsistente basada en, por lo menos, un axioma que contradecía de modo directo a un axioma euclidiano. El resultado sería una geometría «no euclidiana» que podría parecer contraria al sentido común, pero que sería internamente autoconsistente y, por lo tanto, matemáticamente válida.

Por un momento, Saccheri titubeó al borde mismo de la inmortalidad matemática y… retrocedió.

¡No podía! Se necesitaba demasiado valor para aceptar la noción de una geometría no euclidiana. Los estudiosos habían llegado tan erróneamente a confundir la geometría euclidiana con la verdad absoluta que cualquier refutación de Euclides habría suscitado intensos remolinos de inquietud en los corazones y en las mentes de los intelectuales de Europa. Dudar de Euclides era dudar de la verdad absoluta, y, si no había ninguna verdad absoluta en Euclides, ¿no podría deducirse rápidamente de ello que no había ninguna verdad absoluta en ninguna parte? Y, puesto que la más firme reivindicación de verdad absoluta procedía de la religión, ¿no podría ser interpretado un ataque a Euclides como un ataque a Dios?

Saccheri era, evidentemente, un matemático de gran capacidad, pero también era sacerdote jesuita y ser humano, por lo que le falló el valor, y realizó la gran negación^[14]. Cuando su gradual desarrollo de la geometría aguda llegó al punto en que ya no podía llevarla más allá, se indujo a sí mismo a imaginar que había encontrado una inconsistencia donde en realidad no la había, y con gran alivio concluyó que había demostrado el quinto de Euclides. En 1733 publicó un libro sobre sus descubrimientos titulado Euclides liberado de todo fallo y, ese mismo año, murió.

Con su negación, Saccheri había perdido la inmortalidad y elegido el olvido. Su libro pasó virtualmente inadvertido hasta que un matemático italiano posterior, Eugenio Beltrami (1835-1900), llamó la atención sobre él después de que otros hubieran dejado patente el fracaso de Saccheri. Lo que ahora sabemos de Saccheri es, simplemente, esto: que puso el dedo sobre un importante descubrimiento matemático un siglo antes que nadie y que no tuvo el valor de mantener el dedo firmemente sobre él.

Avancemos casi un siglo para acercarnos al matemático alemán Karl F. Gauss (1777-1855). Puede afirmarse que Gauss fue el matemático más grande que jamás haya vivido. Ya de joven asombró a Europa y al mundo científico con su talento.

Hacia 1815 consideró el quinto de Euclides y llegó a la misma conclusión a que había llegado Euclides, que el quinto tenía que ser tomado como axioma porque no podía ser demostrado a partir de los otros axiomas. Gauss llegó además a la conclusión que Saccheri había rehuido, que había otras geometrías autoconsistentes que eran no euclidianas en cuanto que un axioma alternativo remplazaba al quinto.

Y, luego, a él también le faltó el valor necesario para publicar su descubrimiento, y aquí yo no le concedo mi simpatía. La situación era diferente. Gauss tenía una reputación infinitamente superior a la de Saccheri; Gauss no era sacerdote; Gauss vivía en un país y en una época en los que había de temerse menos el poder de la Iglesia. Gauss, genio o no, fue un cobarde.

Y esto nos lleva al matemático ruso Nikolai Ivanovich Lobachevski (1793-1856^[15]). En 1826, Lobachevski empezó a pensar, también, si una geometría podría ser no euclidiana y ser, sin embargo, consistente. Con esa idea, desarrolló los teoremas de la «geometría aguda» como había hecho Saccheri un siglo antes, pero en 1829 Lobachevski hizo lo que no había hecho ni Saccheri ni Gauss. No se echó atrás, y publicó. Desgraciadamente, lo que publicó fue un artículo en ruso titulado «Sobre los principios de la geometría» en un periódico local (trabajaba en la Universidad de Kazán, en el interior de la Rusia campesina).

¿Quién lee ruso? Lobachevski permaneció generalmente desconocido. Fue sólo en 1840 cuando publicó su obra en alemán que atrajo sobre si la atención del mundo de la matemática.

Pero, mientras tanto, un matemático húngaro, János Bolyai (1802-1860), estaba haciendo lo mismo. Bolyai es una de las figuras más románticas de la historia de las matemáticas, ya que se especializó también en cosas tales como el violín y el duelo a espada…, dentro de la más pura tradición de la aristocracia húngara. Se dice que, en cierta ocasión, se batió con trece espadachines, uno tras otro, venciéndolos a todos… y tocando el violín entre asalto y asalto.

En 1831, el padre de Bolyai publicó un libro sobre matemáticas. El joven Bolyai llevaba ya varios años reflexionando sobre el quinto de Euclides y persuadió ahora a su padre para que incluyera un apéndice de veintiséis páginas en el que se describían los principios de la geometría aguda. Esto fue dos años después de que Lobachevski hubiera publicado, pero nadie había oído hablar aún del ruso, y en la actualidad Lobachevski y Bolyai comparten en líneas generales el mérito de haber descubierto la geometría no euclidiana.

Como los Bolyai publicaron su obra en alemán, Gauss tuvo conocimiento inmediato de ella. Su apoyo habría significado mucho para el joven Bolyai. Sin embargo, Gauss no tuvo el valor de poner en letras de molde su aprobación, si bien alabó verbalmente la obra de Bolyai. Y luego no pudo resistir más y dijo a Bolyai que él había tenido las mismas ideas unos años antes pero no las había publicado, y le enseñó el trabajo.

Gauss no necesitaba hacer eso. Su reputación era inconmovible; aun sin la geometría no euclidiana, había hecho suficiente para una docena de matemáticos. Puesto que le había faltado valor para publicar, podía haber tenido la decencia de dejar que Bolyai se llevara el crédito. Pero no lo hizo. Genio o no, Gauss era un hombre mezquino en algunos aspectos.

El pobre Bolyai se sintió tan turbado y humillado por la revelación de Gauss, que no volvió a realizar ningún trabajo más en matemáticas.

¿Y la geometría obtusa? Saccheri la había investigado y se había visto enredado en la contradicción, así que había sido desechada. Sin embargo, una vez establecida la validez de la geometría no euclidiana, ¿no habría forma de rehabilitar también la geometría obtusa?

Sí, la había…, pero sólo a costa de romper más radicalmente aún con Euclides. Al investigar la geometría obtusa, Saccheri había hecho uso de una tácita presunción que también había utilizado el propio Euclides, que una línea podía tener una longitud infinita. Esta presunción no introducía ninguna contradicción en la geometría aguda, ni en la geometría de ángulo recto (la de Euclides), pero creaba problemas en la geometría obtusa.

Pero prescindamos de ella también. Supongamos que, con independencia del «sentido común», adoptamos la presunción de que toda línea debe tener una longitud finita máxima. En ese caso, desaparecerían todas las contradicciones de la geometría obtusa y habría una segunda variedad de geometría no euclidiana. Esto fue demostrado por primera vez en 1854 por el matemático alemán Georg F. Riemann (1826-1866).

Así, pues, tenemos ahora tres clases de geometría, que podemos distinguir utilizando proposiciones equivalentes a la variedad del quinto postulado empleada en cada caso:

A) Geometría aguda (no euclidiana): Por un punto exterior a una línea dada se pueden trazar un número infinito de líneas paralelas a la línea dada.

B) Geometría de ángulo recto (euclidiana): Por un punto exterior a una línea dada, se puede trazar una y solamente una línea paralela a la línea dada.

C) Geometría obtusa (no euclidiana): Por un punto exterior a una línea dada no se puede trazar ninguna línea paralela a la línea dada.

Se puede hacer la distinción de otra manera, equivalente a la anterior:

A) Geometría aguda (no euclidiana): Los ángulos de un triángulo suman menos de 180 grados.

B) Geometría de ángulo recto (euclidiana): Los ángulos de un triángulo suman exactamente 180 grados.

C) Geometría obtusa (no euclidiana): Los ángulos de un triángulo suman más de 180 grados.

Puede que usted pregunte ahora: ¿Pero qué geometría es verdadera?

Si definimos «verdadera» como internamente autoconsistente, entonces las tres geometrías son igualmente verdaderas.

Desde luego, son inconsistentes entre sí, y quizá solamente una se corresponda con la realidad. Podríamos, por consiguiente, preguntar: ¿Qué geometría corresponde a las propiedades del Universo real?

La contestación es, de nuevo, que todas.

Consideremos, por ejemplo, el problema de viajar desde el punto A de la superficie de la Tierra hasta el punto B de la superficie de la Tierra, y supongamos que queremos ir desde A hasta B de tal forma que recorramos la menor distancia posible.

Con el fin de simplificar los resultados, realicemos dos presunciones. En primer lugar, presumamos que la Tierra es una esfera perfectamente lisa. Esto es casi verdadero, en realidad, y podemos eliminar montañas y valles, e incluso el abultamiento ecuatorial, sin producir demasiada distorsión.

En segundo lugar, presumamos que en nuestros viajes nos encontramos limitados a la superficie de la esfera y que no podemos, por ejemplo, horadarla.

Para determinar la distancia más corta desde A hasta B sobre la superficie de la Tierra, podríamos tender un hilo desde un punto hasta el otro y estirarlo hasta ponerlo tenso. Si esto lo hiciéramos entre dos puntos de un plano, es decir, sobre una superficie como la de una pizarra lisa extendida infinitamente en todas direcciones, el resultado sería lo que ordinariamente llamamos una «línea recta».

Sobre la superficie de la esfera, sin embargo, el resultado es una curva, y esa curva es, no obstante, el análogo de una línea recta, ya que esa curva es la distancia más corta entre dos puntos situados sobre la superficie de una esfera. Encontramos una cierta dificultad en forzamos a aceptar una curva como análoga a una línea recta, porque toda nuestra vida hemos estado pensando «recta». Utilicemos, entonces, una palabra diferente. Llamemos a la distancia más corta entre dos puntos de cualquier superficie dada una «geodésica^[16]».

En un plano, una geodésica es una línea recta; en una esfera, una geodésica es una curva, y, específicamente, el arco de un «círculo máximo». Ese círculo máximo tiene una longitud igual a la circunferencia de la esfera y se halla situado en un plano que pasa por el centro de la esfera. En la Tierra, el ecuador es un ejemplo de círculo máximo, y también todos los meridianos. Sobre la superficie de cualquier esfera se pueden trazar un número infinito de círculos máximos. Si elige usted cualquier par de puntos sobre una esfera y une cada par con un hilo tenso, tendrá en cada caso el arco de un círculo máximo distinto.

Ya puede usted darse cuenta de que en la superficie de una esfera no existe cosa tal como una geodésica de longitud infinita. Si se prolonga, acaba, simplemente, encontrándose consigo misma y se convierte en una curva cerrada. En la superficie de la Tierra, una geodésica no puede tener más de 40.000 kilómetros.

Además, cualesquiera dos geodésicas trazadas sobre una esfera se cortan si se prolongan indefinidamente, y se cortan en dos puntos. En la superficie de la Tierra, por ejemplo, dos meridianos cualesquiera se encuentran en el polo norte y en el polo sur. Esto significa que, en la superficie de una esfera, por cualquier punto exterior a una geodésica dada no puede trazarse ninguna paralela a la geodésica dada. Por ese punto no puede trazarse ninguna geodésica que no corte tarde o temprano a la geodésica dada.

Y luego, también, si traza usted un triángulo sobre la superficie de una esfera, siendo cada uno de sus lados el arco de un círculo máximo, los ángulos tendrán una suma mayor que 180 grados. Si tiene usted un globo terráqueo, imagine un triángulo con uno de sus vértices en el polo norte, otro en el ecuador y a 10 grados de longitud Oeste, y el tercero en el ecuador y a 100 grados de longitud Oeste. Se encontrará con que tiene un triángulo equilátero cada uno de cuyos ángulos es igual a 90 grados. La suma de los tres ángulos es 270 grados.

Ésta es precisamente la geometría que desarrolló Riemann, si se considera que las geodésicas son análogas a las líneas rectas. Es una geometría de líneas finitas, sin paralelas y con sumas de ángulos de triángulos mayores de 180 grados. Lo que hemos venido llamando «geometría obtusa» podría entonces llamarse también «geometría esférica». Y lo que hemos venido llamando «geometría de ángulo recto», o «geometría euclidiana», podría denominarse también «geometría plana».

En 1865, Eugenio Beltrami llamó la atención sobre una forma llamada «seudoesfera», que tiene el aspecto de dos cucuruchos unidos por la boca, extendiéndose cada uno de ellos infinitamente en cada dirección, estrechándose continuamente, pero sin llegar a cerrarse nunca. Las geodésicas trazadas sobre la superficie de una seudoesfera cumplen los requisitos de la geometría aguda.

En una seudoesfera, las geodésicas son infinitamente largas, y es posible que dos geodésicas se prolonguen indefinidamente sin cortarse y ser, por lo tanto, paralelas. De hecho, es posible trazar en la superficie de una seudoesfera dos geodésicas que sí se corten y, sin embargo, hacer que ninguna de ellas corte a una geodésica exterior a las dos^[17]. De hecho, puesto que entre las dos geodésicas que se cortan puede trazarse un número infinito de geodésicas que se corten todas en el mismo punto, existe un número infinito de geodésicas posibles por un punto dado, todas las cuales son paralelas a otra geodésica que no pase por ese punto.

En otras palabras, la «geometría aguda» puede ser considerada como una «geometría seudoesférica».

Pero ahora —admitido que las tres geometrías son igualmente válidas en las circunstancias adecuadas a cada una—, ¿cuál es la mejor descripción del Universo como un todo?

Esto no siempre es fácil de decir. Si traza usted un triángulo con geodésicas de una longitud dada en una esfera pequeña y lo hace luego en una esfera grande, la suma de los ángulos del triángulo será mayor de 180 grados en ambos casos, pero el exceso será mayor en el caso de la esfera pequeña.

Si imagina usted una esfera que va aumentando paulatinamente de tamaño, un triángulo de unas determinadas dimensiones trazado en su superficie irá teniendo como suma de sus ángulos una cifra cada vez más próxima a 180 grados, y finalmente ni la medición más refinada podrá detectar la diferencia. En resumen, una pequeña sección de una esfera muy grande es casi tan llana como un plano, y resulta imposible distinguir la diferencia.

Esto es cierto con respecto a la Tierra, por ejemplo. La Humanidad tardó tanto tiempo en convencerse de que la Tierra es esférica porque es una esfera tan grande que pequeñas partes de ella parecen planas.

Bien, pues un problema similar existe por lo que se refiere al Universo en general.

La luz viaja de un punto a otro en el espacio: desde el Sol hasta la Tierra, o desde una lejana galaxia hasta otra, a lo largo de distancias muchas veces superiores a las posibles en la superficie de la Tierra.

Nosotros damos por supuesto que la luz, al viajar a lo largo de los parsecs lo hace en línea recta, pero, naturalmente, lo hace en una geodésica, que puede ser, o no, una línea recta.

Si el Universo obedece a la geometría euclidiana, la geodésica es una línea recta. Si el Universo obedece a alguna geometría no euclidiana, entonces las geodésicas son curvas de una clase u otra.

A Gauss se le ocurrió formar triángulos con rayos de luz que recorrieran el espacio desde la cumbre de una montaña a otra y medir la suma de los ángulos así obtenidos. Desde luego, las sumas resultaron ser de unos 180 grados, ¿pero eran exactamente 180 grados? Imposible decirlo. Si el Universo fuese una esfera de millones de años-luz de diámetro y si los rayos de luz siguieran la curvatura de esa esfera, ninguna medición directa concebible posible hoy podría detectar la minúscula cantidad en que la suma de los ángulos excedía de 180 grados.

Pero en 1916 Einstein elaboró la Teoría General de la Relatividad y encontró que para explicar los efectos de la gravitación tenía que presumir un Universo en el que la luz (y todo lo demás) se desplazara sobre geodésicas no euclidianas.

Conforme a la teoría de Einstein, el Universo es no euclidiano y, de hecho, constituye un ejemplo de «geometría obtusa».

Por expresarlo brevemente, pues, la geometría euclidiana, lejos de ser la verdad absoluta y eterna que durante dos mil años se presumió que era, es tan sólo la geometría sumamente limitada y abstracta del plano, mera aproximación a la geometría de cosas tan importantes como el Universo y la superficie de la Tierra.

No es la verdad lisa y llana que tantos años han dado por sentado que era, sino sólo la verdad del plano.