X. EL QUINTO DE EUCLIDES

Las matemáticas siempre han parecido estar un peldaño por encima de las ciencias. Las ciencias son, en gran medida, inductivas, uno observa, y a partir de ahí induce reglas generales. En las matemáticas uno deduce consecuencias a partir de primeros principios, procedimiento que, en cierto modo, parece más elevado y seguro.

Pero ¿y si los primeros principios son erróneos? La conmoción que produce descubrir tal cosa es más traumática aún que descubrir que una observación ha sido mal interpretada. Incluyo a continuación dos ensayos que servirán para demostrarlo.

Algunos de mis artículos suscitan más comentarios que otros en los lectores, y uno de los más eficaces en este aspecto fue uno que escribí una vez, en el que relacionaba los que, en mi opinión, eran científicos de primera magnitud y concluía presentando una lista personal de los diez científicos más grandes de todos los tiempos.

Naturalmente, recibí cartas que propugnaban la omisión de uno o más de mis diez mejores en favor de uno o más distintos, y las sigo recibiendo, aun ahora, siete años y medio después de haber escrito el artículo.

De ordinario respondo a tales cartas explicando que las estimaciones respecto a cuáles son los diez científicos más grandes (siempre con la excepción de Isaac Newton, respecto al cual no puede haber desacuerdo razonable) son cuestión fundamentalmente subjetiva en la que no cabe verdadera discusión.

No hace mucho, recibí una carta de un lector que sostenía que Arquímedes, uno de mis diez, debía ser sustituido por Euclides, que no era uno de mis diez. Respondí con mi habitual tono conciliador, pero continué diciendo que Euclides era «simplemente un sistematizador», mientras que Arquímedes había realizado progresos muy importantes en física y en matemáticas.

Pero luego mi conciencia empezó a rebullir. Yo seguía manteniendo mi opinión que situaba a Arquímedes por encima de Euclides, pero la expresión «simplemente un sistematizador» me turbaba. No hay nada necesariamente «simple» en ser un sistematizador^[11].

Durante tres siglos antes de Euclides (que floreció hacia el año 300 antes de Cristo) los geómetras griegos se habían esforzado en demostrar un teorema geométrico tras otro, y ya habían sido desarrollados muchos.

Lo que Euclides hizo fue elaborar un sistema de todo ello. Comenzó con ciertas definiciones y presunciones y las utilizó luego para demostrar unos pocos teoremas. Utilizando esas definiciones y presunciones, juntamente con los pocos teoremas que ya había demostrado, demostró unos cuantos teoremas adicionales más, y así sucesivamente.

Que nosotros sepamos, fue el primero en construir un elaborado sistema matemático basado en la explícita actitud de que era inútil tratar de demostrar todo; que era esencial partir inicialmente de algunas cosas que no podían ser demostradas pero que se podían aceptar sin prueba porque satisfacían a la intuición. Esas presunciones intuitivas, sin prueba, recibieron el nombre de «axiomas».

Por sí solo esto ya constituía un gran avance intelectual, pero Euclides hizo algo más. Eligió buenos axiomas.

Para comprender lo que esto significa, considere que uno necesitaría que su lista de axiomas fuese completa, es decir, que fuera suficiente para demostrar todos los teoremas útiles en el campo especial de conocimiento que se está estudiando. Por otra parte, no deben ser redundantes. Uno no necesita poder demostrar todos esos teoremas aun después de haber omitido uno o más de los axiomas de su lista; ni poder demostrar uno o más de sus axiomas mediante el uso de los axiomas restantes. Finalmente, los axiomas deben ser consistentes. Es decir, no quiere uno utilizar unos axiomas para demostrar que algo es así y utilizar luego otros axiomas para demostrar que la misma cosa no es así.

Durante dos mil años, el sistema axiomático de Euclides resistió la prueba. Nadie consideró jamás necesario añadir otro axioma, y nadie pudo jamás eliminar uno o modificarlo sustancialmente…, lo que dice mucho en favor del buen criterio de Euclides.

Pero hacia finales del siglo XIX, en que se habían consolidado ya las nociones de rigor matemático, se comprendió que había muchas presunciones tácitas en el sistema euclidiano; esto es, presunciones que Euclides hizo sin decir específicamente que las había hecho, y que todos sus lectores hacían también, aparentemente sin decírselo específicamente a sí mismos.

Por ejemplo, entre sus primeros teoremas hay varios que demuestran que dos triángulos son iguales en forma y en tamaño mediante una prueba que exige imaginar que un triángulo se mueve en el espacio de tal modo que queda superpuesto al otro. Pero eso presupone que una figura geométrica no cambia de forma ni de tamaño cuando se mueve. Claro que no cambia, dirá usted. Bueno, usted presume que no cambia, y yo presumo que no cambia, y Euclides presumió que no cambia…, pero Euclides nunca dijo que lo presumía.

Igualmente, Euclides presumía que una línea recta podía prolongarse indefinidamente en ambas direcciones…, pero nunca dijo que estuviera realizando esa presunción.

Además, él nunca consideró que propiedades básicas tan importantes como el orden de puntos en una línea, y algunas de sus definiciones básicas, fuesen inadecuadas…

Pero no importa. En el último siglo se ha hecho descansar la geometría euclidiana sobre una base del máximo rigor, y, si bien eso significaba que se alteraba el sistema de axiomas y definiciones, la geometría de Euclides permanecía idéntica. Significaba solamente que los sistemas y las definiciones de Euclides, más sus presunciones no expresadas, eran adecuados para el fin pretendido.

Consideremos ahora los axiomas de Euclides. Eran diez, y él los dividió en dos grupos de cinco. Un grupo de cinco fue denominado «nociones comunes» porque eran comunes a todas las ciencias.

1) Las cosas que son iguales a la misma cosa son también iguales unas a otras.

2) Si se añaden iguales a iguales, las sumas son iguales.

3) Si se sustraen iguales de iguales, los restos son iguales.

4) Las cosas que coinciden unas con otras son iguales unas a otras.

5) El todo es mayor que la parte.

Estas «nociones comunes» parecen tan comunes, tan evidentes, tan inmediatamente aceptables por intuición, tan incapaces de contradicción, que parecen representar la verdad absoluta. Parecen algo que una persona podría comprender tan pronto como hubiera desarrollado la luz de la razón. Sin percibir jamás el Universo de ninguna manera, sino viviendo tan sólo en la luminosa oscuridad de su propia mente, vería que las cosas iguales a la misma cosa son iguales unas a otras y todo lo demás.

Podría entonces, utilizando los axiomas de Euclides, elaborar todos los teoremas de la geometría y, por consiguiente, las propiedades básicas del Universo a partir de primeros principios sin haber observado nada.

Los griegos se sintieron tan fascinados con esta idea de que todo el conocimiento matemático procede de dentro que perdieron un importante estímulo que podría haberles conducido al desarrollo de la ciencia experimental. Hubo experimentadores entre los griegos, en particular Ctesibio y Herón, pero los estudiosos griegos consideraban su trabajo como una especie de artesanado, más que como ciencia.

En uno de los diálogos de Platón, Sócrates formula a un esclavo ciertas preguntas sobre un diagrama geométrico y le hace contestar y demostrar con ello un teorema. Éste era el método de Sócrates de mostrar que incluso un hombre carente por completo de instrucción podía extraer la verdad desde dentro de sí mismo. Se necesitaba, sin embargo, un hombre extremadamente sofisticado, Sócrates, para formular las preguntas, y el esclavo no carecía en absoluto de instrucción, pues con sólo haber estado vivo y perceptivo durante años había aprendido a realizar numerosas presunciones mediante la observación y el ejemplo, sin que ni él ni (aparentemente) Sócrates se dieran cuenta completa de ello.

Sin embargo, todavía en 1800, influyentes filósofos tales como Immanuel Kant sostenían que los axiomas de Euclides representaban la verdad absoluta.

¿Pero la representaban realmente? ¿Discutiría alguien la proposición de que «el todo es mayor que la parte»? Dado que 10 puede fraccionarse en 6 + 4, ¿no estamos legitimados para presumir que 10 es mayor que 6 ó que 4? Si un astronauta puede entrar en una cápsula espacial, ¿no tendríamos derecho a presumir que el volumen de la cápsula es mayor que el volumen del astronauta? ¿Cómo podríamos dudar de la verdad general del axioma?

Bien, cualquier lista de números consecutivos puede ser dividida en números pares y números impares, por lo que podríamos concluir que en cualquier lista de números consecutivos el total de todos los números presentes debe ser mayor que el total de números pares. Y, sin embargo, si consideramos una lista infinita de números consecutivos, resulta que el número total de todos los números es igual al número total de todos los números pares. En las denominadas «matemáticas transfinitas», el axioma concreto de que el todo es mayor que la parte no es, simplemente, aplicable.

Supongamos, igualmente, que dos automóviles circulan entre los puntos A y B por rutas idénticas. Las dos rutas coinciden. ¿Son iguales? No necesariamente. El primer automóvil circulaba de A a B, mientras que el segundo viajaba de B a A.

En otras palabras, dos líneas podrían coincidir y, sin embargo, no ser iguales, ya que la dirección de una podría ser diferente de la dirección de la otra.

¿Es esto hablar por hablar? ¿Se puede decir que una línea tiene dirección? Sí, en efecto. Una línea con dirección es un «vector», y en las «matemáticas vectoriales» las reglas no son las mismas que en las matemáticas ordinarias, y las cosas pueden coincidir sin ser iguales.

En resumen, pues, los axiomas no son ejemplos de verdad absoluta, y es muy probable que la verdad absoluta no exista. Los axiomas de Euclides son axiomas no porque aparezcan como verdad absoluta a consecuencia de alguna iluminación interior, sino solamente porque parecen verdaderos en el contexto del mundo real.

Es posible comenzar con cualquier conjunto de axiomas, siempre que no sean contradictorios entre sí, y elaborar un sistema de teoremas congruentes con esos axiomas y recíprocamente entre ellos, aun cuando no sean congruentes con lo que consideramos el mundo real. Esto no hace a las «matemáticas arbitrarias» menos «verdaderas» que la que arranca de los axiomas de Euclides, sólo menos útiles quizá. De hecho, una «matemática arbitraria» puede ser más útil que las matemáticas ordinarias «de sentido común» en terrenos especiales tales como los de los transfinitos o los vectores.

Aun así, no debemos confundir «útil» y «verdadero». Aunque un sistema axiomático sea tan extraño que no resulte útil en ningún sentido práctico concebible, no podemos, sin embargo, decir nada acerca de su «verdad». Si es internamente congruente, eso es todo lo que tenemos derecho a pedir a cualquier sistema de pensamiento. «Verdad» y «realidad» son palabras teológicas, no científicas.

Pero volvamos a los axiomas de Euclides. Hasta el momento sólo hemos presentado las cinco «nociones comunes». Había también en la lista cinco axiomas más que eran específicamente aplicables a la geometría, y éstos fueron más tarde denominados «postulados». El primero de estos postulados era:

1) Es posible trazar una línea recta desde cualquier punto a cualquier otro punto.

Esto parece eminentemente aceptable, pero ¿está usted seguro? ¿Puede usted demostrar que puede trazar una línea desde la Tierra hasta el Sol? Si pudiera usted de alguna manera situarse en el Sol y mantener a la Tierra inmóvil en su órbita, y de alguna manera tender una cuerda desde la Tierra hasta el Sol y ponerla absolutamente tirante, esa cuerda representaría una línea de la Tierra al Sol. Usted está seguro de que éste es un razonable «experimento mental», y yo también estoy seguro de ello, pero sólo suponemos que las cosas pueden ser así. No podemos presentarlas de forma práctica ni demostrarlas matemáticamente.

Y, dicho sea de paso, ¿qué es una línea recta? Yo acabo de realizar, simplemente, la suposición de que, si se tensa una cuerda hasta dejarla completamente tirante, tiene una forma que nosotros reconoceríamos como lo que llamamos una línea recta. Pero ¿qué es esa forma? Simplemente, no podemos hacer nada mejor que decir: «Una línea recta es algo muy muy fino y muy, muy recto», o, parafraseando a Gertrude Stein: «Una línea recta es una línea recta que es una línea recta…».

Euclides define una línea recta como «una línea que reposa uniformemente con los puntos que contiene», pero no me agradaría tener que intentar describir lo que quiere decir con eso a un estudiante que se estuviera iniciando en el estudio de la geometría.

Otra definición dice que: Una línea recta es la distancia más corta entre dos puntos.

Pero si se pone absolutamente tirante una cuerda, no puede ir desde el punto situado en un extremo hasta el punto situado en el otro extremo por ninguna distancia más corta, de modo que decir que una línea recta es la distancia más corta entre dos puntos es lo mismo que decir que tiene la forma de una cuerda absolutamente tirante, y todavía podemos decir: «¿Y qué forma es ésa?».

En la geometría moderna, las líneas rectas no se definen. Lo que se dice, en esencia, es esto: Llamemos línea a algo que tenga las siguientes propiedades en relación con otros términos indefinidos tales como «punto», «plano», «entre», «continuo», etcétera. Y se enuncian luego las propiedades.

Sea como sea, he aquí los restantes postulados de Euclides:

2) Una línea recta finita puede prolongarse continuamente en una línea recta.

3) Se puede describir un círculo con cualquier punto como centro y cualquier distancia como radio.

4) Todos los ángulos rectos son iguales.

5) Si una línea recta que incide sobre dos líneas rectas forma los ángulos interiores del mismo lado menores de dos ángulos rectos, las dos líneas rectas, si se prolongan indefinidamente, se encuentran en el lado en que están los ángulos menores que dos ángulos rectos.

Tome a cualquier persona inteligente que haya estudiado aritmética y que haya oído hablar de líneas rectas y de círculos, dele los diez axiomas uno a uno, dejándole pensar unos momentos, y a cada uno de los nueve primeros responderá: «¡Claro!». Recite luego el quinto postulado, y seguramente exclamará: «¿Qué?».

Y pasará bastante tiempo antes de que comprenda de qué se trata. De hecho, yo no me pondría a explicarlo sin servirme de un diagrama como el siguiente.

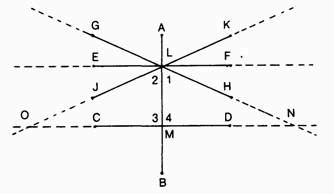
Consideremos dos de las líneas de trazo continuo que aparecen en el diagrama: la que va desde el punto C hasta el punto D pasando por el punto M (a la que llamaremos CD, por los puntos de sus extremos) y la que pasa por los puntos G, L y H (línea GH). Una tercera línea, que pasa por los puntos A, L, M y B (línea AB), atraviesa las líneas GH y CD, formando ángulos con ambas.

Si suponemos que la línea CD es perfectamente horizontal y la línea AB perfectamente vertical, entonces los cuatro ángulos formados al cruzarse las dos líneas (ángulos CMB, BMD, DML y LMC) son ángulos rectos y son todos iguales (por el postulado 4). En particular, los ángulos DML y LMC, que he señalado en el diagrama como 3 y 4, son iguales y son ambos ángulos rectos.

(No me he molestado en definir «perfectamente horizontal», «perfectamente vertical» ni «cruzar», y tampoco en explicar por qué el cruce de una línea perfectamente horizontal con una línea perfectamente vertical produce cuatro ángulos rectos, pero no pretendo ser completamente riguroso. Esta clase de cosa se puede hacer rigurosa, pero sólo a costa de muchas más explicaciones de las que estoy dispuesto a dar).

Consideremos ahora la línea GH. No es perfectamente horizontal. Eso significa que los ángulos que produce en su intersección (no he definido «intersección») con la línea AB no son ángulos rectos y no son todos iguales. Se puede mostrar que los ángulos ALH y GLB son iguales y que los ángulos HLB y GLA son iguales, pero que ninguno de los que componen el primer par es igual a ninguno de los que componen el segundo par. En particular, el ángulo GLB (rotulado con el número 2) no es igual al ángulo HLB (rotulado con el número 1).

Supongamos que trazamos la línea EF, pasando a través de L, y que la línea EF es (como la línea CD) perfectamente horizontal. En ese caso forma cuatro ángulos rectos iguales en su intersección con la línea AB. En particular, los ángulos FLB y ELB son ángulos rectos. Pero el ángulo HLB está contenido dentro del ángulo FLB (¿qué significa «está contenido dentro de»?) y sobra espacio. Puesto que el ángulo HLB es solamente parte de FLB y este último es un ángulo recto, entonces el ángulo HLB (ángulo 1) es menor que un ángulo recto, de acuerdo con la quinta «noción común».

Del mismo modo, comparando el ángulo ELB, que se sabe que es un ángulo recto, con el ángulo GLB (ángulo 2), podemos mostrar que el ángulo 2 es mayor que un ángulo recto.

Los «ángulos interiores» del diagrama son los del lado de la línea GH situado frente a la línea CD, y los del lado de línea CD situado frente a la línea GH. En otras palabras, son los ángulos 1,2,3 y 4.

El quinto postulado habla de «los ángulos interiores del mismo lado», esto es, el 1 y el 4 en un lado y el 2 y el 3 en el otro. Puesto que sabemos que 3 y 4 son ángulos rectos, que 1 es menor que un ángulo recto y que 2 es mayor que un ángulo recto, podemos decir que los ángulos interiores de un lado, 1 y 4, suman menos de dos ángulos rectos, mientras que los ángulos interiores del otro suman más de dos ángulos rectos.

El quinto postulado afirma ahora que, si se prolongan, las líneas GH y CD se cortarán en el lado en que se hallan situados los ángulos interiores cuya suma es menor de dos rectos. Y, en efecto, si mira usted el diagrama, verá que, si se prolongan las líneas GH y CD a ambos lados (líneas de puntos), se cortarán en el punto N, en el lado de los ángulos interiores 1 y 4. Por el otro lado se irán separando cada vez más y, evidentemente, nunca se cortarán.

Por otra parte, si se traza la línea JK a través de L, la situación se invertiría. El ángulo 2 sería menor que un ángulo recto y el ángulo 1 sería mayor que un ángulo recto (donde el ángulo 2 es ahora el ángulo JLB y el ángulo 1 es ahora el ángulo KLB). En ese caso, los ángulos interiores 2 y 3 tendrían una suma menor que dos ángulos rectos, y los ángulos interiores 1 y 4 sumarían más que dos rectos. Si se prolongaran las líneas JK y CD (líneas de puntos), se cortarían en el punto O, en el lado de los ángulos interiores 2 y 3. Por el otro lado irían divergiendo cada vez más.

Ahora que he explicado largamente el quinto postulado (y aun y todo sólo a costa de ser muy poco riguroso), tal vez estaría usted dispuesto a exclamar: «Oh, sí, claro. ¡Desde luego! ¡Es evidente!».

Tal vez, pero si algo es evidente no debería necesitar centenares de palabras de explicación. No he tenido que explayarme respecto a ninguno de los otros nueve axiomas, ¿verdad?

Pues bien, habiendo explicado el quinto postulado, ¿lo he demostrado? No, solamente he interpretado el significado de las palabras y, luego, he señalado al diagrama y he dicho: «Y, efectivamente, si mira usted el diagrama, verá…».

Pero eso no es más que un solo diagrama. Y se refiere a una línea perfectamente vertical que cruza dos líneas, una de las cuales es perfectamente horizontal. ¿Y si ninguna de las líneas es vertical ni horizontal y ninguno de los ángulos interiores son ángulos rectos? El quinto postulado se aplica a cualquier línea que atraviese cualesquiera otras dos líneas, y, ciertamente, yo no he demostrado eso.

Yo puedo trazar un millón de diagramas de tipos diferentes y mostrar que el postulado se cumple en cada caso concreto, pero eso no es suficiente. Tengo que demostrar que se cumple en todos los casos concebibles, y eso no se puede hacer por medio de diagramas. Un diagrama solamente puede aclarar la demostración; la demostración misma debe ser derivada mediante una lógica permisible de premisas más básicas ya demostradas, o presuntas. Esto es lo que yo no he hecho.

Consideremos ahora el quinto postulado desde el punto de vista de las líneas móviles. Supongamos que se hace a la línea GH girar en torno a L como pivote, de tal modo que va acercándose cada vez más a la línea EF, hasta coincidir con ella. (¿Continúa una línea recta siendo línea recta mientras gira de esta manera? Solamente podemos presumir que sí). A medida que la línea GH gira hacia la línea EF, el punto de intersección con la línea CD (punto N) se va alejando más y más hacia la derecha.

Si empezáramos con la línea JK y la hiciéramos girar de modo que acabase coincidiendo con la línea EF, el punto de intersección O se iría alejando más y más a la izquierda. Si considera usted el diagrama y hace unas cuantas señales en él (si tiene que hacerlas), lo verá por usted mismo.

Pero considere la propia línea EF. Cuando GH ha girado finalmente hasta coincidir con la línea EF, podríamos decir que el punto de intersección N se ha alejado una distancia infinita hacia la derecha (cualquier cosa que sea lo que designamos como «distancia infinita»), y cuando la línea JK coincide con la línea EF el punto de intersección O se ha alejado una distancia infinita hacia la izquierda. Por consiguiente, podemos decir que la línea EF y la línea CD se cortan en dos puntos, uno a una distancia infinita a la derecha y otro a una distancia infinita a la izquierda.

O mirémoslo de otra manera. La línea EF, siendo perfectamente horizontal, corta a la línea AB y forma cuatro ángulos rectos iguales. En ese caso, los ángulos 1,2,3 y 4 son todos ángulos rectos y todos iguales. Los ángulos 1 y 4 suman dos ángulos rectos, y también los ángulos 2 y 3.

Pero el quinto postulado dice que la intersección se produce en el lado en que los dos ángulos interiores suman menos que dos ángulos rectos. En el caso de las líneas EF y CD cruzadas por la línea AB, ningún conjunto de ángulos interiores tiene una suma menor que dos ángulos rectos y no puede haber una intersección en ninguno de los dos lados.

Así, pues, hemos demostrado, con dos series de argumentos, primero, que las líneas EF y CD se cortan en dos puntos, localizado cada uno de ellos a una distancia infinita, y, segundo, que las líneas EF y CD no se cortan en absoluto. ¿Hemos encontrado una contradicción y demostrado con ello que algo falla en el conjunto de axiomas de Euclides?

Para evitar una contradicción, podemos decir que producir una intersección a una distancia infinita equivale a decir que no existe intersección. Hay diferentes formas de decir la misma cosa. Aceptar que «decir a» es igual a «decir b» en este caso es congruente con todo el resto de la geometría, así que podemos seguir adelante.

Digamos ahora que dos líneas, tales como EF y CD, que no se cortan mutuamente, son «paralelas» cuando se prolongan a lo largo de cualquier distancia finita.

Evidentemente, sólo hay una línea que pase por L que pueda ser paralela a la línea CD, y esa línea es EF. Cualquier línea que pase por L y que no coincida con la línea EF es (por ligeramente que así sea) o del tipo de la línea GH o de la línea JK, con un ángulo interior en un lado u otro menor que un ángulo recto. Este argumento es pura prestidigitación y carece de rigor, pero nos permite comprender la cuestión y decir: Dada una línea recta y un punto exterior a esa línea, es posible trazar una y solamente una línea recta paralela por ese punto a la línea dada.

Esta proposición es por completo equivalente al quinto postulado de Euclides. Si se suprime el quinto postulado de Euclides y se coloca esta proposición en su lugar, el entero edificio de la geometría euclidiana se mantiene en pie sin el más mínimo temblor.

La versión del postulado que se refiere a las líneas paralelas suena más clara y más fácil de entender que la forma en que Euclides lo expresa porque incluso los escolares principiantes tienen alguna noción del aspecto que ofrecen las paralelas, mientras que pueden no tener ni la más remota idea de lo que son ángulos interiores. Por eso es por lo que los libros de geometría elemental suelen presentar el postulado en esta forma «paralela».

Pero, en realidad, no resulta más claro y más sencillo en esta forma, ya que en cuanto intente uno explicar lo que entiende por «paralela» va a tener que entrar en la cuestión de los ángulos interiores. O, si trata de evitarlo, se meterá en el problema de hablar de líneas de longitud infinita, de intersecciones a una distancia infinita que equivalen a una ausencia de intersección, y eso es peor aún.

Pero el hecho de que yo no haya demostrado el quinto postulado no quiere decir que no pueda demostrarse. Quizás utilizando alguna argumentación extraordinariamente larga, sutil e ingeniosa, sea posible demostrar el quinto postulado por medio de los otros cuatro postulados y de las cinco nociones comunes (o recurriendo a algún axioma adicional no incluido en la lista que, no obstante, sea mucho más simple y más «evidente» que el quinto postulado).

Ay, no. Durante dos mil años los matemáticos han intentado de vez en cuando demostrar el quinto postulado a partir de los otros axiomas, simplemente porque ese maldito quinto postulado era tan largo y tan poco evidente que parecía imposible que fuese un axioma. Bien, pues siempre fracasaron, y parece seguro que deben fracasar. El quinto postulado no se halla contenido en los otros axiomas ni en ninguna lista de axiomas útiles en geometría y más simples que él mismo.

Se puede afirmar, de hecho, que el quinto postulado es el logro más grande de Euclides. En virtud de una extraordinaria percepción, comprendió que, dados los nueve breves y claramente «evidentes» axiomas, no podía demostrar el quinto postulado y que tampoco podía prescindir de él, y que, por consiguiente, pese a lo largo y complicado que era el quinto postulado, tenía que incluirlo entre sus presunciones.

Así, pues, el quinto postulado se mantuvo allí durante dos mil años: largo, desmañanado, desconcertante. Era como una mácula en la perfección, un permanente reproche a una línea de argumentación infinitamente majestuosa por lo demás. Sacaba de sus casillas a los matemáticos.

Y entonces, en 1733, un sacerdote italiano, Girolamo Saccheri, tuvo con respecto al quinto postulado la idea más brillante que jamás había tenido nadie desde los tiempos de Euclides, pero no era lo bastante brillante como para que él mismo se ocupara de ella…

Examinemos eso en el ensayo siguiente.