11

Le forze della natura e l’unificazione della fisica

Come abbiamo spiegato nel capitolo 3, sarebbe molto difficile costruire di getto una teoria unificata completa di tutto ciò che è presente nell’universo. Gli uomini hanno quindi fatto una serie di successivi progressi trovando teorie parziali che descrivono un ambito limitato di accadimenti e trascurando altri effetti o approssimandoli per mezzo di determinati valori numerici. Le leggi della scienza, come le conosciamo oggi, contengono molti numeri – come la misura della carica elettrica dell’elettrone e il rapporto fra la massa del protone e quella dell’elettrone – che non possiamo, almeno per il momento, ricavare dalla teoria. Dobbiamo invece trovarli attraverso l’osservazione e quindi inserirli nelle equazioni. Qualcuno chiama questi numeri «costanti fondamentali», mentre altri li vedono come semplici fattori di correzione.

Qualunque sia il vostro punto di vista, il fatto degno di nota è che i valori di questi numeri sembrano essere stati regolati con estrema precisione al fine di rendere possibile lo sviluppo della vita. Per esempio, se la carica elettrica dell’elettrone fosse stata anche solo leggermente diversa, ciò avrebbe deteriorato l’equilibrio della forza elettromagnetica e gravitazionale nelle stelle, le quali o non sarebbero state in grado di bruciare l’idrogeno e l’elio, o non sarebbero esplose. Alla fine, si spera che troveremo una teoria unificata, completa e coerente, che includa tutte queste teorie parziali come approssimazioni, e che non abbia bisogno di essere corretta in modo da adattarsi ai fatti con l’inserimento di valori numerici arbitrari, come l’intensità della carica dell’elettrone.

La ricerca di una tale teoria è nota come «unificazione della fisica». Einstein spese la maggior parte dei suoi ultimi anni nell’infruttuosa ricerca di una teoria unificata, ma i tempi non erano ancora maturi: c’erano teorie parziali per la gravità e le forze elettromagnetiche, ma si sapeva ancora molto poco sulle forze nucleari. Inoltre, come abbiamo detto nel capitolo 9, Einstein si rifiutava di credere nella realtà della meccanica quantistica. Tuttavia, sembra che il principio di indeterminazione costituisca un carattere fondamentale dell’universo in cui viviamo; una teoria unificata, per poter raggiungere il proprio obiettivo, dovrà quindi necessariamente incorporare questo principio.

Oggi le prospettive di trovare una tale teoria sembrano essere notevolmente migliorate, poiché conosciamo molte più cose intorno all’universo. Dobbiamo comunque guardarci da un eccesso di fiducia – non sarebbe la prima volta che nutriamo false speranze! Agli inizi del XX secolo, per esempio, si pensava che fosse possibile spiegare ogni cosa nei termini delle proprietà della materia continua, come l’elasticità e la conduzione del calore. La scoperta della struttura dell’atomo e del principio di indeterminazione posero clamorosamente fine a queste illusioni. Poi, di nuovo, nel 1928, il fisico e premio Nobel Max Born disse a un gruppo di persone in visita all’Università di Gottinga che «La fisica, come la conosciamo oggi, entro sei mesi potrà dirsi una scienza compiuta». La sua fiducia si basava sulla recente scoperta, da parte di Dirac, dell’equazione che governava l’elettrone. Si pensava che un’equazione simile governasse anche il protone, l’unica altra particella conosciuta all’epoca, e che la sua scoperta avrebbe segnato la conclusione della ricerca nell’ambito della fisica teorica. Arrivò invece la scoperta del neutrone e delle forze nucleari, che seppellì anche questa illusione. Detto questo, ci sono comunque motivi di cauto ottimismo per sperare che oggi potremmo essere vicini alla fine della ricerca delle leggi ultime della natura.

Nella meccanica quantistica si ritiene che le forze o interazioni tra le particelle materiali siano tutte trasportate da particelle. Una particella materiale, come un elettrone o un quark, emette cioè una particella portatrice di forza. Il rinculo dovuto a questa emissione altera la velocità della particella materiale, per lo stesso motivo per cui un cannone si ritrae indietro dopo aver sparato. La particella portatrice di forza entra quindi in collisione con un’altra particella materiale e ne viene assorbita, modificando così il moto di quest’ultima particella. Il risultato netto di questo processo di emissione e assorbimento è lo stesso che si avrebbe se tra le due particelle materiali fosse stata esercitata direttamente una forza.

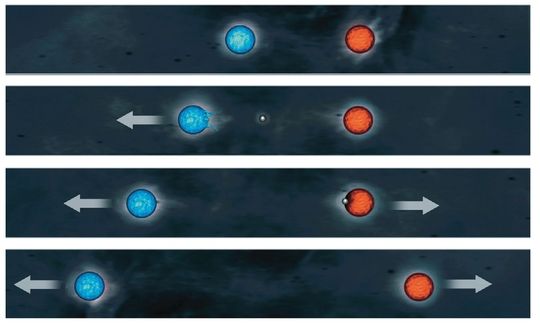
Figura 33. Scambio di particelle Secondo la teoria quantistica, le forze hanno origine dallo scambio di particelle portatrici di forza.

Ciascuna forza viene trasmessa da un proprio particolare tipo di particelle portatrici di forza. Se le particelle portatrici di forza hanno una massa elevata, sarà difficile produrle e scambiarle su grande distanza: le forze da esse trasportate avranno quindi solo un breve raggio d’azione. Dal lato opposto, se particelle portatrici di forza non hanno una massa propria, le forze corrispondenti avranno un lungo raggio d’azione. Le particelle portatrici di forza scambiate tra particelle materiali vengono chiamate «particelle virtuali» poiché, a differenza delle particelle reali, non possono essere individuate direttamente da un rilevatore di particelle. Sappiamo comunque che esistono perché hanno un effetto che possiamo misurare: esse danno cioè origine alle forze che agiscono tra le particelle materiali.

Le particelle portatrici di forza possono essere raggruppate in quattro categorie. Occorrerebbe però sottolineare che questa divisione in quattro classi è qualcosa di artificiale; essa risulta utile per la costruzione di teorie parziali, ma potrebbe non corrispondere a una realtà più profonda. In definitiva, la maggior parte dei fisici spera di trovare una teoria unificata che spieghi tutte le quattro forze come diversi aspetti di una singola forza. In effetti, molti direbbero che questo è oggi l’obiettivo principale della fisica.

La prima categoria è la forza gravitazionale. Questa forza è universale: ogni particella, cioè, risente della forza di gravità, a seconda della sua massa o energia. L’attrazione gravitazionale è attribuita allo scambio di particelle virtuali dette gravitoni. La gravità è di gran lunga la più debole tra le quattro forze; è talmente debole che non ci renderemmo neppure conto della sua esistenza se non fosse per due proprietà speciali da essa possedute: può agire su grandi distanze ed è sempre attrattiva. Ciò significa che le debolissime forze gravitazionali tra le singole particelle di due corpi di grande massa, come la Terra e il Sole, possono sommarsi fino a produrre una forza significativa. Le altre tre forze, invece, o hanno un breve raggio d’azione, o sono a volte attrattive e a volte repulsive, così che tendono a cancellarsi.

La categoria successiva è quella della forza elettromagnetica, che interagisce con le particelle dotate di carica elettrica, come gli elettroni e i quark, ma non con quelle prive di carica, come i neutrini. Essa è molto più forte della forza gravitazionale: la forza elettromagnetica tra due elettroni è circa un milione di milioni di milioni di milioni di milioni di milioni di milioni (1 seguito da 42 zeri) di volte superiore alla forza gravitazionale. Esistono però due tipi di carica elettrica: quella positiva e quella negativa. La forza esercitata tra due cariche positive è repulsiva, così come la forza tra due cariche negative, mentre quella tra una carica positiva e una negativa è attrattiva.

Un corpo di grandi dimensioni, come la Terra o il Sole, contiene grosso modo lo stesso numero di cariche positive e negative. Pertanto, le forze attrattive e repulsive esercitate tra le singole particelle si cancellano quasi totalmente a vicenda, e la forza elettromagnetica netta è quindi estremamente bassa. Le forze elettromagnetiche dominano però sulle piccole scale, a livello di atomi e molecole. L’attrazione elettromagnetica tra gli elettroni (che hanno carica negativa) e i protoni del nucleo (dotati di carica positiva) fa sì che gli elettroni orbitino intorno al nucleo dell’atomo, così come l’attrazione gravitazionale fa sì che la Terra orbiti intorno al Sole. L’attrazione elettromagnetica è attribuita allo scambio di un gran numero di particelle virtuali dette fotoni. Anche in questo caso, i fotoni che vengono scambiati sono particelle virtuali. Tuttavia, quando un elettrone passa da un’orbita più esterna a una più vicina al nucleo, viene liberata una certa quantità di energia e viene emesso un fotone reale, che può essere osservato dall’occhio umano sotto forma di luce visibile, se ha la giusta lunghezza d’onda, o da un rilevatore di fotoni, come una pellicola fotografica. Analogamente, se un fotone reale si scontra con un atomo, può far spostare un elettrone da un’orbita più vicina al nucleo a una più esterna. Questo spostamento consuma l’energia del fotone, che viene così assorbito.

La terza categoria è costituita dalla cosiddetta forza nucleare debole. Nella nostra vita quotidiana, noi non entriamo direttamente in contatto con questa forza. Essa, comunque, è responsabile della radioattività, cioè del decadimento dei nuclei atomici. La forza nucleare debole non fu chiaramente compresa fino al 1967, quando Abdus Salam (dell’Imperial College di Londra) e Steven Weinberg (di Harvard) proposero due teorie che unificavano questa interazione con la forza elettromagnetica, così come – circa un secolo prima – Maxwell aveva unificato l’elettricità e il magnetismo. Le predizioni della teoria concordavano così bene con gli esperimenti che, nel 1979, Salam e Weinberg ricevettero il premio Nobel per la fisica, insieme a Sheldon Glashow (anche lui di Harvard), che aveva a sua volta proposto simili teorie unificate delle forze elettromagnetica e nucleare debole.

La quarta categoria, quella della forza nucleare forte, è la più forte tra le quattro interazioni fondamentali. Si tratta di un’altra forza con cui non abbiamo diretto contatto, ma è quella che garantisce la coesione della maggior parte del mondo in cui viviamo. Essa è responsabile del legame che unisce i quark all’interno del protone e del neutrone, e di quello fra i protoni e i neutroni nel nucleo di un atomo. Senza la forza nucleare forte, la repulsione elettrica fra i protoni (carichi positivamente) farebbe esplodere tutti i nuclei atomici presenti nell’universo – tranne quelli dell’idrogeno, i cui nuclei sono formati da un singolo protone. Si ritiene che questa forza sia trasportata da una particella, chiamata gluone, che interagisce solo con se stessa e con i quark.

Il successo dell’unificazione delle forze elettromagnetica e nucleare debole condusse a una serie di tentativi volti a combinare queste ultime con la forza nucleare forte in una cosiddetta «grande teoria unificata» (GTU). Questo appellativo, però, è un po’ esagerato: le teorie nate da tali sforzi, infatti, non sono poi così grandi, né sono pienamente unificate, dato che non includono la gravità. Esse, inoltre, non si possono propriamente considerare come teorie complete, poiché contengono un numero di parametri i cui valori non possono essere ricavati dalla teoria stessa ma devono essere scelti appositamente in modo da ottenere una concordanza con gli esperimenti. Ciononostante, queste teorie potrebbero rappresentare un passo avanti verso una teoria completa, pienamente unificata.

La principale difficoltà nell’individuazione di una teoria che unifichi la gravità con le altre forze consiste nel fatto che la teoria della gravità – la relatività generale – è l’unica a non essere una teoria quantistica: essa, cioè, non tiene conto del principio di indeterminazione. Dunque, dato che le teorie parziali delle altre forze dipendono sostanzialmente dalla meccanica quantistica, per unificare la gravità con le altre teorie occorrerà trovare un modo per incorporare questo principio nella relatività generale; in altre parole, bisognerà trovare una teoria quantistica della gravità, un compito che finora nessuno è stato in grado di portare a termine.

Il motivo per cui l’elaborazione di una teoria quantistica della gravità si è dimostrata un compito tanto arduo ha a che vedere con il fatto che il principio di indeterminazione implica che persino lo spazio «vuoto» sia pieno di coppie di particelle e antiparticelle virtuali. Se non ci fossero – se cioè lo spazio «vuoto» fosse davvero completamente vuoto –, significherebbe che tutti i campi, come il campo gravitazionale e quello elettromagnetico, dovrebbero avere un valore pari esattamente a zero. Il valore di un campo e la sua velocità di variazione nel tempo sono però simili alla posizione e alla velocità (ossia, alla variazione di posizione) di una particella. Ora, il principio di indeterminazione implica che quanto più è alta la precisione con cui conosciamo una di queste quantità, tanto più è bassa l’accuratezza con cui possiamo conoscere l’altra. Pertanto, qualora un campo nello spazio vuoto avesse un valore fisso pari esattamente a zero, avremmo allora sia un valore preciso (zero, appunto), sia una velocità di variazione altrettanto precisa (zero anche in questo caso, visto che il valore sarebbe fisso), in violazione del suddetto principio. Nel valore del campo deve quindi esserci una certa quantità minima di indeterminazione, le cosiddette fluttuazioni quantistiche.

Possiamo concepire queste fluttuazioni come coppie di particelle che appaiono insieme in un determinato istante, quindi si separano e infine tornano a unirsi e si annichilano a vicenda. Si tratta di particelle virtuali, come le particelle che trasportano la forza: a differenza delle particelle reali, non è possibile osservarle direttamente con un rilevatore di particelle. È però possibile misurare i loro effetti indiretti, per esempio piccole variazioni nell’energia delle orbite degli elettroni, e tali effetti risultano in accordo, con un notevole grado di precisione, con le predizioni teoriche. Nel caso di fluttuazioni del campo elettromagnetico, queste particelle sono fotoni virtuali, e nel caso di fluttuazioni del campo gravitazionale, esse sono gravitoni virtuali. Nel caso di fluttuazioni dei campi della forza debole e di quella forte, invece, queste coppie virtuali sono coppie di particelle materiali, come elettroni o quark, e delle loro rispettive antiparticelle.

Figura 34. Diagramma di Feynman di una coppia virtuale di particella/antiparticella

Applicato all’elettrone, il principio di indeterminazione ci dice che anche nello spazio vuoto appaiono continuamente coppie virtuali di particelle/antiparticelle, che si annichilano poi a vicenda.

Il problema è che le particelle virtuali hanno una loro energia. Di fatto, poiché esistono un numero infinito di coppie virtuali di particelle, esse dovrebbero avere una quantità infinita di energia e quindi, secondo la famosa equazione di Einstein E = mc² (si veda il capitolo 5), dovrebbero avere una quantità infinita di massa. Stando alla relatività generale, ciò significa che la loro gravità dovrebbe incurvare l’universo riducendolo a dimensioni infinitamente piccole. Ma questo, come possiamo ben vedere, non accade! Simili quantità infinite apparentemente assurde compaiono anche nelle altre teorie parziali – quelle delle forze elettromagnetica, nucleare debole e nucleare forte –, ma in tutti questi casi è possibile rimuovere le infinità attraverso un procedimento chiamato «rinormalizzazione», così che per tali forze siamo riusciti a creare le rispettive teorie quantistiche.

Con la rinormalizzazione vengono introdotte nuove quantità infinite che hanno l’effetto di cancellare le infinità che emergono nella teoria. Non è però necessario che le cancellino esattamente: è possibile scegliere le nuove infinità in modo tale da lasciare alcuni piccoli resti, che vengono indicati come le quantità rinormalizzate presenti nella teoria.

Anche se questa tecnica è alquanto dubbia sotto il profilo matematico, in pratica essa sembra comunque funzionare, ed è stata usata con le teorie della forza forte, di quella debole e di quella elettromagnetica per fare delle predizioni che si accordano, con uno straordinario grado di precisione, con le osservazioni empiriche. Dal punto di vista del tentativo di trovare una teoria completa, la rinormalizzazione presenta però un grave inconveniente, poiché di fatto essa prevede che i valori reali delle masse e delle intensità delle forze non possano essere ricavati dalla teoria stessa, ma debbano essere scelti in modo da adeguarsi alle osservazioni. Quando si cerca di usare la rinormalizzazione per rimuovere le quantità infinite dalla relatività generale, sono soltanto due quantità che possono essere corrette: la forza di gravità e il valore della costante cosmologica, il termine che Einstein introdusse nelle sue equazioni mosso dalla convinzione che l’universo non si stesse espandendo (si veda il capitolo 7). È emerso però che la correzione di questi valori non è sufficiente a rimuovere tutte le infinità. Ci resta quindi in mano una teoria quantistica della gravità che sembra predire che certe quantità, come la curvatura dello spazio-tempo, siano realmente infinite, mentre possiamo osservare e misurare che esse sono perfettamente finite.

Si sospettava da tempo che sarebbe emerso questo problema nel combinare la relatività generale e il principio di indeterminazione, ma tali sospetti vennero infine confermati nel 1972 da calcoli dettagliati. Quattro anni dopo fu avanzata l’ipotesi di una possibile soluzione, chiamata «supergravità». Sfortunatamente, i calcoli richiesti per scoprire se nella supergravità rimanesse o meno qualche infinità non cancellata erano talmente lunghi e difficili che nessuno era preparato ad affrontarli. Si stimava che anche con un computer ci sarebbero voluti anni, e le possibilità di compiere almeno un errore – e probabilmente anche più di uno – erano altissime. In sostanza, si avrebbe avuto la certezza di essere giunti alla risposta corretta solo se qualcun altro avesse ripetuto i calcoli attendendo la stessa risposta: una prospettiva che non sembrava davvero molto promettente. Nonostante questi problemi, e nonostante il fatto che le particelle delle teorie della supergravità non sembravano corrispondere alle particelle effettivamente osservate, la maggior parte degli scienziati credeva che la teoria potesse essere migliorata e che costituisse probabilmente la risposta giusta al problema dell’unificazione della gravità con le altre forze. Nel 1984, però, ci fu un notevole cambiamento d’opinione in favore delle cosiddette teorie delle stringhe (o corde).

Prima dell’avvento della teoria delle stringhe, si pensava che ogni particella fondamentale occupasse un singolo punto dello spazio. Nelle teorie delle stringhe, invece, gli oggetti fondamentali non sono particelle puntiformi, bensì entità che hanno una lunghezza ma nessun’altra dimensione, come un pezzo di filo infinitamente sottile. Queste stringhe possono avere dei capi (le cosiddette stringhe aperte) o possono congiungersi con se stesse in anelli chiusi (stringhe chiuse). Una particella occupa un determinato punto dello spazio in ogni istante del tempo. Una stringa, invece, occupa una linea nello spazio in ogni istante del tempo. Due stringhe possono unirsi insieme per formare una singola stringa; nel caso delle stringhe aperte, esse si uniscono semplicemente alle estremità, mentre nel caso delle stringhe chiuse si ha una struttura simile a quella delle due gambe di un paio di pantaloni. Analogamente, una singola stringa può dividersi in due stringhe.

Ma se gli oggetti fondamentali dell’universo sono stringhe, che cosa sono allora le particelle puntiformi che ci sembra di osservare nei nostri esperimenti? Nelle teorie delle stringhe, quelle che prima erano concepite come differenti particelle puntiformi sono ora rappresentate come diverse onde che si propagano sulla stringa stessa, come le onde sul filo vibrante di un aquilone. Tuttavia le stringhe, e le vibrazioni che si propagano su di esse, sono talmente sottili che nemmeno con le nostre migliori tecnologie siamo in grado di definire la loro forma; e così, in tutti i nostri esperimenti, esse si comportano come minuscoli punti privi di caratteri distintivi. Immaginate di osservare un granello di polvere: guardandolo molto da vicino, o sotto una lente d’ingrandimento, potreste scoprire che ha una forma irregolare, o magari anche simile a quella di una corda, ma da una certa distanza esso sembra un semplice punto privo di tratti distintivi.

Nella teoria delle stringhe, l’emissione o l’assorbimento di una particella da parte di un’altra corrisponde alla divisione o al congiungimento delle stringhe. Per esempio, nelle teorie delle particelle la forza gravitazionale che il Sole esercita sulla Terra veniva rappresentata come causata dall’emissione delle particelle portatrici di forza dette gravitoni da parte di una particella materiale situata nel Sole e dal loro assorbimento da una particella materiale situata nella Terra. Nella teoria delle stringhe, invece, questo processo corrisponde a un tubo o a un condotto a forma di H (in un certo senso, la teoria delle stringhe assomiglia un po’ all’idraulica). I due trattini verticali dell’H corrispondono alle particelle nel Sole e nella Terra, mentre la barretta orizzontale corrisponde al gravitone che viaggia tra di loro.

La teoria delle stringhe ha una storia curiosa. Essa venne inventata sul finire degli anni Sessanta nel tentativo di trovare una teoria per descrivere la forza forte. L’idea di fondo era che le particelle come il protone e il neutrone potessero essere considerate come onde in movimento lungo una corda. Le forze forti tra le particelle corrisponderebbero così a pezzi di corda che verrebbero a sistemarsi tra altri pezzi di corda, un po’ come in una ragnatela. Perché questa teoria potesse dare il valore effettivamente osservato della forza forte tra le particelle, tali corde – o stringhe – dovevano essere simili a elastici con un potenziale di trazione di circa dieci tonnellate.

Nel 1974, Joël Scherk (dell’École Normale Supérieure di Parigi) e John Schwarz (del California Institute of Technology) pubblicarono un articolo in cui dimostravano che la teoria delle stringhe potrebbe descrivere la natura della forza gravitazionale, ma solo se la tensione nella stringa fosse di circa un migliaio di milioni di milioni di milioni di milioni di milioni di milioni di tonnellate (1 seguito da 39 zeri). Su scale di lunghezza ordinarie, le predizioni della teoria delle stringhe coinciderebbero esattamente con quelle della relatività generale, differenziandosi però da queste ultime su distanze estremamente piccole, minori di un millesimo di milionesimo di milionesimo di milionesimo di milionesimo di milionesimo di centimetro (vale a dire, un centimetro diviso per 1 seguito da 33 zeri). Il loro lavoro, tuttavia, non ricevette molta attenzione, poiché proprio intorno a quel periodo la maggior parte degli scienziati abbandonò la teoria originaria delle stringhe sulla forza forte a favore della teoria basata su quark e gluoni, che sembrava accordarsi meglio con i dati delle osservazioni. Scherk morì in circostanze tragiche (soffriva di diabete, e cadde in coma mentre vicino a lui non c’era nessuno che gli potesse praticare un’iniezione di insulina), così Schwarz rimase da solo come quasi unico sostenitore della teoria delle stringhe, ma ora con la proposta di un valore molto più elevato per la tensione delle corde.

Figura 35. Diagramma di Feynman nella teoria delle stringhe Nella teoria delle stringhe, l’origine delle forze a lungo raggio non è vista in uno scambio di particelle portatrici di forza, quanto piuttosto in una connessione di tubi.

Nel 1984 l’interesse per le stringhe si riaccese all’improvviso, a quanto pare per due ragioni. Una era che, in realtà, non si stavano facendo molti progressi sulla strada della dimostrazione che la supergravità garantisse valori finiti o che potesse spiegare i tipi di particelle che di fatto osserviamo. L’altra fu la pubblicazione di un ulteriore articolo di John Schwarz, questa volta insieme a Mike Green, del Queen Mary College di Londra. L’articolo dimostrava che la teoria delle stringhe potrebbe essere in grado di spiegare l’esistenza di particelle dotate di chiralità sinistrorsa intrinseca, come alcune delle particelle che osserviamo nella realtà, reciprocamente speculari ma non direttamente sovrapponibili. (Il comportamento della maggior parte delle particelle rimarrebbe lo stesso anche se cambiassimo la configurazione dell’esperimento riflettendo il tutto in uno specchio; il comportamento di queste particelle, però, verrebbe a cambiare. È un po’ come se fossero mancine – o destrorse – anziché essere ambidestre.) Quali che fossero le ragioni, un gran numero di persone iniziarono comunque ben presto a lavorare sulla teoria delle stringhe e ne venne sviluppata una nuova versione, che sembrava in grado di spiegare i tipi di particelle che osserviamo.

Anche le teorie delle stringhe conducono a certe quantità infinite, ma si pensa che, nella versione corretta, queste infinità verranno eliminate (benché la cosa non sia ancora del tutto certa). Le teorie delle stringhe, però, presentano un problema più grande: sembrano cioè essere consistenti solo a condizione che lo spazio-tempo abbia o dieci o 26 dimensioni, al posto delle solite quattro! Naturalmente, le ulteriori dimensioni spazio-temporali sono un luogo comune nella fantascienza. In effetti, esse offrono un modo ideale per superare la normale restrizione imposta dalla relatività generale, per la quale non è possibile viaggiare indietro nel tempo o a una velocità superiore a quella della luce (si veda il capitolo 10). L’idea è quella di prendere una scorciatoia passando per le ulteriori dimensioni. Possiamo raffigurarci questo concetto nel modo seguente. Immaginiamo che lo spazio in cui viviamo abbia soltanto due dimensioni e sia incurvato come la superficie di un anello dell’ancora o di una ciambella. Se ci trovassimo sul bordo interno dell’anello e volessimo raggiungere un punto sul lato opposto, dovremmo muoverci in cerchio lungo il bordo interno dell’anello stesso fino a raggiungere la nostra destinazione. Se però fossimo in grado di viaggiare in una terza dimensione, potremmo abbandonare la superficie dell’anello e tagliare passando dritti per il buco.

Ma perché, se tutte queste ulteriori dimensioni esistono realmente, noi non le percepiamo? Perché vediamo soltanto tre dimensioni spaziali e una temporale? L’ipotesi è che le altre dimensioni non siano come quelle alle quali siamo abituati. Esse sarebbero cioè arrotolate in uno spazio estremamente ridotto, dell’ordine di un milionesimo di milionesimo di milionesimo di milionesimo di milionesimo di centimetro. Si tratta di uno spazio talmente piccolo che semplicemente non lo percepiamo; vediamo soltanto le tre dimensioni spaziali e quella temporale, nelle quali lo spazio-tempo è quasi piatto. Per visualizzare questo concetto, pensate alla superficie di un filo di paglia. Se la guardate da vicino, vedete che la superficie è bidimensionale. In altre parole, la posizione di un punto sul filo di paglia è descritta da due numeri, uno misurato sulla lunghezza del filo e l’altro sulla sua circonferenza. Quest’ultima, però, è di gran lunga più piccola della sua lunghezza. Così, se guardiamo il filo di paglia da lontano, non vediamo il suo spessore e ci sembra essere unidimensionale: in altri termini, ci sembra che per specificare la posizione di un punto ci sia bisogno soltanto di indicare la misura presa sulla lunghezza del filo. Secondo i teorici delle stringhe, lo stesso discorso vale anche per lo spazio-tempo: su una scala estremamente ridotta è decadimensionale e altamente incurvato, ma su scale maggiori noi non ne vediamo la curvatura o le ulteriori dimensioni.

Se questo quadro è corretto, esso porta cattive notizie per gli aspiranti viaggiatori dello spazio: le ulteriori dimensioni, infatti, sarebbero di gran lunga troppo piccole per permettere il passaggio di un’astronave. Ma emerge anche un altro problema considerevole, questa volta per gli scienziati: perché alcune delle dimensioni, ma non tutte, dovrebbero essere arrotolate in una piccola palla? Presumibilmente, nei primissimi stadi della vita dell’universo, tutte le dimensioni saranno state molto incurvate. Ma perché, allora, una dimensione temporale e tre spaziali si sono poi spianate, mentre le altre dimensioni sono rimaste saldamente arrotolate?

Una possibile risposta è data dal principio antropico, che si può parafrasare dicendo: vediamo che l’universo è fatto in questo particolare modo perché, se esso fosse diverso, non potremmo essere qui a contemplarlo. Ci sono due versioni del principio antropico, quella debole e quella forte. Il principio antropico debole afferma che in un universo molto grande o infinito nello spazio e/o nel tempo, le condizioni necessarie per lo sviluppo della vita intelligente si troveranno solo in certe regioni delimitate nello spazio e nel tempo. Gli esseri intelligenti presenti in tali regioni non dovrebbero pertanto stupirsi nel constatare che la regione dell’universo in cui essi vivono soddisfi le condizioni necessarie per la loro esistenza. È un po’ come nel caso di una persona facoltosa che viva in un quartiere ricco senza vedere alcuna traccia di povertà.

Alcuni si spingono molto oltre e propongono una versione forte di questo principio. Secondo questa teoria, esistono o molti universi differenti, o molte regioni differenti di un singolo universo, ciascuna con una propria configurazione iniziale e, forse, con un proprio peculiare insieme di leggi scientifiche. Nella maggior parte di questi universi le condizioni non sarebbero idonee allo sviluppo di organismi complessi; solo nei pochi universi simili al nostro si potrebbero sviluppare degli esseri intelligenti in grado di chiedersi: perché l’universo è fatto proprio in questo particolare modo in cui lo vediamo? La risposta è allora semplice: se fosse stato differente, noi non saremmo qui oggi a porci una tale domanda!

Poche persone contesterebbero la validità o l’utilità del principio antropico debole, mentre ci sono numerose obiezioni che si possono sollevare contro il principio antropico forte come spiegazione dello stato osservato dell’universo. Per esempio, in che senso potremmo dire che tutti questi universi differenti esistono? Se sono veramente separati l’uno dall’altro, ciò che accade in un altro universo non può avere conseguenze osservabili nel nostro. Dovremmo quindi ricorrere al principio di economia ed escludere questi ulteriori universi dalle nostre teorie. Se poi, d’altro lato, essi fossero invece soltanto regioni differenti di un singolo universo, le leggi della scienza dovrebbero essere identiche in ogni regione, dato che altrimenti non sarebbe possibile muoversi senza soluzione di continuità da una regione a un’altra. In questo caso, l’unica differenza tra le regioni sarebbe data dalle loro diverse configurazioni iniziali, così che il principio antropico forte si ridurrebbe di fatto a quello debole.

Il principio antropico ci offre una possibile risposta alla domanda sul perché le ulteriori dimensioni previste dalla teoria delle stringhe sono arrotolate su se stesse. Due dimensioni spaziali non sembrano sufficienti per consentire lo sviluppo di esseri complessi come noi. Per esempio, degli animali bidimensionali che vivessero su una Terra unidimensionale dovrebbero scavalcarsi a vicenda per potersi superare. Se una creatura bidimensionale mangiasse qualcosa che non fosse in grado di digerire completamente, dovrebbe espellere i resti per la stessa via attraverso cui li ha ingeriti, perché se avesse un canale digerente tale da attraversare tutto il suo corpo da una parte all’altra, esso verrebbe di fatto a dividerla in due metà separate: il nostro essere bidimensionale cadrebbe così a pezzi. Similmente, è difficile immaginare come in una creatura bidimensionale potrebbe esistere una forma di circolazione sanguigna.

Ci sarebbero però dei problemi anche nel caso in cui le dimensioni spaziali fossero più di tre. L’attrazione gravitazionale fra due corpi diminuirebbe con l’aumentare della distanza più rapidamente di quanto non faccia in tre dimensioni. (In tre dimensioni, al raddoppiare della distanza la forza gravitazionale si riduce a un quarto. In quattro dimensioni, essa si ridurrebbe a un ottavo, in cinque dimensioni a un sedicesimo e così via.) Di conseguenza, le orbite dei pianeti che, come la Terra, si muovono intorno al Sole, sarebbero instabili: basterebbe la più piccola deviazione da un’orbita perfettamente circolare (come quelle che sarebbero causate dall’attrazione gravitazionale di altri pianeti) per far immettere la Terra su una traiettoria a spirale che la porterebbe ad allontanarsi sempre di più dal Sole o a precipitare in esso. In altre parole, il genere umano finirebbe o congelato o incenerito. Di fatto, poi, a causa di questo comportamento della gravità in relazione alla distanza in più di tre dimensioni spaziali, nemmeno lo stesso Sole potrebbe esistere in uno stato stabile, con un equilibrio tra la pressione interna e la gravità. Esso finirebbe o per andare in pezzi, o per collassare su se stesso fino a formare un buco nero – e, in un caso come nell’altro, non potrebbe più essere molto utile come fonte di luce e di calore per la vita sulla Terra. Su una scala più piccola, le forze elettriche che causano il movimento orbitale degli elettroni intorno al nucleo di un atomo si comporterebbero nello stesso modo delle forze gravitazionali. Di conseguenza, gli elettroni o sfuggirebbero completamente dall’atomo, oppure cadrebbero nel suo nucleo seguendo una traiettoria a spirale; nell’uno come nell’altro caso, non potrebbero esistere gli atomi quali li conosciamo oggi.

Sembra quindi chiaro che la vita, almeno come la conosciamo noi, può esistere solo in regioni dello spazio-tempo in cui una dimensione temporale ed esattamente tre dimensioni spaziali non siano fortemente arrotolate su se stesse. Ciò significa che ci potremmo appellare al principio antropico debole, ammesso che sia possibile dimostrare che la teoria delle stringhe perlomeno permetta l’esistenza di tali regioni dell’universo – e, in effetti, sembra che la teoria delle stringhe la permetta. Potrebbero benissimo esistere anche altre regioni dell’universo (o altri universi, qualunque cosa possa significare quest’espressione) in cui tutte le dimensioni siano fortemente arrotolate su se stesse, o in cui le dimensioni quasi piatte siano più di quattro; tuttavia, in tali regioni non ci sarebbero esseri intelligenti in grado di osservare questa differenza nel numero delle dimensioni effettive.

Un altro problema legato alla teoria delle stringhe è che ce ne sono almeno cinque varianti diverse (due delle stringhe aperte e tre teorie differenti delle stringhe chiuse) e milioni di modi in cui le ulteriori dimensioni previste dalla teoria delle stringhe potrebbero arrotolarsi su se stesse. Perché dovremmo scegliere proprio una determinata teoria delle stringhe e un particolare tipo di arrotolamento? Per un certo tempo sembrò che non ci fossero risposte a questa domanda, così che i progressi rimasero fermi. Poi, a partire dal 1994 circa, i ricercatori iniziarono a scoprire le cosiddette dualità: differenti teorie delle stringhe e diversi tipi di arrotolamento delle dimensioni extra potevano condurre ai medesimi risultati sul piano delle nostre quattro dimensioni standard. Inoltre, a fianco delle particelle (che occupano un singolo punto dello spazio) e delle stringhe (che sono delle linee), i ricercatori scoprirono anche altri oggetti chiamati «p-brane», che si estendevano in due o più dimensioni nello spazio. (Una particella può essere considerata come una 0-brana e una stringa come una 1-brana, ma c’erano anche p-brane con p compreso tra 2 e 9. Una 2-brana può essere pensata come qualcosa di simile a una membrana bidimensionale. È però più difficile rappresentarsi visivamente le p-brane che si sviluppano in un numero più alto di dimensioni.) Ciò che queste scoperte sembrano indicare è che c’è una sorta di democrazia (nel senso di avere uguali voci in capitolo) tra le teorie della supergravità, delle stringhe e delle p-brane: esse, cioè, sembrano essere in accordo le une con le altre, ma nessuna di loro può essere ritenuta più basilare delle altre. Pare piuttosto che tutte queste teorie siano delle differenti approssimazioni, valide in diverse situazioni, di una teoria più fondamentale.

Figura 36. L’importanza di essere tridimensionali In uno spazio con più di tre dimensioni, le orbite planetarie sarebbero instabili e i pianeti finirebbero o per precipitare sul Sole, o per sfuggire completamente al suo campo di attrazione gravitazionale.

Gli uomini hanno cercato di scoprire questa teoria fondamentale ma, fino a oggi, i loro sforzi non sono stati coronati dal successo. Può anche darsi che non ci sia una singola formulazione della teoria fondamentale, così come – secondo quanto ha dimostrato Gödel – non è possibile formulare l’aritmetica nei termini di un singolo insieme di assiomi. Forse la situazione potrebbe essere simile a quella che si ha con le mappe – non possiamo usare una singola mappa piana per descrivere la superficie rotonda della Terra o la superficie di un anello dell’ancora: per coprire ogni punto, ci servono almeno due mappe nel caso della Terra e quattro per l’anello dell’ancora. Ciascuna mappa è valida solo in una regione limitata, ma mappe differenti avranno comunque una zona in cui si sovrappongono e dove sono quindi valide entrambe. L’intera serie delle diverse mappe ci offre una descrizione completa della superficie. Analogamente, in fisica potrebbe essere necessario usare differenti formulazioni nell’ambito delle diverse situazioni, ma due formulazioni differenti verrebbero comunque a trovarsi in accordo in quelle situazioni dove possono essere entrambe applicate.

Se ciò è vero, l’intera serie di differenti formulazioni potrebbe essere considerata come una teoria unificata completa, anche se sarebbe una teoria unificata che non potrebbe essere espressa nei termini di un singolo insieme di postulati. Ma anche questo potrebbe essere più di quanto la natura consenta. È possibile che non esista nessuna teoria unificata? Stiamo forse solo inseguendo un miraggio? Pare che le possibilità siano tre:

1. Esiste realmente una teoria unificata completa (o una serie di formulazioni in parte sovrapposte), che un giorno, se saremo abbastanza intelligenti, riusciremo a scoprire.
2. Non esiste una teoria definitiva dell’universo, ma solo un’infinita sequenza di teorie che lo descrivono in modo sempre più accurato, senza però mai raggiungere l’esattezza.
3. Non esiste alcuna teoria dell’universo: gli eventi non possono essere predetti al di là di un certo limite, ma si verificano in modo casuale e arbitrario.

Alcuni argomenterebbero a favore della terza possibilità sostenendo che, se ci fosse un insieme completo di leggi, verrebbe violata la libertà di Dio di cambiare parere e intervenire nel mondo. Tuttavia, dato che Dio è onnipotente, non potrebbe forse limitare Egli stesso la propria libertà, qualora volesse farlo? È un po’ come il vecchio paradosso: Dio potrebbe creare una pietra così pesante da non essere in grado di sollevarla? In verità, però, l’idea stessa che Dio possa voler cambiare parere è un esempio di quella fallacia, evidenziata da sant’Agostino, che consiste nell’immaginare Dio come un essere esistente nel tempo: il tempo è una proprietà che si riferisce esclusivamente all’universo che Dio ha creato. E presumibilmente, quando lo creò, Egli sapeva ciò che voleva fare!

Con l’avvento della meccanica quantistica, siamo giunti a riconoscere che gli eventi non possono essere predetti con un’accuratezza assoluta, ma che rimane sempre un certo grado di indeterminazione. Volendo, si potrebbe anche ascrivere questa casualità all’intervento di Dio. Si tratterebbe però di un tipo di intervento alquanto strano: non c’è infatti prova che sia diretto a un qualche fine. Anzi, se così fosse, non sarebbe più – per definizione – qualcosa di casuale. In tempi moderni, abbiamo effettivamente rimosso la terza possibilità ridefinendo lo scopo della scienza: il nostro obiettivo, cioè, è oggi quello di formulare un insieme di leggi che ci permettano di predire gli eventi solo entro il limite stabilito dal principio di indeterminazione.

La seconda possibilità, che è quella di una sequenza infinita di teorie sempre più perfezionate, è in accordo con tutta l’esperienza che abbiamo finora maturato. In numerose occasioni, abbiamo accresciuto la sensibilità delle nostre misurazioni o abbiamo effettuato una nuova classe di osservazioni solo per poi scoprire nuovi fenomeni che non erano predetti dalla teoria esistente, e per spiegare questi nuovi fenomeni abbiamo dovuto sviluppare una teoria più avanzata. Attraverso lo studio di particelle che interagiscono con quantità di energia sempre più elevate, potremmo in effetti aspettarci di trovare nuovi livelli di struttura più basilari dei quark e degli elettroni, che oggi consideriamo come particelle «elementari».

La gravità potrebbe porre un limite a questa sequenza di «scatole cinesi». Se avessimo una particella con un’energia superiore alla cosiddetta energia di Planck, la sua massa sarebbe talmente concentrata che essa si separerebbe dal resto dell’universo e formerebbe un piccolo buco nero. Pare quindi che, procedendo verso energie sempre più elevate, la serie di teorie via via più raffinate dovrebbe infine incontrare un limite, così che dovrebbe esistere una teoria definitiva dell’universo. Tuttavia, l’energia di Planck è qualcosa di incredibilmente lontano dalle energie che possiamo attualmente produrre in laboratorio, e gli acceleratori di particelle che potremo costruire nel futuro prevedibile non ci permetteranno certo di colmare questa immensa distanza. Energie di questo livello, però, devono essersi dispiegate nei primissimi stadi della vita dell’universo. Ci sono buone probabilità che lo studio dell’universo primordiale e i requisiti di coerenza matematica ci possano condurre a una teoria unificata completa quando qualcuno di noi sarà ancora vivo, sempre ammesso che non facciamo in modo di estinguerci prima!

Che significato avrebbe questa nostra eventuale scoperta della teoria ultima dell’universo?

Come abbiamo spiegato nel capitolo 3, non potremo mai essere del tutto sicuri di aver effettivamente trovato la teoria corretta, poiché le teorie non possono essere dimostrate. Ma se questa teoria fosse matematicamente coerente e fornisse sempre predizioni in accordo con le osservazioni, potremmo essere ragionevolmente fiduciosi di aver trovato la teoria giusta. Essa metterebbe fine a un lungo e glorioso capitolo nella storia dello sforzo intellettuale condotto dall’umanità al fine di comprendere l’universo, ma rivoluzionerebbe anche la comprensione che la gente comune ha delle leggi che lo governano.

Ai tempi di Newton, una persona istruita poteva ancora conoscere, almeno per sommi capi, l’intero ambito del sapere umano. In seguito, però, il ritmo dello sviluppo della scienza ha reso impossibile una simile impresa. Dato che le teorie vengono continuamente modificate per tener conto di nuove osservazioni, non vengono mai debitamente assimilate o semplificate in modo che anche la gente comune possa capirle. Per comprenderle occorre essere degli specialisti, e anche in questo caso tutto ciò che si può sperare di raggiungere è una comprensione adeguata di una piccola parte delle teorie scientifiche. Inoltre, il ritmo del progresso è talmente rapido che ciò che si impara a scuola o all’università è sempre un po’ superato. Solo poche persone possono tenersi al passo con la rapida avanzata della frontiera del sapere, e per farlo devono dedicarvi tutto il loro tempo e specializzarsi in una ristretta area tematica. Il resto della popolazione sa ben poco dei progressi che vengono compiuti o dell’entusiasmo che essi suscitano. D’altro lato, se dobbiamo credere a quanto disse Eddington, settant’anni fa solo due persone capivano la teoria della relatività generale. Oggi invece la comprendono decine di migliaia di laureati, e molti milioni di persone hanno perlomeno acquisito una certa familiarità con la sua idea di fondo. Se scoprissimo una teoria unificata completa, anch’essa verrebbe assimilata e semplificata allo stesso modo e, almeno a grandi linee, verrebbe insegnata nelle scuole; sarebbe solo questione di tempo. Tutti noi potremmo allora avere una certa comprensione delle leggi che governano l’universo e dalle quali dipende la nostra esistenza.

Tuttavia, quand’anche scoprissimo una teoria unificata completa, ciò non significherebbe acquisire una capacità di predizione generale degli eventi, per due ragioni. La prima è la restrizione che il principio di indeterminazione della meccanica quantistica pone alla nostra capacità di predizione. Non c’è nulla che possiamo fare per aggirare questo limite. Dal punto di vista pratico, però, questa prima limitazione è meno restrittiva della seconda, che deriva dal fatto di non poter quasi certamente risolvere le equazioni di una tale teoria, tranne che per situazioni molto semplici. Come abbiamo detto, nessuno è in grado di risolvere esattamente le equazioni quantistiche per un atomo formato da un nucleo con più di un singolo elettrone che gli orbita intorno. Non riusciamo nemmeno a risolvere esattamente le equazioni per il moto di tre corpi in una teoria semplice come la teoria della gravità di Newton, e la difficoltà cresce con l’aumentare del numero dei corpi e della complessità della teoria. Di solito, le soluzioni approssimative sono sufficienti ai fini pratici, ma è ben difficile dire che siano all’altezza delle grandi aspettative suscitate dall’espressione «teoria unificata del tutto».

Oggi conosciamo già le leggi che governano il comportamento della materia in tutte le condizioni tranne quelle più estreme. In particolare, conosciamo le leggi fondamentali che stanno alla base di tutta la chimica e la biologia. Ciononostante, non abbiamo certamente ridotto queste discipline allo status di problemi risolti. E, finora, abbiamo avuto ben poco successo nel predire il comportamento umano a partire da equazioni matematiche! Così, anche se scoprissimo un insieme completo di leggi fondamentali, ci resterebbe ancora, negli anni a venire, la sfida intellettuale di sviluppare metodi di approssimazione migliori, così da poter fare utili predizioni dei probabili risultati in situazioni complesse e realistiche. Una teoria unificata, completa e coerente costituisce solo il primo passo: il nostro obiettivo è quello di una comprensione completa degli eventi che ci circondano e della nostra stessa esistenza.