6

Lo spazio curvo

La teoria della relatività generale di Einstein si basa sull’idea rivoluzionaria secondo la quale la gravità non è una forza come le altre, bensì una conseguenza del fatto che lo spazio-tempo non è piatto, come si era supposto in precedenza. Nella relatività generale, lo spazio-tempo è incurvato (o «distorto») dalla distribuzione della massa e dell’energia in esso presenti. I corpi come la Terra non sono costretti a muoversi lungo orbite curve dall’azione di una forza chiamata gravità; essi, invece, seguono delle orbite curve perché queste ultime sono la cosa che più si avvicina a una traiettoria rettilinea all’interno di uno spazio curvo, ossia una geodetica. In termini tecnici, una geodetica è definita come la traiettoria più breve (o più lunga) tra due punti vicini.

Un piano geometrico costituisce un esempio di uno spazio bidimensionale piatto, sul quale le geodetiche sono linee rette. La superficie della Terra, invece, è uno spazio bidimensionale curvo. Sulla Terra, una geodetica è indicata con il termine «cerchio massimo». L’equatore è un cerchio massimo, così come ogni altro cerchio tracciato sul globo il cui centro coincida con il centro della Terra. (L’espressione «cerchio massimo» deriva dal fatto che si tratta dei cerchi più grandi che si possano tracciare sulla superficie del globo terrestre.) Dato che la geodetica è la traiettoria più breve tra due aeroporti, essa sarà il percorso che l’ufficiale di rotta dirà al pilota di seguire. Per esempio, per volare da New York a Madrid potreste seguire la vostra bussola viaggiando sempre verso est per 5966 chilometri, seguendo cioè la linea latitudinale che passa per queste due città. Se però decidete di volare lungo un cerchio massimo – facendo dapprima rotta in direzione nordest, quindi girando gradualmente verso est e infine verso sudest –, percorrerete in tutto soltanto 5802 chilometri. La rappresentazione di questi due percorsi su di una mappa – nella quale la superficie del globo viene appiattita e, quindi, distorta – ci può trarre in inganno. Quando viaggiamo «direttamente» (in linea retta) verso est da un punto all’altro della superficie terrestre, in realtà non stiamo procedendo direttamente, almeno non nel senso del tragitto più diretto – la geodetica, appunto.

Figura 10. Le distanze sul globo terrestre

Il percorso più breve che collega due punti sulla Terra si trova lungo un «cerchio massimo», che non corrisponde a una linea retta se lo si osserva su una mappa bidimensionale.

Nella relatività generale, i corpi seguono sempre le geodetiche nello spazio-tempo quadridimensionale. In assenza di materia, queste linee rette nello spazio-tempo quadridimensionale corrispondono a delle linee rette anche nello spazio tridimensionale. In presenza di materia, però, lo spazio-tempo quadridimensionale è distorto, e ciò fa sì che nello spazio tridimensionale i corpi risultino seguire delle traiettorie curve (in un modo che, nella vecchia teoria newtoniana, veniva spiegato tramite gli effetti dell’attrazione gravitazionale). È un po’ come osservare un aeroplano che vola sopra una zona collinare. Nello spazio tridimensionale, l’aereo potrebbe anche volare lungo una linea retta, ma provate a togliere la terza dimensione – l’altezza – e vedrete che la sua ombra sulla superficie bidimensionale delle colline segue una traiettoria incurvata. Oppure, potete anche immaginare un’astronave che viaggia in linea retta attraverso lo spazio, passando esattamente sopra il Polo Nord. Provate quindi a proiettare il suo percorso sulla superficie bidimensionale della Terra, e vedrete che si tratta di un semicerchio che traccia una linea longitudinale nell’emisfero settentrionale. Per quanto ciò possa essere più difficile da rappresentare, la massa del Sole incurva lo spazio-tempo in modo tale che anche se in realtà la Terra segue una traiettoria rettilinea nello spazio-tempo quadridimensionale, nello spazio tridimensionale essa ci appare muoversi lungo un’orbita quasi circolare.

In realtà, per quanto vengano calcolate in modi diversi, le orbite dei pianeti predette dalla relatività generale sono quasi esattamente identiche a quelle predette dalla teoria newtoniana della gravità. La maggiore differenza riguarda l’orbita di Mercurio che, essendo il pianeta più vicino al Sole, è soggetto agli effetti gravitazionali più intensi e ha un’orbita ellittica piuttosto allungata. La relatività generale predice che l’asse maggiore di questa ellisse dovrebbe ruotare intorno al Sole spostandosi di circa un grado ogni diecimila anni. Per quanto piccolo possa essere, tale effetto era già stato notato (si veda il capitolo 3) molto tempo prima del 1915, e costituì una delle prime conferme della teoria di Einstein. In anni recenti, gli scarti ancora più piccoli delle orbite degli altri pianeti rispetto alle traiettorie predette da Newton sono stati misurati con il radar e si è visto come siano in accordo con le predizioni della relatività generale.

Anche i raggi di luce devono seguire le geodetiche nello spazio-tempo. E anche in questo caso, il fatto che lo spazio sia incurvato ha come conseguenza che la luce non ci appaia propagarsi nello spazio in linea retta. La relatività generale predice quindi che i campi gravitazionali dovrebbero incurvare i raggi luminosi. Per esempio, la teoria predice che la traiettoria seguita dalla luce in prossimità del Sole dovrebbe essere leggermente incurvata verso l’interno, proprio a causa della presenza della massa solare. Ciò significa che i raggi luminosi provenienti da una stella lontana che si trovassero a passare vicino al Sole verrebbero deviati di un piccolo angolo, così che un osservatore sulla Terra vedrebbe la stella in una posizione diversa da quella reale. Naturalmente, se la luce di questa stella passasse sempre in prossimità del Sole, noi non saremmo in grado di dire se questa luce venga davvero deviata o se invece la stella si trovi realmente dove la vediamo. Tuttavia, mentre la Terra compie la propria orbita intorno al Sole, diverse stelle passano dietro il disco solare e la loro luce subisce così una deflessione. Di conseguenza, la posizione apparente di queste stelle in rapporto alle altre viene a cambiare.

Figura 11. Il tracciato dell’ombra di un’astronave

Proiettato sulla superficie bidimensionale della Terra, il percorso di un’astronave che viaggia in linea retta attraverso lo spazio apparirà curvo.

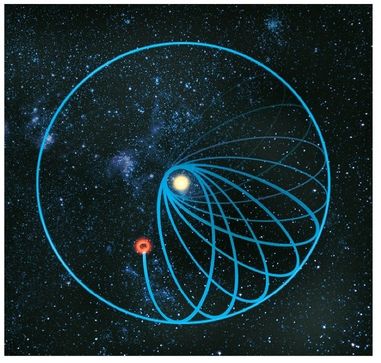
Figura 12. La precessione dell’orbita di Mercurio

Man mano che Mercurio compie le proprie rivoluzioni intorno al Sole, l’asse maggiore della sua orbita ellittica ruota a sua volta – molto più lentamente – intorno alla stella, tornando alla posizione di partenza ogni 360.000 anni circa.

In condizioni normali è molto difficile osservare questo effetto, poiché la luce del Sole rende impossibile la visione delle stelle che si trovano in prossimità del disco solare stesso. La situazione cambia però radicalmente durante un’eclisse di Sole, quando l’interposizione della Luna impedisce alla luce solare di giungere alla Terra. La predizione fatta da Einstein sulla deflessione della luce non poté essere verificata immediatamente nel 1915, poiché era allora in corso la Prima guerra mondiale. Fu solo nel 1919 che una spedizione britannica, osservando un’eclisse dalle coste dell’Africa occidentale, confermò che la luce veniva effettivamente deflessa dal Sole secondo le previsioni della teoria. Questa prova sperimentale di una teoria tedesca da parte di scienziati britannici fu salutata come un grande gesto di riconciliazione fra i due Paesi dopo la guerra. È pertanto un’ironia della sorte che un successivo esame delle fotografie scattate nel corso di quella spedizione abbia dimostrato la presenza di errori dello stesso ordine di grandezza dell’effetto che si cercava di misurare. La misurazione di questi scienziati era quindi stata un caso di mera fortuna, o magari era stata influenzata dal fatto di conoscere in anticipo i risultati che si volevano ottenere – cosa non rara in ambito scientifico. In seguito, comunque, la deflessione della luce è stata confermata da un gran numero di osservazioni accurate.

Figura 13. Deflessione della luce in prossimità del Sole

Quando il Sole si trova quasi direttamente interposto tra la Terra e una stella lontana, il suo campo gravitazionale deflette la luce di questa stella, alterandone la posizione apparente.

Un’altra predizione della relatività generale afferma che in prossimità di un corpo di massa elevata, come la Terra, lo scorrere del tempo dovrebbe apparire più lento. Einstein lo comprese già nel 1907, cinque anni prima di capire che la gravità alterava anche la forma dello spazio e otto anni prima di completare la propria teoria. Dedusse questo effetto in base al principio di equivalenza, che nella relatività generale giocò lo stesso ruolo che il postulato fondamentale aveva rivestito nel quadro della relatività speciale.

Il postulato fondamentale, come ricorderete, affermava che le leggi della scienza dovrebbero essere le stesse per tutti gli osservatori che si muovono liberamente, a prescindere dalla loro velocità. Ora, per dirla in parole semplici, il principio di equivalenza estende questo postulato anche agli osservatori che non si muovono liberamente, ma si trovano sotto l’influenza di un campo gravitazionale. Se volessimo essere precisi, dovremmo tener conto del fatto che nella formulazione di tale principio rientrano anche alcuni aspetti strettamente tecnici – come il fatto che se il campo gravitazionale non è uniforme, bisogna applicare il principio separatamente a una serie di piccoli settori parzialmente sovrapposti l’uno all’altro –, ma noi non ci soffermeremo su questi punti. Per quanto ci riguarda, possiamo formulare il principio in questi termini: in una regione dello spazio sufficientemente piccola, è impossibile dire se un corpo si trovi in uno stato di quiete all’interno di un campo gravitazionale, o se stia accelerando uniformemente nello spazio vuoto.

Immaginate di trovarvi in un ascensore collocato nello spazio vuoto. Non c’è gravità, quindi non ci sono neppure un «alto» e un «basso». State fluttuando liberamente. Ora l’ascensore inizia a muoversi con un’accelerazione costante. Improvvisamente vi sentite pesanti, ossia avvertite una forza che vi attrae verso una delle estremità dell’ascensore, che all’improvviso vi sembra essere diventata il suo pavimento! Se avevate in mano una mela e ora la lasciate andare, essa cadrà sul pavimento. Ora che state accelerando, tutto ciò che avviene all’interno dell’ascensore sarà di fatto indistinguibile da ciò che accadrebbe se l’ascensore fosse immobile all’interno di un campo gravitazionale uniforme. Einstein comprese che proprio come è impossibile dire se il treno in cui ci troviamo sia fermo o se si stia muovendo a velocità uniforme, è anche impossibile stabilire dall’interno se l’ascensore stia accelerando uniformemente o se sia invece fermo in un campo gravitazionale uniforme. Da questa considerazione egli dedusse il suo principio di equivalenza.

Il principio di equivalenza (e, con esso, l’esempio riportato qui sopra) vale soltanto se la massa inerziale (ossia la massa che compare nella seconda legge di Newton, che determina il grado di accelerazione di un corpo in seguito all’applicazione di una determinata forza) e la massa gravitazionale (ossia la massa a cui si fa riferimento nella legge di gravità di Newton, che determina l’intensità dell’attrazione gravitazionale a cui questo corpo è soggetto) sono la stessa cosa (si veda il capitolo 4). Ciò è dovuto al fatto che se i due tipi di massa coincidono, tutti gli oggetti all’interno di un campo gravitazionale cadranno alla stessa velocità, indipendentemente dalle loro masse. Se però questa equivalenza non valesse, sotto l’influenza della gravità alcuni oggetti cadrebbero più velocemente di altri, e sarebbe quindi possibile distinguere l’attrazione gravitazionale dall’accelerazione uniforme (con la quale la velocità di caduta – all’interno dell’ascensore, per rimanere al nostro esempio – resterebbe la stessa per tutti i corpi). Einstein si servì dell’equivalenza di massa inerziale e massa gravitazionale per derivare il proprio principio di equivalenza e, in ultima analisi, l’intera relatività generale: tutto questo suo rigoroso procedimento deduttivo, basato su una ferrea logica, non trova uguali nella storia del pensiero umano.

Ora che conosciamo il principio di equivalenza, possiamo iniziare a seguire il ragionamento di Einstein attraverso un altro esperimento mentale, che ci permette di comprendere perché il tempo deve essere influenzato dalla gravità. Provate a immaginare un razzo nello spazio. Per comodità, supponiamo che la sua lunghezza sia tale che la luce impieghi un secondo per percorrerlo da un estremo all’altro. Infine, supponiamo che in questo razzo ci siano due osservatori, uno nella cupola superiore e l’altro alla base, dotati di due orologi identici che emettono un ticchettio ogni secondo.

Immaginiamo ora che l’osservatore nella cupola attenda il rintocco dell’orologio e mandi quindi immediatamente un segnale luminoso al suo collega situato alla base. Egli ripete poi questa operazione anche al rintocco successivo. Stando alla nostra ipotesi iniziale, ciascun segnale viaggia per un secondo e viene quindi ricevuto dall’osservatore che si trova alla base del razzo. Così, dato che l’osservatore nella cupola invia due segnali luminosi a un secondo di distanza l’uno dall’altro, quello alla base riceverà due segnali, sempre a un secondo di distanza.

Ma se invece che fluttuare liberamente nello spazio il nostro razzo fosse fermo sulla Terra, sotto l’influsso della gravità, che cosa accadrebbe di diverso? Stando alla teoria di Newton, la gravità non influisce in alcun modo su questa situazione: se l’osservatore nella cupola manda i due segnali a un secondo di distanza, quello alla base li riceverà sempre a un secondo di distanza. Il principio di equivalenza, però, non fa questa stessa predizione. Possiamo vedere ciò che accade – ci dice questo principio – prendendo in esame, anziché l’effetto della gravità, l’effetto dell’accelerazione uniforme. Questo è un esempio del modo in cui Einstein ha sfruttato il principio di equivalenza per creare la sua nuova teoria della gravità.

Supponiamo quindi che il nostro razzo stia accelerando. (Immagineremo che stia accelerando lentamente, senza avvicinarsi alla velocità della luce!) Dato che il razzo si muove verso l’alto, il primo segnale dovrà percorrere una distanza più breve rispetto a quella dell’esempio precedente, e pertanto impiegherà meno di un secondo per arrivare a destinazione. Se il razzo si muovesse a velocità costante, il secondo segnale impiegherebbe esattamente questo stesso tempo per giungere all’osservatore posto alla base del razzo, e pertanto l’intervallo tra i due segnali resterebbe sempre di un secondo. A causa dell’accelerazione, però, quando l’osservatore nella cupola invia il secondo segnale, il razzo si starà muovendo più velocemente di quando aveva inviato il primo: di conseguenza, il secondo segnale dovrà percorrere una distanza ancora più ridotta rispetto a quella attraversata dal primo, e arriverà quindi a destinazione in un tempo ancora più breve. L’osservatore posto alla base misurerà pertanto sul proprio orologio meno di un secondo tra i due segnali, trovandosi così in disaccordo con l’osservatore della cupola, che afferma di averli inviati a un secondo esatto di distanza l’uno dall’altro.

Probabilmente, nel caso dell’accelerazione del razzo questo fatto non ci sorprenderà – dopotutto, l’abbiamo appena spiegato! Dobbiamo però tenere a mente come il principio di equivalenza affermi che tali considerazioni possano essere applicate anche a un razzo immobile all’interno di un campo gravitazionale. In altre parole, anche se il razzo non sta accelerando, ma – per esempio – è fermo su una rampa di lancio posta sulla superficie terrestre, se l’osservatore nella cupola manda dei segnali a quello alla base a intervalli di un secondo (stando al suo orologio), l’osservatore alla base (stando al proprio orologio) li riceverà a intervalli più brevi. E questo sì che è un fatto sorprendente!

Ci si potrebbe ancora chiedere: ciò significa che la gravità altera il tempo, oppure semplicemente che danneggia gli orologi? Supponiamo che l’osservatore alla base del razzo salga fin nella cupola per confrontare il proprio orologio con quello del suo collega. Si tratta di orologi identici e, com’è prevedibile, gli osservatori vedranno che ora segnano la stessa durata di ogni secondo. L’orologio dell’osservatore alla base, quindi, non è stato danneggiato: in qualunque luogo si trovi, misura lo scorrere del tempo locale. Pertanto, proprio come la relatività speciale ci dice che lo scorrere del tempo è diverso per gli osservatori che si trovano in movimento l’uno rispetto all’altro, la relatività generale indica che il tempo scorre in maniera differente anche per gli osservatori che si trovano in campi gravitazionali diversi. Stando alla relatività generale, l’osservatore alla base ha misurato un intervallo di tempo più breve tra un segnale e l’altro perché, se ci si trova più vicini alla superficie della Terra, il tempo scorre più lentamente per via della maggiore intensità della gravità. Quanto più forte è il campo gravitazionale, tanto maggiore sarà questo suo effetto. Le leggi del moto di Newton misero fine all’idea di una posizione assoluta nello spazio. Ora, come abbiamo visto, la teoria della relatività si lascia alle spalle anche l’assolutezza del tempo.

Questa predizione venne provata empiricamente nel 1962, usando una coppia di orologi estremamente precisi collocati sulla cima e alla base di una torre serbatoio. L’orologio posto alla base, più vicino alla superficie terrestre, risultò funzionare più lentamente, proprio come prediceva la relatività generale. L’effetto è di per sé piccolo: un orologio collocato sulla superficie del Sole rimarrebbe indietro soltanto di circa un minuto all’anno rispetto a un altro orologio posto sulla superficie della Terra. Ciononostante, la differenza nella velocità degli orologi posti ad altitudini diverse sopra la superficie terrestre ha acquistato oggi – con l’avvento di sistemi di navigazione molto accurati basati sui segnali emessi dai satelliti – un’importanza pratica considerevole. Se si ignorassero le predizioni della relatività generale, le posizioni calcolate risulterebbero sbagliate di diversi chilometri!

Anche i nostri orologi biologici risentono allo stesso modo di queste alterazioni nello scorrere del tempo. Consideriamo una coppia di gemelli. Supponiamo che uno di loro vada a vivere sulla cima di una montagna, mentre l’altro rimanga al livello del mare. Il primo gemello invecchierà più rapidamente del secondo e pertanto, se si rincontrassero, uno dei due sarebbe più vecchio dell’altro. In questo caso, la differenza di età sarebbe molto piccola; essa sarebbe però di gran lunga più grande se uno dei gemelli partisse per un lungo viaggio su un’astronave, accelerando fino a sfiorare la velocità della luce. Al suo ritorno, egli sarebbe molto più giovane del suo gemello rimasto sulla Terra. Questo caso è noto come il paradosso dei gemelli, ma è un paradosso solo se non riusciamo a sbarazzarci dell’idea di un tempo assoluto. Nella teoria della relatività non esiste un unico tempo assoluto, ma ogni singolo individuo ha una propria personale misura del tempo, che dipende da dove si trova e da come si sta muovendo.

Prima del 1915, lo spazio e il tempo erano concepiti come un palcoscenico fisso sul quale gli eventi avevano luogo, ma che non risentiva di ciò che accadeva in esso. Ciò valeva anche per la teoria della relatività speciale. I corpi si muovevano, le forze attraevano e respingevano, ma il tempo e lo spazio continuavano semplicemente la loro esistenza, senza subire alcuna alterazione. Era naturale pensare che spazio e tempo durassero per sempre. Nel quadro della teoria della relatività generale, però, la situazione è completamente diversa. In essa, infatti, lo spazio e il tempo sono quantità dinamiche: quando un corpo si muove o una forza agisce, ciò viene a incidere sulla curvatura dello spazio-tempo; e, a sua volta, la struttura dello spazio-tempo influisce sul modo in cui i corpi si muovono e le forze agiscono. Spazio e tempo non solo influiscono su tutto ciò che accade nell’universo, ma risentono a loro volta di tutto ciò che accade nell’universo. Come non si può parlare di eventi che si verificano nell’universo senza far ricorso alle nozioni di spazio e di tempo, così nella relatività generale non ha più alcun senso parlare di spazio e di tempo al di fuori dei confini dell’universo. Nei decenni successivi al 1915, questa nuova comprensione dello spazio e del tempo avrebbe rivoluzionato la nostra concezione dell’universo. Come vedremo, la vecchia idea di un universo sostanzialmente immutabile, che potrebbe essere esistito da (e potrebbe continuare a esistere per) sempre, fu sostituita dalla concezione di un universo dinamico, in espansione, che sembrava aver avuto inizio in un determinato momento del passato e che poteva finire in un determinato momento del futuro.