Pendant les années où je résidais aux États-Unis, je suis retourné en Italie chaque été, et souvent Abhay Ashtekar, ou Lee Smolin, ou les deux, m'accompagnaient. Ils étaient devenus mes amis et principaux collaborateurs. Nous profitions de ces vacances en Italie pour travailler ensemble.

Plusieurs étapes dans le développement de notre théorie ont été atteintes en Italie, pendant ces visites. Par exemple, c'est à Trente, tous les trois, que nous avons commencé à comprendre comment décrire l'espace macroscopique en mettant ensemble un grand nombre de boucles. C'est aussi à Trente que nous avons compris, suite à un calcul qui ne marchait pas, que la taille des boucles n'était pas infinitésimale, comme nous le pensions au début : leur taille était très petite mais finie.

Il y avait un aspect étrange de la théorie que nous n'arrivions pas à comprendre : d'un point de vue mathématique, on constatait que ces boucles qui constituent l'espace présentaient des intersections : elles passaient l'une dans l'autre à certains endroits. Nous ne parvenions pas à comprendre ce que représentaient ces intersections.

Réseaux de spin

Vers le milieu des années quatre-vingt-dix, pendant que Lee était à Vérone, nous avons travaillé à l'aide d'une méthode de calcul assez classique en mécanique quantique. En mécanique quantique, comme on l'a vu, beaucoup de grandeurs sont « quantifiées ». Cela signifie qu'elles ne peuvent pas prendre n'importe quelle valeur, mais seulement certaines valeurs discontinues. L'énergie d'un atome, par exemple, ne peut pas avoir une valeur arbitraire, mais seulement certaines valeurs particulières : les niveaux d'énergie de l'atome. Pour calculer les valeurs qu'une grandeur physique peut prendre, on utilise une technique qui s'appelle « calcul du spectre de l'opérateur ». En ce qui nous concerne, nous étions intéressés par une grandeur physique particulière : le volume.

Qu'est-ce qu'un volume ? C'est la mesure de la quantité d'espace. Le volume d'une pièce est la quantité d'espace qu'il y a dans cette pièce. Mais comme l'espace est devenu le champ gravitationnel, le volume mesure le champ gravitationnel. Et comme nous étions aux prises avec une théorie quantique, il y avait de fortes chances que le volume ait des valeurs discontinues, et donc qu'il puisse y avoir des « grains » de volume. Les calculs se sont avérés compliqués. Nous avons réussi à les résoudre, grâce aussi à l'aide d'un grand mathématicien anglais, Roger Penrose, que nous sommes allés consulter lorsque nous nous sommes aperçus que nos calculs conduisaient à des objets mathématiques que Roger avait étudiés vingt ans plus tôt, et qu'il avait appelé spin networks, ou « réseaux de spin ».

Résultat du calcul : le volume était en effet une variable non continue, et donc l'espace est constitué de quanta de volume, ou de quanta d'espace. Or, nous avons découvert que ces quanta d'espace se trouvent exactement aux intersections des boucles. Autrement dit, le volume est composé de quanta, de grains d'espace, et les intersections des boucles représentent justement ces grains d'espace. Elles sont les grains d'espace que nous cherchions.

Ces résultats ont quelque peu changé notre représentation initiale. Les intersections sont devenues plus importantes que les lignes. Nous avons cessé de parler d'un ensemble de boucles avec des points d'intersection, pour parler d'un ensemble de points, les intersections, reliés entre eux par des liens, c'est-à-dire par un réseau. Sur un même lien allant d'une intersection à l'autre on peut rencontrer plus qu'une seule ligne de Faraday. Le nombre de lignes de Faraday superposées sur le même lien est un nombre entier qu'on associe à chaque lien, et qui s'appelle le spin du lien. (Pour des raisons historiques, on utilise la moitié de ce nombre, qui est un nombre demi-entier, comme ½, 1, 3/2, 2, 5/2…). De là, le nom de réseau de spin.

L'image qui résulte de l'espace quantique est surprenante : les nœuds du réseau de spin sont les grains d'espace. Les lignes reliant les points les uns aux autres représentent les relations spatiales entre eux. Elles expriment quel grain se trouve en contact avec quel autre grain. C'est ce qu'illustre la figure 5.

Fig. 5.1  Un « réseau de spin » (à gauche) est formé des lignes de Faraday du champ gravitationnel ; les points d'intersection, indiqués par des points noirs, sont les « nœuds » du réseau. Ceux-ci représentent des « grains d'espace » (à droite). Les liens du réseau représentent les relations de voisinage entre les grains d'espace.

Le calcul du « spectre de volume » fournit exactement les valeurs du volume qui peuvent être observées. Le même calcul peut être fait pour l'aire d'une surface. Dans ce cas, on calcule le « spectre de l'aire ». La théorie prédit avec précision un ensemble de nombres représentant les résultats possibles pour des mesures très précises du volume et de la surface.

Donc la théorie de la gravitation à boucles prédit que si nous mesurons une surface de façon exacte, nous ne pouvons pas trouver n'importe quel nombre, mais seulement l'un de ces nombres qui sont sur la liste obtenue par le calcul du spectre.

Quand nous disons que le volume d'une boîte est d'un mètre cube, nous comptons en réalité combien de grains d'espace, ou plutôt combien de « quanta du champ gravitationnel » il y a dans la boîte. Les quanta sont évidemment très petits. Dans une boîte d'un mètre cube, leur quantité est donnée par un nombre d'une centaine de chiffres.

De la même façon, quand nous disons que la surface d'une page de ce livre est, disons, de deux cents centimètres carrés, nous comptons en réalité le nombre de liens du réseau, ou mieux de boucles élémentaires, qui traversent la page. À travers une page de ce livre, cette quantité est donnée par un nombre d'environ soixante-dix chiffres. C'est ce que montre la figure 6.

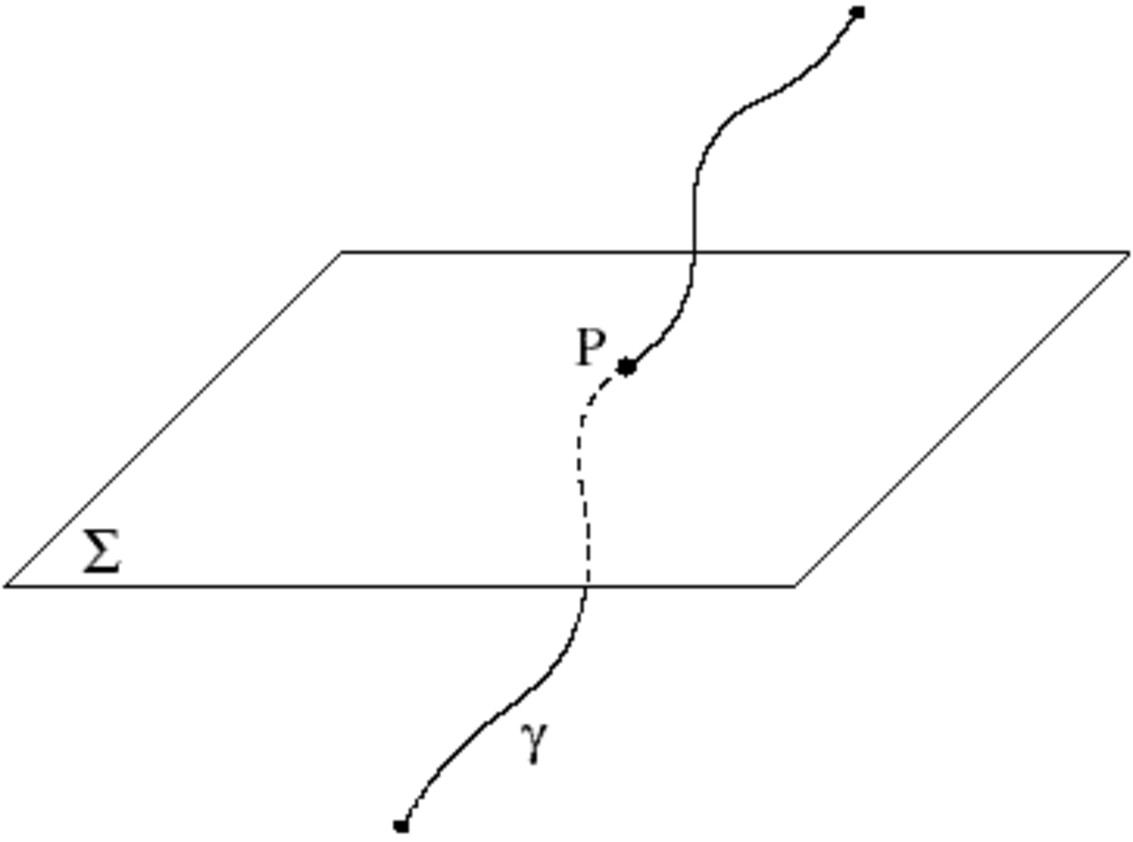
Fig. 5.2  Une surface Σ est traversée par une boucle (dont on n'a dessiné qu'un segment), au point P. La mesure de la surface est déterminée par le nombre de boucles qui la traversent. Une page de ce livre est traversée par environ 10⁷⁰ boucles, c'est-à-dire un nombre à soixante-dix chiffres.

La technologie actuelle n'est pas suffisante pour vérifier ces prédictions. Mais il est très important que la théorie fournisse des prédictions précises et, au moins en principe, vérifiables. Si elle ne le faisait pas, ce ne serait pas une théorie scientifique. Jusqu'à ce jour, la théorie de la gravitation à boucles est la seule théorie de gravitation quantique qui fournit un ensemble de prédictions non ambiguës et articulées, en principe vérifiables.

Les réseaux de spin fournissent une description mathématiquement précise de la structure quantique de l'espace. Plus précisément, du fait que nous avons affaire à la mécanique quantique – et donc aux probabilités – la théorie est formulée en termes de nuages de probabilités associés à ces réseaux de spin. Il faut s'imaginer que ces réseaux de spin qui constituent le monde fluctuent, vibrent et fourmillent, un peu comme les points noirs et blancs d'une télévision analogique sans antenne, et les mathématiques de la théorie décrivent cette agitation des réseaux spin. L'espace physique peut donc être décrit par un nuage de probabilité de réseaux de spin.

Un aspect assez surprenant de cette histoire est le fait que Roger Penrose avait « inventé » les réseaux de spin sur la base de sa seule imagination, comme une tentative de décrire l'espace quantique. Et voilà que nous avions retrouvé ces mêmes réseaux de spin comme une conséquence de la théorie de la relativité générale et de la mécanique quantique.

John Wheeler

L'idée intuitive d'un espace qui n'est plus continu à très petite échelle avait déjà été suggérée par John Wheeler, un des deux auteurs de l'équation de Wheeler-DeWitt, dans les années soixante. La théorie des boucles est une concrétisation mathématique précise de cette idée.

Le jour où John Wheeler, ce grand homme et vétéran de la gravitation quantique, m'a envoyé un mot plein d'affection et d'enthousiasme pour nos résultats et m'a invité à Princeton pour exposer notre théorie, fut un jour de grande émotion pour moi.

Dans sa jeunesse, John Wheeler avait été un collaborateur de Niels Bohr, l'un des géants de la physique du début du XX^e siècle. Il avait participé avec lui à la naissance de la mécanique quantique. Puis il s'était consacré à la physique nucléaire et il comptait parmi les créateurs de l'un des premiers modèles du noyau atomique. Il avait passé la guerre aux États-Unis, où il a joué un rôle central dans les événements tragiques liés à la bombe atomique. C'est lors d'une discussion dans son bureau que la décision a été prise d'écrire à Roosevelt pour l'inciter à fabriquer la bombe atomique parce qu'on craignait que les Allemands ne la fabriquent les premiers – crainte qui s'est révélée infondée par la suite. Après la guerre, Wheeler a travaillé sur la gravitation et est devenu le collaborateur principal d'Einstein. C'est lui qui a introduit le terme si populaire de « trou noir ». Et c'est lui qui a eu une série d'intuitions et d'idées très importantes qui sont à la base de la recherche en gravitation quantique. Il a suggéré que l'espace-temps, à l'échelle la plus petite, était une sorte de mousse fluctuante (une mousse d'espace-temps). Avec Bryce DeWitt, un autre grand scientifique américain, il a formulé la fameuse équation qui allait devenir l'équation fondamentale de la gravitation quantique. Parmi ses étudiants se trouvait Richard Feynman, peut-être le plus grand physicien de la seconde moitié du XX^e siècle. Bref, ce fut un protagoniste de premier plan de tout le développement de la physique moderne. Vous pouvez donc imaginer quelle fut mon émotion en recevant sa lettre !

Dès mon arrivée, Wheeler est venu me voir dans le Bed and Breakfeast où j'avais trouvé à me loger. Nous avons pris le petit-déjeuner ensemble et puis il m'a accompagné dans une longue promenade à travers le campus. Je lui ai expliqué les résultats de nos calculs, tandis que lui me racontait ses histoires extraordinaires : Bohr, la bombe atomique… « Tu vois, Carlo, me disait-il, quand Einstein est arrivé ici la première fois, fuyant l'Allemagne nazie, je suis allé le chercher au petit matin, comme je viens de le faire avec toi, et nous nous sommes promenés le long du même parcours… ». Pourquoi le voisinage, même indirect, des hommes qui ont laissé le plus de traces dans notre pensée nous donne-t-il tant d'émotion ? Ce sont des hommes comme les autres, bien sûr, avec leurs faiblesses et leur humanité comme tout le monde, mais la fascination que nous avons éprouvée pour leurs idées leur confère une aura qui nous enchante. Ils nous ont ouvert des chemins que nous avons le privilège de pouvoir suivre, et de ce fait éveillent admiration, gratitude et affection.

John me parlait à voix basse. Il était âgé, et faible, mais son énergie intérieure était encore là, intacte. Il défendait avec passion sa participation à l'horrible aventure de la bombe atomique, contre mes objections de pacifiste radical. Quand je lui ai montré mon image de la structure de l'espace (la figure 3 de la page…), il a souri comme un enfant et il est allé chercher une image très similaire qu'il avait dessinée longtemps auparavant, et qui se trouve dans l'un de ses livres (figure 7)…

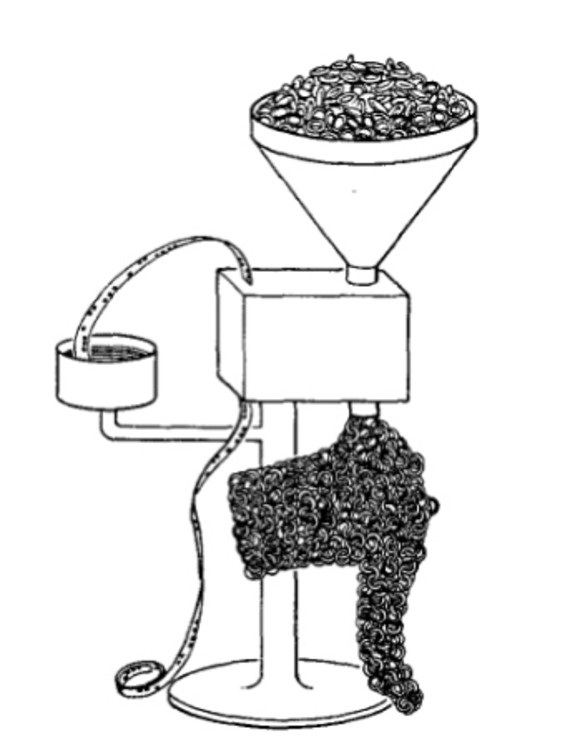
Fig. 5.3  L'image des « Dix milles boucles qui peuvent former l'espace temps », dans le livre « Gravitation » de Misner, Thorne et Wheeler, que John Wheeler m'a montré à Princeton, quand je lui ai parlé de mes boucles (figure 3)

Tester la théorie ?

Aujourd'hui, la gravitation quantique à boucles est étudiée par un grand nombre de chercheurs dans le monde entier, qui l'ont développée dans différentes directions. La théorie trouve des applications dans des champs variés, par exemple en cosmologie, pour étudier le Big Bang – les tout premiers moments de l'Univers –, et aussi pour étudier les propriétés des trous noirs, en particulier leurs propriétés thermiques.

L'application de la théorie des boucles aux trous noirs rejoint une étrange découverte faite dans les années soixante-dix par Stephen Hawking. Stephen est célèbre parce qu'il est parvenu à poursuivre son travail scientifique alors qu'une terrible maladie le force à vivre en chaise roulante et à communiquer au moyen d'un ordinateur qu'il commande à la main. Un de ses résultats les plus importants est la découverte théorique que les trous noirs sont « chauds », c'est-à-dire qu'ils se comportent exactement comme des corps chauds : ils émettent une radiation thermique d'une certaine température.

Or, nous savons qu'en général les objets sont chauds parce que leurs constituants microscopiques sont en mouvement. Un morceau de fer chaud est un morceau de fer dans lequel les atomes de fer vibrent rapidement autour de leurs positions d'équilibre. Mais si un trou noir est chaud, que sont ces « atomes » élémentaires qui vibrent ?

La théorie des boucles apporte une réponse. Les « atomes » élémentaires d'un trou noir, qui vibrent et sont responsables de sa température, sont précisément les boucles individuelles qui se trouvent à la surface du trou noir. En utilisant cette théorie, on est capable de comprendre et de dériver le résultat de Hawking en termes des « vibrations » microscopiques des boucles. C'est un test important de la cohérence de la théorie des boucles, et donc un de ses succès. Mais ce n'est pas un vrai test expérimental.

Pendant longtemps, on a cru que toute possibilité de vérification expérimentale réelle resterait hors de notre portée. Mais récemment plusieurs idées ont surgi qui permettraient de tester la théorie en observant des conséquences indirectes de la granularité de l'espace.

Par exemple, si la structure de l'espace est granulaire, cela devrait avoir un effet sur la propagation de la lumière. Des rayons de couleurs différentes qui traversent l'espace granulaire devraient en principe se déplacer à des vitesses très légèrement différentes (exactement comme dans un cristal : la lumière est dispersée et le rouge avance plus vite que le bleu : on voit donc arriver l'image rouge un peu avant l'image bleue). L'effet est infime, mais il s'accumule tout au long du trajet. On pourrait donc pouvoir le détecter sur les rayons de lumière venant de galaxies très lointaines. À l'heure actuelle, les mesures ne sont pas assez précises pour détecter une granularité inférieure à 10^-29 cm. Or la théorie prévoit que la taille des « grains » d'espace est de l'ordre de 10^-33 cm seulement. Il faut donc attendre d'avoir des instruments de mesure encore dix mille fois plus précis que ceux d'aujourd'hui pour pouvoir mettre cette prédiction à l'épreuve. Ce n'est pas hors de portée. Mais le vrai problème, c'est qu'il n'est pas du tout sûr que la théorie des boucles produise un tel effet qui, en fait, violerait une symétrie importante de la nature, que l'on appelle la « symétrie de Lorentz locale ». Au contraire, de nombreux arguments suggèrent que la théorie des boucles respecte cette symétrie, et les calculs plus récents tendent à confirmer ce résultat, éloignant la possibilité que la théorie puisse être testée par cette voie.

Les conséquences de la théorie qui ont le plus de chance de devenir observables se trouvent dans un autre domaine : la cosmologie.

La cosmologie primordiale

La cosmologie a connu un développement impressionnant ces dernières décennies. Nous avons maintenant une connaissance considérable de l'histoire de l'Univers et de son expansion, et nous en apprenons toujours davantage. Ainsi, en 1998 nous avons découvert que l'Univers n'est pas seulement en expansion, mais que cette expansion est accélérée : l'Univers grandit de plus en plus vite. Cette expansion accélérée est souvent présentée sous les auspices d'une mystérieuse « énergie sombre », mais elle est très bien décrite par la théorie classique d'Einstein, si l'on tient compte d'un terme appelé « constante cosmologique ». Einstein avait déjà montré que ce terme entre dans les équations de la théorie, mais il n'avait pas été pris au sérieux jusqu'à la découverte de l'expansion accélérée. Le futur de l'Univers semble donc être, dans l'état actuel de nos connaissances, une expansion toujours accélérée et un éloignement perpétuel des galaxies les unes des autres.

C'est à l'autre extrémité de l'histoire que le mystère est le plus dense : au début. Et c'est là que la gravité quantique à boucles a quelque chose à offrir. L'application de la théorie des boucles à la cosmologie a connu un développement énorme ces dernières années et c'est l'un des domaines où la théorie engrange ses plus grands succès. Juste après le Big Bang, l'Univers était très petit ; on peut dire qu'il était seulement fait d'un très petit nombre de grains d'espace. Ces grains originels pourraient avoir laissé des traces dans la structure actuelle de l'Univers, notamment dans le fond de radiation cosmique (le fameux « rayonnement fossile ») qui a été très précisément mesuré, et qui est en train de nous dévoiler beaucoup de choses sur la structure de l'Univers. Il est impossible de modéliser l'évolution initiale de l'Univers par un espace continu, comme on le fait lorsque l'Univers est grand. Il faut prendre en compte la granularité de manière explicite, et, pour ce faire, on peut utiliser les équations de la théorie des boucles. De cette manière, on obtient une description des instants immédiatement postérieurs au Big Bang, et même du Big Bang lui-même.

La théorie des boucles nous donne donc un instrument possible pour étudier la cosmologie primordiale, le début de la vie de notre Univers. Les résultats sont assez surprenants. La relativité générale d'Einstein ne fonctionne plus quand on arrive au Big Bang, et donc sans une théorie de la gravité quantique vous ne pouvez rien dire sur ce qui s'est passé au moment du Big Bang. Même les tentatives d'appliquer la mécanique quantique au problème n'ont pas donné de résultats satisfaisants. Par exemple, si vous essayez de calculer ce qui s'est passé dans l'Univers au moment du Big Bang en utilisant la vieille équation de Wheeler et DeWitt, vous retrouvez les mêmes incohérences que dans la théorie classique d'Einstein : l'évolution dans le temps s'arrête au Big Bang et les équations perdent tout leur sens. En revanche, si vous utilisez les équations qui viennent de la théorie des boucles, tout à coup les équations fonctionnent également pour le Big Bang. La raison en est précisément la granularité de l'espace. L'Univers se contracte de plus en plus à mesure qu'on se rapproche du Big Bang, mais il ne peut pas devenir arbitrairement petit, parce que dans la théorie des boucles il n'existe pas de volume arbitrairement petit : l'espace est quantifié.

Le premier qui a trouvé le moyen d'appliquer la théorie des boucles à la cosmologie était un jeune chercheur allemand : Martin Bojowald. Ses idées ont ensuite été développées par beaucoup, en particulier par lui-même et Abhay Ashetar avec son groupe de recherche aux États-Unis.

Les résultats assez surprenants de ce champ de recherche sont que, dans un certain sens, le Big Bang ne constitue pas un vrai début, mais pourrait être vu comme un « rebond » qui fait suite à une phase où l'Univers était en contraction.

Ce résultat est solide : il a été dérivé de différentes façons et en utilisant des modèles de complexité variable. Du point de vue théorique, la chose étonnante est que les équations ne deviennent plus insensées à l'approche du Big Bang. Elles ne donnent plus comme résultats des quantités infinies absurdes, il devient ainsi possible de calculer ce qui se passe au-delà du Big Bang.

Du point de vue de l'observation, ce résultat est de grande valeur, car les équations de l'évolution de l'Univers modifiées par la gravité quantique sont légèrement différentes de celles de la théorie classique habituellement utilisées par les cosmologistes. Cette différence pourrait avoir des effets détectables, en particulier dans l'observation du fond diffus cosmologique, cette faible lumière diffuse présente dans l'espace et étudiée par des satellites comme COBE, WMAP, et Planck. Avec ces nouveaux outils, on observe le fond de radiation cosmique avec une précision de plus en plus grande, et l'espoir augmente de pouvoir observer des effets calculables de la théorie des boucles.

Cependant, le travail de calcul qui relie les équations de base de la théorie à des observations éventuelles est tout sauf facile. Il implique des approximations, une vaste connaissance de la gravité quantique en même temps que de la cosmologie, dont peu de gens disposent, et beaucoup d'intuition. Les meilleurs scientifiques du domaine qui travaillent dans cette direction se trouvent en France. Je pense en particulier à Aurélien Barrau, à Grenoble, qui est aujourd'hui à la pointe de cet effort de recherche et me semble extrêmement prometteur.

Du point de vue conceptuel, cependant, je reste un peu perplexe quant à la possibilité d'interpréter tous ces résultats simplement en termes d'un univers « avant » le Big Bang. Les résultats théoriques sont justes, et les observations qui pourraient en être dérivées sont concrètes, mais la signification physique précise de ces découvertes est encore, à mon avis, un grand mystère à élucider. En particulier, est-ce qu'il y a vraiment du sens à se demander ce qui s'est passé « avant » le Big Bang ?

Ce que la théorie nous dit, c'est qu'aux alentours du Big Bang, l'Univers se trouve dans un état quantique tel que le temps et l'espace ne sont pas bien définis, tout comme dans la mécanique quantique la trajectoire d'une particule n'est pas bien définie. Mais si l'espace et le temps ne sont pas définis dans cette zone de l'espace-temps, que signifie encore l'expression « avant » ?

Finalement, qu'est-ce que le temps dans une théorie où l'espace-temps lui-même devient probabiliste ?