Note

1. E, per inciso, la radioattività dei nostri corpi è un elemento ingiustamente ignorato dai più. Siamo infatti esposti in continuazione a gas, liquidi e solidi che sono naturalmente radioattivi, e di conseguenza lo siamo anche noi, che assumiamo queste sostanze. Insomma, la radioattività non è pericolosa di per sé – tant’è che si parla anche di radioattività naturale, appunto – ma può diventarlo se troppo alta. E, da questo punto di vista, non c’è ragione di preoccuparsi: non siamo un pericolo né per noi né per chi ci sta attorno.

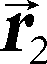1. In un sistema di riferimento in cui i due corpi hanno posizione data dai vettori e , la loro separazione è data dal vettore differenza tra i due, 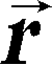= – 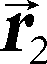, la cui grandezza (o modulo) è |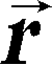| = r.

2. Il secondo d’arco è un’unità di misura utilizzata sia in navigazione sia in astronomia, e rappresenta una maniera alternativa di esprimere l’ampiezza dell’angolo sottinteso da un arco. In pratica, oltre a misurare l’ampiezza di un angolo in gradi – sistema cui siamo tutti abituati – si utilizzano unità più piccole: i minuti d’arco e i secondi d’arco. Un arco di un grado è dunque suddiviso in 60 minuti (ciascuno corrispondente a 0,017 gradi) o in 3600 secondi (ciascuno corrispondente a 0,00028 gradi). Utilizzando l’unità di misura più diffusa, potremmo dire che il perielio di Mercurio cambia di soli 0,0121 gradi ogni secolo!

1. Per chi fosse interessato a un linguaggio più rigoroso dal punto di vista matematico, si definisce lo spaziotempo una varietà matematica avente gli eventi come elementi. A tale varietà è possibile associare una «mappa» di coordinate attraverso la quale misurare le distanze invarianti tra eventi. Tale mappa è descritta da un tensore di rango secondo, detto tensore metrico, o metrica. La distanza tra eventi è quindi misurata attraverso il prodotto scalare – mediato dalla metrica – delle separazioni tra eventi, ed è un’invariante scalare.

2. A voler essere precisi, la m nell’equazione (3.II) indica la cosiddetta massa a riposo, ossia la porzione di massa che non dipende dallo stato di moto dell’oggetto, e non ha quindi valore nel caso di un fotone, che ha massa a riposo nulla. Un’espressione più generale dell’equazione (3.II), e valida per tutti i tipi di particella, è: E² = m² c⁴ + p² c², dove p è la quantità di moto (o linear momentum, in inglese) dell’oggetto. Quest’espressione è valida anche per un fotone, che ha sempre quantità di moto non-nulla e proporzionale alla sua frequenza.

3. Per i lettori interessati, posso brevemente aggiungere che le equazioni di Einstein sintetizzate nella formula (3.III) sono dieci equazioni differenziali alle derivate parziali del secondo ordine, e sono altamente non-lineari. Esse sono scritte in forma covariante attraverso l’uso di due tensori di secondo rango, ossia il tensore di Einstein (G_µν) e quello energia-impulso (T_µν).

4. È importante sottolineare che l’esempio del lenzuolo e della palla da bowling presenta una falla logica: descrive la gravità attraverso l’effetto della palla da bowling, ma essa è già soggetta a un campo gravitazionale. Approfondiremo la questione più avanti nel capitolo, dimostrando come si possa misurare la curvatura anche senza bisogno di un «lenzuolo»; per il momento è sufficiente sottolineare che questa analogia è perfettamente valida: ciò che è importante comprendere, qui, è che la presenza di materia produce curvatura.

5. Se volete tentare un piccolo quiz, provate a chiedervi: presi due punti A e B sulla superficie terrestre, qual è invece il percorso più lungo percorribile per raggiungere B partendo da A?

La risposta è: il cerchio massimo che li unisce, ossia un cerchio passante per A, B e il centro della Terra. Se ad esempio immaginiamo che i due punti abbiano la stessa longitudine, quel percorso seguirebbe il meridiano che li unisce e che passa attraverso il Polo Nord e quello Sud. Sarebbe una via decisamente lunga per raggiungere la propria meta…

1. Come ricorderete dal capitolo 2, la costante gravitazionale G è uguale a 6,67408 × 10^–11 m³/(kg s²), dove m, kg, e s stanno rispettivamente per metri, chilogrammi e secondi; ne consegue che il risultato di GM/(c² R) non ha un’unità di misura specifica legata al sistema internazionale (o SI), ossia è un numero puro.

2. Il simbolo è utilizzato in astronomia per indicare il pianeta Terra; quindi, per fare un esempio, indica la massa del nostro pianeta. In modo analogo il simbolo , che useremo presto, è utilizzato per indicare il Sole e quantità a esso relative.

3. Il parsec è un’unità di misura molto comune in astronomia, in quanto permette di dar conto delle enormi distanze che si incontrano al di fuori del sistema solare. È proprio per questa ragione che in astronomia non si usano mai i chilometri, ma piuttosto gli anni luce e i suoi multipli. Ricordo che un «anno luce» non misura un intervallo di tempo, ma di spazio: quello percorso da un fascio di luce in un anno, ossia circa 10.000 miliardi (10¹³) di chilometri. Un parsec, invece, corrisponde a 3,26 anni luce, vale a dire 30.000 miliardi di chilometri circa.

1. Un fenomeno ondoso come quello delle onde elettromagnetiche è caratterizzato da due grandezze fondamentali: la lunghezza d’onda (ovvero la distanza tra due «picchi» nell’onda) e la frequenza (cioè il numero di picchi che giungono in un intervallo di tempo). La lunghezza d’onda, λ, e la frequenza, f, della radiazione elettromagnetica sono inversamente proporzionali; a livello matematico, possiamo dire che λ = c/f, dove c è la velocità della luce.

2. La radiazione di questo tipo è anche detta a raggi X soffici, per distinguerli da quelli a più alta energia che sono invece definiti duri. La durezza di un fotone nella banda X è dunque misurata attraverso la sua energia (o, in modo equivalente, la sua frequenza): i raggi X soffici hanno di norma un’energia compresa tra 0,1 e 0,3 keV (chiloelettronvolt), mentre quelli duri tra 10 e 100 keV.

3. Sarà qui bene ricordare che le prime classificazioni raggruppavano i tipi di stelle in classi di «colore», a seconda appunto del colore dominante nel loro spettro di emissione: dal blu-bianco delle più calde all’arancione-rosso delle più «fredde». In ordine di calore decrescente, dal blu al rosso, le classi erano: O, B, A, F, G, K, M. Per ricordarle in ordine esiste anche una frase in inglese, introdotta dall’astronoma statunitense che sistematizzò tale suddivisione, Annie Jump Cannon (1863-1941): Oh, be a fine girl/guy, kiss me! (che tradotto suona più o meno: «Oh, sii una ragazza/un ragazzo gentile, baciami!»).

4. I. Šklovskij, in «Soviet astronomy», 11, 749 (1968).

5. W. Baade – F. Zwicky, in «Proceedings of the National Academy of Sciences of the United States of America», 20, 254 (1934).

6. A. Hewish, S.J. Bell, J.D.H. Pilkington, P.F. Scott, R.A. Collins, in «Nature», 217, 709 (1968).

7. La massa atomica è il numero che indica quanti neutroni e protoni sono contenuti all’interno di un certo nucleo atomico. Una quantità simile, ma distinta, è il numero atomico, che conta invece solo il numero di protoni in un nucleo atomico. Ad esempio l’idrogeno ha massa atomica 1 e numero atomico 1 perché il suo nucleo è formato da un solo protone, mentre l’elio ha massa atomica 4 e numero atomico 2 visto che il suo nucleo è formato da due protoni e due neutroni.

8. I neutroni sono particelle di tipo fermionico, ossia seguono una distribuzione statistica di Fermi-Dirac e sono quindi soggetti al principio di esclusione di Pauli. Esso stabilisce che uno stato quantico possa essere occupato al massimo da una singola particella di questo tipo. Proprio tale principio è responsabile della pressione di degenerazione. Usando un’analogia purtroppo fin troppo chiara ai nostri giorni, è come se le particelle fermioniche fossero costrette al «distanziamento sociale» e non potessero quindi trovarsi troppo vicine le une alla altre. Quando si avvicinano in modo eccessivo, generano una grossa pressione che impedisce una compressione ulteriore.

9. In meccanica quantistica la funzione d’onda rappresenta lo stato di un sistema fisico, ad esempio una particella elementare. Essa è funzione del tempo e della posizione, sicché può essere utilizzata per misurare la probabilità che una particella sia in una certa regione dello spazio a un certo istante.

10. G. Gamow – M. Schoenberg, in «Physical Review», 59, 539 (1941).

11. Il modello che ho proposto prende il nome di blitzar e coinvolge la nascita di un buco nero da una stella di neutroni che collassi perdendo il suo campo magnetico. Simulazioni numeriche di questo processo mostrano che esso produrrebbe un segnale molto vicino a quello osservato, sia per durata sia per quantità di energia emessa. Ovviamente ciò non significa che il modello sia corretto e spieghi davvero le osservazioni: la sentenza deve ancora essere emessa…

12. F. Pacini, in «Nature», 219, 145 (1968).

13. Ho deciso, qui, di fornire un esempio diverso da PSR J0437-4715 affinché sia chiaro che non si tratta di pulsar «speciali».

1. Almeno per un certo periodo, il nome «buco nero» ebbe anche un rivale: stella congelata. Quest’ultimo era nato per sottolineare che, quando una stella collassa e dà vita a un buco nero, sembra appunto «congelarsi» nel tempo: a un’osservatrice esterna la sua evoluzione pare bloccata. Tuttavia, la rivalità tra i due nomi non durò a lungo e la comunità scientifica finì presto per adottare la forma che oggi conosciamo tutti, tanto efficace quanto evocativa.

2. Sì, lo so, normalmente si dice osservatore. Questo è però un retaggio del passato in cui la scienza – specie la fisica teorica – era prettamente maschile. Considero questo retaggio anacronistico e vorrei che ragazze e donne si sentano ugualmente protagoniste della scienza e in particolare della fisica teorica. È per questo che nel resto del libro userò il femminile lì dove normalmente è usato il maschile. È un piccolo gesto ma spero che le faccia sentire meno estranee a questa scienza. E lo so, suona po’ strano all’inizio, ma ci si fa presto l’abitudine.

3. Al contrario, se il buco nero avesse una massa dell’ordine di qualche massa solare, le forze mareali – vale a dire quelle generate dal rapido cambiamento del campo gravitazionale tra un punto e l’altro – sarebbero così differenti anche su distanze ristrette da allontanare la vostra testa dai vostri piedi come foste un elastico. In sostanza vi ritrovereste «spaghettificati». Un’esperienza che, francamente, non mi sento di consigliarvi…

4. J. Michell, in «Philosophical Transactions of the Royal Society of London», 74, 35 (1784).

5. R.P. Kerr, R. Kerr, in «Physical Review Letters», 11, 237 (1963).

6. R. Ruffini – J.A. Wheeler, in «Physics Today» 24, 30 (1971).

7. S.W. Hawking, in «Communications of Mathematical Physics», 43, 199 (1975); S.W. Hawking, in «Nature» 248, 3031 (1974).

8. Come già accennato, i buchi neri supermassicci hanno campi gravitazionali che variano in maniera molto graduale se confrontati alla scala umana (quindi di «oggetti» con dimensioni dell’ordine di un paio di metri). Ecco perché ne ho scelto uno per il mio esempio.

9. Le due caratteristiche non sono necessariamente collegate: esistono infatti soluzioni di buco nero che posseggono un orizzonte degli eventi ma non una singolarità fisica al proprio centro, e prendono pertanto il nome di buchi neri regolari.

10. P.O. Mazur – E. Mottola, in «Proceedigns of the National Academy of Sciences, USA», 101, 9545 (2004).

11. C. Misner – J.A. Wheeler, in «Annals of Physics», 2, 525 (1957).

1. Il plasma è uno dei quattro stati della materia, assieme a quello solido, liquido e gassoso. È caratterizzato da una miscela di ioni (atomi privati di alcuni dei loro elettroni) ed elettroni liberi. Lo stato di plasma è molto diffuso in astrofisica, a causa delle alte energie che possono essere raggiunte nel cosmo (ad esempio sulla superficie di una stella).

2. H. Falcke, M. Kramer, L. Rezzolla, ERC Synergy Grant “BlackHoleCam: Imaging the Event Horizon of Black Holes”; Grant No. 610058 (2013-2021).

3. Il parametro d’impatto è usato in fisica delle particelle, ma anche in fisica gravitazionale, per misurare la distanza perpendicolare tra un bersaglio e il punto più vicino a esso raggiunto da una particella lungo la sua traiettoria.

4. Come ovvio, vista la simmetria sferica di un buco nero di Schwarzschild, l’orbita circolare instabile è in realtà un’intera superficie sferica di raggio pari al raggio dell’anello di luce. Il concetto di anello di luce può inoltre essere esteso anche ai buchi neri rotanti, ma in questo caso il quadro si fa decisamente più complicato. In aggiunta alla distinzione tra traiettorie corotanti e controrotanti rispetto al buco nero, infatti, la superficie sferica dell’anello di luce viene sostituita da una regione che è solo approssimativamente sferica.

5. R. Penrose – R.M. Floyd, in «Nature Physical Science», 229, 177 (1971).

6. Quello appena descritto prende in realtà il nome di effetto Doppler relativistico longitudinale, perché ne esiste anche uno trasverso, che porta a una variazione della frequenza anche quando il moto è in una direzione trasversa rispetto a quella di emissione della luce. Quest’ultimo tipo di effetto, però, non gioca un ruolo importante in quanto stiamo discutendo qui.

7. In ambito matematico tutto ciò si esprime attraverso il grado di non-linearità delle equazioni, vale a dire una misura che indichi come a una piccola variazione in una delle proprietà del plasma possano corrispondere enormi variazioni del suo comportamento.

8. Un positrone è la controparte di antimateria di un elettrone, ed è pertanto una particella con la stessa massa a riposo di un elettrone ma carica positiva.

9. Esiste tutta una serie di scenari che potenzialmente potrebbero fornire tale energia. Una possibilità è che essa venga direttamente dall’energia di rotazione del buco nero, attraverso quello che è noto come processo di Blandford-Znajek (si veda R.D. Blandford – R.L. Znajek, in «Monthly Notices of the Royal Astronomical Society», 179, 433 (1977)), mentre un’altra è che sia invece fornita dall’energia rotazionale del disco, attraverso quello che è noto come processo di Blandford-Payne (e qui si veda R.D. Blandford – D.G. Payne, in «Monthly Notices of the Royal Astronomical Society», 199, 883 (1982)). Per finire, un ultimo scenario prevede che l’accelerazione venga fornita tramite processi dissipativi all’interno del plasma magnetizzato.

10. T. Karras, S. Laine, T. Aila, A Style-Based Generator Architecture for Generative Adversarial Networks, arXiv:1812.04948.

11. Y. Mizuno, Z. Younsi, C. M. Fromm, O. Porth, M. De Laurentis, H. Olivares, H. Falcke, M. Kramer, L. Rezzolla, in «Nature Astronomy», 2, 585 (2018); H. Olivares, Z. Younsi, C. M. Fromm, M. De Laurentis, O. Porth, Y. Mizuno, H. Falcke, M. Kramer, L. Rezzolla, in «Monthly Notices of the Royal Astronomical Society», 497, 521 (2020)

1. Un’equazione d’onda per un campo scalare φ può dunque essere scritta semplicemente come 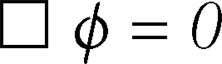, dove è l’operatore differenziale di D’Alambert e rappresenta l’indicazione sintetica di una serie di derivate parziali del secondo ordine. Per fare un esempio, in un sistema di coordinate cartesiane in tre dimensioni spaziali: , dove υ è la velocità di propagazione.

2. Come specificato, quella proposta è una descrizione al primo ordine nella perturbazione. Se volessimo considerare anche effetti non-lineari – ossia contributi alla dinamica di ordine superiore al primo – il materassino si sposterebbe anche nella direzione di propagazione dell’onda, in quanto quest’ultima è parzialmente longitudinale e trasferisce anche una certa quantità di moto.

3. Accanto a queste due polarizzazioni lineari ne esistono anche due circolari – una per ogni senso di rotazione – in cui la deformazione ruota intorno alla direzione di propagazione dell’onda. Facendo di nuovo riferimento alla Figura 8.2, in questo caso l’Uomo vitruviano sarebbe stiracchiato e compresso lungo una direzione che ruota nel tempo man mano che l’onda si propaga.

4. Nei primissimi istanti di vita, l’universo era estremamente caldo e denso, sicché la materia e la radiazione erano «accoppiate» e le loro temperature evolvevano nella stessa maniera. Quando l’universo si è espanso e raffreddato abbastanza, materia e radiazione si sono «disaccoppiate» e, in termini di evoluzione termica, ognuna è «andata per la sua strada». Il momento del disaccoppiamento è stato molto speciale in quanto i fotoni sono stati finalmente «liberi» di propagarsi senza urtare in continuazione con qualche particella. Questi fotoni, che sono stati prodotti solo 380.000 anni dopo il Big-Bang, sono ancora visibili in quella che si chiama radiazione cosmica di fondo, un bagno di radiazione molto uniforme. Se avessimo occhi sensibili alle microonde, il cielo di notte non ci apparirebbe scuro ma illuminato tenuemente da questa radiazione primordiale.

5. Mentre è facile definire un orizzonte degli eventi nel caso di uno spaziotempo statico o stazionario, è molto più difficile calcolarlo nel caso di uno spaziotempo dinamico, come quello che caratterizza due buchi neri prima di fondere o una stella prima di collassare a buco nero. In questi casi si utilizza dunque il concetto di orizzonte apparente, per definire la superficie bidimensionale entro la quale la luce è intrappolata. Nel caso di spazitempi statici o stazionari, i due tipi di orizzonte coincidono.

6. Il Love number non ha niente a che fare con i sentimenti: prende il nome dal fisico britannico Augustus Love (1863-1940), che per primo lo definì nella sua teoria dell’elasticità.

7. Va da sé che se la massa dell’oggetto è al di sopra di circa 3 masse solari non si potrà trattare di una stella di neutroni, ma sarà piuttosto un buco nero; tuttavia esistono osservazioni, ad esempio quella dell’evento GW190814, in cui l’oggetto meno massiccio ha una massa di circa 2,6 masse solari e non è quindi chiaro se prima della fusione fosse il buco nero meno massiccio mai osservato o la stella di neutroni più massiccia. Si veda The LIGO Collaboration and Virgo Collaboration, in «Astrophysical Journal Letters», 896, L44 (2020).

8. Gran parte di ciò che abbiamo visto per sistemi binari di buchi neri o di stelle di neutroni vale anche nel caso di un sistema binario misto, composto da un buco nero e una stella di neutroni, ma con due importanti differenze. La prima è legata al rapporto di massa tra i due oggetti, che può essere di 10 a 1 o anche maggiore viste le masse caratteristiche in gioco (il buco nero avrà una massa tra 15-25 masse solari, mentre la stella di neutroni tra 1,3-2,3 masse solari). La seconda differenza è che la coalescenza di un sistema misto non può portare alla formazione di una stella ipermassiva. In questo caso, infatti, la stella di neutroni viene distrutta marealmente o addirittura «assorbita intera».

9. Si veda E. Nakar, in «Physics Reports», 442, 166 (2007) per un saggio sulla letteratura a riguardo.

10. Si veda S.E. Woosley – J. S. Bloom, in «Annual Review of Astronomy and Astrophysics», 44, 507 (2006) per un saggio sulla letteratura a riguardo.

11. I rivelatori di onde gravitazionali sono generalmente sensibili in quasi tutte le direzioni di provenienza del segnale, ma non proprio in tutte e non in tutte con la stessa sensitività. Esistono infatti direzioni in cui la sensitività è massima, e altre in cui è minima o quasi nulla, al punto che – esattamente come per un’antenna radio – è possibile definire una mappa di sensitività del rivelatore interferometrico. Nel caso di GW170817, il fatto che Virgo non l’avesse misurato ha comunque fornito informazioni preziose, che hanno consentito di restringere l’area di ricerca del segnale elettromagnetico e quindi di scoprire GRB 170817A.

12. Nel caso della coalescenza di sistemi binari di buchi neri di massa stellare una forte controparte elettromagnetica non è generalmente attesa. La ragione è che questi sistemi rappresentano lo stadio finale di un sistema binario che ha essenzialmente perso ogni traccia di materia, o attraverso i processi di collasso che hanno prodotto i buchi neri o attraverso le esplosioni di supernova e le onde d’urto associate.

13. L. Rezzolla, B. Giacomazzo, L. Baiotti, J. Granot, K. Koveliotou, M.-A. Aloy, in «The Astrophysical Journal Letters», 732, L6 (2011).

14. L.-X. Li – B. Paczy–ski, in «The Astrophysical Journal Letters», 507, L59 (1998).

15. In astronomia, si indica come nova un’esplosione termonucleare sulla superficie di una nana bianca, provocata dall’accumulo di idrogeno per via di un processo di accrescimento da una stella compagna in un sistema binario. L’esplosione può essere visibile per diversi giorni e raggiunge una luminosità che varia tra 10.000 e 100.000 volte quella del Sole. Si tratta di esplosioni molto poco energetiche se confrontate con i lampi gamma.

16. J.M. Lattimer – D.N. Schramm, in «The Astrophysical Journal», 210, 549 (1976).