L'irresistibile attrazione della gravità Luciano Rezzolla

Prev Next

Abbiamo visto nel capitolo precedente come l’avvento dell’astronomia X abbia lasciato «spiazzati» gli astrofisici alla fine degli anni Sessanta. Le osservazioni ottenute dagli appositi rivelatori posti su razzi e satelliti avevano infatti mostrato l’esistenza di oggetti mai visti prima: dotati di masse considerevoli ma dimensioni estremamente compatte. Sorgenti come Sco-X1 e Cyg-X1 rappresentavano non solo delle sorprese inspiegabili nel quadro dell’astrofisica noto a quei tempi, ma offrivano sfide all’intera comprensione della fisica moderna. Tuttavia, mentre per Sco-X1 era possibile formulare una spiegazione in qualche modo plausibile delle osservazioni, grazie all’ipotetica esistenza di una fantomatica stella di neutroni, la fenomenologia di Cyg-X1 rappresentava un vero e proprio enigma.

Con una massa pari a circa quindici masse solari non era certo possibile invocare la presenza di una stella di neutroni. D’altro canto, la variabilità dell’emissione nella banda X da parte di Cyg-X1 – che era di norma nell’ordine del secondo, ma arrivava a scendere addirittura a qualche millisecondo appena – suggeriva la presenza di un oggetto diverso e molto più compatto, con una scala di lunghezza che poteva essere dell’ordine di qualche decina di chilometri. Oggi sappiamo che Cyg-X1 è un rappresentante abbastanza ordinario di tutta una classe di oggetti celesti: gli HMXB, appunto. Si tratta, ancora una volta, di sistemi binari in cui c’è passaggio di massa da una stella ordinaria a un altro oggetto, molto ma molto più compatto; tale passaggio avviene di nuovo tramite un disco di accrescimento, attraverso il quale la materia cade sull’oggetto compatto riscaldandosi ed emettendo una radiazione molto intensa nella banda X. La differenza più rilevante con quanto visto per Sco-X1 è che in questo caso la stella ordinaria risulta l’oggetto con la massa più alta, mentre l’altro – quello molto più compatto – oggi sappiamo essere… un buco nero!

Questi corpi celesti sono ormai diventati parte integrante dell’immaginario collettivo, tant’è vero che la risposta più sagace e divertente alla domanda «Cos’è un buco nero?» mi è arrivata da una bambina. A darmela fu mia figlia Anna; al tempo non andava ancora a scuola, ma – come fanno spesso i bimbi – si pronunciò con il tipico distacco di chi sa già tutto della vita. «Be’, è chiaro: è semplicemente un buco che non si riempie…» Un’affermazione che non può dirsi sbagliata – anzi, è perfettamente corretta – sebbene si tratti di una descrizione meramente qualitativa, che in realtà non spiega cosa siano davvero i buchi neri. E, siccome non è infrequente che persino i canali d’informazione generalista diano descrizioni quantomeno confuse di questi oggetti, sarà bene mettere un po’ di ordine nella mole di informazioni che circolano a riguardo.

Così, nella speranza di liberare il campo dalle leggende metropolitane e dalle descrizioni superficiali più diffuse, nelle pagine che seguiranno cercherò di spiegare – in maniera semplice, ma via via più accurata e approfondita – cosa siano i buchi neri e quali caratteristiche abbiano, partendo dalla loro genesi e terminando con una discussione sulle difficoltà che gli scienziati ancora hanno nel confrontarsi con un’idea fondamentalmente difficile da accettare.

Una soluzione stravagante

L’approccio più semplice e al contempo più rigoroso per spiegare cosa siano i buchi neri non può che partire dalla loro definizione, e in particolare dall’affascinante – per quanto tragica – genesi della prima soluzione alle equazioni di Einstein, proposta da un fisico di Francoforte di nome Karl Schwarzschild (1873-1916).

Vi ricordo che nel novembre 1915, sugli atti dell’allora Regia accademia delle scienze di Berlino, apparvero le equazioni di campo di Albert Einstein, fondamento della sua Relatività Generale. A quel tempo Karl Schwarzschild era già un astronomo rinomato, tanto da essere diventato direttore dell’Osservatorio astrofisico di Potsdam, a pochi chilometri da Berlino. Nonostante il ruolo prestigioso che ricopriva, come molti degli ebrei tedeschi suoi contemporanei Schwarzschild avvertiva il bisogno di testimoniare la propria lealtà al Paese e il senso di appartenenza che lo legava alla società tedesca. Per questa ragione nel 1914, allo scoppio della Prima guerra mondiale, si era arruolato come volontario ed era stato mandato in battaglia. Sebbene avesse già raggiunto i quarant’anni, combatté prima sul fronte occidentale e poi su quello orientale. Proprio mentre si trovava in Russia si ammalò gravemente, anche a causa delle durissime condizioni incontrate dai militari, e la sua salute si deteriorò in fretta. Morì nel 1916, ma negli ultimi mesi di vita riuscì comunque a trovare la prima soluzione alle equazioni di Einstein.

Ignaro dell’impatto che essa avrebbe avuto, Schwarzschild non le diede alcun nome; solo nel 1967 (di nuovo quell’anno…) il fisico americano John Archibald Wheeler usò l’espressione «buco nero» per descriverla.¹ Quella di Schwarzschild rappresenta in effetti la soluzione più semplice alle equazioni di campo della Relatività Generale; eppure, all’interno del corso che tengo a Francoforte ci si arriva solo verso la fine delle lezioni, e dopo aver introdotto per mesi la matematica necessaria alla sua derivazione. Essa fu ottenuta sotto tre importanti ipotesi:

la presenza di una simmetria sferica;
l’indipendenza dal tempo, ovvero l’assunzione di staticità della soluzione;
l’assenza di materia, ovvero l’assunzione che si tratti di una soluzione nel vuoto.

Adesso sappiamo che quella di Schwarzschild è anche l’unica soluzione alle equazioni di Einstein che soddisfi tali condizioni (un risultato che rappresenta addirittura la tesi del celebre teorema di Birkhoff, del quale parleremo più avanti). È però improbabile che lo stesso Schwarzschild abbia apprezzato appieno la dirompente novità delle sue implicazioni: alla stregua di molti scienziati dopo di lui, deve averla considerata una «stramberia» della nuova teoria, al punto che avviò in fretta un fitto scambio epistolare con Einstein, chiedendo la sua opinione.

In effetti, diversi aspetti rendevano la soluzione di Schwarzschild a dir poco bizzarra. Tanto per cominciare è a simmetria sferica, e ha pertanto un «centro» e una zona da esso più «lontana», tecnicamente definita asintotica. Lontano dal centro della soluzione – e quindi dell’oggetto che descrive – il quadro sembra analogo a quello di una sorgente gravitazionale nella teoria classica di Newton. Fin qui, dunque, nulla di particolarmente strano. Tuttavia, mentre nella visione newtoniana questo risultato è possibile solo in presenza di materia (visto che il campo gravitazionale dev’essere prodotto da un oggetto dotato di massa) la soluzione di Schwarzschild è – come si è detto – nel vuoto. Insomma, essa suggeriva che fosse possibile creare un campo gravitazionale anche dal… niente. Una conclusione decisamente stravagante.

Ulteriore stranezza, essa prevede l’esistenza di una superficie sferica avente un raggio preciso – r = r_S, poi ribattezzato raggio di Schwarzschild e ormai diventato una delle lunghezze-scala fondamentali in astronomia – il cui valore è dato dalla seguente equazione:

Esattamente a questo raggio si verifica una serie di fenomeni particolari dei quali parleremo presto, ma la questione più pressante era che, lì, la soluzione di Schwarzschild non è ben definita: in quel punto le funzioni matematiche che la descrivono divergono, ossia assumono valori infinitamente grandi.

Com’è evidente già a prima vista, l’espressione (6.I) ci dice in sostanza che il raggio di Schwarzschild è pari a due volte la massa M dell’oggetto in questione, ossia del buco nero. (Ancora una volta, ho marcato in grigio le costanti che non hanno un «significato specifico» ai fini della comprensione.) Oggi sappiamo che r_S rappresenta il raggio del cosiddetto orizzonte degli eventi – del quale parleremo in dettaglio poco più avanti – e che il divergere della soluzione al suo valore non è particolarmente preoccupante: è solo il frutto di una scelta non adeguata delle coordinate utilizzate per descriverla. In effetti – ma lo si scoprì molto dopo – è possibile utilizzare tutta una serie intelligente di trasformazioni di coordinate che «eliminano» tale singolarità e rendono il raggio r = 2GM/c² perfettamente regolare, cioè senza divergenze. Restano, però, altre peculiarità. In particolare, è impossibile per un raggio di luce e per qualsiasi oggetto dotato di massa propagarsi da lì verso l’esterno, sebbene tutto possa entrarvi. In sostanza, la superficie con raggio pari a quello di Schwarzschild sembra comportarsi proprio come una membrana unidirezionale, che consente l’assorbimento di oggetti ma non ne lascia scappare nessuno. Vedremo più avanti cosa significhi tutto ciò da un punto di vista fisico.

Infine, la terza stranezza della soluzione di Schwarzschild – e quella che implica la complicazione più seria – consiste nel fatto che essa non diverge solo all’orizzonte degli eventi, ma anche al centro, ossia a r = 0, quando il raggio diventa nullo. A differenza della singolarità all’orizzonte, questa al centro è molto più severa e non può essere sanata, neanche attraverso un’intelligente trasformazione di coordinate. Tutti i possibili indicatori di cosa succeda quando ci si avvicina al raggio zero suggeriscono infatti che ogni quantità fisica e geometrica diventi infinitamente grande. Per questa ragione, a r = 0 fu assegnato il nome affascinante ma un po’ inquietante di singolarità dello spaziotempo.

Oggi definiamo la zona della soluzione di Schwarzschild intorno a r = 0 una singolarità fisica, vale a dire una zona dello spaziotempo dove il comportamento divergente delle equazioni è tale che esse sono matematicamente impossibili da risolvere. Ciò significa che, in prossimità della singolarità, le leggi della fisica cessano di essere valide e siamo pertanto incapaci di predire e addirittura comprendere cosa vi possa accadere. Questa singolarità fisica rimane ancora oggi la spina più grande nel fianco della teoria di Einstein: la manifestazione palese del fatto che, per quanto corretta, essa rimane incompleta. Sebbene la Relatività Generale abbia ormai dimostrato di saper fornire predizioni corrette sul comportamento della gravità a grandi scale, è palese che resta incapace di descrivere la gravità in presenza di piccolissime dimensioni e grandi curvature, vale a dire le dimensioni in cui entrano in gioco le leggi della meccanica quantistica. Ancora oggi – nonostante gli sforzi di generazioni di fisici teorici – siamo sprovvisti di una teoria della gravità quantistica. Ma non temete: ne riparleremo alla fine del nostro viaggio.

Insomma, quando fu proposta nel 1916, la soluzione di buco nero di Schwarzschild suscitò reazioni contrastanti. Da un lato dimostrava che le equazioni di Einstein non solo erano estremamente interessanti, ma avevano anche delle soluzioni; dall’altro, però, le domande che sollevava erano più delle risposte che offriva.

Come potete immaginare, la soluzione di Schwarzschild non rappresentava la via migliore per cominciare a comprendere la Relatività Generale. Di conseguenza, la nuova teoria proposta da Einstein fu accolta dalla comunità scientifica di quegli anni con atteggiamento di distaccato interesse e scettica curiosità. E ciò era vero tanto per i matematici, attratti dalle sue implicazioni di geometria e curvatura, quanto per i fisici, interessati alle ricadute a livello gravitazionale e sperimentale.

In questo clima diffuso di paternalistico apprezzamento ma fondamentale distacco – peggiorato dalla difficoltà nel risolvere le equazioni di Einstein e quindi comprenderne le predizioni – la teoria della Relatività Generale fu «vittima» di un disinteresse generalizzato da parte della comunità della fisica teorica. Sentimento peraltro alimentato da alcune comprensibili «distrazioni»: a quel tempo iniziavano infatti a comparire teorie altrettanto interessanti, ad esempio la meccanica quantistica, che però offrivano predizioni molto più facili da comprendere e, soprattutto, da verificare sperimentalmente.

Insomma, la teoria di Einstein sembrava condannata a scivolare pian piano nel dimenticatoio. Per fortuna, l’avvento dell’astronomia X e l’osservazione di oggetti come Cyg-X1 costrinsero la comunità scientifica a riconsiderarne – a distanza di cinquant’anni – le predizioni.

Velocità di fuga, orizzonte degli eventi e singolarità

Dopo aver menzionato le principali stravaganze che la soluzione di buco nero proposta da Schwarzschild sottoponeva agli studiosi, cercheremo adesso di comprenderle più nel dettaglio. In particolare, discuteremo di cosa sia l’orizzonte degli eventi, quali siano le proprietà peculiari di questa superficie matematica e, infine, cosa sia la singolarità al centro di un buco nero. Tuttavia, per rendere più comprensibili le caratteristiche dell’orizzonte degli eventi, è bene partire da un fenomeno che ognuno di noi può sperimentare in maniera diretta.

Immaginate di prendere una pallina da tennis e lanciarla verso l’alto, facendo attenzione a imprimerle una traiettoria il più possibile verticale. Ciò che osserverete è che, data una certa velocità iniziale, la pallina sarà soggetta a una decelerazione: durante l’ascesa la sua velocità diminuirà pian piano fino a raggiungere – in un punto particolare del suo moto verticale – un valore nullo. In quel momento la pallina smetterà di salire e tornerà indietro, accelerando mentre torna verso di voi. Esiste quindi un’altezza massima associata al moto della pallina, e legata alla forza con cui l’avete scagliata. E, come vi suggerirà l’esperienza, se la lanciate di nuovo a una velocità diversa, l’altezza massima raggiunta al punto di inversione del moto cambierà. In particolare, tale altezza sarà minore se è minore la velocità iniziale impartita, e sarà maggiore se è maggiore la velocità di partenza. È quindi chiaro che esiste una relazione precisa tra la velocità iniziale con cui lanciate la pallina e l’altezza massima che essa raggiunge. In realtà, quell’altezza rappresenta la posizione in cui l’energia cinetica iniziale della pallina viene convertita interamente in energia potenziale gravitazionale.

L’aspetto forse più importante da sottolineare, in questo semplice esempio, è il motivo per cui la pallina torna indietro, ovvero il fatto che sia legata gravitazionalmente: il campo gravitazionale prodotto dalla Terra è così dominante sulla sua dinamica che l’oggetto in questione non è in grado di sottrarvisi. A questo punto è lecito chiedersi se esista una velocità iniziale che consenta alla pallina di sottrarsi al campo gravitazionale. La riposta è sì: è quella che chiamiamo velocità di fuga. Calcolarne il valore è abbastanza semplice e richiede di confrontare l’energia cinetica con quella potenziale gravitazionale. In questo modo si ottiene un’espressione valida sia nella fisica gravitazionale di Newton sia in quella di Einstein:

Questa espressione ci dice che, per una sorgente di campo gravitazionale – ad esempio la Terra – di massa M e raggio R, la velocità di fuga di un piccolo oggetto dotato di massa è proporzionale alla radice quadrata della massa e inversamente proporzionale alla radice quadrata del raggio. In sostanza, essa cresce con l’aumentare della massa del pianeta (più è massiccio quest’ultimo maggiore sarà la velocità necessaria ad abbandonarlo) e decresce con l’aumentare delle sue dimensioni.

Se volessimo lanciare la nostra pallina e farla scappare dal campo gravitazionale terrestre, dovremmo quindi lanciarla a circa 11,2 chilometri al secondo, ovvero 40.320 chilometri l’ora. Si tratta di una velocità considerevole, ed è proprio per questo che nemmeno il miglior tennista della storia riuscirà mai a mandare in orbita una pallina, sul nostro pianeta. Il che è una fortuna: sarebbe decisamente frustrante assistere a un match nel quale non si possano fare pallonetti perché si rischierebbe di perdere la palla…

Ora, l’espressione (6.II) è interessante per almeno due ragioni diverse. La prima è che la velocità di fuga è indipendente dalla massa M dell’oggetto lanciato (nella formula, infatti, compare solo la massa della sorgente del campo gravitazionale): serve dunque la stessa velocità per spedire sulla Luna un granello di sabbia e una navicella spaziale (ovviamente l’energia spesa sarebbe molto diversa…). La seconda è che la velocità di fuga, ve ne sarete accorti, dipende da una quantità che abbiamo già incontrato: la compattezza M/R della sorgente del campo gravitazionale. Ciò significa che oggetti celesti differenti – la Terra, la Luna, il Sole… – avranno differenti velocità di fuga, perché diversa è la loro compattezza e, di riflesso, il loro campo gravitazionale. Così, sulla Luna, la velocità di fuga è quasi cinque volte più bassa che sulla Terra: circa 2,4 chilometri al secondo. Nemmeno sul nostro satellite naturale saremmo in grado di lanciare la pallina al di fuori del campo gravitazionale con la semplice forza dei muscoli, ma di certo la scaglieremmo molto più in alto che sulla Terra. Viceversa, se ci provassimo sul Sole sarebbe difficile anche solo lanciarla, visto che lì la velocità di fuga è all’incirca di 615 chilometri al secondo.

Per inciso, proprio il fatto che la velocità di fuga sulla Luna sia così bassa – e in particolare più bassa della velocità media delle molecole di un gas di azoto – spiega perché il nostro satellite naturale non abbia un’atmosfera. Al contrario, la velocità di fuga della Terra le ha permesso di trattenere un’atmosfera, la cui presenza è fondamentale per la vita sul pianeta.

Ma c’è un altro aspetto dell’espressione (6.II) che vale la pena sottolineare. Sappiamo infatti che esiste una velocità massima alla quale gli oggetti possono muoversi: quella della luce. Ebbene, possiamo utilizzare la formula (6.II) per calcolare la compattezza necessaria affinché la velocità di fuga di un oggetto celeste sia pari, appunto, a quella della luce. Scopriremo così che, al netto di costanti quali G e c², tale valore è 1/2. Ecco che il raggio di Schwarzschild, così come dato dall’espressione (6.I), diventa ora molto più semplice da comprendere: esso è il raggio di un oggetto – nello specifico, un buco nero – la cui compattezza è M/R = 1/2, che è anche la compattezza massima vista finora. Ciò ci permette di introdurre una nuova definizione dell’orizzonte degli eventi: esso è la superficie alla quale la velocità di fuga è la massima possibile, ovvero quella della luce. In altre parole, qualora fosse emessa esattamente dall’orizzonte degli eventi, la luce non potrebbe lasciare il campo gravitazionale del buco nero perché avrebbe bisogno di una velocità di fuga maggiore della propria.

Immaginate di trovarvi su questa superficie matematica e lanciare un fascio di luce laser verso una stella lontana: a causa del fortissimo campo gravitazionale, esso non potrà propagarsi verso l’esterno e dovrà invece tornare indie- tro! È bene sottolineare che questo concetto è vero soltanto esattamente all’orizzonte degli eventi: se noi ci piazzassimo poco oltre e ripetessimo l’esperimento, parte del nostro fascio laser riuscirebbe a evadere dal campo gravitazionale e raggiungere un’osservatrice posta a grande distanza.² In sostanza, questa proprietà peculiare è valida solo finché r = r_S; al di fuori dell’orizzonte degli eventi, ossia a raggi superiori, il campo gravitazionale resta sì estremamente intenso ma non è «invincibile». Al contrario, se emettessimo un fascio di luce mentre ci troviamo all’interno dell’orizzonte degli eventi, esso potrebbe spostarsi solo in direzione di aree con raggio minore, viaggiando quindi verso il centro e la singolarità.

Torniamo però a considerare il fascio di luce emesso poco oltre l’orizzonte degli eventi. Abbiamo visto che parte di questo raggio raggiungerebbe un’osservatrice posta anche a notevole distanza, ad esempio sulla Terra. Tuttavia, la luce percepita da tale osservatrice sarebbe molto diversa, a livello di colore, da quella rilasciata in origine. Poniamo che la luce fosse a una lunghezza d’onda del visibile spostata verso la parte blu dello spettro: ebbene, l’osservatrice la vedrebbe invece tendente al rosso. Inoltre questa tendenza ad «arrossarsi» sarebbe tanto maggiore quanto più il punto di emissione è vicino al raggio di Schwarzschild. Poiché sappiamo che la lunghezza d’onda di un fascio di luce è indice dell’energia dei fotoni che lo compongono – per essere precisi, l’energia di un fotone è inversamente proporzionale alla sua lunghezza d’onda – il fenomeno della tendenza al rosso sembrerebbe indicare che il fascio di luce abbia perso energia nel propagarsi dal punto in cui è stato emesso, vicino all’orizzonte degli eventi, fino all’osservatrice.

Questo processo in apparenza bizzarro acquista senso se torniamo a pensare alla nostra pallina da tennis lanciata verso l’alto: anch’essa, infatti, perde energia cinetica – che si trasforma in energia potenziale gravitazionale – e a un certo punto è costretta ad arrestare la propria avanzata, per tornare indietro. Dal momento che un fotone non può rallentare, perché costretto per definizione a muoversi alla velocità della luce, esso mostra la perdita di energia cambiando lunghezza d’onda. Si tratta di un fenomeno ben noto in astrofisica, e incarna una proprietà molto comune di oggetti celesti compatti: lo spostamento verso il rosso – o redshift – gravitazionale. Tale fenomeno raggiunge il suo apice proprio nel caso di buchi neri, e diventa matematicamente infinito per un fotone emesso dall’orizzonte degli eventi. Come ovvio, se il redshift di un fotone emesso a r = r_S è infinito, l’osservatrice non lo riceverà mai. Ecco dunque una diversa spiegazione del perché un fotone emesso all’orizzonte degli eventi non possa propagarsi verso l’esterno, ma possa al massimo restare su orbite tangenti a questa superficie.

Per rendere il più digeribile possibile questo concetto, proviamo a fare un gedanken Experiment. Immaginate di trovarvi a una certa distanza dall’orizzonte degli eventi – magari a bordo di una navicella spaziale posizionata in una delle orbite circolari stabili che sono ammesse intorno a un buco nero – e di lasciar cadere verso il corpo celeste un dispositivo che lampeggi a intervalli regolari, come una boa di segnalazione di quelle che si usano in mare. Ebbene, man mano che la boa si allontana da voi e si avvicina all’orizzonte degli eventi, vedrete aumentare l’intervallo tra un lampo e l’altro, mentre la luce prodotta dal dispositivo – inizialmente di un bianco intenso – tenderà sempre più al rosso. Il processo continuerà finché sarete raggiunti da fotoni, ma questi saranno sempre meno e sempre più rossi, e a un certo punto – quando la boa sarà molto vicina all’orizzonte degli eventi – non scorgerete più alcuna luce. Questo, però, non significa che il dispositivo abbia smesso di funzionare o sia andato distrutto prima di varcare l’orizzonte degli eventi! Se infatti vi lanciaste assieme alla boa, vedreste che essa emette i propri lampi sempre con lo stesso periodo, e che la luce non cambia affatto colore. Inoltre, dopo un intervallo di tempo abbastanza semplice da calcolare, attraversereste l’orizzonte degli eventi e vi ritrovereste al suo interno, impossibilitati a comunicare con l’esterno. A seconda della massa del buco nero – e in particolare se si tratta di un buco nero supermassiccio – il passaggio attraverso l’orizzonte degli eventi non sarebbe nemmeno accompagnato da eventi particolarmente drammatici.³ Questa divergenza nella percezione dei processi fisici da parte di osservatori differenti è alla base della Relatività Generale, e in effetti le dà il nome; può sembrare qualcosa di spiazzante, ma si annulla quando si tratta di discutere non delle percezioni osservative, bensì dei processi fisici in se stessi. A quel punto, infatti, tutti gli osservatori converranno sulla medesima conclusione.

Sulla base dell’esempio della boa di segnalazione, possiamo concludere che è impossibile osservare direttamente un orizzonte degli eventi o la nascita di un buco nero finché tali osservazioni coinvolgono fotoni, e quindi l’emissione e ricezione di radiazione elettromagnetica. Tuttavia è comunque possibile ottenere evidenze indirette della presenza di un buco nero attraverso l’emissione di radiazione elettromagnetica (come vedremo nel capitolo 7), o addirittura in assenza di luce emessa e attraverso le onde gravitazionali (argomento del capitolo 8).

Giunti a questo punto, sono consapevole di avervi fornito parecchie informazioni circa i buchi neri e il loro orizzonte degli eventi; al fine di evitare possibili confusioni e mettere bene a fuoco quanto visto, sarà dunque il caso di ricapitolarle in modo schematico.

Da un punto posto ben al di fuori dell’orizzonte degli eventi è possibile proiettare un fascio di luce verso l’esterno: esso si propagherà raggiungendo regioni a raggio maggiore, senza cambiare percettibilmente la propria lunghezza d’onda.
Da un punto vicino all’orizzonte degli eventi ma ancora al di fuori di esso è comunque possibile proiettare un fascio di luce all’esterno, ma in questo caso una parte del fascio piegherà verso l’orizzonte stesso. La quantità di luce che non riesce a propagarsi verso l’esterno aumenta man mano che ci si avvicina all’orizzonte degli eventi.
La luce emessa in prossimità dell’orizzonte degli eventi cambierà lunghezza d’onda, tendendo al rosso a causa dell’effetto di redshift gravitazionale. L’intensità di tale fenomeno aumenta con l’approssimarsi all’orizzonte e diventa infinita per un fotone emesso esattamente da quella superficie.
Un fascio di luce emesso esattamente dall’orizzonte degli eventi – ossia a un raggio r pari a 2M – non può propagarsi verso l’esterno: se non è assorbito dal buco nero, il suo destino è restare per sempre tangente a quella superficie sferica.
Molto di quanto detto è vero anche per una particella dotata di massa, alla quale sarà necessaria – man mano che si avvicina all’orizzonte degli eventi – un’energia sempre più elevata per sottrarsi all’attrazione gravitazionale del buco nero. Tale energia diventa infinita se la particella è posta esattamente all’orizzonte degli eventi.

Spero che ora sia un po’ più chiaro in cosa consista l’orizzonte degli eventi e cosa accada alla luce emessa nelle sue vicinanze. È bene sottolineare – qualora non fosse chiaro – che quella dell’orizzonte degli eventi è una superficie sferica puramente matematica. In altre parole, sebbene sia possibile immaginarla come la superficie esterna di un buco nero, essa non è solida, al contrario di quella di una stella di neutroni. Piuttosto, va intesa come un confine matematico che riflette la transizione tra due possibili processi fisici: uno in cui un fotone diretto verso l’esterno riesce a propagarsi in quella direzione, e l’altro in cui un identico fotone è invece costretto a «tornare» verso l’interno.

Vorrei concludere questa parte con una considerazione storica. Ho già accennato al fatto che l’espressione della velocità di fuga (6.II) si può derivare anche all’interno della teoria gravitazionale di Newton, ed essa era perciò nota già dagli inizi del Settecento. Tant’è vero che a intuire per primo un’idea embrionale di orizzonte degli eventi fu il naturalista britannico John Michell (1724-1793); in un articolo pubblicato nel 1783,⁴ egli introdusse infatti il concetto di «stelle scure»: corpi celesti la cui compattezza era tale che la velocità di fuga era pari a quella della luce. A quei tempi la Relatività Generale era di là da venire, così come il concetto di orizzonte degli eventi, e le osservazioni non avevano ancora rivelato la presenza di oggetti come Cyg-X1. Insomma: è interessante notare come la descrizione di fenomeni estremi quali quelli legati ai buchi neri, che appaiono rivoluzionari e mai esplorati prima, può ritrovarsi – sebbene in forma diversa e, appunto, embrionale – anche in riflessioni datate decenni o secoli prima della loro effettiva scoperta.

Quando il tempo si prende gioco di noi

È ora giunto il momento di affrontare un altro fenomeno fisico che si verifica in prossimità dell’orizzonte degli eventi, e che rappresenta lo spunto per un’immancabile e disorientante scena presente in pressoché tutti i film di fantascienza a tema buchi neri: la dilatazione del tempo.

Nel capitolo 4 abbiamo visto come sia perfettamente plausibile che, se la presenza di massa o energia curva lo spazio, altrettanto accada con il tempo. Inoltre abbiamo appena detto che la lunghezza d’onda di un fotone emesso vicino a un orizzonte degli eventi e diretto verso il suo esterno si allunga, causando il cosiddetto redshift gravitazionale. Adesso non ci resta che mettere insieme questi due concetti.

Per farlo utilizzerò due osservatrici ipotetiche, Anna ed Emilia, la prima più vicina all’orizzonte degli eventi e la seconda a una certa distanza da esso. Entrambe si trovano a bordo di navicelle spaziali poste su orbite circolari stabili, e nessuna di loro corre dunque alcun rischio. Le loro navicelle orbiteranno mantenendo costante la distanza dal buco nero. Supponiamo ora che Anna faccia partire un fascio di luce blu diretto verso Emilia: come abbiamo visto, quest’ultima lo riceverà a una lunghezza d’onda del rosso. Abbiamo interpretato tale fenomeno come una conseguenza dell’energia spesa da un fotone per uscire dalla buca gravitazionale da cui è stato emesso. Tuttavia, c’è anche un altro modo di descriverlo. Infatti, poiché il numero di creste del fotone dev’essere lo stesso sia per Anna, che l’ha inviato, sia per Emilia, che l’ha ricevuto, e siccome il fotone deve comunque muoversi alla velocità della luce, il cambiamento di lunghezza d’onda può essere interpretato quale una variazione del progredire del tempo così come misurato da Anna e da Emilia. In altre parole, il fatto che le due registrino frequenze diverse per lo stesso fotone (e vi ricordo che la frequenza di un fotone è inversamente proporzionale alla sua lunghezza d’onda: f = c/λ) può essere visto come la conseguenza del fatto che il tempo necessario a contare lo stesso numero di creste differisce tra le due osservatrici.

Abbiamo già incontrato qualcosa di simile nel capitolo 4, quando abbiamo discusso della piccola discrepanza di avanzamento tra gli orologi posti a terra e quelli sui satelliti. Ebbene, al pari di quel fenomeno, il redshift gravitazionale sperimentato da Anna ed Emilia può essere descritto come la manifestazione dell’elasticità del tempo. L’importante differenza, rispetto a quanto accade per il sistema GPS, è che in questo caso la curvatura è estrema perché ci troviamo in prossimità di un buco nero, e altrettanto estrema è la variazione del progredire del tempo da un punto all’altro dello spaziotempo. Essa può essere così grande da divergere in prossimità dell’orizzonte degli eventi; ecco allora che il redshift infinito di un fotone emesso all’orizzonte degli eventi può essere interpretato come dovuto a un «rallentamento» tale che l’avanzare del tempo diventa pressoché nullo quando confrontato con l’avanzare in un punto leggermente più lontano dall’orizzonte. In altre parole, per un’osservatrice infinitamente lontana da un buco nero il tempo progredisce a un tasso da spaziotempo piatto, mentre per una che vi si trovi vicino esso dovrà progredire più lentamente, in quanto quella regione dello spaziotempo è più curva. E per un’osservatrice posta all’orizzonte degli eventi il tempo virtualmente si congelerebbe. È bene sottolineare che questo rallentamento è solo apparente: risulta dal confronto tra il tasso di progressione di due orologi posti a distanze diverse rispetto all’orizzonte degli eventi.

Forse, per comprendere meglio questo concetto, abbiamo bisogno di un altro dei nostri gedanken Experiment, anche se in questo caso sarà un po’ meno intuitivo. Dovremo infatti spingere un po’ più in alto l’asticella dell’immaginazione, visto che ci troveremo a utilizzare condizioni fisiche estreme, seppur perfettamente plausibili. Immaginiamo quindi due astronauti, Carolin e Dominik, a bordo di un’astronave posta su un’orbita circolare a distanza di sicurezza da un buco nero supermassiccio, ad esempio quello al centro della galassia ellittica M87. I due, annoiati, decidono di concedersi una «gita spaziale» a bordo della navicella di servizio. Siccome in quell’area gran parte dell’azione si verifica proprio intorno al buco nero – pare che in un modo o nell’altro tutto finisca letteralmente per caderci dentro – decidono di avvicinarsi al corpo celeste, pur rimanendo a debita distanza dall’orizzonte degli eventi. Entrambi sanno bene che esistono orbite sicure per la navicella, calcolate in base alla potenza dei suoi motori. Dopo aver controllato che tutto sia in ordine, scrivono una nota sul diario di bordo elettronico, segnano le coordinate esatte nonché la data e l’ora astrale in cui lasciano l’astronave madre, e poi escono.

I campi gravitazionali in prossimità di un buco nero supermassiccio come quello al centro di M87 variano in modo molto graduale; o, per usare un linguaggio più tecnicamente corretto, dovremmo dire che il raggio di curvatura nei pressi di questi oggetti è estremamente grande e i campi mareali sono parecchio deboli. Per questa ragione, anziché accendere i razzi della navicella, Carolin e Dominik decidono di lasciarsi semplicemente attrarre e godersi la «caduta». Per fare un raffronto, sulla Terra, si tratterebbe di una graduale discesa da una montagna che ha dimensioni orizzontali enormi. In realtà, l’attrazione gravitazionale del buco nero è così grande che, anche in caduta libera, ben presto Carolin e Dominik raggiungono velocità elevatissime, vicine a quella della luce.

I due, intanto, si godono il panorama mozzafiato del materiale in accrescimento che si scorge oltre gli oblò della navicella, davanti a un tè caldo e a una confezione di pasticcini freschi. Poi decidono che è il momento di tornare indietro. Gli strumenti confermano che, alla distanza cui si trovano dall’orizzonte degli eventi, possono ancora invertire la rotta; accendono quindi i motori e puntano la navicella verso l’astronave madre, impiegando – è bene dirlo – una quantità notevole di energia per risalire la buca gravitazionale nella quale erano gradualmente scesi. Insomma: proprio come in montagna, anche in prossimità di un buco nero la salita costa fatica…

Giunti all’astronave principale, i due controllano gli strumenti. Il calendario segna una data astrale ben diversa da quella in cui sono partiti e da quella della loro navicella: secondo il computer di bordo la loro gita è durata diversi mesi. Carolin e Dominik, però, non ne rimangono sorpresi; in effetti sapevano che sarebbe accaduto, ed è per questo che alla partenza hanno portato con sé i pasticcini freschi anziché lasciarli nel frigo dell’astronave. Lì, infatti, il tempo è trascorso molto più in fretta rispetto a quanto sperimentato da loro sulla navicella, ma per i due astronauti si tratta di un fenomeno del tutto prevedibile. Prima di partire, Dominik aveva anche calcolato il tempo che avrebbero «misurato» a bordo della navicella mentre si dirigevano verso l’orizzonte degli eventi, e persino quello necessario se avessero deciso di proseguire oltre, puntando alla singolarità al suo centro. Conoscendo la differenza tra il «loro» tempo e quello misurato dagli strumenti di bordo dell’astronave madre, aveva quindi calcolato la rotta in modo che la differenza tra i due non fosse eccessiva: non voleva che l’astronave madre restasse senza equipaggio per troppo tempo. Insomma, questa gita rivela che Carolin e Dominik conoscono bene la Relatività Generale.

Che il tempo possa rallentare e addirittura fermarsi è qualcosa che ci pare assurdo, per questo sarà utile riflettere su due aspetti importanti legati a questo fenomeno. Il primo: non dobbiamo mai dimenticare che quanto a noi sembra implausibile e addirittura controintuitivo può essere plausibilissimo e consentito dalla fisica. Questo perché la nostra intuizione è costruita sulla base dell’esperienza accumulata su questo pianeta, a condizioni fisiche particolari: curvature impercettibili, temperature e densità basse eccetera. Quindi, per stabilire ciò che è possibile a livello fisico dobbiamo far affidamento sulle equazioni che descrivono le varie leggi della fisica, e affidarci a esse quasi ciecamente. Se una teoria è corretta e le sue equazioni consentono che un certo processo si realizzi, allora tale processo è plausibile (anche se non necessariamente probabile). Il secondo aspetto da tenere sempre a mente è che il fenomeno della dilatazione del tempo non è qualcosa di fantascientifico, ma una realtà misurata anche sulla Terra da parecchie evidenze esperimentali. In effetti ne verifichiamo la correttezza ogni volta che utilizziamo un navigatore satellitare. L’unica differenza rispetto a quanto hanno sperimentato Carolin e Dominik sulla loro navicella spaziale è la magnitudine di tale fenomeno, che in prossimità di un buco nero o di una stella di neutroni è amplificata enormemente. Del resto è proprio per questo che simili oggetti ci affascinano tanto!

Come si produce un buco nero?

Adesso che abbiamo un’idea un po’ più chiara di cosa sia un buco nero e quali siano le sue caratteristiche salienti, è giunto il momento di porsi una domanda fondamentale: «Come nascono questi oggetti?».

La risposta non è propriamente semplice, ma nemmeno troppo complicata se si tralasciano un po’ di dettagli, cosa che intendo fare in questa sezione. Inoltre limiterò la discussione a buchi neri con una massa compresa fra 3 e 100 masse solari circa – detti, più semplicemente, buchi neri stellari – in quanto il loro processo di formazione è molto più chiaro rispetto a quello dei buchi neri supermassicci, la cui origine cosmologica è attualmente oggetto di dibattito. Così potrò anche sfruttare quanto abbiamo imparato nel capitolo 5 circa le stelle di neutroni, e impiegare un importante teorema per illustrare il processo.

Ma procediamo con ordine. Per spiegare come si crei un buco nero stellare ho bisogno di richiamare un importante teorema dell’astrofisica teorica legato al matematico tedesco naturalizzato australiano Hans Adolf Buchdahl (1919-2010). Il teorema è molto semplice da enunciare, e la sua tesi è espressa così: dato un oggetto autogravitante dotato di materia avente una massa M_★ e un raggio R_★, la sua compattezza M_★/R_★ è vincolata a essere:

GM*

In altre parole, dato un oggetto autogravitante, il suo raggio R_★ deve essere maggiore di 9/4 = 2,25 volte la sua massa M_★. Attenzione: il teorema non pone un limite alla massa – che può quindi essere minuscola o enorme – né al raggio necessari per creare un buco nero. Quello che ci dice, piuttosto, è che per ogni massa – qualunque essa sia – esiste un raggio limite al di sotto del quale non è possibile trovare una soluzione di equilibrio alle equazioni di Einstein. Inoltre la tesi del teorema (6.III) ci dice anche che questo raggio limite è pari a 9/8, ossia 1,125 volte, il raggio di Schwarzschild r_S = 2GM/c². C’è quindi un altro modo di descrivere le implicazioni del teorema di Buchdahl: preso un oggetto compatto dotato di una superficie solida, non è possibile ridurne il raggio a nostro piacimento e ottenere comunque una soluzione di equilibrio. Esiste invece un limite, e questo è dato da un raggio che è solo del 13 per cento più grande di quello dell’orizzonte degli eventi di un buco nero avente la stessa massa.

La dimostrazione della tesi del teorema di Buchdahl procede per assurdo, mostrando che se si costruisse un oggetto dotato di materia di tipo ordinario – ossia con una densità di energia e una pressione positiva – che abbia compattezza superiore a 4/9, allora la pressione al suo centro sarebbe infinita. E dal momento che la pressione deve essere necessariamente finita, ne consegue che un oggetto di questo tipo non potrebbe esistere. Vedremo più in là che, in realtà, è possibile costruire oggetti con una compattezza anche maggiore, ma in questo caso dovremo affidarci a un tipo di materia decisamente… esotica.

Questo teorema ci offre lo spunto per un altro dei nostri esperimenti mentali. In particolare, possiamo pensare di prendere un oggetto che ha massa M_★ e ridurne progressivamente le dimensioni allo scopo di aumentarne la compattezza. Come ricorderete, avevamo già fatto qualcosa del genere nel capitolo 4, immaginando di comprimere il Sole fino a portare il suo raggio a soli cinque chilometri, per poi calcolare la curvatura prodotta. L’esperimento che vi propongo ora è simile, ma solo in parte, perché qui vogliamo imparare cosa accada alla curvatura quando superiamo il limite imposto dal teorema di Buchdahl.

Per aiutarci possiamo usare i tre riquadri della Figura 6.1, che mostrano la curvatura dello spaziotempo prodotta dal Sole quando ne riduciamo il raggio mantenendo stabile la massa. Sotto ogni immagine ho indicato la relativa compattezza M/R.

Il riquadro a sinistra mostra la curvatura prodotta dal Sole con il suo vero raggio, di circa 700.000 chilometri. Come già visto nel capitolo 4, in questo caso la compattezza è di qualche parte su un milione e la curvatura pressoché nulla, tant’è vero che la superficie raffigurata appare piatta. Il pannello al centro, invece, mostra la curvatura prodotta comprimendo tutti gli atomi del Sole in una stella ultracompatta, vale a dire, al limite previsto dal teorema di Buchdahl. In questo caso la compattezza è esattamente di 4/9 ≃ 0,444 e la curvatura è ben visibile: al centro della superficie si è sviluppata una depressione con pareti molto ripide. Infine, l’immagine a destra mostra cosa accadrebbe se prendessimo la stella ultracompatta e la comprimessimo ancora, anche solo di pochissimo, sempre mantenendo inalterata la massa a riposo (vale a dire il numero di atomi che compongono il Sole). In questo caso si produrrebbe un oggetto con una superficie sferica con un raggio di soli 1,5 chilometri e una compattezza di 0,5. Ovvero, un buco nero! Infatti, quando nell’espressione (6.I) abbiamo definito il raggio di Schwarzschild come pari a due volte la massa del buco nero, abbiamo implicitamente anche dichiarato che la compattezza di un buco nero di Schwarzschild è esattamente pari a M/R = 1/2 = 0,5. Nel terzo riquadro della Figura 6.1 ho anche riportato la posizione dell’orizzonte degli eventi, dato da una circonferenza di raggio r = r_S, e quella della singolarità fisica, che dev’essere immaginata al centro della «gola» per r = 0 e che quindi non è direttamente visibile nel pannello.

Fig. 6.1 La curvatura dello spaziotempo prodotta dal Sole, a sinistra, e quella creata quando ne riduciamo il raggio mantenendone la massa. Il riquadro al centro raffigura il limite di Buchdahl, mentre in quello di destra il suo raggio è stato portato a soli 1,5 chilometri, generando un buco nero.

Ancora una volta, sarà utile una serie di riflessioni ispirate alla sequenza della Figura 6.1. La prima considerazione è che possiamo utilizzare il pannello di destra, quello relativo al buco nero, per introdurre un’analogia meccanica che forse vi aiuterà a comprendere il ruolo giocato dalla gravità e dall’orizzonte degli eventi. Immaginate che la superficie curva rappresenti il letto di un lago non molto profondo, con un foro al centro: come ovvio, la presenza del buco creerà una corrente che trascinerà l’acqua del lago verso il fondo, creando un’enorme cascata (ignoriamo per il momento la presenza di momento angolare, sicché l’acqua non produce un vortice ma cade lungo traiettorie radiali, proprio come in una cascata circolare). A questo punto, pensate di trovarvi a bordo di un’imbarcazione dai motori estremamente potenti, che vi consentano non solo di avvicinarvi al bordo esterno della cascata, ma addirittura di spingervi su di essa, anche se le pareti sono pressoché verticali. La corrente d’acqua aumenterà man mano che vi avvicinate al foro, ma i vostri fuoribordo sono così potenti da essere comunque in grado di tirarvi fuori da quella situazione. Ebbene: ciò sarà possibile solo fino a un certo punto. Esiste infatti un «confine» superato il quale i vostri motori non ce la faranno a spingervi controcorrente, a prescindere da quanto potenti siano. Anzi, anche se la loro potenza fosse pressoché infinita, non sarebbe comunque sufficiente. Ecco, per voi quel limite rappresenta a tutti gli effetti un «orizzonte»: potrete varcarlo, ma non uscirne!

La seconda considerazione è che non esistono soluzioni intermedie tra le due configurazioni nei pannelli al centro e a destra della Figura 6.1. In altre parole, quando comprimiamo anche a livello infinitesimale una stella ultracompatta che abbia già raggiunto il limite di Buchdahl, le equazioni di Einstein non ammettono altra soluzione statica che quella del buco nero. Si crea dunque una transizione netta tra le soluzioni di oggetti composti di materia e aventi una superficie solida, ossia le stelle compatte, e quelle prive di materia e senza una superficie solida, ossia i buchi neri.

Terza considerazione: se osservate la deformazione della curvatura mostrata negli ultimi due riquadri, avrete come l’impressione che lo spaziotempo sia stato «lacerato», quasi che il suo stesso tessuto avesse ceduto sotto l’azione irresistibile della gravità. In realtà lo spaziotempo non può essere lacerato visto che si tratta di un continuo regolare ovunque – con la sola eccezione della singolarità – e dovete piuttosto pensare che un buco nero ne spinga al massimo l’elasticità. In altre parole, sebbene abbiamo visto che lo spaziotempo è in generale piuttosto rigido, nel caso della soluzione di buco nero la gravità è tale che la sua deformabilità raggiunge il valore massimo.

Una quarta considerazione emerge dal fatto che, nel passaggio da una stella ultracompatta a un buco nero, abbiamo essenzialmente concentrato tutta la materia in un singolo punto infinitesimale. Un buco nero è quindi «vuoto», in quanto tutta la massa che lo ha generato è ormai concentrata in un punto di dimensione nulla. Ne consegue che all’interno dell’orizzonte gli eventi non c’è niente. Sono dunque sbagliate tutte quelle affermazioni – purtroppo ripetute spesso – che lasciano intendere l’esistenza di una densità di materia all’interno di un buco nero, o suggeriscono che sia possibile calcolare tale densità. La densità di materia di un buco nero è esattamente zero, perché esso è una soluzione nel vuoto.

Infine, un’ultima considerazione può essere dedicata al tempo-scala nel quale si genera un buco nero. Come penso sia ormai chiaro, niente in fisica avviene istantaneamente, e ciò vale anche per la nascita di un buco nero. Altrettanto chiaro – a questo punto – dovrebbe essere che, nell’ambito della teoria della Relatività Generale, tale tempo-scala dipende inevitabilmente dalla posizione dell’osservatrice. Chi si trovi lontano da un orizzonte degli eventi non vedrà mai un oggetto cadere su di esso; e, allo stesso modo, chi si trovi lontano da una stella in procinto di collassare non la vedrà mai scomparire al di sotto dell’orizzonte stesso. Piuttosto, vedrà una stella che si contrae progressivamente emettendo luce sempre più spostata verso il rosso, fino a scomparire quando la radiazione emessa non potrà più essere ricevuta. Se invece l’osservatrice si trovasse a cadere insieme alla materia, la durata precisa del fenomeno da lei sperimentato sarà legata a una serie di fattori quali il tipo di materia in questione o il suo stato di rotazione. Fondamentalmente, però, quando il collasso è avviato – e quindi la gravità domina ormai ogni altra interazione fisica – il processo dovrà avvenire sul tempo-scala della caduta libera. Il valore di tale tempo-scala è calcolabile per qualsiasi oggetto, ed è dato da un’espressione molto semplice che lo vuole inversamente proporzionale alla radice quadrata della densità dell’oggetto collassante. In altre parole, più è denso l’oggetto che collassa e più breve sarà il tempo di caduta libera. Nel caso del Sole, ad esempio, il tempo di caduta libera è circa di ventisette minuti. In altre parole, se potessimo «spegnere» per magia tutte le reazioni termonucleari all’interno della nostra stella, così da lasciarla collassare a partire dalle sue dimensioni attuali, la superficie raggiungerebbe il centro dopo mezz’ora scarsa di caduta. Decisamente poco, se si pensa che la materia in superficie deve coprire i 700.000 chilometri che la separano dal cuore del nucleo.

Tutte le considerazioni fatte finora ci aiutano a immaginare cosa sia avvenuto circa cinque milioni di anni fa, quando l’esplosione di supernova di una stella molto massiccia (superiore alle quaranta masse solari) ha dato vita al buco nero in Cyg-X1. La differenza più rilevante tra quanto avviene con una supernova che dà vita a una stella di neutroni e una che genera un buco nero è che, in quest’ultimo caso, il nucleo di ferro è molto più massiccio, nell’ordine di una decina di masse solari. In condizioni del genere, la densità raggiunta durante il collasso è tale che nessuna pressione – neanche quella di degenerazione – è in grado di contrastare la caduta del materiale del nucleo. Così, quando una massa abbastanza elevata si sarà concentrata in un raggio nell’ordine di quello di Schwarzschild, un buco nero sarà stato prodotto.

Ormai, grazie alla soluzione numerica delle equazioni di Einstein e di quelle dell’idrodinamica relativistica, conosciamo in modo abbastanza preciso il processo di formazione di un buco nero in Relatività Generale. Intorno al 2005, insieme a colleghi europei e statunitensi, io stesso ho condotto alcune ricerche volte a studiare questo processo, realizzando le prime simulazioni numeriche che lo descrivono in tre dimensioni. A tale comprensione dell’aspetto gravitazionale, però, non fa riscontro un’altrettanto chiara cognizione della genesi astrofisica dei buchi neri: in questo campo, infatti, le zone d’ombra restano ampie, tanto per i buchi neri stellari quanto per quelli supermassicci. Nel caso dei primi, le osservazioni elettromagnetiche ci informano che ne esistono con masse tra le 5 e le 10 masse solari, mentre le rivelazioni di onde gravitazionali – delle quali parleremo nel capitolo 8 – ci suggeriscono che ne esistano con masse tra le 10 e le 40 masse solari. La situazione si fa ancor più incerta quando si considerano i buchi neri supermassicci, con una maggior indeterminazione della massa e della fase cosmologica in cui vengono creati. Sembra chiaro, tuttavia, che anche in un contesto cosmologico la nascita di un buco nero supermassiccio debba coinvolgere, in un qualche momento, la condensazione in una regione estremamente piccola – paragonabile al raggio di Schwarzschild, se non minore – di enormi quantità di materia. Ecco perché il gedanken Experiment che abbiamo condotto rimane perfettamente valido, ed è un utile riferimento a prescindere dalla massa del buco nero preso in considerazione.

I buchi neri non hanno capelli

Finora, per descrivere i diversi tipi di buchi neri ho usato sempre la massa quale unico parametro distintivo, parlando di buchi neri più piccoli (o stellari) e più grandi (o supermassicci). Tuttavia, è lecito chiedersi se un oggetto tanto complesso, descritto da equazioni estremamente difficili da maneggiare e ancor più da risolvere, possa essere descritto solo in termini della sua massa. In altre parole, è arrivato il momento di domandarsi: «Quanto sono complessi i buchi neri?». Per fornire una risposta, però, dovrò fare una breve digressione.

Sin da bambini, la nostra percezione della realtà – e di conseguenza la nostra comprensione del mondo – ci ha insegnato che la complessità è immancabilmente accompagnata dalla ricchezza di dettagli: ci appare scontato che un fenomeno naturale dalla manifestazione complessa debba essere pieno di sfumature. Per essere più chiaro, lasciatemi ricorrere a qualche esempio. Partiamo da un contesto noto a tutti, almeno a livello generale: la musica. Penso sia ovvio per chiunque che una sinfonia di musica classica eseguita da una grande orchestra è molto più ricca di contenuti, e quindi di sfumature, del semplice suono prodotto da un diapason. Anche convenendo che parlare di «sfumature» o «ricchezza di contenuti» sembri vago e poco obiettivo, possiamo correre ai ripari prendendo in considerazione il numero di strumenti impegnati in una sinfonia di media durata e moltiplicarlo per quello delle note eseguite: otterremo così una misura quantitativa e obiettiva della complessità di tale sinfonia. Lo stesso calcolo si può poi fare per un diapason che ripeta la propria nota a intervalli regolari lungo lo stesso arco di tempo. Se confrontiamo i dati in questi termini, è banale concludere che una sinfonia orchestrale è più complessa dello «spartito» eseguito da un diapason.

Proviamo ora a cambiare contesto, e a prendere un esempio di tipo biologico. Consideriamo quindi tre organismi viventi molto comuni: un batterio quale Escherichia coli, un moscerino del genere Drosophila e un lombrico. Essi sono caratterizzati da complessità crescente, nel senso che per descriverli è necessaria una mole di informazioni via via maggiore. E, se volessimo quantificare tale complessità in termini numerici, potremmo considerare il loro corredo genetico: 5000 geni per Escherichia coli, 13.000 per il moscerino del genere Drosophila e 19.000 per il lombrico (i nostri sono circa 30.000). Ogni gene, poi, è a sua volta descrivibile in termini di una certa combinazione di amminoacidi… È dunque chiaro che serve una mole enorme di informazioni per descrivere anche il più semplice degli esseri viventi.

Insomma, la nostra esperienza quotidiana, così come la nostra conoscenza del mondo, ci suggerisce che, più è complesso un oggetto, un organismo o un fenomeno fisico, maggiore è la quantità di informazioni necessarie per descriverlo. Ebbene, i buchi neri rappresentano un’eccezione stridente a questa ragionevolissima regola.

Sulla scorta degli esempi appena visti, infatti, saremmo portati a concludere che per descrivere un buco nero – il risultato più estremo delle equazioni matematicamente più complesse della fisica teorica – serva un quantitativo enorme di informazioni, e che la massa sia solo una delle innumerevoli sfumature che lo contraddistinguono. Ebbene, non è così: in realtà i buchi neri sono gli oggetti fisici macroscopici più semplici in assoluto! Questa conclusione, che forse vi apparirà sorprendente, è la semplice conseguenza matematica del fatto che per descrivere un qualsiasi buco nero abbiamo bisogno unicamente di tre numeri, che incarnano altrettante proprietà. Ancora una volta, il concetto di buco nero ci sorprende: esso è enormemente più semplice da descrivere anche del più elementare dei batteri.

Quali sono, dunque, le sole tre proprietà di un buco nero? Eccole: la massa, di cui abbiamo già discusso; lo spin, ossia la quantità di rotazione intrinseca; e infine la carica elettrica. Tali caratteristiche sono in genere descritte tramite tre lettere: M per la massa, J per il momento angolare di spin e Q per la carica elettrica. Così, preso un qualsiasi buco nero, potremo assegnargli un posto nella «banca dati» dell’universo semplicemente riportando i tre valori di M, J, e Q. A dirla tutta, in un contesto astrofisico realistico il quadro è persino più semplice, perché ci si aspetta che la carica elettrica di un buco nero sia essenzialmente nulla (Q = 0), sicché possiamo anche dimenticarcene. La ragione è facile da comprendere: se anche si generasse un buco nero con carica netta di un certo segno, le cariche libere – vale a dire l’insieme di elettroni, protoni e altre particelle cariche che circolano liberamente nello spazio interstellare, alcune delle quali avrebbero giocoforza segno opposto rispetto alla carica del buco nero – ne sarebbero attratte elettricamente e verrebbero assorbite. Così, però, la carica del buco nero andrebbe scemando in fretta, fino a diventare nulla. A quel punto il buco nero sarebbe elettricamente neutro, dunque incapace di attirare altre cariche. Ecco perché, in realtà, per descrivere a livello astrofisico questi incredibili corpi celesti bastano due numeri: M e J.

A rendere le cose ancor più semplici, il valore del momento angolare di spin J – ossia la misura di quanto in fretta ruoti il buco nero – dev’essere compreso in un intervallo ben definito. In particolare, se utilizziamo la quantità adimensionale – ossia priva di dimensioni e quindi un numero puro – data dal rapporto tra il momento angolare di spin e il quadrato della massa del buco nero, a = J/M², questo numero deve essere compreso tra –1 e 1 (il cambio di segno indica l’orientamento dell’asse di rotazione rispetto a un asse di riferimento). La quantità a prende anche il nome di spin adimensionale, ed è nulla (a = 0) per un buco nero di Schwarzschild, che può dunque essere visto come un buco nero privo di rotazione (d’ora in poi userò in modo equivalente la forma buco nero di Schwazschild e quella buco nero non-rotante). Se, al contrario, a ha valore non-nullo si parlerà di un buco nero rotante, o buco nero di Kerr, dal matematico neozelandese Roy Kerr che per primo ne trovò la soluzione.⁵ Siccome in genere i buchi neri accrescono materia che ha una certa quantità di momento angolare, in contesto astrofisico ci si aspetta che i buchi neri siano sempre di tipo Kerr, anche se alcuni possono avere una rotazione appena accennata.

Il fatto, a dir poco singolare, che un buco nero sia descritto da tre proprietà soltanto è espresso anche in un teorema molto famoso: quello dell’assenza di capelli (in inglese, no-hair theorem). La denominazione scherzosa si deve al già citato John Wheeler e all’astrofisico italiano Remo Ruffini,⁶ ed è in realtà tesa a sottolineare che se un buco nero è visto come una sfera, essa è appunto priva di dettagli: proprio come una testa può essere priva di capelli. La tesi del teorema, molto semplice da formulare, afferma essenzialmente che: in Relatività Generale un buco nero che sia isolato e in uno spaziotempo asintoticamente piatto (ovvero che a grandi distanze diventa piatto) può essere descritto da questi tre valori soltanto: M, J e Q. E se anche qualcosa dovesse intervenire a modificare una di queste caratteristiche – magari della materia con rotazione che cada sul buco nero e che cambi i valori di M e J – la variazione dei parametri verrà seguita da uno stato in cui tutte le perturbazioni sono rimosse e resta solo un «nuovo» buco nero, diverso dal precedente ma comunque descritto dai valori di M, J e Q (torneremo su questo punto nel capitolo 8).

In tal senso, i buchi neri possono essere visti – almeno a livello concettuale – come «macchine cosmiche» in grado di assorbire materia dall’esterno e modificare così la propria massa, il proprio momento angolare e la propria carica elettrica (si veda la Figura 6.2). Le tre leggi della loro dinamica ci dicono come, attraverso l’interazione con il mondo esterno, le proprietà M, J, Q possano cambiare nel tempo. Lasciando da parte la carica Q, della cui evoluzione abbiamo già parlato, queste leggi – derivate in un contesto classico della Relatività Generale – ci insegnano dunque che la massa di un buco nero può solo aumentare, mentre il suo momento angolare può aumentare ma anche diminuire, arrivando persino a zero. In sostanza, è possibile che un buco nero rotante rallenti – attraverso perdite di energia rotazionale – fino a diventare un buco non-rotante. Quando si verifica questo processo di riduzione del momento angolare è in effetti possibile che la massa del buco nero si riduca, ma non interamente: a diminuire sarà la parte di massa associata alla rotazione, vale a dire quella che dipende da J, detta appunto massa riducibile del buco nero. Ma esiste una parte della massa del buco nero che non è legata alla rotazione (ossia non dipende da J) e che non può diminuire, solo aumentare; per tale ragione essa prende il nome di massa irriducibile.

Fig. 6.2 No-hair theorem: indipendentemente dal tipo di oggetti che i buchi neri possono accrescere, essi producono unicamente un cambiamento di uno dei tre numeri che caratterizzano un buco nero: la massa M, il momento angolare J e la carica elettrica Q.

Il principio in base al quale in un buco nero non è possibile alcuna perdita di massa irriducibile, almeno in una formulazione classica della teoria della Relatività Generale, fu rivoluzionato negli anni Settanta dal fisico britannico Stephen Hawking, il quale propose un nuovo meccanismo legato ai principi della meccanica quantistica. Egli suggerì che un buco nero possa in realtà «evaporare», e quindi perdere massa attraverso l’emissione di una radiazione di tipo termico, detta appunto radiazione di Hawking.⁷ Il fenomeno alla base di tale processo coinvolge la produzione – in una sottile regione vicino all’orizzonte degli eventi – di una serie di particelle e antiparticelle (ossia particelle con «energia negativa») virtuali. Sappiamo che ciò è possibile ovunque nello spaziotempo, dove non ha un effetto netto visto che il numero di antiparticelle prodotte è bilanciato da quello delle particelle corrispondenti. Tuttavia, quando il fenomeno si verifica vicino a un orizzonte degli eventi – che può solo assorbire particelle, non emetterle – un risultato netto è possibile e l’effetto globale è che il buco nero emette radiazione, mentre la sua massa diminuisce a causa dell’accrescimento di antiparticelle.

Non c’è ancora una prova sperimentale dell’esistenza della radiazione di Hawking e la ragione principale è che, ovviamente, non è possibile creare un buco nero in laboratorio (anche se è possibile, in linea di principio, generare oggetti con proprietà simili, che prendono il nome di buchi neri analoghi). Ma non è l’unico motivo: la radiazione di Hawking è infatti molto debole, sia nel caso di buchi neri stellari sia in quello di buchi neri supermassicci, e aumenta d’intensità per masse molto piccole, nel qual caso è difficile compiere osservazioni astronomiche. Nonostante ciò, la comunità scientifica è abbastanza concorde nel ritenere che la radiazione di Hawking sia possibile e che quindi – almeno in teoria – un buco nero possa variare anche la massa, arrivando addirittura a scomparire o a lasciare solo una piccolissima singolarità dietro di sé.

In pratica, la massa persa attraverso la radiazione di Hawking da un buco nero di massa realistica è di norma molto scarsa: la luminosità di Hawking – vale a dire la quantità di massa-energia persa da un buco nero per unità di tempo – è infatti inversamente proporzionale al quadrato della massa del buco nero. Ne consegue che anche un buco nero «leggero», di una sola massa solare, impiegherebbe circa 10⁶⁷ anni per evaporare. Considerando che l’universo ha circa 10¹⁰ anni, è chiaro che un buco nero di questa massa impiegherebbe miliardi di miliardi di miliardi di miliardi di volte l’età dell’universo per evaporare. I tempi-scala diventano ancor più enormi se si considerano buchi neri più massicci, ad esempio quello al centro della nostra galassia. Ecco perché l’unica occasione di osservare la radiazione di Hawking è offerta da buchi neri estremamente piccoli. In particolare, un buco nero che fosse stato generato nell’universo primordiale e avesse una massa di 10¹¹ chilogrammi – vale a dire un miliardesimo di quella di un asteroide – emetterebbe abbastanza radiazione di Hawking da essere ormai giunto sul punto di evaporare.

Insomma, quando si parla di massa i buchi neri sembrano comportarsi proprio come noi umani: possono talvolta «dimagrire», ma nella stragrande maggioranza dei casi – e a lungo andare – tendono inevitabilmente a «ingrassare», mettendo su massa.

Un’idea difficile da digerire

Quanto abbiamo visto parlando di «assenza di capelli» nei buchi neri mi fornisce lo spunto per un’importante riflessione su come l’idea stessa di questi oggetti, e in particolare la presenza di un orizzonte degli eventi, sia ancora molto difficile da accettare, persino più che da comprendere. È infatti importante sottolineare che la presenza di un orizzonte degli eventi rende il funzionamento di un buco nero decisamente «eccezionale», nel senso che esso costituisce davvero un’eccezione a quanto conosciamo e siamo abituati ad accettare in fisica. Una volta attraversata quella superficie matematica, infatti, tutta l’informazione circa le proprietà degli oggetti che vi entrano viene persa, e convertita – assieme alla complessità associata agli oggetti stessi – nelle uniche tre proprietà che noi osservatori esterni possiamo misurare: M, J e Q.

Se ci pensate è un comportamento a dir poco anomalo, cui di certo non siamo abituati in fisica. Per rendere meglio l’idea, vorrei farvi un esempio. Immaginate di prendere della legna e accendere un fuoco: una volta bruciati, dei ciocchi non rimarranno che ceneri informi. Potreste pensare che esse non contengano alcuna informazione sulle proprietà originarie della legna da cui derivano e sulle caratteristiche chimiche delle cellule vegetali che la componevano; che sia insomma impossibile recuperare tracce di chimica organica grazie alle quali stabilire se i ciocchi provenivano da un faggio o un rovere. Ogni informazione a riguardo sembrerebbe andata in fumo… Ma il punto è esattamente questo: la cenere non è l’unico prodotto del falò, ed è infatti possibile risalire alle proprietà del legno studiando quelle del fumo prodotto durante la combustione.

Questo esempio ci mostra come, in fisica, le informazioni circa le proprietà di un certo sistema non vadano mai perse. Possono essere – e in effetti sono sistematicamente – trasformate, ed è plausibile che diventi più difficile raccoglierle (pensiamo al fumo); tuttavia, per ragioni che coinvolgono le radici stesse della nostra comprensione della fisica, non sono mai perse. L’unica eccezione a questa logica è quanto avviene con un buco nero! In quel singolo caso, infatti, perdiamo ogni informazione circa le proprietà di ciò che ha generato la massa o il momento angolare del buco nero, sebbene si tratti di oggetti assolutamente noti e che fino a un istante prima di varcare l’orizzonte degli eventi avremmo potuto descrivere sino all’ultimo atomo.

L’impossibilità di estrarre informazione da un buco nero prende il nome di paradosso della perdita di informazione (in inglese, information-loss paradox), ed è qualcosa di ben più grave di quanto potrebbe apparire. Esso, infatti, mina i fondamenti della meccanica quantistica, in base ai quali l’insieme delle informazioni di un sistema fisico non può andare perso. Per essere più precisi, il paradosso nasce dal fatto che, se descriviamo lo stato di un sistema attraverso una funzione d’onda (e vi ricordo che un postulato fondamentale della meccanica quantistica è appunto che l’intera informazione di un sistema fisico sia racchiusa nella sua funzione d’onda), l’evoluzione di tale funzione debba essere unitaria. In altre parole, una volta specificate le condizioni iniziali della funzione d’onda del sistema, la sua evoluzione è pienamente determinata. Tuttavia, nel caso di un buco nero questa unitarietà sembrerebbe violata, sicché diversi stati inizialmente distinti andrebbero a confluire in uno solo, divenendo indistinguibili.

Il paradosso della perdita di informazione rimane tuttora irrisolto, nonostante decenni di studi in merito. Nessuna delle teorie introdotte per rimuoverlo sembra accettabile, al momento. Questa è l’ennesima, stridente conferma dell’incompatibilità tra la Relatività Generale così come formulata da Einstein e i principi della meccanica quantistica.

Esiste poi un altro aspetto che rende l’orizzonte degli eventi un concetto piuttosto «indigesto» per i fisici. Se ricordate, all’inizio del volume ho sottolineato l’importanza del lavoro di Galileo nel definire e introdurre il metodo scientifico, il solo faro che illumini la notte delle speculazioni umane. Nel corso dei secoli, esso ci ha consentito di giungere a un punto fermo nei dibattiti – durati anche decenni – che hanno caratterizzato l’esplorazione scientifica: cosa sia vero e cosa falso, cosa giusto e cosa sbagliato… Galileo stesso sintetizzò l’importanza di tale metodo in quello che è uno dei suoi aforismi più noti. Rivolgendosi a Tommaso Campanella, egli affermò: «Io stimo più il trovar un vero, benché di cosa leggiera, che ’l disputar lungamente delle massime questioni senza conseguir verità nissuna». Ebbene, nel caso di un buco nero, varcato l’orizzonte degli eventi è di fatto impossibile trovare «un vero», almeno secondo la definizione del metodo scientifico. E questo non perché le leggi della fisica smettano di essere valide!

Cerco di spiegarmi meglio. Immaginiamo una coppia di osservatori che si trovi all’esterno di un buco nero supermassiccio: Simplicio e Salviati.⁸ I due stanno discutendo, chiedendosi se sia possibile o meno condurre un esperimento all’interno dell’orizzonte degli eventi. Seguendo una logica tutta sua Simplicio afferma che, varcato l’orizzonte degli eventi, deve trovarsi un mondo fantastico, un paradiso nel quale ognuno può ottenere ciò che desidera semplicemente pensandolo. Secondo lui, una volta varcato quel limite troverà una tavola imbandita di ogni ben di Dio, e tutti i suoi gusti di gelato preferiti. (Che Simplicio sia goloso, in particolare di gelato, è noto a tutti.)

Per Salviati, al contrario, all’interno dell’orizzonte gli eventi di un buco nero supermassiccio non succede nulla di tutto questo. Le leggi della fisica rimangono valide anche lì, almeno finché ci si tiene alla larga dal centro del buco nero, sul quale ammette di non poter dire niente. In particolare, ragiona Salviati, se la massa è così grande allora un oggetto delle dimensioni di un essere umano sperimenterà forze mareali limitate, e attraversato l’orizzonte degli eventi non avvertirà alcuna variazione apprezzabile alle proprietà gravitazionali incontrate subito prima. A parte il fatto di non poter più comunicare con l’esterno, ovvio.

Ora, sulla base della nostra comprensione della fisica saremo tutti d’accordo che la tesi di Simplicio è campata in aria: non ha nessun supporto logico o scientifico, e non c’è motivo di ritenerla corretta. Tuttavia – ed è proprio questo il problema – la discussione tra i due non può essere risolta, anche se si tratta «di cosa leggiera». La ragione è semplice: né Salviati né nessun altro è in grado di andare all’interno dell’orizzonte degli eventi e dimostrare che lì non ci sono tavole imbandite, per poi divulgare a tutti la scoperta. A rendere ancora più irritante l’intero quadro, Salviati sa benissimo che sarebbe possibile eseguire quell’esperimento: il problema sarebbe semmai diffonderne i risultati all’esterno, visto che una volta entrati nell’orizzonte degli eventi si è impossibilitati a comunicare con il resto dell’universo.

Accettare l’esistenza di un orizzonte degli eventi equivale quindi ad ammettere la presenza, nel nostro universo, di regioni accessibili fisicamente ma precluse a un’indagine basata sul metodo scientifico e sulla sperimentazione. E questo non perché lì la fisica cessi di essere valida: come abbiamo visto, al centro del buco nero c’è un solo punto infinitesimale per il quale la teoria della Relatività Generale non è in grado di fornire previsioni. Il problema, più banalmente, è che non si potrebbe divulgare il risultato di esperimenti condotti entro l’orizzonte degli eventi. Una prospettiva che di certo fa rivoltare nella tomba il povero Galileo…

Se vogliamo ricorrere a un’analogia un po’ azzardata, l’orizzonte degli eventi pone le stesse complicazioni dell’aldilà, alla cui esistenza molti credono ma che nessuno può dimostrare, visto che – a parte eccezioni ben note – nessuno è mai tornato per raccontarci cosa ci sia dopo la morte.

Considerazioni del genere mostrano perché l’idea di un orizzonte degli eventi sia tanto difficile da digerire per i fisici, i quali – per aspirazione o ambizione – sentono il bisogno di vantare una conoscenza che si estenda a ogni angolo dell’universo. Per noi, quella superficie matematica è come una porta che si possa varcare in una sola direzione, e poi si chiuda per sempre alle nostre spalle. Ecco perché nel corso degli anni, e in particolare dell’ultimo decennio, si sono investite tante energie intellettuali nello studio dei cosiddetti buchi neri contraffatti: oggetti attraverso i quali si tenta di mitigare alcune delle difficoltà concettuali poste dai buchi neri, e che vedremo meglio nella prossima sezione.

Buchi neri contraffatti

Abbiamo visto che la presenza di un orizzonte degli eventi e di una singolarità fisica al suo centro rende difficile da digerire l’idea stessa di buco nero. A questo punto, è lecito chiedersi se tale idea sia davvero necessaria. In altre parole: «È possibile fare a meno dei buchi neri?».

In molti si sono misurati con questa domanda, specie negli ultimi anni, quando sono state effettuate osservazioni dirette di oggetti compatibili con i buchi neri, sia attraverso rivelazione di onde gravitazionali (da parte della collaborazione LIGO/Virgo) sia grazie alla prima «fotografia» mai realizzata di un buco nero (da parte della collaborazione Event Horizon Telescope, o EHT). Prima di addentrarci nella risposta, però, dobbiamo fare una considerazione più generale su come progredisce la nostra conoscenza scientifica, specie in astrofisica.

L’astrofisica – unica branca della fisica che fornisca evidenze sull’esistenza di buchi neri – è una scienza osservativa e non sperimentale. Ciò significa che in questo campo, a differenza di ambiti quali la fisica dello stato solido o quella delle particelle elementari, non è possibile eseguire esperimenti veri e propri, costruendo un dispositivo sperimentale che consenta di produrre in maniera controllata – ossia con una chiara idea di quali siano gli errori in cui si può incorrere – le condizioni fisiche sotto le quali un certo fenomeno fisico si realizza. Al contrario, essa deve necessariamente affidarsi alle osservazioni astronomiche per formulare delle teorie, e poi deve confermarle o confutarle attraverso ulteriori osservazioni. Questo aspetto dell’astrofisica – che a volte tendiamo a trascurare, se non addirittura a ignorare – aggiunge una considerevole complessità all’applicazione del metodo scientifico, per almeno due ragioni.

La prima è che, siccome si effettuano solo osservazioni, è in genere difficile predire il numero di sorgenti che verranno studiate e le relative proprietà. Per fare un paragone, quando si costruisce un acceleratore di particelle come quello del CERN si ha un’idea molto precisa del numero di eventi o collisioni che sarà possibile produrre in un certo periodo di tempo, una volta specificate le condizioni iniziali (ad esempio l’energia del fascio incidente o le proprietà del fascio bersaglio). In astrofisica non è così semplice: a meno che non si intendano ripetere osservazioni di sorgenti ben note, la costruzione di un telescopio è in genere accompagnata da una grande incertezza sul numero di nuovi oggetti che verranno osservati. È per questo, ad esempio, che quando sono entrati in funzione i rivelatori di onde gravitazionali della collaborazione LIGO – non dimentichiamo che anche l’astronomia delle onde gravitazionali è una scienza osservativa – l’incertezza sul numero di eventi che sarebbe stato possibile misurare era di tre ordini di grandezza. In altre parole, non si sapeva se si sarebbero visti 400 eventi di fusione all’anno o soli 0,4.

La seconda ragione che rende più arduo il progresso scientifico in astrofisica è che, siccome si tratta appunto di una scienza osservativa, essa soffre di degenerazioni in quelle che sono le possibili spiegazioni alle osservazioni. Ancora una volta, ricorrerò a un’analogia per illustrare questo concetto. Immaginate di avere davanti un vecchio orologio a muro, che potete osservare quanto vi pare. Ebbene, cosa notereste? Probabilmente che ha due lancette, una lunga e una corta, e che quella corta ruota di 360 gradi ogni 12 ore mentre quella lunga ruota dello stesso angolo ogni 60 minuti. Bene, queste sono le vostre «osservazioni»: ora supponete di dover costruire un modello matematicamente completo e fisicamente plausibile del meccanismo interno che consente all’orologio di funzionare. Com’è facile immaginare, potreste trovare un gran numero di modelli matematici e combinazioni di meccanismi in grado di spiegare alla perfezione la rotazione della lancetta lunga ogni 60 minuti e di quella corta ogni 12 ore. Tuttavia, solo una delle possibili spiegazioni è quella giusta, ed è persino possibile che non l’abbiate nemmeno presa in considerazione. Così, per rimediare a questa palese difficoltà, dovreste dar fondo a tutta la vostra immaginazione e arguzia nel tentativo di ottenere informazioni addizionali. Potreste utilizzare dei microfoni per ascoltare il rumore prodotto dal meccanismo responsabile del movimento, e poi sfruttare le registrazioni per escludere alcuni modelli che non siano compatibili con le «osservazioni acustiche». Oppure potreste misurare le vibrazioni che l’orologio trasmette al muro, e lavorare sui modelli con esse compatibili.

Ebbene, i progressi in astrofisica si ottengono in modo analogo. Anche in questo campo, infatti, tutte le informazioni disponibili vengono raccolte unicamente tramite osservazioni, che gli scienziati cercano poi di spiegare attraverso modelli matematici costruiti in base alle leggi della fisica. Le informazioni complementari provengono da osservazioni in diverse bande elettromagnetiche o in diversi canali osservativi, nel qual caso si parla di astronomia a lunghezze d’onda multiple o astronomia multimessaggera (dall’inglese multi-wavelength astronomy e multi-messenger astronomy). E, come nel caso dell’orologio a parete, capita che i modelli in apparenza più accurati e plausibili per spiegare le osservazioni si rivelino poi errati, proprio perché esiste una degenerazione tra le osservazioni e i modelli in grado di spiegarle. Infine, la creatività degli astrofisici consente loro di utilizzare tutte le possibili osservazioni – e le relative connessioni – per sfoltire l’insieme dei modelli che sono in accordo con le osservazioni, o per fare predizioni circa i comportamenti che, qualora osservati o meno, potrebbero confermare o confutare la correttezza del modello.

Ma torniamo a noi. Perché questa digressione sugli aspetti più prettamente epistemologici dell’astrofisica? Per illustrare come, sebbene la soluzione di buco nero rappresenti la più naturale e semplice spiegazione alla fenomenologia osservata in oggetti astrofisici compatti quali Cyg-X1, essa non sia tuttavia l’unica. Ne esistono infatti altre, che non richiedono la presenza di un buco nero. Le caratteristiche di queste soluzioni alternative sono abbastanza semplici da indovinare: devono riferirsi a oggetti estremamente compatti ma privi di un orizzonte degli eventi o di una singolarità fisica.⁹ In effetti, sia la Relatività Generale sia teorie alternative della gravità consentono l’esistenza di un’intera classe di oggetti astrofisici compatti con queste proprietà: sono le cosiddette imitazioni di buchi neri (in inglese, black-hole mimickers), chiamate così perché possiedono molte proprietà simili a quelle dei buchi neri, tanto da essere a volte quasi indistinguibili da essi (almeno per quanto può misurare un’osservatrice distante).

Come accennato, esistono parecchie tipologie di oggetti simili in moltissimi aspetti ai buchi neri, tutte decisamente interessanti, ma per darvene un’idea più precisa ne approfondiremo due. Il primo di questi imitatori è la cosiddetta stella gravitazionale, o più semplicemente gravastar. Si tratta di una soluzione alle equazioni di Einstein in simmetria sferica – quindi perfettamente compatibile con quanto sappiamo sulla Relatività Generale – proposta nel 2000 dai fisici Pawel Mazur ed Emil Mottola.¹⁰ La soluzione suppone l’esistenza di una stella a strati il cui nucleo interno – che ne rappresenta la gran parte – è caratterizzato da materia con proprietà abbastanza inusuali: al contrario di tutta quella cui siamo abituati, ha infatti pressione negativa anziché positiva. Questo nucleo è circondato da una «buccia» molto sottile di materia dalle proprietà altrettanto estreme: in questo caso una pressione positiva elevatissima.

La materia a pressione negativa può essere considerata come un piccolo universo che vuole espandersi; si tratta infatti di uno spaziotempo di de Sitter (dal nome del suo scopritore, lo scienziato olandese Willem de Sitter): una soluzione alle equazioni di Einstein che riteniamo collegata all’espansione accelerata che stiamo misurando in cosmologia. Al contempo, però, la strisciolina di materia ad altissima pressione vuole collassare, e questa sua tendenza riesce a contrastare quella del nucleo, generando un equilibrio stabile. In altre parole, una gravastar è come un palloncino che abbia pressione interna negativa – ma gradiente positivo verso l’esterno – e in cui la sottile superficie esterna impedisce al nucleo di espandersi.

La peculiarità più importante di questa soluzione è che essa può essere costruita in modo da avere una compattezza assai vicina al limite di un buco nero (quindi con un rapporto M/R pari quasi a 1/2), ma leggermente al di sotto di esso. In particolare, è possibile costruire – almeno come soluzioni matematiche – delle gravastar la cui superficie superi di pochissimo il punto in cui si troverebbe l’orizzonte degli eventi di un buco nero con la stessa massa, ovvero che abbiano un raggio infinitesimamente più grande di quello di Schwarzschild. Le gravastar hanno così una superficie rigida come le stelle di neutroni (da qui il nome azzeccato di stella gravitazionale) ma non contengono alcuna singolarità al proprio interno, presentandosi come soluzioni perfettamente regolari.

Il secondo esempio di buco nero contraffatto è ormai diventato quasi un «classico»: in italiano dovremmo chiamarlo cunicolo spaziotemporale, ma è molto più noto come wormhole. Come per black hole, anche il suo evocativo nome fu coniato da John Wheeler, in un articolo del 1957 scritto insieme a Charles Misner.¹¹

Ancora una volta si tratta di una soluzione perfettamente plausibile delle equazioni di Einstein per un oggetto nel vuoto ed estremamente compatto, ma la cui compattezza è leggermente minore di quella di un buco nero. In questo modo, attraverso la curvatura locale che esso produce, è in linea di principio possibile unire due regioni dello spaziotempo estremamente distanti e asintoticamente piatte. In sostanza, la soluzione di wormhole può essere vista come un tunnel nel tessuto elastico dello spaziotempo, che ci fornisce una «scorciatoia» per collegare due regioni fisicamente distanti. Immaginate infatti di prendere una sezione di uno spaziotempo piatto in due dimensioni – il nostro caro lenzuolo – e considerarne due punti posti a una grande distanza l’uno dall’altro. Se adesso piegaste un’estremità del lenzuolo in modo da ottenere due strati paralleli, ecco che i punti non sarebbero più così lontani: basterebbe poter viaggiare attraverso il lenzuolo anziché lungo di esso. Adesso immaginate una sorgente di gravità abbastanza intensa da distorcere il lenzuolo così da creare una doppia gola, e il gioco è fatto: avete creato una scorciatoia tra i due punti prima lontani, e adesso molto vicini. È stato dimostrato da tempo che i wormhole – almeno nei modelli più semplici – sono dinamicamente instabili: se aperti, tenderebbero a richiudersi in maniera estremamente rapida. Allo stesso tempo, esistono modelli di wormhole che possono essere stabilizzati dalla presenza nella gola di materia esotica, vale a dire con massa o energia negativa.

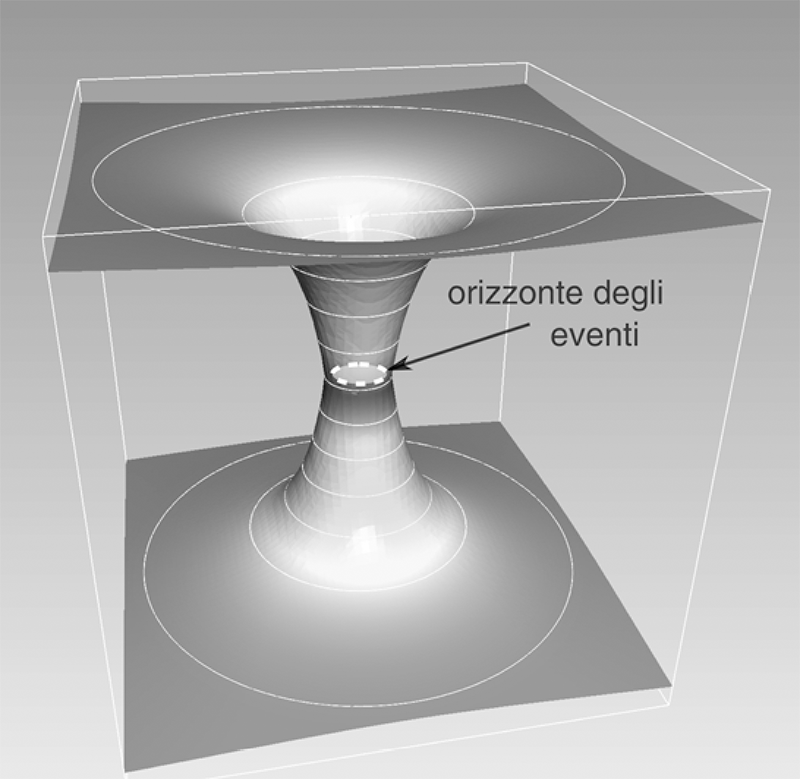
Fig. 6.3 Wormhole con due «gole» identiche e simmetriche, le quali possono unire due regioni dello spaziotempo che a grandi distanze sono piatte. La sezione più piccola della gola è leggermente più grande di quella di un buco nero di Schwarzschild con la stessa massa.

Il diagramma schematico di un wormhole illustrato nella Figura 6.3 mostra la tipica «gola» cui siamo abituati in presenza di forte curvatura. In questo caso, però, le gole sono due, esattamente simmetriche, e possono così unire due regioni dello spaziotempo che a grandi distanze sono piatte. È importante notare che anche in questo caso la sezione più piccola della gola è in realtà leggermente più grande di quella che avrebbe un buco nero di Schwarzschild con la stessa massa (come mostrato dalla circonferenza bianca tratteggiata).

Almeno in un aspetto, una gravastar e un wormhole differiscono in modo significativo: la prima è infatti dotata di una superficie solida – al pari di una stella di neutroni – mentre il secondo non ha superficie solida e – almeno nei modelli più semplici – è addirittura una soluzione nel vuoto. Allo stesso tempo, esistono almeno due proprietà che una gravastar e un wormhole hanno in comune. Entrambi hanno una compattezza M/R estremamente elevata, molto vicina a quella di un buco nero, 1/2, ma anche leggermente inferiore.

La seconda proprietà che hanno in comune riguarda la loro genesi: in entrambi i casi ne abbiamo solo una vaga idea, per non dire che la ignoriamo quasi completamente. In altre parole, sebbene quelle di gravastar e wormhole siano soluzioni consentite e perfettamente lecite delle equazioni di Einstein, non sono noti – almeno in questo momento – i processi astrofisici che potrebbero condurre alla formazione di uno dei due. Per oggetti ugualmente compatti, come le stelle di neutroni o i buchi neri, la situazione è molto diversa. Abbiamo infatti individuato precise tracce evolutive che ci consentono di partire da stelle tra le 10 e le 100 masse solari e di giungere – attraverso una dettagliata evoluzione di astrofisica nucleare – a un fenomeno di supernova, e quindi alla formazione di una stella di neutroni o di un buco nero a seconda della massa della stella progenitrice. Anche facendo uso di tutte le conoscenze che abbiamo oggi dell’astrofisica nucleare e dei processi microfisici che possono avvenire in un contesto stellare, non è invece chiaro come sia possibile produrre una gravastar o un wormhole.

La complicazione forse più seria nel considerare uno scenario astrofisico in grado di generare questo tipo di soluzioni è che entrambe richiedono la presenza di materia esotica, le cui proprietà – ad esempio energia o pressione negative – sono apertamente in contrasto con quelle che caratterizzano la materia a noi nota, sia sulla Terra sia nell’universo accessibile tramite osservazioni astronomiche.

Se volessimo ancora una volta sottoporci alla severa logica imposta dal rasoio di Occam, dovremmo considerare tali soluzioni come irrealistiche. Tuttavia, se accantoniamo per un momento le difficoltà e le stravaganze che circondano la genesi di questi oggetti, rimane comunque chiaro che soluzioni di questo tipo avrebbero molte delle proprietà che pensiamo caratterizzare un buco nero. È per questo che, se torniamo all’esempio del viaggio di Carolin e Dominik verso l’orizzonte degli eventi di un buco nero supermassiccio, sarebbe molto difficile per i due astronauti comprendere se l’oggetto a cui si stanno avvicinando sia un buco nero o piuttosto una gravastar, perché quest’ultima si comporterebbe in modo molto simile al primo, generando un redshift gravitazionale estremamente forte e quindi assorbendo – almeno in apparenza – ogni forma di luce.

Per nostra fortuna – ma non poteva essere altrimenti per una teoria che sia fisicamente accettabile – la Relatività Generale gode della proprietà di unicità delle sue soluzioni. In altri termini, essa ci dice che non possono esistere due soluzioni alle equazioni di Einstein che siano diverse ma che abbiano esattamente le stesse proprietà. Sebbene molto simili, esse dovranno necessariamente differire in qualcosa, e possedere dunque caratteristiche che le rendano distinguibili. È per questa ragione – e per eliminare quindi una degenerazione sconcertante – che gli scienziati nel corso degli ultimi anni hanno studiato in dettaglio non solo i buchi neri contraffatti, ma soprattutto gli aspetti di questi oggetti che li rendono distinguibili dai buchi neri veri e propri.

Anche io mi sono impegnato in questa ricerca. Ho mostrato, ad esempio, che una gravastar può essere essenzialmente indistinguibile da un buco nero fintanto che si fa uso di radiazione elettromagnetica, ma è comunque discernibile da esso studiando l’emissione di onde gravitazionali. Per quanto simili in termini di dimensioni, una gravastar e un buco nero hanno infatti una parte interna radicalmente diversa: piena di materia esotica la prima, il vuoto per il secondo. Così, una volta perturbati, i due oggetti producono emissioni in onde gravitazionali decisamente diverse (torneremo sull’argomento nel capitolo 7, quando considereremo un altro oggetto esotico).

Possiamo ora tornare all’esempio dell’orologio appeso alla parete. Avevamo visto come in quel caso diversi modelli di funzionamento interno potessero essere esclusi perché inconsistenti con le osservazioni. In maniera analoga, il compito dell’astrofisica moderna è quello di produrre modelli in grado di spiegare le osservazioni, e utilizzare tutte le informazioni disponibili per escludere quelle spiegazioni degeneri o alternative che non corrispondono più alle osservazioni. Per la stessa ragione, lo sforzo che fisici e astrofisici stanno portando avanti negli ultimi anni è appunto quello di predisporsi in maniera quasi «agnostica» alle osservazioni astronomiche di oggetti compatti come i buchi neri, e lasciare che siano esse – non i nostri preconcetti – a mostrarci se provengono da un buco nero, da una gravastar, da un wormhole, o da qualsiasi altro imitatore di buco nero.

Come nota conclusiva a questo capitolo, è importante sottolineare un concetto che dobbiamo avere ben chiaro. Per quanto esista una degenerazione nella possibilità di spiegare la fenomenologia astronomica di oggetti come Cyg-X1, ed esistano soluzioni alternative che hanno il vantaggio molto importante di non soffrire di nessuna delle problematiche inerenti ai buchi neri – o perché non posseggono un orizzonte gli eventi o perché non hanno una singolarità al centro – la soluzione di buco nero rimane, al netto di tutte le considerazioni possibili, la spiegazione più semplice e più naturale all’interno della teoria della Relatività Generale, che finora si è sempre rivelata corretta.

In aggiunta – e, a parer mio, si tratta di un vantaggio enorme rispetto a qualsiasi scenario alternativo – la genesi di un buco nero rappresenta una risposta naturale alla sequenza di eventi che sappiamo caratterizzare la vita di alcuni oggetti stellari. Essa non richiede assunzioni improbabili, né la presenza di materia dalle proprietà radicalmente diverse rispetto a quelle cui siamo abituati. In altre parole, per quanto la soluzione di buco nero rappresenti innegabilmente un’idea difficile da digerire, quelle alternative lo sono per molti versi ancora di più.