Spaziotempo, curvatura e gravità

Questo capitolo ha l’arduo compito e l’ardita ambizione di spiegare in modo semplice una serie di concetti alla base della Relatività Generale di Einstein. La matematica di tale teoria ne enuncia i concetti in maniera trasparente ed elegante, e per un fisico o un matematico tutto è chiaro – o quasi – appena si trova davanti le relative equazioni. Potrei quindi limitarmi a mostrarvele e dire: «È tutto lì, non vedete?». So, però, che un approccio del genere non ci porterebbe molto lontano, mentre il mio impegno è farvi da guida premurosa in questo viaggio.

Quindi, ciò che tenterò di fare è decisamente più difficile: illustrare questa nuova interpretazione della gravità utilizzando concetti a cui siamo tutti abituati. La sfida, in un approccio simile, non è legata alla complessità degli argomenti – che sta tutta nella matematica – ma allo sforzo necessario fare per accettare un’interpretazione della realtà fisica in contrasto con la nostra esperienza quotidiana. In altre parole, lo sforzo che vi è richiesto è immaginare una realtà anche molto lontana da quella a cui siete abituati. Del resto, è uno dei requisiti di questo viaggio…

Cominciamo quindi da dove abbiamo concluso il capitolo precedente, quando abbiamo detto che le equazioni di Einstein sintetizzano con eleganza l’equivalenza tra gravità e curvatura dello spaziotempo. A voler essere più precisi, esse affermano in sostanza che:

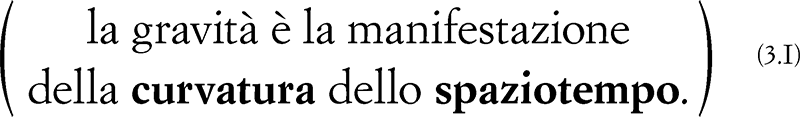
So per esperienza – e per averlo letto sulla faccia di fin troppi studenti quando campeggia per la prima volta su una lavagna – che questa frase suona fondamentalmente oscura, sebbene sia corretta e vera, almeno per quanto possiamo verificare attraverso gli esperimenti scientifici. Tuttavia, non disperate; e, soprattutto, non mollate adesso! Quando ci torneremo, tra qualche pagina, vi scoprirete in grado di comprenderla e addirittura di apprezzarne le profonde implicazioni.

Lo spaziotempo: tutto quello che è accaduto e accadrà

Per comprendere l’affermazione (3.I) possiamo partire facendo un’analisi dei termini che vi compaiono. Partiamo quindi dal concetto di spaziotempo. Innanzitutto, è bene notare che non ho scritto «spazio-e-tempo», né «spazio-tempo». Può sembrare una differenza minima, irrilevante, ma è invece fondamentale, perché rappresenta una delle prime lezioni della teoria della Relatività Generale. In essa, infatti, Einstein postula che la nostra idea di spazio e tempo come entità distinte sia in realtà incorretta, perché i due elementi sono del tutto equivalenti. Ne consegue che uno spostamento nello spazio da un punto a un altro equivale – e così è, nelle equazioni – a uno spostamento nel tempo da un momento a un altro. Andare a destra o a sinistra, in alto o in basso, non è dissimile – almeno a livello matematico – dall’andare avanti e indietro nel tempo.

Nella concezione di Einstein, quindi, lo spaziotempo è un singolo oggetto, che può essere visto in essenza come un «contenitore» di elementi (ossia un insieme) i quali prendono il nome di eventi. Facciamo un esempio per intenderci meglio. L’Unione Europea può essere considerata come un «insieme» di cittadini dei suoi diversi Paesi; quei cittadini sono pertanto gli elementi costitutivi dell’insieme UE. In maniera del tutto analoga, lo spaziotempo è l’insieme di tutti gli eventi: passati, presenti e futuri. Un evento – ossia un elemento dello spaziotempo – è da intendersi come qualcosa che è avvenuto, sta avvenendo o avverrà da qualche parte in qualche momento. La sveglia che avete puntato questa mattina, l’aver fatto colazione, l’aver preso un mezzo di trasporto per andare al lavoro… Sono tutti eventi. Anche il leggere questo libro in questo momento è un evento, in quanto è possibile stabilire che avviene in un posto specifico (ad esempio il vostro divano) e in un certo istante (adesso). Dal momento che ogni evento necessita, per essere definito, della specificazione di quattro diversi pezzi di informazione – tre per la posizione nello spazio e uno per quella nel tempo – è abbastanza semplice concludere che lo spaziotempo è un contenitore in quattro dimensioni (tre spaziali e una temporale) di elementi detti eventi.

A questa definizione Einstein aggiunge che, preso da solo e senza ulteriori regole, questo contenitore di eventi non è particolarmente utile. È dunque necessario associarvi regole precise per individuare la posizione relativa dei vari elementi, ossia la loro distanza. In altre parole, presi gli eventi A e B, è necessario stabilire se A è avvenuto prima o dopo B, alla sua destra o alla sua sinistra, sopra o sotto, e infine se i due sono in qualche maniera collegati o, al contrario, del tutto indipendenti.

Tali regole possono essere fissate solo compiendo una scelta di coordinate, ossia dopo aver introdotto una serie ordinata di numeri che stabiliscano la sequenza degli eventi e consentano di conoscere quindi la posizione relativa di A e B. È essenziale notare che questa scelta di coordinate è del tutto arbitraria – da cui la relatività della teoria – ma l’ordine che ne consegue è lo stesso, indipendentemente dalla scelta fatta. È per questo che, all’interno della teoria della Relatività Generale, è comunque possibile stabilire con certezza quale delle due cose abbiate fatto prima questa mattina: svegliarvi o fare colazione.¹ Inoltre questo stesso ordine sarà stato registrato da chiunque vi abbia osservato, quale che fosse il suo stato di moto.

La curvatura

Adesso che abbiamo compreso cosa sia lo spaziotempo, torniamo alla nostra affermazione (3.I) e concentriamoci sul secondo concetto che vi appare, quello di curvatura.

Anche in questo caso, la matematica ci offre strumenti sofisticati ed eleganti per misurare la curvatura di una superficie in uno spazio di dimensioni arbitrarie. Senza entrare nel dettaglio, quello che ci interessa sapere è che esistono superfici «curve» e che il loro grado di curvatura può essere misurato attraverso dispositivi matematici piuttosto semplici; ad esempio introducendo il concetto di trasporto parallelo in un circuito chiuso: in termini tecnici, potremmo dire che preso un vettore (ossia una «freccia» di una certa lunghezza) in una certa varietà (ossia una porzione di spaziotempo) e sottoposto a un trasporto parallelo lungo un circuito chiuso, esiste uno strumento matematico (denominato il tensore di Riemann, o della curvatura) che misurerà l’ammontare della curvatura presente.

Forse un paio di esempi possono aiutare a chiarire questo concetto. Consideriamo quindi una superficie in due dimensioni, partendo dalla più semplice possibile, ossia un piano. Immaginiamo di rappresentare il circuito chiuso mediante un triangolo A-B-C e di utilizzare come referenza per una certa direzione una freccia di una data lunghezza, la cui origine coincide con il punto A e che si sviluppa lungo il lato A-B. In matematica e fisica una freccia di questo tipo è detta appunto vettore, ed è caratterizzata da una certa lunghezza, una direzione e un verso indicato dalla freccia stessa. Ora possiamo far scorrere il nostro vettore lungo A-B, portarlo fino al punto B e spostarlo poi verso il punto C. Nel farlo, però, è importante mantenere fissa la direzione iniziale della freccia, visto che è questa l’idea dietro il trasporto parallelo. Giunti in C, trasporteremo il vettore sul lato C-A e chiuderemo il circuito così come mostrato nella Figura 3.1. A questo punto possiamo confrontare il vettore finale con quello iniziale, concludendo che sono identici: niente è cambiato nel trasportarlo parallelamente lungo un circuito chiuso contenuto in un piano. Diremo che questa assenza di cambiamento è legata all’assenza di curvatura sulla superficie, ossia, che il piano è una superficie piatta, perché ha curvatura nulla.

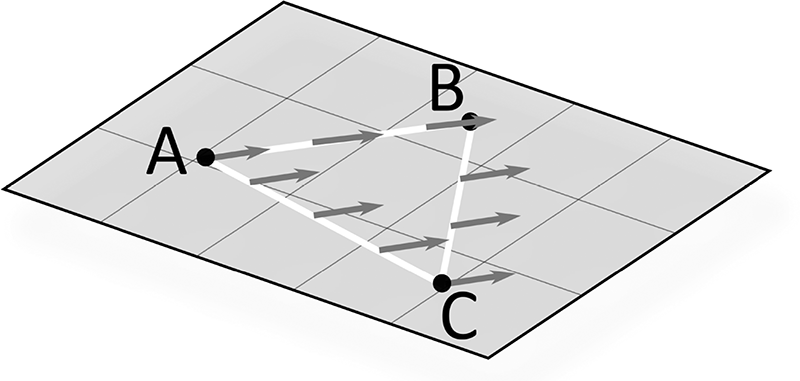
Fig. 3.1 Trasporto parallelo di una freccia (vettore) lungo il triangolo A-B-C su un piano in due dimensioni. Il confronto tra il vettore finale e quello iniziale in A ci mostra che sono identici: il piano è una superficie piatta, perché ha una curvatura nulla.

Quello di cui abbiamo bisogno adesso è un esempio di superficie non banalmente piatta. Prendiamo dunque in considerazione una superficie in due dimensioni che i matematici adorano per la sua semplicità e per la ricchezza delle sue proprietà: una due-sfera, vale a dire la superficie di una sfera a raggio costante. In sostanza, possiamo pensare a una due-sfera come alla buccia di un’arancia se fosse liscia e sottilissima, o alla rappresentazione semplificata della superficie della Terra.

Fig. 3.2 Trasporto parallelo di un vettore lungo un circuito chiuso su una due-sfera. Il confronto tra il vettore finale e quello iniziale mostra che i due sono diversi, perché hanno direzioni ortogonali: la due-sfera è una superficie curva, in quanto ha una curvatura non-nulla.

In questo caso, potremmo costruire il nostro circuito chiuso – sempre rappresentato da un triangolo A-B-C – collegando due meridiani attraverso la sezione di un parallelo che li interseca. Immaginiamo quindi di partire dal punto A, magari una bella isola nei Caraibi, e puntare a nord con l’ausilio di una bussola. Finché ci muoviamo seguendo con precisione l’ago, stiamo in sostanza trasportando in maniera parallela il nostro vettore lungo il primo meridiano, fino ad arrivare al Polo Nord, ossia il punto B. Lì – facendo attenzione a non voltarci, quindi continuando a guardare sempre nella stessa direzione – scendiamo verso sud seguendo un altro meridiano, ad esempio quello posto ad angolo retto rispetto al primo, e raggiungiamo il punto C da qualche parte nell’Africa settentrionale. Una volta arrivati a destinazione, alla latitudine di A, ci muoviamo verso ovest lungo il parallelo che forma il lato C-A, ma continuiamo a guardare nella direzione in cui ci siamo trovati quando siamo giunti al Polo Nord.

Tornati in A e chiuso il circuito, come mostrato nella Figura 3.2, potremo confrontare il vettore finale con quello iniziale, concludendo che questa volta non sono affatto identici: puntano in direzioni ortogonali, a nord il primo e a est l’ultimo. Abbiamo scoperto che il trasporto parallelo di un vettore lungo un circuito chiuso su una due-sfera introduce un cambiamento nella direzione in cui punta il vettore stesso, e questo cambiamento è legato alla presenza di una curvatura sulla superficie sferica. In altre parole, abbiamo appreso che una due-sfera è una superficie curva, perché ha una curvatura non-nulla.

Ovviamente questo semplice esperimento dovrebbe essere sufficiente per convincere i terrapiattisti di quanto insensata sia la loro teoria. Ma rivela anche a noi qualcosa di molto interessante, e ci invita a una serie di importanti riflessioni a margine. La prima: com’è facile intuire, se avessimo scelto un triangolo molto piccolo la variazione tra i due vettori sarebbe stata meno evidente. Se ad esempio considerassimo un triangolo con lati di un centinaio di metri appena, sarebbe molto difficile misurare lo scarto tra i vettori senza strumenti abbastanza sofisticati. Quindi una superficie curva può essere approssimata, almeno localmente, cioè nelle vicinanze di ogni suo punto, con una superficie piatta. In altre parole, gli effetti della curvatura sono evidenti solo su scale confrontabili con il cosiddetto raggio di curvatura della superficie curva.

Per comprendere meglio questo punto, e semplificando enormemente, possiamo dire che è sempre possibile approssimare, almeno localmente, una superficie curva con una sferica. In questo caso, la due-sfera che approssima la superficie curva – e che è anche detta osculante – avrà un raggio pari al raggio di curvatura locale della superficie curva. Se ci limitiamo a una superficie in una sola dimensione spaziale – ossia a una curva – essa è sempre approssimabile localmente con una circonferenza il cui raggio rappresenta il raggio di curvatura locale. Se invece volessimo prendere in considerazione lo spaziotempo nelle sue quattro dimensioni, avremmo una sfera quadridimensionale – che è difficile da immaginare, sono il primo ad ammetterlo – osculante in ogni punto la curvatura locale dello spaziotempo quadridimensionale.

Alla luce di tutto ciò e della definizione di raggio di curvatura, non sorprenderà l’affermazione che una superficie piana – che abbiamo visto avere curvatura nulla – abbia comunque un raggio di curvatura: solo che esso è infinito. Nel caso della Terra, il raggio di curvatura è pari al suo raggio, ossia a circa 6400 chilometri, ed è per questo che è necessario andare dai Caraibi al Polo Nord per misurare la differenza tra i vettori. Se conducessimo l’esperimento in una piazza grande come San Marco a Venezia, misurare una differenza tra i vettori sarebbe molto più difficile, anche se non impossibile.

La seconda considerazione discende direttamente dalla prima, e ci insegna una nozione fondamentale che utilizzeremo molte volte nel corso di questo viaggio. Dal momento che la nostra esperienza del mondo fisico si sviluppa su scale di lunghezza di qualche decina di chilometri – la nostra vista non si spinge oltre – e si costruisce sulla base delle condizioni di gravità presenti sulla Terra, è inevitabile la percezione che le leggi della fisica siano quelle di uno spaziotempo piatto, ossia con curvatura nulla. In realtà è un’impressione incorretta, tanto quanto supporre che la Terra sia piatta solo perché è difficile apprezzarne la curvatura. Bisognerà ancora una volta far affidamento all’intuizione di Einstein per rompere i vincoli della nostra percezione di uno spaziotempo piatto. Torneremo su questo punto nel prossimo capitolo.

La terza considerazione è che lo strumento appena discusso – ossia il trasporto parallelo di un vettore lungo un circuito chiuso – è del tutto generale e può dunque essere applicato anche a superfici la cui curvatura è molto più complessa di quella considerata finora. Prendendo in esame la Figura 3.3, ci troveremo di fronte una superficie bidimensionale con curvature diverse da punto a punto, tranne in quelli equidistanti dal centro. In particolare, se si pensa al raggio di curvatura locale, esso è molto piccolo vicino all’origine e diventa più grande man mano che ci si allontana dal centro. Esattamente all’origine il raggio di curvatura è infinito, perché ho scelto di rappresentare una funzione – ossia sin(r)/r – che ha un valore costante e vicino a uno all’origine. Inoltre l’illustrazione mostra che la curvatura può cambiare segno, diventando positiva o negativa a seconda che la superficie sia convessa – come nel caso della due-sfera – o concava.

La teoria della Relatività Generale utilizza strumenti matematici sofisticati – molti dei quali sviluppati da italiani come Tullio Levi-Civita e Gregorio Ricci-Curbastro all’inizio del Novecento – per misurare il raggio di curvatura e il suo segno. Grazie a essi non è fantascientifico immaginare applicazioni, da utilizzare magari nei nostri smartphone, che un giorno consentiranno di misurare la curvatura locale, in maniera analoga a quelle che misurano il valore locale dell’altitudine.

Fig. 3.3 Una superficie curva generica può essere complessa e avere un raggio di curvatura locale che dipende dalla posizione, anche con valore positivo o negativo a seconda che la superficie sia convessa o concava.

Infine, gli esempi fatti finora ci portano a un’ultima considerazione. È possibile misurare il livello di curvatura di una superficie in due dimensioni, allora si può fare lo stesso per una superficie in tre dimensioni (ossia in un volume) e, per estensione, anche in quattro dimensioni (come lo spaziotempo) o addirittura in una superficie di dimensioni arbitrarie. In altre parole, è possibile utilizzare la stessa logica e gli stessi strumenti matematici per misurare la curvatura dello spaziotempo e dedurre se esso sia piatto o meno.

La curvatura e le equazioni di Einstein

Ora che abbiamo visto come si manifesti la curvatura e quali strumenti matematici utilizzare per misurarla, possiamo fare un importante passo avanti a livello concettuale e scoprire come la teoria della Relatività Generale leghi in maniera indissolubile la presenza di curvatura a quella di materia o energia. Questo legame è espresso dalle equazioni di Einstein, che egli propose nel 1915 e che hanno segnato uno dei capitoli più importanti della fisica moderna. Prima di discuterne, però, è necessario ricordare un’altra equazione (attenzione al singolare!), che è sempre legata ad Einstein ma non ha niente a che fare con la gravità. Fu infatti introdotta ben dieci anni prima della Relatività Generale, nell’ambito della cosiddetta teoria della Relatività Speciale (1905), e può essere espressa come:

Questa formula, anche nota come equazione di Einstein, è ormai diventata un’icona del contributo scientifico del fisico tedesco; e, sebbene sia stata ottenuta senza pensare alla gravità, esprime un concetto importante che utilizzeremo di frequente in seguito. In breve, attraverso il segno =, indica un’equivalenza tra l’energia (E, a sinistra del segno di uguale) e la massa (m, a destra). La presenza del quadrato della velocità della luce, c², è in sostanza irrilevante per quanto ci interessa discutere qui: serve solo a rendere i due membri confrontabili in termini di unità (per questa ragione è mostrata in grigio).² In altre parole, l’equazione (3.II) ci dice che ogni volta che abbiamo una massa – sia essa rappresentata da una piuma o da un macigno, da una particella elementare o da una stella – abbiamo a nostra disposizione una certa quantità di energia.

Questa profonda verità sta dietro il funzionamento delle stelle, che producono energia fondendo – attraverso il processo di fusione termonucleare – due atomi di idrogeno per formarne uno di elio, la cui massa è leggermente minore della somma delle masse dei due atomi di partenza. Questa piccola differenza in massa è rilasciata sotto forma di energia. Lo stesso principio vale per le centrali nucleari: attraverso il processo di fissione nucleare si «rompe» un atomo complesso come quello di uranio per crearne molti più piccoli, la cui massa sommata è inferiore a quella originaria. Ancora una volta, la differenza è rilasciata sotto forma di energia.

Ecco perché d’ora in poi parleremo sempre di massa-energia, senza specificare se si tratti di una massa intesa come agglomerato di particelle elementari (quali elettroni, protoni o neutroni) a cui si può associare una massa a riposo, o di pura energia.

Adesso, senza altri preamboli, possiamo passare a scrivere le equazioni di Einstein (in questo caso al plurale!):

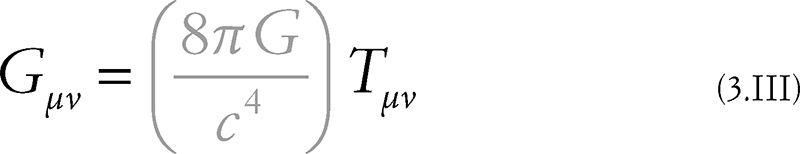
È facile intuire come, per la stragrande maggioranza di voi, tali equazioni siano chiare quanto un testo in cinese. Almeno se non conoscete il cinese, ecco. Il che è perfettamente normale: per capirle, infatti, bisognerebbe frequentare per intero un corso universitario di Relatività Generale. Quello che tengo a Francoforte, ad esempio, dura circa sei mesi e fornisce tutta una serie di strumenti matematici necessari a comprenderle in dettaglio e manipolarle.³ Anche in questo caso, però, non dobbiamo lasciarci «distrarre» dalla matematica: concentriamoci piuttosto sul significato profondo di queste equazioni, che rappresentano la pietra di volta della teoria della Relatività Generale e sono quindi al centro della visione rivoluzionaria della gravità di Einstein.

Partiamo ancora una volta dal segno di uguaglianza, che esprime un’equazione tra quanto compare alla sua sinistra – ovvero il tensore di Einstein (G_µν) – e quanto c’è a destra. Quest’ultimo elemento è il prodotto di due fattori: uno tra parentesi, che serve solo a far tornare le unità ma non ha un significato fisico (per questo è mostrato in grigio), e un altro tensore, ossia quello energia-impulso (T_µν). In buona sostanza, le equazioni di Einstein (3.III) possono anche essere lette come un’equazione concettuale:

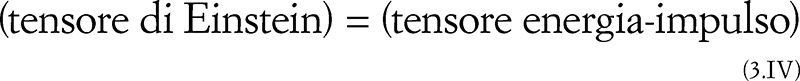
E dal momento che il tensore di Einstein rappresenta una misura della curvatura dello spaziotempo – in effetti è proporzionale al tensore di Riemann, che misura appunto la curvatura – mentre il tensore energia-impulso fornisce una misura della quantità di materia-energia presente nello spaziotempo – maggiori sono la materia e la sua concentrazione, maggiore è numericamente questo tensore – le complesse equazioni (3.III) esprimono, in sostanza, un’uguaglianza di questo genere:

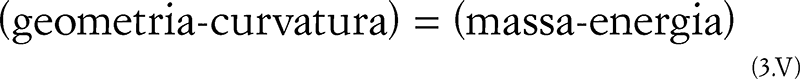
Questo è senza dubbio il concetto più importante di tutto il libro. Esprime esattamente ciò che in maniera molto più complessa – ma anche matematicamente elegante e fisicamente rivoluzionaria – è sancito dalle equazioni di Einstein. In altre parole: ogni volta che c’è materia (o energia), essa produce una curvatura. Questo è vero sempre, non importa che si stia parlando della massa di una galassia o di quella di un granello di sabbia, di un raggio di luce o di un proiettile di cannone. A variare sarà solo la grandezza di tale curvatura, cioè quanto pronunciata o meno sia. Nel prossimo capitolo impareremo a distinguere curvature di diversa intensità, e capiremo anche come la natura sia in grado di produrle. Prima, però, dobbiamo introdurre la gravità in questo quadro concettuale.

Lo spaziotempo è un tessuto elastico

In effetti, per quanto ricca di importanti implicazioni che approfondiremo nel resto del libro, l’espressione (3.V) ancora non spiega come la gravità rientri in tutto questo discorso. In altre parole, non è necessariamente chiaro come le equazioni di Einstein possano spiegare il fenomeno che porta una mela a cadere dall’albero. È questo il prossimo passo che dobbiamo compiere a livello concettuale. Servirà ancora un po’ di concentrazione.

Per comprendere come curvatura e gravità siano indissolubilmente legate, cominciamo immaginando una superficie piana ma elastica e deformabile, ad esempio il lenzuolo di un letto appena rifatto. In assenza di pesi, esso appare perfettamente liscio, piatto, e così rimane finché qualcosa non ne perturba la superficie. È ciò che mostra la Figura 3.4, che ci aiuta a comprendere il significato delle equazioni di Einstein: l’assenza di materia-energia dà vita a uno spaziotempo con curvatura nulla, quindi piatto. All’interno di esso possiamo prendere un vettore, trasportarlo parallelamente lungo un circuito chiuso e ritrovarlo identico alla fine del processo.

Fig. 3.4 L’assenza di materia-energia dà vita a uno spaziotempo privo di curvatura, quindi piatto.

A voler essere pignoli, uno spaziotempo di questo tipo – ossia strettamente vuoto – non può esistere, in quanto la presenza di materia, per quanto di massa minuscola, creerebbe una perturbazione, con tanti saluti alla sua «piattezza». Ma l’esempio è comunque utile, perché è spesso possibile prendere in considerazione spazitempi «pressoché piatti» o «localmente piatti» (che, pur non essendo piatti in assoluto e su grandi scale, lo sono in una piccola regione).

Proviamo dunque a pensare: cosa accadrebbe se posassimo un oggetto pesante, ad esempio una palla da bowling, su quel lenzuolo? Come è facile intuire, esso si «curverebbe» intorno al peso, esattamente come mostrato nella Figura 3.5. Ciò ci offre un’utile analogia con quanto espresso dalle equazioni di Einstein: la presenza di materia (o energia) produce uno spaziotempo dotato di curvatura non-nulla, e quindi curvo. Se prendessimo un vettore e lo trasportassimo parallelamente lungo un circuito chiuso al suo interno, alla fine del percorso lo troveremmo diverso da quello iniziale.⁴

Fig. 3.5 La presenza di materia-energia – qui rappresentata da una sfera, che potrebbe essere un pianeta o un granello di sabbia – dà vita a uno spaziotempo con curvatura non-nulla, quindi curvo.

L’esempio del lenzuolo ci fornisce lo spunto per tre diverse considerazioni «a margine». La prima ha a che fare con un aspetto molto importante della Figura 3.5, qualcosa su cui vorrei richiamare la vostra attenzione: la curvatura prodotta dalla palla da bowling non è identica ovunque, ma varia da punto a punto. In particolare sarà molto lieve ai margini del lenzuolo, che appariranno quasi piatti, e sempre più pronunciata avvicinandosi al punto in cui è posato l’oggetto, dove sarà massima. Detto in altre parole: è naturale aspettarsi che, in condizioni generiche, la curvatura sia una funzione della posizione; solo in circostanze molto speciali – come nel caso di una due-sfera – essa è costante.

La seconda considerazione riguarda la «sagoma» della deformazione. Sebbene possa sembrare ovvio che la presenza della palla da bowling produca una curvatura concava – ossia positiva – nel lenzuolo, per le equazioni di Einstein è possibile, in modo del tutto equivalente, che essa sia convessa. A livello fisico sappiamo che tutta la materia conosciuta intorno a noi, e con la quale possiamo condurre esperimenti, produce una curvatura positiva, esattamente come illustrato nella Figura 3.5. Tuttavia, non è escluso – anzi, le equazioni di Einstein lo consentono – che esista materia che produce una curvatura negativa.

L’ultima considerazione, infine, ha a che fare con l’impatto della curvatura. È infatti importante comprendere che la presenza di una curvatura influenzerà la dinamica (ossia il moto) di eventuali oggetti intorno a essa. Immaginiamo di aggiungere accanto alla palla da bowling un’altra sfera più piccola e leggera, tale da non produrre una curvatura nel lenzuolo paragonabile alla prima; in un simile scenario – e in assenza di attrito – il secondo oggetto sarà costretto a muoversi, «cadendo» verso il centro della curvatura prodotta dalla palla da bowling. Con questo esempio possiamo comprendere come la gravità si manifesti in termini geometrici. Modificando lo spaziotempo in cui avviene il moto, essa produce una variazione nella dinamica dei corpi che, altrimenti, rimarrebbero nello stato di moto rettilineo o di quiete.

Curvatura e gravità

Ora – introdotti e approfonditi a sufficienza concetti quali spaziotempo e curvatura – penso sia finalmente giunto il momento della verità: siamo pronti a tornare alla semplice ma oscura l’affermazione (3.I). Essa recitava:

In genere, nel mio corso, è a questo punto che lo sguardo smarrito e scettico comparso sul volto degli studenti quando avevano incontrato per la prima volta tale affermazione viene sostituito da un sottile sorriso di compiaciuta soddisfazione. L’espressione di chi pensa: «Ma certo! Come potrebbe essere altrimenti?». Non solo la frase non risulta più criptica, ma è anzi diventata profondamente affascinante.

Detto in altre parole, Einstein afferma che se lo spaziotempo è vuoto – nel senso che è privo di materia così massiccia da produrre una curvatura – allora è anche piatto, e in esso ogni oggetto manterrà il proprio stato di moto: rimarrà fermo o continuerà a procedere con velocità costante lungo una linea retta, a seconda di quale delle due era la sua condizione iniziale (è il principio di inerzia). Tuttavia, se lo spaziotempo è dotato di materia che produce una curvatura, allora ogni oggetto in esso presente verrà coinvolto da tale curvatura attraverso una modificazione del proprio stato di moto. Quelli inizialmente fermi non potranno restare tali, a meno che non si trovino in un punto dello spaziotempo localmente piatto; quelli che si muovevano in linea retta a velocità constante, invece, vedranno modificata la propria traiettoria.

Ne consegue che, in questa visione differente e decisamente rivoluzionaria della gravità, se la mela cade non è perché ci sia una forza che l’attiri verso la Terra. Quello che avviene, in realtà, è che la Terra – con il suo contenuto di materia ed energia – curva lo spaziotempo intorno a sé e costringe gli oggetti a muoversi di conseguenza. Quando una mela non è più attaccata all’albero – elemento che le impediva di muoversi liberamente – non può che spostarsi seguendo la curvatura locale, quindi verso il centro della Terra. Ed è in effetti ciò che fa, finché la stessa superficie del pianeta non le impedisce di continuare oltre. È quanto ci mostra in modo molto schematico – e ovviamente fuori scala – la Figura 3.6.

Si potrebbe qui aggiungere un ulteriore commento, che a questo punto sarete in grado di comprendere alla perfezione: la ragione per la quale, una volta libera dall’albero, la mela non si allontana nello spazio interplanetario è legata al segno della curvatura, ossia al fatto che la Terra produce una curvatura positiva (o concava). Se però ammettessimo l’esistenza – in via del tutto ipotetica – di un tipo di materia ancora sconosciuta che produca una curvatura negativa, allora la superficie del «lenzuolo» nella Figura 3.5 sarebbe deformata con una curvatura convessa: come potete facilmente immaginare, il segno della gravità sarebbe dunque opposto ed essa risulterebbe non attrattiva bensì repulsiva! Per fortuna, anche in presenza di questo «cambio di segno» il titolo del libro che tenete fra le mani resterebbe valido: anzi, la gravità sarebbe ancor più attraente!

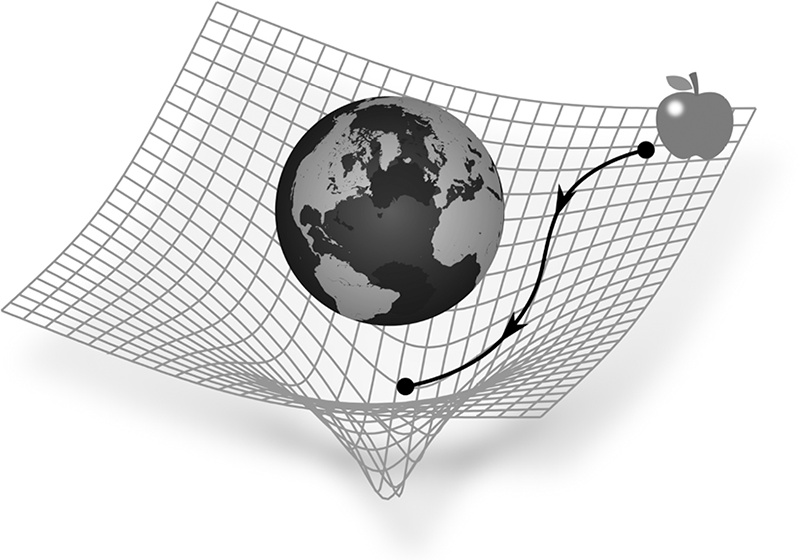
Fig. 3.6 Interpretazione della caduta di una mela nella teoria della gravitazione di Einstein: la Terra produce una curvatura dello spaziotempo e la mela deve muoversi seguendola, dunque «cadendo» verso il centro del pianeta.

Per quanto l’esempio appena suggerito di una gravità repulsiva possa sembrare assurdo, è esattamente ciò che pensiamo stia accadendo in questo momento all’universo, nella sua interezza. Osservando esplosioni di supernove lontane, infatti, è possibile dedurre che l’universo si trova attualmente in una fase di espansione accelerata. La causa di tale fenomeno non è ancora chiara, ma potrebbe essere legata all’energia oscura: una tenue forma di energia che genererebbe una curvatura negativa anziché positiva. Di conseguenza, su scala cosmica, essa sembrerebbe produrre un’azione simile a un’antigravità!

Niente si muove in linea retta

Abbiamo già evidenziato, in una nota, come l’esempio proposto a commento della Figura 3.5 contenga una falla logica. Per spiegare la gravità abbiamo infatti ipotizzato di utilizzare una palla da bowling, che è già soggetta a un campo gravitazionale, ovvero quello terrestre; di conseguenza, essa curva il lenzuolo proprio in virtù del fatto di trovarsi in tale campo. Stiamo quindi sfruttando la dinamica di un oggetto in un campo gravitazionale per spiegare cosa sia la curvatura, che poi diciamo essere l’origine stessa della gravità. La circolarità dell’argomentazione è evidente. Per fortuna, però, è anche innocua: si limita a mostrarci che l’analogia del lenzuolo è molto utile, ma non calza alla perfezione.

A questo punto siamo pronti a dedurre come sia possibile visualizzare e misurare la curvatura senza l’ausilio di lenzuoli e palle da bowling. Per arrivarci servirà ancora un po’ di attenzione, ma vi assicuro che ne varrà la pena: scopriremo insieme uno degli strumenti più efficaci e utilizzati nell’astronomia moderna.

Torniamo all’idea di uno spaziotempo vuoto e quindi piatto. In esso un oggetto dotato di massa segue il principio di inerzia: rimane fermo se inizialmente fermo, altrimenti continua nel suo moto rettilineo uniforme (ossia a velocità costante). È chiaro che, se lo spaziotempo è curvo, lo scenario sarà differente: in questo caso, infatti, la traiettoria dell’oggetto dotato di massa sarà modificata dalla curvatura, e dovrà adeguarsi di conseguenza. Ne consegue che il moto rettilineo uniforme non può più esistere in uno spaziotempo curvo, nel quale ogni moto dovrà essere necessariamente curvo. In altre parole, in uno spaziotempo contenente materia niente si muove in linea retta, se non per tratti molto brevi.

La conclusione appena raggiunta ha due conseguenze interessanti. La prima è legata all’esperienza comune che una linea retta rappresenti la distanza minima tra due punti, ossia la geodetica tra essi. Questo è ovviamente vero in uno spaziotempo piatto, ma cessa di esserlo in uno spaziotempo curvo, dove la distanza minima non è più rappresentata da una linea retta.

Tale considerazione è in realtà meno bizzarra di quanto possa apparire, e due esempi concreti ci aiuteranno a capire come sia anzi abbastanza ovvia. Supponete di muovervi lungo una superficie curva e di dover andare da un punto A a un punto B, così come illustrato nella Figura 3.7.

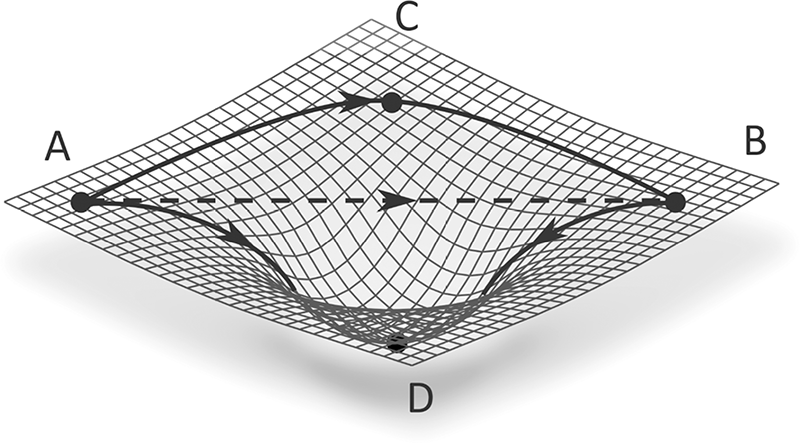
Fig. 3.7 In uno spaziotempo curvo una linea retta non è la traiettoria più breve per connettere due punti (ossia una geodetica). Nel caso in figura, il tragitto A-C-B rappresenta la geodetica tra A e B.

Potreste trovarvi in una situazione del genere durante una passeggiata nel Carso triestino, attività cui personalmente mi dedico appena ne ho tempo: lì avvallamenti di questo tipo sono molto frequenti e sono chiamati doline. Come ovvio, non potreste raggiungere B da A in linea retta – a meno di volare, ma considereremo questo caso nell’esempio successivo – e sareste invece costretti a seguire la superficie del terreno attraverso il percorso A-C-B o quello A-D-B, scegliendo il più breve e meno faticoso. Supponiamo, per fissare le idee, che sia il primo (anche se in condizioni diverse potrebbe essere il secondo): ecco, A-C-B rappresenta la geodetica tra A e B, ossia la curva che quando percorsa misura la distanza più breve tra i due punti.⁵

Per il secondo esempio ci basterà pensare alle rotte che seguono gli aerei o le navi per spostarsi da un punto a un altro del nostro pianeta. Anche esse rappresentano infatti delle geodetiche, visto che sono calcolate per minimizzare i costi di carburante e tracciano quindi la distanza più breve tra i due punti. Tuttavia, siccome aerei e navi sono comunque costretti a muoversi lungo la superficie curva della Terra, queste geodetiche non possono essere linee rette: devono per forza essere archi di curva, ossia le geodetiche di uno spaziotempo curvo. Ciò ha un’implicazione a cui è importante fare attenzione: abbiamo visto che è possibile approssimare localmente uno spaziotempo curvo con uno spaziotempo piatto; per lo stesso principio gli aerei e le navi sembreranno muoversi lungo traiettorie che appaiono come rette su piccola scala, ma che si rivelano curve su scale confrontabili con il raggio di curvatura terrestre.

La seconda conseguenza importante è invece legata in maniera più stretta all’astronomia, le cui osservazioni ci dicono che l’universo è fondamentalmente vuoto, a eccezione di concentrazioni locali di materia che si manifestano sotto forma di pianeti, stelle, galassie, ammassi di galassie e così via. Perciò nello spaziotempo che descrive il nostro universo ci sono vaste regioni – di gran lunga dominanti in volume – che sono pressoché piatte. Lì gli oggetti dotati di massa si muovono lungo linee rette che rimangono parallele se inizialmente parallele. In zone molto più limitate e rare, dove è presente materia in maniera rilevante, lo spaziotempo è invece curvo e la traiettoria degli oggetti dotati di massa non potrà essere rettilinea: percorsi che partono come paralleli dovranno necessariamente divergere o convergere.

Sulla scorta di queste considerazioni, potremo «facilmente» realizzare strumenti che ci consentano di verificare se lo spaziotempo sia, in effetti, piatto o curvo, anche senza ricorrere all’ausilio di lenzuoli e palle da bowling. «Basterà» prendere piccoli oggetti dotati di massa, ad esempio dei microsatelliti, e lanciarli verso un corpo celeste abbastanza lontano – come Proxima Centauri, che è la stella più vicina a noi dopo il Sole e dista solo 4,24 anni luce – facendo attenzione che le loro traiettorie siano inizialmente parallele. A questo punto sarà sufficiente controllare la separazione tra gli oggetti quando essi avranno raggiunto la destinazione, nel nostro caso dopo circa 270.000 anni (assumendo che si muovano alla massima velocità raggiunta finora da un satellite artificiale). A seconda che la separazione sia diminuita o aumentata rispetto a quella iniziale, sapremo se durante il tragitto avranno incontrato regioni di spaziotempo con curvatura positiva o negativa.

Basta un minimo di realismo, però, per capire che questa proposta sperimentale – per quanto concettualmente corretta – è irrealizzabile in pratica: in sostanza si tratta solo dell’idea astrusa di un fisico teorico. Per nostra fortuna, già cento anni fa Einstein suggerì un esperimento simile a livello concettuale e fisicamente realizzabile anche per la tecnologia di quei tempi. Anzi, proprio attraverso quell’esperimento convinse anche i più scettici della correttezza della sua bizzarra teoria della gravitazione.

Per capire meglio cosa propose Einstein dobbiamo tornare alla sua equazione sull’equivalenza tra massa ed energia, ossia l’espressione (3.II). Essa ci permette di dedurre che, se in uno spaziotempo curvo il moto di un oggetto dotato di massa non è rettilineo, lo stesso varrà comunque per il moto di un oggetto privo di massa, ad esempio un fotone. In altre parole, neanche un raggio di luce che si propaghi in uno spaziotempo curvo potrà procedere in linea retta: sarà costretto a seguire una linea curva. È bene notare che un raggio di luce si muove sempre lungo una geodetica – ossia una linea di separazione minima – ma essa sarà una linea retta solo in uno spaziotempo piatto, e sarà invece una linea curva in condizioni più generali di uno spaziotempo curvo.

I fotoni, rispetto all’uso dei satelliti, offrono inoltre due vantaggi: sono molto più veloci di qualsiasi oggetto dotato di massa (viaggiano infatti alla massima velocità consentita) e sono emessi in abbondanza da corpi celesti come Proxima Centauri. Tutto quello che dobbiamo fare, quindi, è utilizzare dei telescopi per intercettare questi fotoni e dedurre se la loro traiettoria sia stata modificata o meno dalla presenza di curvatura.

È esattamente questo che Einstein propose circa cento anni fa con il famoso esperimento dell’eclissi solare totale del 1919, il cui funzionamento di base è mostrato nella Figura 3.8.

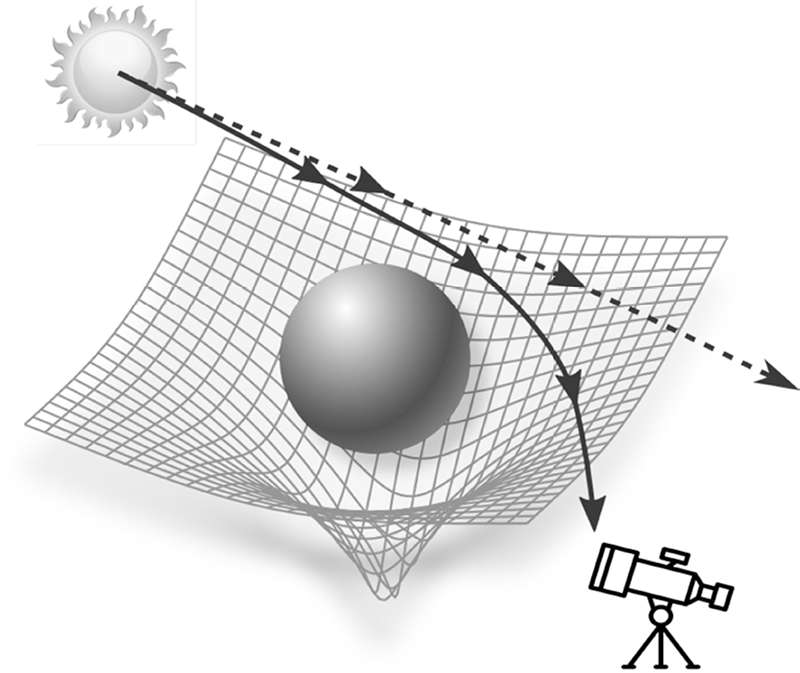
Fig. 3.8 Una delle più importanti predizioni di Einstein è che la luce non può propagarsi in linea retta in uno spaziotempo curvo. Ne consegue che è possibile osservare corpi celesti anche quando sono nascosti da altri oggetti in primo piano.

In sostanza, Einstein fece un’osservazione a dir poco sagace: se un raggio di luce viene deflesso dalla presenza di un oggetto massiccio – ad esempio il Sole – che curva lo spaziotempo e tende ad «attirarlo» a sé, allora in linea di principio è possibile «vedere» anche ciò che sta dietro quell’oggetto!

Ovviamente la capacità di deflettere la traiettoria altrimenti rettilinea di un raggio di luce dipende dall’intensità della curvatura prodotta dal corpo celeste (e quindi, come vedremo nel prossimo capitolo, dalla sua massa e dal suo raggio). Facendo alcuni conti con una versione approssimata delle sue equazioni, Einstein concluse che non si potevano vedere oggetti posizionati esattamente dietro il Sole, ma la curvatura generata dalla nostra stella era sufficiente a mostrarci oggetti posti a ridosso della sua superficie proiettata.

Rimaneva un solo problema da risolvere: il Sole è la sorgente di luce dominante intorno a noi, ed è quindi impossibile identificare il piccolo contributo in luminosità di una stella che si trovi nei pressi del suo bordo: per riuscirci bisognerebbe «spegnerlo». Per nostra fortuna non si può fare, ma è in sostanza ciò che accade durante un’eclissi totale; in quel caso, infatti, la luce proveniente dal Sole è praticamente soppressa e si possono scorgere anche oggetti celesti vicini al suo disco. L’esperimento suggerito da Einstein consisteva quindi nell’osservare un’eclissi solare totale da una posizione ottimale e determinare quali tra le stelle vicine al suo bordo – e in teoria invisibili perché coperte – fossero in realtà visibili.

Tralascio qui i dettagli storici dell’affascinante spedizione condotta dall’astronomo inglese Sir Arthur Eddington, grande ammiratore di Einstein nonché uno dei pochi sostenitori iniziali della teoria della Relatività Generale. Le osservazioni realizzate da Eddington il 29 maggio 1919 sull’isola Príncipe – al tempo territorio portoghese, ora parte della Repubblica Democratica di São Tomé e Príncipe, un arcipelago atlantico posto nel golfo di Guinea – rivelarono che era in effetti possibile misurare una deflessione della luce prodotta da stelle lontane, pari a circa 1,75 secondi d’arco. La misura di un fenomeno fisico ignorato dai principi della gravitazione newtoniana, ma previsto dalla rivoluzionaria Relatività Generale, rappresentò la spallata finale alla teoria di Newton e la consacrazione delle «bizzarre» idee discusse in questo capitolo: spaziotempo, energia, materia, curvatura… Idee che, a quanto pare, non erano poi così bizzarre!

La previsione del fenomeno appena descritto – vale a dire l’impossibilità per la luce di propagarsi in linea retta all’interno di uno spaziotempo curvo – è una delle più utili nella teoria del geniale fisico tedesco, tanto da essere stata scherzosamente ribattezzata «il regalo di Einstein all’astronomia». Il perché è facile da comprendere; al pari del Sole, infatti, qualsiasi oggetto astronomico può agire da lente gravitazionale: deflettere la luce proveniente da altri oggetti e distorcerne l’apparenza, ma anche amplificarla, rendendo dunque visibili oggetti la cui immagine sarebbe altrimenti troppo debole. Proprio come fa una lente che concentri in un punto – il suo fuoco – un fascio di raggi di luce paralleli.

È sfruttando questi interessantissimi effetti di deflessione che gli astronomi possono ottenere immagini multiple e amplificate di centri galattici posti a enorme distanza da noi, e ciò ha segnato la nascita di quella che è nota come astronomia da lenti gravitazionali (in inglese: gravitational lensing astronomy).

Oltretutto, tale fenomeno può verificarsi anche quando l’oggetto che agisce da lente non è visibile perché non emette luce, sebbene abbia una massa a volte considerevole. In questo caso, la presenza dell’oggetto-lente può essere desunta dalla curvatura dello spaziotempo che esso induce intorno a sé, e che si manifesta attraverso la distorsione delle immagini di altri oggetti lontani. Un esempio classico di questo tipo di lente è rappresentato dalla cosiddetta materia oscura, che non emette luce ma la cui presenza è comunque rivelabile attraverso l’azione gravitazionale prodotta su scala galattica: la curva di rotazione delle galassie a spirale ci rivela infatti come la materia oscura sia presente in pressoché tutte le galassie, sotto forma di enorme alone sferico.

La Figura 3.9 illustra in maniera schematica come la presenza di materia oscura non visibile produca comunque una curvatura dello spaziotempo locale, che genera immagini multiple e distorte di galassie lontane. In questo caso, analizzando il modo in cui le immagini degli oggetti celesti vengono distorte, si possono utilizzare le osservazioni per studiare le proprietà della materia oscura, quali la sua massa e distribuzione.

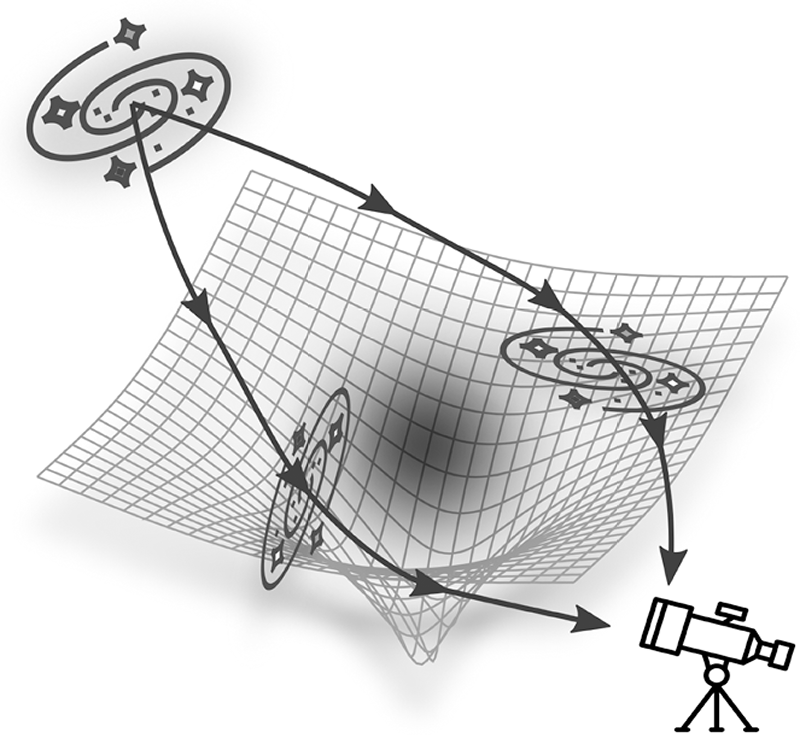
Fig. 3.9 Oggetti astronomici compatti possono agire da lenti gravitazionali e concentrare le emissioni di sorgenti lontane o produrre immagini multiple. Le lenti gravitazionali possono anche essere invisibili, come nel caso della materia oscura.

Ma non finisce qui: nel capitolo 7 vedremo come la deviazione di un raggio di luce in prossimità di una sorgente di forte curvatura dia vita a fenomeni bizzarri quali immagini doppie e triple, amplificazioni e assorbimenti. Nello stesso capitolo, inoltre, vi spiegherò in che modo sia possibile produrre l’immagine di un buco nero, come ha fatto il mio gruppo di ricerca in collaborazione con l’Event Horizon Telescope.