18. Fermat, el príncep dels amateurs

Ah, l’olor de la mimosa!

Al rerepaís del Var, a dalt a Bòrma, les mimoses incendiaven el paisatge. Tot un esdeveniment, la primera olor després del gran buit olfactiu de l’hivern! Ara la natura tornava a fer olor. Les boletes vellutades feien pessigolles a la galta del senyor Ruche.

I tot perquè, en passar pel davant de la floristeria del carrer Lepic, havia ficat el nas en un ram que estava en un gran vas de gres. Li hauria vingut molt de gust baixar. Baixar, pel senyor Ruche, volia dir anar al Mediterrani. En comptes d’un bitllet de tren cap a la costa, va comprar el ram i el va regalar a la Perrette, que el va col·locar sobre la caixa de la llibreria, on durant uns quants dies va tenyir la botiga de groc.

Les equacions algèbriques havien esgotat el senyor Ruche. Pràcticament tant com si les hagués hagut de resoldre personalment. Va sentir la necessitat de fer una pausa. Descans durant uns quants dies. Ni Biblioteca de la Selva, ni Grosrouvre, ni Manaus, ni fidel company. Sentia la necessitat de fer vacances. VACANCES! Era una paraula que havia desaparegut del seu vocabulari. Realment ara treballava. I si treballava, tenia dret a fer vacances. Però cinc setmanes no, sobretot. No n’hauria sortit viu.

No havia tornat a veure l’Albert des del pont de les Arts. El va avisar i ell de seguida ho va acceptar. L’endemà tenia el dia lliure i podien fer com abans de tot aquest daltabaix: passarien el dia tots dos sols. Llàstima que encara no fes prou calor per a un pícnic. Però ja trobarien una fonda que els anés bé.

Cap a les deu, el 404 es va aparcar davant dels Mil i un Fulls. El gris metàl·lic de la carrosseria acabada de pintar brillava, els plats de les rodes eren com miralls. «Els cotxes són com les persones», repetia l’Albert, «com més vells es fan, més s’han de cuidar. Si hi vas amb compte, canvi d’oli, greixatge, bugies, antioxidant, duren toooota la vida!».

Els preparatius per a la marxa no havien passat desapercebuts a les velletes que anaven al mercat. En les mirades dures que els feien no hi havia ni condemna ni retret. Sinó enveja. Si haguessin gosat, haurien abandonat allà mateix cistells i cabassos i s’haurien ficat al cotxe amb aquells dos vells per passar un dia inesperat.

Per les vies perifèriques, el 404 de seguida va ser a l’autopista de l’oest. Van sortir a Mantes-la-Jolie, van agafar la nacional en direcció Vernon. Just abans de la pujada de Rolleboise, van girar i van continuar al llarg del Sena. L’Albert va afluixar: una resclosa travessava el riu. Una xalana, per fortuna, entrava als canals d’enllaç. L’Albert va aparcar de cara al Sena i, sense deixar el cotxe, amb les finestres obertes, van observar a través del parabrisa immaculat el pas laboriós de la barca. Feia el mateix temps que el dia del pont de les Arts i començaven a tenir gana.

La carretera deixava la vora de l’aigua i s’enfilava per una pujada cap a l’altiplà que dominava el riu. El 404 va travessar un bosquet; els rètols indicaven «pas de salvatgines». L’Albert va afluixar. El bosc es va acabar de sobte. Vista panoràmica del paisatge fins que, sense avisar, la carretera topava amb el Sena. En aquell punt, com en un conte de fades, a la vora de l’aigua hi havia una fonda vella tota de vidre amb el sostre de palla: Au Rendez-vous des Canotiers.

Hi van entrar. La sala era buida. Ni un client. ¿Era un lloc encantat? Una escalforeta suau entelava lleugerament els vidres. La vista aguda del senyor Ruche va descobrir un cartellet.

—Llatí!, —va exclamar—. «Curva Sequana, mens recta».

El cigarret de l’Albert va trontollar.

—«El Sena fa corbes, la nostra ment és recta» —va traduir el senyor Ruche mentre un home jove, que havia sortit d’un bar petitó de l’altra banda de la carretera, entrava amb el menú a la mà. Van haver de rumiar tant per triar el menjar com per saber on seure.

A més davant per davant, a l’altra banda del Sena, hi havia una església preciosa. L’havien fet una mica enlairada perquè es pogués veure bé des de l’altra riba. Com en un somni, el senyor Ruche, tot i que estava segur que no hi havia estat mai, la va reconèixer. Ho va confessar en veu baixa a l’Albert, tot i que a la sala del restaurant no hi havia ningú més. L’Albert va parlar dels falsos records: deixar un client en una adreça on no has estat mai i tanmateix… reconèixer una persona que veus per primer cop, reviure un fet que sembla que ja hagis viscut… Com tothom, el senyor Ruche coneixia aquesta manera de domesticar les novetats que de vegades té l’esperit, que redueix el que és inèdit a una simple repetició.

Parlant de coses inèdites, va preguntar a l’Albert si últimament no havia conegut cap país nou. «Ciutats noves!», va rectificar l’Albert, «els països no existeixen, les ciutats són les úniques que tenen una realitat», etc.

Havia fet força voltes fins a l’aeroport. «Quan París és una ciutat trista, és hora de viatjar». Entre les ciutats que havia conegut, n’hi havia una que l’havia impressionat especialment. Perquè no tenia una realitat, sinó dues: Johannesburg. Havia carregat al taxi negres i blancs, alternativament. La constatació era clara, no vivien a la mateixa ciutat! Vivien en dos mons diferents. Això no li havia passat mai, un tall tan gran! I això que no havia pas parlat amb els habitants dels townships.

Una muntanya de carbó va passar arran del restaurant, un remolcador llarg com un tren, ple a vessar, frenava amb tota la força dels motors per agafar un dels revolts més difícils de tot el trajecte de París a Rouen.

El pollastre era de pagès; els cargols, de Borgonya; el vi rosat, del Tarn. La temperatura era molt agradable. Darrere els vidres, es trobaven com flors en un hivernacle.

L’endemà, el senyor Ruche estava en forma. Tot i així va decidir no fer res. El dia va ser molt llarg. Va aterrar a la llibreria unes quantes vegades. La primera va ser per consultar un llibre sobre els impressionistes. Va acabar trobant el que buscava: l’església que es veia des del Rendez-vous des Canotiers era la de Vétheuil pintada per Monet. Pintada des d’un bot-taller amarrat ben bé al costat del lloc on havien dinat.

La mimosa, al gerro sobre la caixa de la llibreria, encara feia molt bona olor. El senyor Ruche donava voltes. Es va avorrir molt i es va preguntar com s’ho feia —abans de les cartes i tota la resta— per passar dies sencers sense morir-se d’avorriment.

A la llista d’en Grosrouvre, el nom següent era Fermat. L’autor d’una de les dues conjectures que assegurava que havia resolt! O sigui que era un matemàtic capital en la història d’en Grosrouvre. Pierre Fermat.

Maquinalment, el senyor Ruche va escriure «πR», igual que en Grosrouvre a la primera carta. Després va escriure «Fermat» a sota i ho va encerclar tot amb un sol cop de ploma.

La similitud entre els dos Pierre s’acabava aquí. Fermat tenia el front ample, un clotet a la barbeta i cinc fills. La posició de llibreter a Montmartre era difícilment comparable a la de conseller al Parlament de Tolosa, comissari de greuges i conseller a la Cambra d’Edictes. Però pel que feia a l’últim títol, «conseller a la Cambra d’Investigacions», el senyor Ruche es va sentir en la mateixa sintonia.

Va fer córrer la cadira de rodes fins als prestatges de la Secció 3: «Matemàtiques occidentals, del 1400 al 1900».

Primera sorpresa, només hi havia una obra de Fermat: les Obres completes. Cinc volums. El senyor Ruche va agafar la fitxa del primer volum. En realitat n’hi havia unes quantes.

Atordit per aquest desbordament, se li va escapar: «I això que només feia matemàtiques en hores perdudes!».

Amb aquest simple resum va entendre que li seria difícil acostar-se a Fermat evitant Pascal i Descartes. El primer li era tan desconegut com familiars li eren els altres dos. Però només en coneixia els escrits filosòfics, no pas els treballs matemàtics. Era una bona oportunitat per completar aquest coneixement coix.

El senyor Ruche es va afanyar a fullejar l’obra. Cartes i més cartes! Efectivament, la major part dels cinc volums eren cartes dirigides als grans matemàtics i als intel·lectuals de tot Europa: Mersenne, Carcavi, Frenicle, Pascal, Descartes, etc.

Una obra per correspondència! El senyor Ruche va començar a entendre el que podia haver atret en Grosrouvre de Fermat. Tots dos eren «amateurs». Ell tampoc no havia escrit cap obra. També estava retirat dels grans centres de producció matemàtica, tot i que, naturalment, la Tolosa del segle XVII no era el Manaus del segle XX i el sud-oest de França no era l’Amazònia. En canvi hi havia una cosa que no els feia gens semblants: Fermat divulgava el que feia pràcticament en directe. Exactament el contrari del secret que havia decidit mantenir en Grosrouvre. De cop i volta el senyor Ruche es va preguntar si en Grosrouvre no havia intercanviat correspondència amb altres matemàtics sobre els seus treballs. Fins aleshores no hi havia res que ho fes pensar. El senyor Ruche va continuar la lectura de la fitxa.

Fermat és un continuador-fundador —escrivia en Grosrouvre—. A les seves cartes no hi ha cap rastre de proclamacions escandaloses. No tenia el propòsit, com Descartes, de revolucionar les matemàtiques. I tanmateix les va transformar radicalment. Com a continuador d’Apol·loni, va fundar la geometria analítica. Com a continuador de Diofant, va fundar la teoria dels nombres. Com a continuador d’Arquimedes, va establir les bases del càlcul integral.

¿Per on es podia entrar a la mola «πR Fermat»?

El senyor Ruche va agafar el full on havia dibuixat el cercle i es va posar a apuntar les grans línies del que acabava de saber.

Fermat, plantificat al mig del segle XVII, es presentava com una veritable rosa dels vents matemàtica. En sortien quatre direccions, cadascuna de les quals donava a un camp immens. Això li va recordar Bagdad, la Ciutat Rodona, amb el palau del califa al mig, d’on sortien les quatre artèries que desembocaven a les quatre portes obertes a la muralla. Va recordar que aquestes portes eren l’única manera de penetrar a la ciutat.

El senyor Ruche ho va entendre: no podia penetrar en Fermat si no agafava aquestes quatre direccions. Segons l’adagi, sempre en necessitem dos de més petits, de manera que va demanar ajut als bessons. Els va ensenyar la rosa dels vents i els va preguntar de quines direccions es podien encarregar. Però allà on el senyor Ruche havia fet servir el plural, ells només hi van voler sentir el singular.

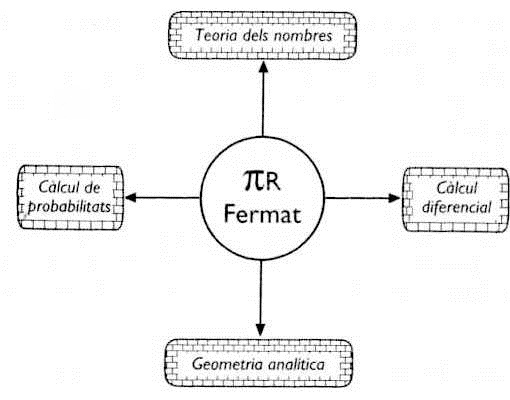
Sense dubtar ni un moment, Jonathan-i-Léa van triar l’oest: el càlcul de probabilitats. La porta es va tancar amb un soroll sec i el senyor Ruche es va quedar sota el pes de les tres direccions que li havien quedat a sobre.

La porta es va obrir. Era la Léa. Bona noia! Ara l’anava a alliberar d’una segona direcció. La Léa es va acostar, va passar de llarg, es va plantificar davant la BDS, en va treure les obres de Pascal i va tornar a marxar.

En homenatge a la mimosa que a hores d’ara devia estar pansida sobre la caixa de la llibreria i devia haver perdut el perfum, el senyor Ruche va decidir començar pel sud.

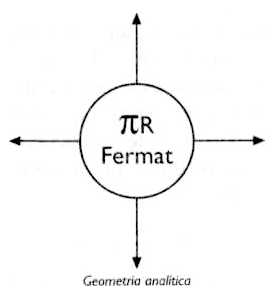
De les quatre fletxes de la rosa dels vents, va passar als dos eixos de la geometria analítica.

Grosrouvre havia escrit:

El principi de la geometria analítica cap en una frase: l’equació d’una corba permet conèixer totes les propietats de la corba —havia escrit en Grosrouvre—. Aquest descobriment, que Fermat i Descartes van fer amb pocs anys de diferència, amb independència l’un de l’altre, va ser anomenat geometria de les coordenades.

El senyor Ruche va saber immediatament de què es tractava i el va sorprendre que en parlar d’aquest tema a l’institut no haguessin citat mai el nom de Fermat. Però Descartes sí, mare de Déu! El preferit dels profes, fins i tot n’havien fet un adjectiu: el punt de referència era cartesià; i les coordenades, cartesianes.

Maquinalment es va posar a dibuixar un eix horitzontal amb la mà, moguda per un automatisme provocat per tants anys d’escola, «x’x, eix de les abscisses», va murmurar. Després va fer l’eix vertical: «y’y, eix de les ordenades», va continuar murmurant. A la intersecció hi va posar un gran 0: «origen de les coordenades».

—A, 8.

—Enfonsat! Guerra de vaixells!

Si n’hi havia jugat vegades i vegades, a batalles navals, quan era petit! Era el joc que preferia. Un joc per a nens assenyats, que no era gens car. Només calien dos llapis, dues gomes i dos fulls de paper, però no pas de qualsevol classe, havien de ser de quadrets!, arrencats de les llibretes d’escola. Ell, que no sabia nedar, patia amb el soroll de l’aigua i s’espantava així que una onada esquitxava l’escullera de Camaret, on havia passat uns quants dies feia un piló d’anys, vivia batalles de Trafalgar tòrrides, interminables lluites a l’Atlàntic. Era successivament capità espanyol o filibuster holandès, almirall de la Royal Navy o pirata bretó, i lliurava combats a tots els mars del planeta. ¿Un joc per a nens assenyats? Les bales de Tartaglia, de trajectòria parabòlica, anaven a petar al pont i obrien vies irreparables d’aigua. Enfonsat! Les desferres suraven en els fulls quadriculats, farcits de creus.

Déu meu, ¿quina hora era? El senyor Ruche s’havia adormit.

Alguna cosa li fregava el crani. Amb un moviment delicat de bec, el Nofutur remenava suaument entre els cabells blancs.

Quin ocellot! Parlava com Jaurès i era afectuós però estrany. Tenia alguna cosa que el senyor Ruche no acabava d’entendre. Posat sobre el secreter, a pocs centímetres de la seva cara, li clavava els iris d’un negre profund, rodejats de groc. La cicatriu que tenia al mig del front blau li donava un aire de Pierrot el Boig just abans de fer-se volar el cap. ¿De quants combats s’havia salvat?

El senyor Ruche li va rascar el clatell, just al mateix lloc on havia vist que li feia en Max. «En el sentit de les plomes!», havia precisat el nen. Després va sucar la ploma de vidre al tinter amb un somriure maliciós als llavis i, sota el dibuix dels eixos de coordenades, a la llibreta de tapes dures, va escriure:

Els punts de la quadrícula es localitzen per les coordenades, igual que els vaixells a alta mar. ¿Com es pot indicar una posició a algú que no està en condicions de veure-la? La localització d’un punt en el pla quadriculat és el seu nom. Igual que les persones per viure, els punts del pla necessiten referències!

En Grosrouvre indicava que els eixos de coordenades es podien situar a qualsevol lloc i que s’hi podia fixar qualsevol llargada com a unitat. També indicava que les coordenades negatives estaven molt mal vistes, especialment per Descartes. Fins que un anglès, John Wallis, els va donar dret de ciutadania. Havia escrit a la fitxa:

Igual que Viète, Wallis va ser un gran desxifrador de cartes secretes.

Una altra referència a les cartes xifrades! Hi havia una nota dedicada a Wallis. Defensava Cromwell i el Parlament en contra del rei Carles I i va desxifrar els missatges secrets enviats pels reialistes i que havien anat a parar a mans dels parlamentaris. Però es va oposar a l’execució del rei. «Es veritat», va pensar el senyor Ruche, «pel que fa a les execucions de reis, els anglesos van ser els primers! I pel que fa a la República també! Van proclamar-ne una, tot i que no va durar gaire, ben bé un segle abans que nosaltres! Un personatge ben curiós, aquest Wallis. Un home que fa tots els estudis a Cambridge i el fan professor… a Oxford!».

Matemàtic, lògic, gramàtic i metge. Aquest també! També es va interessar pel Postulat Número 5, i a més va traduir les obres de Nàssir-ad-Din at-Tussí. Si en feia de dies! Hayyam, Alamut, el carretó de llibres… Wallis va ser el primer savi que es va atrevir a defensar públicament la tesi de la circulació de la sang que acabava de descobrir el seu compatriota William Harvey. Va obrir la primera escola per a sordmuts de la Gran Bretanya.

En Max no havia anat mai a una escola de sordmuts. La seva sordesa no li havia afectat mai la capacitat de paraula. Tenia una manera molt personal de parlar. Lenta, intensa, pronunciant cada paraula, respectant els silencis. I tenia una manera molt personal de sentir, en Max l’Eòlic!

Les coordenades negatives encara eren lluny. El senyor Ruche va passar revista. Tal com succeeix de vegades, quan tornem a pensar en alguna cosa després de no haver-hi pensat durant molt de temps, va copsar amb una claredat nova el valor del descobriment de Fermat i de Descartes. Aquells eixos que feien tan mala pinta eren els agents d’una veritable «desnaturalització» de l’espai. En aquesta òptica, era la paraula justa, un ésser geomètric era «vist» com un ésser algèbric: el punt M es metamorfosava en una parella de nombres (x,y)! Era realment una revolució, que acabava de foragitar la geometria pura.

I la corba geomètrica igual. L’equació es convertia en el seu nom algèbric. Funcionava com un dispositiu que permetia produir a voluntat el nom de cadascun dels punts de la corba.

I el més fort encara no havia arribat: el coneixement d’aquesta equació permetia descobrir totes les propietats geomètriques de la corba! I el senyor Ruche va retrobar, amb emoció, la famosa representació gràfica de quan era jove!

Fermat havia elaborat aquest sistema per oferir a la vella geometria les riqueses noves de l’àlgebra. Era indiscutible que per ell la geometria continuava essent el centre de tot l’edifici matemàtic. En canvi per Descartes l’àlgebra era una ciència d’una magnitud molt més general que la geometria, que, a partir d’aleshores, s’havia de tractar com una ciència de pur càlcul.

Els grecs havien fet de les matemàtiques una ciència geomètrica. Al segle XVII es van convertir en una ciència algebraica. Descartes va instal·lar, al tron encara calent de la geometria, l’àlgebra triomfant.

Després de la revolució, la libació. El senyor Ruche es va fer el te de les cinc. Aquesta vegada va triar un Earl Grey.

Descartes va escriure molt. Però als prestatges de la BDS hi havia poques obres. La Geometria, en un volum enquadernat a part. Després el Discurs del mètode. Per conduir bé la raó i buscar la veritat en les ciències. I finalment les Regulae ad directionem ingenii.

El senyor Ruche se sabia de memòria el començament d’aquesta última obra: «Els actors que han de sortir a l’escenari, per no deixar veure la vermellor de la cara, es posen una màscara. Igual que ells, quan he de pujar en aquest teatre del món on fins ara només havia estat espectador, ho faig emmascarat».

El senyor Ruche va treure la Geometria del prestatge. El llibre era increïblement prim. De tots els assaigs, sens dubte era la millor relació «grau de celebritat / quantitat de pàgines».

En aquest grapat de pàgines, Descartes proposava un veritable programa en cinc punts. Qualsevol persona que es trobés davant d’un problema de geometria havia de seguir les indicacions següents:

El senyor Ruche, admiratiu però no entusiasta, va entendre que l’extraordinària eficàcia de la geometria analítica venia d’aquest programa. S’havien acabat les construccions pas per pas. Ara n’hi havia prou determinant l’equació i ja teníem la figura traçada de cop.

Al Discurs del mètode, Descartes afirmava: «No podem prescindir d’un mètode per posar-nos a buscar la veritat de les coses». Per ell, l’àlgebra no era una ciència, era un mètode. Un mètode universal. El senyor Ruche va recordar que mètode prové de meta-odos. Odos significa «el camí»! El mètode és un camí que porta a un objectiu. Si el segueixes.

¿Quin mètode havia seguit ell durant la investigació?

¿Almenys havia pensat a seguir algun mètode? Havia buscat cap aquí i cap allà, sense programa, comportant-se com un gosset. ¿Quin mapa indicava el camí que l’havia de conduir a l’objectiu?

Si en Jonathan i la Léa havien triat l’oest a la rosa dels vents de πR Fermat era perquè cada vespre, a les golfes, s’havien acostumat a fugir en aquella direcció. Cap a Manaus, a l’altra banda de l’Atlàntic, remuntant el riu Amazones.

En Jonathan va buscar la lluna; es va haver d’enfilar sobre el llit per descobrir-la fregant el límit del vidre de la lluerna. Entrava en la primera fase, «en quadratura» amb el sol.

La lluna en quadratura és el moment en què, als mars i als oceans del planeta, les marees són més baixes. Tot i això, al riu Amazones, es va deixar sentir a més de mil quilòmetres cap amunt, a l’interior del bosc. No va arribar fins a Manaus, però sí que va arribar a Santarém.

Tot i que el cor li bategava de valent, Henry Alexander Wickham va respondre plàcidament al cap de la duana brasilera que inspeccionava la nau: «M’enduc uns quants espècimens delicats que d’aquí a uns quants dies jo mateix plantaré als hivernacles del jardí botànic de Kew». Tranquil·litzat sobre el contingut del carregament, el cap de la duana va baixar de la nau.

Wickham es va precipitar a la bodega i va mirar amb amor les dotzenes de coves estibats amb cura. Contenien un tresor. Un tresor que seria la fortuna dels anglesos i havia de provocar la ruïna de Manaus. El vapor es va allunyar de Santarém, va arribar a Belém i es va endinsar a l’oceà. També es deia Amazones i també es dirigia a Liverpool. Aquest viatge es duia a terme al final del mes de maig de 1876, just un quart de segle després del de Wallace.

No hi va haver cap tempestat ni cap incendi durant la travessia.

¿Quines eren les plantes delicades destinades al jardí botànic de Kew? No eren plantes, sinó llavors; no eren delicades, sinó extraordinàriament precioses, i no n’hi havia unes quantes, sinó setanta mil. Curosament dipositades entre capes de fulles seques de plataners salvatges, ben col·locades a l’abric en dotzenes de coves de fibra de canya de sucre. Setanta mil llavors d’hevea brasiliensis! El millor arbre de cautxú de l’Amazònia, el més resistent i alhora el més productiu en làtex.

L’exportació d’aquelles llavors no estava permesa. L’engany de Wickham havia tingut èxit, per desgràcia per a Manaus.

Uns quants decennis més tard, les llavors de Wickham, trasplantades als boscos de Malàisia, van produir grans plantacions d’hevees de les quals el làtex rajava a dojo. Això va ser la ruïna de Manaus. La ciutat es va despoblar i es va arruïnar.

Els castells importats d’Europa, pedra per pedra, i tornats a muntar al llarg de les grans artèries. El mercat cobert, construït per Gustave Eiffel a Anglaterra, transportat a l’Amazònia i reconstruït a Manaus. Els carrers amb llambordes vingudes directament de Lisboa. El primer tramvia elèctric de tot Amèrica del Sud. El telèfon en plena selva, la il·luminació elèctrica des del final del segle XIX. I l’òpera! Amb mil quatre-centes localitats! L’òpera on havia cantat Caruso en persona. Amb teules envernissades procedents d’Alsàcia, marbre importat de Carrara, marqueteria de França, ferro forjat d’Anglaterra, aranyes d’Itàlia, i les onades de mosaic que adornaven la plaça i es venien a morir al peu de les columnes de marbre de l’entrada de l’Òpera…

S’havia acabat Manaus!

En llegir aquestes línies, en Jonathan es va preguntar si no podia ser que aquesta història hagués influït en Grosrouvre. Si no podia ser que s’hagués dit: «Vet aquí el que passa si et deixes desposseir del que has produït!». ¿El robatori de les llavors l’havia convençut que calia conservar secret el que havia creat? Conservar per a un mateix el secret de la selva. «Segur, segur», va pensar en Jonathan. «Però una llavor no és una demostració. ¿Una demostració es trasplanta?».

La Léa el va sacsejar:

—Te’n faig un resum.

Mentre en Jonathan, al seu llit, vivia el final de Manaus, la Léa, al seu, s’havia preocupat pels inicis de Pascal, a qui s’atribuïa l’inici de les «probabilitats».

—Pascal tenia un pare, dues germanes i un cunyat. Mare, no; s’havia mort quan ell tenia tres anys. Jacqueline, la gran, es va fer monja i Gilberte, la petita, es va convertir en la senyora Périer. Étienne Pascal, el pare, era el tipus exacte de pare de nen prodigi! Com el pare de Mozart, va insistir a ensenyar-li tot ell. De manera que el petit Blaise no va anar a l’escola, no va tenir amiguets per fer el ximple. I no va tenir més mestre que el seu pare.

—Terrible per a la psicologia, això —va exclamar en Jonathan.

—I tant! Étienne era president de la sala d’ajudes de Clermont i matemàtic. Fins i tot va inventar una corba que en porta el nom, el Cargol de Pascal pare, que és una concoide, ¿m’entens? Una concoide que, en un cas particular, és un oval de Descartes i en un altre cas, una… trisectriu! Tot es barreja, podríem dir. ¿Em segueixes o no?

—Bec tot el que em dius. Però no tinc gaire set.

—Pascal pare va prohibir al fill que fes geometria, perquè tenia por que li cansés el cap. ¿Què va passar?

—Que va fer geometria d’amagatotis! I a més, quan en feia, l’excitava perquè tenia por que el pare ho descobrís!

—Exacte! Quan Blaise va tenir l’edat d’en Max, va redescobrir, tot sol, com una personeta gran, que la suma dels angles d’un triangle era igual a 180 graus! La trenta-dosena proposició d’Euclides! Vaja, ho explica la seva germana. I no sabia ni el nom d’Euclides, el seu pare l’hi havia amagat. Quan aquest pare va saber el que acabava de (re)descobrir el seu fill, va plorar d’alegria i va estar tan content que li va regalar… els tretze llibres dels Elements d’Euclides.

—Caram!

—Atenció, no funciona sempre, això. Hi ha pilons de pares que encara que han prohibit als seus fills que fessin matemàtiques, no han pogut impedir que els fills no en fessin. Les mateixes causes no sempre produeixen els mateixos efectes.

—Abel, vint-i-un anys; Galois, divuit. I ara Pascal, dotze. Progressió decreixent. Amb tendència a 0! —va engegar en Jonathan, que es començava a posar nerviós amb la llista de genis. Va pensar: «I jo què semblo, a disset anys i sense cap idea genial!». Va continuar en veu alta—: I en Grosrouvre que vol demostrar les seves conjectures a seixanta anys! Si és veritat que se’n va sortir, em trec el barret! Una súper notícia, no tan sols pel fet d’haver-se’n sortit, sinó per haver-ho fet a seixanta anys.

—Un dia vaig llegir que un matemàtic que no ho hagi parit tot abans de fer vint primaveres no té pràcticament cap oportunitat de descobrir res d’important més endavant.

—¿Pràcticament cap oportunitat? ¿Quantes? Això són probabilitats. Ja hi acabarem arribant. Els gimnastes també, després de vint anys estan cardats.

—És clar. Les matemàtiques són la gimnàstica de la ment. I parlant de gimnàstica de la ment, aquest Blaise era una fera! A setze anys va escriure Essay pour les còniques. És a la BDS. Només se’n van trobar dos exemplars, qui sap com s’ho va fer en Grosrouvre per procurar-se’n un. A dins, Pascal demostra un teorema que va fer molt de soroll, quan va sortir. Agafa un polígon de sis costats.

—Digues un hexàgon! No s’ha de tenir por de les paraules.

—No et facis l’espavilat. Un hexàgon inscrit en un cercle. Amb sis costats, per força té tres parelles de costats oposats. Quan es tallen, tots tres punts estan en línia. Què te’n sembla.

—Malparit…

—I això només és el principi! Perquè la bona és aquesta. Va demostrar que també és veritat quan l’hexàgon està inscrit en una cònica qualsevol! El·lipse, paràbola, hipèrbole…

—¿Entens tot el que m’estàs explicant? —li va preguntar bruscament en Jonathan.

—La meitat! Una frase de cada dues.

—¿Per què m’ho expliques?

—Perquè no vull que moris essent burro.

—Vols que em mori? —en Jonathan es va estirar.

—T’ofereixo el teorema més bonic de la geometria i tu parles de tu! Escolta els noms! Aquest hexàgon, Pascal el va anomenar l’hexagram místic. I el teorema, algú el va batejar el bressol del gat.

—¿Saps què et diu el gat, en aquesta hora?

Un segon després en Jonathan roncava embolicat amb la flassada.

La Léa no veia per què no havia de fer com el senyor Ruche, que es buscava un lloc diferent cada vegada que abordava un matemàtic nou: el Louvre, l’IMA, l’Institut… La Léa en va buscar un per al seu Pascal.

En Max havia decidit afegir-s’hi. Hi va anar amb el Nofutur, que no havia sortit des de feia molt de temps. A partir de l’Òpera, van pujar pels Grans Bulevards, en sentit invers del de la circulació dels cotxes, fins a la porta Saint-Martin. Just abans, a la porta Saint-Denis, van ensenyar a en Max el baix relleu que representava la batalla de Maastricht on va morir d’Artagnan. Mentre caminaven, van intentar inútilment recordar on havien mort els altres tres mosqueters.

Tot d’una, la Léa els va parlar del carretó de Pascal! Els dos germans van fer com si fos normal i es van negar a sorprendre’s que Pascal hagués pogut fer la teoria del carretó i encara menys que hagués aportat a l’artefacte millores tècniques que s’han conservat fins avui. Malauradament, això no es trobava al CNAO, el Centre Nacional d’Arts i Oficis, on la Léa els va portar. Però hi havia un altre invent de Pascal.

El CNAO, creat durant la Revolució, està situat en una antiga abadia de la qual es conserven més que restes. En passar, van clavar un cop d’ull a l’antic refectori, d’una altura que tallava l’alè. Havia estat transformat en biblioteca. Després van penetrar a l’església. Allà hi havia avions suspesos de fils! I el famós pèndol de Foucault, que Umberto Eco havia fet servir de títol d’una de les seves novel·les semiòtiques, que en Jonathan havia llegit.

Davant d’un espai com aquest, el Nofutur no es va poder dominar. Va abandonar l’espatlla d’en Max i es va posar a voleiar i a fer una sèrie de loopings sorprenents al voltant de les ales dels avions suspesos. Amb gran alegria dels visitants, fins que va intervenir un guàrdia. Ah, si tingués un fusell!

El guàrdia va parlar i parlar. En Max no va entendre ni una paraula. Era impossible llegir-li els llavis, els sons li sortien de la boca com la carn de botifarra d’una màquina de fer carn picada. En Max odiava aquesta mena de persones, els engolidors de paraules, els ingurgitadors de puntuació. Aquesta gent el tornaven realment sord.

El Nofutur va tornar a l’espatlla d’en Max. El guàrdia els volia fotre fora. Davant la desaprovació dels visitants, però sobretot davant la mala cara d’en Max, va acceptar que el quartet continués la visita, amb la condició que el Nofutur no abandonés l’espatlla d’en Max. El Nofutur ho va prometre.

Bé havien d’anar per feina, o sigui que van tornar a Pascal. La Léa, transformada en guia, va començar a parlar-los del pare: per guanyar-se la vida, Étienne Pascal recaptava els impostos a Normandia. Una feina generosament retribuïda; com més diners reculls, més te’n quedes. No cal dir que això motiva molt. L’únic problema és que s’han de fer moltes sumes. Com que en Blaise estimava molt el seu pare, ¿què va fer? Va inventar una meravella de màquina de calcular: la Pascalina. En aquell temps en deien «una màquina aritmètica».

Tenien la màquina sota els ulls, en una vitrina. Una capsa de fusta amb sis rodes grises proveïdes de deu seccions daurades, per materialitzar les deu xifres.

—En suma, una capsa força clàssica —va comentar la Léa.

—Bravo pel joc de paraules! Vaja, suposo que la Pascalina funciona a cops de suma!

En veure la cara bocabadada de la Léa, va afegir:

—I no ho ha fet exprés, a més!

—Bravo pel joc de paraules. A més!

—¿Puc saber com s’acaba? —va insistir en Max.

—Tot el problema per calcular mecànicament és què passa quan ja has arribat a 9 i n’has d’afegir 1 —va dir la Léa—. És el problema de quants en portes.

—Com portar els que portes, és clar —va dir en Max.

—Bravo pel joc de paraules! —li va llançar en Jonathan.

En Max, capbaix, va confessar:

—No ho he fet exprés.

—Pascal es va empescar un mecanisme amb el qual ningú havia pensat abans, un «portador que salta», que traslladava les quantitats que portava.

El guàrdia d’abans, que no els havia perdut de vista, els va convidar a marxar. El museu volia tancar.

En el riu de visitants que avançava cap a la sortida, ple de somriures per al Nofutur, la Léa els va explicar com en Blaise es va convertir en empresari. Va muntar una empresa, va fer els plànols de la màquina, va contractar uns quants obrers, va patentar el procediment i va fabricar una cinquantena de pascalines. Les produïa en sèrie i les venia a cent lliures cadascuna, i va guanyar un munt de duros. Van sortir del CNAO.

—Als Pensaments —va explicar la Léa—, Pascal diu que la pascalina s’acosta més al pensament que tot el que fan els animals.

Per culpa del soroll dels cotxes, en Max no ho havia sentit bé. Va alçar el cap d’una manera que la Léa coneixia prou bé. Ho va repetir:

—Diu que la seva màquina és més semblant al pensament dels homes que tot el que fan els animals. I també va afegir: «però res del que fa no permet dir que té voluntat com els animals».

—¿I tu què en penses? —va preguntar en Max al Nofutur, que reposava dels loopings de l’església al voltant del vell avió suspès del CNAO.

Era evident que al Nofutur se li en fotia del que Pascal hagués pogut pensar dels animals. Gairebé tant com Pascal del que el Nofutur pogués pensar dels filòsofs matemàtics jansenistes del segle XVII.

Tots dos tenien raó.

Un altre avió, però aquest gros, va aterrar a l’aeròdrom de Roissy. L’home es va dirigir cap al taxi més proper. Per la finestra oberta li va preguntar:

—¿Em pot dur a París?

Sorprenentment, el xofer, en comptes de preguntar-li on anava, li va preguntar:

—¿D’on ve?

L’home va dubtar, però després va respondre:

—De Tokyo.

—No m’interessa —va respondre el xofer mentre engegava… i es tornava a aturar davant d’una altra entrada de l’aeroport, una mica més enllà.

Desconcertat, l’home es va dirigir a la fila de taxis més propera. Mentre esperava que li toqués la tanda, va veure de lluny que el taxi que l’havia rebutjat agafava uns passatgers i marxava.

Quan li va tocar, l’home va pujar en un familiar molt nou i va agafar la direcció de l’autopista del nord cap a París. Plovisquejava.

L’home no s’aconseguia apartar del pensament el xofer del taxi que l’havia engegat. De cop i volta va agafar el maletí, va marcar el codi, el va obrir, va remenar entre els papers i en va treure una carpeta. Tot just començava a examinar el document i…

—Déu meu senyor! —va exclamar.

—¿Algun maldecap, senyor? —li va preguntar el conductor mirant-lo pel retrovisor.

L’home continuava observant el document. No es podia permetre cap dubte.

A la foto del Louvre, el paio que estava dret al costat del nen que tenia el lloro a l’espatlla era el xofer del primer taxi. Increïble! La mateixa gorra. El va envair l’alegria. «Quina llet!». Va estar punt de fer el senyal de la creu. No em creurà ningú. Va remugar: «El tenia al davant del nas i li he deixat tocar el dos!». Es va inclinar cap al xofer:

—Hi ha un taxi que ha sortit de l’aeroport pocs minuts abans que nosaltres. L’hem d’atrapar.

—Amb aquest temps és difícil anar més de pressa, senyor.

—He dit que l’hem d’atrapar.

El xofer va examinar el passatger pel retrovisor i va prendre la mida d’aquell individu mudat, d’aires decidits i cepat!

—Si l’atrapa no haurà perdut el matí —va avançar l’home.

—¿De quina marca era el taxi que he d’atrapar?

—Un 404.

—¿I la companyia? ¿Ha vist de quina companyia era?

—Aa… no.

—Doncs serà difícil. Miri la quantitat de taxis que tenim al voltant.

Estaven rodejats d’un núvol de taxis, gairebé tots procedents de l’aeroport. I cap 404!

—¿Està segur que era un taxi?

—¿Per qui em pren? —va preguntar el TBVA, amenaçador.

—Vull dir si era un taxi oficial. ¿Segur que tenia el rètol lluminós al sostre?

—Sí, encès. Estava lliure.

—¿I al darrere? ¿Ha vist si duia un plafonet lluminós a la plataforma de darrere el seient? ¿Com aquest? —va assenyalar un plafó molt a prop del cap de l’home—. Des de l’interior no pot veure el que diu: indica l’horari en què el taxi acaba el servei i el dia de l’any. L’hi dic perquè cada cop hi ha més taxis falsos. Els paios fins i tot es compren la maquineta de contraban. L’única manera d’estar segur que tracta amb un taxi de veritat és aquesta! —va assenyalar un paper rosa clavat al parabrisa—. Indica si realment estàs inscrit per a aquest any al registre dels taxis.

—¿On es troba aquest registre?

—A la PP.

—La Prefectura de Policia!

Ja havien arribat al perifèric; el familiar no podia atrapar el 404. Tot perdut!

Tot perdut per ara. Però el TBVA posseïa una pista més. Pensava tornar a trobar el taxi. Era com la Giulietta, quan havia vist alguna cosa una vegada… En canvi el pobre Luigi, amb el temps que feia que la cagava…

L’amo estaria content. Ara ja tenien dues pistes: la de la foto i la del taxi.

Amb la mimosa passa el mateix que amb els trèvols de quatre fulles, no cal mirar gaire estona per adonar-se que no n’hi ha. «Si manca el que és efímer, t’has de conformar amb el que és permanent!». Amb la força d’aquest proverbi, la florista del carrer Lepic va proposar roses al senyor Ruche, que va tornar-se’n amb un ram i el va oferir a la Perrette, que el va posar en un gerro, sobre la caixa de la llibreria.

A la BDS, sobre el secreter, l’esperava una altra rosa. Dominant els vents, amb un cop d’ull va repassar la situació.

En Jonathan i la Léa havien marxat en direcció de ponent i navegaven cap a terres probabilistes. Quan tornessin d’aquell viatge de reconeixement, ¿de què portarien plenes les bodegues? Pel que feia a ell mateix, tornava ben tip d’un llarg periple per les terres meridionals, on, amb la companyia sòlida del parell de coordenades, s’havia passejat algèbricament pel món ordenat de la geometria analítica.

Quedaven el nord i l’est. Estava convençut que el nord indicava la direcció que en Grosrouvre li volia fer agafar. Se la pensava guardar per al final.

Es va preparar a guillar cap a llevant, absolutament decidit a descobrir aquella terra incògnita que per ell representava el càlcul diferencial.

La llista dels qui havien contribuït a fer néixer aquesta nova ciència matemàtica constituïa el Who’s who dels matemàtics del segle XVII. Dos italians, Bonaventura Cavalieri i Evangelista Torricelli; un munt de francesos, naturalment Fermat, però també Roberval, Pascal, Descartes, el marquès de l’Hôpital; un holandès, Christiaan Huygens; dos suïssos, els Bernoulli, Jakob —que va inventar la paraula integral— i el seu germà Johann; una colla de britànics, Isaac Barrow, Christopher Wren, John Wallis, James Gregory, Brook Taylor, Colin Maclaurin. I els mestres d’aquesta arquitectura considerada com el monument més bonic de les matemàtiques, Isaac Newton i Gottfried Wilhelm Leibniz (N-i-L).

El senyor Ruche es va regirar a la cadira. Tenia mal de cul. Feia deu anys que hi estava assegut! El coixí pla que li havia regalat la Perrette encara no se li havia adaptat. Era suau i resistent, airejat i flexible, ¿quant temps necessitava per «agafar la forma»? El coixí vell havia quedat fet miques, triturat com una pell vella esqueixada per la cirurgia estètica. Va alçar una galta, va desplaçar el coixí, res, un pèl. Ja en tenia prou. Ben ancorat a la cadira, va poder tirar endavant cap a la quarta direcció de la rosa dels vents de πR Fermat.

Una corba.

¿Què es veu al primer cop d’ull?

Els màxims i els mínims, els llocs on arriba més amunt o més avall; els punts d’inflexió, on la corba passa de ser oberta cap a dalt a oberta cap a baix; els punts de discontinuïtat, etc.

¿Què són exactament el màxim i el mínim? Si ens ho mirem bé, ens adonem que just abans és ben bé igual que just després! Aquesta és la propietat que caracteritza un «extrem»! Fermat la va situar a la base del seu mètode per buscar els màxims i els mínims, traduint-la en llenguatge algèbric, és a dir, per equacions.

«Abans» no és difícil de traduir. Però «just abans»! ¿Com es diu «just», en matemàtiques? Aquest era justament el problema.

La diferència entre un punt i «just abans» d’aquest punt és petita, molt petita, tan petita com petita vulguis que sigui. És infinitament petita!

«L’esperit diferencial» va envair el segle XVII.

Va ser l’època en què, inoculant una sensibilitat microscòpia al saber, en molts terrenys es va anar a «mirar de més a prop». Fins aleshores, de vegades un coneixement local feia possible un coneixement global. Ara es va fer un pas: un coneixement microscòpic permetia un coneixement global.

Els «infinitament petits». ¿Qui eren aquests? ¿Eren magnituds geomètriques, com deia Cavalieri? ¿O magnituds numèriques, com deia Fermat? En canvi Leibniz els considerava ficcions, ficcions útils! El mateix número que amb els imaginaris: sense saber gaire bé qui eren, els van fer actuar. I van produir resultats miraculosos!

La llibreta de tapes dures s’omplia a mesura que el senyor Ruche penetrava amb excitació en l’univers d’aquests infinitament petits. I pensar que quan estudiava vaig passar-hi a dos dits! ¿A dos dits o «just» a dos dits? A molt més de dos dits. Durant la carrera havia hagut de tractar aquests temes per força, però s’havia sentit tan poc atret per aquestes coses que els objectius se li havien escapat totalment. Amb seixanta anys de retard, el senyor Ruche va entendre el que Fermat havia entès feia tres segles: un arc infinitament petit d’una corba es pot assimilar al segment corresponent de la tocant. A més, les paraules eren exquisides! Va entendre el que Roberval havia entès: la direcció del moviment d’un punt que descriu una corba és la tocant a la corba en cada posició del punt. I finalment va entendre això: la forma d’una corba depèn únicament de la direcció de la tocant. El coneixement d’una família de rectes permet el coneixement de tota la corba! En realitat tota la història equivalia a conèixer la corba per la recta.

Era l’època en què els infinitament petits es deien evanescents, i en què les tangents es deien tocants. Dues nocions clau. Newton va definir les primeres de «quantitats que disminueixen, no pas abans d’esvanir-se, ni després, sinó just quan s’esvaneixen». Just quan s’esvaneixen! Semblava un poema sobre la histèria.

¿I una tocant? És el límit d’una secant quan dos punts M i M’ on talla la corba «s’acosten l’un a l’altre infinitament».

Tocar no és tallar! És un frec amb contacte. El senyor Ruche va dibuixar una tocant.

A les matemàtiques passava el contrari que a la vida: es va començar per la «penetració» de la secant i es va acabar pel flirt de la tocant. Encara més, el segon estat era el resultat de l’abandó progressiu del primer. Quina figura eròtica!

Les fotos anaven passant. Vint-i-cinc, trenta per foto. Les dues primeres files, asseguts; les dues de darrere, drets. Criatures, criatures i criatures! Si almenys hagués estat pedòfil! No suportava les criatures: havia estat minyó escolta. Tots s’assemblaven! Encara que se’ls hagués mirat amb lupa, tots feien la mateixa cara. Però no n’hi havia cap que s’assemblés al mocós dels encants. El TBVB estava a punt de defallir. La demanda que havia fet als fotògrafs no havia resultat inútil, les fotografies de classes de primer i segon el colgaven. Vinga fotos i fotos, i l’amo s’impacientava.

El senyor Ruche, immers en el càlcul diferencial, començava a trobar que aquesta direcció de la rosa dels vents l’arrossegava molt lluny. ¿Necessitava tots aquests coneixements per continuar la investigació, les funcions, les variacions, els límits, les derivades…? Segur que no. Tant li feia. ¿Com podia saber on s’havia d’aturar?

A propòsit de la derivada, noció que no li havia deixat cap bon record, li semblava haver entès de què es tractava: de mesurar la variació instantània d’una funció. Tal com el seu nom indica, una funció varia en funció de la variable. Conèixer la variació de la funció en un interval és fàcil. ¿Però i conèixer aquesta variació per a un valor precís de la variable? És el paper que li toca a la derivació. Fer la derivada volia dir mesurar la variació instantània. ¿Com? Simplement calculant la relació entre un canvi infinitament petit de la funció i el que correspon a la variable. I després fent tendir l’últim a zero.

Ja hi som, s’havia perdut! Hi havia una fórmula per definir la derivada f’(x) de la funció f(x).

No entenia ben bé res! Però l’aparició de la noció de límit li va agradar. Tendir cap a un límit, acostar-se a alguna cosa tan a prop com volgués… sense arribar-hi mai! En tota aquesta matemàtica hi havia una manera preciosa de parlar del plaer… Encara més erotisme. ¿Però què tenia avui? Un retorn del foc, una bafarada de desig! ¿Era primavera o què? Era primavera. Era el 22 de març. Un dia més…!

El senyor Ruche estava content. No sabia per què aquests infinitament petits, aquests indivisibles, aquestes tocants li feien un efecte tonificant. Qüestió de punt de vista.

Igual com havia aparegut un «esperit diferencial», naixia un «punt de vista integral». Quan tota aquesta gent del segle XVII es va posar a mirar una superfície, la va veure no com un tot d’una peça, sinó com un compost de tiretes que, posades de costat, l’omplien totalment.

Això li va recordar una altra cosa. Alamut! Just abans que els bessons anessin a esquiar. Quan Hassan Sabbah havia arribat a Alamut havia desplegat una pell de xai o de bou i havia proposat al comandant de la plaça donar-li cinc mil peces d’or a canvi de tant terreny com pogués delimitar amb la pell.

En comptes d’estirar la pell a terra, Hassan l’havia tallat a tiretes i les havia lligat l’una darrere l’altra per fer-ne una corda. Com Cavalieri, havia descompost la superfície de la pell en una multitud de línies! Com més fines les tallés, més llarga li sortiria la corda i més gran seria la superfície que pogués contenir. I així Hassan Sabbah no es va apoderar de la fortalesa inexpugnable d’Alamut per les armes, sinó pel càlcul integral.

Mmm… El senyor Ruche va admetre que l’analogia no era del tot exacta. D’acord. Va deixar estar Hassan i va tornar al «punt de vista integral». Segons aquest, l’àrea d’una figura era una suma. Però una suma d’un tipus particular. Una «suma» d’una quasi infinitat de «línies», cadascuna de superfície gairebé nul·la! El senyor Ruche va repetir la frase: «suma» d’una quasi infinitat de «línies», cadascuna de superfície gairebé nul·la.

Tot l’entrellat estava a saber què podia significar la «suma» d’una infinitat d’elements i a més d’una infinitat d’elements infinitament petits.

Una operació ben estranya, una suma que no suma un nombre finit de quantitats ben finites, sinó una «infinitat» d’elements ínfims. I que, al capdavall, arriba a una quantitat finita. Aquesta totalització d’un tipus nou és la integració.

El senyor Ruche va sentir necessitat de fer un repàs. Després de rumiar un moment, va concloure que la integració equivalia a ajuntar una infinitat «d’infimitats» i acabar aconseguint una cosa ben definida. Li va semblar que havia tirat endavant.

Per simbolitzar aquesta totalització, Leibniz va introduir una S allargada: el símbol de la integral, suma d’un nombre infinitament gran de rectangles infinitament petits, l’àrea total dels quals constitueix l’àrea de la figura.

¿De què servia tot això? No pas a fora de les matemàtiques, el senyor Ruche recordava perfectament la pregunta que el deixeble havia fet a Euclides i també la de la bleda del bar de la Sorbona. No, volia saber de què servia EN MATEMÀTIQUES.

A la vida, rectificar vol dir corregir, fer correcte. En matemàtiques vol dir fer recte. I quan una línia és recta, si és finita, se’n pot calcular la llargada. Rectificar una corba equival a «redreçar-la» de manera que se’n pugui calcular la llargada.

El senyor Ruche va trobar la resposta: tot això servia per rectificar corbes, quadrar superfícies, cubicar sòlids. Es a dir, calcular una llargada, una àrea, un volum.

Van «quadrar» com mai! L’espiral d’Arquimedes, paràboles, hipèrboles, la cicloide… Quant de camí s’havia recorregut des de la quadratura de les lúnules d’Hipòcrates de Quios! Però també, quant de temps que havia passat: dos mil anys!

Al costat de la geometria i de l’àlgebra, que feien cara d’«antigues», va aparèixer la joveneta Anàlisi, un terreny nou que reunia el càlcul diferencial i el càlcul integral, adornada amb totes les belleses. La van anomenar Anàlisi sublim. El senyor Ruche va alçar el cap, el cartell encara era a la paret. Va fer córrer la cadira i, al costat de les vuit seccions que ja feia tant de temps que havia dibuixat en Max, va afegir:

Aquí és on van intervenir els dos veritables fundadors de l’anàlisi. N-i-L, Newton i Leibniz, els pares enemics que es van esbatussar perquè se’ls reconegués la paternitat! Els devem dos descobriments essencials.

El primer: van descobrir que les dues direccions diferents en què havien treballat els matemàtics fins aleshores, la determinació de les tangents i el càlcul d’àrees, en realitat constituïen les dues cares del mateix fenomen i que es podia passar de l’una a l’altra. A partir de les tangents es podia tornar a la corba, a partir de la funció derivada es podia tornar a la funció de la qual era la derivada. Havien passat d’una rectificació a una quadratura! Si ho haguessin vist els grecs!

Va ser una revelació en el món dels matemàtics. Una sola eina capaç d’efectuar accions tan diferents com calcular la llargada d’una corba, determinar l’àrea d’una figura, calcular el volum d’un sòlid, situar el centre de gravetat d’una figura, localitzar els mínims i els màxims d’una corba, determinar les tangents, expressar les velocitats i les acceleracions! Una mena d’eina universal que va entusiasmar els qui s’interessaven per la física. Amb aquesta tècnica, en el futur es podrien estudiar les variacions de tota mena de fenòmens. La porta que donava al coneixement dels fenòmens físics s’obria de bat a bat. La física i la mecànica havien trobat l’eina que els convenia! I era una eina matemàtica.

Conseqüència: el «moviment», que normalment havia quedat exclòs de les matemàtiques, feia una entrada sonada. Al final del segle XVII, el món immòbil de les figures de la Grècia antiga es va animar. Es va passar de la fotografia al cinema.

El segon: «N-i-L» van convertir aquest camp nou en un «càlcul» proveït de regles, el càlcul infinitesimal. La derivació es va convertir en una operació. Una operació d’un tipus nou que no actuava sobre nombres sinó sobre quantitats variables lligades a corbes. Una operació que es podia efectuar amb l’ajuda d’un algoritme sistemàtic.

Després de segles en què el món només disposava de les quatre operacions aritmètiques i de l’extracció d’arrels, en pocs anys van sorgir la diferenciació i la integració. Igual que les primeres, que anaven per parelles inverses: suma/resta, multiplicació/divisió, elevar al quadrat / arrel quadrada, el duo nou també funcionava d’una manera similar: diferenciació i integració eren inverses l’una de l’altra. Però la primera tenia prioritat sobre la segona.

Diuen que quan Newton va néixer era tan menut que cabia en un pot d’un litre… A deu anys fabricava estels i hi fixava llanternes enceses. A la nit, la gent del poble, espantada, fugia pensant-se que veien volar ratpenats en flames.

Amb una cura poc corrent, en Grosrouvre havia copiat dues frases. La primera era de Newton:

Ignoro de quina manera em veu el món; però a mi mateix em sembla que no he estat sinó un nen jugant a la vora de l’aigua i divertint-se a trobar, de tant en tant, una pedreta polida o una carculla més bonica que les altres; mentre el gran oceà de la veritat es desplegava davant meu sense que jo el conegués.

La segona era de Pascal:

Els qui vegin clarament la veritat de la Geometria dels indivisibles podran admirar la grandesa i el poder de la natura en aquesta infinitud doble que ens envolta per tots costats, i mitjançant aquesta consideració meravellosa es podran aprendre a conèixer ells mateixos en veure’s situats entre una infinitud i un no-res d’espai, entre una infinitud i un no-res de nombres, entre una infinitud i un no-res de moviment, entre una infinitud i un no-res de temps, i amb això podran aprendre a estimar-se en el preu que valen i formar reflexions que valen més que tota la resta de la geometria.

Situats entre una infinitud i un no-res! Separar els braços. Amb una mà tocar-ne un, i amb l’altra acariciar l’altre. I estimar-se en el preu just. El soroll de les ones va ressonar molta estona al cap del senyor Ruche… Després va arribar la marea i ho va oblidar tot. Es va adormir a la cadira al mig de la BDS. Tota la nit va córrer descalç per la sorra.