-
Statistics needed to understand the material in this book and in particular this chapter:
-
Statistics Review 1: Summation notation, mean and variance.
-
Statistics Review 2: Normal distribution .
-
Statistics Review 3: Covariance and the variance of the sum of two variables.
-
Statistics Review 4: Regression and correlation.
The basic concepts of the
mean and variance of a set of scores and the use of the summation
(sigma— ) notation, essential for
understanding the material in this book, are reviewed in Statistics Review 1 in Appendix D.
) notation, essential for
understanding the material in this book, are reviewed in Statistics Review 1 in Appendix D.
Classical Test Theory (CTT) is the oldest formalization of a theory of test scores. An excellent review of its history is provided by Traub (1997). CTT , which was introduced by the British Psychologist Charles Spearman early in the twentieth century, dominated test analysis in education and psychology till the latter part of the twentieth century. In many areas, it is becoming superseded by what is known as modern test theory . In this book, we study in detail one of the two theories of modern test theory , that of Rasch Measurement Theory (RMT) .
We introduce, and briefly study, the elements of CTT here for four related reasons. First, because it is the oldest theory, it gives some indication of how the field of test theory began and how it has evolved. Second, the theory continues to be used by many researchers in applied assessment . Third, many of the ideas that have been developed in the theory are relevant in all theories of measurement . Fourth, by studying CTT , and comparing and contrasting its features with RMT , the special features of RMT can be understood better than if it were studied on its own. We will see some fundamental similarities and differences between them.
Much of CTT rests on the assumption that traits assessed in social measurement are normally distributed. The normal distribution is reviewed in Statistics Review 2.
Elements of CTT
Although CTT can be conceptualized in the assessment of variables such as attitude as well as proficiency and is used in both contexts, for ease of exposition we will illustrate points primarily with tests of proficiency but also with assessments of attitude. We use the term proficiency in a generic sense as it pertains to some kind of achievement or attainment as is found in educational assessments and performance assessments which appear in health outcomes. Other relevant examples include intelligence and aptitude assessments which focus on the possible prediction of future achievement rather than primarily assessing material explicitly taught. CTT was developed in this area. Often the term ability is used to characterize all these traits, for example, reference to a person’s ability in relation to an item’s difficulty. However, because the ability is often thought of as some innate ability unaffected by any education and experience, which is not the case in the exposition of CTT and RMT of this book, we will consider generally assessments of proficiency.
The Total Score on an Instrument
You will have noticed that most tests and questionnaires have multiple items . There are two main reasons for this. First, by having more items, there are potentially more score points and therefore greater precision of the assessment . As we will see, precision is related to the concept of reliability which we begin to formalize in this chapter. Second, although all items are intended to assess the same trait, each is also intended to assess some unique aspect of the trait. Thus, there would be no point repeating exactly the same question in an achievement test in mathematics or the same statement in an attitude questionnaire . Having more than one item, each of which assesses both a common and a unique aspect of the trait, potentially enhances the validity of the instrument . We consider validity throughout. We focus here on the formalization of reliability in CTT .
It is intended that every item included in an instrument , should add to the precision and validity of that instrument . However, in anticipation of much of the work in CTT and in RMT , we note that any particular item might not contribute to either precision or validity , or not contribute as much as is required. Whether it does so or not is an empirical question to be answered in the analysis.
A feature of CTT is that it takes the score of a person on an instrument as simply the sum of the person’s scores on the items. Although a mean of the sum of the scores is not taken, only the sum of the scores, the idea is the same. Thus, just as the mean of replications of a response in general settings gives more information than just one response, the total score on an instrument composed of many items should give more information than one item.
Reliability, True and Error Scores
A key concept of CTT is reliability . As the term implies, the idea of reliability has the connotations of repeatability, consistency and predictability. It is a desirable property. Reliability can be considered from a number of perspectives. One of the main ones is when parallel instruments are applied to the same people. The one we consider arises from this perspective and where the items themselves are taken as parallel to each other in assessing the same trait.
Two other important concepts of CTT that are related to reliability are those of each person’s true score and each person’s error score. An observed score , the total score on the items of an instrument , is taken to be the sum of a true score and an error score. The true score is never observed but needs to be estimated.
The concept of a latent trait variable was introduced in Chap. 1. The concept of a true score variable introduced above is identical to a latent trait variable. The latter is simply a more general term, while the term true score variable is identified with CTT . Then, referenced to some defined population of persons, reliability is defined as the ratio of the variance of the true scores among members of the population to the variance of their observed scores.
It should be evident that if the instrument as a whole has an error, then this error must have arisen as a result of some potential error in each response to each item. The kind of error we are referring to is one which, by definition, would not repeat itself systematically and that errors will tend to cancel each other out. For example, through carelessness, a very proficient person may answer an item incorrectly and therefore would generally not answer other items of the same kind and difficulty incorrectly, or a person disagrees to a statement on a questionnaire but would not generally disagree with similar statements.
Statistics Reviews
The theory and implications of CTT are formalized in terms of variances, covariance , correlation and regression. Therefore, it is necessary to understand the concepts of variance, covariance , correlation and regression (Statistics Reviews 3 and 4). These calculations can be performed by even relatively modest calculators. However, it is important to understand the ideas behind the calculations; therefore some simple examples are shown, and it is suggested you carry out some calculations on equally simple exercises. Besides the use of the ideas in CTT , these concepts are important in other areas of data analysis, and therefore reviewing them will be useful to you beyond the needs of this book.
Responses of 50 persons on a 10-item test
|
Person |
Item |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Total score |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Max score |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
3 |
4 |
||
|
1 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
3 |
3 |
17 |
|
|
2 |
0 |
1 |
1 |
0 |
1 |
3 |
0 |
0 |
1 |
0 |
7 |
|
|
3 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
3 |
4 |
18 |
|
|
4 |
1 |
1 |
1 |
1 |
1 |
3 |
0 |
1 |
3 |
2 |
14 |
|
|
5 |
1 |
1 |
1 |
1 |
1 |
2 |
0 |
1 |
3 |
3 |
14 |
|
|
6 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
3 |
1 |
15 |
|
|
7 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
2 |
2 |
15 |
|
|
8 |
1 |
1 |
0 |
1 |
1 |
4 |
1 |
0 |
1 |
1 |
11 |
|
|
9 |
1 |
1 |
1 |
1 |
0 |
2 |
1 |
1 |
3 |
1 |
12 |
|
|
10 |
1 |
1 |
1 |
1 |
1 |
4 |
0 |
0 |
3 |
4 |
16 |
|
|
11 |
0 |
1 |
1 |
1 |
1 |
3 |
0 |
1 |
3 |
1 |
12 |
|
|
12 |
1 |
1 |
1 |
1 |
1 |
3 |
1 |
1 |
0 |
4 |
14 |
|
|
13 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
0 |
3 |
2 |
13 |
|
|
14 |
1 |
1 |
0 |
1 |
1 |
3 |
1 |
1 |
2 |
3 |
14 |
|
|
15 |
1 |
1 |
1 |
1 |
1 |
4 |
0 |
1 |
1 |
3 |
14 |
|
|
16 |
1 |
1 |
1 |
1 |
1 |
4 |
0 |
1 |
3 |
1 |
14 |
|
|
17 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
0 |
3 |
1 |
14 |
|
|
18 |
1 |
1 |
1 |
1 |
0 |
4 |
1 |
1 |
2 |
1 |
13 |
|
|
19 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
3 |
2 |
16 |
|
|
20 |
1 |
1 |
0 |
1 |
1 |
3 |
1 |
1 |
3 |
1 |
13 |
|
|
21 |
1 |
1 |
1 |
1 |
1 |
3 |
0 |
1 |
2 |
3 |
14 |
|
|
22 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
1 |
1 |
13 |
|
|
23 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
0 |
3 |
2 |
15 |
|
|
24 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
3 |
1 |
15 |
|
|
25 |
1 |
1 |
0 |
1 |
1 |
4 |
1 |
0 |
2 |
1 |
12 |
|
|
26 |
1 |
1 |
1 |
1 |
1 |
3 |
1 |
1 |
3 |
3 |
16 |
|
|
27 |
1 |
0 |
1 |
0 |
1 |
4 |
1 |
0 |
2 |
3 |
13 |
|
|
28 |
1 |
1 |
1 |
1 |
1 |
3 |
1 |
1 |
3 |
4 |
17 |
|
|
29 |
1 |
1 |
1 |
0 |
1 |
3 |
1 |
0 |
3 |
1 |
12 |
|
|
30 |
0 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
3 |
4 |
17 |
|
|
31 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
3 |
2 |
16 |
|
|
32 |
1 |
1 |
1 |
1 |
1 |
3 |
1 |
1 |
2 |
1 |
13 |
|
|
33 |
1 |
1 |
0 |
1 |
1 |
4 |
1 |
1 |
3 |
3 |
16 |
|
|
34 |
1 |
1 |
1 |
1 |
1 |
3 |
0 |
1 |
2 |
2 |
13 |
|
|
35 |
1 |
1 |
1 |
1 |
1 |
3 |
1 |
0 |
2 |
0 |
11 |
|
|
36 |
1 |
1 |
1 |
1 |
1 |
3 |
1 |
1 |
2 |
1 |
13 |
|
|
37 |
1 |
1 |
1 |
0 |
1 |
4 |
1 |
1 |
3 |
0 |
13 |
|
|
38 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
2 |
0 |
6 |
|
|
39 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
3 |
3 |
17 |
|
|
40 |
1 |
0 |
1 |
1 |
0 |
3 |
0 |
1 |
1 |
0 |
8 |
|
|
41 |
1 |
1 |
1 |
0 |
1 |
3 |
1 |
0 |
2 |
0 |
10 |
|
|
42 |
1 |
1 |
1 |
1 |
0 |
2 |
0 |
0 |
3 |
1 |
10 |
|
|
43 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
0 |
2 |
1 |
13 |
|
|
44 |
1 |
1 |
1 |
0 |
1 |
3 |
1 |
0 |
3 |
0 |
11 |
|
|
45 |
1 |
1 |
1 |
1 |
1 |
3 |
1 |
0 |
3 |
2 |
14 |
|
|
46 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
3 |
2 |
12 |
|
|
47 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
3 |
3 |
17 |
|
|
48 |
1 |
1 |
0 |
1 |
1 |
4 |
1 |
1 |
2 |
1 |
13 |
|
|
49 |
1 |
1 |
1 |
1 |
1 |
4 |
0 |
1 |
3 |
2 |
15 |
|
|
50 |
1 |
1 |
1 |
1 |
1 |
3 |
0 |
1 |
3 |
3 |
15 |
|
|
Total |
46 |
48 |
44 |
43 |
46 |
166 |
36 |
34 |
123 |
90 |
676 |
|
|
Facility |
0.92 |
0.96 |
0.88 |
0.86 |
0.92 |
0.83 |
0.72 |
0.68 |
0.82 |
0.45 |
||
|
Discrimination |
0.36 |
0.25 |
0.05 |
0.52 |
0.33 |
0.51 |
0.31 |
0.48 |
0.47 |
0.76 |
The evidence of the performances on the test is analysed in two stages. The first stage is termed the item analysis. It checks how well the items have worked relative to expectation. Following the item analysis, the analysis of the results focuses on the persons. This stage is termed the person analysis.
Item Analysis
Facility of an Item
The first main concept of an item
analysis is concerned with the difficulty of items relative to the
population of persons administered the test to assess a variable. It is required that
the item is not so difficult that a person cannot engage with it,
or that it is so easy that it is trivial. Although such an index is
calculated, we see when we formalize CTT
in terms of equations, that the relative difficulties of items are
only implied, and not formally part of the theory. This is one of
its weaknesses and contrasts with RMT .
Although the relative difficulty of an
item can be conceptualized in the assessment of variables such as attitude, for
present, and for ease of exposition, we continue to refer to tests
of proficiency. In dichotomously scored items, the index of item
difficulty is simply the
proportion of persons who answered the item correctly, called the
facility of the item, and
usually denoted by  . In dichotomously scored items, the
proportion correct is the same as the average score on the
item.
. In dichotomously scored items, the
proportion correct is the same as the average score on the
item.
To obtain the facility of a polytomously scored item, this relationship between the average and the proportion correct is generalized. Thus to obtain the facility of a polytomous item , the average score of an item is calculated. However, if the maximum score of an item is say m, then this average will be a number between 0 and m. Therefore, to appreciate the item’s facility without having to consider its maximum score, the average is divided by the item’s maximum score m. This number is, as with dichotomous items, a number between 0 and 1. The facility of each item is shown in Table 3.1. The easiest item was item 2, with a facility of 0.96. The most difficult item was item 10, with a facility of 0.45.
Discrimination of an Item
The term discrimination is used to indicate a statistical index which describes the degree to which an item is consistent with the other items in helping distinguish the proficiencies of the persons. The term discrimination in this context is not used pejoratively. It is used to summarize the expectation that if an item assesses the same variable as the majority of the items of an instrument , then those persons who obtain a high score on the item, should also tend to obtain a high score on the test . Likewise, those persons who obtain a low score on the item should tend to obtain a low total score on the test . Although there are different calculations of the discrimination, we simply take it as the correlation between the scores on the item and the total scores on the test across all the persons.
Because the index of discrimination is a correlation, it cannot have a value less than −1.0 and greater than +1.0. However, it also follows from the reasoning above regarding the expected relationship between scores on an item and scores on the test , that the discrimination of each is expected to be greater than 0. Consistent with this expectation, it is taken in CTT in general, that the greater the discrimination of an item, the better. There is no a priori specific value that CTT provides that indicates the ideal magnitude of this correlation. However, if there were no errors, then this correlation would be 1. We see that there is a counterpart to this correlation in RMT .
The discrimination of each item is shown in Table 3.1. The least discriminating item was item 3, with a correlation of 0.05. The most discriminating item was item 10, with a correlation of 0.76.
Person Analysis
In Statistics Review 1, we used the letter
 to represent a score on an item and
then also the mean of the scores. However, in this chapter, we
distinguish between the variable for an item and the variable for
the sum of scores across items. As you will see, we use the letter
x for the value of a response
to an item and the letter y for
the sum of the scores across items. This notation will be
consistent with the one we use with RMT
.
to represent a score on an item and
then also the mean of the scores. However, in this chapter, we
distinguish between the variable for an item and the variable for
the sum of scores across items. As you will see, we use the letter
x for the value of a response
to an item and the letter y for
the sum of the scores across items. This notation will be
consistent with the one we use with RMT
.
We now formalize the concepts and relationship between observed score , true score and the error score in CTT . The governing requirement and approach to the theory is that the series of items that make up an instrument are indicators of the same variable.
Notation and Assumptions of CTT
 be the
score of person n on item
be the
score of person n on item
 where
where  can take the integer values
can take the integer values
 and where there are
and where there are  items on the test :
items on the test :
- (i)
each person n has a true score
 ,
, - (ii)
the best overall indicator of the person’s true score is the total score
 on the items,
on the items, - (iii)
the observed score
 has an additive error to the
true score
has an additive error to the
true score  for each person denoted by
for each person denoted by
 ,
, - (iv)
the errors
 are not correlated with the true
scores of the persons or with each other and
are not correlated with the true
scores of the persons or with each other and - (v)
across a population of persons, the errors sum to 0 and they are normally distributed.
Basic Equations of CTT
From these assumptions, derivations and definitions, Eqs. (3.1)–(3.5) follow. The derivations of Eqs. (3.4) and (3.5) are in Part IV of this book. We apply these equations in an example in this chapter.


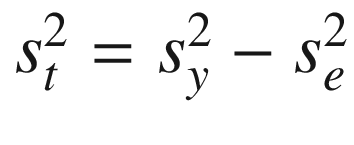 , where
, where 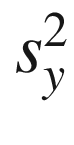 is the variance of the observed
scores in a population of persons,
is the variance of the observed
scores in a population of persons, 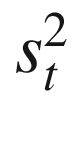 is the variance of their true scores
and
is the variance of their true scores
and 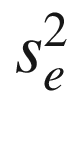 is the error variance.
is the error variance.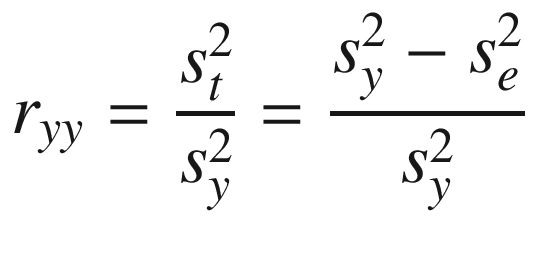

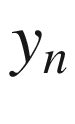 and
and  is the mean of the observed scores.
is the mean of the observed scores.
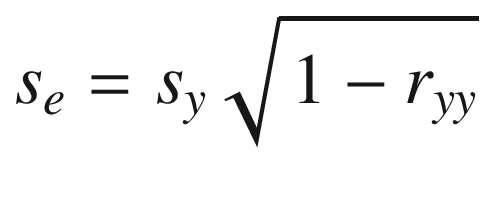
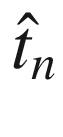 of a person and is the same for all
persons. We note that the errors specified are considered random
among each other. As a result of the nature of the randomness, they
cancel each other out rather than propagate and become
larger.
of a person and is the same for all
persons. We note that the errors specified are considered random
among each other. As a result of the nature of the randomness, they
cancel each other out rather than propagate and become
larger.Reliability of a Test in CTT 
The proportion of true variance relative to the total variance of the test , specified in Eq. (3.3) is defined as the reliability of a test . Equation (3.3) summarizes the next most important concept of CTT after Eq. (3.1). The double subscript of the same variable (e.g. yy) is used often to denote reliability because it can also be interpreted as an observed correlation between the observed scores on two parallel forms of a test .
- (i)
the number of items;
- (ii)
the discrimination of the items;
- (iii)
the alignment of the items to the persons, that is, their relative difficulties;
- (iv)
the variation of the true scores in the population.
If all assumptions hold, the greater the number of items the closer the facilities are to 0.5 and the greater the variation in the true scores, the greater the reliability . We reconsider each of these relationships as we proceed through the book. We consolidate this idea in the next chapter where we show one method of estimating reliability .
The Standard Error of Measurement 
The standard error
of measurement in Eq. (3.5) pertains to a person.
The square of this term is the error variance,  , which also appears in
Eq. (3.2)
where it is a variance across persons. It is no coincidence that
there is a single term
, which also appears in
Eq. (3.2)
where it is a variance across persons. It is no coincidence that
there is a single term  for both of these concepts. The
reason only one term is necessary for these two conceptualizations
of error is that all errors are postulated to come from the same
distribution of errors. Thus although each person will have a
different actual error, it is postulated that these errors have a
mean of 0, that they are normally distributed, and that they have a
variance of
for both of these concepts. The
reason only one term is necessary for these two conceptualizations
of error is that all errors are postulated to come from the same
distribution of errors. Thus although each person will have a
different actual error, it is postulated that these errors have a
mean of 0, that they are normally distributed, and that they have a
variance of  . This holds whether we conceptualize
one person being assessed on multiple occasions or multiple people
assessed on one occasion. This is a contrast with the error in RMT . Given an estimate of the
reliability of a test , Eq. (3.5) can be used to
estimate the error variance
. This holds whether we conceptualize
one person being assessed on multiple occasions or multiple people
assessed on one occasion. This is a contrast with the error in RMT . Given an estimate of the
reliability of a test , Eq. (3.5) can be used to
estimate the error variance  .
.
It is evident from Eqs. (3.1) to (3.5) that they contain no formalization of the facility or difficulty of an item. This is another of the contrasts with RMT .
Statistics Reviews
Statistics Reviews 3 and 4 belong together and should be seen as a whole. Covariance is explained first in Review 3 and then used in the formula for correlation in Review 4. Correlation explained in Review 4, however, is needed to understand the variance of the sum of two uncorrelated variables, explained in Review 3.
Example
We now briefly apply
Eqs. (3.4) and (3.5) to the data of Table 3.1. The mean score for
the data from Table 3.1 is 13.52 and the variance of the scores is
6.42. We see in the next chapter how the reliability coefficient  can be calculated. In this example
can be calculated. In this example
 = 0.47.
= 0.47.
- (i)

- (ii)

- (iii)
From the normal curve table, 95% of the area is contained between z = −1.96 and z = 1.96.
Therefore, the 95% confidence interval is given by

10.60–17.83, which is a relatively wide range.
- (iv)
From
 above,
above,  .
.
Therefore, from  ,
,  .
.
We need to appreciate that we do not have an independent absolute unit in the above calculations. The calculations are relative to an arbitrary origin and an arbitrary unit that are a property of the data. We examine this assertion when we study RMT .