The origin and fate of the Universe is, for many researchers, the fundamental question. Many answers were provided over the ages, a few of them built over scientific observations and reasoning. During the last century important scientific theoretical and experimental breakthroughs occurred after Einstein’s proposal of the General Theory of Relativity in 1915, with precise and systematic measurements establishing the expansion of the Universe, the existence the cosmic microwave background, and the abundances of light elements in the Universe. The fate of the Universe can be predicted from its energy content—but, although the chemical composition of the Universe and the physical nature of its constituent matter have occupied scientists for centuries, we do not know yet this energy content well enough.
We are made of protons, neutrons, and electrons, combined into atoms in which most of the energy is concentrated in the nuclei (baryonic matter), and we know a few more particles (photons, neutrinos, ...) accounting for a limited fraction of the total energy of atoms. However, the motion of stars in galaxies as well as results about background radiation and the large-scale structure of the Universe (both will be discussed in the rest of this chapter) is inconsistent with the presently known laws of physics, unless we assume that a new form of matter exists. This matter is not visible, showing little or no interaction with photons—we call it “dark matter” . It is, however, important in the composition of the Universe, because its energy is a factor of five larger than the energy of baryonic matter.
Recently, the composition of the Universe has become even more puzzling, as observations imply an accelerated expansion. Such an acceleration can be explained by a new, unknown, form of energy—we call it “dark energy”—generating a repulsive gravitational force. Something is ripping the Universe apart.
The current view on the distribution of the total budget between these forms of energy is shown in Fig. 1.8. Note that we are facing a new Copernican revolution: we are not made of the same matter that most of the Universe is made of. Moreover, the Universe displays a global behavior difficult to explain, as we shall see in Sect. 8.1.1.
Today, at the beginning of the twenty-first century, the Big Bang model with a large fraction of dark matter (DM) and dark energy is widely accepted as “the standard model of cosmology,” but no one knows what the “dark” part really is, and thus the Universe and its ultimate fate remain basically unknown.
8.1 Experimental Cosmology

Wavelength shifts observed in spectra of galaxies depending on their distance. From J. Silk, “The Big Bang,” Times Books 2000
8.1.1 The Universe Is Expanding

 68 km s
68 km s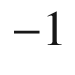 Mpc
Mpc is the so-called Hubble constant (we shall see that it is not at all
constant and can change during the history of the Universe) which
is often expressed as a function of a dimensionless parameter
h defined as
is the so-called Hubble constant (we shall see that it is not at all
constant and can change during the history of the Universe) which
is often expressed as a function of a dimensionless parameter
h defined as


A redshift occurs whenever  which is the case for the large
majority of galaxies. There are notable exceptions (
which is the case for the large
majority of galaxies. There are notable exceptions ( , a blueshift) as the one of M31, the
nearby Andromeda galaxy, explained by a large intrinsic velocity
(peculiar velocity) oriented toward
us.
, a blueshift) as the one of M31, the
nearby Andromeda galaxy, explained by a large intrinsic velocity
(peculiar velocity) oriented toward
us.
Wavelength shifts were first observed by the US astronomer James Keeler at the end of the nineteenth century in the spectrum of the light reflected by the rings of Saturn, and later on, at the beginning of twentieth century, by the US astronomer Vesto Slipher, in the spectral lines of several galaxies. In 1925 spectral lines had been measured for around 40 galaxies.

 becomes
becomes


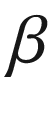 is not valid for high redshift
objects with z as high as 11
that have been observed in the last years—the list of the most
distant object comprises more than 100 objects with
is not valid for high redshift
objects with z as high as 11
that have been observed in the last years—the list of the most
distant object comprises more than 100 objects with  among galaxies (the most abundant
category), black holes, and even stars. On the other hand, high
redshift supernovae (typically
among galaxies (the most abundant
category), black holes, and even stars. On the other hand, high
redshift supernovae (typically  to 1) have been extensively studied.
From these studies an interpretation of the expansion based on
special relativity is clearly excluded: one has to invoke general
relativity.
to 1) have been extensively studied.
From these studies an interpretation of the expansion based on
special relativity is clearly excluded: one has to invoke general
relativity.In terms of general relativity (see
Sect. 8.2) the observed redshift is not due to any
movement of the cosmic objects but to the expansion of the proper
space between them. This expansion has no center: an observer at
any point of the Universe will see the expansion in the same way
with all objects in all directions receding with radial velocities
given by the same Hubble law and not limited by the speed of light
(in fact for  radial velocities are, in a large
range of cosmological models, higher than c): it is the distance scale in the
Universe that is changing.
radial velocities are, in a large
range of cosmological models, higher than c): it is the distance scale in the
Universe that is changing.

 ) distance between the objects
(
) distance between the objects
( that does not change with time
(comoving distance). Then
that does not change with time
(comoving distance). Then




The velocity–distance relation measured by Hubble (the original “Hubble plot”). From E. Hubble, Proceedings of the National Academy of Sciences 15 (1929) 168


 (if
(if  the expansion slows down) defined as
the expansion slows down) defined as


However, in an expanding Universe the
computation of the distance is much more subtle. Various distance
measures are usually defined between two objects: in particular,
the proper distance  and the luminosity distance
and the luminosity distance  .
.
-
 is defined as the length measured on
the spatial geodesic connecting the two objects at a fixed time (a
geodesic is defined to be a curve whose
tangent vectors remain parallel if they are transported along it.
Geodesics are (locally) the shortest path between points in space,
and describe locally the infinitesimal path of a test inertial
particle). It can be shown (see Ref. [F8.2]) that
for small z the usual linear Hubble law is recovered.
is defined as the length measured on
the spatial geodesic connecting the two objects at a fixed time (a
geodesic is defined to be a curve whose
tangent vectors remain parallel if they are transported along it.
Geodesics are (locally) the shortest path between points in space,
and describe locally the infinitesimal path of a test inertial
particle). It can be shown (see Ref. [F8.2]) that
for small z the usual linear Hubble law is recovered. (8.13)
(8.13) -
 is defined as the distance that is
experimentally determined using a standard candle assuming a static
and Euclidean Universe as noted above:
is defined as the distance that is
experimentally determined using a standard candle assuming a static
and Euclidean Universe as noted above:
 (8.14)
(8.14)
 and
and  depends on the curvature of the
Universe (see Sect. 8.2.3). Even in a flat (Euclidean) Universe
(see Sect. 8.2.3 for a formal definition; for the moment,
we rely on an intuitive one, and think of flat space as a space in
which the sum of the internal angles of a triangle is always
depends on the curvature of the
Universe (see Sect. 8.2.3). Even in a flat (Euclidean) Universe
(see Sect. 8.2.3 for a formal definition; for the moment,
we rely on an intuitive one, and think of flat space as a space in
which the sum of the internal angles of a triangle is always
 ) the flux of light emitted by an
object with a redshift z and
received at Earth is attenuated by a factor
) the flux of light emitted by an
object with a redshift z and
received at Earth is attenuated by a factor  due to the dilation of time
(
due to the dilation of time
( ) and the increase of the photon’s
wavelength (
) and the increase of the photon’s
wavelength ( ). Then if the Universe was basically
flat
). Then if the Universe was basically
flat
![$$\begin{aligned} d_L={d}_p\left( 1+z\right) \simeq \frac{c}{H_0}z\left[ 1+\frac{ 1-q_0}{2}z\right] \, . \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_8_Chapter/304327_2_En_8_Chapter_TeX_Equ15.png)
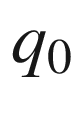 one needs to extend the range of
distances in the Hubble plot by a large amount. New and brighter
standard candles are needed.
one needs to extend the range of
distances in the Hubble plot by a large amount. New and brighter
standard candles are needed.8.1.2 Expansion Is Accelerating
Type Ia
supernovae have been revealed themselves as an optimal option to
extend the range of distances in the Hubble plot. Supernovae Ia
occur whenever, in a binary system formed by a white dwarf (a compact Earth-size stellar endproduct of
mass close to the solar mass) and another star (for instance a red
giant, a luminous giant star in a late
phase of stellar evolution), the white dwarf accretes matter from
its companion reaching a total critical mass of about 1.4 solar
masses. At this point a nuclear fusion reaction starts, leading to
a gigantic explosion (with a luminosity about  times larger than the brightest
Cepheids; see Fig. 8.3 for an artistic representation).
times larger than the brightest
Cepheids; see Fig. 8.3 for an artistic representation).
 data leads to negative values of
data leads to negative values of
 meaning that, contrary to what was
expected, the expansion of the Universe is nowadays accelerating.
meaning that, contrary to what was
expected, the expansion of the Universe is nowadays accelerating.

Artistic representation of the formation and explosion of a supernova Ia
(Image from A. Hardy, David A. Hardy/www.astroart.org)

Left: The “Hubble plot” obtained by the “High-z Supernova Search Team” and by the “Supernova Cosmology Project.” The lines represent the prediction of several models with different energy contents of the Universe (see Sect. 8.4). The best fit corresponds to an accelerating expansion scenario. From “Measuring Cosmology with Supernovae,” by Saul Perlmutter and Brian P. Schmidt; Lecture Notes in Physics 2003, Springer. Right: an updated version by the “Supernova Legacy Survey” and the “Sloan Digital Sky Survey” projects, M. Betoule et al. arXiv:1401.4064
 by the simple formula:
by the simple formula:

 is known as the angular diameter
distance. In a curved and/or expanding
Universe
is known as the angular diameter
distance. In a curved and/or expanding
Universe  does not coincide with the proper
(
does not coincide with the proper
( ) and the luminosity (
) and the luminosity ( ) distances defined above but it can
be shown (see Ref. [8.2]) that:
) distances defined above but it can
be shown (see Ref. [8.2]) that:

 between pairs of galaxies is just the
excess probability that the two galaxies are at the distance
r and thus a sharp peak in
between pairs of galaxies is just the
excess probability that the two galaxies are at the distance
r and thus a sharp peak in
 will correspond in its Fourier
transform to an oscillation spectrum with a well-defined
frequency.
will correspond in its Fourier
transform to an oscillation spectrum with a well-defined
frequency.8.1.2.1 Dark Energy
There is no
classical explanation for the accelerated expansion of the
Universe. A new form of energy is invoked, permeating the space and
exerting a negative pressure. This kind of energy can be described
in the general theory of relativity (see later) and associated,
e.g., to a “cosmological constant” term  ; from a physical point of view, it
corresponds to a “dark” energy component—and to the present
knowledge has the largest energy share in the Universe.
; from a physical point of view, it
corresponds to a “dark” energy component—and to the present
knowledge has the largest energy share in the Universe.
In Sect. 8.4 the current overall
best picture able to accommodate all present experimental results
(the so-called  CDM model) will be discussed.
CDM model) will be discussed.
8.1.3 Cosmic Microwave Background
In 1965 Penzias and Wilson,3 two radio astronomers working at Bell Laboratories in New Jersey, discovered by accident that the Universe is filled with a mysterious isotropic and constant microwave radiation corresponding to a blackbody temperature around 3 K.
 cm while the spectrum peaks
around
cm while the spectrum peaks
around mm. To fully measure the density
spectrum it is necessary to go above the Earth’s atmosphere, which
absorbs wavelengths lower than
mm. To fully measure the density
spectrum it is necessary to go above the Earth’s atmosphere, which
absorbs wavelengths lower than  cm. These measurements were
eventually performed in several balloon and satellite experiments.
In particular, the Cosmic Background Explorer (COBE), launched in
1989, was the first to show that in the 0.1 to 5 mm range the
spectrum, after correction for the proper motion of the Earth, is
well described by the Planck blackbody formula
cm. These measurements were
eventually performed in several balloon and satellite experiments.
In particular, the Cosmic Background Explorer (COBE), launched in
1989, was the first to show that in the 0.1 to 5 mm range the
spectrum, after correction for the proper motion of the Earth, is
well described by the Planck blackbody formula

 is the Boltzmann constant. Other
measurements at longer wavelengths confirmed that the cosmic
microwave background (CMB) spectrum is well described by the
spectrum of a single temperature blackbody (Fig. 8.5) with a mean
temperature of
is the Boltzmann constant. Other
measurements at longer wavelengths confirmed that the cosmic
microwave background (CMB) spectrum is well described by the
spectrum of a single temperature blackbody (Fig. 8.5) with a mean
temperature of


The CMB intensity plot as measured by COBE and other experiments


8.1.3.1 Recombination and Decoupling
In the Big Bang model the expanding Universe cools down going through successive stages of lower energy density (temperature) and more complex structures. Radiation materializes into pairs of particles and antiparticles, which, in turn, give origin to the existing objects and structures in the Universe (nuclei, atoms, planets, stars, galaxies, ...). In this context, the CMB is the electromagnetic radiation left over when electrons and protons combine to form neutral atoms (the, so-called, recombination phase). After this stage, the absence of charged matter allows photons to be basically free of interactions, and evolve independently in the expanding Universe (photon decoupling ).

 H as nonrelativistic particles) the
number density of electrons, protons, and hydrogen atoms may be
approximated by the Maxwell–Boltzmann distribution (see
Sect. 8.3.1)
H as nonrelativistic particles) the
number density of electrons, protons, and hydrogen atoms may be
approximated by the Maxwell–Boltzmann distribution (see
Sect. 8.3.1)

 is a statistical factor accounting for
the spin (the subscript x
refers to each particle type).
is a statistical factor accounting for
the spin (the subscript x
refers to each particle type). can then be approximately modeled by
the Saha equation
can then be approximately modeled by
the Saha equation


 for complete ionization, whereas,
for complete ionization, whereas,
 when all protons are inside neutral
atoms),
when all protons are inside neutral
atoms),

 , the Saha equation can be rewritten
as
, the Saha equation can be rewritten
as

 follows the usual blackbody
distribution corresponding, as we have seen before, to a photon
density number of:
follows the usual blackbody
distribution corresponding, as we have seen before, to a photon
density number of:



 is the total number of baryons, which
in this simple approximation is defined as
is the total number of baryons, which
in this simple approximation is defined as
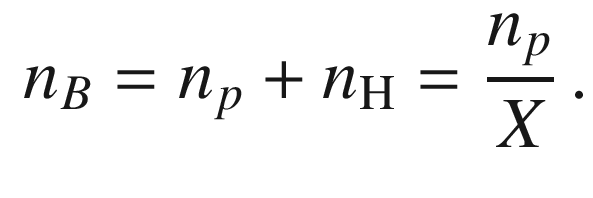

 and
and  evolve independently both as
evolve independently both as
 , where a(t)
is the scale factor of the Universe, see Sect. 8.1.1. Thus,
, where a(t)
is the scale factor of the Universe, see Sect. 8.1.1. Thus,  is basically a constant, which can be
measured at the present time through the measurement of the content
of light elements in the Universe (see Sect. 8.1.4):
is basically a constant, which can be
measured at the present time through the measurement of the content
of light elements in the Universe (see Sect. 8.1.4):

 and T, and used to determine the
recombination temperature (assuming
and T, and used to determine the
recombination temperature (assuming
 :
:

 . For instance
. For instance  results into
results into


X as a function of z in the Saha equation. Time on the abscissa increases from left to right (as z decreases).
Adapted from B. Ryden, lectures at ICTP Trieste, 2006
 . The entire CMB spectrum was expanded
by this factor, and then it can be estimated that recombination had
occurred (see Fig. 8.6) at
. The entire CMB spectrum was expanded
by this factor, and then it can be estimated that recombination had
occurred (see Fig. 8.6) at

 equals the expansion rate of the
Universe (which is given by the Hubble parameter)
equals the expansion rate of the
Universe (which is given by the Hubble parameter)


 and
and  are, respectively, the free electron
density number and the Thomson cross section.
are, respectively, the free electron
density number and the Thomson cross section. can be related to the fractional
ionization X(z) and the baryon density number
(
can be related to the fractional
ionization X(z) and the baryon density number
( ), the redshift at which the photon
decoupling occurs (
), the redshift at which the photon
decoupling occurs ( ) is given by
) is given by

 is subtle. Both
is subtle. Both  and H evolve during the expansion (for
instance in a matter-dominated flat Universe, as it will be
discussed in Sect. 8.2,
and H evolve during the expansion (for
instance in a matter-dominated flat Universe, as it will be
discussed in Sect. 8.2,  and
and  ). Furthermore, the Saha equation is
not valid after recombination since electrons and photons are no
longer in thermal equilibrium. The exact value of
). Furthermore, the Saha equation is
not valid after recombination since electrons and photons are no
longer in thermal equilibrium. The exact value of  depends thus on the specific model
for the evolution of the Universe and the final result is of the
order of
depends thus on the specific model
for the evolution of the Universe and the final result is of the
order of

 ) when the Universe was still small
enough for neutral hydrogen formed at recombination to be ionized
by the radiation emitted by stars. Still, the scattering
probability of CMB photons during this epoch is small. To account
for it, the reionization optical depth parameter
) when the Universe was still small
enough for neutral hydrogen formed at recombination to be ionized
by the radiation emitted by stars. Still, the scattering
probability of CMB photons during this epoch is small. To account
for it, the reionization optical depth parameter  is
introduced, in terms of which the scattering probability is given
by
is
introduced, in terms of which the scattering probability is given
by
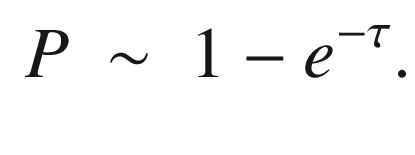
 arcminutes.
arcminutes. , very close to
, very close to 

 the Universe is opaque to photons and
to be able to observe it other messengers, e.g., gravitational
waves, have to be studied. On the other hand, the measurement of
the primordial nucleosynthesis (Sect. 8.1.4) allows us to
indirectly test the Big Bang model at times well before the
recombination epoch.
the Universe is opaque to photons and
to be able to observe it other messengers, e.g., gravitational
waves, have to be studied. On the other hand, the measurement of
the primordial nucleosynthesis (Sect. 8.1.4) allows us to
indirectly test the Big Bang model at times well before the
recombination epoch.8.1.3.2 Temperature Fluctuations


 , the temperature fluctuations are of
the order of
, the temperature fluctuations are of
the order of  : the observed CMB spectrum is
remarkably isotropic.
: the observed CMB spectrum is
remarkably isotropic.

Sky map (in Galactic coordinates) of CMB temperatures measured by COBE after the subtraction of the emission from our Galaxy. A dipole component is clearly visible.

CMB temperature fluctuations sky map as measured by COBE after the subtraction of the dipole component and of the emission from our Galaxy.


 , was confirmed and greatly improved
by the Wilkinson Microwave Anisotropy Probe WMAP, which obtained
full sky maps with a
, was confirmed and greatly improved
by the Wilkinson Microwave Anisotropy Probe WMAP, which obtained
full sky maps with a  angular resolution. The Planck
satellite delivered more recently sky maps with three times
improved resolution and ten times higher sensitivity
(Fig. 8.9), also covering a larger frequency range.
angular resolution. The Planck
satellite delivered more recently sky maps with three times
improved resolution and ten times higher sensitivity
(Fig. 8.9), also covering a larger frequency range.

CMB temperature fluctuations sky map as measured by the Planck mission after the subtraction of the dipole component and of the emission from our Galaxy.
Once these maps are obtained it is possible to establish two-point correlations between any two spatial directions.

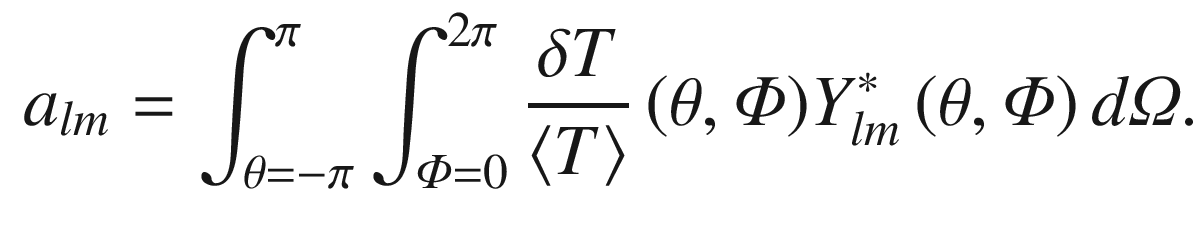
 and
and  separated by an angle
separated by an angle  is defined as
is defined as

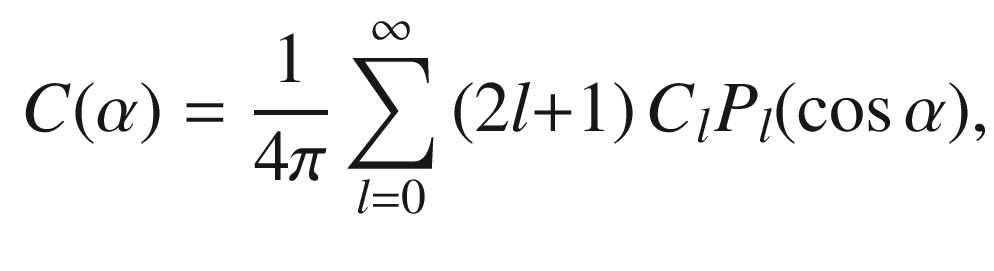
 are the Legendre polynomials and the
are the Legendre polynomials and the
 , the multipole moments, are given by
the variance of the harmonic coefficients
, the multipole moments, are given by
the variance of the harmonic coefficients  :
:

 such that
such that


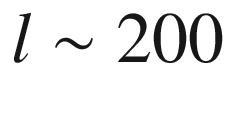 followed by several smaller peaks.
followed by several smaller peaks.

Temperature power spectrum from the Planck, WMAP, ACT, and SPT experiments. The abscissa is logarithmic for l less than 30, linear otherwise. The curve is the best-fit Planck model. From C. Patrignani et al. (Particle Data Group), Chin. Phys. C, 40, 100001 (2016)
The first peak at an angular scale of
 defines the size of the “sound
horizon” at the time of last scattering (see
Sect. 8.1.4) and the other peaks (acoustic peaks)
are extremely sensitive to the specific
contents and evolution model of the Universe at that time. The
observation of very tiny fluctuations at large scales (much greater
than the horizon,
defines the size of the “sound
horizon” at the time of last scattering (see
Sect. 8.1.4) and the other peaks (acoustic peaks)
are extremely sensitive to the specific
contents and evolution model of the Universe at that time. The
observation of very tiny fluctuations at large scales (much greater
than the horizon,  ) leads to the hypothesis that the
Universe, to be casually connected, went through a very early stage
of exponential expansion, called inflation .
) leads to the hypothesis that the
Universe, to be casually connected, went through a very early stage
of exponential expansion, called inflation .
Anisotropies can also be found studying the polarization of CMB photons. Indeed at the recombination and reionization epochs the CMB may be partially polarized by Thomson scattering with electrons. It can be shown that linear polarization may be originated by quadrupole temperature anisotropies. In general the polarization pattern is decomposed in two orthogonal modes, respectively, called B-mode (curl-like) and E-mode (gradient-like). The E-mode comes from density fluctuations, while primordial gravitational waves are expected to display both polarization modes. Gravitational lensing of the CMB E-modes may also be a source of B-modes. E-modes were first measured in 2002 by the DASItelescope in Antarctica and later on the Planck collaboration published high-resolution maps of the CMB polarization over the full sky. The detection and the interpretation of B-modes are very challenging since the signals are tiny and foreground contaminations, as the emission by Galactic dust, are not always easy to estimate. The arrival angles of CMB photons are smeared, due to the microlensing effects, by dispersions that are function of the integrated mass distribution along the photon paths. It is possible, however, to deduce these dispersions statistically from the observed temperature angular power spectra and/or from polarized E- and B-mode fields. The precise measurement of these dispersions will give valuable information for the determination of the cosmological parameters. It will also help constraining parameters, such as the sum of the neutrino masses or the dark energy content, that are relevant for the growth of structures in the Universe, and evaluating contributions to the B-mode patterns from possible primordial gravity waves.
The detection of gravitational lensing was reported by several experiments such as the Atacama Cosmology Telescope, the South Pole Telescope, and the POLARBEAR experiment. The Planck collaboration has measured its effect with high significance using temperature and polarization data, establishing a map of the lensing potential.
Some of these aspects will be discussed briefly in Sect. 8.3, but a detailed discussion of the theoretical and experimental aspects of this fast-moving field is far beyond the scope of this book.
8.1.4 Primordial Nucleosynthesis
 He,
He,  He,
He,  Li,
Li,  Li) is the third observational
“pillar” of the Big Bang model, after the Hubble expansion and the
CMB. As it was proposed, and first computed, by the Russian
American physicists Ralph Alpher and George Gamow in 1948, the
expanding Universe cools down, and when it reaches temperatures of
the order of the nuclei-binding energies per nucleon (
Li) is the third observational
“pillar” of the Big Bang model, after the Hubble expansion and the
CMB. As it was proposed, and first computed, by the Russian
American physicists Ralph Alpher and George Gamow in 1948, the
expanding Universe cools down, and when it reaches temperatures of
the order of the nuclei-binding energies per nucleon ( MeV) nucleosynthesis occurs if there
are enough protons and neutrons available. The main nuclear fusion
reactions are
MeV) nucleosynthesis occurs if there
are enough protons and neutrons available. The main nuclear fusion
reactions are
-
proton–neutron fusion:

-
deuterium–deuterium fusion:



-
other
 formation reactions:
formation reactions:




-
and finally the lithium and beryllium formation reactions (there are no stable nuclei with
 :
:




The absence of stable nuclei with
 basically stops the primordial Big
Bang nucleosynthesis chain. Heavier nuclei are produced in stellar (up to Fe), or supernova
nucleosynthesis.5
basically stops the primordial Big
Bang nucleosynthesis chain. Heavier nuclei are produced in stellar (up to Fe), or supernova
nucleosynthesis.5

 ; if
; if  .
.
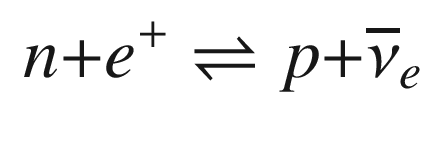
 is greater than the expansion rate of
the Universe,
is greater than the expansion rate of
the Universe,

 and H diminish during the expansion, the
former much faster than the latter. Indeed in a flat Universe
dominated by radiation (Sect. 8.2)
and H diminish during the expansion, the
former much faster than the latter. Indeed in a flat Universe
dominated by radiation (Sect. 8.2)


 is the Fermi weak interaction
constant and
is the Fermi weak interaction
constant and  the number of degrees of freedom that
depends on the relativistic particles content of the Universe
(namely on the number of generations of light neutrinos
the number of degrees of freedom that
depends on the relativistic particles content of the Universe
(namely on the number of generations of light neutrinos
 , which, in turn, allows to set a
limit on
, which, in turn, allows to set a
limit on  ).
). at which
at which

 are a little below the MeV scale:
are a little below the MeV scale:



 ratio will decrease slowly while all
the neutrons will not be bound inside nuclei, so that
ratio will decrease slowly while all
the neutrons will not be bound inside nuclei, so that

 s is the neutron lifetime.
s is the neutron lifetime.
 is quite small (
is quite small ( ) makes photodissociation of the
deuterium nuclei possible at temperatures lower than the blackbody
peak temperature
) makes photodissociation of the
deuterium nuclei possible at temperatures lower than the blackbody
peak temperature  (the Planck function has a long
tail). The relative number of free protons, free neutrons, and
deuterium nuclei can be expressed, using a Saha-like equation
(Sect. 8.1.3), as follows:
(the Planck function has a long
tail). The relative number of free protons, free neutrons, and
deuterium nuclei can be expressed, using a Saha-like equation
(Sect. 8.1.3), as follows:


 as a function of
as a function of  and
and  and performing an order of magnitude
estimation, we obtain
and performing an order of magnitude
estimation, we obtain

 by the Planck distribution
by the Planck distribution

 gives a remarkably stable value of
temperature. In fact there is a sharp transition around
gives a remarkably stable value of
temperature. In fact there is a sharp transition around
 MeV: above this value neutrons and
protons are basically free; below this value all neutrons are
substantially bound first inside D nuclei and finally inside
MeV: above this value neutrons and
protons are basically free; below this value all neutrons are
substantially bound first inside D nuclei and finally inside
 nuclei, provided that there is enough
time before the fusion rate of nuclei becomes smaller than the
expansion rate of the Universe. Indeed, since the
nuclei, provided that there is enough
time before the fusion rate of nuclei becomes smaller than the
expansion rate of the Universe. Indeed, since the 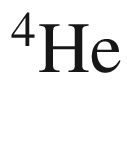 binding energy per nucleon is much
higher than those of D,
binding energy per nucleon is much
higher than those of D,  H, and
H, and  , and since there are no stable nuclei
with
, and since there are no stable nuclei
with  , then
, then  is the favorite final state.
is the favorite final state.

The observed and predicted abundances of
 , D,
, D,  , and
, and  Li. The bands show the 95% CL range.
Boxes represent the measured abundances. The narrow vertical band represents the constraints
at 95% CL on
Li. The bands show the 95% CL range.
Boxes represent the measured abundances. The narrow vertical band represents the constraints
at 95% CL on  (expressed in units of 10
(expressed in units of 10 ) from the CMB power spectrum analysis
while the wider is the Big Bang nucleosynthesis concordance range
From C. Patrignani et al. (Particle Data Group), Chin. Phys. C, 40,
100001 (2016)
) from the CMB power spectrum analysis
while the wider is the Big Bang nucleosynthesis concordance range
From C. Patrignani et al. (Particle Data Group), Chin. Phys. C, 40,
100001 (2016)
 He,
He,  , is
defined usually as the fraction of mass density of
, is
defined usually as the fraction of mass density of  He nuclei,
He nuclei,  (
( He), over the total baryonic mass
density,
He), over the total baryonic mass
density, 

 , i.e., that
, i.e., that


 ,
,  .
. MeV and
MeV and  0.1 MeV
0.1 MeV

 is in the range
is in the range

 and around three quarters is made of
hydrogen. There are however small fractions of
and around three quarters is made of
hydrogen. There are however small fractions of 
 , and
, and  H that did not turn into
H that did not turn into  , and there are, thus, tiny fractions
of
, and there are, thus, tiny fractions
of  Li and
Li and  Be that could have formed after the
production of
Be that could have formed after the
production of  and before the dilution of the nuclei
due to the expansion of the Universe. Although their abundances are
quantitatively quite small, the comparison of the expected and
measured ratios are important because they are rather sensitive to
the ratio of baryons to photons,
and before the dilution of the nuclei
due to the expansion of the Universe. Although their abundances are
quantitatively quite small, the comparison of the expected and
measured ratios are important because they are rather sensitive to
the ratio of baryons to photons, 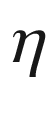 .
.In Fig. 8.11 the predicted
abundances of  ,
, 
 , and
, and  Li computed in the framework of the
standard model of Big Bang nucleosynthesis as a function of
Li computed in the framework of the
standard model of Big Bang nucleosynthesis as a function of
 are compared with measurements (for
details see the Particle Data Book). An increase in
are compared with measurements (for
details see the Particle Data Book). An increase in  will increase slightly the deuterium
formation temperature
will increase slightly the deuterium
formation temperature  (there are less
(there are less  per baryon available for the
photodissociation of the deuterium), and therefore, there is more
time for the development of the chain fusion processes ending at
the formation of the
per baryon available for the
photodissociation of the deuterium), and therefore, there is more
time for the development of the chain fusion processes ending at
the formation of the  . Therefore, the fraction of
. Therefore, the fraction of
 will increase slightly, in relative
terms, and the fraction of
will increase slightly, in relative
terms, and the fraction of  and
and  will decrease much more
significantly, again in relative terms. The evolution of the
fraction of
will decrease much more
significantly, again in relative terms. The evolution of the
fraction of  Li is, on the contrary, not
monotonous; it shows a minimum due to the fact that it is built up
from two processes that have a different behavior (the fusion of
Li is, on the contrary, not
monotonous; it shows a minimum due to the fact that it is built up
from two processes that have a different behavior (the fusion of
 and
and  H is a decreasing function of
H is a decreasing function of
 ; the production via
; the production via  Be is an increasing function of
Be is an increasing function of
 ).
).
Apart from the measured value for the
fraction of  Li all the other measurements converge
to a common value of
Li all the other measurements converge
to a common value of  that is, within the uncertainties,
compatible with the value indirectly determined by the study of the
acoustic peaks in the CMB power spectrum (see
Sect. 8.4).
that is, within the uncertainties,
compatible with the value indirectly determined by the study of the
acoustic peaks in the CMB power spectrum (see
Sect. 8.4).
8.1.5 Astrophysical Evidence for Dark Matter
Evidence thatthe Newtonian physics applied to visible matter does not describe the dynamics of stars, galaxies, and galaxy clusters were well established in the twentieth century.
As a first approximation, one can estimate the mass of a galaxy based on its brightness: brighter galaxies contain more stars than dimmer galaxies. However, there are other ways to assess the total mass of a galaxy. In spiral galaxies, for example, stars rotate in quasi-circular orbits around the center. The rotational speed of peripheral stars depends, according to Newton’s law, on the total mass of the galaxy, and one has thus an independent measurement of this mass. Do these two methods give consistent results?
 and for a spherical system
and for a spherical system
 , where the constant
, where the constant  depends on the density profile and it
is generally of order one. Since a generic astronomical object is
not at rest with respect to the Sun (because of the expansion of
the Universe, of the peculiar motion, etc.), the application of the
virial theorem to Coma requires the velocity to be measured with
respect to its center-of-mass. Accordingly,
depends on the density profile and it
is generally of order one. Since a generic astronomical object is
not at rest with respect to the Sun (because of the expansion of
the Universe, of the peculiar motion, etc.), the application of the
virial theorem to Coma requires the velocity to be measured with
respect to its center-of-mass. Accordingly,  should be replaced by
should be replaced by  , where
, where  is the three-dimensional velocity
dispersion of the Coma galaxies. Further, since only the
line-of-sight velocity dispersion
is the three-dimensional velocity
dispersion of the Coma galaxies. Further, since only the
line-of-sight velocity dispersion  of the galaxies can be measured,
Zwicky made the simplest possible assumption that Coma galaxies are
isotropically distributed, so that
of the galaxies can be measured,
Zwicky made the simplest possible assumption that Coma galaxies are
isotropically distributed, so that  . As far as the potential energy is
concerned, Zwicky assumed that galaxies are uniformly distributed
inside Coma, which yields
. As far as the potential energy is
concerned, Zwicky assumed that galaxies are uniformly distributed
inside Coma, which yields  . Thus, the virial theorem now reads
. Thus, the virial theorem now reads
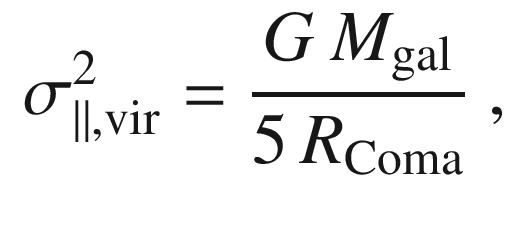
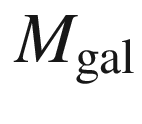 is the total mass of Coma in term of
galaxies (no intracluster gas was known at that time). Zwicky was
able to measure the line of sight of only seven galaxies of the
cluster; assuming them to be representative of the whole galaxy
population of Coma he found
is the total mass of Coma in term of
galaxies (no intracluster gas was known at that time). Zwicky was
able to measure the line of sight of only seven galaxies of the
cluster; assuming them to be representative of the whole galaxy
population of Coma he found  and
and  . Further, from the measured angular
diameter of Coma and its distance as derived from the Hubble law he
estimated
. Further, from the measured angular
diameter of Coma and its distance as derived from the Hubble law he
estimated  . Finally, Zwicky supposed that Coma
contains about N = 800 galaxies with mass
. Finally, Zwicky supposed that Coma
contains about N = 800 galaxies with mass  – which at that time was considered
typical for galaxies—thereby getting
– which at that time was considered
typical for galaxies—thereby getting  . Therefore Eq. (8.55) yields
. Therefore Eq. (8.55) yields  . Since
. Since  , in order to bring
, in order to bring  in agreement with
in agreement with  , Zwicky had to increase
, Zwicky had to increase  by a factor of about 200 (he wrote
400), thereby obtaining for the Coma galaxies
by a factor of about 200 (he wrote
400), thereby obtaining for the Coma galaxies  (he wrote
(he wrote  ). Thus, Zwicky ended up with the
conclusion that Coma galaxies have a mass about two orders of
magnitudes larger than expected: his explanation was that these
galaxies are totally dominated by dark matter.
). Thus, Zwicky ended up with the
conclusion that Coma galaxies have a mass about two orders of
magnitudes larger than expected: his explanation was that these
galaxies are totally dominated by dark matter.Despite this early evidence, it was only in the 1970s that scientists began to explore this discrepancy in a systematic way and that the existence of dark matter started to be quantified. It was realized that the discovery of dark matter would not only have solved the problem of the lack of mass in clusters of galaxies, but would also have had much more far-reaching consequences on our prediction of the evolution and fate of the Universe.
An important observational evidence of the need for dark matter was provided by the rotation curves of spiral galaxies—the Milky Way is one of them. Spiral galaxies contain a large population of stars placed on nearly circular orbits around the Galactic center. Astronomers have conducted observations of the orbital velocities of stars in the peripheral regions of a large number of spiral galaxies and found that the orbital speeds remain constant, contrary to the expected prediction of reduction at larger radii. The mass enclosed within the orbits radius must therefore gradually increase in regions even beyond the edge of the visible galaxy.
Later, another independent confirmation of Zwicky’s findings came from gravitational lensing. Lensing is the effect that bends the light coming from distant objects, due to large massive bodies in the path to the observer. As such it constitutes another method of measuring the total content of gravitational matter. The obtained mass-to-light ratios in distant clusters match the dynamical estimates of dark matter in those clusters.
8.1.5.1 How Is Dark Matter Distributed in Galaxies?
 the mass of a star, we have
the mass of a star, we have
 where M(r)
is the total mass inside the radius r of the orbit of the star:
where M(r)
is the total mass inside the radius r of the orbit of the star:

 ; Eq. 8.56 yields
; Eq. 8.56 yields  . This behavior is called Keplerian because it is identical to that
of the rotation velocity of the planets orbiting the Sun. Yet, the
observations of Rubin and collaborators showed that v(r)
rises close enough to the center, and then reaches a maximum and
stays constant as r increases,
failing to exhibit the expected Keplerian fall-off. According to
Eq. 8.56 the
observed behavior implies that in order to have
. This behavior is called Keplerian because it is identical to that
of the rotation velocity of the planets orbiting the Sun. Yet, the
observations of Rubin and collaborators showed that v(r)
rises close enough to the center, and then reaches a maximum and
stays constant as r increases,
failing to exhibit the expected Keplerian fall-off. According to
Eq. 8.56 the
observed behavior implies that in order to have  it is necessary that
it is necessary that  . But since
. But since
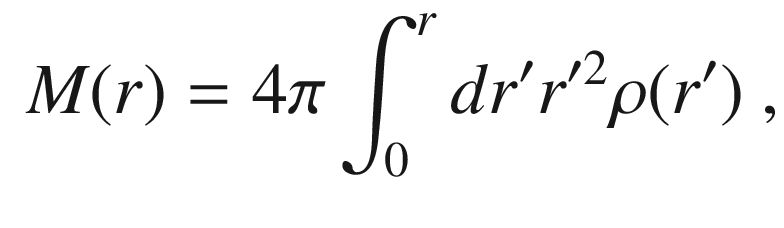
 is the mass density, the conclusion
is that at large enough galactocentric distance the mass density
goes like
is the mass density, the conclusion
is that at large enough galactocentric distance the mass density
goes like  . In analogy with the behavior of a
self-gravitating isothermal gas sphere, the behavior is called
singular isothermal. As a
consequence, spiral galaxies turn out to be surrounded in first
approximation by a singular isothermal halo made of dark matter. In
order to get rid of the central singularity, it is often assumed
that the halo profile is pseudo-isothermal, assuming a density:
. In analogy with the behavior of a
self-gravitating isothermal gas sphere, the behavior is called
singular isothermal. As a
consequence, spiral galaxies turn out to be surrounded in first
approximation by a singular isothermal halo made of dark matter. In
order to get rid of the central singularity, it is often assumed
that the halo profile is pseudo-isothermal, assuming a density:

 , too small to draw waterproof
conclusion when errors are taken into account. Luckily, the disks
of spirals also contain neutral atomic hydrogen (HI) clouds; like
stars they move on nearly circular orbits, but the gaseous disk
extends typically twice, and in some cases even more. According to
relativistic quantum mechanics, the nonrelativistic ground state of
hydrogen at
, too small to draw waterproof
conclusion when errors are taken into account. Luckily, the disks
of spirals also contain neutral atomic hydrogen (HI) clouds; like
stars they move on nearly circular orbits, but the gaseous disk
extends typically twice, and in some cases even more. According to
relativistic quantum mechanics, the nonrelativistic ground state of
hydrogen at  splits into a pair of levels,
depending on the relative orientation of
the spins of the proton and the electron; the energy splitting is
only
splits into a pair of levels,
depending on the relative orientation of
the spins of the proton and the electron; the energy splitting is
only  eV (hyperfine splitting). Both levels
are populated thanks to collisional excitation and interaction with
the CMB; thus, HI clouds can be detected by radio-telescopes since
photons emitted during the transition to the ground state have a
wavelength of about 21 cm. In 1985 Van Albada, Bahcall, Begeman and
Sancisi performed this measurement for the spiral NGC 3198, whose
gaseous disks is more extended than the stellar disk by a factor of
2.7, and could construct the rotation curve out to
eV (hyperfine splitting). Both levels
are populated thanks to collisional excitation and interaction with
the CMB; thus, HI clouds can be detected by radio-telescopes since
photons emitted during the transition to the ground state have a
wavelength of about 21 cm. In 1985 Van Albada, Bahcall, Begeman and
Sancisi performed this measurement for the spiral NGC 3198, whose
gaseous disks is more extended than the stellar disk by a factor of
2.7, and could construct the rotation curve out to  . They found that the flat behavior
persists, and this was regarded as a clear-cut evidence for dark
matter halos around spiral galaxies. Measurements now include a
large set of galaxies (Fig. 8.12), including the Milky Way
(Fig. 8.13).
. They found that the flat behavior
persists, and this was regarded as a clear-cut evidence for dark
matter halos around spiral galaxies. Measurements now include a
large set of galaxies (Fig. 8.12), including the Milky Way
(Fig. 8.13).

Rotation curve of the galaxy M33 (from Wikimedia Commons, public domain)

Rotation curve of the Milky Way (from http://abyss.uoregon.edu)
Profiles obtained in numerical
simulations of dark matter including baryons are steeper in the
center than those obtained from simulations with dark matter only.
The Navarro, Frenk, and White (NFW) profile, often used as a benchmark, follows a  distribution at the center. On the
contrary, the Einasto profile does not
follow a power law near the center of galaxies, is smoother at kpc
scales, and seems to fit better more recent numerical simulations.
A value of about 0.17 for the shape parameter
distribution at the center. On the
contrary, the Einasto profile does not
follow a power law near the center of galaxies, is smoother at kpc
scales, and seems to fit better more recent numerical simulations.
A value of about 0.17 for the shape parameter  in Eq. 8.59 is consistent with
present data and simulations. Moore and collaborators have
suggested profiles steeper than NFW.
in Eq. 8.59 is consistent with
present data and simulations. Moore and collaborators have
suggested profiles steeper than NFW.
![$$\begin{aligned} \begin{array}{rrcl} \mathrm{NFW}: &{} \rho _\mathrm{NFW}(r) &{} = &{} \displaystyle \rho _{s}\frac{r_{s}}{r}\left( 1+\frac{r}{r_{s}}\right) ^{-2} \\ \mathrm{Einasto}: &{} \rho _\mathrm{Einasto}(r) &{} = &{} \displaystyle \rho _{s}\exp \left\{ -\frac{2}{\alpha }\left[ \left( \frac{r}{r_{s}}\right) ^{\alpha }-1\right] \right\} \\ \mathrm{Moore}: &{} \rho _\mathrm{Moore}(r) &{} = &{} \displaystyle \rho _{s} \left( \frac{r_s}{r}\right) ^{1.16} \left( 1+\frac{r}{r_s}\right) ^{-1.84} . \end{array} \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_8_Chapter/304327_2_En_8_Chapter_TeX_Equ59.png)


Comparison of the densities as a function of
the radius for DM profiles used in the literature, with values
adequate to fit the radial distribution of velocities in the halo
of the Milky Way. The curve EinastoB indicates an Einasto curve
with a different  parameter. From M. Cirelli et al.,
“PPPC 4 DM ID: A Poor Particle Physicist Cookbook for Dark Matter
Indirect Detection”, arXiv:1012.4515, JCAP 1103 (2011) 051
parameter. From M. Cirelli et al.,
“PPPC 4 DM ID: A Poor Particle Physicist Cookbook for Dark Matter
Indirect Detection”, arXiv:1012.4515, JCAP 1103 (2011) 051
 –
– , to be compared with the
, to be compared with the  of our Galaxy. For these galaxies the
ratio between the estimate of the total mass M inferred from the velocity dispersion
(velocities of single stars are measured with an accuracy of a few
kilometers per second thanks to optical measurements) and the
luminous mass L, inferred from
the count of the number of stars, can be very large. The dwarf
spheroidal satellites of the Milky Way could become tidally
disrupted if they did not have enough dark matter. In addition
these objects are not far from us: a possible DM signal should not
be attenuated by distance dimming. Table 8.1 shows some
characteristics of dSph in the Milky Way; their position is shown
in Fig. 8.15.
of our Galaxy. For these galaxies the
ratio between the estimate of the total mass M inferred from the velocity dispersion
(velocities of single stars are measured with an accuracy of a few
kilometers per second thanks to optical measurements) and the
luminous mass L, inferred from
the count of the number of stars, can be very large. The dwarf
spheroidal satellites of the Milky Way could become tidally
disrupted if they did not have enough dark matter. In addition
these objects are not far from us: a possible DM signal should not
be attenuated by distance dimming. Table 8.1 shows some
characteristics of dSph in the Milky Way; their position is shown
in Fig. 8.15.
A list of dSph satellites of the Milky Way that may represent the best candidates for DM searches according to their distance from the Sun, luminosity, and inferred M / L ratio
|
dSph |
|
L
( |
M / L ratio |
|---|---|---|---|
|
Segue 1 |
23 |
0.3 |
>1000 |
|
UMa II |
32 |
2.8 |
1100 |
|
Willman 1 |
38 |
0.9 |
700 |
|
Coma Berenices |
44 |
2.6 |
450 |
|
UMi |
66 |
290 |
580 |
|
Sculptor |
79 |
2200 |
7 |
|
Draco |
82 |
260 |
320 |
|
Sextans |
86 |
500 |
90 |
|
Carina |
101 |
430 |
40 |
|
Fornax |
138 |
15500 |
10 |

The Local Group of galaxies around the Milky Way (from http://abyss.uoregon.edu/~js/ast123/lectures/lec11.html). The largest galaxies are the Milky Way, Andromeda, and M33, and have a spiral form. Most of the other galaxies are rather small and with a spheroidal form. These orbit closely the large galaxies, as is also the case of the irregular Magellanic Clouds, best visible in the Southern hemisphere, and located at a distance of about 120,000 ly, to be compared with the Milky Way radius of about 50,000 ly
The observations of the dynamics of galaxies and clusters of galaxies, however, are not the only astrophysical evidence of the presence of DM. Cosmological models for the formation of galaxies and clusters of galaxies indicate that these structures fail to form without DM.
8.1.5.2 An Alternative Explanation: Modified Gravity
The dependence of  on the mass M(r)
on which the evidence for DM is based relies on the virial theorem,
stating that the kinetic energy is on average equal to the absolute
value of the total energy for a bound state, defining zero
potential energy at infinite distance. The departure from this
Newtonian prediction could also be related to a departure from
Newtonian gravity.
on the mass M(r)
on which the evidence for DM is based relies on the virial theorem,
stating that the kinetic energy is on average equal to the absolute
value of the total energy for a bound state, defining zero
potential energy at infinite distance. The departure from this
Newtonian prediction could also be related to a departure from
Newtonian gravity.
Alternative theories do not necessarily require dark matter, and replace it with a modified Newtonian gravitational dynamics. Notice that, in a historical perspective, deviations from expected gravitational dynamics already led to the discovery of previously unknown matter sources. Indeed, the planet Neptune was discovered following the prediction by Le Verrier in the 1840s of its position based on the detailed observation of the orbit of Uranus and Newtonian dynamics. In the late nineteenth century, the disturbances to the expected orbit of Neptune led to the discovery of Pluto. On the other hand, the precession of the perihelion of Mercury, which could not be quantitatively explained by Newtonian gravity, confirmed the prediction of general relativity—and thus a modified dynamics.
 at small values of the acceleration,
and proposes the following modification:
at small values of the acceleration,
and proposes the following modification:

 is positive, smooth, and
monotonically increasing; it is approximately equal to its argument
when the argument takes small values compared to unity (deep MOND
limit), but approaches unity when that argument is large.
is positive, smooth, and
monotonically increasing; it is approximately equal to its argument
when the argument takes small values compared to unity (deep MOND
limit), but approaches unity when that argument is large.
 is a constant of the order of
is a constant of the order of
 .
. and we can approximate
and we can approximate  . One has then
. One has then

 given by
given by
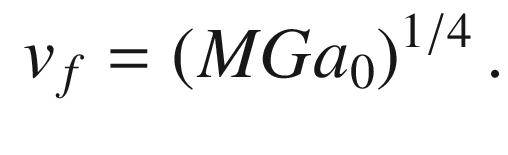
 .
.

The matter in the “bullet cluster” is shown in this composite image
(from http://apod.nasa.gov/apod/ap060824.html, credits: NASA/CXC/CfA/ M. Markevitch et al.). In this image depicting the collision of two clusters of galaxies, the bluish areas show the distributions of dark matter in the clusters, as obtained from gravitational lensing, and the red areas correspond to the hot X-ray emitting gases. The individual galaxies observed in the optical image data have a total mass much smaller than the mass in the gas, but the sum of these masses is far less than the mass of dark matter. The clear separation of dark matter and gas clouds is a direct evidence of the existence of dark matter
One could also consider the fact that galaxies may contain invisible matter of known nature, either baryons in a form which is hard to detect optically, or massive neutrinos—MOND reduces the amount of invisible matter needed to explain the observations.
8.1.6 Age of the Universe: A First Estimate
The age of the Universe is an old question. Has the Universe a finite age? Or is the Universe eternal and always equal to itself (steady state Universe)?
For sure the Universe must be older than
the oldest object that it contains and the first question has been
then: how old is the Earth? In the eleventh century, the Persian
astronomer Abu Rayhan al-Biruni had already realized that Earth
should have a finite age, but he just stated that the origin of
Earth was too far away to possibly measure it. In the nineteenth
century the first quantitative estimates finally came. From
considerations, both, on the formation of the geological layers,
and on the thermodynamics of the formation and cooling of Earth, it
was estimated that the age of the Earth should be of the order of
tens of millions of years. These estimates were in contradiction
with both, some religious beliefs, and Darwin’s theory of
evolution. Rev. James Ussher, an Irish Archbishop, published in
1650 a detailed calculation concluding that according to the Bible
“God created Heaven and Earth” some six thousand years ago, more
precisely “at the beginning of the night of October 23rd in the
year 710 of the Julian period”, which means 4004 B.C.. On the other
hand, tens or even a few hundred million years seemed to be a too
short time to allow for the slow evolution advocated by Darwin.
Only the discovery of radioactivity at the end of nineteenth
century provided precise clocks to date rocks and meteorite debris
with, and thus to allow for reliable estimates of the age of the
Earth. Surveys in the Hudson Bay in Canada found rocks with ages of
over four billion ( ) years. On the other hand
measurements on several meteorites, in particular on the Canyon
Diablo meteorite found in Arizona, USA, established dates of the
order of
) years. On the other hand
measurements on several meteorites, in particular on the Canyon
Diablo meteorite found in Arizona, USA, established dates of the
order of  years. Darwin had the time he
needed!
years. Darwin had the time he
needed!
The proportion of elements other than hydrogen and helium (defined as the metallicity) in a celestial object can be used as an indication of its age. After primordial nucleosynthesis (Sect. 8.1.4) the Universe was basically composed by hydrogen and helium. Thus the older (first) stars should have lower metallicity than the younger ones (for instance our Sun). The measurement of the age of low metallicity stars imposes, therefore, an important constraint on the age of the Universe. Oldest stars with a well-determined age found so far are, for instance, HE 1523-0901, a red giant at around 7500 light-years away from us, and HD 140283, denominated the Methuselah star, located around 190 light years away. The age of HE 1523-0901 was measured to be 13.2 Gyr, using mainly the decay of uranium and thorium. The age of HD 140283 was determined to be (14.5 ± 0.8) Gyr.

 CDM model (see Sect. 8.4) the best-fit value,
taking into account the present knowledge of such parameters, is
CDM model (see Sect. 8.4) the best-fit value,
taking into account the present knowledge of such parameters, is

Finally, we stress that a Universe with
a finite age and in expansion will escape the nineteenth-century
Olbers’ Paradox: “How can the night be
dark?” This paradox relies on the argument that in an infinite
static Universe with uniform star density (as the Universe was
believed to be by most scientists until the mid of last century)
the night should be as bright as the day. In fact, the light coming
from a star is inversely proportional to the square of its
distance, but the number of stars in a shell at a distance between
r and  is proportional to the square of the
distance r. From this it seems
that any shell in the Universe should contribute the same amount
light. Apart from some too crude approximations (such as, not
taking into account the finite life of stars), redshift and the
finite size of the Universe solve the paradox.
is proportional to the square of the
distance r. From this it seems
that any shell in the Universe should contribute the same amount
light. Apart from some too crude approximations (such as, not
taking into account the finite life of stars), redshift and the
finite size of the Universe solve the paradox.
8.2 General Relativity
Special relativity, introduced in Chap. 2, states that one cannot distinguish on the basis of the laws of physics between two inertial frames moving at constant speed one with respect to the other. Experience tells that it is possible to distinguish between an inertial frame and an accelerated frame. Can the picture change if we include gravity?
 ; this, in turn, is proportional to
the inertial mass
; this, in turn, is proportional to
the inertial mass  , that characterizes the body’s
inertia to be accelerated by a force. The net result is that the
local acceleration of a body, g, due to a gravitational field created
by a mass M at a distance
r, is proportional to the ratio
, that characterizes the body’s
inertia to be accelerated by a force. The net result is that the
local acceleration of a body, g, due to a gravitational field created
by a mass M at a distance
r, is proportional to the ratio
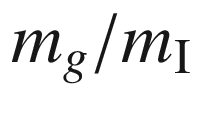


Thus if  were proportional to
were proportional to  the movement of a body in a
gravitational field would be independent of its mass and
composition. In fact the experiments of Galilei on inclined planes
showed the universality of the movement of rolling balls of
different compositions and weights. Such universality was also
found by measuring the period of pendulums with different weights
and compositions but identical lengths, first again by Galilei, and
later on with a much higher precision (better than 0.1%) by Newton.
Nowadays,
the movement of a body in a
gravitational field would be independent of its mass and
composition. In fact the experiments of Galilei on inclined planes
showed the universality of the movement of rolling balls of
different compositions and weights. Such universality was also
found by measuring the period of pendulums with different weights
and compositions but identical lengths, first again by Galilei, and
later on with a much higher precision (better than 0.1%) by Newton.
Nowadays,  is experimentally known to be
constant for all bodies, independent of their nature, mass, and
composition, up to a relative resolution of
is experimentally known to be
constant for all bodies, independent of their nature, mass, and
composition, up to a relative resolution of  . We then choose G in such a way that
. We then choose G in such a way that  . Space-based experiments, allowing
improved sensitivities up to
. Space-based experiments, allowing
improved sensitivities up to  on
on  , are planned for the next years.
, are planned for the next years.
8.2.1 Equivalence Principle
It is difficult to believe that such a precise equality is just a coincidence. This equality has been thus promoted to the level of a principle, named the weak equivalence principle , and it led Einstein to formulate the strong equivalence principle which is a fundamental postulate of General Relativity (GR) . Einstein stated that it is not possible to distinguish infinitesimal movements occurring in an inertial frame due to gravity (which are proportional to the gravitational mass), from movements occurring in an accelerated frame due to “fictitious” inertial forces (which are proportional to the inertial mass).

Scientists performing experiments in an accelerating spaceship moving with an upward acceleration g (left) obtain the same results as if they were on a planet with gravitational acceleration g (right). From A. Zimmerman Jones, D. Robbins, “String Theory For Dummies”, Wiley 2009
8.2.2 Light and Time in a Gravitational Field
In the same way, if an observer is inside a free-falling elevator, gravity is locally canceled out by the “fictitious” forces due to the acceleration of the frame. Free-falling frames are equivalent to inertial frames. A horizontal light beam in such a free falling elevator then moves in a straight line for an observer inside the elevator, but it curves down for an observer outside the elevator (Fig. 8.18). Light therefore curves in a gravitational field.

Trajectory of a light beam in an elevator freely falling seen by an observer inside (left) and outside (right): Icons made by Freepik from www.flaticon.com

Rocket on the left: Two clocks onboard an accelerating rocket. Two rockets on the right: Why the clock at the head appears to run faster than the clock at the tail
 and the second flash travels the
shorter distance L
and the second flash travels the
shorter distance L , because the ship is accelerating and
has a higher speed at the time of the second flash. You can see,
then, that if the two flashes were emitted from clock A one second
apart, they would arrive at clock B with a separation somewhat less
than one second, since the second flash does not spend as much time
on the way. The same will also happen for all the later flashes. So
if you were sitting in the tail you would conclude that clock A was
running faster than clock B. If the rocket is at rest in a
gravitational field, the principle of equivalence guarantees that
the same thing happens. We have the relation
, because the ship is accelerating and
has a higher speed at the time of the second flash. You can see,
then, that if the two flashes were emitted from clock A one second
apart, they would arrive at clock B with a separation somewhat less
than one second, since the second flash does not spend as much time
on the way. The same will also happen for all the later flashes. So
if you were sitting in the tail you would conclude that clock A was
running faster than clock B. If the rocket is at rest in a
gravitational field, the principle of equivalence guarantees that
the same thing happens. We have the relation


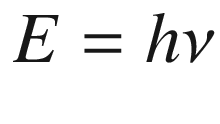 :
:

8.2.3 Flat and Curved Spaces
Gravity in GR is no longer a force (whose sources are the masses) acting in a flat spacetime Universe. Gravity is embedded in the geometry of spacetime that is determined by the energy and momentum contents of the Universe.
Classical mechanics considers that we
are living in a Euclidean three-dimensional space (flat, i.e., with vanishing curvature),
where through each point outside a “straight” line (a geodesic)
there is one, and only one, straight line
parallel to the first one; the sum of the internal angles of a
triangle is  ; the circumference of a circle of
radius R is
; the circumference of a circle of
radius R is  , and so on. However, it is
interesting to consider what would happen if this were not the
case.
, and so on. However, it is
interesting to consider what would happen if this were not the
case.
 ; the circumference of a circle of
radius R is less than
; the circumference of a circle of
radius R is less than
 . Alternatively, let us imagine that
we were living on a saddle, which has a negative curvature (the
surface can curve away from the tangent plane in two different
directions): then the sum of the angles of a triangle is less than
. Alternatively, let us imagine that
we were living on a saddle, which has a negative curvature (the
surface can curve away from the tangent plane in two different
directions): then the sum of the angles of a triangle is less than
 ; the perimeter of a circumference is
greater than
; the perimeter of a circumference is
greater than  , and so on. The three cases are
visualized in Fig. 8.20. The metric of the sphere and of the
saddle are not Euclidean.
, and so on. The three cases are
visualized in Fig. 8.20. The metric of the sphere and of the
saddle are not Euclidean.

2D surfaces with positive, negative, and null curvatures
(from http://thesimplephysicist.com,
 2014 Bill
Halman/tdotwebcreations)
2014 Bill
Halman/tdotwebcreations)
8.2.3.1 2D Space



 of the 2D flat surface is constant
and the geodesics are straight lines.
of the 2D flat surface is constant
and the geodesics are straight lines.

Distances on a sphere of radius a. From A. Tan et al. DOI:10.5772/50508
The maximum distance between two points
on the sphere is bounded by  : the two points are the extrema of a
half great circle.
: the two points are the extrema of a
half great circle.

 term. It is not possible to cover the
entire sphere with one unique plane without somewhat distorting the
plane, although it is always possible to define locally at each
point one tangent plane. The geodesics are not straight lines; they
are indeed part of great circles, as it can be deduced directly
from the metrics and its derivatives.
term. It is not possible to cover the
entire sphere with one unique plane without somewhat distorting the
plane, although it is always possible to define locally at each
point one tangent plane. The geodesics are not straight lines; they
are indeed part of great circles, as it can be deduced directly
from the metrics and its derivatives. as
as


 ) curvature at any point of its
surface. However, the above expressions are valid both for the case
of negative (
) curvature at any point of its
surface. However, the above expressions are valid both for the case
of negative ( ) and null (
) and null ( ) curvature. In the case of a flat
surface, indeed, the usual expression in polar coordinates is
recovered:
) curvature. In the case of a flat
surface, indeed, the usual expression in polar coordinates is
recovered:

 and, respectively,
and, respectively,  and
and  , is given by:
, is given by:




 :
:
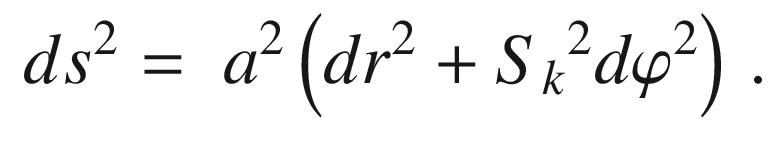
8.2.3.2 3D Space
 are independent variables) leading
to:
are independent variables) leading
to:
![$$\begin{aligned} ds^2=\ a^2\left[ \frac{dr^2}{1-Kr^2}+r^2\ \left( d{\theta }^2+{\sin }^2\theta \ d{\varphi }^2\right) \right] \, . \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_8_Chapter/304327_2_En_8_Chapter_TeX_Equ235.png)
8.2.3.3 4D Spacetime
 :
:
![$$\begin{aligned} ds^2=\ dt^2-\ a^2(t) \left[ \frac{dr^2}{1-Kr^2}+r^2\ \left( d{\theta }^2+{\sin }^2\theta \ d{\varphi }^2\right) \right] \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_8_Chapter/304327_2_En_8_Chapter_TeX_Equ76.png)
 , the FLRW metric can be written as
, the FLRW metric can be written as
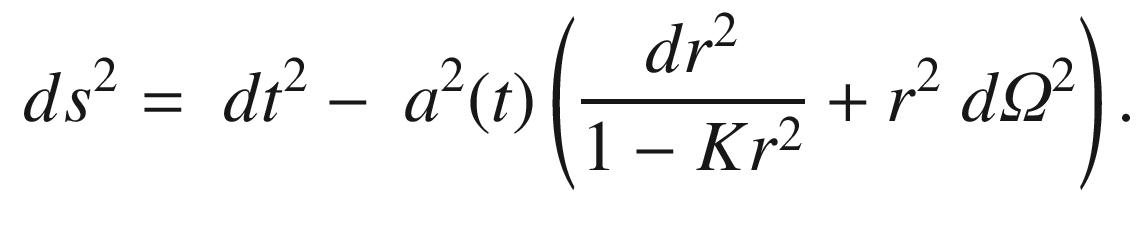
 introduced above as
introduced above as

 ) of the FLRW metric.
) of the FLRW metric.The geodesics in a 4D spacetime correspond to the extremal (maximum or minimum depending on the metric definition) world lines joining two events in spacetime and not to the 3D space paths between the two points. The geodesics are determined, as before, just from the metric and its derivatives.
8.2.4 Einstein’s Equations

 and
and  are, respectively, the Einstein and
the Ricci tensors, which are built from the metric and its
derivatives;
are, respectively, the Einstein and
the Ricci tensors, which are built from the metric and its
derivatives;  is the Ricci scalar
is the Ricci scalar  and
and  is the energy–momentum tensor.
is the energy–momentum tensor.The energy and the momentum of the particles determine the geometry of the Universe which then determines the trajectories of the particles. Gravity is embedded in the geometry of spacetime. Time runs slower in the presence of gravitational fields.
Einstein’s equations are tensor equations and thus independent on the reference frame (the covariance of the physics laws is automatically ensured). They involve 4D symmetric tensors and represent in fact 10 independent nonlinear partial differential equations whose solutions, the metrics of spacetime, are in general difficult to sort out. However, in particular and relevant cases, exact or approximate solutions can be found. Examples are the Minkowski metric (empty Universe); the Schwarzschild metric (spacetime metric outside a noncharged spherically symmetric nonrotating massive object—see Sect. 8.2.8); the Kerr metric (a cylindrically symmetric vacuum solution); the FLRW metric (homogeneous and isotropic Universe—see Sect. 8.2.5).
 constant in space and time, the
so-called “cosmological constant”):
constant in space and time, the
so-called “cosmological constant”):

 in a
Universe of free noninteracting particles with four-momentum
in a
Universe of free noninteracting particles with four-momentum
 moving along trajectories
moving along trajectories
 is defined as
is defined as

 terms can be seen as “charges” and
the
terms can be seen as “charges” and
the  terms as “currents”, which then obey
a continuity equation ensuring energy–momentum conservation. In
general relativity local energy–momentum conservation generalizes
the corresponding results in special relativity,
terms as “currents”, which then obey
a continuity equation ensuring energy–momentum conservation. In
general relativity local energy–momentum conservation generalizes
the corresponding results in special relativity,

 and pressure
and pressure 

 and accounts for the “kinetic energy”
of the fluid.
and accounts for the “kinetic energy”
of the fluid. and pressure
and pressure  the weak gravity field predicted by
Newton is given by
the weak gravity field predicted by
Newton is given by





 are the Christoffel symbols given by
are the Christoffel symbols given by

 , and then
, and then

8.2.5 The Friedmann–Lemaitre–Robertson–Walker Model (Friedmann Equations)
The present standard model of cosmology assumes the so-called cosmological principle, which in turn assumes a homogeneous and isotropic Universe at large scales. Homogeneity means that, in Einstein’s words, “all places in the Universe are alike” and isotropic just means that all directions are equivalent.
The FLRW metric discussed before (Sect. 8.2.3) embodies these symmetries leaving two independent functions, a(t) and K(t), which represent, respectively, the evolution of the scale and of the curvature of the Universe. The Russian physicist Alexander Friedmann in 1922, and independently the Belgian Georges Lemaitre in 1927, solved Einstein’s equations for such a metric leading to the famous Friedmann equations, which are still the starting point for the standard cosmological model, also known as the Friedmann–Lemaitre–Robertson–Walker (FLRW) model.
 ) as
) as



 with the volume V we can recognize adiabatic energy
conservation
with the volume V we can recognize adiabatic energy
conservation



8.2.5.1 Classical Newtonian Mechanics
- 1.
From Newton law of gravitation and from the Newton second law of motion we can write
 (8.94)
(8.94) - 2.
From energy conservation
 (8.95)
(8.95)
The two Friedmann equations are
“almost” recovered. The striking differences are that in classical
mechanics the pressure does not contribute to the “gravitational
mass”, and that the  term must be introduced by hand as a
form of repulsive potential.
term must be introduced by hand as a
form of repulsive potential.
The curvature of spacetime is, in this “classical” version, associated to (minus) the total energy of the system, which can somehow be interpreted as a “binding energy”.
8.2.5.2 Single Component Universes
The two Friedmann equations determine,
once the energy density  and the pressure
and the pressure  are known, the evolution of the scale
a(t) and of the curvature K(t)
of the Universe. However,
are known, the evolution of the scale
a(t) and of the curvature K(t)
of the Universe. However,  and
and  are nontrivial quantities, depending
critically on the amount of the different forms of energy and
matter that exist in the Universe at each evolution stage.
are nontrivial quantities, depending
critically on the amount of the different forms of energy and
matter that exist in the Universe at each evolution stage.
 ) and the Friedmann equations can be
approximated as
) and the Friedmann equations can be
approximated as


 and
and  of the type
of the type  , the solutions are
, the solutions are

 , and we obtain
, and we obtain

 ) combines with a decrease in the mean
photon energy (
) combines with a decrease in the mean
photon energy ( ) corresponding to wavelength
dilation.
) corresponding to wavelength
dilation.8.2.5.3 Static Universe and Vacuum Energy Density
 ,
,  ) one should have:
) one should have:

 ) and
) and  . This requires a “new form of energy”
with negative
. This requires a “new form of energy”
with negative  , which can be related to the
“cosmological” constant term. By reading this term on the
right-hand side of Einstein’s equations, we can formally include it
in the energy–momentum tensor, thus defining a “vacuum” tensor as
, which can be related to the
“cosmological” constant term. By reading this term on the
right-hand side of Einstein’s equations, we can formally include it
in the energy–momentum tensor, thus defining a “vacuum” tensor as


 :
:



8.2.5.4 De Sitter Universe
 ), as first discussed by de Sitter,
), as first discussed by de Sitter,




8.2.6 Critical Density of the Universe; Normalized Densities



 this corresponds to
this corresponds to

8.2.6.1
Normalized Densities  , H, and
, H, and 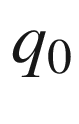





 ,
,  ).
).

 can also be expressed as a function
of the normalized densities
can also be expressed as a function
of the normalized densities  . In fact
. In fact 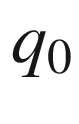 was defined as
(Sect. 8.1.1)
was defined as
(Sect. 8.1.1)

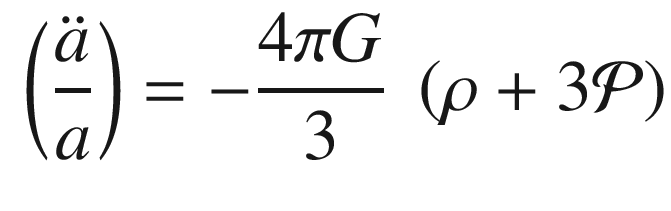




 are of the utmost importance, since
they connect directly the experimentally measured quantities
are of the utmost importance, since
they connect directly the experimentally measured quantities
 and
and  to the densities of the various
energy species in the Universe.
to the densities of the various
energy species in the Universe.8.2.6.2 Experimental Determination of the Normalized Densities

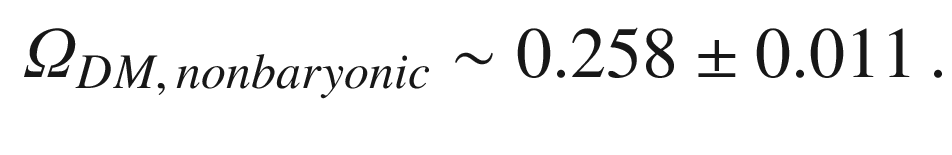
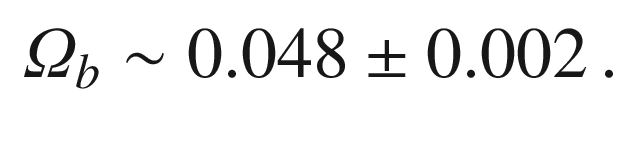
In summary, a remarkable agreement of independent astrophysical observations with cosmological global fits indicates that the energy content of DM in the Universe could be about 25% of the total energy of the Universe, compared to some 5% due to ordinary matter.


 is the sum of
is the sum of  ,
,  and
and  , with
, with  being negligible. This means that, in
general,
being negligible. This means that, in
general,  is a function of time, unless
is a function of time, unless
 and thus
and thus  (flat Universe).
(flat Universe).
 is identically one. For this reason
this fact is at the heart of the standard model of cosmology, the
is identically one. For this reason
this fact is at the heart of the standard model of cosmology, the
 CDM model,
which postulates
CDM model,
which postulates  .
.8.2.7 Age of the Universe from the Friedmann Equations and Evolution Scenarios



 and radiation
and radiation  dominated Universes the solutions
are, respectively,
dominated Universes the solutions
are, respectively,


 ,
,  ) we obtain
) we obtain

8.2.7.1 Evolution Scenarios
-
the present value of the Hubble parameter,
 ;
; -
the present value of the energy density of radiation,
 (we shall omit the subscript 0);
(we shall omit the subscript 0); -
the present value of the energy density of matter,
 ;
; -
the present value of the energy density of vacuum,
 .
.

The different ages the Universe passed through since the Big Bang
(from
http://scienceblogs.com/startswithabang/files/2013/06/AT_7e_Figure_27_01.jpeg,
 2011 Pearson education, Pearson
Addison Wesley)
2011 Pearson education, Pearson
Addison Wesley)
However, as we have discussed above, the evolution of the energy density of the different components scales with different powers of the scale parameter of the Universe a. Therefore, there are “eras” where a single component dominates. It is then reasonable to suppose that, initially, the Universe was radiation dominated (apart for a very short period where it is believed that inflation occurred—see Sect. 8.3.2), then that it was matter dominated and finally, at the present time, that it is the vacuum energy (mostly “dark” energy, i.e., not coming from quantum fluctuations of the vacuum of the known interactions) that is starting to dominate (Fig. 8.22).
 ) between the matter and radiation
ages can be obtained, in first approximation, by just equalizing
the corresponding densities:
) between the matter and radiation
ages can be obtained, in first approximation, by just equalizing
the corresponding densities:





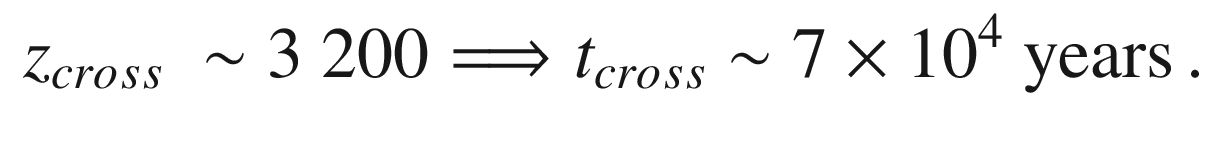
 and
and  . Although this is a restricted
parameter phase space, there are several different possible
evolution scenarios as shown in Fig. 8.23:
. Although this is a restricted
parameter phase space, there are several different possible
evolution scenarios as shown in Fig. 8.23:
- 1.
If
 the Universe is flat but it can
expand forever (
the Universe is flat but it can
expand forever ( ) or eventually recollapses
(
) or eventually recollapses
( ).
). - 2.
If
 the Universe is closed (positive
curvature).
the Universe is closed (positive
curvature). - 3.
If
 the Universe is open (negative
curvature).
the Universe is open (negative
curvature). - 4.
In a small phase space region with
 and
and  there is a solution for which the
Universe bounces between a minimum and a maximum scale factor.
there is a solution for which the
Universe bounces between a minimum and a maximum scale factor.
Some of these evolution scenarios are represented as functions of time in Fig. 8.24 for selected points in the parameter space discussed above. The green curve represents a flat, matter-dominated, critical density Universe (the expansion rate is slowing down forever). The blue curve shows an open, low density, matter-dominated Universe (the expansion is slowing down, but not as much). The orange curve shows a closed, high-density Universe (the expansion reverts to a “big crunch” ). The red curve shows a Universe with a large fraction of “dark energy” (the expansion of the Universe accelerates).

Different scenarios for the expansion of the
Universe. The Hubble constant was fixed to  (km/s)/Mpc. From J.A. Peacock,
“Cosmological Physics”, Cambridge University Press 1998
(km/s)/Mpc. From J.A. Peacock,
“Cosmological Physics”, Cambridge University Press 1998

Evolution of the Universe in a two-component
model (matter and vacuum) for different ( ,
,  values.
values.
8.2.8 Black Holes
The first analytical solution of Einstein’s equations was found in 1915, just a month after the publication of Einstein’s original paper, by Karl Schwarzschild , a German physicist who died one year later from a disease contracted on the First World War battlefield.


 , we recover flat spacetime. According
to this solution, a clock with period
, we recover flat spacetime. According
to this solution, a clock with period  placed at a point r is seen by an observer placed at
placed at a point r is seen by an observer placed at
 with a period
with a period  given by:
given by:

 (the Schwarzschild radius) the metric shows a coordinate singularity: the
time component goes to zero and the radial component goes to
infinity. From the point of view of an asymptotic observer, the
period
(the Schwarzschild radius) the metric shows a coordinate singularity: the
time component goes to zero and the radial component goes to
infinity. From the point of view of an asymptotic observer, the
period  is seen now as infinitely large. No
light emitted at
is seen now as infinitely large. No
light emitted at  is able to reach the
is able to reach the  world. This is what is usually
called, following John Wheeler, a “black hole”.
world. This is what is usually
called, following John Wheeler, a “black hole”.

The singularity observed in the Schwarzschild metric is not in fact a real physics singularity; it depends on the reference frame chosen (see [F8.3] for a discussion). An observer in free-fall frame will cross the Schwarzschild surface without feeling any discontinuity; (s)he will go on receiving signals from the outside world but (s)he will not be able to escape from the unavoidable, i.e., from crunching, at last, at the center of the black hole (the real physical singularity).
Schwarzschild black holes are however just a specific case. In 1963, New Zealand mathematician Roy Kerr found an exact solution to Einstein’s equations for the case of a rotating noncharged black hole and two years later the US Ezra Newman extended it to the more general case of rotating charged black holes. In fact it can be proved that a black hole can be completely described by three parameters: mass, angular momentum, and electric charge (the so-called no-hair theorem) .
Black holes are not just exotic solutions of the General Theory of Relativity. They may be formed either by gravitational collapse or particle high-energy collisions. While so far there is no evidence of their formation in human-made accelerators, there is striking indirect evidence that they are part of several binary systems and that they are present in the center of most galaxies, including our own (the Milky Way hosts in its center a black hole of roughly 4 million solar masses, as determined from the orbit of nearby stars). Extreme high-energy phenomena in the Universe, generating the most energetic cosmic rays, may also be caused by supermassive black holes inside AGN (Active Galactic Nuclei—see Chap. 10).
8.2.9 Gravitational Waves
Soon afterthe discovery of the electromagnetic radiation the existence of gravitational waves was suggested. The analogy was appealing but it took a long way before a firm prediction by Einstein and only very recently the direct experimental detection has been possible (see Chap. 10). According to Einstein’s equations the structure of spacetime is determined by the energy-momentum distributions but the solutions of such equations are far from being trivial. In particular, in the case of gravitational waves, where the components of the spacetime metric have to be time dependent (contrary for instance to the cases discussed in the previous section where the metric was assumed to be static), general exact analytic solutions are, still nowadays, impossible to obtain.

 is the Minkowski metric and
is the Minkowski metric and
 for all
for all  .
.

 and
and  are respectively the wave amplitude
and the wave vector. These waves are transverse,
are respectively the wave amplitude
and the wave vector. These waves are transverse,

 is a null-vector:
is a null-vector:


 (
( ;
;  ), may be nonzero. The general
solution for a propagation along the z axis with fixed frequency w can thus be written as:
), may be nonzero. The general
solution for a propagation along the z axis with fixed frequency w can thus be written as:

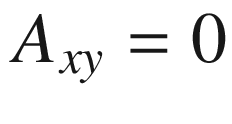 , the space-time metric produced by
such a wave is given by:
, the space-time metric produced by
such a wave is given by:


 . This wave is said to be “plus”
polarized (denoted by +). On the other hand, if
. This wave is said to be “plus”
polarized (denoted by +). On the other hand, if  a similar effect may be observed for
axis rotated by
a similar effect may be observed for
axis rotated by  and then the wave is said to be
“cross” polarized (denoted by
and then the wave is said to be
“cross” polarized (denoted by  ). Such effects are graphically
represented in Fig. 8.25.
). Such effects are graphically
represented in Fig. 8.25. is proportional to
1 / R where
R is the distance to the
source). The relative change of the distance between two tests
masses at Earth, the strain
, which is the variable measured by
gravitational wave detectors (see Sect. 4.6), is of the of the order of
is proportional to
1 / R where
R is the distance to the
source). The relative change of the distance between two tests
masses at Earth, the strain
, which is the variable measured by
gravitational wave detectors (see Sect. 4.6), is of the of the order of
 for the Hulse–Taylor binary pulsar
and of
for the Hulse–Taylor binary pulsar
and of  for the coalescence of a binary
stellar-mass black hole system (see Sect. 10.4.4).
for the coalescence of a binary
stellar-mass black hole system (see Sect. 10.4.4).

Graphical representation of the effects of
polarized waves (top,  polarization; bottom,
polarization; bottom,  polarization) From K. Riles,
“Gravitational Waves: Sources, Detectors and Searches”, Prog. Part.
Nucl. Phys. 68 (2013) 1
polarization) From K. Riles,
“Gravitational Waves: Sources, Detectors and Searches”, Prog. Part.
Nucl. Phys. 68 (2013) 1
In summary, gravitational waves are “ripples in space-time” propagating in free space with the velocity of light and their effect on the relative distances between free mass particles have been detected, as it will be discussed in Chap. 10.
8.3 Past, Present, and Future of the Universe
8.3.1 Early Universe
 (
( , where n is the number density,
, where n is the number density,  is the cross section, and v is the relative velocity) and the
Hubble parameter H
(
is the cross section, and v is the relative velocity) and the
Hubble parameter H
( ) evolve with the energy density
) evolve with the energy density
 as
as







 are the internal degrees of freedom
of the particles—the +/– signs are for bosons (Bose–Einstein
statistics) and fermions (Fermi–Dirac statistics),
respectively.
are the internal degrees of freedom
of the particles—the +/– signs are for bosons (Bose–Einstein
statistics) and fermions (Fermi–Dirac statistics),
respectively. (relativistic limit)
(relativistic limit)
![$$\begin{aligned} n_i =\left\{ \begin{array}{l} g_{i}\frac{\zeta \left( { 3}\right) }{{\pi }^2}{\left( \frac{k_BT}{\hbar { c}}\right) }^3{,\mathrm{for\, bosons}} \\ \frac{3}{{ 4}}\left[ g_{i}\frac{\zeta \left( { 3}\right) }{{\pi }^2}{\left( \frac{k_BT}{\hbar { c}}\right) }^{{ 3}}\right] { ,\ \mathrm{for}\ \mathrm{fermions}} \end{array} \right. \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_8_Chapter/304327_2_En_8_Chapter_TeX_Equ156.png)
![$$\begin{aligned} \rho _i{{ c}}^2 =\left\{ \begin{array}{l} g_{i}\frac{{\pi }^2}{{ 30\ }}k_BT{\left( \frac{k_BT}{\hbar { c}}\right) }^3{ ,\ \mathrm{for}\ \mathrm{bosons}} \\ \frac{{ 7}}{{ 8}}\left[ g_{i}\frac{{\pi }^2}{{ 30\ }}k_B{ \ }T{\left( \frac{k_BT}{\hbar { c}}\right) }^3\right] { ,\ \mathrm{for}\ \mathrm{fermions}} \end{array} \right. \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_8_Chapter/304327_2_En_8_Chapter_TeX_Equ157.png)

 is the Riemann zeta function
(
is the Riemann zeta function
( ).
). the classical Maxwell–Boltzmann
distribution is recovered:
the classical Maxwell–Boltzmann
distribution is recovered:
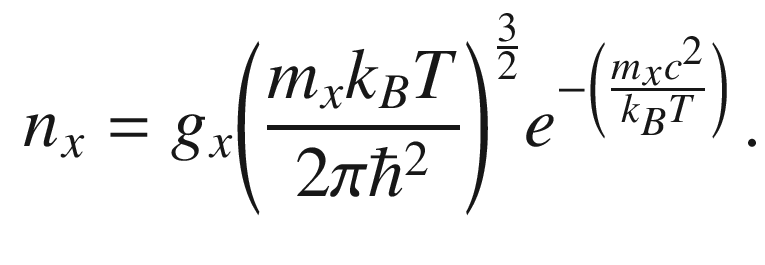

 is defined as the total “effective”
number of degrees of freedom and is given by
is defined as the total “effective”
number of degrees of freedom and is given by

 independently of the temperature of
the other particles. The individual temperatures
independently of the temperature of
the other particles. The individual temperatures 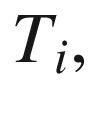
 may be introduced in the definition
of the “effective” number of degrees of freedom as
may be introduced in the definition
of the “effective” number of degrees of freedom as

 is of course a function of the age of
the Universe). At a given time all the particles with
is of course a function of the age of
the Universe). At a given time all the particles with  contribute.
contribute.





Finally, the expansion of the Universe is assumed to be adiabatic. In fact there is, by definition, no outside system and the total entropy is much higher than the small variations due to irreversible processes. The entropy of the early Universe can then be assumed to be constant.


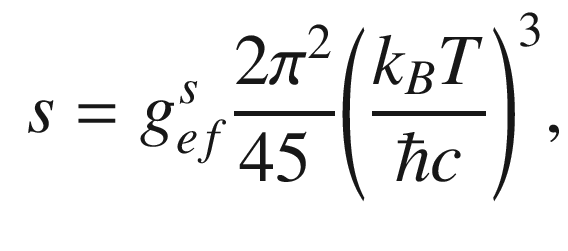
 is defined similarly to
is defined similarly to  as
as

 TeV (
TeV ( K,
K,  s) all the standard model particles
should contribute. In the SM there are six different types of
bosons (
s) all the standard model particles
should contribute. In the SM there are six different types of
bosons ( ,
,  , Z, g,
, Z, g,
 ) and 24 types of fermions and
antifermions (quarks and leptons): thus the total “effective”
number of degrees of freedom is
) and 24 types of fermions and
antifermions (quarks and leptons): thus the total “effective”
number of degrees of freedom is

 s), where general relativity meets
quantum mechanics and all the interactions may become unified,
remains basically unknown. Quantum gravity theories like string
theory or loop quantum gravity have been extensively explored in
the last years, but, for the moment, are still more elegant
mathematical constructions than real physical theories. The review
of such attempts is out of the scope of the present book; only the
decoupling of a possible stable heavy dark matter particle will be
discussed in the following.
s), where general relativity meets
quantum mechanics and all the interactions may become unified,
remains basically unknown. Quantum gravity theories like string
theory or loop quantum gravity have been extensively explored in
the last years, but, for the moment, are still more elegant
mathematical constructions than real physical theories. The review
of such attempts is out of the scope of the present book; only the
decoupling of a possible stable heavy dark matter particle will be
discussed in the following.At later times the temperature
decreases, and  decreases as well. At
decreases as well. At  GeV hadronization occurs and quarks
and gluons become confined into massive hadrons. At
GeV hadronization occurs and quarks
and gluons become confined into massive hadrons. At  MeV
MeV  s) the light elements are formed
(primordial nucleosynthesis, see Sect. 8.1.4). Around the same
temperature neutrinos also decouple as it will be discussed below.
At
s) the light elements are formed
(primordial nucleosynthesis, see Sect. 8.1.4). Around the same
temperature neutrinos also decouple as it will be discussed below.
At  0.8 eV the total energy density of
nonrelativistic particles is higher than the total energy density
of relativistic particles and then the Universe enters a
matter-dominated era (see Sect. 8.2.5). Finally at
0.8 eV the total energy density of
nonrelativistic particles is higher than the total energy density
of relativistic particles and then the Universe enters a
matter-dominated era (see Sect. 8.2.5). Finally at
 0.3 eV recombination and decoupling
occur (see Sect. 8.1.3). At that moment, the hot plasma of
photons, baryons, and electrons, which was coherently oscillating
under the combined action of gravity (attraction) and radiation
pressure (repulsion), breaks apart: photons propagate away
originating the CMB while the baryon oscillations stop (no more
radiation pressure) leaving a density excess at a fixed radius (the
sound horizon) which, convoluted with the initial density
fluctuations, are the seeds for the subsequent structure formation.
This entire evolution scenario is strongly constrained by the
existence of dark matter which is gravitationally coupled to
baryons.
0.3 eV recombination and decoupling
occur (see Sect. 8.1.3). At that moment, the hot plasma of
photons, baryons, and electrons, which was coherently oscillating
under the combined action of gravity (attraction) and radiation
pressure (repulsion), breaks apart: photons propagate away
originating the CMB while the baryon oscillations stop (no more
radiation pressure) leaving a density excess at a fixed radius (the
sound horizon) which, convoluted with the initial density
fluctuations, are the seeds for the subsequent structure formation.
This entire evolution scenario is strongly constrained by the
existence of dark matter which is gravitationally coupled to
baryons.
8.3.1.1
Neutrino Decoupling and 
 Annihilations
Annihilations
 is of the order of the expansion rate
of the Universe
is of the order of the expansion rate
of the Universe

 ) and thus their cross sections have a
magnitude for
) and thus their cross sections have a
magnitude for  of the order of
of the order of

 is proportional to
is proportional to  (
( and
and  ) while H, as seen above (Eq. 8.166), is proportional
to
) while H, as seen above (Eq. 8.166), is proportional
to  . Therefore, there will be a crossing
point, which, indeed, occurs for temperatures around a few
MeV.
. Therefore, there will be a crossing
point, which, indeed, occurs for temperatures around a few
MeV. , while photons are still in thermal
equilibrium with a plasma of electrons and positrons through
production (
, while photons are still in thermal
equilibrium with a plasma of electrons and positrons through
production ( ) and annihilation (
) and annihilation ( ) reactions. For temperatures below 1
MeV this equilibrium breaks down as the production reaction is no
more possible (
) reactions. For temperatures below 1
MeV this equilibrium breaks down as the production reaction is no
more possible ( MeV). However, entropy should be
conserved and therefore
MeV). However, entropy should be
conserved and therefore





 /cm
/cm , the number density of cosmological
neutrinos should be:
, the number density of cosmological
neutrinos should be:

8.3.2 Inflation and Large-Scale Structures
The early Universe should have been
remarkably flat, isotropic, and homogeneous to be consistent with
the present measurements of the total energy density of the
Universe (equal or very near of the critical density) and with the
extremely tiny temperature fluctuations ( ) observed in the CMB. On the
contrary, at scales
) observed in the CMB. On the
contrary, at scales  Mpc, the observed Universe is filled
with rather inhomogeneous structures, like galaxies, clusters,
superclusters, and voids. The solution for this apparent paradox
was given introducing in the very early Universe an exponential
superluminal (recessional velocities much greater than the speed of
light) expansion. It is the, so-called, inflation .
Mpc, the observed Universe is filled
with rather inhomogeneous structures, like galaxies, clusters,
superclusters, and voids. The solution for this apparent paradox
was given introducing in the very early Universe an exponential
superluminal (recessional velocities much greater than the speed of
light) expansion. It is the, so-called, inflation .
8.3.2.1 The Inflaton Field
The possibilityof a kind of exponential expansion was
already discussed above in the framework of a Universe dominated by
the cosmological constant (Sect. 8.2). The novelty was to
introduce a mechanism that could, for a while, provide a vacuum
energy density and a state equation ( , with
, with  ) ensuring thus the necessary
negative pressure. A scalar field filling the entire Universe (the
“inflaton field”) can serve these purposes.
) ensuring thus the necessary
negative pressure. A scalar field filling the entire Universe (the
“inflaton field”) can serve these purposes.
 with an associated potential energy
with an associated potential energy
 are given by (For a discussion see [F
8.5]):
are given by (For a discussion see [F
8.5]):



An example of an inflaton potential. (from K. Dimopoulos, J. Phys.: Conf. Ser. 283 012010 (doi:10.1088/1742-6596/283/1/012010))
In the first phase the inflaton field
rolls down slowly starting from a state of false vacuum
( ) and inflation occurs. In this case
the inflation period ends when the potential changes abruptly its
shape going to a minimum (the true vacuum). The field then
oscillates around this minimum dissipating its energy: this process
will refill the empty Universe originated by the exponential
expansion with radiation (reheating), which will then be the
starting point of a “classical” hot big bang expansion.
) and inflation occurs. In this case
the inflation period ends when the potential changes abruptly its
shape going to a minimum (the true vacuum). The field then
oscillates around this minimum dissipating its energy: this process
will refill the empty Universe originated by the exponential
expansion with radiation (reheating), which will then be the
starting point of a “classical” hot big bang expansion.



 .
.8.3.2.2 Flatness, Horizon, and Monopole Problems

 s) the deviation from the critical
density should be
s) the deviation from the critical
density should be 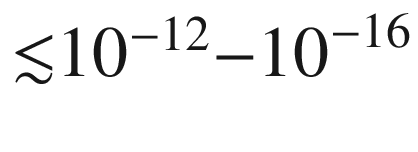 .
.The exponential expansion will also give a solution to the puzzle that arises from the observations of the extreme uniformity of the CMB temperature measured all over the sky (the so-called horizon problem).
 years,
years,  ) is given by
) is given by

 would be as expected to be just
would be as expected to be just
 .
.Basically, the horizon distance is just a consequence of the finite speed of light (which also solves the Olbers’ paradox as referred in Sect. 8.1.6).
 Gyr) is given by
Gyr) is given by

 and
and  , respectively. The crossing point was
computed to be around
, respectively. The crossing point was
computed to be around  years.
years.


 factor accounts for the expansion
between the time of last scattering and the present.
factor accounts for the expansion
between the time of last scattering and the present.Regions separated by more than this angular distance have in the standard Big Bang model no way to be in thermal equilibrium. Inflation, by postulating a superluminal expansion at a very early time, ensures that the entire Universe that we can now observe was causally connected in those first moments before inflation.
Finally, according to the Big Bang picture, at the very early moments of the Universe all the interactions should be unified. When later temperature decreases, successive phase transitions, due to spontaneous symmetry breaking, originated the present world we live in, in which the different interactions are well individualized. The problem is that Grand Unified Theories (GUT) phase transition should give rise to a high density of magnetic monopoles. Although none of these monopoles were ever observed (the so-called “monopole problem”), if inflation had occurred just after the GUT phase transition the monopoles (or any other possible relics) would be extremely diluted and this problem would be solved.
It is then tempting to associate the inflaton field to some GUT breaking mechanism, but it was shown that potentials derived from GUTs do not work, and for this reason the inflaton potential is still, for the moment, an empirical choice.
8.3.2.3 Structure Formation
Nowadays, the most relevant and falsifiable aspect of inflationary models is their predictions for the origin and evolution of the structures that are observed in the present Universe.
Quantum fluctuations of the inflaton field originate primeval density perturbations at all distance scales. During the inflationary period all scales that can be observed today went out of the horizon (the number of e-foldings is set accordingly) to reenter later (starting from the small scales and progressively moving to large scales) during the classical expansion (the horizon grows faster than the Universe scale). They evolve under the combined action of gravity, pressure, and dissipation, giving rise first to the observed acoustic peaks in the CMB power spectrum and, finally, to the observed structures in the Universe.
 , and
, and


 (Harrison–Zel’dovich spectrum) the
amplitudes in the corresponding gravitational potential are equal
at all scales.
(Harrison–Zel’dovich spectrum) the
amplitudes in the corresponding gravitational potential are equal
at all scales.This power spectrum is distorted (in particular for high k, i.e., small scales) as each scale mode will reenter the horizon at a different moment and thus will evolve differently.
In the radiation-dominated phase baryonic matter is coupled to photons and thus the density perturbation modes that had reentered the horizon cannot grow due the existence of a strong radiation pressure which opposes gravity (the sound speed is high and therefore the Jeans scale, at which one would expect collapse, is greater than the horizon). These perturbations on very small scales can be strongly (or even completely) suppressed, while on larger scales a pattern of acoustic oscillations is built up.
At recombination baryons and photons decouple, the sound speed decreases dramatically, and the Jeans scale goes to zero (there is no more photon pressure to sustain gravitation). The baryonic density perturbations will then grow by coalescing onto already formed DM halos.
 and the Doppler shift, the
temperature fluctuations at each point in space are proportional to
the gravitational potential
and the Doppler shift, the
temperature fluctuations at each point in space are proportional to
the gravitational potential

The pattern of the density oscillations at recombination should be also somehow imprinted in the matter distribution in the Universe, what starts to be revealed by the observation of the Baryon Acoustic Oscillations (see Sect. 8.1.1).
Dark matter is, by definition, not coupled to photons and therefore it is not subject to any dramatic change at recombination time. Whenever dark matter became cold (nonrelativistic) associated density perturbations could start to grow and build gravitational potential wells that have, then, been “filled” by baryons after recombination and boosted the formation of gravitational structures. The relative proportion of hot (for instance neutrinos) and cold (for instance WIMPs) dark matter may lead to different scenarios for the formation of large-scale structures. In presence of hot dark matter, a top to bottom formation scenario (from superclusters to galaxies) is favored, while in a cold dark matter (CDM) scenario, it is just the contrary: this second case is in agreement with observational evidence of the existence of supernovae almost as old as the Universe.
8.4 The
 CDM Model
CDM Model
 CDM model
, also denominated as the concordance model or the Standard Model of Cosmology, is a
parametrization of the Big Bang cosmological model based on general
relativity with a reduced set of parameters. We can assume the
evolution of the Universe under GR to be represented through the
first Friedmann equation
CDM model
, also denominated as the concordance model or the Standard Model of Cosmology, is a
parametrization of the Big Bang cosmological model based on general
relativity with a reduced set of parameters. We can assume the
evolution of the Universe under GR to be represented through the
first Friedmann equation

 the density. The
the density. The  CDM model postulates that we live in a
flat Universe (
CDM model postulates that we live in a
flat Universe ( and
and  ) with
) with  ,
,  being the baryonic density and
being the baryonic density and
 the cold dark matter (CDM) density.
The Universe is dominated by dark energy in the form of a nonzero
cosmological constant
the cold dark matter (CDM) density.
The Universe is dominated by dark energy in the form of a nonzero
cosmological constant  and cold dark matter, CDM. The
and cold dark matter, CDM. The
 CDM model also assumes homogeneity,
isotropy, and a power law spectrum of primordial fluctuations. It
is the simplest model describing the existence and structure of the
CMB, of the large-scale structure in the distribution of galaxies,
of the abundances of nucleons, of the accelerating expansion of the
universe.
CDM model also assumes homogeneity,
isotropy, and a power law spectrum of primordial fluctuations. It
is the simplest model describing the existence and structure of the
CMB, of the large-scale structure in the distribution of galaxies,
of the abundances of nucleons, of the accelerating expansion of the
universe. is motivated by the fact that
observations are consistent with this value with extreme accuracy.
Indeed
is motivated by the fact that
observations are consistent with this value with extreme accuracy.
Indeed

 , then
, then  . The minimal
. The minimal  CDM model has six free parameters,
which can be chosen as:
CDM model has six free parameters,
which can be chosen as:
- 1.
 , the Hubble parameter;
, the Hubble parameter; - 2.
 , the baryonic matter density in units
of the critical density;
, the baryonic matter density in units
of the critical density; - 3.
 , the cold dark matter density in
units of the critical density;
, the cold dark matter density in
units of the critical density; - 4.
 , the optical depth to reionization
(see Sect. 8.1.3.1);
, the optical depth to reionization
(see Sect. 8.1.3.1); - 5.
 and
and  , related to the primordial
fluctuation spectrum (we shall not make use of these parameters in
the following).
, related to the primordial
fluctuation spectrum (we shall not make use of these parameters in
the following).
 and
and  (Fig. 8.27). The present best
fit for observational data by the PDG (2018) provides for the main
(Fig. 8.27). The present best
fit for observational data by the PDG (2018) provides for the main
 CDM parameters from 1 to 4 the
following values:
CDM parameters from 1 to 4 the
following values:
- 1.
 km s
km s Mpc
Mpc , with
, with 
- 2.

- 3.

- 4.
 .
.
 CDM model, extra parameters like, for
example, the total mass of the neutrinos, the number of neutrino
families, the dark energy equation of state, the spatial curvature,
can be added.
CDM model, extra parameters like, for
example, the total mass of the neutrinos, the number of neutrino
families, the dark energy equation of state, the spatial curvature,
can be added.


The density, temperature, age, and redshift for the several Universe epochs. From E. Linder, “First principles of Cosmology,” Addison-Wesley 1997

Timeline of the Universe. Adapted from G. Sigl, “Astroparticle Physics: Theory and Phenomenology”, Springer 2017. Taken from Yinweichen – Own work, CC BY-SA 3.0, Wikimedia Commons
Finally, the standard model of cosmology gives us a coherent picture of the evolution of the Universe (Figs. 8.28 and 8.29) starting from close to Planck time, where even General Relativity is no longer valid. What happened before? Was there a single beginning, or our Universe is one of many? What will happen in the future? Is our Universe condemned to a thermal death? Questions for the twenty-first century. Questions for the present students and the future researchers.
8.4.1 Dark Matter Decoupling and the “WIMP Miracle”
The  CDM model
assumes that dark matter is formed by stable massive
nonrelativistic particles. These
particles must have an interaction strength weaker than the
electromagnetic one—otherwise they would have been found (see
later); the acronym WIMP (Weakly
Interactive Massive Particle) is often used to name them, since for
several reasons that will be discussed below, the favorite
theoretical guess compatible with experiment is that they are
heavier than
CDM model
assumes that dark matter is formed by stable massive
nonrelativistic particles. These
particles must have an interaction strength weaker than the
electromagnetic one—otherwise they would have been found (see
later); the acronym WIMP (Weakly
Interactive Massive Particle) is often used to name them, since for
several reasons that will be discussed below, the favorite
theoretical guess compatible with experiment is that they are
heavier than  GeV. The lightest supersymmetric
particle, possibly one of the neutralinos
GeV. The lightest supersymmetric
particle, possibly one of the neutralinos  (the lightest SUperSYmmetric
particles, see the previous Chapter), is for many the most likely
candidate; we shall use often the symbol
(the lightest SUperSYmmetric
particles, see the previous Chapter), is for many the most likely
candidate; we shall use often the symbol  to indicate a generic WIMP. WIMPs
must be neutral and, if there is only one kind of WIMP, we can
assume that they coincide with their antiparticle (as it is the
case for the neutralino).
to indicate a generic WIMP. WIMPs
must be neutral and, if there is only one kind of WIMP, we can
assume that they coincide with their antiparticle (as it is the
case for the neutralino).
- 1.
We can think that in the early Universe, in the radiation dominated era, WIMPs were produced in collisions between particles of the thermal plasma. Important reactions were the production and annihilation of WIMP pairs in particle-antiparticle collisions. At temperatures corresponding to energies much higher than the WIMP mass,
 , the colliding particle-antiparticle
pairs in the plasma had enough energy to create WIMP pairs, the
rate of the process being
where
, the colliding particle-antiparticle
pairs in the plasma had enough energy to create WIMP pairs, the
rate of the process being
where
 is the number density of WIMPs,
is the number density of WIMPs,
 the annihilation cross section, and
v the speed. The inverse
reactions converting pairs of WIMPs into SM particles were in
equilibrium with the WIMP-producing processes.
the annihilation cross section, and
v the speed. The inverse
reactions converting pairs of WIMPs into SM particles were in
equilibrium with the WIMP-producing processes. - 2.
As the Universe expanded, temperature decreased, and the number of particles capable to produce a WIMP decreased exponentially as the Boltzmann factorIn addition, the expansion decreased the density
 (8.184)
(8.184) and with it the production and
annihilation rates.
and with it the production and
annihilation rates. - 3.
When the mean free path for WIMP-producing collisions became of the same order of the radius:or equivalently the WIMP annihilation rate became smaller than the expansion rate of the universe H:
 production of WIMPs ceased (decoupling). After this, the number of WIMPs in a comoving volume remained approximately constant and their number density decreased as
production of WIMPs ceased (decoupling). After this, the number of WIMPs in a comoving volume remained approximately constant and their number density decreased as (8.185)
(8.185) . The value of the decoupling density
is therefore a decreasing function of
. The value of the decoupling density
is therefore a decreasing function of  , where the velocity v is small for a large mass particle. In
Fig. 8.30 the number density of a hypothetical dark
matter particle as a function of time (expressed in terms of the
ratio
, where the velocity v is small for a large mass particle. In
Fig. 8.30 the number density of a hypothetical dark
matter particle as a function of time (expressed in terms of the
ratio  ) for different assumed values of
) for different assumed values of
 is shown.A numerical solution provideswith
is shown.A numerical solution provideswith (8.186)
(8.186) in the range 10 GeV
in the range 10 GeV  TeV, and
An important property illustrated in Fig. 8.30 is that smaller annihilation cross sections lead to larger relic densities: the weakest wins. This fact can be understood from the fact that WIMPs with stronger interactions remain in thermodynamical equilibrium for a longer time: hence they decouple when the Universe is colder, and their density is further suppressed by a smaller Boltzmann factor. This leads to the inverse relation between
TeV, and
An important property illustrated in Fig. 8.30 is that smaller annihilation cross sections lead to larger relic densities: the weakest wins. This fact can be understood from the fact that WIMPs with stronger interactions remain in thermodynamical equilibrium for a longer time: hence they decouple when the Universe is colder, and their density is further suppressed by a smaller Boltzmann factor. This leads to the inverse relation between (8.187)
(8.187) and
and  in Eq. 8.187.
in Eq. 8.187. - 4.
If the
 particle interacts via weak
interactions (Chap. 6) its annihilation cross section for
low energies can be expressed as
where
particle interacts via weak
interactions (Chap. 6) its annihilation cross section for
low energies can be expressed as
where (8.188)
(8.188) is the weak elementary coupling
constant,
is the weak elementary coupling
constant,  nb GeV
nb GeV . Inserting for
. Inserting for  a value of the order of 100 GeV in
Eq. 8.187
one finds the right density of dark matter to saturate the energy
budget of the Universe with just one particle, and no need for a
new interaction.Eq. 8.187 is often expressed using the thermally-averaged product of the cross section times velocity
a value of the order of 100 GeV in
Eq. 8.187
one finds the right density of dark matter to saturate the energy
budget of the Universe with just one particle, and no need for a
new interaction.Eq. 8.187 is often expressed using the thermally-averaged product of the cross section times velocity . For
. For  ,
,  , and one has
The value
, and one has
The value
 is a benchmark value for the
velocity-averaged annihilation cross section of dark matter
particles.
is a benchmark value for the
velocity-averaged annihilation cross section of dark matter
particles.

The comoving number density of a
nonrelativistic massive particle as a function of time (expressed
in terms of the ratio  ) for different values of
) for different values of  . Adapted from D. Hooper, “TASI 2008
Lectures on Dark Matter”, arXiv:0901.4090 [hep-ph])
. Adapted from D. Hooper, “TASI 2008
Lectures on Dark Matter”, arXiv:0901.4090 [hep-ph])
An appropriate relation between
 and
and  can thus ensure a density of
particles at decoupling saturating the total DM content of the
Universe. In addition the expected values for a WIMP with
can thus ensure a density of
particles at decoupling saturating the total DM content of the
Universe. In addition the expected values for a WIMP with
 GeV and
GeV and  , corresponding to the electroweak
coupling, provides the right scale for the observed dark matter
density (
, corresponding to the electroweak
coupling, provides the right scale for the observed dark matter
density ( –0.3, see Sect. 8.4); this coincidence is
called the WIMP miracle
. A WIMP can indeed be the mysterious
missing dark particle, but the WIMP miracle is not the only
possible solution: we take it just as a benchmark. In the opinion
of Andrej Sacharov, dark matter could just be gravitationally
coupled–and if he was right, it will be extremely difficult to
detect it experimentally. A value
–0.3, see Sect. 8.4); this coincidence is
called the WIMP miracle
. A WIMP can indeed be the mysterious
missing dark particle, but the WIMP miracle is not the only
possible solution: we take it just as a benchmark. In the opinion
of Andrej Sacharov, dark matter could just be gravitationally
coupled–and if he was right, it will be extremely difficult to
detect it experimentally. A value  of the order of
of the order of  is the resulting benchmark value for
the velocity-averaged annihilation cross section of dark matter
particles in a range of weak interactions and of DM masses of the
order8 of 50 GeV–10 TeV.
is the resulting benchmark value for
the velocity-averaged annihilation cross section of dark matter
particles in a range of weak interactions and of DM masses of the
order8 of 50 GeV–10 TeV.
8.5 What Is Dark Matter Made of, and How Can It Be Found?
Observations indicate a large amount of dark matteror substantial modifications of the standard theory of gravitation (see Sect. 8.1.5).
Dark matter is unlikely to consist of baryons.
-
First, the
 CDM model (Sect. 8.4) computes the total
content of baryonic DM (i.e., nonluminous matter made by ordinary
baryons) from the fit to the CMB
spectrum, and the result obtained is only some 4% of the total
energy of the Universe; the structure of the Universe, computed
from astrophysical simulations, is consistent with the fractions
within the
CDM model (Sect. 8.4) computes the total
content of baryonic DM (i.e., nonluminous matter made by ordinary
baryons) from the fit to the CMB
spectrum, and the result obtained is only some 4% of the total
energy of the Universe; the structure of the Universe, computed
from astrophysical simulations, is consistent with the fractions
within the  CDM model.
CDM model. -
Second, the abundances of light elements depend on the baryon density, and the observed abundances are again consistent with those coming from the fit to
 coming from the CMB data.
coming from the CMB data.
A direct search for baryonic dark matter has been however motivated by the fact that some of the hypotheses on which cosmological measurements are based might be wrong (as in the case of MOND, for example).
Baryonic DM should cluster into massive astrophysical compact objects, the so-called MACHOs,9 or into molecular clouds.

Principle of gravitational microlensing. By Adam Rogers, blog “The Amateur Realist”
The main baryonic component should be thus concentrated in massive objects (MACHOs), including black holes. We can estimate the amount of this component using the gravitational field generated by it: a MACHO may be detected when it passes in front of a star and the star light is bent by the MACHO’s gravity. This causes more light to reach the observer and the star to look brighter, an effect known as gravitational microlensing (Fig. 8.31) , very important also in the search for extrasolar planets (see Chap. 11). Several research groups have searched for MACHOs and found that only less than 20% of the total DM can be attributed to them. Therefore, MACHOs do not solve the missing mass problem.
Candidates for nonbaryonic DM must
interact very “weakly” with electromagnetic radiation (otherwise
they would not be dark), and they must have the right density to
explain about one-quarter of the energy content of the Universe. A
new particle of mass above the eV and below some  would have been already found by LEP:
DM particles must be very heavy or very light if they exist. They
must also be stable on cosmological timescales (otherwise they
would have decayed by now). We use the acronyms WIMP (weakly interacting massive particle) to
indicate possible new “heavy” particles, and WISP (weakly interacting slim particle, or sub-eV
particle) to indicate possible new light particles. Part of the
rationale for WIMPs has been discussed in Sect. 8.4.1.
would have been already found by LEP:
DM particles must be very heavy or very light if they exist. They
must also be stable on cosmological timescales (otherwise they
would have decayed by now). We use the acronyms WIMP (weakly interacting massive particle) to
indicate possible new “heavy” particles, and WISP (weakly interacting slim particle, or sub-eV
particle) to indicate possible new light particles. Part of the
rationale for WIMPs has been discussed in Sect. 8.4.1.
We shall present in this chapter the results of direct searches for dark matter, searches at accelerators, and shortly of indirect searches; a more detailed discussion of indirect signatures in the context of multimessenger astrophysics will be presented in Chap. 10.
8.5.1 WISPs: Neutrinos, Axions and ALPs

 ) particle originally postulated to
explain the so-called strong CP
problem. In principle, CP should not be a symmetry of the QCD
Lagrangian; however, CP (and
T) appear to be conserved, as
opposed to what happens for weak interactions; this fact has been
verified with very good accuracy. To fix this problem, Peccei and
Quinn (1977) proposed a new global symmetry, spontaneously broken
at a very-high-energy scale, and giving rise to an associated boson
called the axion (see Sect. 7.3.2). Being pseudoscalar (like
the
) particle originally postulated to
explain the so-called strong CP
problem. In principle, CP should not be a symmetry of the QCD
Lagrangian; however, CP (and
T) appear to be conserved, as
opposed to what happens for weak interactions; this fact has been
verified with very good accuracy. To fix this problem, Peccei and
Quinn (1977) proposed a new global symmetry, spontaneously broken
at a very-high-energy scale, and giving rise to an associated boson
called the axion (see Sect. 7.3.2). Being pseudoscalar (like
the  ), the axion can decay into two
photons, at a rate determined by the (small) coupling
), the axion can decay into two
photons, at a rate determined by the (small) coupling  —all quantities here are expressed in
NU. The standard axion mass
—all quantities here are expressed in
NU. The standard axion mass  is related to the coupling by the
formula
is related to the coupling by the
formula

 , which is larger than the age of the
Universe for
, which is larger than the age of the
Universe for  eV. An axion below this mass would
thus be stable.
eV. An axion below this mass would
thus be stable.Since the axion couples to two photons,
in a magnetic or electric field it could convert to a photon; vice
versa, a photon in an external magnetic or electric field could
convert into an axion (Primakoff effect) ; the amplitude of the process would be
proportional to  .
.
Axion-like particles (ALPs) are a generalization of the axion: while the
axion is characterized by a strict relationship between its mass
 and
and  , these two parameters are unrelated
for ALPs. Depending on the actual values of their mass and coupling
constant, ALPs can play an important role in cosmology, either as
cold dark matter particles or as quintessential dark energy.
, these two parameters are unrelated
for ALPs. Depending on the actual values of their mass and coupling
constant, ALPs can play an important role in cosmology, either as
cold dark matter particles or as quintessential dark energy.
In order to account for dark matter, that is, to reach an energy density of the order of the critical density, axion masses should be at least 0.1 meV. Light axions and ALPs could still be DM candidates, since they are produced nonthermally via Bose-Einstein condensation, and thus they can be “cold”.
- 1.
Using the light-shining-through-a-wall (LSW) technique: a laser beam travels through a region of high magnetic field, allowing the possible conversion of photons into axions. These axions can then pass through a wall, and on the other side they can be converted back into photons in a magnetic field. An example is the OSQAR experiment at CERN.
- 2.
Trying to spot solar axions using helioscopes: the CAST (CERN Axion Solar Telescope) experiment looks for the X-rays that would result from the conversion of solar axions produced in the Sun back into photons, using a 9-tons superconducting magnet.
- 3.
Searching for axions in the local galactic dark matter halo (haloscopes). Axion conversion into photons is stimulated by strong magnetic field in a microwave cavity. When the cavity’s resonant frequency is tuned to the axion mass, the interaction between local axions and the magnetic field is enhanced. The Axion Dark Matter eXperiment (ADMX) in Seattle uses a resonant microwave cavity within a 8 T superconducting magnet.
Indirect searches are also possible.
- 4.
The vacuum magnetic birefringence (VMB) in high magnetic fields due to photon–axion mixing can be investigated. Different polarizations often experience a different refractive index in matter—a common example is a uniaxial crystal. The vacuum is also expected to become birefringent in presence of an external magnetic field perpendicular to the propagation direction, due to the orientation of the virtual
 loops. The magnitude of this
birefringence could be enhanced by the presence of an axion field,
which provides further magnetic-dependent mixing of light to a
virtual field (experiment PVLAS by E. Zavattini and collaborators,
2006).
loops. The magnitude of this
birefringence could be enhanced by the presence of an axion field,
which provides further magnetic-dependent mixing of light to a
virtual field (experiment PVLAS by E. Zavattini and collaborators,
2006). - 5.
Study of possible anomalies in the cooling times of stars and of cataclismic stellar events. An example is given by SNe, which produce vast quantities of weakly interacting particles, like neutrinos and possibly gravitons, axions, and other unknown particles. Although this flux of particles cannot be measured directly, the properties of the cooling depend on the ways of losing energy. The results on the cooling times and the photon fluxes (since photons are coupled to axions) constrain the characteristics of the invisible axions: emission of very weakly interacting particles would “steal” energy from the neutrino burst and shorten it. The best limits come from SN1987A. However, significant limits come also from the cooling time of stars on the horizontal branchin the color-magnitude diagram, which have reached the helium burning phase.
- 6.
ALPs can also directly affect the propagation of photons coming from astrophysical sources, by mixing to them. This possibility has been suggested in 2007 by De Angelis, Roncadelli, and Mansutti (DARMa), and by Simet, Hooper, and Serpico. The conversion of photons into axions in the random extragalactic magnetic fields, or at the source and in the Milky Way, could give rise to a sort of cosmic light-shining-through-a-wall effect. This might enhance the yield of very-high-energy photons from distant active galactic nuclei, which would be otherwise suppressed by the interaction of these photons with the background photons in the Universe (see Chap. 10). These effects are in the sensitivity range of Fermi-LAT and of the Cherenkov telescopes.
- 7.
The line emission from the two-photon decay of axions in galaxy clusters can be searched with optical and near-infrared telescopes.


Axion and ALP coupling to photons versus the ALP mass. The labels are explained in the text. Adapted from C. Patrignani et al. (Particle Data Group), Chin. Phys. C, 40, 100001 (2016) and 2017 update
A hint for ALPs comes from possible anomalies in the propagation of very-high-energy photons from astrophysical sources (see Chap. 10).
A summary of exclusion limits, and of a possible observational window indicated by the cosmological propagation of VHE photons (see Chap. 10), is shown in Fig. 8.32. The topic is very hot and many new experimental results are expected in the next years.
8.5.2 WIMPs
If dark matter (DM) particles
 are massive they must be “weakly”
(i.e., with a strength corresponding to the weak interaction or
even weaker) interacting (WIMPs). A lower limit for the strength of
the interaction is given by the gravitational strength. They must
be neutral and, for a large range of interaction strengths, of mass
larger than
are massive they must be “weakly”
(i.e., with a strength corresponding to the weak interaction or
even weaker) interacting (WIMPs). A lower limit for the strength of
the interaction is given by the gravitational strength. They must
be neutral and, for a large range of interaction strengths, of mass
larger than  , otherwise they would have been found
at the LEP
, otherwise they would have been found
at the LEP  collider.
collider.
The “WIMP miracle”, discussed in Sect.
8.4.1,
guarantees that a single type of WIMP of mass  of the order of 50 GeV - few TeV,
emerged from a standard thermal decoupling, can saturate the energy
budget of the Universe for dark matter if the interaction
characterizing WIMPs is the well-known electroweak interaction.
WIMPs should be stable or should have a lifetime large enough in
order to have survived from the early Universe until the present
time.
of the order of 50 GeV - few TeV,
emerged from a standard thermal decoupling, can saturate the energy
budget of the Universe for dark matter if the interaction
characterizing WIMPs is the well-known electroweak interaction.
WIMPs should be stable or should have a lifetime large enough in
order to have survived from the early Universe until the present
time.
 , coincident with its antiparticle, we
expect an annihilation cross section
, coincident with its antiparticle, we
expect an annihilation cross section 


Several extensions to the SM have
proposed WIMP candidates, most notably supersymmetric models (SUSY)
with  parity conservation, in which the
lightest supersymmetric particle, the putative neutralino
parity conservation, in which the
lightest supersymmetric particle, the putative neutralino
 , is
stable and thus a serious candidate (Sect. 7.6.1) with a range of annihilation
cross sections including the desired ones–the spectrum of cross
section can vary in some 5 orders of magnitude depending on the
many free parameters of SUSY. For this reason the neutralino is
usually thought to be a “natural” DM candidate. However, more
general models are also allowed.
, is
stable and thus a serious candidate (Sect. 7.6.1) with a range of annihilation
cross sections including the desired ones–the spectrum of cross
section can vary in some 5 orders of magnitude depending on the
many free parameters of SUSY. For this reason the neutralino is
usually thought to be a “natural” DM candidate. However, more
general models are also allowed.
- 1.
At accelerators, where they can be produced.
- 2.
Directly, via elastic scattering with targets on Earth. If the DM conjecture is correct, we live in a sea of WIMPs. For a WIMP mass of 50 GeV, there might be in our surroundings some 10
 particles per cubic meter, moving at
a speed smaller than the revolution velocity of the Earth around
the Sun. From astrophysical observations the local WIMP density is
about 0.4 GeV/cm
particles per cubic meter, moving at
a speed smaller than the revolution velocity of the Earth around
the Sun. From astrophysical observations the local WIMP density is
about 0.4 GeV/cm ; the velocity distribution is
Maxwellian, truncated by the Galactic escape velocity of 650 km/s.
For a mass of 50 GeV, the RMS velocity is comparable to the speed
of the solar system in the Galaxy,
; the velocity distribution is
Maxwellian, truncated by the Galactic escape velocity of 650 km/s.
For a mass of 50 GeV, the RMS velocity is comparable to the speed
of the solar system in the Galaxy,  230 km/s. Direct detection relies on
observation of the scattering or other interaction of the WIMPs
inside low-background Earth-based detectors.
230 km/s. Direct detection relies on
observation of the scattering or other interaction of the WIMPs
inside low-background Earth-based detectors. - 3.
Indirectly, by their decay products if they are unstable (WIMPs can be unstable, provided their lifetime is larger than the Hubble time), or by their self-annihilation products in high-density DM environments. The annihilation products of pairs of WIMPs—for example, in the halo of the Galaxy, or as a result of their accumulation in the core of the Sun or of the Earth, is likely to happen if the WIMP is a boson or a Majorana fermion as the SUSY neutralino.

Different proceses used to investigate on WIMPs
8.5.2.1 Production and Detection of WIMPs at Accelerators
WIMPs can be created at colliders, but they are difficult to detect, since they are neutral and weakly interacting. However, it is possible to infer their existence. Their signature would be missing momentum when one tries to reconstruct the dynamics of a collision into a final state involving dark matter particles and standard model particles—notice that a collision producing dark matter particles only would not be triggered. There has been a huge effort to search for the appearance of these new particles.
The production of WIMPs is severely
constrained by LEP up to a mass close to  . WIMPs with
. WIMPs with  GeV can be constrained with the
branching ratio for invisible Higgs boson decays which is measured
at LHC to be
GeV can be constrained with the
branching ratio for invisible Higgs boson decays which is measured
at LHC to be  . This does not appear as a strong
constraint, but in many scenarios the Higgs boson coupling to WIMPs
is stronger than to SM particles.
. This does not appear as a strong
constraint, but in many scenarios the Higgs boson coupling to WIMPs
is stronger than to SM particles.
Accelerator searches are complementary
to the direct searches that will be described later; however, to
compare with noncollider searches, the limits need to be translated
via a theory into upper limits on WIMP-nucleon scattering or on
WIMP annihilation cross sections, introducing model dependence–for
example, the comparison can be done in the framework of SUSY
(Fig. 8.36). In particular, searches at accelerators
can exclude the region below 10 GeV and a cross section per nucleon
of the order of 10 cm
cm , where direct searches are not very
sensitive.
, where direct searches are not very
sensitive.
8.5.2.2 Direct Detection of WIMPs in Underground Detectors
Experimental detection is based on the nuclear recoil that would be caused by WIMP elastic scattering.

 of the solar system with respect to
the center of the Galaxy, which is of the order of
of the solar system with respect to
the center of the Galaxy, which is of the order of  .
. flux on the Earth should be about
flux on the Earth should be about

 has been used to compute the number
density of DM particles). This flux is rather large and a
potentially measurable fraction might scatter off nuclei.
has been used to compute the number
density of DM particles). This flux is rather large and a
potentially measurable fraction might scatter off nuclei. of a particle of mass M initially at rest after a
nonrelativistic collision with a particle of mass
of a particle of mass M initially at rest after a
nonrelativistic collision with a particle of mass  traveling at a speed
traveling at a speed  is approximately
is approximately
![$$\begin{aligned} E_K \simeq 50\,{\mathrm{keV}} \left[ \frac{M}{100 \, {\mathrm{GeV}}} \left( \frac{2}{1+M/m_\chi }\right) ^2 \right] \, . \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_8_Chapter/304327_2_En_8_Chapter_TeX_Equ193.png)
 per day in a kilogram of material for
a 50 GeV particle weakly interacting.
per day in a kilogram of material for
a 50 GeV particle weakly interacting.Translating a number of collisions into
a cross section per nucleon is not trivial in this case. The
WIMP-nucleon scattering cross section has a spin-dependent (SD) and
a spin-independent (SI) part. When the scattering is coherent, the
SI cross section has a quadratic dependence on the mass number
 which leads to strong enhancement for
heavy elements. A nucleus can only recoil coherently for
which leads to strong enhancement for
heavy elements. A nucleus can only recoil coherently for
 SD scattering on the other hand
depends on the total nuclear angular momentum. In the case of
spin-dependent interaction the cross section is smaller by a factor
of order
SD scattering on the other hand
depends on the total nuclear angular momentum. In the case of
spin-dependent interaction the cross section is smaller by a factor
of order  than for coherent scattering.
than for coherent scattering.
Detectors sensitive to WIMP interactions should have a low energy threshold, a low-background noise, and a large mass. The energy of a nucleus after a scattering from a WIMP is converted into a signal corresponding to (1) ionization, (2) scintillation light; (3) vibration quanta (phonons). The main experimental problem is to distinguish the genuine nuclear recoil induced by a WIMP from the huge background due to environmental radioactivity. It would be useful to do experiments which can measure the nuclear recoil energy and if possible the direction. The intrinsic rejection power of these detectors can be enhanced by the simultaneous detection of different observables (for example, heat and ionization or heat and scintillation).

Left: the directions of the Sun’s and the Earth’s motions during a year. Assuming the WIMPs to be on average at rest in the Galaxy, the average speed of the WIMPs relative to the Earth is modulated with a period of 1 year. Right: annual modulation of the total counting rate (background plus possible dark matter signal) in 7 years of data with the DAMA detector. A constant counting rate has been subtracted. From R. Bernabei et al., Riv. Nuovo Cim. 26 (2003) 1
-
The thickness of the rock (to isolate from muons and from the secondary products of their interaction).
-
The geology (radioactive materials produce neutrons that should be shielded) and the presence of Radon.
-
The volume available (none of the present installations could host a megaton detector).
-
The logistics.
Some of the largest underground detectors in the world are shown in Fig. 8.35.

Underground laboratories for research in particle physics (1–10) listed with their depth in meters water equivalent. Laboratories for research in the million-year scale isolation of nuclear waste are also shown (11–20). The NELSAM laboratory (21) is for earthquake research.
Essentially three types of detectors operate searching directly for dark matter in underground facilities all around the world.
-
Semiconductor detectors. The recoil nucleus or an energetic charged particle or radiation ionizes the traversed material and produces a small electric signal proportional to the deposited energy. Germanium crystals, which have a very small value of the gap energy (3 eV) and thus have a good resolution of 1 per thousand at 1 MeV, are commonly used as very good detectors since some years. The leading detectors are the CDMS, CoGeNT, CRESST, and EDELWEISS experiments. The bolometric technique (bolometers are ionization-sensitive detectors kept cold in a Wheatstone bridge; the effects measured are: the change in electric resistance consequent to the heating, i.e., the deposited energy, and ionization) increases the power of background rejection, and allows a direct estimate of the mass of the scattering particle.
-
Scintillating crystals. Although their resolution is worse than Germanium detectors, no cooling is required. The scintillation technique is simple and well known, and large volumes can be attained because the cost per mass unit is low. However, these detectors are not performant enough to allow an event-by-event analysis. For this reason, some experiments are looking for a time-dependent modulation of a WIMP signal in their data. As the Earth moves around the Sun, the WIMP flux should be maximum in June (when the revolution velocity of the Earth adds to the velocity of the solar system in the Galaxy) and minimum in December, with an expected amplitude variation of a few percent. DAMA (now called in its upgrade DAMA/LIBRA) is the first experiment using this detection strategy. The apparatus is made of highly radio-pure NaI(Tl) crystals, each with a mass of about 10 kg, with two PMTs at the two opposing faces.
-
Noble liquid detectors. Certainly the best technique, in particular in a low-background environment, it uses noble elements as detectors (this implies low background from the source itself) such as argon (A = 40) and xenon (A = 131). Liquid xenon (LXe) and liquid argon (LAr) are good scintillators and ionizers in response to the passage of radiation. Using pulse-shape discrimination of the signal, events induced by a WIMP can be distinguished from background electron recoil. The main technique is to the present knowledge the “double phase” technique. A vessel is partially filled with noble liquid, with the rest of the vessel containing the same element in a gaseous state. Electric fields of about 1 kV/cm and 10 kV/cm are established across the liquid and gas volumes, respectively. An interaction in the liquid produces excitation and ionization processes. Photomultiplier tubes are present in the gas volume and in the liquid. The double phase allows reconstruction of the topology of the interaction (the gas allowing a TPC reconstruction), thus helping background removal. The leading experiments are:
-
The XENON100 detector, a 165 kg liquid xenon detector located in LGNS with 62 kg in the target region and the remaining xenon in an active veto together with high purity Germanium detectors. A new liquid xenon-based project, XENON1t, is planned in the LNGS, with 3.5 tons of liquid xenon.
-
The LUX detector, a 370 kg xenon detector installed in the Homestake laboratory (now called SURF) in the US. LUX was decommissioned in 2016 and a new experiment, LUX-ZEPLIN (LZ), with 7 tons of active liquid xenon is in preparation.
-
 the flux decreases as
the flux decreases as  and the sensitivity for fixed mass
densities also drops. The best sensitivity is attained for WIMP
masses close to the mass of the recoiling nucleus.
and the sensitivity for fixed mass
densities also drops. The best sensitivity is attained for WIMP
masses close to the mass of the recoiling nucleus.

Compilation of experimental results on cross sections of WIMPs versus masses. The areas labeled as DAMA/LIBRA and CDMS-Si indicate regions of possible signals from those experiments. Supersymmetry implications are also shown. New experiments to hunt for dark matter are becoming so sensitive that neutrino will soon show up as background; the “neutrino flooris shown in the plot. From C. Patrignani et al. (Particle Data Group), Chin. Phys. C, 40, 100001 (2016) and 2017 update, in which experiments are also described in detail
The experimental situation is not
completely clear (Fig. 8.36). Possible WIMP detection signals were
claimed by the experiment DAMA, based on
a large scintillator (NaI (Tl)) volume, and the CRESST and CoGeNT
data show some stress with respect to experiments finding no
signal. The data analyzed by DAMA corresponded to 7 years of
exposure with a detector mass of 250 kg, to be added to 6 years of
exposure done earlier with a detector mass of 100 kg. Based on the
observation of a signal at 9.3  (Fig. 8.34, right) modulated
with the expected period of 1 year and the correct phase (with a
maximum near June 2, as expected from the Earth’s motion around the
Sun), DAMA proposes two possible scenarios: a WIMP with
(Fig. 8.34, right) modulated
with the expected period of 1 year and the correct phase (with a
maximum near June 2, as expected from the Earth’s motion around the
Sun), DAMA proposes two possible scenarios: a WIMP with
 GeV and a cross section per nucleon
GeV and a cross section per nucleon
 pb, and a WIMP with
pb, and a WIMP with  GeV and
GeV and  pb. The DAMA signal is controversial,
as it has not presently been reproduced by other experiments with
comparable sensitivity but with different types of detectors (we
remind that there is some model dependence in the rescaling from
the probability of interaction to the cross section per
nucleon).
pb. The DAMA signal is controversial,
as it has not presently been reproduced by other experiments with
comparable sensitivity but with different types of detectors (we
remind that there is some model dependence in the rescaling from
the probability of interaction to the cross section per
nucleon).
In the next years the sensitivity of direct DM detectors will touch the “neutrino floor” for WIMP masses above 10 GeV, in particular thanks to the DARWIN detector, a 50-ton LXe detector planned to start in the mid-2020s at LNGS.
In the meantime the DarkSide collaboration at LNGS has proposed a
20-ton liquid argon dual-phase detector, with the goal to be
sensitive to a cross section of  cm
cm for a mass of 1 TeV/
for a mass of 1 TeV/ , based on extrapolations of the
demonstrated efficiency of a 50 kg pathfinder.
, based on extrapolations of the
demonstrated efficiency of a 50 kg pathfinder.
8.5.2.3 Indirect Detection of WIMPs
WIMPs are likely to annihilate in pairs; it is also possible that they are unstable, with lifetimes comparable with the Hubble time, or larger. In these cases one can detect secondary products of WIMP decays. Let us concentrate now on the case of annihilation in pairs—most of the considerations apply to decays as well.
If the WIMP mass is below the
W mass, the annihilation of a
pair of WIMPs should proceed mostly through  pairs. The state coming from the
annihilation should be mostly a spin-0 state (in the case of small
mutual velocity the s-wave
state is favored in the annihilation; one can derive a more general
demonstration using the Clebsch–Gordan coefficients). Helicity
suppression entails that the decay in the heaviest accessible
fermion pair is preferred, similar to what seen in
Chap. 6 when studying the
pairs. The state coming from the
annihilation should be mostly a spin-0 state (in the case of small
mutual velocity the s-wave
state is favored in the annihilation; one can derive a more general
demonstration using the Clebsch–Gordan coefficients). Helicity
suppression entails that the decay in the heaviest accessible
fermion pair is preferred, similar to what seen in
Chap. 6 when studying the  decay (Sect. 6.3.4): the decay probability into
a fermion–antifermion pair is proportional to the square of the
mass of the fermion. In the mass region between 10 and 80 GeV, the
decay into
decay (Sect. 6.3.4): the decay probability into
a fermion–antifermion pair is proportional to the square of the
mass of the fermion. In the mass region between 10 and 80 GeV, the
decay into  pairs is thus preferred (this
consideration does not hold if the decay is radiative, and in this
case a generic
pairs is thus preferred (this
consideration does not hold if the decay is radiative, and in this
case a generic  pair will be produced). The
pair will be produced). The
 pair will then hadronize and produce
a number of secondary particles.
pair will then hadronize and produce
a number of secondary particles.
In the case of the annihilation in the cores of stars, the only secondary products which could be detected would be neutrinos. However, no evidence for a significant extra flux of high-energy neutrinos from the direction of the Sun or from the Earth’s core has ever been found.
One could have annihilations in the halos of galaxies or in accretion regions close to black holes or generic cusps of dark matter density. In this case one could have generation of secondary particles, including gamma rays, or antimatter which would appear in excess to the standard rate.
We shortly present here the possible scenarios for detections, which will be discussed in larger details in Chap. 10, in the context of multimessenger astrophysics.
Gamma
Rays. The self-annihilation of a heavy WIMP  can generate photons
(Fig. 8.37) in three main ways.
can generate photons
(Fig. 8.37) in three main ways.
- (a)
Directly, via annihilation into a photon pair (
 ) or into a photon—Z pair (
) or into a photon—Z pair ( ) with
) with  or
or  , respectively; these processes give a
clear signature at high energies, as the energy is monochromatic,
but the process is suppressed at one loop, so the flux is expected
to be very faint.
, respectively; these processes give a
clear signature at high energies, as the energy is monochromatic,
but the process is suppressed at one loop, so the flux is expected
to be very faint. - (b)
Via annihilation into a quark pair which produces jets emitting in turn a large number of
 photons (
photons ( jets
jets  many
photons); this process produces a continuum of gamma rays with
energies below the WIMP mass. The flux can be large but the
signature might be difficult to detect, since it might be masked by
astrophysical sources of photons.
many
photons); this process produces a continuum of gamma rays with
energies below the WIMP mass. The flux can be large but the
signature might be difficult to detect, since it might be masked by
astrophysical sources of photons. - (c)
Via internal bremsstrahlung; also in this case one has an excess of low energy gamma rays with respect to a background which is not so well known. Besides the internal bremsstrahlung photons, one will still have the photons coming from the processes described at the two previous items.

 -ray signature of neutralino
self-annihilation or of neutralino decay. Simulation from the
Fermi-LAT collaboration
-ray signature of neutralino
self-annihilation or of neutralino decay. Simulation from the
Fermi-LAT collaboration
 -ray flux from the annihilation of a
pair of WIMPs of mass
-ray flux from the annihilation of a
pair of WIMPs of mass  can be expressed as the product of a
particle physics component times an astrophysics component:
can be expressed as the product of a
particle physics component times an astrophysics component:

 , the velocity-weighted annihilation
cross section (there is indeed a possible component from cosmology
in v), and
, the velocity-weighted annihilation
cross section (there is indeed a possible component from cosmology
in v), and  , the
, the  -ray energy spectrum for all final
states convoluted with the respective branching rations. The part
of the integral over line of sight (l.o.s.) in the observed solid angle of
the squared density of the dark matter distribution constitutes the
astrophysical contribution.
-ray energy spectrum for all final
states convoluted with the respective branching rations. The part
of the integral over line of sight (l.o.s.) in the observed solid angle of
the squared density of the dark matter distribution constitutes the
astrophysical contribution.It is clear that the expected flux of
photons from dark matter annihilations, and thus its detectability,
depend crucially on the knowledge of the annihilation cross section
 (which even within SUSY has
uncertainties of one to two orders of magnitude for a given WIMP
mass) and of
(which even within SUSY has
uncertainties of one to two orders of magnitude for a given WIMP
mass) and of  , which is even more uncertain, and
enters squared in the calculation. Cusps in the dark matter
profile, or even the presence of local clumps, could make the
detection easier by enhancing
, which is even more uncertain, and
enters squared in the calculation. Cusps in the dark matter
profile, or even the presence of local clumps, could make the
detection easier by enhancing  —and we saw that the density in the
cusps is uncertain by several orders of magnitude within current
models (Sect. 8.1.5.1). In the case of WIMP decays, the
density term will be linear.
—and we saw that the density in the
cusps is uncertain by several orders of magnitude within current
models (Sect. 8.1.5.1). In the case of WIMP decays, the
density term will be linear.
The targets for dark matter searches should be not extended, with the highest density, with no associated astrophysical sources, close to us, and possibly with some indication of small luminosity/mass ratio from the stellar dynamics.
-
The Galactic center is at a distance of about 8 kpc from the Earth. A black hole of about
 solar masses, Sgr A
solar masses, Sgr A , lies there. Because of its
proximity, this region might be the best candidate for indirect
searches of dark matter. Unfortunately, there are other
astrophysical
, lies there. Because of its
proximity, this region might be the best candidate for indirect
searches of dark matter. Unfortunately, there are other
astrophysical  -ray sources in the field of view
(e.g., the supernova remnant Sgr A East), and the halo
core radius makes it an extended rather than a point-like
source.
-ray sources in the field of view
(e.g., the supernova remnant Sgr A East), and the halo
core radius makes it an extended rather than a point-like
source. -
The best observational targets for dark matter detection outside the Galaxy are the Milky Way’s dwarf spheroidal satellite galaxies (for example, Carina, Draco, Fornax, Sculptor, Sextans, Ursa Minor). For all of them (e.g., Draco), there is observational evidence of a mass excess with respect to what can be estimated from luminous objects, i.e., a high M/L ratio. In addition, the gamma-ray signal expected in the absence of WIMP annihilation is zero.
The results of the experimental searches will be discussed in Sect. 10.5.3.
Neutrinos. Neutrino–antineutrino pairs can also be used for probing WIMP annihilation or decay, along the same line discussed for gamma rays, apart from the fact that neutrino radiation is negligible. Besides the smaller astrophysical background, the advantage of neutrinos is that they can be observed even if the annihilation happens in the cores of opaque astrophysical objects (the Sun or compact objects in particular); apart fromm these cases the sensitivity of the gamma-ray channel is by far superior, due to the experimental difficulty of detecting neutrinos for the present and next generation of detectors.
Matter–Antimatter and Electron Signatures. Another indirect manifestation of the presence of WIMPs would be given by their decay (or self-annihilation) producing democratically antimatter and matter.
A possible observable could be related
to electron and positron pairs. A smoking gun would be the presence
of a peak in the energy of the collected electrons, indicating a
two-body decay. A shoulder reaching  could also be a signature, but, in
this last case, one could hypothesize astrophysical sources as
well.
could also be a signature, but, in
this last case, one could hypothesize astrophysical sources as
well.
An excess of antimatter with respect to
the prediction of models in which antimatter is just coming from
secondary interactions of cosmic rays and astrophysical sources
could be seen very clearly in the positron and antiproton spectrum.
The PAMELA space mission observed a positron abundance in cosmic
radiation higher than that predicted by current models (see
Chap. 10). This has been confirmed by the
AMS-02 mission, reaching unprecedented accuracy. AMS-02 has also
found an excess of antiprotons with respect to models in which only
secondary production is accounted. A smoking gun signature for the
origin of positrons from the decay of a  or from a
or from a  annihilation would be a steep
drop-off of the ratio at a given energy. A more detailed discussion
of experimental data will be presented in Chap. 10.
annihilation would be a steep
drop-off of the ratio at a given energy. A more detailed discussion
of experimental data will be presented in Chap. 10.
8.5.3 Other Nonbaryonic Candidates
Additional candidates, more or less theoretically motivated, have been proposed in the literature. We list them shortly here; they are less economic than the ones discussed before (WIMPs in particular).
Sterile Neutrinos. A possible DM candidate is a “sterile” neutrino, i.e., a neutrino which does not interact via weak interactions. We know that such neutrino states exist: the right-handed component of neutrinos in the standard model are sterile. Constraints from cosmology make it, however, unlikely that light sterile neutrinos can be the main component of dark matter. Sterile neutrinos with masses of the order of the keV and above could be, with some difficulty, accommodated in the present theories.
Kaluza–Klein States. If particles propagate in extra spacetime dimensions, they will have an infinite spectroscopy of partner states with identical quantum numbers; these states could be a DM candidate.
Matter in Parallel Branes; Shadow or Mirror Matter. Some theories postulate the presence of matter in parallel branes, interacting with our world only via gravity or via a super-weak interaction. In theories popular in the 1960s, a “mirror matter” was postulated to form astronomical mirror objects; the cosmology in the mirror sector could be different from our cosmology, possibly explaining the formation of dark halos. This mirror-matter cosmology has been claimed to explain a wide range of phenomena.
Superheavy Particles (WIMPzillas). Superheavy particles above the GZK cutoff (WIMPzillas) could have been produced in the early Universe; their presence could be detected by an excess of cosmic rays at ultrahigh energies.
Further Reading
- [F8.1]
-
J. Silk, “The big bang”, Times Books 2000.
- [F8.2]
-
B. Ryden, “Introduction to Cosmology”, Cambridge 2016. This book provides a clear introduction to cosmology for upper-level undergraduates.
- [F8.3]
-
E.F. Taylor and J.A. Wheeler, “Exploring Black Holes, introduction to general relativity”, Addison-Wesley 2000. This book provides an enlightening introduction to the physics of black holes emphasizing how they are “seen” by observers in different reference frames.
- [F8.4]
-
M.V. Berry, “Principles of Cosmology and Gravitation”, Adam Hilger 1989. This book presents the fundamentals of general relativity and cosmology with many worked examples and exercises without requiring the use of tensor calculus.
- [F8.5]
-
V. Mukhanov, “Physical Foundations of Cosmology”, Cambridge 2005. This book provides a comprehensive introduction to inflationary cosmology at early graduate level.
- [F8.6]
-
B. Schutz, “A first Course in General Relativity”, second edition, Cambridge University Press 2009. This is a classic and comprehensive textbook.
- [F8.7]
-
R. Feynman, “The Feynman Lectures on Physics”, www.feynmanlectures.caltech.edu. The classic book by Feynman on Web.
Exercises
- 1.
Cosmological principle and Hubble law. Show that the Hubble law does not contradict the cosmological principle (all points in space and time are equivalent).
- 2.
Olbers Paradox. Why is the night dark? Does the existence of interstellar dust (explanation studied by Olbers himself) solve the paradox?
- 3.
Steady state Universe. In a steady state Universe with Hubble law, matter has to be permanently created. Compute in that scenario the creation rate of matter.
- 4.
Blackbody form of the Cosmic Microwave Background. In 1965 Penzias and Wilson discovered that nowadays the Universe is filled with a cosmic microwave background which follows an almost perfect Planck blackbody formula. Show that the blackbody form of the energy density of the background photons was preserved during the expansion and the cooling that had occurred in the Universe after photon decoupling.
- 5.
The CMB and our body. If CMB photons are absorbed by the human body (which is a reasonable assumption), what is the power received by a human in space because of CMB?
- 6.
CMB, infrared and visible photons. Estimate the number of near-visible photons (
 from 0.3
from 0.3  m to 1
m to 1  m) in a cubic centimeter of
interstellar space. Estimate the number of far-infrared photons in
the region of
m) in a cubic centimeter of
interstellar space. Estimate the number of far-infrared photons in
the region of  from 1000
from 1000  m to 1
m to 1  m.
m. - 7.
Requirements for a cosmic neutrino background detector. Let the typical energy of a neutrino in the Cosmic Neutrino Background be
 meV. What is the approximate
interaction cross section for cosmic neutrinos? How far would
typically a cosmic neutrino travel in ice before interacting?
meV. What is the approximate
interaction cross section for cosmic neutrinos? How far would
typically a cosmic neutrino travel in ice before interacting? - 8.
Dark Matter and mini-BHs. If BHs of mass
 made up all the dark matter in the
halo of our Galaxy, how far away would the nearest such BH on
average? How frequently would you expect such a BH to pass within 1
AU of the Sun?
made up all the dark matter in the
halo of our Galaxy, how far away would the nearest such BH on
average? How frequently would you expect such a BH to pass within 1
AU of the Sun? - 9.
Nucleosynthesis and neutron lifetime. The value of the neutron lifetime, which is abnormally long for weak decay processes (why?), is determinant in the evolution of the Universe. Discuss what would have been the primordial fraction of He if the neutron lifetime would have been one-tenth of its real value.
- 10.
GPS time corrections. Identical clocks situated in a GPS satellite and at the Earth surface have different periods due general relativity effects. Compute the time difference in one day between a clock situated in a satellite in a circular orbit around Earth with a period of 12 h and a clock situated on the Equator at the Earth surface. Consider that Earth has a spherical symmetry and use the Schwarzschild metric.
- 11.
Asymptotically Matter-dominated Universe. Consider a Universe composed only by matter and radiation. Show that whatever would have been the initial proportion of matter and radiation energy densities this Universe will be asymptotically matter dominated.
- 12.
Cosmological distances. Consider a light source at a redshift of
 in an Einstein-de Sitter Universe.
(a) How far has the light from this object traveled to reach us?
(b) How distant is this object today?
in an Einstein-de Sitter Universe.
(a) How far has the light from this object traveled to reach us?
(b) How distant is this object today? - 13.
Decoupling. What are the characteristic temperatures (or energies) at which (a) neutrinos decouple; (b) electron-positron pairs annihilate; (c) protons and neutrons drop out of equilibrium; (d) light atomic nuclei form; (e) neutral He atoms form; (f) neutral hydrogen atoms form; (g) photons decouple from baryonic matter?
- 14.
Evolution of momentum. How does the momentum of a free particle evolve with redshift (or scale factor)?
- 15.
 CDM and
distances. Estimate the expected apparent magnitude of a type
Ia supernova (absolute magnitude
CDM and
distances. Estimate the expected apparent magnitude of a type
Ia supernova (absolute magnitude  at a redshift
at a redshift  in the
in the  CDM Universe.
CDM Universe. - 16.
Flatness of the Early Universe. The present experimental data indicate a value for the normalized total energy density of the Universe compatible with one within a few per mil. Compute the maximum possible value of
 at the scale of the electroweak
symmetry breaking consistent with the measurements at the present
time.
at the scale of the electroweak
symmetry breaking consistent with the measurements at the present
time. - 17.
WIMP “miracle”. Show that a possible Weak Interacting Massive Particle (WIMP) with a mass of the order of
 100 GeV would have the relic density
needed to be the cosmic dark matter (this is the so-called WIMP
“miracle”).
100 GeV would have the relic density
needed to be the cosmic dark matter (this is the so-called WIMP
“miracle”). - 18.
Recoil energy in a DM detector. Calculate the recoil energy of a target nucleus in a DM detector.



