1.1 Particle and Astroparticle Physics
The Universe around us, the objects surrounding us, display an enormous diversity. Is this diversity built over small hidden structures? This interrogation started out, as it often happens, as a philosophical question, only to become, several thousand years later, a scientific one. In the sixth and fifth century BC in India and Greece the atomic concept was proposed: matter was formed by small, invisible, indivisible, and eternal particles: the atoms—a word invented by Leucippus (460 BC) and made popular by his disciple Democritus. In the late eighteenth and early nineteenth century, chemistry gave finally to atomism the status of a scientific theory (mass conservation law, Lavoisier 1789; ideal gas laws, Gay-Lussac 1802; multiple proportional law, Dalton 1805), which was strongly reinforced with the establishment of the periodic table of elements by Mendeleev in 1869—the chemical properties of an element depend on a “magic” number, its atomic number.

Sketch of the atom according to atomic models by several scientists in the early twentieth century: from left to right, the Lenard model, the Nagaoka model, the Thomson model, and the Bohr model with the constraints from the Rutherford experiment.
Natural radioactivity was the first way to investigate the intimate structure of matter; then people needed higher energy particles to access smaller distance scales. These particles came again from natural sources: it was discovered in the beginning of the twentieth century that the Earth is bombarded by very high-energy particles coming from extraterrestrial sources. These particles were named “cosmic rays.” A rich and not predicted spectrum of new particles was discovered. Particle physics, the study of the elementary structure of matter, also called “high-energy physics,” was born.
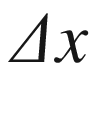 we can sample is inversely
proportional to the momentum (which approximately equals the ratio
of the energy E by the speed of
light c for large energies) of
the probe we are using for the investigation itself:
we can sample is inversely
proportional to the momentum (which approximately equals the ratio
of the energy E by the speed of
light c for large energies) of
the probe we are using for the investigation itself:

 J s is the so-called
Planck2 constant (sometimes the name of Planck
constant is given to h).
Accelerating machines, developed in the mid-twentieth century,
provided higher and higher energy particle beams in optimal
experimental conditions. The collision point was well-defined and
multilayer detectors could be built around it. Subnuclear particles
(quarks) were discovered, and a “standard model of particle physics” was built, piece by
piece, until its final consecration with the recent discovery of
the Higgs boson. The TeV energy scale (that corresponds to
distances down to
J s is the so-called
Planck2 constant (sometimes the name of Planck
constant is given to h).
Accelerating machines, developed in the mid-twentieth century,
provided higher and higher energy particle beams in optimal
experimental conditions. The collision point was well-defined and
multilayer detectors could be built around it. Subnuclear particles
(quarks) were discovered, and a “standard model of particle physics” was built, piece by
piece, until its final consecration with the recent discovery of
the Higgs boson. The TeV energy scale (that corresponds to
distances down to  –
– m) is, for the time being,
understood.
m) is, for the time being,
understood.However, at the end of the twentieth century, the “end of fundamental physics research” announced once again by some, was dramatically dismissed by new and striking experimental evidence which led to the discovery of neutrino oscillations, which meant nonzero neutrino mass, and by the proof that the Universe is in a state of accelerated expansion and that we are immersed in a dark Universe composed mainly of dark matter and dark energy—whatever those entities, presently unknown to us, are. While the discovery that neutrinos have nonzero mass could be incorporated in the standard model by a simple extension, the problems of dark matter and dark energy are still wide open.
The way to our final understanding of the
fundamental constituents of the Universe, which we think will occur
at energies of 10 GeV (the so-called Planck scale), is hopelessly long. What is worse,
despite the enormous progress made by particle acceleration
technology, the energies we shall be able to reach at Earth will
always be lower than those of the most energetic cosmic
rays—particles reaching the Earth from not yet understood
extraterrestrial accelerators. These high-energy beams from space
may advance our knowledge of fundamental physics and interactions,
and of astrophysical phenomena; last but not least, the messengers
from space may advance our knowledge of the Universe on a large
scale, from cosmology to the ultimate quest on the origins of life,
astrobiology. That is the domain and the ambition of the new field
of fundamental physics called astroparticle physics. This book
addresses this field.
GeV (the so-called Planck scale), is hopelessly long. What is worse,
despite the enormous progress made by particle acceleration
technology, the energies we shall be able to reach at Earth will
always be lower than those of the most energetic cosmic
rays—particles reaching the Earth from not yet understood
extraterrestrial accelerators. These high-energy beams from space
may advance our knowledge of fundamental physics and interactions,
and of astrophysical phenomena; last but not least, the messengers
from space may advance our knowledge of the Universe on a large
scale, from cosmology to the ultimate quest on the origins of life,
astrobiology. That is the domain and the ambition of the new field
of fundamental physics called astroparticle physics. This book
addresses this field.
Let us start from the fundamental entities: particles and their interactions.
1.2 Particles and Fields
The paradigm which is currently accepted by most researchers, and which is at the basis of the so-called standard model of particle physics, is that there is a set of elementary particles constituting matter. From a philosophical point of view, even the very issue of the existence of elementary particles is far from being established: the concept of elementarity may just depend on the energy scale at which matter is investigated—i.e., ultimately, on the experiment itself. And since we use finite energies, a limit exists to the scale one can probe. The mathematical description of particles, in the modern quantum mechanical view, is that of fields, i.e., of complex amplitudes associated to points in spacetime, to which a local probability can be associated.
Interactions between elementary particles are described by fields representing the forces; in the quantum theory of fields, these fields can be seen as particles themselves. In classical mechanics fields were just a mathematical abstraction; the real thing were the forces. The paradigmatic example was Newton’s3 instantaneous and universal gravitation law. Later, Maxwell gave to the electromagnetic field the status of a physical entity: it transports energy and momentum in the form of electromagnetic waves and propagates at a finite velocity—the speed of light. Then, Einstein4 explained the photoelectric effect postulating the existence of photons—the interaction of the electromagnetic waves with free electrons, as discovered by Compton,5 was equivalent to elastic collisions between two particles: the photon and the electron. Finally with quantum mechanics the wave-particle duality was extended to all “field” and “matter” particles.
Field particles and matter particles have different behaviors. Whereas matter particles comply with the Pauli6 exclusion principle—only one particle can occupy a given quantum state (matter particles obey Fermi-Dirac statistics and are called “fermions” )—there is no limit to the number of identical and indistinguishable field particles that can occupy the same quantum state (field particles obey Bose–Einstein statisticsand are called “bosons” ). Lasers (coherent streams of photons) and the electronic structure of atoms are thus justified. The spin of a particle and the statistics it obeys are connected by the spin-statistics theorem: according to this highly nontrivial theorem, demonstrated by Fierz (1939) and Pauli (1940), fermions have half-integer spins, whereas bosonshave integer spins.
 , and the neutrino, neutral), and 6 quarks
(a state of 3 bound quarks constitutes a nucleon, like the protonor the neutron).
Each big family can be divided into three generations of two
particles each; generations have similar properties—but different
masses. This is summarized in Fig. 1.2. A good scale for
masses is one GeV/
, and the neutrino, neutral), and 6 quarks
(a state of 3 bound quarks constitutes a nucleon, like the protonor the neutron).
Each big family can be divided into three generations of two
particles each; generations have similar properties—but different
masses. This is summarized in Fig. 1.2. A good scale for
masses is one GeV/ , approximately equal to 1.79
, approximately equal to 1.79
 kg— we are implicitly using the
relation
kg— we are implicitly using the
relation  ; the proton mass is about 0.938
GeV/
; the proton mass is about 0.938
GeV/ . Notice, however, that masses of the
elementary “matter” particles vary by many orders of magnitude,
from the neutrino masses which are of the order of a fraction of
eV/
. Notice, however, that masses of the
elementary “matter” particles vary by many orders of magnitude,
from the neutrino masses which are of the order of a fraction of
eV/ , to the electron mass (about half a
MeV/
, to the electron mass (about half a
MeV/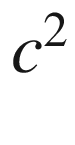 ), to the top quark mass (about 173
GeV/
), to the top quark mass (about 173
GeV/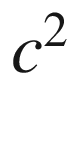 ). Quarks have fractional charges with
respect to the absolute value of the electron charge, e:
). Quarks have fractional charges with
respect to the absolute value of the electron charge, e:  for the up, charm, top quark, and
for the up, charm, top quark, and
 for the down, strange, bottom. Quark
names are just fantasy names.
for the down, strange, bottom. Quark
names are just fantasy names.

Presently observed elementary particles. Fermions (the matter particles) are listed in the first three columns; gauge bosons (the field particles) are listed in the fourth column.
The Higgs boson is standing alone. Adapted from MissMJ [CC BY 3.0 (http://creativecommons.org/licenses/by/3.0)], via Wikimedia Commons
The material constituting Earth can be basically explained by only three particles: the electron, the up quark, and the down quark (the proton being made of two up quarks and one down, uud, and the neutron by one up and two down, udd).
For each known particle there is an
antiparticle (antimatter) counterpart,
with the same mass and opposite charge quantum numbers. To indicate
antiparticles, the following convention holds: if a particle is
indicated by P, its
antiparticle is in general written with a bar over it, i.e.,
 . For example, to every quark,
q, an antiquark,
. For example, to every quark,
q, an antiquark,  , is associated; the antiparticle of
the proton p (uud) is the antiproton
, is associated; the antiparticle of
the proton p (uud) is the antiproton  (
( ), with negative electric charge. The
antineutron
), with negative electric charge. The
antineutron  is the antiparticle of the neutron
(note the different quark composition of the two). To the electron
neutrino
is the antiparticle of the neutron
(note the different quark composition of the two). To the electron
neutrino  an anti-electron neutrino
an anti-electron neutrino
 corresponds (we shall see later in
the book that neutrinos, although electrically neutral, have
quantum numbers allowing them to be distinguished from their
antiparticles). A different naming convention is used in the case
of the anti-electron or positron
corresponds (we shall see later in
the book that neutrinos, although electrically neutral, have
quantum numbers allowing them to be distinguished from their
antiparticles). A different naming convention is used in the case
of the anti-electron or positron  : the superscript denoting the charge
makes explicit the fact that the antiparticle has the opposite
electric charge to that of its associated particle. The same
applies to the heavier leptons (
: the superscript denoting the charge
makes explicit the fact that the antiparticle has the opposite
electric charge to that of its associated particle. The same
applies to the heavier leptons ( ,
,  ) and to the “field particles”
) and to the “field particles”
 .
.
- 1.
The gravitational interaction, acting between whatever pair of bodies and dominant at macroscopic scales.
- 2.
The electromagnetic interaction, acting between pairs of electrically charged particles (i.e., all matter particles, excluding neutrinos).
- 3.
The weak interaction, also affecting all matter particles (with certain selection rules) and responsible, for instance, for the beta decay and thus for the energy production in the Sun.
- 4.
The color force, acting among quarks. The strong interaction,7 responsible for binding the atomic nuclei (it ensures electromagnetic repulsion among protons in nuclei does not break them up) and for the interaction of cosmic protons with the atmosphere, is just a residual shadow (à la van der Waals) of the very strong interaction between quarks.
The relative intensity of such
interactions spans many orders of magnitude. In a  H atom, in a scale where the intensity
of strong interactions between the nucleons is 1, the intensity of
electromagnetic interactions between electrons and the nucleus is
10
H atom, in a scale where the intensity
of strong interactions between the nucleons is 1, the intensity of
electromagnetic interactions between electrons and the nucleus is
10 , the intensity of weak interactions
is 10
, the intensity of weak interactions
is 10 , and the intensity of gravitational
interactions between the electron and the nucleus is 10
, and the intensity of gravitational
interactions between the electron and the nucleus is 10 . However, intensity is not the only
relevant characteristic in this context: one should consider also
the range of the interactions and the characteristics of the
charges. The weak and strong interactions act at subatomic
distances, smaller than
. However, intensity is not the only
relevant characteristic in this context: one should consider also
the range of the interactions and the characteristics of the
charges. The weak and strong interactions act at subatomic
distances, smaller than  1 fm, and they are not very
important at astronomical scales. The electromagnetic and
gravitational forces have instead a
1 fm, and they are not very
important at astronomical scales. The electromagnetic and
gravitational forces have instead a  dependence. On small (molecular)
scales, gravity is negligible compared to electromagnetic forces;
but on large scales, the universe is electrically neutral, so that
electrostatic forces become negligible. Gravity, the weakest of all
forces from a particle physics point of view, is the force
determining the evolution of the Universe at large scales.
dependence. On small (molecular)
scales, gravity is negligible compared to electromagnetic forces;
but on large scales, the universe is electrically neutral, so that
electrostatic forces become negligible. Gravity, the weakest of all
forces from a particle physics point of view, is the force
determining the evolution of the Universe at large scales.
|
Quanta of the interaction fields |
|
|---|---|
|
Strong interaction |
Eight gluons |
|
Electromagnetic interaction |
Photon ( |
|
Weak interaction |
Bosons |
|
Gravitational interaction |
Graviton (?) |
According to most scientists, the
gravitational interaction is mediated by the graviton, an electrically neutral boson of mass 0 and spin
2, yet undiscovered. The weak interaction is mediated by three
vectors: two are charged, the  (of mass
(of mass  80.4 GeV/
80.4 GeV/ ) and its antiparticle, the
) and its antiparticle, the
 ; one is neutral, the Z
(with mass
; one is neutral, the Z
(with mass  91.2 GeV/
91.2 GeV/ ). The electromagnetic interaction is
mediated by the well-known photon. The color interaction is
exchanged by eight massless neutral particles called gluons. The couplings of each particle to the
boson(s) associated to a given interaction are determined by the
strength of the interaction and by “magic” numbers, called charges.
The gravitational charge of a particle is proportional to its mass
(energy); the weak charge is the weak isospin charge (
). The electromagnetic interaction is
mediated by the well-known photon. The color interaction is
exchanged by eight massless neutral particles called gluons. The couplings of each particle to the
boson(s) associated to a given interaction are determined by the
strength of the interaction and by “magic” numbers, called charges.
The gravitational charge of a particle is proportional to its mass
(energy); the weak charge is the weak isospin charge ( for the fermions sensitive to the
weak interaction, 0,
for the fermions sensitive to the
weak interaction, 0,  for bosons); the electrical charge is
the well-known (positive and negative) charge; the strong charge
comes in three types designated by color names (red, green, blue).
Particles or combinations of particles can be neutral to the
electromagnetic, weak or strong interaction, but not to the
gravitational interaction. For instance, electrons have electric
and weak charges but no color charge, and atoms are electrically
neutral. At astrophysical scales, the dominant interaction is
gravitation; at atomic scales,
for bosons); the electrical charge is
the well-known (positive and negative) charge; the strong charge
comes in three types designated by color names (red, green, blue).
Particles or combinations of particles can be neutral to the
electromagnetic, weak or strong interaction, but not to the
gravitational interaction. For instance, electrons have electric
and weak charges but no color charge, and atoms are electrically
neutral. At astrophysical scales, the dominant interaction is
gravitation; at atomic scales,  (1 nm), it is the electromagnetic
interaction; and at the scale of nuclei,
(1 nm), it is the electromagnetic
interaction; and at the scale of nuclei,  (1fm), it is the strong
interaction.
(1fm), it is the strong
interaction.
In quantum physics the vacuumis not empty at all. Heisenberg’s
uncertainty relations allow energy conservation violations by a
quantity  within small time intervals
within small time intervals
 such that
such that  . Massive particles that live in such
tiny time intervals are called “virtual.” But, besides these
particles which are at the origin of measurable effects (like the
Casimir effect, see Chap. 6), we have just discovered that
space is filled by an extra field to which is associated the Higgs
boson, a neutral spinless particle with mass about 125
GeV/
. Massive particles that live in such
tiny time intervals are called “virtual.” But, besides these
particles which are at the origin of measurable effects (like the
Casimir effect, see Chap. 6), we have just discovered that
space is filled by an extra field to which is associated the Higgs
boson, a neutral spinless particle with mass about 125
GeV/ . Particles in the present theory are
intrinsically massless, and it is their interaction with the Higgs
field that originates their mass: the physical properties of
particles are related to the properties of the quantum vacuum.
. Particles in the present theory are
intrinsically massless, and it is their interaction with the Higgs
field that originates their mass: the physical properties of
particles are related to the properties of the quantum vacuum.
1.3 The Particles of Everyday Life
As we have seen, matter around us is
essentially made of atoms; these atoms can be explained by just
three particles: protons and neutrons (making up the atomic nuclei)
and electrons. Electrons are believed to be elementary particles,
while protons and neutrons are believed to be triplets of quarks –
uud and udd, respectively. Particles made of
triplets of quarks are called baryons.
Electrons and protons are stable particles to the best of our
present knowledge, while neutrons have an average lifetime
( ) of about 15 min if free, and
then they decay, mostly into a proton, an electron and an
antineutrino—the so-called
) of about 15 min if free, and
then they decay, mostly into a proton, an electron and an
antineutrino—the so-called  decay. Neutrons in atoms, however,
can be stable: the binding energy constraining them in the atomic
nucleus can be such that the decay becomes energetically
forbidden.
decay. Neutrons in atoms, however,
can be stable: the binding energy constraining them in the atomic
nucleus can be such that the decay becomes energetically
forbidden.
Baryons are not the only allowed
combination of quarks: notably, mesons
are allowed combinations of a quark and an antiquark. All mesons
are unstable. The lightest mesons, called pions, are combinations
of u and d quarks and their antiparticles; they
come in a triplet of charge ( ,
,  ,
,  ) and have masses of about 0.14
GeV/
) and have masses of about 0.14
GeV/ . Although unstable (
. Although unstable ( ns, mostly decaying through
ns, mostly decaying through
 and similarly for
and similarly for  ;
;  s, mostly decaying through
s, mostly decaying through
 ), pions are also quite common, since
they are one of the final products of the chain of interactions of
particles coming from the cosmos (cosmic rays, see later) with the
Earth’s atmosphere.
), pions are also quite common, since
they are one of the final products of the chain of interactions of
particles coming from the cosmos (cosmic rays, see later) with the
Earth’s atmosphere.
All baryons and mesons (i.e., hadrons)
considered up to now are combinations of u and d quarks and of their antiparticles.
Strange hadrons (this is the
term we use for baryons and mesons involving the s, or strange, quark) are less common, since
the mass of the s is larger and
the lifetimes of strange particles are of the order of 1 ns.
The lightest strange mesons are called the K mesons, which can be charged
( ,
,  ) or neutral; the lightest strange baryon
(uds) is called the
) or neutral; the lightest strange baryon
(uds) is called the
 .
.
The heavier brothers of the electrons,
the muons (with masses of about 0.11
GeV/ ), are also common, since they have a
relatively long lifetime (
), are also common, since they have a
relatively long lifetime ( s) and they can propagate for long
distances in the atmosphere. They also appear in the chain of
interactions/decays of the products of cosmic rays.
s) and they can propagate for long
distances in the atmosphere. They also appear in the chain of
interactions/decays of the products of cosmic rays.
Last but not least, a “field particle”
is fundamental for our everyday life: the quantum of
electromagnetic radiation, the photon ( ). The photon is massless to the best of our knowledge,
and electrically neutral. Photon energies are related to their
wavelength
). The photon is massless to the best of our knowledge,
and electrically neutral. Photon energies are related to their
wavelength  through
through  , and the photons of wavelengths
between about 0.4 and 0.7
, and the photons of wavelengths
between about 0.4 and 0.7  m can be perceived by our eyes as
light.
m can be perceived by our eyes as
light.
1.4 The Modern View of Interactions: Quantum Fields and Feynman Diagrams
The purpose of physics is to describe (and possibly predict) change with time. A general concept related to change is the concept of interaction, i.e., the action that occurs as two or more objects have an effect upon one another. Scattering and decay are examples of interactions, leading from an initial state to a final state. The concept of interaction is thus a generalization of the concept of force exchange in classical physics.
Quantum field theories (QFT), which provide in modern physics
the description of interactions, describe nature in terms of
fields, i.e., of wavefunctions defined in
spacetime. A force between two particles (described by “particle
fields”) is described in terms of the exchange of virtual force
carrier particles (again described by appropriate fields) between
them. For example, the electromagnetic force is mediated by the
photon field; weak interactions are mediated by the Z and  fields, while the mediators of the
strong interaction are called gluons. “Virtual” means that these
particles can be off-shell; i.e., they do not need to have the
“right” relationship between mass, momentum, and energy—this is
related to the virtual particles that we
discussed when introducing the uncertainty relations, which can
violate energy–momentum conservation for short times.
fields, while the mediators of the
strong interaction are called gluons. “Virtual” means that these
particles can be off-shell; i.e., they do not need to have the
“right” relationship between mass, momentum, and energy—this is
related to the virtual particles that we
discussed when introducing the uncertainty relations, which can
violate energy–momentum conservation for short times.
Feynman diagrams are pictorial representations of interactions, used in particular for interactions involving subatomic particles, introduced by Richard Feynman8 in the late 1940s.
 and Z). Two important rules that the Feynman
diagrams must satisfy clarify the meaning of such representation:
and Z). Two important rules that the Feynman
diagrams must satisfy clarify the meaning of such representation:
-
conservation of energy and momentum is required at every vertex;
-
lines entering or leaving the diagram represent real particles and must have
 (see in the next chapter the
discussion on Einstein’s special relativity).
(see in the next chapter the
discussion on Einstein’s special relativity).
Associated with Feynman diagrams are mathematical rules (called the “Feynman rules”) that enable the calculation of the probability (quantum mechanically, the square of the absolute value of the amplitude) for a given reaction to occur; we shall describe the quantitative aspects in larger detail in Chaps. 6 and 7. Figure 1.3, left, represents a simple Feynman diagram, in which an electron and a proton are mutually scattered as the result of an electromagnetic interaction (virtual photon exchange) between them. This process requires two vertices in which the photon interacts with the charged particle (one for each particle), and for this kind of scattering this is the minimum number of vertices—we say that this is the representation of the process at leading order.


Electromagnetic scattering: interaction between an electron and a proton. Left: via the exchange of one virtual photon. Right: the same process with one more virtual photon—the amplitude decreases by a factor of approximately 1/137
1.5 A Quick Look at the Universe
The origin and destiny of the Universe
are, for most researchers, the fundamental question. Many answers
were provided over the ages, a few of them built over scientific
observations and reasoning. Over the last century enormous
scientific theoretical and experimental breakthroughs have
occurred: less than a century ago, people believed that the Milky
Way, our own galaxy, was the only galaxy in the Universe; now we
know that there are 10 galaxies within the observable
universe, each containing some 10
galaxies within the observable
universe, each containing some 10 stars. Most of them are so far away
that we cannot even hope to explore them.
stars. Most of them are so far away
that we cannot even hope to explore them.
 , which comes from its hieroglyphic
representation). The latter is a star with a mass of about
, which comes from its hieroglyphic
representation). The latter is a star with a mass of about
 kg located at a distance from us of
about 150 million km (i.e., 500 light seconds). We call the average
Earth–Sun distance the astronomical unit, in short AU or au. The ensemble of planets orbiting the Sun
is called the solar system. Looking to the aphelion of the orbit of
the farthest acknowledged planet, Neptune, the solar system has a
diameter of 9 billion km (about 10 light hours, or 60 AU).
kg located at a distance from us of
about 150 million km (i.e., 500 light seconds). We call the average
Earth–Sun distance the astronomical unit, in short AU or au. The ensemble of planets orbiting the Sun
is called the solar system. Looking to the aphelion of the orbit of
the farthest acknowledged planet, Neptune, the solar system has a
diameter of 9 billion km (about 10 light hours, or 60 AU).

The Milky Way seen from top and from side.
The Milky Way (Fig. 1.4) is the galaxy that contains our solar system. Its name “milky” is derived from its appearance as a dim glowing band arching across the night sky in which the naked eye cannot distinguish individual stars. The ancient Romans named it “via lactea,” which literally corresponds to the present name (being lac the latin word for milk)—the term “galaxy,” too, descends from a Greek word indicating milk. Seen from Earth with the unaided eye, the Milky Way appears as a band because its disk-shaped structure is viewed edge-on from the periphery of the galaxy itself. Galilei9 first resolved such band of light into individual stars with his telescope, in 1610.
The Milky Way is a spiral galaxy some
100 000 light-years (ly) across, 1000 ly to 2000 ly thick,
with the solar system located within the disk, about 30 000 ly
away from the galactic center in the so-called Orion arm. The stars
in the inner 10 000 ly form a bulge and a few bars that
radiate from the bulge. The very center of the galaxy, in the
constellation of Sagittarius, hosts a supermassive black hole of
some 4 million solar masses, as determined by studying the orbits
of nearby stars. The interstellar medium (ISM) is filled by partly
ionized gas, dust, and cosmic rays, and it accounts for some 15% of
the total mass of the disk. The gas is inhomogeneously distributed
and it is mostly confined to discrete clouds occupying a few
percent of the volume. A magnetic field of a few  G interacts with the ISM.
G interacts with the ISM.
With its  10
10 stars, the Milky Way is a relatively
large galaxy. Teaming up with a similar-sized partner (called the
Andromeda galaxy), it has gravitationally
trapped many smaller galaxies: together, they all constitute the
so-called Local Group. The Local Group
comprises more than 50 galaxies, including numerous dwarf
galaxies—some are just spherical collections of hundreds of stars
that are called globular clusters. Its gravitational center is
located somewhere between the Milky Way and the Andromeda galaxies.
The Local Group covers a diameter of 10 million light-years, or 10
Mly (i.e., 3.1 megaparsec,10 Mpc); it has a total mass of about
stars, the Milky Way is a relatively
large galaxy. Teaming up with a similar-sized partner (called the
Andromeda galaxy), it has gravitationally
trapped many smaller galaxies: together, they all constitute the
so-called Local Group. The Local Group
comprises more than 50 galaxies, including numerous dwarf
galaxies—some are just spherical collections of hundreds of stars
that are called globular clusters. Its gravitational center is
located somewhere between the Milky Way and the Andromeda galaxies.
The Local Group covers a diameter of 10 million light-years, or 10
Mly (i.e., 3.1 megaparsec,10 Mpc); it has a total mass of about
 solar masses.
solar masses.
Galaxies are not uniformly distributed; most of them are arranged into groups (containing some dozens of galaxies) and clusters (up to several thousand galaxies); groups and clusters and additional isolated galaxies form even larger structures called superclusters that may span up to 100 Mly.
This is how far our observations can go.

 is a parameter called the Hubble constant (whose value is known today to be
about 68 km s
is a parameter called the Hubble constant (whose value is known today to be
about 68 km s Mpc
Mpc , i.e., 21 km s
, i.e., 21 km s Mly
Mly ). The above relation is called
Hubble’s law (Fig. 1.6). Note that at that
time galaxies beyond the Milky Way had just been discovered.
). The above relation is called
Hubble’s law (Fig. 1.6). Note that at that
time galaxies beyond the Milky Way had just been discovered.

Redshift of emission spectrum of stars and galaxies at different distances. A star in our galaxy is shown at the bottom left with its spectrum on the bottom right. The spectrum shows the dark absorption lines, which can be used to identify the chemical elements involved. The other three spectra and pictures from bottom to top show a nearby galaxy, a medium distance galaxy, and a distant galaxy. Using the redshift we can calculate the relative radial velocity between these objects and the Earth.

Experimental plot of the relative velocity (in km/s) of known astrophysical objects as a function of distance from Earth (in Mpc). Several methods are used to determine the distances. Distances up to hundreds of parsecs are measured using stellar parallax (i.e., the difference between the angular positions from the Earth with a time difference of 6 months). Distances up to 50 Mpc are measured using Cepheids, i.e., periodically pulsating stars for which the luminosity is related to the pulsation period (the distance can thus be inferred by comparing the intrinsic luminosity with the apparent luminosity). Finally, distances from 1 to 1000 Mpc can be measured with another type of standard candle, Type Ia supernova, a class of remnants of imploded stars. From 15 to 200 Mpc, the Tully–Fisher relation, an empirical relationship between the intrinsic luminosity of a spiral galaxy and the width of its emission lines (a measure of its rotation velocity), can be used. The methods, having large superposition regions, can be cross-calibrated. The line is a Hubble law fit to the data.
From A. G. Riess, W. H. Press and R. P. Kirshner, Astrophys. J. 473 (1996) 88

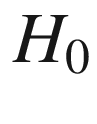 means, the speed of revolution of the
Earth around the Sun is about 30 km/s. Andromeda, the large
galaxy closest to the Milky Way, is at a distance of about 2.5 Mly
from us—however we and Andromeda are indeed approaching: this is an
example of the effect of local motions.
means, the speed of revolution of the
Earth around the Sun is about 30 km/s. Andromeda, the large
galaxy closest to the Milky Way, is at a distance of about 2.5 Mly
from us—however we and Andromeda are indeed approaching: this is an
example of the effect of local motions.Dimensionally, we note that  is the inverse of a time:
is the inverse of a time:
 . A simple interpretation of the
Hubble law is that, if the Universe had always been expanding at a
constant rate, about 14 billion years ago
its volume was zero—naively, we can think that it exploded through
a quantum singularity, such an explosion being usually called the
“Big Bang.” This age is consistent with present estimates of the
age of the Universe within gravitational theories, which we shall
discuss later in this book, and slightly larger than the age of the
oldest stars, which can be measured from the presence of heavy
nuclei. The picture looks consistent.
. A simple interpretation of the
Hubble law is that, if the Universe had always been expanding at a
constant rate, about 14 billion years ago
its volume was zero—naively, we can think that it exploded through
a quantum singularity, such an explosion being usually called the
“Big Bang.” This age is consistent with present estimates of the
age of the Universe within gravitational theories, which we shall
discuss later in this book, and slightly larger than the age of the
oldest stars, which can be measured from the presence of heavy
nuclei. The picture looks consistent.

Tiny quantum fluctuations in the
distribution of cosmic energy at epochs corresponding to fractions
of a second after the Big Bang led to galaxy formation. Density
fluctuations grew with time into proto-structures which, after
accreting enough mass from their surroundings, overcame the pull of
the expanding universe and after the end of an initial era
dominated by radiation collapsed into bound, stable structures. The
average density of such structures was reminiscent of the average
density of the Universe when they broke away from the Hubble
expansion: so, earlier-forming structures have a higher mean
density than later-forming structures. Proto-galaxies were
initially dark. Only later, when enough gas had fallen into their
potential well, stars started to form—again, by gravitational
instability in the gas—and shine due to the nuclear fusion
processes activated by the high temperatures caused by
gravitational forces. The big picture of the process of galaxy
formation is probably understood by now, but the details are not.
The morphological difference between disk (i.e., spiral) galaxies
and spheroidal (i.e., elliptical) galaxies are interpreted as due
to the competition between the characteristic timescale of the
infall of gas into the protogalaxy’s gravitational well and the
timescale of star formation: if the latter is shorter than the
former, a spheroidal (i.e., three-dimensional) galaxy likely forms;
if it is longer, a disk (i.e., two-dimensional) galaxy forms. A
disk galaxy is rotation supported, whereas a spheroidal galaxy is
pressure supported—stars behaving in this case like gas molecules.
It is conjectured that the velocity dispersion ( 200 km/s) among proto-galaxies in
the early Universe may have triggered rotation motions in disk
galaxies, randomly among galaxies but orderly within individual
galaxies.
200 km/s) among proto-galaxies in
the early Universe may have triggered rotation motions in disk
galaxies, randomly among galaxies but orderly within individual
galaxies.
Stars also formed by gravitational instabilities of the gas. For given conditions of density and temperature, gas (mostly hydrogen and helium) clouds collapse and, if their mass is suitable, eventually form stars. Stellar masses are limited by the conditions that (i) nuclear reactions can switch on in the stellar core (>0.1 solar masses), and (ii) the radiation drag of the produced luminosity on the plasma does not disrupt the star’s structure (<100 solar masses). For a star of the mass of the Sun, formation takes 50 million years—the total lifetime is about 11 billion years before collapsing to a “white dwarf,” and in the case of our Sun some 4.5 billion years are already gone.
Stars span a wide range of luminosities and colors and can be classified according to these characteristics. The smallest stars, known as red dwarfs, may contain as little as 10% the mass of the Sun and emit only 0.01% as much energy, having typical surface temperatures of 3000 K, i.e., roughly half the surface temperature of the Sun. Red dwarfs are by far the most numerous stars in the Universe and have lifetimes of tens of billions of years, much larger than the age of the Universe. On the other hand, the most massive stars, known as hypergiants, may be 100 or more times more massive than the Sun, and have surface temperatures of more than 40 000 K. Hypergiants emit hundreds of thousands of times more energy than the Sun, but have lifetimes of only a few million years. They are thus extremely rare today and the Milky Way contains only a handful of them.

Hertzsprung–Russell diagramplotting the luminosities of stars versus their stellar classification or effective temperature (color).
 J—mostly in neutrinos from the nuclear
processes occurring in the core, and just 1% in kinetic energies of
the ejecta—in a few tens of seconds.12 For a period of days to
weeks, a supernova may outshine its entire host galaxy. Being the
energy of the explosion large enough to generate hadronic
interactions, basically any element and many subatomic particles
are produced in these explosions. On average, in a typical galaxy
(e.g., the Milky Way) supernova explosions occur just once or twice
per century. Supernovae leave behind neutron stars or black
holes.13
J—mostly in neutrinos from the nuclear
processes occurring in the core, and just 1% in kinetic energies of
the ejecta—in a few tens of seconds.12 For a period of days to
weeks, a supernova may outshine its entire host galaxy. Being the
energy of the explosion large enough to generate hadronic
interactions, basically any element and many subatomic particles
are produced in these explosions. On average, in a typical galaxy
(e.g., the Milky Way) supernova explosions occur just once or twice
per century. Supernovae leave behind neutron stars or black
holes.13

Binding energy per
nucleon for stable atoms. Iron ( Fe) is the stable element for which
the binding energy per nucleon is the largest (about 8.8 MeV); it
is thus the natural endpoint of processes of fusion of lighter
elements, and of fission of heavier elements (although
Fe) is the stable element for which
the binding energy per nucleon is the largest (about 8.8 MeV); it
is thus the natural endpoint of processes of fusion of lighter
elements, and of fission of heavier elements (although  Fe and
Fe and  Ni have a slightly higher binding
energy, by less than 0.05%, they are subject to nuclear
photodisintegration).
Ni have a slightly higher binding
energy, by less than 0.05%, they are subject to nuclear
photodisintegration).
The heavier the star, the more effective the fusion process, and the shorter the lifetime. We need a star like our Sun, having a lifetime of a few tens of billion of years, to both give enough time to life to develop and to guarantee high enough temperatures for humans. The solar system is estimated to be some 4.6 billion years old and to have started from a molecular cloud. Most of the collapsing mass collected in the center, forming the Sun, while the rest flattened into a disk out of which the planets formed. The Sun is too young to have created heavy elements in such an abundance to justify carbon-based life on Earth. The carbon, nitrogen, and oxygen atoms in our bodies, as well as atoms of all other heavy elements, were created in previous generations of stars somewhere in the Universe.

Present energy budget of the Universe
 of an astrophysical object of mass
m at a distance r from a given point can be computed from
the relation
of an astrophysical object of mass
m at a distance r from a given point can be computed from
the relation
![$$ \frac{m v^2_{\mathrm{esc}}}{2} - G M \frac{m}{r} = \frac{m v^2_{\mathrm{esc}}}{2} - G \left[ \left( \frac{4}{3} \pi r^3 \right) \frac{\rho }{c^2} \right] \frac{m}{r} = 0 \Longrightarrow v_{\mathrm{esc}} = \sqrt{\frac{8}{3} \pi G r^2 \frac{\rho }{c^2}} \, , $$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_1_Chapter/304327_2_En_1_Chapter_TeX_Equ6.png)
 is the amount of mass in the sphere
of radius r,
is the amount of mass in the sphere
of radius r,  being the average energy density, and
G the gravitational constant.
Given Hubble’s law, if
being the average energy density, and
G the gravitational constant.
Given Hubble’s law, if

 , about 5 GeV/m
, about 5 GeV/m , is called the critical energy
density of the Universe.
, is called the critical energy
density of the Universe.
Energy spectrum (number of incident particles per unit of energy, per second, per unit area, and per unit of solid angle) of the primary cosmic rays. The vertical band on the left indicates the energy region in which the emission from the Sun is supposed to be dominant; the central band the region in which most of the emission is presumably of galactic origin; the band on the right the region of extragalactic origin.
By Sven Lafebre (own work) [GFDL http://www.gnu.org/copyleft/fdl.html], via Wikimedia Commons
1.6 Cosmic Rays
The distribution in energy (the
so-called energy spectrum) of cosmic
rays14 is quite well described by a power law
 with p a positive number
(Fig. 1.10). The spectral index p is around 3 on average. After the
low-energy region dominated by cosmic rays from the Sun (the solar
wind), the spectrum becomes steeper for energy values of less than
with p a positive number
(Fig. 1.10). The spectral index p is around 3 on average. After the
low-energy region dominated by cosmic rays from the Sun (the solar
wind), the spectrum becomes steeper for energy values of less than
 1000 TeV (150 times the maximum energy
foreseen for the beams of the LHC
collider at CERN) : this is the energy
region that we know to be dominated by cosmic rays produced by
astrophysical sources in our Galaxy, the Milky Way. For higher
energies a further steepening occurs, the point at which this
change of slope takes place being called the “knee.” Some believe
that the region above this energy is dominated by cosmic rays
produced by extragalactic sources, mostly supermassive black holes
growing at the centers of other galaxies. For even higher energies
(more than one million TeV) the cosmic-ray spectrum becomes less
steep, resulting in another change of slope, called the “ankle”;
some others believe that the knee is caused by a propagation
effect, and the threshold for the dominance of extragalactic
sources is indeed close to the ankle. Finally, at the highest
energies in the figure a drastic suppression is present—as expected
from the interaction of long-traveling particles with the cosmic
microwave background, remnant of the origin of the
Universe.15
1000 TeV (150 times the maximum energy
foreseen for the beams of the LHC
collider at CERN) : this is the energy
region that we know to be dominated by cosmic rays produced by
astrophysical sources in our Galaxy, the Milky Way. For higher
energies a further steepening occurs, the point at which this
change of slope takes place being called the “knee.” Some believe
that the region above this energy is dominated by cosmic rays
produced by extragalactic sources, mostly supermassive black holes
growing at the centers of other galaxies. For even higher energies
(more than one million TeV) the cosmic-ray spectrum becomes less
steep, resulting in another change of slope, called the “ankle”;
some others believe that the knee is caused by a propagation
effect, and the threshold for the dominance of extragalactic
sources is indeed close to the ankle. Finally, at the highest
energies in the figure a drastic suppression is present—as expected
from the interaction of long-traveling particles with the cosmic
microwave background, remnant of the origin of the
Universe.15
The majority of high-energy particles in cosmic rays are protons (hydrogen nuclei); about 10% are helium nuclei (nuclear physicists usually call them alpha particles), and 1% are neutrons or nuclei of heavier elements. Together, these account for 99% of cosmic rays, and electrons and photons make up the remaining 1%. Note that the composition is expected to vary with energy; given the energy dependence of the flux, however, only the energies below the knee are responsible for this proportion. The number of neutrinos is estimated to be comparable to that of high-energy photons, but it is very high at low energies because of the nuclear processes that occur in the Sun: such processes involve a large production of neutrinos.
Neutral and stable cosmic messengers
(gamma rays, high-energy neutrinos, gravitational waves) are very
precious since they are not deflected by extragalactic (order of 1
nG–1 fG) or by galactic (order of 1  G) magnetic fields and allow pointing
directly to the source. While we detect a large flux of gamma rays
and we know several cosmic production sites, evidence for
astrophysical neutrinos and gravitational
waves was only recently published,
respectively in 2014 and in 2016.
G) magnetic fields and allow pointing
directly to the source. While we detect a large flux of gamma rays
and we know several cosmic production sites, evidence for
astrophysical neutrinos and gravitational
waves was only recently published,
respectively in 2014 and in 2016.
Cosmic rays hitting the atmosphere (called primary cosmic rays) generally produce secondary particles that can reach the Earth’s surface, through multiplicative showers.

Left: The remnant of the supernova in the Crab region (Crab nebula), a powerful gamma emitter in our Galaxy. The supernova exploded in 1054 and the phenomenon was recorded by Chinese astronomers. Until 2010, most astronomers regarded the Crab as a standard candle for high-energy photon emission, but recently it was discovered that the Crab Nebula from time to time flickers. Anyway, most plots of sensitivity of detectors refer to a “standard Crab” as a reference unit. The vortex around the center is visible; a neutron star rapidly rotating (with a period of around 30 ms) and emitting pulsed gamma-ray streams (pulsar) powers the system. Some supernova remnants, seen from Earth, have an apparent dimension of a few tenths of a degree—about the dimension of the Moon. Right: A supermassive black hole accretes, swallowing neighboring stellar bodies and molecular clouds, and emits jets of charged particles and gamma rays.
Credits: NASA
The reason why the maximum energy
attained by human-made accelerators with the presently known
acceleration technologies cannot compete with the still mysterious
cosmic accelerators is simple. The most efficient way to accelerate
particles requires their confinement within a radius R by a magnetic field B, and the final energy is proportional
to the product  . On Earth, it is difficult to imagine
reasonable confinement radii greater than one hundred kilometers,
and magnetic fields stronger than 10 T (i.e., one hundred
thousand times the Earth’s magnetic field). This combination can
provide energies of a few tens of TeV, such as those of the LHC
accelerator at CERN. In nature, accelerators with much larger radii
exist, such as supernova remnants (light-years) and active galactic
nuclei (tens of thousands of light-years). Of course human-made
accelerators have important advantages, such as being able to
control the flux and the possibility of knowing the initial
conditions (cosmic ray researchers do not know a-priori the initial
conditions of the phenomena they study).
. On Earth, it is difficult to imagine
reasonable confinement radii greater than one hundred kilometers,
and magnetic fields stronger than 10 T (i.e., one hundred
thousand times the Earth’s magnetic field). This combination can
provide energies of a few tens of TeV, such as those of the LHC
accelerator at CERN. In nature, accelerators with much larger radii
exist, such as supernova remnants (light-years) and active galactic
nuclei (tens of thousands of light-years). Of course human-made
accelerators have important advantages, such as being able to
control the flux and the possibility of knowing the initial
conditions (cosmic ray researchers do not know a-priori the initial
conditions of the phenomena they study).

Map of the emitters of photons above 100 GeV in the Universe, in galactic coordinates (from the TeVCAT catalog). The sources are indicated as circles—the colors represent different kinds of emitters which will be explained in Chap. 10.
From http://tevcat.uchicago.edu/ (February 2018)
A sky map of the emitters of very high-energy photons in galactic coordinates16 is shown in Fig. 1.12. One can identify both galactic emitters (in the equatorial plane) and extragalactic emitters. The vast majority of the galactic emitters is associated to remnants of supernovae, while extragalactic emitters are positionally consistent with active galaxies—instruments do not have the resolution needed to study the morphology of galaxies outside the local group.
1.7 Multimessenger Astrophysics
Physicists and astronomers have studied during millennia the visible light coming from astrophysical objects. The twentieth century has been the century of multiwavelength astronomy: information from light at different wavelengths (radio, microwave, infrared, UV, X-ray, and gamma ray) became available and is allowing us, in a joint effort with optical astronomy, to learn more about the various physical processes that occur throughout the Universe.
In the last decade, the detections of astrophysical neutrinos, and especially the detection of gravitational waves, allowed us to learn about objects that were invisible to other astronomical methods, for example merging black hole systems. The new observations paved the way for a new field of research called multimessenger astrophysics: combining the information obtained from the detection of photons, neutrinos, charged particles, and gravitational waves can shed light on completely new phenomena and objects.
- [F1.1]
A. Einstein and L. Infeld, “The Evolution of Physics,” Touchstone. This inspiring book is about the main ideas in physics. With simplicity and a limited amount of formulas it gives an exciting account for the advancement of science down to the early quantum theory.
- [F1.2]
L. Lederman and D. Teresi, “The God Particle: If the Universe Is the Answer, What Is the Question?”, Dell. This book provides a history of particle physics starting from Greek philosophers down to modern quantum physics.
- [F1.3]
G. Smoot and K. Davidson, “Wrinkles in Time,” Harper. This book discusses modern cosmology in a simple way.
- [F1.4]
S. Weinberg, “To Explain the World,” Harper. This book discusses the evolution of modern science.
- 1.
Size of a molecule. Explain how you will be able to find the order of magnitude of the size of a molecule using a drop of oil. Make the experiment and check the result.
- 2.
Thomson atom. Consider the Thomson model of the atom applied to a helium atom (the two electrons are in equilibrium inside a homogeneous positive-charged sphere of radius
 m).
m).- (a)
Determine the distance of the electrons to the center of the sphere.
- (b)
Determine the vibration frequency of the electrons in this model and compare it to the first line of the spectrum of hydrogen, at
 eV.
eV.
- (a)
- 3.
Atom as a box. Consider a simplified model where the hydrogen atom is described by a one-dimensional box of length r with the proton at its center and where the electron is free to move around. Compute, considering the Heisenberg uncertainty principle, the total energy of the electron as a function of r and determine the value of r for which this energy is minimized.
- 4.
Naming conventions for particles. Write down the symbol, charge, and approximate mass for the following particles:
- (a)
tau lepton;
- (b)
antimuon-neutrino;
- (c)
charm quark;
- (d)
anti-electron;
- (e)
antibottom quark.
- (a)
- 5.
Strange mesons. How many quark combinations can you make to build a strange neutral meson, using u, d, and s quarks?
- 6.
The Universe. Find a dark place close to where you live, and go there in the night. Try to locate the Milky Way and the galactic center. Comment on your success (or failure).
- 7.
Telescopes. Research the differences between Newtonian and Galileian telescopes; discuss such differences.
- 8.
Number of stars in the Milky Way. Our Galaxy consists of a disk of a radius
 kpc about
kpc about  300 pc thick, and a spherical bulge
at its center roughly 3 kpc in diameter. The distance between our
Sun and our nearest neighboring stars, the Alpha Centauri system,
is about 1.3 pc. Estimate the number of stars in our galaxy.
300 pc thick, and a spherical bulge
at its center roughly 3 kpc in diameter. The distance between our
Sun and our nearest neighboring stars, the Alpha Centauri system,
is about 1.3 pc. Estimate the number of stars in our galaxy. - 9.
Number of nucleons in the Universe. Estimate the number of nucleons in the Universe.
- 10.
Hubble’s law. The velocity of a galaxy can be measured using the Doppler effect. The radiation coming from a moving object is shifted in wavelength, the relation being, for
 ,
where
,
where
 is the rest wavelength of the
radiation,
is the rest wavelength of the
radiation,  is the observed wavelength minus the
rest wavelength, and v is
defined as positive when the object parts away from the observer.
Notice that (for v small
compared to the speed of light) the formula is the same as for the
classical Doppler effect.
is the observed wavelength minus the
rest wavelength, and v is
defined as positive when the object parts away from the observer.
Notice that (for v small
compared to the speed of light) the formula is the same as for the
classical Doppler effect.An absorption line that is found at 500 nm in the laboratory is measured at 505 nm when analyzing the spectrum of a particular galaxy. Estimate the distance of the galaxy.
- 11.
Luminosity and magnitude. Suppose that you burn a car on the Moon, heating it at a temperature of 3000 K. What is the absolute magnitude of the car? What is the apparent magnitude m seen at Earth?
- 12.
Cosmic ray fluxes and wavelength. The most energetic particles ever observed at Earth are cosmic rays. Make an estimation of the number of such events with an energy between 3
 and
and  eV that may be detected in one year
by an experiment with a footprint of 1000 km
eV that may be detected in one year
by an experiment with a footprint of 1000 km . Evaluate the structure scale that
can be probed by such particles.
. Evaluate the structure scale that
can be probed by such particles. - 13.
Energy from cosmic rays: Nikola Tesla’s “free” energy generator. “This new power for the driving of the world’s machinery will be derived from the energy which operates the universe, the cosmic energy, whose central source for the Earth is the Sun and which is everywhere present in unlimited quantities.” Immediately after the discovery of natural radioactivity, in 1901, Nikola Tesla patented an engine using the energy involved (and expressed a conjecture about the origin of such radioactivity). Below, we show a drawing (made by Tesla himself) of Tesla’s first radiant energy receiver. If an antenna (the higher the better: why?) is wired to one side of a capacitor (the other going to ground), the potential difference will charge the capacitor. Suppose you can intercept all high-energy cosmic radiation (assume 1 particle per square centimeter per second with an average energy of 3 GeV); what is the power you could collect with a 1 m
 antenna, and how does it compare with
solar energy?
antenna, and how does it compare with
solar energy?

- 14.
Galactic and extragalactic emitters of gamma rays. In Fig. 1.12, more than half of the emitters of high-energy photons lie in the galactic plane (the equatorial line). Guess why.


