Particle detectors measure physical quantities related to the result of a collision; they should ideally identify all the outcoming (and the incoming, if unknown) particles and measure their kinematic characteristics (momentum, energy, velocity).
In order to detect a particle, one must make use of its interaction with a sensitive material. The interaction should possibly not destroy the particle that one wants to detect; however, for some particles this is the only way to obtain information.
In order to study the properties of detectors, we shall thus first need to review the characteristics of the interaction of particles with matter.
4.1 Interaction of Particles with Matter
4.1.1 Charged Particle Interactions
Charged particles interact basically with atoms, and the interaction is mostly electromagnetic: they might expel electrons (ionization), promote electrons to upper energy levels (excitation), or radiate photons (bremsstrahlung, Cherenkov radiation, transition radiation). High-energy particles may also interact directly with the atomic nuclei.
4.1.1.1 Ionization Energy Loss
 is described by the so-called Bethe
formula.1 This expression
has an accuracy of a few % in the region
is described by the so-called Bethe
formula.1 This expression
has an accuracy of a few % in the region  for materials with intermediate
atomic number.
for materials with intermediate
atomic number.
![$$\begin{aligned} -\frac{dE}{dx} \simeq \rho D \left( \frac{Z}{A} \right) \frac{(z_p)^2}{\beta ^2} \left[ \frac{1}{2}\ln \left( \frac{2m_e c^2 \beta ^2 \gamma ^2}{I} \right) - \beta ^2 - \frac{\delta (\beta ,\rho )}{2} \right] \, , \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_4_Chapter/304327_2_En_4_Chapter_TeX_Equ1.png)
-
 is the material density, in
g/cm
is the material density, in
g/cm ;
; -
Z and A are the atomic and mass number of the material, respectively;
-
 is the charge of the incoming
particle, in units of the electron charge;
is the charge of the incoming
particle, in units of the electron charge; -
 MeV cm
MeV cm /g;
/g; -
 is the energy corresponding to the
electron mass,
is the energy corresponding to the
electron mass,  0.5 MeV;
0.5 MeV; -
I is the mean excitation energy in the material; it can be approximated as
 for
for  ;
; -
 is a correction term that becomes
important at high energies. It accounts for the reduction in energy
loss due to the so-called density
effect. As the incident particle velocity increases, media
become polarized and their atoms can no longer be considered as
isolated.
is a correction term that becomes
important at high energies. It accounts for the reduction in energy
loss due to the so-called density
effect. As the incident particle velocity increases, media
become polarized and their atoms can no longer be considered as
isolated.
-
independent of the particle’s mass;
-
typically small for high-energy particles (about 2 MeV/cm in water; one can roughly assume a proportionality to the density of the material);
-
proportional to 1/
 for
for  (the minimum of ionization: minimum
ionizing particle, often just called a “mip” );
(the minimum of ionization: minimum
ionizing particle, often just called a “mip” ); -
basically constant for
 0.96 (logarithmic increase after the
minimum);
0.96 (logarithmic increase after the
minimum); -
proportional to Z / A (Z / A being about equal to 0.5 for all elements but hydrogen and the heaviest nuclei).


Specific ionization energy loss for muons, pions, and protons in different materials.
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001

Distribution of the energy loss (Landau distribution) in silicon for 500 MeV pions, normalized to unity at the most probable value. w is the full width at half maximum.
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
 passes at a distance b from a target of mass M and charge Z. The momentum
passes at a distance b from a target of mass M and charge Z. The momentum  transferred to the target depends on
the electric field
transferred to the target depends on
the electric field  produced by the charged traveling
particle. Given the symmetry of the problem only the transverse
component of the electric field with the respect to the particle
track
produced by the charged traveling
particle. Given the symmetry of the problem only the transverse
component of the electric field with the respect to the particle
track  matters. Relating the interaction
time t with the velocity of the
particle,
matters. Relating the interaction
time t with the velocity of the
particle,  , one can write for the momentum
transfer:
, one can write for the momentum
transfer:

 . Therefore, the momentum transferred
to the target particle can be written as
. Therefore, the momentum transferred
to the target particle can be written as


 0.003 pm:
0.003 pm:

 ) and low mass particles (
) and low mass particles ( ) are the most important with respect
to energy loss; thus one can neglect the effect of nuclei.
) are the most important with respect
to energy loss; thus one can neglect the effect of nuclei.Photoluminescence. In some transparent
media, part ofthe ionization energy loss
goes into the emission of visible or near-visible light by the
excitation of atoms and/or molecules. This phenomenon is called
photoluminescence; often it results into a fast ( 100
100  s) excitation/de-excitation—in this
last case we talk of fluorescence, or scintillation. Specialists
often use definitions which distinguish between fluorescence and
scintillation; this separation is, however, not universally
accepted. We shall discuss later fluorescence in the context of the
detection of large showers induced in the atmosphere by high-energy
cosmic rays.
s) excitation/de-excitation—in this
last case we talk of fluorescence, or scintillation. Specialists
often use definitions which distinguish between fluorescence and
scintillation; this separation is, however, not universally
accepted. We shall discuss later fluorescence in the context of the
detection of large showers induced in the atmosphere by high-energy
cosmic rays.
4.1.1.2 High-Energy Radiation Effects
According to classical electromagnetism, a charged particle undergoing acceleration radiates electromagnetic waves. The intensity of the emitted radiation from a dipole is proportional to the square of the acceleration.

The stopping power  for positive muons in copper as a
function of
for positive muons in copper as a
function of  is shown over nine orders of
magnitude in momentum (corresponding to 12 orders of magnitude in
kinetic energy).
is shown over nine orders of
magnitude in momentum (corresponding to 12 orders of magnitude in
kinetic energy).
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
To first order, the emitted energy is
(as in the classical case) proportional to the inverse of the
square of the mass. On top of the ionization energy loss described
by Eq. 4.1, above  (which means an extremely high energy
for a proton,
(which means an extremely high energy
for a proton,  TeV, but just
TeV, but just  GeV for a muon), such radiation
effects become important (Fig. 4.3).
GeV for a muon), such radiation
effects become important (Fig. 4.3).
 is approximately independent of the
energy itself, and can be described by
is approximately independent of the
energy itself, and can be described by

 is called the radiation length, and is characteristic of the material—for
example, it is about 300 m for air at Normal Temperature and
Pressure (NTP),4 about 36 cm for water, about
0.5 cm for lead.
is called the radiation length, and is characteristic of the material—for
example, it is about 300 m for air at Normal Temperature and
Pressure (NTP),4 about 36 cm for water, about
0.5 cm for lead.

Fractional energy loss per radiation length in lead as a function of the electron or positron energy.
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
 ) is
) is

 and
and  is the density of atoms per cubic
centimeter in the medium, or more simply
is the density of atoms per cubic
centimeter in the medium, or more simply

 ) decreases
with increasing atomic number:
) decreases
with increasing atomic number:


 , which anyway does not contradict
energy conservation: the integral of the energy released for each
energy bin is constant.
, which anyway does not contradict
energy conservation: the integral of the energy released for each
energy bin is constant.The emitted photons are collimated: the
typical angle of emission is  .
.
4.1.1.3 Cherenkov Radiation
The Vavilov–Cherenkov5 radiation (commonly called just Cherenkov radiation) occurs when a charged particle moves through a medium faster than the speed of light in that medium. The total energy loss due to this process is negligible; however, Cherenkov radiation is important due to the possibility of use in detectors.

 , where n is the refractive index of the medium.
The presence of a coherent wavefront can be easily derived by using
the Huygens–Fresnel principle.
, where n is the refractive index of the medium.
The presence of a coherent wavefront can be easily derived by using
the Huygens–Fresnel principle. at the maximum (limiting) angle is
at the maximum (limiting) angle is


Emission of Cherenkov radiation by a charged particle. User Harp, Creative Commons Attribution-Share Alike 2.5 Generic license via Wikimedia Commons

 and the medium is transparent, and
this happens close to the range of visible light).
and the medium is transparent, and
this happens close to the range of visible light).The total energy radiated is small, some
 times the energy lost by ionization.
In the visible range (300–700 nm), the total number of emitted
photons is about 40/m in air, about 500/cm in water. Due to the
dependence on
times the energy lost by ionization.
In the visible range (300–700 nm), the total number of emitted
photons is about 40/m in air, about 500/cm in water. Due to the
dependence on  , it is important that Cherenkov
detectors are sensitive close to the ultraviolet region.
, it is important that Cherenkov
detectors are sensitive close to the ultraviolet region.
Dense media can be transparent not only to visible light, but also to radio waves. The development of Cherenkov radiation in the radiowave region due to the interactions with electrons in the medium is often referred to as the Askar’yan effect. This effect has been experimentally confirmed for different media (namely sand, rock salt, and ice) in accelerator experiments at SLAC; presently attempts are in progress to use this effect in particle detectors.
4.1.1.4 Transition Radiation
X-ray transition radiation (XTR) occurs when a relativistic charged particle crosses from one medium to another with different dielectric permittivity.
The energy radiated when a particle with
charge  and
and  crosses the boundary between vacuum
and a different transparent medium is typically concentrated in the
soft X-ray range 2–40 keV.
crosses the boundary between vacuum
and a different transparent medium is typically concentrated in the
soft X-ray range 2–40 keV.

Range per unit of density and of mass for
heavy charged particles in liquid (bubble chamber) hydrogen, helium
gas, carbon, iron, and lead. Example: a  with momentum 700 MeV/c,
with momentum 700 MeV/c,  1.42, and we read
1.42, and we read  in lead, corresponding to a range of
195 g/cm
in lead, corresponding to a range of
195 g/cm .
.
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
4.1.2 Range

4.1.3 Multiple Scattering

Multiple Coulomb scattering.
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
 to determine the standard deviation
in space):
to determine the standard deviation
in space):
![$$ \theta _0 \simeq \frac{13.6\,\text {MeV}}{\beta c p} z_p \sqrt{\frac{x}{X_0}} \left[ 1 + 0.038 \ln \frac{x}{X_0} \right] \, . $$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_4_Chapter/304327_2_En_4_Chapter_TeX_Equ29.png)
 is the radiation length defined
before. The above expression comes from the so-called Molière
theory, and is accurate to some 10% or better for
is the radiation length defined
before. The above expression comes from the so-called Molière
theory, and is accurate to some 10% or better for  . For an ultrarelativistic particle of
absolute charge 1 it simplifies to
. For an ultrarelativistic particle of
absolute charge 1 it simplifies to

4.1.4 Photon Interactions
High-energy photons mostly interact with matter via photoelectric effect, Compton scattering, and electron–positron pair production. Other processes, like Rayleigh scattering and photonuclear interactions, have in general much smaller cross sections.
4.1.4.1 Photoelectric Effect
The photoelectric effect is the ejection of an electron from a material that has just absorbed a photon. The ejected electron is called a photoelectron.
The photoelectric effect was pivotal in
the development of quantum physics (for the explanation of this
effect Albert Einstein was awarded the Nobel Prize). Due to
photoelectric effect, a photon of angular frequency  can eject from a metal an electron,
which pops up with a kinetic energy
can eject from a metal an electron,
which pops up with a kinetic energy  , where V is the minimum gap of energy of
electrons trapped in the metal (V is frequently called the work function of the metal).
, where V is the minimum gap of energy of
electrons trapped in the metal (V is frequently called the work function of the metal).
 is
is

 varying between 4 and 5 depending on
the energy. The cross section rapidly decreases with energy above
the typical electron binding energies (Fig. 4.8).
varying between 4 and 5 depending on
the energy. The cross section rapidly decreases with energy above
the typical electron binding energies (Fig. 4.8).
Photon mass attenuation coefficient (cross section per gram of material) as a function of energy in lead tungstate (data from the NIST XCOM database)
4.1.4.2 Compton Scattering
 ) and suppose that the electron is
initially free and at rest. After the collision, the photon is
scattered at an angle
) and suppose that the electron is
initially free and at rest. After the collision, the photon is
scattered at an angle  and comes out with a reduced energy
and comes out with a reduced energy
 , corresponding to a wavelength
, corresponding to a wavelength
 ; the electron acquires an energy
; the electron acquires an energy
 . The conservation laws of energy and
momentum yield the following relation (Compton formula):
. The conservation laws of energy and
momentum yield the following relation (Compton formula):

 is the scattering angle of the
emitted photon;
is the scattering angle of the
emitted photon;  pm is the Compton wavelength of the
electron.
pm is the Compton wavelength of the
electron.It should be noted that, in the case when the target electron is not at rest, the energy of the scattered photon can be larger than the energy of the incoming one. This regime is called inverse Compton, and it has great importance in the emission of high-energy photons by astrophysical sources: in practice, thanks to inverse Compton, photons can be “accelerated.”
 (so the scattered electrons are
nonrelativistic) then the total cross section is given by the
Thomson cross section. This is known as the Thomson limit. The
cross section for
(so the scattered electrons are
nonrelativistic) then the total cross section is given by the
Thomson cross section. This is known as the Thomson limit. The
cross section for  (Thomson regime) is about
(Thomson regime) is about

 0.003 pm is the classical radius of
the electron. If the photon energy is
0.003 pm is the classical radius of
the electron. If the photon energy is  , we are in the so-called
Klein–Nishina regime and the total cross section falls off rapidly
with increasing energy (Fig. 4.8):
, we are in the so-called
Klein–Nishina regime and the total cross section falls off rapidly
with increasing energy (Fig. 4.8):

4.1.4.3 Pair Production
Pair production is the most important interaction process for a photon above an energy of a few tens of MeV. In the electric field in the neighborhood of a nucleus, a high-energy photon has a non-negligible probability of transforming itself into a negative and a positive electron—the process being kinematically forbidden unless an external field, regardless of how little, is present.
 of the electrons:
of the electrons:

 MeV the fraction of energy
MeV the fraction of energy
 taken by the secondary
electron/positron is uniformly distributed between 0 and 1
(becoming peaked at the extremes as the energy increases to values
above 1 PeV).
taken by the secondary
electron/positron is uniformly distributed between 0 and 1
(becoming peaked at the extremes as the energy increases to values
above 1 PeV).
 is the density of atomic nuclei per
unit volume, in such a way that the interaction length is
is the density of atomic nuclei per
unit volume, in such a way that the interaction length is

 .
.4.1.4.4 Rayleigh Scattering and Photonuclear Interactions
Rayleigh
scattering (the dispersion of electromagnetic radiation by
particles with radii  1/10 the wavelength of the radiation)
is usually of minor importance for the conditions of high-energy
particle and astroparticle physics, but it can be important for
light in the atmosphere, and thus for the design of instruments
detecting visible light. The photonuclear effect, i.e., the excitation of nuclei by photons,
is mostly restricted to the region around 10 MeV, and it may
amount to as much as 10% of the total cross section due to
electrodynamic effects.
1/10 the wavelength of the radiation)
is usually of minor importance for the conditions of high-energy
particle and astroparticle physics, but it can be important for
light in the atmosphere, and thus for the design of instruments
detecting visible light. The photonuclear effect, i.e., the excitation of nuclei by photons,
is mostly restricted to the region around 10 MeV, and it may
amount to as much as 10% of the total cross section due to
electrodynamic effects.
4.1.4.5 Comparison Between Different Processes for Photons
The total Compton scattering probability decreases rapidly when the photon energy increases. Conversely, the total pair production probability is a slowly increasing function of energy. At large energies, most photons are thus absorbed by pair production, while photon absorption by the Compton effect dominates at low energies (being the photoelectric effect characteristic of even smaller energies). The absorption of photons by pair production, Compton, and photoelectric effect is compared in Fig. 4.8.
As a matter of fact, above about
30 MeV the dominant process is pair production, and the
interaction length of a photon is, to an extremely good
approximation, equal to  .
.
At extremely high matter densities
and/or at extremely high energies (typically above 10 –10
–10 eV, depending on the medium
composition and density) collisions cannot be treated
independently, and the result of the collective quantum mechanical
treatment is a reduction of the cross section. The result is the
so-called Landau–Pomeranchuk–Migdal
effect, or simply LPM effect,
which entails a reduction of the pair production cross section, as
well as of bremsstrahlung.
eV, depending on the medium
composition and density) collisions cannot be treated
independently, and the result of the collective quantum mechanical
treatment is a reduction of the cross section. The result is the
so-called Landau–Pomeranchuk–Migdal
effect, or simply LPM effect,
which entails a reduction of the pair production cross section, as
well as of bremsstrahlung.
4.1.5 Nuclear (Hadronic) Interactions
The nuclear force is felt by hadrons, charged and neutral; at high energies (above a few GeV), the inelastic cross section for hadrons is dominated by nuclear interaction.
High-energy nuclear interactions are
difficult to model. A useful approximation is to describe them by
an inelastic interaction length  . Values
for
. Values
for  are typically of the order of
100 g/cm
are typically of the order of
100 g/cm ; a listing for some common materials
is provided in Appendix B—where the inelastic interaction length
; a listing for some common materials
is provided in Appendix B—where the inelastic interaction length
 and the total interaction length
and the total interaction length
 are separately listed, and the rule
for the composition is
are separately listed, and the rule
for the composition is  .
.
The final state products of inelastic high-energy hadronic collisions are mostly pions, since these are the lightest hadrons. The rate of positive, negative, and neutral pions is more or less equal—as we shall see, this fact is due to an approximate symmetry of hadronic interactions, called the strong isospin symmetry.
4.1.6 Interaction of Neutrinos
The case of neutrinos is a special one.
Neutrinos have a very low interaction cross section. High-energy
neutrinos mainly interact with nucleons, being the neutrino-lepton
cross section smaller—with the exception of the peak corresponding
to the production of the  boson in neutrino-lepton interactions
at
boson in neutrino-lepton interactions
at  eV.
eV.
 10 TeV (Fig. 4.9) as
10 TeV (Fig. 4.9) as

 TeV (
TeV ( eV), a parametrization is
eV), a parametrization is


Measurements of muon neutrino and antineutrino inclusive scattering cross sections divided by neutrino energy as a function of neutrino energy; different symbols represent measurements by different experiments. Note the transition between logarithmic and linear scales at 100 GeV.
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
4.1.7 Electromagnetic Showers
High-energy electrons lose most of their energy by radiation. Thus, in their interaction with matter, most of the energy is spent in the production of high-energy photons and only a small fraction is dissipated. The secondary photons, in turn, undergo pair production (or, at lower energies, Compton scattering); secondary electrons and positrons can in turn radiate. This phenomenon continues generating cascades (showers) of electromagnetic particles; at each step the number of particles increases while the average energy decreases, until the energy falls below the critical energy.

 is the radiation length), and of the
scaled energy
is the radiation length), and of the
scaled energy

 is the critical energy); the
radiation length and the critical energy have been defined in
Sect. 4.1.1.2. Since the opening angles for
bremsstrahlung and pair production are small, the process can be in
first approximation (above the critical energy) considered as
one-dimensional (the lateral spread will be discussed at the end of
this section).
is the critical energy); the
radiation length and the critical energy have been defined in
Sect. 4.1.1.2. Since the opening angles for
bremsstrahlung and pair production are small, the process can be in
first approximation (above the critical energy) considered as
one-dimensional (the lateral spread will be discussed at the end of
this section).-
the incoming charged particle has an initial energy
 much larger than the critical energy
much larger than the critical energy
 ;
; -
each electron travels one radiation length and then gives half of its energy to a bremsstrahlung photon;
-
each photon travels one radiation length and then creates an electron–positron pair; the electron and the positron each carry half of the energy of the original photon.
 , and then electrons and positrons
lose their energy by ionization.
, and then electrons and positrons
lose their energy by ionization.

Left: Scheme of the Heitler approximation for the development of an electromagnetic shower. From J. Matthews, Astropart. Phys. 22 (2005) 387. Right: Image of an electromagnetic shower developing through a number of brass plates 1.25 cm thick placed across a cloud chamber (from B. Rossi, “Cosmic rays,” McGraw-Hill 1964)
 particles and there will be roughly
the same number of electrons, positrons, and photons, each with an
average energy
particles and there will be roughly
the same number of electrons, positrons, and photons, each with an
average energy

 , at a thickness of absorber
, at a thickness of absorber
 that can be written in terms of the
initial and critical energies as
that can be written in terms of the
initial and critical energies as


Shower parameters for a particle on energy
 according to Rossi’s approximation B
(y
according to Rossi’s approximation B
(y 
 )
)
|
Incident electron |
Incident photon |
|
|---|---|---|
|
Peak of shower |
|
|
|
Center of gravity |
|
|
|
Number of |
|
|
|
Total track length |
y |
y |

Logarithm of the number of electrons for
electron-initiated showers, calculated under Rossi approximation B,
as a function of the number of radiation lengths traversed.
Multiplication by  (
( is called
is called  in the figure) yields the specific
ionization energy loss [F4.1]
in the figure) yields the specific
ionization energy loss [F4.1]
 is
is

 is Euler’s Gamma function
is Euler’s Gamma function
 . In the above approximation,
. In the above approximation,
 , which should be thus equal to
, which should be thus equal to
 with
with  for an electron and
for an electron and  for a photon.
for a photon.

A Monte Carlo simulation of a 30 GeV
electron-induced cascade in iron. The histogram shows the
fractional energy deposition per radiation length, and the curve is
a fit to the distribution using Eq. 4.13. The circles
indicate the number of electrons with total energy greater than
1.5 MeV crossing planes at  intervals (scale on the right) and
the squares the number of photons above the same energy crossing
the planes (scaled down to have the same area as the electron
distribution).
intervals (scale on the right) and
the squares the number of photons above the same energy crossing
the planes (scaled down to have the same area as the electron
distribution).
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
 . An incomplete longitudinal
containment of the shower badly increases fluctuations on the
deposited energy. A rule of thumb for the longitudinal containment
of 95% of the shower is
. An incomplete longitudinal
containment of the shower badly increases fluctuations on the
deposited energy. A rule of thumb for the longitudinal containment
of 95% of the shower is

Despite the elegance of Rossi’s calculations, one can do better using computers, and most calculations are performed nowadays by Monte Carlo methods.6 Monte Carlo calculations of electromagnetic cascades have the advantages of using accurate cross sections for bremsstrahlung and pair production, the correct energy dependence of ionization loss, and including all electromagnetic interactions. Monte Carlo calculations, in addition, give correct account for the fluctuations in the shower development, as well as for the angular and lateral distribution of the shower particles. Rossi’s approximation B, however, is faster and represents a rather accurate model.


 is the electron shower size,
r is the distance from the
shower axis, and
is the electron shower size,
r is the distance from the
shower axis, and  is a transverse scale called the
Molière radius described below, is accurate for a shower age
is a transverse scale called the
Molière radius described below, is accurate for a shower age
 . A variety of transverse distribution
functions can be found in the literature (Greisen, Greisen–Linsley,
etc.) and are mostly specific modifications of the NKG
function.
. A variety of transverse distribution
functions can be found in the literature (Greisen, Greisen–Linsley,
etc.) and are mostly specific modifications of the NKG
function.
 ; about 95% is contained in a radius
of
; about 95% is contained in a radius
of  , and about 99% in a radius of
, and about 99% in a radius of
 . In air at NTP,
. In air at NTP,  m; in water
m; in water  cm.
cm.4.1.8 Hadronic Showers
The concept of hadronic showers is similar to the concept of
electromagnetic showers: primary hadrons can undergo a sequence of
interactions and decays creating a cascade. However, on top of
electromagnetic interactions one has now nuclear reactions. In
addition, in hadronic collisions with the nuclei of the material, a
significant part of the primary energy is consumed in the nuclear
processes (excitation, emission of low-energy nucleons, etc.). One
thus needs ad hoc Monte Carlo
corrections to account for the energy lost, and fluctuations are
larger. The development of appropriate Monte Carlo codes for
hadronic interactions has been a problem in itself, and still the
calculation requires huge computational “loads.” At the end of a
hadronic cascade, most of the particles are pions, and one-third of
the pions are neutral and decay almost instantaneously  s) into a pair of photons; thus
on average one third of the hadronic cascade is indeed
electromagnetic (and the fraction of energy detected in
electromagnetic form is larger, since roughly three quarters of the
energy of charged pions is “wasted” into neutrinos). As an example,
the image of a hadronic shower in a cloud chamber is shown in
Fig. 4.13.
s) into a pair of photons; thus
on average one third of the hadronic cascade is indeed
electromagnetic (and the fraction of energy detected in
electromagnetic form is larger, since roughly three quarters of the
energy of charged pions is “wasted” into neutrinos). As an example,
the image of a hadronic shower in a cloud chamber is shown in
Fig. 4.13.
 ; however, the approximation is less
accurate than the one we did when we assumed electromagnetic
reactions to scale with the radiation length
; however, the approximation is less
accurate than the one we did when we assumed electromagnetic
reactions to scale with the radiation length  , and intrinsic fluctuations are
larger.
, and intrinsic fluctuations are
larger.

Image of a hadronic shower developing through a number of brass plates 1.25 cm thick placed across a cloud chamber (from B. Rossi, “Cosmic rays,” McGraw-Hill 1964). To be compared to Fig. 4.10, right
4.2 Particle Detectors
The aim of a particle detector is to measure the momenta and to identify the particles that pass through it after being produced in a collision or a decay; this is called an “event.” The position in space where the event occurs is known as the interaction point.
In order to identify every particle produced by the collision, and plot the paths they have taken—i.e., to “completely reconstruct the event”—it is necessary to know the masses and momenta of the particles themselves. The mass can be computed by measuring the momentum and either the velocity or the energy.
The characteristics of the different instruments that allow for these measurements are presented in what follows.
4.2.1 Track Detectors

 is the component of the magnetic
field perpendicular to the particle velocity, expressed in tesla
(which is the order of magnitude of typical fields in detectors),
the momentum p is expressed in
GeV/c, and R is the radius of curvature (Larmor
radius) of the helix in meters.
is the component of the magnetic
field perpendicular to the particle velocity, expressed in tesla
(which is the order of magnitude of typical fields in detectors),
the momentum p is expressed in
GeV/c, and R is the radius of curvature (Larmor
radius) of the helix in meters.A source of uncertainty for this determination is given by the errors in the measurement of the hits; another (intrinsic) noise is given by multiple scattering. In what follows we shall review some detectors used to determine the trajectory of charged tracks.
4.2.1.1 Cloud Chamber and Bubble Chamber
The cloud chamber was invented by C.T.R. Wilson in the beginning of the twentieth century and was used as a detector for reconstructing the trajectories of charged cosmic rays. The instrument, already discussed in the previous chapter, is a container with a glass window, filled with air and saturated water vapor (Fig. 3.8); the volume can be suddenly expanded, and the adiabatic expansion causes the temperature to decrease, bringing the vapor to a supersaturated (metastable) state. A charged particle crossing the chamber produces ions, which act as seeds for the generation of droplets along the trajectory. One can record the trajectory by taking a photographic picture. If the chamber is immersed in a magnetic field B, momentum and charge can be measured by the curvature.

Left: The BEBC bubble chamber. Center: A picture taken in BEBC, and right: its interpretation.
Credits: CERN
Due to the higher density of liquids compared with gases, the interaction probability is larger for bubble chambers than for gas chambers, and bubble chambers act at the same time both as an effective target and as a detector. Different liquids can be used, depending on the type of experiment: hydrogen to have protons as a target nucleus, deuterium to study interactions on neutrons, etc. From 1950 to the mid-1980s, before the advent of electronic detectors, bubble chambers were the reference tracking detectors. Very large chambers were built (the Big European Bubble Chamber BEBC now displayed at the entrance of the CERN exhibition is a cylinder with an active volume of 35 cubic meters), and wonderful pictures were recorded.
Bubble and cloud chambers provide a
complete information: the measurement of the bubble density (their
number per unit length) provides an estimate of the specific
ionization energy loss dE / dx, hence  ; the range, i.e., the total track
length before the particle eventually stops (if the stopping point
is recorded), provides an estimate for the initial energy; the
multiple scattering (see below) provides an estimate for the
momentum.
; the range, i.e., the total track
length before the particle eventually stops (if the stopping point
is recorded), provides an estimate for the initial energy; the
multiple scattering (see below) provides an estimate for the
momentum.
A weak point of cloud and bubble chambers is their dead time: after an expansion, the fluid must be re-compressed. This might take a time ranging from about 50 ms for small chambers (LEBC, the LExan Bubble Chamber, used in the beginning of the 1980s for the study of the production and decay of particles containing the quark charm, had an active volume of less than a liter) to several seconds. Due to this limitation and to the labor-consuming visual scanning of the photographs, bubble chambers were abandoned in the mid-1980s—cloud chambers had been abandoned much earlier.
4.2.1.2 Nuclear Emulsions
A nuclear emulsion is a photographic plate with a thick emulsion layer and very uniform grain size. Like bubble chambers and cloud chambers they record the tracks of charged particles passing through, by changing the chemical status of grains that have absorbed photons (which makes them visible after photographic processing). They are compact, have high density, but have the disadvantages that the plates must be developed before the tracks can be observed, and they must be visually examined.
 m. They had great importance in the
beginning of cosmic-ray physics, and they are still used in
neutrino experiments (where interactions are rare) due to the lower
cost per unit of volume compared to semiconductor detectors and to
the fact that they are unsurpassed for what concerns to the
single-point space resolution. They recently had a revival with the
OPERA experiment at the LNGS underground laboratory in Gran Sasso,
Italy, detecting the interactions of a beam of muon neutrinos sent
from the CERN SPS in Geneva, 730 km away.
m. They had great importance in the
beginning of cosmic-ray physics, and they are still used in
neutrino experiments (where interactions are rare) due to the lower
cost per unit of volume compared to semiconductor detectors and to
the fact that they are unsurpassed for what concerns to the
single-point space resolution. They recently had a revival with the
OPERA experiment at the LNGS underground laboratory in Gran Sasso,
Italy, detecting the interactions of a beam of muon neutrinos sent
from the CERN SPS in Geneva, 730 km away.

Left: Operational scheme of an ionization chamber. Right: A chamber made in a “tube” shape, using coaxial cylindrical electrodes.
From Braibant, Giacomelli and Spurio, “Particles and fundamental interactions,” Springer 2014
4.2.1.3 Ionization Counter, Proportional Counter and Geiger–Müller Counter

Practical gaseous ionization detector regions: variation of the ion charge with applied voltage in a counter, for a constant incident radiation. By Doug Sim (own work) [CC BY-SA 3.0 http://creativecommons.org/licenses/by-sa/3.0], via Wikimedia Commons
-
The ionization chamber regime when
 (I is the ionization energy of the gas,
and e the electron charge). The
primary ions produced by the track are collected by the wire, and
the signal is then proportional to the energy released by the
particle.
(I is the ionization energy of the gas,
and e the electron charge). The
primary ions produced by the track are collected by the wire, and
the signal is then proportional to the energy released by the
particle. -
The proportional counter regime when
 , but V is smaller than a breakdown potential
, but V is smaller than a breakdown potential
 (see below) . The ions and the electrons are then accelerated
at an energy such that they can ionize the gas. The signal is thus
amplified and it generates an avalanche of electrons around the
anode. The signal is then proportional to the wire tension.
(see below) . The ions and the electrons are then accelerated
at an energy such that they can ionize the gas. The signal is thus
amplified and it generates an avalanche of electrons around the
anode. The signal is then proportional to the wire tension. -
Above a potential
 , the gas is completely ionized; the
signal is then a short pulse of height independent of the energy of
the particle (Geiger–Müller regime)
. Geiger–Müller tubes are also
appropriate for detecting gamma radiation, since a photoelectron
can generate an avalanche.
, the gas is completely ionized; the
signal is then a short pulse of height independent of the energy of
the particle (Geiger–Müller regime)
. Geiger–Müller tubes are also
appropriate for detecting gamma radiation, since a photoelectron
can generate an avalanche.
4.2.1.4 Wire Chamber

Scheme of a multiwire chamber. By Michael Schmid (own work) [GFDL http://www.gnu.org/copyleft/fdl.html], via Wikimedia Commons

The spark chamber built by LIP (Laboratório de Instrumentação e Partículas, Portugal) for educational purposes records a cosmic ray shower
4.2.1.5 Streamer Chamber and Spark Chamber
These are typically multianode (can be multiwire) chambers operating in the Geiger–Müller regime. Short electric pulses of the order of 10 kV/cm are sent between subsequent planes; when a particle passes in the chamber, it can generate a series of discharges which can be visible—a sequence of sparks along the trajectory, Fig. 4.18.
4.2.1.6 Drift Chamber
The drift chamberis a multiwire chamber in which spatial resolution is achieved by measuring the time electrons need to reach the anode wire. This results in wider wire spacing with respect to what can be used in multiwire proportional chambers. Fewer channels have to be equipped with electronics in order to obtain a comparable overall space resolution; in addition, drift chambers are often coupled to high-precision space measurement devices like silicon detectors (see below).
Drift chambers use longer drift distances than multiwire chambers, hence their response can be slower. Since the drift distance can be long and drift velocity needs to be well known, the shape and constancy of the electric field need to be carefully adjusted and controlled. To do this, besides the anode wires (also called “signal” or “sense” wires), thick field-shaping cathode wires called “field wires” are often used.
An extreme case is the time projection chamber (TPC), for which drift lengths can be very large (up to 2 m), and sense wires are arranged at one end; signals in pads or strips near the signal wire plane are used to obtain three-dimensional information.
4.2.1.7 Semiconductor Detectors
Silicon detectors are solid-state particle detectors, whose principle of operation is similar to that of an ionization chamber: the passage of ionizing particles produces in them a number of electron–hole pairs proportional to the energy released. The detector is like a diode (p-n junction) with reverse polarization, the active area being the depleted region. The electron–hole pairs are collected thanks to the electric field, and generate an electrical signal.
The main feature of silicon detectors is the small energy required to create a electron–hole pair—about 3.6 eV, compared with about 30 eV necessary to ionize an atom in an Ar gas ionization chamber.
Furthermore, compared to gaseous
detectors, they are characterized by a high density and a high
stopping power, much greater than that of the gaseous detectors:
they can thus be very thin, typically about 300  m.
m.
 m, as the width of each strip.
m, as the width of each strip.

Scheme of a silicon microstrip detector, arranged in a double-side geometry (strips are perpendicular).
Source: http://spie.org/x20060.xml
From the signal collected on the strip
one can tell if a particle has passed through the detector. The
accuracy can be smaller than the size and the pitch: the charge
sharing between adjacent strips improves the resolution to some
10  m. As in the case of multiwire
chambers, the usual geometry involves adjacent parallel planes of
mutually perpendicular strips.
m. As in the case of multiwire
chambers, the usual geometry involves adjacent parallel planes of
mutually perpendicular strips.
A recent implementation of
semiconductor detectors is the silicon pixel detector. Wafers of
silicon are segmented into little squares (pixels) that are as
small as 100  m on a side. Electronics is more
expensive (however with modern technology it can be bonded to the
sensors themselves); the advantage is that one can measure directly
the hits without ambiguities.
m on a side. Electronics is more
expensive (however with modern technology it can be bonded to the
sensors themselves); the advantage is that one can measure directly
the hits without ambiguities.
4.2.1.8 Scintillators
 photons per MeV of energy
deposited—and the time of formation of the signal is very fast,
typically less than 1 ns: they are
appropriate for trigger9 systems.
photons per MeV of energy
deposited—and the time of formation of the signal is very fast,
typically less than 1 ns: they are
appropriate for trigger9 systems.

To make the light travel efficiently toward the photosensor (photomultiplier), light guides are frequently used (Fig. 4.20). Sometimes the fluorescence is dominated by low wavelengths; in this case it is appropriate to match the photosensor optical efficiency with a wavelength shifter (a material inducing absorption of light and re-emission in an appropriate wavelength).
The scintillators can be used as tracking devices, in the so-called hodoscopeconfiguration (from the Greek “hodos” for path, and “skope” for observation) as in the case of silicon strips. Hodoscopes are characterized by being made up of many detecting planes, made in turn by segments; the combination of which segments record a detection is then used to reconstruct the particle trajectory. Detecting planes can be arranged in pairs of layers. The strips of the two layers should be arranged in perpendicular directions (let us call them horizontal and vertical). A particle passing through hits a strip in each layer; the vertical scintillator strip reveals the horizontal position of the particle, and the horizontal strip indicates its vertical position (as in the case of two wire chambers with perpendicular orientation of the wires, but with poorer resolution). Scintillator hodoscopes are among the cheapest detectors for tracking charged particles.
Among scintillators, some are polymeric (plastic); plastic scintillators are particularly important due to their good performance at low price, to their high light output and relatively quick (few ns) signal, and in particular to their ability to be shaped into almost any desired form.
4.2.1.9 Resistive Plate Chambers
The resistive plate chamber (RPC) is a lower-cost alternative to large scintillator planes. An RPC is usually constructed from two parallel high-resistivity glass or melaminic plates with a gap of a few millimeters between them, which is filled with gas at atmospheric pressure. A high potential (of the order of 10 kV) is maintained between the plates.
A charged particle passing through the chamber initiates an electric discharge, whose size and duration are limited by the fact that the current brings the local potential below the minimum required to maintain it. The signal induced is read by metallic strips on both sides of the detector and outside the gas chamber, which are separated from the high voltage coatings by thin insulating sheets.
Typical characteristics of different kinds of tracking detectors. Data come from K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
|
Detector type |
Spatial resolution |
Time resolution |
Dead time |
|---|---|---|---|
|
RPC |
|
|
– |
|
Scintillation counter |
10 mm |
0.1 ns |
10 ns |
|
Emulsion |
1 |
– |
– |
|
Bubble chamber |
10–100 |
1 ms |
50 ms–1 s |
|
Proportional chamber |
50–100 |
2 ns |
20–200 ns |
|
Drift chamber |
50–100 |
few ns |
20–200 ns |
|
Silicon strip |
Pitch/5 (few |
few ns |
50 ns |
|
Silicon pixel |
10 |
few ns |
50 ns |
4.2.1.10 Comparison of the Performance of Tracking Detectors
The main characteristics of tracking detectors are summarized in Table 4.2.
4.2.2 Photosensors
Most detectors in particle physics and astrophysics rely on the detection of photons near the visible range, i.e., in the eV energy range. This range covers scintillation and Cherenkov radiation as well as the light detected in many astronomical observations.
Essentially, one needs to extract a measurable signal from a (usually very small) number of incident photons. This goal can be achieved with the generation of a primary photoelectron or electron–hole pair by an incident photon (typically via photoelectric effect), amplifying the signal to a detectable level (usually by a sequence of avalanche processes), and collecting the secondary charges to form the electrical signal.
-
the quantum efficiency QE , namely the probability that a primary photon generates a photoelectron;
-
the collection efficiency C related to the overall acceptance;
-
the gain G , i.e., the number of electrons collected for each photoelectron generated;
-
the dark noise DN , i.e., the electrical signal when there is no incoming photon;
-
the intrinsic response time of the detector.

Scheme of a photomultiplier attached to a scintillator.
Source: Colin Eberhardt [public domain], via Wikimedia Commons
4.2.2.1 Photomultiplier Tubes
Photomultiplier tubes (photomultipliers or PMTs) are detectors of light in the ultraviolet, visible, and near-infrared regions of the electromagnetic spectrum; they are the oldest photon detectors used in high-energy particle and astroparticle physics.
They are constructed (Fig. 4.21) from a glass envelope with a high vacuum inside, housing a photocathode, several intermediate electrodes called dynodes, and an anode. As incident photons hit the photocathode material (a thin deposit on the entrance window of the device) electrons are produced by photoelectric effect and directed by the focusing electrode toward the electron multiplier chain, where they are multiplied by secondary emission.
The electron multiplier consists of several dynodes, each held at a higher positive voltage than the previous one (the typical total voltage in the avalanche process being of 1–2 kV). The electrons produced in the photocathode have the energy of the incoming photon (minus the work function of the photocathode, i.e., the energy needed to extract the electron itself from the metal, which typically amounts to a few eV). As the electrons enter the multiplier chain, they are accelerated by the electric field. They hit the first dynode with an already much higher energy. Low-energy electrons are then emitted, which in turn are accelerated toward the second dynode. The dynode chain is arranged in such a way that an increasing number of electrons are produced at each stage. When the electrons finally reach the anode, the accumulation of charge results in a sharp current pulse. This is the result of the arrival of a photon at the photocathode.
Photocathodes can be made of a variety of materials with different properties. Typically materials with a low work function are chosen.
The typical quantum efficiency of a
photomultiplier is about 30% in the range from 300 to 800 nm
of wavelength for the light, and the gain G is in the range  –
– .
.
A recent improvement to the
photomultiplier was obtained thanks to hybrid photon detectors
(HPD), in which a vacuum PMT is coupled to a silicon sensor. A
photoelectron ejected from the photocathode is accelerated through
a potential difference of about  20 kV before it hits a silicon
sensor/anode. The number of electron–hole pairs that can be created
in a single acceleration step is
20 kV before it hits a silicon
sensor/anode. The number of electron–hole pairs that can be created
in a single acceleration step is  V), the denominator being the
mean voltage required to create an electron–hole pair. The linear
behavior of the gain is helpful because, unlike exponential gain
devices, high voltage stability translates in gain stability. HPD
detectors can work as single-photon counters.
V), the denominator being the
mean voltage required to create an electron–hole pair. The linear
behavior of the gain is helpful because, unlike exponential gain
devices, high voltage stability translates in gain stability. HPD
detectors can work as single-photon counters.
4.2.2.2 Gaseous Photon Detectors
In gaseous photomultipliers (GPM) a photoelectron entering a suitably chosen gas mixture (a gas with low photoionization work function, like the tetra dimethylamine ethylene (TMAE)) starts an avalanche in a high-field region. Similarly to what happens in gaseous tracking detectors, a large number of secondary ionization electrons are produced and collected.
Since GPMs can have a good space resolution and can be made into flat panels to cover large areas, they are often used as position-sensitive photon detectors. Many of the ring-imaging Cherenkov (RICH) detectors (see later) use GPM as sensors.
4.2.2.3 Solid-State Photon Detectors
Semiconductor photodiodes were
developed during World War II, approximately at the same time
photomultiplier tubes became a commercial product. Only in recent
years, however, a technique which allows the Geiger-mode avalanche
in silicon was engineered, and the semiconductor photodetectors
reached sensitivities comparable to photomultiplier tubes.
Solid-state photodetectors (often called SiPM) are more compact, lightweight, and they
might become cheaper than traditional PMTs in the near future. They
also allow fine pixelization, of the order of 1 mm
 1 mm, are easy to integrate in
large systems and can operate at low electric potentials.
1 mm, are easy to integrate in
large systems and can operate at low electric potentials.
One of the recent developments in the field was the construction of large arrays of tiny avalanche photodiodes (APD) packed over a small area and operated in Geiger mode.
The main advantages of SiPM with respect to the standard PMT are compact size, low power consumption, low operating voltage (less than 100 V), and immunity to electromagnetic field. The main disadvantages of SiPM are dark current caused by thermally generated avalanches even in the absence of an incoming photon, cross talk between different channels, and the dependence of gain on temperature, of the order of 1% per kelvin at standard temperatures (temperature needs thus to be stabilized, or at least monitored).
4.2.3 Cherenkov Detectors
The main ingredients of Cherenkov detectors are a medium to produce Cherenkov radiation (usually called the radiator) and a system of photodetectors to detect Cherenkov photons. The yield of Cherenkov radiation is usually generous so as to make these detectors perform well.
If one does not need particle
identification, a cheap medium (radiator) with large refractive
index n can be used so to have
a threshold for the emission as low as possible. A typical radiator
is water, with  The IceCube detector in Antarctica
uses ice as a radiator (the photomultipliers are embedded in the
ice).
The IceCube detector in Antarctica
uses ice as a radiator (the photomultipliers are embedded in the
ice).
Since the photon yield and the emission angle depend on the mass of the particle, some Cherenkov detectors are also used for particle identification.
Threshold Cherenkov detectors make a yes/no decision based on whether a particle velocity is or not above the Cherenkov threshold velocity c / n—this depends exclusively on the velocity and, if the momentum has been measured, provides a threshold measurement of the value of the mass. A more advanced version uses the number of detected photoelectrons to discriminate between particle species.
Imaging Cherenkov detectors measure the ring-correlated angles of emission of the individual Cherenkov photons. Low-energy photon detectors measure the position (and sometimes the arrival time) of each photon. These must then be “imaged” onto a detector so that the emission angles can be derived. Typically the optics maps the Cherenkov cone onto (a portion of) a conical section at the photodetector.

Left: Image of the hits on the photon
detectors of the RICHs of the LHCb experiment at CERN with
superimposed rings. Credit: LHCb collaboration. Right: Dependence
of the Cherenkov angle measured by the RICH of the ALICE experiment
at CERN on the particle momentum; the angle can be used to measure
the mass through Eq. 4.6 ( ).
).
Credit: ALICE Collaboration
Atmospheric Cherenkov telescopes for
high-energy  astrophysics are also in use. If one
uses a parabolic telescope, again the projection of the Cherenkov
emission by a particle along its trajectory is a conical section in
the focal plane. If the particle has generated through a
multiplicative cascade a shower of secondary particles (see later),
the projection is a spot, whose shape can enable us to distinguish
whether the primary particle was a hadron or an electromagnetic
particle (electron, positron, or photon).
astrophysics are also in use. If one
uses a parabolic telescope, again the projection of the Cherenkov
emission by a particle along its trajectory is a conical section in
the focal plane. If the particle has generated through a
multiplicative cascade a shower of secondary particles (see later),
the projection is a spot, whose shape can enable us to distinguish
whether the primary particle was a hadron or an electromagnetic
particle (electron, positron, or photon).
4.2.4 Transition Radiation Detectors
Similar to Cherenkov detectors,
transition radiation detectors (TRD)
couple interfaces between different media (used as radiators) to
photon detectors. Thin foils of lithium, polyethylene, or carbon
are common; randomly spaced radiators are also in use, like foams.
The main problem in the TRD is the low number of photons. In order
to intensify the photon flux, periodic arrangements of a large
number of foils are used, interleaved with X-ray detectors such as
multiwire proportional chambers filled with xenon or a
Xe/CO mixture.
mixture.
4.2.5 Calorimeters
Once entering an absorbing medium, particles undergo successive interactions and decays, until their energy is degraded, as we have seen in Sect. 4.1.7. Calorimeters are blocks of matter in which the energy of a particle is measured through the absorption to the level of detectable atomic ionizations and excitations. Such detectors can be used to measure not only the energy, but also the position in space, the direction, and in some cases the nature of the particle.
4.2.5.1 Electromagnetic Calorimeters
An ideal material used for an electromagnetic calorimeter —a calorimeter especially sensitive to electrons/positrons and photons—should have a short radiation length, so that one can contain the electromagnetic shower in a compact detector, and the signal should travel unimpeded through the absorber (homogeneous calorimeters). However, sometimes materials which can be good converters and conductors of the signals are very expensive: one then uses sampling calorimeters, where the degraded energy is measured in a number of sensitive layers separated by passive absorbers.
The performance of calorimeters is limited both by the unavoidable fluctuations of the elementary phenomena through which the energy is degraded and by the technique chosen to measure the final products of the cascade processes.
Homogeneous Calorimeters. Homogeneous calorimeters may be built with heavy (high density, high Z) scintillating crystals, i.e., crystals in which ionization energy loss results in the emission of visible light, or Cherenkov radiators such as lead glass and lead fluoride. The material acts as a medium for the development of the shower, as a transducer of the electron signal into photons, and as a light guide toward the photodetector. Scintillation light and/or ionization can be detected also in noble liquids.
Sampling Calorimeters. Layers of absorbers are typically interspersed with layers of active material (sandwich geometry). The absorber helps the development of the electromagnetic shower, while the active material transforms part of the energy into photons, which are guided toward the photodetector. Different geometries can be used: for example, sometimes rods of active material cross the absorber (spaghetti geometry).
Converters have high density, short radiation length. Typical materials are iron (Fe), lead (Pb), uranium, tungsten (W). Typical active materials are plastic scintillator, silicon, liquid ionization chamber gas detectors.
Disadvantages of sampling calorimeters are that only part of the deposited particle energy is detected in the active layers, typically a few percent (and even one or two orders of magnitude less in the case of gaseous detectors). Sampling fluctuations typically result in a worse energy resolution for sampling calorimeters.
 of a calorimeter can be parameterized as
of a calorimeter can be parameterized as

 represents addition in quadrature.
The stochastic term a
originates from statistics-related effects such as the intrinsic
fluctuations in the shower, number of photoelectrons, dead material
in front of the calorimeter, and sampling fluctuations—we remind
that the number of particles is roughly proportional to the energy,
and thus the Poisson statistics gives fluctuations proportional to
represents addition in quadrature.
The stochastic term a
originates from statistics-related effects such as the intrinsic
fluctuations in the shower, number of photoelectrons, dead material
in front of the calorimeter, and sampling fluctuations—we remind
that the number of particles is roughly proportional to the energy,
and thus the Poisson statistics gives fluctuations proportional to
 . The a term is at a few percent level for a
homogeneous calorimeter and typically 10% for sampling
calorimeters. The systematic or constant b term represents contributions from the
detector nonuniformity and calibration uncertainty, and from
incomplete containment of the shower. In the case of hadronic
cascades (discussed below), the different response of the
instrument to hadrons and leptons, called noncompensation, also
contributes to the constant term. The constant term b can be reduced to below one percent.
The c term is due to electronic
noise. Some of the above terms can be negligible in
calorimeters.
. The a term is at a few percent level for a
homogeneous calorimeter and typically 10% for sampling
calorimeters. The systematic or constant b term represents contributions from the
detector nonuniformity and calibration uncertainty, and from
incomplete containment of the shower. In the case of hadronic
cascades (discussed below), the different response of the
instrument to hadrons and leptons, called noncompensation, also
contributes to the constant term. The constant term b can be reduced to below one percent.
The c term is due to electronic
noise. Some of the above terms can be negligible in
calorimeters.The best energy resolution for
electromagnetic shower measurement is obtained with total
absorption, homogeneous calorimeters, such as those built with
heavy crystal scintillators like Bi Ge
Ge O
O , called BGO. They are used when
optimal performance is required. A relatively cheap scintillator
with relatively short
, called BGO. They are used when
optimal performance is required. A relatively cheap scintillator
with relatively short  is the cesium iodide (CsI), which
becomes more luminescent when activated with thallium, and is
called CsI(Tl); this is frequently used for dosimetry in medical
applications, and in space applications, where high technological
readiness and reliability are needed.
is the cesium iodide (CsI), which
becomes more luminescent when activated with thallium, and is
called CsI(Tl); this is frequently used for dosimetry in medical
applications, and in space applications, where high technological
readiness and reliability are needed.
Energy resolutions for some homogeneous and sampling calorimeters are listed in Table 4.3.
4.2.5.2 Hadronic Calorimeters
We have examined the main characteristics of hadronic showers in Sect. 4.1.8.
Detectors capable of absorbing hadrons and detecting a signal were developed around 1950 for the measurement of the energy of cosmic rays. It can be assumed that the energy of the incident particle is proportional to the multiplicity of charged particles.
Most large hadron calorimeters are sampling calorimeters installed as part of complex detectors at accelerator experiments. The basic structure typically consists of absorber plates (Fe, Pb, Cu, or occasionally U or W) alternating with plastic scintillators (shaped as plates, tiles, bars), liquid argon (LAr) chambers, or gaseous detectors (Fig. 4.23). The ionization is measured directly, as in LAr calorimeters, or via scintillation light observed in photodetectors (usually photomultipliers).
Main characteristics of some electromagnetic calorimeters. Data from K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001. The accelerators quoted in the table are discussed in the next section
|
Technology (experiment) |
Depth ( |
Energy resolution (relative) |
|---|---|---|
|
BGO (L3 at LEP) |
22 |
|
|
CsI (kTeV at the FNAL K beam) |
27 |
|
|
PbWO |
25 |
|
|
Lead glass (DELPHI, OPAL at LEP) |
20 |
|
|
Scintillator/Pb (CDF at the Tevatron) |
18 |
|
|
Liquid Ar/Pb (SLD at SLC) |
21 |
|
A hadron with energy E generates a cascade in which there are
repeated hadronic collisions. In each of these, neutral pions are
also produced, which immediately ( fs) decay into photons: a
fraction of the energy is converted to a potentially observable
signal with an efficiency which is in general different, usually
larger, than the hadronic detection efficiency. The response of the
calorimeters to hadrons is thus not compensated with respect to the
response to electromagnetic particles (or to the electromagnetic
part of the hadronic shower).
fs) decay into photons: a
fraction of the energy is converted to a potentially observable
signal with an efficiency which is in general different, usually
larger, than the hadronic detection efficiency. The response of the
calorimeters to hadrons is thus not compensated with respect to the
response to electromagnetic particles (or to the electromagnetic
part of the hadronic shower).
Due to all these problems, typical
fractional energy resolutions are in the order of
30–50%/ .
.

Hadronic calorimeters of the ATLAS experiments at LHC.
Credit: CERN
4.3 High-Energy Particles
 of a wave packet is given by
of a wave packet is given by

In addition, we might be interested in using high-energy particles to produce new particles in collisions. This requires more energy, the more massive the particles we want to produce.
4.3.1 Artificial Accelerators
A particle accelerator is an instrument using electromagnetic fields to accelerate charged particles at high energies.
-
collision with a fixed target (fixed-target experiments) ;
-
collision of a beam with another beam running in the opposite direction (collider experiments) .
We also distinguish two main categories of accelerators depending on the geometry: linear accelerators and circular accelerators. In linear accelerators the bremsstrahlung energy loss is much reduced since there is no centripetal acceleration, but particles are wasted after a collision, while in circular accelerators the particles which did not interact can be reused.
The center-of-mass energy  sets the scale for the maximum mass
of the particles we can produce (the actual value of the available
energy being in general smaller due to constraints related to
conservation laws).
sets the scale for the maximum mass
of the particles we can produce (the actual value of the available
energy being in general smaller due to constraints related to
conservation laws).
We want now to compare fixed-target and colliding beam experiments concerning the available energy.

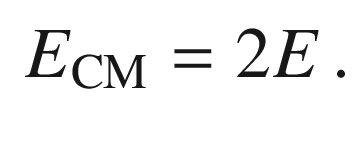
Making two beams collide, however, is not trivial: one must control the fact that the beams tend to defocus due to mutual repulsion of the particles. In addition, Liouville’s theorem states that the phase space volume (the product of the spread in terms of the space coordinates times the spread in the momentum coordinate) of an isolated beam is constant: reducing the momentum dispersion is done at the expense of the space dispersion—and one needs small space dispersion in order that the particles in the beam actually collide. Beating Liouville’s theorem requires feedback on the beam itself.10
Since beams are circulated for several hours, circular accelerators are based on beams of stable particles and antiparticles, such as electrons, protons, and their antiparticles. In the future, muon colliders are an interesting candidate: as “clean” as electrons, since they are not sensitive to the hadronic interaction, muons have a lower energy dissipation (due to synchrotron radiation and bremsstrahlung) thanks to their mass being 200 times larger than electrons.
Particle accelerators and detectors are often situated underground in order to provide the maximal shielding possible from natural radiation such as cosmic rays that would otherwise mask the events taking place inside the detector.
4.3.1.1 Acceleration Methods
 in an electric field
in an electric field  and a magnetic field
and a magnetic field  feels a force
feels a force
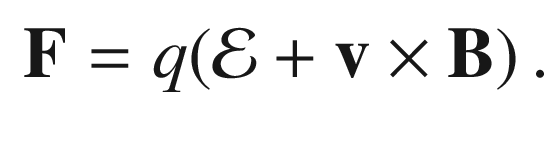
 can constrain the particle along a
circular trajectory perpendicular to
can constrain the particle along a
circular trajectory perpendicular to  .
.If a single potential were applied, increasing energy would demand increasing voltages. The solution is to apply multiple times a limited potential.
An acceleration line (which corresponds roughly to a linear accelerator) works as follows. In a beam pipe (a cylindrical tube in which vacuum has been made) cylindrical electrodes are aligned. A pulsed radiofrequency (RF) source of electromotive force V is applied. Thus particles are accelerated when passing in the RF cavity (Fig. 4.24); the period is adjusted in such a way that half of the period corresponds of the time needed for the particle to cross the cavity. The potential between the cylinders is reversed when the particle is located within them.

Scheme of an acceleration line displayed at two different times. By Sgbeer (own work) [GFDL http://www.gnu.org/copyleft/fdl.html], via Wikimedia Commons
A collider consists of two circular or almost circular accelerator structures with vacuum pipes, magnets and accelerating cavities, in which two beams of particles travel in opposite directions. The particles may be protons in both beams, or protons and antiprotons, or electrons and positrons, or electrons and protons, or also nuclei and nuclei. The two rings intercept each other at a few positions along the circumference, where bunches can cross and particles can interact. In a particle–antiparticle collider (electron–positron or proton–antiproton), as particles and antiparticles have opposite charges and the same mass, a single magnetic structure is sufficient to keep the two beams circulating in opposite directions.
4.3.1.2 Parameters of an Accelerator
An important parameter for an
accelerator is the maximum center-of-mass (c.m.) energy
 available, since this sets the
maximum mass of new particles that can be produced.
available, since this sets the
maximum mass of new particles that can be produced.
 ; the number of outcomes of this
process per unit time can be expressed as
; the number of outcomes of this
process per unit time can be expressed as

 s
s ; however, for practical reasons it is
customary to use “inverse barns” and its multiples instead of
cm
; however, for practical reasons it is
customary to use “inverse barns” and its multiples instead of
cm (careful: due to the definition, 1
mbarn
(careful: due to the definition, 1
mbarn ).
).
 and
and  in the two beams. Notice that in a
proton–antiproton collider the number of antiprotons is in general
smaller than that of protons, due to the “cost” of the antiprotons
(antiprotons are difficult to store and to accumulate, since they
easily annihilate). The luminosity is also proportional to the
number of crossings in a second f and inversely proportional to the
transverse section
in the two beams. Notice that in a
proton–antiproton collider the number of antiprotons is in general
smaller than that of protons, due to the “cost” of the antiprotons
(antiprotons are difficult to store and to accumulate, since they
easily annihilate). The luminosity is also proportional to the
number of crossings in a second f and inversely proportional to the
transverse section  at the intersection point
at the intersection point

4.3.2 Cosmic Rays as Very-High-Energy Beams
As we have already shown, cosmic rays can attain energies much larger than the particles produced at human-made accelerators. The main characteristics of cosmic rays have been explained in Sect. 1.6 and in Chap. 3.
We just recall here that the
distribution in energy (the so-called spectrum) of cosmic rays is
quite well described by a power law  , with the so-called spectral index
p around 3 on average
(Fig. 1.8), extending up to about
, with the so-called spectral index
p around 3 on average
(Fig. 1.8), extending up to about
 eV (above this energy the GZK
cutoff, explained in the previous chapters, stops the cosmic travel
of particles; a similar mechanism works for heavier nuclei, which
undergo photodisintegration during their cosmic travel). The
majority of the high-energy particles in cosmic rays are protons
(hydrogen nuclei); about 10% are helium nuclei (nuclear physicists
call them usually “alpha particles”), and 1% are neutrons or nuclei
of heavier elements. These together account for 99% of the cosmic
rays, and electrons, photons, and neutrinos dominate the remaining
1%. The number of neutrinos is estimated to be comparable to that
of high-energy photons, but it is very high at low energy because
of the nuclear processes that occur in the Sun. Cosmic rays hitting
the atmosphere (called primary cosmic rays) generally produce
secondary particles that can reach the Earth’s surface, through
multiplicative showers.
eV (above this energy the GZK
cutoff, explained in the previous chapters, stops the cosmic travel
of particles; a similar mechanism works for heavier nuclei, which
undergo photodisintegration during their cosmic travel). The
majority of the high-energy particles in cosmic rays are protons
(hydrogen nuclei); about 10% are helium nuclei (nuclear physicists
call them usually “alpha particles”), and 1% are neutrons or nuclei
of heavier elements. These together account for 99% of the cosmic
rays, and electrons, photons, and neutrinos dominate the remaining
1%. The number of neutrinos is estimated to be comparable to that
of high-energy photons, but it is very high at low energy because
of the nuclear processes that occur in the Sun. Cosmic rays hitting
the atmosphere (called primary cosmic rays) generally produce
secondary particles that can reach the Earth’s surface, through
multiplicative showers.
The reason why human-made accelerators
cannot compete with cosmic accelerators from the point of view of
the maximum attainable energy is that with the present technologies
acceleration requires confinement within a radius R by a magnetic field B, and the final energy is
proportional to R times
B. On Earth, it is difficult to
imagine reasonable radii of confinement larger than one hundred
kilometers and magnetic fields stronger than ten tesla (one hundred
thousand times the Earth’s magnetic field). This combination can
provide energies of a few tens of TeV, such as those of the LHC
accelerator at CERN. In nature there are accelerators with much
larger radii, as the remnants of supernovae (hundreds of light
years) and active galactic nuclei (tens of thousands of light
years): one can thus reach energies as large as 10 eV, i.e., 1 ZeV (the
so-called extremely high-energy (EHE) cosmic rays; cosmic rays above 10
eV, i.e., 1 ZeV (the
so-called extremely high-energy (EHE) cosmic rays; cosmic rays above 10 eV, i.e., 1 EeV, are often
called ultrahigh energy, UHE) . Of course
terrestrial accelerators have great advantages like luminosity and
the possibility of knowing the initial conditions.
eV, i.e., 1 EeV, are often
called ultrahigh energy, UHE) . Of course
terrestrial accelerators have great advantages like luminosity and
the possibility of knowing the initial conditions.
The conditions are synthetically illustrated in the so-called Hillas plot (Fig. 10.32), a scatter plot in which different cosmic objects are grouped according to their sizes and magnetic fields; this will be discussed in larger detail in Chap. 10. UHE can be reached in the surroundings of active galactic nuclei, or in gamma-ray bursts. R times B in supernova remnants is such that particles can reach energies of some PeV.
4.4 Detector Systems and Experiments at Accelerators
Detectors at experimental facilities are in general hybrid, i.e., they combine many of the detectors discussed so far, such as drift chambers, Cherenkov detectors, electromagnetic, and hadronic calorimeters. They are built up in a sequence of layers, each one designed to measure a specific aspect of the particles produced after the collision.
-
A tracking system: this is designed to track all the charged particles and allow for complete event reconstruction. It is in general the first layer crossed by the particles, in such a way that their properties have not yet been deteriorated by the interaction with the material of the detector. It should have as little material as possible, so as to preserve the particles for the subsequent layer.
-
A layer devoted to electromagnetic calorimetry.
-
A layer devoted to hadronic calorimetry.
-
A layer of muon tracking chambers: any particle releasing signal on these tracking detectors (often drift chambers) has necessarily traveled through all the other layers and is very likely a muon (neutrinos have extremely low interaction cross sections, and most probably they cross also the muon chambers without leaving any signal) .
A layer containing a solenoid can be inserted after the tracking system, or after the calorimeter. Tracking in a magnetic field allows for momentum measurement.
-
Photons leave no tracks in the tracking detectors (unless they undergo pair production) but produce a shower in the electromagnetic calorimeter.
-
Electrons and positrons leave a track in the tracking detectors and produce a shower in the electromagnetic calorimeter.
-
Muons leave tracks in all the detectors (likely as a minimum ionizing particle in the calorimeters).
-
Longlived charged hadrons (protons for example) leave tracks in all the detectors up to the hadronic calorimeter where they shower and deposit all their energy.
-
Neutrinos are identified by missing energy-momentum when the relevant conservation law is applied to the event.

Overview of the signatures by a particle in a multilayer hybrid detector.
Credit: CERN
4.4.1 Examples of Detectors for Fixed-Target Experiments
In a fixed-target experiment,
relativistic effects make the interaction products highly
collimated. In such experiments then, in order to enhance the
possibility of detection in the small- (
( , where
, where  is the momentum component
perpendicular to the beam direction), different stages are
separated by magnets opening up the charged particles in the final
state (lever arms).
is the momentum component
perpendicular to the beam direction), different stages are
separated by magnets opening up the charged particles in the final
state (lever arms).

A configuration of the European Hybrid Spectrometer (a fixed-target detector at the CERN Super Proton Synchrotron).
From M. Aguilar-Benitez et al., “The European hybrid spectrometer,” Nucl. Instr. Methods 258 (1987) 26
4.4.1.1 The European Hybrid Spectrometer at the SPS
The European Hybrid Spectrometer EHSwas operational during the 1970s and in the beginning of the 1980s at the North Area of CERN, where beams of protons were extracted from the SPS (Super Proton Synchrotron)11 accelerator at energies ranging from 300 to 400 GeV. Such particles might possibly generate secondary beams of charged pions of slightly smaller energies by a beam-dump and a velocity selector based on magnetic field. EHS was a multi-stage detector serving different experiments (NA16, NA22, NA23, NA27). Here we describe a typical configuration; Fig. 4.26 shows a schematic drawing of the EHS setup.
In the figure, the beam particles come
in from the left. Their direction is determined by the two small
wire chambers U1 and U3. From the collision point inside a rapid
cycling bubble chamber (RCBC; the previously described LEBC is an
example, with a space resolution of 10  m) most of the particles produced
enter the downstream part of the spectrometer.
m) most of the particles produced
enter the downstream part of the spectrometer.
The RCBC acts both as a target and as a vertex detector. If an event is triggered, stereoscopic pictures are taken with 3 cameras and recorded on film.
The momentum resolution of the
secondary particles depends on the number of detector element hits
available for the track fits. For low momentum particles, typically
 GeV/c, length and direction of the
momentum vector at the collision point can be well determined from
RCBC. On the other hand, tracks with
GeV/c, length and direction of the
momentum vector at the collision point can be well determined from
RCBC. On the other hand, tracks with  GeV/c have a very good chance to enter the
so-called first lever arm. This is defined by the group of four
wire chambers W2, D1, D2, and D3 placed between the two magnets M1
and M2. Very fast particles (typically with momentum
GeV/c have a very good chance to enter the
so-called first lever arm. This is defined by the group of four
wire chambers W2, D1, D2, and D3 placed between the two magnets M1
and M2. Very fast particles (typically with momentum  GeV/c) will go through the aperture of the
magnet M2 to the so-called second lever arm, consisting of the
three drift chambers D4, D5, and D6.
GeV/c) will go through the aperture of the
magnet M2 to the so-called second lever arm, consisting of the
three drift chambers D4, D5, and D6.
To detect gamma rays, two
electromagnetic calorimeters are used in EHS, the intermediate
gamma detector (IGD) and the forward gamma detector (FGD). IGD is
placed before the magnet M2. It has a central hole to allow fast
particles to proceed to the second lever arm. FGD covers this hole
at the end of the spectrometer. The IGD has been designed to
measure both the position and the energy of a shower in a
two-dimensional matrix of lead-glass counters 5 cm
 5 cm in size, each of them
connected to a PMT. The FGD consists of three separate sections.
The first section is the converter (a lead-glass wall), to initiate
the electromagnetic shower. The second section (the position
detector) is a three-plane scintillator hodoscope. The third
section is the absorber, a lead-glass matrix deep enough (60
radiation length) to totally absorb showers up to the highest
available energies. For both calorimeters, the relative accuracy on
energy reconstruction is
5 cm in size, each of them
connected to a PMT. The FGD consists of three separate sections.
The first section is the converter (a lead-glass wall), to initiate
the electromagnetic shower. The second section (the position
detector) is a three-plane scintillator hodoscope. The third
section is the absorber, a lead-glass matrix deep enough (60
radiation length) to totally absorb showers up to the highest
available energies. For both calorimeters, the relative accuracy on
energy reconstruction is  .
.
The spectrometer included also three detectors devoted to particle identification: the silica-aerogel Cherenkov detector (SAD), the ISIS chamber measuring specific ionization, and the transition radiation detector TRD.
4.4.1.2 LHCb at LHC

Sketch of the LHCb detector.
Credit: CERN
Although, in strict terms, LHCb is a colliding beam experiment, it is done as a fixed-target one: the strongly boosted b-hadrons fly along the beam direction, and one side is instrumented.
At the heart of the detector is the
vertex detector, recording the decays of the b particles, which have typical lifetimes
of about 1 ps and will travel only about 10 mm before
decaying. It has 17 planes of silicon (radius 6 cm) spaced
over a meter and consisting of two disks (in order to measure
radial and polar coordinates) and provides a hit resolution of
about 10 and 40  m for the impact parameter of high
momentum tracks.
m for the impact parameter of high
momentum tracks.
Downstream of the vertex detector, the tracking system (made of 11 tracking chambers) reconstructs the trajectories of emerging particles. LHCb’s 1.1 T superconducting dipole spectrometer magnet (inherited from the DELPHI detector at LEP, see later) opens up the tracks.
Particle identification is performed by
two ring-imaging Cherenkov (RICH) detector stations. The first RICH
is located just behind the vertex detector and equipped with a
5 cm silica aerogel and 1 m C F
F gas radiators, while the second one
consists of 2 m of CF
gas radiators, while the second one
consists of 2 m of CF gas radiator behind the tracker.
Cherenkov photons are picked up by a hybrid photodiode array.
gas radiator behind the tracker.
Cherenkov photons are picked up by a hybrid photodiode array.
The electromagnetic calorimeter, installed following the second RICH, is a “shashlik” structure of scintillator and lead read out by wavelength-shifting fibers. It has three annular regions with different granularities in order to optimize readout. A lead-scintillator preshower detector improves electromagnetic particle identification.
The hadron calorimeter is made of scintillator tiles embedded in iron. Like the electromagnetic calorimeter upstream, it has three zones of granularity. Downstream, shielded by the calorimetry, are four layers of muon detectors. These are multigap resistive plate chambers and cathode pad chambers embedded in iron, with an additional layer of cathode pad chambers mounted before the calorimeters. Besides muon identification, this provides important input for triggering.
There are four levels of triggering. The initial (level 0) decisions are based on a high transverse momentum particle and use the calorimeters and muon detectors. This reduces by a factor of 40 the 40 MHz input rate. The next trigger level (level 1) is based on vertex detector (to look for secondary vertices) and tracking information, and reduces the data by a factor of 25 to an output rate of 40 kHz. Level 2, suppressing fake secondary decay vertices, achieves further eightfold compression. Level 3 reconstructs B decays to select specific decay channels, achieving another compression factor of 25. Data are written to tape at 200 Hz.
4.4.2 Examples of Detectors for Colliders
The modern particle detectors in use today at colliders are as much as possible hermetic detectors. They are designed to cover most of the solid angle around the interaction point (a limitation being given by the presence of the beam pipe). The typical detector consists of a cylindrical section covering the “barrel” region and two endcaps covering the “forward” regions.
In the standard coordinate system, the
z axis is along the beam
direction, the x axis points
toward the center of the ring, and the y axis points upwards. The polar angle to
the z axis is called
 and the azimuthal angle is called
and the azimuthal angle is called
 ; the radial coordinate is
; the radial coordinate is

 and
defined as
and
defined as
![$$\begin{aligned} \eta = \ln \left[ \tan \left( \frac{\theta }{2} \right) \right] \, ; \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_4_Chapter/304327_2_En_4_Chapter_TeX_Equ52.png)
 corresponds to
corresponds to  , and is called the central region.
When in Chap. 6 we shall discuss the theory of
hadronic interactions, quantum chromodynamics, we shall clarify the
physical significance of this variable.
, and is called the central region.
When in Chap. 6 we shall discuss the theory of
hadronic interactions, quantum chromodynamics, we shall clarify the
physical significance of this variable.The detector has the typical onion-like structure described in the previous section: a sequence of layers, the innermost being the most precise for tracking.
The configuration of the endcaps is similar to that in a fixed-target experiment except for the necessary presence of a beam pipe, which makes it impossible to detect particles at very small polar angles, and entails the possible production of secondary particles in the pipe wall.
In the following sections we shall
briefly describe three generations of collider detectors operating
at the European Organization for Particle Physics, CERN: UA1 at the
S S
S  accelerator, DELPHI at the LEP
accelerator, DELPHI at the LEP
 accelerator, and the main detectors
at the LHC pp accelerator: CMS
and ATLAS. We shall see how much the technology developed and the
required labor increased; the basic ideas are anyway still common
to the prototype detector, UA1.
accelerator, and the main detectors
at the LHC pp accelerator: CMS
and ATLAS. We shall see how much the technology developed and the
required labor increased; the basic ideas are anyway still common
to the prototype detector, UA1.
4.4.2.1 UA1
at the S S
S
The UA1 experiment, named as the first experiment in the
CERN Underground Area (UA), was operating at CERN’s S S (Super proton–antiproton
Synchrotron) accelerator–collider from
1981 till 1993. The discovery of the W and Z bosons, mediators of the weak
interaction, by this experiment in 1983, led to the Nobel Prize for
physics to Carlo Rubbia and Simon van der Meer in 1984 (the
motivation of the prize being more related to the development of
the collider technology). The S
S (Super proton–antiproton
Synchrotron) accelerator–collider from
1981 till 1993. The discovery of the W and Z bosons, mediators of the weak
interaction, by this experiment in 1983, led to the Nobel Prize for
physics to Carlo Rubbia and Simon van der Meer in 1984 (the
motivation of the prize being more related to the development of
the collider technology). The S S was colliding protons and
antiprotons at a typical c.m. energy of 540 GeV; three bunches
of protons and three bunches of antiprotons, 10
S was colliding protons and
antiprotons at a typical c.m. energy of 540 GeV; three bunches
of protons and three bunches of antiprotons, 10 particles per bunch, were present in
the ring at the same time, and the luminosity was about
particles per bunch, were present in
the ring at the same time, and the luminosity was about
 cm
cm /s (5 inverse millibarn per
second).
/s (5 inverse millibarn per
second).

Left: The UA1 detector, and Carlo Rubbia. Right: A Z boson decaying into a muon–antimuon pair as seen at the event display of UA1
(Source: CERN)
UA1 was a general-purpose detector. The
central tracking system was an assembly of six drift chambers
5.8 m long and 2.3 m in diameter. It recorded the tracks
of charged particles curving in a 0.7 T magnetic field,
measuring their momenta with typical accuracy  (where
(where  is the momentum component transverse
to the beam axis, also called the transverse
momentum12; p
is expressed in GeV/c) and
possibly identifying them by the specific energy loss dE / dx. The geometrical arrangement of the
approximately 17 000 field wires and 6125 sense wires allowed
a three-dimensional reconstruction of events. UA1 introduced also
the concept of event display (Fig. 4.28).
is the momentum component transverse
to the beam axis, also called the transverse
momentum12; p
is expressed in GeV/c) and
possibly identifying them by the specific energy loss dE / dx. The geometrical arrangement of the
approximately 17 000 field wires and 6125 sense wires allowed
a three-dimensional reconstruction of events. UA1 introduced also
the concept of event display (Fig. 4.28).
After the tracking chamber and an air
gap of 0.5 m, the particles next encountered the calorimeter
plus 60 cm of additional iron shielding, including the magnet
yoke. The calorimeter started with an electromagnetic calorimeter
made of a sandwich of lead and scintillator, with a total relative
energy resolution about  . The iron shielding was partially
instrumented with streamer tubes13 measuring the position and
the number of minimum ionizing particles, and thus, acting as a
hadronic calorimeter with relative energy resolution about
. The iron shielding was partially
instrumented with streamer tubes13 measuring the position and
the number of minimum ionizing particles, and thus, acting as a
hadronic calorimeter with relative energy resolution about
 . Together, the calorimeter and the
shielding corresponded to more than eight interaction lengths of
material, which almost completely absorbed strongly interacting
particles. Finally, muons were detected in the outer muon chambers,
which covered about 75% of the solid angle in the pseudorapidity
range
. Together, the calorimeter and the
shielding corresponded to more than eight interaction lengths of
material, which almost completely absorbed strongly interacting
particles. Finally, muons were detected in the outer muon chambers,
which covered about 75% of the solid angle in the pseudorapidity
range  2.3. Muon trigger processors required
tracks in the muon chambers pointing back to the interaction region
to retain an event as significant.
2.3. Muon trigger processors required
tracks in the muon chambers pointing back to the interaction region
to retain an event as significant.
4.4.2.2 DELPHI at LEP
 cm
cm /s (20 inverse microbarn per second).
DELPHI was built and operated by approximately 600 scientists from
50 laboratories all over the world.
/s (20 inverse microbarn per second).
DELPHI was built and operated by approximately 600 scientists from
50 laboratories all over the world.

The DELPHI detector at LEP.
Source: CERN
DELPHI consisted of a central cylindrical section and two endcaps, in a solenoidal magnetic field of 1.2 T provided by a superconducting coil. The overall length and the diameter were over 10 m and the total weight was 2500 tons. The electron–positron collisions took place inside the vacuum pipe at the center of DELPHI and the products of the annihilations would fly radially outwards, tracked by several detection layers and read out via about 200 000 electronic channels. A typical event was about one million bits of information.
The DELPHI detector was composed of
subdetectors as shown in Fig. 4.29. In the barrel part
of the detector, covering approximately the region of polar angle
 between 40
between 40 and 140
and 140 , there was an onion-like structure of
tracking detectors, the ones closest to the collision point being
characterized by best resolution: the silicon Vertex Detector (VD),
a cylinder of proportional counters called the Inner Detector (ID),
the Time Projection Chamber (TPC), another cylinder of proportional
counters called the Outer Detector (OD) and the Barrel Muon
Chambers (MUB). The Time Projection Chamber (TPC), shown as the big
cylinder in the Figure, was the main tracking device of DELPHI,
helping as well in charged particle identification by measuring the
specific ionization energy loss dE / dx. The detector provided points per
particle trajectory at radii from 40 to 110 cm.
, there was an onion-like structure of
tracking detectors, the ones closest to the collision point being
characterized by best resolution: the silicon Vertex Detector (VD),
a cylinder of proportional counters called the Inner Detector (ID),
the Time Projection Chamber (TPC), another cylinder of proportional
counters called the Outer Detector (OD) and the Barrel Muon
Chambers (MUB). The Time Projection Chamber (TPC), shown as the big
cylinder in the Figure, was the main tracking device of DELPHI,
helping as well in charged particle identification by measuring the
specific ionization energy loss dE / dx. The detector provided points per
particle trajectory at radii from 40 to 110 cm.
Also in the forward part, a sequence of tracking chambers was present: the Forward Silicon Detector, the Forward Chambers A and B (FCA and FCB), the Forward Muon Chambers (MUF) were devoted to precise measurement of the trajectories of charged particles, and hence to the precise determination of the directions and momenta of the charged particles.
Electron and photon identification was
provided primarily by the electromagnetic calorimetry system. This
was composed of a barrel calorimeter (the High-density Projection
Chamber, HPC) and a forward calorimeter (FEMC); a smaller
calorimeter in the very forward region was used mainly for
luminosity measurement.14 The HPC was installed as a
cylindrical layer outside the Outer Detector, inside the solenoid;
it was an accordion of lead filled with gas as sensitive detector.
The Forward ElectroMagnetic Calorimeter (FEMC) consisted of two
5 m diameter disks made of lead glass, with the front faces
placed at  cm; it detected the Cherenkov
light emitted by charged particles in the shower.
cm; it detected the Cherenkov
light emitted by charged particles in the shower.
The hadron calorimeter (HCAL) was a sampling gas detector incorporated in the magnet yoke (made mainly of iron), covering both the barrel and the endcap regions. It provided calorimetric energy measurements of charged and neutral hadrons (strongly interacting particles).
The identification of charged hadrons in DELPHI relied also on the specific ionization energy loss per unit length in the TPC, and on ring-imaging Cherenkov (RICH) detectors in the barrel and in the forward regions.



Two events reconstructed by DELPHI, projected on the xz plane (left) and on the xy plane (right).
Credits: CERN
4.4.2.3 CMS at LHC

The CMS detector at the LHC.
Source: CERN
As customary for collider detectors, CMS in structured in layers arranged in an onion-like structure.
Layer 1 is devoted to tracking. The
inner silicon tracker is located immediately around the interaction
point. It is used to identify the tracks of individual particles
and match them to the vertices from which they originated. The
curvature of charged particle tracks in the magnetic field allows
their charge and momentum to be measured. The CMS silicon tracker
consists of 13 layers in the central region and 14 layers in the
endcaps. The three innermost layers (up to 11 cm radius)
are made of 
 m pixels (a total of 66 million
pixels) and the next four (up to 55 cm radius) are
silicon strips (9.6 million strip channels in total). The CMS
silicon tracker is the world’s largest silicon detector, with
205 m
m pixels (a total of 66 million
pixels) and the next four (up to 55 cm radius) are
silicon strips (9.6 million strip channels in total). The CMS
silicon tracker is the world’s largest silicon detector, with
205 m of silicon sensors (approximately the
area of a tennis court) and 76 million channels.
of silicon sensors (approximately the
area of a tennis court) and 76 million channels.
Layer 2 is devoted to electromagnetic
calorimetry. The Electromagnetic Calorimeter (ECAL) is constructed
from crystals of lead tungstate, PbWO , a very dense but optically clear
material. It has a radiation length of 0.89 cm, and a rapid
light yield (80% of light yield within one crossing time of
25 ns) of about 30 photons per MeV of incident energy. The
crystals front size is 22 mm
, a very dense but optically clear
material. It has a radiation length of 0.89 cm, and a rapid
light yield (80% of light yield within one crossing time of
25 ns) of about 30 photons per MeV of incident energy. The
crystals front size is 22 mm  22 mm, with a depth of
23 cm. They are readout by silicon avalanche photodiodes and
sit in a matrix of carbon fiber that ensures optical isolation. The
barrel region consists of
22 mm, with a depth of
23 cm. They are readout by silicon avalanche photodiodes and
sit in a matrix of carbon fiber that ensures optical isolation. The
barrel region consists of  60 000 crystals, with a further
60 000 crystals, with a further
 7000 in each of the endcaps.
7000 in each of the endcaps.
Layer 3 is devoted to hadronic calorimetry. The Hadronic Calorimeter (HCAL) consists of layers of dense material (brass or steel) interleaved with tiles of plastic scintillators, read out via wavelength-shifting fibers by hybrid photodiodes. This combination was optimized to guarantee the maximum amount of absorbing material inside the magnet coil.
Layer 4 is the magnet. It is 13 m
long and 6 m in diameter, and it is a refrigerated
superconducting niobium-titanium coil providing a solenoidal field
of 3.8 T (the current being  18 000 A, giving a total stored
energy of about 2.5 GJ, equivalent to about 500 kg of
TNT: dump circuits to safely dissipate this energy are in place,
should the magnet quench).
18 000 A, giving a total stored
energy of about 2.5 GJ, equivalent to about 500 kg of
TNT: dump circuits to safely dissipate this energy are in place,
should the magnet quench).
Layer 5 is occupied by the muon detectors and the return yoke. To identify muons and measure their momenta, CMS uses mostly drift tubes and resistive plate chambers. The drift tubes provide precise trajectory measurements in the central barrel region. The RPC provides an accurate timing signal at the passage of a muon.
The amount of raw data from each
crossing is approximately 1 MB, which at the 40 MHz
crossing rate would result in 40 TB of data per second. A
multi-stage trigger system reduces the rate of interesting events
down to about 100/s. At the first stage, the data from each
crossing are held in buffers within the detector and some key
information is used to identify interesting features (such as large
transverse momentum particles, high-energy jets, muons or missing
momentum). This task is completed in around 1  s, and the event rate is reduced by a
factor of about thousand down to 50 kHz. The data
corresponding to the selected events are sent over fiber-optic
links to a higher level trigger stage, which is a software trigger.
The lower rate allows for a much more detailed analysis of the
event, and the event rate is again reduced by a further factor of
about a thousand, down to around 100 events per second. In a
high-luminosity collider as the LHC, one single bunch crossing may
produce several separate events, called pile-up events. Trigger systems must thus be very
effective.
s, and the event rate is reduced by a
factor of about thousand down to 50 kHz. The data
corresponding to the selected events are sent over fiber-optic
links to a higher level trigger stage, which is a software trigger.
The lower rate allows for a much more detailed analysis of the
event, and the event rate is again reduced by a further factor of
about a thousand, down to around 100 events per second. In a
high-luminosity collider as the LHC, one single bunch crossing may
produce several separate events, called pile-up events. Trigger systems must thus be very
effective.


A reconstructed event is seen in Fig. 4.32.
4.4.2.4 ATLAS at LHC
-
An inner tracking system: operating inside an axial magnetic field of 2 T, it is based on three types of tracking devices—an innermost silicon pixel detector is followed by a silicon strip detector and finally by straw tubes with particle identification capabilities based on transition radiation in the outer tracker.
-
A hybrid calorimeter system: liquid argon with different types of absorber materials is used for the electromagnetic part, the hadronic endcap and the forward calorimeter. The central hadronic calorimeter is a sampling calorimeter with steel as the absorber material and scintillator as the active medium.
-
A large muon spectrometer: an air-core toroid system generates an average field of 0.5 T (1 T), in the barrel (endcap) region of this spectrometer, resulting in a bending power between 2.0 and 7.5 Tm. Tracks are measured by monitored drift tubes and cathode strip chambers. Trigger information is provided by Thin Gap Chambers (TGC) in the endcap and RPC in the barrel.

An event reconstructed by CMS as shown in different projections by the CMS event display.
Source: CERN

Sketch of the ATLAS detector.
Credit: CERN
An electromagnetic calorimeter and a Cherenkov counter instrument the endcap region. Two scintillator wheels were mounted in front of the electromagnetic endcaps to provide trigger signals with minimum bias.
The ATLAS trigger and data acquisition is a multi-level system with buffering at all levels. Trigger decisions are based on calculations done at three consecutive trigger levels.


Comparison of the main design parameters of CMS and ATLAS
|
Parameter |
ATLAS |
CMS |
|---|---|---|
|
Total weight (tons) |
7000 |
12 500 |
|
Overall diameter (m) |
22 |
15 |
|
Overall length (m) |
46 |
20 |
|
Magnetic field for tracking (T) |
2 |
4 |
|
Solid angel for precision measurement
( |
|
|
|
Solid angel for energy measurement
( |
|
|
|
Total cost (million euros) |
550 |
550 |
4.5 Cosmic-Ray Detectors
The strong decrease in the flux
 of cosmic rays with energy, in first
approximation
of cosmic rays with energy, in first
approximation  , poses a big challenge to the
dimensions and the running times of the experimental installations
when high energies are studied. Among cosmic rays, a small fraction
of about 10
, poses a big challenge to the
dimensions and the running times of the experimental installations
when high energies are studied. Among cosmic rays, a small fraction
of about 10 are photons, which are particularly
interesting since they are not deflected by intergalactic magnetic
fields, and thus point directly to their sources; the large
background from charged cosmic rays makes the detection even more
complicated. Neutrinos are expected to be even less numerous than
photons, and their detection is even more complicated due to the
small cross section.
are photons, which are particularly
interesting since they are not deflected by intergalactic magnetic
fields, and thus point directly to their sources; the large
background from charged cosmic rays makes the detection even more
complicated. Neutrinos are expected to be even less numerous than
photons, and their detection is even more complicated due to the
small cross section.
We shall examine first the detectors of cosmic rays which have a relatively large probability of interactions with the atmosphere: nuclei, electrons/positrons, and photons. We shall then discuss neutrinos, and finally the recently discovered gravitational waves, for which detection techniques are completely different.
Balloon and satellite-borne detectors operate at an altitude of above 15 km where they can detect the interaction of the primary particle inside the detector, but they are limited in detection area and therefore also limited in the energy range they can measure. The maximum primary energy that can be measured by means of direct observations is of the order of 1 PeV; above this energy the observations are performed by exploiting the cascades induced in atmosphere by the interactions of cosmic rays.
4.5.1 Interaction of Cosmic Rays with the Atmosphere: Extensive Air Showers
The physics of electromagnetic and hadronic showers has been described before; here we particularize the results obtained to the development of the showers due to the interaction of high-energy particles with the atmosphere. These are called extensive air showers (EAS) .

Schematic representation of two atmospheric showers initiated by a photon (left) and by a proton (right).
From R.M. Wagner, dissertation, MPI Munich 2007
For photons and electrons above a few
hundred MeV, the cascade process is dominated by the pair
production and the bremsstrahlung mechanisms: an energetic photon
scatters on an atmospheric nucleus and produces an  pair, which emits secondary photons
via bremsstrahlung; such photons produce in turn a pair, and so on,
giving rise to a shower of charged particles and photons, degrading
the energy down to the critical energy
pair, which emits secondary photons
via bremsstrahlung; such photons produce in turn a pair, and so on,
giving rise to a shower of charged particles and photons, degrading
the energy down to the critical energy  where the ionization energy loss of
charged particles starts dominating over bremsstrahlung.
where the ionization energy loss of
charged particles starts dominating over bremsstrahlung.
 radiation lengths, the radiation
length for air being about 37 g/cm
radiation lengths, the radiation
length for air being about 37 g/cm (approximately 300 m at sea
level and NTP). The critical energy
(approximately 300 m at sea
level and NTP). The critical energy  is about 80 MeV in
air.16
is about 80 MeV in
air.16

Longitudinal shower development from a photon-initiated cascade. The parameter s describes the shower age.
From R.M. Wagner, dissertation, MPI Munich 2007; adapted from reference [F4.1] in the “Further reading”
The hadronic interaction length in air
is about 90 g/cm for protons (750 m for air at
NTP), being shorter for heavier nuclei—the dependence of the cross
section on the mass number A is
approximately
for protons (750 m for air at
NTP), being shorter for heavier nuclei—the dependence of the cross
section on the mass number A is
approximately  . The transverse profile of hadronic
showers is in general wider than for electromagnetic showers, and
fluctuations are larger.
. The transverse profile of hadronic
showers is in general wider than for electromagnetic showers, and
fluctuations are larger.
Particles release energy in the atmosphere, which acts like a calorimeter, through different mechanisms—which give rise to a measurable signal. We have discussed these mechanisms in Sect. 4.1.1; now we reexamine them in relation to their use in detectors.
4.5.1.1 Fluorescence
As the charged particles in an extensive air shower go through the atmosphere, they ionize and excite the gas molecules (mostly nitrogen). In the de-excitation processes that follow, visible and ultraviolet (UV) radiations are emitted. This is the so-called fluorescence light associated to the shower.
The number of emitted fluorescence photons is small—of the order of a few photons per electron per meter in air. This implies that the fluorescence technique can be used only at high energies. However, it is not directional as in the case of Cherenkov photons (see below), and thus it can be used in serendipitous observations.
4.5.1.2 Cherenkov Emission
Many secondary particles in the EAS are superluminal, and they thus emit Cherenkov light that can be detected. The properties of the Cherenkov emission have been discussed in Sects. 4.1.1 and 4.2.
At sea level, the value of the
Cherenkov angle  in air for a speed
in air for a speed  is about 1.3
is about 1.3 , while at 8 km a.s.l. it is
about 1
, while at 8 km a.s.l. it is
about 1 . The energy threshold for Cherenkov
emission at sea level is 21 MeV for a primary electron and
44 GeV for a primary muon.
. The energy threshold for Cherenkov
emission at sea level is 21 MeV for a primary electron and
44 GeV for a primary muon.
Half of the emission occurs within
20 m of the shower axis (about 70 m for a proton shower).
Since the intrinsic angular spread of the charged particles in an
electromagnetic shower is about 0.5 , the opening of the light cone is
dominated by the Cherenkov angle. As a consequence, the ground area
illuminated by Cherenkov photons from a shower of 1 TeV (the
so-called light pool of the shower) has a radius of about
120 m, with an approximately constant density of photons per
unit area. The height of maximal emission for a primary photon of
energy of 1 TeV is approximately 8 km a.s.l., and about
150 photons per m
, the opening of the light cone is
dominated by the Cherenkov angle. As a consequence, the ground area
illuminated by Cherenkov photons from a shower of 1 TeV (the
so-called light pool of the shower) has a radius of about
120 m, with an approximately constant density of photons per
unit area. The height of maximal emission for a primary photon of
energy of 1 TeV is approximately 8 km a.s.l., and about
150 photons per m arrive at 2000 m a.s.l. (where
typically Cherenkov telescopes are located, see later) in the
visible and near UV frequencies. This dependence is not linear,
being the yield of about 10 photons per square meter at
100 GeV.
arrive at 2000 m a.s.l. (where
typically Cherenkov telescopes are located, see later) in the
visible and near UV frequencies. This dependence is not linear,
being the yield of about 10 photons per square meter at
100 GeV.
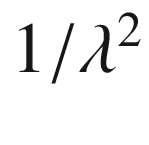 ) arriving at the detectors, in
particular suppressing the UV component (Fig. 4.36) which is still
dominant. There are several sources of extinction: absorption bands
of several molecules, molecular (Rayleigh) and aerosol (Mie)
scattering.
) arriving at the detectors, in
particular suppressing the UV component (Fig. 4.36) which is still
dominant. There are several sources of extinction: absorption bands
of several molecules, molecular (Rayleigh) and aerosol (Mie)
scattering.

Spectrum of the Cherenkov radiation emitted by gamma-ray showers at different energies initiated at 10 km a.s.l. (solid curves) and the corresponding spectra detected at 2200 meters a.s.l. (lower curve).
From R.M. Wagner, dissertation, MPI Munich 2007
Radio Emission. Cosmic-ray air showers alsoemit radio waves in the frequency range from a few to a few hundred MHz, an effect that opens many interesting possibilities in the study of UHE and EHE extensive air showers. At present, however, open questions still remain concerning both the emission mechanism and its strength.
4.5.2 Detectors of Charged Cosmic Rays
The detection of charged cosmic rays may be done above the Earth’s atmosphere in balloon or satellite-based experiments whenever the fluxes are large enough (typically below tens or hundreds of GeV) and otherwise in an indirect way by the observation of the extensive air showers produced in their interaction with the atmosphere (see Sect. 4.5.1).
-
The Advanced Composition Explorer (ACE) launched in 1997 and still in operation (with enough propellant to last until
 ) has been producing a large set of
measurements on the composition (from H to Ni) of solar and
Galactic Cosmic rays covering energies from 1 keV/nucleon to
500 MeV/nucleon. ACE has several instruments which are able to
identify the particle charge and mass using different types of
detectors (e.g., silicon detectors, gas proportional counters,
optical fiber hodoscopes) and techniques (e.g., the specific energy
loss dE / dx, the time-of-flight, electrostatic
deflection). The total mass at launch (including fuel) was about
800 kg.
) has been producing a large set of
measurements on the composition (from H to Ni) of solar and
Galactic Cosmic rays covering energies from 1 keV/nucleon to
500 MeV/nucleon. ACE has several instruments which are able to
identify the particle charge and mass using different types of
detectors (e.g., silicon detectors, gas proportional counters,
optical fiber hodoscopes) and techniques (e.g., the specific energy
loss dE / dx, the time-of-flight, electrostatic
deflection). The total mass at launch (including fuel) was about
800 kg. -
The Balloon-borne Experiment with Superconducting Spectrometer (BESS) performed successive flights starting in 1993 with the main aim to measure the low-energy antiproton spectrum and to search for antimatter, namely antihelium. The last two flights (BESS-Polar) were over Antarctica and had a long duration (8.5 days in 2004 and 29.5 days in 2007/2008). The instrument, improved before every flight, had to ensure a good charge separation and good particle identification. It had a horizontal cylindrical configuration and its main components were as follows: a thin-wall superconducting magnet; a central tracker composed of drift chambers; time-of-flight scintillation counter hodoscopes; an aerogel (an ultralight porous material derived from a gel by replacing its liquid component with a gas) Cherenkov counter.
-
The PAMELA experiment, launched in June 2006, measured charged particles and antiparticles out of the Earth’s atmosphere during a long (six years) period. A permanent magnet of 0.43 T and a microstrip silicon tracking system ensured a good charge separation between electrons and positrons up to energies of the order of hundred GeV measured by a silicon/tungsten electromagnetic calorimeter complemented by a neutron counter to enhance the electromagnetic/hadronic discrimination power. The trigger was provided by a system of plastic scintillators which were also used to measure the time of flight and an estimation of the specific ionization energy loss (dE / dX).
-
The Alpha Magnetic Spectrometer (AMS-02) was installed in May 2011 on the International Space Station. Its concept is similar to PAMELA but with a much larger acceptance and a more complete set of sophisticated and higher performing detectors. Apart from the permanent magnet and the precision silicon tracker it consists of a transition radiation detector, time-of-flight and anticoincidence counters, a ring-imaging Cherenkov detector, and an electromagnetic calorimeter (Fig. 4.37). Its total weight is 8500 kg and its cost was over 2 billion euros.
-
ISS-CREAM (Cosmic Ray Energetics and Mass for the International Space Station) is in orbit since 2017. It uses a Si detector, timing detectors, and scintillating fiber hodoscopes to detect the charge of incident particles up to iron at energies up to the knee. Energies are measured with a transition radiation detector (TRD), and with a calorimeter. The mission follows successful balloon flights of the CREAM detector.

The AMS-02 detector layout.
Credit: AMS Collaboration
-
The measurement of a fraction of the EAS particles arriving at the Earth’s surface through an array of surface detectors (SD);
-
The measurement in moonless nights of the fluorescence light emitted mainly by the de-excitation of the atmosphere nitrogen molecules excited by the shower low energy electrons through an array of ultraviolet fluorescence detectors (FD) placed on the Earth surface or even in satellites; and
-
The measurement of the Cherenkov light emitted by the ultrarelativistic air shower particles in a narrow cone around the shower axis, through telescopes as the Imaging Atmosphere Cherenkov Telescopes (IACTs), which will be discussed in the next section in the context of gamma-ray detection.
Other possible techniques (radio detection for example) might be exploited in the future.
Surface detectors measure at specific space locations the time of arrival of individual particles. The most widely used surface detectors are scintillation counters and water Cherenkov counters. More sophisticated tracking detectors as resistive plate chambers, drift chambers, and streamer tube detectors have been also used or proposed.

Air shower front arriving at the Earth surface; arrival times are measured by surface detectors and allow for the determination of the shower arrival direction
 eV. The measured densities show
a fast decrease with the distance to the core and are usually
parameterized by empirical or phenomenologically inspired
formulae—the most popular being the NKG function, introduced in
Sect. 4.1.7—which depend also on the shower age (the
level of development of the shower when it reaches ground). Such
functions allow for a better determination of the shower core and
for the extrapolation of the particle density to a reference
distance of the core, which is then used as an estimator of the
shower size and thus of the shower energy. The exact function and
the reference distance depend on the particular experimental setup.
eV. The measured densities show
a fast decrease with the distance to the core and are usually
parameterized by empirical or phenomenologically inspired
formulae—the most popular being the NKG function, introduced in
Sect. 4.1.7—which depend also on the shower age (the
level of development of the shower when it reaches ground). Such
functions allow for a better determination of the shower core and
for the extrapolation of the particle density to a reference
distance of the core, which is then used as an estimator of the
shower size and thus of the shower energy. The exact function and
the reference distance depend on the particular experimental setup.

Left: Map of the observed particle density pattern of the highest-energy event at the AGASA experiment. The cross corresponds to the fitted position of the shower core. From http://www.icrr.u-tokyo.ac.jp. Right: Shower longitudinal profile of the most energetic event observed by the Fly’s Eye experiment. From D.J. Bird et al., Astrophys. J. 441 (1995) 144

Display of one shower in the focal plane of one of the Pierre Auger fluorescence telescopes. Left: Pattern of the pixels with signals. Right: response (signal versus time, with a time bin of 100 ns) of the selected pixels (marked with a black dot in the left panel). The development of the shower in the atmosphere can be qualitatively pictured.

Shower geometry as seen by a fluorescence telescope.
From K.-H. Kampert and A. Watson, “Extensive Air Showers and Ultra High Energy Cosmic Rays: A Historical Review,” EPJ-H 37 (2012) 359
Simultaneous observations of the shower by two (stereo) or more fluorescence detectors or by a surface detector array (hybrid detection) provide further geometric constraints improving considerably the resolution of the shower geometric reconstruction.
The intensity of collected light along the shower axis is corrected for the detector efficiency, the solid angle seen by each detector pixel, the attenuation in the atmosphere, the night sky background, and the contributions of fluorescence (dominant unless the shower axis points in the direction of the telescope) and of Cherenkov light are estimated. Finally, the shower longitudinal profile (Fig. 4.39, right) is obtained assuming proportionality between the fluorescence light emitted and the number of particles in the shower. The integral of such a profile is a good estimator of the energy of the shower (small “missing momentum” corrections due to low interacting particles in the atmosphere, like muons and neutrinos, have to be taken into account).
The Pierre Auger Observatory. The Pierre Auger Observatory in Malargue, Argentina, is the largest cosmic-ray detector ever built. It covers a surface of about 3000 square kilometers with 1600 surface detector stations (Cherenkov water tanks) arranged in a grid of 1.5 km side complemented by 27 fluorescence telescopes, grouped into four locations to cover the atmosphere above the detector area (Fig. 4.42).
 base by 1.5 m height filled with
12 tons of water (Fig. 4.43). The inner walls of the tank are covered
with a high reflectivity material. The Cherenkov light, produced by
the charged particles crossing the water, is collected by three
PMTs placed at the top of the tank. Each tank is autonomous being
the time given by a GPS unit and the power provided by a solar
panel; it communicates via radio with the central data acquisition
system.
base by 1.5 m height filled with
12 tons of water (Fig. 4.43). The inner walls of the tank are covered
with a high reflectivity material. The Cherenkov light, produced by
the charged particles crossing the water, is collected by three
PMTs placed at the top of the tank. Each tank is autonomous being
the time given by a GPS unit and the power provided by a solar
panel; it communicates via radio with the central data acquisition
system.

The Pierre Auger Observatory near Malargue, Argentina. The radial lines point to the fluorescence detectors. The black dots are the 1600 surface detectors (SD). Sites with specialized equipment are also indicated. By Darko Veberic [GFDL http://www.gnu.org/copyleft/fdl.html], via Wikimedia Commons
 in azimuth and 29
in azimuth and 29 in elevation (Fig. 4.43). Light enters the
telescope through an ultraviolet filter installed over the
telescope and is collected in a 3.5 m diameter spherical
mirror which focuses it in a 440 PMT camera.
in elevation (Fig. 4.43). Light enters the
telescope through an ultraviolet filter installed over the
telescope and is collected in a 3.5 m diameter spherical
mirror which focuses it in a 440 PMT camera.

Sketch of one of the Pierre Auger surface detectors (left); a fluorescence telescope (right).

A 30 EeV event at a zenith angle of
about 88 recorded by the Auger detector. The
inset shows a simulation of an event of the same energy and
angle.
recorded by the Auger detector. The
inset shows a simulation of an event of the same energy and
angle.
The
Telescope Array. The largest cosmic-ray detector in the
Northern hemisphere is the Telescope Array (TA) in Utah, USA. Similar to Auger, it is
also a hybrid detector composed of a surface array of 507
scintillator detectors, each 3 m in size, located on a
1.2 km square grid, plus three fluorescence stations, each
with a dozen of telescopes instrumented with a 256 PMT camera
covering 3 –33
–33 in elevation. The total surface
covered is about 800 km
in elevation. The total surface
covered is about 800 km .
.
 ), one can cover a large surface on
Earth (above 1.9
), one can cover a large surface on
Earth (above 1.9  10
10 km
km ), but the energy threshold is high
(around 3
), but the energy threshold is high
(around 3  10
10 eV).
eV).

4.5.3 Detection of Hard Photons
Most photons in astrophysics are produced by systems near thermal equilibrium, approximately blackbodies. The bulk of astrophysical photons is due to CMB at a temperature of about 2.7 K (corresponding to an energy of about 0.1 meV). The highest-energy thermalized systems emit at energies of about a keV, i.e., in the X-ray range. We are interested in this book mainly on nonthermal processes, and thus, on photons in the keV range and above.
Nonthermal photons, in the keV range and above, are expected to be generated in astrophysical objects mostly by leptonic acceleration mechanisms (see Chap. 10), and by the decays of neutral pions produced in cosmic-ray interactions with radiation or gas—as these pions decay, they produce photons with typical energies one order of magnitude smaller than those of the cosmic-ray nucleons generating them. Photons in the MeV range can come also from nuclear de-excitation processes.
 pair production dominates above these
energies.
pair production dominates above these
energies.

Transparency of the atmosphere for different photon energies and possible detection techniques.
Source: A. De Angelis and L. Peruzzo, “Le magie del telescopio MAGIC,” Le Scienze, April 2007
- 1.
Hard X-ray region (or keV region) the energy region between 3 and 300 keV.
- 2.
Low-energy gamma-ray region (or MeV region) the energy region between 0.3 and 30 MeV. This is the region in which the Compton interaction probability is comparable with the pair production probability.
- 3.
High-energy (HE) gamma-ray region (or GeV region) the energy region between 30 MeV and 30 GeV. The pair production process becomes dominant.
- 4.
Very-high-energy (VHE) gamma-ray region (or TeV region) the energy region between 30 GeV and 30 TeV. Electromagnetic showers in the atmosphere start becoming visible.
- 5.
PeV region the energy region between 30 TeV and 30 PeV. Charged particles from electromagnetic showers in the atmosphere can reach instruments at mountain-top altitudes. As we shall see in Chap. 10, however, the mean free path of photons at these energies is such that we expect photons from very few extragalactic sources to reach the Earth.
This classification, in particular, corresponds to different detection techniques, as we shall see now. The MeV, GeV, and TeV regions are especially important related to the physics of cosmic rays and to fundamental physics. Note the difference in range with respect to highest-energy charged cosmic rays—do not forget that the flux in the latter case is three orders of magnitude larger in the MeV–GeV region.
Main figures of merit for a detector are its effective area (i.e., the product of the area times the detection efficiency), the energy resolution, the space or angular resolution (called as well point spread function, or PSF). In particular the effective area has to be appropriate for the flux one wants to measure.
 -rays – and thus gamma rays below the
TeV region. Satellites are small, about 1 m
-rays – and thus gamma rays below the
TeV region. Satellites are small, about 1 m in area at maximum, because of the
cost of space technology. The area sampled by ground-based
detectors can be much larger than this. Since the fluxes of
high-energy photons are low and decrease rapidly with increasing
energy, TeV and PeV gamma rays can be detected only from the
atmospheric showers they produce, i.e., by means of ground-based
detectors. This fact clarifies another meaning of the division
between HE and VHE photons: HE photons are detected using
satellites, while for VHE photons the detection using ground-based
instruments becomes possible.
in area at maximum, because of the
cost of space technology. The area sampled by ground-based
detectors can be much larger than this. Since the fluxes of
high-energy photons are low and decrease rapidly with increasing
energy, TeV and PeV gamma rays can be detected only from the
atmospheric showers they produce, i.e., by means of ground-based
detectors. This fact clarifies another meaning of the division
between HE and VHE photons: HE photons are detected using
satellites, while for VHE photons the detection using ground-based
instruments becomes possible.

Principles of operation of focusing grazing incident mirrors (left, credits: NASA) and of coded mask apertures (right, credits: Wikimedia Commons)
4.5.3.1 Satellites
Satellite-based telescopes for hard
photons can detect the primary particles at energies lower than
ground-based telescopes. They have a small effective area, of the
order of 1 m maximum, which limits their
sensitivity. They have a large duty cycle, and they suffer a low
rate of background events, since they can be coupled to
anticoincidence systems rejecting the charged cosmic rays. They
have a large cost, dominated by the costs of launch and by the
strong requirements of instruments to be sent into space, with
little or no possibility of intervention to fix possible bugs.
maximum, which limits their
sensitivity. They have a large duty cycle, and they suffer a low
rate of background events, since they can be coupled to
anticoincidence systems rejecting the charged cosmic rays. They
have a large cost, dominated by the costs of launch and by the
strong requirements of instruments to be sent into space, with
little or no possibility of intervention to fix possible bugs.
- 1.
Satellites operational in the keV regime use different focal plane detectors and optical system. Optical systems (Fig. 4.47) are constituted by focusing grazing incident mirrors or by collimating elements such as coded mask systems (grids of materials opaque to various wavelengths of light: by blocking light in a known pattern, a coded “shadow” is cast upon a sensitive plane, and the properties of the original light sources can then be mathematically reconstructed from this shadow).
1a. In the energy band of a few keV, satellites in use today include NASA’s Chandra mission and ESA’s XMM-Newton observatory, both launched in 1999; they both use X-ray grazing incident mirrors. Chandra has an effective area of 800 and 400 cm
 at 0.25 and 5 keV, respectively.
Different instruments can be inserted in
the focal plane; at 1 keV, the typical field of view (FoV) is
at 0.25 and 5 keV, respectively.
Different instruments can be inserted in
the focal plane; at 1 keV, the typical field of view (FoV) is
 and space resolution is as good as
0.5 arcsec; the spectral resolving power
and space resolution is as good as
0.5 arcsec; the spectral resolving power  is between 30 and 2000. ESA’s X-ray
Multi-Mirror Mission (XMM-Newton) uses three co-aligned grazing
incidence gold-coated imaging X-ray telescopes each with an
effective area of
is between 30 and 2000. ESA’s X-ray
Multi-Mirror Mission (XMM-Newton) uses three co-aligned grazing
incidence gold-coated imaging X-ray telescopes each with an
effective area of  1500 cm
1500 cm at 1 keV with a spatial
resolution of 6 arcsec. Also in this case there are different
instruments. Typical effective area is of the order of
1000 cm
at 1 keV with a spatial
resolution of 6 arcsec. Also in this case there are different
instruments. Typical effective area is of the order of
1000 cm at 1 keV for a spectral
resolving power of 20; of the order of 200 cm
at 1 keV for a spectral
resolving power of 20; of the order of 200 cm for a resolving power of 1000. The
maximum energy detected by these detectors is around
15 keV.
for a resolving power of 1000. The
maximum energy detected by these detectors is around
15 keV.NASA’s NuSTAR (Nuclear Spectroscopic Telescope Array), launched in 2012, is a space-based X-ray telescope that operates in the range of 3–80 keV. NuSTAR is the first telescope using imaging techniques at energies above 15 keV. The NuSTAR grazing mirrors have a focal length of 10.15 m and are held at the end of a long deployable mast. The point spread function for the flight mirrors is 43 arc seconds, an unprecedentedly good resolution for focusing hard X-ray optics.
In the future (launch is planned for 2028), the ATHENA (Advanced Telescope for High Energy Astrophysics) satellite, one hundred times more sensitive than the best existing X-ray telescopes, will fly within ESA’s Cosmic Vision program.
1b. At higher energies, collimating elements are used to image photons of energy in the range from 100 keV to few MeV. Coded mask systems are used both by the Swift Burst Alert Telescope (BAT) and by the main instruments on board the INTEGRAL satellite.
The Neil Gehrels Swift Observatory (shortly Swift) is a NASA international mission launched in 2004. The primary scientific objectives are to determine the origin of Gamma Ray Bursts (GRB) and to pioneer their use as probes of the early Universe. Swift is a multiwavelength observatory carrying three instruments. The Burst Alert Telescope (BAT; 15–150 keV) is a wide field-of-view coded aperture imager with an effective area 5240 cm
 and a FoV of 1.4 sr half coded and a
position accuracy of
and a FoV of 1.4 sr half coded and a
position accuracy of  . The X-Ray Telescope (XRT;
0.2–10.0 keV) uses a X-ray grazing mirror system and has a CCD
Imaging spectrometer with an effective area of
110 cm
. The X-Ray Telescope (XRT;
0.2–10.0 keV) uses a X-ray grazing mirror system and has a CCD
Imaging spectrometer with an effective area of
110 cm at 1.5 keV, a FoV of
at 1.5 keV, a FoV of
 and a
and a  position accuracy. The UV/Optical
Telescope (UVOT; 170–650 nm) is a CCD detector with a FoV of
position accuracy. The UV/Optical
Telescope (UVOT; 170–650 nm) is a CCD detector with a FoV of
 and 0.3 arcsec position accuracy. The
key characteristics of Swift are the rapid response to newly
detected GRB and rapid data dissemination. As soon as the BAT discovers a new GRB, Swift rapidly releases
its first position estimate, with (1–4) arcmin accuracy, to the
ground segment, and an autonomous trigger allows the burst entering
within the field of view of XRT and
UVOT to follow up the afterglow.
and 0.3 arcsec position accuracy. The
key characteristics of Swift are the rapid response to newly
detected GRB and rapid data dissemination. As soon as the BAT discovers a new GRB, Swift rapidly releases
its first position estimate, with (1–4) arcmin accuracy, to the
ground segment, and an autonomous trigger allows the burst entering
within the field of view of XRT and
UVOT to follow up the afterglow.ESA’s International Gamma-Ray Astrophysics Laboratory (INTEGRAL) was launched in 2002. It is producing a complete map of the sky in the soft gamma-ray waveband and it is capable of performing high spectral and spatial observations in gamma rays. The observatory is also equipped with X-ray and optical detectors to provide simultaneous observations in these wavebands. The payload hosts several gamma-ray instruments. The Spectrometer (SPI; 20 keV–8 MeV) has a coded aperture mask with a FoV of
 and a detection plane made of a
Germanium array with a detector area of 500 cm
and a detection plane made of a
Germanium array with a detector area of 500 cm , a spectral resolution
, a spectral resolution  of 500 at 1 MeV and a spatial
resolution of 2
of 500 at 1 MeV and a spatial
resolution of 2 . The Imager (IBIS;
15 keV–10 MeV) is also equipped with a coded aperture
mask. Its FoV is
. The Imager (IBIS;
15 keV–10 MeV) is also equipped with a coded aperture
mask. Its FoV is  , and it has a detector area of
2600 cm
, and it has a detector area of
2600 cm (CdTe array - ISGRI) and of
3100 cm
(CdTe array - ISGRI) and of
3100 cm (CsI array - PICSIT) with a spatial
resolution of
(CsI array - PICSIT) with a spatial
resolution of  . The Joint European X-Ray Monitor
(JEM-X) makes observations simultaneously with the main gamma-ray
instruments and provides images in the 3–35 keV prime energy
band with an angular resolution of 3 arcmin.
. The Joint European X-Ray Monitor
(JEM-X) makes observations simultaneously with the main gamma-ray
instruments and provides images in the 3–35 keV prime energy
band with an angular resolution of 3 arcmin.In this energy range not collimated systems use scintillation materials to detect photons up to tens of MeV. The Fermi (see later) Gamma-ray Burst Monitor (GBM) is equipped with 12 NaI detectors sensitive from a few keV to about 1 MeV and two BGO detectors operating up to 40 MeV.
- 2.
In the MeV regime, the state of the art for Compton imaging is mostly frozen at the COMPTEL instrument on the Compton Gamma Ray Observatory (CGRO), launched in 1991 aboard the space shuttle Atlantis, and safely deorbited in 2000. CGRO had four instruments that covered six decades of the electromagnetic spectrum, from 30 keV to 30 GeV. In order of increasing spectral energy coverage, these instruments were the Burst And Transient Source Experiment (BATSE), the Oriented Scintillation Spectrometer Experiment (OSSE), the Imaging Compton Telescope (COMPTEL), and the Energetic Gamma Ray Experiment Telescope (EGRET). The Imaging Compton Telescope (COMPTEL) used the Compton effect and two layers of gamma-ray detectors to reconstruct an image of a gamma-ray source in the energy range 1–30 MeV. COMPTEL’s upper layer of detectors were filled with a liquid scintillator which scattered an incoming gamma-ray photon. This photon was then absorbed by NaI crystals in the lower detectors. The instrument recorded the time, location, and energy of the events in each layer of detectors, making it possible to determine the direction and energy of the original gamma-ray photon and reconstruct an image and energy spectrum of the source.
The silicon detector technology allows today improving the sensitivity of COMPTEL by two orders of magnitude, and also crucially improving the localization accuracy. Two detectors are under evaluation, e-ASTROGAM by a mostly European consortium and AMEGO by NASA, which use silicon detector planes without converter to build a hodoscope sensitive to both Compton interaction and pair production (Fig. 4.48) .
- 3.
In the GeV regime, pair production is mostly used to detect photons. Three modern gamma-ray telescopes sensitive to photons in the HE region are in orbit; they are called AGILE, Fermi Large Area Telescope (LAT) (Fig. 4.49), and DAMPE.
Their technology has been inherited from the smaller and less technological EGRET instrument, operational in the years 1991–2000 on the Compton Gamma-Ray Observatory, and from particle physics. The direction of an incident photon is determined through the geometry of its conversion into an
 pair in foils of heavy materials
which compose the instrument, and detected by planes of silicon
detectors. The presence of an anticoincidence apparatus realizes a
veto against unwanted incoming charged particles. The principle of
operation is illustrated in Fig. 4.49, right.
pair in foils of heavy materials
which compose the instrument, and detected by planes of silicon
detectors. The presence of an anticoincidence apparatus realizes a
veto against unwanted incoming charged particles. The principle of
operation is illustrated in Fig. 4.49, right.The angular resolution of these telescopes is limited by the opening angle of the
 pair, approximately
pair, approximately  , and especially by the effect of
multiple scattering. To achieve a good energy resolution, in this
kind of detector, a calorimeter in the bottom of the tracker is
possibly used, depending on the weight that the payload can comply
with. Due to weight limitations, however, it is difficult to fit in
a calorimeter that completely contains the showers; this leakage
degrades the energy resolution. Since at low energies multiple
scattering is the dominant process, the optimal detector design is
a trade-off between small radiation length (which decreases the
conversion efficiency) and large number of samplings (which
increases the power consumption, limited by the problems of heat
dissipation in space).
, and especially by the effect of
multiple scattering. To achieve a good energy resolution, in this
kind of detector, a calorimeter in the bottom of the tracker is
possibly used, depending on the weight that the payload can comply
with. Due to weight limitations, however, it is difficult to fit in
a calorimeter that completely contains the showers; this leakage
degrades the energy resolution. Since at low energies multiple
scattering is the dominant process, the optimal detector design is
a trade-off between small radiation length (which decreases the
conversion efficiency) and large number of samplings (which
increases the power consumption, limited by the problems of heat
dissipation in space). The largest gamma-ray space-based
detector ever built is up to now the Fermi observatory, launched in June 2008—and called
GLAST before the successful positioning in orbit. It is composed of
the spacecraft and two instruments: the Large Area Telescope (LAT)
and the Fermi Gamma Burst
Monitor (GBM); the two instruments are integrated and they work as
a single observatory.
The largest gamma-ray space-based
detector ever built is up to now the Fermi observatory, launched in June 2008—and called
GLAST before the successful positioning in orbit. It is composed of
the spacecraft and two instruments: the Large Area Telescope (LAT)
and the Fermi Gamma Burst
Monitor (GBM); the two instruments are integrated and they work as
a single observatory.The structure of the LAT consists mainly of a tracker, an anticoincidence apparatus and a calorimeter (see Fig. 4.49). Its energy range goes from 20 MeV to about 300 GeV and above, while the energy range explored by the GBM is 10–25 MeV. Fermi was built and it is operated by an international collaboration with contributions from space agencies, high-energy particle physics institutes, and universities in France, Italy, Japan, Sweden, and the United States; it involves about 600 scientists. After the first year, data are public, i.e., every scientist in the world can in principle analyze them.
The scientific objectives of the LAT include the understanding of the nature of unidentified gamma-ray sources and origins of diffuse Galactic emission; of particle acceleration mechanisms at the sources, particularly in active galactic nuclei, pulsars, supernova remnants, and the Sun; of the high-energy behavior of gamma-ray burst and transient sources. The observations will also be used to probe dark matter and, at high energy, the early universe and the cosmic evolution of high-energy sources to redshift
 .
.The characteristics and performance of the LAT are enabling significant progress in the understanding of the high-energy sky. In particular, it has good angular resolution for source localization and multiwavelength study, high sensitivity in a broad field of view to detect transients and monitor variability, good calorimetry over an extended energy band for detailed emission spectrum studies, and good calibration and stability for absolute, long-term flux measurements.
The LAT tracker is composed of 16 planes of high-Z material (W) in which incident
 rays can convert to an
rays can convert to an  pair. The converter planes are
interleaved with 18 two-layer planes of silicon detectors that
measure the tracks of the particles resulting from pair conversion.
This information is used to reconstruct the directions of the
incident
pair. The converter planes are
interleaved with 18 two-layer planes of silicon detectors that
measure the tracks of the particles resulting from pair conversion.
This information is used to reconstruct the directions of the
incident  rays. After the tracker, a
calorimeter can measure the energy. It is made of CsI(Tl) crystals
with a total depth of 8.6 radiation lengths, arranged in a
hodoscope configuration in order to provide longitudinal and
transverse information on the energy deposition. The depth and the
segmentation of the calorimeter enable the high-energy reach of the
LAT and significantly contribute to background rejection. The
aspect ratio of the tracker (height/width) is 0.4 (the width being
about 1.7 m), resulting in a large field of view (2.4 sr) and
ensuring that most pair-conversion showers initiated in the tracker
will reach the calorimeter for energy measurement. Around the
tracker, an anticoincidence detector (ACD) made of plastic
scintillator provides charged particle background rejection.The overall performance of Fermi can be summarized as follows in the region of main interest (30 MeV–30 GeV):
rays. After the tracker, a
calorimeter can measure the energy. It is made of CsI(Tl) crystals
with a total depth of 8.6 radiation lengths, arranged in a
hodoscope configuration in order to provide longitudinal and
transverse information on the energy deposition. The depth and the
segmentation of the calorimeter enable the high-energy reach of the
LAT and significantly contribute to background rejection. The
aspect ratio of the tracker (height/width) is 0.4 (the width being
about 1.7 m), resulting in a large field of view (2.4 sr) and
ensuring that most pair-conversion showers initiated in the tracker
will reach the calorimeter for energy measurement. Around the
tracker, an anticoincidence detector (ACD) made of plastic
scintillator provides charged particle background rejection.The overall performance of Fermi can be summarized as follows in the region of main interest (30 MeV–30 GeV):-
Effective area of about 1 m
 ;
; -
Relative energy resolution decreasing between 10% at 100 MeV and 5% at 1 GeV, increasing again to 10% at 30 GeV;
-
Angular resolution of 0.1
 at 10 GeV, and approximately
varying as
at 10 GeV, and approximately
varying as  .
.
AGILE, the precursor of Fermi, is a completely Italian satellite launched in April 2007. Its structure is very similar to Fermi, but its effective area is about one order of magnitude smaller. However, many remarkable physics results were obtained thanks to the AGILE data.
Finally DAMPE, launched in 2015, has also a structure and an effective area similar to AGILE. It is however characterized by an imaging calorimeter of about 31 radiation lengths thickness, made up of 14 layers of Bismuth Germanium Oxide (BGO) bars in a hodoscopic arrangement—this is the deepest calorimeter ever used in space.
-

Representative event topologies for a Compton event (left) and for a pair event (right). Photon tracks are shown in pale blue, dashed, and electron and/or positron tracks in red, solid.
Courtesy of Alex Moiseev

On the left, the Fermi satellite. On the right, the layout of the Large Area Telescope (LAT), and principle of operation.
Credits: NASA
4.5.3.2 Ground-Based Gamma-Ray Detectors
Ground-based VHE gamma-ray detectors–such as HAWC, H.E.S.S. , MAGIC, and VERITAS –detect the atmospheric showers produced by primary photons and cosmic rays of energy higher than those observed by satellites.
The two kinds of detectors (on
satellite and at the ground) are complementary. At energies below
1 GeV or so, the showers generated by photons do not have the
time to develop properly, and thus the only way to detect photons
below this energy is with the use of satellites. At TeV energies,
however, the flux is too low to be detected with satellite-based
detectors: due to their cost, and in particular to the cost of the
launch, the satellites have areas of the order of
1 m at most, and at these energies even
the most luminous gamma-ray sources have a flux smaller than one
photon per square meter every ten hours. Ground-based detectors
have a huge effective area, so their sensitivity is high; they
detect a huge amount of background events, but they have low
cost.
at most, and at these energies even
the most luminous gamma-ray sources have a flux smaller than one
photon per square meter every ten hours. Ground-based detectors
have a huge effective area, so their sensitivity is high; they
detect a huge amount of background events, but they have low
cost.
The main problem of ground-based
detection is the rejection of the background from showers generated
by protons. As an example to evaluate the entity of the problem, we
consider a source with an emission energy distribution like the
Crab Nebula, a nearby ( 2 kpc away) pulsar wind nebula
and the first source detected in VHE gamma rays, and the brightest
VHE gamma-ray source visible from both hemispheres—therefore, it
has become the so-called standard
reference in VHE gamma-ray astronomy.
2 kpc away) pulsar wind nebula
and the first source detected in VHE gamma rays, and the brightest
VHE gamma-ray source visible from both hemispheres—therefore, it
has become the so-called standard
reference in VHE gamma-ray astronomy.


The number of photons from the Crab per
m per second above a given threshold is
shown in Fig. 4.50, and compared to the background from
cosmic rays in a square degree. From this it becomes clear that in
order to separate the gamma-ray signal from the background the
angular resolution should be of one degree or better, and possibly
there should be a way to distinguish electromagnetic showers from
hadronic showers (e.g., by their topology or by the presence of
muons in hadronic showers).
per second above a given threshold is
shown in Fig. 4.50, and compared to the background from
cosmic rays in a square degree. From this it becomes clear that in
order to separate the gamma-ray signal from the background the
angular resolution should be of one degree or better, and possibly
there should be a way to distinguish electromagnetic showers from
hadronic showers (e.g., by their topology or by the presence of
muons in hadronic showers).

Left: Signal above a given energy on an
effective area of 10 000 m , integrated over 1 s: Crab
(solid line) and background from charged cosmic rays within one
square degree (dashed line). Right: ratio signal/background from
the plot on the left
, integrated over 1 s: Crab
(solid line) and background from charged cosmic rays within one
square degree (dashed line). Right: ratio signal/background from
the plot on the left

Sketch of the operation of Cherenkov telescopes and of EAS detectors
EAS Detectors. The EAS detectors, such as MILAGRO, Tibet-AS and ARGO-YBJ in the past, and HAWC which is presently in operation, are large arrays of detectors sensitive to charged secondary particles generated in the atmospheric showers. They have a high duty cycle and a large field of view, but a relatively poor sensitivity. The energy threshold of such detectors is rather large—a shower initiated by a 1 TeV photon typically has its maximum at about 8 km a.s.l.
-
either using a sparse array of scintillator-based detectors, as, for example, in Tibet-AS (located at 4100 m a.s.l. to reduce the threshold; for an energy of 100 TeV there are about 50 000 electrons at mountain-top altitudes);
-
or by effective covering of the ground, to ensure efficient collection and hence lower the energy threshold.
-
The ARGO-YBJ detector at the Tibet site followed this approach. It was an array of resistive plate counters. Its energy threshold was in the 0.5–1 TeV range. The Crab Nebula could be detected with a significance of about 5 standard deviations (
 ) in 50 days of observation.
) in 50 days of observation. -
MILAGRO was a water Cherenkov instrument located in New Mexico (at an altitude of about 2600 m a.s.l.). It detected the Cherenkov light produced by the secondary particles of the shower when entering the water pool instrumented with photomultipliers. MILAGRO could detect the Crab Nebula with a significance of about 5
 in 100 days of
observation, at a median energy of about 20 TeV.
in 100 days of
observation, at a median energy of about 20 TeV.
-
The energy threshold of EAS detectors
is at best in the 0.5–1 TeV range, so they are built to detect
UHE photons as well as the most energetic VHE gamma rays. At such
energies fluxes are small and large effective areas of the order of
10 m
m are required. We remind here that the
effective area is the product of the collection area times the
detection efficiency; the collection area can be larger than the
area covered by the detector, since one can detect showers
partially contained—this fact is more relevant for Cherenkov
telescopes, see later.
are required. We remind here that the
effective area is the product of the collection area times the
detection efficiency; the collection area can be larger than the
area covered by the detector, since one can detect showers
partially contained—this fact is more relevant for Cherenkov
telescopes, see later.
Concerning the discrimination from the
charged cosmic ray background, muon detectors devoted to hadron
rejection may be present. Otherwise, this discrimination is based
on the reconstructed shower shape. The direction of the detected
primary particles is computed from the arrival times with an
angular precision of about 1 to 2
to 2 . The calibration can be performed by
studying the shadow in the reconstructed directions caused by the
Moon. Energy resolution is poor.
. The calibration can be performed by
studying the shadow in the reconstructed directions caused by the
Moon. Energy resolution is poor.
Somehow, the past generation EAS detectors were not sensitive enough and just detected a handful of sources. This lesson led to a new EAS observatory with much better sensitivity: the High Altitude Water Cherenkov detector HAWC, inaugurated in 2015.
HAWC (Fig. 4.52) is a very high-energy gamma-ray observatory
located in Mexico at an altitude of 4100 m. It consists of 300
steel tanks of 7.3 m diameter and 4.5 m deep, covering an
instrumented area of about 22 000 m . Each tank is filled with purified
water and contains three PMTs of 20 cm diameter, which observe
the Cherenkov light emitted in water by superluminal particles in
atmospheric air showers. Photons traveling through the water
typically undergo Compton scattering or produce an
electron–positron pair, also resulting in Cherenkov light emission.
This is an advantage of the water Cherenkov technique, as photons
constitute a large fraction of the electromagnetic component of an
air shower at ground.
. Each tank is filled with purified
water and contains three PMTs of 20 cm diameter, which observe
the Cherenkov light emitted in water by superluminal particles in
atmospheric air showers. Photons traveling through the water
typically undergo Compton scattering or produce an
electron–positron pair, also resulting in Cherenkov light emission.
This is an advantage of the water Cherenkov technique, as photons
constitute a large fraction of the electromagnetic component of an
air shower at ground.

Left: The HAWC detector. Right: Sketch of a water tank.
Credit: HAWC Collaboration
A future installation in the Northern
hemisphere, a hybrid detector called LHAASO, is in construction in China. LHAASO
covers a total area of about  m
m with more than 5000 scintillation
detectors, each of 1 m
with more than 5000 scintillation
detectors, each of 1 m area. A central detector of
80 000 square meters (four times the HAWC detector) of surface
water pools is equipped with PMTs to study gamma-ray astronomy in
the sub-TeV/TeV energy range. About 1200 water tanks underground,
with a total sensitive area of about 42 000 m
area. A central detector of
80 000 square meters (four times the HAWC detector) of surface
water pools is equipped with PMTs to study gamma-ray astronomy in
the sub-TeV/TeV energy range. About 1200 water tanks underground,
with a total sensitive area of about 42 000 m , pick out muons, to separate
gamma-ray initiated showers from hadronic showers. 18 wide
field-of-view Cherenkov telescopes will complete the observatory.
LHAASO will have the best sensitivity on gamma-ray initiated
showers above some 10 TeV. One-quarter of the observatory
should be ready by 2018, and completion is expected in 2021.
, pick out muons, to separate
gamma-ray initiated showers from hadronic showers. 18 wide
field-of-view Cherenkov telescopes will complete the observatory.
LHAASO will have the best sensitivity on gamma-ray initiated
showers above some 10 TeV. One-quarter of the observatory
should be ready by 2018, and completion is expected in 2021.
Cherenkov Telescopes. Most of the experimental results on VHE photons are presently due to Imaging Atmospheric Cherenkov Telescopes (IACTs), which detect the Cherenkov photons produced in air by charged, locally superluminal particles in atmospheric showers.
WHIPPLE in Arizona was the first IACT to see a significant signal (from the Crab Nebula, in 1989). The second-generation instruments HEGRA and CANGAROO improved the technology, and presently the third-generation instruments H.E.S.S. in Namibia, MAGIC in the Canary Islands and VERITAS in Arizona are running smoothly and detecting tens of sources every year. For reasons explained below, these instruments have a low duty cycle (about 1000–1500 h/year) and a small field of view (FoV), but they have a high sensitivity and a low energy threshold.
The observational technique used by the
IACTs is to project the Cherenkov light collected by a large
optical reflector onto a focal camera which is basically an array
of photomultipliers, with a typical quantum efficiency of about
30%, in the focal plane of the reflector (see
Fig. 4.53). The camera has a typical diameter of
about 1 m, and covers a FoV of about 5 . The signal collected by the camera
is analogically transmitted to trigger systems, similar to the ones
used in high-energy physics. The events which pass the trigger
levels are sent to the data acquisition system, which typically
operates at a frequency of a few hundreds Hz. The typical
resolution on the arrival time of a signal on a photomultiplier is
better than 1 ns.
. The signal collected by the camera
is analogically transmitted to trigger systems, similar to the ones
used in high-energy physics. The events which pass the trigger
levels are sent to the data acquisition system, which typically
operates at a frequency of a few hundreds Hz. The typical
resolution on the arrival time of a signal on a photomultiplier is
better than 1 ns.

Observational technique adopted by Cherenkov telescopes.
From R.M. Wagner, dissertation, MPI Munich 2007
Since, as discussed above, about 10
photons per square meter arrive in the light pool for a primary
photon of 100 GeV, a light collector of area
100 m is sufficient to detect gamma-ray
showers if placed at mountain-top altitudes. Due to the faintness
of the signal, data can typically be taken only in moonless time,
or with moderate moonlight, and without clouds, which limits the
total observation time to some 1000–1500 h/year.
is sufficient to detect gamma-ray
showers if placed at mountain-top altitudes. Due to the faintness
of the signal, data can typically be taken only in moonless time,
or with moderate moonlight, and without clouds, which limits the
total observation time to some 1000–1500 h/year.

Development of a vertical 1 TeV photon (left) and proton (right) showers in the atmosphere. The upper panels show the positions in the atmosphere of all shower electrons above the Cherenkov threshold; the lower panels show the resulting Cherenkov images in the focal plane of a 10 m reflecting mirror when the showers fall 100 m from the detector (the center of the focal plane is indicated by a star).
From C.M. Hoffmann et al., “Gamma-ray astronomy at high energies,” Reviews of Modern Physics 71 (1999) 897

Images from the focal camera of a Cherenkov telescope. The electromagnetic events differ from the hadronic events by several features: the envelope of the electromagnetic shower can be quite well described by an ellipse whereas the important fraction of large transverse momentum particles in hadronic showers will result in a more scattered reconstructed image. Muons are characterized by a conical section.

The H.E.S.S. telescopes.
Credit: H.E.S.S. Collaboration
The time structure of Cherenkov images provides an additional discriminator against the hadronic background, which can be used by isochronous detectors (with parabolic shape) and with a signal integration time smaller than the duration of the shower (i.e., better than 1–2 GHz).
Systems of more than one Cherenkov telescope provide a better background rejection, and a better angular and energy resolution than a single telescope.
There are three large operating IACTs: H.E.S.S. , MAGIC, and VERITAS; the first located in the Southern hemisphere and the last two in the Northern hemisphere.
-
The H.E.S.S. observatory (Fig. 4.56) in Namibia is composed of four telescopes with a diameter of 12 m each, working since early 2003. A fifth large telescope, a surface of about 600 m
 , is located in the center; it was
inaugurated in 2012.
, is located in the center; it was
inaugurated in 2012. -
The MAGIC observatory (Fig. 4.57) in the Canary Island of La Palma is a twin telescope system; each parabola has a diameter of 17 m and a reflecting surface of 236 m
 .
. -
VERITAS is constituted by an array of four telescopes with a diameter of 12 m and is located near Tucson, Arizona. It is operational since April 2007.
These instruments are managed by international collaborations of some 150 scientists.
Typical sensitivities of H.E.S.S.,
MAGIC, and VERITAS are such that a source less than 1% of the flux
of the Crab Nebula can be detected at a 5 significance in 50 h of
observation.
significance in 50 h of
observation.
An overlap in the regions of the sky explored by the IACTs allows an almost continuous observation of sources placed at midlatitude; there is, however, space for two more installations, one in South America and one (MACE, in construction) in India.

One of the MAGIC telescopes.
Credit: Robert Wagner, University of Stockholm
A comparison of the characteristics of Fermi, the IACTs and of the EAS particle detector arrays. Sensitivity computed over one year for Fermi and the EAS, and over 50 h for the IACTs
|
Quantity |
Fermi |
IACTs |
EAS |
|---|---|---|---|
|
Energy range |
20 MeV–200 GeV |
100 GeV–50 TeV |
400 GeV–100 TeV |
|
Energy res. |
5–10% |
15–20% |
|
|
Duty cycle |
80% |
15% |
>90% |
|
FoV |
|
5 |
|
|
PSF (deg) |
0.1 |
0.07 |
0.5 |
|
Sensitivity |
1% Crab (1 GeV) |
1% Crab (0.5 TeV) |
0.5 Crab (5 TeV) |
4.5.3.3 Summary of the Performance of Gamma-Ray Detectors
A simplified comparison of the characteristics of the Fermi LAT satellite detector, of the IACTs and of the EAS detectors (ground-based), is shown in Table 4.5. The sensitivities of the above described high-energy detectors are shown in Fig. 4.58.
A Cherenkov Telescope: MAGIC. We shall now describe in larger detail one of the Cherenkov telescopes: MAGIC. The MAGIC experiment, located at an altitude of 2200 m a.s.l. on the Canary island of La Palma, is composed of two 17 m diameter IACTs devoted to the observation of VHE gamma rays with a lower energy threshold of 30 GeV. The first of the MAGIC telescopes started operations in 2004; the second was built some years later allowing stereo observations since autumn 2009.
MAGIC II was constructed like a
copy of MAGIC I with a few improvements. Both are built using
a lightweight carbon-fiber structure, and the size of the mirror
dish (17 m diameter) and the camera field of view
(3.5 ) are the same. Each MAGIC camera is
composed of 1039
) are the same. Each MAGIC camera is
composed of 1039  hexagonal pixels (a hexagonal
reflecting cone, called Winston cone, collecting the light onto a
photomultiplier).
hexagonal pixels (a hexagonal
reflecting cone, called Winston cone, collecting the light onto a
photomultiplier).
The reflectors are made of square
mirrors with a curved surface; each mirror is 1 m in size. Their position can be
corrected thanks to an automatic mirror control (AMC) in such a way that they point to the focal
camera.
in size. Their position can be
corrected thanks to an automatic mirror control (AMC) in such a way that they point to the focal
camera.
In both telescopes the signals from the PMT in each pixel are optically transmitted to the countinghouse where trigger and digitization of the signals take place. The signals of both telescopes are digitized using a frequency of 2 GSample/s.

Point source continuum differential
sensitivity of different X- and  -ray instruments. The curves for
INTEGRAL/JEM-X, IBIS (ISGRI and
PICsIT), and SPI are for an effective observation time
-ray instruments. The curves for
INTEGRAL/JEM-X, IBIS (ISGRI and
PICsIT), and SPI are for an effective observation time  Ms. The COMPTEL and EGRET
sensitivities are given for the typical observation time
accumulated during the
Ms. The COMPTEL and EGRET
sensitivities are given for the typical observation time
accumulated during the  9 years of the CGRO mission. The
Fermi/LAT sensitivity is for a
high Galactic latitude source in 10 years of observation in survey
mode. For MAGIC, H.E.S.S./VERITAS, and CTA, the sensitivities are
given for
9 years of the CGRO mission. The
Fermi/LAT sensitivity is for a
high Galactic latitude source in 10 years of observation in survey
mode. For MAGIC, H.E.S.S./VERITAS, and CTA, the sensitivities are
given for  h. For HAWC
h. For HAWC  year, for LHAASO
year, for LHAASO  year, and for HiSCORE
year, and for HiSCORE
 h. The e-ASTROGAM sensitivity is
calculated at
h. The e-ASTROGAM sensitivity is
calculated at  for an effective exposure of 1 year
and for a source at high Galactic latitude. Compilation by V.
Tatischeff
for an effective exposure of 1 year
and for a source at high Galactic latitude. Compilation by V.
Tatischeff
4.5.3.4 Future Detectors for High-Energy Photons
It is difficult to think for this century of an instrument for GeV photons improving substantially the performance of the Fermi LAT: the cost of space missions is such that the size of Fermi cannot be reasonably overcome with present technologies. New satellites already approved (like the Chinese-Italian mission HERD, for which launch is expected after 2024) will improve some of the aspects of Fermi, – in this particular case, calorimetry.
-
keV astrophysics. The launch of ATHENA is foreseen in 2028 and will improve the sensitivity by two orders of magnitude.
-
MeV astrophysics. The possible launches of e-ASTROGAM and/or AMEGO in 2028/29 will improve the sensitivity by two orders of magnitude, with a comparable improvement in the quality of data (localization accuracy, measurement of polarization, etc.).
-
TeV gamma-ray astrophysics. VHE gamma-ray astrophysics in the current era has been dominated by Cherenkov telescopes. We know today that the previous generation EAS telescopes were underdimensioned in relation to the strength of the sources.
The research in the future will push both on EAS and IACT, which have mutual advantages and disadvantages. The sensitivities of the main present and future detectors are illustrated in Fig. 4.58. We have already seen the characteristics of HAWC, which is under upgrade with the construction of an outrigger; a very large Cherenkov Telescope Array (CTA) is also in construction.
The CTA is a future observatory for VHE gamma-ray astrophysics that is expected to provide an order of magnitude improvement in sensitivity over existing instruments.
An array of tens of telescopes will detect gamma-ray-induced showers over a large area on the ground, increasing the efficiency and the sensitivity, while providing a much larger number of views of each cascade. This will result in both improved angular resolution and better suppression of charged cosmic-ray background events. Three types of telescopes are foreseen:-
The low-energy (the goal is to detect showers starting from an energy of 20 GeV) instrumentation will consist of 23 m large-size telescopes (LST) with a FoV of about 4–5
 .
. -
The medium energy range, from around 100 GeV–1 TeV, will be covered by medium-size telescopes (MST) of the 12 m class with a FoV of 6–8
 .
. -
The high-energy instruments, dominating the performance above 10 TeV, will be small size (SST, 4–6 m in diameter) telescopes with a FoV of around 10
 .
.
CTA will be deployed in two sites. The Southern hemisphere site is less than 10 km from the Paranal Observatory in the Atacama Desert in Chile; it will cover about three square kilometers of land with telescopes that will monitor all the energy ranges in the center of the Milky Way’s Galactic plane. It will consist of all three types of telescopes with different mirror sizes (4 LSTs, 25 MSTs, and 70 SSTs in the present design). The Northern hemisphere site is located on the existing Roque de los Muchachos Observatory on the Canary island of La Palma, close to MAGIC; only the two larger telescope types (4 LSTs and 15 MSTs in the present design) would be deployed, on a surface of about one square kilometer. These telescopes will be mostly targeted at extragalactic astronomy. The telescopes of different sizes will be arranged in concentric circles, the largest in the center (Fig. 4.59).
Different modes of operation will be possible for CTA: deep field observation; pointing mode; scanning mode—also pointing to different targets.
-
-
PeV gamma-ray astrophysics. Besides LHAASO, already in construction in the Northern hemisphere, another large-FoV detector is in construction in Russia, called HiSCORE (Hundred Square-km Cosmic ORigin Explorer). Together with a system of Cherenkov telescopes, HiSCORE should form the hybrid array TAIGA. There is a strong case for a PeV wide-FoV detector in the Southern hemisphere in order to study the highest-energy emissions of accelerators in the Galaxy. Several collaborations are proposing designs for such a detector, and convergence could be reached in the next years.

Left: Possible layout of the CTA. Right: Project of the large telescope (LST).
Credit: CTA Collaboration
4.5.4 Neutrino Detection
The energy spectrum of neutrinos
interesting for particle and astroparticle physics spans more than
20 orders of magnitude, from the  2 K (
2 K ( 0.2 meV) of relic neutrinos from
the big bang, to the MeV of reactors, to the few MeV of the solar
neutrinos, to the few GeV of the neutrinos produced by the
interaction of cosmic rays with the atmosphere (atmospheric
neutrinos), to the region of extremely high energy where the
production from astrophysical sources is dominant. We concentrate
here on the detection of neutrinos of at least some MeV, and we
present some of the most important neutrino detectors
operating.
0.2 meV) of relic neutrinos from
the big bang, to the MeV of reactors, to the few MeV of the solar
neutrinos, to the few GeV of the neutrinos produced by the
interaction of cosmic rays with the atmosphere (atmospheric
neutrinos), to the region of extremely high energy where the
production from astrophysical sources is dominant. We concentrate
here on the detection of neutrinos of at least some MeV, and we
present some of the most important neutrino detectors
operating.
Since neutrino cross section is small, it is important that neutrino detectors be located underground or underwater to shield from cosmic rays.
4.5.4.1 MeV Neutrinos
Detectors of neutrinos in the MeV range
mostly use the detection of the products of induced  decays. The first setups used a
solution of cadmium chloride in water and two scintillation
detectors as a veto against charged cosmic rays. Antineutrinos with
an energy above the 1.8 MeV threshold can cause inverse beta
decay interactions with protons in water, producing a positron
which in turn annihilates, generating photon pairs that can be
detected.
decays. The first setups used a
solution of cadmium chloride in water and two scintillation
detectors as a veto against charged cosmic rays. Antineutrinos with
an energy above the 1.8 MeV threshold can cause inverse beta
decay interactions with protons in water, producing a positron
which in turn annihilates, generating photon pairs that can be
detected.
Radiochemical chlorine detectors
consist instead of a tank filled with a chlorine solution in a
fluid. A neutrino converts a  Cl atom into a
Cl atom into a  Ar; the threshold neutrino energy for
this reaction is 0.814 MeV. From time to time the argon atoms
are counted to measure the number of radioactive decays. The first
detection of solar neutrinos was achieved using a chlorine detector
containing 470 tons of fluid in the former Homestake Mine near
Lead, South Dakota. This measurement evidenced a deficit of
electron neutrinos from what expected by the power radiated from
the Sun. For this discovery the leader of the experiment, Ray
Davis, won the Nobel Prize in
physics.19 A similar detector design, with a lower
detection threshold of 0.233 MeV, uses the
Ga
Ar; the threshold neutrino energy for
this reaction is 0.814 MeV. From time to time the argon atoms
are counted to measure the number of radioactive decays. The first
detection of solar neutrinos was achieved using a chlorine detector
containing 470 tons of fluid in the former Homestake Mine near
Lead, South Dakota. This measurement evidenced a deficit of
electron neutrinos from what expected by the power radiated from
the Sun. For this discovery the leader of the experiment, Ray
Davis, won the Nobel Prize in
physics.19 A similar detector design, with a lower
detection threshold of 0.233 MeV, uses the
Ga  Ge transition.
Ge transition.
4.5.4.2 MeV to GeV Neutrinos
Probably the most important results in the sector of MeV to GeV neutrinos in the recent years are due to a Cherenkov-based neutrino detector, Kamiokande, in Japan. We give here a short description of this detector in its present version, called Super-Kamiokande.

The Super-Kamiokande detector.
Credit: Super-Kamiokande Collaboration
Super-K (Fig. 4.60) consists of a cylindrical tank about 40 m tall and 40 m in diameter containing 50 000 tons of ultrapure water. The volume is divided by a stainless steel structure into an inner detector (ID) region (33.8 m in diameter and 36.2 m in height) and an outer detector (OD) consisting of the remaining tank volume. Mounted on the structure are about 11 000 PMT 50 cm in diameter that face the ID and 2000 20 cm PMT facing the OD.
The interaction of a neutrino with the electrons or nuclei in the water can produce a superluminal charged particle generating Cherenkov radiation, which is projected as a ring on the wall of the detector and recorded by a PMT. The information recorded is the timing and charge information by each PMT, from which one can reconstruct the interaction vertex, the direction and the size of the cone.
Typical threshold for the detection of electron neutrinos is of about 6 MeV. Electrons lose quickly their energy, and, if generated in the ID, are likely to be fully contained (not penetrating inside the OD). Muons instead can penetrate, and the muon events can be partially contained (or not) in the detector. The threshold for the detection of muon neutrinos is about 2 GeV.
A new detector called Hyper-Kamiokande is envisaged, with a volume 20 times larger than Super-Kamiokande. Construction is expected to start around 2020, and to take about seven years.
The
SNO Detector. The Sudbury Neutrino Observatory (SNO) used
1000 tons of heavy water (D O) contained in a 12 m diameter
spherical vessel surrounded by a cylinder of ordinary water,
22 m in diameter and 34 m high. In addition to the
neutrino interactions visible in a detector as SK, the presence of
deuterium allows the reaction producing a neutron, which is
captured releasing a gamma-ray that can be detected. SNO was
recently upgraded to SNO+, using the same sphere filled with a
liquid scintillator (linear alkylbenzene) to act as detector and
target material.
O) contained in a 12 m diameter
spherical vessel surrounded by a cylinder of ordinary water,
22 m in diameter and 34 m high. In addition to the
neutrino interactions visible in a detector as SK, the presence of
deuterium allows the reaction producing a neutron, which is
captured releasing a gamma-ray that can be detected. SNO was
recently upgraded to SNO+, using the same sphere filled with a
liquid scintillator (linear alkylbenzene) to act as detector and
target material.
4.5.4.3 Very-High-Energy Neutrinos
Very-high-energy neutrinos are expected to be produced in astrophysical objects by the decays of charged pions produced in primary cosmic ray interactions with radiation or molecular clouds in astrophysical objects (this is called “hadronic” mechanism). As these pions decay, they produce neutrinos with typical energies one order of magnitude smaller than those of the cosmic-ray nucleons—more or less the same energies as photons. These neutrinos can travel long distances undisturbed by either the absorption experienced by high-energy photons or the magnetic deflection experienced by charged particles, making them a unique tracer of cosmic-ray acceleration. Additional sources can be the interactions of cosmic rays with the atmosphere (atmospheric neutrinos), and decays of heavier particles formed by the interaction of cosmic rays with the CMB, or decays of new, heavy particles.
Above an energy of 100 TeV, the expected atmospheric neutrino background falls to the level of one event per year per cubic kilometer, and any (harder) astrophysical flux can be clearly seen.
The challenge in the field of UHE neutrinos is to build telescopes with good enough sensitivity to see events, since the flux is expected to be lower than the photon flux (the main mechanism for the production of neutrinos, i.e., the hadronic mechanism, is common to photons, which in addition can be produced via a “leptonic” mechanism, as we shall see in Chap. 10). This requires instrumenting very large volumes. Efforts to use large quantities of water and ice as detectors are ongoing. Several experiments are completed, operating, or in development using Antarctic ice, the oceans, and lakes, with detection methods including optical and coherent radio detection as well as particle production.
Among the experiments in operation, the largest sensitivity detectors are Baikal NT-200 and IceCube.

The
IceCube Experiment. IceCube, a cube of
1 km instrumented in the Antarctica ices,
has been in operation at the South Pole since 2010
(Fig. 4.61). The telescope views the ice through
approximately 5160 sensors called digital optical modules (DOMs).
The DOMs are attached to vertical strings, frozen into 86
boreholes, and arrayed over a cubic kilometer from 1 450 to
2 450 m depth. The strings are deployed on a hexagonal
grid with 125 m spacing and hold 60 DOMs each. The vertical
separation of the DOMs is 17 m. Eight of these strings at the
center of the array were deployed more compactly, with a horizontal
separation of about 70 m and a vertical DOM spacing of
7 m. This denser configuration forms the DeepCore subdetector,
which lowers the neutrino energy threshold to about 10 GeV,
creating the opportunity to study neutrino oscillations. At the
surface, an air shower array is coupled to the detector. As the
Earth is opaque to UHE neutrinos, detection of extremely
high-energy neutrinos must come from neutrinos incident at or above
the horizon, while intermediate energy neutrinos are more likely to
be seen from below.
instrumented in the Antarctica ices,
has been in operation at the South Pole since 2010
(Fig. 4.61). The telescope views the ice through
approximately 5160 sensors called digital optical modules (DOMs).
The DOMs are attached to vertical strings, frozen into 86
boreholes, and arrayed over a cubic kilometer from 1 450 to
2 450 m depth. The strings are deployed on a hexagonal
grid with 125 m spacing and hold 60 DOMs each. The vertical
separation of the DOMs is 17 m. Eight of these strings at the
center of the array were deployed more compactly, with a horizontal
separation of about 70 m and a vertical DOM spacing of
7 m. This denser configuration forms the DeepCore subdetector,
which lowers the neutrino energy threshold to about 10 GeV,
creating the opportunity to study neutrino oscillations. At the
surface, an air shower array is coupled to the detector. As the
Earth is opaque to UHE neutrinos, detection of extremely
high-energy neutrinos must come from neutrinos incident at or above
the horizon, while intermediate energy neutrinos are more likely to
be seen from below.
IceCube detects a dozen of very-high-energy events per year consistent with astrophysical sources. The IceCube sensitivity will soon reach the high-energy neutrino fluxes predicted in cosmogenic neutrino models.
KM3NeT. A large underwater neutrino detector, KM3NeT, is planned. KM3NeT will host a neutrino telescope with a volume of several cubic kilometers at the bottom of the Mediterranean sea. This telescope is foreseen to contain of the order of 12 000 pressure-resistant glass spheres attached to about 300 detection units—vertical structures with nearly one kilometer in height. Each glass sphere will contain 31 photomultipliers and be connected to shore via a high-bandwidth optical link. At shore, a computer farm will perform the first data filtering in the search for the signal of cosmic neutrinos. KM3NeT builds on the experience of three pilot projects in the Mediterranean sea: the ANTARES detector near Marseille, the NEMO project in Sicily, and the NESTOR project in Greece. ANTARES was completed in 2008 and is the largest neutrino telescope in the Northern hemisphere.
4.6 Detection of Gravitational Waves
Gravitational waves are generated by
aspherical motions of matter distributions; they propagate at the
speed of light, bringing curvature of space–time information. Their
effect on matter is to change the relative distances. This effect
is however small, and even the most violent astrophysical phenomena
(e.g., colliding black holes or neutron stars, collapsing stars)
emit gravitational waves which, given the typical distance to the
event, are expected to cause relative shifts on distances of only
10 on Earth. In fact, gravitational
waves were predicted by Albert Einstein in his theory of general
relativity roughly 100 years ago, but only recently has
technology enabled us to detect them.
on Earth. In fact, gravitational
waves were predicted by Albert Einstein in his theory of general
relativity roughly 100 years ago, but only recently has
technology enabled us to detect them.
 :
:

 is its variation. Another one is the
horizon distance, i.e., the maximum range out to which it could see
the coalescence of two 1.4
is its variation. Another one is the
horizon distance, i.e., the maximum range out to which it could see
the coalescence of two 1.4  neutron stars.
neutron stars.The idea explored first to detect
gravitational waves was to detect the elastic energy induced by the
compression/relaxation of a metal bar due to the
compression/relaxation of distance. Detectors were metal cylinders,
and the energy converted to longitudinal oscillations of the bar
was measured by piezoelectric transducers. The first large
gravitational wave detector, built by Joseph Weber in the early
1960s, was a 1.2 ton aluminum cylindrical bar of 1.5 m length
and 61 cm diameter (Fig. 4.62) working at room
temperature and isolated as much as possible from acoustic and
ground vibrations. The mechanical oscillation of the bar was
translated into electric signals by piezoelectric sensors placed in
its surface close to the central region. The detector behaved as a
narrow band high (quality factor) mechanical resonator
with a central frequency of about 1600 Hz. The attenuation of
the oscillations is, in such devices, very small and therefore the
bar should oscillate for long periods well after the excitation
induced by the gravitational waves. The sensitivity of Weber’s
gravitational antenna was of the order of
(quality factor) mechanical resonator
with a central frequency of about 1600 Hz. The attenuation of
the oscillations is, in such devices, very small and therefore the
bar should oscillate for long periods well after the excitation
induced by the gravitational waves. The sensitivity of Weber’s
gravitational antenna was of the order of  over timescales of
over timescales of  s. Bar detectors (ALLEGRO,
AURIGA, Nautilus, Explorer, Niobe) reached sensitivities of
s. Bar detectors (ALLEGRO,
AURIGA, Nautilus, Explorer, Niobe) reached sensitivities of
 , thanks to the introduction of
cryogenic techniques which allow for a substantial reduction in the
thermal noise as well as the use of very performing superconducting
sensors. However, their frequency bandwidths remain very narrow
, thanks to the introduction of
cryogenic techniques which allow for a substantial reduction in the
thermal noise as well as the use of very performing superconducting
sensors. However, their frequency bandwidths remain very narrow
 tens of Hz) and the resonant
frequencies (
tens of Hz) and the resonant
frequencies ( 1 kHz) correspond typically to
acoustic wavelengths of the order of the detector length. A further
increase in sensitivity implies a particular attention to the
quantum noise, and thus a considerable increase of the detector
mass (bars with hundred tons of mass are being considered).
1 kHz) correspond typically to
acoustic wavelengths of the order of the detector length. A further
increase in sensitivity implies a particular attention to the
quantum noise, and thus a considerable increase of the detector
mass (bars with hundred tons of mass are being considered).
 correspond to interferences over
distances many orders of magnitude (
correspond to interferences over
distances many orders of magnitude ( 10
10 –10
–10 ) smaller than the dimension of an
atom, and thus both the stability of the laser beam and the control
of all possible noise sources are critical.
) smaller than the dimension of an
atom, and thus both the stability of the laser beam and the control
of all possible noise sources are critical.

Joseph Weber working on his gravitational antenna (1965).
-
The thermal noise is associated to the Brownian motion of the test masses due to the impact of the surrounding air molecules, to their internal vibrations, and to the mirror suspensions. To minimize such effects the rest masses should be placed in a high vacuum environment and the frequencies of the intrinsic resonances of the system should be set as far as possible from the target signal frequency band.
-
The intrinsic readout noise is due to the fluctuations induced by the quantum nature of the interaction of the laser light beams with the mirrors. The light beams may be modeled as discrete sets of photons obeying in their arrival time to the mirror to Poisson statistics. The number of photons measured in a time window has a statistical intrinsic fluctuation (“shot noise”); its effects on sensitivity decrease with the increase of the laser power. On the other hand, the increase of the laser power increases the momentum transfer to the mirrors (“radiation pressure”), which will change the phase of the beams. To minimize such contradictory effects, the tests masses should be as heavy as possible and the Heisenberg uncertainties relations (the quantum limit) carefully handled.
-
The seismic noise accounts for all the natural or human-made perturbations comprising a large range of diversified phenomena like earthquakes, environment perturbations or nearby automobile traffic. The measured spectrum of such noise, in a quiet location, decreases with the frequency and imposes already an important sensitivity constraint to the next generation of laser interferometer detectors. To minimize such effects, the test masses are isolated from ground through several attenuation stages characterized by resonance frequencies much lower than the expected signal frequencies. To access lower frequencies (1–10 Hz), the possibility to build large interferometers underground in a low seismic region is being studied. To go further into the 10
 –10
–10 Hz region it will be necessary to
build a large arm interferometer in space.
Hz region it will be necessary to
build a large arm interferometer in space.

Sketch of a Michelson interferometer. A monochromatic laser light is split into two beams which travel along the two perpendicular arms. The laser light moves back and forth in the two arms between the two mirrors depicted as test masses (Fabry–Perot cavity) and is then made to combine again to form an interference pattern. A gravitational wave passing through (also depicted in the figure) will change the length of one arm with respect to the other, causing relative phase shift of the laser light and thus in the interference pattern.
Credit: LIGO Collaboration

Proposed LISA detector (the size is increased by a factor of 10). From M. Pitkin et al., “Gravitational Wave Detection by Interferometry (Ground and Space),” http://www.livingreviews.org/lrr-2011-5
The largest gravitational wave observatories operating at present are the Laser Interferometer Gravitational Wave Observatory (LIGO) and Virgo. LIGO is built over two sites in the US (at Hanford, Washington, and at Livingston, Louisiana, 3 000 km apart), each one with a 4 km arm interferometer, while Virgo is installed near Pisa, Italy, and consists of a 3 km arm interferometer. A Japanese underground detector known as KAGRA which is 3 km in arm length is being commissioned and should start operating in 2019. A third LIGO detector is planned to be built in India before 2024. A close collaboration among all the gravitational waves observatories is in place.
The first detection of gravitational
waves was performed by LIGO in 2015; the signal was generated by
two black holes with, respectively, 36 and 29 solar masses that
merged into a 62 solar masses BH, thus releasing an energy
corresponding to 3  mostly in gravitational waves. Now we
have a handful of signals of different phenomena, as we shall
discuss in Chap. 10.
mostly in gravitational waves. Now we
have a handful of signals of different phenomena, as we shall
discuss in Chap. 10.
The development of new detectors (e.g.,
interferometers in space) will allow us to explore different
frequency bands, and to detect gravitational waves generated by
different astrophysical processes. In a more distant future a space
observatory will be built extending the detection sensitivity to a
much lower frequency range (10 –10
–10 Hz). The LISA project, comprising three satellite
detectors spaced by more than 2.5 million kilometers
(Fig. 4.64), has been approved by ESA; launch is
scheduled for the year 2034. Meanwhile a LISA Pathfinder mission
was launched and demonstrated the feasibility to achieve the
low-frequency noise requirements of the LISA mission.
Hz). The LISA project, comprising three satellite
detectors spaced by more than 2.5 million kilometers
(Fig. 4.64), has been approved by ESA; launch is
scheduled for the year 2034. Meanwhile a LISA Pathfinder mission
was launched and demonstrated the feasibility to achieve the
low-frequency noise requirements of the LISA mission.

Present and expected sensitivities of gravitational wave detectors.
From M. Hendry and G. Woan, Astronomy and Geophysics 48 (2007) 1
Further Reading
- [F4.1]
-
B. Rossi, “High-Energy Particles,” Prentice-Hall, New York 1952. Still a fundamental book on particle detection, in particular related to the interaction of particles with matter and to multiplicative showers.
- [F4.2]
-
K. Kleinknecht, “Detectors for Particle Radiation” Cambridge University Press 1986.
- [F4.3]
-
W.R. Leo, “Techniques for Nuclear and Particle Physics Experiments,” Springer Verlag 1994.
Exercises
- 1.
Muon energy loss. A muon of 100 GeV crosses a layer of 1 m of iron. Determine the energy loss and the expected scattering angle.
- 2.
Energy loss in a water Cherenkov detector. In the Pierre Auger Observatory the surface detectors are composed of water Cherenkov tanks 1.2 m high, each containing 12 tons of water. These detectors are able to measure the light produced by charged particles crossing them. Consider one tank crossed by a single vertical muon with an energy of 5 GeV. The refraction index of water is
 and can be in good approximation
considered constant for all the relevant photon wavelengths.
Determine the energy lost by ionization, and compare it with the
energy lost by Cherenkov emission.
and can be in good approximation
considered constant for all the relevant photon wavelengths.
Determine the energy lost by ionization, and compare it with the
energy lost by Cherenkov emission. - 3.
Cherenkov radiation. A proton with momentum 1.0 GeV/c passes through a gas at high pressure. The refraction index of the gas can be changed by changing the pressure. Compute: (a) the minimum refraction index at which the proton will emit Cherenkov radiation; (b) the Cherenkov radiation emission angle when the refraction index of the gas is 1.6.
- 4.
Pair production and multiple scattering. What is the optimal thickness (in radiation lengths) of a layer of silicon in a gamma-ray telescope with hodoscopic structure in order that the multiple scattering does not deteriorate the information from the opening angle of the electron-positron pair in a photon conversion?
- 5.
Compton scattering. A photon of wavelength
 is scattered off a free electron
initially at rest. Let
is scattered off a free electron
initially at rest. Let  be the wavelength of the photon
scattered in the direction
be the wavelength of the photon
scattered in the direction  . Compute: (a)
. Compute: (a)  as a function of
as a function of  ,
,  and universal parameters; (b) the
kinetic energy of the recoiling electron.
and universal parameters; (b) the
kinetic energy of the recoiling electron. - 6.
Reconstruction of a Compton interaction event. Detecting gamma rays by Compton scattering in a gamma-ray telescope with hodoscopic structure (Fig. 4.48) is more complicated than for pair production. The Compton scattering of the incident photon occurs in one of the tracker planes, creating an electron and a scattered photon. The tracker measures the interaction location, the electron energy, and in some cases the electron direction. The scattered photon can be absorbed in the calorimeter where its energy and absorption position are measured.
Suppose that an incident gamma-ray Compton scatters by an angle
 in one layer of the tracker,
transferring energy
in one layer of the tracker,
transferring energy  to an electron. The scattered photon
is then absorbed in the calorimeter, depositing its energy
to an electron. The scattered photon
is then absorbed in the calorimeter, depositing its energy
 . Demonstrate that the scattering
angle is given by
. Demonstrate that the scattering
angle is given by  , where
, where  is the electron mass. With this
information, one can derive an “event circle” from which the
original photon arrived—this sort of Compton events are called
“untracked.” Multiple photons from the same source enable a full
deconvolution of the image, using probabilistic techniques.
is the electron mass. With this
information, one can derive an “event circle” from which the
original photon arrived—this sort of Compton events are called
“untracked.” Multiple photons from the same source enable a full
deconvolution of the image, using probabilistic techniques.For energetic incident gamma rays (above
 1 MeV), measurement of the track
of the scattered electron might in addition be possible, resulting
in a reduction of the event circle to a definite direction. If the
scattered electron direction is measured, the event circle reduces
to an event arc with length due to the uncertainty in the electron
direction reconstruction, allowing improved source localization.
This event is called “tracked,” and its direction reconstruction is
somewhat similar to that for pair event—the primary photon
direction is reconstructed from the direction and energy of two
secondary particles: scattered electron and photon. Comment.
1 MeV), measurement of the track
of the scattered electron might in addition be possible, resulting
in a reduction of the event circle to a definite direction. If the
scattered electron direction is measured, the event circle reduces
to an event arc with length due to the uncertainty in the electron
direction reconstruction, allowing improved source localization.
This event is called “tracked,” and its direction reconstruction is
somewhat similar to that for pair event—the primary photon
direction is reconstructed from the direction and energy of two
secondary particles: scattered electron and photon. Comment. - 7.
Nuclear reactions. The mean free path of fast neutrons in lead is of the order of 5 cm. What is the total fast neutron cross section in lead?
- 8.
Range. Compare approximately the ranges of two particles of equal velocity and different mass and charge traveling through the same medium.
- 9.
Hadron therapy. The use of proton and carbon ion beams for cancer therapy can reduce the complications on the healthy tissue compared to the irradiation with MeV gamma rays. Discuss why.
- 10.
Neutrino interaction in matter. For neutrinos produced in nuclear reactors typical energies are
 MeV. What is the probability to
interact in a water detector with the thickness of one meter? What
is the probability to interact inside the Earth traveling along a
trajectory that passes through its center? Answer the same
questions for a neutrino of energy 1 PeV.
MeV. What is the probability to
interact in a water detector with the thickness of one meter? What
is the probability to interact inside the Earth traveling along a
trajectory that passes through its center? Answer the same
questions for a neutrino of energy 1 PeV. - 11.
Electromagnetic showers. How does an electromagnetic shower evolve as a function of the penetration depth in a homogeneous calorimeter? What is the difference between an incoming photon and an incoming electron/positron?
- 12.
Hadronic showers. Let us approximate the effective cross section for protons on nucleons in air with a value of 20 mb. Calculate the interaction length of a proton (in g/cm
 , and in meters at NTP). What is the
average altitude above the sea level where this interaction takes
place? In hadronic showers we find also an electromagnetic
component, and muons. Where do these come from?
, and in meters at NTP). What is the
average altitude above the sea level where this interaction takes
place? In hadronic showers we find also an electromagnetic
component, and muons. Where do these come from? - 13.
Tracking detectors. Could you build a tracking detector for photons? And for neutrinos?
- 14.
Photodetectors. What gain would be required from a photomultiplier in order to resolve the signal produced by three photoelectrons from that due to two or four photoelectrons? Assume that the fluctuations in the signal are described by Poisson statistics, and consider that two peaks can be resolved when their centers are separated by more than the sum of their standard deviations.
- 15.
Cherenkov counters. Estimate the minimum length of a gas Cherenkov counter used in the threshold mode to be able to distinguish between pions and kaons with momentum 20 GeV. Assume that 200 photons need to be radiated to ensure a high probability of detection and that radiation covers the whole visible spectrum (neglect the variation with wavelength of the refractive index of the gas).
- 16.
Electromagnetic calorimeters. Electromagnetic calorimeters have usually 20 radiation lengths of material. Calculate the thickness (in cm) for calorimeters made of BGO, PbWO
 (as in the CMS experiment at the
LHC), uranium, iron, tungsten, and lead. Take the radiation lengths
from Appendix B or from the Particle Data Book.
(as in the CMS experiment at the
LHC), uranium, iron, tungsten, and lead. Take the radiation lengths
from Appendix B or from the Particle Data Book. - 17.
The HERA collider. The HERA accelerator collided protons at energy
 820 GeV with electrons at
820 GeV with electrons at
 820 GeV. Which value of
820 GeV. Which value of
 would be needed to obtain the same
center-of-mass energy at an ep
fixed-target experiment?
would be needed to obtain the same
center-of-mass energy at an ep
fixed-target experiment? - 18.
The LHC collider. What is the maximum energy for a tunnel 27 km long with a maximum magnetic field in the vacuum tube of 8.36 T?
- 19.
Focusing in the LHC. The diameter of the vacuum tube in the LHC is 18 mm. How many turns and for how long can a proton beam stay vertically in the tube if you do not focus it?
- 20.
Collisions in the LHC. In the LHC ring there are 2835 bunches in each ring which collide with each other once in each detector. How many collisions of bunches are there in
- (a)
one second,
- (b)
one run which will last about 10 h?
- (a)
- 21.
Luminosity. How much integrated luminosity does an experiment need to collect in order to measure at better than 1% the rate of a process with cross section of 1 pb?
- 22.
Luminosity measurement at the LEP collider. The luminosity at the Large Electron–Positron Collider (LEP) was determined by measuring the elastic
 scattering (Bhabha scattering) as its
cross section at low angles is well known from QED. In fact,
assuming small polar angles, the Bhabha scattering cross section
integrated between a polar angle
scattering (Bhabha scattering) as its
cross section at low angles is well known from QED. In fact,
assuming small polar angles, the Bhabha scattering cross section
integrated between a polar angle  and
and  is given at first order by
Determine the luminosity of a run of LEP knowing that this run lasted 4 h, and the number of identified Bhabha scattering events was 1200 in the polar range of
is given at first order by
Determine the luminosity of a run of LEP knowing that this run lasted 4 h, and the number of identified Bhabha scattering events was 1200 in the polar range of
![$$\theta \in [29; 185]$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_4_Chapter/304327_2_En_4_Chapter_TeX_IEq424.png) mrad. Take into account a
detection efficiency of 95% and a background of 10% at
mrad. Take into account a
detection efficiency of 95% and a background of 10% at  .
. - 23.
Luminosity and cross section. The cross section of a reaction to produce the Z boson at the LEP
 collider is 32 nb at the beam
energy 91 GeV. How long did LEP have to wait for the first
event if the luminosity was
collider is 32 nb at the beam
energy 91 GeV. How long did LEP have to wait for the first
event if the luminosity was  cm
cm s
s ?
? - 24.
Synchrotron radiation. Consider a circular synchrotron of radius
 which is capable of accelerating
charged particles up to an energy
which is capable of accelerating
charged particles up to an energy  . Compare the radiation emitted by a
proton and an electron and discuss the difficulties to accelerate
these particles with this technology.
. Compare the radiation emitted by a
proton and an electron and discuss the difficulties to accelerate
these particles with this technology. - 25.
Initial state radiation. The effective energy of the elastic
 scattering can be changed by the
radiation of a photon by the particles of the beam (initial state
radiation), which is peaked at very small angles. Supposing that a
measured
scattering can be changed by the
radiation of a photon by the particles of the beam (initial state
radiation), which is peaked at very small angles. Supposing that a
measured  pair has the following transverse
momenta:
pair has the following transverse
momenta:  GeV, and the radiated photon is
collinear with the beam and has an energy of 10 GeV, determine
the effective energy of the interaction of the electron and
positron in the center of mass,
GeV, and the radiated photon is
collinear with the beam and has an energy of 10 GeV, determine
the effective energy of the interaction of the electron and
positron in the center of mass,  . Consider that the beam was tuned for
. Consider that the beam was tuned for
 .
. - 26.
Bending radius of cosmic rays from the Sun. What is the bending radius of a solar proton, 1 MeV kinetic energy, in the Earth’s magnetic field (0.5 G), for vertical incidence with respect to the field?
- 27.
Low Equatorial Orbit. Low-Earth Orbits (LEOs) are orbits between 300 and 2000 km from the ground; the altitude is optimal in order to protect them from cosmic rays, thanks to the Van Allen radiation belts. Due to atmospheric drag, satellites do not usually orbit below 300 km. What is the velocity of an Earth satellite in a LEO and how does it compare to the escape velocity from Earth? How many revolutions per day does it make? Suppose that the satellite sees a solid angle of 2
 /5, and that it rolls: after how many
hours will it observe all the sky?
/5, and that it rolls: after how many
hours will it observe all the sky? - 28.
Electromagnetic showers in the atmosphere. If a shower is generated by a gamma ray of
 1 TeV penetrating the atmosphere
vertically, considering that the radiation length
1 TeV penetrating the atmosphere
vertically, considering that the radiation length  of air is approximately
37 g/cm
of air is approximately
37 g/cm and its critical energy
and its critical energy  is about 88 MeV, calculate the
height
is about 88 MeV, calculate the
height  of the maximum of the shower in the
Heitler model and in Rossi’s approximation B.
of the maximum of the shower in the
Heitler model and in Rossi’s approximation B. - 29.
Extensive electromagnetic air showers. The main characteristic of an electromagnetic shower (say, initiated by a photon) can be obtained using a simple Heitler model. Let
 be the energy of the primary particle
and consider that the electrons, positrons and photons in the
cascade always interact after traveling a certain atmospheric depth
be the energy of the primary particle
and consider that the electrons, positrons and photons in the
cascade always interact after traveling a certain atmospheric depth
 , and that the energy is always
equally shared between the two particles. With this assumptions, we
can schematically represent the cascade as in
Fig. 4.10.
, and that the energy is always
equally shared between the two particles. With this assumptions, we
can schematically represent the cascade as in
Fig. 4.10.- (a)
Write the analytical expressions for the number of particles and for the energy of each particle at depth X as a function of d, n and
 .
. - (b)
The multiplication of the cascade stops when the particles reach a critical energy,
 (when the decay probability surpasses
the interaction probability). Using the expressions obtained in the
previous question, write as a function of
(when the decay probability surpasses
the interaction probability). Using the expressions obtained in the
previous question, write as a function of  ,
,  and
and  , the expressions, at the shower
maximum, for:
, the expressions, at the shower
maximum, for:
- i.
the average energy of the particles,
- ii.
the number of particles,
 ,
, - iii.
the atmospheric depth,
 .
.
- i.
- (a)
- 30.
Extensive hadronic air showers. Consider a shower initiated by a proton of energy
 . We will describe it with a simple
Heitler-like model: after each depth d an equal number of pions,
. We will describe it with a simple
Heitler-like model: after each depth d an equal number of pions,  , of each of the 3 types is produced:
, of each of the 3 types is produced:
 ,
,  ,
,  . Neutral pions decay through
. Neutral pions decay through
 and their energy is transferred to
the electromagnetic cascade. Only the charged pions will feed the
hadronic cascade. We consider that the cascade ends when these
particles decay as they reach a given decay energy
and their energy is transferred to
the electromagnetic cascade. Only the charged pions will feed the
hadronic cascade. We consider that the cascade ends when these
particles decay as they reach a given decay energy  , after n interactions, originating a muon (plus
an undetected neutrino).
, after n interactions, originating a muon (plus
an undetected neutrino).- (a)
How many generations are needed to have more that
 of the primary energy,
of the primary energy,  in the electromagnetic component?
in the electromagnetic component? - (b)
Assuming the validity of the superposition principle, according to which a nucleus of mass number A and energy
 behaves like A nucleons of energy
behaves like A nucleons of energy  , derive expressions for:
, derive expressions for:
- i.
the depth where this maximum is reached,
 ,
, - ii.
the number of particles at the shower maximum,
 ,
, - iii.
the number of muons produced in the shower,
 .
.
- i.
- (a)
- 31.
Cherenkov telescopes. Suppose you have a Cherenkov telescope with 7 m diameter, and your camera can detect a signal only when you collect 100 photons from a source. Assuming a global efficiency of 0.1 for the acquisition system (including reflectivity of the surface and quantum efficiency of the PMT), what is the minimum energy (neglecting the background) that such a system can detect at a height of 2 km a.s.l.?
- 32.
Cherenkov telescopes and muon signals. Show that the image of the Cherenkov emission from a muon in the focal plane of a parabolic IACT is a conical section (approximate the Cherenkov angle as a constant).
- 33.
Imaging Atmospheric Cherenkov Telescopes. In the isothermal approximation, the depth x of the atmosphere at a height h (i.e., the amount of atmosphere above h) can be approximated aswith

 g/cm
g/cm . If a shower is generated by a gamma
ray of
. If a shower is generated by a gamma
ray of  TeV penetrating the atmosphere
vertically, considering that the radiation length
TeV penetrating the atmosphere
vertically, considering that the radiation length  of air is approximately
36.6 g/cm
of air is approximately
36.6 g/cm (440 m) and its critical energy
(440 m) and its critical energy
 is about 88 MeV and using Rossi’s
approximation B (Table 4.1):
is about 88 MeV and using Rossi’s
approximation B (Table 4.1):
- (a)
Calculate the height
 of the maximum of the shower in the
Heitler model and in Rossi’s approximation B.
of the maximum of the shower in the
Heitler model and in Rossi’s approximation B. - (b)
If 2000 useful Cherenkov photons per radiation length are emitted by charged particles in the visible and near UV, compute the total number
 of Cherenkov photons generated by the
shower (note: the critical energy is larger than the Cherenkov
threshold).
of Cherenkov photons generated by the
shower (note: the critical energy is larger than the Cherenkov
threshold). - (c)
Supposing that the Cherenkov photons are all emitted at the center of gravity of the shower (that in the Heitler approximation is just the maximum of the shower minus one radiation length), compute how many photons per square meter arrive to a detector at an altitude
 of 2000 m, supposing that the
average attenuation length of photons in air is 3 km, and that
the light pool can be derived by an opening angle of
of 2000 m, supposing that the
average attenuation length of photons in air is 3 km, and that
the light pool can be derived by an opening angle of  1.3
1.3 from the shower maximum
(1.3
from the shower maximum
(1.3 is the Cherenkov angle and
0.5
is the Cherenkov angle and
0.5 , to be added in quadrature, comes
from the intrinsic shower spread). Comment on the size of a
Cherenkov telescope, considering an average reflectivity of the
mirrors (including absorption in transmission) of 70%, and a
photodetection efficiency (including all the chains of acquisition)
of 20%.
, to be added in quadrature, comes
from the intrinsic shower spread). Comment on the size of a
Cherenkov telescope, considering an average reflectivity of the
mirrors (including absorption in transmission) of 70%, and a
photodetection efficiency (including all the chains of acquisition)
of 20%. - (d)
Redo the calculations for
 GeV, and comment.
GeV, and comment.
- (a)






































