5.1 A Zoo of Particles
In the beginning of the 1930s, just a few particles were
known: the proton and the electron, the charged constituents of the
atom; the neutron, which was ensuring the stability of the atomic
nuclei; the neutrino (predicted but by then not discovered yet),
whose existence was conjectured to guarantee the conservation of
energy and momentum in beta decays; and the photon, i.e., the
quantum of the electromagnetic field. Then, as we discussed in
Chap. 3, new and often unexpected particles
were discovered in cosmic rays: the positron, the antiparticle of
the electron; the muon, the heavy brother of the electron; the
charged pion, identified as the particle postulated by Yukawa as
the mediator of the strong interaction; the strange “V” particles
 and
and  (called “V” from the topology of
their decays in bubble chambers).
(called “V” from the topology of
their decays in bubble chambers).
 14 TeV with the Large Hadron Collider
(LHC) at CERN.
14 TeV with the Large Hadron Collider
(LHC) at CERN.

Livingston plot, representing the maximum energies attained by accelerators as a function of the year: original (left) and updated (right). For colliders, energies are translated into the laboratory system.
Original figures from M.S. Livingston and J.P. Blewett, “Particle Accelerators,” MacGraw Hill 1962; A. Chao et al. “2001 Snowmass Accelerator R&D Report,” eConf C010630 (2001) MT100
Accelerators provide the possibility to
explore in a systematic way the energy scale up to a few TeV,
and thanks to this a huge number of new particles have been
discovered. Already in the 1950s, many discoveries of particles
with different masses, spins, charges, properties took place. Their
names almost exhausted the Greek alphabet: these particles were
called  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 

Classifications had to be devised to put an order in such a complex zoology. Particles were first classified according to their masses in classes with names inspired, once again, to Greek words: heavy particles like the proton were called baryons ; light particles like the electron were called leptons ; and particles with intermediate masses were called mesons . The strict meaning of the class names was soon lost, and now we know a lepton, the tau, heavier than the proton. According to the present definition, leptons are those fermions (particles with half-integer spins) that do not interact strongly with the nuclei of atoms, while baryons are the fermions that do. Mesons are bosons (particles with integer spins) subject to strong interactions. Baryons and mesons interact thus mainly via the strong nuclear force and have a common designation of hadrons .
The detailed study of these particles
shows that there are several conserved quantities in their
interactions and decays. The total electric charge, for example, is
always conserved, but also the total number of baryons appears to
be conserved, and thus, the proton, being the lightest baryon,
cannot decay (the present experimental limit for the proton
lifetime is of about 10 years). Strange particles if they
decay by strong interactions give always birth to a lighter strange
particle, but the same is not true when they decay via weak
interactions. To each (totally or partially) conserved quantity, a
new quantum number was associated: baryons, for instance, have
“baryonic quantum number”
years). Strange particles if they
decay by strong interactions give always birth to a lighter strange
particle, but the same is not true when they decay via weak
interactions. To each (totally or partially) conserved quantity, a
new quantum number was associated: baryons, for instance, have
“baryonic quantum number”  (antibaryons have baryonic quantum number
(antibaryons have baryonic quantum number  , and mesons have baryonic quantum
number 0).
, and mesons have baryonic quantum
number 0).
As a consequence of baryon number
conservation, for example, the most economic way to produce an
antiproton in a proton–proton collision
is the reaction  . A proton beam with energy above the
corresponding kinematic threshold is needed to make this process
possible. The Bevatron, a proton synchrotron at the Lawrence
Berkeley National Laboratory providing beams with energy of
6.2 GeV, was designed for this purpose and started operation
in 1954. In the following year, Chamberlain, Segrè, Wiegand, and
Ypsilantis announced the discovery of the antiproton; the new
particle was identified by measuring its momentum and mass using a
spectrometer with a known magnetic field, a Cherenkov detector, and
a time-of-flight system. This discovery confirmed that indeed, as
predicted by the Dirac equation, to each particle corresponds an
oppositely charged particle with the same mass and spin.
. A proton beam with energy above the
corresponding kinematic threshold is needed to make this process
possible. The Bevatron, a proton synchrotron at the Lawrence
Berkeley National Laboratory providing beams with energy of
6.2 GeV, was designed for this purpose and started operation
in 1954. In the following year, Chamberlain, Segrè, Wiegand, and
Ypsilantis announced the discovery of the antiproton; the new
particle was identified by measuring its momentum and mass using a
spectrometer with a known magnetic field, a Cherenkov detector, and
a time-of-flight system. This discovery confirmed that indeed, as
predicted by the Dirac equation, to each particle corresponds an
oppositely charged particle with the same mass and spin.
The existence of particles and antiparticles is an example of symmetry, and symmetries became more and more present in the characterization of particles and of their interactions. Particle physicists had to study or reinvent group theory in order to profit of the possible simplifications guaranteed by the existence of symmetries.
5.2 Symmetries and Conservation Laws: The Noether Theorem
Being a part of the Universe, it is difficult to imagine how humans can expect to understand it. But we can simplify the representation of the Universe if we find that its description is symmetrical with respect to some transformations. For example, if the representation of the physical world is invariant with respect to translation in space, we can say that the laws of physics are the same everywhere, and this fact greatly simplifies our description of Nature.
 of the particles themselves, by their
momenta
of the particles themselves, by their
momenta  and by the potentials of the
interactions within the system. One way to express this is to use
the so-called Hamiltonian function
and by the potentials of the
interactions within the system. One way to express this is to use
the so-called Hamiltonian function


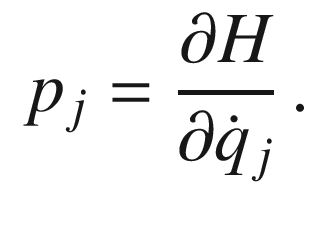



Symmetries of a Hamiltonian with respect to given operations entail conservation laws: this fact is demonstrated by the famous Noether theorem.1 In the opinion of the authors, this is one of the most elegant theorems in physics.

5.3 Symmetries and Groups
 }, finite or infinite, of objects or
transformations (called hereafter elements of the group) form a group
}, finite or infinite, of objects or
transformations (called hereafter elements of the group) form a group  if there is an operation (called
hereafter product and represented by the symbol
if there is an operation (called
hereafter product and represented by the symbol  between any two of its elements such
that
between any two of its elements such
that
- 1.
It is closed: the product of any of two elements a, b is an element c of the group
 (5.8)
(5.8) - 2.
There is one and only one identity element: the product of any element a by the identity element e is the proper element a
 (5.9)
(5.9) - 3.
Each element has an inverse: the product of an element a by its inverse element b (designated also as a
 ) is the identity e
) is the identity e
 (5.10)
(5.10) - 4.
The associativity law holds: the product between three elements a, b, c can be carried out as the product of one element by the product of the other two or as the product of the product of two elements by the other element, keeping however the order of the elements:
 (5.11)
(5.11)

A symmetry is an invariance over a transformation or a group of transformations. In physics, there are well-known symmetries, some related to fundamental properties of space and time. For instance in mechanics, the description of isolated systems is invariant with respect to space and time translations as well as to space rotations. Noether’s theorem grants that for each symmetry of a system there is a corresponding conservation law and therefore a conserved quantity. The formulation of Noether’s theorem in quantum mechanics is particularly elegant.
5.3.1 A Quantum Mechanical View of the Noether’s Theorem


 is the Hermitian conjugate of
U. Weshall use in what follows without distinction
the terms Hermitian conjugate, conjugate transpose, Hermitian
transpose, or adjoint of an
is the Hermitian conjugate of
U. Weshall use in what follows without distinction
the terms Hermitian conjugate, conjugate transpose, Hermitian
transpose, or adjoint of an  complex matrix A to indicate the
complex matrix A to indicate the  matrix obtained from A by taking the transpose and then taking
the complex conjugate of each entry.
matrix obtained from A by taking the transpose and then taking
the complex conjugate of each entry.


 , eigenstates of the Hamiltonian, are
a complete basis, U commutes
with the Hamiltonian:
, eigenstates of the Hamiltonian, are
a complete basis, U commutes
with the Hamiltonian:
![$$\begin{aligned}{}[\hat{H}, U] = \hat{H}U-U\hat{H} = 0 \, . \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ18.png)
![$$\begin{aligned} \frac{d}{dt} \langle \psi |U|\psi \rangle = -\frac{i}{\hbar } \langle \psi |[U, H]|\psi \rangle = 0. \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ19.png)
5.3.1.1 Continuum Symmetries



![$$\begin{aligned}{}[H, I + i\epsilon G ] = 0 \Longrightarrow [H, G ] = 0 \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ23.png)
![$$[H, I] = 0$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_IEq29.png) ), and since the time evolution of the
expectation value of G is given
by the equation
), and since the time evolution of the
expectation value of G is given
by the equation
![$$\begin{aligned} \frac{d}{dt} \langle G \rangle = \frac{i}{\hbar } \langle [H, G] \rangle = 0 \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ24.png)
 is conserved.
is conserved.Continuum symmetries in quantum mechanics are thus associated to conservation laws related to the group generators. In the next section, we shall make examples; in particular, we shall see how translational invariance entails momentum conservation (the momentum operator being the generator of space translations).
Let us see now how Noether’s theorem can be extended to discrete symmetries.
5.3.1.2 Discrete Symmetries
 which commutes with the Hamiltonian
which commutes with the Hamiltonian
![$$\begin{aligned}{}[ \hat{H}, \hat{P} ] = 0 \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ25.png)

 .
.Parity-invariant Hamiltonians represent interaction which conserve parity.
Let us examine now some examples of symmetries.
5.3.2 Some Fundamental Symmetries in Quantum Mechanics
5.3.2.1 Phase Shift Invariance

 is a real number, then
is a real number, then

 associated to this transformation is
a unitary operator: this means that its Hermitian conjugate
associated to this transformation is
a unitary operator: this means that its Hermitian conjugate
 is equal to its inverse operator
is equal to its inverse operator
 .
.5.3.2.2 Space Translation Invariance




 along x
along x

 .
.The operator  commutes with the Hamiltonian of an
isolated system, and the associated conserved quantity is the
linear momentum
commutes with the Hamiltonian of an
isolated system, and the associated conserved quantity is the
linear momentum  .
.
 , just the first terms may be retained
and
, just the first terms may be retained
and

5.3.2.3 Rotational Invariance

 , the angular momentum operator about
the z-axis, is the generator of
the rotation:
, the angular momentum operator about
the z-axis, is the generator of
the rotation:


 , the angular momentum can be replaced
in the perturbative expansion of the rotation by the matrix
, the angular momentum can be replaced
in the perturbative expansion of the rotation by the matrix



![$$\begin{aligned} { R}_{x}\left( {\theta }_{x}\right) { R}_{{ y}}\left( {\theta }_{y}\right) { R}_{{ z}}\left( {\theta }_{z}\right) \ne { \exp }\left[ \frac{i}{\hbar }\left( {\theta }_{x}{\hat{L}}_{x}+{\theta }_{y}{\hat{L}}_{y}+{\theta }_{z}{\hat{L}}_{z}\right) \right] : \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ41.png)
 and
and  two operators, the following relation
holds:
two operators, the following relation
holds:
![$$\begin{aligned} \exp \left( \hat{A} { + } \hat{B}\right) =\exp \left( \frac{1}{2}\left[ \hat{A},\hat{B}\right] \right) \exp { (}\hat{A}{ )\exp }(\hat{B}) \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ42.png)
![$$\left[ \hat{A},\hat{B}\right] $$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_IEq46.png) is the commutator of the two
operators.
is the commutator of the two
operators.![$$\begin{aligned} \left[ {\hat{L}}_{x},{\hat{L}}_{y}\right] =i\hbar {\hat{L}}_{z} \; ; \; \left[ {\hat{L}}_{y},{\hat{L}}_{z}\right] =i\hbar {\hat{L}}_{x} \; ; \; \left[ {\hat{L}}_{z},{\hat{L}}_{x}\right] =i\hbar {\hat{L}}_{y} \, . \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ43.png)
Once a basis is defined, operators can in most cases be associated to matrices; there is a isomorphism between vectors and states, matrices and operators.2 In the following, whenever there is no ambiguity, we shall identify operators and matrices, and we shall omit when there is no ambiguity the “hat” associated to operators.
5.3.3 Unitary Groups and Special Unitary Groups
Unitary groups U(n) and Special Unitary groups SU(n) of a generic rank n play a central role in particle physics both related to the classification of the elementary particles and to the theories of fundamental interactions.
 matrix has
matrix has  parameters, but the unitarity
condition (
parameters, but the unitarity
condition ( imposes
imposes  constrains, and thus, the number of
free parameters is
constrains, and thus, the number of
free parameters is  . A particularly important group is
the group U(1) which has just one free parameter and so one
generator. It corresponds to a phase transformation:
. A particularly important group is
the group U(1) which has just one free parameter and so one
generator. It corresponds to a phase transformation:

 is a real number and
is a real number and  is a Hermitian operator. Relevant
cases are
is a Hermitian operator. Relevant
cases are  being the identity operator (like a
global change of the phase of the wave function as discussed above)
or an operator associated to a single measurable quantity (like the
electric charge or the baryonic number). Noether’s theorem ensures
that the invariance of the Hamiltonian with respect to such
transformation entails the conservation of a corresponding
measurable quantity.
being the identity operator (like a
global change of the phase of the wave function as discussed above)
or an operator associated to a single measurable quantity (like the
electric charge or the baryonic number). Noether’s theorem ensures
that the invariance of the Hamiltonian with respect to such
transformation entails the conservation of a corresponding
measurable quantity.The special unitary group SU(n) is the
group of unitary complex matrices of dimension  and with determinant equal to 1. The
number of free parameters and generators of the group is thus
and with determinant equal to 1. The
number of free parameters and generators of the group is thus
 . Particularly important groups will
be the groups SU(2) and SU(3).
. Particularly important groups will
be the groups SU(2) and SU(3).
5.3.4 SU(2)

 . This group has three free parameters
and thus three generators. SU(2) operates in an internal space of
particle spinors , which in this context are complex
two-dimensional vectors introduced to describe the spin
. This group has three free parameters
and thus three generators. SU(2) operates in an internal space of
particle spinors , which in this context are complex
two-dimensional vectors introduced to describe the spin
 (as the electron) polarization
states. For instance in a (
(as the electron) polarization
states. For instance in a ( ,
,  basis, the polarization states along
z, x, and y can be written as
basis, the polarization states along
z, x, and y can be written as

 angular momentum operators, can be
for example (it is not a unique choice) the
Pauli matrices
angular momentum operators, can be
for example (it is not a unique choice) the
Pauli matrices  ,
,  e and
e and 


![$$\begin{aligned} \left[ {\hat{S}}_{i},{\hat{S}}_{j}\right] =i\hbar \ {\varepsilon }_{ijk}{\hat{S}}_{k} \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ48.png)
 , the Levi-Civita symbol, is the
completely antisymmetric matrix which takes the value 1 if
i, j, k, is obtained by an even number of
permutations of x, y, z, the value
, the Levi-Civita symbol, is the
completely antisymmetric matrix which takes the value 1 if
i, j, k, is obtained by an even number of
permutations of x, y, z, the value  if i, j,
k, is obtained by a odd number for permutations of x, y, z, and is zero otherwise.
if i, j,
k, is obtained by a odd number for permutations of x, y, z, and is zero otherwise.These commutation relations are
identical to those discussed above for the generators of space
rotations (the normal angular momentum operators) in three
dimensions, which form a SO(3) group (group of real orthogonal
matrices of dimension  with determinant equal to 1). SU(2)
and SO(3) have
thus the same algebra, and there is a mapping between the elements
of SU(2) and elements of SO(3) which respect the respective group
operations. But, while in our example SO(3) operates in the real
space transforming particle wave functions, SU(2) operates in the
internal space of particle spinors.
with determinant equal to 1). SU(2)
and SO(3) have
thus the same algebra, and there is a mapping between the elements
of SU(2) and elements of SO(3) which respect the respective group
operations. But, while in our example SO(3) operates in the real
space transforming particle wave functions, SU(2) operates in the
internal space of particle spinors.

 where the
where the  are the unit vectors of the
coordinate axes, and aligning the rotation axis to a unit vector
are the unit vectors of the
coordinate axes, and aligning the rotation axis to a unit vector
 :
:

 matrix.
matrix. operators (called the Casimir
operators) which do commute with all the
SU(n) generators. Then in the case of SU(2) there is one Casimir
operator which is usually chosen as the square of the total spin:
operators (called the Casimir
operators) which do commute with all the
SU(n) generators. Then in the case of SU(2) there is one Casimir
operator which is usually chosen as the square of the total spin:

 where s is the total spin:
where s is the total spin:

 is chosen as the projection operator
is chosen as the projection operator

 of the projection operator along a
given axis and by the total spin s. The two other operators
of the projection operator along a
given axis and by the total spin s. The two other operators  and
and  can be combined forming the so-called
raising and lowering operators
can be combined forming the so-called
raising and lowering operators  and
and  :
:






 have to be accommodated in SU(n)
representations of higher order. For example, for spin 1 particles,
the spin projection operator has three eigenvalues (1, 0,
have to be accommodated in SU(n)
representations of higher order. For example, for spin 1 particles,
the spin projection operator has three eigenvalues (1, 0,
 ) and therefore the spin states are
described by a three-component vector. In this case, the spin
operators are
) and therefore the spin states are
described by a three-component vector. In this case, the spin
operators are  matrices. For instance, in a
matrices. For instance, in a
 basis:
basis:

 fundamental representation.
fundamental representation. ) nodes aligned along an axis
) nodes aligned along an axis
 (Fig. 5.2).
(Fig. 5.2).

Graphical representation of SU(2) multiplets
5.3.5 SU(3)
SU(3) is the group behind the so-called eightfold way (the organization of baryons and mesons in octets and decuplets, which was the first successful attempt of classification of hadrons) and behind QCD (quantum chromodynamics, the modern theory of strong interactions). Indeed, SU(3) operates in an internal space of three-dimensional complex vectors and thus can accommodate at the same level rotations among three different elements (flavors u, d, s or colors Red, Green, Blue). The eightfold way will be discussed later in this chapter, while QCD will be discussed in Chap. 6; here, we present the basics of SU(3).

 3 matrices
3 matrices  are the generators. Since for a
generic matrix A
are the generators. Since for a
generic matrix A

 matrices should be traceless. SU(3)
has thus
matrices should be traceless. SU(3)
has thus  traceless, and Hermitian generators
that in analogy with SU(2) Pauli matrices can be defined as
traceless, and Hermitian generators
that in analogy with SU(2) Pauli matrices can be defined as

 are the Gell-Mann matrices:
are the Gell-Mann matrices:




 are
permutations of the following:
are
permutations of the following:

 matrices are built as the extension
of the SU(2) generators we have discussed before.
matrices are built as the extension
of the SU(2) generators we have discussed before. and
and  commute, and thus, they have common
eigenstates; their eigenvalues can thus be used to label the
eigenstates. We call the corresponding quantum numbers “third
isospin component” I
commute, and thus, they have common
eigenstates; their eigenvalues can thus be used to label the
eigenstates. We call the corresponding quantum numbers “third
isospin component” I and “hypercharge” Y quantum numbers. The other operators can be, in a
similar way as it was done for SU(2), combined two by two to form
raising and lowering (step) operators. Then the standard SU(3) generators will be defined
as:
and “hypercharge” Y quantum numbers. The other operators can be, in a
similar way as it was done for SU(2), combined two by two to form
raising and lowering (step) operators. Then the standard SU(3) generators will be defined
as:




-
 leaves Y unchanged and changes
leaves Y unchanged and changes
 by ±1,
by ±1, -
 changes Y by
changes Y by  and changes
and changes  by ±1/2,
by ±1/2, -
 changes Y by
changes Y by  and changes
and changes  by ±1/2.
by ±1/2.
5.3.6 Discrete Symmetries: Parity, Charge Conjugation, and Time Reversal
Let us examine now in larger detail three fundamental discrete symmetries: parity, charge conjugation, and time reversal.
5.3.6.1 Parity

 once and twice to a wave function
leads to
once and twice to a wave function
leads to

 operator are
operator are  . The parity group has just two
elements:
. The parity group has just two
elements:  and the identity operator
and the identity operator
 .
.  is thus Hermitian, and a measurable
quantity, parity, can be
associated to its eigenvalues: parity is a legal quantum
number.
is thus Hermitian, and a measurable
quantity, parity, can be
associated to its eigenvalues: parity is a legal quantum
number.Electromagnetic and strong interactions appear to be invariant under parity transformations (and therefore the parity quantum number is conserved in these interactions) but, as it will be discussed in the next chapter, weak interactions, with the surprise of most of physicists in the 1950s, are not.

 to
to  and
and  to
to  . One can prove that
. One can prove that

 , since a generic free-particle
Hamiltonian is with good approximation parity invariant, and an
“intrinsic” parity is assigned to each particle. Fermions and
antifermions have opposite parities; bosons and antibosons have the
same parity.
, since a generic free-particle
Hamiltonian is with good approximation parity invariant, and an
“intrinsic” parity is assigned to each particle. Fermions and
antifermions have opposite parities; bosons and antibosons have the
same parity.The photon has a negative parity: this can be seen by the fact that the basic atomic transition is characterized by the emission of a photon and a change of orbital angular momentum by one unit. All vector bosons have a negative parity, while the axial vector bosons have a positive parity.
Example: Experimental Determination of the Pion
Parity. By convention, we define that protons and neutrons
have positive intrinsic parity. The negative parity of pions can be
determined by assuming parity and angular momentum conservation in
the capture at rest of a  by a deuterium nucleus producing two
neutrons in the final state (
by a deuterium nucleus producing two
neutrons in the final state ( . The parity of a system of two
particles is the product of the parities of the two particles
multiplied by a (
. The parity of a system of two
particles is the product of the parities of the two particles
multiplied by a ( )
) factor where l is the orbital angular momentum of the
system (
factor where l is the orbital angular momentum of the
system ( is the ground state). In the case of
the nn system discussed above,
is the ground state). In the case of
the nn system discussed above,
 and thus the final state parity is
and thus the final state parity is
 . Pseudo-scalar mesons (like pions)
have negative parity, while scalar mesons have positive parity.
. Pseudo-scalar mesons (like pions)
have negative parity, while scalar mesons have positive parity.

5.3.6.2 Charge Conjugation
Charge conjugation reverses the sign of
all “internal” quantum numbers (electric charge, baryon number,
strangeness, ...) keeping the values of mass, momentum, energy, and
spin. It transforms a particle in its own antiparticle. Applying
the charge conjugation operator  twice brings the state back to its
original state, as in the case of parity. The eigenvalues of
twice brings the state back to its
original state, as in the case of parity. The eigenvalues of
 are again
are again  , but most of the elementary particles
are not eigenstates of
, but most of the elementary particles
are not eigenstates of  (particle and antiparticle are not
usually the same); this is trivial for electrically charged
particles.
(particle and antiparticle are not
usually the same); this is trivial for electrically charged
particles.
Once again electromagnetic and strong
interactions appear to be invariant under charge conjugation, but
weak interactions are not (they are “almost” invariant with respect
to the product  as it will be discussed later
on).
as it will be discussed later
on).
Electric charge changes sign under
charge conjugation and so do electric and magnetic fields. The
photon has thus a negative  eigenvalue. The neutral pion
eigenvalue. The neutral pion
 decays into two photons: its
decays into two photons: its
 eigenvalue is positive. Now you
should be able to answer the question: is the decay
eigenvalue is positive. Now you
should be able to answer the question: is the decay  possible?
possible?
5.3.6.3 Time Reversal and CPT

 CL on the mass difference between the
CL on the mass difference between the
 and the
and the  :
:
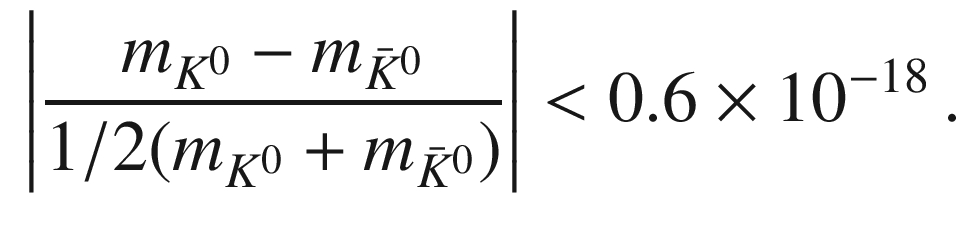
5.3.7 Isospin
In 1932, J. Chadwick discovered the
neutron after more than 10 years of intensive experimental
searches following the observation by Rutherford that to explain
the mass and charges of all atoms, and excluding hydrogen, the
nucleus should consist of protons and of neutral bound states of
electrons and protons. The particle discovered was not a bound
state of electron and proton—meanwhile, the uncertainty relations
demonstrated by Heisenberg in 1927 had indeed forbidden it. The
neutron wasindeed a particle like the
proton with almost the same mass ( MeV/
MeV/ ,
,  MeV/
MeV/ ), the same behavior with respect to
nuclear interaction, but with no electric charge. It was the
neutral “brother” of the proton.
), the same behavior with respect to
nuclear interaction, but with no electric charge. It was the
neutral “brother” of the proton.
Soon after neutron discovery, Heisenberg
proposed to regard proton and neutron as two states of a single
particle later on called the nucleon. The formalism was borrowed from
the Pauli spin theory and Wigner, in 1937, called “isospin”
symmetry this new internal symmetry with respect to rotations in
the space defined by the vectors (p, 0) and (0, n). Strong interactions should be
invariant with respect to an internal SU(2) symmetry group, the
nucleons would have isospin  , and their states would be described
by isospin spinors. By convention, the proton is identified with
the isospin-up
, and their states would be described
by isospin spinors. By convention, the proton is identified with
the isospin-up  projection and the neutron with the
isospin-down
projection and the neutron with the
isospin-down  projection.
projection.
As we have discussed in
Chap. 3, Yukawa postulated in 1935 that the
short-range nuclear interaction might be explained by the exchange
of a massive meson, the pion. The charge independence of nuclear
interactions suggested later on that three pions ( ,
,  ,
,  ) should exist. Nuclear interaction
could thus be seen as an interaction between the nucleon isospin
doublet
) should exist. Nuclear interaction
could thus be seen as an interaction between the nucleon isospin
doublet  and a isovector
and a isovector  triplet of pions. Three spin 0 and
isospin 1 pions (
triplet of pions. Three spin 0 and
isospin 1 pions ( with
with  ,
,  with
with  ,
,  with
with  ) with almost the same masses
(
) with almost the same masses
( 139.6 MeV/
139.6 MeV/ ,
,  135.0 MeV/
135.0 MeV/ ) were indeed discovered in the late
1940s and in the beginning of the 1950s. The isospin theory of
nuclear interactions was established.
) were indeed discovered in the late
1940s and in the beginning of the 1950s. The isospin theory of
nuclear interactions was established.
5.3.7.1 The Isospin of a System of Particles
The isospin of a system of particles can be expressed as a function of the isospin of the individual particles using the same addition rules valid for the sum of ordinary spins or angular momenta.
 , while the total spin s can take values from |
, while the total spin s can take values from | to
to  . The weights of the different final
states in the total amplitude are given by the squares of the
so-called Clebsch–Gordan coefficients
C
. The weights of the different final
states in the total amplitude are given by the squares of the
so-called Clebsch–Gordan coefficients
C . The calculation of these
coefficients is not relevant for the purpose of this book; they can
be found in tables, an example being given in
Fig. 5.4.
. The calculation of these
coefficients is not relevant for the purpose of this book; they can
be found in tables, an example being given in
Fig. 5.4.

Clebsch–Gordan coefficients and spherical
harmonics. From K.A. Olive et al. (Particle Data Group), Chin.
Phys. C 38 (2014) 090001. Note: a square-root sign is to be
understood over every coefficient, e.g., for  read
read 
 particles gives
particles gives






5.3.7.2 Isospin and Cross Section
Strong interactions are invariant under
SU(2) rotations in the internal isospin space and according to
Noether’s theorem, total isospin is conserved in such interactions.
The transition amplitudes between initial and final states are a
function of the isospin I and
can be labeled as  .
.
- 1.

- 2.

- 3.
 .
.
The deuteron d is a
pn bound state and must have
isospin  ; otherwise, the bound states
pp and nn should exist (experimentally, they do
not exist). The isospin quantum numbers
; otherwise, the bound states
pp and nn should exist (experimentally, they do
not exist). The isospin quantum numbers  of the final states are thus those of
the
of the final states are thus those of
the  , which means
, which means  ,
,  ,
,  , respectively. The isospins of the
initial states follow the rules of the addition of two isospin
1 / 2 states discussed above, and are, respectively,
, respectively. The isospins of the
initial states follow the rules of the addition of two isospin
1 / 2 states discussed above, and are, respectively,
 ,
, 
 and
and  . As the final state is a pure
. As the final state is a pure
 state, only the transition amplitude
corresponding to
state, only the transition amplitude
corresponding to  is possible. The cross section
(proportional to the square of the sum of the scattering
amplitudes) for the reaction
is possible. The cross section
(proportional to the square of the sum of the scattering
amplitudes) for the reaction  should then be half of each of the
cross sections of any of the other reactions.
should then be half of each of the
cross sections of any of the other reactions.
 and
and  collisions:
collisions:
- 1.

- 2.

- 3.
 .
.

 and
and  corresponding to
corresponding to  and
and  , respectively, and
, respectively, and


Total cross section for the collision of positive and negative pions with protons as a function of the pion kinetic energy.
Credit: E.M Henley and A. Garcia, Subatomic physics, World Scientific 2007
 elastic scattering channel an
unexpected and dramatic increase at center-of-mass energies of 1232
MeV (Fig. 5.5). Such increase was soon after interpreted
by Keith Brueckner (Fermi was not convinced) as evidence that the
pion and the proton form at that energy a short-lived bound state
with isospin number
elastic scattering channel an
unexpected and dramatic increase at center-of-mass energies of 1232
MeV (Fig. 5.5). Such increase was soon after interpreted
by Keith Brueckner (Fermi was not convinced) as evidence that the
pion and the proton form at that energy a short-lived bound state
with isospin number  . Indeed, whenever
. Indeed, whenever  ,
,

This resonance is now called the
 ; being a
; being a
 state it has, as expected, four
projections, called
state it has, as expected, four
projections, called  .
.
5.3.8 The Eightfold Way

Dharma wheel representing the Buddhist “eightfold path” to liberation from pain.
From Wikimedia Commons
As discussed in Chap. 3, strange particles had been
discovered in the late 1940s in cosmic rays, and later abundantly
produced in early accelerator experiments in the beginning of the
1950s. These particles were indeed strange considering the
knowledge at that time: they have large masses, and they are
produced in pairs with large cross sections, but they have large
lifetimes as compared with what expected for nuclear resonances.
Their production is ruled by strong interactions while they decay
weakly. A new quantum number, strangeness ,
was assigned in 1953 to these particles by Nakano and Nishijima
and, independently, by Gell-Mann. By convention, positive
K mesons (kaons) have
strangeness  , while
, while  baryons have strangeness
baryons have strangeness  . “Ordinary” (nonstrange) particles
(proton, neutron, pions,
. “Ordinary” (nonstrange) particles
(proton, neutron, pions,  ) have strangeness 0.
) have strangeness 0.


 the antiparticle of the
the antiparticle of the  and the
and the 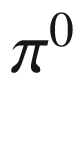 its own antiparticle. For kaons, the
existence of the strangeness quantum number implies that there are
four different states which are organized in two isospin doublets:
its own antiparticle. For kaons, the
existence of the strangeness quantum number implies that there are
four different states which are organized in two isospin doublets:
 and
and  having, respectively, strangeness
having, respectively, strangeness
 and
and  and being the antiparticles of each
other.
and being the antiparticles of each
other. , and a new quantum number, the
hypercharge
, and a new quantum number, the
hypercharge  , defined
as the sum of the baryonic number B (being B = 0 for mesons,
, defined
as the sum of the baryonic number B (being B = 0 for mesons,  for baryons and
for baryons and  for antibaryons) and
strangeness S:
for antibaryons) and
strangeness S:

 Y) plane (examples in
Figs. 5.7
and 5.8). The
masses of the particles in each multiplet were similar but not
strictly equal (they would be if the symmetry were perfect).
Indeed, while particles lying on the horizontal lines with the same
isospin have almost equal masses, the masses of the particles in
consecutive horizontal lines differ by 130–150 MeV/
Y) plane (examples in
Figs. 5.7
and 5.8). The
masses of the particles in each multiplet were similar but not
strictly equal (they would be if the symmetry were perfect).
Indeed, while particles lying on the horizontal lines with the same
isospin have almost equal masses, the masses of the particles in
consecutive horizontal lines differ by 130–150 MeV/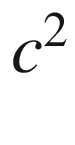 .
.

Fundamental meson and baryon octets: on the
left spin 0, parity −1 (pseudo-scalar mesons); on the right the
spin 1/2 baryons. The  axis is the abscissa, while the
Y axis is the ordinate
axis is the abscissa, while the
Y axis is the ordinate

Spin 3/2, parity 1 baryon decuplet. The
 axis is the abscissa, while the
Y axis is the ordinate. The
axis is the abscissa, while the
Y axis is the ordinate. The
 has
has  , and the
, and the  s have
s have 

 : one with
: one with  (
( ,
,  ) and one with
) and one with  1 (
1 ( ,
,  ). In the triangle (decuplet) 10 spin
3/2 baryons could be accommodated.
). In the triangle (decuplet) 10 spin
3/2 baryons could be accommodated.

Bubble chamber picture of the first
 .
.
From V.E. Barnes et al., “Observation of a Hyperon with Strangeness Minus Three”, Physical Review Letters 12 (1964) 204
There was however an empty spot in the
decuplet: a baryon with  ,
,  ,
,  ,
,  and a mass around 1670
MeV/
and a mass around 1670
MeV/ was missing. This particle, which we
call now the
was missing. This particle, which we
call now the  , was indeed
discovered in the Brookhaven National Laboratory 2-meter hydrogen
bubble chamber in 1964 (Fig. 5.9). A
, was indeed
discovered in the Brookhaven National Laboratory 2-meter hydrogen
bubble chamber in 1964 (Fig. 5.9). A  meson interacts with a proton in the
liquid hydrogen of bubble chamber producing a
meson interacts with a proton in the
liquid hydrogen of bubble chamber producing a  , a
, a  , and a
, and a  , which then decays according to the
following scheme:
, which then decays according to the
following scheme:

Measuring the final state charged
particles and applying energy–momentum conservation, the mass of
the  was reconstructed with a value of (1686
± 12) MeV/
was reconstructed with a value of (1686
± 12) MeV/ , in agreement with the prediction of
Gell-Mann and Ne’eman.
, in agreement with the prediction of
Gell-Mann and Ne’eman.
This “exoteric” classification was thus widely accepted, but something more fundamental should be behind it!
5.4 The Quark Model
5.4.1
SU(3)
 would be the triplet of antiquarks. Two
of the quarks (named up, u, and
down, d, quarks) formed a
isospin duplet and the other (named strange, s), which has strangeness quantum number
different from zero, a isospin singlet. The fundamental
representations of quarks and antiquarks formed triangles in the
(
would be the triplet of antiquarks. Two
of the quarks (named up, u, and
down, d, quarks) formed a
isospin duplet and the other (named strange, s), which has strangeness quantum number
different from zero, a isospin singlet. The fundamental
representations of quarks and antiquarks formed triangles in the
( Y) plane (Fig. 5.10).
Y) plane (Fig. 5.10).

Fundamental representations  and
and  of SU(3)
of SU(3)
This classification of quarks into
u, d, and s states introduces a new symmetry called
flavor symmetry , and the
corresponding SU(3) group is labeled as SU(3) (shortly SU(3)
(shortly SU(3) ) whenever confusion is possible with
the group
) whenever confusion is possible with
the group  (shortly
(shortly  ) of strong interactions that will be
discussed in the next chapter.
) of strong interactions that will be
discussed in the next chapter.
|
Q |
I |
|
S |
B |
Y |
|
|---|---|---|---|---|---|---|
|
u |
|
1/2 |
|
0 |
1/3 |
1/3 |
|
d |
|
1/2 |
|
0 |
1/3 |
1/3 |
|
s |
|
0 |
0 |
|
1/3 |
|
 and
and  SU(3) representations, which gives an
octet and a singlet:
SU(3) representations, which gives an
octet and a singlet:


“nonet” (octet  singlet) of pseudo-scalars mesons
singlet) of pseudo-scalars mesons
There are three states with  and
and  both for pseudo-scalars (
both for pseudo-scalars ( ,
,  ,
,  ) and vectors (
) and vectors ( ,
,  ,
,  ). The
). The  and the
and the  are the already well-known states
with
are the already well-known states
with 
 . The other states should then
correspond to the SU(3) symmetric singlet
. The other states should then
correspond to the SU(3) symmetric singlet  , and to the octet isospin singlet,
orthogonal to the SU(3) singlet,
, and to the octet isospin singlet,
orthogonal to the SU(3) singlet,  ; however, the physically observed
states are mixtures of these two “mathematical” singlets. Due to
these mixings, there is in fact a combination of the SU(3) octet
and singlet which is commonly designated as the “nonet.”
; however, the physically observed
states are mixtures of these two “mathematical” singlets. Due to
these mixings, there is in fact a combination of the SU(3) octet
and singlet which is commonly designated as the “nonet.”
The quark content of a meson can be accessed studying its decay modes.
 SU(3) representations. The 27
possible three quark combinations are then organized in a decuplet,
two octets, and a singlet:
SU(3) representations. The 27
possible three quark combinations are then organized in a decuplet,
two octets, and a singlet:

5.4.2 Color
Color is at the basis of the present
theory of strong interactions, QCD (see Sect. 6.4), and its introduction solves
the so-called  puzzle. The
puzzle. The
 is formed by three u quarks with orbital angular momentum
is formed by three u quarks with orbital angular momentum
 (it is a ground state) and in the
same spin projection state (the total spin is
(it is a ground state) and in the
same spin projection state (the total spin is  ). Therefore, its flavor, spin, and
orbital wave functions are symmetric, while the Pauli exclusion
principle imposes that the total wave functions of states of
identical fermions (as it is the case) should be antisymmetric.
). Therefore, its flavor, spin, and
orbital wave functions are symmetric, while the Pauli exclusion
principle imposes that the total wave functions of states of
identical fermions (as it is the case) should be antisymmetric.
In color space, quarks are represented
by complex three-vectors (the generalization of the two-dimensional
spinors). The number of colors in QCD is  , as we shall see later in this
Chapter; the quark colors are usually designated as Red, Blue and Green, having the antiquark the
corresponding anticolors.
, as we shall see later in this
Chapter; the quark colors are usually designated as Red, Blue and Green, having the antiquark the
corresponding anticolors.
Quarks interact via the emission or absorption of color field bosons, the gluons. There are eight gluons corresponding to the eight generators of the SU(3) group (see Sect. 5.3.5). Gluons are in turn colored, and the emission of a gluon changes the color.
(Anti)baryons are singlet states obtained by the combination of three (anti)quarks; mesons are singlet states obtained by the combination of one quark and one antiquark. All stable hadrons are color singlets, i.e., they are neutral in color.
 the decay into a pair of kaons which
is experimentally favored (86 % branching ratio) in relation
to the decay into three pions which however has a much larger phase
space. The suppression of the 3
the decay into a pair of kaons which
is experimentally favored (86 % branching ratio) in relation
to the decay into three pions which however has a much larger phase
space. The suppression of the 3 mode can be seen as a consequence of
the fact that “decays with disconnected quark lines are suppressed”
(Fig. 5.12). Being the
mode can be seen as a consequence of
the fact that “decays with disconnected quark lines are suppressed”
(Fig. 5.12). Being the  state a color singlet, the initial
and the final state in the right plot cannot be connected by a
single gluon, being the gluon a colored object (see
Sect. 6.4). Indeed, one can prove that the
“disconnected” decay would need the exchange of at least three
gluons.
state a color singlet, the initial
and the final state in the right plot cannot be connected by a
single gluon, being the gluon a colored object (see
Sect. 6.4). Indeed, one can prove that the
“disconnected” decay would need the exchange of at least three
gluons.

OZI favored (left) and suppressed (right)
 decay diagrams
decay diagrams

Baryon ground states in the quark model: the
spin 1/2 octet (left), and the spin 3/2 decuplet (right). The
vertical (S)-axis corresponds
to the Y-axis, shifted by 1
( corresponds to
corresponds to  ).
).
By Trassiorf [own work, public domain], via Wikimedia Commons
In color space, the physical states are antisymmetric singlets (the total color charge of hadrons is zero, the strong interactions are short range, confined to the interior of hadrons and nuclei). The product of the spin wave function and the flavor wave function in ground states (angular orbital momentum = 0) must then be symmetric. The net result is that the ground-state baryons are organized in a symmetric spin 1/2 octet and in a symmetric spin 3/2 decuplet (Fig. 5.13).
5.4.3 Excited States (Nonzero Angular Momenta Between Quarks)
Hundreds of excited states have been discovered with nonzero orbital angular momentum; they can be organized in successive SU(3) multiplets.

 invariant mass plot in
invariant mass plot in  annihilations (left) and in
proton–beryllium interactions (right).
annihilations (left) and in
proton–beryllium interactions (right).
Credits: Nobel foundation
5.4.4 The Charm Quark
 ”; it was finally decided to name it
“J/
”; it was finally decided to name it
“J/ .” The resonance was too narrow to be
an excited state—in this case, a hadronic decay would have been
expected, and thus a width of
.” The resonance was too narrow to be
an excited state—in this case, a hadronic decay would have been
expected, and thus a width of  150 MeV/
150 MeV/ .
.

Left: 16-plets for the pseudo-scalar
(a) and vector
(b) mesons made of the
u, d, s, and c quarks as a function of isospin
 , charm C, and hypercharge
, charm C, and hypercharge
 . The nonets of light mesons occupy
the central planes to which the
. The nonets of light mesons occupy
the central planes to which the  states have been added. Right: SU(4)
multiplets of baryons made of u, d,
s, and c quarks: (a) The 20-plets including an SU(3)
octet; (b) The 20-plets
with an SU(3) decuplet.
states have been added. Right: SU(4)
multiplets of baryons made of u, d,
s, and c quarks: (a) The 20-plets including an SU(3)
octet; (b) The 20-plets
with an SU(3) decuplet.
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
In terms of the quark model, the
J/ can be interpreted as a
can be interpreted as a  (where c stands for a new quark flavor, called
the charm, which has an
electric charge of 2/3) vector (being produced in
(where c stands for a new quark flavor, called
the charm, which has an
electric charge of 2/3) vector (being produced in  ) meson. The possibility of the
existence of a fourth flavor was suggested in 1964 by, among
others, Bjorken and Glashow for symmetry reasons: at that time,
four leptons—the electron, the muon, and their respective
neutrinos—were known, and just three quarks. Later, in 1970,
Glashow, Iliopoulos, and Maiani demonstrated that a fourth quark
was indeed needed to explain the suppression of some neutral current weak processes—this is
the so-called GIM mechanism that will be discussed in
Sect. 6.3.6.
) meson. The possibility of the
existence of a fourth flavor was suggested in 1964 by, among
others, Bjorken and Glashow for symmetry reasons: at that time,
four leptons—the electron, the muon, and their respective
neutrinos—were known, and just three quarks. Later, in 1970,
Glashow, Iliopoulos, and Maiani demonstrated that a fourth quark
was indeed needed to explain the suppression of some neutral current weak processes—this is
the so-called GIM mechanism that will be discussed in
Sect. 6.3.6.
With the existence of a fourth flavor,
the flavor symmetry group changes from SU(3) to SU(4) giving rise
to more complex multiplets which were named “supermultiplets.”
Supermultiplets can be visualized (Fig. 5.15) as solids in a
three-dimensional space  , Y, C,
where C is the new charm
quantum number.
, Y, C,
where C is the new charm
quantum number.
A rich spectroscopy of charmed hadrons
was open. For instance, the pseudo-scalar SU(3) octet becomes a
15-particle SU(4) multiplet with seven new mesons with at least a
c quark ( ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ), and the spin 3/2 decuplet of
baryons becomes a 20-particle multiplet.
), and the spin 3/2 decuplet of
baryons becomes a 20-particle multiplet.
5.4.4.1 Quarkonia: The Charmonium
 states, named charmonium states, are particularly interesting; they
correspond to nonrelativistic particle/antiparticle bound states.
Charmonium states have thus a structure of excited states similar
to positronium (an
states, named charmonium states, are particularly interesting; they
correspond to nonrelativistic particle/antiparticle bound states.
Charmonium states have thus a structure of excited states similar
to positronium (an  bound state), but their energy levels
can be explained by a potential in which a linear term is added to
the Coulomb-like potential, which ensures that an infinite energy
is needed to separate the quark and the antiquark (no free quarks
have been observed up to now, and we found a clever
explanation for this fact, as we shall see):
bound state), but their energy levels
can be explained by a potential in which a linear term is added to
the Coulomb-like potential, which ensures that an infinite energy
is needed to separate the quark and the antiquark (no free quarks
have been observed up to now, and we found a clever
explanation for this fact, as we shall see):

 is the equivalent for the strong
interactions of the fine structure constant
is the equivalent for the strong
interactions of the fine structure constant  ,
,  is a positive constant, and the
coefficient 4/3 has to do with the color structure of strong
interactions; we shall discuss it in larger detail in
Sect. 6.4.6.
is a positive constant, and the
coefficient 4/3 has to do with the color structure of strong
interactions; we shall discuss it in larger detail in
Sect. 6.4.6.
Hadronization: the string mechanism
 ; the result is
; the result is

 of the system, which in the case of
hydrogen is approximately equal to the electron mass
of the system, which in the case of
hydrogen is approximately equal to the electron mass  while in the case of positronium, it
is exactly
while in the case of positronium, it
is exactly  The spin–orbit interaction splits the
energy levels (fine splitting), and a further splitting (hyperfine
splitting) is provided by the spin–spin interactions.
The spin–orbit interaction splits the
energy levels (fine splitting), and a further splitting (hyperfine
splitting) is provided by the spin–spin interactions. (n is the principal quantum number,
S is the total spin, L indicates the orbital angular momentum
in the spectroscopic notation (S being the
(n is the principal quantum number,
S is the total spin, L indicates the orbital angular momentum
in the spectroscopic notation (S being the  state), and s is the spin projection).
state), and s is the spin projection).

Energy levels for (a) the positronium and (b) the charmonium states.
From S. Braibant, G. Giacomelli, and M. Spurio, “Particles and fundamental interactions,” Springer 2012
The right plot of
Fig. 5.17 shows the energy levels of charmonium;
they can be obtained inserting the potential (5.86) into the
Schrödinger equation. One obtains  GeV/fm, and
GeV/fm, and 
The bottom quark, which will be introduced in the next section, has an even larger mass, and it gives rise to a similar spectroscopy of quarkonia.
5.4.5 Beauty and Top
A fifth quark was discovered a few
years later. In 1977, an experiment in Fermilab led by Leon
Lederman studied the mass spectrum of  pairs produced in the interaction of
a 400 GeV proton beam on copper and platinum targets. A new heavy
and narrow resonance, named the upsilon
pairs produced in the interaction of
a 400 GeV proton beam on copper and platinum targets. A new heavy
and narrow resonance, named the upsilon  , was found, with a mass of around
9.46 GeV/
, was found, with a mass of around
9.46 GeV/ .
.
The  was interpreted as a
was interpreted as a  vector meson where b stands for a new quark flavor, the
bottom or beauty
, which has,
like the d and the s, an electric charge of
vector meson where b stands for a new quark flavor, the
bottom or beauty
, which has,
like the d and the s, an electric charge of  . Several hadrons containing at least
a b quark were discovered. A
family of
. Several hadrons containing at least
a b quark were discovered. A
family of  mesons, called the bottomium and indicated by the letter
mesons, called the bottomium and indicated by the letter  , was there, as well as mesons and
baryons resulting from the combination of b quarks with lighter quarks:
pseudo-scalar mesons like the
, was there, as well as mesons and
baryons resulting from the combination of b quarks with lighter quarks:
pseudo-scalar mesons like the  ,
,  , the
, the  , and the
, and the  ; bottom baryons like
; bottom baryons like  ,
,  ,
,  ,
,  . Heavy mesons and baryons with a
single heavy quark are very interesting. The light quarks surround
the heavy quark in a strong force analogy of electrons around the
proton in the electromagnetically bound hydrogen atom.
. Heavy mesons and baryons with a
single heavy quark are very interesting. The light quarks surround
the heavy quark in a strong force analogy of electrons around the
proton in the electromagnetically bound hydrogen atom.
The discovery of the b quark inaugurated a third generation or
family of quarks. Each family is formed
by two quarks, one with electric charge  and the other with electric charge
and the other with electric charge
 (the first family is formed by quarks
u and d; the second by quarks c and s). In the lepton sector, as will be
discussed at the end of this chapter, there were at that time
already five known leptons (the electron, the muon, their
corresponding neutrinos, and a recently discovered heavy charged
lepton, the tau) . With the bottom quark,
the symmetry was restored between quarks and leptons but the sixth
partners both in the quark and in lepton (the tau neutrino) sector
were missing. The existence of a third family of quarks had indeed
been predicted already in 1973, before the discovery of the
(the first family is formed by quarks
u and d; the second by quarks c and s). In the lepton sector, as will be
discussed at the end of this chapter, there were at that time
already five known leptons (the electron, the muon, their
corresponding neutrinos, and a recently discovered heavy charged
lepton, the tau) . With the bottom quark,
the symmetry was restored between quarks and leptons but the sixth
partners both in the quark and in lepton (the tau neutrino) sector
were missing. The existence of a third family of quarks had indeed
been predicted already in 1973, before the discovery of the
 , by Makoto Kobayashi and Toshihide
Maskawa, to accommodate in the quark model the CP violation observed in the
, by Makoto Kobayashi and Toshihide
Maskawa, to accommodate in the quark model the CP violation observed in the  system (this will be discussed in
Chap. 6). The hypothetical sixth quark was
named before its discovery the “top” quark .
system (this will be discussed in
Chap. 6). The hypothetical sixth quark was
named before its discovery the “top” quark .
The top quark was missing and for many
years, and many people looked for it in many laboratories (in the
USA and in Germany, Japan, CERN), both at electron–positron and at
proton–(anti)proton colliders. A strong indication of a top with a
mass around 40 GeV/ was even announced in 1984 but soon
dismissed. Lower limits on the top mass were later established, and
indications on the value of the mass were derived from the standard
model (see Chap. 7); finally, in 1995, the discovery
of the top quark was published by the CDF experiment (and soon
after by the D0 experiment) at Fermilab, at a mass of (176 ± 18)
GeV/
was even announced in 1984 but soon
dismissed. Lower limits on the top mass were later established, and
indications on the value of the mass were derived from the standard
model (see Chap. 7); finally, in 1995, the discovery
of the top quark was published by the CDF experiment (and soon
after by the D0 experiment) at Fermilab, at a mass of (176 ± 18)
GeV/ . The present (2018) world average of
the direct measurements is (173.1 ± 0.6) GeV/
. The present (2018) world average of
the direct measurements is (173.1 ± 0.6) GeV/ . The top is heavier than a gold
nucleus; with such a large mass, its decay phase space is huge and
its lifetime is very short, even if the decay is mediated by the
weak force. It is so short (the estimated value is around
. The top is heavier than a gold
nucleus; with such a large mass, its decay phase space is huge and
its lifetime is very short, even if the decay is mediated by the
weak force. It is so short (the estimated value is around
 s) that the top does not live
long enough to hadronize: there are no top hadrons.
s) that the top does not live
long enough to hadronize: there are no top hadrons.
5.4.6 Exotic Hadrons
It is evident that it is possible to
form other color singlet bound states than the ordinary mesons
( ) and baryons (qqq). Indeed many states are predicted
formed by: just gluons (glueballs); two
quarks and two antiquarks (tetraquarks);
four quarks and one antiquark (pentaquarks); or six quarks (hexaquarks). These hadrons had been searched for
long and many candidates did exist, but only recently (2014 and
2015) the LHCb collaboration at CERN confirmed the existence of a
tetraquark (the Z(4430), a
bound
) and baryons (qqq). Indeed many states are predicted
formed by: just gluons (glueballs); two
quarks and two antiquarks (tetraquarks);
four quarks and one antiquark (pentaquarks); or six quarks (hexaquarks). These hadrons had been searched for
long and many candidates did exist, but only recently (2014 and
2015) the LHCb collaboration at CERN confirmed the existence of a
tetraquark (the Z(4430), a
bound  state) and two pentaquarks (the
state) and two pentaquarks (the
 and the
and the  , both bound
, both bound  states). A rich spectroscopy can be
studied in the future.
states). A rich spectroscopy can be
studied in the future.
5.4.7 Quark Families
 are known, and they can be organized
into three families:
are known, and they can be organized
into three families:

 for the u and the d quarks,5 to the almost 200
GeV/
for the u and the d quarks,5 to the almost 200
GeV/ for the t quark. The flavor symmetry that was the
clue to organize the many discovered hadrons is strongly violated.
Why? Is there a fourth, a fifth (
for the t quark. The flavor symmetry that was the
clue to organize the many discovered hadrons is strongly violated.
Why? Is there a fourth, a fifth ( ), family to be discovered? Are quarks
really elementary? These are questions we hope to answer during
this century.
), family to be discovered? Are quarks
really elementary? These are questions we hope to answer during
this century.5.5 Quarks and Partons
In the words of Murray Gell-Mann in 1967, quarks seemed to be just mathematical entities. This picture was deeply changed in a few years by the results of deep inelastic scattering experiments.
Indeed in the 1950s Robert
Hofstadter,6 in a series of Rutherford-like experiments
using a beam of electrons instead of  particles (electrons have no strong
interactions), showed departures from the expected elastic point
cross section. Nucleons (protons and neutrons) are not point-like
particles. The proton must have a structure and the quarks could be
thought as its constituents.
particles (electrons have no strong
interactions), showed departures from the expected elastic point
cross section. Nucleons (protons and neutrons) are not point-like
particles. The proton must have a structure and the quarks could be
thought as its constituents.
5.5.1 Elastic Scattering
 , was calculated by Rosenbluth (Sect. 6.2.8):
, was calculated by Rosenbluth (Sect. 6.2.8):
![$$\begin{aligned} \frac{d\sigma }{d\varOmega }=\frac{\alpha ^{2}\cos ^{2}\left( \frac{\theta }{2}\right) }{4 E^{2}\sin ^{4}\left( \frac{\theta }{2}\right) }\frac{{ E'}}{E}\left[ 1+\frac{Q^{2}}{2m_{p}^{2}} \tan ^{2}\left( \frac{\theta }{2}\right) \right] \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ87.png)
 takes into account the energy lost in
the recoil of the proton; and the third factor is the spin/spin
interaction. Note that for a given energy of the incident electron
there is just one independent variable, which is usually chosen by
experimentalists to be the scattering angle,
takes into account the energy lost in
the recoil of the proton; and the third factor is the spin/spin
interaction. Note that for a given energy of the incident electron
there is just one independent variable, which is usually chosen by
experimentalists to be the scattering angle,  . In fact, the energy of the scattered
electron,
. In fact, the energy of the scattered
electron, 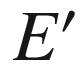 , can be expressed as a function of
, can be expressed as a function of
 as
as

 dependence as would be expected in
the case of a finite size proton. This cross section was
parameterized as:
dependence as would be expected in
the case of a finite size proton. This cross section was
parameterized as:
![$$\begin{aligned} \frac{d\sigma }{d\varOmega }=\frac{{\alpha }^{2}\cos ^{2}\left( \frac{\theta }{2}\right) }{4\ E^{2}\sin ^{4}\left( \frac{\theta }{2}\right) }\frac{{ E'}}{E}\left[ \frac{G_{E}^{2}\left( Q^{2}\right) +\frac{Q^{2}}{4m_{p}^{2}}G_{M}^{2}\left( Q^{2}\right) }{1+\frac{Q^{2}}{4m_{p}^{2}}}+2\frac{Q^{2}}{4m_{p}^{2}}\ G_{M}^{2}\left( Q^{2}\right) \tan ^{2}\left( \frac{\theta }{2}\right) \right] \nonumber \\ \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ89.png)
 and
and 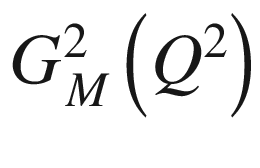 are called, respectively, the
electric and the magnetic form factors (if
are called, respectively, the
electric and the magnetic form factors (if  , the Rosenbluth formula (5.87) is
recovered).
, the Rosenbluth formula (5.87) is
recovered).At low  ,
,  and
and  can be interpreted as the Fourier
transforms of the electric charge and of the magnetization current
density inside the proton. In the limit
can be interpreted as the Fourier
transforms of the electric charge and of the magnetization current
density inside the proton. In the limit  (
( for the exchanged virtual photon),
the electron “sees” the entire proton and it could be expected that
for the exchanged virtual photon),
the electron “sees” the entire proton and it could be expected that
 . This is what the experiment tells
for
. This is what the experiment tells
for  , but it is not the case for
, but it is not the case for
 . In fact, the measured value is
. In fact, the measured value is
 . The proton has an anomalous magnetic
moment
. The proton has an anomalous magnetic
moment  which reveals already that the proton
is not a Dirac point-like particle. The same is observed for the
neutron which has
which reveals already that the proton
is not a Dirac point-like particle. The same is observed for the
neutron which has  .
.
 (
(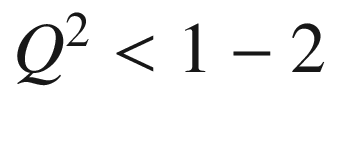 GeV
GeV ), the experimental data on
), the experimental data on
 and
and  are well described by the dipole
formula
are well described by the dipole
formula

 using polarized beams showed a much
richer picture reflecting a complex structure of constituents and
their interactions.
using polarized beams showed a much
richer picture reflecting a complex structure of constituents and
their interactions.5.5.2 Inelastic Scattering Kinematics
 with four-momentum:
with four-momentum:

 and
and 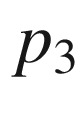 are, respectively, the four-momentum
of the incoming and outgoing electron,
are, respectively, the four-momentum
of the incoming and outgoing electron,  is the target four-momentum, and
is the target four-momentum, and
 is the four-momentum of the final
hadronic state which has an invariant mass
is the four-momentum of the final
hadronic state which has an invariant mass  (see Fig. 5.18). In case of elastic
scattering,
(see Fig. 5.18). In case of elastic
scattering,  .
.

Deep inelastic scattering kinematics


 ) by:
) by:

-
the lost energy

 (5.96)
(5.96) in the laboratory reference frame is
the energy lost by the electron:
in the laboratory reference frame is
the energy lost by the electron:
 (5.97)
(5.97) -
the inelasticity yy is dimensionless, and it is limited to the interval
 (5.98)
(5.98) . In the laboratory frame is the
fraction of the energy lost by the electron:
. In the laboratory frame is the
fraction of the energy lost by the electron:
 (5.99)
(5.99) -
the Bjorken variable, xx is also dimensionless and limited to the interval
 (5.100)
(5.100) . Using the definition of
. Using the definition of  , x can also be expressed as:
or imposing energy and momentum conservation at the hadronic vertex:
, x can also be expressed as:
or imposing energy and momentum conservation at the hadronic vertex: (5.101)If
(5.101)If (5.102)
(5.102) then
then  , the elastic scattering formula is
recovered.
, the elastic scattering formula is
recovered.
At a fixed center-of-mass energy,
 , the inelastic scattering final state
can be characterized by the Lorentz invariant variables,
, the inelastic scattering final state
can be characterized by the Lorentz invariant variables,
 ,
,  , x, y,
as well as by the scattered electron energy
, x, y,
as well as by the scattered electron energy  and scattered angle
and scattered angle  in the laboratory reference frame.
However, from all those variables, only two are independent. The
experimental choice is usually the directly measured variables
in the laboratory reference frame.
However, from all those variables, only two are independent. The
experimental choice is usually the directly measured variables
 and
and  , while the theoretical interpretation
is usually done in terms of
, while the theoretical interpretation
is usually done in terms of  and
and  or
or  and x.
and x.




5.5.3 Deep Inelastic Scattering
 and
and  , can be expressed as a function of
any two of the kinematic variables discussed in the previous
section. Hereafter, the choice will be
, can be expressed as a function of
any two of the kinematic variables discussed in the previous
section. Hereafter, the choice will be  and
and  . Hence,
. Hence,
![$$\begin{aligned} \frac{d\sigma }{d\varOmega { d}E'}= \ \frac{{\alpha }^{2}{\cos }^{2}\left( \frac{\theta }{2}\right) }{4\ E^{2}\,{\sin }^{4}\left( \frac{\theta }{2}\right) }\frac{{ E'}}{E}\left[ W_{2}\left( Q^{2},\nu \right) +2W_{1}\left( Q^{2},\nu \right) \ {\tan }^{2}\left( \frac{\theta }{2}\right) \right] . \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ107.png)
 describes the interaction between the
electron and the proton magnetic moments and can be neglected for
low
describes the interaction between the
electron and the proton magnetic moments and can be neglected for
low  .
. ,
,  ), these structure functions should
reproduce the elastic cross section formula discussed above:
), these structure functions should
reproduce the elastic cross section formula discussed above:


 (elastic scattering of electrons on a
point 1/2 spin particle with mass
(elastic scattering of electrons on a
point 1/2 spin particle with mass  and charge e) the Rosenbluth formula (5.87) is recovered and:
and charge e) the Rosenbluth formula (5.87) is recovered and:

 and
and  . In the case of a scattering over
point-like particles, the exchanged virtual photon “sees” always
the same charge whatever the
. In the case of a scattering over
point-like particles, the exchanged virtual photon “sees” always
the same charge whatever the  . In the case of a finite size
particle, the photon wavelength (
. In the case of a finite size
particle, the photon wavelength ( ) limits the observed volume inside the target. For
smooth charge distributions inside the target, it is therefore
trivial to predict that when
) limits the observed volume inside the target. For
smooth charge distributions inside the target, it is therefore
trivial to predict that when  :
:

 and
and  , the scaling of the structure
functions:
, the scaling of the structure
functions:


 and
and  are dimensionless functions, while
are dimensionless functions, while
 and
and  have dimensions
have dimensions  .
.While Bjorken was suggesting the
scaling hypothesis, the groups lead by J. Friedman, H. Kendall, and
R. Taylor7 designed and built at SLAC electron
spectrometers able to measure energies up to 20 GeV for
different scattering angles. The strong  dependence of the elastic form
factors was then confirmed up to
dependence of the elastic form
factors was then confirmed up to  30 GeV
30 GeV while, surprisingly, in the region
while, surprisingly, in the region
 GeV, the inelastic cross section
showed a very mild
GeV, the inelastic cross section
showed a very mild  dependence (Fig. 5.19, left).
dependence (Fig. 5.19, left).
 structure function showed, at these
relative small energies, already an approximate Bjorken scaling. In
fact,
structure function showed, at these
relative small energies, already an approximate Bjorken scaling. In
fact, 
 was found to be a universal function
of
was found to be a universal function
of  as demonstrated by measurements at
different energies and angles of the scattered particle
(Fig. 5.19, right) or at different
as demonstrated by measurements at
different energies and angles of the scattered particle
(Fig. 5.19, right) or at different  but keeping w constant (Fig. 5.20).
but keeping w constant (Fig. 5.20).

Left: Deep inelastic electron–proton
differential cross section normalized to the Mott cross section, as
measured by SLAC. From Ref. [F5.2] in the “Further readings.”
Adapted from Nobel Foundation, 1990. Right:  scaling: measurements at different
scattered energies and angles. From W. Atwood, “Lepton Nucleon
Scattering,” Proc. 1979 SLAC Summer Institute (SLAC-R-224)
scaling: measurements at different
scattered energies and angles. From W. Atwood, “Lepton Nucleon
Scattering,” Proc. 1979 SLAC Summer Institute (SLAC-R-224)

 scaling for the proton: measurements
at fixed x and at different
scaling for the proton: measurements
at fixed x and at different
 .
.
From J.I. Friedman and H.W. Kendall, Annual Rev. Nucl. Science 22 (1972) 203

Representation of electron–parton scattering in Feynman’s Quark–Parton Model
The Feynman partons were soon after identified as the Gell-Mann and Ne’eman quarks. However, nowadays, the term “parton” is used often to denominate all the nucleon constituents, i.e., the quarks and antiquarks and even the gluons.
5.5.4 The Quark–Parton Model
 of the nucleon momentum and energy:
of the nucleon momentum and energy:

 of the nucleon mass
of the nucleon mass  :
:

 and the proton moves with a very high
momentum toward the photon. However, even if the parton model was
built in such an extreme frame, its results are valid whenever
and the proton moves with a very high
momentum toward the photon. However, even if the parton model was
built in such an extreme frame, its results are valid whenever
 .
. particle with electric charge
particle with electric charge
 and mass
and mass  can be written as
can be written as

 function:
function:  , and remembering that
, and remembering that  and
and  , the electron–parton form factors
are:
, the electron–parton form factors
are:

 and
and  :
:

 function imposes that
function imposes that  . That means that, to comply with the
elastic kinematics constraints, the exchanged virtual photon has to
pick up a parton with precisely a fraction x of the nucleon momentum.
. That means that, to comply with the
elastic kinematics constraints, the exchanged virtual photon has to
pick up a parton with precisely a fraction x of the nucleon momentum. the density probability function to
find a parton carrying a fraction of momentum
the density probability function to
find a parton carrying a fraction of momentum  . The electron–nucleon form factors
are thus obtained integrating over all the entire
. The electron–nucleon form factors
are thus obtained integrating over all the entire  range and summing up all the partons:
range and summing up all the partons:


 are called the parton density functions (PDFs) .
are called the parton density functions (PDFs) .

Validation of the Callan–Gross relation.
Adapted from S. Braibant, G. Giacomelli and M. Spurio, “Particles and fundamental interactions,” Springer 2012
 and
and  , the so-called Callan–Gross relationis established:
, the so-called Callan–Gross relationis established:

 ) and was well verified experimentally
(Fig. 5.22).
) and was well verified experimentally
(Fig. 5.22).

Quarks in hadrons may have different
flavors and thus different charges and masses. The corresponding
PDFs are denominated according to the corresponding flavor:
u(x), d(x),
s(x), c(x),
b(x) t(x)
for quarks; 

 for antiquarks.
for antiquarks.
 for the electron–proton scattering
can now, for instance, be written as a function of the specific
quarks PDFs:
for the electron–proton scattering
can now, for instance, be written as a function of the specific
quarks PDFs:
![$$\begin{aligned} {F_{2}}^{ep}\left( Q^{2}, x\right) \simeq x\ \left[ \frac{4}{9}\left( u(x)+\bar{u}(x)\right) +\frac{1}{9}\left( d(x)+\bar{d}(x)+s(x)+\bar{s}(x)\right) \right] . \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ121.png)

 antiquark PDF, we should remember
that in the proton there are no valence antiquarks, just sea
antiquarks. Moreover, as the sea quarks and antiquarks appear in
pairs, the sea quarks and antiquarks PDFs with the same flavor
should be similar. Therefore, the
antiquark PDF, we should remember
that in the proton there are no valence antiquarks, just sea
antiquarks. Moreover, as the sea quarks and antiquarks appear in
pairs, the sea quarks and antiquarks PDFs with the same flavor
should be similar. Therefore, the  component in the proton can be
expressed as
component in the proton can be
expressed as

 . However, the physical observable
xf(x) (the carried momentum) are better
behaved (Fig. 5.24).
. However, the physical observable
xf(x) (the carried momentum) are better
behaved (Fig. 5.24).

 and
and  distributions have a maximum around
1 / 3 as expected but the sum of the momenta carried out
by the valence quarks is (as it was discussed before) smaller than
the total momentum:
distributions have a maximum around
1 / 3 as expected but the sum of the momenta carried out
by the valence quarks is (as it was discussed before) smaller than
the total momentum:

 for electron–proton and
electron–neutron scattering.
for electron–proton and
electron–neutron scattering.

Parton distribution functions at
Q GeV
GeV (left) and Q
(left) and Q GeV
GeV (right). The gluon and sea
distributions are scaled down by a factor of 10. The experimental,
model, and parameterization uncertainties are shown.
(right). The gluon and sea
distributions are scaled down by a factor of 10. The experimental,
model, and parameterization uncertainties are shown.
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001



![$$\begin{aligned} {F_{2}}^{ep}\left( Q^{2}, x\right) \simeq \ x\ \left[ \frac{4}{9} u_v^p(x) + \frac{1}{9} d_v^p(x) + \frac{10}{9} \bar{u}^p(x) + \frac{2}{9} \bar{s}^p(x) \right] \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ127.png)
![$$\begin{aligned} {F_{2}}^{en}\left( Q^{2}, x\right) \simeq \ x\ \left[ \frac{1}{9} u_v^p(x) + \frac{4}{9} d_v^p(x) + \frac{10}{9} \bar{u}^p(x) + \frac{2}{9} \bar{s}^p(x) \right] \end{aligned}$$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ128.png)

 range, one has
range, one has

 ) showing the limits of the naïve
quark–parton model. There is probably an isospin violation in the
sea quark distributions.
) showing the limits of the naïve
quark–parton model. There is probably an isospin violation in the
sea quark distributions.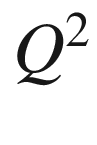 dependence of the structure functions (Fig. 5.25) was measured
systematically by several experiments, in particular, at the HERA
electron–proton collider, where a wide
dependence of the structure functions (Fig. 5.25) was measured
systematically by several experiments, in particular, at the HERA
electron–proton collider, where a wide  and
and  range was covered (
range was covered ( GeV
GeV ;
;  ). For
). For  , the scaling is reasonably satisfied
but for small x, the
, the scaling is reasonably satisfied
but for small x, the
 structure function clearly increases
with
structure function clearly increases
with  . This behavior is well predicted by
the theory of strong interactions, DGLAP
(Dokshitzer–Gribov–Lipatov–Altarelli–Parisi) equations, and
basically reflects the resolution power of the exchanged virtual
photon. A higher
. This behavior is well predicted by
the theory of strong interactions, DGLAP
(Dokshitzer–Gribov–Lipatov–Altarelli–Parisi) equations, and
basically reflects the resolution power of the exchanged virtual
photon. A higher  corresponds to a smaller wavelength
(
corresponds to a smaller wavelength
( ), and therefore a much larger number
of sea quarks with a very small
), and therefore a much larger number
of sea quarks with a very small  can be seen.
can be seen.

 dependence of
dependence of  .
.
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
5.5.5 The Number of Quark Colors
 comes from the measurement of the
R ratio of the hadronic cross
section in
comes from the measurement of the
R ratio of the hadronic cross
section in  annihilations to the
annihilations to the  cross section, defined as:
cross section, defined as:

 these processes are basically
electromagnetic and are mediated at the first order by one virtual
photon (
these processes are basically
electromagnetic and are mediated at the first order by one virtual
photon ( . The cross sections are thus
proportional to the square of the electric charge q of the final state particles f and
. The cross sections are thus
proportional to the square of the electric charge q of the final state particles f and  . A rule-of-thumb that can frequently
be helpful (note the analogies with the Rutherford cross section)
above production threshold and outside the regions in which
resonances are produced is:
. A rule-of-thumb that can frequently
be helpful (note the analogies with the Rutherford cross section)
above production threshold and outside the regions in which
resonances are produced is:


 , and over all colors. For
, and over all colors. For
 GeV, just the u, d
and s quarks can contribute.
Then,
GeV, just the u, d
and s quarks can contribute.
Then,

 GeV, there is also the contribution
of the c quark and
GeV, there is also the contribution
of the c quark and

 GeV, the b quark contributes
GeV, the b quark contributes

 pair production to be accessible at the
past and present
pair production to be accessible at the
past and present  colliders.
colliders. GeV, summarized in
Fig. 5.26, show, apart from regions close to the
resonances, a fair agreement between the data and this naïve
predictions, provided
GeV, summarized in
Fig. 5.26, show, apart from regions close to the
resonances, a fair agreement between the data and this naïve
predictions, provided  . Above
. Above  GeV, the annihilation via the
exchange of a Z boson starts to
be nonnegligible and the interference between the two channels is
visible, the calculation in Eq. (5.133) being no more
valid (see Chap. 7).
GeV, the annihilation via the
exchange of a Z boson starts to
be nonnegligible and the interference between the two channels is
visible, the calculation in Eq. (5.133) being no more
valid (see Chap. 7).

Measurements of  .
.
Adapted from [F5.2] in the “further readings”; the data are taken from K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
5.6 Leptons
 and it is one of the fundamental
constituents of the atoms. Later on, the neutral neutrino had to be
postulated to save the energy-momentum conservation law, as seen in
Chap. 2. Finally, three families each made
by one charged and one neutral leptons (and their corresponding
antiparticles) were discovered, symmetrically with the structure of
the three quark families:
and it is one of the fundamental
constituents of the atoms. Later on, the neutral neutrino had to be
postulated to save the energy-momentum conservation law, as seen in
Chap. 2. Finally, three families each made
by one charged and one neutral leptons (and their corresponding
antiparticles) were discovered, symmetrically with the structure of
the three quark families:

The  (tau) lepton, with its neutrino, was
the last discovered.
(tau) lepton, with its neutrino, was
the last discovered.
5.6.1 The
Discovery of the  Lepton
Lepton
 (tau), was
discovered in a series of experiments lead by Martin Perl, using
the Mark I detector at the SPEAR
(tau), was
discovered in a series of experiments lead by Martin Perl, using
the Mark I detector at the SPEAR  storage ring in the years 1974–1976.
The first evidence was the observation of events with only two
charged particles in the final state: an electron or a positron and
an opposite sign muon, with missing energy and momentum
(Fig. 5.27, left). The conservation of energy and
momentum indicated the existence in such events of at least two
undetected particles (neutrinos).
storage ring in the years 1974–1976.
The first evidence was the observation of events with only two
charged particles in the final state: an electron or a positron and
an opposite sign muon, with missing energy and momentum
(Fig. 5.27, left). The conservation of energy and
momentum indicated the existence in such events of at least two
undetected particles (neutrinos).

Left: An  event observed at Mark I. The muon
moves upward and the electron downward. The numbers 13 and 113 give
the relative amount of the electromagnetic energy deposited.
Credit: Martin Perl et al., M. L. Perl et al., “Evidence for
Anomalous Lepton Production in
event observed at Mark I. The muon
moves upward and the electron downward. The numbers 13 and 113 give
the relative amount of the electromagnetic energy deposited.
Credit: Martin Perl et al., M. L. Perl et al., “Evidence for
Anomalous Lepton Production in  Annihilation,” Phys. Rev. Lett. 35
(1975) 1489. Right: Feynman diagram for the
Annihilation,” Phys. Rev. Lett. 35
(1975) 1489. Right: Feynman diagram for the  decay in
decay in  ,
,  ,
,  .
.
By en:User: JabberWok and Time 3000 [GFDL http://www.gnu.org/copyleft/fdl.html], via Wikimedia Commons
 . In this case, a
. In this case, a  pair could have been produced,
pair could have been produced,

 into its (anti)neutrino plus a
W boson (Fig. 5.27, right); the
W boson, as it will be
explained in the next chapter, can then decay in one of the known
charged leptons
into its (anti)neutrino plus a
W boson (Fig. 5.27, right); the
W boson, as it will be
explained in the next chapter, can then decay in one of the known
charged leptons  ) plus the corresponding neutrino or
antineutrino:
) plus the corresponding neutrino or
antineutrino:

 hadronic decay modes:
hadronic decay modes:

 is massive enough (
is massive enough ( GeV) to allow such decays (the
GeV) to allow such decays (the
 being virtual).
being virtual).5.6.2 Three Neutrinos

 the antiparticle of
the antiparticle of  ? Lee and Yang were convinced, in
1960, that it should not be so (otherwise the Feynman diagram
represented in Fig. 5.28, would be possible and then the branching
fraction for
? Lee and Yang were convinced, in
1960, that it should not be so (otherwise the Feynman diagram
represented in Fig. 5.28, would be possible and then the branching
fraction for  would be large). At least two
different species of neutrinos should exist.
would be large). At least two
different species of neutrinos should exist.

Feynman diagram for the decay  in the case where just one neutrino
species exists
in the case where just one neutrino
species exists
Around the same time, the possibility
to produce a neutrino beam from the decay of pions created in the
collision of GeV protons on a target was intensively discussed in
the cafeteria of the Columbia University. In 1962, a kind of a
neutrino beam was finally available at Brookhaven National
Laboratory (BNL): the idea was to put an internal target in a long
straight section of the proton accelerator and to drive with a
magnet the proton beam on it; the pions coming from the proton
interactions were then decaying into pions. An experiment led by
Leon Lederman, Melvin Schwartz, and Jack Steinberger was set to
observe the neutrino reaction within a 10-ton spark chamber.
Hundreds of millions of neutrinos were produced mostly accompanied
by a muon ( as it will be discussed in the next
chapter). Forty neutrino interactions in the detector were clearly
identified; in six of them, the final state was an electron, and in
thirty-four, the final state was a muon. The
as it will be discussed in the next
chapter). Forty neutrino interactions in the detector were clearly
identified; in six of them, the final state was an electron, and in
thirty-four, the final state was a muon. The  and
and  are, thus, different particles,
otherwise the same number of events with one electron and with one
muon in the final state should have been observed.
are, thus, different particles,
otherwise the same number of events with one electron and with one
muon in the final state should have been observed.
 lepton was clearly identified. In
these events, the reconstruction of the charged tracks in the
iron/emulsion target showed a characteristic kink indicating at
least one invisible particle produced in the decay of a heavy
particle into a muon (Fig. 5.29).
lepton was clearly identified. In
these events, the reconstruction of the charged tracks in the
iron/emulsion target showed a characteristic kink indicating at
least one invisible particle produced in the decay of a heavy
particle into a muon (Fig. 5.29).

Tau-neutrino event in DONUT. A tau neutrino produces several charged particles. Among them a tau particle, which decays to another charged particle with missing energy (at least one neutrino).
From K. Kodama et al., DONUT Collaboration, “Observation of tau-neutrino interactions,” Phys. Lett. B 504 (2001) 218
5.7 The Particle Data Group and the Particle Data Book
How can one manage all this information about so many particles? How can one remember all these names? The explosion of particle discoveries has been so great, that Fermi said, “If I could remember the names of all these particles, I’d be a botanist.”
Fortunately, a book, called the Review of Particle Physics (also known as the Particle Data Book) , can help us. It is edited by the Particle Data Group (in short PDG), an international collaboration of about 150 particle physicists, helped by some 500 consultants, that compiles and organizes published results related to the properties of particles and fundamental interactions, reviewing in addition theoretical advancements relevant for experimental physics. The PDG publishes the Review of Particle Physics and its pocket version, the Particle Physics Booklet, which are printed biennially in paper, and updated annually in the Web. The PDG also maintains the standard numbering scheme for particles in event generators (Monte Carlo simulations).
-
Particle physics summary tables—Brief tables with the properties of of particles.
-
Reviews, tables, and plots—Review of fundamental concepts from mathematics and statistics, tables related to the chemical and physical properties of materials, review of current status in the fields of standard model, cosmology, and experimental methods of particle physics, tables of fundamental physical and astronomical constants, summaries of relevant theoretical subjects.
-
Particle listings—Extended version of the Particle Physics Summary Tables, with reference to the experimental measurements.
The Particle Physics Booklet (about 300 pages) is a condensed version of the Review, including the summary tables, and a shortened section of reviews, tables, and plots.
The publication of the Review of Particle Physics in its present form started in 1970; formally, it is a journal publication, appearing in different journals depending on the year.
5.7.1 PDG: Estimates of Physical Quantities
The “particle listings” (from which the “summary tables” are extracted) contain all relevant data known to the PDG team that are published in journals. From these data, “world averages” are calculated.
-
it is superseded by or included in later results.
-
no error is given.
-
it involves questionable assumptions.
-
it has a poor signal-to-noise ratio, low statistical significance, or is otherwise of poorer quality than other data available.
-
it is clearly inconsistent with other results that appear to be more reliable.
-
OUR AVERAGE—From a weighted average of selected data.
-
OUR FIT—From a constrained or overdetermined multiparameter fit of data.
-
OUR EVALUATION—Not from a direct measurement, but evaluated from measurements of related quantities.
-
OUR ESTIMATE—Based on the observed range of the data, not from a formal statistical procedure.
5.7.2 Averaging Procedures by the PDG
The average is computed by a
 minimization. There is an attempt to
use uncorrelated variables as much as possible, but correlations
are taken into account.
minimization. There is an attempt to
use uncorrelated variables as much as possible, but correlations
are taken into account.
When the error for a measurement
x is asymmetric, the error used
is a continuous function of the errors  and
and  . When the resultant average
x is less than
. When the resultant average
x is less than  ,
,  is used; when it is greater than
is used; when it is greater than
 ,
,  is used; in between, the error is a
linear function of x.
is used; in between, the error is a
linear function of x.
 , as follows. The PDG calculates a
weighted average and error as
, as follows. The PDG calculates a
weighted average and error as

 .
.-
If
 is less than or equal to 1, and there
are no known problems with the data, the results are accepted.
is less than or equal to 1, and there
are no known problems with the data, the results are accepted. -
If
 is very large, the PDG may
is very large, the PDG may
-
not to use the average at all, or
-
quote the calculated average, making an educated (conservative) guess of the error.
-
-
If
 is greater than 1, but not so much,
the PDG still averages the data, but then also increases the error
by
is greater than 1, but not so much,
the PDG still averages the data, but then also increases the error
by  . This scaling procedure for errors
does not affect central values.
. This scaling procedure for errors
does not affect central values.
 is greater than 1.25, an ideogram of
the data is shown in the Particle Listings.
Figure 5.30 is an example. Each measurement is shown
as a Gaussian with a central value
is greater than 1.25, an ideogram of
the data is shown in the Particle Listings.
Figure 5.30 is an example. Each measurement is shown
as a Gaussian with a central value  , error
, error  , and area proportional to
, and area proportional to
 .
.

An ideogram representing clearly inconsistent data—the measurements of the mass of the charged kaon. The arrow at the top shows the position of the weighted average, while the width of the shaded pattern shows the error in the average after scaling by the factor S.
From K.A. Olive et al. (Particle Data Group), Chin. Phys. C 38 (2014) 090001
A short summary of particle properties is also listed in the Appendix D of this book.
Further Reading
- [F5.1]
S. Haywood, “Symmetries and Conservation laws in Particle Physics: an introduction to group theory for experimental physicists,” Imperial College Press 2011. An excellent introduction to group theory and its application in particle physics.
- [F5.2]
A. Bettini, “Introduction to Elementary Particle Physics,” Cambridge University Press 2014. A very good introduction to Particle Physics at the undergraduate level putting together experimental and theoretical aspects and discussing basic and relevant experiments.
- [F5.3]
M. Thomson, “Modern Particle Physics,” Cambridge University Press, 2013. A recent, pedagogical and rigorous book covering the main aspects of Particle Physics at advanced undergraduate and early graduate level.
- [F5.4]
PDG 2017, C. Patrignani et al. (Particle Data Group), Chin. Phys. C, 40, 100001 (2016) and 2017 update. URL: http://pdg.lbl.gov/. Including the previous editions, this is the most quoted reference in this book.
- 1.
Kinematic thresholds and conservation laws. Compute the kinematic threshold of the reaction
 in a fixed target experiment.
in a fixed target experiment. - 2.
Can neutron be a bound state of electron and proton? The hypothesis that the neutron is a bound state of electron and proton is inconsistent with Heisenberg’s uncertainty principle. Why?
- 3.
- 4.
Parity. Verify explicitly if the spherical harmonicsare eigenstates of the parity operator, and in case they are determine the corresponding eigenvalues.

- 5.
Constructing baryons. How many different baryon combinations can you make with 1, 2, 3, 4, 5, or 6 different quark flavors? What’s the general formula for n flavors?
- 6.
Baryons. Using four quarks (u, d, s, and c), construct a table of all the possible baryon species. How many combinations carry a charm of
 1? How many carry charm
1? How many carry charm  2, and
2, and  3?
3? - 7.
Compositeness of quarks? M. Shupe [Phys. Lett. B 611, 87 (1979)] has proposed that all quarks and leptons are composed of two even more elementary constituents: c (with charge −1/3) and n (with charge zero) - and their respective antiparticles. You are allowed to combine them in groups of three particles or three antiparticles (ccn, for example, or nnn). Construct all of the eight quarks and leptons in the first generation in this manner. (The other generations are supposed to be excited states.) Notice that each of the quark states admits three possible permutations (ccn, cnc, ncc, for example)—these correspond to the three colors.
- 8.
Decays of the
 baryon. Which decay do you think would be
more likely:
Draw the Feynman diagrams at leading order, and explain your answer.
baryon. Which decay do you think would be
more likely:
Draw the Feynman diagrams at leading order, and explain your answer.
- 9.
Decay of charmed mesons. Which decay do you think would be least likely:Draw the Feynman diagrams at leading order, and explain your answer.

- 10.
Cross sections and isospin. Determine the ratio of the following interactions cross sections at the
 resonance:
resonance: 


- 11.
Decay branching ratios and isospin. Consider the decays of the
 into
into  ,
,  and
and  . Determine the ratios between the
decay rates in these decay channels.
. Determine the ratios between the
decay rates in these decay channels. - 12.
Quantum numbers. Verify if the following reactions/decays are possible and if not say why:
- (a)
 ,
, - (b)
 ,
, - (c)
 ,
, - (d)

 ,
, - (e)
 ,
, - (f)
 ,
, - (g)

 ,
, - (h)




- (a)
- 13.
Width and lifetime of the
 . The width of the
. The width of the  meson is
meson is  keV. What is its lifetime? Could you
imagine an experiment to measure it directly?
keV. What is its lifetime? Could you
imagine an experiment to measure it directly? - 14.
 mass.
Verify the relations between the masses of all the particles lying
in the fundamental baryon decuplet but the
mass.
Verify the relations between the masses of all the particles lying
in the fundamental baryon decuplet but the  and predict the mass of this one. Compare
your prediction with the measured values.
and predict the mass of this one. Compare
your prediction with the measured values. - 15.
Decays and conservation laws. Is the decay
 possible?
possible? - 16.
Experimental resolution in deep inelastic scattering. Consider an
 deep inelastic scattering experiment
where the electron scattering angle is
deep inelastic scattering experiment
where the electron scattering angle is  6
6 . Make an estimation of the
experimental resolution in the measurement of the energy of the
scattered electron that is needed to distinguish the elastic
channel (
. Make an estimation of the
experimental resolution in the measurement of the energy of the
scattered electron that is needed to distinguish the elastic
channel ( ) from the first inelastic channel
(
) from the first inelastic channel
( ).
). - 17.
e
 deep
inelastic scattering kinematics. Consider the
deep
inelastic scattering kinematics. Consider the  deep inelastic scattering and deduce
the following formulae:
deep inelastic scattering and deduce
the following formulae:



- 18.
Gottfried sum rule. Deduce in the framework of the quark–parton model the Gottfried sum ruleand comment the fact that the value measured in

 and
and  deep inelastic scattering experiments
is approximately 1/4.
deep inelastic scattering experiments
is approximately 1/4.












![$$ \exp \left( \hat{A}{ +}\hat{B}\right) =\exp \left( \frac{1}{2}\left[ \hat{A},\hat{B}\right] \right) \exp (\hat{A})\exp (\hat{B}) \, . $$](/epubstore/A/A-D-Angelis/Introduction-To-Particle-And-Astroparticle-Physics/OEBPS/images/304327_2_En_5_Chapter/304327_2_En_5_Chapter_TeX_Equ159.png)