IGAZSÁG, BIZONYÍTÁS, MEGLÁTÁS

Hilbert programja a matematikában

Mi az igazság? Hogyan alakítjuk ki ítéleteinket arról, hogy a világban mi igaz és mi nem? Követünk-e valamilyen algoritmust — amelyet a természetes kiválasztás erőteljes folyamata kétséget kizáróan előnyben részesít más, kevésbé hatásos algoritmusokkal szemben? Vagy az igazság kiderítésének lehet más, esetleg nem-algoritmikus módja? Nehéz kérdésnek látszik. ítéleteink az érzetek, érvelések és becslések bonyolult kombinációitól függnek. Mi több, sok e világi helyzetben nem létezhet általános egyezség arról, hogy mi igaz és mi hamis.

Hogy a kérdést egyszerűsítsük, tekintsük csupán a matematikai igazságot. Hogyan alakítjuk ki ítéleteinket — talán még „bizonyos” tudásunkat is — a matematikai kérdésekben? Itt legalább sokkal világosabbak a dolgok. Nem lehet kérdéses, hogy az adott esetben mi igaz, és mi hamis — vagy mégis? Mi valójában a matematikai igazság?

A matematikai igazság kérdése nagyon messzire nyúlik vissza, a korai görög filozófusok és matematikusok idejére és még régebbre. Egyes nagyon nagy tisztába tételek és meglepő új meglátások azonban nagyjából az elmúlt száz év eredményei. Ezeket az új fejleményeket próbáljuk megérteni. A problémák egészen alapvetőek, és azt a kérdést érintik, hogy vajon gondolkodási folyamatunk valóban lehet-e teljesen algoritmikus természetű. Fontos, hogy ezekkel tisztába jöjjünk.

A 19. század vége felé a matematika nagy lépéseket tett előre, részben azért, mert a matematikai bizonyításnak egyre több és több hatásos módszere fejlődött ki. (David Hilbert és Georg Cantor, akikkel korábban már találkoztunk, és a kiváló francia matematikus, Henri Poincaré, akivel később fogunk megismerkedni, ők hárman voltak e fejlődés élharcosai.) A matematikusok biztonságot szereztek e hatékony módszerek használatában. Sok ilyen módszer használta a végtelen számú tagot tartalmazó halmaz* fogalmát, és a bizonyítások gyakran éppen azért voltak sikeresek, mert a halmazokat valódi „dolgoknak” — teljes, létező egészeknek — tudták tekinteni, nem csupán potenciális lehetőségeknek. Sok hatásos elképzelés Cantor nagyon eredeti végtelen számok fogalmából keletkezett, amelyet ő következetesen, a végtelen sorozatokat használva fejlesztett ki. (Az előző fejezetben már vetettünk erre egy pillantást.)

Ez a magabiztosság azonban megtört, amikor 1902-ben a brit logista és filozófus, Bertrand Russell előállt ma már híres paradoxonjával (amelyet már Cantor is előre látott, lévén közvetlen leszármazottja az ő „átlós metszés” eljárásának). Hogy Russell érvelését megértsük, először némi elképzelésünk kell legyen a halmazokról, mint teljes egészekről. Képzeljünk el egy olyan halmazt, amelyet egy speciális tulajdonság jellemez. A piros dolgok halmazára például a pirosság a jellemző tulajdonság: valami akkor és csak akkor tartozik a halmazhoz, ha van pirossága. Ez megengedi, hogy fordítsunk egyet a dolgokon, és egy tulajdonságról egyetlen objektum, nevezetesen az ilyen tulajdonságú dolgok teljes halmaza formájában beszéljünk. E nézőpont szerint a „pirosság” az összes piros dolog halmaza. (Elgondolhatjuk azt is, hogy „ott” vannak más halmazok is, amelyek elemeit nem ennyire egyszerű tulajdonság jellemez.)

A fogalmak halmazokkal való definiálásának ez az elképzelése központi helyet foglalt el abban az eljárásban, amelyet 1884-ben vezetett be a jelentős hatású német logista, Gottlob Frege, mert a számokat is lehet halmazok segítségével definiálni. Mit értünk például a 3 számon? Tudjuk, mi a „hármasság” tulajdonság, de mi maga a 3? A „hármasság” objektumok gyűjteményeinek, azaz halmazoknak egy tulajdonsága: egy halmaznak akkor és csak akkor van meg ez a „hármasság” tulajdonsága, ha pontosan három eleme van. Egy kiválasztott olimpiai versenyszám érmesei halmazának például megvan ez a „hármasság” tulajdonsága. Ugyanígy megvan egy tricikli kerékgumijai halmazának, vagy egy közönséges lóhere levelei halmazának, vagy az x³ — 6x² + 11x — 6 = 0 egyenlet megoldásai halmazának. Mi hát akkor a 3 szám Frege-féle definíciója? Szerinte a 3 halmazoknak egy halmaza kell legyen: minden, e „hármasság” tulajdonsággal rendelkező halmaz halmaza.¹ Egy halmaznak így akkor és csak akkor van három eleme, ha hozzátartozik Frege 3 halmazához.

Mindez kissé körülményesnek tűnhet, de igazán nem az. Általánosan úgy definiálhatjuk a számokat, mint ekvivalens halmazok összességeit; az „ekvivalens” most azt jelenti, hogy „az elemeket egy-egy párosításba lehet egymással állítani” (azaz közönséges kifejezéssel „ugyanannyi tagjuk van”). A 3 szám az egyike ezeknek a halmazoknak, amelynek egyik eleme például egy almát, egy narancsot és egy körtét tartalmaz.

*Egy halmaz dolgoknak — fizikai objektumoknak vagy matematikai fogalmaknak — gyűjteményét jelenti, amely úgy kezelhető, mint egy egész. A matematikában egy halmaz elemei (azaz tagjai) nagyon gyakran maguk is halmazok, mert a halmazokat össze lehet gyűjteni és új halmazokat képezni. így tekinthetjük halmazok halmazát, halmazok halmazainak halmazát stb.

 

Jegyezzük meg, hogy a „3” e definíciója egészen különböző Churchnek a 89. oldalon megadott „3”-jától. Más definíciókat is lehet adni, amelyek manapság sokkal népszerűbbek. Na már most, mi a Russell-paradoxon? Az egy R halmazra vonatkozik, amelynek definíciója a következő:

R a halmaza minden halmaznak, amely nem eleme saját magának.

R így halmazok bizonyos gyűjteménye; annak feltétele, hogy egy X halmaz a gyűjteményhez tartozzék, az, hogy ő maga ne legyen saját elemei között.

Abszurd feltételezés-e az, hogy egy halmaz eleme saját magának? Nem igazán. Tekintsük például a végtelen (végtelen sok elemű) halmazok I halmazát. Biztos, hogy végtelen sok különböző végtelen halmaz van, így I maga végtelen, tehát valóban hozzátartozik saját magához! Miért van akkor az, hogy Russell elgondolása paradoxonhoz vezet? Azt kérdezzük: Russell R halmaza eleme-e saját magának vagy sem? Ha nem, akkor R-hez kell tartozzon, mert R pontosan azokat a halmazokat tartalmazza, amelyek nem elemei saját maguknak. Ezért R végül is R-hez tartozik — ami ellentmondás. Ha viszont R eleme saját magának, akkor mivel „saját maga” valójában R, ezért olyan halmazhoz tartozik, amelynek elemeire az jellemző, hogy nem elemei saját maguknak, azaz végül is R nem eleme saját magának — ami megint ellentmondás!*

Ez a gondolatmenet nem volt komolytalan. Russel csupán ugyanazt a típusú, nagyon általános, matematikai halmazelméleti okfejtést használta nagyon szélsőséges formában, mint amelyet a matematikusok kezdtek bizonyításaikban alkalmazni. A dolgok nyilvánvalóan kicsúsztak a matematikusok kezeiből, és sürgetővé vált, hogy sokkal pontosabban fogalmazzák meg, milyen típusú okfejtés megengedett, és milyen nem. Az feltétlenül szükséges, hogy a megengedett gondolatmenetben ne legyen ellentmondás, és hogy csak igaz állításokat engedjen meg levezetni előzőleg igaznak ismert állításokból. Russell munkatársával, Alfréd North Whiteheaddel nekilátott, hogy kidolgozza axiómáknak és eljárási szabályoknak egy nagymértékben formális matematikai rendszerét. Céljuk az volt, hogy a korrekt matematikai gondolatmenetek minden típusát le lehessen ebbe fordítani. A szabályokat gondosan válogatták, hogy megakadályozzák a paradoxon jellegű gondolatmeneteket, amilyen a Russell- paradoxonhoz is vezetett. A Russell és Whitehead által készített különleges rendszer nagyszabású munka volt. Ám sok fáradsággal járt, és eléggé korlátozta a megengedett matematikai okfejtések típusait.

*A Russell-paradoxon szórakoztató módon kifejezhető lényegében köznapi fogalmakkal. Képzeljünk el egy könyvtárat, amelyben két katalógus van, az egyik felsorolja a könyvtár minden olyan könyvét, amelyik valahol hivatkozik saját magára, a másik meg pontosan azokat, amelyek nem hivatkoznak magukra. Melyik katalógusba kell besorolni a második katalógust?

 

David Hilbert, a nagy német matematikus, akivel először a 2. fejezetben találkoztunk, belekezdett egy sokkal jobban használható és átfogóbb rendszerbe. Minden korrekt matematikai típusú gondolatmenetet be kívánt illeszteni a matematika minden területéről. Mi több, Hilbert arra törekedett, hogy bizonyítani lehessen, hogy a rendszer ellentmondásmentes. Így a matematika egyszer s mindenkorra megtámadhatatlan alapzatra kerülne.

Hilbertnek és követőinek reményei azonban semmivé váltak, amikor 1931-ben a 25 éves ragyogó osztrák matematikai logista, Kurt Gödel egy olyan meglepő tétellel állt elő, amely hatásosan rombolta le Hilbert programját. Gödel azt mutatta meg, hogy axiómáknak és eljárási szabályoknak tetszőleges ilyen pontos („formális”) matematikai rendszere, feltéve hogy elég széles, hogy tartalmazza egyszerű aritmetikai propozíciók (állítások) leírásait (mint a 2. fejezetben tárgyalt „Fermat utolsó tétele”), és feltéve hogy ellentmondásmentes, kell tartalmazzon olyan állítást, amely a rendszeren belül megengedett módokon nem bizonyítható és nem cáfolható. Az ilyen állítások igazsága tehát a jóváhagyott eljárásokkal „nem dönthető el”. Gödel ténylegesen meg tudta mutatni, hogy magának az axiómarendszer következetességének állítása, átalakítva megfelelő aritmetikai állítássá, szintén ilyen „eldönthetetlen” állítás. Fontos, hogy megértsük ezen „eldönthetetlenség” természetét. Látni fogjuk, miért hatolt le Gödel bizonyítása egészen a magjáig Hilbert programjának. Látni fogjuk azt is, hogyan tesz képessé Gödel tétele a meglátás felhasználásával arra, hogy túllépjünk bármely speciális formális matematikai rendszer korlátain. Ennek megértése döntő lesz sok elkövetkező fejtegetésünk szempontjából.

Formális matematikai rendszerek

Egy kicsit világosabban meg kell mondanunk, mit értünk „axiómák és eljárási szabályok formális matematikai rendszerén”. Fel kell tételeznünk, hogy a szimbólumoknak, amelyekkel matematikai állításainkat ki akarjuk fejezni, van ábécéjük.

E szimbólumoknak bizonyára alkalmasaknak kell lenniük arra, hogy megengedjék a természetes számok jelölését, hogy az „aritmetika” beépíthető legyen rendszerünkbe. Ha akarjuk, a számokra éppen használhatjuk a szokásos 0, 1, 3, .. .,9, 10, 11, 12, .. .arab jelölést, bár ez a szabályok leírását a szükségesnél kissé bonyolultabbá teszi. Sokkal egyszerűbb leírást eredményez, ha a természetes számok sorozatára mondjuk a 0, 01, 011, 0111, 01111, .. .jelölést alkalmazzuk (vagy kompromisszumként használhatjuk a bináris jelölést). Mivel azonban ez a következő gondolatmenetekben zavart okozna, leírásomban tartani fogom magam a szokásos arab jelöléshez, bármilyen jelölést használjon is ténylegesen a rendszer.

Szükségünk lehet egy „helyköz” szimbólumra rendszerünk különböző „szavainak” vagy „számainak” elválasztására, de mivel ez is zavart okozhat, e célra, ahol kell, használhatjuk éppen a vesszőt (,).

Kellenek majd betűk is a tetszőleges („változó”) természetes számok (vagy esetleg egészek, vagy racionális számok stb. — de maradjunk most a természetes számoknál) jelölésére, mondjuk t, u, v,w,x, y, z, t’, t’’, t’’’ — A t’, t’’,... vesszős betűkre is szükség lehet, mert nem akarjuk korlátozni egy kifejezésben előfordulható változók számát. A vesszőt (’) a formális rendszer külön szimbólumának tekintjük, ezért a szimbólumok aktuális száma véges.

Szükségünk lesz az aritmetikai alapműveletek =, +, x, stb. szimbólumaira, esetleg különféle zárójelekre, (, ), [, ], és a logikai szimbólumokra, mint például az A („és”), → („implikálja”), V („vagy”), <-> („akkor és csak akkor”), ~ („nem”, vagy „nem igaz, hogy ... ”).

Ezekhez jönnek még a logikai „kvantorok”: a egzisztenciális kvantor („van olyan ..., hogy”) és az V univerzális kvantor („minden”).

Most már tehetünk állításokat, ilyen például „Fermat utolsó tétele”:

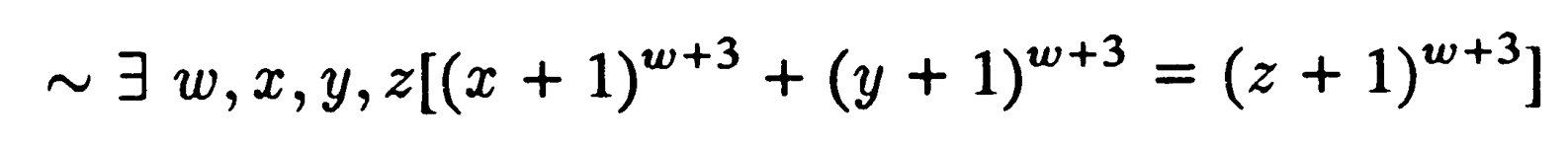
(lásd 2. fejezet 77. o.). (írhattam volna „0111”-et a „3” helyett, és talán használhattam volna külön jelölést a „hatványra emelés”-re, ami jobban illenék a formalizmushoz; de amint mondtam, tartom magam a hagyományos szimbólumokhoz, hogy ne okozzak felesleges bonyodalmakat.) A fenti állítást így olvassuk (az első szögletes zárójelig):

„Nem léteznek olyan w,x,y,z természetes számok, hogy Átírhatjuk Fermat utolsó tételét a V szimbólumot használva:

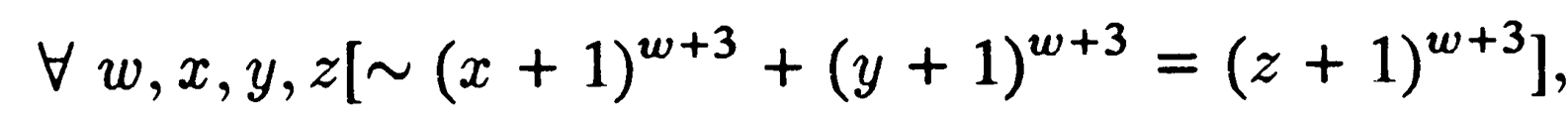
amit így olvasunk (az első zárójel utáni „nem” szimbólummal befejezve): „Minden w,x,y,z természetes számra nem igaz, hogy ... ”, ami logikailag azonos az előzővel.

A teljes állítások, szakkifejezéssel élve propozíciók, jelölésére szükségünk van betűkre, erre a P,Q,R,S,... nagybetűket fogom használni. Például ilyen propozíció lehet Fermat előbbi állítása:

Egy prepozíció függhet is egy vagy több változótól; például érdeklődhetünk Fermat állításában valamilyen speciális w + 3 hatvány iránt:

így G(O) azt állítja, hogy „köb nem lehet pozitív köbök összege”, G(1) ugyanezt negyedik hatványokra, és így tovább. (Vegyük észre hogy „” után hiányzik a „w".)* A Fermat-állítás most az, hogy G(w) fennáll minden w-re:

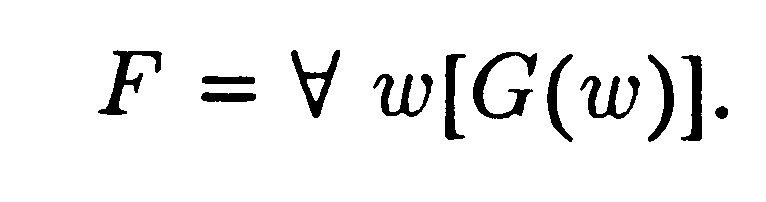
G( ) példája annak, amit propozíciós függvénynek nevezünk, olyan propozíció, amely egy változótól függ.

A rendszer axiómái általános prepozíciók egy véges listáját alkotják, igazságukat a szimbólumok jelentésének ismeretében magától értetődőnek tételezzük fel. Tetszőleges P,Q,R( ) prepozíciókra vagy propozíciós függvényekre például egyebek között érvényesek a következő axiómák:

amelyek „magától értetődő igazságáról” jelentésükből könnyen meggyőződhetünk. (Az első egyszerűen azt állítja, hogy „ha mind P, mind Q igaz, akkor P igaz”; a második a „nem igaz, hogy P hamis” és a ,P igaz” ekvivalenciáját; a harmadikat Fermat utolsó tételének az előbbiekben megadott kétféle megfogalmazása közötti logikai ekvivalencia példázza.) Bevehetnénk aritmetikai alapaxiómákat is, mint például

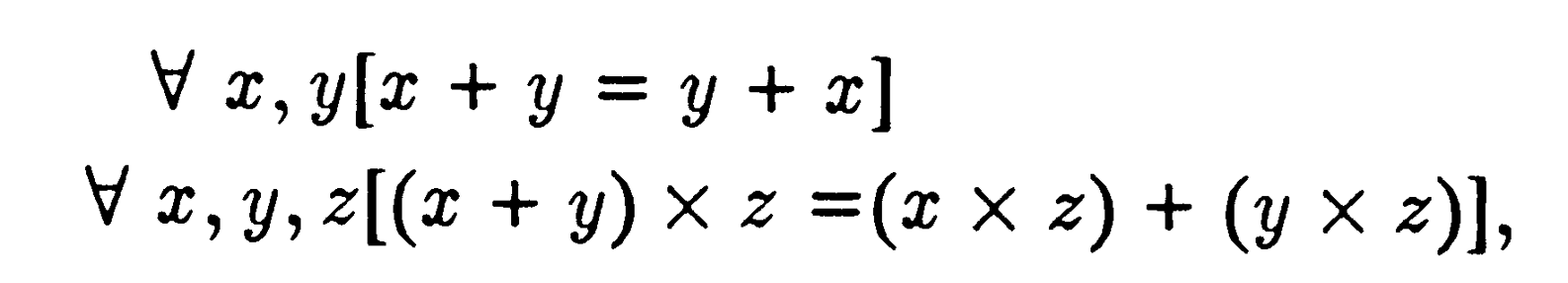
bár lehet, hogy valaki jobban szereti ezeket az aritmetikai műveleteket egyszerűbb dolgokból felépíteni és az állításokat tételként származtatni. Az eljárási szabályok olyan (maguktól értetődő) dolgok, mint például„P-ből és P => Q-ból levezethetjük Q-1”,

„V k[R(x)]-ből levezethetünk minden olyan prepozíciót, amelyet úgy kapunk, hogy R(x)-ben x helyébe speciális természetes számot helyettesítünk”.

*Bár az F teljes Fermat-propozíció igazsága még nem ismert, a G(0), G(l), G(2), G(3),... egyedi prepozíciók igazságát kb. G(125000)-ig ismerjük. Azaz tudjuk, hogy köb nem lehet pozitív köbök összege, negyedik hatvány nem lehet negyedik hatványok összege stb., a 125000. hatványokra vonatkozó megfelelő állításig.

 

Ezek olyan utasítások, amelyek megmondják, hogyan származtathatunk már elfogadott propozíciókból újabbakat.

Na már most, az axiómákból kiindulva és az eljárási szabályokat újra és újra alkalmazva felépíthetjük a prepozíciók hosszú listáját. Minden lépésnél újra játékba hozhatjuk bármelyik axiómát, és mindig újra felhasználhatjuk bármelyik prepozíciót, amelyet már csatoltunk egyre hosszabbodó listánkhoz. A helyesen összeállított listák propozícióiról mint tételekről beszélünk (bár sok közülük, mint matematikai állítás egészen triviális vagy érdektelen). Ha van egy speciális P prepozíciónk, amelyet bizonyítani akarunk, akkor próbálunk olyan, a szabályok szerint helyesen összeállított listát találni, amelyik a P propozícióval végződik. Ez a lista P bizonyítását nyújtaná a rendszeren belül; P ennek megfelelően tétel lenne.

Hilbert programjának az volt az elképzelése, hogy a matematika bármely jól meghatározott területén megtalálja az axiómáknak és eljárási szabályoknak egy elegendően széles listáját, hogy a területhez tartozó helyes matematikai gondolatmenetek minden formája rajta legyen. Rögzítsük, hogy matematikai területünk az aritmetika (ahol ott vannak a Ǝ és V kvantorok, így Fermat utolsó tételéhez hasonló állítások tehetők). Semmi előnnyel nem járna, ha ennél általánosabb területet vizsgálnánk. Az aritmetika már elég általános ahhoz, hogy Gödel eljárása alkalmazható legyen. Ha el tudjuk fogadni, hogy Hilbert programjával összhangban az aritmetikára vonatkozóan valóban adott az axiómáknak és eljárási szabályoknak egy átfogó rendszere, akkor meghatározott kritériummal rendelkezünk az aritmetika bármely prepozíciója matematikai bizonyításának „helyességére”. A remény az volt, hogy az ilyen axióma- és szabályrendszer teljes lehet olyan értelemben, hogy elvileg képessé tehet bennünket a rendszeren belül megfogalmazható bármely matematikai állítás igazságának vagy hamisságának eldöntésére.

Hilbert abban bízott, hogy egy matematikai prepozíciót ábrázoló szimbólumfüzérre, mondjuk P-re, bebizonyítható vagy P vagy ~ P, attól függően, hogy P igaz vagy hamis. Itt fel kell tételeznünk, hogy a füzér szintaktikuson helyesen felépített — a „szintaktikusan helyes” lényegében „nyelvtanilag helyeset” jelent, azaz kielégíti a formalizmus minden jelölési szabályát, hogy például a zárójeleket helyesen kell párosítani stb. — úgy, hogy P-nek jól meghatározott igaz vagy hamis jelentése van. Ha Hilbert reménye megvalósulhatna, akkor nem kellene azon problémáznunk, mit jelentenek a prepozíciók együttesen! P egy szintaktikusan helyes szimbólumfüzér volna. A P szimbólumfüzér igazságértéke igaz, ha P tétel (azaz P a rendszeren belül bizonyítható); hamis, ha ellenkezőleg: ~ P tétel. Hogy ennek értelme legyen, a teljesség mellett megköveteljük a konzisztenciát. Nem létezhet tehát olyan P szimbólumfüzér, amelyre mind P, mind ~ P tétel. Máskülönben P egyszerre lehetne igaz és hamis!

Az a nézőpont, hogy a matematikai állítások értelmét nélkülözhetjük, nem tekintve azokat másnak, mint szimbólumfüzéreknek egy formális matematikai rendszerben, a formalizmus matematikai álláspontja. Vannak, akik szeretik ezt az elképzelést, ami által a matematika egyfajta „értelmetlen játékká” válik. Nekem azonban ez az idea nem tetszik. Valójában az „értelem” — nem pedig a vak algoritmikus számítás — az, ami a matematikának megadja a lényegét. Szerencsére Gödel megsemmisítő csapást mért a formalizmusra! Nézzük meg, hogyan tette ezt.

Gödel tétele

Gödel bizonyításának egy része nagyon aprólékos és bonyolult. E bonyodalmakon azonban nem szükséges magunkat átrágnunk. A központi gondolat viszont egyszerű, szép és mély. Ezt képesek leszünk értékelni. A bonyolult rész (amelyben sok a leleményesség is) azt mutatja meg részletesen, hogyan lehet a formális rendszer egyedi eljárási szabályait és változatos axiómáinak használatát is aritmetikai műveletekbe kódolni. (A mély rész egyik gondolata viszont annak felismerése, hogy gyümölcsöző dolog ezt megtenni!)

E kódolás végrehajtásához alkalmas módját kell találnunk a propozíciók természetes számokkal való megjelölésének. Használhatnánk egyszerű „alfabetikus” rendezést a formális rendszer meghatározott hosszúságú szimbólumfüzéreire, emellett rendezést a füzérek hosszúsága szerint. (Alfabetikusán rendeznénk az egy hosszúságú füzéreket, ezután jönnének a szintén alfabetikusán rendezett kettő, majd a három stb. hosszúságúak.) Ezt hívják lexikografikus (szótáríró) rendezésnek.* Gödel eredetileg bonyolultabb számozást használt, az ebből adódó eltérések azonban számunkra nem fontosak. Különös figyelmet fordítunk azokra a propozíciós függvényekre, amelyek egyetlen változó függvényei, mint az előzőkben G(w).

Legyen a w-re alkalmazott (a szimbólumfüzérek választott rendezésében)

*A lexikografikus rendezésre úgy gondolhatunk, mint a természetes számok közönséges, ,k + 1 bázisban” felírt rendezésére, a k + 1 számjegy helyett a formális rendszer különböző szimbólumait használva egy új,.zérussal” együtt, amelyet sohasem használunk. (Ez utóbbi bonyodalom azért lép fel, mert a zérussal kezdődő számok ugyanazok, mint az e zérus elhagyásával kapottak.) Füzérek egy egyszerű, kilenc szimbólumot használó, lexikografikus rendezése a közönséges tízes rendszerben felírt, a nullát nem tartalmazó természetes számokkal valósítható meg: 1, 2, 3, 4,..., 8, 9,11, 12,... ,19, 21, 22       99, 111, 112,....

 

n-edik ilyen propozíciós függvény

P_n(w).

Megengedhetjük, hogy számozásuk kissé „felületes” legyen, egyes kifejezések szintaktikusan helytelenek lehetnek. (így az aritmetikai kódolás sokkal könnyebb, mintha megpróbálnánk elhagyni minden szintaktikusan helytelen kifejezést.) Ha P_n(w) szintaktikusan helyes, akkor van a két természetes számra, n-re és w-re vonatkozó, tökéletesen jól meghatározott, speciális aritmetikai állítás. Hogy ez pontosan melyik, az a választott számozási rendszer részleteitől függ. Ez a bizonyítás bonyolult részéhez tartozik, bennünket most nem érdekel. A propozíció füzérek, amelyek a rendszerben tételek bizonyításait képezik, szintén megjelölhetők a természetes számokkal a választott rendezési sémában. Jelölje

_∏n

az n-edik bizonyítást. (Ismét használhatunk „felületes számozást”, amikor egyes n értékekre a „∏_n” kifejezés szintaktikusan nem helyes, így nem bizonyít tételt.)

Tekintsük most a w természetes szám következő propozíciós függvényét:

Az állítás a szögletes zárójelben részben szavakkal van kifejezve, de tökéletesen pontosan meghatározott. Azt mondja ki, hogy az x-edik bizonyítás annak a propozíciónak bizonyítása, amelyik P_w( ) alkalmazva magára a w értékre. A szögletes zárójelen kívül a tagadott egzisztenciális kvantor az egyik változó eltávolítására szolgál („nincs olyan x, amelyre... ”), így az aritmetikai propozíciós függvény végül csak az egyetlen w változótól függ. Az egész kifejezés azt állítja, hogy P_w(w)-nek nincs bizonyítása. Feltételezem, hogy szintaktikusan helyesen van megszerkesztve, még akkor is, ha P_w(w) nem — ebben az esetben az állítás igaz, mert egy szintaktikusan nem helyes kifejezésnek nem lehet bizonyítása. Az aritmetikára való lefordítás miatt, ami feltételezésünk szerint megtörtént, a fenti propozíció valójában a w természetes számra vonatkozó aritmetikai állítás (a szögletes zárójelben álló rész jól definiált aritmetikai állítás az x és w természetes számokról). Nem feltételeztük, hogy az állítás nyilvánvalóan átkódolható az aritmetikába, de ez megtehető. Ennek megmutatása volt a „kemény munka” Gödel bizonyításának bonyolult részében. Mint előbb, most is a számozási rendszer részleteitől függ, hogy pontosan melyik aritmetikai állításról van szó, e rendszer pedig nagyon függ formális rendszerünk axiómáinak és szabályainak részletes szerkezetétől. Mivel mindez a bonyolult részhez tartozik, ezért a részletek nem érdekelnek bennünket.

Megszámoztunk minden egyváltozós propozíciós függvényt, ezért a most leírtnak is kell legyen száma. Legyen ez k. Propozíciós függvényünk a listán a k-adik. így

Vizsgáljuk most e függvényt a speciális w =/= k érték mellett. Azt kapjuk, hogy

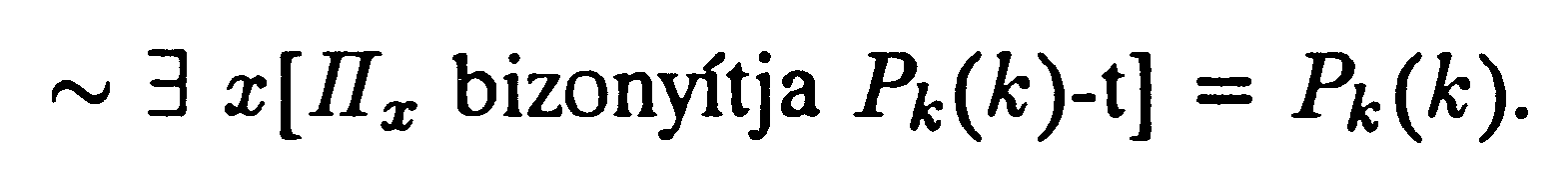
A speciális P_k(k) propozíció egy tökéletesen jól definiált (szintaktikusan helyes) aritmetikai állítás. Van-e bizonyítása formális rendszerünkön belül? Van-e tagadásának, ~ P_k(k)-nak bizonyítása? A válasz mindkét kérdésre „nem” kell legyen. Ezt úgy láthatjuk, hogy megvizsgáljuk a Gödel-eljárás mögött húzódó jelentést. Noha P_k(k) aritmetikai propozíció, konstrukciója szerint azt állítja, ami a bal oldalon áll: „a rendszeren belül a P_k(k) propozíciónak nincs bizonyítása”. Ha axiómáinkat és eljárási szabályainkat gondosan fektettük le, és ha a számozást helyesen végeztük, akkor a rendszeren belül ennek a P_k(k)-nak nem lehet bizonyítása. Mert ha lenne, akkor P_k(k) állítás „jelentése”, nevezetesen, hogy nincs bizonyítás, hamis lenne, így P_k(k) mint aritmetikai propozíció hamis kellene legyen. Formális rendszerünk nem lehet olyan rosszul felépített, hogy megengedje hamis propozíciók bizonyítását! Ezért a helyzet az kell legyen, hogy P_k(k)-nak ténylegesen nincs bizonyítása. Azonban pontosan ez az, amit P_k(k) mondani próbál nekünk. Ezért amit P_k(k) mond, az igaz állítás kell legyen, így P_k(k), mint aritmetikai propozíció igaz kell legyen. Találtunk egy igaz propozíciót, amelynek a rendszeren belül nincs bizonyításai

Mi a helyzet tagadásával, ~ P_k(k)-val? Az előbbiekből következik, hogy ennek sem lehet bizonyítása. Épp most állapítottuk meg, hogy ~ P_k(k) hamis kell legyen (mert P_k(k) igaz), és hamis propozíciókat a feltevés szerint a rendszeren belül nem tudunk bebizonyítani! így sem P_k(k), sem ~ P_k(k) nem bizonyítható formális rendszerünkben. Ez Gödel tétele.

Matematikai meglátás

Vegyük észre, hogy itt most valami nagyon figyelemreméltó dolog történt. Az emberek gyakran gondolnak a Gödel-tételre negatívumként — mint amely a formális matematikai gondolkodás szükségszerű korlátait mutatja meg. Akármilyen átfogónak is gondoljuk rendszerünket, mindig lesznek propozíciók, amelyek kiszöknek a hálóból. De kell-e izgasson bennünket ez a speciális Pk(k) propozíció? A fenti gondolatmenet során megállapítottuk, hogy Pk(k) igaz állítás! Sikerült valahogy meglátnunk, hogy P_k(k) igaz, annak ellenére, hogy a rendszeren belül formálisan nem bizonyítható. A szigorú matematikai formalistáknak valóban aggódniuk kell, mert éppen a fenti gondolatmenettel állapítottuk meg, hogy a formalista „igazság” fogalom szükségképpen nem teljes. Akármilyen (következetes) formális rendszert használunk is az aritmetikára, lesznek olyan állítások, amelyekről láthatjuk, hogy igazak, de amelyekhez az előbb leírt formalista eljárással nem tudjuk hozzárendelni az igaz igazságértéket. A szigorú formalista talán úgy próbálhatja ezt megkerülni, hogy egyáltalán nem beszél az igazság fogalmáról, hanem csak egy rögzített formális rendszeren belüli bizonyíthatóságról. Ez azonban nagyon korlátozónak látszik. E nézőpontot elfogadva még az előző Gödel-féle érvelést sem tudnánk elmondani, mert annak lényeges részei használnak meggondolásokat arról, mi igaz, és mi nem igaz.² Egyes formalisták „pragmatistább” álláspontra helyezkednek, azt állítják, hogy az olyan állítások miatt, mint P_k(k), nem kell aggódni, mert ezek szélsőségesen bonyolultak és érdektelenek mint aritmetikai propozíciók. Ezek az emberek azt mondanák:

Igen, vannak ezek a furcsa állítások, mint amelyekre az én bizonyíthatósági vagy igazságfogalmam nem esik egybe az Önök ösztönös igazságfogalmával, de ezek az állítások soha nem fordulnak elő a komoly matematikában (legalábbis abban, amely engem érdekel), mert abszurd módon bonyolultak és mint matematika természetellenesek.

Valóban az a helyzet, hogy a P_k(k)-hoz hasonló propozíciók, amikor teljesen kiírjuk azokat, rendkívül furcsán néznek ki, mint számokra vonatkozó matematikai állítások. A legutóbbi években azonban matematikailag nagyon elfogadható, ésszerűen egyszerű állítások kerültek színre, amelyek ténylegesen Gödel típusú prepozíciókkal egyenértékűek.³ Ezek az aritmetika normál axiómáiból nem bizonyíthatók, mégis következnek magának az axiómarendszernek egy „nyilvánvalóan igaz” tulajdonságából.

A formalista bevallott érdektelensége a „matematikai igazságban” számomra nagyon különös nézőpont mint matematikai filozófia. Továbbmenve: nem igazán a pragmatizmus teteje. Amikor a matematikusok gondolatmeneteiket végigviszik, nem akarják, hogy állandóan ellenőrizni kelljen, kifejezhetők-e érveléseik egy bonyolult formális rendszer axiómáival és eljárási szabályaival. Csak abban kell biztosaknak lenniük, hogy gondolatmeneteik az igazság kiderítésének érvényes módjai. A Gödel-féle bizonyítás egy másik ilyen érvényes eljárás, így nekem úgy tetszik, hogy P_k(k) éppen olyan jó matematikai igazság, mint bármi más, ami az előre lefektethető axiómák és eljárási szabályok hagyományosabb használatával kapható.

Egy kínálkozó eljárás a következő. Fogadjuk el, hogy P_k(k), amit egyelőre G₀-lal fogok jelölni, valóban tökéletesen érvényes propozíció; így mint további axiómát, csatolhatjuk rendszerünkhöz. Új, kiegészített rendszerünknek természetesen meglesz a saját Gödel-propozíciója, mondjuk G₁, amelyről szintén látható, hogy tökéletesen érvényes állítás a számokról. Ennek megfelelően G₁-et szintén csatoljuk rendszerünkhöz. Így újabb kiegészített rendszerhez jutunk, amelynek meglesz a saját G₂ Gödel-propozíciója (megint tökéletesen érvényes), ezt is csatolhatjuk, megkapjuk a következő Gödel-propozíciót, G₃-at, amelyet szintén csatolunk, és így tovább az eljárást a végtelenségig ismételve. Mit mondhatunk az így létrejövő rendszerről, ha megengedjük, hogy a G₀, G₁, G₂, G₃, ... teljes listát további axiómákként használjuk? Lehetséges-e, hogy ez teljes? Mivel axiómarendszerünk most nem korlátos (végtelen), ezért esetleg nem világos, hogy alkalmazható-e rá a Gödel-eljárás. Azonban a Gödel-propozícióknak ez a folytatólagos csatolása tökéletesen szisztematikus, és újrafogalmazható mint axiómáknak és eljárási szabályoknak közönséges, véges logikai rendszere. Ennek a rendszernek is meglesz a saját Gödel-propozíciója, mondjuk G_w, amelyet újra csatolhatunk, és azután képezhetjük a kapott rendszer G_W+1 Gödel-propozícióját. Megismételve ezt ugyanúgy, mint az előbb, a propozíciók G_w, G_W+1, G_w+2, G_w+3, ... listáját kapjuk, mindegyik tökéletesen érvényes állítás a természetes számokról, mindegyik csatolható formális rendszerünkhöz. E csatolás megint teljesen szisztematikus, és az egész sokaságot összefogó, új rendszerhez vezet; ám ennek újra lesz Gödel-propozíciója, mondjuk G_w+w, amelyet G_w2-ként is írhatunk. Az egész eljárás újra kezdhető, így kapunk egy új, végtelen, de szisztematikus G_w2, G_w2+1, G_w2+2 stb. axiómalistát, amely megint új rendszerhez — és új G_w3 Gödel-propozícióhoz vezet. Megismételve a teljes eljárást kapjuk G_W4-et, majd G_W5-öt, és így tovább. Most ez az eljárás teljesen szisztematikus, és van saját G_(w)² Gödel-propozíciója.

Véget ér-e ez valaha? Egyfajta értelemben nem; azonban ez nehéz matematikai megfontolásokhoz vezet, amelyek részleteibe most nem mehetünk bele. Az előző eljárást Alan Turing tárgyalta egy 1939-es cikkében.⁴ Nagyon figyelemreméltó, hogy az aritmetikában tetszőleges igaz (de univerzálisan kvantifikált) propozíció megkapható ilyen típusú ismételt „gödelizációs” eljárással! [Lásd Feferman (1988).] Ám ezzel bizonyos fokig elintézettnek tekinthetjük azt a kérdést, hogyan döntjük el ténylegesen, hogy egy propozíció igaz vagy hamis. A kritikus pont minden szakaszban annak kérdése, hogyan kell úgy kódolnunk a Gödel-propozíciók egy végtelen családjának csatolását, hogy egyetlen (vagy véges számú) további axiómát kapjunk. Ez megköveteli, hogy végtelen családunk algoritmikus módon rendszerezhető legyen. Hogy biztosak legyünk abban, hogy e rendszerezés helyesen csinálja meg azt, amit feltételezés szerint meg kell csinálnia, szükségünk lesz a rendszeren kívülről jövő meglátásokra — éppen úgy, mint amikor azért tettük ezt, hogy a P_k(k) propozíció igaz voltát lássuk. E meglátásokat nem lehet rendszerezni — és valóban kívül kell lenniük bármilyen algoritmikus cselekményen!

A meglátás, amely által arra következtettünk, hogy a P_k(k) Gödel-propozíció valóban igaz állítás az aritmetikában, általános példája annak az eljárásnak, amelyet a logisták tükrözési elvként ismernek: „tükrözve” az axiómarendszer és az eljárási szabályok értelmét, és meggyőződve arról, hogy ezekkel valóban érvényes módon juthatunk el matematikai igazságokig, képesek lehetünk e meglátást újabb igaz matematikai állításokba kódolni, amelyek magukból az axiómákból és szabályokból nem vezethetők le. P_k(k) igazságának leszármaztatása, mint előbb körvonalaztam, ilyen elvre támaszkodott. Egy másik, az eredeti Gödel-féle érvelés számára lényeges (bár az előzőekben nem megadott) tükrözési elvre támaszkodik az, ahogy új matematikai igazságokat származtatnak abból a tényből, hogy egy axiómarendszer, amelyet matematikai igazságok előállítására már érvényesnek hiszünk, ténylegesen konzisztens. A tükrözési elvek gyakran tartalmaznak végtelen halmazokra vonatkozó gondolatmeneteket, és használatuknál mindig vigyáznunk kell arra, hogy ne kerüljünk túl közel az olyan jellegű érveléshez, amely Russell-típusú paradoxonhoz vezethet. A tükrözési elvek szolgáltatják a formalista gondolkodás antitézisét. Ha óvatosak vagyunk, akkor ezek képessé tesznek arra, hogy kiszökjünk egy formális rendszer merev falai közül és új matematikai meglátásokhoz jussunk, amelyek korábban nem látszottak elérhetőnek. Matematikai irodalmunkban sok teljesen elfogadható eredmény van, amelyek bizonyításai olyan meglátásokat követelnek, amelyek távol esnek az aritmetikára használatos szabványos formális rendszerek eredeti szabályaitól és axiómáitól. Mindez azt mutatja, hogy a szellemi eljárások, amelyek segítségével a matematikusok meghozzák ítéleteiket, nem egyszerűen valamely speciális formális rendszer eljárásaiban gyökereznek. Látjuk a P_k(k) Gödel-propozíció érvényességét, bár az axiómákból levezetni nem tudjuk. Az a fajta „látás”, amelyet egy tükrözési elv magában foglal, olyan matematikai meglátást követel, amely nem eredménye tisztán algoritmikus műveleteknek, amelyeket egy formális matematikai rendszerbe lehetne kódolni. Erre a 10. fejezetben majd visszatérünk.

Az Olvasó észrevehet bizonyos hasonlóságot a P_k(k) igazságát, mégis „bizonyíthatatlanságát” megalapozó érvelés és a Russell-paradoxon gondolatmenete között. Van hasonlóság Turing bizonyításával is, amely megállapítja, hogy nem létezik olyan Turing-gép, amely megoldja a megállási problémát. E hasonlóságok nem véletlenek. A három között erős történeti szál teremt kapcsolatot. Turing Gödel munkájának tanulmányozása után találta meg bizonyítását. Gödel jól ismerte a Russell-paradoxont, és képes volt az ilyen paradox gondolatmenetet érvényes matematikai bizonyítássá alakítani. (Mindezek a gondolatmenetek Cantornak az előző fejezetben, a 106. oldalon leírt „átlós metszésiéből származnak.)

Miért fogadjuk el Gödel és Turing bizonyításait, noha a Russell-paradoxon- hoz vezető gondolatmenetet el kellett vetnünk? Az előbbiek sokkal világosabbak és mint matematikai bizonyítások kifogástalanok, míg a Russell-paradoxon ködösebb, „óriási” halmazokkal operáló érvelésre támaszkodik. Ám el kell ismernünk, hogy a különbségek nem annyira tiszták, mint amennyire szeretnénk. A különbségek világossá tételének szándéka komoly hajtóereje volt a formalizmus egész elképzelésének. Gödel bizonyítása azt mutatja, hogy a szigorú formalista nézőpont nem tartható igazán; mégsem kínál egészében megbízható, alternatív nézőpontot. A kérdés szerintem nem megoldott. A matematikában jelenleg elfogadott eljárás* az olyan típusú „óriási” halmazokat használó érvelés elkerülésére, mint amilyen a Russell-paradoxonhoz vezet, nem teljesen kielégítő. Mi több, határozottan formalista módon igyekeznek megfogalmazni vagy másképpen olyan formában, amely nem győz meg teljesen arról, hogy nem fordulhatnak elő ellentmondások.

Akármi is a helyzet, én úgy látom, hogy a Gödel-féle bizonyításnak világos következménye az, hogy a matematikai igazság fogalma nem zárható be formális sémába, az túlmegy a puszta formalizmuson. Ez talán még a Gödel-tétel nélkül is világos. Mert hogyan döntjük el, mely axiómákat és eljárási szabályokat fogadjuk el, amikor egy formális rendszert próbálunk felállítani? Döntésünkben mindig intuitív megértésünk kell vezessen, mi az, ami „magától értetődően igaz”, ha ismerjük a rendszer szimbólumainak „értelmét”. Hogyan döntjük el, milyen formális rendszereket ésszerű elfogadni — összhangban intuitív érzéseinkkel a „magától értetődő”-ről és „értelem”-ről — és milyeneket nem? Az önkonzisztencia követelménye erre bizonyára nem megfelelő. Sok önkonzisztens rendszer lehet ebben az értelemben nem „ésszerű”, ezeknél az axiómák és eljárási szabályok olyan állítások, amelyeket mint hamisakat vagy esetleg értelmetleneket elvetünk. „Magától értetődő” és „értelem” olyan fogalmak, amelyekre még a Gödel-tétel nélkül is szükség volna.

A Gödel-tétel nélkül azonban elképzelhetnénk, hogy a „magától értetődő” és „értelem” intuitív fogalmait csupán a formális rendszer felállításánál alkalmazzuk, utána, az igazság meghatározására szolgáló tiszta matematikai érvelésben eltekintünk tőlük. Ekkor, a formalista nézettel összhangban, ezek a „homályos” intuitív fogalmak a matematikus előzetes gondolkodásának részeként jutnának szerephez, útmutatóként az alkalmas formális érvelés megtalálásához; de nem játszanának szerepet a matematikai igazság tényleges bemutatásában.

*Különbséget tesznek „halmazok” és „osztályok” között. A halmazokat össze lehet gyűjteni és belőlük más halmazokat vagy esetleg osztályokat csinálni, de az osztályokra ez nem megengedett, belőlük nem lehet semmilyen nagyobb gyűjteményt kialakítani, ehhez „túl nagyoknak” tekintik őket. Nincs szabály azonban annak eldöntésére, mikor tekinthető egy gyűjtemény halmaznak, és mikor kell szükségszerűen osztálynak tekinteni, eltekintve attól a körbezáródótól, amely szerint a halmazok azok a gyűjtemények, amelyeket össze lehet gyűjteni, hogy más gyűjteményeket formáljanak belőlük!

 

Gödel tétele azt mutatja, hogy ez a nézőpont egy matematikai alapfilozófiában nem igazán tartható. A matematikai igazság fogalma túlmegy a formalizmus egész koncepcióján. Van benne valami abszolút és „Isten-adta”. Ez az, amiről az előző fejezet végén tárgyalt matematikai platonizmusban szó van. Bármilyen speciális formális rendszer ideiglenes és „emberalkotta” minőséget fejez ki róla. E rendszerek valóban nagyon értékes szerepet játszanak a matematikai vizsgálatokban, de az igazsághoz csak részleges (vagy közelítő) útmutatással szolgálhatnak. Az igazi matematikai igazság túlmegy a csupán ember alkotta konstrukciókon.

Platonizmus vagy intuicionizmus?

Bemutattam a matematikai filozófia két szembenálló iskoláját, és a formalista nézettel szemben határozottan a platonista mellé álltam. A különbségeket igen leegyszerűsítettem. A nézőpontokat illetően sok finomítás tehető. A „platonizmus” címke alatt lehet vitatkozni például arról, hogy vajon a matematikai gondolkodás objektumainak van-e tényleges „létezésük”, vagy csak a matematikai „igazság” fogalma abszolút. Ezekkel a különbségekkel most nem foglalkozom. Fejemben a matematikai igazság abszolút volta és a matematikai fogalmak platóni létezése ugyanaz a dolog. A „létezés”, amelyet például a Mandelbrot-halmaznak tulajdonítanunk kell, az „abszolút” természetének egy tulajdonsága. Hogy az Argand-sík egy pontja hozzátartozik-e a Mandelbrot-halmazhoz vagy sem, ez abszolút kérdés, független attól, melyik matematikus vagy melyik számítógép vizsgálja. A Mandelbrot-halmaz „matematikusfüggetlensége” adja meg platóni létezését. Továbbmenve, a legfinomabb részletei túl vannak azon, ami számítógépek használatával számunkra elérhető. Ezek az eszközök csak közelítéseit adhatják egy szerkezetnek, amelynek megvan a maga mélyebb és „számítógép-független” létezése. Elfogadom azonban, hogy sok más nézőpont létezhet, amely ésszerűen közelíti meg ezt a kérdést. Ezeken a különbségeken most nem kell sokat töprengnünk.

Vannak nézőpontbeli különbségek abban is, meddig megy el valaki platonizmusában — ha valóban platonistának vallja magát. Gödel nagyon erősen platonista volt. Az olyan típusú matematikai állítások, mint amilyenekkel eddig foglalkoztunk, meglehetősen „szelídek” ahhoz képest, ahogy az ilyen dolgok mennek.⁵ Vitathatóbb állítások is előjöhetnek, különösen a halmazelméletben. Amikor végigtekintünk a halmazelmélet összes elágazásán, annyira vadul óriási és ködösen felépített halmazokkal találkozunk, hogy még az olyan határozott platonista is, mint jómagam, kételkedni kezd, hogy létezésük valóban „abszolút” dolog-e.⁶ Eljuthatunk egy szintre, ahol a halmazok definíciója annyira nyakatekert és fogalmilag annyira kétes, hogy a rájuk vonatkozó matematikai állítások igazságának vagy hamisságának kérdése már inkább „felfogás dolga” lehet, mintsem „Isten adta” minőség. Hogy valaki, Gödellel együtt, kész-e végigvinni a platonizmust, és kitart amellett, hogy az ilyen óriási halmazokra vonatkozó matematikai állítások igazsága vagy hamissága mindig abszolút vagy „platóni” dolog, vagy megáll egy pontnál, és abszolút igazságot vagy hamisságot csak akkor követel, ha a halmazok felépítése ésszerű, nem túlságosan vad; e kérdésnek további vizsgálataink során nem lesz lényeges jelentősége. A számunkra fontos (véges vagy végtelen) halmazok azokhoz képest, amelyekre most utaltam, nevetségesen kicsik! Ezért e különböző platonista nézetek közötti eltérések nem nagyon érintenek bennünket.

Vannak azonban más matematikai álláspontok, például az intuicionizmus (vagy egy másik, a finitizmus), amely a másik szélsőséget képviseli, semmiféle végtelen halmaznak nem ismeri el befejezett létezését.* Az intuicionizmust a holland matematikus, C. E. J. Brouwer indította el alternatív — a formalizmustól eltérő — válaszként az olyan paradoxonokra (például a Russell-félére), amelyek úgy keletkeznek, hogy a matematikai érvelésben túl szabadon használják a végtelen halmazokat. E nézőpont gyökerei Arisztotelészig nyúlnak vissza, aki Platón tanítványa volt, de elutasította tanítójának a matematikai dolgok abszolút létezéséről és a végtelen halmazok elfogadhatóságáról vallott nézeteit. Az intuicionizmus szerint a halmazokra (végtelenekre vagy végesekre) nem úgy kell gondolnunk, mint önmagukban „létezőkre”, hanem csupán a tagságot meghatározó szabályokon keresztül kell elképzelnünk azokat.

Brouwer intuicionizmusának egy jellemző sajátossága a „kizárt harmadik törvényének” elvetése. E törvény azt állítja, hogy egy állítás tagadásának tagadása ekvivalens az állítással. (Jelölésben: ~ (~ P) P, egy reláció, amellyel már találkoztunk.) Arisztotelész talán boldogtalan lett volna valami logikailag annyira „nyilvánvaló” tagadásától, mint ez! A „józan ész” közönséges nyelvén kifejezve a kizárt harmadik törvénye magától értetődő igazságnak tekinthető: ha az hamis, hogy valami nem igaz, akkor az a valami biztosan igaz! (Ez a törvény az alapja a „reductio ad absurdum” matematikai eljárásnak, vö. 78. o.) Az intuicionisták azonban képesek e törvény tagadására. Alapvetően azért van így, mert a „létezés” fogalmához eltérő módon állnak hozzá, megkövetelik, hogy mielőtt egy matematikai objektum tényleges létezését elfogadják, legyen megadva annak egy határozott (elvi) felépítése. így az intuicionista számára a „létezés” „konstruktív létezést” jelent. Egy, a reductio ad absurdum szerint eljáró matematikai bizonyítás felvet valamilyen hipotézist azzal a szándékkal, hogy megmutassa, következményei ellentmondáshoz vezetnek, ez az ellentmondás szolgáltatja a kívánt bizonyítást, hogy a kérdéses hipotézis hamis.

*Az intuicionizmust azért hívják így, mert a feltételezés szerint az emberi gondolkodást tükrözi.

 

A hipotézis lehet olyan állítás, hogy egy bizonyos megkövetelt tulajdonságokkal rendelkező matematikai dolog nem létezik. Amikor ez ellentmondáshoz vezet, akkor a közönséges matematikában arra következtetünk, hogy a szóban forgó dolog valójában létezik. Azonban az ilyen bizonyítás önmagában nem kínál módot a dolog valóságos felépítésére. Az intuicionista számára ez a fajta létezés egyáltalán nem számít létezésnek; ebben az értelemben utasítják el a kizárt harmadik törvényét és a reductio ad absurdum eljárást. Brouwer valóban mélyen elégedetlen volt az ilyen nem konstruktív „létezéssel”.⁷ Tényleges felépítés nélkül, állította, az ilyen létezésfogalom értelmetlen. A brouweri logikában egy objektum nem létezésének hamisságából nem lehet az objektum tényleges létezésére következtetni!

Nézetem szerint, bár némileg dicsérhető, ha a matematikai létezésben a konstruktivitást keressük, az intuicionizmus Brouwer-féle nézőpontja mégis nagyon szélsőséges. Brouwer először 1924-ben tette közzé elképzeléseit, több mint tíz évvel Church és Turing munkái előtt. Most, hogy a konstruktivitás fogalma — Turingnak a kiszámíthatóságról kifejtett elképzelései alapján — a matematikai filozófia hagyományos keretei között tanulmányozható, nem szükséges olyan szélsőségekig elmenni, mint amilyenekhez Brouwer szándékozott elvinni. A konstruktivitást a matematikai létezés kérdésétől elkülönítve tárgyalhatjuk. Ha bemegyünk az intuicionizmus utcájába, akkor a matematikában meg kell tagadnunk magunktól az érvelés nagyon erőteljes fajtáinak használatát, és a dolog valahogy kifullad, tehetetlenné válik.

Nem kívánok hosszan időzni a különböző nehézségeknél és látható abszurditásoknál, amelyekhez az intuicionista nézőpont vezet; de talán hasznos lesz, ha utalok néhány problémára. Egy Brouwer által gyakran emlegetett példa a π szám

3,141592653589793...

tizedestört kifejtésével függ össze. Előfordul-e valahol a kifejtésben tíz egymást követő hetes, azaz

π = 3,141592653589793...7777777777...

vagy sem? A közönséges matematika szerint minden, amit mondhatunk, az, hogy vagy előfordul, vagy nem — és nem tudjuk, melyik az igaz! Ez eléggé ártalmatlan állításnak látszik. Az intuicionista azonban tagadná, hogy érvényes a „vagy létezik a π tizedes kifejtésében valahol tíz egymás utáni hetesből álló sorozat, vagy nem” állítás — hacsak és amíg valaki (az intuicionista számára elfogadható, konstruktív módon) vagy meg nem állapítja, hogy valóban van ilyen sorozat, vagy pedig azt, hogy nincs! Közvetlen számítás elegendő lenne annak megmutatására, hogy a π tizedes kifejtésében valahol valóban előfordul tíz hetes egymás után, de annak megállapítására, hogy ilyen sorozat nincs, matematikai tétel volna szükséges. Számítógéppel még nem találtak a π kifejtésében ilyen sorozatot. Valószínűségi alapon azt várjuk, hogy létezik ilyen sorozat, de még ha számítógép adná is ki folyamatosan a számjegyeket, mondjuk másodpercenként egyet, akkor is nagyságrendben száz és ezer év közötti idő kellene a sorozat megtalálásához! Sokkal valószínűbbnek látszik, hogy közvetlen számítás helyett egyszer majd matematikailag fogják a sorozat létezését megállapítani (valószínűleg egy sokkal jelentősebb és érdekesebb eredmény folyományaként) — bár esetleg nem az intuicionisták számára elfogadható módon!

E speciális problémának igazi matematikai érdekessége nincs. Szélsőséges intuicionizmusában Brouwer azt állítaná, hogy „a π decimális kifejtésében előfordul valahol tíz egymás utáni hetesből álló sorozat” állítás sem nem igaz, sem nem hamis. Ha valamikor később a kérdést számítással vagy (intuitív) matematikai bizonyítással így vagy úgy eldöntik, akkor az állítás „igazzá” vagy „hamissá” válik. Hasonló példa „Fermat utolsó tétele”. Brouwer szélsőséges intuicionizmusa szerint jelenleg ez is sem nem igaz, sem nem hamis, de később egyikké vagy másikká válhat. Számomra a matematikai igazság ilyen szubjektív volta és időfüggősége elrémítő. Az valóban nagyon szubjektív dolog, hogy egy matematikai eredmény elfogadható-e, vagy mikor fogadható el hivatalosan „bizonyítottnak”. A matematikai igazság nem nyugodhat ilyen társadalomfüggő kritériumokon. Időben változó fogalma túlzás nélkül a legkínosabb és nem kielégítő a matematika számára, amely matematikától azt reméljük, hogy megbízhatóan alkalmazhatjuk a fizikai világ leírására. Nem minden intuicionista követ ennyire kemény vonalat, mint Brouwer. Az intuicionista nézőpont mindazonáltal különösen kellemetlen még a konstruktivizmus céljaival rokonszenvezők számára is. Néhány mai matematikus örömmel követi az intuicionizmust, bár csak azért, mert nagyon korlátozza a matematikai okfejtés megengedhető típusait.

Nagy vonalakban leírtam a mai matematikai filozófia három fő áramlatát: a formalizmust, a platonizmust és az intuicionizmust. Nem csináltam titkot abból, hogy rokonszenvem erősen a platonista nézeté, amely szerint a matematikai igazság abszolút, külső és örök, és nem alapszik emberalkotta ismérveken; a matematikai objektumoknak saját időtlen létezésük van, amely nem függ emberi társadalomtól, sem speciális fizikai objektumoktól. E nézet mellett szóló érveimet ebben a szakaszban, az előzőben és a 3. fejezet végén próbáltam kifejteni. Remélem az Olvasó a legtöbb dologban kész velem tartani. Ez a későbbiekben sok mindenben fontos lesz.

Gödel-típusú tételek Turing eredményéből

A Gödel-tétel bemutatásánál sok részletet elhagytam, azt is, ami az érvelésnek történetileg talán a legfontosabb része; az utalást az axiómák következetességének „eldönthetetlenségére”. Célom nem az volt, hogy a Hilbert és kortársai számára annyira fontos „axióma-konzisztencia-bizonyíthatósági problémát” hangsúlyozzam, hanem hogy megmutassam, egy speciális Gödel-propozícióról, amely a vizsgált formális rendszer axiómáinak és szabályainak használatával nem bizonyítható vagy cáfolható — a kérdéses műveletek értelmére vonatkozó meglátásainkat használva világosan láthatjuk, hogy igaz propozíció!

Említettem, hogy Turing Gödel munkájának tanulmányozása után dolgozta ki saját bizonyítását a megállási probléma megoldhatatlanságáról. A két bizonyításban sok a közös vonás, és valóban, Turing eljárását használva közvetlenül le lehet vezetni Gödel eredményének kulcsfontosságú részeit. Nézzük meg, hogy megy ez; így némileg eltérő képet kapunk a Gödel-tétel hátteréről.

Egy formális matematikai rendszer lényeges sajátossága, hogy kiszámítható módon eldönthető, egy adott szimbólumfüzér a rendszeren belül egy matematikai állítás bizonyítását képezi-e vagy sem. A matematikai bizonyítás formálissá tételének lényeges pontja végül is az, hogy további ítéleteket nem kell alkotnunk arról, mi érvényes gondolatmenet, és mi nem az. Teljesen mechanikus és előre meghatározott módon ellenőrizhető kell legyen, hogy vajon egy feltételezett bizonyítás valóban bizonyítás-e; azaz a bizonyítások ellenőrzésére kell legyen algoritmus. Azt viszont nem követeljük meg, hogy szükségszerűen algoritmikus dolog legyen megtalálni javasolt matematikai állítások bizonyításait (vagy cáfolatait).

Ténylegesen az a helyzet, hogy tetszőleges formális rendszeren belül mindig van algoritmus egy bizonyítás találására, amikor csak bizonyítás létezik. Ehhez fel kell tételeznünk, hogy rendszerünket valamilyen szimbolikus nyelven fogalmaztuk meg, és ez a nyelv kifejezhető a szimbólumok véges „ábécé”-jének segítségével. Szimbólumfüzéreinket, mint előbb, rendezzük lexikografikusan, ami, emlékezzünk vissza, alfabetikus rendezést jelent a rögzített hosszúságú füzérekre, először az egy hosszúságú füzéreket rendezzük, majd a kettő, három stb. hosszúságúakat (128. o.). Így minden helyesen felépített bizonyítást számszerűen rendeztünk e lexikografikus séma szerint. A bizonyítások listája mellett van egy listánk a formális rendszer minden tételéről. Ugyanis a tételek pontosan azok a propozíciók, amelyek helyesen felépített bizonyítások utolsó sorai. A listázás tökéletesen kiszámítható: tekinthetjük ugyanis a rendszer összes szimbólumfüzérének lexikografikus listáját, akár értelmesek mint bizonyítások, akár nem, utána bizonyítás-ellenőrző algoritmusunkkal ellenőrizzük az első füzért, hogy bizonyítás-e, és eldobjuk, ha nem az; utána ugyanúgy ellenőrizzük a másodikat, és eldobjuk, ha nem bizonyítás, majd a harmadikat, negyediket és így tovább. Ha van bizonyítás, akkor ezen az úton végül megtaláljuk azt valahol a listán.

Így ha Hilbertnek sikerült volna megtalálnia matematikai rendszerét — axiómák és eljárási szabályok egy rendszerét, amely elég erős, hogy formális bizonyítással eldönthessük a rendszeren belül megfogalmazott, tetszőleges matematikai propozíció igazságát vagy hamisságát — akkor volna általános, algoritmikus módszerünk az ilyen propozíciók igazságának eldöntésére. Miért? Mert ha az előbb vázolt eljárással egy bizonyítás utolsó sorában végül is ráakadunk a keresett prepozícióra, akkor bebizonyítottuk ezt a prepozíciót. Ha, ellenkezőleg, prepozíciónk tagadását találjuk meg, mint utolsó sort, akkor megcáfoltuk azt. Ha Hilbert rendszere teljes volna, akkor e két lehetőség egyike mindig bekövetkezne (és ha konzisztens, akkor soha nem következnének be egyszerre). Mechanikus eljárásunk így valamelyik lépésben mindig megszakadna, és univerzális algoritmusunk volna a rendszer minden prepozíciója igazságának vagy az ellenkezőjének meghatározására. Ez ellentmondana Turing eredményének, hogy matematikai propozíciók eldöntésére nincs általános algoritmus, amint azt a 2. fejezetben bemutattuk. Következésképpen bebizonyítottuk Gödel tételét, hogy semmilyen, Hilbert által áhított rendszer nem lehet teljes a megtárgyalt értelemben.

Gödel tétele ennél valójában kevesebbet állít, mert a formális rendszertől Gödel csak azt követelte meg, hogy az aritmetikai prepozícióknak legyen megfelelő, nem a matematikai propozíciók számára általában. El tudjuk-e érni, hogy a Turing-gépek minden szükséges művelete végrehajtható legyen csak aritmetikát használva? Másképpen megfogalmazva: ki lehet-e fejezni a természetes számok minden kiszámítható függvényét (azaz rekurzív vagy algoritmikus függvényeket — a Turing-gép munkájának eredményeit) a közönséges aritmetikával? Majdnem igaz, hogy igen, de nem egészen. Egy extra műveletet hozzá kell csatolnunk az aritmetika és logika megszokott szabályaihoz (amelyek között a 3 és V már ott van). Ez a művelet egyszerűen kiválasztja

„az x legkisebb természetes számot, amelyre K(x) igaz”,

ahol K( ) tetszőlegesen adott, aritmetikailag kiszámítható propozíciós függvény — amelyre feltételeztük, hogy van ilyen szám, azaz hogy x[K(x)] igaz. (Ha nem volna, akkor műveletünk „örökké futna”,* próbálná megtalálni a kívánt, de nem létező x-et.) Mindenesetre az említett bizonyítás Turing eredménye alapján megállapítja, hogy Hilbert programja a matematika egész ágainak egy formális rendszeren belül végzett számításokká való redukálására valóban tarthatatlan.

 

*Lényeges megengedni az ilyen szerencsétlen eseteket is, hogy lehetőségünk legyen tetszőleges algoritmikus művelet leírására. Emlékezzünk vissza, ahhoz, hogy a Turing-gépeket általánosan leírhassuk, meg kell engednünk azokat is, amelyek soha nem állnak meg.

 

Ez az eljárás önmagában nem mutatja annyira világosan, hogy van egy Gödel-propozíciónk [mint Pk(k)], amely igaz, de a rendszeren belül nem bizonyítható. Ám ha felidézzük a 2. fejezetben leírt „hogyan győzzünk le egy algoritmust” gondolatmenetet (vö. 83. o.), akkor látni fogjuk, hogy csinálhatunk valami nagyon hasonlót. Azzal a gondolatmenettel meg tudtuk mutatni, hogy ha adott egy tetszőleges algoritmus, amely eldönti, hogy egy Turing-gép megáll-e vagy sem, akkor tudunk csinálni olyan Turing-gépet, amelyről mi látjuk, hogy nem áll meg, de az algoritmus nem. (Emlékezzünk vissza, ragaszkodtunk ahhoz, hogy az algoritmusnak helyesen kell tájékoztatnia bennünket, amikor egy Turing-gép meg fog állni, bár olykor elmulaszthatja megmondani, hogy a Turing-gép nem fog megállni — mert maga is a végtelenségig fut.) Így ugyanúgy, mint az előbb a Gödel-tételnél, most is van egy prepozíciónk, amelyről meglátásunk elárulja, hogy igaz kell legyen (hogy a Turing-gép nem áll meg), de az adott algoritmus nem képes ezt megmondani nekünk.

Rekurzívan felsorolható halmazok

Turing és Gödel eredményeinek alapvető kellékeit leírhatjuk grafikus módon a halmazelmélet nyelvén. Ezáltal megszabadulhatunk a formális rendszerektől, a különleges szimbólumoktól, a lényeges pontok mégis megérthetőek. Csak a 0, 2, 3,4,... természetes számok (véges vagy végtelen) halmazait tekintjük, ezek gyűjteményeit fogjuk vizsgálni, mint például {4,5,8}, {0,57,100003}, {6}, {0}, {1,2,3,4,..., 9999}, {1,2,3,4,...}, {0,2,4,6,8,...}, vagy éppen a teljes N = {0,1,2,3,4,...} halmaz, vagy a 0 = { } üres halmaz. Csak kiszámíthatósági kérdésekkel fogunk foglalkozni, nevezetesen: „A természetes számok mely típusú halmazait lehet és melyeket nem lehet algoritmus segítségével előállítani?”

Hogy nevet adjunk a dolgoknak, ha akarjuk, gondolhatjuk azt, hogy minden egyes n természetes szám egy formális rendszer egy speciális szimbólumfüzérét jelöli. Ez lenne az „n-edik” szimbólumfüzér, mondjuk Q_n, a rendszer („szintaktikusan helyesen” kifejezett) propozícióinak egy lexikografikus rendezésében. Így minden egyes természetes szám egy propozíciót ábrázol. A formális rendszer összes propozíciójának halmazát a teljes N halmaz ábrázolná, és például a formális rendszer tételei a természetes számok egy kisebb halmazát képeznék, mondjuk a P halmazt. A propozíciók speciális számozási rendszerének részletei azonban nem fontosak. Mindössze két algoritmusra lenne szükségünk, hogy megfeleltetést létesítsünk a természetes számok és a propozíciók között. Az egyik a (megfelelő szimbolikus jelöléssel felírt) Q_n propozíciót állítja elő a megfelelő n természetes számból, a másik n-et állítja elő Q_n-ből. Ha e két algoritmust adottnak vesszük, akkor jogunkban áll azonosítani a természetes számok N halmazát egy speciális formális rendszer propozícióinak halmazával.

Válasszunk egy formális rendszert, amely konzisztens és elég széles ahhoz, hogy tartalmazza minden Turing-gép minden hatását — és mi több, „ésszerű” abban az értelemben, hogy axiómái és eljárási szabályai „maguktól értetődően igazaknak" vehetők. A formális rendszer Q₀, Q₁, Q₂, Q₃,. . prepozíciói közül egyeseknek lesz bizonyításuk a rendszeren belül. E „bizonyítható” propozíciók számai egy halmazt alkotnak N-ben, mégpedig a „tételek” előbb említett P halmazát. Láttuk már, hogy van algoritmus, amellyel adott formális rendszerben minden bizonyítással rendelkező propozíció előállítható, egyik a másik után. (Mint korábban körvonalaztam, az „n-edik bizonyítás”, ∏_n, algoritmikusan megkapható n-ből. Ezért mindössze annyit kell tennünk, hogy az n-edik bizonyítás utolsó sorában megkeressük „a rendszeren belül bizonyítható n-edik propozíciót”, azaz az n-edik „tételt”.) Így van algoritmusunk, amely előállítja P elemeit, egyiket a másik után (esetleg ismétlődésekkel, ami nem számít.)

Egy halmazt, mint P-t is, amely ezen a módon algoritmussal előállítható, rekurzívan felsorolhatónak neveznek. Jegyezzük meg, hogy azon propozíciók halmaza, amelyek a rendszeren belül cáfolhatók — azaz, amelyek tagadása bizonyítható —, hasonlóképpen rekurzívan felsorolható, hiszen egyszerűen felsorolhatjuk a bizonyítható prepozíciókat, és vesszük tagadásaikat. N-nek van sok egyéb rekurzívan felsorolható részhalmaza, és nem kell hivatkoznunk a formális rendszerre, hogy meghatározzuk azokat. Egyszerű példák a páros számok

{0,2,4,6,8,...}

halmaza, a négyzetszámok

{0,1,4,9,16,...}

halmaza és a prímszámok

{2,3,5,7,11,...}

halmaza. Nyilvánvalóan mindhárom halmazt előállíthatjuk algoritmussal. A halmaz kiegészítő halmaza — azon természetes számok halmaza, amelyek nincsenek a halmazban — mindhárom példában szintén rekurzívan felsorolható. A fenti halmazok kiegészítő halmazai rendre:

{1,3,5,7,9,...};

{2,3,5,6,7,8,10,...};

{0,1,4,6,8,9,10,12,...}.

Egyszerű dolog algoritmust adni e kiegészítő halmazokra is. Tetszőlegesen adott n természetes számról algoritmikusan eldönthetjük, hogy páros szám-e vagy sem, hogy négyzetszám-e vagy sem, hogy prímszám-e vagy sem. Így mind a halmazt, mind a kiegészítő halmazt előállíthatjuk egy algoritmussal, mert végigfuthatunk sorban a természetes számokon, és mindegyikről eldönthetjük, hogy az eredeti vagy a kiegészítő halmazhoz tartozik-e. Egy halmazt, amely olyan tulajdonságú, hogy maga is és kiegészítő halmaza is rekurzívan felsorolható, rekurzív halmaznak nevezünk. Rekurzív halmaz kiegészítő halmaza nyilvánvalóan szintén rekurzív.

Van-e már most olyan halmaz, amely rekurzívan felsorolható, de nem rekurzív? Tartsunk egy pillanatnyi szünetet, hogy megjegyezzük, mit vonna ez maga után. Mivel az ilyen halmaz elemeit elő lehet állítani algoritmussal, módunkban áll eldönteni, hogy egy gyaníthatóan a halmazhoz tartozó elem — és amely, tételezzük fel egy pillanatra, ténylegesen a halmaz eleme — valóban a halmazban van-e. Mindössze annyit kell tennünk, hogy algoritmusunkat végigfuttatjuk a halmaz elemein, amíg végül megtaláljuk a vizsgálandó elemet. Tegyük fel azonban, hogy gyanúsított elemünk ténylegesen nincs a halmazban. Algoritmusunk ebben az esetben semmi jóval nem kecsegtet, mert fut a végtelenségig, soha nem jut döntésre. Ehhez a kiegészítő halmazt előállító algoritmusra volna szükségünk. Ha az megtalálja gyanúsítottunkat, akkor biztosan tudjuk, hogy az elem nincs a halmazban. Mindkét algoritmussal könnyű dolgunk lenne. Egyszerűen váltogatnánk a két algoritmust, és valamelyik elkapná a gyanúsítottat. Ez a kellemes helyzet azonban csak a rekurzív halmazoknál valósul meg. Halmazunk most a feltevés szerint csupán rekurzívan felsorolható, de nem rekurzív: a kiegészítő halmaz előállítására nem létezik algoritmus! Így az a furcsa helyzet áll elő, hogy egy halmazban lévő elemről algoritmikusan eldönthetjük, hogy az valóban a halmazban van-e, de algoritmussal nem tudjuk biztosan eldönteni e kérdést olyan elemekre, amelyek nincsenek a halmazban!

Előfordulhat-e valaha ilyen furcsa helyzet? Valóban vannak-e rekurzívan felsorolható halmazok, amelyek nem rekurzívak? Mi a helyzet a P halmazzal? Ez rekurzív-e? Tudjuk, hogy rekurzívan felsorolható, ezért azt kell eldöntenünk, hogy kiegészítő halmaza is rekurzívan felsorolható-e. Kiderül, hogy nem! Hogyan tudjuk ezt megmondani? Nos, emlékezzünk vissza, hogy a Turing- gépek műveletei feltevés szerint megengedettek formális rendszerünkön belül. Jelöljük az n-edik Turing-gépet T_n-nel. Ekkor a

,,T_n(n) megáll”

állítás egy propozíció — jelöljük S(n)-nel —, amely formális rendszerünkben minden n természetes számra kifejezhető. Az S(n) propozíció egyes n értékekre igaz, másokra hamis. Az összes S(n) halmaza, miközben n végigfut a 0, 1, 2, 3,.. .természetes számokon, részhalmaza lesz N-nek. Idézzük most fel Turing alapvető eredményét (2. fejezet, 78. o.), amely szerint pontosan azokban az esetekben nincs algoritmus, amely megállapítja, hogy ,,T„(n) nem áll meg”, amelyekben T„(n) ténylegesen nem áll meg. Ez azt mutatja, hogy a hamis S(n)-ek halmaza nem sorolható fel rekurzívan.

Figyeljük meg, hogy 5-nek az a része, amely P-ben fekszik, pontosan az igaz S(n)-ekét tartalmazza. Miért? Ha egy S(n) bizonyítható, akkor igaznak kell lennie (mert formális rendszerünket „ésszerűnek” választottuk!), így S- nek P-ben fekvő része kizárólag az igaz S(n) propozíciókat tartalmazhatja. Továbbmenve, igaz S(n) propozíció nem lehet P-n kívül, mert ha T_n(n) megáll, akkor a rendszeren belül bebizonyíthatjuk, hogy valóban ezt teszi.*

Tegyük most fel, hogy P kiegészítője rekurzívan felsorolható. Ekkor van algoritmusunk e kiegészítő halmaz elemeinek előállítására. Futtathatjuk ezt az algoritmust, és lejegyezhetünk minden S (n) propozíciót, amelyet megkapunk. Ez az összes hamis S(n), így eljárásunk a hamis S(n)-ek halmazának rekurzív felsorolását adná. De az előbb már megjegyeztük, hogy a hamis 5(n)-ek nem sorolhatók fel rekurzívan. Az ellentmondásból következik, hogy P kiegészítője nem lehet rekurzívan felsorolható; így a P halmaz nem rekurzív, amit bizonyítani akartunk.

Ezek a tulajdonságok azt bizonyítják, hogy formális rendszerünk nem lehet teljes: azaz kell, hogy legyenek propozíciók, amelyek a rendszeren belül sem nem bizonyíthatók, sem nem cáfolhatók. Mert ha ilyen „eldönthetetlen” propozíció nem lenne, akkor a P halmaz kiegészítője a cáfolható propozíciók halmaza kellene legyen (minden, ami nem bizonyítható, cáfolható kellene legyen). Láttuk azonban, hogy a cáfolható propozíciók rekurzívan felsorolható halmazt képeznek, így ez P-t rekurzívvá tenné. Ám P nem rekurzív — ez ellentmondás, amely bizonyítja a nemteljességet. Ez Gödel tételének fő döfése.

Mit mondhatunk N T részhalmazáról, amely formális rendszerünk igaz prepozícióit ábrázolja? Rekurzív-e T? Rekurzívan felsorolható-e? T kiegészítője rekurzívan felsorolható-e? Mindezen kérdésekre a válasz: „nem”. Egy lehetséges út ennek megmutatására az, hogy észrevesszük, hogy a

,,T_n(n) megáll”

alakú hamis propozíciók, mint előbb megjegyeztük, nem állíthatók elő algoritmussal. Ezért a hamis propozíciók összességükben nem állíthatók elő algoritmussal, mert tetszőleges ilyen algoritmus egyebek között felsorolná az összes fenti ,,T_n(n) megáll” hamis propozíciót. Hasonlóképpen az összes igaz propozíció sem állítható elő algoritmussal (mert egy ilyen algoritmus triviálisan módosítható volna, hogy az összes hamis propozíciót állítsa elő: egyszerűen venni kellene minden előállított propozíció tagadását).

*A bizonyítás egy olyan lépéssorozatból állhatna, amely tükrözné a futó gép hatását, amíg meg nem áll. A bizonyítás befejeződne, amikor a gép megáll.

 

Mivel így az igaz propozíciók nem rekurzívan felsorolhatók (és a hamisak sem), ezért lényegesen összetettebb és mélyebb elrendezést képeznek, mint a rendszeren belül bizonyítható propozíciók. Ez megint Gödel tételének egy megvilágítása: a matematikai igazság fogalma formális bizonyítással csak részben hozzáférhető.

4.1. ábra. Egy rekurzív halmaz nagyon vázlatos ábrázolása

Az igaz aritmetikai prepozícióknak vannak bizonyos egyszerű osztályai, amelyek rekurzívan felsorolható halmazokat alkotnak. Például a

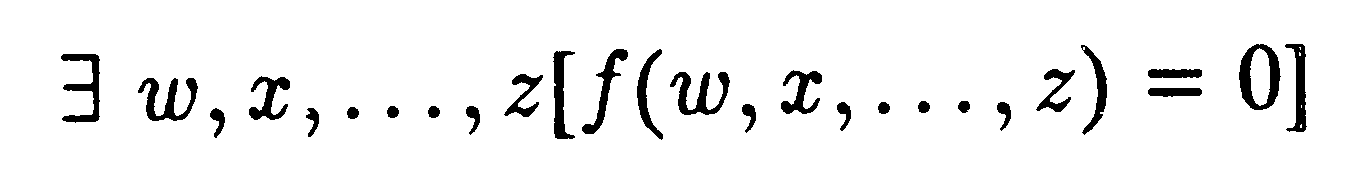
alakú igaz propozíciók, ahol f( ) az összeadás, kivonás, szorzás és hatványozás közönséges aritmetikai műveleteiből felépített függvény, rekurzívan felsorolható halmazt alkotnak (amelyet A-val fogok jelölni), amit nem túl nehéz látni.⁸ Ilyen alakú prepozícióra példa — noha nem tudjuk, hogy igaz-e — „Fermat utolsó tételének” tagadása, amelynél az f( ) függvényt a következőképpen írhatjuk:

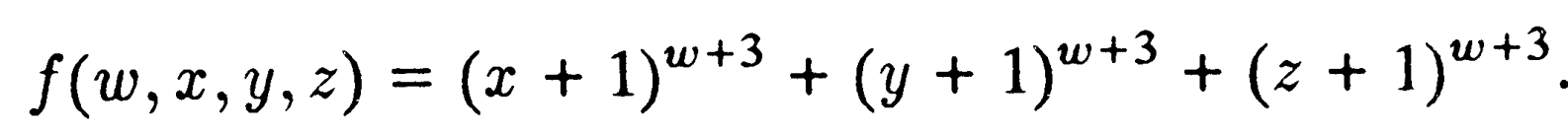
Az A halmaz azonban nem rekurzív (ezt nem túl könnyű látni — bár következménye Gödel eredeti gondolatmenetének). így algoritmikus módon még elvileg sem tudjuk eldönteni „Fermat utolsó tételének” igazságát vagy hamisságát!

A 4.1. ábrán egy rekurzív halmazt próbáltam vázlatosan ábrázolni, mint egy szép egyszerű határvonalakkal rendelkező tartományt; elképzelhetjük, hogy közvetlenül meg lehet mondani, egy adott pont a halmazhoz tartozik-e vagy sem.

4.2 ábra. Egy rekurzívan felsorolható, de nem rekurzív halmaz (fekete tartomány) nagyon vázlatos ábrázolása. Az elgondolás az, hogy a fehér tartomány csak azzal van meghatározva, „ami marad”, ha a kiszámíthatóan előállított fekete tartományt előállítjuk; és nem kiszámítható dolog azt kideríteni, hogy egy pont ténylegesen a fehér tartományban van-e

4.3 ábra. Propozíciók különböző halmazai nagyon vázlatosan ábrázolva. A rendszeren belül bizonyítható propozíciók P halmaza rekurzívan felsorolható, de nem rekurzív; az igaz propozíciók T halmaza még csak nem is sorolható fel rekurzívan

A képen minden pont egy természetes számot ábrázol. A kiegészítő halmazt szintén egyszerűnek látszó tartomány ábrázolja. A 4.2. ábrán egy rekurzívan felsorolható, de nem rekurzív halmazt próbáltam ábrázolni, mint egy bonyolult határvonalú halmazt. A határ egyik oldalán lévő halmaz — a rekurzívan felsorolható oldal — az elképzelés szerint egyszerűbbnek látszik, mint a másik halmaz. Az ábrák nagyon vázlatosak, és semmilyen értelemben nem szántam „geometriailag pontosnak” azokat. Így nincs jelentősége annak sem, hogy e képeket sima kétdimenziós síkon ábrázoltam! A 4.3. ábrán azt mutattam be vázlatosan, hogyan fekszenek a P, T és A tartományok az N halmazon belül.

Rekurzív-e a Mandelbrot-halmaz?

A nem rekurzív halmazoknak meg kell legyen az a tulajdonságuk, hogy nagyon lényeges módon bonyolultak. Bonyolultságuknak bizonyos értelemben le kell győznie minden rendszerezési kísérletet, különben maga a rendszerezés vezetne megfelelő algoritmikus eljáráshoz. Nem rekurzív halmaznál nincs általános algoritmikus út annak eldöntésére, hogy egy elem (vagy „pont”) a halmazhoz tartozik-e vagy sem. A 3. fejezet elején láttunk egy rendkívül bonyolultan kinéző halmazt, a Mandelbrot-halmazt. Bár a meghatározását adó szabályok meglepően egyszerűek, maga a halmaz nagyon bonyolult szerkezetek végtelen változatosságát mutatja. Lehet, hogy a nem rekurzív halmazok egyike mutatkozott meg halandó szemeink előtt?

Ám az Olvasónak hamar eszébe jut majd, hogy a bonyolultságnak ezt a mintapéldányát a modern nagy sebességű elektronikus számítógépek technológiájának varázslata idézte fel szemünk számára láthatóan. Nem az algoritmikus működés megtestesülései-e az elektronikus számítógépek? Valóban, ez biztosan igaz, de nem szabad elfelejtenünk, milyen módon hozza létre a számítógép ezeket a képeket. A számítógép úgy ellenőrzi, hogy az Argand-sík egy pontja egy c komplex szám — a (feketére színezett) Mandelbrot-halmazhoz vagy a (fehéren hagyott) kiegészítő halmazhoz tartozik-e, hogy elindul a 0-tól, majd z = 0-ra alkalmazza a

z -> z² + c

leképezést, így kapja c-t, akkor z = c-re alkalmazva c² + c-t, majd z = c² + c- re alkalmazva c⁴ + 2c³ + c² + c-t és így tovább. Ha ez a 0, c, c² + c, c⁴ + 2c³ + c²+c, ... sorozat korlátos marad, akkor a c-t ábrázoló pontot feketére színezzük, egyébként fehér marad. Hogyan mondja meg a gép, hogy az ilyen sorozat korlátos marad-e vagy sem? Elvileg ismernie kell a sorozat végtelen számú tagját!' Ez nem kiszámítható dolog. Szerencsére vannak módok arra, hogy a sorozatnak csak véges tagját ismerve megmondjuk, ha a sorozat nemkorlátossá válik. (Ha eléri az origó középpontú, 1 + gyök(2) sugarú kört, akkor biztos, hogy nem korlátos.)

Így bizonyos értelemben a Mandelbrot-halmaz kiegészítője (azaz a fehér tartomány) rekurzívan felsorolható. Ha a c komplex szám a fehér tartományban van, akkor ennek a ténynek kiderítésére van algoritmus. Mi a helyzet magával a Mandelbrot-halmazzal — a fekete tartománnyal? Van-e algoritmus annak biztos megállapítására, hogy egy, a fekete tartományban sejtett pont valóban a fekete tartományban van-e? Erre a kérdésre a válasz jelenleg nem ismert.⁹ Sok munkatársammal, szakértőkkel konzultáltam, egyikük sem tudott ilyen algoritmusról. Nem találkoztak annak bizonyításával sem, hogy ilyen algoritmus nem létezik. A fekete tartományra, legalábbis úgy látszik, nincs ismert algoritmus. Lehet, hogy a Mandelbrot-halmaz kiegészítő halmaza valóban olyan rekurzívan felsorolható halmaz, amely nem rekurzív!

Mielőtt e sejtést tovább nyomoznánk, meg kell beszélnünk bizonyos problémákat, amelyeket eddig elkendőztem. Ezeknek majd jelentőségük lesz későbbi vizsgálatainkban a kiszámíthatóságról a fizikában. Az előzőekben valamennyire pontatlan voltam. A „rekurzívan felsorolható” és „rekurzív” kifejezéseket az Argand-sík pontjainak halmazaira alkalmaztam, azaz komplex számok halmazaira. Ezeket a kifejezéseket szigorúan véve csak a természetes számokra vagy más, megszámlálható halmazokra használhatjuk. A 3. fejezetben (105. o.) láttuk, hogy a valós számok nem megszámlálhatóak, így a komplex számok sem lehetnek azok — mert a valós számok speciális komplex számoknak tekinthetők, nevezetesen olyanoknak, amelyek képzetes része eltűnik (vő. 110. o.). A valóságban pontosan „olyan sok” komplex szám van, mint amennyi valós, nevezetesen „C”. (A komplex és valós számok között úgy lehet például egy-egy értelmű kapcsolatot létesíteni, hogy vesszük minden komplex szám valós és képzetes részének tizedes kifejtését, és ezekből felváltva véve jegyeket, összefésüljük őket: a 3,6781...+ i 512,975... komplex szám például az 50132,6977851 valós számnak felel meg.)

E probléma elkerülésének egyik módja az lehetne, ha csak a kiszámítható komplex számokra szorítkoznánk, mert a 3. fejezetben láttuk, hogy a kiszámítható valós számok — és ezért a kiszámítható komplex számok is — valóban megszámlálhatók. Ám van ezzel egy komoly nehézség: nincs általános algoritmus annak eldöntésére, hogy két, megfelelő algoritmusukkal adott, kiszámítható szám egyenlő-e egymással vagy sem! (Különbségüket képezhetjük algoritmikusan, de azt nem tudjuk algoritmikusan eldönteni, hogy e különbség nulla-e vagy sem. Képzeljünk el két algoritmust, amelyek rendre a 0,99999... és 1,00000... jegyeket állítják elő, de soha nem tudhatjuk, hogy a 9-esek vagy a 0-k a végtelenségig folytatódnak-e, azaz a két szám egyenlő, vagy egyszer csak más jegy is megjelenik, és a számok nem egyenlőek.) így soha nem tudhatjuk, hogy e két szám egyenlő-e. Ennek velejárója, hogy még az olyan egyszerű halmazra, mint az Argand-sík egység-körlemeze (azon pontok halmaza, amelyek távolsága az origótól nem nagyobb egy egységnél, azaz a fekete tartomány a 4.4. ábrán) nem lenne algoritmus annak biztos eldöntésére, hogy egy komplex szám rajta van-e a körlemezen. A probléma nem a tartomány belső pontjainál (nem is a körlemezen kívül lévőknél), hanem pont a körlemez szélén, azaz magán az egységkörön fekvőknél lép fel. Az egységkört a körlemez részének tekintjük. Tegyük fel, hogy van egy algoritmusunk, amely előállítja egy komplex szám valós és képzetes részének jegyeit. Ha gyanítjuk is, hogy e komplex szám ténylegesen az egységkörön fekszik, nem tudunk erről kétséget kizáróan megbizonyosodni. Nincs algoritmus annak eldöntésére, hogy az

x² + y²

kiszámítható szám valóban egyenlő-e 1-gyel vagy sem, lévén ez a feltétele annak, hogy az x + iy kiszámítható komplex szám az egységkörön fekszik-e vagy sem.

4.4. ábra. Az egység-körlemeznek kétségtelenül „rekurzívnak” kellene számítania, ám ehhez megfelelő nézőpont szükséges

Világos, hogy nem ez az, amit akarunk. Az egység-körlemeznek bizonyára rekurzívnak kellene számítania! Nincs sok nála egyszerűbb halmaz! A probléma megkerülésének egy módja az volna, hogy a határvonalat figyelmen kívül hagyjuk. A belső vagy a külső rész pontjainál biztosan létezik algoritmus e tény kiderítésére. (Állítsuk elő egyszerűen x² + y² jegyeit, egyiket a másik után, és egyszer csak találunk a tizedespont után egy 9-től különböző jegyet a 0,99999... -ben vagy egy 0-tól különböző jegyet az 1,00000... -ban.) Ebben az értelemben az egység-körlemez rekurzív. Matematikailag azonban e nézőpont eléggé veszélyes, mert a bizonyításokban gyakran az a lényeges, mi történik a határokon. Lehet viszont, hogy a fizika számára megfelelő az ilyen szemlélet. Később majd újra meg kell fontolnunk ezt a kérdést.

Elfogadhatunk egy másik, rokon nézőpontot, amely egyáltalán nem hivatkozik a kiszámítható komplex számokra. Ahelyett, hogy a kérdéses halmazon belül vagy kívül fekvő komplex számokat próbálnánk felsorolni, olyan algoritmust keresünk, amely adott komplex számra eldönti, hogy a halmazban vagy a halmaz kiegészítőjében fekszik-e. Az „adott” szón azt értem, hogy minden ellenőrzésre kerülő komplex számnál — esetleg valamilyen bűvös úton — megkapjuk a valós és képzetes rész egymás után következő jegyeit, annyit, amennyit csak óhajtunk. Nem követelem meg, hogy e jegyek megismerésére legyen ismert vagy ismeretlen algoritmus. A komplex számok egy halmazát „rekurzívan felsorol- hatónak” tekintenénk, ha létezne a következő tulajdonságú algoritmus: amikor csak az elmondott módon megkapná a jegyek ilyen sorozatát, akkor véges számú lépés után akkor és csak akkor mondaná azt, hogy „igen”, ha a komplex szám ténylegesen a halmazban fekszik. Kiderül, hogy ez a nézőpont, akárcsak az előbb javasolt első, „nem vesz tudomást” a határokról. Így ebben az értelemben az egység-körlemez belseje és külseje is rekurzívan felsorolhatónak számítana, míg maga a határvonal nem.

Számomra nem egészen világos, hogy e nézőpontok egyike vagy másika az, amire igazán szükségünk van.¹⁰ A Mandelbrot-halmazra alkalmazva a „határról nem veszünk tudomást” filozófia sokat elveszthet a halmaz bonyolultságából. E halmaz részben „foltokból” — belső résszel rendelkező tartományokból —, részben „indákból” áll. A legszélsőségesebb bonyodalmak az indáknál látszanak, amelyek a legvadabbul tekereghetnek. Az indák azonban nem fekszenek a halmaz belsejében, így „nem vennénk tudomást róluk”, ha elfogadnánk e két filozófia egyikét. Még így, csak a foltokat tekintve sem világos, hogy a Mandelbrot-halmaz rekurzív-e. A kérdés, úgy látszik, egy a halmazra vonatkozó, nem bizonyított sejtésen nyugszik: olyan-e ez a halmaz, mint amilyet „lokálisan összefüggő”-nek neveznek? Nem szándékozom most magyarázni e kijelentés értelmét vagy fontosságát. Csupán azt kívánom jelezni, hogy ezek nehéz problémák, és a Mandelbrot-halmazzal kapcsolatban olyan kérdéseket vetnek fel, amelyek még megoldatlanok, és amelyek közül egyesek a jelenlegi matematikai kutatások élvonalába tartoznak.

Vannak más elfogadható nézőpontok is annak a problémának megkerülésére, hogy a komplex számok nem megszámlálhatóak. Ahelyett, hogy az összes kiszámítható komplex számot tekintenénk, szorítkozhatunk e számok egy megfelelő részhalmazára, amelynek az a tulajdonsága, hogy kiszámítható módon eldönthető, egyenlő-e két eleme vagy sem. Egy egyszerű ilyen részhalmaz a ,racionális" komplex számok halmaza, amelyek valós és képzetes része egyaránt racionális. Nem hiszem azonban, hogy sokat mondana a Mandelbrot- halmaz indáiról, lévén e nézőpont nagyon korlátozó. Valamivel kielégítőbb lenne az algebrai számok használata — azoké a komplex számoké, amelyek egész együtthatós algebrai egyenletek megoldásai.

4.5. ábra. Az y >= e^x exponenciális összefüggés által definiált halmaz is „rekurzívnak” kellene számítson

 

Például a

12 9z⁷ – 33z⁵ + 725z⁴ + 16z³ -2z-3=0

egyenlet minden megoldása algebrai szám. Az algebrai számok megszámlálhatók és kiszámíthatók, és kiszámítható dolog annak eldöntése, hogy két ilyen szám egyenlő-e. (Kiderül, hogy közülük sok van az egységkörön és a Mandelbrot-halmaz indáin.) A kérdés, ha tetszik, úgy fogalmazható, hogy e számok szerint rekurzív-e a Mandelbrot-halmaz vagy sem.

Lehet, hogy az algebrai számok alkalmasak lennének e két most tárgyalt halmaz esetében, de nem oldják meg általánosságban az összes nehézséget. Tekintsük ugyanis az

y>=e^x

összefüggéssel meghatározott halmazt (a 4.5. ábra fekete tartományát), ahol x + iy(= z) az Argand-sík pontja. A halmaznak és kiegészítőjének belseje rekurzívan felsorolható bármelyik előbb kifejtett nézőpont szerint, azonban a határ, az y = e^x (F. Lindemann 1882-ben bebizonyított nevezetes tétele szerint) csak egyetlen algebrai pontot tartalmaz, nevezetesen a z = i pontot. Ebben az esetben a határ algoritmikus természetének felkutatásában az algebrai számok nem segítenek! Nem lenne nehéz megtalálni a kiszámítható számok egy másik alosztályát, amely kielégítő lenne e speciális esetben, de az emberben megmarad az az erős érzés, hogy a helyes nézőpontot még nem találtuk meg.

A nemrekurzív matematika néhány példája

A matematika nagyon sok területén merülnek fel nem rekurzív problémák. így vizsgálhatjuk az olyan problémák osztályát, amelyekre a válasz vagy „igen”, vagy „nem”, de e két lehetőség közötti választásra nem létezik általános algoritmus. A problémák egyes ilyen osztályai különösen egyszerűnek látszanak.

Először tekintsük azt a problémát, amely az egész együtthatós algebrai egyenletek rendszerének egész megoldásaival foglalkozik. Az ilyen egyenleteket diofantoszi egyenleteknek nevezik (Diofantosz görög matematikus után, aki az i. e. 3. században élt, és az ilyen típusú egyenleteket tanulmányozta). Ilyen egyenletrendszer lehet a következő:

és a probléma annak meghatározása, hogy van-e egész x,y,z megoldás. E speciális esetben van,

x = 13, y = 7, z = 2

megoldása az egyenletrendszernek. Nincs azonban algoritmus a kérdés eldöntésére tetszőleges diofantoszi egyenletek rendszerénél: a diofantoszi aritmetika, alkotórészeinek elemi természete ellenére, a nemalgoritmikus matematika része!*

Valamivel kevésbé elemi példa a sokaságok topologikus ekvivalenciája. Ezt csak röviden említem, mert elképzelhető, hogy van szerepe a 8. fejezetben vizsgált kérdésekben. Hogy megértsük, mi egy „sokaság” , tekintsünk először egy füzér hurkot, amely egydimenziós sokaság, azután egy zárt felületet, egy kétdimenziós sokaságot. Majd próbáljunk elképzelni egyfajta „felületet”, amelynek három vagy magasabb számú dimenziója lehet. Két sokaság „topologikus ekvivalenciája” azt jelenti, hogy az egyik folytonos módon — vágás vagy ragasztás nélkül — a másikba deformálható. így egy gömbfelület és egy kocka felszíne topologikusan ekvivalensek, viszont mindkettő topologikusan inekvivalens egy gyűrű vagy egy teáscsésze felületével — az utóbbi kettő egymással topologikusan ekvivalens. Kétdimenziós sokaságoknál van algoritmus annak eldöntésére, hogy közülük kettő topologikusan ekvivalens-e — ez valójában az egyes felületek „fogantyúi” számának megszámlálása.

*Ez negatív választ ad Hilbertnek a 51. oldalon említett tizedik problémájára. (Lásd például Devlin 1988.) Itt a változók száma nincs megszorítva. Ismert azonban, hogy valójában nincs szükség kilencnél többre, hogy e nemalgoritmikus tulajdonság fennálljon.

 

Három dimenzióban a kérdésre válasz az írás időpontjában nem ismeretes, de négy vagy több dimenzióban az ekvivalencia eldöntésére nincs algoritmus. A négydimenziós esetnek feltehetően van jelentősége a fizikában, mert Einstein általános relativitáselmélete szerint a tér és az idő együtt négyes sokaságot képez (lásd 5. fejezet 232. o.). Geroch és Hartle (1987) azt vetette fel, hogy e nem algoritmikus tulajdonságnak jelentősége lehet a „kvantumgravitációban” (vö. még 8. fejezet).

Tekintsünk egy más típusú, az ún. szóproblémát.¹¹ Tegyük fel, hogy van egy szimbólum ábécénk, és tekintsük e szimbólumok különböző füzéreit, a szavakat. Önmagukban nem kell értelmük legyen, de kapunk egy listát a közöttük fennálló „egyenlőségekről”, amelyet felhasználhatunk, hogy további ilyen „ egyenlőségeket” vezessünk le. Ezt úgy csináljuk, hogy az eredeti listáról szavakat helyettesítünk más (általában hosszabb) szavakba, amelyek részként tartalmazzák azokat. Minden ilyen rész helyettesíthető másikkal, amely a lista szerint egyenlő vele. A probléma annak eldöntése egy adott szópárra, hogy e szabályok szerint „egyenlőek-e” vagy sem.

Kezdeti listánk lehet például a következő:

ÉSZ = ÉS,

VÉS = S,

VÉSZ = CSER,

CSERÉP = ETET,

TETTES = SZŐ.

Ezekből levezethetjük például azt, hogy

ŐSI = ŐSZI

a második, az első majd megint a második egyenlőség behelyettesítésével:

ŐSI = ŐVÉSI = ő VÉSZI = ŐSZI.

A probléma most az, hogy megkaphatjuk-e ilyen helyettesítésekkel egy adott szópár egyik tagját a másikból? Átalakíthatjuk-e például a SZÉPTEVÉS szót az ESŐ szóba vagy a TETTET szót a SŐT szóba? Az első esetben a válasz „igen”, a másodikban „nem”. „Igen” válasz esetén a bizonyítás rendes módja az, hogy mutatunk egy egyenlőségfüzért, amelyben minden szót az előzőből a megengedett „egyenlőségek” felhasználásával kapunk. Így (kövérrel jelölve a cserére kerülő, dőlttel az éppen kicserélt betűket):

SZÉPTEVÉS = VÉSZÉPTEVÉS = VÉSZÉPTES = CSERÉPTES =

= ETETTES = ESZŐ = EVÉSZŐ = EVÉSŐ = ESŐ.

Hogyan állapíthatjuk meg, hogy a megengedett szabályokkal lehetetlen megkapni a TETTET-ből a SŐT-t? Ehhez valamivel többet kell gondolkoznunk, de a dolog nem nehéz, és többféleképpen is megoldható. A legegyszerűbb talán a következő: kezdeti listánk minden „egyenlőségében” az S, a P, a T és az ö betűk összegének párossága mindkét oldalon ugyanolyan. Így e párosság a megengedett helyettesítések során nem változhat. Azonban a TETTET szóban a felsorolt betűk összes száma 4, azaz páros, a SŐT szóban 3, azaz páratlan, következésképp egyik a másikból a megengedett helyettesítésekkel nem kapható meg.

Vegyük észre, hogy amikor két szó „egyenlő”, akkor ezt egy megengedett formális szimbólumfüzérrel tudjuk megmutatni a megadott szabályokat használva; míg abban az esetben, amikor „nem egyenlőek”, akkor az adott szabályokra vonatkozó érvekhez kell folyamodnunk. A szavak „egyenlőségének” megállapítására világos algoritmust használhatunk, amikor csak a szavak ténylegesen egyenlőek. Mindössze lexikografikus listát kell készítenünk a szavak összes lehetséges sorozatáról, majd kihúzni erről minden olyan füzért, amelyben vannak olyan egymást követő szavak, ahol a második a megengedett szabályok alapján nem következik az elsőből. A megmaradt sorozatok adják az összes keresett „egyenlőséget” a szavak között. Nincs azonban ilyen nyilvánvaló általános algoritmus a döntésre, amikor két szó nem „egyenlő”, ekkor e tény megállapítására az „értelemhez” kell folyamodnunk. (Valóban kell némi idő, míg észrevesszük az előbbi „trükköt”, aminek segítségével megállapítottuk, hogy a TETTET és SÓT szavak nem „egyenlőek”. Az értelem esetleg hasznos — de nem szükséges — egy „egyenlőség” létezésének megállapításához is.)

Valójában az előző speciális esetben, amikor a kezdeti listán mindössze öt „egyenlőség” állt, nem túlságosan nehéz algoritmust adni annak kiderítésére, hogy két szó „nem egyenlő”, ha azok valóban „nem egyenlőek”. Ám az ebben az esetben működő algoritmus megtalálásához bizonyos mennyiségű értelem gyakorlatoztatására van szükségünk! Valójában az a helyzet, hogy nincs egyetlen algoritmus, amelyet minden lehetséges kezdeti listára, általánosan fel lehet használni. Ebben az értelemben a szóproblémának nincs algoritmikus megoldása. Az általános szóprobléma a nem rekurzív matematikához tartozik!

Vannak bizonyos speciális kezdeti listák, amelyeknél nincs algoritmus a döntésre, ha két szó nem egyenlő. Egy ilyen a következő:

AH = HA,

OH = HO,

AT = TA,

OT = TO,

TAI = IT,

HOI = IH,

THAT = ITHT.

(Ezt a listát egy G. S. Tseitin és Dana Scott által 1955-ben megadott lista átdolgozásával kaptuk; lásd Gardner 1958, 144. o.) Így ez a speciális szóprobléma önmagában példája a nem rekurzív matematikának abban az értelemben, hogy e speciális kezdeti listát használva nem dönthetjük el algoritmikusan, hogy két adott szó „egyenlő-e” vagy sem.

Az általános szóprobléma a formális matematikai logika („formális rendszerek” stb., amint korábban tárgyaltuk) megfontolásaiból nőtt ki. A kezdeti lista egy axiómarendszer szerepét játssza, a szavak helyettesítési szabálya pedig az eljárás formális szabályaiét. A nem rekurzivitás bizonyítása is ilyen meggondolásokból ered.

Utolsó nem rekurzív matematikai példaként nézzük az euklideszi sík sokszögekkel való lefedésének kérdését. Adott véges számú különböző alakzat, és azt kérdezzük, le lehet-e fedni kizárólag ezekkel a síkot tökéletesen, rések és átfedések nélkül. Az alakzatok ilyen elrendezését a sík egy parkettázásának nevezik. Jól tudjuk, hogy csak négyzetekkel vagy csak egyenlő oldalú háromszögekkel vagy csak szabályos hatszögekkel (10. fejezet, 10.2. ábra) az ilyen parkettázás lehetséges, de csak szabályos ötszögekkel nem. A sík sokféle más alakzattal parkettázható, mint például a 4.6. ábrákon bemutatott kétféle szabálytalan ötszög bármelyikével. Két alakzattal a parkettázás szebben kidolgozott lehet. A 4.7. ábrán két egyszerű példa látható. Mindezeknek a példáknak megvan az a tulajdonsága, hogy periodikusak, két független irányban pontosan ismétlődnek. Matematikai nyelven azt mondjuk, hogy van egy periódusparalelogramma — egy paralelogramma, amelyet valahogy megjelölve és a két irányban oldalaival párhuzamosan újra és újra lerakva megkapjuk az adott parkettamintát. Egy példa a 4.8. ábrán látható, a bal oldal periodikus parkettázást mutat egy kürt alakú parkettával, a jobb oldal a kapcsolatot mutatja a periódus-paralelogrammával való periodikus parkettázással.

A síknak sok olyan parkettázása van, amely nem periodikus. A 4.9. ábra három nem periodikus „spirális” parkettázást mutat, ugyanazzal a kürt alakú parkettával, mint amely a 4.8. ábrán látható. E speciális parkettaalak (nyilvánvaló okokból!) „sokoldalú” néven ismert, B. Grünbaum és G. C. Shephard (1981, 1987) javasolták, H. Voderberg egy korábbi alakzatából kiindulva. Érdekes, hogy a sokoldalúval periodikusan és nem periodikusan egyaránt lehet parkettázni.

 

E tulajdonságban osztozik sok más, egyetlen parkettából vagy több alakzatból álló rendszer is. Van-e olyan egyetlen parketta vagy parketta rendszer, amellyel a síkot csak nem periodikusan lehet a síkot lefedni? A kérdésre a válasz „igen”. A 4.10. ábrán egy hat parkettából álló halmaz látható, amelyet Raphael Robinson amerikai matematikus szerkesztett; ezzel a teljes sík lefedhető, de csak nem periodikus módon.

4.9. ábra. Három nem periodikus, „spirális” parkettázás, mindhárom azzal a „sokoldalú” alakzattal, amely a 4.8. ábrán látható

 

Érdemes egy kicsit áttekinteni annak történetét, hogyan születtek ezek a nem periodikus parkettázások (vö. Grünbaum és Shephard 1987). A kínai-amerikai logista, Hao Wang 1961-ben azt a kérdést vetette fel, hogy létezik-e vagy sem döntési eljárás a parkettázási problémára, azaz van-e algoritmus annak eldöntésére, hogy a teljes sík lefedhető-e vagy sem különböző sokszögek véges halmazával!* Meg tudta mutatni, hogy valóban volna ilyen döntési eljárás, ha meg lehetne mutatni azt, hogy különböző parketták minden véges halmazával, amelyekkel a sík valahogy lefedhető, lefedhető periodikusan is. Gondolom, akkoriban úgy érezték, nagyon valószínűtlen, hogy létezhet ezt a feltételt sértő halmaz — azaz parketták egy „aperiodikus” halmaza.

*Hao Wang ténylegesen egy kissé különböző problémát vizsgált — négyszög parkettával, forgatás nélkül és a színnel megjelölt élek összeillesztésével, de az eltérések nem lényegesek számunkra.

 

4.10. ábra. Raphael Robinson hat parkettája, amelyekkel a sík csak nem periodikusan fedhető le

 

 

Azonban 1966-ban, egyes Hao Wang által javasolt példákat követve, Róbert Berger meg tudta mutatni, hogy a parkettázási problémára nincs döntési eljárás: ez is a nem rekurzív matematika része!¹²

Így Hao Wang korábbi eredményéből következik, hogy léteznie kell aperiodikus parkettahalmaznak, és Berger meg tudta szerkeszteni az első ilyet. Gondolatmenetének bonyolultsága miatt azonban halmaza rettenetesen nagyszámú különböző parkettát tartalmazott — eredetileg 20426-ot. További ügyeskedéssel ezt a számot később 104-re tudta csökkenteni. 1971-ben Raphael Robinsonnak sikerült 6-ra csökkenteni, ez a halmaz látható a 4.10. ábrán.

4.12. ábra. Két pár, mindkettővel csak nemperiodikus parkettázás készíthető („Penrose-parketták”); és a sík egy-egy tartományának lefedése az egyes párokkal

 

Egy másik, hat parkettából álló aperiodikus halmaz a 4.11. ábrán látható. Ezt én szerkesztettem 1973 körül teljesen független gondolatmenetet követve. (A 10. fejezetben majd visszatérek erre, ott a 10.3. ábrán látható egy elrendezés ezekkel az alakzatokkal.) Mikor Robinson hatos aperiodikus halmaza tudomásomra jutott, gondolkodni kezdtem a szám csökkentésén; és változatos vágásokkal és újraragasztásokkal le tudtam menni kettőre. Két különböző lehetőség látható a 4.12. ábrán. A teljes parkettázás szükségszerűen nem periodikus mintázatainak figyelemre méltó tulajdonságaik vannak, közöttük egy látszólagos, kristálytanilag lehetetlen, ötfogású szimmetriát mutató kváziperiodikus szerkezet.

Talán figyelemre méltó, hogy a matematika egy ilyen nyilvánvalóan „triviális” területe — nevezetesen a sík lefedése egyforma alakzatokkal —, amely majdnem a „gyermekjátékhoz” hasonlít, valójában a nem rekurzív matematika része. E területen sok a nehéz és megoldatlan probléma. Nem tudjuk például azt, van-e egyetlen parkettából álló aperiodikus halmaz.

Wang, Berger és Robinson a parkettázási problémában négyszög alapú parkettákat használt. Magam tetszőleges alakú sokszögeket megengedtem; az egyes parketták alakjának kiderítésére szükség volna valamilyen megfelelően kiszámítható módszerre. Egy lehetőség az volna, ha a csúcsokat az Argand- sík pontjaiként adnánk meg, ekkor tökéletesen jól leírhatnánk azokat algebrai számokkal.

A Mandelbrot-halmaz és a nemrekurzív matematika

Térjünk most vissza a Madelbrot-halmazzal foglalkozó korábbi fejtegetésünkhöz. Az illusztráció kedvéért fel fogom tételezni, hogy valamilyen megfelelő értelemben a halmaz nem rekurzív. Ekkor, mivel kiegészítője rekurzívan felsorolható, ezért a halmaz maga nem lehet olyan. Úgy vélem, hogy a Mandelbrot- halmaz egy pár dologra megtanít bennünket a nem rekurzív halmazok és a nem rekurzív matematika természetét illetően.

Térjünk vissza a 3.2. ábrához, amellyel a 3. fejezet elején találkoztunk. Vegyük észre, hogy a halmaz legnagyobb része az a nagy szív alakú tartomány, amelyet a 4.13. ábrán A-val jelöltem. Az alakzat neve kardioid, belsejét úgy lehet matematikailag definiálni, mint az Argand-sík azon c pontjainak halmaza, amelyekre

c = z — z²,

ahol 2 olyan komplex szám, amelynek távolsága a kezdőponttól kisebb, mint 1/2. Ez a halmaz a korábban javasolt értelemben biztosan rekurzívan felsorolható: létezik algoritmus, amely a tartomány egy belső pontjára alkalmazva kimutatja, hogy a pont valóban a tartomány belsejében van. A tényleges algoritmus a fenti képletből könnyen megkapható.

Tekintsük most a fő kardioidtól közvetlenül balra lévő, korongszerű tartományt (a 4.13. ábrán a B tartományt). Belseje a

c = z — 1

pontok halmaza, ahol z távolsága a kezdőponttól kisebb, mint 1/4. E tartomány valóban egy korong belseje — egy egzakt kör belsejében lévő pontok halmaza. Ez a fenti értelemben ismét rekurzívan felsorolható. Mi a helyzet a kardioid többi „szemölcsével”? Nézzük meg közülük a két legnagyobbat. Ezek azok a nagyjából kör alakú foltok, amelyek a 3.2. ábrán közelítőleg a kardioid tetején és alján helyezkednek el, és amelyeket a 4.13. ábrán C₁-gyel és C₂-vel jelöltem. Ezek pontjai a

c³ + 2c² + (1 - z)c + (1 – z)² = 0

egyenlettel adhatók meg, ahol z most a kezdőponttól 1/8-nál kisebb távolságra lévő pontokon fut végig. Valójában az egyenlet nem csak ezt a két foltot adja meg, hanem a 3.2. ábrán balra látható „bébi”-kardioid-szerű alakzatot is a 3.1. ábra fő tartományát — amelyet a 4.13. ábrán C₃-mal jelöltem. E tartományok (együtt vagy külön-külön) újra rekurzívan felsorolható halmazokat képeznek (a korábban javasolt értelemben) egyszerűen azért, mert a fenti képlet létezik.

Korábbi sugalmazásom ellenére, mely szerint a Mandelbrot-halmaz esetleg nem rekurzív, a legnagyobb területeket már tisztába tudtuk tenni teljesen jól területeken a legáltalánosabb problémákat, amelyekbe sokszor beleütközünk, gyakran tudjuk egyszerű algoritmikus eljárásokkal kezelni — amelyek esetleg már évszázadok óta ismertek. Egyesek azonban kiszöknek a hálóból, és kezelésükhöz kifinomultabb eljárásokra van szükség. Az ilyenek természetesen különösen felkeltik a matematikusok érdeklődését, és még hatékonyabb módszerek kidolgozására ösztönzik őket. Ehhez pedig mélyebb és mélyebb bepillantásokra van szükség a matematika e részének természetébe. Talán így értjük meg a fizikai világot is.

A most bemutatott szóproblémákban és parkettázási problémákban egy pillantást vethettünk az ilyen dolgokra (bár ezeken a területeken a matematika gépezetét még nem nagyon fejlesztették ki). Az egyik speciális esetben elég egyszerű érveléssel meg tudtuk mutatni, hogy a megengedett szabályokat alkalmazva egy szó nem kapható meg egy másikból. Nem nehéz elképzelni, hogy a bonyolultabb esetek kezelésére sokkal kifinomultabb gondolatmenetekre lehet szükség. Előfordulhat, hogy ezek az új gondolatmenetek algoritmikus eljárásokká fejleszthetők. Tudjuk, hogy semmiféle eljárás nem oldhatja meg egyszerre az összes szóproblémát, de nagy körültekintéssel és elmésséggel kellene megszerkeszteni a hálóból kiszökő példákat. Mihelyt tudjuk, hogyan épülnek fel ezek a példák — mihelyt biztosan tudjuk, hogy egy speciális eset elillant algoritmusunk elől —, meg tudjuk javítani algoritmusunkat úgy, hogy befogja azt az esetet is. Csak olyan szópárok szökhetnek meg, amelyek nem „egyenlőek”, így amint megtudjuk, hogy megszöktek, tudjuk azt is, hogy nem „egyenlőek”, és ezt a tényt hozzáadhatjuk algoritmusunkhoz. Bepillantásunk tökéletesebb lett, és ez tökéletesebb algoritmushoz vezet!

Bonyolultságelmélet

Az algoritmusok természetéről, létezéséről és korlátairól most és az előző fejezetekben kifejtett érveim nagyon sok tekintetben „elvi” jellegűek voltak. Egyáltalán nem vizsgáltam annak kérdését, hogy a felmerülő algoritmusoknak várhatóan lesz-e gyakorlati értékük. Még azoknál a problémáknál is, amelyeknél világos, hogy léteznek algoritmusok, és az is, hogy hogyan kell ezeket felépíteni, sok ötletességre és kemény munkára lehet szükség, hogy használhatóvá tegyék ezeket az algoritmusokat. Egy kis meglátás és ügyesség olykor jelentősen csökkentheti egy algoritmus bonyolultságát, óriási javuláshoz vezethet a sebességet illetően. Ezek a kérdések gyakran nagyon is a részleteket érintik, technikai jellegűek. Az utóbbi években, sok különböző összefüggésben, nagy munkát végeztek az algoritmusok felépítését, megértését és javítását illetően — gyorsan bővülő és fejlődő munkaterület ez. Nem volna célszerű, ha el akarnék mélyedni e kérdések részletes vizsgálatában. Vannak azonban különféle általános dolgok, ismertek vagy sejtettek, arra vonatkozóan, milyen abszolút korlátai vannak egy algoritmus sebessége növelésének. Kiderül, hogy még az algoritmikus természetű matematikai problémák között is vannak olyan osztályok, amelyekbe tartozókat belső sajátságaiknál fogva sokkal nehezebb algoritmikusan megoldani, mint másokat. A nehezeket csak nagyon lassú algoritmusokkal lehet megoldani (vagy esetleg olyanokkal, amelyek hatalmas tárterületet stb. követelnek). Az ilyen jellegű kérdésekkel foglalkozó elméletet bonyolultságelméletnek nevezik.

A bonyolultságelmélet nem annyira az egyes problémák algoritmikus megoldásának nehézségeivel foglalkozik, hanem végtelen problémacsaládokéval, ahol létezik egy általános algoritmus, amelynek segítségével egy család minden problémája megválaszolható. A család különböző problémái különböző „méretűek”, a probléma méretét egy n természetes szám méri. (Mindjárt mondok majd többet arról, hogyan is jellemzi ez az n szám a probléma méretét.) Az időtartam — vagy helyesebben az elemi lépések száma —, amelyre az algoritmusnak az osztály egyes speciális problémáinál szüksége van, valamely N természetes számmal adható meg, amely függ n-től. Egy kicsit pontosabban mondjuk azt, hogy az összes n méretű probléma közül az algoritmus által megtett legnagyobb lépésszám N. Na már most: ahogy n egyre nagyobb és nagyobb, a N szám is egyre nagyobb és nagyobb lesz. N általában sokkal gyorsabban nő, mint n. Például N közelítőleg arányos lehet n²-tel vagy n³-bel vagy esetleg 2ⁿ-nel (ami nagy n-re sokkal nagyobb, mint n, n², n³, n⁴ és n⁵ akármelyiké — valójában nagyobb, mint n^r minden rögzített r mellett), sőt közelítőleg arányos lehet (2²)ⁿ-nel (ami még sokkal nagyobb).

A „lépések” száma természetesen függhet a számítógép típusától, amelyen az algoritmus fut. Ha a számítógép a 2. fejezetben leírt típusú Turing-gép, amelynél csak egyetlen szalag van — ami igen rossz hatásfokú — akkor az N szám gyorsabban nőhet (azaz a gép lassabban futhat), mint ha két vagy több szalagot is megengedünk. Az ilyen jellegű bizonytalanságok elkerülésére nagyon széles osztályokat állítottak fel aszerint, hogy n milyen függvénye szerint nő az N, így — függetlenül a használt Turing-gép típusától — N növekedési sebességének mértéke mindig ugyanabba az osztályba esik. Az egyik ilyen osztály, amelyet P-vel jelölnek (a „polinomiális időre” utalva), magában foglalja az összes sebességet, amely legfeljebb az n, n², n³, n⁴, n⁵,... valamelyikének rögzített számszorosa.* Azaz minden, a P osztályba tartozó problémára (ahol „problémán” tulajdonképpen problémák egy általános algoritmussal megoldható családját értem) fennáll, hogy

N <= K • n^r,

a K és r számok (n-től független) állandók. Ez azt jelenti, hogy az N nem nagyobb, mint az n valamilyen hatványának számszorosa.

Egy egyszerű problématípus, amely biztosan P-be tartozik, két szám összeszorzása. Ennek magyarázatához először azt mondom el, hogyan jellemzi az n szám annak a speciális számpárnak a méretét, amelyeket össze akarunk szorozni. Elképzelhetjük, hogy mindkét számot kettes számrendszerben írjuk fel, és hogy n/ 2 az egyes számok bináris jegyeinek száma, ami összesen n bináris jegy — azaz n bit. (Ha az egyik szám hosszabb, mint a másik, akkor a rövidebbet annyi nullával kezdjük, hogy a hosszuk egyenlő legyen.) Ha például n = 14 akkor tekinthetjük a

1011010 • 0011011

szorzást (ami 1011010 • 11011, csak a rövidebb szám elé nullákat írtunk).

A szorzás elvégzése előtt emlékeztetünk arra, hogy bináris rendszerben:

 

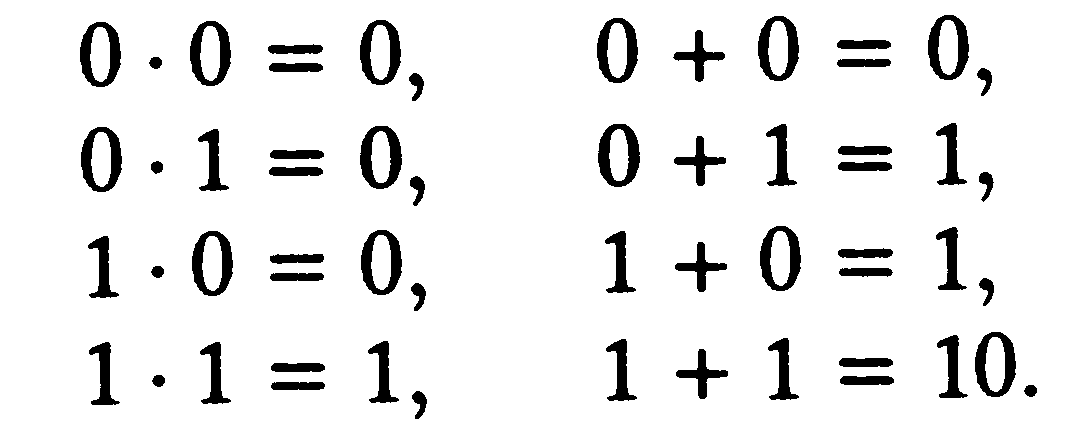
*A „polinomiális” szó tulajdonképpen olyan általánosabb kifejezésre utal, mint például 7n⁴ — 3n⁵ + 6n + 15, de ez igazából nem jelent nagyobb általánosságot. Minden ilyen kifejezésben n összes alacsonyabb hatványa lényegtelenné válik, amikor n nagyon nagy (így speciális példánkban a 7n⁴ kivételével az összes tagot elhagyhatjuk).

 

A szorzás végrehajtásának legközvetlenebb módja az, hogy kiírjuk:

Az egyedi bináris szorzások száma (n/2) •(n/2) = n²/4, és lehet még legfeljebb (n²)/4 - (n/2) egyedi bináris összeadás (az átvitellel együtt). Ez összesen (n²/2) - (n/2) egyedi aritmetikai műveletet jelent — amihez jön még néhány, az átvitelben fellépő logikai lépések miatt. A lépések teljes száma lényegében N = n²/2 (elhagyva az alacsonyabb rendű tagokat), ami biztosan polinomiális¹³.

Egy problémaosztályon belül a probléma „méretének” n nagysága a bináris jegyek (vagy bitek) teljes száma, amely az ilyen méretű probléma szabad adatainak leírásához szükséges. Ez azt jelenti, hogy adott n mellett az ilyen méretű problémának 2ⁿ különböző példánya lehet (mert minden jegy kétféle lehet, 0 vagy 1, és összesen n jegy van), és az algoritmusnak ezekkel egyformán kell megbirkóznia nem több, mint N lépésben.

Sok olyan probléma(osztály) van, amelyek nem P-ben vannak. Amikor például az r természetes számból kiszámítjuk 2^2r értékét, csak a válasz leírásához kb. 2ⁿ lépésre van szükségünk, nem is beszélve a számítás végrehajtásáról; n a bináris jegyek száma r bináris ábrázolásában. 2² kiszámításánál csupán a leírás 2^2r körüli lépést vesz igénybe stb.! Ezek a polinomiálisnál sokkal nagyobbak, így biztosan nincsenek P-ben!

Érdekesebbek azok a problémák, amelyeknél polinomiális idő alatt le lehet írni a választ, sőt még ellenőrizni is lehet helyességét. A problémák (algoritmikusan megoldható részének) fontos osztályát jellemzi ez a tulajdonság. Ezeket NP problémáknak (osztályoknak) nevezik. Pontosabban szólva, ha egy NP-ben lévő problémaosztály egy problémájának van megoldása, akkor az algoritmus megadja ezt a megoldást, és polinomiális idő alatt ellenőrizhető kell legyen, hogy a javasolt megoldás valóban megoldás. Azokban az esetekben, amikor a problémának nincs megoldása, az algoritmus ezt megmondja, de ellenőrizni nem kell — polinomiális időben vagy máshogy —, hogy valóban nincs megoldás.¹⁴

4.14. ábra. Egy gráf, benne egy (valamivel sötétebb vonallal jelzett) Hamilton-körrel. Van még egy másik is benne, amelyet az Olvasó kereshet meg

 

NP problémák sok összefüggésben felbukkannak mind magán a matematikán belül, mind a gyakorlati világban. Mondok egy egyszerű matematikai példát: azt a problémát, hogyan találjunk egy gráfban olyat, amit „Hamilton- kör”-nek neveznek (meglehetősen ijesztő név egy rendkívül egyszerű dologra). „Gráfon” pontok vagy „csúcsok” véges együttesét értjük, amelyben bizonyos számú pár össze van kötve vonalakkal — ezek a gráf „élei . (Most nem érdekelnek a geometriai vagy a „távolság”-tulajdonságok, csak az, melyik csúcs melyik csúccsal van összekötve. így nem számít, hogy a csúcsok egy síkban vannak-e — feltéve, hogy nem törődünk az élek kereszteződéseivel vagy háromdimenziós térben.) A Hamilton-kör egy zárt út (vagy hurok), amely csak a gráf éleiből áll, és minden csúcson pontosan egyszer megy keresztül. A 4.14. ábrán példaként egy gráf látható, benne egy Hamilton-körrel. A Hamilton-kör probléma annak eldöntése, hogy tetszőlegesen adott gráfban létezik-e Hamilton-kör vagy sem, és, amikor létezik, akkor egy ilyen explicit megadása.

Sokféle módon lehet gráfokat bináris jegyek segítségével megadni. Nem sokat számít, melyik módszert használjuk. Egy lehetséges eljárás a csúcsok 1, 3, 4, 5, ... megszámozása, majd a párok felsorolása alkalmasan rögzített sorrendben:

(1,2), (1,3), (2,3), (1,4), (2,4), (3,4), (1,5), (2,5), (3,5), (4,5), (1,6),... Ezután ehhez illeszkedő, pontos listát készítünk „0”-kból és „1”-ekből: „1”-et teszünk, ha a pár megfelel a gráf egy élének, „0”-t, ha nem. Így a

10010110110...

bináris sorozat azt jelöli, hogy az 1 csúcs össze van kötve a 2, a 4 és az 5 csúccsal, ... a 3 csúcs össze van kötve a 4 és az 5 csúccsal, ... a 4 csúcs össze van kötve az 5 csúccsal, ... stb. (mint a 4.14. ábrán látható). A Hamilton-kört, ha tetszik, meg lehet adni úgy, mint ezen élek egy alrendszerét, amelyet az előbbinél sokkal több nullát tartalmazó sorozat ír le. Az ellenőrzés sokkal gyorsabban hajtható végre, mint a Hamilton-kör megtalálása. Mindössze azt kell ellenőrizni, hogy a javasolt kör valóban kör-e, élei valóban az eredeti gráf élei között vannak-e, és hogy a gráf minden csúcsa pontosan kétszer szerepel-e egyszer-egyszer két él végpontjaként. Az ellenőrzési eljárás könnyen végrehajtható polinomiális időben.

E probléma valójában nemcsak NP, hanem ún. NP-teljes. Ez azt jelenti, hogy tetszőleges más NP probléma átalakítható ebbe polinomiális idő alatt — így ha valaki elegendően okos lenne, és találna egy algoritmust, amely polinomiális idő alatt megoldja a Hamilton-kör problémát, azaz megmutatná, hogy a probléma valóban P-ben van, akkor ebből következne, hogy minden NP probléma P-ben van! Ebből nagyon fontos dolgok következnének. Egy P-ben lévő problémát általánosan kezelhetőnek” (azaz „elfogadható idő alatt megoldhatónak”) tekintenek, gyors modern számítógépen, ésszerűen nagy n mellett, míg egy NP-ben lévőt, amely nincs P-ben, „Kezelhetetlennek" (azaz bár elvileg megoldhatónak, „gyakorlatilag megoldhatatlannak”) ésszerűen nagy n mellett — függetlenül a számítógépek műveleti sebességében bekövetkezhető, bármilyen jellegű növekedéstől. (Az az idő, amennyit egy nem P-ben lévő NP probléma megoldása ténylegesen igénybe venne, nagy n-re gyorsan felülmúlná a világegyetem életkorát, ami gyakorlati problémánál nem sok reménnyel kecsegtet!) Bármilyen okos algoritmus, amely polinomiális idő alatt megoldja a Hamilton- kör problémát, átalakítható volna olyan algoritmusba, amely polinomiális idő alatt megold tetszőleges más NP problémát!

Egy másik, NP-teljes probléma^ls „az utazó kereskedő problémája”, amely meglehetősen hasonlít a Hamilton-kör problémához, csak ebben az élekhez számok vannak rendelve, és azt a Hamilton-kört keresi, amelyre a számok összege (a kereskedő által beutazott „távolság”) minimális. Az utazó kereskedő problémájának polinomiális idő alatti megoldása ismét minden más NP probléma polinomiális idő alatti megoldásához vezetne. (Ha ilyen megoldást találnának, az címoldalra kerülő újsághír lenne! Ott vannak ugyanis a titkos kódrendszerek, amelyeket az elmúlt néhány év során vezettek be, és amelyek a nagy egész számok szorzattá bontásának problémájára támaszkodnak, lévén ez egy másik NP probléma. Ha ez megoldható volna polinomiális idő alatt, ak

kor az ilyen kódokat a nagy teljesítményű, modern számítógépek valószínűleg könnyen megfejtenék, de ha nem, akkor a kódok biztonságban vannak. (Lásd Gardner 1989.)

A szakértők között általános az a vélemény, hogy tetszőleges Turing-gép- szerű eszközzel lehetetlen polinomiális idő alatt megoldani egy NP-teljes problémát, és következésképp P és NP nem azonos. Nagyon valószínű, hogy e sejtés igaz, de még senkinek sem sikerült bebizonyítania. Ez marad a bonyolultságelmélet legfontosabb megoldatlan problémája.

Bonyolultság és kiszámíthatóság a fizikai dolgokban

A bonyolultságelmélet fontos a könyvünkben található fejtegetések szempontjából, mert egy másik kérdést kínál, valamennyire eltérőt attól, hogy a dolgok algoritmikusak-e vagy sem: nevezetesen azt, hogy vajon azok a dolgok, amelyekről tudjuk, hogy algoritmikusak, hasznos módon algoritmikusak-e. A későbbi fejezetekben kevesebbet kell majd foglalkoznom a bonyolultságelmélet kérdéseivel, többet a kiszámíthatósággal. Hajlok ugyanis azt hinni (bár kétségtelen, hogy teljesen megalapozatlanul), hogy eltérően a kiszámíthatóság alapvető kérdésétől, a bonyolultságelmélet nem játszik központi szerepet a szellemi jelenségekben. Mi több, úgy érzem, hogy az algoritmusok gyakorlatiasságának kérdéseit a bonyolultságelmélet mai állásában alig érinti.

Persze tévedhetek is a bonyolultság szerepének megítélésében. Amint azt később majd kifejtem (9. fejezet, 430. o.), a bonyolultságelmélet a valódi fizikai objektumokra jelentősen eltérő lehet attól, amit éppen most tárgyaltunk. Hogy e lehetséges különbség láthatóvá váljék, ahhoz ki kellene használni a kvantummechanikának — az atomok és molekulák viselkedése és sok más, esetleg sokkal nagyobb skálán is fontos jelenség e titokzatos, mégis hatékony és pontos elméletének — mágikus tulajdonságait. Ezzel az elmélettel a 6. fejezetben fogunk megismerkedni. A David Deutsch (1985) által felvetett legújabb elképzelések szerint elvileg lehetséges „kvantumszámítógépet” készíteni, amely polinomiális idő alatt megoldhat nem P-ben lévő problémákat. Jelenleg egyáltalán nem világos, hogyan kell olyan valódi fizikai eszközt készíteni, amely (megbízhatóan) úgy viselkedik, mint egy kvantumszámítógép — és ráadásul az eddig számításba vett problémaosztály határozottan mesterséges —, ám az elméleti lehetőség, hogy egy kvantumfizikai eszköz képes lehet tökéletesíteni egy Turing-gépet, úgy látszik, az asztalunkon van.

Lehetséges-e, hogy az emberi agy, amelyet e tárgyalásban „fizikai eszköznek” tekintek, noha meghökkentően finom tervezésűnek és bonyolultnak tartom, kihasználja a kvantumelmélet varázslatait? Értjük-e a módját, hogyan lehet a kvantumos jelenségeket előnyösen felhasználni problémák megoldásában vagy ítéletek kialakításában? Elképzelhető-e, hogy még a mai kvantumelméletnél is „mélyebbre” kell mennünk, hogy e lehetséges előnyöket kiaknázzuk? Reális-e az a lehetőség, hogy valóságos fizikai eszközök tökéletesíthetik a Turing-gépek bonyolultságelméletét? És mit mond a kiszámíthatóság elmélete ezekre az eszközökre?

Hogy e kérdésekkel foglalkozhassunk, el kell hagynunk a tiszta matematikát, és a következő fejezetekben azt kell megvizsgálnunk, hogyan viselkedik a fizika: világ!

Jegyzetek

1. Ha olyan halmazokkal foglalkozunk, amelyek elemei is halmazok lehetnek, óvatosnak kell lennünk a halmaz elemeinek és a halmaz elemei elemeinek megkülönböztetésében. Tegyük fel például, hogy S egy bizonyos T halmaz nem üres részhalmazainak halmaza, T elemei pedig egy alma és egy narancs. T „kettesség” és nem „hármasság” tulajdonságú, S azonban „hármasság” tulajdonságú; három eleme van ugyanis: egy egyetlen almát tartalmazó halmaz, egy egyetlen narancsot tartalmazó halmaz, és egy halmaz, amelyben egy alma és egy narancs van — ez összesen három halmaz. Hasonlóképpen az a halmaz, amelynek egyetlen eleme az üres halmaz₉ „egyesség” és nem „nullaság” tulajdonságú — egy eleme van, nevezetesen az üres halmaz! Magának az üres halmaznak természetesen nulla eleme van.
2. A Gödel-tétel bizonyítását el lehet mondani úgy, hogy az olyan propozícióknál, mint Pk(k), ne támaszkodjék egy teljesen külső „igazság” fogalomra. Ám még ekkor is függ egyes szimbólumok tényleges „jelentésének” értelmezésétől: speciálisan, hogy „~3” valóban azt jelenti, hogy „nincs olyan (természetes szám) ..., hogy ...
3. A következőkben a kis betűk a természetes számokat, a nagyok a természetes számok véges halmazait jelölik. Jelentse m => [n, k, r] a következő állítást: „Ha X természetes számoknak tetszőleges m-elemű halmaza, amelynek k-elemű részhalmazait szétosztottuk r dobozba, akkor X-nek van olyan „nagy” n-elemű Y részhalmaza, hogy Y minden k-elemű részhalmaza ugyanabban a dobozban van.” Itt a „nagy” azt jelenti, hogy Y-nak több eleme van, mint az a természetes szám, amely Y legkisebb eleme. Tekintsük a következő propozíciót: k, r és n tetszőleges megválasztásánál létezik olyan hogy minden m₀-nál nagyobb m-re igaz az m => [n, k, r] állítás”. J. Paris és L. Harrington megmutatták, hogy ez a propozíció az aritmetika szabványos (Peano-féle) axiómái mellett ekvivalens egy Gödel-típusú propozícióval, azokból az axiómákból nem bizonyítható, mégis állít valamit róluk, ami „nyilvánvalóan igaz” (ebben az esetben azt, hogy az axiómákból levezethető propozíciók igazak).
4. A cím: „A logika ordinálokon alapuló rendszerei”, egyes Olvasók számára ismerős lesz a cantori ordinális számok jelölése, amelyet az alsó indexeknél alkalmaztam. A logikai rendszereknek azt a hierarchiáját, amelyet a leírt eljárással kapunk, a kiszámítható ordinális számok jellemzik. Vannak matematikai tételek, amelyek egészen természetesen és könnyen megfogalmazhatók, de ha az aritmetika szokásos (Peano-féle) szabályait használva akarjuk bizonyítani azokat, akkor a fenti „gödelizációs” eljárást kell iszonyatos mértékben alkalmazni (sokkal szélesebbre kiterjesztve, mint amit bemutattam). E tételek matematikai bizonyításai egyáltalán nem támaszkodnak homályos vagy megkérdőjelezhető gondolatmenetekre, amelyek láthatóan kívül fekszenek a rendes matematikai bizonyítási eljárásokon (lásd Smorynski 1983).
5. A kontinuumhipotézis, amelyre a 3. fejezetben, a 107. oldalon utaltunk (és amely azt állítja, hogy C = N₀), a „legszélsőségesebb” matematikai állítás, amellyel e könyvben találkozunk (bár gyakran lehet találkozni ennél sokkal szélsőségesebb állításokkal). Különös érdekessége van, mert maga Gödel, Paul J. Cohennel együtt, megállapította, hogy valójában független a halmazelmélet szabványos axiómáitól és eljárási szabályaitól. így a kontinuumhipotézishez való viszonyulás megkülönbözteti a formalista és platonista nézőpontot. Egy formalista számára a hipotézis „eldönthetetlen”, mert a szokásos (Zermelo—Frankel-féle) formális rendszert használva sem bizonyítani, sem cáfolni nem lehet, ezért „értelmetlen” akár „igaznak”, akár „hamisnak” mondani. Egy jó platonista számára azonban a hipotézis vagy igaz, vagy hamis, de hogy melyik, annak megállapításához a bizonyítás új formáira van szükség — túl kell menni azon, hogy Gödel-típusú propozíciókat a Zermelo—Frankel-féle formális rendszerre alkalmazzanak. [Cohen (1966) egy tükrözési elvet javasolt, amely a kontinuumhipotézist „nyilvánvalóan hamissá” teszi!]
6. E kérdések érdekes és határozottan nem technikai jellegű tárgyalását illetően lásd Rucker (1984).
7. Brouwer, úgy tetszik, részben azért indult el ezen a vonalon, mert gondok gyötörték egyik saját tétele, a topológia „Brouwer-féle fixpont tétele” bizonyításának „nem konstruktív” jellege miatt. A tétel azt állítja, hogy ha veszünk egy korongot — egy kört belsejével együtt —, és folytonosan leképezzük annak a tartománynak a belsejébe, ahol eredetileg volt, akkor lesz legalább egy pontja — egy fix pont —, amely pontosan oda kerül, ahonnan indult. Nem tudhatjuk, hol van pontosan ez a pont, azt sem, hogy lehet-e sok ilyen pont, a tétel csak egy ilyen pont létezését állítja. (A matematikai egzisztenciatételekhez képest ez meglehetősen „konstruktív”. A nemkonstruktivitás más nagyságrendjét jelentik azok az egzisztenciatételek, amelyek a „választási axióma” vagy „Zorn-lemma” néven ismert kijelentésre támaszkodnak (vö. Cohen 1966, Rucker 1984). A Brouwer-féle esetben a nehézség a következőhöz hasonló: találjunk egy pontot, amelyben / egy valós változó valósértékű, folytonos függvénye, amely mind pozitív, mind negatív értékeket felvesz. A szokásos eljárás ismételten felosztja azt a tartományt, ahol/jelet vált, de a Brouwer által megkövetelt értelemben nem lehet „konstruktívan” eldönteni, hogy/közbenső értékei pozitívak, negatívak vagy zérusok.
8. A {v, w, x,… z} halmazokat, ahol v az f függvényt ábrázolja, felsoroljuk valamilyen lexikografikus séma szerint. Minden lépésben (rekurzívan) ellenőrizzük, hogy f(w, x,… z) = 0 fennáll-e, és csak ha igen, akkor tartjuk meg a Ǝ w, x,… z [ f(w, x, ... ,z) = 0 ] propozíciót.
9. Legújabban Leonore Blum arról informált, hogy (a könyv első, keményfedeles kiadásában található megjegyzéseimtől ösztönözve) bebizonyította, a Mandelbrot-halmaz (és kiegészítő halmaza) az alábbi 10. megjegyzésben említett értelemben valóban nem rekurzív, mint ahogy azt a szövegben felvetettem.
10. Blum, Shub és Smale (1989) kidolgozták a kiszámíthatóság egy új elméletét valós számok valósértékű függvényeire (ellentétben a hagyományos természetes számok természetes számértékű függvényeivel), ennek részleteivel csak legújabban találkoztam. Az elmélet komplexértékű függvényekre is alkalmazható lesz, és jelentős hatása lehet a szövegben felmerülő kérdésekre.
11. E speciális problémát helyesebb a „félcsoportok szóproblémájának” nevezni. A szóproblémának vannak más formái is, amelyeknél a szabályok egy kissé különböznek. Ezekkel nem fogunk foglalkozni.
12. Hanf (1974) és Myers (1974) azt is megmutatták, hogy van egy (nagyszámú parkettát tartalmazó) egyetlen halmaz, amellyel a sík csak nem kiszámítható módon fedhető le.
13. Megfelelő ötletekkel ez a lépésszám nagy n esetén n log n log log n nagyságrendűvé csökkenthető — ami természetesen még mindig P-ben van. A témáról további információ a Knuth (1981) hivatkozásban található.
14. Pontosabban kifejezve a P, NP és NP-teljes osztályokat (lásd 168. o.) igen/nem típusú problémákra definiálták (például adott a, b és c mellett igaz-e, hogy a • b = c), de a szöveg leírásai megfelelnek céljainknak.
15. Szigorúan véve ennek igen/nem változatára van szükségünk: van-e a kereskedőnek olyan útja, amelynek hossza kisebb, mint ennyi meg ennyi? (Lásd az előbbi megjegyzést.)