Prev Next

ALGORITMUSOK ÉS TURING-GÉPEK

Az algoritmusfogalom háttere

Mi pontosan egy algoritmus vagy egy Turing-gép, vagy egy univerzális Turing- gép? Miért annyira alapvetőek e fogalmak annak modern megítélésében, hogy mi képezhet „gondolkodó eszközt”? Vannak-e abszolút korlátai annak, mit érhet el elvileg egy algoritmus? Hogy ezeket a kérdéseket megfelelő formában tudjuk felvetni, meg kell vizsgálnunk az algoritmus és a Turing-gépek fogalmát kicsit részletesebben.

Az elkövetkező fejtegetések során néha majd matematikai kifejezésekre kell hivatkoznom. Elismerem, hogy egyeseket az ilyen dolgok elijeszthetnek. Ha Ön ezek közé tartozik, akkor türelmét kérem, és azt ajánlom, kövesse a „Tanács az Olvasónak” jegyzetben a 15. oldalon adott tanácsomat! A gondolatmenetek nem követelnek az elemi iskolain túlmenő matematikai tudást, de részletes követésükhöz néhol komoly elmélyedésre lesz szükség. Azt hiszem, a legtöbb leírás egészen világos, és a részletek követésével jól meg lehet érteni. De még úgy is sokat lehet nyerni, ha valaki a bizonyításokat csak átfutja, hogy a dolgok ízét megérezze. Ha viszont Ön, éppen ellenkezőleg, szakértője a témának, akkor megint csak türelmét kérem. Azt hiszem, így is érdemes lehet átnéznie, amit el kell mondanom, egy-két dolog bizonyára érdeklődésére tarthat számot.

Az „algoritmus” szó a kilencedik századbeli perzsa matematikus, Abu Dzsáfár Mohammed ibn Músza al-Hvárizmi nevéből származik, aki i. sz. 825 körül nagy hatású matematikai tankönyvet írt „Kitab al jabr w’al-muqabala” címmel. Az „algoritmus” ma használatos, a korábbi és pontosabb „algorizmus”-tól eltérő alakja valószínűleg az „aritmetika” szóhoz való társítás következménye. (Érdemes megjegyezni, hogy az „algebra” szó az említett könyv címében előforduló arab „al jabr” szóból származik.)

Algoritmusokra példákat azonban al-Hvárizmi könyvénél már sokkal korábban ismertek. Az egyik legnépszerűbb az ókori görög időkből (kb. i. e. 300-ból) származó, ma euklideszi algoritmus néven ismert eljárás, két szám legnagyobb közös osztójának meghatározására. Nézzük meg, hogyan működik ez. Segíteni fog, ha meghatározott számpárra gondolunk, legyen ez mondjuk 1365 és 3654. A legnagyobb közös osztó az a legnagyobb egész szám, amellyel mindkét szám maradék nélkül osztható. Alkalmazva Eukleidész algoritmusát osszuk el az egyik számot a másikkal, és vegyük a maradékot: 1365 kétszer van meg 3654- ben, a maradék 924( = 3654 - 2 • 1365). Helyettesítsük most eredeti két számunkat ezzel a maradékkal, nevezetesen 924-gyel és azzal a számmal, amellyel osztottunk, nevezetesen 1365-tel, ebben a sorrendben. Az új párral megismételjük, amit az előbb csináltunk: 924 egyszer van meg 1365-ben, a maradék 441(= 1365 - 924). így megint egy új párt kapunk, ez 441 és 924, utóbbit az előbbivel osztva a maradék 42(= 924-2-441), és így tovább, amíg egy maradék nélküli osztáshoz nem jutunk. Összefoglaljuk az egészet:

3654	1365	a maradék	924
1365	924	a maradék	441
924	441	a maradék	42
441	42	a maradék	21
42 :	21	a maradék	0.

Amivel utoljára osztottunk, nevezetesen a 21, a keresett legnagyobb közös osztó. Eukleidész algoritmusa maga az a szisztematikus eljárás, amellyel megtaláltuk ezt az osztót. Ezt az eljárást most éppen egy meghatározott számpárra alkalmaztuk, de egészen általánosan akármilyen nagy számokra alkalmazható. Nagyon nagy számokra az eljárás végrehajtása nagyon hosszú időt vehet igénybe, és minél nagyobbak a számok, általában annál tovább tart. Azonban minden meghatározott esetben végül is befejeződik, és véges számú lépésben határozott választ ad. Minden egyes lépésnél teljesen világos, mi az a művelet, amelyet el kell végezni, és amikor az egész eljárás befejeződik, abban a pillanatban tökéletesen világos a végeredmény is. Továbbmenve, az egész eljárás leírása véges alakban megadható annak ellenére, hogy korlátlan nagyságú természetes számokra alkalmazható. (A „természetes számok” a közönséges nemnegatív¹ egész számok: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...). Könnyű olyan (véges) „folyamatábrát” készíteni, amely leírja Eukleidész algoritmusának teljes logikai működését (lásd 2.1. ábra).

Meg kell jegyeznem, hogy az eljárás még nincs széttördelve legelemibb részeire, mivel hallgatólagosan feltételeztük, hogy már „tudjuk”, hogyan kell elvégezni azt a szükséges alapvető műveletet, amely két tetszőleges A és B természetes számra megadja az osztás maradékát. Ez a művelet megint algoritmikus — az osztásnak az a nagyon közismert eljárása, amelyet az iskolában tanulunk. Ez az eljárás valójában sokkal bonyolultabb, mint az euklideszi algoritmus többi része, de erre is lehet készíteni folyamatábrát. A fő bonyodalom abból származik, hogy a természetes számokra (feltehetően) a szabványos „tizes” jelölést használnánk, így fel kellene jegyeznünk az összes szorzótáblát, és gondoskodnunk kellene az átvitelekről stb.

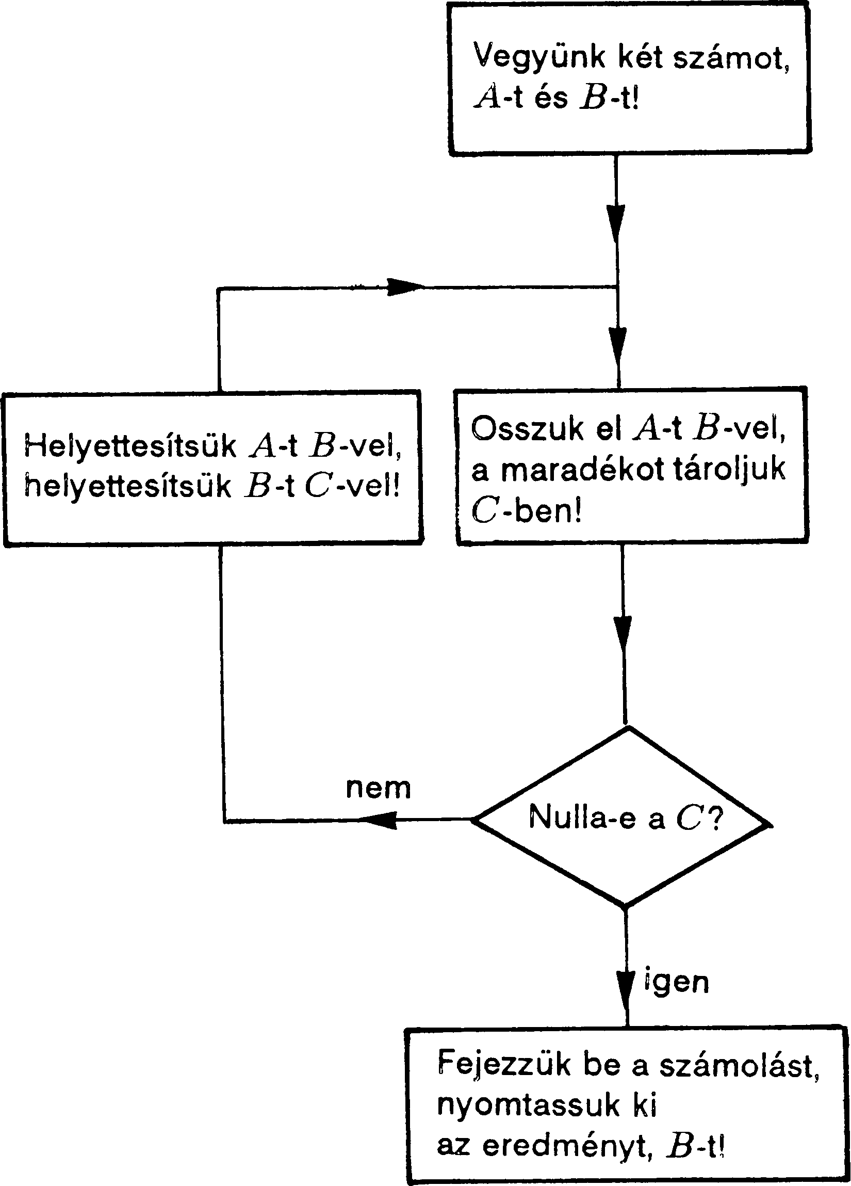
2.1. ábra. Eukleidész algoritmusának folyamatábrája

Ha az n szám ábrázolására egyszerűen n darab valamilyen jelből álló sorozatot használnánk — például • • • • • ábrázolná az ötöt —, akkor a maradék képzése nagyon elemi algoritmikus művelet lenne. Hogy A-nak B-vel való osztásánál megkapjuk a maradékot, egyszerűen addig vesszük el a B-t ábrázoló jelsorozatot az A-t ábrázolóból, amíg már nem marad elegendő jel ahhoz, hogy a műveletet újra elvégezzük. Az utoljára megmaradó jelsorozat adja a kívánt választ. Például, hogy megkapjuk a maradékot, amikor a tizenhetet osztjuk öttel, egyszerűen eltávolítunk • • • • • sorozatokat a • • • • • • • • • • • • • • • • • • • • -ből:

• • • • • • • • • • • • • • • • • • • •

• • • • • • • • • • • • • •

• • • • • • • • •

• •

és a válasz nyilván a kettő, mert a műveletet nem tudjuk újra elvégezni.

2.2. ábra. Az ismételt levonásos eljárás folyamatábrája

Egy folyamatábra, amely egy osztás maradékát ilyen ismételt levonással találja meg, a 2.2. ábrán megadott módon nézhet ki.

Hogy Eukleidész algoritmusának teljes folyamatábráját megkapjuk, a maradékképzés fenti ábráját behelyettesítjük az eredeti ábra jobb oldalán, középen álló keretbe. Egy algoritmusnak egy másikba való ilyen behelyettesítése általános számítógép-programozási eljárás. A fenti maradékkereső algoritmus a szubrutinok egy példája. A szubrutin egy olyan (általában előre ismert) algoritmus, amelyet a fő algoritmus „hív be” és használ működése közben.

Az n számnak n köröcskével való egyszerű ábrázolása természetesen nagyon rossz hatásfokú, amikor nagy számokról van szó. Ez az, amiért általában tömörebb jelölést használunk, például a szabványos (tizes) rendszert. Most azonban a műveletek vagy jelölések hatékonyságával nem fogunk sokat törődni. Ehelyett azt a kérdést vizsgáljuk, milyen műveleteket lehet elvileg algoritmikusan elvégezni. Ami algoritmikus a számok egyik jelölésénél, az algoritmikus akkor is, ha egy másik jelölést használunk. Különbség csupán a részletekben és a bonyolultság fokában van.

Eukleidész algoritmusa csak egy a számos, gyakran nagyon régóta ismert, algoritmikus eljárás közül, amelyek a matematika minden területén megtalálhatóak. Figyelemre méltó azonban, hogy algoritmusok speciális példáinak ókori történeti eredete ellenére az általános algoritmusfogalom pontos megalkotása csak ebben a században történt meg. Valójában e fogalom változatos alternatív leírásait adták meg, mindet az 1930-as években. Ezek közül a legközvetlenebb, a leginkább meggyőző és történetileg is a legfontosabb az, amelyik a Turing- gép néven ismert fogalmat használja. Helyénvaló, ha egy kicsit részletesebben megvizsgáljuk ezeket a „gépeket”.

Amit egy Turing-„gépről” tudnunk kell, hogy az egy darab „absztrakt matematika”, és nem fizikai objektum. A fogalmat az angol matematikus, kódfejtő szakértő és úttörő számítógéptudós, Alán Turing vezette be 1935 —36-ban (Turing 1937), hogy segítségével megbirkózzon egy nagyon széles körű, az eldönthetőségi probléma (Entscheidungsproblem) néven ismert kérdéssel, amelyet a nagy német matematikus, David Hilbert vetett fel, részben már az 1900-as Párizsi Nemzetközi Matematikai Kongresszuson („Hilbert tizedik problémája”), teljesebben pedig a Bolognai Nemzetközi Kongresszuson 1928-ban. Hilbert nem kevesebbet keresett, mint egy általános algoritmikus eljárást a matematikai problémák megoldására, vagy inkább választ arra a kérdésre, hogy ilyen eljárás elvileg létezhet-e vagy sem. Hilbertnek volt olyan programja is, hogy a matematikát egyszer s mindenkorra lefektetett axiómákkal és eljárási szabályokkal megtámadhatatlan, tökéletes alapra helyezze, de mire Turing nagy munkájával előállt, addigra erre a programra már megsemmisítő csapást mért egy meglepő tétel, amelyet 1931-ben bizonyított be a briliáns osztrák logista, Kurt Gödel. A Gödel-tételt és jelentőségét a 4. fejezetben fogjuk áttekinteni. Hilbertnek az a problémája, amellyel Turing foglalkozott (az eldönthetőségi probléma), túlment a matematika minden speciális, axiomatikus rendszerek formájában való megfogalmazásán. A kérdés a következő volt: van-e általános, mechanikus eljárás, amellyel elvileg megoldható lenne a matematika minden (alkalmasan meghatározott osztályba tartozó) problémája, egyik a másik után?

A kérdés megválaszolásának nehézsége részben annak eldöntése volt, mit értsünk „mechanikus eljárás” alatt. E fogalom kívül esett az akkori idők rendes matematikai elképzelésein. Hogy ezzel megmérkőzzön, Turing megpróbálta elképzelni, hogyan lehetne a „gép” fogalmát formálissá tenni, működését elemi egységekre bontani. Világosan látszik, hogy Turing saját értelmezésében az emberi agyat is a „gépek” egyikének tekintette, úgy hogy bármilyen tevékenységet hajtsanak is végre a matematikával foglalkozó emberek, amikor matematikai problémáikkal birkóznak, ezekre is a „mechanikus eljárás” címkéjét ragasztotta volna.

Noha az emberi gondolkodásról alkotott ilyen szemlélet, úgy tetszik, értékes volt Turing számára, felettébb fontos koncepciójának kialakításában, nekünk semmiképp sem szükséges ragaszkodnunk hozzá. Turing ténylegesen megmutatta, hogy vannak olyan tökéletesen jól meghatározott matematikai műveletek, amelyeket semmilyen közönséges értelemben nem lehet mechanikusnak nevezni! Van talán némi irónia abban, hogy éppen Turing munkájának ez az oldala jelenthet közvetett módon egérutat számunkra, amelyen kiléphetünk a szellemi jelenségek természetének Turing-féle koncepciójából. Jelenleg azonban nem ez a gondunk. Először meg kell tudnunk, mi valójában Turingnak a mechanikus eljárásról alkotott koncepciója.

Turing koncepciója

Próbáljunk elképzelni egy gépet, amely valamilyen (végesen definiálható) számítási eljárást hajt végre. Milyen lenne ennek általános alakja? Fel kell készülnünk arra, hogy egy kicsit idealizáljunk, és ne törődjünk túl sokat a gyakorlati dolgokkal: valójában egy matematikailag idealizált „gépről” gondolkodunk. Gépünktől azt várjuk, hogy különböző lehetséges állapotai egy diszkrét sorozatot alkossanak, számuk véges (bár esetleg nagyon nagy szám) legyen. Ezeket a gép belső állapotainak nevezzük. Nem akarjuk azonban korlátozni a számítások méretét, amelyeket gépünk elvileg végre fog hajtani. Emlékezzünk Eukleidész előbbiekben leírt algoritmusára. Ott elvileg nincs korlát a számok nagyságára, amelyekkel az az algoritmus dolgozhat. Az algoritmus — vagy az általános számítási eljárás — pontosan ugyanaz, függetlenül attól, milyen nagyok a számok. Nagyon nagy számokra az eljárás valóban nagyon hosszú időt vehet igénybe, és jelentős mennyiségű „durva papírra” lehet szükség, a mindenkori számítások elvégzésére. Az algoritmus azonban az utasításoknak ugyanaz a véges sorozata, akármilyen nagyok is a számok.

így bár gépünknek véges számú belső állapota van, tudnia kell kezelni olyan adatbevitelt is, amely méretében nem korlátozott. Mi több, meg kell engedni, hogy számításaihoz korlátlan külső tárolóterületet („durva papírt”) vegyen igénybe, és hogy szintén korlátlan méretű adatkivitelt legyen képes létrehozni. Mivel gépünknek csak véges számú különböző belső állapota van, nem lehet tőle elvárni azt, hogy az összes külső adatot vagy számításainak összes eredményét „magában hordozza”. Ehelyett az adatoknak vagy az előző számításoknak csak azokat a részeit kell vizsgálnia, amelyekkel közvetlenül foglalkozik, ezeken kell elvégeznie a szükséges műveletet. Lejegyezheti, esetleg a külső tárolóterületen a művelet lényeges eredményeit, azután pontosan meghatározott módon áttérhet feladatának következő szakaszára. A korlátlan bevitel, számítási terület és kivitel az, ami elárulja, hogy csak egy matematikai idealizációról beszélünk, és nem valami olyanról, amit a gyakorlatban valóban meg lehetne valósítani (2.3. ábra). Ez azonban nagy jelentőségű idealizáció.

A modern számítógép-technológia csodái olyan elektronikus tárolóeszközökkel láttak el bennünket, amelyek a legtöbb gyakorlati cél szempontjából valóban korlátlannak tekinthetők.

A tárolóterületnek az a fajtája, amelyre a fenti fejtegetés során, mint „külsőre” hivatkoztunk, valójában egy modern számítógép belső munkaterülete részének tekinthető. Talán csak technikai részlet, hogy a tárolóterület egy bizonyos részét belsőnek vagy külsőnek tekintjük-e. A „gép” és a „külső” rész közötti szétválasztásra való utalás egyik módja a hardver és szoftver megkülönböztetés. A belső rész lehetne a hardver, a külső a szoftver. Nem fogok ehhez feltétlenül ragaszkodni, de akármilyen szemmel nézünk is rá, Turing idealizációját valóban figyelemreméltóan jól megközelítik a mai elektronikus számítógépek.

Turing a külső adat- és tárolóterületet úgy jelenítette meg, mint egy jelekkel ellátott „szalagot”. Ezt a szalagot hívja be és „olvassa” a gép szükség szerint, működésének részeként hátra vagy előre tudja mozgatni azt. Ahol szükséges, új jeleket is el tud helyezni a szalagon, és ki tud törölni régieket, lehetővé téve, hogy ugyanaz a szalag szolgáljon külső tárolóként (azaz „durva papírként”) és bevitelként is. Valójában segít, ha nem teszünk semmiféle világos különbséget a „külső tároló” és a „bevitel” között, mert sok műveletben egy számítás közbenső eredményei éppen olyan szerepet játszhatnak, mint az új adatok. Emlékezzünk vissza, hogy az euklideszi algoritmusban eredeti bevitelünket (az A és B számot) a számítás különböző szakaszainak eredményeivel helyettesítettük. Hasonlóképpen ugyanaz a szalag használható a végső kivitelre (azaz a „válaszra”) is. A szalag állandóan előre vagy hátra fut az eszközben mindaddig, amíg további számításokat kell elvégezni. Amikor a számítás véglegesen befejeződött, az eszköz megáll, és a számítás eredménye megjelenik a szalagnak azon a részén, amelyik az eszköz egyik oldalán található. A határozottság kedvéért tegyük fel, hogy a válasz mindig a bal oldalon jelenik meg, míg a bevitelben lévő összes numerikus adat, a megoldandó probléma leírásával együtt, mindig a jobb oldalon.

Ami engem illet, kicsit kényelmetlennek érzem, hogy véges eszközünk egy potenciálisan végtelen szalagot mozgasson hátra és előre. Legyen anyaga bármennyire is pehelykönnyű, egy végtelen szalagot nehéz lehet megmozdítani! Jobban szeretek ehelyett úgy gondolni a szalagra, mint ami valamilyen külső környezetet képvisel, amelyben véges eszközünk mozoghat. (A modern elektronikában természetesen sem a „szalagnak” sem az „eszköznek” nem kell a közönséges fizikai értelemben „mozognia”, de az ilyen „mozgás” kényelmes módja a dolgok megjelenítésének.) Ebben a képben az eszköz minden bevitelét környezetéből kapja. Úgy használja a környezetet, mint saját „durva papírját”. Kivitelét végül ugyanebbe a környezetbe írja ki.

Turing leírásában a „szalag” négyzeteknek egy lineáris sorozatából áll, amely mindkét irányban végtelen. A szalagon minden négyzet vagy üres, vagy egyetlen jelet tartalmaz.* A megjelölt és jelöletlen négyzetek használata azt mutatja, hogy megengedjük „környezetünk” (azaz a szalag) lebontását, és (a folytonossal szemben) diszkrét elemekkel való leírását. Ez ésszerűnek látszik, ha azt kívánjuk, hogy eszközünk megbízható és abszolút meghatározott módon működjék. Megengedjük azonban, hogy ez a „környezet” (potenciálisan) végtelen legyen, ami az általunk használt matematikai idealizáció sajátossága, de a bevitel, a számítás és a kivitel bármelyik speciális esetben mindig véges kell maradjon. így bár a szalagot végtelen hosszúnak vesszük, csak véges számú jel lehet rajta. Egy bizonyos ponton túl mindkét irányban teljesen üresnek kell lennie.

Az üres négyzetet a „0”, a megjelöltet az „1” szimbólummal jelöljük, például:

Gépünknek „olvasnia” kell a szalagot. Fel fogjuk tételezni, hogy egyszerre egy négyzetet olvas el, és minden művelet után egy négyzetnyit mozdul el jobbra vagy balra. Ez nem megy az általánosság rovására. Egy eszköz, amely egyszerre n négyzetet olvas el, vagy egyszerre k négyzetnyit mozog, könnyen modellezhető egy másikkal, amely egyszerre egy négyzetet olvas, és ennyit is mozdul el. Egy k négyzetnyi elmozdulás felépíthető k számú egy négyzetnyi elmozdulásból, és ha n egy négyzetnyi olvasás eredményét tárolja, akkor az eszköz úgy tud viselkedni, mintha mind az n négyzetet egyszerre olvasná el.

*Eredeti leírásában Turing megengedte, hogy a szalag bonyolultabb módon legyen megjelölve, de ez nem jelent valódi különbséget. A bonyolultabb jelek mindig lebonthatók egyszerű jelek és üres helyek sorozataira. Még majd teszek néhány lényegtelen, önkényes módosítást Turing eredeti leírásához képest.

Mi mindent tud csinálni egy ilyen eszköz? Mi a legáltalánosabb módja annak, ahogy valami, amit „mechanikusnak” írnánk le, működni tud? Emlékezzünk rá, hogy gépünk belső állapotainak száma véges. E végességen túl csupán azt kell tudnunk, hogy viselkedését belső állapotai és a bevitel tökéletesen meghatározzák. A bevitelt úgy egyszerűsítettük, hogy az a „0” és „1” szimbólumok valamelyike. Ha ez a bevitel és a gép kezdeti állapota adott, akkor az tökéletesen determinisztikusán működik: belső állapotát valamelyik másikra változtatja (vagy változatlanul hagyja); az éppen beolvasott 0 vagy 1 szimbólumot ugyanazzal vagy a másikkal helyettesíti; elmozdul egy négyzettel jobbra vagy balra; végül eldönti, folytassa-e a számítást, vagy szakítsa meg és álljon le.

Hogy eszközünk működését explicit módon definiáljuk, először számozzuk meg a különböző belső állapotokat mondjuk a 0, 1, 2,3, 4,5, .. .jegyekkel; ekkor az eszköz vagy Turing-gép működését tökéletesen megadja valamilyen explicit helyettesítési lista, mint például a következő:

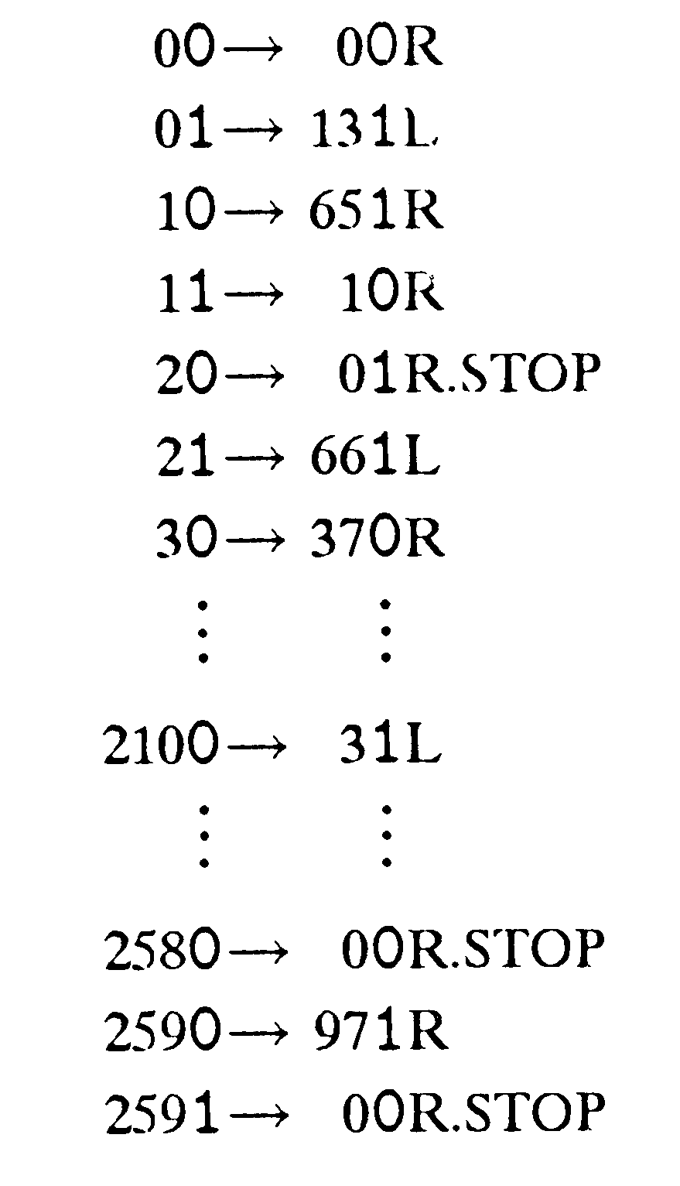
A nyíl bal oldalán álló nagy számjegy a szalagon lévő szimbólum, amit a gép beolvas, és a jobb oldal közepén álló nagy számjeggyel helyettesít. R azt mutatja, hogy a gép egy négyzetet lépjen a szalag mentén jobbra, L azt, hogy egy négyzetet balra. (Ha, Turing eredeti leírásának megfelelően, azt gondoljuk, hogy nem a gép mozog, hanem a szalag, akkor R-et, illetve L-et olyan utasításként kell értelmeznünk, hogy a szalag mozduljon el egy négyzetet balra, illetve jobbra. R és L az angol right és left szó kezdőbetűi.) A stop szó azt jelzi, hogy a számítás befejeződött, a gépnek meg kell állnia. A második utasítás, 01 -> 131L például azt mondja, hogy ha a gép a o belső állapotban van, és a szalagról l-et olvas, akkor át kell mennie a 13-as belső állapotba, a szalagon meg kell hagynia az l-et, és a szalag mentén egy négyzettel balra kell lépnie. Az utolsó utasítás, 2591 —> OOR.STOP azt mondja, hogy ha a gép a 259 állapotban van, és a szalagról l-et olvas, akkor vissza kell térnie a o állapotba, a szalagon az l-et 0-val kell helyettesítenie, a szalag mentén egy négyzettel jobbra kell lépnie, és meg kell szakítania a számítást.

Ahelyett, hogy a belső állapotokat a o, 1, 2,3,4,5,... számjegyekkel címkéznénk, jobban összhangban lenne a szalagon használt jelöléssel, ha csak o-kból és i-ekből álló szimbólumokat használnánk. Ha akarnánk, használhatnánk az n állapot jelölésére egy n darab i-esből álló sorozatot, ez azonban rossz hatásfokú. Használjuk helyette a bináris (kettes) számrendszert, ami mostanában megszokott jelölésmód:

Itt a jobb oldalon álló utolsó jegy az „egyeseket” jelenti éppen úgy, mint a szabványos (tízes) jelölésben, de az előtte lévő jegy nem a „tízesekre”, hanem a „kettesekre” vonatkozik. Az ezelőtt álló a „négyeseket” jelenti, nem a „százasokat”, a következő a „nyolcasokat” és nem az „ezreseket”, és így tovább, balra haladva az egymás utáni jegyek a 2 egymás utáni hatványait: 1(= 2°), 2(= 2¹), 4(= 2² = 2 • 2), 8(= 2³ = 2-2-2), 16(= 2⁴ = 2-2-2-2), 32(= 2⁵ = 2-2-2-2-2) stb. (Másféle célból, amelyről később lesz szó, olykor hasznosnak fogjuk találni, ha a természetes számok ábrázolására más alapú számrendszert használunk, mint a kettest vagy a tízest: például hármas alap esetén a tízes rendszerbeli 64 számot 2101-nek kellene írni, mindegyik jegynek olyan értéke van, amely most a 3 valamelyik hatványa: 64 = 2 • 3³ + 1 • 3² + + 0 • 3¹ + 1 • 3°, ahol 3° = 1; vö. 4. fejezet, 128. o., lábjegyzet.)

A belső állapotokra ilyen bináris jelölést használva az előző Turing-gép leírása a következő:

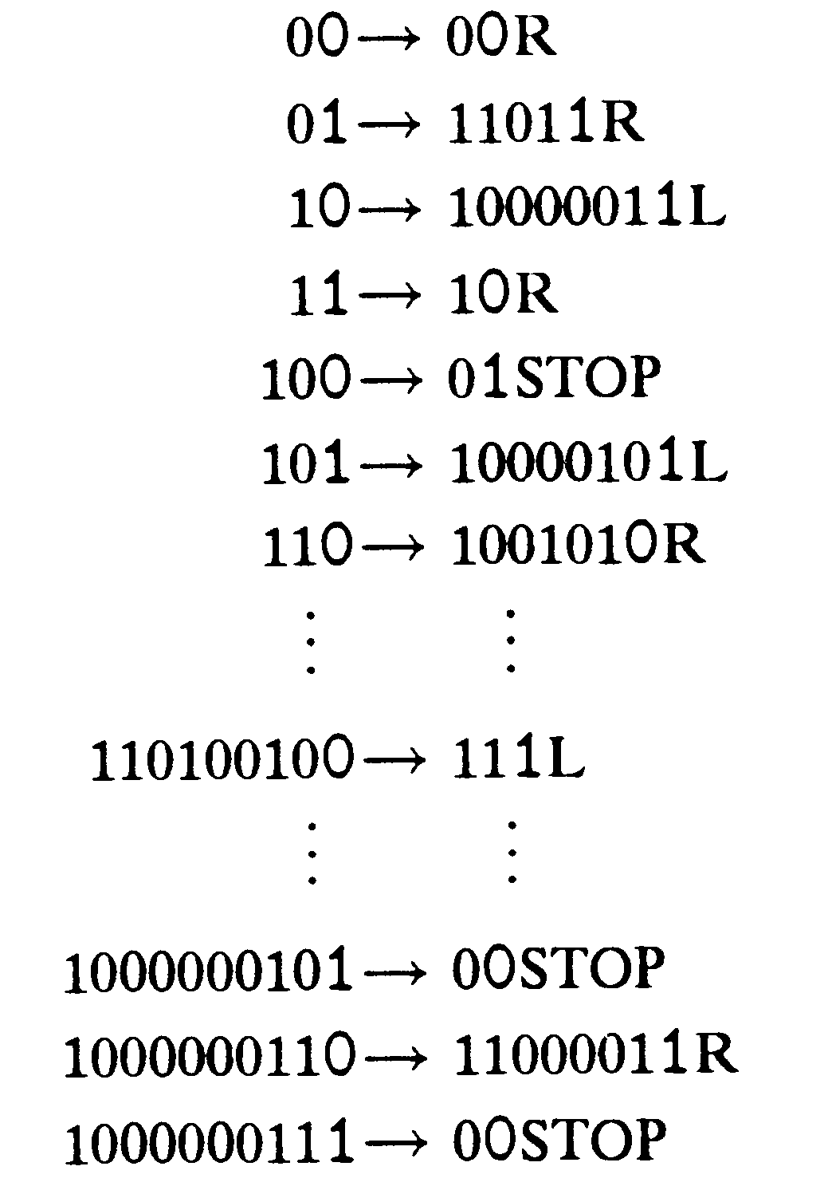
A fentiekben az R.STOP-ot is rövidítettem STOP-ra, mert feltehetjük, hogy L.STOP soha nem fordul elő, így a számítás utolsó lépésének eredménye mindig az eszköz bal oldalán jelenik meg, mint része a válasznak.

Tegyük fel, hogy gépünk éppen abban a belső állapotban van, amelyet a 11010010 bináris sorozat ábrázol, és annak a számításnak a közepén, amelynek szalagja az 54. oldalon látható; a sorban a 110100100->-111L utasítás következik:

Azt a jegyet, amelyet a gép éppen beolvas (most a „0”), a szalagon nagyobb számmal jelöltem a belső állapotot ábrázoló szimbólumfüzértől jobbra. A Turing-gép e példájában, amelyet az előbbiekben részben leírtam (és többé-kevésbé véletlenszerűen adtam meg), a most beolvasott „0”-t „1”-essel kell helyettesíteni, a belső állapotot pedig a „11”-esre változtatni; ezután az eszköz egyet lép balra:

A gép most készen áll, hogy beolvasson egy újabb jegyet, újra egy „0”-t. A táblázat szerint ezt a „0”-t most változatlanul hagyja, de az „100101” belső állapotba megy át, és a szalag mentén egyet lép jobbra. Most „1”-est olvas be, és valahol lent a táblázatban volna egy további utasítás, hogy milyen belső állapotba menjen át, megváltoztassa-e a beolvasott jegyet, és milyen irányban mozogjon a szalag mentén. Ez így folytatódna addig, amíg egy stop-hoz nem érkezik, amelyik pontban (miután még lép egyet jobbra) elképzelünk egy csengőt, amely megszólal, és a gép figyelmezteti kezelőjét, hogy a számítás befejeződött.

Fel fogjuk tételezni, hogy a gép mindig a „o” belső állapotból indul, és hogy az olvasóeszköztől balra kezdetben az egész szalag üres. Az utasításokat és az adatokat mind a jobb oldalon tápláljuk be. Mint korábban említettem, ez a betáplált információ mindig egy O-kból és 1-esekből álló véges füzér, amelyet üres szalag követ (azaz 0-k). Amikor a gép STOP-hoz ér, a számítás eredménye az olvasóeszköz bal oldalán lévő szalagon látható.

Mivel azt szeretnénk, ha a bevitel részeként numerikus adatokat is be tudnánk adni, ezért valahogy le kell tudnunk írni a közönséges számokat is (ezek alatt most a 0, 1, 2, 3, 4, ... természetes számokat értem) mint a bevitel részét. Ennek egyik módja az lehet, hogy az n természetes szám ábrázolására egy n darab 1-esből álló füzért használunk (bár így a nulla természetes számmal nehézségeink lehetnek):

1 ->1 , 2 -> 11, 3 -> 111, 4 -> 1111, 5 -> 11111 stb.

Ezt a primitív számrendszert (eléggé logikátlanul) unáris (egyes) rendszernek nevezik. Ekkor a „0” szimbólum helyközként használható a különböző számok egymástól való elválasztására. Fontos, hogy erre legyen módunk, mert sok algoritmus nem egyes számokkal, hanem számok sorozatával dolgozik. Az euklideszi algoritmusnál például eszközünknek az A és B számokból álló párokkal kell dolgoznia. Nagyobb nehézség nélkül le lehet írni olyan Turing-gépeket, amelyek végrehajtják ezt az algoritmust. Egyes hozzáértő olvasók gyakorlatként talán vehetik a fáradságot, és igazolhatják, hogy a következő explicit leírással megadott Turing-gép (amelyet EUC-nak fogok hívni), valóban végrehajtja az euklideszi algoritmust, ha egymástól egy 0-val elválasztott unáris számpárra alkalmazzuk:

Mielőtt azonban az Olvasó ennek nekikezdene, bölcsebben teszi, ha valami sokkal egyszerűbbel próbálkozik, mint amilyen például az UN+1 Turing-gép:

00-> OOR, 01-> 11R, 10—> 01 STOP, 11-> 11R.

Ez egyszerűen egyet ad egy unáris számhoz. Hogy ellenőrizzük, hogy az UN + 1 éppen ezt teszi, képzeljük el, hogy alkalmazzuk mondjuk a

...00000111100000...

szalagra, amely a 4-es számot ábrázolja. Az eszköz kezdetben valahol az 1-esektől balra helyezkedik el. A o belső állapotban van, és a szalagon 0-t olvas. Ezt, az első utasítás szerint, meghagyja 0-nak, és megmaradva a o belső állapotban egyet lép jobbra. Ezt addig csinálja, amíg az első 1-essel nem találkozik. Ekkor a második utasítás lép életbe: meghagyja az 1-est 1-esnek, és megint jobbra lép, de most az l belső állapotban. A negyedik utasítás szerint az 1 belső állapotban marad, az 1-eseket változatlanul hagyja, jobbra mozog a szalag mentén, amíg el nem éri az 1-esek után következő első 0-t. A harmadik utasítás ekkor azt mondja neki, hogy változtassa azt 1-esre, lépjen még egyet jobbra (emlékezzünk rá, hogy a STOP tulajdonképpen az R.STOP utasítást jelöli), és álljon meg. Így az 1-esek füzéréhez egy további 1 adódik, és példánkban a 4 valóban 5-re változik, ahogy azt elvártuk.

Valamivel komolyabb gyakorlatként ellenőrizni lehet, hogy a

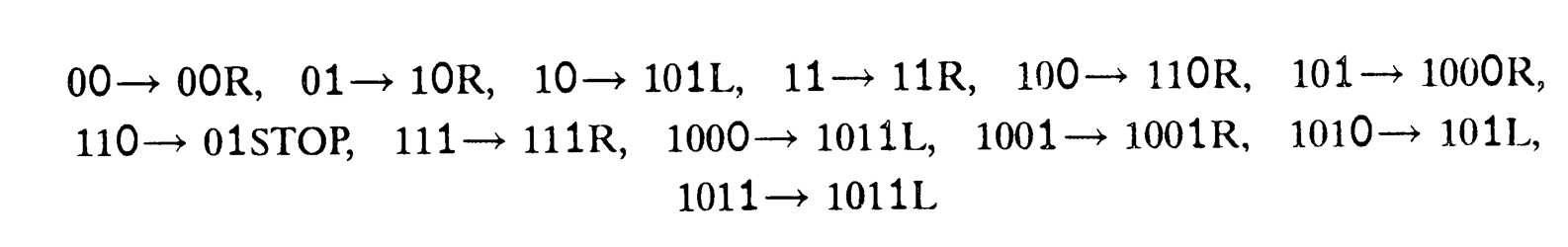
utasításokkal definiált UNx2 gép megkétszerez egy unáris számot.

Hogy az EUC alapeszméjét megértsük, ki lehet próbálni valamely alkalmas explicit számpárra, legyen ez mondjuk a 6 és a 8. Az olvasóeszköz, mint előbb, kezdetben a o belső állapotban van a bal oldalon, és a szalag kezdeti jelölése most a következő:

.. .0000000000011111101111111100000

Miután sok lépéssel később a Turing-gép megáll, a szalagon a

...000011000000000000...

jelölés lesz látható, az olvasóeszköz a nem zérus jegyektől jobbra fog elhelyezkedni. így a keresett legnagyobb közös osztóra (helyesen) 2-t kapunk.

Annak teljes magyarázata, miért csinálja meg az EUC (vagy az UNx2) azt, amit elvárunk tőle, tartalmaz bizonyos finomságokat, és sokkal bonyolultabb lenne elmondani, mint amennyire bonyolult a gép maga — nem szokatlan tulajdonsága ez a számítógépprogramoknak! (Hogy miért csinálja egy algoritmikus eljárás meg azt, amit feltételeznek róla, ennek teljes megértéséhez meglátások kellenek. Algoritmikusak-e maguk a „meglátások”? Ez olyan kérdés, amely a későbbiekben fontos lesz számunkra.) Nem szándékozom most ilyen magyarázattal szolgálni az EUC vagy az UNx2 esetében. Az Olvasó, aki az ellenőrzést elvégzi, azt fogja találni, hogy az igazi euklideszi algoritmustól nagyon csekély mértékben eltértem, hogy a dolgokat tömörebben fejezzem ki a kívánt formában. Az EUC leírása így is egy kissé bonyolult, 11 különböző belső állapotra 22 elemi utasítást tartalmaz. A bonyodalmak legnagyobb része tisztán szervezési jellegű. Megfigyelhető például, hogy a 22 utasításból csak 3 változtatja meg a jelet a szalagon! (Még az UNx2-nél is, ahol 12 utasítást használtam, csak 6-ban van jelváltoztatás.)

A numerikus adatok kettes rendszerbeli kódolása

Az egyes számrendszer nagy számok ábrázolására rendkívül rossz hatásfokú. Ezért általában a korábban leírt kettes számrendszert fogjuk használni. Azonban ezt nem tudjuk közvetlenül megtenni, úgy nem tudjuk olvasni a szalagot, hogy azon csak kettes rendszerbeli számok vannak. A dolgok eddigi állása szerint nincs módunk annak megállapítására, hol fejeződik be egy szám kettes rendszerbeli ábrázolása, és hol kezdődik a 0-k végtelen sorozatával ábrázolt jobb oldali üres szalag. Szükség van valamilyen jelölésre, hogy hol szakad meg egy szám kettes rendszerbeli ábrázolása. Továbbá gyakran akarunk majd több számot betáplálni, mint például az euklideszi algoritmus számpárját.² Egyelőre nem tudjuk megkülönböztetni a számok közötti helyközöket a O-któl vagy a 0-kból álló füzérektől, amelyek egyes számok kettes rendszerbeli ábrázolásának részei. Ehhez jön még az, hogy néha mindenféle bonyolult utasítást és számokat akarhatunk a bemeneti szalagra rátenni. Hogy ezeket a nehézségeket legyűrjük, fogadjunk el egy eljárást, amelyet kontrakciónak fogok nevezni, és amely szerint bármely 0-kból és (véges számú) 1-esből álló füzért nem egyszerűen kettes rendszerbeli számként olvassuk, hanem egy 0-kból, 1-esekből, 2-esekből, 3-asokból stb. álló füzérrel helyettesítjük, olyan előírás szerint, hogy a második sorozat mindegyik jegye egyszerűen az első sorozat 0-i között álló 1-esek. számát adja meg. Eszerint például a

01000101101010110100011101010111100110

sorozatot a következőképp helyettesítjük:

A 2, 3, 4, ... számokat most valamilyen jelként vagy utasításként olvashatjuk. Valóban tekintsük a 2-t egyszerű „vesszőnek”, amely a két szám közötti helyközt jelöli, míg a 3, 4, 5, ... kívánság szerint ábrázolhatnak különféle fontos utasításokat és jelöléseket, mint a „mínusz”, „plusz” jeleket, a szorzás jelét, ugrást a következő szám által jelzett helyre, az előző műveletnek a következő számszor való iterálását stb. Most változatos füzéreink vannak 0-kból és 1-kből, és ezek nagyobb számjegyekkel vannak egymástól elválasztva. A füzérek a közönséges számokat ábrázolják a kettes rendszerben. így az előző sorozat a következőképp olvasandó (ha a „2” a „vessző”):

(bináris szám 1001) vessző (bináris szám 11) vessző ...

A szabványos arab „9”, „3”, „4”, „0” jelölést használva a megfelelő 1001, 11, 100, 0 bináris számokra, a teljes sorozat a következőképp fest:

9,3,4 (utasítás 3) 3 (utasítás 4) 0,

Ez az eljárás módot ad arra, hogy úgy fejezzük be egy szám leírását, hogy egyszerűen vesszőt teszünk a végére (és ezáltal megkülönböztessük a jobb oldalon található végtelen hosszú üres szalagtól). Mi több, lehetőséget nyújt bináris jelölésben felírt természetes számok bármilyen véges sorozatának egyetlen, 0-kból és 1-ékből álló sorozatként való kódolására, amelyben a számok elválasztására vesszőket használunk. Nézzük meg, hogyan működik ez egy konkrét esetben. Tekintsük például az

5, 13, 0, 1, 1, 4,

sorozatot. Bináris jelölésben ez

101, 1101, 0, 1, 1, 100,

ami a szalagon expanzióval (azaz az előbbi kontrakciós eljárás fordítottjával) a következőképpen lesz kódolva: ...000010010110101001011001101011010110100011000 …

Hogy ezt a kódolást egyszerű és közvetlen módon megkapjuk, az eredeti bináris számokból álló sorozatban a következő helyettesítéseket kell elvégeznünk:

0 -> 0

1 -> 10

, -> 110

és mindkét végére hozzá kell még tennünk végtelen sok 0-t. Világosabban lehet mindezt látni, ha helyközöket szúrunk be:

0000 10 0 10 110 10 10 0 10 110 0 110 10 110 10 110 10 0 0 110 00

A számok (számsorozatok) ilyen jelölésére mint kiterjesztett bináris jelölésre fogok hivatkozni. (így például a 13 kiterjesztett bináris alakja 1010010.)

Van végül még valami, amit meg kell csinálni ennél a kódolásnál. Ez csupán technikai dolog, de a teljesség érdekében szükség van rá.³ A természetes számok bináris (vagy decimális) ábrázolásában van egy csekély redundancia, amennyiben a szám elejére írt 0-k nem számítanak — ezeket általában elhagyjuk. Például a 00110010 ugyanaz a bináris szám, mint az 110010 (és a 0050 ugyanaz a tízes számrendszerbeli szám, mint az 50). Ez a redundancia kiterjed magára a zérus számra is, amely például 000 vagy 00 alakban éppen úgy írható, mint 0-ként. Logikailag egy üres hely is zérust jelentene! A közönséges jelölésben ez nagy zavart okozna, viszont nagyon jól illeszkedik az épp most leírt jelöléshez. így ugyanúgy írható egy zérus két vessző között, mint két vessző egymás után („), ami a szalagon úgy jelenne meg, mint két 11 pár egyetlen 0-val elválasztva:

...001101100...

így a fenti, hat számból álló sorozat bináris jelölésben úgy is írható, mint

101,1101,,1,1,100,

és a szalagon kiterjesztett bináris jelölésben a

. ..00001001011010100101101101011010110100011000...

sorozattal kódolható (amely egy 0-val kevesebbet tartalmaz, mint az előző sorozat).

Most már tekinthetünk egy olyan Turing-gépet, amely mondjuk az euklideszi algoritmust hajtja végre, kiterjesztett bináris jelölésben felírt számpárokra alkalmazva. Például a korábban vizsgált (6, 8) pár esetén az ott használt

.. .0000000000011111101111111100000...

sorozat helyett tekintsük a 6 és a 8 bináris alakját, nevezetesen rendre az 110 és 1000 számokat. A pár ezek szerint

8, azaz bináris jelölésben 110,1000,

ami expanzió után a szalagon a

...00000101001101000011000000...

kódsorozatként jelenik meg. Ennél a számpárnál a tömörségnek nincs előnye az egyes rendszerbeli alakkal szemben. Tegyük fel azonban, hogy mondjuk a 1583169 és 8610 (tízes rendszerbeli) számokat vesszük. Bináris jelölésben ezek

110000010100001000001, 10000110100010,

úgy, hogy a szalagon a

.. .001010000001001000001000000101101000001010010000100110...

kódot kapjuk, az egész elfér egy sorban, míg az egyes rendszerbeli jelölésben a „1583169, 8610” párt ábrázoló szalag az egész könyvbe se férne bele!

Egy, az euklideszi algoritmust a kiterjesztett bináris jelöléssel ábrázolt számokra végrehajtó Turing-gép, ha kell, egyszerűen megkapható úgy, hogy az EUC-hoz egyszerűen hozzáteszünk egy megfelelő szubrutinalgoritmus párt, amely az egyes és a kiterjesztett bináris rendszer között fordít oda és vissza. Ez azonban ténylegesen rendkívül rossz hatásfokú lenne, mivel „belsőleg” még jelen lenne az egyes számrendszer rossz hatásfoka, és ez az eszköz lassúságában és a mértéktelen mennyiségű külső „durva papír” igényben (a szalag bal oldali részén) mutatkozna meg. Az euklideszi algoritmusra hatékonyabb Turing-gép is megadható, amely teljes egészében a kiterjesztett bináris rendszerben operál, de számunkra ez itt most nem lenne különösebben tanulságos.

Ehelyett inkább próbáljuk meg egy, az euklideszi algoritmusnál sokkal egyszerűbb példán, nevezetesen az egy természetes számhoz egyet hozzáadó eljáráson bemutatni, hogyan lehet kiterjesztett bináris számokkal operáló Turing- gépet készíteni. A következő Turing-gép (amelyet XN+1-nek fogok nevezni) ezt a műveletet hajtja végre:

Egyes lelkes Olvasók ismét vehetik a fáradságot, és ellenőrizhetik, hogy ez a Turing-gép valóban megteszi azt, amit várunk tőle, alkalmazva, mondjuk a 167-es számra, amelynek bináris ábrázolása 10100111, tehát a következő szalag adja meg:

.. .0000100100010101011000...

Egy bináris számhoz úgy kell hozzáadni egyet, hogy megkeressük az utolsó 0 jegyet, ezt 1-re változtatjuk, és az utána következő összes 1-t 0-val helyettesítjük. Például 167 + 1 = 168 bináris jelölésben a következőképp írható:

10100111 + 1 = 10101000.

Így az „egyet hozzáadó” Turing-gépünknek az előbbi szalagot a .. .0000100100100001100000...

szalaggal kell helyettesítenie, és valóban ezt is teszi.

Vegyük észre, hogy ebben a jelölésben még az egy hozzáadásának nagyon elemi művelete is bonyolult egy kissé, tizenöt utasítást és nyolc különböző belső állapotot használ! A dolgok természetesen sokkal egyszerűbbek voltak az egyes rendszerbeli jelöléssel, mivel „egy hozzáadása” egyszerűen azt jelenti, hogy az 1-ékből álló füzért egy további 1-gyel meghosszabbítjuk. Így nem meglepő, hogy UN+1 gépünk elemibb volt. Nagyon nagy számokra azonban az UN+1 a megkövetelt, túl hosszú szalag miatt rendkívül lassú lenne, és jobb lenne a bonyolultabb XN+1 gép, amely a tömörebb kiterjesztett bináris jelölést használja.

Egy kis kitérőként mutatok egy olyan műveletet, ahol a Turing-gép ténylegesen egyszerűbben néz ki a kiterjesztett kettes számrendszerbeli jelöléssel, mint az egyessel. A művelet a kettővel való szorzás. A

00-> 00R, 01->11R, 10—>00R, 11->100R, 100—>111R, 110 -> OOSTOP

utasításokkal megadott XNx2 Turing-gép a kiterjesztett binárisban hajtja végre feladatát, míg a megfelelő egyes rendszerbeli jelölést használó, korábban leírt, UNx2 gép jóval bonyolultabb!

A fentiek adnak némi elképzelést arról, mire képesek a Turing-gépek nagyon elemi szinten. Ahogy az várható, ezek a gépek roppant bonyolulttá válhatnak és ténylegesen azzá is válnak, ha némileg összetett műveleteket kell végrehajtaniuk. Mi tehát végül az ilyen eszközök működési területe? Ezt a kérdést vizsgáljuk a következőkben.

A Church-Turing-tétel

Ha valaki szerzett már némi jártasságot egyszerű Turing-gépek készítésében, akkor könnyen meggyőződhet arról, hogy a különféle aritmetikai alapműveletek, mint két szám összeadása vagy összeszorzása, egy szám hatványozása, speciális Turing-gépekkel valóban végrehajthatók. Nem túl nehéz explicit módon megadni ilyen gépeket, de most nem fogok ezzel bajlódni. El lehet végezni olyan műveleteket is, ahol az eredmény egy természetes számpár, ilyen a maradékos osztás — vagy olyanokat, amelyek eredménye számok egy tetszőlegesen nagy véges sorozata. Még továbbmenve, olyan Turing-gépeket is lehet készíteni, amelyeknél nincs előre rögzítve, milyen aritmetikai műveletet kell végrehajtani, de az erre szolgáló utasítások rajta vannak a szalagon. Lehet, hogy valamelyik lépésben az éppen elvégzendő művelet függ valamelyik olyan számítás eredményétől, amelyet a gépnek egy korábbi szakaszban kellett elvégeznie. („Ha ennek a számításnak az eredménye nagyobb, mint ez és ez, akkor csináld ezt; egyébként csináld azt.”) Ha egyszer meggyőződtünk arról, hogy lehet olyan Turing-gépeket csinálni, amelyek aritmetikai vagy egyszerű logikai műveleteket végrehajtanak, akkor könnyebben el tudjuk képzelni, hogyan lehet velük bonyolultabb, algoritmikus természetű feladatokat elvégeztetni. Ha az ember játszott már ilyen dolgokkal, akkor könnyen megnyugszik abban, hogy egy effajta géppel bármilyen mechanikus műveletet el lehet végeztetni! Ésszerűnek látszik matematikailag úgy definiálni egy mechanikus műveletet, mint amit egy ilyen gép végre tud hajtani. Az „algoritmus”, főnevet és a „kiszámítható”, „rekurzív” és „végrehajtható” mellékneveket a matematikusok mind az olyan mechanikus műveletek megjelölésére használják, amelyeket ilyen típusú elméleti gépekkel a Turing-gépekkel — végre lehet hajtani. Amennyiben egy eljárás elég világos és mechanikus, akkor joggal gondolhatjuk, hogy valóban lehet találni olyan Turing-gépet, amely végrehajtja azt. Ez volt végül is a lényege bevezető fejtegetésünknek (azaz Turingénak), ez motiválja magát a Turing-gép fogalmát.

Másrészről esetleg még úgy érezhető, hogy az ilyen gépek tervezését talán szükségtelenül korlátoztuk. Első pillantásra ilyen korlátozásnak tűnik az, hogy az eszköz egyszerre csak egy bináris jegyet (0-t vagy 1-t) olvashat el, és hogy egyszerre csak egy lépésnyit mozdulhat el, és csak egyetlen egydimenziós szalag mentén. Miért nem engedünk meg négy vagy öt, vagy esetleg ezer különálló szalagot, nagyszámú vagy egymással összekapcsolt, egy időben működő olvasóeszközökkel? Miért nem engedjük meg inkább 0-t vagy 1-et tartalmazó négyzetek egy egész síkját (vagy esetleg háromdimenziós elrendezését) ahelyett, hogy ragaszkodunk az egydimenziós szalaghoz? Miért nem engedünk meg más jeleket bonyolultabb számrendszerekből vagy ábécékből? Valójában egyik ilyen változtatás sem módosítja még a legcsekélyebb mértékben sem azt, amit elvileg el lehet érni, bár egyesek bizonyos mértékben különbségeket eredményeznek a műveletek gazdaságosságában (bizonyára ez lenne a helyzet, ha egynél több szalagot engednénk meg). Az elvégezhető műveletek osztálya, és így az, ami az algoritmus (vagy „számítások” vagy „végrehajtható eljárások” vagy „ismétlődő műveletek”) címke alá tartozik, pontosan ugyanaz volna, mint előbb, még ha gépeink definícióját az összes felsorolt módon egyszerre szélesítenénk is ki!

Láthatjuk, hogy amíg a Turing-gép talál üres helyet az adott szalagon, addig nincs szükség egynél több szalagra. Ehhez viszont szükség lehet arra, hogy a szalagon az adatokat áthelyezze egyik helyről a másikra. Lehet, hogy ez „rossz hatásfokú”, de nem korlátozza azt, ami elvileg elérhető.⁴ Hasonlóképpen, elvileg nem nyerünk semmit több Turing-gép párhuzamos működtetésével (ami az utóbbi évek divatossá vált elképzelése az emberi agy jobb modellezésének szándékától hajtva), bár bizonyos körülmények között a működési sebesség megnövekedhet. Két, egymással közvetlenül nem kommunikáló, különálló géppel nem lehet többet elérni, mint két egymással kommunikálóval, ha pedig kapcsolat van közöttük, akkor valójában egyetlen gépnek számítanak!

Mi a helyzet Turingnak azzal a megszorításával, hogy a szalag egydimenziós? Ha úgy gondolunk a szalagra, hogy az a „környezetet” képviseli, akkor lehet, hogy jobban szeretnénk, ha nem egydimenziós lenne, hanem egy sík felület, esetleg háromdimenziós szerkezet. Egy sík felület látszólag közelebb állhat ahhoz, ami egy „folyamattáblához” szükséges (például az euklideszi algoritmus működésének előbbi leírásában).* Elvi nehézség azonban nincs abban, hogy egy folyamatábra működését „egydimenziós” formában (például a táblázat közönséges szóbeli leírásával) adjuk meg. A kétdimenziós síkbeli megjelenítés csak saját kényelmünket és a könnyebb érthetőséget szolgálja, és nem befolyásolja azt, hogy elvileg mit lehet elérni. Egy jel vagy objektum helyzetét a kétdimenziós síkon, sőt a háromdimenziós térben is mindig világos módon fel lehet jegyezni egydimenziós szalagra. (Egy kétdimenziós sík használata valójában tökéletesen ekvivalens két szalag használatával. A két szalag szolgáltatná a két „koordinátát”, amelyre szükség van a kétdimenziós sík egy pontjának megadásához; hasonlóképpen három szalag elő tudja állítani a háromdimenziós tér egy pontjának koordinátáit.)

*Maga ez a folyamattábla, ahogy a dolgokról most beszélünk, inkább az „eszköz” része lenne, mint a külső környezet „szalagé”. Az A, B, A-B stb. számok voltak azok, amiket a szalagon ábrázoltunk. Azonban az eszköz leírását is lineáris, egydimenziós alakban akarjuk majd kifejezni. Mint később az univerzális Turing-géppel kapcsolatban látni fogjuk, szoros összefüggés van egy meghatározott „eszköz” és a számára lehetséges „adatok” (vagy „program”) megadása között. Ezért kényelmes, ha mindkettő egydimenziós alakban áll rendelkezésünkre.

Ez az egydimenziós kódolás megint „rossz hatásfokú” lehet, de ez nem befolyásolja azt, hogy mit lehet elvileg elérni.

Mindezek ellenére megkérdezhetjük, hogy vajon összefog-e a Turing-gép fogalma minden logikai vagy matematikai műveletet, amelyet „mechanikusnak” óhajtanánk nevezni. Amikor Turing korszakos cikkét írta, akkor ez sokkal kevésbé volt világos, mint ma, így ő szükségesnek találta, hogy érveit részletesen kifejtse. Érvelése további támogatást talált abban a tényben, hogy tőle teljesen függetlenül (valójában valamivel korábban) az amerikai logista, Alonzo Church (S. C. Kleene segítségével) közétett egy elgondolást — a lambda-kalkulust —, szintén a Hilbert-féle eldönthetőségi probléma megoldására. Bár ez sokkal kevésbé nyilvánvalóan volt teljes, átfogó, mechanikus séma, mint Turingé, azonban matematikai szerkezetének meglepő gazdaságossága jelentett némi előnyt. (Church figyelemre méltó kalkulusát e fejezet végén fogom leírni.) Hilbert problémájának megoldására voltak egyéb, Turingétól szintén független javaslatok is (lásd Gandy 1988), legfőképp a lengyel-amerikai logistáé, Emil Posté (valamivel később Turingnál, de sokkal inkább az övéhez, mint a Churchéhez hasonló elképzelésekkel). Hamarosan megmutatták, hogy mindezek a sémák teljesen ekvivalensek egymással. Ez jelentősen megerősítette azt a nézőpontot, amely a Church —Turing-tétel néven vált ismertté, hogy a Turing-gép (vagy az azzal ekvivalens) fogalom valójában definiálja azt, amit matematikailag algoritmikus (végrehajtható, rekurzív, mechanikus) eljárás alatt értünk. Most, hogy a nagy sebességű elektronikus számítógépek életünknek annyira megszokott részévé váltak, láthatóan nem sok ember érzi szükségesnek megkérdőjelezni ezt a tézist eredeti formájában. Ehelyett inkább arra irányul a figyelem, hogy vajon a valódi fizikai rendszerek (ideértve feltehetően az emberi agyat is) — amelyek pontos fizikai törvények szerint működnek —, többet, kevesebbet vagy pontosan ugyanazokat a logikai és matematikai műveleteket képesek-e végrehajtani, mint a Turing-gépek. Én nagyon boldogan elfogadom a Church-Turing-tétel eredeti matematikai alakját. A valóságos fizikai rendszerek viselkedésével való kapcsolata viszont külön probléma, amely könyvünkben később az egyik fő kérdés lesz.

Számok, amelyek nem természetes számok

Az előző vizsgálatban természetes számokkal végzett műveleteket néztünk, és megjegyeztük azt a figyelemre méltó tényt, hogy egy önmagában álló Turing-gép tetszőlegesen nagy természetes számokat képes kezelni annak ellenére, hogy minden gépnek meghatározott, véges számú, különböző belső állapota van. Gyakran kell azonban bonyolultabb számokkal dolgozni, negatív számokkal, törtekkel vagy végtelen tizedestörtekkel. A negatív számok és a törtek (például az olyan számok, mint a —597/26) könnyen kezelhetők Turing-gépekkel, és a számlálók és nevezők akármilyen nagyok lehetnek. Nincs másra szükségünk, csak a „ — ” és „/” jelek valamilyen alkalmas kódolására, és ez könnyen elvégezhető a korábban leírt, kiterjesztett bináris jelölés használatával (például „3” a és „4” a jelre - rendre 1110 és 11110 alakban kódolva a kiterjesztett bináris jelölésben). A negatív számok és a törtek így természetes számok véges sorozataival kezelhetőek, ezért a kiszámíthatóság általános kérdését illetően semmi újat nem hoznak.

Hasonlóképpen nem adnak semmi újat a tetszőleges hosszúságú véges tizedestörtek sem, mivel ezek csupán a törtek speciális esetei. Például a π irracionális szám 3,14159265 véges tizedestört közelítése egyszerűen a 314159265/100000000 tört. Azonban a végtelen tizedestörtek, mint a π = 3,14159265358979... teljes, meg nem szakadó kifejtés, jelentenek bizonyos nehézséget. Egy Turing-gépnek szigorúan véve sem a bevitele, sem a kivitele nem lehet végtelen tizedestört. Azt gondolhatnánk, hogy találhatunk olyan Turing-gépet, amely a kiviteli szalagon kidobja π fenti kifejezésének összes egymás utáni 3, 1, 4, 5, 9, .. .jegyét, egyiket a másik után, egyszerűen csak azt kell megengednünk, hogy a gép örökké fusson. Ez azonban egy Turing-gépnek nincs megengedve. Meg kell várnunk, míg a gép megáll (ezt jelzi a csengőszó!), csak ezután vizsgálhatjuk meg a kivitelt. Amíg a gép stop utasításhoz nem ér, addig a kivitel megváltozhat, és így nem bízhatunk meg benne. Másrészt, miután STOP-hoz ért, a kivitel szükségszerűen véges.

Van azonban egy eljárás, amely során egy Turing-gép szabályszerűen adhat ki jegyeket, egyiket a másik után, az előzőhöz nagyon hasonló módon. Ha egy végtelen tizedestört kifejtést óhajtunk létrehozni, mondjuk a π-ét, akkor egy Turing-géppel kiadathatjuk először az egész részt, a 3-t úgy, hogy a gép a 0-ra hasson, azután az első tizedesjegyet, 1-t úgy, hogy a gép az 1-re hasson, azután a második tizedesjegyet, 4-et úgy, hogy a 2-re hasson, azután a harmadikat, 1-t úgy, hogy a 3-ra hasson stb. A valóságban bizonyára létezik olyan Turing-gép, amely ebben az értelemben kiadja a ír teljes tizedestört kifejtését, bár egy kissé bonyolult volna explicit módon kidolgozni azt. Hasonló megjegyzés érvényes sok más irracionális számra, mint például a gyök(2) = 1,414213562.. .-re. A helyzet azonban az, hogy egyes irracionális számok (figyelemre méltóan) egyáltalán nem állíthatók elő semmiféle Turing-géppel, amint azt a következő fejezetben látni fogjuk. Azokat a számokat, amelyeket elő lehet ilyen módon állítani, kiszámíthatóaknak nevezik (Turing 1937). Amelyeket nem lehet (a hatalmas többség ilyen!), azok a nem kiszámíthatóak. Erre és rokon problémákra a későbbi fejezetekben vissza fogok térni. Lesz bizonyos jelentőség* számunkra azzal a kérdéssel kapcsolatban, hogy vajon egy valóságos fizikai objektum (például az emberi agy) fizikai elméleteink szerint megfelelően leírható-e kiszámítható matematikai szerkezetekkel kifejezve.

A kiszámíthatóság kérdése a matematikában általánosságban fontos. Nem úgy kell gondolni rá, mint ami csak számokra mint olyanokra vonatkozik. Lehetnek olyan Turing-gépek, amelyek közvetlenül matematikai képletekkel, például algebrai vagy trigonometrikus kifejezésekkel dolgoznak, vagy amelyek a kalkulus formális manipulációit csinálják végig. Nincs másra szükség, mint az összes előforduló matematikai szimbólum 0-kból és 1-ekből álló sorozatokba való pontos kódolásának valamilyen formájára, és ekkor a Turing-gép fogalma alkalmazható. Végül is ez járhatott Turing fejében, amikor nekilátott az eldönthetőségi probléma megoldásához, amely algoritmikus eljárást keres általános természetű matematikai kérdések megválaszolására. Hamarosan visszatérünk erre a kérdésre.

Az univerzális Turing-gép

Nem írtam még le az univerzális Turing-gép fogalmát. Az elvet nem túl nehéz megadni, bár a részletek bonyolultak. Az alapeszme az, hogy egy tetszőleges T Turing-gép utasításainak listáját egy 0-kból és 1-kből álló füzérbe kódoljuk át, ezt szalagon lehet ábrázolni. Ezt a szalagot használjuk azután valamilyen speciális U Turing-gép bevitele kezdeti részének — U-1 nevezzük majd univerzális Turing-gépnek. A bevitel maradék részére U éppen úgy hat, mint ahogy T tenné. Az univerzális Turing-gép egy univerzális utánzó. A szalag kezdeti része megadja az U univerzális gépnek a teljes információt, amire annak szüksége van, hogy pontosan utánozzon bármilyen adott T gépet!

Működésének megértéséhez először szükségünk van a Turing-gépek szisztematikus megszámozására. Tekintsük a valamilyen speciális Turing-gépet definiáló utasítások listáját, mondjuk az előzőekben leírtak egyikét. Ezt a listát valamilyen pontos előírás szerint 0-kból és 1-kből álló füzérré kell átkódolni. Az előbbiekben elfogadott „kontrakciós” eljárás szerint ez megtehető. Ha az R, L, STOP, nyíl (—>) és vessző szimbólumokat rendre a 2, 3, 4, 5 és 6 számokkal ábrázoljuk, akkor ezek a kontrakcióval az 110, 1110, 11110, 111110 és 1111110 füzérekbe kódolhatók. Ezután a 0 és 1 jegyek, rendre 0 és 10 alakban kódolva használhatók a táblázatban megjelenő aktuális szimbólumfüzérekre. Nincs szükség arra, hogy külön jelöléssel megkülönböztessük a Turing-gép táblázatában álló 0 és 1 nagy számjegyeket a kisebb kövérektől, mert a nagy jegyek helyzete a bináris számozás végén elegendő a többitől való megkülönböztetésre. így például 1101-et a bináris 1101 számként kell olvasni és szalagon 1010010-ként kódolni. Speciálisan a 00-t OO-nak kell olvasni, ami egyértelműen kódolható 0-val, vagy egy olyan szimbólumnak, amely egészében elhagyható. Jelentős megtakarítást érhetünk el, ha nem bajlódunk sem a nyilak, sem az azokat közvetlenül megelőző szimbólumok kódolásával, hanem ehelyett az utasítások szám szerinti rendezésére támaszkodunk, ezzel írjuk elő, milyenek legyenek azok a szimbólumok — bár elfogadva ezt az eljárást biztosítanunk kell azt, hogy e rendezésben ne legyenek rések, így ahol szükséges, egy néhány extra „statisztáló” utasítást kell beírnunk. (Az XN+1 Turing-gép például nem rendelkezik arról, mit kell csinálni 1100-val, mivel ez a kombináció a gép futtatása során soha nem fordul elő, ezért be kell szúrnunk egy „statiszta” utasítást, mondjuk 1100—>00R-et, ami beilleszthető a listába anélkül, hogy bármi megváltozna. Hasonlóképpen az XNx2 gépbe be kell illesztenünk az 101—>00R utasítást.) Ilyen „statiszták” nélkül a listán egymás után következő utasítások kódolása el lenne rontva. Az egyes utasítások végén álló vesszőre valójában nincs szükségünk, mivel az L vagy R szimbólum elegendő az utasítások egymástól való elválasztására. Ezért egyszerűen a következő kódolást fogadjuk el:

a o-ra vagy 0-ra,

10 az l-re vagy 1-re,

110 az R-re,

1110 az L-re,

11110 a STOP-ra.

Példaként kódoljuk az XN+1 Turing-gépet (beszúrva az 1100—>00r utasítást). Elhagyva a nyilakat, az ezeket közvetlenül megelőző jegyeket és a vesszőket is, ez áll előttünk:

00R 11R 00R 101R HOL 101R OlSTOP 1000L 1011L 1001L 1100R 101R OOR llllR HÍR lllOR.

Ezen még javíthatunk úgy, hogy a korábban mondottakkal összhangban elhagyunk minden 00-t, és egyszerűen 1-gyel helyettesítünk minden 01-et, így a következőt kapjuk:

RURRIOIRHOLIOIRISTOPIOOOLIO ÍILIOOILIIOORIOIRRIIIIRIURIIIOR.

Ez a szalagon a következő kódsorozatként jelenik meg:

110101011011010010110101001110100101101011110100001110

100101011101000101110101000110100101101101010101011010

10101101010100110

Két további apró rövidítés: mindig elhagyhatjuk a kezdeti 110-t (az ezt megelőző végtelen hosszú üres szalagdarabbal együtt), minthogy ez a 00—>00R kezdő utasítást ábrázolja, amit hallgatólagosan minden Turing-gépben közösnek tekintek — az eszköz így a jelektől balra tetszőlegesen távolról indulhat, és addig megy jobbra, amíg az első jelet meg nem találja —, és mindig kihúzhatjuk a végső 110-t (és a 0-k ezt követő feltételezett végtelen sorozatát), mert minden Turing-gép leírása így kell végződjék (mert mindegyik vége R, L vagy STOP). Az eredményül kapott bináris szám a Turing-gép száma, amely az XN+1 esetében

101011011010010110101001110100101101011110100001110100

101011101000101110101000110100101101101010101011010101

01101010100

A szabványos tízes jelölésben ez a szám a

450813704461563958982113775643437908.

Olykor, kissé pongyolán, úgy hivatkozunk a Turing-gépre, amelynek száma n, mint az n-edik Turing-gép, és azt T„-nel jelöljük. Így XN+1 a

450813704461563958982113775643437908

-dik Turing-gép!

Meglepő, hogy a Turing-gépek „listáján” ilyen messzire el kell mennünk, míg találunk egyet, amely elvégez egy olyan triviális műveletet, mint az 1 hozzáadása (a kiterjesztett bináris jelölésben) egy természetes számhoz! (Nem hiszem, hogy kódolásom nagyon rossz hatásfokú lenne, bár kis javításokat el tudok képzelni.) Vannak alacsonyabb számú Turing-gépek, amelyeknek van jelentőségük. Például az UN+1 kettes rendszerbeli száma

101011010111101010,

ami tízes jelölésben csak 177642! Így a különösen egyszerű Turing-gép, amely csupán egy további l-et rak egy egyesekből álló sorozat végére, a 177642-dik Turing-gép. Pusztán az érdekesség kedvéért megjegyezhetjük, hogy a „kettővel való szorzás”, mindkét jelölésben valahol az előző kettő között van a Turing-gépek listáján, mivel az XNx2 száma 1456581339, míg az UNx2-é 1492923420919872026917547669.

E számok nagyságát látva talán nem meglepő, hogy a természetes számok hatalmas többségéhez egyáltalán nem tartozik működő Turing-gép. Írjuk le a számozás szerinti első tizenhárom Turing-gépet:

T₀ egyszerűen jobbra mozog, kitöröl mindent, amit talál, és soha nem áll meg. T₁ félénkebb, mert amint jobbra menve talál egy jelet a szalagon, kitörli azt, és visszaugrik balra, és ezt folytatja a végtelenségig. A T₂ gép a T₀-hoz hasonlóan szintén állandóan jobbra mozog, de tisztelettudóbb, mint az, egyszerűen mindent változatlanul hagy a szalagon. Turing-gépnek igazán egyik sem jó, mert egyik sem áll meg sohasem. T₃ az első elfogadható Turing-gép. Ez csakugyan megáll, szerényen, miután az első (bal szélső) 1-et 0-ra változtatta.

A T₄-gyel komoly probléma van. Miután megtalálja a szalagon az első 1-et, olyan belső állapotba lép be, amely nincs a listán, így nincs utasítása arra, mit kell ezután csinálnia. Ugyanez a probléma a T₈,T₉,T₁₀ gépekkel. Még alapvetőbb a nehézség a TV-tel. Az őt kódoló 0 és 1 füzérben öt egyes áll egymás után: 110111110. Az ilyen sorozatot nem lehet értelmezni, ezért T₇ elakad, amint megtalálja a szalagon az első 1-t. (Ty-re vagy bármelyik másik T_n gépre, amelynél n bináris kifejtése négynél több egymás utáni 1-t tartalmaz, úgy fogok hivatkozni, mint aminek leírása nem helyes.) A T₅, T₆ és T₁₂ gépeknek hasonló problémájuk van, mint T₀-nak, T₁-nek és T₂-nek. Egyszerűen a végtelenségig futnak, soha meg nem állnak. A T₀,T₁,T₂, T₄,T₅,T₆,T₇,T_&, T₉,T₁₀ és T₁₂ gépek mind haszontalanok! Csak T₃ és T₁₁ igazán működő Turing-gép, és ráadásul egyik sem nagyon érdekes. T₁₁ még szerényebb, mint T₃. Megáll, amikor az első 1-gyel találkozik, és nem változtat meg semmit!

Meg kell jegyeznünk, hogy a listában átfedések is vannak. A T₁₂ gép azonos T₆-tal és működésében T₁-gyel is, mert T₆ és T₁₂ 1-es belső állapota soha nem jelenik meg. Sem ezen átfedések, sem a haszontalan Turing-gépek szaporasága miatt nem kell zavartatnunk magunkat. Kódolásunkat meg lehetne úgy javítani, hogy az értelmetlenségek tekintélyes része eltűnjön, és az átfedések is jelentősen csökkenjenek. Mindezt azon az áron, hogy bonyolultabbá tesszük szegény univerzális Turing-gépünket, amelynek meg kell fejtenie a kódot, és amely az a T_n Turing-gép szándékozik lenni, amelyiknek n számát olvassa. Ezt akkor lenne érdemes megtenni, ha az összes használhatatlan dolgot (vagy átfedést) el tudnánk távolítani. Ez azonban, amint azt hamarosan látni fogjuk, nem lehetséges! Hagyjuk hát a kódolást úgy, ahogy van.

Kényelmes lesz úgy értelmezni a szalagon egy jelsorozatot, például a következőt:

...0001101110010000...,

mint valamely szám bináris ábrázolását. Emlékezzünk vissza, hogy a 0-k mindkét oldalon a végtelenségig folytatódnak, az 1-ek száma viszont véges. Feltételezem azt is, hogy az 1-ek száma nem nulla (azaz legalább egy 1 van). Választhatnánk azt, hogy az első és utolsó egyes közötti véges szimbólumfüzért olvassuk be, mint egy természetes szám bináris leírását (beleértve az l-eket is), ami az előző példában

110111001

lenne (ami most tízes jelölésben 441). Azonban ez az eljárás csak páratlan számokat adna (olyanokat, amelyek bináris ábrázolása 1-gyel végződik), mi pedig azt szeretnénk, ha minden természetes számot ábrázolni tudnánk. Ezért egyszerűen úgy segítünk magunkon, hogy elhagyjuk az utolsó l-et (ezt csupán egy jelnek tekintjük, amely a kifejezés végét jelzi), és ami marad, azt bináris számként elolvassuk.⁵ Így a fenti példában az

11011100

bináris számot kapjuk, amely tízes jelölésben 220. Az eljárás előnye, hogy a nullát is egy jelzett szalag ábrázolja, nevezetesen a

.. .0000001000000

Tekintsük a T_n Turing-gép hatását egy 0-kból és 1-ékből álló (véges) füzérre, amit a szalagon a jobb oldalon táplálunk be. Kényelmes lesz ezt a füzért is valamely szám, mondjuk m, bináris ábrázolásának tekinteni az előbb megadott előírás szerint. Tegyük fel, hogy egy lépéssorozat után a T_n gép végül megáll (azaz STOP-hoz ér). A bináris jegyekből álló füzér, amit most a gép a bal oldalon kiad, a számítás eredménye. Olvassuk ezt is úgy, mint egy szám, mondjuk p, ugyanolyan módon értelmezett bináris ábrázolását. Ezt a kapcsolatot, amely azt fejezi ki, hogy ha az n-edik Turing-gép m-re hat, akkor p-t ad ki, a következőképpen írjuk fel:

T_n(m) = p.

Tekintsünk most egy kicsit másképpen erre a kapcsolatra. Gondoljuk azt, hogy egy speciális műveletet fejez ki, amelyet egy (n, m) számpárra kell alkalmazni, hogy eredményül a p számot kapjuk. (Tehát: ha adva van két szám, n és m, akkor p-t úgy tudjuk meghatározni, hogy megnézzük, mit csinál az n-edik Turing-gép m-mel.) Ez a speciális művelet egy teljesen algoritmikus eljárás. Ezért el tudja azt végezni egy speciális U Turing-gép; azaz U az (n, m) párra hat, és eredményül p-t ad. Mivel az U gépnek mindkét számra, n-re és m-re is hatnia kell, hogy kijöjjön az egyetlen p eredmény, ezért szükségünk van az (n, m) pár valamilyen kódolására az egyetlen szalagon. Ehhez feltételezhetjük, hogy n le van írva a közönséges bináris jelölésben, és ezt közvetlenül határolja az 111110 sorozat. (Emlékezzünk rá, hogy minden helyesen megadott Turing-gép bináris száma egy, a0, 10, 110, 1110 és 11110 jelekből álló sorozat, és ezért nem tartalmaz olyan részsorozatot, amiben négy 1-esnél több van. Így ha T_n egy helyesen megadott gép, akkor az 111110 előfordulása valóban azt jelzi, hogy az n szám leírása befejeződött.) Minden, ami ezt követi, egyszerűen az m-et ábrázoló szalag a fenti előírásaink szerint (azaz az m bináris szám, utána pedig 1000...). Így ez a második rész egyszerűen az a szalag, amelyre a feltételezés szerint T_n hat.

Ha például n = 11 és m = 6, akkor í7-nak a következő jelsorozatot tartalmazó szalagra kell hatnia:

...000101111111011010000

Ez a következőképpen áll össze:

... 0000 (kezdeti üres szalag)

1011 (11 bináris ábrázolása)

111110 (n-t határolja)

110 (6 bináris ábrázolása)

10000 ... (a szalag maradék része)

Az V Turing-gépnek az a dolga, hogy utánozva T_n m-mel való műveletének egymás utáni lépéseit, megvizsgálja n kifejezésében a jegyek egymásutánjának szerkezetét, így tudja elvégezni a megfelelő helyettesítéseket m jegyeiben (azaz T_n „szalagján”). Valójában elvileg nem túl nehéz (de a gyakorlatban határozottan fárasztó) végignézni, hogyan lehet készíteni egy ilyen gépet. Saját utasításlistája egyszerűen arra irányulna, hogy elolvassa a megfelelő jegyeket azon a „listán”, amelyen az n számot kódolja, és tegye ezt az m-et megadó „szalag” jegyeire való alkalmazás minden egyes szakaszában. Kétségkívül sokat ugrálna előre és hátra az m és az n jegyei között, és az eljárás általában rendkívül lassú volna. Azonban egy utasításlistát bizonyára meg lehet adni; és egy ilyen gépet nevezünk univerzális Turing-gépnek. A gép hatását az (n, m) számpárra U(n, m)-mel jelölve azt írhatjuk, hogy

U(n, m) = T„(m)

minden egyes (n, m) párra, amelyre T_n egy helyesen megadott Turing-gép.⁶ Az U gép, ha először az n számot tápláljuk bele, pontosan utánozza az n-edik Turing-gépet!

Mivel U Turing-gép, neki is van száma; azaz

U =T_U

valamilyen u számra. Milyen nagy u! Pontosan meg tudjuk adni:

u = 724485533533931757719839503961571123795236067255655963110814479 6606505059404241090310483613632359365644443458382226883278767626556 1446928141177150178425517075540856576897533463569424784885970469347 2573998858228382779529468346052106116983594593879188554632644092552 5505820555989451890716537414896033096753020431553625034984529832320
6515830476641421307088193297172341510569802627346864299218381721573 3348282307345371342147505974034518437235959309064002432107734217885 1492760797597634415123079586396354492269159479654614711345700145048 1673375621725734645227310544829807849651269887889645697609066342044 7798902191443793283001949357096392170390483327088259620130177372720 2718625919914428275437422351355675134084222299889374410534305471044 3686958764051781280194375308138706399427728231564252892375145654438 9905278079324114482614235728619311833261065612275553181020751108533 7633806031082361675045635852164214869542347187426437544428790062485 8270912404220765387542644541334517485662915742999095026230097337381 3772416217274772361020678685400289356608569682262014198248621698902 6091309402985706001743006700868967590344734174127874255812015493663 9389969058177385916540553567040928213322216314109787108145997866959 9704509681841906299443656015145490488092208448003482249207730403043 1884298993931352668823496621019471619107014619685231928474820344958 9770955356110702758174873332729667899879847328409819076485127263100 1740166787363477605857245036964434897992034489997455662402937487668 8397514044516657077500605138839916688140725455446652220507242623923 7921152531816251253630509317286314220040645713052758023076651833519 95689139748137504926429605010013651980186945639498

(vagy valamilyen más, legalább ugyanilyen méretű lehetséges szám). Ez a szám kétségtelenül riasztóan nagynak látszik! És valóban az is, de nem látom módját, hogyan lehetne jelentősen csökkenteni. A kódolási eljárások és előírások, amelyeket a Turing-gépekre megadtam, egészen ésszerűek és egyszerűek, mégis elkerülhetetlenül ilyen méretű számhoz jutunk egy igazi univerzális Turing-gép kódolásakor.⁷

Már említettem, hogy minden modern, általános célú számítógép valójában univerzális Turing-gép. Nem akarom ezzel azt mondani, hogy az ilyen számítógépek logikai tervezetének hasonlítania kell az univerzális Turing-gép olyan fajta leírásához, amelyet éppen megadtam. A lényeg egyszerűen az, hogy bármelyik univerzális Turing-gépet először megfelelő programmal (a bemeneti szalag kezdeti részével) ellátva elérhető, hogy utánozza bármelyik Turing-gép viselkedését! A fenti leírásban a program egyetlen szám (az n szám) alakját veszi fel, de lehetséges más eljárás is; sok változat létezik Turing eredeti témájára. Leírásomban valójában valamennyire eltértem attól, amit Turing eredetileg megadott. Számunkra azonban most e különbségek egyike sem lényeges.

A Hilbert-féle probléma megoldhatatlansága

Térjünk most rá arra, amiért Turing elképzeléseit eredetileg felvetette, hogy megadja a választ Hilbert nagyon általános eldönthetőségi problémájára: létezik-e mechanikus eljárás valamilyen széles, de jól meghatározott osztályba tartozó matematikai problémák megoldására? Turing rájött, hogy a kérdést át tudja fogalmazni annak a problémának eldöntésére, hogy megáll-e vagy sem valamikor az n-edik Turing-gép, amikor az m számra hat. Erre a problémára, mint megállási problémára hivatkoztak. Könnyű olyan utasításlistát készíteni, amellyel a gép semmilyen m számra nem áll meg (ilyen például az előbbiekben megadott n =1 vagy 2 eset, vagy bármely másik, ahol nincs stop utasítás. Van sok olyan utasításlista is, amellyel a gép mindig megáll, bármilyen számra alkalmazza is azt (például az n = 11), és egyes gépek egyes számokra megállnak, másokra nem. Annyit bizonyára mondhatunk, hogy egy feltételezett algoritmusnak nincs sok haszna, ha megállás nélkül a végtelenségig fut. Az ilyen nem is algoritmus. Így fontos, hogy képesek legyünk eldönteni, hogy m-re alkalmazva T_n ad-e egyáltalán valamikor valamilyen választ! Ha nem (azaz ha a számítás nem áll meg), akkor azt fogom írni, hogy

T_n(m) = □.

(Ide tartoznak azok az esetek is, amikor a Turing-gép a számítás valamelyik szakaszában azért kerül bajba, mert nem talál megfelelő utasítást, amely megmondaná, mit kell csinálnia — ilyenek az előbb vizsgált, haszontalan gépek, T4 és T₇. Sajnos a látszólag sikeres T₃ gépünket is ide kell sorolnunk: T₃(m) = □, mert a gép működésének eredménye mindig csak üres szalag, míg ahhoz, hogy a számítás eredménye valamilyen szám legyen, legalább egy 1-esnek kell lennie a kivitelben! A T₁₁ gép viszont szabályszerű, mert egyetlen 1-est ad ki. Ez a kivitel a 0 számú szalag, így T₁₁(m) = 0, minden m-re.)

A matematika számára fontos lenne, hogy képesek legyünk eldönteni, mikor állnak le a Turing-gépek. Tekintsük például a következő egyenletet:

(x + i)^w+3 + (y + 1)^w+3 = (z + i)^w+3

(Ha Ön a matematikai egyenleteket nem igazán kedveli, ez még ne szegje kedvét! Ezt most csak példaként mutatom, nincs szükség arra, hogy a részleteket is értse.) Ez a speciális egyenlet a matematika egyik híres megoldatlan problémájához kapcsolódik — talán mind közül a leghíresebbhez. A probléma a következő: vannak-e olyan w,x,y,z természetes számok, amelyekre a fenti egyenlet teljesül? A „Fermat utolsó tétele” (nagy Fermat-tétel) néven ismert híres állítás, amelyet a tizenhetedik századbeli kiváló francia matematikus, Pierre de Fermat (1601 — 1665) Diofantosz Arithmeticá}ának margójára írt, azt mondja, hogy az egyenlet soha nem teljesül.⁸* Bár foglalkozására nézve jogász (és Descartes kortársa), Fermat korának legkitűnőbb matematikusa volt. Azt állította, hogy tételére „igazán csodálatos bizonyítása” van, de a margó túl kicsi volt, így nem fért rá; azonban mind a mai napig senki nem volt képes rekonstruálni egy ilyen bizonyítást, viszont ellenpéldát sem tudtak a nagy Fermat-tételre találni!

Világos, hogy ha adott a (w, x, y, z) számnégyes, akkor csupán számolás kérdése annak eldöntése, hogy az egyenlőség fennáll-e vagy sem. Ezért el tudunk képzelni olyan számítógép-algoritmust, amely végigfut egymás után minden számnégyesen, és csak akkor áll meg, ha az egyenlet teljesül. (Láttuk, hogy vannak módok véges számsorozatok kiszámítható kódolására egyetlen szalagon, azaz egyetlen számként, így „végigfuthatunk” minden számnégyesen, követve ezen egyetlen számok természetes sorrendjét.) Ha meg tudnánk állapítani, hogy ez az algoritmus nem áll meg, akkor bizonyításunk lenne Fermat tételére.

Sok más megoldatlan matematikai problémát is meg lehet fogalmazni hasonló módon, a Turing-gép megállási problémájaként. Egy ilyen példa a „Goldbach-sejtés”, amely szerint minden 2-nél nagyobb páros szám felbontható két prímszám összegére.** Eldönteni, hogy egy adott természetes szám prímszám-e vagy sem, ez algoritmikus folyamat, mert csak nála kisebb számokkal való oszthatóságot kell ellenőrizni, ami véges számítás.

*Emlékezzünk rá, hogy a természetes számok a 0, 1, 2, 3, 4, 5, 6,.... Hogy a nagy Fermat- tétel szokásosabb alakja (x^w + y^w = z^w; x, y, z > 0, w> 2 ) helyett ,x + l”-et, „w+3”-at stb. írtunk, annak oka az, hogy x,w stb. értékére 0-tól kezdve minden természetes számot megengedünk.

** Emlékezzünk rá, hogy a prímszámok, 2, 3, 5, 7, 11, 13, 17,... azok a természetes számok, amelyek csak önmagukkal és eggyel oszthatók. Sem a 0-t, sem az l-et nem tekintjük prímszámnak.

Ki tudnánk gondolni egy Turing-gépet, amely végigfut a 6, 8, 10,12,14,... páros számokon, az összes lehetséges módon két páratlan szám összegére bontja azokat, és ellenőrzi, hogy van-e mindegyik páros számnak olyan felbontása, amelyben mindkét tag prímszám:

6 = 3 + 3,8 = 3 + 5,10 = 3 + 7 = 5 + 5,12 = 5 + 7,14 = 3 + 11 = 7 + 7,...

(A páros tagokból álló felbontásokat, a 2 + 2 kivételével, nyilván nem kell megvizsgálni, mert a 2 kivételével minden prímszám páratlan.) Gépünk csak akkor áll meg, amikor olyan páros számhoz érkezik, amelyiknél egyik felbontás sem tartalmaz két prímszámot. Ebben az esetben ellenpéldánk volna a Goldbach-sejtésre, nevezetesen egy olyan (2-nél nagyobb) páros szám, amely nem két prímszám összege. Így ha el tudnánk dönteni, hogy ez a Turing-gép megáll-e valamikor vagy sem, akkor módunk lenne a Goldbach-sejtés helyességének eldöntésére is.

Felvetődik egy természetes kérdés: hogyan döntsük el, hogy bármelyik speciális Turing-gép (meghatározott bemeneti adatokat betáplálva) megáll-e valamikor? Sok Turing-gépre ezt nem lehet nehéz megválaszolni; de a válasz, mint előbb láttuk, olykor egy komoly matematikai probléma megoldását foglalja magában. Van-e tehát valamilyen algoritmikus eljárás az általános kérdés — a megállási probléma — teljesen automatikus megválaszolására? Turing megmutatta, hogy nincs.

Érvelése lényegében a következő volt. Először feltesszük az ellenkezőjét, azt, hogy van egy ilyen algoritmus.* Ekkor kell legyen valamilyen H Turing-gép, amely eldönti, hogy az n-edik Turing-gép, amikor az m számra hat, megáll-e végül vagy sem. Mondjuk, hogy a kivitel a 0 számú szalag, ha nem áll meg, az 1 számú, ha megáll:

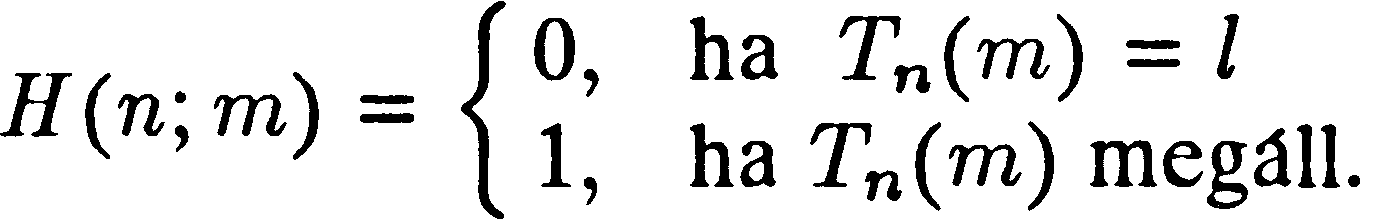
Itt az (n, m) számpár kódolására ugyanazt a szabályt használhatjuk, mint amelyet az U univerzális gépnél elfogadtunk. Ez azonban ahhoz a technikai problémához vezethet, hogy bizonyos n számokra (például n = 7-re) T_n nincs helyesen megadva; és az 11110 jelzés nem lenne megfelelő n és m elválasztására a szalagon. Hogy e problémát megelőzzük, tételezzük fel, hogy n-et az egyszerű helyett a kiterjesztett bináris jelölés szerint kódoljuk, m- re pedig megtartjuk a közönséges binárist, mint korábban.

*Ez az indirekt bizonyítás (reductio ad absurdum) néven ismert, megszokott — és hatásos — matematikai eljárás, amelynek során először feltesszük, hogy amit bizonyítani akarunk, az hamis, és ebből ellentmondást vezetünk le, megállapítva így, hogy az állítás valójában igaz.

Ekkor a 110 jel elegendő lesz n és m elválasztására. A pontosvessző használata H(n;m)-ben, eltérően az U(n,m)-ben használt vesszőtől, e változtatás jelzésére szolgál.

Képzeljünk most el egy végtelen elrendezést, amely felsorolja minden lehetséges Turing-gép minden kivitelét, minden lehetséges különböző bevitel esetén. Az elrendezés n-edik sora az n-edik Turing-gép kiviteleit mutatja a 0, 1, 2, 3, ... bevitelek mellett:

A fenti táblázatban egy kicsit csaltam, nem úgy soroltam fel a Turing-gépeket, ahogy valójában számozva vannak. Ha így tettem volna, akkor a táblázat eleje kicsit unalmasan nézett volna ki, mert minden gép, amelynél n kisebb, mint 11, csak □-eket ad, n = 11 esetén pedig csak 0-kat kapunk. Hogy a lista eleje érdekesebben nézzen ki, feltételeztem, hogy valamilyen hatékonyabb kódolást sikerült találni. Valójában egyszerűen csak véletlenszerűen állítottam össze a táblázatot, hogy éppen csak némi benyomást adjak, milyen lehetne annak általános kinézete.

Nem állítom azt, hogy ténylegesen kiszámítottuk ezt az elrendezést, mondjuk valamilyen algoritmus segítségével. (Valójában nincs is ilyen algoritmus, mint azt egy pillanaton belül látni fogjuk.) Éppen csak el kell képzelnünk, hogy az igazi listát valaki, talán a Jóisten, elénk terítette! A □-k előfordulása az, ami nehézségeket okozna, ha számítani akarnánk, mivel nem tudnánk biztosan, mikor tegyünk valamelyik helyre □-t, hiszen ezek a számítások egyszerűen a végtelenségig tartanának!

Tudnánk azonban számítási eljárást adni a táblázat létrehozására, ha használhatnánk feltételezett H gépünket, mivel az megmondaná nekünk, hol jelennek meg a □ -ek. Használjuk azonban ehelyett a H-t minden □ kiküszöbölésére, helyettesítsük mindegyiket 0-val. Tegyük ezt úgy, hogy T_n m-re való hatását megelőzzük H(n;m) kiszámításával; T_n-1 csak akkor engedjük m-re hatni, ha H(n; m) = 1 (azaz csak ha T_n(m) számítása valóban ad eredményt), és egyszerűen 0-t írunk, ha H(n; m) = 0 (azaz ha T_n(m) = □). Új eljárásunkat — azaz amelyet úgy kapunk, hogy T_n(m)-et megelőzzük H(n; m) hatásával — a

T_n(m) X H(n;m)

alakban írhatjuk. (Itt a matematikai műveletek sorrendjére vonatkozó általános konvenciót használom: először a jobbra állót kell elvégezni. Figyeljük meg, hogy, szimbolikusan, □ x 0 = 0.)

A táblázat most így alakul:

Figyeljük meg, hogy — H létezését feltételezve —, a táblázat sorai kiszámítható sorozatokból állnak. (Kiszámítható sorozaton olyan végtelen sorozatot értek, amelynek egymás után következő tagjai egy algoritmus segítségével képezhetők; azaz van valamilyen Turing-gép, amely az m = 0, 1, 2, 3, 4, .. természetes számokra alkalmazva sorban kiadja a sorozat egymást követő tagjait.) Feljegyzünk most két tényt a táblázatról. Elsőként azt, hogy a természetes számok minden kiszámítható sorozatának meg kell jelennie valamelyik sorban (esetleg többször is). Ez már igaz volt az eredeti táblázatra is a maga □-eivel. Ahhoz egyszerűen hozzátettünk sorokat, hogy helyettesítsük a „haszontalan” Turing-gépeket (azaz azokat, amelyek legalább egy □-et produkálnak). Másodszor azt, hogy feltételeztük: a H Turing-gép valóban létezik, a táblázat kiszámíthatóan készült (azaz valamilyen meghatározott algoritmussal), nevezetesen a T_n(m) x H(n; m) eljárás szerint. Van tehát valamilyen Q Turing-gép, amely az (n,m) számpárra hatva kiadja a táblázat megfelelő elemét. Ehhez n-et és m-et ugyanúgy kódolhatjuk Q szalagján, mint tettük azt H számára, és így

Q(n; m) = T_n(m) x H(n;m).

Most egy elmés és hatásos fogásnak, Georg Cantor „átlós metszés”-ének egy változatát alkalmazzuk. (Cantor átlós metszésének eredeti változatát a következő fejezetben fogjuk látni.) Tekintsük a főátló elemeit, amelyeket most kövér jegyekkel jelöltünk:

Ezek az elemek valamilyen 0, 0, 1, 2, 1, 0, 3, 7, 1, ... sorozatot alkotnak, amelynek minden tagjához most hozzáadunk l-et:

1,1,2,3,2,1,4,8,2,...

Ez nyilvánvalóan kiszámítható eljárás, és mivel táblázatunk kiszámíthatóan készült, ezért egy új kiszámítható sorozatot kapunk, az 1 + Q(n;n), azaz az

1 + T_n(n) X H(n; n)

sorozatot (mivel az átlós elemeknél m egyenlő n-nel). De táblázatunk minden kiszámítható sorozatot tartalmaz, ezért az új sorozatnak is benne kell valahol lennie. Ez azonban nem lehetséges! Új sorozatunk ugyanis különbözik az első sortól az első tagban, a másodiktól a másodikban, a harmadiktól a harmadikban, és így tovább. Ez nyilvánvaló ellentmondás. Ez az ellentmondás teremti meg az alapját annak, amit bizonyítani akartunk, nevezetesen, hogy a H Turing-gép valójában nem létezik! Nincs univerzális algoritmus annak eldöntésére, hogy egy Turing-gép megáll-e vagy sem.

Az érvelés egy más megfogalmazása a következő. Feltételezve, hogy H létezik, az 1 + Q(n;n) algoritmusnak van valamilyen Turing-gép száma, mondjuk k, így

1 + T„(n) x H(n;n) = T_k(n).

De ha ebbe az összefüggésbe n = k-t helyettesítünk (átlós eljárás!), akkor a következőt kapjuk:

1 + T_k(k) x H(k;k) = T_k(k).

Ez ellentmondás, mert ha T_k(k) megáll, akkor az

1 + T_k(k) = T_k(k)

lehetetlen összefüggést kapjuk (mivel H(k;k) = 1), míg ha T_k(k) nem áll meg (így H(k; k) = 0), akkor a szintén ellentmondó

1 + 0 = □

egyenlőséget.

Az a kérdés, hogy egy Turing-gép megáll-e vagy sem, a matematikának egy tökéletesen jól meghatározott darabja (és már láttuk, hogy megfordítva: változatos, jelentős matematikai kérdések fogalmazhatók meg Turing-gépek megállásának problémájaként). Így megmutatva, hogy nem létezik algoritmus annak a kérdésnek eldöntésére, hogy megállnak-e a Turing-gépek, Turing bebizonyította (és ezt tette Church is saját, meglehetősen különböző megközelítésében), hogy a matematikai kérdések eldöntésére nem létezhet általános algoritmus. Hilbert eldönthetőségi problémájának nincs megoldása!

Ez nem jelenti azt, hogy bármelyik egyedi esetben ne lehetnénk képesek kideríteni az igazságot, megválaszolni egyes matematikai kérdéseket; vagy eldönteni, hogy valamely adott Turing-gép megáll-e vagy sem. A leleményesség vagy éppen csak a józan ész segítségével adott esetben képesek lehetünk eldönteni egy ilyen kérdést. (Ha például egy Turing-gép utasításlistáján nincs STOP utasítás, vagy csak STOP utasítások vannak, akkor a józan ész önmagában elegendő, hogy megmondjuk, megáll-e vagy sem!) Nincs azonban algoritmus, amely minden matematikai kérdésnél működik, nincs ilyen minden Turing- gépre és minden számra, amelyre a gépek hathatnak.

Úgy tűnhet, most azt állapítottuk meg, hogy van legalább néhány eldönthetetlen matematikai kérdés. Azonban semmi ilyet nem csináltunk. Nem azt mutattuk meg, hogy van valamilyen különösen szörnyűséges Turing-gép táblázat, amelynél, valamiféle abszolút értelemben, lehetetlen eldönteni, megáll-e a gép vagy sem, amikor valamilyen különösen szörnyű számot táplálunk belé — a helyzet valójában éppen az ellenkező, amint azt egy pillanaton belül látni fogjuk. Nem mondtunk semmit egyes problémák megoldhatatlanságáról, csak problémák egyes családjainak algoritmikus megoldhatatlanságáról. A válasz bármelyik egyedi esetben vagy „igen”, vagy „nem”, így az adott eset eldöntésére bizonyára van algoritmus, nevezetesen az, amely egyszerűen „igen”-t mond, amikor feladjuk neki a problémát, vagy amelyik egyszerűen „nem”-et mond, ami szintén előfordulhat! A nehézség természetesen az, hogy nem tudhatjuk, melyik algoritmust használjuk. Ez egyetlen állítás matematikai igazsága kiderítésének, nem pedig állítások egy családja szisztematikus eldöntésének kérdése. Fontos felismerni azt, hogy az algoritmusok magukban nem döntik el a matematikai igazságot. Egy algoritmus érvényességét mindig külső eszközökkel kell megállapítani.

Hogyan győzzünk le egy algoritmust?

A matematikai állítások igazsága eldöntésének kérdésére később, Gödel-tételével kapcsolatban visszatérünk (lásd a 4. fejezetet). Most rá szeretnék mutatni arra, hogy Turing érvelése valójában sokkal építőbb és kevésbé negatív, mint amilyennek eddig látszólag bemutattam. Nem mutattunk még olyan speciális Turing-gépet, amelynél, valamilyen abszolút értelemben, eldönthetetlen, hogy megáll-e vagy sem. Ha azonban gondosan megvizsgáljuk az érvelést, akkor azt találjuk, hogy eljárásunk maga hallgatólagosan már megadja a választ a látszólag „különösen szörnyűséges” gépeket illetően. Most Turing eljárását használva fogunk egy ilyet készíteni!

Lássuk, hogy történik ez. Tegyük fel, hogy van valamilyen algoritmusunk, amely olykor meg tudja mondani, hogy egy Turing-gép nem áll meg. Turing fentebb körvonalazott eljárása explicit módon megad egy Turing-gép számítást, amelyről ez a speciális algoritmus nem képes eldönteni, hogy megáll-e vagy sem. Azonban követve az eljárást, az bennünket képessé tesz, hogy ebben az esetben megadjuk a választ. A speciális Turing-gép számítás, amelyet bemutatunk, nem fog megállni.

Hogy lássuk, hogyan állnak össze a részletek, tegyük fel, hogy van egy olyan algoritmusunk, amely néha hatásosan működik. Mint előbb, jelöljük ezt az algoritmust (Turing-gépet) H-val, most azonban megengedjük, hogy az algoritmus ne tudja mindig biztosan megmondani, hogy egy Turing-gép a valóságban nem fog megállni:

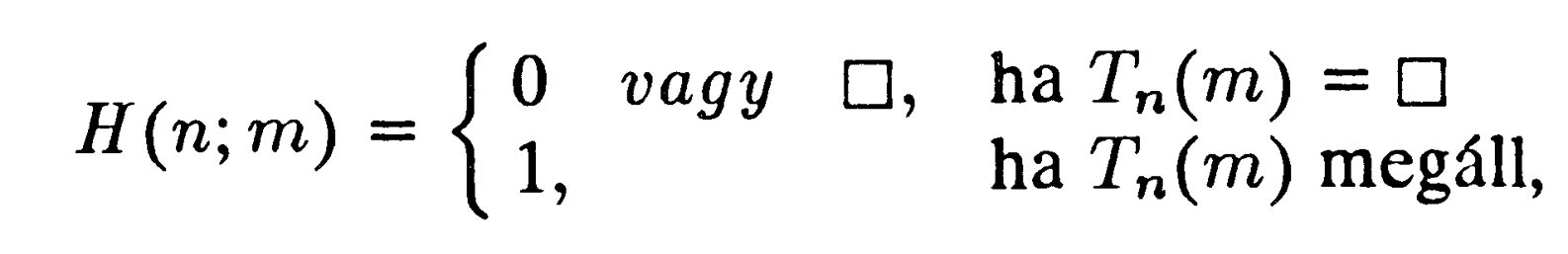
így H(n;m) = □ egy lehetőség, amikor T„(m) = □. Ténylegesen sok ilyen H(n; m) algoritmus létezik. (Például H(n;m) kiadhat egyszerűen egy 1-et, amint T_n(m) megáll, bár ennek a speciális algoritmusnak aligha lenne sok gyakorlati haszna!)

Követhetjük Turing eljárását részleteiben, ahogy a fentiekben megadtuk, azzal a kivétellel, hogy nem helyettesítünk minden □-et 0-val, hanem most egyes □-eket meghagyunk. Átlós eljárásunk, mint előbb, az

1 + T_n(n) X H(n; n)

kifejezést adja az átló n-edik tagjára. (□-et kapunk, amikor csak H(n;n) = □. Jegyezzük meg, hogy □ x □ = □, 1 + □ = □) Ez tökéletesen jó számítás, így elvégezhető valamilyen Turing-géppel, mondjuk a k-adikkal, és most fennáll, hogy

1 + T„(n) x H(n;n) = T_k(n).

A k-adik átlós tagra, azaz n = k-ra azt kapjuk, hogy

1 + T_k(k) x H(k;k) = T_k(k).

Ha a T_k(k) számítás megáll, akkor ellentmondásra jutottunk [mivel H(k;k) a feltevés szerint 1, amikor csak T_k(k) megáll, és az egyenlet ekkor az 1 + T_k(k) = T_k(k) értelmetlenséget adja], Így T_k(k) nem állhat meg, azaz T_k(k) = □.

Az algoritmus azonban ezt nem „tudhatja”, mivel ha H(k;k) = 0-át adna, akkor ismét ellentmondásra jutnánk (szimbolikusan az 1 + 0 = □ érvénytelen összefüggést kapnánk).

Így ha meg tudjuk találni k-t, akkor tudjuk, hogyan építsük fel az algoritmus legyőzésére speciális számításunkat, azt, amelyre mi ismerjük a választ! Hogyan találjuk meg k-t? Ez kemény munka. Azt kell tennünk, hogy részleteiben megvizsgáljuk H(n;m) és T_n(m) felépítését, és ezután részletesen azt, hogyan hat 1 + T_n(n) x H(n;n) mint Turing-gép. Megtaláljuk ezen Turing-gép számát, ami k. Ezt részleteiben bizonyára bonyolult lenne végrehajtani, de meg lehetne tenni.* A bonyodalmak miatt T_k(k) számítása egyáltalán nem érdekel ne bennünket, ha nem az volna a helyzet, hogy speciálisan állítjuk azt elő, a H algoritmus legyőzésére!

*A legnehezebb részét valójában már elvégeztük azzal, hogy az előbbiekben felépítettük az U univerzális Turing-gépet, mivel ez lehetővé teszi, hogy leírjuk T_n(n)-et mint az n-re ható Turing- gépet.

Az a fontos, hogy bármelyik H is adott, jól meghatározott eljárásunk van egy megfelelő k megtalálására, amelyikről mi tudjuk, hogy Tk(k) legyőzi H-t, és amelyikkel ezért jobbak vagyunk, mint az algoritmus. Talán megvigasztal egy kicsit, ha arra gondolunk, hogy jobbak vagyunk, mint a puszta algoritmusok!

Az eljárás ténylegesen olyannyira jól meghatározott, hogy adott H mellett egy algoritmust találhatnánk k előállítására. Így mielőtt túl önelégültté válnánk, rá kell ébrednünk arra, hogy ez az algoritmus H-nak segíthet⁹, mivel ez „tudja”, hogy Tk(k) = □. Biztosan így van ez? A megfogalmazásban segített az antropomorf „tudja” kifejezés egy algoritmusra vonatkoztatva. Azonban nem mi vagyunk-e, akik a „tudást” csináljuk, míg az algoritmus éppen csak követi a szabályokat, amelyeket mi mondtunk neki? Vagy magunk is csupán szabályokat követünk, amire agyunk felépítése és környezetünk által be vagyunk programozva? A kérdés nem egyszerűen az algoritmusok kérdése, hanem azé is, hogyan ítéljük meg, mi igaz és mi nem. Ezek központi problémák, később vissza kell térnünk rájuk. A matematikai igazság kérdésével (és annak nem-algoritmikus természetével) a 4. fejezetben foglalkozunk. Most legalább valami érzésünk kellene legyen az „algoritmus” és a „kiszámíthatóság” kifejezések jelentéséről, és értenünk kellene egyes kapcsolódó problémákat.

Church lambda-kalkulusa

A kiszámíthatóság fogalma nagyon fontos és szép matematikai elképzelés. Figyelemre méltóan új is — ahhoz képest, ahogy az ilyen alapvető dolgok mennek a matematikában —, hiszen először az 1930-as években vetették fel. Olyan elképzelés, amely végigvonul a matematika minden területén (jóllehet a legtöbb matematikus egyelőre nem nagyon izgatja magát a kiszámíthatósági kérdésekkel). Ereje részben abból a tényből táplálkozik, hogy a matematikában egyes jól meghatározott műveletek valójában nem kiszámíthatóak (ilyen egy Turing-gép megállásának eldöntése; a 4. fejezetben látunk majd egyéb példákat is). Ha ilyen nem kiszámítható dolgok nem lennének, akkor a kiszámíthatóság fogalmának nem lenne sok matematikai érdekessége. A matematikusok szeretik a rejtvényeket. Számukra érdekes rejtvény lehet annak eldöntése, hogy valamilyen matematikai művelet kiszámítható-e vagy sem. És különösen érdekes azért, mivel ennek a rejtvénynek az általános megoldása maga nem kiszámítható!

Egy dolgot világosan kell lássunk. A kiszámíthatóság igazi „abszolút” matematikai fogalom. Egy absztrakt idea, amely minden speciális, „Turing-gépek” formájában való megvalósítás mögött rejtőzik, amint azokat leírtam. Ahogy korábban megjegyeztem, a „szalagoknak”, „belső állapotoknak” stb., amelyek Turing szellemes, de speciális megközelítését jellemzik, nem kell különleges jelentőséget tulajdonítanunk. A kiszámíthatóság eszméjének kifejezésére vannak másféle módok is, ezek között történetileg az első az amerikai logistának, Alonzo Churchnek Stephen C. Kleene közreműködésével kidolgozott, figyelemre méltó „lambda-kalkulusa”. Church eljárása egészen különböző és határozottan absztraktabb volt Turingénál. Valójában abban a formában, ahogy Church elképzeléseit megfogalmazta, a látható kapcsolat a kettő között meglehetősen csekély, és kevés az utóbbiban bármi olyan is, ami „mechanikusnak” nevezhető. Church eljárásának alapgondolata velejéig absztrakt — egy olyan matematikai művelet, amiről Church úgy beszél, mint „absztrakcióról”.

Úgy érzem, megéri a fáradságot, hogy megadjuk Church elgondolásának rövid leírását, nemcsak azért, mert ez hangsúlyozza, hogy a kiszámíthatóság a számítógép bármelyik speciális koncepciójától független matematikai gondolat, hanem azért is, mert megvilágítja az absztrakt gondolatok erejét a matematikában. Az Olvasó, aki nem igazán jártas a matematikai ideák terén, és azok önmagukban nem is nagyon érdeklik, ennél a résznél esetleg jobbnak találhatja, ha áttér a következő fejezetre — jelentős veszteség az érvelés folyamatában nem fogja őt érni. Mégis azt hiszem, hogy az ilyen Olvasók számára hasznos lehet, ha még egy kicsit türelmesek, és tanúi lesznek Church rendszere bűvös gazdaságosságának (lásd Church 1941).

Ebben a rendszerben objektumok egy „világával” van dolgunk, jelölésük legyen mondjuk mindegyik egy matematikai műveletet vagy függvényt jelöl. (A vesszős jelölés oka egyszerűen az, hogy korlátlan szimbólumkészlet álljon rendelkezésre az ilyen függvények jelölésére.) E függvények „argumentumai” — azaz amikre e függvények hatnak — más, ugyanilyen típusú dolgok, azaz szintén függvények. Mi több, egy ilyen függvény egy másikra való hatásának eredménye (vagy „értéke”) újra egy függvény. (Valóban csodálatos a fogalmak gazdaságossága Church rendszerében.)

Így amikor azt írjuk,* hogy

a = bc,

akkor ezen azt értjük, hogy a b függvény a c függvényre való hatásának eredménye egy másik, a függvény. Nehézség nélkül ki lehet fejezni azt, hogy egy függvénynek két vagy több változója van. Ha úgy akarunk gondolni az f függvényre, mint két változó, mondjuk p és q, függvényére, egyszerűen azt írhatjuk, hogy

(fp)q

(ami az fp függvény q-ra való hatásának eredménye). Három változó függvényét

((fp)q)r

alakban írhatjuk, és így tovább.

Most jön az absztrakció nagy erejű művelete. Erre a görög λ (lambda) betűt használjuk, ezt követi közvetlenül egy Church-függvényt jelölő betű, mondjuk x, amit „néma változónak” tekintünk. Az ezt közvetlenül követő szögletes zárójeles kifejezésben az x változó minden előfordulása csupán egy „helynek” tekintendő, ahová bármi behelyettesíthető, ami az egész kifejezést követi. így ha azt írjuk, hogy

λ x.[fx],

akkor ezen azt a függvényt értjük, amely mondjuk a-ra hatva az fa eredményt adja. Azaz

(λ x.[fx])a = fa.

Más szavakkal λ x[fx] egyszerűen az f függvény, azaz

λ x.[fx] = f.

Érdemes egy kicsit elgondolkodni. Egyike ez azoknak a matematikai szépségeknek, amelyek első ránézésre olyan szőrszálhasogatóak és maguktól értetődőek, hogy hajlamosak vagyunk a lényeget teljesen elveszteni. Vegyünk egy példát a jól ismert iskolai matematikából. Legyen az f függvény egy trigonometriai művelet, egy szög szinusza, ekkor a „sin” absztrakt függvény definíciója a következő:

λx [sin x] = sin .

*Megszokottabb jelölés lenne mondjuk a = b(c), de ezek a zárójelek nem igazán szükségesek, és jobb, ha hozzászokunk elhagyásukhoz. Következetes megtartásuk meglehetősen kényelmetlen képletekhez vezetne, mint például (f(p))(g) és ((f(p))(í))(r) rendre (fp)q és ((fp)g)r helyett.

(Ne törődjünk azzal, hogyan lehet az x „függvény” egy szög. Rövidesen látni fogjuk, hogyan lehet számokat függvényeknek tekinteni; és a szög a számok egy fajtája.) Eddig ez valóban meglehetősen triviális. Képzeljük azonban azt, hogy a „sin” jelölést nem találták ki, ismerjük azonban a sin x hatványsoros kifejezését:

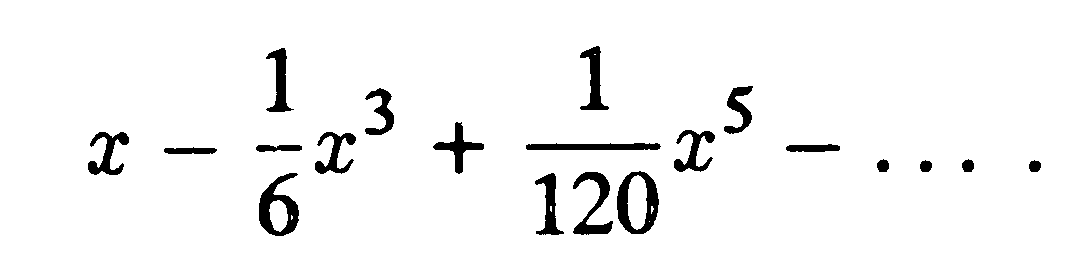
Ekkor definiálhatnánk, hogy

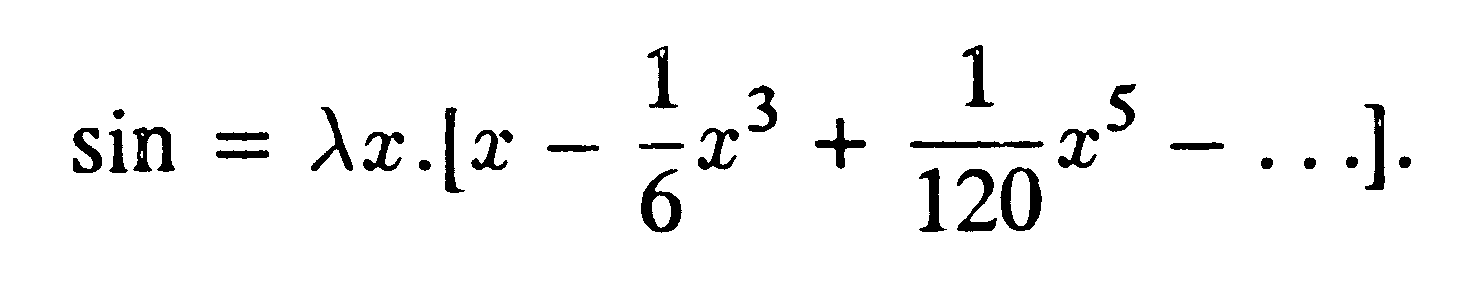
Jegyezzük meg, hogy definiálhatnánk a még egyszerűbb, mondjuk „egyhatod köb” műveletet, amelyre nincs szabványos „függvény” jelölés:

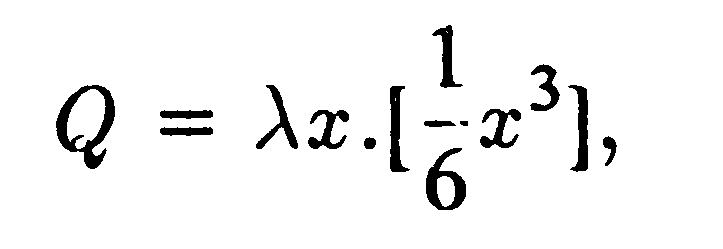
és például azt találnánk, hogy

Jelenlegi fejtegetésünkhöz jobban illenek azok a kifejezések, amelyek egyszerűen Church elemi függvényműveleteiből épülnek fel, mint például

Ez az a függvény, amely egy másik, mondjuk g függvényre hatva azt adja, amit g ad kétszer hatva x-re, azaz

Először az x-et is „elabsztrahálhatnánk”, azt kapnánk, hogy

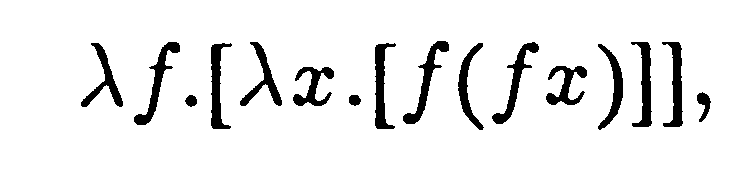
amit rövidíthetünk:

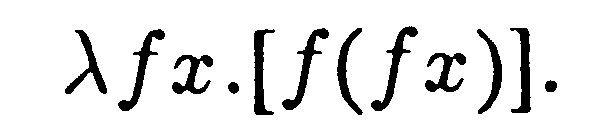
Ez az a művelet, amely g-re hatva a „kétszer iterált g” függvényt adja. Valóban, ez pontosan az a függvény, amit Church a 2 természetes számmal azonosít:

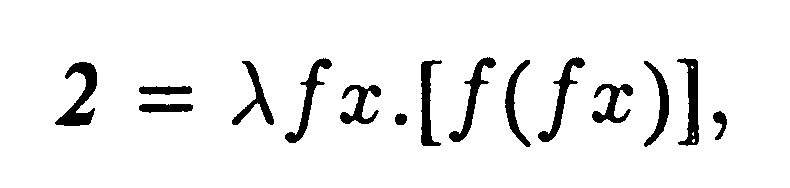
így (2g)y = g(gy). Hasonlóképpen definiálja Church a következőket:

valamint ezekkel együtt:

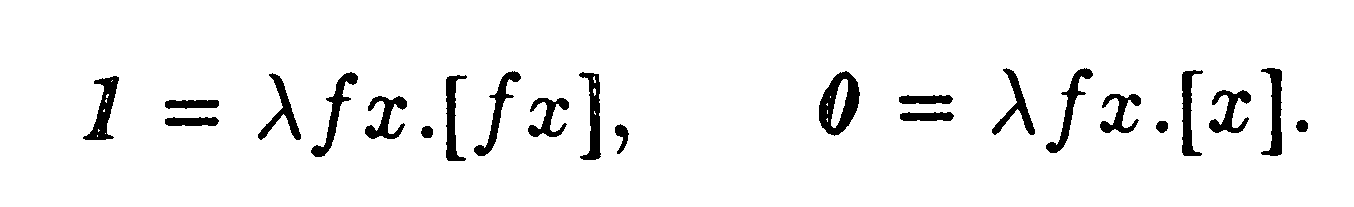
Church „2”-je valójában inkább hasonlít a „kétszerihez, „3”-ja a „háromszöghöz, stb. Így a 3 hatása az f függvényre, nevezetesen 3 f, az „iteráld f-et háromszor” művelet. 3 f hatása y-ra ezért a következő lenne: (3 f)y = f(f(f(y))).

Lássuk, hogyan fejezhető ki egy nagyon egyszerű aritmetikai művelet, nevezetesen 1 hozzáadása egy számhoz, Church rendszerében. Definiáljuk a következőt:

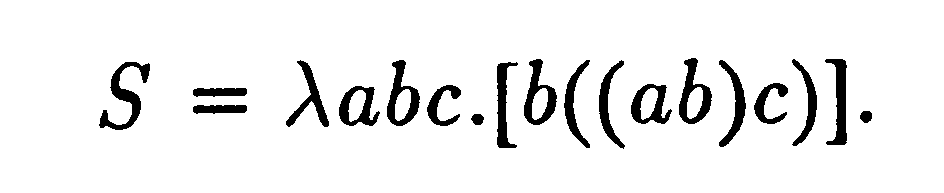
Illusztrálandó, hogy 5 valóban egyszerűen 1-et ad egy Church jelölésével leírt számhoz, nézzük meg a 3-ra:

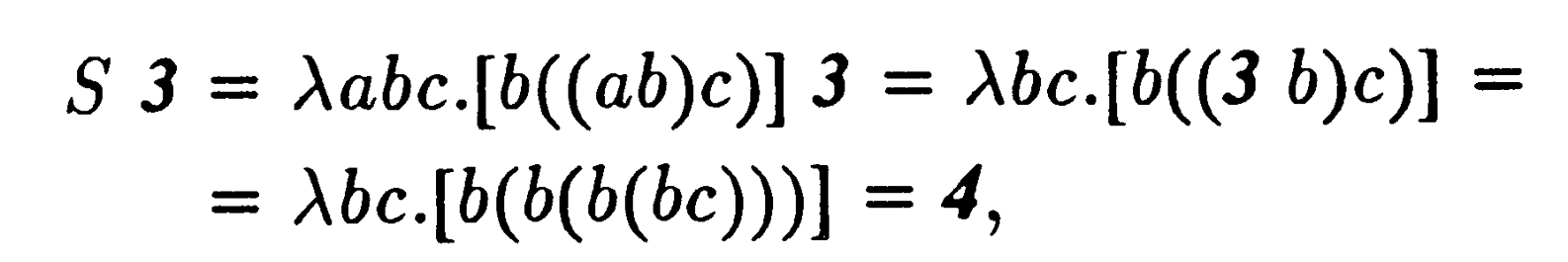
mivel (3 b)c = b(b(bc)). Világos, hogy ez ugyanígy alkalmazható bármilyen más természetes számra. (Ténylegesen λabc.[(ab)(bc)] ugyanolyan jó lenne, mint S)

Hogyan kell egy számot kettővel megszorozni? Ez a kétszerezés

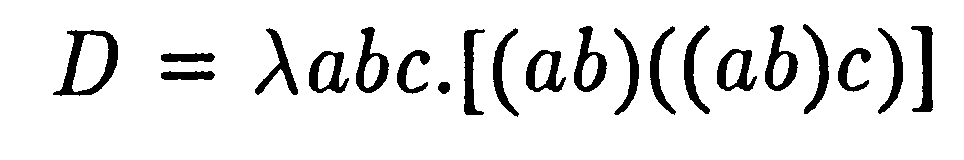
segítségével érhető el, amit megint a 3-ra való hatásával mutatunk be:

Az alapvető aritmetikai műveletek, az összeadás, szorzás és hatványozás rendre a következőképpen definiálhatók:

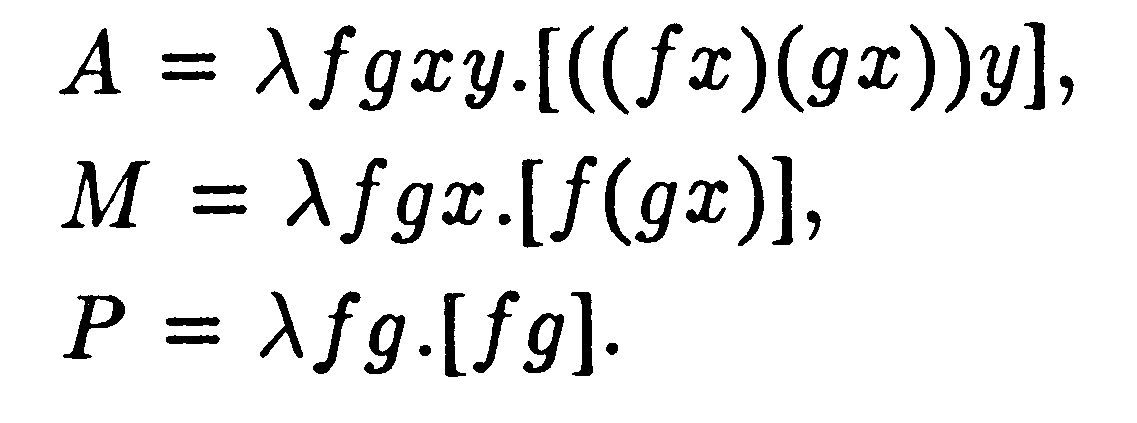
Az Olvasó meggyőződhet róla — vagy ha nem, hát elhiheti —, hogy valóban

ahol m és n két természetes szám Church-függvénye, m + n az összegük Church-függvénye stb. Az utolsó a legmeglepőbb. Ellenőrizzük az m = 2, n = 3 esetre:

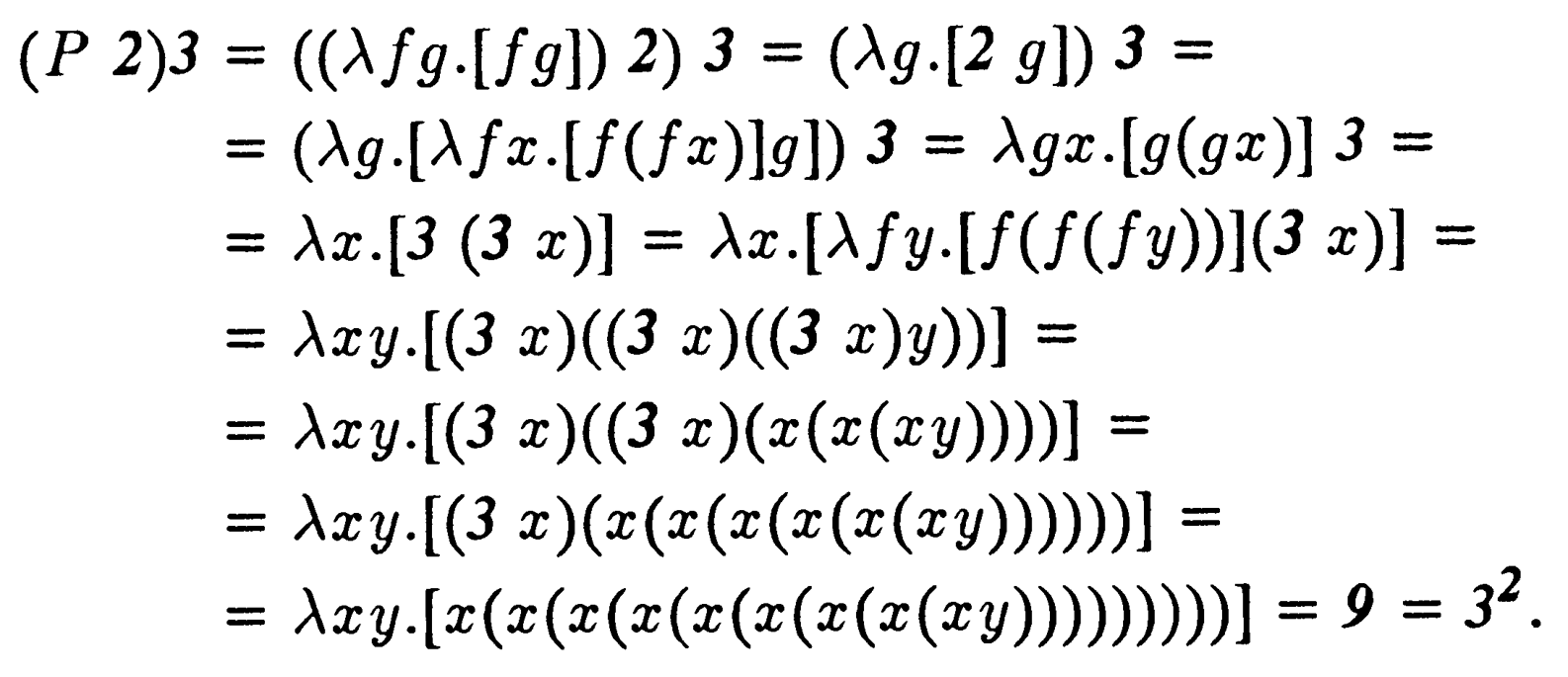
A kivonás és osztás műveletét nem olyan könnyű definiálni (és ténylegesen valamilyen megállapodásra van szükség, mit csináljunk „m — n”-nel, amikor m kisebb, mint n, és „m / n”-nel, ha m nem osztható n-nel). Fontos határkövet jelentett a korai 1930-as években, hogy Kleene felfedezte, hogyan lehet a kivonás műveletét kifejezni Church rendszerében! Ezt követték más műveletek. Végül 1937-ben Church és Turing egymástól függetlenül megmutatták, hogy minden kiszámítható (vagy algoritmikus) művelet — most Turing-gépek értelmében — megadható valamilyen Church-kifejezéssel (és fordítva).

Ez igazán figyelemreméltó tény, és hangsúlyozható vele a kiszámíthatóság fogalmának alapvetően objektív és matematikai jellege. Church kiszámíthatóság-fogalmának, első ránézésre, nagyon kevés köze van a számítógépekhez. Mégis vannak bizonyos alapvető kapcsolatai a gyakorlati számítással. Nevezetesen a LISP, ami egy igen hatékony és rugalmas számítógép-nyelv, lényeges módon felhasználja Church kalkulusának alapszerkezetét.

Mint azt korábban jeleztem, vannak más lehetőségek is a kiszámíthatóság fogalmának definiálására. Post számítógépfogalma nagyon közel áll Turingé- hoz, és attól függetlenül keletkezett, azzal majdnem egy időben. J. Herbrand és Gödel a kiszámíthatóság (rekurzivitás) egy sokkal inkább használható definícióját is megadta abban az időben. H. B. Curry 1929-ben és M. Schönfin-kel is 1924-ben, tehát valamivel korábban, másféle megközelítéseket dolgoztak ki, részben ezekből fejlődött ki Church kalkulusa (lásd Gandy 1988). A kiszámíthatóság modern megközelítései (mint a Cutland 1980 hivatkozásban leírt korlátozatlan számlálógép), a részletekben jelentősen különböznek Turing eredetijétől, és ezek sokkal inkább gyakorlatiak. A kiszámíthatóság fogalma mégis ugyanaz marad, bármelyiket fogadjuk is el a változatos megközelítések közül.

Sok más matematikai gondolathoz hasonlóan, különösen a mélyebben szépségesekhez és alapvetőekhez, a kiszámíthatóság ideájának, úgy tűnik, van egyfajta saját platóni valósága. Általában a matematikai fogalmak platóni valóságának ez a titokzatos kérdése az, amivel a következő két fejezetben foglalkoznunk kell.

Jegyzetek

A szokásos modern terminológiát fogadom el, amely most a nullát a „természetes számok” közé sorolja.
Sokféle más módon lehet számpárokat, számhármasokat stb. egyetlen számmal kódolni, ezeket a matematikusok jól ismerik, mostani céljainkhoz azonban kevésbé kényelmesek. Az ½ ((a + b)² + 3a + b) formula például az (a, b) természetes számokból álló párt egyértelműen adja meg egyetlen természetes számmal. Próbálja ki!
Nem bajlódtam azzal, hogy bevezessek valamilyen jelet, amely a számok (vagy utasítások stb.) sorozatának kezdetét mutatja. A bevitelnél erre nincs szükség, mert a dolgok ott kezdődnek, amikor az első 1 megjelenik. A kivitelnél azonban szükség lehet valami másra, mivel a priori nem tudhatjuk, milyen messze kell mennünk a kiviteli szalag mentén, hogy elérjük az első (azaz a bal szélső) l-et. Bár balra haladva a 0-k hosszú füzérét találhatjuk, ez nem biztosíték arra, hogy még messzebb balra nem lehet egy 1. Ezzel kapcsolatban változatos nézőpontokat lehet elfogadni. Az egyik ilyen mindig egy speciális jelet (mondjuk a kontrakciós eljárásban a 6-tal kódoltat) használ a teljes kivitel bevezetésére. Leírásomban az egyszerűség kedvéért azonban egy másik álláspontra helyezkedem, nevezetesen arra, hogy mindig „tudjuk”, hogy az olvasóeszköz a szalag mekkora részével találkozott (például elképzelhető, hogy valamilyen „nyomot” hagy maga után), így elvileg nem kell végtelen hosszú szalagot megvizsgálnunk, hogy biztosak legyünk abban, hogy a teljes kivitelt áttekintettük.
Egy mód arra, hogy két szalag információját egyetlen szalagon kódoljuk, az, hogy a kettőt összefésüljük. így például az egyetlen szalagon a páratlan számú jelek ábrázolhatják az első szalag jeleit, a páros számúak a másodikéit. Hasonló módszer három vagy több szalagra is működik. Ennek az eljárásnak a „rossz hatásfoka” abból ered, hogy az olvasóeszköznek előre-hátra kell ugrálnia a szalag mentén, és jeleket hagynia rajta, hogy ne veszítse el, hol tart mind a páros, mind a páratlan szalagrész olvasásában.
Ez az eljárás csak arra az esetre vonatkozik, amikor egy megjelölt szalag természetes számként értelmezhető. Nem változtatja meg speciális Turing-gépeink, az EUC vagy XN+1 értelmét.
Ha T_n előírása nem helyes, akkor U úgy megy előre, mintha az n szám megszakadna, amikor az első füzérhez vagy n bináris kifejezésében több mint négy 1-eshez ér. E kifejezés maradékát az m szalag részeként olvassa el, ezért valamilyen értelmetlen számítást fog végrehajtani! Ezt a tulajdonságot, ha akarjuk, kiküszöbölhetjük úgy, hogy n-et a kiterjesztett bináris jelöléssel adjuk meg. Úgy gondoltam, hogy ezt már nem csinálom meg, hogy ne bonyolítsam tovább a szegény univerzális U gép leírását!
Hálás vagyok David Deutschnak, hogy u alább megadott bináris alakjából meghatározta a tízes rendszerbeli alakot. Köszönet illeti őt azért is, mert ellenőrizte, hogy u-nak ez a bináris értéke valóban megad egy univerzális Turing-gépet! u bináris alakja a következő:

10000000010111010011010001001010101101000110100010100000110101001101000101

01001011010000110100010100101011010010011101001010010010111010100011101010

10010010101110101010011010001010001010110100000110100100000101011010001001

11010010100001010111010010001110100101010000101110100101001101000010000111

01010000111010100001001001110100010101011010100101011010000011010101001011

01001001000110100000000110100000011101010010101010111010000100111010010101

01010101011101000010101011101000010100010111010001010011010010000101001101

00101001001101001000101101010001011101001001010111010010100011101010010100

10011101010101000011010010101010111010100100010110101000010110101000100110

10101010100010110100101010010010110101001001011101010100101011101010010100

11010101000011101000100100101011101010100101011101010100000111010100100000

11010101010010111010100101011010001001000111010000000111010010100101010101

11010010100100101011101000001010111010000100011101000001010100111010000101

00111010000010001011101000100001110100001001010011101000100001011010001010

01011101000101001011010010000010110100010101001001101000101010101110100100

00011101001001010101011101010101001101001000101011010010010010110100000001

01101000001000110100000100101101000000000110100101000101110100101010001101

00101001010110100000100111010010101001011010010011101010000001010111010100

00001101010100010101011010010101011010100001010111010100100101011101010001

00101101010010000101110100000011101010010001011010100101001101010100010111

01010010100101110101010000010111010101000001011101000000111010101000010101

11010010101011010101000010111010100010101011101010100100101110101010100001

11010100000001110100100100001101001001000101101010101010011101000000001011

01001000011010101010100101110100100001101001000101010111010000100011101000

10000111010000110100000001011010000010010111010101001010101101000100010010

11101000001001110101010011010000010101011010000100001110100100001000111010

10101010100111010000100100111010001001000011101000010100101101000010100001

11010101010101011101000100100110100010010011010100101001011101000100010101

11010000000111010001001001011101001101001001000010110101010100110100010100

01011101000011010100001000101101010011010101001010010110101010011010010010

10111010011010010000010110100010101010001110100100001010110100000010011010

01000100101110100100001101010000010010111010010010100110100100101010110100

11010010010100101101001101001010000010110100100000111010100100110101010100

00101110100101000010111010010101010111010100010010110100100111010010101000

10111010001001110101000010110100100111010010101010101110100100011101001010

10100101110100100011101010000010101011100110101000001011010010011101010000

00101110100101101010000010101101001010010111010100001001011101000011010100

01000010110101001101010001000101101010101001011101010001010010110100010101

01011101001000010101101010001011101010010010101011101010100100101110101000

11101010001110101001001001011101010001110101001010001011101010001011101010

00010010111010100011101000101000101110100101001011101010010101001011101001

01010101010110101000010101010110100001001110100001010101010111010101000101

01110101010001010111010000001110101010001001011101000000111010101001000101

11010100000011010100001011010000001110100100000010111010100011101010010001

01011101010011010101010001010110100000110101010100101010110100000010011010

10101001001110101001101010101001001011010100110100100100111010000011010101

01010010101101010001001101000101001010101110100000110101010101010010110100

01000111010001010101010101101000100011101000010101110100010010000111010011

01000000010011101000000100101110100010001010011101000000100101110100101010

10100101101000010101010111010001001010010111010000010001011101010100101101

00010001001110100000100101011101000000101010110100001000111001111010000100

00011101000010010011101000001010010111010000010100101101000010001010111010

00010001001101000100001110101111010000100100101110100001001001011101000000

01010111010000101010001101000100101110100001000001110100001001110100010000

01011101010100101101000100000101110100001010101011101000000101010111010001

00001010111010001000010101110100100000111010100100100110100000010101110100

01000100101110101010000111010100101011010010101010000110100000101001101000

00001110100000100100111010010110100100010100101101010100110100010100100101

10101010011010001010100010110011010100100101110101010011010001010101010110

01101010001010101100110100100010101010111010001000111010010010101010101101

00101001010001101001000000101110100000110101010010101010110100101010110100

10001000101110100010101011010100000101011010001000001101001000101011010000

10011101010010101010101110100101101001001000101011001101001001001010101110

10011010010010010101101001011010010010010010110100101101001001010001011001

10100100101001010111010001010111010010010111001101001001010100101110011010

01010001010101110100010001110100001010010110100101000101110100101000101011

01000100111010010100010010111010001001110100101001000101110011010010001000

11101000100111010010100101010111001101001010000011100110101010101011010000

00011101001010100101010111010010001110100101010010101110011010000101001001

10011010100000110100000001110100101010100101011100110101000100001101000000

01110100010010101010111010001000111010101010101010101101000010011101001000

10010101110100101010001001101010000000101101001001110101000010101110100100

00110101000000010110100100011101010010010111010000110101000010101011010100

01011101010000101001011101010001011101010001010101011100110101000101011010

0001101010001001010

A vállalkozó szellemű Olvasó jó házi számítógéppel a szövegben közölt előírások alapján ellenőrizheti, hogy a fenti kód valóban megadja egy univerzális Turing-gép hatását, ha különböző egyszerű Turing-gép számokra alkalmazza azt!
A Turing-gép másféle megadásával u értéke esetleg valamivel csökkenthető. Eltekinthetünk például a STOP-tól, elfogadva helyette azt a szabályt, hogy a gép akkor ál! meg, amikor valamilyen más belső állapotból visszalép a 0 belső állapotba. Ezzel sokat nem nyerhetünk (ha egyáltalán valamit). Nagyobb nyereséget eredményezne, ha megengednénk, hogy a szalagon más jelek is lehessenek, mint 0 vagy 1. Ténylegesen leírtak az irodalomban nagyon tömörnek kinéző univerzális Turing-gépeket, de ez a tömörség csalóka, mert a gépek leírásának kódolása általában rendkívül bonyolult.

E híres állításhoz kapcsolódó nem technikai részleteket illetően lásd Devlin (1988).

Természetesen e megjavított algoritmust is legyőzhetnénk úgy, hogy egyszerűen újra alkalmazzuk az egész előbb említett eljárást. Az így szerzett új tudásunkkal algoritmusunkat még tovább javíthatjuk; de azt megint legyőzhetnénk stb. Azt a fajta meggondolást, amihez ez az iteratív eljárás vezet, Gödel tételével kapcsolatban, a 4. fejezetben fogjuk tárgyalni, vö. 131. o.