Notas

^[1] Quod Erat Demostrandum: lo que se quería demostrar. (N. del T.) <<

^[2] En la conferencia, Feynman toma AB y Bc por bases de los dos triángulos. Los dos tienen la misma altura, que se forma prolongando hacia abajo la línea ABc y trazando una perpendicular que pase por S. Su prueba y la nuestra funcionan igual de bien. <<

^[3] Feynman comenta este punto en su charla dedicándole sólo una línea. No es tan sencillo, sin embargo, y tampoco nosotros lo hemos probado en realidad. He aquí una prueba más completa. Pensemos en dos segmentos orbitales cualesquiera que tengan ángulos centrales iguales:

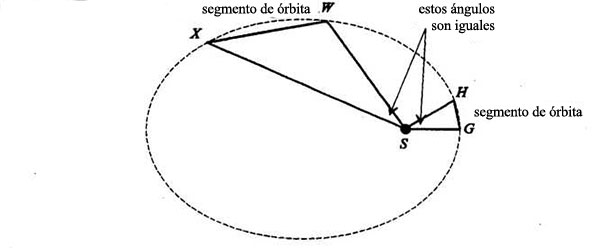
Pongamos el triángulo SWX encima de SGH, de este modo:

Siempre es posible trazar una línea que pase por WX, que sea paralela a HG y tal que los dos triángulos pequeños que resulten tengan áreas iguales:

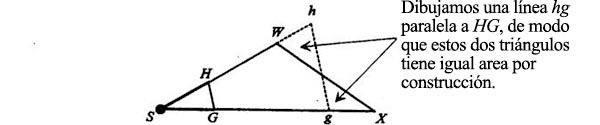
El triángulo Sgh tiene la misma área que SWX (aumenta lo que mide uno de los triángulos pequeños y disminuye lo que mide el otro) y es semejante a SGH. Tracemos ahora una línea desde S hasta el punto donde WX cruza hg:

Llamemos SZ, o Sz, a la distancia del Sol a la órbita. Según la propiedad de los triángulos semejantes (base y altura aumentan con la dimensión de modo que el área es proporcional al cuadrado de la dimensión), los triángulos semejantes SGH y Sgh tienen áreas proporcionales al cuadrado de las longitudes SZ y Sz. Pero SWXtiene la misma área que Sgh, así que el área de SWX también es proporcional al cuadrado de Sz. Si imaginamos ahora que reducimos el ángulo central hasta el infinito, la línea SZz queda siempre dentro del ángulo, y como los puntos Wy Xde la órbita están cada vez más juntos, la longitud Sz se vuelve al final igual a SW o a SX que es lo que antes llamábamos distancia al Sol. QED. <<

^[4] Feynman está diciendo que Δv/Δt es proporcional a v/T. Aquí llama «aceleración centrípeta» a Δv/Δt: más abajo dice «aceleración centrífuga». <<

^[5] Este es el punto que se explica en la nota 3. <<

^[6] Materia y movimiento (N. del T.) <<