La conferencia:
«El movimiento de los planetas alrededor del Sol»

(13 de marzo de 1964)

El título de esta lección es «El movimiento de los planetas alrededor del Sol». …Después de daros esta mala noticia, os daré otra buena, y es que, dado que el martes que viene hay exámenes, no es cuestión de dar una clase que os obligue a estudiar, de manera que voy a daros una charla por puro placer, para pasar el rato [aplausos]. Basta, basta, o no me dejaréis empezar. Guardaos todo eso para el final y decidid entonces.

La historia de nuestro tema físico llegó a uno de sus momentos culminantes cuando Newton, repentinamente, comprendió tanto partiendo de tan poco. La historia de este descubrimiento es también la larga historia de Copérnico, de Tycho Brahe cuando midió las posiciones de los planetas, y de Kepler cuando averiguó las leyes que empíricamente describían el movimiento de esos planetas. Fue entonces cuando Newton descubrió que podía entender el movimiento planetario formulando otra ley. Todo esto lo sabéis ya por la lección sobre la gravedad, así que continuaré desde aquí con un rápido resumen de la cuestión.

Primero, Kepler observó que los planetas describían elipses alrededor del Sol, con éste como foco de cada elipse. Observó también (se apoyó en tres observaciones para describir las órbitas) que el área barrida por una línea trazada desde el Sol a la órbita es proporcional —esta área de aquí—, es proporcional al tiempo. Por último, para comparar planetas con distintas órbitas, descubrió que los planetas con órbitas diferentes tienen periodos (los tiempos que tardan en completar una órbita) que guardan con el eje mayor de la elipse una razón proporcional a la potencia 3/2. Si fueran círculos (para simplificar las cosas), el cuadrado del tiempo que se tarda en recorrer la circunferencia del círculo sería proporcional al cubo del radio del círculo.

Ahora bien, Newton supo extraer dos consecuencias de esto. Primero advirtió que áreas iguales y tiempos iguales significaban, según su concepción de la inercia, que el móvil seguiría en línea recta a velocidad uniforme si no sufriera ninguna perturbación, que las desviaciones de la velocidad uniforme se dirigen siempre hacia el Sol, y que áreas iguales en tiempos iguales equivale a decir que las fuerzas se dirigen hacia el Sol. Así aplicó una de las leyes de Kepler para deducir que las fuerzas eran hacia el Sol; y entonces resulta fácil argumentar (sobre todo cuando se aplica la tercera ley al caso especial de los círculos) que, en estos círculos, la fuerza dirigida hacia el Sol debe ser inversamente proporcional al cuadrado de la distancia.

La razón es más o menos como sigue. Supongamos que tomamos una fracción de la órbita, un cierto ángulo (un ángulo pequeño) y que una partícula tiene cierta velocidad en una parte de la órbita y otra después. Luego los cambios de velocidad en un ángulo determinado son evidentemente proporcionales a la velocidad; y el cambio de velocidad durante un cierto intervalo de tiempo, que es la fuerza, es evidentemente proporcional a la velocidad orbital por el tiempo que se tarda en recorrer esa fracción de la órbita (quiero decir, partida por el tiempo). Así, la velocidad cambia proporcionalmente a la velocidad, y el tiempo que ha durado este cambio es proporcional al tiempo que se tarda en completar la órbita. Por lo tanto, la aceleración centrípeta, es decir, el cambio por segundo de la velocidad en la dirección del centro, es proporcional a la velocidad en la órbita partida por el periodo de la misma.^[4]

Se puede decir de muchas otras formas, porque, lógicamente el periodo de revolución está relacionado con la velocidad a través de esta proporción. Se puede decir que la aceleración por el tiempo es la distancia o mejor dicho, que la aceleración por el tiempo es proporcional al radio, y así podemos sustituir el tiempo y obtener nuestra famosa v/R. Mejor aún, yo sustituiré la velocidad R/T. La velocidad es evidentemente proporcional al radio partido por el periodo de revolución, así que la aceleración centrífuga está en razón directamente proporcional al radio e inversamente proporcional al cuadrado del periodo de revolución. Ahora bien, Kepler nos dice que el periodo al cuadrado es proporcional al cubo del radio. Es decir, que el denominador es proporcional al cubo del radio y, por tanto, la aceleración hacia el centro es inversamente proporcional al cuadrado de la distancia. Así dedujo Newton (la verdad es que Robert Hooke dedujo lo mismo antes que Newton) que esta fuerza tendría que ser inversamente proporcional al cuadrado de la distancia. Partiendo de dos leyes de Kepler llegamos a dos únicas conclusiones. Nadie puede verificar nada de este modo. Quizá no tenga ningún interés, porque el número de hipótesis introducidas es igual al número de hechos cotejados y al número de supuestos.

Por otra parte, lo que Newton descubrió (y fue el más espectacular de sus descubrimientos) fue que la tercera ley de Kepler [Feynman se refiere en realidad a la primera] era ahora consecuencia de las otras dos. Dado que la fuerza es hacia el Sol, y dado que varía en razón inversa al cuadrado de la distancia, calcular esta sutil combinación de variaciones y velocidad para determinar la forma de la órbita y averiguar que es una elipse es una aportación de Newton; supo que la ciencia estaba avanzando porque podía conocer tres cosas formulando dos.

Como ya sabéis, al final conoció mucho más, que las órbitas en realidad no son elipses perfectas, que se perturban mutuamente, que el movimiento de los satélites de Júpiter se explica de la misma manera, así como el movimiento de la Luna alrededor de la Tierra, etc.; pero concentrémonos en un caso en el que pueda desestimarse la interacción mutua entre los planetas.

Resumamos lo que dijo Newton sobre el movimiento de un planeta: que los cambios de velocidad en tiempos iguales se dirigen hacia el Sol, y que en magnitud son inversamente proporcionales al cuadrado de la distancia. Nuestro problema ahora es demostrar (y el objetivo de esta charla es sobre todo demostrar) que en consecuencia la órbita es una elipse.

No es difícil, si se sabe escribir las ecuaciones diferenciales y resolverlas, demostrar que es una elipse. Creo que en las clases que os han dado, o por lo menos en el manual, calculáis la órbita mediante métodos numéricos y veis que parece una elipse. Esto no es lo mismo que demostrar que es exactamente una elipse. La demostración se suele confiar al departamento de matemáticas: ¡allí se las compongan con sus ecuaciones diferenciales! [Risas].

Prefiero demostraros que es una elipse de un modo completamente extraño, original y distinto del que soléis emplear. Voy a daros lo que yo llamaría una demostración elemental. Pero «elemental» no quiere decir fácil de entender [risas], «Elemental» significa que para comprenderlo se necesitan muy pocos conocimientos previos, además de una cantidad infinita de inteligencia [risas]. Para entender una demostración elemental no hacen falta conocimientos, sino inteligencia. Tal vez haya muchos pasos difíciles de seguir, pero son pasos que no exigen saber cálculo de antemano, ni transformadas de Fourier etc. Así, cuando digo «demostración elemental» quiero decir una demostración que retrocede todo lo que se puede en relación con lo aprendido.

Como es lógico, una demostración elemental en este sentido podría consistir en enseñaros cálculo primero y luego explicar la demostración igual. Pero esto sería más largo que la demostración que deseo presentaros aquí. En segundo lugar, esta demostración es interesante por otro motivo: se sirve sólo de métodos geométricos. Puede que a alguno de vosotros le gustara la geometría del bachillerato y se divirtiera probando, o descubriendo con ingenio, las líneas correctas de una construcción. Mucha gente sabe apreciar la elegancia y belleza de las demostraciones geométricas. Por otro lado, después de Descartes toda la geometría se puede reducir a álgebra y actualmente toda la mecánica y demás se reduce a análisis con símbolos escritos en papel, y no se emplean métodos geométricos.

Además, en los comienzos de nuestra ciencia, es decir, en la época de Newton, el método de análisis geométrico de tradición euclidiana era la forma habitual de hacer las cosas. En realidad, los Principia de Newton se escribieron casi totalmente de forma geométrica; todos los cálculos de esta obra se hicieron mediante diagramas geométricos. Hoy se hacen escribiendo símbolos analíticos en la pizarra, pero para entreteneros y hacerlo más interesante quiero que viajéis en coche de caballos, por su elegancia, en vez de subir a un coche de carreras. Así que vamos a deducir este hecho mediante argumentos puramente geométricos (bueno, esencialmente geométricos, porque no sé qué significa eso de argumentos puramente geométricos) y veamos lo bien que nos sale.

Así pues, nuestro problema es demostrar que si es cierto que los cambios de velocidad se dirigen hacia el Sol y que son inversamente proporcionales al cuadrado de la distancia a tiempos iguales, entonces la órbita es una elipse. Primero (por algún sitio hay que empezar) tenemos que saber qué es una elipse. Si no disponemos de una definición de la elipse, será imposible demostrar la teoría. Más aún: si no se entiende su significado, no se puede demostrar el teorema. Así que muchos dirán: «Todo esto está muy bien, pero hay que partir de un conocimiento de la elipse». Es verdad; pero, al margen de esto, no creo que haga falta mucho conocimiento extra, sólo mucha atención, por favor, y meditación cuidadosa. No es fácil, cuesta lo suyo y no vale la pena. Es mucho más fácil recurrir al cálculo, pero lo vamos a hacer de este otro modo, y recordad que lo hacemos únicamente para ver cómo resulta.

Hay varias formas de definir una elipse y elegiré una. Supongo que todo el mundo sabe que una elipse puede trazarse (o que la elipse es la curva que puede trazarse) cogiendo un cordel y dos clavos, poniendo un lápiz aquí y dando una vuelta. Dicho matemáticamente, es el lugar… hoy se dice conjunto de puntos, pues muy bien, el conjunto de puntos… tal que la suma de la distancia FP y la distancia FP, donde F y F’ son los dos puntos fijos, permanece constante. Supongo que ya sabéis que esto es la definición de la elipse. Puede que hayáis oído otra definición; si queréis, llamaremos focos a estos dos puntos, y esto significa que la luz emitida en F llegará a F’ tras rebotar en un punto cualquiera de la elipse.

Permitidme demostrar por lo menos la equivalencia de estas dos proposiciones. El siguiente paso será pues, demostrar que la luz se refleja de F a F’. La luz se refleja como si la superficie fuera aquí un plano tangente a la curva real. Ya sabéis que la ley de la reflexión de la luz en un plano dice que los ángulos de incidencia y reflexión son iguales. Por lo tanto, lo que tengo que probar es esto: si trazo una línea aquí tal que sus ángulos con las líneas FP y F’P sean iguales, entonces esta línea es tangente a la elipse.

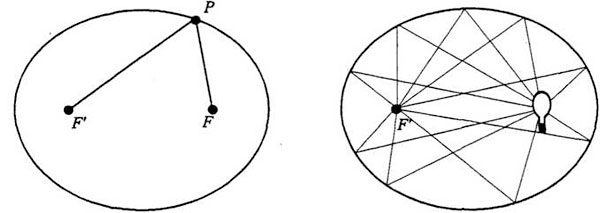
Demostración: He aquí la línea trazada tal como he descrito. Tracemos el punto imagen de F’ según esta línea: o lo que es lo mismo, prolonguemos la perpendicular que va de F a la línea hasta la misma distancia por el otro lado para obtener G’ imagen refleja de F’. Adviértase que, como los ángulos son iguales, este ángulo de aquí es el ángulo vertical. Pues bien, este ángulo es igual a este otro, porque estos dos triángulos rectos son exactamente iguales. Es una imagen refleja, así que este lado es igual a este otro, y estos dos ángulos son iguales; esto es una línea recta. Así que PG’, esta línea de aquí, es igual al segmento F’P y, dicho sea de paso, FG’ es una recta, así que FP + F’P que es la suma de estas dos distancias, es en realidad FP + G’P, porque F’P = G’P. Ahora bien, la cuestión es que, si tomamos cualquier otro punto de la tangente, por ejemplo Q, y llevamos a Q la suma de estas dos distancias, vemos fácilmente que la distancia F’Q es, nuevamente, la misma que G’Q. Así pues, la suma de estas dos distancias, de F’ a Q y de Q a F es la misma que la distancia de F a Q y de Q a G’ En otras palabras, la suma de las distancias entre ambos focos y un punto cualquiera de la línea es igual a la distancia de F a G’, subiendo hasta este punto y pasando al otro lado. Evidentemente es más larga, evidentemente es siempre más larga que pasar al otro lado en línea recta. En otras palabras, la suma de las dos distancias hasta un punto Q es mayor que para la elipse (para cualquier punto Q menos el punto P). Así pues, para cualquier punto de esta línea, la suma de las distancias a estos dos puntos es mayor que en el caso de un punto de la elipse.

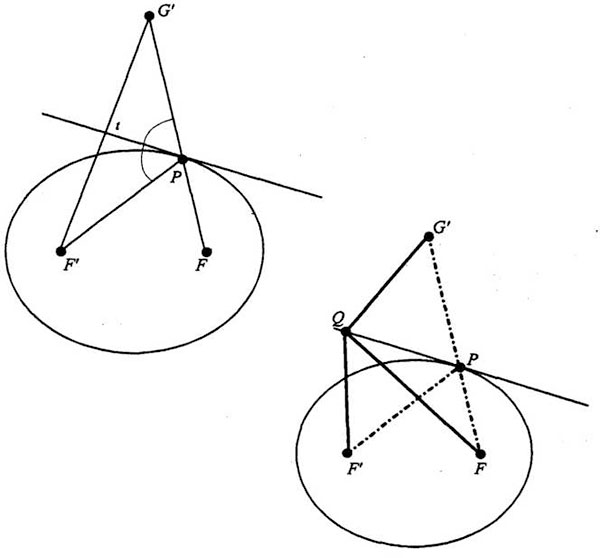
Ahora daré por evidente lo que sigue, para que ideéis vosotros mismos una prueba satisfactoria: si la elipse es la curva tal que la suma de los dos puntos es constante, entonces los puntos exteriores a la elipse darán una suma mayor, y los puntos interiores a la elipse darán una suma menor; y como estos puntos de la línea suman más que un punto de la elipse, toda esta línea queda fuera de la elipse, exceptuando únicamente el punto P que por tanto debe ser tangencial, porque la recta no se cruza por dos puntos ni entra en ningún momento en la elipse. Muy bien, la cosa es, pues, tangente y sabemos que la ley de la reflexión dice la verdad.

Las elipses tienen otra propiedad que quisiera describir, el porqué será un misterio absoluto para todos, pero es algo que necesitaré más tarde para esta demostración.

Permitidme decir que, aunque los métodos de Newton eran geométricos, en su época todo el mundo sabía muy bien qué eran las secciones cónicas, por eso recurre continuamente a propiedades de las secciones cónicas totalmente misteriosas (para mí) y yo, como es lógico, tengo que demostrar las propiedades de que hablo mientras procedo. Me gustaría, sin embargo, que nos fijáramos otra vez en el mismo diagrama, el que he trazado aquí, y lo repitiéramos. Se dibuja exactamente igual: F’ y F, aquí está la tangente, aquí el punto imagen de F’, G’. Pero me gustaría que imaginarais lo que le ocurre al punto imagen G’ cuando P recorre la elipse. Es evidente, como ya he señalado, que PG’ es igual a F’P, de manera que FP + F’P es constante, lo que implica que FP + PG’ es constante. En otras palabras, FG’ es constante. En resumen: el punto imagen G’ da la vuelta alrededor del punto F describiendo un círculo de radio constante. Muy bien. Al mismo tiempo, trazo una línea de F’ a G’ y veo que mi tangente es perpendicular a ella. Es lo mismo que dije antes. Sólo quiero resumirlo, recordaros una propiedad de las elipses, que es la siguiente: cuando un punto G’ describe un círculo, una línea trazada entre un punto excéntrico y un punto G’ (este punto es excéntrico respecto de G’ será siempre perpendicular a la tangente. Dicho al revés: la tangente es siempre perpendicular a la línea, o a una línea, trazada desde un punto excéntrico. Muy bien, esto es todo, volveremos sobre ello, lo recordaremos y lo repasaremos otra vez, así que no hay por qué preocuparse. Esto es sólo un resumen de una propiedad de las elipses, partiendo de los hechos. Aquí está la elipse.

Por otro lado tenemos que saber dinámica, así que explicaré ahora qué es la dinámica. Quiero esta proposición, esto es la geometría: ahora la dinámica, qué sentido tiene esta proposición. Lo que Newton quiere decir con esto es lo siguiente: si esto es el Sol, por ejemplo, el centro de la atracción, y en un instante dado una partícula, por ejemplo, estuviera aquí (y permitidme suponer que se mueve hasta otro punto, de A a B, en cierto intervalo de tiempo), entonces, si no hay fuerzas ejercidas hacia el Sol, esta partícula seguiría en la misma dirección y recorrería exactamente la misma distancia hasta un punto c. Pero durante este movimiento hay un impulso hacia el Sol, y en beneficio del análisis imaginaremos todas las curvas en el instante medio (en este instante). En otras palabras, concentramos todos nuestros impulsos, como si dijéramos, en este momento medio. En consecuencia, el impulso es en la dirección del Sol y esto podría representar el cambio de movimiento. Esto significa que en vez de moverse de aquí hasta aquí, se mueve hasta otro punto, que es C, que a su vez es diferente de c, porque el movimiento resultante es el movimiento compuesto del original más el impulso adicional hacia el centro del Sol. Así que el movimiento final es a lo largo de la línea BC, y al final del segundo intervalo de tiempo la partícula estará en C. Subrayo que Cc es paralela e igual a BV a saber, la tracción ejercida por el Sol. Es por tanto paralela a una línea trazada de B al centro del Sol. Por último, el resto de la proposición es que el tamaño de BV variará en razón inversa al cuadrado de la distancia conforme recorramos la órbita.

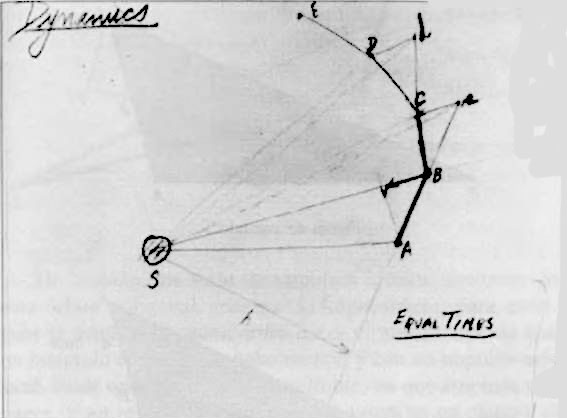
He dibujado aquí otra vez lo mismo, exactamente del mismo modo, sin más cambios que el color, para hacerlo más atractivo. He aquí el movimiento que la partícula tendría (que tiene en el primer instante) y el movimiento que seguiría si pasara al segundo intervalo de tiempo sin fuerzas de por medio. Permitidme señalaros que las áreas barridas en este caso serían iguales durante estos dos intervalos de tiempo. Porque estas dos distancias, AB y Bc, son evidentemente iguales, y por tanto los dos triángulos, SAB y SBc, que son las dos áreas, serán iguales: porque tienen bases iguales y comparten la altura. Si prolongáis la base y trazáis la altura, es la misma altura en ambos triángulos; y puesto que las bases son iguales, las áreas barridas son también iguales.

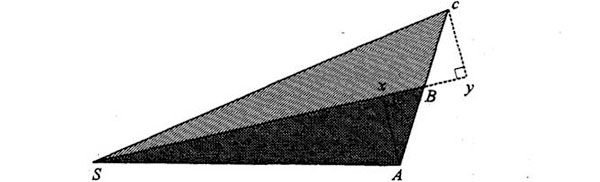
Figura del capítulo 3

Feynman, sin embargo, lo dibuja así:

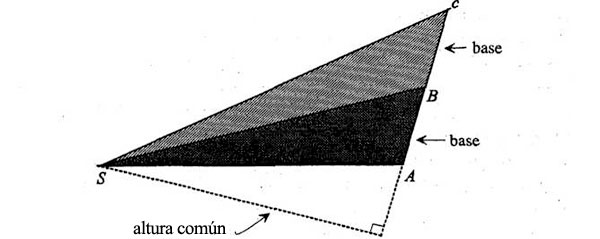
Por otro lado, el movimiento real no es hacia el punto c, sino hacia el punto C, que se diferencia de la posición c por un desplazamiento en la dirección del Sol en el momento B es decir, en la línea azul paralela a la línea azul original. Me gustaría deciros ahora que el área más ocupada (quiero decir la barrida en el segundo intervalo de tiempo si hubiera una fuerza, a saber, el área SBC) es la misma que el área que habría si no hubiera fuerza, a saber. SBc. El motivo es que tenemos dos triángulos que tienen una base común y la misma altura, ya que están entre dos paralelas. Como el área del triángulo SBC y la del triángulo SAB son iguales, pero los puntos A, B y C representaban posiciones sucesivas en la órbita en tiempos iguales, vemos que las áreas recorridas en tiempos iguales son iguales. Vemos igualmente que la órbita sigue siendo un plano, que estando el punto c en el plano y estando la línea Cc en el plano de ABS, el movimiento restante está en el plano ABS.

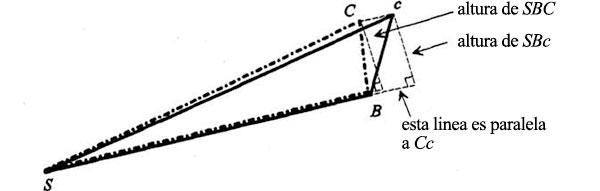
He trazado una serie de impulsos iguales alrededor de esta órbita poligonal imaginaria. Lógicamente, para averiguar la órbita real necesitamos hacer el mismo análisis con un intervalo de tiempo mucho menor, y con un impulso más sutil, hasta que llegamos al caso límite, en que tenemos una curva. Y en este caso límite la curva estará en un plano y el área barrida será proporcional al tiempo. Así sabemos que tenemos áreas iguales en tiempos iguales. La demostración que acabáis de ver es una reproducción exacta de otra que hay en los Principia mathematica de Newton, y el ingenio y la belleza que podáis o no ver en ella ya existía de buen principio.

La prueba que falta no procede de Newton, porque me di cuenta de que no podía seguirla bien, pues comporta muchísimas propiedades de las secciones cónicas. Así que ideé otra.

Tenemos áreas iguales y tiempos iguales. Me gustaría pensar ahora qué aspecto tendría la órbita si en vez de emplear tiempos iguales imagináramos la sucesión de posiciones correspondientes a ángulos iguales desde el centro del Sol. En otras palabras, vuelvo a trazar la órbita con la sucesión de puntos J, K, L, M, N, que corresponden, no a instantes iguales, como en el diagrama anterior, sino a ángulos de inclinación iguales, desde la posición inicial.

Para simplificarlo un poco, aunque esto no es esencial en absoluto, he supuesto que el movimiento inicial era perpendicular al Sol en el primer punto; pero esto no es esencial, sólo nos da un diagrama más limpio.

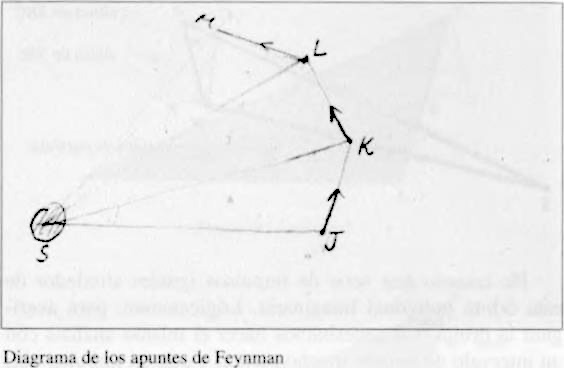
Diagrama de los apuntes de Feynman

Sabemos ya por la proposición anterior que las áreas iguales tardan tiempos iguales en ser barridas. Escuchad ahora: me gustaría señalaros que… ángulos iguales, y a esto es a lo que voy, no significa que las áreas sean iguales, no, sino que son proporcionales al cuadrado de la distancia al Sol; pues si tengo un triángulo con un ángulo dado, está claro que si construyo dos, serán semejantes; y el área proporcional de los triángulos semejantes es proporcional al cuadrado de sus dimensiones^[5]. Ángulos iguales significa, por tanto, que el tiempo que se tarda en barrer estos ángulos iguales es proporcional al cuadrado de la distancia. En otras palabras, los puntos J, K, L, etc., no representan imágenes de la órbita en tiempos iguales, sino imágenes de la órbita en tiempos sucesivos que son proporcionales al cuadrado de la distancia.

Ahora bien, la ley dinámica dice que hay cambios de velocidad iguales… mejor dicho, que los cambios de velocidad varían en razón inversa al cuadrado de la distancia al Sol (los cambios de velocidad en tiempos iguales). Otra forma de decirlo es que los cambios iguales de velocidad emplearán tiempos proporcionales al cuadrado de la distancia. Es lo mismo. Si invierto más tiempo, más cambio de velocidad, y si hago mis tiempos proporcionales al cuadrado de la distancia entonces los cambios de velocidad serán iguales. O, como reza la ley dinámica: hay cambios iguales de velocidad en tiempos proporcionales al cuadrado de la distancia. Ahora bien, fijaos en que los ángulos iguales equivalían a tiempos proporcionales al cuadrado de la distancia. Así llegamos a la conclusión, por la ley de la gravedad, de que habrá cambios iguales de velocidad describiendo ángulos iguales en la órbita. Aquí tenemos el núcleo central del que se deducirá todo: tenemos cambios iguales de velocidad cuando la órbita se mueve mediante ángulos iguales. Trazo ahora en este diagrama una pequeña línea que representa las velocidades. A diferencia del otro diagrama, estas líneas no son la línea completa de J a K, porque en aquel diagrama eran proporcionales a las velocidades, ya que los tiempos eran iguales y la longitud partida por tiempos iguales representaba las velocidades. Aquí tengo que emplear otra escala para representar lo lejos que la partícula habría ido en una unidad dada de tiempo, y no en los tiempos que son de hecho proporcionales al cuadrado de la distancia. Así pues, estas líneas representan la sucesión de velocidades. Es difícil apreciar qué ha cambiado en este diagrama.

Dibujaré, por lo tanto, otro diagrama (que llamaré diagrama de velocidades) a escala

ampliada, sólo para entendernos. Las líneas representadas son, se supone, las mismas. Éstarepresenta el movimiento por segundo (o por un intervalo de tiempo dado) de una partículaen J. Ésta representa el movimiento que tendría una partícula desde el comienzo en unintervalo de tiempo dado. A todas les doy un origen común, para poder comparar lasvelocidades. Así pues, tengo una serie de velocidades para la sucesión de estos puntos.

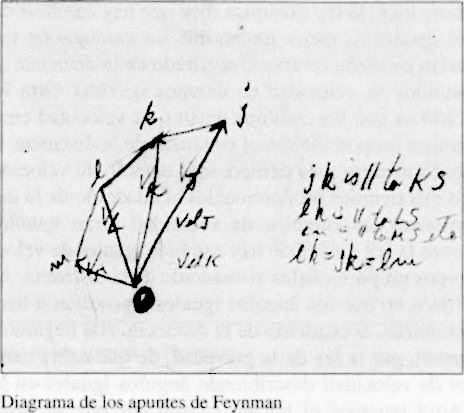
Diagrama de los apuntes de Feynman

Ahora bien, ¿qué son los cambios de velocidad? El punto en el primer movimiento está aquí y esto es la velocidad. Sin embargo, hay un impulso hacia el Sol, y por tanto hay un cambio de velocidad, señalado por la línea verde que genera la segunda velocidad v_K. Hay igualmente otro impulso hacia el Sol, pero esta vez con un ángulo diferente, que produce el siguiente cambio de velocidad v_L, etc. Ahora bien, la proposición de que los cambios de velocidad eran iguales (para ángulos iguales, que es lo que dedujimos) quiere decir que las longitudes de estos segmentos en sucesión son iguales. Eso es lo que quiere decir.

¿Y qué hay de sus ángulos comunes? Puesto que esta línea va en la dirección del Sol con este radio, puesto que esta otra va en la dirección del Sol con este radio, puesto que esta otra va en la dirección del Sol con este radio, etc., etc., y como estos radios tienen ángulos comunes sucesivos, es igualmente cierto que estos pequeños cambios de velocidad tienen ángulos comunes iguales. En resumen, estamos construyendo un polígono regular. Una serie de pasos iguales, con cambios de sentido en ángulos iguales, dará una serie de puntos en la superficie, aproximándose a un círculo. Dará un círculo. Por lo tanto, el extremo del vector velocidad (si se le llama así, el extremo de cada punto de velocidad; no hace falta saber lo que es un vector en esta descripción elemental) se encontrará en un círculo. Dibujo el círculo otra vez.

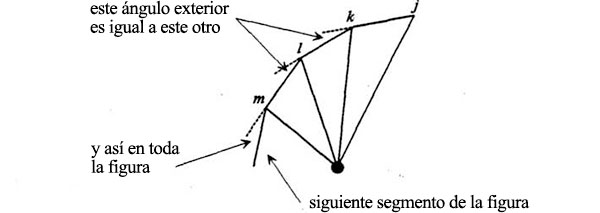
Repaso lo que hemos obtenido. Tomo el límite continuo, donde los intervalos angulares son muy pequeños, para obtener una curva continua. Pongamos que θ es el ángulo, ángulo total, hasta un punto P, y pongamos que v_p representa la velocidad de dicho punto del mismo modo que antes. Entonces el diagrama de velocidades tendrá este aspecto. Este punto es el origen del diagrama de velocidades, lo mismo que aquí, y esto es el vector velocidad correspondiente a este punto P. Así pues, este punto está en el círculo, pero no es necesariamente el centro de dicho círculo. Sin embargo, el ángulo que hemos descrito siguiendo el círculo es el mismo θ. El motivo es que el ángulo descrito desde el comienzo por esta cosa es proporcional al ángulo descrito por la órbita porque es la sucesión de la misma cantidad de ángulos pequeños. Por lo tanto, este ángulo de aquí es el mismo que este otro.

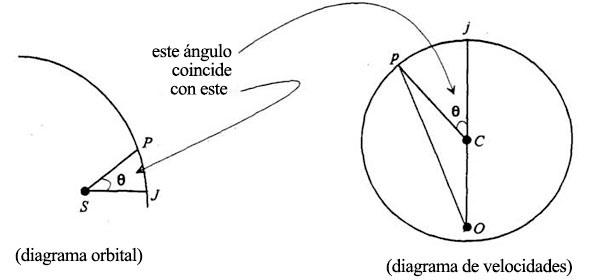
He aquí, pues, lo que hemos descubierto: si trazamos un círculo y tomamos un punto excéntrico, y luego tomamos un ángulo de la órbita (cualquier ángulo de la órbita que queramos) y trazamos el correspondiente ángulo dentro de este círculo, y trazamos luego una línea que salga del punto excéntrico, entonces esta línea será la dirección de la tangente. Porque la velocidad es, evidentemente, la dirección del movimiento en el momento, y lleva la dirección de la tangente a la curva. Así, nuestro problema es hallar la curva tal que si trazamos un punto a partir de un centro excéntrico, la dirección de la tangente a esa curva sea siempre paralela a ésta cuando el ángulo de la curva venga dado por el ángulo en el centro de ese círculo.

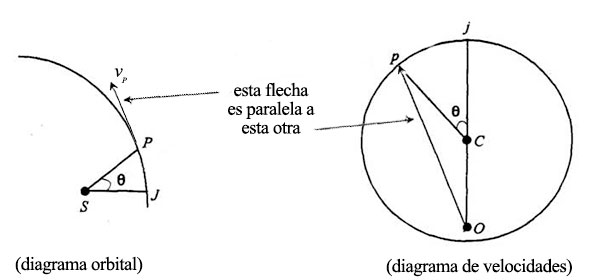
Para aclarar aún más por qué debe salir de este modo, giraré 90° el diagrama de velocidades de manera que los ángulos se correspondan exactamente y sean paralelos entre sí. Este diagrama de abajo es, pues, el mismo diagrama de arriba, pero girado 90°, para que la cosa se vea mejor. Esto de aquí es el vector velocidad, sólo que girado 90° (todo el diagrama ha girado 90°). Es evidente que esta línea es perpendicular a esta otra y es también evidente que ésta es perpendicular a ésta. En resumen, hay que hallar la curva tal que si ponemos en ella la órbita, y creo que ya lo estoy haciendo… (bueno, ahora me limitaré a decirlo y luego la dibujaré…) si ponemos en ella la órbita en un punto dado, aquí, donde esta línea corta la órbita (olvidaos de las escalas, todas son imaginarias, quiero decir que todo está en proporción), donde esta línea corta la órbita, la tangente debería ser perpendicular a esta línea trazada desde un punto excéntrico.

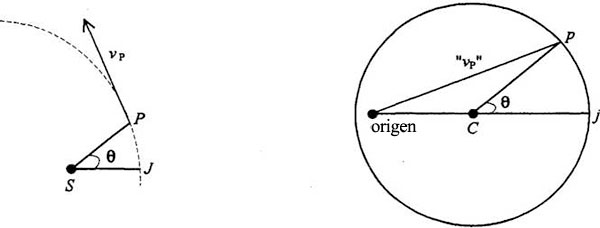
La vuelvo a dibujar para enseñaros cómo es. Ya sabéis cuál es la solución. Aquí tenemos otra vez un dibujo del mismo círculo de velocidades, pero esta vez la órbita se traza en el interior a una escala distinta, para que podamos ver este dibujo superpuesto a este otro,de manera que los ángulos se correspondan. Así pues, como los ángulos se corresponden, puedo trazar la línea que representa tanto el punto P de la órbita como el puntop del círculo de velocidades. Ahora bien, lo que hemos descubierto es que la órbita tiene tal naturaleza que una línea trazada desde el punto excéntrico, aquí, por la prolongación de este punto que está en un círculo exterior, será siempre perpendicular a la tangente a la curva. Bueno, esa curva es una elipse, y lo podéis averiguar mediante la siguiente construcción.

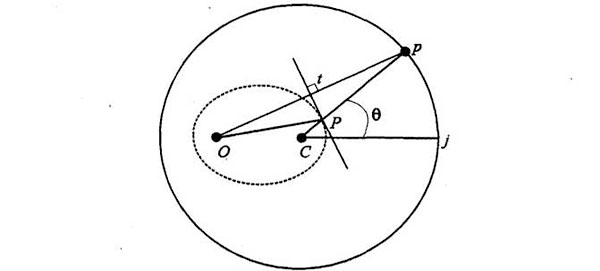
Construid la curva siguiente. La curva que voy a construir satisfará todas las condiciones. Tomad siempre la bisectriz de esta línea, fijaos por dónde se cruza con la otra línea. Cp, y llamad P a la intersección. Esta es la bisectriz. Ahora probaré dos cosas: primero, que el lugar geométrico de este punto es una elipse y, segundo, que esta línea es una tangente, quiero decir tangente a la elipse, y por lo tanto satisface las condiciones.

Primero, que es una elipse: como ésta era la bisectriz, está a igual distancia de O y de p; está claro por tanto que Pp es igual a PO; esto quiere decir que CP + PO que es por tanto igual que CP + Pp, es el radio del círculo, que es constante, evidentemente. Así pues, la curva es una elipse, o lo que es lo mismo, la suma de estas dos distancias es constante.

A continuación, que esta línea es tangente a la elipse: porque, como… los dos triángulos son congruentes, este ángulo de aquí es igual a este otro ángulo de aquí.

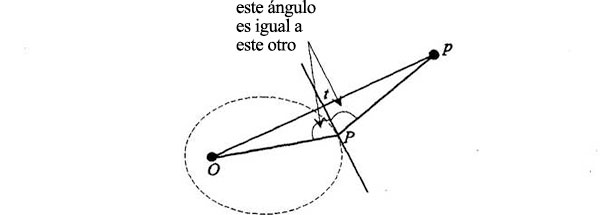
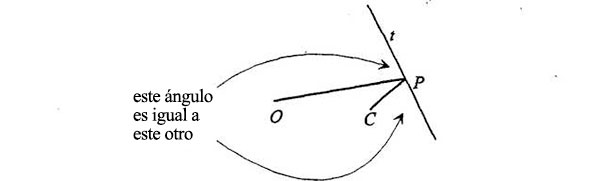
Pero si prolongo la línea por el otro lado, entonces también este ángulo es igual. Así pues, la línea en cuestión forma un ángulo igual con las dos líneas trazadas hasta los focos. Ya demostramos que eso era una de las propiedades de las elipses, la propiedad de reflexión. Por lo tanto, la solución del problema es una elipse (aunque lo que he probado es lo mismo pero al revés, que la elipse es una solución posible del problema). Y es esta solución. Así que las órbitas son elipses. Elemental, pero difícil.

Aún me queda mucho tiempo, así que añadiré algo al respecto. Primero me gustaría decir cómo supe de esta demostración, el hecho de que las velocidades describan un círculo. La demostración fue idea del señor Fano y yo la leí. Para demostrar después que la órbita era una elipse tardé un tiempo espantosamente largo, me refiero al paso evidente y simple, girar de este modo y trazar esto y aquello. Muy difícil, y es que todas estas demostraciones elementales exigen una elevada cantidad (como cualquier otra demostración geométrica) de ingenio. Pero una vez presentada, es elegante y sencilla. Quiero decir que está acabada. Lo divertido es que resulta una especie de mecano.

No es fácil utilizar el método geométrico para descubrir cosas. Es muy difícil, pero la elegancia de las demostraciones, una vez hechos los descubrimientos, es tremenda. La fuerza del método analítico es que es mucho más fácil descubrir cosas que demostrarlas. Pero no si se quiere un poco de elegancia. Hay mucho papel emborronado, con equis, íes y tachaduras, cancelaciones, etc.

Me gustaría señalar algunos casos interesantes. Puede suceder, desde luego, que el punto O esté en el círculo, incluso que esté fuera de él. Resulta que cuando el punto O está en el círculo no genera una elipse, sino una parábola. Cuando el punto O está fuera del círculo, que es otra posibilidad, genera una curva distinta, una hipérbola. Os dejo algunos de estos objetos para que juguéis con ellos. Por otro lado, me gustaría hacer ahora algunas aplicaciones de lo que sabemos y volver al argumento del señor Fano con otra finalidad. Él iba en una dirección diferente y me gustaría explicarlo.

Lo que el señor Fano buscaba era una prueba elemental de una ley que fue muy importante para la historia de la física en 1914: la llamada ley de la dispersión de Rutherford. Si tenemos un núcleo infinitamente pesado (que no es el caso, pero supongamos que sí) y disparamos una partícula contra dicho núcleo, ésta saldrá despedida en virtud de la ley de la inversa del cuadrado, a causa de la fuerza eléctrica. Si q_e es la carga de un electrón, la carga del núcleo será Z por q_e, donde Z es el número atómico. Luego la fuerza mutua será 4_πεο por el cuadrado de la distancia, que para simplificar escribiré provisionalmente como z/R² la constante partida por R². No sé si lo habéis hecho en clase o no, pero lo supondré: para abreviar, escribiré q_e² /4_πεο como e² . Luego esto no es más que Ze²/R² . Bueno, esto es la fuerza en razón inversamente proporcional al cuadrado de la distancia, pero es repulsiva en vez de atractiva. El problema ahora es como sigue: si disparo muchas partículas contra estos núcleos, que no veo, ¿cuántas saldrán desviadas con cualquier ángulo? ¿Qué porcentaje se desviará en más de 30°? ¿Qué porcentaje se desviará en más de 45°? ¿Cómo se distribuirán los ángulos de desviación? Este era el problema que Rutherford quería resolver, y cuando tuvo la solución buena la comprobó experimentalmente.

[Feynman parte en dirección contraria en este momento. No tardará en dar la vuelta.]

Rutherford averiguó que las partículas que en teoría tenían que desviarse con ángulos grandes no estaban allí. En otras palabras, la cantidad de partículas desviadas con ángulos grandes era mucho menor de lo esperado y, en consecuencia, dedujo que la fuerza era inferior a 1/R² en las distancias cortas. Porque es evidente que ángulos de desviación grandes requieren mucha fuerza, y esto corresponde a las partículas que golpean el núcleo casi de cabeza. Así, las que se acercaban mucho al núcleo no parecían salir como debían, y la razón es que el núcleo tiene cierto tamaño… Estoy contándolo al revés. Si el núcleo fuera lo bastante grande, entonces las partículas que en teoría deberían salir con un ángulo grande no serían repelidas con toda la fuerza, porque entrarían en la distribución de carga y se desviarían menos. Me he hecho un lío. Disculpadme. Empiezo de nuevo.

Rutherford dedujo cómo debería funcionar el asunto si todas las fuerzas estuvieran concentradas en el centro. En su época se creía que la carga del átomo estaba distribuida de manera uniforme por todo el átomo, y para confirmar esta distribución pensó que, si dispersaba las partículas, éstas nunca tendrían una desviación muy grande, como correspondería a una aproximación máxima al centro de repulsión, porque en realidad no habría centro. Rutherford, sin embargo, observó desviaciones con ángulos grandes, de lo cual dedujo que el átomo tenía toda su masa concentrada en un punto central muy pequeño. Lo expongo al revés. Fue después cuando se probó, otra vez por lo mismo, que el núcleo tenía cierto tamaño. Pero lo primero que se probó fue que el átomo no es tan grande a efectos eléctricos como el átomo entero a todos los efectos: es decir, que toda la carga estaba concentrada en el centro, y así se descubrió el núcleo. Sin embargo, lo que hay que entender es que necesitamos saber cuál es la ley del ángulo de desviación, y sólo podemos averiguarlo de este modo.

Supongamos que repetimos lo anterior y dibujamos la órbita. He aquí la carga y aquí el movimiento de una partícula cercana, solo que esta vez se trata de una repulsión. Comienzo el dibujo en este punto, porque me da la gana, y trazo mis círculos de velocidades como antes. Esto es la velocidad. Sabemos que la velocidad, la velocidad inicial en este punto (debería emplear los mismos colores para que sepáis lo que estoy haciendo… esto debería ser azul, esta órbita roja), lo que quiero decir es que los cambios de velocidad están en un círculo. Ahora bien, los cambios de velocidad son esta vez repulsiones, por lo que el signo se invierte. Tras pensar un poco, vemos que las desviaciones van así, y que el centro del cálculo, que solía llamarse origen del espacio de velocidades O, está fuera del círculo. La sucesión de pequeños cambios de velocidad está en el círculo, y entonces la sucesión de velocidades sobre la órbita corresponde a estas líneas, hasta que llegamos a algo muy interesante: esta tangente.

¿Qué significa este punto tangente a la curva? Quiere decir que todos los cambios de velocidad se hacen en la dirección de la velocidad. Pero los cambios de la velocidad son en la dirección del Sol, lo que significa que esta velocidad, en esta parte del diagrama, está en la dirección del Sol, porque está en la dirección de los cambios. Es decir, este punto de aquí, cuando nos aproximamos a este punto de aquí, que llamaré x, corresponde al acercamiento hacia el Sol desde el infinito por esta línea de aquí. Es decir: desde muy lejos llegamos hasta muy cerca del Sol (no del Sol, sino del núcleo) y entonces, tras dar la vuelta por aquí… (este diagrama debería estar al revés, las flechas deberían estar aquí) se va por este lado, e irse por este lado equivale a salir con la velocidad en esta dirección.

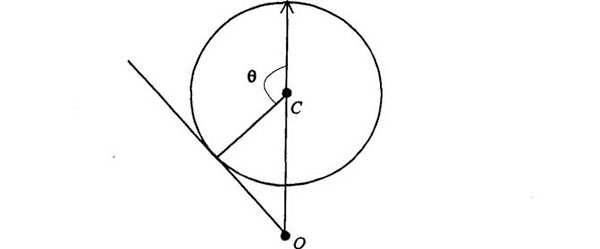
Ahora bien, si dibujamos la órbita con más cuidado, se parecerá mucho a esto. Si a este punto de aquí lo llamo V_∞, entonces la velocidad de la partícula al comienzo es V_∞. A la misma escala, llamo V al radio de este círculo (la velocidad correspondiente al radio del círculo). Tengo que hacer una ecuación, no voy a hacerlo de modo totalmente geométrico; pero, para ahorrar tiempo y demás, ya traigo el trabajo hecho. No hay que ir todo el tiempo en coche de caballos. La cosa se disfruta y luego se deja. Ahora quiero hallar primero la velocidad del centro, el radio del círculo de velocidades. En otras palabras, voy a apearme para hacer más analíticas algunas de estas cosas geométricas.

Supondré que la fuerza es una constante: la fuerza (mejor dicho, la aceleración) es una constante partida por R² . Para la gravedad, esta constante es GM, y para la electricidad es Ze²/m. Es decir, los cambios de velocidad son siempre igual a z/R² por el tiempo. Llamemos ahora a (que es una constante para el movimiento) al área barrida por la órbita cada segundo. Entonces, cambiando esto a ángulo, tengo que R²ΔΦ sería el área. Si divido esto por el área barrida por unidad de tiempo… esto me dice cuánto tiempo se tarda en barrer un ángulo. Así pues, el tiempo es, dados los ángulos, proporcional al cuadrado de la distancia. Ahora expresaré analíticamente todo lo que antes expresé con palabras. Sustituyendo este Δt de aquí para averiguar cómo son los cambios de velocidad en relación con el ángulo, obtenemos R²ΔΦ/α, donde R² se elimina, lo que significa que los cambios de velocidad son como dice la publicidad: iguales para ángulos iguales.

En el diagrama de velocidades (aunque no sea ésta la órbita que obtengáis, no importa), estos son cambios de velocidad y estos son cambios en el ángulo de la órbita. Así, ΔVes igual, por la geometría de este círculo, al radio del círculo, que llamo V_RxΔΦ. En otras palabras, tenemos que el radio del círculo de velocidades es igual a z/α donde α es el área barrida por segundo, y z es una constante que tiene que ver con la ley de la fuerza. Ahora bien, el ángulo en que este planeta se ha desviado es este de aquí (quiero decir el ángulo de desviación de la partícula cargada respecto del núcleo). Salta a la vista, por lo que vengo diciendo, que es igual a este ángulo de aquí, Φ, porque estas velocidades son paralelas a las dos direcciones primeras. Está claro, pues, que podemos hallar Φ si obtenemos la relación con V_∞ y V_R. Bueno, ya lo veis: tangente de Φ/2 = V_r/V_∞, y esto nos da el ángulo. Lo único que necesitamos es sustituir V_R por z/αR, y ya lo tenemos.

Sin embargo, no nos servirá de mucho mientras no conozcamos α en esta órbita. He aquí una idea atractiva: pensemos en este objeto que se dirige hacia este otro, de modo que si no hubiera ninguna fuerza fallase por cierta distancia, b. Esto se llama parámetro de impacto. Imaginemos que el objeto viene del infinito orientado por el centro de la fuerza, pero falla porque es desviado. ¿Cuál es la desviación si la orientación le hizo fallar por b? He aquí la cuestión. Si la orientación le hizo fallar por una distancia b, ¿qué desviación tendrá?

Así que ahora sólo necesitamos determinar cómo está relacionado α con b. V_∞ es la distancia recorrida por segundo, de modo que si yo dibujara aquí al lado un área de aspecto horrible, un triángulo, un triángulo horrible, entonces… (tengo un factor 2 en algún sitio, sí) el área del triángulo es 1/2 R² . Hay dos factores, dos, que os pido que resolváis cuando llegue el momento. Hay 1/2 aquí y hay 1/2 en algún otro sitio que voy a construir ahora. El área de este triángulo es la base V_∞ por la altura b por 1/2. Este triángulo es el que una partícula barrería (el radio barrería) en 1 segundo. Y esto, por lo tanto, es α. Así pues, tenemos que esto equivale a z/bV_∞². Dada la distancia de impacto, el margen de acierto, esto nos dice qué ángulo describiría la desviación según la rapidez a la que llega la partícula y la conocida ley de la fuerza. Así se acaba todo.

Una cosa más que me parece muy interesante. Supongamos que quisiéramos saber la probabilidad de obtener una desviación superior a un cierto ángulo. Tomemos un cierto Φ (digamos Φ₀) y queremos una desviación mayor que Φ₀. Esto sólo significa que tenemos que acertar en un área más céntrica que la b correspondiente a esta Φ. Cualquier impacto más centrado que b_Q producirá una desviación mayor que Φ₀. Si nos alejamos, tenemos menos desviación, menos fuerza. Así pues, la sección del área en que hay que acertar para que la desviación sea mayor que Φ (borro el cero) es πb², donde b es z/V_∞² tg² Φ/2. En otras palabras, πZ²/V_∞ tg² Φ/2. Y esta es la ley de la dispersión de Rutherford. La ley nos dice la probabilidad del área en que hay que acertar, el área efectiva de incidencia, para obtener una desviación mayor que determinada cantidad. Esta z es igual a Ze²/m; es una cuarta potencia y es una fórmula muy famosa.

Es tan famosa que, como suele suceder, no se escribió así cuando se dedujo, por eso yo, a causa de su «famosidad», la escribiré de otra forma… bueno, dejaré que la escribáis vosotros. Yo sólo daré la solución y vosotros veréis si podéis demostrarla. En vez de preguntarnos por la sección correspondiente a una desviación mayor que cierto ángulo, podemos preguntamos por el elemento de sección, dσ , que corresponde a la desviación en el intervalo dΦ en que debería estar el ángulo, entre… aquí y ahí. Sólo hay que diferenciar esta cosa y el resultado final es la famosa fórmula de Rutherford: 4Z²e⁴ por 2π senΦ dΦ partido por 4m²V_∞⁴ por el seno de Φ/2 elevado a la cuarta potencia. Lo escribo sólo porque es una fórmula famosa que aparece mucho en física. La combinación 2π senΦ dΦ es en realidad el ángulo sólido que tenemos en el intervalo dΦ. Así en una unidad de ángulo sólido, la sección está en razón inversa a la cuarta potencia del seno de Φ/2. Y esta ley se vio que era verdadera para la dispersión de partículas alfa por los átomos, lo que demostraba que los átomos tenían un punto duro en el centro, un núcleo. Y a través de esta fórmula se descubrió el núcleo atómico.

Muchas gracias.