3. Tales, el hombre de la sombra

—Sucedió en tiempos de Maricastaña. A orillas del mar Egeo, cerca de la ciudad jonia de Mileto, el hijo de Examio y Cleobulina, cuyo nombre era Tales, paseaba por la campiña.

¿Quién se atrevía a despertar a Jonathan tan temprano un domingo por la mañana? ¡Maldición! Era Léa. El grano que Jonathan tenía bajo la barbilla comenzó a lanzar destellos a la vez que él entreabría un ojo que parecía de bulldog. La puerta que separaba los dos dormitorios estaba abierta, como de costumbre. La voz, nasal y ronca, prosiguió:

—Tales iba por los campos y, a su lado, caminaba una criada.

Eso no era Léa. Sin duda era la radio. ¡SU radio!, se dijo Jonathan.

—Tales observaba el cielo mientras andaba. No era su radio. Jonathan saltó de la cama y se lanzó hacia la puerta.

—¡Yo alucino!

¡El loro! Ahí estaba, agarrado al marco de la puerta. Al otro lado, la atónita Léa contemplaba al pájaro dispuesto a proseguir con su letanía. Lo ignoraron y bajaron las escaleras.

El reloj de péndulo del salón comedor señalaba las once. Ruche aparentaba leer un periódico mientras Max recogía las tazas del desayuno.

Léa le recriminó:

—¿Le parece bonito que un loro nos despierte un domingo a estas horas? ¿Un loro que repite con voz nasal todo lo que le ha metido en la cabeza?

Con un batir de alas, el ave cambió de lugar y sentenció con un cloqueo:

—Lo mío no es repetir, recitar, informar o avisar. ¡Yo cuento!

Alrededor de la cicatriz, las plumas erizadas como púas ponían de manifiesto lo enfadado que se sentía. La bata entreabierta de Léa dejaba ver sus senos desnudos y se la abrochó. Pellizcándose el pendiente, Jonathan preguntó:

—¿Por qué nos habla de Tales en ayunas?

Ruche hizo oídos sordos a las preguntas, dejó el periódico y habló:

—¿Así que Sinfuturo os contaba —y Ruche insistió en el verbo y continuó— que Tales observaba el cielo para descubrir secretos sobre el curso de los astros? La sirvienta que lo acompañaba vio un hoyo en el campo y lo evitó. Tales, absorto en la contemplación de la bóveda celeste, cayó dentro. En tanto que la mujer le ayudaba a salir le dijo: «No ves lo que está a tus pies y quieres conocer lo que ocurre en el cielo». —Ruche concluyó—: Como veis, todo empieza por una caída.

La puerta se abrió y, cargada con las cestas de la compra, entró Perrette, que oyó la última frase. Jonathan-y-Léa la miraron y, al ver su cara tensa, emprendieron el camino de regreso a sus habitaciones. Léa, antes de desaparecer, no pudo evitar hacer un comentario socarrón:

—Y tuvo un montón de hijos.

—¡Craso error! —respondió Ruche regocijado—. Tales no tuvo hijos. Adoptó el de su hermana Kibistos.

Jonathan, como todos los estudiantes del mundo, había estudiado a Tales en diversas ocasiones. En cada una de ellas, el profesor había hablado del teorema pero nunca del autor. En las clases de matemáticas nunca se hablaba de las personas sino de sus teorías. De vez en cuando se mencionaba a Tales, Pitágoras, Pascal o Descartes, pero eran solamente nombres, como los de una parada de metro o una marca de queso, de quienes no se decía ni dónde ni cuándo habían vivido. Las fórmulas, demostraciones y teoremas llenaban la pizarra sin indicar quién los había creado, como si existieran desde siempre, al igual que las montañas y los ríos, aunque ni las unas ni los otros fueran eternos. Con ello se conseguía que los teoremas parecieran aún más eternos que las montañas y los ríos. Las matemáticas… no eran como la historia, la geografía o la geología. Pero ¿qué eran con exactitud? La respuesta no interesaba a la mayoría.

—Lo tuyo ha sido fabuloso. —Max alisaba las plumas de Sinfuturo—. Has contestado muy bien. —Se bamboleó y frunció los labios imitando al loro—. «No repito, ¡cuento!». ¡Bien! Estaban estupefactos. Reconozco de todos modos que tienes una memoria diabólica.

Ésa era exactamente la reflexión que Jonathan se estaba haciendo en el piso superior.

«Creo que se ha recuperado demasiado bien para ser un loro mudo». Y preguntó a Léa:

—¿Alguna vez habías oído a un loro hablar tanto y tan seguido?

La chica no respondió.

—Perrette nos llevaba a las tiendas de animales que hay junto al Sena, ¿recuerdas? Nos quedábamos atentos delante de las jaulas de los loros durante más de una hora. ¡No dijeron ni pío jamás!

—No debían de ser de los habladores —sugirió Léa.

Su mente estaba en otra parte.

—Es que éste no es un hablador, ¡es un charlatán!

La hermana cortó la conversación, bajó al comedor y digiriéndose a Ruche, que la esperaba con cara inocente, le espetó con agresividad:

—¿Qué es lo que empezó con la caída de Tales?

Y se sentó a desayunar. Perrette escuchaba atentamente mientras trajinaba en la cocina americana que estaba en el mismo comedor. Ruche guardó un reflexivo silencio, luego dijo:

—Tales fue el primer «pensador» de la historia. Lo cual no quiere decir que nadie hubiera pensado antes que él. ¡Qué va! Se piensa desde hace muchísimo tiempo. Antes que él hubo muchos magos, escribas, sacerdotes, contables, narradores, unos recitaban oraciones, otros efectuaban cálculos y otros narraban mitos. No obstante, Tales hizo algo más: se planteó preguntas. Por ejemplo: ¿qué es pensar?, o ¿qué relación existe entre lo que pienso y lo que es?, y también: ¿hay cosas que escapan a mi pensamiento? ¿De qué está hecha la naturaleza? Lo que hoy nos extraña es que nadie se hubiera planteado antes preguntas como ésas.

Ruche disfrutaba navegando en pleno mar de la filosofía. Jonathan se unió a ellos, vestido con una especie de sari indio y calzado con sandalias de cuerda. Se sirvió un cuenco de leche en el que vertió dos puñados de cereales.

—Esto es filosofía, ¿verdad, Ruche? —inquirió Léa.

—Creía que Tales era matemático —le secundó Jonathan.

Ruche disfrutaba, los había «enganchado». Y se apresuró a aclarar:

—En la época de Tales, el siglo VI antes de nuestra era, la filosofía y las matemáticas estaban totalmente unidas. De hecho, esas palabras no existían. Fueron inventadas más tarde y, bastante después, se separaron. Hoy todos pretenden olvidar que, en su origen, marchaban al unísono.

Ya que les había puesto a Tales ante los ojos, Ruche se dijo que no podía parar. Conocía muy bien al pensador, era uno de los que había situado en lo más alto de su Panteón particular. Sin embargo, debía refrescar su memoria con respecto a la vertiente matemática de la obra del griego.

¿Dónde obtener esa información? En la Biblioteca Nacional, por supuesto. La BN, como se la ha llamado siempre. Allí había pasado muchas horas con Grosrouvre, cuando era estudiante, por supuesto.

En la BN no se entra con la misma facilidad que en un cine. Se necesita un carné de lector. El acceso se concede o se rechaza después de una entrevista muy formal con un miembro de la administración. La bibliotecaria que lo recibió le preguntó si era profesor o investigador, cuál era el tema de su investigación, qué profesor le dirigía dicha investigación, si tenía carné de estudiante, si… De repente, consciente de la edad de su interlocutor, dijo confusa, como excusándose:

—Preguntamos esto a todos…

Y él pensó que podía haberle contestado: «Vivo con una mujer, Perrette Liard, que cayó en una alcantarilla cuando tenía veinte años, etc., etc., y ahora me he decidido a investigar porque los gemelos…». La bibliotecaria no lo habría entendido.

Le dedicó una amplia sonrisa.

—Me llamo Pierre Ruche, soy librero en Montmartre, tengo ochenta y cuatro años. Mi director de tesis murió en 1944. Nunca la acabé. Luego he intentado espabilarme solo. Mis investigaciones son a título personal; tampoco tengo en perspectiva ninguna publicación. Me gustaría consultar obras sobre Tales y los comienzos de las matemáticas griegas.

La funcionaría levantó la mano dando a entender que era suficiente.

—¿Quiere usted un carné válido para un año o sólo para diez veces?

—Con mi edad, sería más razonable tomar el de diez pases, pero ¡venga el anual!

Ruche pagó y fue a hacerse una fotografía. La foto, revelada al instante, quedó impresa directamente en la tarjeta de lector plastificada. Sin echar una mirada a la tarjeta, la agarró con fuerza y se la metió en un bolsillo de la chaqueta.

A la entrada cambió el carné por una ficha en la que estaba grabado un número de asiento. La sala de lectura no había cambiado.

Bastantes años antes, Ruche trotaba entre las filas de los lectores sentados; ahora, la conducción de su silla de ruedas le dio algunos problemas: derribó una silla, aplastó una carpeta abandonada en el suelo y rozó una estantería atestada de manuales. Por fin llegó a su sitio, situado en el centro de una fila. Recobrando antiguos reflejos, se familiarizó rápidamente con la situación. Encendió la lámpara, vieja costumbre en la BN, cuyas luces se encendían sin importar la hora ni la cantidad de luz diurna. Los catálogos y los ficheros se hallaban en una sala del entresuelo, y sólo se accedía a ella por una escalera. Iba a protestar con furia al director de la biblioteca, cuando recordó que el Catálogo general de los libros impresos también estaba disponible en la sala de lectura. Podía consultarlo cómodamente. Anotó las signaturas y rellenó las fichas de solicitud de las obras.

Más tarde, en una callejuela adyacente, compartiendo la mesa con un grupo de habituales, se tomó un bocadillo y un vaso de burdeos.

La una y media. El bar se vació y Ruche permaneció un momento disfrutando del recién conquistado silencio. Volvía a sentirse como un estudiante. Un viejo estudiante. Sacó del bolsillo su carné de lector y miró la foto. Era minúscula pero de una nitidez extraordinaria. Contempló dos ojos claros, casi transparentes, finos y abundantes cabellos peinados hacia atrás, mejillas hundidas, barbilla firme, nariz recta y una piel casi sin arrugas. Sonrió: ¡las arrugas están en el interior! Hacía mucho que no se miraba a sí mismo con tanto detenimiento. Colocó de nuevo la tarjeta en la cartera.

En la papelería situada a la vuelta de la esquina le enseñaron diversos tipos de cuadernos. Como era muy maniático en todo lo concerniente a los objetos de escritorio, acabó escogiendo uno grueso, con tapas de cartón negro y cuyas páginas de cuadrícula grande tenían un margen ancho. Luego regresó en taxi a la calle Ravignan.

Se dirigió directamente al segundo estudio, precisamente el que estaba acabando de acondicionar el carpintero de la calle Trois-Frères. Había explicado sus ideas sobre la transformación del local para que el resultado se adecuara a sus propósitos, y el carpintero las siguió con exactitud.

Ruche entró en el garaje-habitación y pasó la tarde desarrollando el proyecto que tenía en mente. Todo debería estar listo para el próximo domingo.

Tras algunas sesiones matinales en la BN, la libreta se llenó. Instalado en un pasillo situado a la derecha de la sala de lectura, Ruche repasó las notas que había tomado hasta el momento.

Ruche los dibujó:

¡Qué dibujo más siniestro! Terriblemente semejante a aquellos que habían llenado de tristeza su juventud. Continuó leyendo lo que había anotado:

Relación entre círculos y triángulos. Demostró que a cada triángulo puede corresponder un círculo: el círculo circunscrito, aquél cuya circunferencia pasa por los tres vértices, del que propuso una construcción general.

Ruche reflexionó y anotó en el margen del cuaderno: «Eso quiere decir que, dados tres puntos, existe un solo círculo cuya circunferencia pasa por ellos».

Lo volvió a leer. ¡No, no! «Tres puntos no alineados», añadió, porque si los tres puntos están en línea recta lo que pasa es una recta y no una circunferencia. Había que ser preciso, de otro modo podían escribirse despropósitos. Luego añadió: «Eso quiere decir que tres puntos que no están alineados definen no sólo un triángulo, lo que es evidente, sino un círculo, que no lo es». Mientras lo dibujaba, a Ruche le impresionó el interés que Tales ponía en los elementos que relacionaban los objetos matemáticos. El dibujo resultante fue tan siniestro como el precedente.

g

Con un lápiz sombreó el interior del círculo. El dibujo mejoró.

Sacó sus instrumentos del estuche y enmarcó la figura; observó el efecto entrecerrando los ojos. Le encantó su propia idea: ¡presentar las figuras geométricas como cuadros de pintura!

La estudiante que estaba sentada en la mesa frente a él le miró sorprendida, intrigada por el comportamiento de ese anciano que dibujaba aplicadamente en un cuaderno. Con la palma de la mano, Ruche limpió la hoja de papel de restos de goma de borrar. Luego, reanudando su tarea, escribió:

Tales demostró que un triángulo isósceles tiene dos ángulos iguales, estableciendo así una relación entre longitudes y ángulos: a lados iguales, ángulos iguales.

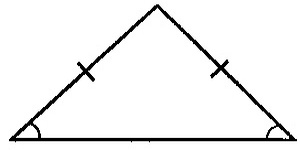
Al leer las líneas que seguían, Ruche no pudo por menos que sonreír; había escrito:

Para referirse a un bisonte los indios americanos dicen un «dos cuernos». A un coche se le llama «dos caballos» por su potencia, a un velero «dos palos». A una figura de tres ángulos se la llama un tri-ángulo. Pero podríamos muy bien llamarla también tri-lado. Los antiguos lo hacían y hablaban de trilátero, palabra formada sobre el mismo esquema que cuadrilátero.

Continuando con su vena etimológica, había añadido:

¿Isósceles? Iso: igual, skelos: piernas. ¡Un triángulo isósceles es un triángulo con dos piernas iguales! Consecuencia de ello, cualquier triángulo con los tres lados desiguales es llamado escaleno, es decir, cojo.

Ruche comenzó a fantasear con un problema de matemáticas que dijese así: «Dado un triángulo cojo…». Eso le trajo a la mente a Perrette y su descendencia trilátera, «dos hijos más uno». Y permaneció un largo rato ensimismado, acordándose de las revelaciones de Perrette respecto de su caída. En rigor, no les había dicho casi nada. Y, sin darse cuenta, estaba de nuevo en el punto de partida de lo que había desencadenado la investigación sobre Tales que ahora efectuaba.

Después de tratar las relaciones que Tales estableció entre círculos y triángulos, y entre ángulos y lados, abordó las que se establecen entre rectas y círculos. Con esa finalidad se enfrascó en la lectura de una obra sobre los comienzos de las matemáticas griegas.

Mientras escribía lo que había extractado, le vino a la memoria un fragmento de la carta de Grosrouvre: Hay en estas obras historias comparables a las de nuestros mejores novelistas. ¿Zola, Balzac, Tolstói en matemáticas? Grosrouvre había cargado las tintas, como solía. Pero Ruche admitió que, por lo menos, era una forma original de ver las matemáticas.

«¿Y si siguiera su consejo? Veamos: ¿qué me cuentan estas páginas?».

La historia sucede en un plano y tiene como personajes principales a una recta y un círculo. ¿Qué puede pasar entre ellos? Puede ser que la recta corte al círculo o bien que no lo corte. Puede rozarlo, observó Ruche. Si lo corta, lo dividirá forzosamente en dos partes. Y para que las partes sean iguales, ¿cómo debe estar situada la recta? Tales le dio la respuesta: para que la recta divida al círculo en dos partes iguales, debe pasar necesariamente por el centro: es el diámetro. El diámetro es el segmento más largo que un círculo puede contener y que lo atraviesa en toda su longitud. Por eso podemos decir que el diámetro «mide» el círculo.

Compás, regla, lápiz. El resultado es:

Ruche reanudó la lectura y luego escribió:

La respuesta de Tales no se refiere a un círculo concreto sino a cualquier círculo. No hace la más mínima alusión a un resultado numérico establecido desde un solo objeto, como habían hecho antes que él los egipcios o los babilonios. Ambiciona llegar a verdades generales acerca de una clase completa de objetos del mundo, infinita, a ser posible. Ello constituye una ambición de absoluta novedad. Para llegar a obtener esas verdades generales, Tales se verá obligado a concebir, sólo con su pensamiento, un ser ideal, «EL círculo», el cual es, de algún modo, ¡EL REPRESENTANTE DE TODOS LOS CÍRCULOS DEL MUNDO! Y como está interesado en todos los círculos existentes y no en un grupo determinado, quiere afirmar verdades que pertenezcan a su naturaleza de círculo. Por ello le podemos otorgar el título de «primer matemático de la historia». Era una manera extremadamente nueva de ver las cosas. Es difícil imaginar la novedad que representó una frase como: Toda recta que pasa por el centro de un círculo lo corta en dos partes iguales.

Con la cabeza llena de círculos y rectas, abandonó la BN.

Con sus cabriolas sobre una rama del laurel del patio, Sinfuturo provocaba la risa de todos.

Perrette, sentada a una mesa de jardín, mientras bebía un vino quinado con fresa, hacía esfuerzos por contenerse. Ruche, encolerizado, estaba a punto de abandonar la lectura de sus apuntes. Sinfuturo, de mala gana, dejó la rama y fue a posarse en el hombro de Max. Cuando Ruche pronunció la frase: «Tales ambiciona llegar a verdades generales acerca de una clase completa de objetos del mundo», Jonathan no pudo contenerse Y dijo:

—Es terrible lo que ahí se afirma. ¿No podría ser que, escondido en algún lugar del mundo, hubiera un círculo clandestino, un círculo guerrillero, que escapara a ese teorema?

—¡Ninguno! ¡Jamás! ¡En ningún sitio! —tronó Ruche.

—¿No lo has oído? —exclamó Léa—. ¡Ha dicho todos los círculos! ¡Sin excepciones!

—¡Me parece demasiado fuerte! —replicó Jonathan.

—¡Más bien totalitario!

Ruche no replicó nada; admiraba su furor adolescente. Los quería así, rebeldes contra el orden del mundo. Le recordaban sus terribles discusiones con Grosrouvre, en el bar lleno de humo de la Sorbona.

—¡No se puede huir de un teorema que se aplica a uno mismo! —sentenció Léa erigida en pitonisa.

Perrette la miró, asombrada ante tanta vehemencia. Se sirvió de nuevo vino quinado en su vaso ya vacío y lo suavizó con un chorrito de jarabe de fresa.

—Sus matemáticas son como el destino en las tragedias, ¿no le parece, Ruche? —dijo Perrette con dulzura.

—¿Mis matemáticas? —repuso furioso el aludido—. ¡Grosrouvre es quien va a estar contento! ¡Ha triunfado! Perrette insistió en su idea.

—¿No hay ninguna relación entre las tragedias y las matemáticas? Ambas nacieron en Grecia por la misma época, ¿no?

Ruche la miró atónito. Jamás se le había ocurrido relacionarlas. ¡La tragedia y las matemáticas! Esquilo, Sófocles, Eurípides… ¡Para morirse, vamos!

Y se dirigió a Jonathan:

—Tranquilízate, los teoremas no se refieren más que a seres ideales.

—Así Jonathan ya no tiene miedo a nada. —Léa soltó una carcajada.

—Por supuesto —aseguró Ruche—. Los teoremas no se aplican a los seres humanos.

—¿Y a los loros? —preguntó Max.

—Tampoco.

Al amanecer hacía ya calor y la temperatura no dejó de aumentar a lo largo de la mañana. La única solución era ir al cine. Jonathan-y-Léa se dirigieron hacia la cercana plaza de Clichy; pasaron por delante de las minisalas con indiferencia estudiada y seleccionaron una sala de cine tradicional, con butacas mullidas, gruesa moqueta, gran telón y una pantalla grande como la vela mayor de un velero de tres palos.

En el descanso se atracaron de helados mientras canturreaban una cancioncilla tonta que inventaron poco tiempo atrás, en la época en que Perrette estaba sin blanca y les llevaba a la primera sesión de los domingos por la tarde porque era la más barata.

Por una de esas casualidades del destino, que parece anticipar futuros acontecimientos, en el cine se proyectaba Tierra de faraones, fabulosa película de 1955, con Jack Hawkins, Dewey Martin y Joan Collins y guión de William Faulkner. El tema era la misteriosa construcción de las pirámides.

La película les entusiasmó, y salieron con pena de la sala refrigerada. Jonathan-y-Léa se dirigieron hacia la Butte de Montmartre, atravesando renuentes el puente Caulaincourt.

El puente Caulaincourt es único: pasa por encima de un cementerio, por lo que los transeúntes caminan por encima de las tumbas. Los partidarios del puente sostienen que es preferible andar por un puente sobre un cementerio que por un túnel que pase por debajo, y argumentan que es mejor tener tumbas bajo los pies que sobre las cabezas.

—¡Ni un solo árbol para refugiarnos a su sombra en tanto que abajo abundan! —masculló Léa—. ¡La misma historia de siempre, todo en grandes cantidades a quien no lo necesita!

La chica odiaba ese puente.

Jonathan la miraba avanzar con paso de sonámbula; observaba su cabeza cubierta de rizos e impenetrables pensamientos, los hombros estrechos, inclinados cerrando un busto de alambre de espino. Pensó en un cuervo con un cuerpo de garza real. Con cariño, le dio con el codo en las costillas y Léa saltó de lado, de tal modo que por poco cayó bajo el único coche que circulaba en esa tórrida tarde.

—¡No me toques! —aulló.

—¡Para! —le dijo Jonathan—, hueles a rancio.

Ésta era una frase que utilizaba siempre para incordiar a su hermana cuando ella «vomitaba sobre el mundo».

Max les observaba desde el umbral de la librería. Les hizo señas para que apresuraran el paso y les precedió hacia el estudio.

El local había quedado irreconocible: el suelo estaba recubierto de alfombras de un espesor considerable, mayor que el de la moqueta del cine de la plaza Clichy, y sobre las alfombras, estratégicamente distribuidas, había finas esteras de esparto. Soberbiamente instalado sobre un taburete cubierto con terciopelo rojo, estaba Sinfuturo. Ruche, desde el fondo de la habitación, les dio la bienvenida con una sonrisa discreta. Max se retiró tras dejarlos instalados en las esteras. Se hizo un largo silencio, durante el cual creyeron oír un vago rumor de olas, Fue la señal. Sinfuturo comenzó con su ronca voz:

—Tales, apoyado en la borda de la embarcación, veía alejarse la tierra donde había vivido toda su vida. Mileto desapareció en la lejanía. Emprendía viaje hacia Egipto. —Sinfuturo hablaba, serio como un papa, desde lo alto de su taburete. Su cuello se henchía con cada palabra, sus ojos lanzaban chispas; afirmándose sobre las patas, buscaba el mejor apoyo para mantener un tono de voz potente, como si hubiera asistido a cursos de dicción—. El navío, impulsado por los vientos etesios, que no soplan más que en verano, en plena canícula, efectuó la travesía sin escalas. Avistó las costas egipcias, puso proa al lago Mariotis y, allí, Tales embarcó en una faluca con la que remontaría el curso del Nilo.

La voz de Sinfuturo se apagó, se le había acabado la cuerda. Max le acarició y le ofreció un pequeño tentempié. Echó en un cuenco el contenido de un sobre de cóctel selecto: cacahuetes fritos y finamente salados, almendras, nueces y anacardos.

Fue Ruche quien prosiguió:

—Al cabo de algunos días de viaje, sólo interrumpido por paradas en las ciudades y pueblos que bordean el Nilo, Tales la vio. ¡La pirámide de Keops! Se alzaba en medio de una amplia elevación del terreno, no muy lejos de la orilla del río. El griego nunca había visto algo tan imponente. Las otras dos pirámides, la de Kefrén y la de Micerinos, estaban cerca, y parecían pequeñas en comparación. Aunque ya se lo habían advertido los otros viajeros durante el trayecto por el Nilo, las dimensiones del monumento sobrepasaban todo lo que Tales podía imaginar. Bajó de la faluca. Anduvo hacia ella aminorando su velocidad a medida que se acercaba, como si la proximidad de la masa del monumento tuviera la propiedad de acortar sus pasos. Se sentó, agotado. Un campesino egipcio, un fellah de edad indefinida, se puso en cuclillas a su lado.

—Extranjero, ¿sabes cuántos muertos ha costado esta pirámide que tanto admiras?

—Miles, sin duda —respondió Tales.

—Di mejor decenas de miles.

—¡Decenas de miles!

—Centenares de miles es más aproximado.

—¡Centenares de miles! —Tales le miró con incredulidad.

—Posiblemente nos quedamos cortos —añadió el fellah—, y ¿para qué tantos muertos? ¿Para abrir un canal? ¿Contener el río? ¿Tender un puente? ¿Construir una carretera? ¿Edificar un palacio? ¿Erigir un templo en honor de los dioses? ¿Excavar una mina? Rotundamente no. Esta pirámide la mandó hacer el faraón Keops con el único fin de obligar a los humanos a convencerse de su pequeñez. La construcción tenía que sobrepasar todos los límites para aplastarnos: cuanto más gigantesca fuera ella, más minúsculos seríamos nosotros. Consiguió su propósito. Me he fijado en ti cuando te acercabas, y he visto dibujarse en tu cara los efectos de esta magnitud. El faraón y sus arquitectos quisieron obligarnos a admitir que, entre la pirámide y nosotros, no hay ninguna medida común.

Tales ya había oído especulaciones parecidas sobre los designios del faraón Keops, pero nunca enunciadas con tanta falta de pudor y tanta precisión a la vez: «¡No hay ninguna medida común!». El monumento deliberadamente desmesurado le desafiaba. Construido hacía ya dos mil años por los hombres, estaba fuera del alcance de su conocimiento. Cualesquiera que fueran los fines del faraón una cosa saltaba a la vista: la altura de la pirámide era imposible de calcular. ¡La construcción más visible del mundo habitado era también la única imposible de medir! Tales decidió aceptar el reto.

El fellah habló toda la noche. Nadie ha sabido jamás lo que dijo.

Cuando el sol apuntaba por el horizonte, Tales se levantó y observó su propia sombra proyectarse en dirección oeste; pensó que, cualquiera que sea el tamaño de un objeto, siempre existirá una iluminación que lo haga parecer grande. Durante un buen rato permaneció de pie, inmóvil, con los ojos fijos en la sombra que proyectaba su cuerpo en el suelo. La vio disminuir a medida que el sol se iba elevando en el cielo.

Se prometió a sí mismo: «Ya que mi mano no puede medir la pirámide, la voy a medir con el pensamiento». Tales miró la pirámide con insistencia durante mucho rato; debía encontrar un aliado que fuese de la talla de su adversario. Varias veces su mirada se desplazó de su cuerpo a su sombra y viceversa, y luego a la pirámide. Por fin levantó los ojos, mientras el sol lanzaba sus rayos terribles. ¡Tales acababa de encontrar a su aliado!

El sol no hace distingos entre las cosas del mundo, y las trata a todas del mismo modo, aunque su nombre sea Helios en Grecia o Ra en Egipto. A ese modo de tratar a todos por igual, si atañe a los hombres, en Grecia se le llamará más tarde democracia.

Si el sol trata de modo semejante al hombre, minúsculo, y a la pirámide, gigantesca, se establece la posibilidad de la medida común.

Tales se aferró a esa idea: «La relación que yo establezco Con mi sombra es la misma que la pirámide establece con la suya». De ahí dedujo: «En el mismo instante en que mi sombra sea igual que mi estatura, la sombra de la pirámide será igual a su altura». Hete aquí la solución que buscaba. No faltaba sino ponerla en práctica.

Tales no podía efectuar la operación solo. Necesitaban ser dos y el fellah accedió a ayudarlo. Es posible que sucediera de ese modo. ¿Cómo llegar a saberlo?

Al día siguiente, al alba, el fellah fue hacia el monumento y se sentó bajo su sombra inmensa. Tales dibujó en la arena un círculo con un radio igual que su propia estatura, se situó en el centro y se puso de pie bien derecho. Luego fijó los ojos en el borde extremo de su sombra.

Cuando la sombra tocó la circunferencia, es decir, cuando la longitud de la sombra fue igual a su estatura, dio un grito convenido. El fellah, atento, plantó un palo inmediatamente en el lugar donde estaba el extremo de la sombra de la pirámide. Tales corrió hacia el palo.

Sin intercambiar una sola palabra, con la ayuda de una cuerda bien tensa, midieron la distancia que separaba el palo de la base de la pirámide y supieron la altura de la pirámide.

Bajo sus pies, la arena se levantaba; el viento del sur estaba empezando a soplar. El jonio y el egipcio se dirigieron hacia la orilla del Nilo, donde acababa de atracar una faluca. El fellah permaneció sonriente en la orilla mientras la embarcación se alejaba por el río.

Tales estaba orgulloso. Con ayuda del fellah había ideado un truco. ¿La vertical me resulta inaccesible? Mido la horizontal. ¿No puedo medir la altura porque se pierde en el cielo? Mediré su sombra estampada en el suelo. Con lo pequeño podré medir lo grande. Con lo accesible podremos medir lo inaccesible. Con lo cercano podremos medir lo lejano.

—Las matemáticas son una astucia del espíritu —concluyó, agotado, Ruche.

Esta última frase iba dirigida no sólo a sus oyentes sino también a sí mismo.

Instalado en lo alto de su taburete de terciopelo rojo, Sinfuturo permanecía en una total inmovilidad. Podía parecer dormido.

—En resumidas cuentas, ¿lo que acaba de contarnos, Ruche, es un peplum? —inquirió Léa.

—Eso que dices es un cumplido que toca mi fibra sensible —replicó Ruche—, me encantan Cecil B. DeMille, Los diez mandamientos, Ben-Hur…

—El sonido no era malo, pero carecíamos de imágenes —dijo Léa con tono afectado—. De todos modos es un mito estupendo.

—¡Un mito! —tronó Ruche—. Tales existió verdaderamente, la ciudad de Mileto también, las pirámides están ahí todavía, los vientos etesios soplan cada verano en la canícula, el Nilo fluye sin parar, y siempre hacia el Mediterráneo. —De pronto se interrumpió—. ¿Y por qué no un mito? ¿Tenéis algo en contra de los mitos? Un mito contado por Plutarco. En cuanto al Teorema de Tales, aún sigue vigente.

—¿Teorema de Tales? Bien, de acuerdo sobre Tales, lo imagino, pero no veo nada sobre el teorema —comentó Jonathan.

Max sonrió con aspecto de complicidad. Le había hecho esa misma observación a Ruche por la tarde cuando ensayaban el espectáculo.

Todo se desarrolló con extremada rapidez: una tupida cortina tapó el ventanal dejando la habitación sumida en la oscuridad, en tanto que por la pared opuesta descendía una tela blanca. Max puso en marcha un proyector, cuyo motor comenzó a zumbar. Una cantidad indeterminada de lamparillas se iluminaron por todas partes proyectando halos de luz en la noche artificial. Sobre la tela se esbozó algo, al principio impreciso, que luego tomó esta forma:

—¿Se parece esto ya a tu teorema? —preguntó Ruche con ironía—. Perfectamente —admitió Jonathan. Léa asintió.

—¡La siguiente! —ordenó Ruche

Max pasó a la diapositiva siguiente.

—¡Uf! —exclamaron con desaliento—. Esto ya no es un peplum, Ruche, es una película underground. Después de Hawks esta tarde, es de verdad mísera…

—Atención, atención, esto es un teorema —les cortó una voz metálica. ¡Y no era Sinfuturo! Se encendió una luz.

En la pared, cerca del techo y colgado sólidamente junto al ventanal, había un altavoz. Era un altavoz antiguo, con una ancha bocina, estilo campo de prisioneros de la segunda guerra mundial, que Max había comprado en las Pulgas. Empezó a vociferar: «Esto es un teorema, esto es un teorema: Un sistema de paralelas, AA', BB', CC', cortadas por dos secantes, D y D', determinan segmentos proporcionales, es decir, que el cociente entre las longitudes de los segmentos AB y AC es igual al cociente entre las longitudes de A'B' y A'C'.»

Jonathan-y-Léa, impresionados, enmudecieron. ¡Un verdadero espectáculo de luz y sonido! Sinfuturo era el único a quien parecía no gustarle el altavoz. Por primera vez en su vida de loro, se encontraba cara a cara a otro no humano capaz, también, de hablar. La verdad es que éste sólo repetía y no comprendía una sola palabra de lo que salía de su bocina. ¡Y, encima, llevaba dibujada en el metal La voz de su amo! ¡Una verdadera provocación para Sinfuturo, el loro libertario!

Max dio al interruptor del magnetófono y la cinta quedó inmóvil. El altavoz calló.

—¡Para empezar, no está mal! —Jonathan-y-Léa sonrieron con complicidad a Ruche.

—¡Efectivamente! Con este teorema comienza lo que se convertirá en uno de los más importantes hallazgos de las matemáticas griegas: la ciencia de las proporciones. Teorema de Tales o Teorema de la proporcionalidad de segmentos. Antes del llamémosle «entreacto», estábamos hablando de la revelación que tuvo Tales de que el sol trataba a todos los objetos por igual. Estaba inmerso en plena similitud. ¡Y por detrás de la similitud está la FORMA! ¡Todas las figuras semejantes tienen la misma forma! Conservar las proporciones es conservar la forma. Con mayor corrección podríamos decir: la forma es lo que se conserva cuando cambiamos las dimensiones guardando las proporciones.

Ruche paró para observar el efecto de su perorata. Jonathan-y-Léa le prestaban gran atención. Una manchita de rojo fluorescente apareció en la pantalla y se puso a revolotear alrededor de la fórmula como una mosca alrededor de una herida.

—¡Que las fórmulas hablen! —exclamó con entusiasmo.

Acababa de recordar lo que Grosrouvre repetía sin cesar cuando estudiaba matemáticas: «¡Hay que hacer hablar a las fórmulas! Si quieres saber lo que tienen dentro, pregúntales». En aquella época, Ruche no había entendido lo que eso significaba.

—¿Qué estaba diciendo?

—Acababa de decir: «Que las fórmulas hablen…», y ha callado bruscamente —le recordó Jonathan.

—¡Ah, sí! «Que las fórmulas hablen». ¿Qué dice la fórmula de Tales? —Silencio por respuesta—. Repito la pregunta.

—AB partido por AC es igual a A'B' dividido por A'C', con barras horizontales por todas partes —contestó Léa con una docilidad aparente.

—¡No! Lo que yo pregunto es: ¿qué quiere decir eso? En la vida, cuando se dice algo es para expresar una idea; bueno, la mayoría de las veces. En matemáticas también. La fórmula de Tales QUIERE hablar. —La mancha fluorescente se posó sobre AB. AB es a AC lo que A'B' es a A'C'.

«Yo soy para ti como ella es suya», pensó Léa para su coleto.

—La fórmula de Tales nos dice —continuó Ruche— que el primer y el segundo par están en la misma relación lógica. ¡He ahí la palabra! Este teorema, aparentemente inocuo, lleva consigo todas las preguntas que las relaciones ponen en juego: cambio de escala, modelos reducidos, planos, mapas, ampliaciones, reducciones.

Ruche hizo una seña a Max, y éste abandonó el proyector para dirigirse a una fotocopiadora, disimulada en un mueble al fondo de la habitación. Con tres simples trazos de rotulador, Max dibujó una especie de loro en una hoja de papel, la puso sobre el vidrio, seleccionó la reducción 50%, puso en marcha la máquina, esperó y mostró el original junto a la fotocopia.

Ruche prosiguió:

—La reducción es lo mismo: igual forma pero menor tamaño. Loro dos veces más pequeño —comentó.

Max colocó de nuevo el original sobre el vidrio, seleccionó esta vez el 150%, y con el nuevo resultado y el original, se acercó a Ruche.

—Ampliación. La misma forma pero mayor tamaño. Véase: loro una vez y media mayor.

Jonathan se levanto de súbito. Tomó la ampliación y la reducción y, a la vez que las enseñaba, imitando la voz de Ruche dijo:

—La misma forma, pero mayor. —Apuntando a Léa con el dedo, continuó—: Loro ampliado, ¿cuántas veces mayor que loro reducido?

Léa, pillada por sorpresa, se ruborizó y remedó:

—No hablaré si no es en presencia de mi abogado. Sinfuturo se agitó. No le gustaban demasiado los ejercicios pedagógicos hechos a su costa. Para cambiar de tema, Léa siguió:

—Sin embargo, ninguna de estas cosas nos explica cómo procedió Tales. Porque se trataba de medir una pirámide real, no de inventar una fórmula sobre el papel.

—Querrás decir sobre el papiro —le corrigió el intratable Jonathan.

—Papiro o papel, la fórmula es la misma. No depende del soporte.

Max imaginó formulas que dependiesen del material sobre el que estuvieran escritas: el signo más se convertía en menos al pasar de la tela al estaño, el aspa de multiplicar era la barra de fracción si pasábamos del pergamino a la vitela…

—¿Cuántas veces mayor? —siguió insistiendo Jonathan.

Le dieron la callada por respuesta.

La fórmula desapareció de la pantalla y Ruche tomó carrerilla:

—Si se hubiera tratado de un árbol o… del Obelisco de la plaza de la Concorde, que estaba en Egipto antes de que lo trajeran aquí, si se hubiese tratado de un cilindro o un prisma, la misión de Tales hubiera sido simple, bastaba con la medida que había tomado. Pero la pirámide se ensancha desde su vértice hasta la base sobre la que reposa. La pirámide de Keops tiene una base cuadrada y su eje pasa exactamente por el centro de la base. La altura de la pirámide es la longitud del eje y la longitud de la sombra del eje es también la longitud del eje. ¡Simple! ¡Diapositiva!

En la pantalla apareció una figura.

—Bien, Tales sólo pudo medir con precisión —Ruche dirigió una insistente mirada a Léa— la parte de sombra que sobresalía de la base. La otra parte, la que está en el interior del monumento, le era inaccesible.

—¡Todo eso no le sirvió de nada! —exclamó indignada Léa.

—Así lo creí yo. Luego reflexioné y di con la solución… en otro libro. Tales lo consiguió porque tomó la medida en el momento en que los rayos del sol eran exactamente perpendiculares al lado de la base.

—¿Es decir? —preguntó Léa.

—¡Uf! Deja que lo recuerde. Perpendiculares al lado de la base… lo que implica que la parte oculta era igual a la mitad del lado. Así, la altura de la pirámide era igual a la longitud de la sombra más la mitad de un lado —concluyó expeditivamente Ruche.

—No he entendido nada —confesó Léa.

—Yo menos —añadió Jonathan—. ¡A cenar!

Ruche pensó: «Salvado por la campana». Perrette les llamaba a la mesa y no tenía que dar explicaciones de algo que no sabía. Y luego, en voz alta dijo:

—¡Tenía ya un hambre de lobo!

Pero no engañó a nadie con esa excusa.

Al día siguiente Jonathan-y-Léa no tenían clase por la tarde. Cuando volvieron a casa después de comer en el colegio, Ruche les recordó:

—Daos prisa, va a venir Albert a buscarnos.

El timbre sonó, era Albert. Con su gorra gris de cuadros, grasienta, gafas con cristales gruesos como lupas y un sempiterno cigarrillo apagado en la comisura de los labios, pasaba ampliamente los sesenta años, muy bien llevados, por cierto.

—¡Buenos días a todos!

Se encargó de Ruche, hombre y silla de ruedas; los manejaba con destreza. En su viejo Peugeot 404, gris metalizado, tapizado en cuero, con techo practicable, tras el accidente llevaba al librero en todos sus desplazamientos. Estos últimos días lo había llevado a la BN.

Ruche, cuando hablaba de Albert, decía: «Es muy independiente». Y era digno de ver el placer que experimentaba al decir eso, porque él también era muy independiente pese a sus limitaciones. Albert nunca había aceptado ser radiotaxi, y se sentía orgulloso de ello. Se preguntaba cómo podían soportar un viaje los clientes oyendo con voz hiriente: «calle Vaugirard, 105; paseo de Belleville, 83; pasaje Guéméné delante del número 8…». Trabajaba como taxi pirata o en la parada de las estaciones de tren. También tenía algunos clientes fijos, como Ruche.

El accidente les había unido. Siempre que Albert se tomaba un día libre, acudía a buscar a Ruche por la mañana temprano, y se marchaban de excursión al campo, donde pasaban todo el día. Un cesto de provisiones bien repleto de cosas buenas ocupaba el asiento de atrás, como en las películas de Renoir.

Max sí que tenía clase, pero, con la autorización de Perrette, siguió a la tropa. Todos, Sinfuturo incluido, se metieron en el 404. De pie junto a la puerta de la librería, Perrette les vio marchar con envidia. Ruche no quiso decir adónde iban. Plaza Pigalle, Nuestra Señora de Lorette, la Trinité, la Ópera Garnier, donde daban El rapto del serrallo. Pasaron luego por la avenida de la Ópera. Cuando circulaban ante la boca del metro de la línea 5, la estación Pirámides, Albert se las arregló para disminuir la velocidad. Pasado el Palais Royal, el coche enfiló por debajo de los arcos del Louvre y entró en la plaza del Carrousel. Albert frenó con brusquedad y en un santiamén estacionó el 404 junto a la acera. En el centro del patio de Napoleón, brillaba, desafiante, la pirámide de vidrio.

Se instalaron en la explanada delantera.

—Entre la pirámide de Keops y esta transparente del Louvre hay 4639 años de diferencia. Una situada a orillas del Nilo y la otra a las del Sena. —A la vez que hablaba, Ruche sacó un bloc de dibujos y unos lapiceros—. Para Tales, la idea de que el sol trata igual a todas las cosas se expresa en el hecho de que todos los rayos del sol son paralelos. El astro está tan lejos y nosotros somos tan pequeños que esta estimación está justificada. Veamos la situación en el momento en que Tales midió la sombra.

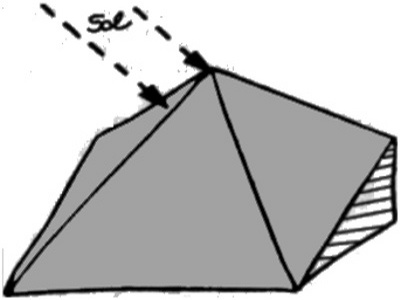
Desde que Ruche empezó a dibujar, Sinfuturo se instaló en su hombro para ver mejor lo que hacía.

—La pirámide que Tales tuvo que medir no era transparente como ésta, por eso le haremos una autopsia. Quito lo que me impide ver el interior, conservo la sombra y dibujo el eje.

Ruche borró el sombreado de las caras, y trazó una vertical desde el extremo superior hasta el centro de la base:

—La altura de la pirámide es la longitud del eje, que es lo que busca Tales.

»¡Sigamos con la autopsia!

Ruche se movía demasiado y Sinfuturo cambió su hombro por el de Max, más tranquilo. Ruche borró las caras, luego trazó una línea horizontal desde el pie del eje hasta el extremo del triángulo de sombra que sobresalía de la base de la pirámide y dijo:

—Si la pirámide hubiera sido transparente, la sombra del eje cuya longitud quería determinar Tales es esta que veis aquí:

»La parte de la sombra que está en el interior de la base, por tanto en el interior de la pirámide, la he dibujado en trazos discontinuos; es inaccesible, Tales no puede medirla; la parte que va desde el lado de la base hasta el extremo de la sombra está en negro continuo, Tales puede medirla. De hecho, en toda esta historia, es la única cosa que puede medir.

Ruche borró el triángulo en sombra, dibujó el eje en trazo continuo, puso la letra A en el pie del eje, H en el punto en que la sombra del eje cortaba al lado de la base, M en el extremo de la sombra. Colocó el primer y el último dibujo, uno junto a otro.

—¡Antes de! ¡Después de! ¡Igual que en la publicidad de los productos adelgazantes!

»Quitar la carne a las cosas. Despojar al monumento de su masa, borrarla, no conservar de ella más que los efectos que pueda producir en la pregunta que nos planteamos. Borrar, purificar, simplificar, olvidar, es lo que hizo Tales. Todos los matemáticos actúan así, pienso yo. A eso le llaman “abstraer”. Para un matemático el problema termina ahí —concluyó Ruche.

—¡Cómo! —se rebelaron Jonathan-y-Léa.

—Si Tales se hubiera fijado en un obelisco, su problema habría acabado porque bastaba con medir la longitud AM directamente en el suelo. Pero quiso ocuparse de una pirámide que, al esconder dentro de ella la parte AH, la hizo inaccesible.

—¡Se fastidió! —gritaron alegres Jonathan-y-Léa.

Ruche no hizo caso de la interrupción. Al levantar los ojos se dio cuenta de que algunos turistas se habían detenido y los observaban desde lejos. Se concentró en Tales.

—¿Qué pasaba en la arena que rodeaba a la pirámide de Keops? Cuando la dirección de los rayos del sol formaba un ángulo cualquiera con el lado de la base, lo que sucedía prácticamente siempre, la sombra formaba un triángulo cualquiera y… Tales no podía hacer nada.

»¡No olvidéis que las matemáticas son una trampa! Tales buscó una situación particular que le permitiera solucionarlo. La encontró trasladando su problema a un momento particular de día, aquél en que los rayos son perpendiculares al lado de la base. Ésta es la situación de la que os he hablado en casa, y de la que parece que no habéis entendido nada. —No estaba muy seguro de conseguir claridad expositiva, ¡con la cantidad de turistas que se estaban congregando a su alrededor!—. Lo que Tales no podía obtener por medición directa iba a deducirlo con el razonamiento. ¿Con qué armas contaba? De la pirámide sólo conocía el lado de la base. Y lo usaría.

Ruche enseñó un nuevo dibujo efectuado con extrema rapidez.

Miró satisfecho a su público. Cada vez se agolpaban a su alrededor más turistas. Cerró su cuaderno de dibujo con lentitud cuando…

—¿Cómo podía saber Tales que la sombra era perpendicular al lado? —preguntó Jonathan.

¡La guinda del pastel! Ruche le miró aviesamente.

—Es una buena pregunta que también me he planteado. —Y, volviendo a abrir de mala gana su cuaderno, explicó—: Tales no tenía escuadra ni cartabón, pero tenía algo mejor: la orientación de la pirámide. Los arquitectos construyeron el monumento de tal manera que una de sus caras estuviese orientada al sur.

Ruche completó su último dibujo.

—La sombra será perpendicular al lado en el momento en que el sol esté en su cénit. Exactamente a mediodía.

—¡En el preciso momento en que hace más calor! —observó Jonathan

—Para saber hay que sufrir —filosofó Léa—. ¿Dicen los libros si Tales pilló una insolación? En pleno desierto y a mediodía ¡es lo menos que podía pasarle!

—A mediodía, por supuesto, pero a la sombra, Léa. Debo recordarte que Tales medía la sombra, no el sol. Y si se mide la sombra es que la hay, y si la hay, uno puede protegerse en ella.

Todos rieron con ganas.

—Ya que hablamos de sombra, Ruche, ¿no nos ha escamoteado algo? ¿Tiene sombra la pirámide a mediodía todos los días del año?

—¡No! —respondió Ruche.

—Si no he entendido mal —dijo Jonathan, que se sentía vencedor—, tiene que haber, en primer lugar, una sombra visible, es decir, que sobrepase el límite de la pirámide.

—Que la sobrepase en el mediodía exacto —siguió Léa—, porque si es en otro momento del día, Tales no tiene nada que hacer.

—La sombra debe ser igual a la pirámide —continuó Jonathan—. Con todo eso tenemos una serie de condiciones bastante difíciles de conseguir.

Ruche esperó que acabara la andanada.

—La pirámide no tiene, cada mediodía, una sombra visible perpendicular al lado. En eso reside toda la dificultad. Para ello es necesario que el sol no esté demasiado alto en el cielo en su trayectoria diurna.

—Resumamos. Dos condiciones son necesarias: la sombra debe ser igual a la pirámide y perpendicular a la base. Para contestar a todo lo que de ahí se deriva, es preciso salir de la pura geometría y entrar en la astronomía, geodesia y geografía. Volvamos al terreno real.

»La pirámide de Keops está en Gizeh, a 30° de latitud en el hemisferio norte, como nosotros, por encima del trópico, pero bastante más abajo. Para que la sombra sea igual que el objeto que la produce, los rayos tienen que tener una inclinación de 45°. En Gizeh, en verano y al mediodía, los rayos del sol son casi verticales y por lo tanto casi no habrá sombra durante todo un periodo del año. Añadamos que, para que la sombra sea perpendicular a la base, ésta debe tener orientación norte-sur. En definitiva: sólo dos días al año se cumplen todas las condiciones mencionadas. Los astrónomos afirman que Tales únicamente pudo efectuar su medición el… —sacó un cuadernillo de su bolsillo y lo hojeó— 21 de noviembre o el 20 de enero. Escoged. ¿Ves, Léa? Era mediodía, pero a la sombra y en invierno. Si Tales pilló algo, debió de ser un catarro, no una insolación.

Un grupo de japoneses se arracimaba alrededor de Ruche; uno quería comprarle los dibujos, otro tomó una foto. Entonces habló Léa:

—El teorema es general, sin duda, pero la medición muy particular. ¿Cuál fue el resultado? Porque se trata de saber la altura de la pirámide, ¿no? —preguntó Léa.

—Tenía una cuerda a mano, pero le faltaba una unidad de medida. Utilizó el tales, es decir, su propia estatura. Midió la sombra con la cuerda ajustada a su estatura. Medía 18 tales; luego midió el lado de la base, dividió por dos y le dio 67 tales. Sumó y anotó el resultado. La pirámide de Keops mide 85 tales. En magnitud local, el tales equivalía a 3,23 codos egipcios, lo que nos da 276,25 codos en total. Hoy sabemos que la altura de la pirámide es de 280 codos, o sea, 147 metros.

Ruche no dijo el tiempo que había pasado la noche anterior efectuando esos cálculos, ni cuántas veces se había equivocado.

—Ésta —y señalaba la del Louvre— mide…

Buscaba los datos en el cuadernillo, cuando sonó la voz de Albert:

—Mide 21,60 metros de altura y 34,40 metros de lado.

Todos le miraron estupefactos, mientras el pobre Albert, sofocado, daba vueltas a la gorra.

—Lo oigo cada vez que traigo turistas a este sitio —añadió como disculpándose.

—Para acabar con las preguntas, os he preparado una serie de dibujos.

Ruche arrancó las hojas y se las enseñó.

de donde se obtiene:

Algunos turistas japoneses quisieron estrecharle la mano. Ruche se excusó.

—Con eso encontráis la fórmula que representa el teorema de Tales, como en la sesión anterior de luz y sonido, tal como conserva en la memoria Jonathan.

Mostró el último dibujo, en el que la abstracción dominaba. Por supuesto sin materia, sin revestimiento alguno; el plano estaba depurado. Tenían un verdadero esquema matemático ante los ojos. Ruche acabó:

—El teorema cuenta, de hecho, lo que sucede cuando un grupo de rectas paralelas se dedican a cortar un par de secantes.

Una ovación celebró la última frase de Ruche. En todos los tonos y acentos imaginables se oyó «taelis», «talais». Tales fue condimentado en todas las salsas lingüísticas, e incluso un norteamericano soltó con entusiasmo: «¡Yeah! Telis».

Los turistas japoneses estaban tan emocionados que quisieron darle dinero… ¡Ah, París!

Días después, en la sección de cultura de un periódico de Tokio, se publicó una foto de Ruche, espléndido en su silla de ruedas; a su lado estaba Max, con Sinfuturo posado en su hombro, y Albert, que, en un acto puramente reflejo, se había quitado la gorra, aunque no se había quitado la colilla de la boca. Al fondo, en segundo plano, los lectores de Tokio podían percibir la famosa pirámide del Louvre. El pie de foto decía:

El sol había desaparecido tras los muros de las Tullerías y empezaba a hacer frío. En vez de ir directamente hacia el norte, el 404 bordeó el Sena y se metió en la plaza de la Concorde en el momento en que encendían las farolas. Dio dos vueltas completas para permitir que todos pudieran contemplar el obelisco. Luego, pasando por la calle Saint-Honoré, Albert les llevó a que admiraran la columna Vendôme.

—Podéis comprobar —dijo Ruche, que empezaba a estar bastante cansado— que las columnas y los obeliscos se trasladan. Las pirámides resultan bastante más difíciles de transportar.

—Y de medir —susurró Max.

«Siempre lo mismo», añadió Ruche en su interior. «En el instituto, mi profesor de matemáticas decía: Para resolver el problema basta con aplicar el teorema, etc., y dejaba la tiza. ¡Fantástico! Basta con…».

—Las matemáticas son sencillas, Ruche —sentenció Léa—. Lo complicado es aplicarlas.

—Sin embargo, yo diría: las matemáticas son complicadas y sus aplicaciones aún lo son más —rectificó Jonathan.

—Siempre dramatizas —repuso Ruche—. Fíjate en Tales; la trascendencia de su teorema va más allá de todas las aplicaciones y, no obstante, para medir su pirámide, lo ha utilizado en un caso muy particular, cuando la relación entre la pirámide y su sombra es igual a 1, porque era más simple.

—Más simple pero menos frecuente —dijo Jonathan.

—Un caso particular normalmente es menos frecuente que el caso general. Es como en la vida, hay que escoger: complicado y frecuente o simple y raro —filosofó Ruche.

—Simple y frecuente preferimos nosotros —dijeron a coro los gemelos.

Max se enderezó.

—En casa, Ruche, dijo al principio que Tales abandonó Mileto en plena canícula, y que no se detuvo, prácticamente, hasta llegar a la pirámide de Keops. Ahora ha dicho que la medición se hizo en invierno. ¿Duró seis meses el viaje?

Ruche cayó inopinadamente de las nubes. ¡Lo habían pillado!

—Quizá se paró alguna vez, no sé, quizás visitó Alejandría. ¡Uy, no! ¡Qué digo! Alejandría se fundó más tarde. Pues visitaría Tebas. En mi opinión, Tales debió de instalarse al pie de la pirámide y esperó la ocasión idónea para medirla.

—¿Y el fellah? —insistió Max—. ¿Qué fue del fellah de Tales?

Ruche meneó la cabeza; se había olvidado completamente del fellah.

—¡No hay medida sin el fellah! —corearon Jonathan-y-Léa.

—Tenéis razón. Tales no hubiera podido medir nada sin él. Le era imposible comprobar que su sombra era igual que su estatura y, a la vez, señalar el extremo de la sombra de la pirámide. Tienen que ser dos para aplicar el teorema.

—Hay que llamarle el Teorema de Tales y el fellah —concluyó Léa—. Demos al fellah lo que es del fellah.

Ruche se prometió preguntar: ¿quién es el fellah aquí?, en cada ocasión que les explicase teoremas.

Por fin, todos se arrellanaron en los asientos y se impuso el silencio en el 404.

Durante el trayecto hacia Montmartre, Ruche hizo balance de lo que había sucedido desde que tomó la decisión de explicarles Tales con una finalidad digamos que personal.

Sus relatos debían ser fieles a todo lo que se sabía y conformes a la historia. Los gemelos habían resultado ser unos interlocutores exigentes. Fue consciente de que no le dejarían pasar ni una. La tarea se presentaba mucho más ardua de lo que había previsto, aunque mucho más excitante.

Albert se colaba por en medio de los embotellamientos con una habilidad al límite de la colisión.

—¿Usted sabía, Ruche, que Tales predijo un eclipse? —preguntó de pronto Jonathan, rompiendo el silencio.

—Sí.

—¡No nos lo ha dicho! —No.

—He leído —volvió Jonathan— que no fue el teorema lo que le hizo famoso en su tiempo, sino que el eclipse, que predijo, tuviese lugar en el momento preciso que él había dicho.

Desconcertada por esta revelación, Léa miró aviesamente a Jonathan. Se recobró de inmediato y preguntó a su vez:

—La boba de la criada que acompañaba a Tales hubiera estado más guapa callada. Su observación, creo yo, tendría que figurar en las inscripciones —se rió—: «No ves lo que está a tus pies y quieres conocer lo que ocurre en el cielo» —pronunció Léa con voz ácida y aguda intentando remedar a la criada, pero sonó a falso.

Albert dio un frenazo y Léa se estampó contra el cristal, aunque siguió imperturbable.

—¿No es verdad?: «Como no ves el hoyo, no puedes ver el cielo», o bien al contrario: «Por haber pasado tu tiempo intentando saber lo que pasa en el cielo, has caído en un hoyo del camino».

Sin dar tiempo a que Ruche replicara Léa pidió a Albert que parase. Bajó y Jonathan la siguió.

Mientras el 404 ascendía hacia Montmartre, Ruche se preguntó por qué no les había hablado del eclipse. No encontró una respuesta. ¿Qué sucede cuando se produce un eclipse? Desaparece bruscamente la luz que cegaba los ojos momentos antes, se pasa del día a la noche de golpe. Tales, el hombre que establece relaciones… Cuando Perrette desapareció en la alcantarilla abierta en medio de la acera, diecisiete años atrás…, ¿qué es lo que la joven no quiso volver a ver y, en cambio, veía con gran claridad en el instante anterior?, se preguntó Ruche.

El coche había dejado a Jonathan-y-Léa en la avenida, entre Pigalle y Blanche. Instantes después Léa preguntó a su hermano:

—¿Por qué no me has contado a mí primero esa historia del eclipse? ¿Vas a la tuya o qué?

—Eres libre de hacer tus propias pesquisas. Quiero recordarte que dos son también dos por uno.

Caminaban por el terraplén central, y pasaron delante del Moulin-Rouge, cuyas aspas de colores agresivos odiaban. Jonathan, furioso, iba delante. «No voy a contarle todo lo que hago. Cada uno debe vivir su propia vida», se decía. Luego recordó de nuevo el eclipse. Al pronosticarlo gracias al estudio del cielo, Tales se liberó a sí mismo del terror que desencadenaría la súbita desaparición del sol.

Esperó que Léa le alcanzase y le comentó:

—En lo que concierne al hoyo, opino que Tales aceptó el riesgo de caer dentro y sumirse en una oscuridad…, cómo diría…

—¿Local? —propuso Léa.

—Local —continuó Jonathan—, a condición de poder estudiar el cielo y escapar a la oscuridad general que invadiría la tierra y aterrorizaría a los hombres.

Léa miró desconcertada a Jonathan. ¿Era posible que la revelación de Perrette con respecto a su origen le hubiera trastornado tanto? ¡Se expresaba de manera tan distinta a como lo hacía habitualmente! Caminaron hombro con hombro. Léa fue consciente por vez primera de la suerte que tenían de haber nacido juntos para poder afrontar y asumir, también juntos, ese problema y pensó: «Dos es también uno más uno». Se detuvo, se masajeó el chichón que se había hecho a consecuencia del frenazo de Albert, y tiró a Jonathan del brazo:

—O sea que, según tú, ¿el hoyo era el precio que tenía que pagar para liberarse del miedo de lo que iba a suceder?

Tales cumplía su misión de forma ponderada. Jonathan-y-Léa decidieron adoptar como amigo a ese gran antepasado que dominó la sombra y domesticó la oscuridad del mundo.