Notas

^[1] Bajo ese título se publican en la edición inglesa de las obras de Aristóteles dirigida por W. D. Ross (Opuscula) y la colección Loeb (Minor Works). <<

^[2] En ese sentido se manifiesta HIRSCH en Der pseudo-Aristotelische Traktat «De lineis insecabilibus» (tesis doctoral inédita, Heidelberg, 1953). No he podido consultarlo; lo cito según las referencias de Timpanaro-Cardini. <<

^[3] HIRSCH, op. cit., cap. IX, ofrece un catálogo de esos pasajes. <<

^[4] Uno de los problemas que planteó fue el siguiente: si se corta un cono mediante un plano paralelo a la base ¿cómo serán las dos secciones, iguales o desiguales? Si son desiguales, la superficie exterior del cono no será recta; si son iguales, será un cilindro. <<

^[5] Los testimonios han sido recogidos por R. HEINZE, Xenokrates…, págs. 175-178. <<

^[6] A History of Greek Mathematics, vol. I, pág. 347. <<

^[7] De ser así debemos incluir este escrito entre los pocos textos de carácter matemático anteriores a Euclides que se nos han conservado y tener presente que sería la única obra completa de esa característica junto con los tratados de AUTÓLICO DE PITANE Sobre la esfera en movimiento y Sobre los ortos y los ocasos. <<

^[1] Comienza en este punto la presentación de los argumentos de quienes defienden la existencia de las líneas indivisibles. <<

^[2] Se refiere a una línea «ideal» en el sentido platónico del término. <<

^[3] También aquí se refiere a cuadrados, triángulos, planos y cuerpos «ideales», previos, en tanto que ideas, a los existentes en el mundo perceptible. <<

^[4] Aristóteles en Física 187a3 hace referencia a este argumento, «el argumento de la dicotomía, que supone magnitudes indivisibles». Para comprender adecuadamente y situar en su contexto el párrafo conviene recurrir a ciertos pasajes de la Física aristotélica que nos transmiten el pensamiento de Zenón (239b9, 239b11, 233a21, 239b14, 239b30, 239b33), reunidos, traducidos y comentados en G. S. KIRK y J. E. RAVEN, Los filósofos presocráticos, Madrid, Gredos, 1981, págs. 408-15. <<

^[5] Para interpretar correctamente este argumento es necesario tener presente el valor de los conceptos matemáticos que en él se utilizan. La mayor parte de las veces encontramos las aclaraciones que nos son precisas recurriendo a los Elementos de Euclides, si bien lo más posible, como señala HEATH (Mathematics in Aristotle, Oxford, 1949, pág. 256) es que este tratado sea de fecha anterior a Euclides y, por tanto, su autor tomara esas nociones de otros matemáticos. Por ejemplo, términos como «binomial» y «apótoma» pueden haber sido tomados de Teeteto, a quien se atribuye, según una noticia de Papo, el descubrimiento y estudio de las irracionales compuestas. La definición que se da aquí de «líneas conmensurables» coincide con la que ofrece EUCLIDES, Elementos X, def. 1. <<

^[6] En cuanto a las rectas racionales e irracionales, hay que recordar que, para la matemática griega, las nociones de racionalidad e irracionalidad son relativas y de carácter geométrico. Así lo señala EUCLIDES en Elem. X, def. 3: «… existen rectas, infinitas en número, conmensurables e inconmensurables, unas sólo en longitud, otras también en cuadrado, con una recta propuesta: llámese, pues, “racional” a la recta propuesta y “racionales” a las que son conmensurables con ella ya sea en longitud y en cuadrado, ya sea sólo en cuadrado, y llámese “irracionales” a las inconmensurables con ella». Para explicar la noción de «conmensurabilidad en cuadrado» resulta aclaradora la nota de HETT: «Dos líneas, cuyas longitudes son respectivamente √3 y √6 son conmensurables en cuadrado porque sus cuadrados, 3 y 6, son conmensurables», aunque hay que tener presente que trasladar el pensamiento geométrico euclidiano a términos numéricos comporta siempre cierta falsedad. <<

^[7] Apótomas y binomiales son dos de los tipos de rectas irracionales estudiadas por EUCLIDES en el libro X (de ahí que, como han indicado Heath y Timpanaro, debamos rechazar la conjetura textual de Apelt). <<

^[8] La definición de la binomial aparece en EUCLIDES, Elementos X 36: «Si se suman dos rectas racionales conmensurables sólo en cuadrado, la recta resultante es irracional: llámesela binomial»; las Segundas Definiciones y las proposiciones 42 y 48-66 se ocupan de la clasificación y características de las binomiales. La definición de la apótoma aparece en X 73: «Si se quita de una recta racional otra racional que sea conmensurable sólo en cuadrado con la recta entera, la restante es irracional: llámesela apótoma»; las proposiciones 74-75 dan la clasificación de las apótomas; las proposiciones 79-81, las Terceras Definiciones y lo que sigue, proposiciones 85-104 y 108-114 describen sus características y propiedades. <<

^[9] Aquí comienza la enumeración de los argumentos con los que el autor pretende refutar a los sostenedores de las líneas indivisibles. La edición de Apelt presenta la conjunción disyuntiva é, que probablemente hay que corregir, a tenor del sentido y de lo expresado por DENNISTON, (The Greek Particles, Oxford, 1978, rp. de la segunda edición, pág. 279 y ss.) por la partícula ê. De hecho, los restantes traductores también han obrado como si lo hubieran corregido. <<

^[10] Se refiere a las «razones que surgirían entre las partes de estas líneas divisibles si éstas fueran cortadas». <<

^[11] Tendrá «las divisiones finitas», se sobreentiende. <<

^[12] En el de los números enteros. <<

^[13] «Las opiniones de los matemáticos», se entiende. <<

^[14] Es decir: «estos argumentos, supuestamente matemáticos, no tienen fuerza bastante como para escapar…». <<

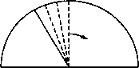
^[15] Es decir, el movimiento del radio que recorre un semicírculo recorre —dice el tratadista— todos los puntos de líneas divisibles, en lugar de —como pretenden sus oponentes— ir saltando del extremo de una indivisible al extremo de la indivisible siguiente. <<

^[16]

JOACHIM (op. cit., nota ad loc.) interpreta este párrafo de la siguiente manera: «En otras palabras: la geometría, asumiendo que el movimiento es un hecho, muestra que el objeto que se mueve atraviesa en efecto la infinidad de puntos intermedios y muestra que no puede haber movimiento en el que esto no se produzca. Quienes defienden las líneas indivisibles no han llevado a cabo intentos de refutar estas pruebas geométricas. Su postulado de “líneas indivisibles”, incluso si esquivan los argumentos de Zenón, entra en colisión con los mucho más sólidos datos de la geometría: porque la geometría muestra que es imposible la clase de movimiento que tendría lugar si existieran las líneas indivisibles. El texto está tan corrupto que parece imposible aclarar el argumento en detalle.» Las enmiendas al texto propuestas por FEDERSPIEL («Notes exégétiques…», págs. 504-7) no producen cambios en el sentido del pasaje. <<

^[17] Da comienzo aquí la serie de argumentos matemáticos contra la existencia de las líneas indivisibles. <<

^[18] Referencia a dos definiciones que a nosotros nos han sido transmitidas por EUCLIDES, Elem. I, def. 3 («Los límites de una recta son puntos») y PLATÓN, Parménides 137e («Recto es aquello cuyo medio queda enfrente de ambos extremos»). <<

^[19] Las cuestiones relativas a la conmensurabilidad de las rectas en longitud y en cuadrado son la materia de la que trata Elem. X. Véase nota 6. <<

^[20] Así, la aceptación de la existencia de las líneas indivisibles entraría en conflicto con las teorías matemáticas —ya bien asentadas en esta época— sobre lo conmensurable y lo inconmensurable y lo racional y lo irracional, y más concretamente con la irracionalidad existente entre el lado del cuadrado y su diagonal. <<

^[21] «En las líneas se usa la de un pie como si fuera indivisible», afirma Aristóteles en Metafísica 1052b33. <<

^[22]

De acuerdo con la explicación, ABCD es el cuadrado que tiene por lado la línea indivisible, AE = 2AB y el rectángulo AEFG ha sido construido de tal manera que AE x EF = AB². Si eso es posible, afirma el tratadista, EF = ½ AB; es decir: se habría dividido por la mitad la línea indivisible, que dejaría de ser tal. <<

^[23] EUCLIDES, en Elementos I 22 ofrece la solución al problema de «construir un triángulo con tres rectas que son iguales a tres rectas dadas», pero con la precisión de que «es necesario que dos de las rectas, tomadas juntas de cualquier manera, sean mayores que la restante», teniendo en cuenta que en I 20 se ha demostrado que esto último es propiedad de todo triángulo. La objeción a la existencia de las indivisibles es la misma que en el argumento anterior. <<

^[24]

«La perpendicular a cualquiera de sus lados», se entiende. En EUCLIDES, Elementos I 10 y 11 se plantean como problemas «dividir en dos partes iguales una recta finita dada» y «trazar una línea recta perpendicular a una recta dada desde un punto dado en ella». Ambos se resuelven mediante la construcción de un triángulo equilátero, de tal manera que la afirmación que se lee en el texto resultaría corolario de las dos proposiciones mencionadas. Sea ABC el triángulo formado por tres indivisibles y AD la perpendicular al lado BC: la supuesta indivisible BC habría resultado dividida en dos partes iguales por la altura del triángulo, luego no sería indivisible. <<

^[25] Es decir, que tenga por lado una recta indivisible. <<

^[26] En efecto, en aplicación del teorema de Pitágoras (EUCLIDES, Elementos I 47), en el cuadrado de AB (que es una línea indivisible) podemos trazar la diagonal AC y una perpendicular a ésta, BE; entonces, AB² = AE² + EB², de donde resulta que AB no es la menor y, por tanto, tampoco sería indivisible.

<<

^[27] Sobreentiéndase «la teoría que sostiene la existencia de las líneas indivisibles». Con esta frase se introduce la segunda serie de argumentos matemáticos contra la existencia de las líneas indivisibles. <<

^[28] Cf. más adelante 971a27 y ss. y nota a ese pasaje. <<

^[29] «Una línea indivisible», se entiende. <<

^[30] Con «estas cosas» se refiere fundamentalmente al espacio y el tiempo, aunque el argumento podía también emplearse para justificar la existencia de indivisibles en otros géneros de magnitudes. <<

^[31] Nueva referencia a las definiciones de EUCLIDES, en este caso a Elem. I, def. 3 (v. más arriba, nota 18). <<

^[32] Se abusa de la polisemia de «último» (éschaton) al emplearlo en su primera aparición en la frase con sentido local-temporal y como sinónimo de «elemental» en la segunda. <<

^[33] Tras la conclusión que se da al primer tema en el párrafo anterior, se aborda la segunda cuestión de las que componen el tratado. Los argumentos que se exponen en ella coinciden en parte con los ya expresados y en parte con los que se contienen en Fís. 231a20-232a22. <<

^[34] Es decir, «como principio general». Ese principio general aparece en ARISTÓTELES, Fís. 231b2: «Y en cuanto al contacto, dos cosas sólo pueden estar en contacto recíproco si el todo de una toca al todo de la otra, o si una parte de una toca a una parte de la otra, o si una parte de una toca el todo de la otra. Pero como los indivisibles no tienen partes, tendrían que tocarse entre sí como un todo con un todo». El pasaje citado forma parte de la argumentación con la que Aristóteles pretende demostrar que «es imposible que algo continuo esté hecho de indivisibles, como, por ejemplo, que una línea esté hecha de puntos, si damos por supuesto que la línea es un continuo y el punto un indivisible». <<

^[35] Como señala JOACHIM (nota ad loc.) si b y c están en contacto con k, puesto que el contacto entre los puntos sólo puede ser del tipo «el todo con el todo», también B y c estarán en contacto entre sí y también en la modalidad «el todo con el todo».

<<

^[36] Por las razones aducidas en el párrafo anterior. <<

^[37] Tal es la traducción literal del texto de Apelt que tomo como base. HETT, que emplea el mismo texto, refleja sin embargo en su traducción la versión latina de Julius Martianus Rota. JOACHIM considera insalvable el corrupto estado del pasaje y prefiere dejarlo en griego sin traducir. M. TIMPANARO CARDINI sugiere invertir el orden de los dos párrafos que nosotros hemos incluido en IX, pero ni aun así, a nuestro entender, se salva el problema de la relación de este argumento con lo anterior y posterior. Entendemos, más bien, que es FEDERSPIEL («Notes exégétiques…», págs. 511-12) quien da la interpretación más acertada al pasaje: de 971a30 a 971b31 el refutador examina tres modos de relación entre los puntos de acuerdo con lo que aparece en ARIST. Fís. V 3, 226b 18 y ss. «El último argumento mostraba que la hipótesis de una relación de consecutividad entre los puntos de una línea o bien nos hacía caer de nuevo en los absurdos de la relación de contacto o bien nos obligaba a cambiar la definición de continuo, lo cual es absurdo. El nuevo argumento prolonga el precedente estudiando una relación aún más general que la de consecutividad, la relación de yuxtaposición. Al revés de lo que se ha venido diciendo, el lazo con el argumento anterior es evidente». Con esta frase Federspiel rechaza la propuesta de M. Timpanaro a la que aludíamos más arriba, y lo justifica de la manera siguiente: la segunda parte del argumento viene a demostrar el aserto contenido en la primera parte, puesto que si esta relación de yuxtaposición tiene consecuencias absurdas, la teoría que afirma que la línea se compone de puntos es falsa. La demostración, igual que en el argumento anterior, se hace en dos tiempos, expresados en las dos frases del segundo párrafo de nuestro argumento IX. <<

^[38] El tratadista da por demostrada su tesis, pero aún ha de abordar otra cuestión en relación con ella: aunque no esté compuesta de puntos, los puntos forman parte de la recta como extremos de la misma, como poco tiempo después recogería Euclides en sus definiciones. Tanto esta segunda cuestión (la línea no está compuesta de puntos) como la tercera (el punto no es lo más pequeño que hay en la recta ni tampoco una articulación indivisible) aparecen ya suscitadas en ARISTÓTELES, Física 215b12-22: «Pero no hay ninguna proporción según la cual el vacío sea superado por un cuerpo, como no hay ninguna proporción entre la nada y el número… por esto tampoco la línea supera al punto, a menos que la línea esté compuesta de indivisibles». <<

^[39] En la tercera parte del tratado, que comienza aquí, se tratará la naturaleza del punto de manera negativa, mediante la refutación de dos definiciones que el tratadista considera erróneas: el punto como «lo más pequeño que hay en la recta» y el punto como «articulación indivisible». Más adelante también EUCLIDES formularía su definición de punto en forma negativa (Elementos I, def. 1): «Punto es lo que no tiene partes». <<

^[40] Los puntos estarían en la línea como extremos de la misma. <<

^[41] «En el espacio». <<

^[42] «La línea». <<

^[43] Algunos autores consideran que este pasaje, corregido de manera diversa pero con sentidos no lejanos por Diels y Timpanaro, debía formar parte de un texto sobre las articulaciones de los animales. <<

^[44] Aceptar la corrección propuesta por M. Timpanaro para la cita de Empédocles un poco más arriba es lo que nos permite interpretar esta última frase, que de otro modo resulta incomprensible: las articulaciones serían exclusivas de los seres vivos. Tal característica haría imposible definir el punto como ninguna clase de articulación. <<

^[1] Se trataba de objetos sumamente llamativos pero basados en principios elementales. Entre ellos se mencionan animales que bebían, grifos maravillosos de los que manaba a veces vino, a veces agua, a veces una mezcla de ambos, pájaros que cantaban y movían las alas, órganos de agua. Donde mayores servicios prestaron estos autómatas fue en la corte bizantina. Según las fuentes, en un salón destinado a la celebración de grandes ceremonias se encontraban las figuras de un buey que bebía y un trono, flanqueado por leones que rugían, que subía y bajaba sin que fuera posible ver el mecanismo, el llamado «trono de Salomón». Embajadores y visitantes debían de quedar muy impresionados por semejante espectáculo. <<

^[2] PROCLO, In primum Euclidis Elementorum librum Commentarii, ed. FRIEDLEIN, Leipzig, 1873, pág. 41; HERÓN, Definitiones, ed. HEIBERG, Leipzig, 1912, pág. 164. <<

^[3] A History of Greek Mathematics, vol. I, pág. 344. <<

^[4] CLAGGETT, M., Greek sciences in Antiquity, Londres, 1979⁶, págs. 93-94. <<

^[5] Sigue viva hoy día en los catecismos y colecciones de problemas resueltos. <<

^[6] Geschichte…, pág. 67. <<

^[7] En su artículo «The Pseudo-Aristotelian Questions of Mechanics in Renaissance Culture», Studies in the Renaissance 18 (1971), 65-104. <<

^[8] Se trata, según un comentario de J. BERTIER, de «un trabajo muy elaborado en lo relativo a la crítica textual y en la presentación de numerosos escolios inéditos». Lamentablemente no me ha sido posible conseguir esta obra para utilizarla como base de mi trabajo. <<

^[9] A. GONZÁLEZ PALENCIA y E. MELE publicaron su biografía junto con la colección de fuentes en las que se basa y diversos índices en una obra de lectura amenísima, Vida y obras de Don Diego Hurtado de Mendoza, 3 vols., Madrid, 1941-43. <<

^[10] Gracias al trabajo del hispanista R. FOULCHÉ-DELBOSC aparecido en Revue Hispanique 5 (1898), 365-405. <<

^[1] La cita está en verso —aunque no es un verso completo— de base trocaica; no disponemos de datos bastantes para identificar al poeta citado. <<

^[2] Lo que se mueve es la circunferencia, y lo que permanece, su centro. <<

^[3] En el sentido de que, al estar el círculo en movimiento, mientras uno de los extremos de un diámetro se mueve de atrás hacia delante, el extremo contrario de ese mismo diámetro se está moviendo en sentido inverso. <<

^[4] «El círculo», se entiende. <<

^[5] Los usos terminológicos y descriptivos en Aristóteles no son siempre iguales a los que más tarde se generalizarán, como podemos ver al compararlo con Autólico o Euclides. En estos últimos autores, para designar un punto se utilizan expresiones como tò semeîon tò E o simplemente tò E («el punto E», «E»); en la Mecánica, sin embargo, encontramos oraciones de relativo del tipo eph’hoû tó A, literalmente «donde está la (letra) A». <<

^[6] También Herón menciona este artilugio, al que da el nombre de hagnistérion. <<

^[7] El «radio» suele ser designado con expresiones que comprenden el verbo grápho «describir, dibujar»; así, en este mismo pasaje (848b10) he gráphousa tòn kýklon, pero también tôn ek toû kéntrou graphousôn toùs kýklous (849a11 y 849a21), pásei kýklon graphoúsei (849a14-15), he AB gráphousa tòn kýklon (849a27). En otras ocasiones, sin embargo, encontramos expresiones más próximas a la euclidiana he ek toû kéntrou, como en 849a2 autÈn apò toû kéntrou. La afirmación de que «el radio es transportado doblemente» vendrá justificada un poco más adelante, como corolario a la demostración del «paralelogramo de las velocidades». <<

^[8] Entiéndase «en determinada proporción del doble movimiento mencionado en la frase anterior». <<

^[9] La cuestión que sigue es, dentro de este tratado, una de las que más ha llamado la atención de los historiadores de la ciencia. Se trata del «paralelogramo de las velocidades», antecedente del «paralelogramo de las fuerzas», que da nombre a la regla básica de la mecánica según la cual «la resultante de dos fuerzas concurrentes viene representada por la diagonal del paralelogramo construido sobre ellas». HEATH comenta esta cuestión en su History of Greek Mathematics, vol. I, pág. 345: «El paralelogramo de las fuerzas se deduce fácilmente del paralelogramo de las velocidades en combinación con el axioma aristotélico de que la fuerza que mueve un peso dado es llevada en la dirección de la línea del movimiento del peso y es proporcional a la distancia recorrida por el peso en un tiempo dado». <<

^[10] La descripción de los movimientos nos parecería más fácilmente inteligible si se nos dijera que se transportan «ΑΓ hacia BH» y «AB hacia ΓΗ». La traducción, como es natural, debe reflejar el original griego aun cuando éste no se exprese de un modo sencillo. <<

^[11] «La proporción», se entiende. <<

^[12] Entiéndase «en ninguna proporción fija». <<

^[13] En términos actuales se diría que el movimiento del punto sobre la circunferencia es consecuencia de dos movimientos: tangencial (ley de inercia) y centrípeto (fuerza que violenta al punto a conservar su distancia al centro). Ésta es la causa dinámica (Galileo y Newton). Lo que el tratadista nos presenta es un análisis, también válido, puramente cinemático, en el que nos da una descripción fenoménica —no una explicación causal— del movimiento del punto sobre la circunferencia. <<

^[14] CAPPELLE propone secluir las palabras entre corchetes, lo que da un texto más coherente; también FORSTER acepta la corrección. <<

^[15] El griego emplea el término diámetros, que habitualmente se refiere al «diámetro de una circunferencia» o a la «diagonal de un paralelogramo»; evidentemente aquí, de acuerdo con la figura, tiene el significado de «cuerda». <<

^[16] La fuerza vertical tangente a la circunferencia (movimiento natural). <<

^[17] La fuerza centrípeta (movimiento violento o contra naturaleza). <<

^[18] Recibe aquí el rectángulo por nombre el adjetivo heteromékes «el de dos longitudes», en lugar de la expresión «la figura comprendida por ΑΒ y ΒΔ» con que suele denominarlo Euclides. <<

^[19] Debemos entender que esa situación es la que concierne al extremo B del radio AB. <<

^[20] Los manuales actuales de mecánica precisan que las fuerzas de inercia y centrípetas, para un mismo período o número de vueltas, son directamente proporcionales al radio. <<

^[21] Entiéndase: «en el tiempo en que X hubiera recorrido la distancia ΧΘ». <<

^[22] Toda la frase es oscura, y tengo la impresión de que se ha producido alguna alteración textual. Las traducciones inglesas de HETT y FORSTER no reflejan el texto griego. <<

^[23] A pesar del esfuerzo por resolver matemáticamente la cuestión que plantea, el tratadista mezcla dos asuntos: la precisión de la balanza y su sensibilidad. Para que una balanza sea precisa se requiere que los brazos de la cruz tengan la misma longitud y el mismo peso, que los platillos tengan el mismo peso y que el centro de gravedad de toda la parte móvil esté situado en la vertical de la cuchilla de apoyo y por debajo de ella. La sensibilidad de las balanzas es directamente proporcional a la longitud de los brazos de la cruz, inversamente proporcional al peso de la cruz y guarda razón inversa de la distancia del centro de gravedad de la parte móvil al eje de suspensión de la cruz. Una balanza con los brazos más largos será, por tanto, más sensible, pero para que sea también más exacta se requerirá, como se indica al final de la cuestión, que los dos brazos tengan la misma longitud y peso, etc. <<

^[24] El término que el griego emplea es spartíon, «cuerdecita»; esa cuerdecita serviría para mantener colgada la balanza. Pero dicho término va ampliando su significado para referirse, como vemos en esta misma frase, al soporte que sostiene la balanza estando debajo de ella. Más adelante, en la cuestión 20, veremos que ese mismo término designa también las posiciones que ocupa —o puede ocupar— la cuerda que sostiene la romana y hace función de fiel en ese tipo de balanza. <<

^[25] El «peso» al que se refiere el párrafo es el del brazo de la balanza que quedó en la parte de arriba (ΠΖ en la figura) al desequilibrarse la balanza en la pesada. <<

^[26] Anota HETT: «Aristóteles está equivocado en los detalles del segundo caso. Si la balanza tiene el soporte debajo está en equilibrio inestable y, por tanto, cualquier peso colocado en un brazo produciría el efecto de hacer bajar ese brazo hasta que la balanza quedara fuera del pivote. La balanza sólo mantendría su posición si el soporte estuviera en el centro de gravedad de la balanza». La precisión —correcta— que añade HETT no invalida el análisis —incompleto pero correcto— del pseudo-Aristóteles. <<

^[27] HEATH, History of Greek Mathematics, vol. 1, pág. 345, al comentar este pasaje afirma: «La idea es que, al ejercer el peso una fuerza mayor, a una distancia mayor produce correspondientemente una mayor velocidad», y relaciona este pasaje con el capítulo 8 del tratado aristotélico Acerca del cielo (289b1-290a6). En ese texto Aristóteles pretende explicar el movimiento de los astros en sus círculos y se ocupa de la cuestión del movimiento circular (cito los textos en la traducción de M. Candel publicada en esta misma colección, núm. 249): «… no es en absoluto absurdo, sino necesario, que los círculos tengan las velocidades proporcionales a sus magnitudes, …» (289b15 y ss.) y «Es lógico que entre círculos fijos alrededor del mismo centro sea mayor la velocidad del círculo mayor pues al igual que en los demás casos el cuerpo mayor se desplaza más rápidamente en su traslación propia, así también ocurre con los cuerpos movidos circularmente; en efecto, entre los segmentos de circunferencia delimitados por líneas trazadas desde el centro (scil., “radios”) es mayor el segmento del circulo mayor, de modo que, lógicamente, el circulo mayor girará en un tiempo igual que el menor…» (289b34 y ss.). <<

^[28] Como señala HEATH (Mathematics in Aristotle, pág. 235), el tratadista pone el principio de la palanca en relación con el movimiento de los radios de círculos concéntricos. También señala este autor, muy acertadamente, que todos los ejemplos de palancas que aparecen en este tratado son considerados palancas de primera clase (es decir, de aquéllas que tienen el fulcro entre la potencia y la resistencia), incluso cuando el caso es diferente (cf. cuestiones 4 y 14). Para encontrar la descripción de una palanca de segunda clase, HEATH nos remite al De Architectura, de Vitruvio (X 3-5). <<

^[29] El tratadista propone erróneamente la tesis de que el remo es una palanca de primera clase —es decir, de aquellas en las que el punto de apoyo (el escálamo) se encuentra entre la potencia (el marinero) y la resistencia (el mar)— cuando, en realidad, el remo es una palanca de segunda clase —es decir, de aquellas en las que la resistencia (el propio peso del barco) se encuentra entre la potencia (el marinero) y el punto de apoyo (el mar)—. En el mismo sentido el extenso comentario de HEATH en Mathematics in Aristotle, pág. 237. La afirmación de que los remos centrales son los más potentes sigue, en todo caso, siendo cierta, puesto que en efecto, el brazo de potencia de esos remos es más largo que el de los otros remos. <<

^[30] Al igual que en la cuestión anterior, el autor relaciona adecuadamente el funcionamiento del timón con el principio de la palanca, pero el planteamiento no es completamente acertado. El timón con su pala, su caña y su timonel, es una palanca de primera clase, en la que el timonel aplica la potencia mediante la caña o la rueda que gobiernan la pala; el punto de apoyo es la cabeza del timón; la resistencia es la pala del timón, más grande y de más peso que la caña. Como mecanismo para variar la derrota del barco también es una palanca de primera clase, pero los elementos que intervienen son: como potencia, la fuerza que emplea el barco en su desplazamiento, fuerza que le viene dada por el empuje de los remos, la vela o el motor; como punto de apoyo, aquél por el que el timón se fija al codaste; la resistencia es la que opone el agua al desplazamiento en su seno de la pala del timón en sentido oblicuo al de la marcha de la nave. Es decir, que el timón funciona mediante la acción simultánea de dos palancas; el tratadista, al considerarlo una sola, las mezcla, y toma la fuerza del timonel que mueve la caña por la potencia que mueve el barco. El autor reconoce con acierto una de las diferencias entre el funcionamiento del remo y el del timón al precisar que el timón actúa en el agua en posición oblicua. <<

^[31] Para HEATH, Mathematics in Aristotle, pág. 239, la interpretación de la vela como una palanca respecto de la nave es un concepto erróneo. HETT, en nota a este pasaje, señala que, efectivamente, una vela colocada en un lugar más alto da mayor velocidad a la nave, pero la altura puede llegar a ser excesiva y entonces, también por el principio de la palanca, el viento en la vela volcaría la nave en lugar de propulsarla. <<

^[32] Tampoco aquí la explicación es exacta. El tratadista pretende explicar la cuestión del gobierno de una nave con viento desfavorable como resultado de las acciones contrapuestas del timón y la vela, pero el asunto es mucho más complejo. En tal situación, los navegantes han de armonizar la acción de la vela —una palanca— con la del timón —una palanca doble— con los efectos producidos por la resistencia de dos fluidos —el agua y el aire— al movimiento de dos cuerpos —la vela y el casco de la nave— en su interior. La explicación detallada de este arte queda, sin lugar a dudas, fuera de los propósitos de esta nota. <<

^[33] Se refiere al ángulo que forma la circunferencia con el suelo, es decir, el llamado ángulo de tangencia que Euclides estudia en Elementos III 26, donde demuestra que es menor que cualquier ángulo rectilíneo, es decir, igual a cero. <<

^[34] Es decir, «la circunferencia». <<

^[35] Cf. 848a3 y ss. y Cuestión 1, 848b34 y ss. <<

^[36] Es decir, «hacia la tangente», colaborando con la tendencia centrífuga. <<

^[37] Cuestión 1, al final (849b20 y ss.). <<

^[38] Como señala HEATH (Mathematics in Aristotle, pág. 240), si la balanza —o las ruedas a que hace referencia el tratadista— estuvieran suspendidas por su centro de gravedad (un punto matemático), cualquier peso, aun muy pequeño, las pondría en movimiento. Pero en realidad están suspendidas de un eje material y, como indican BLANCANO y CAPPELLE, la fricción es tanto mayor cuanto más peso hay en la balanza o en las ruedas. <<

^[39] El texto es difícil, como se comprueba al ver que los diversos traductores y comentaristas han dado interpretaciones claramente divergentes. La traducción que doy no coincide con ninguna de las más recientes, pero sí con la interpretación que Hurtado de Mendoza dio a este mismo pasaje. Entiendo que esta versión es preferible puesto que (1) tiene un significado coherente ella misma, (2) no se sale de la tónica del resto de las cuestiones planteadas (cosa que sí sucede en otras interpretaciones) y (3) no ha requerido ninguna corrección textual. Ha bastado la interpretación del término zygón no con el valor habitual de «yugo, balanza, puente de la lira», sino como referida a una máquina que, en efecto, se asemeja a los objetos mencionados: el torno. El término «árgana» que emplea aquí Hurtado de Mendoza es, evidentemente de procedencia vitrubiana, con cuya clasificación de las máquinas es coincidente. <<

^[40] Hay que entender «a la misma distancia de la rodilla»; pero tanto en ese caso como en el expuesto a continuación —un extremo del palo en el suelo y el pie como fulcro— el tratadista nos presenta palancas de segunda clase —doble en la primera situación, simple en la segunda—. Cf. HEATH, Mathematics in Aristotle, pág. 241. <<

^[41] Se refiere a «la parte de en medio de las piedras y conchas» y a «la distancia de los bordes de esas piedras y conchas hasta el centro de las mismas». <<

^[42] Da la impresión de que se hace referencia a experimentos llevados a cabo con pesos controlados. La mina tenía un peso aproximado de medio kilo (431 gramos la mina ático-euboica y 630 gramos la mina egineta). <<

^[43]

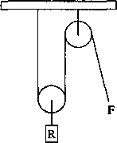
Creo que el tratadista se refiere a un sistema de dos poleas, una móvil y una fija. La polea fija, como se explica en los manuales de mecánica, tendría como utilidad cambiar la dirección de la fuerza sin alterarla, pero al añadir una polea móvil, habría que aplicar la fórmula correspondiente, cuyo resultado viene a ser, en el caso más habitual —cordones de las dos poleas paralelos y cuerda abrazada por la polea móvil igual a su diámetro— que la fuerza necesaria para mover la resistencia es la mitad de ésta. Cf. INCLÁN LÓPEZ, A. y MAÑAS BONVÍ, J., Curso de Física, pág. 45. V. también el extenso comentario de HEATH (Mathematics in Aristotle, págs. 242-43). <<

^[44] Hay que sobreentender «el hacha» como sujeto de la frase. <<

^[45] La palabra spartion designaría aquí, a mi entender, no sólo la cuerdecita o soporte del que se cuelga lo que se quiere pesar en la romana, sino también las marcas en la barra de la romana que acreditan el peso. En relación con este término, cf. nota a la cuestión 2. Aunque el funcionamiento práctico de la romana es sencillo y aún podemos verlo en uso entre los vendedores ambulantes, la explicación física de su regulación y control no lo es tanto. El lector interesado puede recurrir, como en otras ocasiones, a HEATH, Mathematics in Aristotle, pág. 244-245. <<

^[46] Se emplea el término específico odontágra, cuyo significado literal sería «cazadientes», y no el general thermastrís, «tenaza», como un poco más adelante. <<

^[47] «El diente», hay que sobreentender. <<

^[48] No reconozco el instrumento al que se refiere el tratadista. Evidentemente es una doble palanca de mecanismo más semejante al de unas tijeras (doble palanca de primera clase) que al de nuestros actuales cascanueces (doble palanca de segunda clase). <<

^[49] Se trata de un caso particular del «paralelogramo de las velocidades» que ya quedó tratado en la cuestión 1. <<

^[50] Se refiere a los «dos movimientos» que ya mencionó antes y que nacen del punto transportado desde un vértice del rombo. <<

^[51] Tenemos aquí el conocidísimo problema de la «rueda de Aristóteles», especialmente interesante por la agudeza matemática que se revela en su planteamiento. En su History of Greek Mathematics, HEATH indica que Herón en el capítulo 7 de su Mecánica —obra que se nos ha conservado sólo en árabe— intenta explicar la aporía de la rueda de Aristóteles. La explicación de Herón, dice HEATH, es que en el caso de que el círculo mayor ruede una distancia determinada, el círculo menor mantiene la misma velocidad que el mayor porque se dan dos movimientos; si consideramos el círculo menor como sujeto al mayor y sin movimiento giratorio, al desplazarse el mayor sobre su circunferencia desplazará también linealmente el centro común, y esa distancia será igual al desarrollo de la rotación del mayor y del menor independientemente de que el menor haya rodado o no. La solución completa del problema, en todo caso, no fue hallada sino por Galileo y publicada en 1638 en los Diálogos referentes a dos nuevas ciencias. Galileo estudia la cuestión observando lo que sucede con polígonos semejantes y situados semejantemente. La descripción y el estudio detallado tanto del problema aristotélico como de la solución de Galileo aparecen en HEATH, Mathematics in Aristotle, págs. 246-252. <<

^[52] Esas líneas serían iguales a la distancia recorrida por un círculo que hubiera cumplido un giro de 360°, es decir, iguales a la longitud de la circunferencia correspondiente. <<

^[53] ARISTÓTELES en Sobre las líneas indivisibles (970a6) y en Metafísica (1052b33) se sirve de la «línea de un pie» (podiaía) para ejemplificar una longitud. <<

^[54] HETT anota: «El aserto de Aristóteles es correcto, aunque está curiosamente expresado. Círculos concéntricos unidos tienen la misma velocidad angular, pero ruedas dentadas desiguales tienen velocidades angulares distintas». <<

^[55] «Musical y blanco» son predicados que se dan unidos por accidente: Aristóteles emplea el mismo ejemplo de lo que aparece unido accidentalmente en Metafísica VI 2 1026b. En ese pasaje afirma que «no es posible estudio alguno sobre lo que es accidentalmente» y que «Los razonamientos de los sofistas tratan… más que nada acerca del accidente». En este caso, pretende el tratadista, tener en cuenta que los círculos tienen el mismo centro es considerar un aspecto accidental de la cuestión. <<

^[56] El pie equivalía a 0,296 cm; el codo del que se habla a continuación equivalía a un pie y medio, o sea, 0,444 cm. Esas equivalencias nos dan para los lechos un tamaño standard de algo más de 1,776 m. por 0,888. <<

^[57] En ísois en el original griego: hay que entender que se refiere a paralelogramos iguales, en los que el ángulo externo es igual al interno y opuesto del mismo lado. <<

^[58] Editores y traductores coinciden en reconocer la corrupción textual en este último párrafo. Para el último aserto, cf. EUCL., El. I 20. <<

^[59] V. Cuestión 1. <<

^[60] «Perpendicular a la tierra», se entiende. <<

^[61] HEATH considera acertadas las consideraciones expuestas y admite, siguiendo a CAPPELLE, que el autor nos ofrece una intuición del principio de inercia. <<

^[62] El principio que le falta al tratadista es el conocimiento de la ley de la gravedad. <<

^[63] Es decir, «a los objetos muy pequeños y a los muy grandes». <<

^[64] «El círculo menor». <<

^[65] Entiéndase «en el mismo círculo». <<

^[66] Las explicaciones que se ofrecen, basadas en los principios expresados al comienzo de la obra, no son acertadas, y la dinámica de fluidos es una de las ramas más complejas de la física. Si en otros pasajes, como en la «rueda de Aristóteles», había que destacar la finura de análisis para percibir los problemas, lo que aquí deja sorprendido al lector es el atrevimiento intelectual que impulsaba a estos primeros tratadistas a intentar explicar de modo racional cualquier fenómeno que llamara su atención. <<

^[1] Dictionnaire historique de la terminologie optique des grecs.- Douze siècles de dialogues avec la lumière, París, 1964. <<

^[2] Definitiones, ed. cit., págs. 102-108. <<

^[3] La óptica «homónima con la general» es, evidentemente, la que se ocupa de las materias que acaba de enumerar. <<

^[4] Los diez libros de Arquitectura, VII Prefacio, 10-11. <<

^[5] Ésta es la razón por la que he preferido no incluir la traducción de la Opticorum recensio Theonis en este trabajo, considerando que el matemático interesado en estos temas preferirá vérselas con el texto más fielmente conservado, mientras que el filólogo no tendrá empacho en recurrir a los originales. <<

^[6] LEJEUNE, Euclide et Ptolémée…, pág. 10. <<

^[7] Papo, en el exordio al libro VI de su Colección (Synagogé), menciona un grupo de escritos cuyo conocimiento es indispensable a quienes, ya formados en los Elementos, desean aplicarse a la astronomía. Puesto que son necesarios para comprender la Sýntaxis (Composición matemática) de Ptolomeo, reciben el nombre de Pequeña colección astronómica (Mikròs astronomoúmenos, en contraposición a la Megále sýntaxis de Ptolomeo); no sabemos con certeza qué obras la compusieron —entre otras razones, porque pudieron variar con las épocas— pero parece que, junto con una serie de tratados astronómicos, figuraban en ella la Óptica y la Catóptrica de Euclides (LORIA, Le scienze esatte nell’antica Grecia, págs. 494 y 495). <<

^[8] A este respecto pueden consultarse los trabajos de LEJEUNE, LINDBERG y THEISEN citados en la bibliografía. <<

^[9] Sobre esta Academia de fundación real puede consultarse la obra de J. Rey Pastor, Los matemáticos españoles del siglo XVI, Madrid, 1938. Este trabajo ha sido puesto al día y ampliado mediante abundantes referencias bibliográficas en la obra que lleva por título Institución de la Academia Real Mathematica (Madrid, 1995) de J. SIMÓN DÍAZ y L. CERVERA VERA, quienes han editado en facsímil y con estudios preliminares el documento en el que J. de Herrera, inspirador y miembro eminente de la Academia, explícita el plan de estudios de la misma. <<

^[1] A pesar de que la denominación hóroi («definiciones») aparece en todos los manuscritos se trata más bien de postulados o lemas. <<

^[2] Interpreto el pasaje de un modo literal y coincido en ello con HEATH (A History…, vol I, págs. 441-2). VER EECKE, sin embargo, traduce «se propagan con divergencia en las grandes magnitudes», y anota que «en la concepción euclidiana los rayos visuales brotan del ojo y se propagan en líneas rectas que divergen de modo que comprendan en su ángulo la magnitud vista». Efectivamente, ésa es la concepción euclidiana, como se desprende de la Definición 2; a mi entender, sin embargo, eso no se dice en la Definición 1. Cabe también que nos planteemos si no se habrá producido una alteración textual. <<

^[3] El hecho es cierto, pero no en razón de fenómenos ópticos, sino por razones de orden fisiológico. <<

^[4] En el original, anisoplatê, «de anchuras distintas»; ése es el único valor que da a la expresión el diccionario griego inglés de LIDDELL-SCOTT e igualmente el de Rodríguez Adrados; el diccionario de Mugler no recoge la palabra; a la vista de la ilustración, sin embargo, entiendo que ése es el significado que hay que dar al término —VER EECKE ofrece esa misma explicación en nota— mientras que la traducción etimológica del mismo deja la frase incomprensible; de ahí que prefiera apartarme de versiones anteriores y hacer el texto comprensible al lector actual. Obsérvese que nos encontramos aquí ante una de las proposiciones fundamentales en perspectiva, la de la coincidencia aparente de las paralelas en la distancia. <<

^[5] No se demuestra que esas dos rectas sean iguales; VER EECKE anota que puede demostrarse sin recurrir a otra figura prolongando ΘΒ y ΚΓ hasta el diámetro paralelo a ΑΔ; teniendo en cuenta que ΘΒ y ΚΓ son equidistantes del centro de la recta ΑΔ, serían también equidistantes del centro y por tanto las prolongaciones mencionadas serían semicuerdas iguales; restándoles la parte igual comprendida entre ΑΔ y el diámetro paralelo a ella, resulta que también ΘΒ y ΚΓ son iguales. <<

^[6] Según HEATH (A History…, vol. I, pág. 442) esta proposición prueba el equivalente del hecho siguiente: si α, β son dos ángulos y se cumple que α < β < ½ π, entonces ig α/tg β < α/β; en fecha algo posterior Aristarco asumiría la fórmula sin prueba. <<

^[7] Euclides emplea el término enalláx, definido en Elementos V, def. 12: «razón enalláx es la relación del antecedente al antecedente y del consecuente al consecuente». Repetidamente se ha señalado que tal definición conviene mejor a una proporción que a una razón; en todo caso, para nuestra traducción hemos aceptado la versión sugerida por CH. MUGLER, Dictionnaire…, artíc. lógos. <<

^[8] En el original, synthénti. Euclides define la sýnthesis lógou en Elementos V, def. 14: «La composición de una razón consiste en tomar el antecedente más el consecuente como uno en relación con el consecuente». Es decir, en la transformación de a/b :: c/d en (a + b)/b :: (c + d)/d. <<

^[9] Ver Eecke considera este corolario carente de sentido y lo tiene por interpolación de un escoliasta. Las implicaciones de esta proposición —y de las siguientes 11, 12, 13 y 14— con la perspectiva están emparentadas con las de la proposición 6. <<

^[10] El teorema se limita a demostrar que los puntos A, Γ, E son comunes a dos planos; de ello el lector deduce que están en línea recta y con ello queda reducido el planteamiento de la hipótesis al caso tratado en la proposición 10. <<

^[11] Por el mismo sistema que en la proposición anterior, el caso queda reducido al tratado anteriormente en la proposición 11. <<

^[12] Evidentemente, tal y como se plantean las proposiciones 15 y 16, parecen estar tratando un problema de perspectiva, a saber: la variación de la apariencia según el punto de vista del observador. Desde el punto de vista geométrico lo razonable hubiera sido comparar la diferencia de tamaño entre las magnitudes según que esa diferencia de tamaño estuviera dispuesta en dirección hacia el ojo o en dirección opuesta al mismo. En 15 —el caso de que la diferencia de tamaño entre los objetos estuviera en dirección al ojo— podemos resolverlo por aplicación de la definición 4: al acercarse el ojo a los objetos se ven bajo un ángulo mayor no sólo los objetos, sino también la diferencia de tamaño entre los mismos, con lo que la proposición resultaría ser un caso particular de la propos. 2.

En 16 —el caso de que la diferencia de tamaño entre los objetos estuviese en dirección opuesta al ojo— se llega a la solución mediante comparación de triángulos semejantes. <<

^[13] Ver Eecke hace notar que para que esto se cumpla el ojo ha de moverse por una línea recta que sea perpendicular a la magnitud. <<

^[14] Sobreentiéndase «el rayo de sol». <<

^[15] Catóptrica, proposición 1. Esta frase hizo pensar durante una época que la Catóptrica euclidiana había sido compuesta antes que la Óptica y así, en algunas ediciones, como la de Basilea de 1537, la Catóptrica precede a la Óptica. Hoy más bien consideramos que se trata de una glosa marginal que en algún momento de la transmisión manuscrita fue incluida en el texto. <<

^[16] En principio, la expresión periphéreia (o periphéreia kýklou) pueden designar tanto la «circunferencia» propiamente dicha como un «arco de circunferencia»; la demostración aquí, como podemos ver por la ilustración y, como se deduce de la última frase, se refiere a un arco de circunferencia. <<

^[17] Al final de la proposición se detecta una laguna que, de momento, ningún estudioso se ha atrevido a colmar y que afecta a la parte final del razonamiento. Para VER EECKE, la demostración se continuaba con la consideración de que la disminución aparente de los rayos sucesivos equivale a las sucesivas retracciones de los puntos Δ, E, Z, etc., lo que produciría el enderezamiento aparente del arco hasta transformarse en una recta perpendicular al rayo visual AZ. <<

^[18] Sobre el diámetro, se entiende. <<

^[19] Este pasaje más que una demostración alternativa es un comentario a la proposición anterior; un editor más crítico probablemente hubiera relegado esta parte del texto a un apéndice. <<

^[20] La insuficiencia del razonamiento es evidente: el hecho de que los objetos no se vean enteros explicaría que no se vea una circunferencia entera pero no explica ni demuestra que haya de verse como una recta. Este segundo «De otra manera», al igual que el anterior, se podría también relegar a un apéndice. <<

^[21] La mayor parte de los manuscritos de la versión latina medieval de la Óptica incluyen entre esta proposición y la anterior dos demostraciones que no se nos han transmitido en la versión griega. Las incluyo aquí por dos razones: la primera, de orden filológico, es que el hecho de que aparezcan en la mayor parte de los manuscritos hace que representen una sólida tradición en la historia del texto; la segunda razón, relacionada con el contenido, es que en ellas aparecen demostraciones que más adelante se dan por supuestas. Para la traducción me he basado en el texto publicado por W. R. THEISEN en «Líber De Visu: The greco-latin translation of Euclid’s Optics» (cf. bibliografía).

Del Líber de Visu (Theisen 24):

Si se coloca una circunferencia en el mismo plano en que está el ojo no se ve la semicircunferencia entera.

Si BZG fuera un semicírculo, puesto que B y DG serían rectas tangentes al círculo, una y otra formarían un ángulo recto con el diámetro BG, según el 17 del Tercero de Euclides.

Luego el triángulo BDG tendrá dos ángulos rectos, lo cual es imposible.

Del Liber de Visu (Theisen 25):

El rayo más largo que llega a una esfera será como una recta tangente.

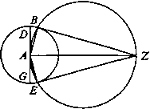
Sea DG una esfera vista por el ojo Z con centro en A) y a distancia del ojo; prolongada una recta desde el centro de la esfera hasta el ojo, dibújese un círculo, y sea la recta AZ el diámetro del círculo y avancen los rayos ZE, ZB a los puntos de corte de los círculos. Digo que éstos son más largos que los que no son tangentes a la esfera.

Así, prolónguense los radios de la esfera hasta los extremos de los rayos tangentes y formen dos ángulos rectos con los rayos aplicados. Así, cada uno de los ángulos está inscrito en un semicírculo. Luego las rectas aplicadas a la circunferencia serán tangentes a ella puesto que forman ángulos rectos con las líneas trazadas desde el centro. Luego, prolongadas, no serán secantes al círculo. Pues si cayeran dentro, sería contra la cola del pavo. Pero si estuviera fuera, puesto que las dos, etcétera. Luego si llegara un rayo más largo ocurriría que dos líneas rectas comprenderían una superficie, lo cual es imposible.

Luego queda que las dos rectas más largas son tangentes.

Respecto al texto de esta segunda demostración hay que señalar que la frase «Pues si cayera dentro sería contra la cola del pavo» aparece en el manuscrito más fiable sólo como glosa marginal. <<

^[22] VER EECKE anota que en los Elementos no aparece ninguna proposición en la que se demuestre que la sección de la esfera es un círculo, aunque tal demostración se nos ofrece, subsidiariamente, en XII 17. La demostración particular, indica, no la encontraremos hasta las Esféricas de TEODOSIO (algo anteriores al final del siglo I d. C.). <<

^[23] Formando ángulos rectos «con los extremos del diámetro del circulo», se entiende a partir de la figura. <<

^[24] Heiberg objeta la contradicción entre el enunciado «visto de cualquier manera» y el desarrollo de la demostración, con el ojo situado «en el mismo plano que la base ΒΓ del cilindro»; Ver Eecke, sin embargo, no da importancia a la contradicción y aduce que la demostración seria la misma si consideráramos el ojo situado en un plano paralelo a la base del cilindro. <<

^[25] En el que debemos situar el ojo. <<

^[26] Se refiere a los ángulos ZBA y ZEA (Elem. III 18). <<

^[27] Esta demostración es la que presenta la Opticorum recensio de Teón. En ambas versiones ha desaparecido la consideración de que el ojo debe estar situado en el mismo plano que la base. Cf. prop. 27 y n. El último párrafo es probablemente un añadido tardío. <<

^[28] Es decir, o bien con el plano de la base del cilindro, si suponemos el ojo situado en ella, o bien con el plano determinado por los rayos visuales que inciden en el cilindro. <<

^[29] Heiberg considera sospechoso el pasaje entre corchetes, que, como puede verse, resulta contradictorio con el enunciado de la proposición y carece de nexo con lo inmediatamente anterior. <<

^[30] Sobreentiéndase «con los diámetros». <<

^[31] «Con ΓΝ y con ΓΕ», se entiende. <<

^[32] Sobreentiéndase «cumple esa condición». <<

^[33] Se entiende que todas esas rectas forman ángulos iguales «con la recta ab cuando ésta se desplaza sobre la circunferencia βδ en posición paralela a la suya primitiva». VER EECKE sugiere que podríamos encontrarnos ante un texto lacunoso y que en este punto debería añadirse que, por tanto, el ángulo ΑΓΒ permanecerá constante y que una magnitud vista bajo ese ángulo constante parecerá siempre igual. <<

^[34] Entiéndase «y que forman un ángulo con la recta que representa la magnitud vista que se traslada sobre la circunferencia». <<

^[35] VER EECKE indica que AZ se construye como antiparalela de ΔΒ respecto al ángulo con vértice en Γ. Dos rectas son antiparalelas respecto a una tercera cuando, sin ser paralelas, forman ángulos iguales con ella (como en el caso de los lados iguales de un triángulo isósceles respecto a la base) y son antiparalelas respecto a un ángulo cuando ambas lo subtienden y forman ángulos iguales con las dos rectas que forman el ángulo. Las antiparalelas no aparecen descritas, usadas ni tratadas en los Elementos, si bien HEATH en su comentario las emplea como recurso para ampliar la demostración de VI 12. A juzgar por el uso que se hace aquí de la antiparalela, parece que se conocían sus propiedades, aunque no exista para ella ninguna denominación específica (de hecho, la palabra griega antiparállelos no se nos ha conservado en ningún texto de carácter matemático, sino sólo como término técnico de métrica). <<

^[36] Es decir, «en la más cercana a E». <<

^[37] Se refiere a «la línea recta sobre la que se desplaza el ojo». <<

^[38] El texto griego emplea el término koinôs; literalmente traducido diríamos «que ocupan en común determinados lugares». Prefiero la versión más libre en beneficio de la claridad. <<

^[39] Sobreentiéndase «el ojo». <<

^[40] Sobreentiéndase como sujeto «el sector ΓΖΔ». <<

^[41] Desde este punto y hasta «el teorema 31 del libro tercero de los planos» da la impresión de ser una glosa marginal que se ha introducido en el texto. De hecho, la demostración puede seguirse perfectamente sin tales referencias a los Elementos. Esta opinión fue ya expresada por Weissenborn, pero Heiberg no la admite en su edición, sino que la relega al aparato crítico. <<

^[42] El texto corrupto de este último párrafo se refiere a la primera parte de la demostración contenida en 44, es decir, a los casos en que «las magnitudes iguales y que ocupan determinados lugares en posición contigua parecen iguales». Por el estado del texto no podemos discernir si ofrecía una demostración alternativa a la de 44 o si se limitaba a repetir la conclusión. <<

^[43] VER EECKE indica que hay que entender que la nueva posición del ojo H se encuentra en el mismo plano ΒΕΔ al que son perpendiculares AB y ΓΔ. <<

^[44] Tomando como referencia el triángulo ΑΘΗ. <<

^[45] La traducción literal del enunciado «Hay ciertos lugares en los cuales, si se pone el ojo, las magnitudes desiguales sumadas en la misma parecerán iguales a cada una de las desiguales» lo hubiera dejado prácticamente incomprensible; de ahí que haya preferido en mi versión resolver el anacoluto del texto griego mejor que respetarlo. <<

^[46] Con relación a la paralela a la recta primera trazada por el ojo. <<

^[47] Llama la atención en esta proposición la referencia a esta recta ΜΛ que, una vez trazada, no vuelve a mencionarse ni a emplearse en el razonamiento. A la vista del texto y de la ilustración, entiendo que cabe la sospecha de algún género de corrupción textual. El elevado número de variantes, raspados, añadidos y sobreeseritos que menciona el aparato crítico de HEIBERG refuerza aún más la sospecha. <<

^[48] Los manuscritos presentan la lectura N, que es evidentemente errónea; adopto la corrección Ξ propuesta por WEISSENBORN. <<

^[49] El texto griego presenta una laguna en todos los manuscritos. <<

^[50] Esta proposición, al igual que la siguiente han sido consideradas sospechosas de ser un añadido. <<

^[51] Para VER EECKE no hay demostración y, además, entra en contradicción con la proposición 22 si suponemos que el ojo está en el mismo plano. Si supusiéramos el ojo situado más arriba o más abajo daría lugar a diversas ilusiones visuales. <<

^[52] Sobreentiéndase «con el plano del cuadrado». <<

^[1] Según ese procedimiento, el punto imagen se localiza en la intersección del rayo visual incidente con la perpendicular trazada del objeto al espejo. La ley es inexacta, pero permitió importantes avances, especialmente en lo relativo al funcionamiento de los espejos planos. Este principio mantuvo su vigencia durante toda la Antigüedad y la Edad Media y, a pesar de ser varios los autores en el siglo XVII que percibieron el error experimentalmente, siguió siendo aceptado hasta principios del XVIII. No sabemos con certeza si su descubrimiento se debe a Arquímedes o a algún otro científico perteneciente a la época que media entre la Catóptrica euclidiana y la de Herón. <<

^[2] En una de sus cartas escribe: «Arguyes que la Catóptrica de Euclides es espuria: erróneamente, a mi juicio. Las palabras claras, nítidas, finas, incluso bien compuestas, las demostraciones rotundas y breves, cuidadosa la distinción entre los supuestos y lo demostrado a partir de los supuestos. Además no es, como dices, torpe error ver qué se sigue a partir de un supuesto falso, sino que asumir algo falso es confesión de la oscuridad de la naturaleza o, si fuera error, desde luego no es increíble en Euclides, que filosofa sobre los rayos visuales de acuerdo con su tiempo, para las entendederas de los hombres aquéllos» (Texto aportado por HEIBERG, Literargeschichtliche Studien…, pág. 90). <<

^[3] Literargeschichtliche Studien…, pág. 152. V. también Geschichte…, págs. 77 y 78. <<

^[4] Cf. introducción a la Óptica, nota 19. <<

^[5] PTOLOMEO, Óptica 88, 9-19. Tomo la referencia de LEJEUNE, op. cit., pág. 33. <<

^[6] Contradicciones encontramos entre los teoremas 9 y 19; entre los teoremas 10 y 20 o entre los teoremas 12 y 28. Como ejemplo de repetición tenemos el de las proposiciones 5 y 24: ambas estudian el caso del ojo puesto en el centro de la esfera de un espejo cóncavo. <<

^[1] El título «Definiciones» no figura en los manuscritos, sino que fue puesto por el editor. Como en la Óptica, no tienen carácter de definiciones, sino que en ellas se mezclan los axiomas con las observaciones tomadas de la realidad. <<

^[2] La definición de recta que se nos ofrece no es la euclidiana (Elementos I 4), sino la platónica (Parménides 137 e) ligeramente modificada: el plural sustituye al dual, el indicativo al subjuntivo, el tardío epiprosthéoa la expresión adverbial epíprosthen eînai. <<

^[3] El aserto es una aplicación de la semejanza de triángulos —basta sustituir «espejo» por «plano de referencia» en el texto para comprobarlo— y presupone la igualdad de los ángulos de incidencia y reflexión, a pesar de que esta ley básica no se nos presenta como un axioma, presupuesto o postulado, sino como deducción probada en la primera proposición. <<

^[4] En su nota a este pasaje VER EECKE afirma: «es decir, que la imagen de un objeto no será vista en la propia superficie del espejo, sino más allá de esta superficie, a determinada profundidad sobre la perpendicular trazada del objeto hacia la superficie del espejo». Efectivamente eso es lo que sucede, pero no veo base ni apoyo alguno para interpretar de ese modo el texto euclidiano. <<

^[5] Sobreentiéndase «la recta». <<

^[6] Aparece junto con las otras definiciones, pero en realidad es un fenómeno observable. Es, además, la única referencia en esta obra al fenómeno de la refracción (aún sin nombre en este estadio de la ciencia griega). Según afirma OLIMPIODORO en sus Comentarios a la Meteorología de Aristóteles este hecho fue demostrado por Arquímedes. La refracción no aparece estudiada con cierta amplitud en el mundo griego hasta las obras de Ptolomeo, en el siglo π de nuestra era, y las principales leyes concernientes a este fenómeno no serían formuladas hasta el siglo XVII. <<

^[7] El fenómeno de la «reflexión» y su efecto, «el rayo reflejado», reciben en griego el nombre único de anáklasis; el verbo correspondiente, que aparece aquí por primera vez, es anakláomai. <<

^[8] En los tratados matemáticos griegos, la referencia a un ángulo suele hacerse bien mediante la mención de su vértice (he A, he pròs tôi A). En la Catóptrica es frecuente que aparezca otra forma más, en expresiones del tipo he A, B: en estos casos suele referirse a un ángulo que es suma de los dos cuyo vértice se menciona. Traduzco la expresión, cuando aparece, como «el ángulo suma de A, B».

Encontramos aquí considerado por primera vez el ángulo formado por una circunferencia y su tangente, al que los griegos denominaban keratoeidés (lit., «en forma de cuerno»), de acuerdo con la clasificación de los ángulos transmitida por Proclo. Euclides se ocupa de él en algunas ocasiones y en Elementos III 16 lo considera menor que cualquier ángulo agudo rectilíneo. Actualmente se le denomina ángulo de contingencia y se le considera nulo. En relación con esta cuestión geométrica puede verse el comentario de HEATH a Elementos I, Def. 8 y 9 (The Thirteen Books of the Elements, vol. I, págs. 176-178), y a las proposiciones I 5 (ibid., vol. I, págs. 252-254) y a III 16 (ibid., vol. II, págs. 39 y ss.), así como, de ese mismo autor, A History of Greek Mathematics, vol. I, págs. 178-179. <<

^[9] Entiendo que la figura que ofrece HEIBERG es errónea. <<

^[10] El ángulo de un semicírculo (hemikyklíou gonía) es el que forma un diámetro con la circunferencia a la que pertenece. Euclides (III 16) lo considera mayor que cualquier ángulo agudo rectilíneo. Para más información sobre esta cuestión geométrica puede recurrirse a los lugares citados más arriba, nota 8. <<

^[11] Como el lector ha podido ya observar, el enunciado de esta proposición es contradictorio con el de la anterior. <<

^[12] Los textos euclídeos utilizan el término periféreia para designar tanto la «circunferencia» como el «arco de circunferencia»; el castellano sí suele distinguir; por eso he preferido optar entre ambos ateniéndome al contexto. <<

^[13] VER EECKE anota que para que tal cosa se cumpla han de estar dispuestas oblicuas o paralelas al espejo, pero no perpendiculares. La figura, como hace notar el mismo autor, es errónea. <<

^[14] La figura, como afirma VER EECKE, es errónea. <<

^[15] Sobreentiéndase «sean ΒΓ, BA». <<

^[16] La figura, afirma VER EECKE, es errónea. <<

^[17] Tomamos la lectura hórois del manuscrito m. <<

^[18] Cf. Def. 1 y nota. <<

^[19] Como en la proposición 16, preferimos la lectura hórois del manuscrito m. <<

^[20] Como en las proposiciones 16 y 17, preferimos la lectura hórois del manuscrito m. <<

^[21] VER EECKE afirma que esta proposición y las dos siguientes son falsas desde el punto de vista de la anatomía. La proposición 26, además, está probada de modo incorrecto. <<

^[1] S. SAMBURSKY, El mundo físico de los griegos, pág. 73. <<

^[2] Sí podían saber cuándo cabía que se produjera un eclipse de sol, habida cuenta de las posiciones del sol y la luna, pero no podían predecirlos con exactitud porque para ello hubieran necesitado conocer, entre otras cosas, los tamaños auténticos de la tierra, el sol y la luna, y no disponían de esos datos. <<

^[3] La fama de buenos astrónomos que acompañaba a los caldeos llevó a exageraciones como la de Simplicio, que afirma que los babilonios disponían de observaciones de las estrellas a lo largo de 1.444.000 años. Más verosímil es la afirmación de Ptolomeo de que los babilonios disponían de observaciones sistemáticas ininterrumpidas desde el reinado de Nabonasar (747-735 a. C.). <<

^[4] Cf. L. GIL, «Ex Aegypto lux: II. 22, 25-32», Quaderni Urbinati di Cultura Classica, N. S. 61 (1999), 35-42. <<

^[5] No cabe pensar que pudo hacer tal predicción sin contar previamente con tablas astronómicas. Como en esta época los griegos no disponían de colecciones de observaciones, es de suponer que se apoyó en materiales babilonios. En cuanto a la veracidad de la anécdota, como hemos indicado algo más atrás, ni Siquiera los babilonios estuvieron en situación de predecir, stricto sensu, los eclipses de sol, sino, simplemente, avisar de cuándo podía producirse. Hace ya más de un siglo que los astrónomos y los historiadores de la ciencia coinciden en afirmar que el acierto en la predicción, si en efecto se produjo, fue en parte fruto del azar. <<

^[6] Aristóteles describe así las opiniones de los pitagóricos: «la mayoría de los que afirman que el cielo es limitado dicen que (la tierra) se halla en el centro, pero los llamados pitagóricos, de Italia, se manifiestan en contra: en efecto, afirman que en el centro hay fuego, y que la tierra, que es uno de los astros, al desplazarse en círculo alrededor del centro, produce la noche y el día. Además postulan otra tierra opuesta a ésta, que designan con el nombre de Antitierra, no buscando argumentos y causas conformes a las apariencias, sino forzando las apariencias e intentando compaginarlas con ciertos argumentos y opiniones suyos» (Acerca del cielo II 13, 293a18-26; en el libro II de este escrito trata diversas cuestiones de detalle sobre la cosmografía pitagórica). Citamos la traducción de M. CANDEL en esta misma colección, vol. 229. <<

^[7] Platón se refiere a la astronomía en Timeo 30c-40d (donde se contiene la exposición más completa de sus puntos de vista astronómicos), República X 614b-621d y Leyes VII 821b-822c. Al leer esos textos hemos de tener presente que no se trata de textos puramente científicos, sino literarios, y que en ellos aparecen elementos poéticos y mitológicos que, formando parte del pensamiento platónico, no pretenden ofrecer ni una visión general ni una presentación ordenada de los conocimientos científicos de la época. <<

^[8] La cuestión se había suscitado ya entre los astrónomos babilonios en el sentido de encontrar un período que contuviera simultáneamente un número completo de días (revoluciones de la esfera de las fijas), meses (revoluciones lunares) y años (revoluciones solares). El interés del asunto radica en que el cómputo lunar, al no coincidir con el cómputo solar, hace que en poco tiempo el calendario se desajuste y los mismos meses lunares dejen de pertenecer a las mismas estaciones del año. El lector interesado encontrará el asunto expuesto de modo claro y detallado en GEMINO, Introducción a los fenómenos, cap. VIII, publicado en esta misma colección, vol. 178. <<

^[9] HEATH, Greek Astronomy, págs. XLVI-XLVII. Las aportaciones del Estagirita aparecen dispersas en sus tratados, pero la Física, el Sobre el cielo y la Metafísica son las obras en las que más referencias a este asunto encontramos. <<

^[10] Esto es, en brevísimo resumen, lo que Aristóteles sostiene en el Acerca del cielo, pero se ha de recordar que los puntos de vista aristotélicos sobre los movimientos celestes variaron a lo largo de su vida. Puede consultarse la Introducción a ese tratado preparada por M. CANDEL para esta misma colección (núm. 229) y la bibliografía que allí se menciona. <<

^[11] Cf. S. SAMBURSKY, El mundo físico de los griegos, págs. 84-85. <<

^[12] Aunque lo que en nuestro tiempo ha concedido su renombre a Aristarco haya sido la anticipación del sistema copernicano, sólo conocemos esa hipótesis suya por una referencia de Arquímedes; de su obra poseemos nada más un breve tratado Sobre los tamaños y las distancias del Sol y la Luna. <<

^[13] Recientemente se ha comprobado que los dos libros son, en realidad, dos redacciones distintas de un único tratado original. <<

^[14] J. B. J. DELAMBRE, Histoire de l’astronomie ancienne, tomo I, pág. 56. <<

^[15] O. NEUGEBAUER, History of the Ancient Mathematical Astronomy, vol. II, pág. 749. <<

^[16] G. LORIA, Le scienze esatte nell’antica Grecia, pág. 503. <<

^[17] La crítica de NEUGEBAUER es mucho más tajante, pero menos argumentada: «Se ha desplegado mucha ingenuidad para establecer los contenidos de una “esférica” preeuclidiana…; sugerir como autor a Eudoxo no hace sino más endeble el argumento… No niego que es bastante obvio que los de Euclides y Autólico no fueron los primeros estudios de geometría esférica, pero me parece inútil postular la existencia de una obra precisa… Creo que ya es hora de olvidar la búsqueda de precedentes.» <<

^[18] Geschichte…, pág. 54. En sus Literargeschichtliche Studien…, págs. 41-51, hace hincapié sobre todo en el estudio de los paralelismos con Autólico y cuestiones relacionadas con la pureza del texto. <<

^[19] HAMA, vol. 2, págs. 706-33. <<

^[20] PAPO, Synagogé VI, págs. 598, 21 y ss. El uso de esta y otras citas de Papo como argumento en la tarea de fijación del texto de los Fenómenos puede verse en HEIBERG, Literargeschichtliche Studien…, págs. 46-50. <<

^[21] V. Introducción a la Óptica, pág. 132. <<

^[22] Cf. BERGGREN y THOMAS, op. cit., págs. 11-12. <<

^[23] La primera, la edición príncipe de Euclides (Venecia, 1505) en la versión latina de Zamberti; medio siglo después (Mesina, 1558) aparecieron los Fenómenos junto con las obras de esférica de Teodosio, Menelao y Autólico en la versión de Maurólico; la tercera versión latina fue la de Auria (Roma, 1591); Dasypodius editó en Estrasburgo (1571) su Euclidis omnes omnium librorum propositiones, en el que aparecían los enunciados en griego y latín. <<

^[24] Entre esos manuscritos el más destacado es el Vaticanus graecus 204. <<

^[25] El Vindobonense XXXI, 13, de gran importancia también para el texto de la Óptica. <<

^[1] El texto que antecede a las proposiciones, que carece de títulos o subtítulos en los manuscritos, es quizá, como señalábamos en la Introducción, de diferente autor que los enunciados y demostraciones. Los subtítulos que introducimos tienen el propósito de facilitar al lector la comprensión y desvelar lo que consideramos la intención de este excurso previo. De acuerdo con Aristóteles, Analíticos Posteriores 71b9-72a38, especialmente 72a15-72a24, existen dos clases de premisas últimas en toda ciencia: los axiomas (axiómata), que contienen principios usados en las demostraciones de todas las ciencias, y los supuestos (théseis) o principios propios de cada ciencia determinada, que se subdividen a su vez en presupuestos (hypothéseis), que, ante dos alternativas, admiten una como cierta, y definiciones (horismoí). Relacionando esas opiniones aristotélicas con el hecho de que en este excurso previo, efectivamente, la primera parte comienza sus asertos con un thetéon («hay que suponer») y se continúa con una serie de definiciones, hemos optado por incluir los subtítulos que aparecen. <<

^[2] En contraposición con las estrellas «errantes» (planetai, de donde el español «planetas»), las «no errantes» (aplaneîs) guardan la misma posición relativa en la bóveda celeste. <<

^[3] Al mencionar los levantes y ponientes se refiere a la aparición y desaparición de los astros cuando alcanzan el horizonte. <<

^[4] La vista sólo dista lo mismo de cualquier punto de la circunferencia si está situada en su centro o se cumplen las condiciones expresadas en Óptica, prop. 34, 35 y lema y 36.; pero en este tratado se supone, de acuerdo con la hipótesis astronómica de origen pitagórico, que el mundo tiene forma esférica y que la tierra ocupa el centro de tal esfera (cf. Prop. 1), por lo que sospechamos que aquí se haya producido alguna interpolación o corrupción del texto. <<

^[5] Según anotan BERGGREN y THOMAS (págs. 48-49 y n.), en época helenística no había ninguna estrella visible que ocupara en efecto el lugar correspondiente al polo celestial del hemisferio norte. Aún así, el nombre de «estrella polar» que recibe hoy αUMi procede, justamente, de que fuera considerada uno de los polos del eje de la esfera celeste. Aunque, al revés que los Elementos, los Fenómenos no presentan unas definiciones completas de los términos que luego emplean en sentido técnico, en el De sphaera, de AUTÓLICO (ed. MOGENET, pág. 195, líns. 9-11) leemos que «Eje de la esfera es el diámetro de la esfera sobre el cual, inmóvil, la esfera gira; polos de la esfera son los extremos del eje». <<

^[6] El redactor de estos presupuestos trabaja siempre en la suposición de que el observador se encuentra en la zona templada del hemisferio norte; los datos fiables que podía manejar eran, desde luego, procedentes de esas latitudes. El círculo ártico que menciona aquí no es el geográfico, sino un círculo celeste cuyas estrellas, para un observador como el descrito, son visibles todo el año. Así se explica que casi siempre se refiera a este círculo como «el mayor de los siempre visibles». Por lo demás, sólo en estos presupuestos y en la prop. 14 se le llama círculo ártico. <<

^[7] En griego, pròs mesembrían, literalmente, «al mediodía». <<

^[8] Es decir, de los arcos que recorre cada astro por encima de la tierra. <<

^[9] Es decir, «el círculo mayor de los siempre visibles». <<

^[10] «Estos» se refiere a «los astros que parecen trasladarse por el círculo mayor de los siempre visibles». <<

^[11] En griego, isemerinós. Preferimos el término «ecuador» frente a versiones más literales como «círculo equinoccial» por entender que de este modo es más fácil emparentarlo con un círculo celeste y no confundirlo con el término geográfico. <<

^[12] En griego, pròs árktous, literalmente, «hacia las Osas». <<

^[13] El Círculo de Leche o Vía Láctea se menciona únicamente aquí y el autor no llega a definirlo ni a especificar su naturaleza. ARATO (Fenómenos, 278-9 y 511, escrito entre 276 y 274 a. C.) considera que la Vía Láctea es otro de los círculos máximos, junto con el ecuador y la eclíptica. Aunque Arato no pueda ser considerado una fuente científica, puesto que su obra debe ser encuadrada en el género de la écfrasis o descripción literaria, resultaría difícil de creer que hubiera incluido en su obra asertos considerados erróneos por los científicos de su época. <<

^[14] Ho zoidiakós (kýklos) y ho tôn zoidíon kýklos son los nombres que se dan a lo largo de la obra al círculo del zodíaco, que nunca es definido (aunque ya se refiere a una abstracción, y no sólo a la serie de constelaciones). Estas constelaciones están situadas en el firmamento de tal manera que el sol parece ir recorriéndolas en su aparente camino anual alrededor de la tierra. En nuestro tiempo, ese camino aparente del sol recibe el nombre de eclíptica porque ahí es donde se producen los eclipses de sol y de luna. Nada hace pensar, sin embargo, que el autor de los Fenómenos tuviera ese hecho presente. Con toda probabilidad la astronomía antigua contemporánea de Euclides ya tenía observado el fenómeno, pero aún así, la expresión ekleiptikos kýklos no está testimoniada con certeza en griego hasta que en el siglo III d. C. la usa Aquiles Tacio. Por estas razones hemos preferido la traducción «el zodíaco» o «el círculo del zodíaco» aunque se encuentre más alejada de nuestra expresión habitual. <<

^[15] Utilizamos «mundo» para verter el término kósmos: según la tradición griega iniciada por los pitagóricos y seguida por Platón, Eudoxo y Autólico, por mencionar sólo algunos nombres destacados, el kósmos comprende las esferas en que giran las estrellas fijas, la luna, el sol y los planetas con la tierra como centro. <<

^[16] Es decir, una elipse. El término que se emplea en griego y que hemos respetado es el habitual hasta Arquímedes; a partir de Apolonio se utilizará y pasará a las lenguas europeas el de «elipse». <<

^[17] El adverbio homalôs es el término usado para referirse a la velocidad uniforme. Coincide con la terminología de Autólico, quien lo define «Se dice que unos puntos se trasladan uniformemente (homalôs) cuando recorren en igual tiempo magnitudes iguales o semejantes; si, al trasladarse uniformemente un punto sobre una línea recorre dos líneas, guardarán la misma razón el tiempo en que el punto recorre una de las líneas con el tiempo en que recorre la otra y la línea con la línea». (AUTÓLICO, ed. MOGENET, pág. 195, líns. 3-8). <<

^[18] Aparece como término técnico horízon para designar al horizonte; supone una diferencia con el modo de expresión de Autólico, quien habitualmente lo llama kýklos horízon tò te aphanès kaì tò phaneròn hemisphairion tês sphaíras: «el círculo que separa el hemisferio invisible y el visible de la esfera». <<

^[19] «Meridiano» y «trópicos», igual que antes «ecuador» y «círculo ártico» se refieren a círculos celestes, no geográficos. <<

^[20] El texto griego emplea la expresión katà syzygían, de donde procede el término español «sicigia», hoy especializado para designar la conjunción o la oposición entre la luna y el sol. <<

^[21] Los arcos semejantes lo son en sentido geométrico; cf. más arriba, n. 17. <<

^[22] La dioptra es un instrumento para medir a distancia. Lo describe Herón en su tratado Sobre la dioptra. <<

^[23] En griego, polos toû horízontos, es decir, «polo del horizonte». <<

^[24] El pasaje entre corchetes es considerado por Heiberg una interpolación posterior a Papo. En la redacción presente, como vemos, la proposición pretende ofrecemos cinco demostraciones. La primera de ellas es rápidamente solventada con un «ya está demostrado» sin más indicaciones. Como señalamos en la referencia entre corchetes, se puede encontrar la demostración en la obra Sobre la esfera en movimiento, de AUTÓLICO, que se nos ha conservado, aunque también cabría la probabilidad de que Euclides conociera la demostración gracias a algún otro tratado de carácter astronómico o a un tratado de esférica que no conocemos. <<

^[25] Para referirse a los trópicos, Euclides emplea siempre las expresiones que vemos aquí, «trópico de verano» (therinòs tropikós) y «trópico de invierno» (cheimerinòs tropikós), nunca la de «trópico de Cáncer» y sólo una vez (prop. 18) «trópico de Capricornio», que son los nombres que se les dan en los Fenómenos de ARATO, tan próximos en el tiempo a este tratado. <<

^[26] Las letras ΩΒΓ designan aquí al horizonte. <<

^[27] Concluye aquí la segunda de las demostraciones pretendidas «el círculo del zodíaco será dos veces perpendicular al horizonte cuando el polo del horizonte esté entre el trópico de verano y el polo visible». <<

^[28] Es decir, el cénit. <<

^[29] Concluye aquí la tercera de las demostraciones pretendidas; «el círculo del zodíaco nunca será perpendicular al horizonte cuando el polo del horizonte esté entre el trópico de verano y el polo visible». Hasta aquí el lector debía servirse de las dos primeras ilustraciones. Reproducimos las del códice Vaticano gr. 204; el códice Vindobonense XXXI, 13 ofrece una ilustración diferente y errónea. El lector interesado en consultarla puede hacerlo en la edición de HEIBERG y en el trabajo de BERGGREN y THOMAS. A partir de aquí se desarrollan las demostraciones de las tesis que HEIBERG considera interpolación tardía, y que van acompañadas de dos ilustraciones más; el códice a presenta otras ilustraciones también claramente erróneas, que HEIBERG reproduce como parte del aparato crítico. <<

^[30] Euclides emplea la expresión asýmptotón esti, cuyo significado, evidentemente, no coincide aún con el que damos a «asíntota». Apolonio será el primero en usarlo en ese sentido. <<

^[31] Como señalan BERGGREN y THOMAS, esta proposición será de especial utilidad cuando el «círculo máximo» considerado sea el del zodíaco (propos. 9, 14,15). <<

^[32] Literalmente, tà pròs taîs árktois, «los que están junto a las Osas». <<

^[33] Literalmente, tà ástra tà katà diámetron ónta, «los astros que están según el diámetro». <<

^[34] La edición de HEIBERG presenta en el texto griego Σ en este lugar, en vez de Z; en la ilustración y la versión latina figura correctamente. <<

^[35] Sobreentiéndase como sujeto «el punto de contacto del círculo del zodíaco y el trópico de verano». <<

^[36] Como en el pasaje al que se refería la nota anterior, hemos de sobreentender como sujeto «el punto de contacto del círculo del zodíaco y el trópico de verano». <<

^[37] La edición de HEIBERG presenta en el texto griego por errata ΘΔ en lugar de ΘΛ. Las letras están correctamente en la versión latina y la ilustración. <<

^[38] Como un poco más arriba, la edición de Heiberg presenta por errata en el texto griego ΔΖ en lugar de ΛΖ, que aparece correctamente en la versión latina y la ilustración. <<

^[39] El griego emplea aquí el término katenantíon, que está sobradamente testimoniado con el significado de «opuesto»; pero en este contexto se hace evidente a la vista de la figura, que sirve para designar arcos «correspondientes» o «semejantes». <<

^[40] Repetidamente a lo largo de esta proposición se dará al ecuador no el nombre habitual de isemerinós, sino el de mégistos tôn parallélon, particularidad terminológica que hemos respetado. <<

^[41] BERGGREN y THOMAS anotan que este «punto de contacto del círculo oblicuo» lo es con el trópico de Cáncer. Es decir, se trata del punto A en el que coinciden la eclíptica, el trópico de Cáncer y el horizonte. <<

^[42] El sujeto de la frase son «los círculos mayores ΣΦ, TX y el horizonte». <<

^[43] Se interrumpe aquí la demostración de la primera parte del enunciado; se concluirá tras la demostración de la segunda parte. <<

^[44] No aparece un término específico para la «cuerda»; se la menciona con una expresión emparentada con la que suele designar la recta, he apó toû O epì tò Ψ: «la [recta, cuerda] que va de O a Ψ». <<

^[45] MENGE considera interpolación el pasaje entre corchetes cuadrados. BERGGREN y THOMAS consideran que la interpolación viene desde algo más atrás, desde «Y lo mismo se demostrará»; comparto la opinión de estos últimos, pues si el pasaje fuera antiguo esta tesis se habría reflejado también en el enunciado. <<

^[46] Se refiere a los dos cuadrantes de la eclíptica. <<

^[47] Como en 12a, se interrumpe la demostración de la primera parte del enunciado; se concluirá tras finalizar la demostración de la segunda parte. <<

^[48] V. n. 40 a la proposición anterior. <<

^[49] La figura que reproducimos junto a estas líneas. <<

^[50] Por errata aparece A en lugar de Λ en el texto griego de Menge. <<

^[51] La demostración es inmediata a partir de lo ya desarrollado en Prop. 6 y 12. <<

^[52] Este lema aparece como tal en algunos de los mss. de la versión a, y como una más de las demostraciones en otros (V 1 L), mientras que en los mss. de la versión b figura como escolio en los más antiguos y como lema en los más recientes. <<

^[53] Entiéndase «trópico de verano». <<

^[54] Es decir, la afirmación es válida para observaciones realizadas desde la zona templada del hemisferio norte. El nombre «círculo ártico», como dejamos señalado más arriba (cf. n. 6), se usa con mucha menos frecuencia que el de «círculo máximo de los siempre visibles». BERGGREN y THOMAS hacen notar que la situación propuesta en la hipótesis de esta proposición es la más restrictiva de toda la obra, si bien, como hemos hecho notar en otras ocasiones, las latitudes son, aproximadamente, aquéllas para las que los astrónomos de la antigüedad podían tener observaciones fiables. <<

^[55] El texto no indica la localización exacta del punto Y; para BERGGREN y THOMAS indicaría la intersección de ΚΦ y la prolongación de ΡΤΠ. <<

^[56] Aquí concluye el texto de los manuscritos que nos ofrecen la versión a. La versión completa de la proposición 16 y las que le siguen se conservan sólo en los manuscritos de la versión b. <<

^[57] El contenido de la presente proposición se sigue de lo demostrado en 14 y 15. <<

^[58] El contenido que figura entre corchetes es adición de Menge. <<

^[59] Estos arcos iguales deben estar situados en el círculo del zodíaco, como se deduce de la demostración y de los enunciados del resto del tratado. <<

^[60] Al igual que ocurría con la Prop. 16, también la presente se sigue de lo demostrado en 14 y 15. <<

^[61] Naturalmente, al hablar de arcos iguales hay que excluir el caso, suficientemente tratado, de los arcos que distan lo mismo por cada parte del punto de contacto con los trópicos. En el enunciado falta la precisión de que uno de los arcos ha de estar situado más cerca del trópico de verano que el otro, pero esto queda claro más adelante, al describir el caso en los términos que corresponden a la figura. La proposición presenta, a mi entender, algunas dificultades de orden lingüístico y terminológico: es el único lugar del tratado en que aparecen las expresiones he tychoúsa (literalmente «uno cualquiera») y he loipé (literalmente «el restante») para referirse a arcos; se hace difícil captar su significado con exactitud; así lo hacen ver BERGGREN y THOMAS, que silencian el pasaje en su versión. <<

^[62] El aserto, tal y como está expresado, es falso; para admitirlo como válido tendríamos que sobreentender la misma precisión que en el enunciado. Lo mismo sucede con la frase final de la proposición. <<