[DEFINICIONES][1]
1. El rayo visual es una recta cuyas partes medias están to das en línea con los extremos[2].
2. Todos los objetos vistos se ven mediante rectas.
3. Si se coloca un espejo en un plano y se contempla cierta altura que es perpendicular al plano, resulta una proporción en la que la recta que hay entre el espejo y el espectador es a la que hay entre el espejo y la altura perpendicular como la altura del espectador es a la altura perpendicular al plano[3].
4. Si en los espejos planos se ocupa el lugar sobre el que cae la perpendicular desde el objeto visto, ya no se ve el objeto visto[4].
5. Y en los espejos convexos, si se ocupa el lugar por el que se traza[5] desde el objeto visto hacia el centro de la esfera, ya no se ve el objeto visto. Y lo mismo ocurre también en los cóncavos.
6. Si se deposita algo en un vaso y se toma una distancia tal que ya no se vea, estando a la misma distancia, si se vierte agua se verá el objeto depositado[6].
PROPOSICIÓN 1
En los espejos planos y convexos y cóncavos los rayos visuales se reflejan[7] en ángulos iguales.
Sea B el ojo y ΑΓ el espejo plano y llévese el rayo BK desde el ojo y refléjese hacia Δ.
Digo que el ángulo E es igual al ángulo Z.

Trácense las rectas ΒΓ, ΔΑ perpendiculares al espejo. Y entonces ΒΓ es a ΓΚ como ΔΑ a AK, pues eso se había supuesto en las definiciones [Def. 3], Entonces el triángulo ΒΓΚ es semejante al triángulo ΔΑΚ. Luego el ángulo Ε es igual al ángulo Z, ya que los triángulos semejantes son equiángulos.
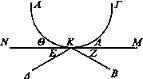
Sea AKΓ un espejo convexo, y sea BK el rayo visual que se refleja en Δ.
Digo que el ángulo suma de Ε, Θ[8] será igual al ángulo suma de Z, Λ.
Coloco el espejo plano NM; entonces, el ángulo E es igual al Z; y también el Θ al Λ, puesto que MN es tangente. Luego todo el ángulo suma de E, Θ es igual a todo el ángulo suma de Λ, Z.
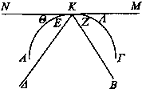
Sea ahora ΑΚΓ un espejo cóncavo y sea BK el rayo visual que se refleja en Δ.
Digo que el ángulo E es igual al Z.
Pues si se coloca un espejo plano resulta igual el ángulo suma de ΘΕ al ángulo suma de ΖΛ. Y el ángulo Θ es igual al Λ; luego el ángulo restante E será igual al Z.
PROPOSICIÓN 2
Si un rayo visual incide en cualquier clase de espejo produciendo ángulos iguales, se reflejará siguiéndose a sí mismo.
Sea ΑΓ un espejo plano y B el ojo y haya incidido el rayo visual BK produciendo los ángulos E, Z cuya suma es igual a Θ.
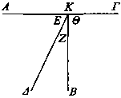
Digo que el rayo visual BK al reflejarse pasará a través de sí mismo, es decir, hacia B.
Pues no sea así, sino que, si es posible, vaya hacia Δ. Y puesto que los rayos visuales se reflejan en ángulos iguales, el ángulo E es igual al Θ. Y se había demostrado que el ángulo suma de E, Z era igual al Θ [Prop. 1], Luego también el ángulo suma de E, Z será igual al ángulo E, el mayor al menor: lo cual es imposible. Luego el rayo BK se reflejará siguiéndose a sí mismo.
Y la misma demostración sería apta en el caso de los espejos convexos y cóncavos.
PROPOSICIÓN 3
Si el rayo visual al incidir en cualquier clase de espejo forma ángulos desiguales, ni se reflejará siguiéndose a sí mismo ni hacia el ángulo menor.
Sea ΑΚΓ un espejo plano, e incida el rayo visual BK formando el ángulo Z mayor que el ángulo suma de Θ, Λ.
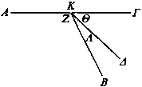
Digo que al reflejarse BK ni se reflejará siguiéndose a sí mismo ni hacia al ángulo suma de Θ, A.
Pues si fuera hacia B, el ángulo Z sería igual al Θ, Λ: lo que es imposible, pues se ha supuesto mayor. Y si fuera hacia Δ, el ángulo Ζ sería igual al Θ: pero es mayor. Luego BK se reflejará hacia el ángulo mayor Ζ, pues es posible quitar del ángulo mayor uno igual al menor.
La misma demostración cabe en el caso de los convexos y cóncavos.
PROPOSICIÓN 4
Los rayos visuales que se reflejan sobre los espejos planos y convexos no serán ni concurrentes entre sí ni paralelos.
Sea AF un espejo plano y B el ojo y ΒΓΔ, BAE los rayos visuales reflejados.
Digo que ΓΔ, AE ni son paralelas ni serán concurrentes hacia Δ, E.
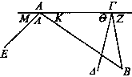
Puesto que el ángulo Z es igual al Θ y el ángulo K es igual al ángulo M, mientras que el ángulo Z es mayor que el K por ser exterior al triángulo ΒΑΓ [Elem. 116], también Θ sería mayor que M. Luego ΓΔ no es paralela a AE ni serán concurrentes hacia Ε, Δ.
Sea ahora ΑΖΓ un espejo convexo y B el ojo y ΒΖΔ, BHE los rayos visuales que se reflejan[9].
Digo que ΖΔ, EH ni son paralelas ni serán concurrentes hacia Ε, Δ.

Trácese la recta HZ y prolónguese por ambos extremos. Puesto que el ángulo suma de Κ, Θ es igual al ángulo Λ por producirse la reflexión en ángulos iguales [Prop. 1], el ángulo suma de Λ, M sería mayor que Κ. Y K es mayor que el ángulo suma de N, Ξ [Elem. I 16] y el ángulo suma de N, Ξ es mayor que el ángulo suma de O, Π, ya que el propio ángulo Ξ es igual a ΟΠ. Luego el ángulo suma de Λ, M es mucho mayor que O. Luego las rectas ΖΔ, HE no serán concurrentes ni son paralelas.
PROPOSICIÓN 5
En los espejos cóncavos, si se pone el ojo en el centro, o en la circunferencia o fuera de la circunferencia, es decir, entre el centro y la circunferencia, los rayos visuales al reflejarse serán concurrentes.
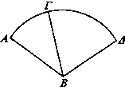
Sea ΑΓΔ un espejo cóncavo, y B el centro de la esfera, y póngase el ojo en B, e incidan desde B en la circunferencia los rayos visuales BA, ΒΓ, ΒΔ.
Entonces, los ángulos con sus vértices en A, Δ, Γ son iguales, pues son de un semicírculo[10]; luego los rayos visuales BA, ΒΓ, ΒΔ, al reflejarse, se reflejarán siguiéndose a sí mismos: eso ya se ha demostrado [Prop. 2]. De manera que serán concurrentes en B.
Sea ahora ΑΓΒ un espejo cóncavo, y el ojo B, y esté sobre la circunferencia de aquél; e incidan desde B los rayos visuales ΒΓ, BA que se reflejan hacia los puntos Δ, E.
Puesto que el segmento ΑΓΒ es mayor que el segmento ΒΓ, el ángulo Z es mayor que el ángulo Θ. Por tanto, también el ángulo H es mayor que el K [Prop. 1], Luego la suma de los ángulos Ζ, H es mayor que la de los ángulos Θ, K. Luego el ángulo restante Λ es menor que M; luego es mucho menor que N. Luego las rectas ΓΔ, AE coincidirán en Ξ.
Se demostrará de la misma manera aunque el ojo caiga fuera de la circunferencia, como en la proposición que sigue.
PROPOSICIÓN 6
En los espejos cóncavos, si pones el ojo entre el centro y la circunferencia, los rayos visuales que se reflejan unas veces coincidirán y otras veces no coincidirán[11].
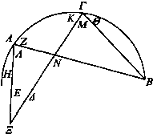
Sea AΓ un espejo cóncavo y A su centro, y esté el ojo B situado entre el centro y la circunferencia, y sean BA, ΒΓ rayos visuales que se reflejan hacia Η, Z y prolónguense los rayos visuales ΑΘ, ΓΚ hasta el espejo.

El rayo visual ΑΘ es mayor, igual o menor que ΓΚ. Si el rayo visual AZ es igual al rayo visual ΓΚ, también el arco de circunferencia[12] ΑΓΘ es igual al arco de circunferencia ΓΘΚ; de ese modo también el ángulo M es igual al ángulo Ξ, puesto que los ángulos correspondientes a arcos de circunferencia iguales son también iguales entre sí [Cf. Elem. III 21]. Entonces, también los ángulos M, Λ son iguales a los ángulos N, Ξ por la reflexión [Prop. 1]. Luego también el ángulo restante O es igual al Π; luego P es mayor que O. Puesto que el ángulo P es mayor que Π por ser exterior [Elem. I 16] y el ángulo Π es igual a O, entonces el P es mayor que el O. Añádase en común el ángulo OPZ: entonces los rayos visuales ΓΖ, AH concurrirán hacia los puntos H, Z.
Lo mismo ocurrirá aunque el rayo visual ΑΘ sea mayor que el ΓΚ. Luego los ángulos Λ, M serán mayores que los N, Ξ, y el ángulo Π será mayor que el O y el P mayor que el O. Pero si la recta ΑΘ es menor que la ΓΚ, por las mismas razones el ángulo O será mayor que el ángulo Π. Y también P es mayor que Π; luego nada impide que P sea igual a O o menor que O y que AH no sea concurrente con ΓΖ. Y es evidente que tanto si el arco de circunferencia ΑΘ es mayor que el ΓΚ como si son iguales, la coincidencia de los rayos reflejados no se producirá ni en la circunferencia del círculo ni fuera de ella, sino sólo en su interior.
PROPOSICIÓN 7
Las alturas y las profundidades de los espejos planos aparecen vueltas cabeza abajo.

Sea AE una altura, y AΛ un espejo plano y B el ojo, y ΒΓ, ΒΔ los rayos visuales que se reflejan hacia los puntos E, K.
Entonces, al ser prolongados en línea recta los rayos visuales, E, que está arriba, aparece en Θ, que está abajo, mientras que K, que está abajo, aparece en Z, que está arriba; de manera que en apariencia están vueltas cabeza abajo.
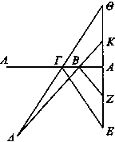
Sea ahora EA una profundidad, y ΑΓ un espejo plano, y Δ el ojo, y ΔΓ, ΔΒ los rayos visuales que se reflejan hacia los puntos E, Z.
De la misma manera, al prolongar los rayos visuales hacia los puntos Θ, K, aparecerá E, que está abajo, en Θ, que está arriba, mientras que Z, que está arriba, aparecerá en K, que está abajo.
PROPOSICIÓN 8
Las alturas y las profundidades en los espejos convexos aparecen vueltas cabeza abajo.
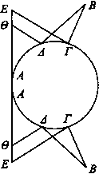
Sea AE una altura y ΑΔΓ un espejo convexo y ΒΔ, ΒΓ rayos visuales que se reflejan hacia los puntos E, Θ.
Se ha demostrado que no serán concurrentes [Prop. 4]. Lo demás, como lo de los espejos planos [Prop. 7].
Sea ahora AE una profundidad, y ΑΓ un espejo convexo, y B el ojo y ΒΓΕ, ΒΔΘ los rayos que se reflejan hacia E, Θ. Lo demás, como en los planos [Prop. 7].
PROPOSICIÓN 9
Las magnitudes alargadas[13], en los espejos planos, aparecen tal y como son en verdad.
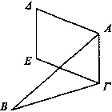
Sea B el ojo y ΔΕ la magnitud alargada y ΑΓ el espejo.
Entonces, al reflejarse los rayos visuales, Δ aparece en A y E en Γ y es en apariencia como es en verdad: lo próximo, próximo; y lo lejano, lejano.
PROPOSICIÓN 10
Las magnitudes oblicuas en los espejos convexos aparecen tal y como son verdaderamente.
Sea ΕΔ la magnitud y B el ojo y ΑΓ el espejo convexo y los rayos que se reflejan hacia Ε, Δ[14]. Lo demás, lo mismo.

PROPOSICIÓN 11
Las alturas y las profundidades en los espejos cóncavos si están dentro de la concurrencia de los rayos visuales aparecen vueltas cabeza abajo como en los espejos planos y convexos, pero si están fuera de la concurrencia aparecen como son.
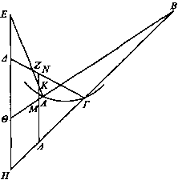
Sea ΑΓ un espejo cóncavo y B el ojo y BA, ΒΓ los rayos visuales que se reflejan y sea Z su punto de concurrencia y sean ΔΕ y KN las alturas y esté KN dentro de la coincidencia Z y ΔΕ fuera de la coincidencia.
Entonces, una vez prolongados los rayos visuales como en los espejos planos y convexos, el punto K aparece en M y el punto N en Λ, de manera que parecen vueltos cabeza abajo. A la vez, en la altura de fuera de la coincidencia, Δ aparece en H, mientras que E aparece en Θ: aparece tal como es.
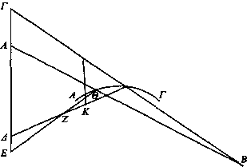
Sean ahora ΔΕ y ΚΘ la profundidad y ΑΓ el espejo cóncavo y B el ojo y[15] los rayos visuales que se reflejan y coinciden en Z.
Entonces, al prolongarse los rayos visuales, los puntos Κ, Θ aparecerán igualmente vueltos cabeza abajo: el K en Γ y el Θ en A, como en los espejos planos y convexos, mientras que Δ, E aparecerán tal como son, E abajo, en A, y Δ arriba en Γ.
PROPOSICIÓN 12
Las magnitudes oblicuas en los espejos cóncavos, cuantas están situadas dentro de la coincidencia de los rayos visuales, aparecen tal y como son, mientras que cuantas están fuera, vueltas cabeza abajo[16].

Sean ΕΔ, ΘΚ magnitudes oblicuas, y ΑΓ un espejo cóncavo y B el ojo y ΒΑΔ, ΒΓΕ los rayos visuales que se reflejan y coinciden en H; y esté la magnitud oblicua ΘΚ por dentro del punto de coincidencia H, y la ΔΕ por fuera.
Entonces, los puntos Θ, K aparecen acordes con la naturaleza, como en los espejos planos y convexos, mientras que E, Δ vueltos del otro lado, puesto que Δ aparece en A y E en Γ.
PROPOSICIÓN 13
Es posible ver lo mismo mediante muchos espejos planos.

Sea A lo que ha de verse y B el ojo y sean ΓΔ, ΔΕ, EZ los tres espejos.
Trácese desde B la recta ΒΓ perpendicular al espejo ΓΔ, y sea ΒΓ igual a ΓΣ, y luego trácese desde A la recta AZ perpendicular a EZ, y sea ΖΘ igual a AZ; y trácese desde Θ la recta ΘΚ perpendicular al espejo ΔΕ y sea KA igual a ΘK y trácese ΛΜΞΣ que una Λ con Σ, y trácese ΜΡΘ que una M con Θ, y trácense también ΑΡ, ΒΞ. Puesto que ΒΓ es igual a ΓΣ y que los ángulos con vértice en Γ son rectos, entonces las dos rectas ΒΓ, ΓΦ son iguales respectivamente a las dos rectas ΣΓ, ΓΦ y el ángulo ΒΓΦ, que es recto, es igual al ángulo ΣΓΦ, que es recto, y los ángulos restantes serán iguales a los ángulos restantes, a los que subtienden los lados iguales [Elem. I 4]: el ángulo de vértice en B al de vértice en Σ, y el de vértice en Ξ al de vértice en T; pero el ángulo T es igual al ángulo N —por opuestos por el vértice—; de manera que el ángulo N es igual al Ξ. Luego el rayo visual ΒΞ se reflejará hacia M. A la vez, puesto que ΘK es igual a KΛ y puesto que los ángulos de vértice en K son rectos, el ángulo O es igual al Π. Luego, el mismo rayo visual ΒΞΜ se refleja hacia P. Por lo mismo también se refleja hacia A, por ser igual el ángulo ZPA al EPM; de manera semejante en las demás demostraciones.
Luego el rayo visual que sale del ojo B ve el punto A mediante los tres espejos planos que hay, ΓΔ, ΔΕ, EZ.
PROPOSICIÓN 14
También es posible ver lo mismo mediante cuantos espejos planos se dispongan. Pero es preciso componer, de acuerdo con el número de los espejos, un polígono equilátero y equiángulo que tenga dos lados más que espejos.

Sea A lo que ha de verse y B el ojo, y trácese AB y a partir de AB constrúyase un polígono equilátero y equiángulo que tenga dos lados más que espejos y sea el polígono ΑΒΔ y tómese el centro Θ del círculo descrito en torno al polígono, y a partir de él trácense las rectas ΘΓ, ΘΕ, ΘΔ, ΘΒ, ΘΑ hacia los ángulos, y colóquense espejos planos formando ángulos rectos con las rectas trazadas.
Puesto que el ángulo suma de Z, Λ es igual al ángulo suma de N, K —pues cada uno de ellos es recto— y de ellos, N es igual a Λ, entonces el ángulo restante Z es igual al K. De manera que el rayo reflejado del rayo visual ΒΓ irá hacia Δ, ya que los reflejos se producen en ángulos iguales. Del mismo modo se demostrará también que los ángulos que se forman en los espejos con vértice en los puntos Δ, E son iguales.
Luego el rayo visual que sale del ojo B, al reflejarse e incidir en todos los espejos llegará al punto A.
PROPOSICIÓN 15
También es posible ver lo mismo mediante espejos convexos y cóncavos.

Sea A lo que ha de verse y B el ojo y de la misma manera constrúyase un polígono equilátero y equiángulo ΑΒΓΔΕ y haya en los puntos Γ, Δ, E espejos planos desde los que se ve A, como se ha demostrado [Prop. 14], y a éstos añádanse espejos cóncavos o convexos en los puntos de contacto de los rayos visuales.
Entonces, el ángulo Z es igual al Θ, y el K al Λ. Luego todo el ángulo KZ es igual al ΘΛ. Luego el rayo visual se reflejará desde el espejo convexo Γ hacia el Δ, y desde el Δ hacia el E, y desde el Ε hacia el A.
Luego es evidente que es posible ver lo mismo tanto si los espejos son todos convexos o cóncavos como si están mezclados.
PROPOSICIÓN 16
En los espejos planos cada uno de los objetos vistos se ve según la perpendicular desde el objeto visto.
Sea ΓΔ un espejo plano y B el ojo y A el objeto visto y sea ΑΓ la perpendicular desde el objeto visto al espejo.
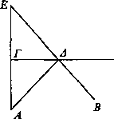
Entonces, puesto que se ha supuesto en las «Definiciones»[17] [Def. 4] que si el lugar de Γ está ocupado no se ve A, se verá A en línea recta con ΑΓ. Y también en línea recta con el rayo visual ΒΔ; luego se verá en E. Y habíamos supuesto que lo recto es aquello cuya parte media está en línea con los extremos[18]: de manera que AE y BE serán una recta.
PROPOSICIÓN 17
En los espejos convexos cada uno de los objetos vistos se ve según la recta trazada desde el objeto visto hacia el centro de la esfera.
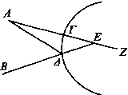
Sea ΓΔ un espejo convexo y B el ojo y ΒΔ un rayo visual que se refleja hacia A, y sea Z el centro de la esfera y trácese AZ y prolónguese el rayo visual ΒΔ hacia E.
Entonces, puesto que se había supuesto en las «Definiciones»[19] [Def. 5] que si Γ está ocupado, A no se ve, se verá en línea recta con ΑΓ en la coincidencia con el rayo visual ΒΔ y dentro de la recta ΑΓ, en el punto E, como en los planos.
PROPOSICIÓN 18
En los espejos cóncavos cada uno de los objetos vistos se ve en la recta trazada desde el objeto visto hacia el centro de la esfera.

Sea ΓΔ un espejo cóncavo y ΒΓ el rayo visual que se refleja hacia el objeto visto, A, y sea E el centro de la esfera y desde A hacia E trácese una recta y prolónguese.
Entonces, puesto que se había supuesto en las «Definiciones»[20] que, si el lugar de Δ está ocupado, no se ve A, ya que aparece en línea recta con AE, se verá en la coincidencia de la recta ΑΔ y el rayo visual ΒΓ en el punto Z.
PROPOSICIÓN 19
En los espejos planos lo de la derecha aparece a la izquierda y lo de la izquierda a la derecha, y la imagen es igual al objeto visto y la distancia desde el espejo es igual.
Sea ΑΓ un espejo plano y B el ojo y BA, ΒΓ los rayos visuales que se reflejan hacia los puntos Ε, Δ y sea ΕΔ el objeto visto, y desde los puntos Ε, Δ trácense las rectas EZ, ΔΘ perpendiculares al espejo y prolónguense; prolónguense también los rayos visuales ΒΓ, BA y coincidan con las perpendiculares en los puntos K, Λ. Y trácese la recta AK.
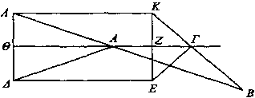
Entonces E aparece en K y Δ en Λ —eso ya se había demostrado [Prop. 16]. Luego lo de la izquierda aparece a la derecha y lo de la derecha a la izquierda. Y puesto que el ángulo ΚΓΖ es igual al ángulo ΖΓΕ y los ángulos con vértice en Z son rectos, entonces también la recta ZK sería igual a ZE. Por lo mismo, también ΔΘ es igual a ΘΛ. Luego la distancia que dista ΕΔ del espejo es la misma que la que dista la imagen ΚΛ.Υ el objeto visto ΕΔ es igual a la imagen KΛ por ser iguales EZ a ZK y ΔΘ a ΘΛ y ser común y estar formando ángulos rectos ΘΖ.
PROPOSICIÓN 20
En los espejos convexos lo de la izquierda aparece a la derecha y lo de la derecha a la izquierda y la imagen tiene menor distancia del espejo.
Sea ΑΓ un espejo convexo y Θ el centro de la esfera y B el ojo y BA, ΒΓ los rayos visuales que se reflejan hacia los puntos Δ, E y sea ΔΕ el objeto visto y trácense desde el centro Θ hacia Δ, E las rectas ΘΔ, ΘΕ y prolónguense los rayos visuales hacia Ζ, H y trácese la imagen ZH.
Entonces Δ aparece en H y E en Z. Luego lo de la derecha aparece a la izquierda y lo de la izquierda a la derecha.
Digo que EΛ es mayor que ΛZ.
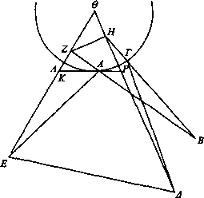
Trácese por el punto A la recta PAK tangente a la circunferencia [Elem. III 17]. Puesto que las rectas BA, AE forman ángulos iguales con la circunferencia por la reflexión [Prop. 1] y la recta KAP es tangente, el ángulo comprendido por EAZ resultaría cortado por la mitad; y el ángulo K es obtuso; luego la recta EK es mayor que la recta KZ; y mucho mayor la recta EΛ que la recta ΛZ. Luego la imagen ZH está menos distante del espejo, mientras que el objeto visto ΕΔ está más distante.
PROPOSICIÓN 21
En los espejos convexos la imagen es menor que los objetos vistos.
Sea ΑΟΓ un espejo convexo, y B el ojo y BA, ΒΓ los rayos visuales que se reflejan hacia los puntos Δ, E.
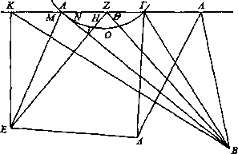
Entonces en el espejo convexo se ve EA en el ángulo comprendido por ΑΒΓ. Póngase al lado el espejo plano ΑΓ que toque a los rayos visuales en A, Γ, Entonces el rayo visual que va a ver E desde el espejo plano no es el rayo BAE, pues no forma ángulos iguales con el espejo plano; ni tampoco se reflejará entre los puntos A, Γ. Pero refléjese, si es posible, y sea el rayo visual BZE. Entonces el ángulo H será igual al ángulo Θ por la reflexión [Prop. 1], Pero el ángulo Θ es mayor que el ángulo suma de N, I y el ángulo M mayor que H. De manera que M también es mayor que la suma de N, I: lo cual es imposible, puesto que el propio ángulo I es mayor que M, pues es igual al ángulo entero con vértice en la circunferencia. Luego se reflejará fuera de A. Refléjese y sea BKE. De manera semejante, también ΒΛΔ caerá fuera. Entonces el objeto ΕΔ se ve en el espejo plano bajo un ángulo mayor, el comprendido por KBA, que en el espejo convexo. Y se había demostrado que la apariencia era igual en el espejo plano [Prop. 19].
Luego es evidente que en el espejo convexo la imagen aparece menor que el objeto visto.
PROPOSICIÓN 22
En los espejos convexos aparecen menores las imágenes de los espejos menores.
Sea ΑΓ la esfera mayor y ΕΛ la esfera menor en torno al mismo centro Θ, y B el ojo y trácese la recta ΒΑΘ y refléjese en la esfera el rayo visual ΒΓΔ.
Digo que el rayo visual que se refleja en la esfera menor hacia Δ no pasará por Γ ni caerá fuera de Γ.

Pues pase primero, si es posible, por Γ, y refléjese en la esfera menor hacia el punto Δ y sea la recta ΒΕΔ y trácese una recta que una Θ y Γ y prolónguese hacia K. La recta ΘΓΚ cortará por la mitad el ángulo ΒΓΔ por formar ΒΓΔ ángulos iguales con la circunferencia por la reflexión [Prop. 1]. Por lo mismo, la recta que va de Θ a E una vez trazada y prolongada cortará por la mitad el ángulo comprendido por ΒΕΔ. Córtelo y sea la recta ΘΕΖ. Puesto que el ángulo comprendido por ΒΓΔ es mayor que el comprendido por ΒΕΔ, también la mitad de la mitad, el ángulo comprendido por ΒΓΚ es mayor que el comprendido por BEZ; pero también es menor, lo cual es imposible. Luego el rayo visual reflejado en la esfera menor no pasará por Γ.

Supóngase de nuevo lo mismo y el rayo visual ΒΕΔ al reflejarse en la esfera menor caiga por fuera de Γ y corte la recta BE la esfera mayor en Z. El rayo visual BZK al reflejarse en Z no coincidirá con ΓΔ —eso ya se ha demostrado [Prop. 4]—. Coincida entonces con ΕΔ en K. Entonces el rayo visual BZK al reflejarse en el espejo mayor ve K y el propio rayo visual BEK al reflejarse en el espejo menor ve el mismo K. Pero eso se había demostrado arriba que era imposible. Luego el rayo visual al reflejarse en el espejo menor hacia Δ caerá entre los puntos Γ, A.
De manera semejante se demostrará también que hace lo mismo el rayo visual de la otra parte. Luego se ve bajo un ángulo menor, el que hay con vértice en B, en el espejo menor que en el mayor [Óptica, def. 4].
Luego la imagen aparece menor en el espejo menor.
PROPOSICIÓN 23
En los espejos convexos las imágenes aparecen convexas.
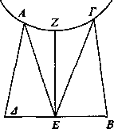
Sea ΑΓ un espejo convexo y E el ojo y EA, ΕΓ los rayos visuales que se reflejan hacia Δ; B y ZE un rayo visual que se refleja sobre sí mismo hacia E.
Entonces, de los rayos visuales los más lejanos son los mayores en longitud, mientras que los del centro, como EZ, son los menores. Luego E parece más próximo al espejo y B y Δ más lejanos.
De manera que todo entero parece convexo.
PROPOSICIÓN 24
En los espejos cóncavos, si se pone el ojo en el centro, sólo aparece el ojo[21].

Sea ΑΓΔ un espejo cóncavo y B su centro y BA, ΒΓ, ΒΔ los rayos visuales.
Entonces, el ángulo E es igual al Z. Luego al reflejarse el rayo visual ΒΓ pasará por B [Prop. 2]. Y lo mismo los restantes rayos visuales.
Luego sólo se ve el propio B.
PROPOSICIÓN 25
En los espejos cóncavos, si pones el ojo en la circunferencia o por fuera de la circunferencia no se ve el ojo.
Sea ΑΓΒ un espejo cóncavo y esté el ojo B en la circunferencia de éste e incidan los rayos visuales BA, ΒΓ y refléjense.
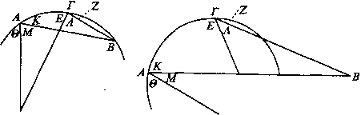
Entonces, el ángulo suma de Μ, Θ es mayor que el K y el ángulo suma de Ε, Λ mayor que el Z. De manera que los rayos visuales BA, ΒΓ no se reflejarán hacia el ojo B: si se reflejaran hacia el ojo, los ángulos de vértice en A, Γ serían iguales.
Y se demostrará que aunque el ojo esté por fuera de la circunferencia ocurre lo mismo, es decir, que el ojo no se ve por no ir hacia él los rayos reflejados.
PROPOSICIÓN 26
En los espejos cóncavos, si sacando el diámetro de la esfera levantas desde el centro una perpendicular y pones el ojo en un extremo, no se verá nada de lo que hay en la parte en la que está el ojo, es decir, ni de lo que esté sobre el diámetro ni de lo que esté por fuera del diámetro.

Sea ΑΓΔ un espejo cóncavo y sea ΑΔ el diámetro de la esfera y desde el centro Z levántese perpendicular a ΑΔ la recta ΖΓ y sea B el ojo y BE el rayo visual.
Entonces, BE al reflejarse no irá ni hacia el punto B ni hacia el Z, puesto que se refleja en ángulos iguales; lúego irá como ΕΘ. De manera semejante, también si el ojo cae por dentro, en donde Θ, o sobre el diámetro, en M, al reflejarse los rayos visuales ΘΚ, MN irán como ΚΛ, ΝΞ.
Luego no se ve nada de lo que hay en la misma parte en la que está el ojo ni de lo que está sobre el diámetro ni de lo de fuera del diámetro.
PROPOSICIÓN 27
En los espejos cóncavos, si se ponen los ojos sobre el diámetro equidistantes del centro, no se verá ninguno de los dos ojos.
Sea ΑΓΔ un espejo cóncavo, ΑΔ el diámetro, Z el centro, ΖΓ perpendicular, Β, E los ojos equidistantes del centro y ΒΓ el rayo visual.
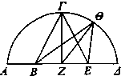
De manera que al reflejarse irá hacia E, puesto que se refleja en ángulos iguales. Ningún otro rayo visual irá al reflejarse desde B hacia E. Pues si fuera, como ΒΘ, trácense ΘΕ, ΘΖ. Entonces el ángulo ΒΘΕ quedará cortado por la mitad por ΖΘ, y ΒΘ será en proporción a ΘΕ como BZ a ZE [Elementos VI 3]: lo cual es imposible, pues ΒΘ es mayor que ΘΕ, mientras que BZ es igual a ZE. Por tanto, ningún rayo visual al reflejarse irá de B hacia E. Luego sólo un rayo visual se reflejará hacia cada uno de los ojos Β, E y E no se verá. Y es que al ser prolongado el rayo ΒΓ no coincidirá con ΒΔ en las partes de Γ, Δ, sino que cada uno de los objetos vistos aparecía sólo en el punto de coincidencia [Prop. 18]. Y tampoco el rayo ΕΓ coincidirá con EA en las partes de Γ, A, pues en los espejos cóncavos cada uno de los objetos vistos se ve según la recta trazada desde el objeto visto hasta el centro de la esfera.
PROPOSICIÓN 28
En los espejos cóncavos, si cortando el radio en dos partes iguales y trazando una perpendicular pones los ojos a la misma distancia del radio, y los pones o entre el diámetro y la perpendicular o sobre la propia perpendicular, no se ve ninguno de los ojos.

Sea ΑΓΔ un espejo cóncavo, ΑΔ el diámetro, K el centro y la perpendicular ΚΓ quede cortada en dos partes iguales por el punto Π y sea perpendicular a ella la recta ΕΠΖ y sean Β, Θ los ojos situados entre el diámetro ΑΔ y la recta EZ en las paralelas EZ, ΒΘ, equidistantes del radio ΚΓ, y sea ΒΓ el rayo visual que se refleja hacia Θ, pues forma ángulos iguales en la circunferencia por ser ZE paralela a ΒΘ e igual BN a ΝΘ. Y una vez trazadas KB, ΚΘ prolónguense y prolónguese también ΓΒ hacia Φ.
Y puesto que ΒΓ es mayor que BK, también el ángulo P es mayor que el ángulo I. De manera que también el ángulo comprendido por ΓΒΘ es mayor que el comprendido por ΘΒΚ, es decir, que el comprendido por ΒΘΚ; luego ΒΓ no coincidirá con ΚΘ; luego Θ no se verá, ya que aparece en el punto de coincidencia de ΒΓ, ΚΘ [Prop. 18].
Sea ahora lo mismo que arriba, pero estén situados los ojos Β, Θ sobre la recta que corta perpendicularmente por la mitad al radio, sobre ΑΔ.
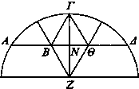
Puesto que la recta ΒΓ es igual a BZ y la recta ΓΘ es igual a ΖΘ, ΒΓ sería paralela a ΖΘ [Cf. Elem. I 34]; luego el rayo visual ΒΓ no coincidirá con el radio, es decir, con ΖΘ, hacia el objeto visto, hacia las partes de Θ, Γ. De manera que el ojo Θ no aparece, puesto que aparecía en el punto de coincidencia de los rayos ΒΓ, ΖΘ.
Sea de nuevo lo mismo pero estén situados los ojos B, Γ, equidistantes del radio ZA, por encima del punto de corte del radio en dos partes iguales.
Digo que aparecen los ojos B, Γ y lo de la derecha a la izquierda y lo de la izquierda a la derecha y la imagen mayor que el rostro y la imagen a mayor distancia del espejo.
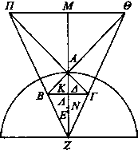
Sea BA el rayo visual que se refleja y trácense desde el centro Z hacia los puntos Β, Γ las rectas ΖΒ, ΖΓ y prolónguese BA.
Puesto que el punto de corte en dos partes iguales es N, BZ es mayor que BA, y el ángulo K es mayor que el E. Y el ángulo K es igual al Δ; luego el ángulo Δ es mayor que el E. Luego, una vez prolongadas ZB, ΓΑ, coincidirán. Coincidan en el punto Π. Por la misma razón también BA, ZΓ coincidirán en el punto Θ. Luego Γ se verá en Θ y B en Π, y aparece lo de la derecha a la izquierda y lo de la izquierda a la derecha; y en efecto, ΘΠ es mayor que ΒΓ, pues son paralelas. Luego la imagen aparece mayor y a mayor distancia del espejo, pues MA es mayor que AΛ.
Y si se ponen los ojos fuera del diámetro, lo de la derecha aparece a la derecha y lo de la izquierda a la izquierda y la imagen menor que el rostro y entre el rostro y el espejo.

Sean Β, Γ los ojos y Z el centro del espejo y sea ΑΖΔ una perpendicular al diámetro y ΒΓ una perpendicular a ella, y sea ΑΓ igual a BA y sea ΒΔ el rayo visual que se refleja hacia Γ y trácense las rectas BZK, ΓΖΕ pasando por el centro y una la recta EK los puntos Ε, K.
Por consiguiente, B aparece en K y Γ en E. Luego lo de la derecha aparece a la derecha y lo de la izquierda a la izquierda y la imagen EK menor que el rostro ΒΓ, pues EK es paralela a ΒΓ. Y la imagen aparece entre el espejo y el rostro.
Y si se mueve hacia atrás el rostro, la imagen aparece aún menor.
Sea MN el mismo rostro que ΒΓ, pero distante de ΒΓ, situado de manera semejante.
La recta trazada desde M hasta el centro Z y prolongada caerá más allá de K, como Λ, y la recta que va de N a Z caerá más allá de E, como Θ. Luego MN aparece como ΘΛ; y ΘΛ es menor que EK y está más próxima al espejo.
PROPOSICIÓN 29
Es posible disponer un espejo de manera que en el mismo aparezcan muchos rostros, unos mayores, otros menores y unos más cerca, otros más lejos y de unos, lo de la derecha a la derecha y lo de la izquierda a la izquierda y de otros lo de la izquierda a la derecha y lo de la derecha a la izquierda.
Sea pues AM un plano. Entonces en él estarían espejos convexos como ΑΟΓ, ΘΡΚ; cóncavos como ΓΔΕ, ΖΗΘ; planos como EZ, AM.

Al colocar el rostro en donde N, de los espejos planos aparecen las imágenes iguales y a la misma distancia [Prop. 9 y 19]; de los convexos, menores y a menor distancia [Prop. 20 y 21]; de los cóncavos, de todas las maneras [Prop. 28], como se ha demostrado.
PROPOSICIÓN 30
De los espejos cóncavos puestos frente al sol se enciende fuego.

Sea ΑΒΓ un espejo cóncavo y EZ el sol y Θ el centro del espejo, y trazada ΔΘ desde un punto Δ hacia el centro Θ prolónguese hacia B, e incida el rayo ΔΓ y refléjese hacia K. Entonces se reflejará por encima del centro K, pues el ángulo Π de vértice en la circunferencia es menor que el ángulo restante de vértice en la circunferencia comprendido por ΒΓΔ. Y sea el arco de circunferencia AB igual al ΒΓ, y desde Δ incida otro rayo, ΔΑ. Así, es evidente que al reflejarse el rayo ΑΔ caerá sobre K por ser igual el arco de circunferencia AB al ΒΓ. De la misma manera se demostrará que todos los rayos que parten de Δ e inciden en el espejo y comprenden arcos de circunferencia iguales coincidirán con ΒΘ en el mismo punto por encima de Θ.
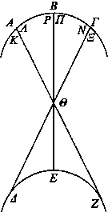
Sea de nuevo ΑΒΓ un espejo cóncavo y ΔΕΖ el sol y sea la recta ΕΘΒ desde un punto E pasando por el centro Θ, y desde otros puntos Δ, Z sean las rectas ΔΘΓ, ΖΘΑ.
En efecto, hemos demostrado antes que los rayos que proceden de E coincidirán consigo mismos por ser iguales los ángulos Π, P [Prop. 3]; pues son diámetros. Y los que proceden de Z por ser iguales los ángulos Κ, A, y los que proceden de Δ hacia la recta ΔΓ por ser iguales los ángulos N, Ξ. Y es evidente que todos éstos se reflejan hacia sí mismos. Pues siendo radios, forman semicírculos y los ángulos de los semicírculos son iguales; y los rayos reflejados se producen mediante ángulos iguales; entonces, se reflejan sobre sí mismos. Luego desde todos los puntos coincidirán todos los rayos hacia los rayos que pasan por el centro y están en el centro.
Luego al calentarse estos rayos en torno al centro se reúne el fuego; de manera que si se pone allí una estopa, se encenderá.