DEFINICIONES[1]
1. Supóngase que las líneas rectas trazadas a partir del ojo se propagan a lo largo de un espacio de grandes magnitudes[2].
2. Y que la figura contenida por los rayos visuales es un cono que tiene el vértice en el ojo y la base en los extremos de los objetos vistos.
3. Y que se ven los objetos en los que los rayos visuales inciden y no se ven aquellos objetos en los que los rayos visuales no inciden.
4. Y que los objetos que se ven bajo un ángulo mayor parecen mayores; los que bajo un ángulo menor, menores, y los que se ven bajo ángulos iguales, iguales.
5. Y los que se ven bajo ángulos más elevados parecen más elevados, y los que se ven bajo ángulos más bajos, más bajos.
6. Y, de manera semejante, parecen más a la derecha los que se ven bajo rayos más a la derecha y más a la izquierda los que se ven bajo rayos más a la izquierda.
7. Los objetos que se ven bajo mayor número de ángulos aparecen con más precisión.
PROPOSICIÓN 1
Ninguno de los objetos vistos se ve entero al mismo tiempo[3].
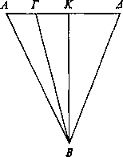
Sea ΑΔ el objeto visto y sea B el ojo a partir del cual incidan los rayos visuales BA, ΒΓ, BK, ΒΔ.
Así, puesto que los rayos visuales incidentes han sido prolongados a lo largo de un espacio, no incidirían continuos sobre ΑΔ. De manera que en ΑΔ se producirían espacios sobre los que no incidirán los rayos visuales [Def. 1].
Luego ΑΔ no se verá entero al mismo tiempo. Pero parece que se ve al mismo tiempo porque los rayos visuales se trasladan rápidamente.
PROPOSICIÓN 2
De los objetos de iguales longitudes que están situados a distancia, se ven con más precisión los que están situados más cerca.
Sea B el ojo y ΓΔγ ΚΛ los objetos vistos —hay que considerarlos iguales y paralelos— y esté situado más cerca ΓΔ e incidan los rayos visuales ΒΓ, ΒΔ, BK, ΒΛ.
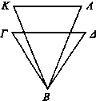
No diríamos que los rayos visuales incidentes sobre ΚΛ a partir del ojo pasen por los puntos Γ, Δ, pues la recta ΚΛ del triángulo ΒΔΛΚΓΒ sería mayor que la recta ΓΔ, y se ha supuesto que era igual. Por tanto, ΓΔ se ve bajo mayor número de rayos visuales que KA.
Luego ΓΔ aparecerá con más precisión que KΛ, ya que los objetos vistos bajo mayor número de ángulos aparecen con más precisión [Def. 7],
PROPOSICIÓN 3
Cada uno de los objetos vistos posee cierta longitud de separación que, una vez situado allí, ya no se ve.
Sea B el ojo y ΓΔ el objeto visto.
Afirmo que ΓΔ, situado a cierta distancia, ya no se verá.

Quede situado ΓΔ a la distancia intermedia entre los rayos visuales a la que está situado K. Así, no incidirá sobre K ninguno de los rayos visuales que parten de B. Y aquello sobre lo cual no inciden los rayos visuales no se ve.
Luego cada uno de los objetos vistos posee cierta longitud de separación que, una vez situado allí, ya no se ve.
PROPOSICIÓN 4
De los objetos que están a distancias iguales y sobre la misma recta los que se ven a mayor distancia parecen menores.
Sean AB, ΒΓ, ΓΔ distancias iguales sobre una recta y trácese formando ángulos rectos AE en la cual esté situado el ojo, E.
Digo que AB parecerá mayor que ΒΓ y ΒΓ mayor que ΓΔ.
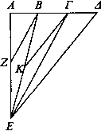
Incidan los rayos EB, ΕΓ, ΕΔ y trácese BZ paralela a la recta ΓΕ por el punto B. Por tanto, AZ es igual a ZE. Puesto que se ha trazado la recta BZ paralela a uno de los lados, el ΓΕ, del triángulo ΑΕΓ, entonces ΓΒ es a BA como EZ a ZA; luego, como se ha dicho, AZ es igual a ZE. Y el lado BZ es mayor que el ZA; luego también es mayor que ZE. Y el ángulo correspondiente a ZEB es mayor que el ángulo correspondiente a ZBE; y el correspondiente a ZBE es igual al correspondiente a ΒΕΓ; por tanto, también el correspondiente a ZEB es mayor que el ángulo correspondiente a ΓΕΒ.
Luego AB se verá mayor que ΒΓ [Def. 4]. Y si de manera semejante de nuevo se trazara una paralela a ΔΕ por el punto Γ, se verá mayor ΒΓ que ΓΔ.
PROPOSICIÓN 5
Las magnitudes iguales situadas a distancias desiguales parecen desiguales, y parece siempre mayor la que está situada más cerca del ojo.
Sean AB, ΓΔ, dos magnitudes iguales y sea E el ojo, respecto al cual están situadas a distancias desiguales, y esté más cerca AB.
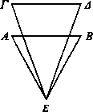
Digo que AB parecerá mayor.
Incidan los rayos AE, EB, ΕΓ, ΕΔ. Puesto que los objetos vistos bajo ángulos mayores parecen mayores [Def. 4] y el ángulo correspondiente a AEB es mayor que el correspondiente a ΓΕΔ, entonces AB parecerá mayor que ΓΔ.
PROPOSICIÓN 6
Los espacios paralelos vistos de lejos parecen convergentes[4].
Sean dos magnitudes paralelas AB, ΓΔ y sea E el ojo.
Digo que AB, ΓΔ parecen convergentes y que el espacio más cercano parece mayor que el más lejano.
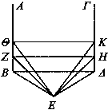
Incidan los rayos EB, EZ, ΕΘ, ΕΔ, EH, EK y trácense las rectas ΒΔ, ZH, ΘΚ. Puesto que el ángulo correspondiente a ΒΕΔ es mayor que el ángulo correspondiente a ZEH, entonces también parece mayor ΒΔ que ZH [Def. 4], A la vez, puesto que el ángulo correspondiente a ZEH es mayor que el ángulo correspondiente a ΘΕΚ, entonces también parece mayor ZH que ΘΚ. Luego la distancia ΒΔ parece mayor que ZH y ZH mayor que ΘΚ.
Luego las distancias que son paralelas ya no se verán de la misma manera, sino convergentes.
En el caso de los espacios que están situados en un plano elevado, trácese la perpendicular AB desde el punto A al plano supuesto y sean paralelas ΛΞ, KN, ΘΜ.
Digo que también así las magnitudes ΓΔ, EZ parecen convergentes.
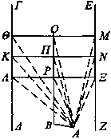
Trácese BP perpendicular desde B a ΛΞ y prolónguese BP hasta O e incidan los rayos ΑΛ, AK, ΑΘ, ΑΞ, ΑΝ, AM y trácense AP, ΑΠ, AO. Puesto que se ha trazado una recta AP desde el punto elevado A hasta ΡΞ, entonces AP es perpendicular a ΡΞ, y AO es perpendicular a OM y ΑΠ a ΠΝ. Luego los triángulos ΑΡΞ, ΑΠΝ, AOM son rectángulos. Y, puesto que son rectángulos, ΠΝ es igual a ΡΞ y ΠΑ es mayor que AP, luego el ángulo correspondiente a ΞΑΡ es mayor que el correspondiente a ΠΑΝ. Luego también se verá mayor ΡΞ que ΠΝ [Def. 4], De manera semejante, también ΡΛ se verá mayor que ΠΚ. Luego toda la magnitud ΛΞ se verá mayor que toda la magnitud ΠΚ.
Luego también así las magnitudes se verán convergentes.
PROPOSICIÓN 7
Las magnitudes iguales que están sobre la misma recta sin estar puestas una a continuación de otra y situadas a distancias desiguales del ojo parecen desiguales.
Sean AB, ΓΔ dos magnitudes iguales sobre la misma recta ΑΔ sin estar puestas una a continuación de otra y situadas a distancias desiguales del ojo E, e incidan los rayos EA, ΕΔ y sea EA mayor que ΕΔ.
Digo que ΓΔ parecerá mayor que AB.
Incidan los rayos EB, ΕΓ y circunscríbase el círculo ΑΕΔ en torno al triángulo ΑΕΔ. Y sean las rectas BZ, ΓΗ prolongación de las rectas EB, ΕΓ; y trácense formando ángulos rectos desde los puntos Β, Γ las rectas iguales[5] ΒΘ, ΓΚ. Por otro lado, AB es igual a ΓΔ, y también el ángulo correspondiente a ΑΒΘ es igual al correspondiente a ΔΓΚ. Por tanto, el arco de circunferencia ΑΘ es igual al arco de circunferencia ΔΚ.
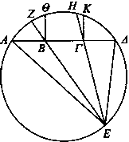
Por tanto, el arco de circunferencia ΚΔ es mayor que el arco de circunferencia ZA. Por tanto, el arco de circunferencia ΗΔ es mucho mayor que el arco de circunferencia ZA. Pero el ángulo correspondiente a AEZ está sobre el arco de circunferencia ZA, y el correspondiente a ΗΕΔ está sobre el arco de circunferencia ΗΔ. Por tanto, el ángulo correspondiente a ΗΕΔ es mayor que el correspondiente a AEZ. Y AB se ve bajo el correspondiente a AEZ y ΓΔ bajo el correspondiente a ΗΕΔ.
Luego ΓΔ parece mayor que AB [Def. 4],
PROPOSICIÓN 8
Las magnitudes iguales y paralelas situadas a distancias distintas del ojo no se ven proporcionalmente a las distancias[6].
Sean dos magnitudes AB, ΓΔ situadas a distancias distintas del ojo E.
Digo que no cabe, como parece ser, que ΓΔ sea a AB como BE a ΕΔ.
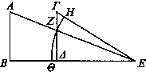
Incidan los rayos AE, ΕΓ y con centro E y radio EZ trácese el arco de circunferencia de un círculo ΗΖΘ. Puesto que el triángulo ΕΖΓ es mayor que el sector EZH, y el triángulo ΕΖΔ es menor que el sector ΕΖΘ, entonces el triángulo ΕΖΓ guarda con el sector EZH una razón mayor que el triángulo ΕΖΔ con el sector ΕΖΘ. Y, tomando la proporción en alternancia[7], el triángulo ΕΖΓ guarda con el triángulo ΕΖΔ una razón mayor que el sector EZH con el sector ΕΖΘ y, por composición[8], el triángulo ΕΓΔ guarda con el triángulo ΕΖΔ una razón mayor que el sector EHZ con el sector ΕΖΘ. Pero el triángulo ΕΔΓ es al ΕΖΔ como ΓΔ a ΔΖ; y ΓΔ es igual a AB, y AB es a ΔΖ como BE es a ΕΔ. Luego BE guarda con ΕΔ una razón mayor que el sector ΕΗΘ con el sector ΕΖΘ. Y como el sector es al sector, así el ángulo correspondiente a ΗΕΘ al ángulo correspondiente a ΖΕΘ. Luego BE guarda con ΕΔ una razón mayor que el ángulo correspondiente a ΗΕΘ con el correspondiente a ΖΕΘ. Y ΓΔ se ve desde el ángulo correspondiente a ΗΕΘ, mientras que AB desde el correspondiente a ΖΕΘ.
Luego las magnitudes iguales no se ven en proporción a las distancias.
PROPOSICIÓN 9
Las magnitudes rectangulares vistas a distancia parecen redondeadas.
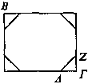
Sea el rectángulo ΒΓ visto a distancia que se encuentra elevado. Puesto que cada uno de los objetos vistos tiene una longitud de separación que una vez que está situado allí ya no se ve [Prop. 3], entonces no se ve el ángulo Γ, sino que sólo aparecen los puntos Δ, Z. Eso sucederá de manera semejante también en cada uno de los restantes ángulos.
De modo que todo entero parecerá redondeado.
PROPOSICIÓN 10
Las partes más lejanas de los planos situados por debajo del ojo parecen más elevadas.
Sea A el ojo situado más elevado que ΒΕΓ, e incidan los rayos AB, AE, ΑΔ, ΑΓ, de los cuales AB sea perpendicular al plano supuesto.
Digo que ΓΔ parece más elevado que ΔΕ y ΔΕ más que BE.
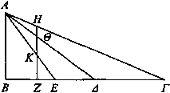
Tómese en BE un punto al azar Z, y trácese ZH formando ángulos rectos. Puesto que los rayos visuales inciden en ZH antes que en ΖΓ, incida ΑΓ en ZH en el punto Η, ΑΔ en el Θ y AE en el K. Puesto que H está más elevado que Θ y Θ más que K, mientras que Γ está en el mismo plano que H y Δ en el mismo que Θ y E en el mismo que K y, al tiempo, ΔΓ se ve mediante ΑΓ, ΑΔ; y ΔΕ mediante ΑΔ, AE; entonces ΓΔ parece más elevado que ΔΕ. De modo semejante también ΔΕ parecerá más elevado que BE, puesto que los objetos vistos bajo rayos más elevados parecen más elevados [Def. 5].
Y es evidente que los objetos situados en un plano más elevado parecerán cóncavos[9].
PROPOSICIÓN 11
Las partes más lejanas de los planos situados por encima del ojo parecen más bajas.

Sea A el ojo situado más bajo que el plano ΒΓ, e incidan los rayos BA, ΑΔ, AE, ΑΓ, de los cuales sea AB perpendicular al plano supuesto. Digo que ΓΕ parece más bajo que ΕΔ.
Por el teorema expuesto previamente, el rayo ΑΓ es más bajo que el AE, el AE más que el ΑΔ, el ΑΔ más que el AB. Y ΓΕ se ve mediante los rayos ΓΑ, AE mientras que ΕΔ se ve mediante EA, ΑΔ y ΔΒ se muestra mediante ΔΑ, AB.
Luego ΓΕ parece más bajo que ΕΔ y ΕΔ más que ΔΒ [Def. 5].
PROPOSICIÓN 12
De los objetos que tienen longitud hacia delante, los que están a la derecha parecen desviarse hacia la izquierda y los que están a la izquierda, hacia la derecha [Def. 9].
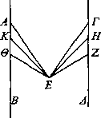
Sean AB, ΓΔ dos magnitudes vistas y sea E el ojo desde el cual incidan los rayos ΕΘ, ΕΚ, EA, EZ, EH, ΕΓ. Digo que EZ, EH, ΕΓ parecen cambiar de dirección hacia la izquierda, mientras que ΕΘ, ΕΚ, EA hacia la derecha.
Puesto que EZ está más a la derecha que EH y EH más que ΕΓ, a partir de ello da entonces la impresión de que ΕΓ cambia de dirección hacia la izquierda de EH y HE a la de EZ. También, de manera semejante, EK, EA, ΕΘ parecen desviarse hacia la derecha [Def. 6].
PROPOSICIÓN 13
De las magnitudes iguales situadas bajo el mismo ojo las más lejanas parecen más elevadas.
Sean AB, ΓΔ, EZ magnitudes iguales y sea H el ojo, situado más elevado que las magnitudes, e incidan los rayos HA, ΗΓ, HE.
Digo que AB parece más elevado que ΓΔ, y ΓΔ más que EZ.
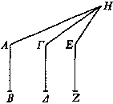
Puesto que HA está más elevado que ΗΓ y ΗΓ más que HE y puesto que los puntos A, Γ, E están en el mismo plano que los rayos HA, ΗΓ, HE y las magnitudes AB, ΓΔ, EZ están en el mismo plano que A, Γ, E, entonces AB parece más elevado que ΓΔ y ΓΔ más que EZ[10].
PROPOSICIÓN 14
De las magnitudes iguales y situadas por encima del ojo, las más lejanas parecen más bajas.
Sean AB, ΓΔ, EZ magnitudes iguales situadas más arriba que el ojo H.
Digo que AB parece más bajo que ΓΔ y ΓΔ más que EZ.
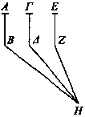
Incidan los rayos HB, ΗΔ, HZ. Puesto que el rayo HB es más bajo que el ΗΔ y el ΗΔ más que el HZ, mientras que los puntos Β, Δ, Z están en el mismo plano que los rayos HB, ΗΔ, HZ y las magnitudes AB, ΓΔ, EZ están en el mismo plano que Β, Δ, Z, entonces AB parece más bajo que ΓΔ y ΓΔ más que EZ[11].
PROPOSICIÓN 15
Cuantos objetos situados bajo el mismo ojo son mayores unos que otros, al acercarse el ojo, el que aparece por encima parece mayor en una magnitud mayor, mientras que al alejarse, en una magnitud menor.
Sean AB, ΓΔ dos magnitudes desiguales y sea mayor AB y sea E el ojo desde el cual incida el rayo EZ que pasa por Γ.
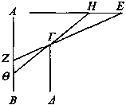
Puesto que ZB, ΓΔ se muestran bajo el ojo y el rayo EZ, entonces AB aparece por encima de ΓΔ en la magnitud AZ.
Cambie de posición el ojo a una más cercana y sea H, desde el cual incida el rayo ΗΘ que pase por Γ. Puesto que ΓΔ y ΘΒ se muestran bajo el ojo y bajo el rayo ΗΘ, entonces AB parecerá mayor que ΓΔ en la magnitud ΑΘ. Y bajo E se veía mayor en AZ, y ΑΘ es mayor que AZ[12].
Luego al acercarse el ojo, el objeto que aparece por encima parece mayor en una magnitud mayor y, al alejarse, en una menor.
PROPOSICIÓN 16
Cuantas magnitudes desiguales entre sí sobresalen por encima del ojo, al acercarse el ojo, la magnitud que sobresale por encima parece mayor en una magnitud menor, mientras que al alejarse, en una mayor.
Sean AB, ΓΔ magnitudes desiguales, de las cuales la mayor es AB. Sea E el ojo desde el cual incida el rayo EZ que pase por Γ.
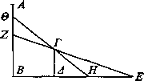
Puesto que las magnitudes ZB, ΓΔ se toman bajo el rayo EZ, entonces BZ, ΓΔ parecen iguales entre sí. Entonces AB parece mayor que ΓΔ en la magnitud AZ. Aproxímese el ojo más cerca y sea H, desde el cual incida el rayo ΗΘ que pase por Γ. Puesto que ΒΘ, ΓΔ se toman bajo el rayo ΗΘ, mientras que ZB, ΓΔ bajo el EZ, y ZA es mayor que ΑΘ, entonces, al acercarse el ojo, el objeto que sobresale por encima parece mayor en una magnitud menor y, al alejarse, en una mayor.
PROPOSICIÓN 17
Cuantos objetos son mayores unos que otros, al acercarse y alejarse el ojo a la magnitud menor en línea recta[13], parecerá siempre que el objeto que sobresale por encima excede al menor en lo mismo.
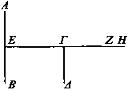
Sean AB, ΓΔ dos magnitudes desiguales, de las cuales la mayor es AB, y sea Z el ojo situado en línea recta con el extremo Γ de la magnitud ΓΔ. Digo que al acercarse y alejarse el ojo Z que está en línea recta parecerá que AB sobresale por encima de ΓΔ en lo mismo.
Incida el rayo ZE que pasa por Γ. Entonces AB apárece por encima de ΓΔ en la magnitud AE.
Cambie de posición el ojo H y esté más lejos y esté en línea recta. Entonces el rayo que incide desde el ojo H pasará por el punto Γ y llegará hasta el punto E y AB aparecerá por encima de ΓΔ en lo mismo.
PROPOSICIÓN 18
Conocer de qué tamaño es una altitud dada cuando brilla el sol.

Sea AB la altura dada y sea necesario conocer de qué tamaño es. Sea Δ el ojo y ΓΑ el rayo de sol que se une con el extremo de la magnitud AB y trácese[14] hasta el ojo Δ. Y sea ΔΒ la sombra de AB. Y póngase otra magnitud EZ que, sin ser en absoluto iluminada por el rayo, se una con él en su extremo Z. Así, se ha aplicado al triángulo ΑΒΔ otro triángulo ΕΖΔ. Por tanto, ΔΕ es a ZE como ΔΒ a BA [Elem. VI 2]. Y la razón de ΔΕ a EZ es conocida, luego también la razón de ΔΒ a BA es conocida. Y ΔΒ es conocido.
Luego también es conocido AB.
PROPOSICIÓN 19
Conocer de qué tamaño es la altitud dada no habiendo sol.
Sea AB la altitud y sea Γ el ojo y sea necesario conocer de qué tamaño es AB sin haber sol.
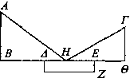
Póngase el espejo ΔΖ y prolónguese ΔΒ en línea recta con ΕΔ hasta que coincida con el extremo B de la magnitud AB, e incida el rayo ΓΗ desde el ojo Γ y refráctese hasta que coincida con el extremo A de la magnitud AB y sea ΕΘ prolongación de ΔΕ y trácese ΓΘ perpendicular a ΕΘ desde Γ. Puesto que el rayo ΓΗ ha incidido y HA es el rayo refractado correspondiente, las refracciones se han producido en ángulos iguales, como dice en los libros de Catóptrica[15]. Por tanto, el ángulo correspondiente a ΓΗΘ es igual al correspondiente a AHB. Pero también el correspondiente a ABH es igual al correspondiente a ΓΘΗ; y por consiguiente, el restante, el correspondiente a ΗΓΘ, es igual al restante, el correspondiente a HAB. Por tanto, el triángulo AHB es equiángulo respecto al triángulo ΓΗΘ. Y en los triángulos equiángulos los lados son proporcionales [Elem. VI 4]. Por tanto, ΓΘ es a ΘΗ como AB a BH. Pero la razón de ΓΘ a BH es conocida; luego también la razón de BA a BH es conocida; y HB es conocido.
Luego también AB es conocido.
PROPOSICIÓN 20
Conocer de qué tamaño es una profundidad dada.
Sea ΑΔ la profundidad dada y sea E el ojo y sea necesario conocer de qué tamaño es la profundidad.

Incida a la vista el rayo del sol ΕΔ que coincide con el plano en el punto B y con la profundidad en Δ. Y prolónguese BZ en línea recta desde B y trácese EZ perpendicular a la recta BZ desde E. Así, puesto que el ángulo correspondiente a EZB es igual al correspondiente a ΒΑΔ mientras que también el correspondiente a ΑΒΔ es igual al correspondiente a EBZ, también el tercero, el correspondiente a BEZ es igual al correspondiente a ΑΔΒ. Por consiguiente, el triángulo ΑΔΒ es equiángulo respecto al triángulo BEZ. Por tanto, los lados serán proporcionales [Elem. VI 4], Luego EZ es a ZB como ΔΑ a AB. Y la razón de EZ a ZB es conocida; luego la razón de ΔΑ a AB también es conocida; y también AB es conocido.
Luego también ΑΔ es conocido.
PROPOSICIÓN 21
Conocer de qué tamaño es la longitud dada.
Sea AB la longitud dada y sea Γ el ojo y sea necesario conocer de qué tamaño es la longitud AB.

Incidan los rayos ΓΑ, ΓΒ y tómese próximo al ojo Γ un punto al azar Δ sobre el rayo, y trácese desde el punto Δ la recta ΔΕ paralela a AB. Puesto que ΔΕ se ha trazado paralela a uno de los lados, BA, del triángulo ΑΒΓ, entonces ΓΔ es a ΔΕ como ΓΑ a AB [Elem. VI 2], Y la razón de ΓΔ a ΔΕ es conocida; luego también la razón de ΑΓ a AB es conocida. Y ΑΓ es conocido.
Luego también AB es conocido.
PROPOSICIÓN 22
Si se pone un arco de circunferencia de un círculo en el mismo plano en que está el ojo, el arco de circunferencia del círculo[16] parece una línea recta.
Sea ΒΓ un arco de circunferencia de un círculo situado en el mismo plano que el ojo A, desde el cual incidan los rayos AB, ΑΔ, AE, AZ, AH, ΑΘ, ΑΓ.
Digo que el arco ΒΓ parece una recta.
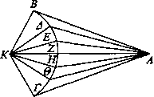
Sitúese el centro de la circunferencia y sea K, y trácense las rectas KB, ΚΔ, KE, KZ, KH, ΚΘ, ΚΓ. Puesto que KB se ve bajo el ángulo correspondiente a KAB y ΚΔ bajo el correspondiente a ΚΑΔ, entonces KB parecerá mayor que ΚΔ, y ΚΔ mayor que KE y KE mayor que KZ y, por la otra parte, ΚΓ parecerá mayor que ΚΘ, ΚΘ mayor que KH y KH mayor que KZ. Por ello, permaneciendo la recta KA †[17], ΒΓ siempre es perpendicular. Lo mismo sucederá también en la parte cóncava de la circunferencia.
DE OTRA MANERA
También es posible decir sobre estos rayos visuales que la recta entre el ojo A y el diámetro es la menor, y que la más cercana a ella es siempre menor que la más lejana. Lo mismo ocurre también siendo AZ una perpendicular sobre él[18]. Por eso la circunferencia envía la representación de una recta, sobre todo si apareciera a tan gran distancia que no pudiéramos percibir su convexidad. Por eso las cuerdas que no están muy tensadas, vistas de lado, parece que tienen holgura, pero desde abajo parecen ser rectas, y las sombras de las argollas situadas en el mismo plano que lo que las ilumina son rectas[19].
DE OTRA MANERA
Si se pone un arco de circunferencia de un circulo en el mismo plano que el ojo, el arco de circunferencia del círculo parece una línea recta.
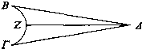
Sea ΒΓ el arco de circunferencia de un círculo, y sea Δ el ojo que está en el mismo plano que el arco de circunferencia ΒΓ, a partir del cual incidan los rayos visuales ΔΒ, ΔΖ, ΔΓ. Así, puesto que ninguno de los objetos vistos se ve entero al mismo tiempo [Prop. 1], BZ es una recta; y de manera semejante ΖΓ.
Por consiguiente, todo el arco de circunferencia ΒΓ parecerá una recta[20].
PROPOSICIÓN 23[21]
Una esfera vista de cualquier manera por un ojo parece siempre menor que una semiesfera y la propia parte vista de la esfera parece una circunferencia de un círculo.

Sea una esfera cuyo centro sea A y sea B el ojo. Y trácese AB y prolónguese el plano que pasa por BA. Producirá como corte un círculo[22]. Produzca el círculo ΓΔΘΗ y, en torno al diámetro AB, dibújese el círculo ΓΒΔ y trácense las rectas ΓΒ, ΒΔ, ΑΔ, ΑΓ. Puesto que ΑΓΒ es un semicírculo, el ángulo correspondiente a ΑΓΒ es recto, e igualmente el correspondiente a ΒΔΑ. Por tanto, ΓΒ, ΒΔ se tocan. Únase ΓΔ y trácese ΗΘ paralela a ΓΔ por el punto A. Entonces, los ángulos con vértice K son rectos. Y si haciendo girar el triángulo ΒΓΚ en torno al ángulo recto K, mientras AB permanece fija, se le lleva de nuevo a la misma posición en la que empezó a moverse, ΒΓ tocará a la esfera en un punto y ΚΓ producirá como corte un círculo.
Por tanto, en la esfera se verá una circunferencia de un círculo.
Digo además que será menor que la semiesfera.
Puesto que ΗΘ es un semicírculo, ΓΔ es menor que un semicírculo. Y mediante los rayos ΒΓ, ΒΔ se ve la misma parte de la esfera. Por tanto ΓΔ es menor que una semiesfera. Y se ve mediante los rayos ΒΓ, ΒΔ.
PROPOSICIÓN 24
Al acercarse el ojo a la esfera, lo que se ve será menor, pero parecerá que se ve mayor.
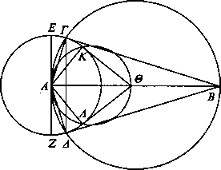
Sea una esfera cuyo centro sea A y sea B el ojo a partir del cual se trace la recta AB. Y circunscríbase en torno a AB el círculo ΓΒΔ, y trácese desde el punto A la recta EZ formando ángulos rectos por ambos lados con la recta AB, y prolónguese el plano que pasa por EZ, AB. Producirá como corte un círculo. Sea ΓΕΖΔ, y trácense ΓΑ, ΑΔ, ΔΒ, ΒΓ, ΓΔ. Como en el teorema previo, los ángulos con vértice en los puntos Γ, Δ son rectos. Por tanto, ΒΓ, ΒΔ, que son rayos, se tocan y bajo el ojo B se ve la parte ΓΔ de la esfera.
Cambie de posición el ojo más cerca de la esfera y sea Θ, y a partir de él trácese la recta ΘΑ y dibújese el círculo ΑΛΚ y trácense las rectas ΘΚ, KA, ΑΛ, ΛΘ. De manera semejante, bajo el ojo Θ se ve la parte KΛ de la esfera, mientras que bajo B se veía ΓΔ. Y KΛ es menor que ΓΔ.
Luego, al acercarse el ojo, lo que se ve es menor, pero da la impresión de que parece mayor, porque el ángulo correspondiente a ΚΘΛ es mayor que el ángulo correspondiente a ΓΒΔ [Def. 4].
PROPOSICIÓN 25
Vista una esfera mediante dos ojos, se verá su semiesfera íntegra si el diámetro de la esfera es igual a la recta que distan los ojos entre sí.

Sea una esfera cuyo centro sea A y dibújese en la esfera en torno al centro A el círculo ΒΓ y trácese su diámetro ΒΓ y desde Β, Γ trácense ΒΔ, ΓΕ formando ángulos rectos[23] y sea paralela a ΒΓ la recta ΔΕ, sobre la cual yazgan los ojos Δ, E.
Digo que se verá la semiesfera íntegra.
Por el punto A trácese AZ paralela a cada una de las rectas ΒΔ, ΓΕ. Entonces ΑΒΔΖ es un paralelogramo. Si al hacerlo girar, permaneciendo fija AZ, llega de nuevo a la misma posición desde la que empezó a moverse la figura que se ha hecho girar, empezará en B, llegará a Γ y B y la figura descrita por la recta AB será un círculo que pasa por el centro de la esfera.
Luego bajo los ojos Δ, E se verá una semiesfera.
PROPOSICIÓN 26
Si la distancia entre los ojos es mayor que el diámetro de la esfera, se verá más de una semiesfera de la esfera.
Sea una esfera cuyo centro sea A y descríbase en torno al centro A el círculo ΕΘΔΗ, y sean los ojos Β, Γ y sea la distancia entre los rayos visuales B, Γ mayor que el diámetro de la esfera y trácese ΒΓ.
Digo que se verá más de una semiesfera.
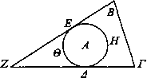
Incidan los rayos BE, ΓΔ y prolónguense hacia las partes E, Δ. Llegan a coincidir uno con otro por ser el diámetro menor que ΒΓ. Coincidan en el punto Z. Puesto que las rectas ZE, ΖΔ han incidido en la circunferencia desde un punto exterior al círculo, ΔΘΗ es menor que un semicírculo [Líber De Visu (Theisen 24)]. Luego ΕΗΔ es mayor que un semicírculo. Y ΕΗΔ se ve bajo Β, Γ. Por tanto, bajo Β, Γ se ve más de la mitad del círculo.
Luego lo mismo se verá de la esfera.
PROPOSICIÓN 27
Si la distancia entre los ojos es menor que el diámetro de la esfera, se verá menos de una semiesfera.
Sea una esfera cuyo centro sea el punto A y descríbase en torno al punto A el círculo ΒΓ y quede entre los ojos la distancia ΔΕ que sea menor que el diámetro de la esfera, a partir del cual trácense las tangentes ΔΒ, ΕΓ y sean ellas mismas también rayos. Digo que se verá menos de una semiesfera.
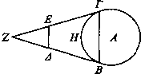
Prolónguense ΒΔ, ΓΕ; irán a coincidir en la parte de Γ, B, H, puesto que ΔΕ es menor que el diámetro de la esfera. Coincidan en el punto Z. Puesto que las rectas ZB, ZΓ han incidido desde un punto Z, ΒΗΓ será menor que un semicírculo [Líber De Visu (Theisen 24)]; pero lo que ocupa el segmento ΒΗΓ, lo ocupa también el de la esfera.
Por tanto, contienen menos de una semiesfera.
PROPOSICIÓN 28
Un cilindro visto de cualquier manera por un ojo se verá menos de un semicilindro.
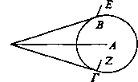
Sea un cilindro del que el punto A sea el centro de la base y descríbase en torno a A el círculo ΒΓ y esté situado el ojo Δ situado en el mismo plano que la base ΒΓ del cilindro y únase la recta ΔΑ desde Δ hasta A y trácense desde Δ los rayos ΔΒ, ΔΓ y sean tangentes al círculo y álcense los lados del cilindro BE, ΓΖ desde los puntos B, Γ formando ángulos rectos y prolónguense el plano que pasa por ΔΒ, BE y el que pasa por ΔΓ, ΓΖ. Ninguno de los dos, por tanto, corta al cilindro, ya que ΔΒ, ΔΓ y BE, ΓΖ son tangentes. Así, ΒΓ se ve mediante los rayos ΒΔ, ΔΓ, lo cual es menor que un semicírculo [Líber De Visu (Theisen 24)].
De la misma manera, también se verá menos de un semicilindro[24].
Y si se viera mediante dos ojos es evidente que ocurrirá también en este caso lo dicho en el caso de la esfera.
DE OTRA MANERA
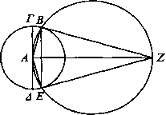
Sea un círculo cuyo centro sea A y sea Z un punto exterior[25] y únase AZ desde A hasta Z y desde el punto A álcese ΓΔ formando ángulos rectos con AZ por ambas partes. Luego ΓΔ es el diámetro del círculo. Y descríbase en torno a la recta AZ el círculo ABZE y trácense AB, BZ, ZE, EA. Luego ZB, ZE son tangentes, puesto que los ángulos con vértice en los puntos Β, E son rectos[26]. Así, puesto que los rayos BZ, ZE han incidido desde un punto Z en la circunferencia del círculo, entonces se verá la parte BE del círculo. Y ΓΒΕΔ es un semicírculo.
Luego BE es menor que un semicírculo.
Este teorema es para los conos y para los cilindros, pues si desde los puntos Β, E se trazan formando ángulos rectos los lados de los cilindros, los rayos serán tangentes a ellos por la parte por la que inciden y quedará cerrada la parte ΒΔΕ de la vista, y se verá la parte BE del semicírculo. Y se verá esa misma parte de los conos, la menor[27].
PROPOSICIÓN 29
Al poner el ojo más cerca del cilindro, la parte del cilindro comprendida por los rayos es menor, pero parecerá que se ve mayor.
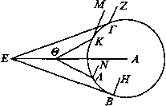
Sea un cilindro cuya base sea el círculo ΒΓ, su centro A y E el ojo desde el cual se trace EA hasta el centro e incidan los rayos EB, ΕΓ y desde los puntos Β, Γ trácense ΓΖ, BH formando ángulos rectos con el cilindro[28]. Por lo anterior, ΗΒΓΖ es menor que un semicilindro. Y se ve mediante el ojo E.
Cambie de posición el ojo Θ a más cerca.
Digo que lo comprendido por el ojo Θ da la impresión de parecer mayor que ΖΒΓΗ, siendo menor que ello.
Incidan los rayos ΘΚ, ΘΛ y trácense formando ángulos rectos desde los puntos K, Λ los lados del cilindro KM, ΛΝ. Mediante los rayos ΘΚ, ΘΛ se verá la parte ΜΚΛΝ del cilindro. Pero también ΖΓΒΗ se ve mediante EB, ΕΓ; y ΖΓΒΗ es mayor que MKΛN. Pero da la impresión de parecer menor, puesto que también el ángulo correspondiente a Θ es mayor que el de E [Def. 4],
PROPOSICIÓN 30
Visto mediante un ojo un cono que tiene un círculo como base y el eje formando ángulos rectos con ella se verá menor que un semicono.
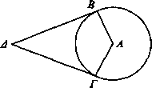
Sea un cono cuya base es el círculo ΒΓ y su vértice el punto A y sea Δ el ojo desde el cual incidan los rayos ΔΒ, ΔΓ. Y puesto que los rayos ΔΒ, ΔΓ han incidido tangentes a ΒΓ, entonces ΒΓ es menor que un semicírculo por lo demostrado anteriormente [Liber De Visu (Theisen 24)]. Trácense desde el vértice A del cono hacia los puntos B, Γ los lados del cono AB, ΑΓ. Luego lo comprendido por las rectas AB, ΑΓ y el sector ΒΓ es menor que un semicono, puesto que también ΒΓ es menor que un semicírculo.
Por tanto se verá menor que un semicono.
PROPOSICIÓN 31
Al colocar el ojo más cerca en el mismo plano en el que está la base del cono, la parte comprendida por los rayos visuales será menor, pero dará la impresión de que se ve mayor.
Sea un cono cuya base sea el círculo AB y su vértice el punto Γ y sea Δ el ojo y tómese el centro del círculo Λ, y trácese la recta ΔΛ e incidan los rayos ΔΑ, ΔΒ y trácense los lados ΑΓ, ΓΒ del cono. Así, la parte ΑΒΓ del cono queda comprendida por el ojo Δ y los rayos visuales ΔΑ, ΔΒ y es menor que un semicono.

Cambie de posición el ojo a más cerca y sea E, e incidan los rayos EZ, EH y trácense los lados ZΓ, ΓΗ. De nuevo, queda comprendida la parte ΖΓΗ del cono por el ojo E y los rayos visuales EZ, EH. Y ΖΓΗ es menor que ΑΒΓ, pero da la impresión de que parece mayor, puesto que el ángulo correspondiente a ZEH es mayor que el ángulo correspondiente a ΑΔΒ.
Y es evidente que también en el caso de un cono visto por dos ojos ocurrirá lo que ocurría en el caso de la esfera y el cilindro vistos de la misma manera.
PROPOSICIÓN 32
Si inciden rayos desde el ojo hacia la base del cono y desde los rayos incidentes y tangentes, desde sus puntos de contacto, se trazan rectas por la superficie del cono hacia su vértice y desde las rectas trazadas y los rayos que inciden desde el ojo hacia la base del cono se prolongan planos; si se pone el ojo en su contacto, es decir, en la sección común de los planos, lo que se ve del cono en total se verá igual mientras el rayo visual esté en un plano paralelo al plano presupuesto.
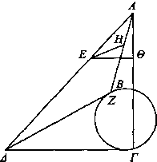
Sea un cono cuya base es el círculo ΒΓ y su vértice el punto A y sea Δ el ojo desde el que incidan los rayos ΔΖ, ΔΓ y trácense desde los puntos de contacto Z, Γ hacia el vértice A del cono los lados ZA, ΓΑ del cono y prolónguese el plano que pasa por ΔΖ, ZA y el que pasa por ΓΔ, ΓΑ. Producirá como corte común una recta. Sea la recta ΑΕΔ. Digo que si el ojo se transporta sobre ΑΕΔ se verá del cono lo mismo que se veía mediante los rayos ΔΓ, ΔΖ.
Esté situado sobre ΑΕΔ el ojo E desde el cual incidan rayos hacia el cono. Irán por AZ, ΑΓ, puesto que el ojo está situado sobre un plano paralelo y los rayos visuales se mueven en líneas rectas. Pues si cayeran fuera de ΑΓ, AZ, los rayos visuales serán quebrados, lo cual es imposible. Sean pues ΕΘ, EH. Puesto que los rayos visuales se mueven en líneas rectas sobre un plano paralelo y que las cosas vistas bajo ángulos iguales parecen iguales, cuantos rayos visuales paralelos se pongan sobre la recta ΑΕΔ contienen ángulos iguales, luego se verá lo mismo del cono [Def. 4] [si ven lo mismo; pero ven una parte menor del cono; luego se verá también una parte menor del cono][29].
PROPOSICIÓN 33
De nuevo, si el ojo cambia de posición desde un plano más bajo, colocado el ojo más alto lo que se ve del cono será mayor, pero dará la impresión de que parece menor, mientras que estando más bajo será menor, pero dará la impresión de que parece mayor.
Sea un cono cuya base sea el círculo ΒΓ y su vértice el punto A, y sean los lados del cono BA, ΑΓ. Trácese ΒΓ y añádase BH a ΒΓ y trácese por un punto Θ al azar la recta ΘΚ paralela a AB.
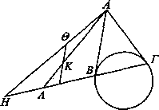
Digo que, si se pone el ojo en el punto Θ, lo que se ve del cono será mayor, pero se verá menor que si se pone en el punto K.
Trácense AK, ΑΘ y prolónguense ΑΘ hacia H y AK hacia Λ. Así, al poner el ojo en H y en Λ será distinto lo que se ve del cono, y será mayor lo que se ve desde el ángulo de H, pero se verá mayor lo que se ve desde el ángulo de Λ a pesar de ser menor. Y lo que se ve desde el ángulo de H es igual que lo que se ve desde el ángulo de Θ y lo que se ve desde el ángulo de Λ, igual a lo que se ve desde el ángulo de K, como se demostró en la proposición anterior.
Luego lo que se ve del cono será mayor si se pone el ojo en Θ que si se pone en K, pero dará la impresión de que es menor.
PROPOSICIÓN 34
Si desde el centro de un círculo se alza una recta formando ángulos rectos con el plano del círculo y se coloca el ojo sobre ella, los diámetros trazados en el plano del círculo parecerán todos iguales.
Sea un círculo cuyo centro sea el punto A y desde él, formando ángulos rectos con el plano del círculo, álcese una recta AB, sobre la cual esté situado el ojo B.
Digo que los diámetros parecerán iguales.

Sean ΓΔ, EZ dos diámetros y trácense ΒΓ, BE, ΒΔ, BZ. Puesto que ZA es igual a ΑΓ y AB es común y los ángulos son rectos, entonces la base ZB y la base ΒΓ son iguales y también los ángulos que están junto a las bases. Por tanto, el ángulo comprendido por ZB, BA es igual al comprendido por AB, ΒΓ. E igualmente también el correspondiente a EBA y el correspondiente a ΑΒΔ. Luego el comprendido por ΓΒ, ΒΔ es igual al comprendido por EB, BZ. Y las cosas vistas bajo ángulos iguales parecen iguales [Def. 4]; luego ΓΔ parece igual a EZ.
* * *
Y si la recta trazada desde el centro no formara ángulos rectos con el plano pero fuera igual al radió, los diámetros parecerán todos iguales.
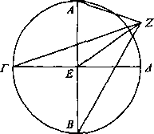
Sea el círculo ΑΒΓΔ y trácense en él dos diámetros AB, ΓΔ y sea ZE, sobre la que está situado el ojo Z, la recta trazada desde el punto E sin formar ángulos rectos, pero igual a cada uno de los radios, y trácense los rayos ZA, ZΓ, ZB, ΖΔ. Puesto que BE es igual a EZ y también EA es igual a EZ, entonces las tres rectas EZ, EA, EB son iguales. Luego el semicírculo descrito en torno al diámetro AB en el plano que pasa por AB, EZ pasará por el punto Z. Luego el ángulo comprendido por AZ, ZB es recto. Y es igualmente recto el comprendido por ΓΖ, ΖΔ. Y los ángulos rectos son iguales y los objetos vistos bajo ángulos iguales parecen iguales. Luego AB parecerá igual a ΓΔ.
* * *
Y ahora ni sea igual AZ al radio ni forme ángulos rectos con el plano del círculo, pero haga iguales los ángulos correspondientes a ΔΑΖ, ΖΑΓ y los correspondientes a EAZ, ZAB.
Digo que también así parecerán iguales los diámetros que forman ángulos iguales.
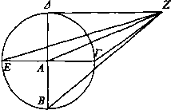
Puesto que las rectas ΓΑ, AZ son iguales a ZA, AΔ y las rectas BA, AZ iguales a ZA, AE, entonces también son iguales los ángulos; luego la base ΔΖ es igual a la base ΖΓ. De manera que también el ángulo correspondiente a ΔΖΑ es igual al correspondiente a ΑΖΓ. De la misma manera demostraremos que el ángulo correspondiente a EZA es igual al correspondiente a AZB. Luego el ángulo entero correspondiente a ΔΖΒ es igual al correspondiente a ΕΖΓ; de manera que también los diámetros ΔΒ, ΕΓ parecerán iguales [Def. 4],
PROPOSICIÓN 35
Si el rayo que incide desde el ojo hacia el centro del círculo ni formara ángulos rectos con el plano del círculo ni fuera igual al radio ni comprendiera ángulos iguales[30], los diámetros con los que forma ángulos desiguales parecerán desiguales.
Sea el círculo ΑΒΓΔ y trácense los dos diámetros AB, ΓΔ que se cortan mutuamente formando ángulos rectos en el punto E; y la línea ZE, trazada desde el punto E, sobre la cual está situado el ojo, no forme ángulos rectos con el plano ni sea igual al radio ni contenga con las rectas ΑΓ, ΔΒ ángulos iguales.

Digo que los diámetros ΑΓ, ΔΒ se verán desiguales.
Trácense ΖΓ, ZA, ΖΔ, ZB. Efectivamente, EZ es mayor que el radio o menor; por eso, efectivamente, el ángulo comprendido por ΔΖ, ZB es mayor que el comprendido por ΓΖ, ZA o el comprendido por ΓΖ, ZA mayor que el comprendido por ΔΖ, ZB, como a continuación demostraremos.
Luego los diámetros se verán desiguales.
LEMA
Sea un círculo cuyo centro sea el punto A y sea B el ojo desde el cual, trazada la perpendicular al círculo, no caiga en el centro A, sino fuera, y sea ΒΓ y trácese ΑΓ desde A hasta Γ y AB desde A hasta B.
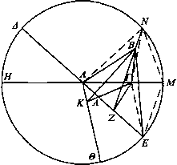
Digo que de todos los ángulos comprendidos por las rectas trazadas por el punto A y que forman un ángulo con la recta AB el menor es el comprendido por ΓΑ, AB.
Trácese por A la recta ΔΑΕ. Digo que el ángulo correspondiente a ΓΑΒ es menor que el correspondiente a EAB.
Trácese desde Γ hasta ΔΕ la perpendicular ΓΖ en el plano, y trácese BZ. Luego también BZ es perpendicular a ΔΕ. Puesto que el ángulo correspondiente a ΓΖΑ es recto, el correspondiente a ΑΓΖ es menor que un recto. Y al ángulo mayor lo subtiende el lado mayor. Luego ΑΓ es mayor que AZ. Pero el ángulo comprendido por ΑΓ, ΓΒ y el comprendido por BZ, ZA son rectos. De modo que las rectas ΓΒ, BZ son desiguales. Y el ángulo comprendido por ZA, AB es mayor que el comprendido por ΓΑ, AB. De manera semejante se demostrará que de todos los ángulos comprendidos por las rectas trazadas por el punto A y que forman un ángulo con la recta AB el menor es el comprendido por ΓΑ, AB.
Y es evidente que si se traza cualquier otra recta por el punto A, como ΑΘ, que esté más lejos de ΑΓ que AZ, el ángulo correspondiente a ΒΑΘ será mayor que el correspondiente a BAZ.
Pues, de nuevo, al trazar ΓΚ perpendicular a ΑΘ, una vez trazada BK será igualmente perpendicular a ΑΘ; y puesto que AΛ es mayor que AK (pues subtiende al ángulo recto AKΛ), entonces AZ es mucho mayor que AK. Y los ángulos correspondientes a BZA, BKA son rectos; luego BZ es menor que BK por ser la suma de los cuadrados de BZ, ZA y los de BK, KA iguales al cuadrado de BA y entre sí y, a la vez, ser mayor el ángulo correspondiente a BAK que el correspondiente a BAZ. Y de todos los ángulos formados por la recta BA y las rectas que pasan por el punto A el mayor es el correspondiente a BAH una vez prolongada ΓΑ hacia H, puesto que también el menor de todos es el correspondiente a ΒΑΓ.
Por otro lado, son iguales las rectas que por cada lado distan lo mismo de MA, la que contiene, junto con BA, el ángulo menor. Pues sea MN igual a EM y trácense EM, MN, ΕΓ, ΓΝ, BE, BN, AN. Puesto que MN es igual a ME y ΜΓ es común y contienen ángulos iguales, entonces ΕΓ es igual a ΓΝ. Y ΓΒ es común y forma ángulos rectos[31]. Luego también EB es igual a BN. Pero también EA es igual a AN, y AB es común. Luego también el ángulo correspondiente a EAB es igual al correspondiente a NAB.
* * *
Sea el círculo ΑΒΓΔ, cuyo centro sea Z, en el cual se tracen rectas que pasen por A, B, Γ, Δ que se corten mutuamente formando ángulos rectos, y sea el ojo E, desde el cual la recta que lo une con el centro formando ángulos rectos con ΓΔ contenga junto con AB un ángulo cualquiera. Y sea EZ mayor que el radio.
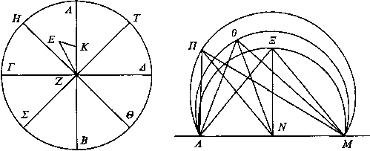
Digo que los diámetros AB, ΓΔ parecerán desiguales y que ΓΔ parecerá el mayor y AB el menor, y que siempre el más cercano al menor parecerá menor que el más lejano, y que sólo dos diámetros parecerán iguales: los que, por cada lado, distan lo mismo de la menor.
Puesto que ΓΔ forma ángulos rectos con cada una de las rectas AB, EZ, entonces también todos los planos que pasan por ΓΔ, al ser prolongados, forman ángulos rectos con el plano que pasa por EZ, AB. De manera que también el supuesto plano del círculo, en el que está ΓΔ[32]. Trácese, pues, desde el punto E una perpendicular al plano supuesto. Por tanto, cae sobre AB, la sección común de los planos. Caiga, pues, y sea EK, y trácese AM igual al diámetro del círculo y divídase en dos partes iguales por el punto N, y trácese desde N la recta ΝΞ formando ángulos rectos con ΛM, y sea ΝΞ igual a EZ. Entonces el segmento descrito en torno a ΛM y que pasa por Ξ es mayor que un semicírculo, puesto que ΝΞ es mayor que cada una de las rectas ΛΝ, NM. Sea el sector ΛΞΜ y trácense ΞΛ, ΞΜ. Entonces el ángulo con vértice en Ξ comprendido por las rectas ΛΞ, ΞΜ es igual al ángulo con vértice en E comprendido por el punto E y los puntos Γ, Δ. Constitúyase en la recta ΛN y en su punto N el ángulo comprendido por ΛN, NO igual al comprendido por HZ, ZE [Elem. I 23], y sea igual NO a EZ y trácense ΛO, OM y descríbase en torno al triángulo ΛOM el sector ΛOM. El ángulo con vértice en O será igual al ángulo con vértice en E correspondiente a ΗΕΘ. Constitúyase además en la recta ΛN y en su punto N el ángulo comprendido por ΛΝ, ΝΠ igual al correspondiente a AZE [Elem. I 23] y sea igual ΝΠ a EZ, y trácense ΛΠ, ΠΜ y descríbase en torno al triángulo ΛΠΜ el sector de círculo ΛΠΜ. Entonces el ángulo con vértice en Π será igual al ángulo correspondiente a AEB. Así, puesto que el ángulo con vértice en Ξ es mayor que el ángulo con vértice en O, mientras que el de vértice en Ξ es igual al correspondiente a ΓΕΔ y el de vértice en O es igual al correspondiente a ΗΕΘ, entonces ΓΔ parecerá mayor que ΗΘ. Y, a la vez, puesto que el ángulo con vértice en el punto O es igual al correspondiente a ΗΕΘ, mientras que el de vértice en Π es igual al correspondiente a AEB, pero el de vértice en O es mayor que el de vértice en Π, entonces también será mayor el correspondiente a ΗΕΘ que el correspondiente a AEB. Luego ΗΘ parecerá mayor que AB. Luego de todas las rectas que pasan por el punto Z y forman ángulos con la recta EZ se verá ΓΔ la mayor y AB la menor, porque también de los ángulos constituidos con vértice en E el mayor es el correspondiente a ΓΕΔ y el menor el correspondiente a AEB, y sólo se podrá constituir otro ángulo igual a ΗΕΘ: el correspondiente a ΤΕΣ, al quitar AT igual a HA y trazar TZ y prolongarla hacia Σ. Eso está claro a partir de los ángulos de los puntos Ξ, O, Π. Y de éstos el menor es el de vértice en Π, puesto que el ángulo correspondiente a ΠΝΛ es igual al ángulo menor, el correspondiente a EZA; y el mayor es el de vértice en Ξ por formar ángulos rectos con ΝΞ, que es la mayor de las rectas trazadas por el punto N en el segmento ΛΞΜ y porque al poner una igual a ella excede el segmento ΛΞΜ y porque el punto Ξ es el que cae más dentro mientras que Π el que cae más fuera por no existir ningún ángulo menor que el correspondiente a ΠΝΛ. Por otro lado, al ser igual el ángulo correspondiente a EZT al correspondiente a EZH, como se ha demostrado antes, también su suplementario, el correspondiente a ΕΖΣ, es igual al correspondiente a ΕΖΘ, es decir, al correspondiente a ONM. De modo que cada uno de los ángulos correspondientes a ΤΕΣ, ΗΕΘ son iguales al de vértice en O.
Luego ΗΘ parecerá igual que ΤΣ.
* * *
Sea menor la recta trazada del ojo al centro que el radio. En ese caso sucederá lo contrario en relación con los diámetros: el que antes parecía mayor ahora parecerá menor; y el menor, mayor.
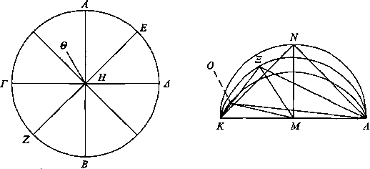
Sea un círculo ΑΒΓΔ y trácense dos diámetros AB, ΓΔ que se cortan mutuamente en ángulos rectos, y trácese otra línea al azar EZ y sea Θ el ojo a partir del cual la línea trazada hasta el centro, ΗΘ, sea menor que cada uno de los radios. Y sea KΛ igual al diámetro del círculo y córtese en dos partes iguales por el punto M, y desde el punto M trácese MN en ángulos rectos y sea MN igual a ΘΗ y descríbase el sector de círculo NKΛ en torno a ΚΛ y el punto N. Ciertamente, es menor que un semicírculo, puesto que MN es menor que el radio. Y con vértice en N habrá un ángulo comprendido por KN, ΛΝ igual al ángulo con vértice en Θ comprendido por ΓΘ, ΘΔ. Y además, sea el ángulo correspondiente a ΚΜΞ igual al correspondiente a ΕΗΘ, y sea ΜΞ igual a ΗΘ y descríbase en torno a KΛ y al punto Ξ el sector ΚΞΛ. Entonces el ángulo con vértice en el punto Ξ comprendido por ΚΞΛ es igual al de vértice en Θ comprendido por ΖΘΕ. Y además, sea el comprendido por KM, MO igual al comprendido por AH, ΗΘ y sea MO igual a ΗΘ, y descríbase un sector en torno a ΚΛ y al punto O. En consecuencia, el ángulo de vértice en O comprendido por ΚΟΛ será igual al de vértice en Θ comprendido por ΑΘΒ. Puesto que el ángulo de vértice en O es mayor que el de vértice en Ξ, mientras que el ángulo de vértice en O es igual al ángulo de Θ comprendido por AΘB y el de vértice en Ξ es igual al de vértice en Θ comprendido por ΕΘΖ, entonces AB parecerá mayor que EZ. A la vez, puesto que el de vértice en Θ comprendido por ΕΘ, ΘΖ es mayor que el de vértice en Θ comprendido por ΓΘΔ, entonces EZ se verá mayor que ΓΔ.
PROPOSICIÓN 36
Las ruedas de los carros parecen unas veces circulares, y otras, oblongas.
Sea ΑΒΓΔ una rueda y trácense los diámetros BA, ΓΔ que se cortan mutuamente formando ángulos rectos en el punto E y no esté el ojo en el plano del círculo.

Por tanto, si la recta trazada del ojo hacia el centro formara ángulos rectos con el plano o fuera igual al radio, los diámetros parecerán todos iguales, de modo que la rueda parece circular.
Pero si la línea trazada desde el ojo hacia el centro no formara ángulos rectos con el plano ni fuera igual al radio, los diámetros parecerán desiguales, uno muy grande y otro muy pequeño, y sólo un diámetro, trazado hacia ambas partes, se verá igual a cualquier otro trazado intermedio entre el mayor y el menor. De modo que la rueda parece oblonga.
PROPOSICIÓN 37
Hay un lugar en el cual, si el ojo permanece fijo y el objeto visto cambia de posición, el objeto visto parece siempre igual.
Sea A el ojo y ΒΓ la magnitud vista y a partir del ojo incidan los rayos AB, ΒΓ y descríbase en torno a ΑΒΓ el círculo ΑΒΓ.
Digo que hay un lugar en el cual si el ojo permanece fijo y la magnitud vista cambia de posición, el objeto visto parece siempre igual.
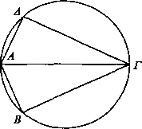
Cambie de posición y sea ΔΓ, y sea ΑΔ igual a AB. Así, puesto que BA es igual a ΑΔ y ΒΓ igual a ΓΔ, entonces el ángulo ΒΑΓ es igual al ángulo ΔΑΓ; pues están sobre arcos de circunferencia iguales; de manera que son iguales. Luego el objeto visto parecerá igual [Def. 4].
Lo mismo sucederá si el ojo permaneciera en el centro del círculo y el objeto visto se moviera sobre la circunferencia.
PROPOSICIÓN 38
Hay un lugar en el cual, si el ojo cambia de posición y el objeto visto permanece fijo, el objeto visto parece siempre igual.
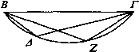
Sea ΒΓ el objeto visto y sea Z el ojo a partir del cual incidan los rayos ZB, ΖΓ y descríbase en torno al triángulo ΒΖΓ un sector de círculo, ΒΖΓ, y cambie de posición el ojo Z hacia Δ e incidan ahora en cambio los rayos ΔΒ, ΔΓ. Por consiguiente, el ángulo Δ es igual a Z, puesto que ocupan el mismo segmento. Y los objetos vistos bajo ángulos iguales parecen iguales [Def. 4].
Luego, en cualquier caso, ΒΓ parecerá igual si el ojo cambia de posición sobre el arco de circunferencia ΒΔΓ.
PROPOSICIÓN 39
Si una magnitud fuera perpendicular al plano supuesto y se pusiera el ojo sobre un punto del plano y el objeto visto cambia de posición sobre la circunferencia del círculo que tiene por centro el ojo, el objeto visto se verá siempre igual al moverse en posición paralela a la del principio.

Sea AB la magnitud vista que es perpendicular al plano y sea Γ el ojo. Y trácese ΓΒ y con centro en Γ y radio ΓΒ descríbase el círculo ΒΔ. Digo que si la magnitud AB cambia de posición sobre la circunferencia del círculo, desde el ojo Γ se verá igual AB.
Pues AB es una recta y forma con ΒΓ un ángulo recto, y todos los radios que inciden desde el centro Γ en la circunferencia del círculo forman ángulos iguales[33]. Luego la magnitud vista se verá igual.
Y si desde el centro Γ se trazara una recta perpendicular y se pusiera el ojo en ella y la magnitud vista fuera transportada por la circunferencia del círculo en posición paralela a la recta sobre la que está el ojo, el objeto visto se verá siempre igual.
PROPOSICIÓN 40
Y si el objeto visto no fuera perpendicular al plano supuesto y, siendo igual al radio, cambiara de posición sobre la circunferencia del círculo, al moverse en posición paralela a la del principio se verá unas veces igual a sí mismo y otras desigual.
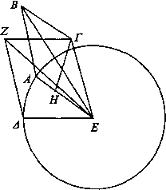
Sea el círculo ΑΔ y tómese el punto Δ sobre su circunferencia y álcese la recta ΔΖ que no forme ángulos rectos con el círculo y que sea igual al radio, y sea E el ojo.
Digo que ΔΖ, si cambia de posición sobre la circunferencia del círculo, a veces parecerá igual, a veces mayor, a veces menor.
Efectivamente, trácese por el punto E, que es el centro, ΓΕ paralela a ΔΖ y sea ΕΓ igual a ΔΖ. Y trácese por el punto Γ la recta ΓΗ perpendicular al plano supuesto y únase con el plano en el punto H. Y, una vez trazada EH, prolónguese y únase con la circunferencia en el punto A y trácese AB paralela a ΓΕ por el punto A, y sea AB igual a ΔΖ.
Digo que de todas las rectas que cambian de posición sobre la circunferencia del círculo AB parecerá la menor.
Trácense las rectas ΕΔ, ΓΖ, ΓΒ, EB, ZE. Puesto que ΓΕ es paralela e igual a AB, entonces también EA es igual y paralela a ΓΒ. Luego ΑΕΓΒ es un paralelogramo; por lo mismo, también ΕΔΖΓ es un paralelogramo. Queda demostrar que la misma magnitud parece menor y mayor. Y es evidente que el ángulo correspondiente a ΓΕΑ es menor que el correspondiente a ΓΕΔ, puesto que se ha demostrado que de todas las rectas trazadas por el centro y que forman un ángulo[34], el ángulo menor es el correspondiente a FEA [Lema que sigue a 35]. Luego también es menor que el correspondiente a ΓΕΔ. Y el ángulo correspondiente a BEA es la mitad del correspondiente a ΓΕΑ, puesto que BE es un paralelogramo equilátero. Por otro lado, el ángulo correspondiente a ΖΕΔ es la mitad del correspondiente a ΓΕΔ, puesto que ZE es un paralelogramo equilátero. Luego el ángulo correspondiente a BEA es menor que el correspondiente a ΖΕΔ. De modo que también la magnitud ΑΒ se verá menor que la ΔΖ.
Y es evidente a partir del lema recién demostrado que se verá lo más pequeño en el punto A, lo más grande en el punto diametralmente opuesto a A e igual cuando dista igual del punto A por cualquiera de los dos lados.
PROPOSICIÓN 41
Si el objeto visto formara ángulos rectos con el plano supuesto y el ojo cambiara de posición sobre la circunferencia de un círculo que tiene por centro el punto en el que se une la magnitud con el plano, el objeto visto parecerá siempre igual.
Sea AB la magnitud vista, que forma ángulos rectos con el plano supuesto, y sea Γ el ojo. Y con centro en B y radio ΒΓ descríbase el círculo ΓΔ.
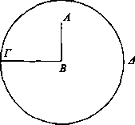
Digo que si Γ cambia de posición sobre la circunferencia del círculo, AB parecerá siempre igual.
Esto es evidente. Pues todos los rayos que inciden desde el punto Γ sobre AB inciden con ángulos iguales, puesto que el ángulo de B es recto.
Luego el objeto visto se verá igual [Def. 4].
PROPOSICIÓN 42
Si el objeto visto permanece fijo y el ojo cambia de posición en una línea recta que es oblicua a la magnitud vista, el objeto visto parece a veces igual y a veces desigual.
Sea el objeto visto AB, [E el ojo] y la recta oblicua ΓΑ y prolónguese ΓΔ en línea recta con BA y únase con ΔΓ en Γ, y cambie de posición sobre ella el ojo.
Digo que AB parece a veces igual y a veces desigual.
Tómese ΓΕ, la media proporcional de ΒΓ, ΓΑ, y sea E el ojo y cambie de posición y esté sobre la misma recta en Δ. Digo que el objeto visto desde E, Δ parece desigual.
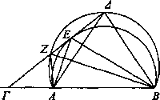
Trácense las rectas AE, EB, ΑΔ, ΒΔ y circunscríbase en torno al triángulo AEB el sector AEB y sea el ángulo comprendido por ΓΑ, AZ igual al ángulo comprendido por ΓΔ, ΔΒ[35] y trácese BZ. Entonces los puntos B, A, Z, Δ están en círculo. Puesto que el ángulo correspondiente a AEB es mayor que el correspondiente a AZB mientras que el correspondiente a AZB es igual al comprendido por ΑΔ, ΔΒ, ya que están en el mismo segmento, entonces también el correspondiente a AEB es mayor que el correspondiente a ΑΔΒ. Pero AB se ve bajo el ángulo correspondiente a ΑΔΒ cuando el ojo está en Δ, mientras que el mismo AB se ve bajo el ángulo correspondiente a AEB cuando el ojo está en E. Por tanto el objeto visto parece desigual al cambiar de posición el ojo sobre la recta ΕΔ [Def. 4].
Y es evidente que también al cambiar el ojo de posición sobre ΕΓ parece desigual, lo más grande desde la posición E, siempre mayor en la posición más cercana a él[36] sobre cualquiera de las rectas ΕΔ, ΕΓ; igual en las posiciones Z y Δ y en las tomadas de la misma manera que éstas, por estar los ángulos en el mismo segmento.
DE OTRA MANERA
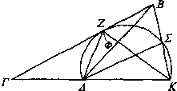
Sea ΚΔ el objeto visto, y ΒΓ la recta coincidente con ΚΔ al prolongar ésta. Tómese la recta ΓΖ, media proporcional de ΓΔ, ΓΚ y trácense ZK y ΖΔ, y descríbase en torno a la recta ΚΔ un segmento que comprenda el ángulo correspondiente a ΚΖΔ, Será tangente a la recta ΒΓ, puesto que ΚΓ es a ΓΖ como ΓΖ a ΓΔ. Esté situado el ojo en el punto B y prolónguense ΔΒ, BK. Trácese ΣΔ. Así, el ángulo Φ es igual al ángulo Σ, puesto que ambos están en el mismo segmento. Y el ángulo Σ es mayor que el ángulo B, luego también el ángulo Φ es mayor que el ángulo B.
Luego ΚΔ parece mayor si el ojo está en Z que si está en B.
PROPOSICIÓN 43
Lo mismo sucederá si la línea recta[37] fuera paralela a la magnitud vista.
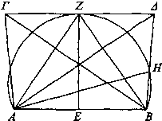
Sea AB la magnitud vista y córtese en dos partes iguales por el punto E y trácese desde E formando ángulos rectos con AB la recta EZ, sobre la cual esté situado el ojo Z, y trácense las rectas ZA, ZB y circunscríbase en torno al triángulo AZB el segmento AZB y trácese ΖΔ paralela a AB por el punto Z y cambie el ojo de posición a Δ e incidan los rayos ΑΔ, ΔΒ.
Digo que desde Δ, Z parecerán desiguales.
Trácese AH. Puesto que el ángulo correspondiente a AZB es igual al correspondiente a AHB, mientras que el correspondiente a AHB es mayor que el correspondiente a ΑΔΒ, entonces también el correspondiente a AZB es mayor que el correspondiente a ΑΔΒ. Y si el ojo está en 2, AB se ve bajo el ángulo correspondiente a AZB, e, igualmente, si está en Δ, bajo el correspondiente a ΑΔΒ.
Luego el objeto visto parece desigual desde los puntos Δ, Z [Def. 4].
Y si se pone ΖΓ igual a ΔΖ, entonces desde Γ parece menor que desde Z, pero desde Γ, Δ parece igual.
PROPOSICIÓN 44
Hay lugares en los cuales, al cambiar el ojo de posición, las magnitudes iguales y que ocupan ciertos lugares en posición contigua[38] parecen unas veces iguales y otras desiguales.
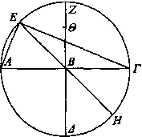
Sea Θ el ojo y AB, ΒΓ las magnitudes y trácese BZ desde B formando ángulos rectos y prolónguese hacia Δ. Es evidente que si el ojo se pone en cualquier parte de ΖΔ las magnitudes AB, ΒΓ parecerán iguales. Cambie de posición el ojo y sea E.
Digo que desde E parecen desiguales.
Incidan los rayos AE, EB, ΕΓ y circunscríbase en torno al triángulo ΑΓΕ el círculo ΑΕΔΓ y sea BH la prolongación de EB. Así, puesto que el arco de circunferencia ΑΔ es igual al arco de circunferencia ΔΓ, mientras que el arco de circunferencia ΑΔΗ es mayor que el arco de circunferencia ΗΓ, entonces AB parecerá mayor que ΒΓ. Y si cambia de posición[39] sobre EH parecerán, del mismo modo, desiguales, y si se pone sobre las partes del círculo, a menos que sea en la recta que forma ángulos rectos, parecen desiguales, y si se pone fuera del círculo sin estar en línea recta con ΔΖ, parecen desiguales.
DE OTRA MANERA
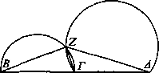
Sea la recta ΒΓ igual a la recta ΓΔ, y descríbase en torno a ΒΓ el semicírculo ΒΖΓ, y en torno a ΓΔ descríbase ΓΖΔ, mayor que un semicírculo. Y es evidente que cortará[40] al semicírculo antes mencionado. Y[41] es posible describir sobre ΓΔ una sección mayor que un semicírculo. Pues si suponemos un ángulo agudo, nos es posible describir sobre ΓΔ un segmento de círculo que admita un ángulo igual al ángulo agudo supuesto, según el teorema 33 del libro tercero de los planos, y el segmento que se forme sobre este ángulo será mayor que un semicírculo, según el teorema 31 del libro tercero de los planos. Y trácense BZ, ZΓ, ΖΔ. Así, el ángulo inscrito en el semicírculo es mayor que el ángulo inscrito en el segmento mayor. Y los objetos vistos bajo un ángulo mayor parecen mayores [Def. 4], Luego ΒΓ parece mayor que ΓΔ. Y era igual. Luego hay un lugar común en el cual, si se pone el ojo, los objetos iguales parecen desiguales.
Pero parecerán iguales cuando estén en los f puntos del principio, de los que están en los <segmentos> ΒΓ, ΓΔ mayores que semicírculos[42].
PROPOSICIÓN 45
Existe un lugar común desde el cual las magnitudes desiguales parecen iguales.

Sea ΒΓ mayor que ΓΔ y descríbase en torno a ΒΓ un segmento mayor que un semicírculo, y en torno a ΓΔ una figura semejante a la descrita en torno a ΒΓ, es decir, que admita un ángulo igual al que hay en ΒΖΓ. Entonces, las secciones se cortarán mutuamente. Córtense en Z y trácense ZB, ΖΓ, ΖΔ. Así, puesto que los ángulos que están inscritos en segmentos semejantes son iguales entre sí, los ángulos de las secciones ΒΖΓ, ΓΖΔ son iguales entre sí. Y los objetos vistos bajo ángulos iguales parecen iguales [Def. 4], Luego al poner en el punto Z el ojo, ΒΓ parecería igual a ΓΔ; y es mayor.
Luego hay un lugar común desde el cual las magnitudes desiguales parecen iguales.
PROPOSICIÓN 46
Existen lugares en los cuales, al cambiar el ojo de sitio, las magnitudes iguales y que están formando ángulos rectos con el plano supuesto parecen a veces iguales y a veces desiguales.
Sean AB, ΓΔ magnitudes iguales que están formando ángulos rectos con el plano supuesto.
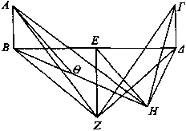
Digo que hay un lugar que, si se pone el ojo en él, AB, ΓΔ parecen iguales.
Trácese ΒΔ desde B hasta Δ y córtese en dos partes iguales por el punto E, y desde E trácese EZ formando ángulos rectos con ΔΒ.
Digo que si se pone el ojo sobre EZ parecerán iguales AB, ΓΔ.
Esté situado el ojo sobre EZ y sea Z, e incidan los rayos AZ, ZB, ZE, ΖΔ, ΖΓ. Efectivamente, la recta ZB es igual a ΖΔ. Pero también se ha supuesto que AB es igual a ΓΔ; luego las dos rectas AB, BZ son iguales a las dos ΓΔ, ΔΖ. Y contienen ángulos rectos; luego el ángulo correspondiente a BZA es igual al correspondiente a ΔΖΓ.
Luego AB, ΓΔ se verán iguales [Def. 4].
Digo que también se verán desiguales.
Cámbiese de posición el ojo y sea H[43], y trácese HE e incidan los rayos HB, HA, ΗΓ, ΗΔ. Entonces HB es mayor que ΗΔ. De HB quítese ΒΘ igual a ΗΔ, y trácese ΑΘ. Por tanto, el ángulo correspondiente a ΒΘΑ es igual al correspondiente a ΓΗΔ; pero el correspondiente a ΒΘΑ es mayor que el correspondiente a BHA, el exterior mayor que el interior[44] [Elem. I 16]. Luego también el correspondiente a ΓΗΔ es mayor que el correspondiente a BHA.
Luego ΓΔ parecerá mayor que AB [Def. 4].
PROPOSICIÓN 47
Hay ciertos lugares en los cuales, si se pone el ojo, la suma en una misma magnitud de las magnitudes desiguales parecerá igual a cada una de las desiguales[45].
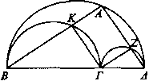
Pues sea ΒΓ mayor que ΓΔ y descríbanse semicírculos en torno a ΒΓ, ΓΔ y en torno a la recta entera ΒΔ. Así, el ángulo inscrito en el semicírculo ΒΑΔ es igual al inscrito en ΒΚΓ, pues cada uno de ellos es recto. Luego ΒΓ parece igual a ΒΔ. De la misma manera también ΒΔ parece igual a ΓΔ si los ojos están situados en los semicírculos ΒΑΔ, ΓΖΔ.
Luego hay ciertos lugares en los que la suma en la misma magnitud de dos magnitudes desiguales parece igual a cada una de las magnitudes desiguales.
PROPOSICIÓN 48
Hallar los lugares desde los cuales la misma magnitud parecerá la mitad o la cuarta parte o, en general, en la proporción en la que se corta el ángulo.
Sea AZ igual a ΒΓ y descríbase en torno a AZ un semicírculo y dibújese en él el ángulo recto K; por otro lado, sea ΒΓ igual a AZ y circunscríbase en torno a ΒΓ un segmento que admita un ángulo que sea la mitad del de Κ [Elem. I 9 y III 33]. Así, el ángulo Κ es el doble que el ángulo Δ.
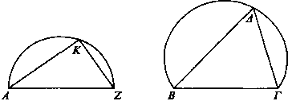
Luego AZ parece doble que ΒΓ si los ojos están situados en los arcos de circunferencia AKZ, ΒΔΓ.
PROPOSICIÓN 49
Sea AB una magnitud vista. Digo que AB tiene lugares que, al poner el ojo en ellos, la misma magnitud parece a veces la mitad, a veces entera, a veces la cuarta parte y, en general, se ve en la razón dada.
Circunscríbase el círculo AEB en torno a la recta AB de manera que AB no sea el diámetro y tómese el centro del círculo y sea Γ, en el cual esté situado el ojo, y trácense las rectas ΑΓ, ΓΒ. Luego AB se ve bajo el ángulo ΑΓΒ.
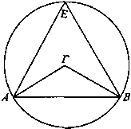
Esté situado el ojo sobre la circunferencia del círculo y sea E, e incidan los rayos EA, EB. Puesto que el ángulo correspondiente a ΑΓΒ es el doble del correspondiente a AEB [Elem. III 20], entonces desde Γ se ve AB el doble que desde E. E igualmente se verá como la cuarta parte si el ángulo fuera la cuarta parte del ángulo, y en la razón dada.
PROPOSICIÓN 50
Si unos objetos que se trasladan a la misma velocidad y que tienen sus extremos del mismo lado sobre una recta que forma ángulos rectos con ellos, se acercan a la paralela a la recta dicha trazada por el ojo, parecerá que lo más lejano al ojo precede a lo más cercano, mientras que al cambiar de lado[46] parecerá que lo que precedía va siguiendo y que lo que iba siguiendo precede.
Trasládense a la misma velocidad ΒΓ, ΔΖ, KA, que tienen los extremos del mismo lado Γ, Z, A, sobre la recta ΓΑ que forma ángulos rectos con ellos, y desde el ojo M trácese MΛ[47] paralela a ΓΑ y únanse ΜΓ, MZ, MA. Así parece que ΒΓ es el que precede y KA el que va siguiendo porque da la impresión de que, de los rayos incidentes desde el ojo, ΜΓ se desvía más hacia Γ que los otros rayos. Luego al acercarse, parecerá que ΜΓ es el que precede, como se ha dicho.
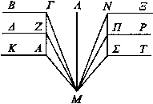
Pero al cambiar de lado ΒΓ, ΔΖ, KA transformados en ΝΞ, ΠΡ, ΣΤ, incidan los rayos MN, ΜΠ, ΜΣ. Así, que ΝΞ se desvía hacia Ξ porque el rayo MN se desvía hacia Ξ[48] más que los otros rayos; y ΣΤ está desviado hacia T porque también el rayo ΜΣ está desviado hacia T más que los otros rayos.
Luego el que precede, ΒΓ, transformado en ΝΞ, parecerá que va siguiendo, mientras que AK, transformado en ΣΤ, parecerá que precede.
PROPOSICIÓN 51
Si al trasladarse varios objetos a distinta velocidad se traslada también con ellos el ojo en la misma dirección, los objetos que se trasladan a la misma velocidad que el ojo parecerán estar fijos; los que se trasladan más despacio, que se trasladan en dirección contraria; los que van más deprisa, que se trasladan hacia lo que les precede.
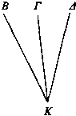
Trasládense a distinta velocidad Β, Γ, Δ y trasládense B más despacio, Γ a la misma velocidad que el ojo y Δ más deprisa que Γ. Incidan desde el ojo K los rayos KB, ΚΓ, ΚΔ. Así, parecerá al ojo que Γ, al trasladarse, está fijo; que B, al ser dejado atrás, se traslada en dirección contraria; y Δ, el que se ha supuesto que va más deprisa de ellos, parecerá que se traslada hacia delante, pues está a mayor distancia de ellos.
PROPOSICIÓN 52
Si al trasladarse ciertos objetos aparece algo que no se traslada, lo que no se traslada parecerá trasladarse hacia atrás.
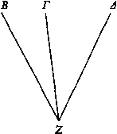
Trasládense Β, Δ y permanezca fijo Γ, e incidan desde el ojo los rayos ZB, ΖΓ, ΖΔ. Así, B, al trasladarse, estará más cerca que Γ, mientras que Δ, al apartarse, más lejos.
Luego parecerá que Γ se traslada en dirección contraria.
PROPOSICIÓN 53
Al acercarse el ojo más cerca del objeto visto parecerá que el objeto visto es más grande.
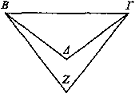
Véase ΒΓ bajo los rayos ZB, ΖΓ estando el ojo situado en Z, y cámbiese de posición el ojo más cerca de ΒΓ y esté situado en Δ y véase el mismo objeto bajo los rayos ΔΒ, ΔΓ. Así, el ángulo Δ es mayor que el ángulo Z, y los objetos vistos bajo un ángulo mayor parecen mayores.
Luego parecerá que ΒΓ es más grande al estar el ojo en Δ que al estar en Z.
PROPOSICIÓN 54
De los objetos que se trasladan a la misma velocidad, los más lejanos parecen trasladarse más despacio.
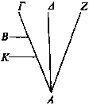
Trasládense Β, Κ a la misma velocidad, y desde el ojo A trácense los rayos ΑΓ, ΑΔ, AZ. Así, B tiene mayores que Κ los rayos trazados desde el ojo.
Luego recorrerá una distancia mayor y después, al cambiar de lado, parecerá que el rayo visual AZ se traslada más despacio.
DE OTRA MANERA
Trasládense dos puntos A, B sobre rectas paralelas y sea Z el ojo desde el cual incidan los rayos ZA, ZB, ZE, ΖΔ.
Digo que el más lejano, A, parece trasladarse más despacio que B.
Puesto que AZ, ZA contienen un ángulo menor que ZB, ZE, entonces BE se ve mayor que ΑΔ. Luego, si prolongamos el rayo ZE en línea recta, que en el caso de los objetos que se trasladan a igual velocidad, B sobre el rayo ZE, †[49] impedido se retrasará por tanto de los objetos que se trasladan a igual velocidad los más lejanos parecen trasladarse más despacio.
DE OTRA MANERA

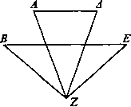
Trasládense dos puntos A, B sobre las rectas paralelas ΑΔ, BE uniformemente. Entonces, en el mismo tiempo recorrerán las mismas distancias.
Sean iguales ΑΔ, BE e incidan desde el ojo Z los rayos ZA, ΖΔ, ZB, ZE. Puesto que el ángulo correspondiente a ΑΖΔ es menor que el correspondiente a BZE, entonces la distancia ΑΔ parecerá menor que BE [Def. 4].
De modo que parecerá que A se traslada más despacio.
PROPOSICIÓN 55
Si el ojo permanece fijo pero los rayos visuales se deslizan, parecerá que los objetos más lejanos son dejados atrás.
Sean A, Γ los objetos vistos, que están sobre las rectas AB, ΓΔ, y sea E el ojo desde el cual incidan los rayos ΕΓ, EΔ, EA, EB.
Digo que parecerá que el objeto A es dejado atrás.
Prolónguese ΕΔ hasta que se una con AB y sea EB. Puesto que el ángulo correspondiente a ΓΕΒ es mayor que el correspondiente a AEB, entonces la distancia ΓΔ parece mayor que la AB [Def. 4]; de manera que, si el ojo permanece fijo en E, los rayos visuales al deslizarse hacia la parte de A, Γ cambiarán de lado más deprisa el objeto A que el Γ.
Luego parecerá que AB es dejado atrás.
PROPOSICIÓN 56
Las magnitudes que crecen parecen acercarse al ojo.

Sea AB la magnitud vista y sea Γ el ojo desde el cual incidan los rayos ΓΑ, ΓΒ. Y crezca BA y sea ΒΔ, e incida el rayo ΓΔ. Puesto que el ángulo correspondiente a ΒΓΔ es mayor que el correspondiente a ΒΓΑ, entonces ΒΔ parecerá mayor que BA. Pero las cosas de las que se opina que son mayores que sí mismas dan la impresión de crecer, y las que están más cerca del ojo parecen mayores.
Luego las magnitudes que crecen parecerán acercarse al ojo.
PROPOSICIÓN 57[50]
Cuantos objetos están situados a la misma distancia sin que sus extremos estén en línea recta con su parte media, forman la figura entera a veces cóncava y a veces convexa.
Véase ΓΒΔ estando el ojo situado en K, e incidan los rayos ΚΓ, KB, ΚΔ. Parecerá que la figura entera es cóncava.

Muévase ahora lo que se ve en la parte media y esté situado más cerca del ojo. Parecerá que ΔΒΓ es convexo[51].
PROPOSICIÓN 58
Si desde el punto de contacto de las diagonales de un cuadrado se traza una recta que forme ángulos rectos[52] y se pone en ella el ojo, los lados del cuadrado parecerán iguales y las diagonales parecerán también iguales.
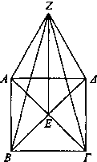
Sea ΑΒΓΔ el cuadrado y trácense sus diagonales ΔΒ, ΓΑ, y trácese desde E una recta elevada EZ que forme ángulos rectos con el plano, sobre la cual esté situado el ojo Z, e incidan los rayos ZA, ZB, ΖΔ, ZΓ. Puesto que ΔΕ es igual a ΕΓ y EZ es común y los ángulos son rectos, entonces la base ZΓ es igual a la base ΔΖ, y de los ángulos adyacentes a la base son iguales aquéllos a los que subtienden los lados iguales. Luego el ángulo correspondiente a ΕΖΓ es igual al correspondiente a ΕΖΔ. Luego ΕΓ parecerá igual a ΕΔ. Del mismo modo, también el ángulo correspondiente a AZE es igual al correspondiente a BZE. Luego ΑΓ parecerá igual a ΒΔ. Y, a la vez, puesto que ΓΖ es igual a ZB, mientras que AZ lo es a ΖΔ y también AB a ΓΔ, las tres, por tanto, son iguales a las tres, y el ángulo igual al ángulo.
Luego el lado parecerá igual al lado, de modo que también los restantes lados parecerán iguales.
Pero si la recta trazada desde el ojo hasta el punto de contacto de las diagonales ni forma ángulos rectos con el plano ni es igual a cada una de las rectas trazadas desde el punto de contacto hasta los ángulos del cuadrado ni forma con ellas ángulos iguales, las diagonales parecerán desiguales. Demostraremos lo que sucede de la misma manera que en los círculos.