Para Salvador Dalí

1. Irracionalidad y predicibilidad

Como se habrán dado cuenta, este título es una transposición libre de uno de los más famosos títulos de Dalí: La conquista de lo irracional (1).

En efecto, mi conferencia tratará dos puntos que constituyen el núcleo de la creación daliniana. El primero es la relación entre el espacio y el tiempo, y, más exactamente, lo que podríamos llamar la «temporalización del espacio». El segundo es la cuestión del pluralismo en nuestra descripción del Universo.

Estos dos puntos son dos de los aspectos concretos de los que Dalí se ocupa en sus escritos y pinturas. Pero ¿qué es irracional? Para empezar, recordemos a Werner Heisenberg. Paseando un día cerca del castillo de Krongberg, Niels Bohr, que le acompañaba, le dijo: «¿No es extraño ver cómo cambia este castillo cuando se imagina uno que Hamlet vivió en él? Como científicos creemos que un castillo está formado sólo por piedras y admiramos la forma en que el arquitecto las compuso. Las piedras, el techo verde de pátina, las tallas de la iglesia, forman el conjunto del castillo. Nada debería cambiar por el hecho de que Hamlet viviera en él, pero, de hecho, cambia completamente. Inesperadamente, las paredes y las murallas hablan un lenguaje diferente. El patio se transforma en todo un mundo, un rincón oscuro nos recuerda la oscuridad del alma… Oímos las palabras de Hamlet: to be or not to be. Sin embargo, todo lo que sabemos realmente de Hamlet es que su nombre aparece en una crónica del siglo XIII. Nadie puede probar que viviera aquí realmente. Pero todo el mundo conoce las preguntas que Shakespeare puso en su boca, las profundidades del alma humana que estaba destinada a revelar, y cada uno sabe que, en consecuencia, también él tendría que ocupar un lugar en la Tierra, aquí en Krongberg» (2).

Esta cita saca a relucir una cuestión tan vieja como la humanidad: ¿cuál es el significado de la realidad? Y, muy relacionada con ella, ¿cuál es el significado de la diferencia entre lo racional y lo irracional?

En este punto, topamos inmediatamente con el problema del tiempo. ¿Es el cambio irreversible un atributo de racionalidad o es la expresión de alguna irracionalidad básica? ¿Cómo está relacionada la racionalidad con el problema del cambio?

En primer lugar, recordemos cómo plantea este problema la física clásica. En el contexto del racionalismo occidental, parecería que el objetivo último de la ciencia, considerada a partir de los éxitos de la dinámica newtoniana, fuera exorcizar el tiempo. Sabemos que la formulación de la ciencia moderna realizada por Isaac Newton se hizo bajo el signo de un Dios Todopoderoso, garante supremo de una racionalidad diseñada en un período de monarquía absoluta. Desde este punto de vista, que otorga omnisciencia a un Dios concebido como soberano, el tiempo podría ser tan sólo una ilusión.

En efecto, este objetivo fue fijado desde el alba de la filosofía natural occidental; y más de una vez se consideró casi conseguido: los componentes intemporales del atomismo, el reino eterno de la legalidad newtoniana, el universo estático de la relatividad general, fueron algunos de los intentos más notables por apartar el tiempo del nivel fundamental de descripción.

En realidad, Einstein puede aparecer como la encarnación más lograda de este camino hacia una formulación de la física en la que no se hace referencia alguna a la irreversibilidad. Llegó incluso a acuñar una célebre negación del tiempo, pronunciada con ocasión de la muerte de su amigo Michele Besso: «Michele se me ha adelantado en abandonar este extraño mundo. No tiene importancia. Para nosotros, físicos convencidos, la distinción entre pasado y futuro es una ilusión, aunque tenaz» (3).

De hecho, es bien sabido que Einstein no aceptó del todo las consecuencias de esta negación, tal como se desprende de sus comentarios a K. Gödel, quien sugirió que, en el marco de la relatividad general, podría ser posible que alguien retrocediera a su propio pasado: «Lo esencial es que el hecho de emitir una señal es, en el sentido termodinámico, un proceso irreversible, un proceso relacionado con el aumento de la entropía (mientras que, de acuerdo con nuestros conocimientos actuales, todos los procesos elementales son reversibles)» (4).

La ciencia clásica, ejemplificada por la dinámica newtoniana, describió un universo que, al nivel fundamental, no contenía referencia alguna al «llegar a ser (becoming)»: una trayectoria nunca comienza y nunca acaba. Lo mismo siguió siendo válido en la física cuántica: en este caso, es la función de onda la que evoluciona continuamente en el tiempo (si despreciamos los efectos perturbadores del proceso de medida).

¡Qué contraste con el mundo de la música, que nace del silencio y vuelve al silencio, o con cualquier obra de arte, que corresponde a una absoluta novedad! ¿Cómo reconciliar, pues, el mundo de la ciencia con el mundo del arte?

Una respuesta, un tanto caricaturesca, puede encontrarse en el universo formalista y sin objetivos de Malevich, que estaba en la misma vena que la descripción literaria de microcosmos incorrelacionado de la novela Watt de Beckett.

Otra respuesta, en la tradición de Friedrich y Turner, tiende a rehusar cualquier primer plano bien formado: Picture of nothing and very like (5). Sabemos que algunos de los pintores más destacados de esta tradición, como Kandinsky o Mondrian, buscaron su verdad en la enseñanza de la teosofía moderna. Exploraron dimensiones de la naturaleza que la ciencia rehusó al principio de nuestro siglo; Pahaut y yo mismo hemos desarrollado ideas parecidas en un breve texto escrito para una exposición montada alrededor del tema «Arte y tiempo» (6).

La respuesta del surrealismo, tal como se expresa enérgicamente en la pintura de Dalí, consistió en trazar figuras bien formadas pero ambiguas, que nos abren el reino de las posibles transformaciones entre objetos verdaderos —no entre objetos virtuales. Este homenaje a la ambigüedad hubo de ser reconocido como una forma más potente de resucitar recursos latentes del «material cultural», a la manera de un «cadáver exquisito» (cadavre exquis) (7).

El conflicto entre la ciencia clásica y el arte es claramente expresado por la aproximación surrealista. La ciencia clásica describirá un universo transparente, inequívoco, abierto a la evidencia de las idees claires et distinctes avanzadas por Descartes. Por el contrario, el surrealismo, elevado al punto culminante por las pinturas de Dalí, subrayó la opacidad fundamental de la naturaleza, la multiplicidad de significados inherente a nuestra relación con el mundo que nos rodea. Curiosamente, esta característica del surrealismo resucita antiguas prácticas del «barroco». Por ejemplo, muchos objetos precolombinos presentan la misma ambigüedad fundamental: según la manera como se miren, puede descubrirse en ellos una diversidad de significados.

La evolución de la ciencia en las últimas décadas ha creado una nueva situación. El mundo del arte y el mundo de la ciencia ya no están ideológicamente enfrentados. La multiplicidad de significados, la opacidad fundamental del mundo, están reflejadas por nuevos lenguajes y nuevos formalismos. Esta evolución de la ciencia es el tema principal de mi conferencia. No hay ningún concepto que describa más vivamente este cambio dramático que el concepto de tiempo. Debemos empezar otra vez con un conflicto. De hecho, al principio del siglo XX hubo realmente cierto consenso sobre la necesidad de este conflicto.

Grandes pensadores como Einstein, Bergson, Heidegger, a pesar de sus diferencias, compartieron la creencia de que el tiempo como irreversibilidad no es y no puede ser el objeto de la ciencia propiamente dicha.

De hecho, el problema del tiempo nos acompaña desde el alba del pensamiento racionalista, desde los progresos de los filósofos griegos en el campo de los problemas ontológicos. Recordemos que el análisis aristotélico del tiempo introduce la idea de una polaridad radical en el mismo (8). La famosa definición de la Física (iv, 219 a-b) es explícita en este punto: el tiempo es algo relacionado con el movimiento, en la perspectiva de lo anterior y de lo posterior. Aristóteles pregunta: ¿de dónde proviene esta perspectiva de lo anterior y de lo posterior? ¿Está inscrita en la naturaleza de las cosas «objetivas», o es una característica del «alma que cuenta»? Éste habría de convertirse en un problema de primer orden para los filósofos desde Aristóteles. El tiempo, ¿es sólo una ilusión humana o es una propiedad cósmica? Encontraremos este problema varias veces a lo largo de esta conferencia. Creo que la característica fundamental de nuestra época es la de que estamos, por primera vez en la historia de la ciencia, en una posición que nos permite escoger entre estas dos posibilidades: recientes avances de la física teórica y de la experimental respaldan la conclusión de que el tiempo como irreversibilidad es un ingrediente esencial de la naturaleza.

Hace unos 120 años, en 1865, Clausius formuló la segunda ley de la termodinámica e introdujo una nueva magnitud, la entropía. La propiedad más importante de la entropía radica en que, a consecuencia de procesos irreversibles, «orientados» en el tiempo, la entropía de nuestro universo (considerado como sistema aislado) va en aumento. Ésta fue una afirmación sorprendente en un tiempo dominado por la física clásica: al formularse por primera vez la segunda ley, en el contexto de la ciencia moderna, se introducía la idea de una historia del universo.

Desde Clausius, la física ha de vérselas con dos conceptos de tiempo: el tiempo como repetición y el tiempo como degradación. Pero es obvio que tenemos que superar esta dualidad. Ni la repetición (la negación del tiempo), ni la decadencia (el tiempo entendido como degradación) pueden hacer justicia a la complejidad del mundo físico. Por tanto, tenemos que conseguir un tercer concepto de tiempo que contenga también aspectos positivos y constructivos.

[Fig. 1.1] Variación de entropía para un sistema sometido a ligaduras externas.

Recordemos que pueden distinguirse dos términos aditivos en la variación de la entropía dS [fig. 1.1.]: d_eS y d_iS, que son, respectivamente, los intercambios (positivos o negativos) entre el sistema y su entorno, y la producción de entropía (siempre positiva). Para un sistema aislado, dS = d_iS es positiva o nula [fig. 1.2]. Pero ¿qué pasa si el sistema está sujeto a ligaduras externas? Obviamente, cualquier contribución de la termodinámica a una teoría de los sistemas naturales tiene que abordar el caso de sistemas sumergidos en algún entorno.

Los primeros pasos de la termodinámica estuvieron asociados a la consideración de los estados de equilibrio. En un sistema aislado en equilibrio, el tiempo no tiene dirección. Más tarde, en 1931, Onsager dio las relaciones generales de la termodinámica del no-equilibrio en la región próxima-al-equilibrio: sistemas sometidos a ligaduras externas débiles responden linealmente a estas ligaduras. Estas relaciones lineales y recíprocas entre flujos y fuerzas sugerían que la termodinámica no-lineal era también digna de estudio. Ampliaban la descripción dada para los sistemas en equilibrio, hecha en términos de los potenciales termodinámicos cuyos extremos corresponden a los estados finales, a una nueva descripción de los sistemas en no-equilibrio en términos de una nueva función potencial, la producción de entropía.

[Fig. 1.2] Aumento monótono de entropía para un sistema aislado.

En 1945, el teorema de la mínima producción de entropía afirmó que, dentro del dominio del validez de las relaciones de Onsager (la región lineal), un sistema evoluciona hacia un estado estacionario caracterizado por la mínima producción de entropía compatible con las ligaduras determinadas por las condiciones del contorno. Este estado estacionario es necesariamente un estado de no-equilibrio en el que ocurren procesos disipativos con ritmos no nulos. Pero, dado que entonces todas las cantidades que describen al sistema tienen que ser independientes del tiempo, la actividad del sistema hace aumentar necesariamente la entropía del entorno: dS = d0 implica un balance entre d_eS y d_iS. El flujo negativo d_eS significa que el sistema transfiere entropía al mundo exterior.

Esta termodinámica lineal del no-equilibrio tenía que ser generalizada para poder construir una termodinámica del no-equilibrio válida para sistemas en condiciones alejadas del equilibrio (9). Los sistemas sometidos a ligaduras fuertes presentan respuestas que ya no son lineales; de acuerdo con esto, su comportamiento muestra una multiplicidad de estados estacionarios así como muchas características dinámicas nuevas relacionadas con ellas, como las bifurcaciones, las histéresis, etc. Damos a continuación dos ejemplos de comportamiento, recientemente descubierto, de los sistemas en no-equilibrio.

La llamada inestabilidad de Bénard es un ejemplo muy ilustrativo de una inestabilidad de un sistema estacionario que da lugar a un fenómeno de autoorganización espontánea; la inestabilidad es debida a un gradiente vertical de temperatura establecido en una capa horizontal del líquido. La cara inferior es mantenida a temperatura mayor que la de la cara superior. Como resultado de estas condiciones de contorno, se establece un flujo permanente de calor que va de abajo a arriba. Para pequeñas diferencias de temperatura, el calor puede transmitirse por conducción, sin que aparezca la convección, pero, cuando el gradiente de temperatura alcanza un valor umbral, el estado estacionario (el estado de «reposo» del fluido) se vuelve inestable: aparece la convección, que corresponde al movimiento coherente de un número enorme de moléculas, y aumenta el ritmo de transferencia de calor. En condiciones apropiadas, la convección produce una compleja organización espacial en el sistema [figura 1.3].

Hay otra manera de enfocar este fenómeno. Dos elementos están implicados en ello: el flujo de calor y la gravitación. En condiciones de equilibrio, la fuerza gravitacional apenas tiene efecto sobre una capa delgada dg unos 10 mm. Sin embargo, lejos del equilibrio, la gravitación da lugar a estructuras macroscópicas. La materia en no-equilibrio se vuelve mucho más sensible a las condiciones del mundo exterior que la materia en equilibrio. Me gusta decir que, en el equilibrio, la materia es ciega; lejos del equilibrio, podría comenzar a ver.

En segundo lugar, consideremos el ejemplo de las oscilaciones químicas. Idealmente hablando, tenemos una reacción química cuyo estado podemos controlar mediante la inyección de productos químicos y la eliminación de los productos de desecho. Supongamos que dos de los componentes están constituidos, respectivamente, por moléculas rojas y azules en cantidades comparables. Sería de esperar que observáramos una especie de color impreciso, con trazas de manchas rojas o azules esparcidas irregularmente. Sin embargo, no es esto lo que ocurre realmente. Para la totalidad de un determinado tipo de reacciones químicas, vemos cómo sucesivamente el recipiente entero se vuelve rojo, después azul y más tarde rojo nuevamente: tenemos de esta forma un «reloj químico». En cierta manera, esto viola toda nuestra intuición sobre las reacciones químicas.

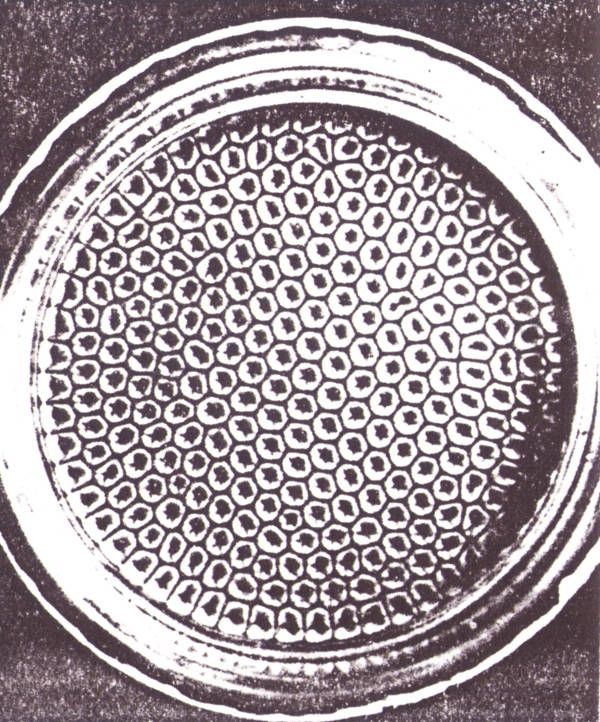
[Fig. 1.3] La inestabilidad hidrodinámica de Bénard (vista desde arriba).

Estábamos acostumbrados a hablar de las reacciones químicas como si estuvieran producidas por moléculas que se mueven de manera desordenada y colisionando al azar. Pero, a fin de sincronizar su cambio periódico, las moléculas deben comunicarse en algún sentido. En otras palabras, estamos tratando aquí con nuevas escalas supermoleculares —tanto en el tiempo como en el espacio— producidas por actividad química.

Las condiciones básicas que deben satisfacerse a fin de que ocurran este tipo de oscilaciones químicas son las relaciones auto reciprocatalíticas, que llevan a un comportamiento «no-lineal», como las descritas en numerosos estudios de la moderna bioquímica. Recordemos que los ácidos nucleicos producen las proteínas, las cuales, a su vez, llevan a la formación de los ácidos nucleicos. Hay un «bucle» autocatalítico que relaciona las proteínas y los ácidos nucleicos. Las situaciones de no-linealidad y alejamiento de equilibrio están íntimamente relacionadas; el efecto de ambas es conducir a una multiplicidad de estados estables (en contraste con las situaciones cerca-del-equilibrio en las cuales sólo encontramos un estado estable). Esta multiplicidad puede verse en un «diagrama de bifurcaciones» [figura 1.4]: hemos trazado la solución del problema, X, respecto a un parámetro de bifurcación, λ, (X podría ser, por ejemplo, la concentración de algún componente químico, y λ podría tener relación con el tiempo durante el cual las moléculas están en el reactor químico). Para un cierto valor crítico del parámetro de control, el valor que denotaremos por λ_c, surgen nuevas soluciones. Por otro lado, cerca del punto de bifurcación, el sistema tiene una «elección» entre dos ramas: podríamos esperar, por tanto, un comportamiento estocástico: cerca de un punto de bifurcación, las fluctuaciones juegan un papel importante.

[Fig. 1.4] Bifurcación entre ramas estacionarias, para un parámetro de control.

2. Dinámica caótica y atractores fractales

El hecho de que los sistemas disipativos presenten un comportamiento que puede ser descrito en términos de atractores implica otra diferencia básica con respecto a la mecánica. Supongamos que tenemos un objeto celeste extraño que se acerca a la Tierra: esto implicaría una deformación de la trayectoria terrestre que permanecería para siempre: los sistemas dinámicos no pueden olvidar las perturbaciones. No es éste el caso cuando incluimos disipación. Un péndulo amortiguado alcanzará una posición de equilibrio, sea cual sea la perturbación inicial.

Podemos ahora entender bien, en términos bastante generales, qué ocurre cuando llevamos un sistema lejos del equilibrio. El «atractor» que dominaba el comportamiento del sistema cerca del equilibrio puede volverse inestable, como resultado del flujo de materia y energía que dirigimos hacia el sistema. El no-equilibrio se transforma en una fuente de orden; nuevos tipos de atractores, tipos más complicados quizás, pueden aparecer y dar lugar a nuevas y extraordinarias propiedades del comportamiento espacio-temporal del sistema. Consideremos dos ejemplos muy estudiados en la actualidad.

Hemos visto cómo los sistemas disipativos pueden olvidar las perturbaciones; estos sistemas están caracterizados por atractores. Los atractores más elementales son puntos o líneas como las que se muestran en las figuras 2.1 y 2.2. En la figura 2.1., hay un punto atractor P en un espacio bidimensional (X₁ y X₂ pueden ser las concentraciones de algunas especies): sean cuales sean las condiciones iniciales, el sistema evolucionará necesariamente hacia P. En la figura 2.2, hay un atractor lineal: sean cuales sean las condiciones iniciales, el sistema evolucionará finalmente sobre esta línea, llamada ciclo límite.

[Fig. 2.1] Atractor puntual en el espacio fásico (x, y).

[Fig. 2.2] Atractor de ciclo límite. Puede verse una contracción del área asociada al efecto de atracción.

Pero los atractores pueden presentar una estructura más compleja: pueden estar formados por un conjunto de puntos [figura 2.3]. Su distribución puede ser suficientemente densa como para permitir atribuirle una dimensionalidad efectiva (no nula). Por ejemplo, la dimensión del atractor de la figura 2.3 puede ser cualquier número real comprendido entre 2 y 3. Siguiendo la terminología de Benoît Mandelbrot, podemos decir que éste es un atractor «fractal». El comportamiento de los sistemas en el entorno de un atractor de este tipo puede ser descrito usando las nueva dinámica cualitativa no-lineal. Por ejemplo, las trayectorias en el atractor caótico de la figura 2.4 convergen en una dimensión y divergen en la otra; estas características están descritas por los correspondientes exponentes de Lyapunov asignados a estas dimensiones.

[Fig. 2.3] Atractor fractal.

[Fig. 2.4] Atractor caótico correspondiente a las ecuaciones de Rossler.

Estos sistemas tienen propiedades únicas, que recuerdan, por ejemplo, la turbulencia conocida por la experiencia diaria. Combinan fluctuaciones y estabilidad. El sistema es llevado hacia el atractor, pero, puesto que éste está formado por tal cantidad de puntos, es de esperar que se produzcan grandes fluctuaciones. Se habla a menudo de «caos atrayente». Estas grandes fluctuaciones están relacionadas con una gran sensibilidad respecto a las condiciones iniciales. La distancia entre trayectorias vecinas aumenta exponencialmente con el tiempo (este aumento viene caracterizado por los llamados exponentes de Lyapunov). El caos atractor ha sido observado en una serie de situaciones que incluyen sistemas químicos o hidrodinámicos; pero la importancia de estos nuevos conceptos va más allá de las simples física y química. Permítanme indicarles algunos ejemplos estudiados recientemente.

Sabemos que el clima ha fluctuado violentamente durante el pasado. Las condiciones climáticas que prevalecieron durante los últimos dos o trescientos millones de años fueron extremadamente diferentes de las actuales. En el transcurso de esos períodos, a excepción de la era cuaternaria (que comenzó hace unos dos millones de años), no hubo prácticamente hielo en los continentes y el nivel del mar fue unos ochenta metros más alto que el actual. Una característica distintiva y sorprendente de la era cuaternaria es la aparición de una serie de glaciaciones, con una periodicidad media de unos cien mil años, a las que se superpone una importante cantidad de «ruido». ¿Cuál es el origen de estas violentas fluctuaciones [figura 2.5] que, evidentemente, han jugado un papel importante en nuestra historia? No hay indicios de que la intensidad de la energía solar pueda ser la responsable.

[Fig. 2.5] Variación del volumen total de hielo continental de la Tierra durante el último millón de años, inferido a partir del registro de isótopos.

Un análisis reciente de C. y G. Nicolis (10) ha mostrado que estas fluctuaciones pueden corresponder a modelos de cuatro variables independientes, formando un sistema dinámico no-lineal que conduce a un atractor caótico de dimensión 3,1 sumergido en un espacio físico de dimensión 4. La variabilidad del clima podría entenderse como el resultado de la interacción de un gran número de variables, actuando de una forma determinista; sería ésta, entonces, una situación similar a la que resulta de la ley de los números grandes. La intuición actual es de que esto no es así. La complejidad temporal debido sólo a cuatro variables independientes. Debemos aceptar, por lo tanto, una complejidad intrínseca o impredicibilidad del clima.

En otro campo, trabajos recientes (11) han mostrado que la actividad eléctrica del cerebro durante el sueño profundo, monitorizada por electroencefalograma (EEG), puede ser modelizada mediante un atractor fractal. El sueño profundo de un EEG puede ser descrito por una dinámica en la que intervienen cinco variables; éste es un hecho muy notable dado que muestra que el cerebro actúa como un sistema que posee no sólo una complejidad intrínseca, sino también impredecibilidad.

Es esta impredicibilidad la que permite las amplificaciones de los inputs relacionados con la impresión sensorial del estado de vigilia. Evidentemente, la complejidad dinámica del cerebro no puede ser un accidente. Debe haber sido seleccionado precisamente por su inestabilidad. ¿Es la evolución biológica el secreto de la inestabilidad dinámica, que sería pues el ingrediente básico de la creatividad característica de la existencia humana?

Los sistemas químicos caóticos desempeñaron probablemente un papel esencial en el origen de la vida. La vida, tal como la conocemos actualmente, está relacionada, esencialmente, con la existencia de biomoléculas. Ahora bien, uno de los rasgos distintivos de las biomoléculas radica en que son portadoras de información. Esta información es muy parecida a la de un texto que debe ser leído en un dirección, exactamente como un texto escrito en lenguaje humano. Las biomoléculas presentan, en este sentido, una rotura de simetría. Es natural que relacionemos esta rotura de simetría con la rotura de simetría expresada por la segunda ley de la termodinámica. Incluso en el simple caso de la inestabilidad de Bénard, la irreversibilidad se convierte en formación de figuras. Sin embargo, la figura del flujo de Bénard permanece sólo mientras el calor atraviesa la capa del líquido. Por otro lado, la vida tiene un extraordinario grado de estabilidad, dado que se originó hace 3.400 millones de años. La vida es, por tanto, como una «inscripción» de irreversibilidad sobre la materia, una inscripción que parece ser bastante diferente de la que observamos en la inestabilidad de Bénard.

Las reacciones químicas caóticas nos dan un modelo simple de esta inscripción de irreversibilidad sobre la materia. Según un trabajo reciente de G. Nicolis y G. y J. Subba Rao (12), consideremos ahora una reacción química en la que intervienen tres componentes: X₁, X₂, X₃. Cada vez que la concentración de alguno de estos componentes supera un determinado valor umbral, suponemos que la molécula del respectivo componente se une a cierto polímero [figura 2.6]. Como resultado, obtenemos una secuencia que lleva consigo una información incompresible. Es verdad que esto habría podido conseguirse con una reacción de ciclo límite, en cuyo caso sólo podríamos esperar una secuencia periódica del tipo xyzxyzxyz. Los autores han demostrado que esta secuencia, al ser leída en la dirección en que crece el tiempo, corresponde a una cadena de Markov. Éste es solamente un modelo supersimplificado. Pero se puede esperar, y esto es lo que está estudiando nuestro grupo de Austin, que puedan realizarse experimentos reales («del mundo real») a fin de producir cadenas de polímeros en condiciones lejos-del-equilibrio, separados de la rama termodinámica por puntos de bifurcación. Podemos esperar encontrar aquí algún tipo de moléculas prebióticas, portadoras de información, que podrían ser plausibles antecesoras de las actuales biomoléculas. De todas formas, una mejor comprensión de la química en condiciones lejos-del-equilibrio podría mostrar que el origen de la vida, lejos de ser un acontecimiento único, es una situación natural (normal) si tenemos en cuenta las condiciones químicas y físicas que reinan en nuestro planeta.

[Fig. 2.6] Dos codificaciones sucesivas de un comportamiento caótico.

3. Irreversibilidad y cosmología

Acabamos de hacer algunas observaciones sobre el problema del origen de la vida, pero, evidentemente, el más sorprendente de esta clase de problemas es el que hace referencia al origen de nuestro universo. La historia moderna de la cosmología ha sido una historia dramática. Como es bien sabido, Einstein propuso en 1917 un modelo estático de universo. La relatividad general le pareció la realización final, dado que ofrecía una unificación de la gravitación con el espacio-tiempo. Pero esta imagen estática tuvo que ser abandonada cuando Friedman demostró que las ecuaciones de Einstein eran inestables, y cuando las observaciones de Hubble sugirieron un universo en expansión, evolutivo. Posteriormente, la famosa radiación residual del cuerpo negro sugirió que, más allá de esta evolución geométrica, hay una evolución térmica más fundamental.

Llegamos así a la moderna cosmología standard [figura 3.1]. Esta presenta dos aspectos fundamentales: la temperatura del universo aumenta monótonamente conforme nos acercamos al Big-Bang, mientras que, de acuerdo con una fase adiabática de la evolución, la entropía del universo permanece constante. No podemos dar aquí los detalles, pero sí destacaremos que todo esto implica dos preguntas obvias: ¿cómo pudo comenzar el universo a partir de una temperatura tan alta?; y, ¿cómo pudo la entropía alcanzar este nivel en el primer momento? A este respecto, se han ideado diferentes modelos, algunos de los cuales introducen la consideración de un fenómeno irreversible en el origen de nuestro universo; me refiero a modelos como el del universo «inflacionario».

[Fig. 3.1] Suposiciones de la moderna cosmología standard para la temperatura y la entropía del universo.

Pero las preguntas sobre el origen de la entropía y sobre el significado de la evolución de la temperatura siguen abiertas. Es muy tentador reconsiderar estas preguntas desde el punto de vista de los procesos irreversibles (13). Encontramos en el universo una cualidad notable: está constituido, esencialmente, por fotones y bariones. Una idea de la estructura del universo muy interesante viene dada por la llamada entropía específica «S», definida por la razón entre la densidad numérica de fotones y la de bariones. El valor generalmente aceptado es de «S» ≃ 10⁸ ~ 10⁹.

Actualmente, los bariones son considerados como objetos en no-equilibrio, que están en un estado metaestable como decayendo, mientras que los fotones son «productos de desecho» que ya no pueden decaer hacia otras formas conocidas de materia. Por lo tanto, la mayor parte de nuestro universo está en equilibro térmico por lo que respecta al punto de vista de estas «partículas»; sin embargo, afortunadamente para nosotros, hay un pequeño residuo en no-equilibrio. Dualidades como ésta son típicas de los procesos acoplados en no-equilibrio. Las radiaciones solares originan una producción positiva de entropía, la mayor parte de la cual lleva a la disipación en forma de fotones. De manera esquemática, tenemos que

Un ejemplo sencillo de proceso acoplado en no-equilibrio es el siguiente: un sistema de dos componentes que contiene una mezcla de hidrógeno y nitrógeno se somete a un flujo externo de calor, manteniéndose un gradiente interno de temperatura [figura 3.2.]. Como resultado, uno de los componentes, el hidrógeno por ejemplo, se acumula en el compartimento I, mientras que el otro lo hace en el compartimento II. De nuevo, la producción de entropía es causada por dos procesos —transferencia de calor y «antidifusión»:

Si, en algún momento, cesamos el flujo de calor, la concentración de los componentes en los compartimentos se irá igualando lentamente. Durante algún tiempo, tendremos una distribución en equilibrio de temperaturas y una distribución en no-equilibrio de materia.

[Fig. 3.2] Un ejemplo de procesos acoplados en no-equilibrio.

Lo que es importante es que la parte del sistema que va evolucionando lentamente hacia el equilibrio ha sido apartada del equilibrio por un proceso de no-equilibrio. ¿Es posible que la materia sea la parte en no-equilibrio de algún proceso cósmico de no-equilibrio que haya producido también la radiación del cuerpo negro? Creemos que hay una posibilidad de que esto sea así cuando reconsideramos el papel que desempeña la segunda ley en la relatividad general.

Consideremos la dualidad básica que aparece en la relatividad general: por una parte, el espacio-tiempo; por otra, la materia. Estos dos aspectos están conectados por medio de las ecuaciones de Einstein. Pero no hay razón alguna para creer que el espacio-tiempo y la materia juegan un papel simétrico con respecto a la entropía. Al contrario, es verosímil que los modos longitudinales en la teoría de Einstein correspondan a un comportamiento coherente y a una entropía que va anulándose. La entropía, desde esta perspectiva, estaría asociada básicamente a la materia. En la cosmología primitiva, una transferencia de energía gravitacional a la materia correspondería entonces a los procesos irreversibles, produciéndose entropía. No entraremos aquí en detalles, pero avanzamos que el resultado principal es la posibilidad de un nuevo tipo de transición de fase, ocurrida en el universo primitivo [figura 3.3].

[Fig. 3.3] Suposiciones propuestas para la temperatura y la entropía del universo.

Es interesante notar que la existencia del máximo está relacionada con la entropía específica del universo (razón de las densidades numéricas de fotones y bariones). Existe sólo cuando la entropía es mayor que un valor umbral, muy cercano o igual al orden de magnitud experimental de 10⁸ ~ 10⁹. El tiempo en que aparece corresponde a los tiempos iniciales en los cuales la «entropía» crece hacia el infinito (agradezco al Dr. Edgard Gunzig por estas observaciones). Parece que hay una especie de transición de fase que calentó el universo primitivo y que está relacionada con la transición desde un universo no-Minkowskiniano abierto hacia un verdadero universo Minkowskiniano.

Resumiremos ahora los principales descubrimientos que hemos mostrado. La irreversabilidad juega un papel constructivo, y no sólo destructivo, en nuestro universo. Cuestiones como la del origen de la vida, la del origen del universo o la del origen de la materia, ya no pueden ser discutidas sin tener que recurrir a la irreversibilidad. Estamos, pues, en una situación paradójica, que nos lleva a un enfrentamiento con el punto de vista tradicional. En efecto, el criterio convencional consiste en que, dado que las leyes fundamentales de la física son simétricas respecto a la inversión temporal, no puede haber base física alguna que fundamente la orientación del tiempo. La aparición de la irreversibilidad en los procesos físicos y la correspondiente «orientación del tiempo» son tan sólo el resultado de una media estadística (o «de grano gordo») que es necesaria, no por ningún aspecto objetivo de los fenómenos físicos, sino simplemente para tener en cuenta nuestra ignorancia (o falta de interés) sobre el estado dinámico del sistema. Así, Born afirma que «la irreversibilidad es una consecuencia de la introducción explícita de la ignorancia en las leyes fundamentales». Esto convertiría una estructura química o biológica en el resultado de nuestra ignorancia, lo cual es paradójico.

Afortunadamente, comenzamos a entrever la solución. Sin embargo, la introducción de la irreversibilidad en el nivel microscópico está lejos de ser una cuestión trivial. Mientras que consideremos las trayectorias o las funciones de onda como objetos fundamentales de la física no podremos abordar la irreversibilidad. Nuestro problema es, por tanto, cómo sustituir estos conceptos por otros nuevos.

4. Inestabilidad e irreversibilidad

Veremos ahora cómo la inestabilidad fuerte, que lleva a la irreversibilidad, implica una forma de no-localidad en los sistemas físicos (14). Consideremos el lanzamiento de una moneda, ejemplo éste ya tratado por Poincaré. El resultado se presenta, tradicionalmente, por probabilidades iguales: P₀ = 0,5 y P₁ = 0,5. ¿Corresponde este resultado a alguna ley fundamental de la naturaleza? Si suponemos que es aplicable una representación determinista (leyes de Newton) al lanzamiento de una moneda, ¿no debería ser 0 o 1 el resultado, según cuáles fueran los condiciones iniciales?

Podemos ahora analizar más detalladamente esta información. Supongamos que vamos limitando las condiciones iniciales dentro de intervalos cada vez menores. Si, comenzando con cierta precisión finita, el resultado corresponde a la predicción determinista 0/1, las leyes son claramente deterministas. Pero si, para unas condiciones arbitrarias, sea cual sea la precisión, el resultado sigue siendo 0,5/0,5, entonces debemos considerar que el problema es indecidible individualmente, pero «decidible» estadísticamente. La ley fundamental de la naturaleza es entonces una ley de naturaleza estadística.

Consta que Bohr afirmó a Planck que en la mecánica cuántica las coordenadas y los momentos no pueden ser determinados simultáneamente. Planck contestó: «¡Pero Dios conoce ambas cosas!», a lo cual Bohr respondió que la física trata sólo de aquello que el hombre puede conocer.

La ilusión de un conocimiento completo (infinito) proviene, al parecer, del hecho histórico que la ciencia clásica empezó con el estudio de los movimientos periódicos. El retorno diario del sol y la regularidad de los fenómenos celestes han influido profundamente en el pensamiento humano desde los tiempos paleolíticos. Pero esta regularidad de los procesos periódicos no es el caso general. El mensaje contenido en el segundo principio de la termodinámica consiste en que no vivimos en un mundo que pueda ser descrito en términos de movimientos periódicos. Es un mundo inestable, que conocemos a través de una ventana finita.

A modo de ejemplo, consideremos la llamada transformación del panadero. Aquí el espacio físico es un cuadrado, sobre el que aplicamos las operaciones bien conocidas por los panaderos: aplanamientos, corte, doblado [figura 4.1a]. En este espacio fásico, consideremos un conjunto determinado de condiciones iniciales sometidas a esta dinámica. Su volumen se conserva, pero los puntos están esparcidos por todo el espacio [figura 4.1b].

[Fig. 4.1a] La transformación del panadero en el espacio fásico (p, q). La transformación del panadero puede ser descrita como una transformación puntual uno-a-uno en el espacio fásico [0,1[ × [0,1[: (x, y) → (x', y'), donde x' = 2x (mod 1) y y' = (y + 2x − x')/2.

[Fig. 4.1b] Conservación y fragmentación del volumen para la transformación del panadero.

Hablando idealmente, sería factible encontrar los membra disjecta y volver a unirlos de nuevo. Pero el nuevo mundo de la física contemporánea ya no es, en absoluto, una especie de museo (como lo fue el mundo clásico, o incluso el mundo cuántico si se desprecian los procesos de medida) en que se supone que cada bit de información se conserva: es un mundo de procesos, en el que se destruye y se genera información y estructura.

Los sistemas de Bernoulli (y, más en general, los K-flujos) nos conducen a conceptos nuevos como es el de operador temporal interno T. En efecto, la transformación del panadero (que es un sistema de Bernoulli) induce en el cuadrado una particular estructura geométrica relacionada con el tiempo. Por ejemplo, de una partición χ_n [figura 4.2.] se puede considerar que da la edad interna que la transformación otorga al sistema. La partición χ₀ tiene la χ₋₁ como su pasado inmediato, y la χ₊₁ como su futuro inmediato, y así sucesivamente: χ_n = Uⁿχ₀: además, es evidente que puntos separados por un intervalo de vertical u horizontal reducirán o aumentarán respectivamente, esta distancia en un factor de 2 en cada iteración. Esto determina dos foliaciones del espacio fásico, una en fibras horizontales (que se dilatan) y otra en fibras verticales (que se contraen).

[Fig. 4.2] Particiones generadoras de la transformación del panadero.

Este nuevo operador T admite a las particiones χ_n como funciones propias; por tanto, no conmuta con el operador U que lleva de una a otra de estas particiones.

Este tipo de sistema nos trae a los conceptos de particiones codificadoras y generadoras. Una representación muy importante de la transformación del panadero es el llamado «cambio de Bernoulli» (1/2, 1/2). Construyamos una partición P = {P₀, P₁), codificada por el alfabeto Q = {0,1}, donde P₀ (respectivamente P₁) es la mitad izquierda (respectivamente derecha) del cuadrado: un estado (o punto) ω es descrito por un símbolo s si ω ∈ P_s. Es fácil ver que la secuencia simbólica (s_t), t ∈ ℤ que corresponde a un punto ω = (x, y) viene dada por el desarrollo binario siguiente:

dado por la aplicación de desplazamiento

s'_k = s_k−1

que es el equivalente a las operaciones del panadero. La partición tiene la propiedad de Bernoulli para esta transformación; en particular, todos los símbolos (s_k), −∞ < k < +∞ que describen un punto cogido al azar (con una distribución uniforme de probabilidad sobre el cuadrado), toman independientemente los valores (0, 1) con probabilidades iguales (1/2, 1/2).

Cualesquiera que sean los datos definidos a través de una ventana finita, pongamos por caso s_−k, …,s_k, no serán capaces de permitir la predicción de la trayectoria después de un tiempo suficiente (t > 2_k+1). Desde el punto de vista que aquí nos interesa, el teorema fundamental es el siguiente: supongamos que consideramos un problema de valores iniciales para un sistema dinámico inestable del tipo del panadero (descrito por un cambio de Bernoulli). Supongamos que nuestro conocimiento de las condiciones iniciales viene descrito por una ventana como la detallada anteriormente, sea cual sea su tamaño. Tenemos que representar entonces nuestro estado inicial por una función de distribución sobre el estado de las secuencias simbólicas. El teorema básico sobre sistemas de Bernoulli y K-sistemas afirma entonces que esta función de distribución satisface una ecuación del tipo Markov, correspondiendo a una aproximación al equilibrio para un tiempo positivo grande.

Tenemos que subrayar que ambas condiciones (inestabilidad y ventana finita) son necesarias. Con una ventana finita y un sistema estable el conjunto que resultaría sería la colectividad de Gibbs en no-equilibrio, que satisface la ecuación temporalmente reversible de Liouville. Para precisión infinita, deberíamos tratar con un punto fásico que siguiera una trayectoria única, y entonces no aparecería problema alguno de irreversibilidad.

Por lo tanto, tenemos ahora una manera de unificar el trabajo de los dos padres fundadores de la física estadística. Para los sistemas estables, recuperamos las colectividades de Gibbs; para los inestables, recuperamos las ecuaciones cinéticas tipo Boltzmann, que llevan a un aumento de entropía. Veamos más detalladamente cómo ocurre todo esto.

A causa de la ventana finita, es evidente que nunca podremos distinguir dos puntos de una variedad contráctil que estén más cerca que una cierta distancia estadística η, En efecto, conforme el tiempo avanza, estos dos puntos convergerán en el mismo punto. En lugar de una trayectoria única, debemos considerar un conjunto de trayectorias. De hecho, a la función δ le corresponde ahora una generalización δ = Λδ, obtenida mediante el operador de deformación Λ, que suaviza las funciones de distribución del espacio fásico a lo largo de las fibras que se contraen, para distancias ~η. Dado que la contracción resulta de la acción de la dinámica, Λ también puede ser expresado como una función de operador Λ = λ(t), donde λ es una auténtica función real decreciente:

1 = λ(−∞) ≥ λ(t) ≥ λ(+∞) = 0

El objeto δ puede jugar ahora el mismo papel fundamental que juega el concepto de trayectoria en la física clásica. Se puede mostrar que el semigrupo mantiene invariante este objeto, de la misma manera que la trayectoria es invariante con respecto a los grupos usuales de la dinámica. Mientras que la colectividad de Gibbs es una superposición de funciones δ, la colectividad de Boltzmann es un superposición de δ.

La transformación de panadero corresponde a un caso muy idealizado. Recientemente, se han encontrado en el campo de la dinámica celeste situaciones del mismo tipo, pero más realistas. El ejemplo al que hago referencia es el trabajo de mi colega T. Petrosky de Austin, realizado bajo la dirección de V. Szebehely, uno de los expertos mundiales sobre el problema de los tres cuerpos. El problema en cuestión consiste en la captura de un cometa en el sistema solar, producida a consecuencia del efecto de Júpiter. Una de las dificultades de este problema radica en que el proceso de captura ocurre por un fuerte efecto de resonancia entre el período de Júpiter y el movimiento del cometa. Todos los efectos que hemos visto anteriormente para la transformación del panadero son también aplicables aquí: las trayectorias individuales dejan de tener sentido, pero es posible hacer un modelo del comportamiento colectivo a partir de la acumulación de movimientos cometarios. Por lo tanto, es un hecho muy notable que las nuevas ideas de irreversibilidad e inestabilidad aparezcan ahora en el baluarte del determinismo, que ha sido tradicionalmente la dinámica celeste clásica (15).

5. Conclusiones

En la aproximación que hemos dado, la racionalidad ya no puede seguir siendo identificada con la «certeza», ni tampoco la probabilidad con la ignorancia. En todos los niveles, la probabilidad juega un papel esencial en la mecánica evolutiva. Las descripciones que damos del mundo exterior y de nuestro propio mundo interior ya no son contradictorias.

Estamos lejos del pesimismo de Sigmund Freud, quien dijo que la historia de la ciencia es una historia de alienación: Zwei grosse Kränkungen ihrer naiven Eigenliebe hat die Menscheit im Laufe der Zeite von der Wissenschaft erduldan müssen (16); desde Copérnico ya no vivimos en el centro del universo; desde Darwin el hombre ya no es diferente de los animales; y desde el mismo Freud la conciencia sólo es la parte emergida de una realidad compleja que nos está oculta. Curiosamente, llegamos ahora a una opinión contraria: el hombre aparece como una realización sorprendente de las leyes básicas de la naturaleza, expresadas éstas por la inestabilidad, el azar y la irreversibilidad.

Como hemos mostrado, la física puede hablar ahora de un nuevo operador temporal, que es intrínseco a los objetos, no exterior a ellos. Realmente, no conozco una mejor ilustración de este nuevo concepto de tiempo que los Relojes blandos que son uno de los motivos recurrentes más famosos de Dalí.

Hemos visto cómo, incluso en el mundo de la dinámica clásica, hemos conseguido un grado de descripción muy similar al famoso principio de complementariedad de Bohr: los diversos lenguajes y puntos de vista posibles con respecto a un sistema físico pueden ser complementarios. La irreductible pluralidad de perspectivas sobre una misma realidad expresa la imposibilidad de un punto de vista divino desde el cual pueda ser contemplada toda la realidad.

De nuevo, y como mencionábamos en la introducción, estamos aquí muy cerca de la ambigüedad básica claramente reflejadas en el trabajo pictórico de Dalí. Más general aún, sabemos que hay una tendencia profunda, perceptible en alguno de los creadores más relevantes de la pintura moderna, a comunicar una sensación de incertidumbre o de inquietud, sobre el mundo que nos rodea.

En esta conferencia hemos hablado de la reciente evolución de la cosmología. En este campo estamos también lejos de la calmada confianza en el poder infinito de la razón clásica. Un universo evolutivo expresa que la realidad no puede ser devuelta a la identidad. El universo es un escenario en transformación incesante, y, en consecuencia, ¿cómo no recordar las infinitas variaciones de significado de los múltiples sueños de Dalí?

¿Cuál podría ser nuestra conclusión? Más que nunca el tiempo aparece en el centro. Quizá podríamos llegar a decir que toda cosmología que comienza con algún guion para el nacimiento de nuestro universo expresa de una forma u otra que el tiempo precede a la existencia.