E quindi, che cosa abbiamo imparato dai nostri errori?

Mentre scrivevo questo libro, io e mia moglie ci siamo presi una pausa dal lavoro e in uno dei nostri molti viaggi abbiamo trascorso una giornata a visitare una città straniera. Piuttosto grande e famosa, per la verità. Ci stavamo dedicando alle solite attività turistiche, quando mi è venuto in mente che eravamo nella città dove si trovava un’opera ingegneristica a cui aveva lavorato un mio amico.

Nel corso degli ultimi decenni, questo mio amico era stato coinvolto nel design e nella costruzione di un progetto d’ingegneria (pensate a qualcosa come un edificio o un ponte). Una volta, tra una birra e l’altra, mi aveva raccontato di uno sbaglio che avevano fatto durante la progettazione, un errore matematico che per fortuna non aveva avuto nessun impatto sulla sicurezza di quella costruzione e che tuttavia aveva portato a un suo leggero cambiamento, una banalità sul piano estetico. Insomma, qualche dettaglio non era venuto proprio secondo il progetto originale. E sì, questa storia è deliberatamente vaga.

Mia moglie (su cui posso sempre fare affidamento) mi ha aiutato a individuare la conseguenza visibile dello sbaglio matematico del mio amico, in modo che potessi scattarmi una foto lì accanto. Non ho idea di che cosa pensassero i passanti vedendomi in posa dove non c’era in apparenza nulla da fotografare, ma io ero eccitatissimo: sarebbe stato un grande esempio contemporaneo da includere nel mio libro. La storia è piena di errori ingegneristici, ma il mio amico è ancora vivo e avrei potuto raccogliere una testimonianza personale su come era stato fatto quello sbaglio. Inoltre, non era nulla di pericoloso, motivo per cui avrei potuto spiegare in modo imparziale il processo che aveva portato all’errore.

Temo che non potrai usarla.

Potevo quasi percepire nella sua voce il pentimento per avermi raccontato di quello sbaglio. Per convincerlo ho provato a mostrargli le foto delle mie vacanze, con me accanto alla prova visibile del loro errore di calcolo, ma non è servito a nulla. Mi ha spiegato che questo genere di cose, pur essendo analizzate e discusse all’interno di un gruppo, non vengono mai rese pubbliche, anche quando si tratta – come in questo caso – di una banalità priva di conseguenze. Il contratto e gli accordi di riservatezza impediscono legalmente agli ingegneri di rivelare quasi ogni cosa che riguardi i progetti, anche quando sono ormai stati completati da decenni.

Così, eccoci qui. L’unica cosa che posso dirvi su quanto è successo è che non posso dirvi nulla. E non sono solo gli ingegneri a non poter divulgare notizie simili. Un altro mio amico svolge un lavoro di consulenza sugli aspetti matematici di un’area della sicurezza con cui il pubblico viene direttamente a contatto. Vengono assunti da un’azienda per fare alcune ricerche e scoprire errori che riguardano l’intero settore; poi però, quando lavorano per un’altra compagnia o anche quando consigliano il governo sull’adozione delle linee guida per la sicurezza, non possono rivelare ciò che hanno in precedenza scoperto per conto di qualcun altro. È tutto un po’ sciocco.

Gli uomini non sembrano molto bravi a imparare dagli errori, e io non ho grandi soluzioni a questo riguardo: mi rendo pienamente conto che le compagnie non vogliono che le loro pecche, o le ricerche che hanno dovuto finanziare, divengano di dominio pubblico. Per quanto riguarda l’errore ingegneristico del mio amico, dato che le conseguenze sono solo estetiche, può anche essere giusto che nessun altro venga mai a scoprirlo. Mi piacerebbe però che ci fosse un meccanismo in grado di assicurare che le lezioni importanti e potenzialmente utili possano essere condivise con chi trarrebbe beneficio dal conoscerle. Scrivendo questo libro ho svolto numerose ricerche consultando i rapporti sulle indagini che sono stati resi di dominio pubblico, ma in genere questo avviene soltanto quando il disastro in questione è sotto gli occhi di tutti; è probabile che ci siano molti più casi in cui errori matematici dalle conseguenze meno appariscenti vengono semplicemente nascosti sotto il tappeto.

Tutti sbagliamo, e lo facciamo incessantemente. E non è una cosa di cui avere paura. Molte persone con cui parlo mi raccontano che, quando andavano a scuola, si lasciavano scoraggiare dalla matematica perché non la capivano. Ma la sfida di imparare la matematica consiste per metà nell’accettare il fatto che, per quanto possiate non essere naturalmente portati per questa disciplina, se vi mettete d’impegno potete comunque apprenderla. Per quanto ne so, l’unica mia frase che è stata inserita su un poster e appesa in classe da alcuni insegnanti è: «I matematici non sono persone che trovano la matematica facile, ma persone a cui piace la sua difficoltà».

Nel 2016, sono diventato mio malgrado il simbolo di quando tutti i vostri sforzi matematici non sono comunque sufficienti. Stavamo filmando un video da caricare su YouTube per il canale Numberphile a proposito dei quadrati magici. Si tratta di griglie di numeri che danno sempre la stessa somma addizionando le righe, le colonne o le diagonali. Sono un grande appassionato di quadrati magici, e mi sembrava interessante che nessuno avesse mai trovato un quadrato magico tre-per-tre composto interamente di numeri quadrati. E, d’altro canto, nessuno era mai riuscito a dimostrare la sua inesistenza. Ok, non sarà stato il più importante problema aperto in ambito matematico, però trovavo stimolante che nessuno l’avesse ancora risolto.

Così decisi di provarci io. Sfidando le mie capacità di programmatore, scrissi un codice per vedere quanto riuscissi ad avvicinarmi alla scoperta di un quadrato magico fatto di quadrati. E trovai il seguente:

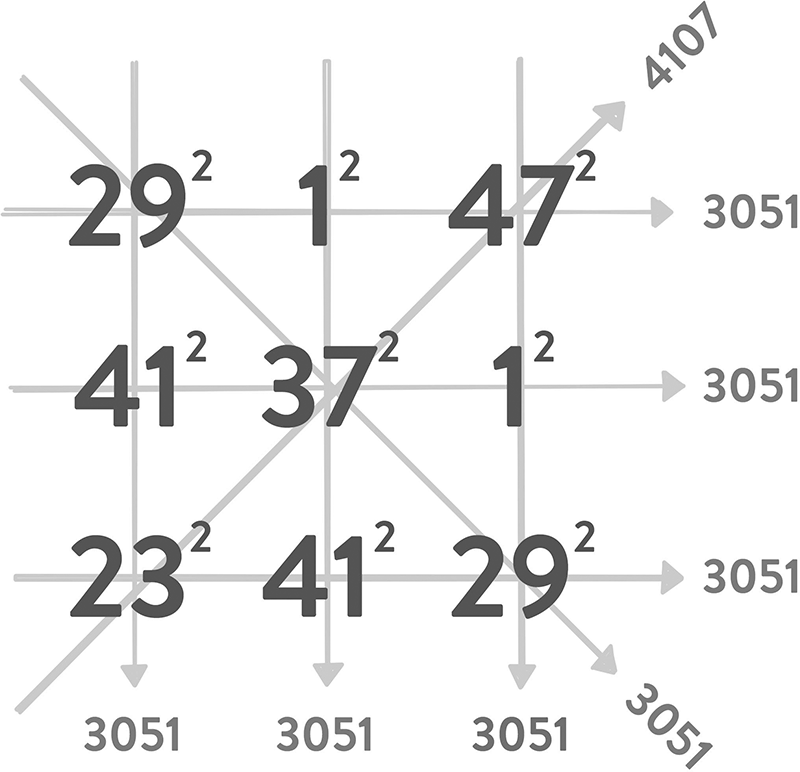
La somma è la stessa su tutte le righe e le colonne, ma solo su una delle due diagonali. Mi mancava una somma perché funzionasse; inoltre, avevo usato più volte gli stessi numeri, mentre in un vero quadrato magico tutti i numeri dovrebbero essere diversi. Il mio tentativo di trovare una soluzione era quindi fallito, ma la cosa non mi sorprese: era già stato dimostrato che ogni quadrato magico tre-per-tre composto da quadrati avrebbe dovuto contenere solo numeri più grandi di centomila miliardi, mentre i miei andavano da 1² = 1 a 47² = 2209. Volevo solo fare una prova per vedere fin dove riuscissi ad arrivare, tutto qui.

Il video venne però filmato da Brady Haran, che si mostrò meno indulgente: in sostanza, sottolineò che la mia soluzione non era per niente buona. Quando mi chiese il nome di quella creazione, capii subito che, se lo avessi chiamato «quadrato di Parker», sarebbe diventato un simbolo del fare le cose nel modo sbagliato. Non che avessi scelta, comunque. Brady intitolò il video The Parker Square («Il quadrato di Parker») e il resto è storia: è diventato un meme su Internet e Brady, invece di «non dare troppa importanza alla cosa», gli ha persino dedicato delle T-shirt e delle tazze. La gente si diverte a indossare le magliette quando viene ad assistere ai miei spettacoli.

Ho tentato di reinterpretare il quadrato di Parker presentandolo come un simbolo dell’importanza di provarci anche quando il fallimento è probabile. A scuola le persone sembrano avere l’impressione che sbagliare in matematica sia qualcosa di terribile, da evitare a ogni costo. Tuttavia, è impossibile migliorarsi e provare nuove sfide senza commettere qualche sbaglio di tanto in tanto; così, come una sorta di compromesso, il quadrato di Parker è diventato «un simbolo delle persone che ci provano ma, alla fine, non ce la fanno».

La mia vita ora è questa.

Detto questo, ci sono comunque situazioni in cui, come ho mostrato nel libro, la matematica dev’essere fatta in modo corretto. Certo, chi gioca con nuovi concetti matematici e li studia può permettersi di fare errori di qualsiasi tipo, ma quando usiamo la matematica in situazioni critiche, di importanza vitale, dovremmo essere in grado di procedere regolarmente nel modo giusto. E dato che, spesso, andiamo oltre i limiti di ciò che l’uomo è per natura capace di fare, ci sarà sempre qualche errore in agguato dietro l’angolo.

Il motore principale dello space shuttle (SSME) è una macchina straordinaria. Ha un rapporto spinta/peso superiore a quello di tutti i motori precedenti. È stato costruito ai limiti dell’esperienza ingegneristica precedente, se non al di là di quei limiti; non c’è quindi da stupirsi che siano emersi differenti tipi di difetti e di difficoltà.

– Appendice F: Osservazioni personali di R.P. Feynman sull’affidabilità dello shuttle, tratte dal Rapporto al Presidente della Commissione presidenziale sull’incidente dello space shuttle Challenger, 6 giugno 1986

Penso che valga la pena di assumere un atteggiamento pragmatico, quando bisogna evitare i disastri. Gli sbagli avverranno inevitabilmente, e i sistemi devono essere in grado di gestirli e di impedire che si trasformino in disastri. Il team di CHI+MED che studia le interazioni tra uomo e computer nell’ambito delle apparecchiature mediche ha elaborato una nuova versione del modello del formaggio svizzero per cui ho un debole: per spiegare il processo causale che porta agli incidenti, hanno introdotto il modello del formaggio fondente.

In questa evoluzione del modello, il formaggio svizzero viene adagiato su un lato: immaginate che le fette di formaggio siano orizzontali e che gli sbagli vi piovano sopra dall’alto. Solo gli errori che riescono a passare attraverso i buchi di ogni strato, arrivando fino in fondo, diventano incidenti. L’elemento di novità è costituito dal fatto che le fette di formaggio in questo caso sono calde e alcune loro parti possono fondere e gocciolare, causando nuovi problemi. Lavorando con le attrezzature mediche, i membri di CHI+MED hanno capito che il modello del formaggio svizzero non rappresentava una causa di incidenti: a volte, possono essere proprio i diversi strati e i passaggi all’interno del sistema a determinare il verificarsi di un errore. Così, la semplice aggiunta di un nuovo strato non riduce automaticamente il numero degli incidenti; i sistemi sono una realtà più complicata e dinamica.

Se il set da fonduta rappresenta il disastro, nessuno vuole delle gocce in più.

Come esempio i membri di CHI+MED usano quello dei sistemi di Barcode Medication Administration, introdotti per usare i codici a barre in modo da ridurre gli errori nella somministrazione dei farmaci. È innegabile che questi sistemi abbiano contribuito a ridurre gli errori nei quali veniva dato il farmaco sbagliato, ma al contempo hanno aperto la strada ad altre possibilità di sbagli del tutto nuove. Per risparmiare tempo, a volte il personale, invece di scansionare il codice a barre sul braccialetto di un paziente, porta con sé delle copie di quei codici legate alla cintura o le custodisce negli armadi delle scorte; inoltre, se ritengono che due pacchetti di farmaci siano identici, scansionano due volte lo stesso anziché scansionarli tutti e due singolarmente. Disporre delle copie dei codici a barre ha causato situazioni in cui pazienti e farmaci vengono controllati con meno attenzione di prima. Quando viene implementato un nuovo sistema, gli uomini sanno essere molto intraprendenti nel trovare modi innovativi di commettere sbagli.

Quando gli uomini diventano troppo sicuri di sé e pensano di saperne di più della matematica, la situazione può diventare molto pericolosa. Nel 1907, su una sezione larga più di mezzo chilometro del fiume San Lorenzo, in Canada, era in costruzione un ponte stradale e ferroviario in acciaio. I lavori erano iniziati da tempo, ma il 29 agosto uno degli operai notò che un rivetto che aveva piantato un’ora prima si era misteriosamente spezzato a metà. Quindi, all’improvviso, l’intera sezione meridionale del ponte crollò con un boato che venne udito fino a 10 chilometri di distanza. Morirono settantacinque delle ottantasei persone che in quel momento stavano lavorando sul ponte.

C’era stato un errore di calcolo inerente il peso che avrebbe avuto il ponte, dovuto in parte al fatto che quando il progetto originale era stato allungato, da 490 a 550 metri, le forze non erano state ricalcolate; di conseguenza, le travi portanti inferiori si erano piegate fino a cedere del tutto. Nel corso dei lavori, gli operai avevano già espresso le loro preoccupazioni per il fatto che le travi si stavano deformando, e qualcuno si era addirittura licenziato per non stare più lì. Tuttavia, gli ingegneri non li ascoltarono. Anche quando l’errore di calcolo del carico venne scoperto, il capo ingegnere decise di procedere comunque con la costruzione, ritenendo che la struttura avrebbe retto bene senza che fossero stati condotti dei test adeguati.

In seguito al crollo, il ponte venne riprogettato e la sezione trasversale delle travi che portavano il carico critico fu raddoppiata rispetto al primo tentativo. Il lavoro ebbe successo e il Ponte del Québec, terminato nel 1917, è in uso ancora oggi, a più di un secolo di distanza. La costruzione non fu però priva di ulteriori problemi: nel 1916, durante il tentativo di collocare al suo posto la sezione centrale (assemblata a riva), l’attrezzatura usata per sollevarla si ruppe e la struttura cadde nel fiume, causando la morte di tredici operai. Quella sezione centrale si trova tuttora sul letto del fiume, accanto al primo ponte crollato. Le costruzioni sono un lavoro pericoloso, dove il più piccolo sbaglio può costare delle vite.

Una foto di poco prima del crollo e una scattata in seguito.

Fare l’ingegnere, o lavorare su qualcosa in cui la matematica ha conseguenze importanti, è un mestiere terrificante. A causa del disastro del Ponte del Québec, a partire dal 1925 gli studenti che si laureano in ingegneria in Canada possono partecipare alla «Cerimonia della vocazione dell’ingegnere», dove ricevono un anello di acciaio come promemoria dell’umiltà e della fallibilità degli ingegneri. È una tragedia quando un matematico commette uno sbaglio che provoca un disastro, ma ciò non significa che possiamo fare a meno della matematica. Abbiamo bisogno di ingegneri che continuino a progettare ponti, nonostante la pressione che questo lavoro comporta.

Il mondo moderno dipende dalla matematica, e quando le cose vanno storte dovremmo considerarlo come monito sulla necessità di tenere un occhio sul formaggio fondente; al contempo, però, questo dovrebbe anche ricordarci di tutta la matematica che continua a funzionare a meraviglia intorno a noi.