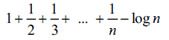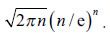Notas

^[1] El original alemán es: «Wir müssen wissen. Wir werden wissen». Se encuentra en una charla que grabó Hilbert para la radio. Ver Constante Reid, Hilbert, Springer, Berlín, 1970, p. 196^[*]. <<

^[2] Simon Singh, Fermat’s Last Theorem, Fourth Estate, 1997. <<

^[3] Gauss, carta a Heinrich Olbers, 21 de marzo de 1816. <<

^[4] El título de Wiles era «Curvas modulares, formas elípticas y representaciones de Galois». <<

^[5] Andrew Wiles, «Modular elliptic curves and Fermat’s last theorem», Annals of Mathematics, n.º 141 (1995), pp. 443-551. <<

^[6] Ian Stewart, Seventeen Equations that Changed the World, Profile, 2012, capítulo 11. <<

^[7] Ibid, capítulo 9. <<

^[8] Los problemas de Hilbert, y su estatus actual, tal como figuran con ligeros cambios en Profesor Stewart’s Hoard of Mathematical Treasures, Profile, 2009^[**], son los siguientes:

^[9] Reimpreso como: Jacques Hadamard, The Psychology of Invention in the Mathematical Field, Dover, 1954. <<

^[10] El algoritmo de Agrawal-Kayal-Saxena es como sigue:

Input: entero n

1. Si n es una potencia exacta de cualquier número más pequeño, resultado COMPUESTO y stop.

2. Encontrar el r más pequeño tal que la potencia más pequeña de r que sea igual a 1 módulo n es al menos (log n)².

3. Si cualquier número menor o igual que r tiene un factor en común con n, resultado COMPUESTO y stop.

4. Si n es menor o igual que r, resultado PRIMO y stop.

5. Para todos los números naturales a desde 1 hasta un límite especificado, comprobar si el polinomio (x + a)ⁿ es igual a xⁿ + a, módulo n y módulo x^r - 1. Si la igualdad se cumple en algún caso, resultado COMPUESTO y stop.

6. Resultado PRIMO. <<

^[11] Un ejemplo de lo que tengo en mente es la fórmula [A³ⁿ], donde los corchetes denotan el máximo entero menor o igual que su contenido. En 1947 W. H. Mills demostró que existe una constante real A tal que esta fórmula da un primo para cualquier n. Suponiendo la hipótesis de Riemann, el mínimo valor de A que funciona es aproximadamente 1,306. Sin embargo, la constante está definida utilizando una secuencia apropiada de primos, y la fórmula es tan solo una forma simbólica de reproducir esta secuencia. Para más de estas fórmulas, incluidas algunas que representan a todos los primos, véase http://mathworld.wolfram.com/PrimeFormulas.html http://en.wikipedia.org/wiki/Formula_for_primes. <<

^[12] Si n es impar entonces n - 3 es par, y si n es mayor que 5 entonces n - 3 es mayor que 2. Por la primera conjetura, n - 3 = p + q, de modo que n = p + q + 3. <<

^[13] Prefiero este término al antiguo, pero quizá más familiar, «progresión aritmética». Nadie habla ya de progresiones, excepto en los casos de la aritmética y la geométrica. <<

^[14] http://www.numberworld.org/misc_runs/pi-5t/details.html. <<

^[15] Lo que menos me gusta en este contexto es «salto cuántico». En el habla coloquial indica algún paso adelante gigantesco, o un cambio enorme, como el descubrimiento de América por los europeos. Sin embargo, en la teoría cuántica un salto cuántico es tan minúsculo que ningún instrumento conocido puede observarlo directamente, un cambio cuyo tamaño es aproximadamente 0,000 … 01 con unos cuarenta ceros. <<

^[16] Encontrar una disección finita de un cuadrado en un círculo se denomina el problema de cuadrar el círculo de Tarski. Miklós Laczovich lo resolvió en 1990. Su método no es constructivo y hace uso del axioma de elección. El número de piezas requerido es enorme, del orden de 10⁵⁰. <<

^[17] Las estrafalarias afirmaciones de los cuadradores del círculo y trisectores del ángulo se exploran en profundidad en Underwood Dudley, A Budget of Trisections, Springer, 1987, y Mathematical Cranks, Mathematical Association of America, 1992. El fenómeno no es nuevo: véase Augustus De Morgan, A Budget of Paradoxes, Longmans, 1872; reimpreso por Books For Libraries Press, 1915. <<

^[18] La cuadratriz de Hippias es la curva que traza el punto de intersección de una recta vertical que se mueve uniformemente a través de un rectángulo y una recta que rota uniformemente en torno al punto central del lado inferior del rectángulo (véase Figura 52). Esta relación convierte cualquier pregunta sobre división de ángulos en la correspondiente sobre división de rectas. Por ejemplo, para trisecar un ángulo simplemente se triseca la recta correspondiente. Véase:

http://www.geom.uiuc.edu/~huberty/math5337/groupe/quadratrix.html

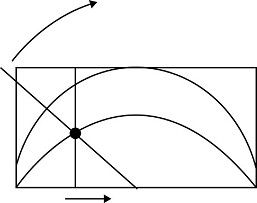
FIGURA 52. La cuadratriz de Hippias (curva inferior). <<

^[19] He aquí un ejemplo explícito. Desde el punto de vista geométrico, si una línea corta a un círculo y no es tangente al mismo, entonces corta al círculo en exactamente dos puntos. Consideremos una línea que es paralela al eje horizontal, a distancia ½ por encima del mismo (véase Figura 53). La ecuación de esta línea es muy sencilla: y = ½. (Cualquiera que sea el valor de χ, siempre obtenemos el mismo valor para y). Cuando y = ½, la ecuación χ² + y² = 1 se hace χ² + ¼ = 1. Por lo tanto χ² = 3/4, de modo que 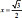o 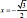. Así, el álgebra nos dice que el círculo unidad corta a nuestra recta escogida exactamente en dos puntos, cuyas coordenadas son y 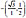. Esto es consistente con la Figura 53 y con un razonamiento puramente geométrico.

FIGURA 53. Una recta horizontal que corta al círculo en dos puntos. <<

^[20] Estrictamente hablando, el polinomio en cuestión debe tener coeficientes enteros y ser irreducible: no es producto de dos polinomios de grado menor con coeficientes enteros. Tener un grado que es una potencia de 2 no siempre es suficiente para que exista una construcción con regla y compás, pero siempre es necesario. Si el grado no es una potencia de 2, no puede existir una construcción. Si es una potencia de 2, se necesita más análisis para decidir si existe una construcción. <<

^[21] La recíproca también es cierta: dadas construcciones para 3-gonos y 5-gonos regulares, puede derivarse una para un 15-gono. La idea subyacente es que 2/5 - 1/3 = 1/15. Un punto sutil concierne a las potencias primas. El argumento no proporciona una construcción para, digamos, un 9-gono dada una para sus factores primos; a saber, un 3-gono. Gauss demostró que no es posible una construcción para potencias primas impares mayores que la primera. <<

^[22] Véase Ian Stewart, Seventeen Equations that Changed the World, Profile, 2012, capítulo 5. <<

^[23] Para dar sentido a esta afirmación, resolvemos la cuadrática en factores lineales. Entonces χ² - 1 = (χ + 1) (χ - 1) que es cero si uno de los factores es cero, de modo que χ = 1 o -1. El mismo razonamiento puede aplicarse a χ² = xx: esto es cero si o bien el primer factor χ = 0 o bien el segundo χ = 0. Sucede así que estas dos soluciones dan el mismo χ, pero la presencia de dos factores χ distingue esta situación de algo como χ(χ - 1) donde solo hay un factor χ. Al contar cuantas soluciones tiene una ecuación algebraica, la respuesta es generalmente mucho más rigurosa si se tienen en cuenta estas «multiplicidades». <<

^[24] Cuando n = 9, el segundo factor es χ⁸ + χ⁷ + x⁶ + x⁵ + x⁴ + x³ + x³ + x + 1 Pero esto tiene factores: es igual a (χ² + x + 1) (x⁶ + x³ + 1). La caracterización de Gauss de números construibles requiere que cada factor irreducible tenga un grado que sea una potencia de 2. Pero el segundo factor tiene grado 6, que no es una potencia de 2. <<

^[25] Gauss demostró que el 17-gono puede construirse siempre que se pueda construir una recta cuya longitud sea

Puesto que siempre se pueden construir raíces cuadradas, esto resuelve efectivamente el problema. Otros matemáticos encontraron construcciones explícitas. Ulrico von Huguenin publicó la primera en 1803, y H. W. Richmond encontró una más sencilla en 1893. En la Figura 54, tomar dos radios perpendiculares AOP₀ y BOC de un círculo. Hacer OJ = 1/4OB y ángulo OJE = 1/4OJP₀. Encontrar F tal que el ángulo EJF es 45 °. Trazar un círculo con FP₀ como diámetro, que corta a OB en K. Trazar el círculo con centro E que pasa por K, que corta a AP₀ en G y H. Trazar HP₃ y GP₅ perpendicular a AP₀. Entonces, P₀, P₃, P₅ son respectivamente los vértices 0-ésimo, tercero y quinto de un 17-gono regular, y los otros vértices se construyen ahora fácilmente.

FIGURA 54. Cómo construir un 17-gono regular. <<

^[26] Para los últimos descubrimientos, véase Wilfrid Keller, «Factores primos de números de Fermat y estatus completo de factorización» http://www.prothsearch.net/fermat.html. <<

^[27] E. J. Richelot publicó una construcción para el 257-gono regular en 1832. J. Hermes de la Lingen University dedicó diez años al polígono de 65.537 lados. Su trabajo no publicado puede encontrarse en la Universidad de Gotinga, pero se cree que contiene errores. <<

^[28] Una típica fracción continua tiene este aspecto:

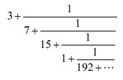
Esta fracción continua concreta es el comienzo de la que representa π. <<

^[29] http://bellar4d.org/pi-challenge/announce220997.html. <<

^[30] Louis H. Kauffman, «Map coloring end the vector cross product, Journal of Combinatorial Theory», B 48, (1990), pp. 145-154. Louis H. Kauffman, «Reformulating the map color theoreme», Discrete Mathematics, n.º 302 (2005), pp. 145-172. <<

^[31] Si se permite que las fronteras sean muy complicadas, no como en un mapa sino mucho más sinuosas, entonces tantos países como uno quiera pueden compartir una «frontera» común. Una construcción llamada los Lagos de Wada demuestra este resultado contraintuitivo. Véase:

http://en.wikipedia.org/wiki/Lakes_of_Wada <<

^[32] El término técnico es «grafo dual», porque tradicionalmente se utilizaba «grafo» en lugar de «red». Pero «red» se está haciendo habitual, es más evocador y evita la confusión con otros usos de la palabra «grafo». <<

^[33] Hasta hace poco se pensaba que la nota en Nature era la última referencia en prensa al problema durante casi un siglo, pero el historiador de las matemáticas Robin Wilson localizó este artículo posterior de Cayley. <<

^[34] Trabajando en la red dual, sea C el número de caras (incluida una gran cara que rodea la red entera), A el número de aristas y V el número de vértices. Podemos suponer que cada cara en la red dual tiene al menos tres aristas; si tiene una cara con solo dos aristas entonces corresponde a un vértice «superfluo» de la red original en donde se encuentran solo dos aristas. Este vértice puede eliminarse y las dos aristas se unen. Cada arista limita dos caras, y cada cara tiene al menos tres aristas, de modo que A ≥ 3C/2, o lo que es equivalente 2A/3 ≥ C. Por el teorema de Euler C + V - A = 2, de modo que 2A/3 + V - A ≥ 2, lo que implica que

12 + 2A ≤ 6V

Supongamos que A_m es el número de vértices con m vecinos. Entonces A₂, A₃, A₄ y A₅ son cero. Por lo tanto

A = A₆ + A₇ + A₈ + …

Puesto que cara arista une dos vértices,

2A = 6V₆ + 7V₇ + 8V₈ + …

Sustituyendo esto en la desigualdad obtenemos

12 + 6V₆ + 7V₇ + 8V₈ + … ≤ 6V₆ + 6V₇ + 6V₈ + …

de modo que

12 + V₇ + 2V₈ + … ≤ 0

que es imposible. <<

^[35] «Cadena» es equívoco, puesto que sugiere una secuencia lineal. Una cadena de Kempe puede contener lazos y puede ramificarse. <<

^[36] La demostración completa se da en Gerhard Ringel, Map Color Theorem, Springer, 1974. Se divide en doce casos, dependiendo de si el género es de la forma 12k, 12k + 1…, 12k + 11. Llamemos a estos casos 0-11. Con un número finito de excepciones, los casos se resolvieron como sigue:

Caso 5: Ringel, 1954

Casos 3, 7 y 10: Ringel en 1961.

Casos 0 y 4: C. M. Ferry, Lloyd Welch y Youngs en 1963.

Caso 1: W. Gustin y Youngs en 1964.

Caso 9: Gustin en 1965.

Caso 6: Youngs en 1966.

Casos 2, 8 y 11: Ringel y Youngs en 1967.

Las excepciones eran los géneros 18, 20, 23 (resuelto por Yves Mayer en 1967) y 30, 35, 47, 659 (resuelto por Ringel y Youngs en 1968). Ellos también trataron el problema análogo para superficies de una cara (como la banda de Möbius pero sin bordes), que también había abordado Heawood. <<

^[37] La notable historia de cómo se descubrió el error, y qué sucedió entonces, puede encontrarse en:

http://en.wikipedia.org/wiki/Pentium_FDIV_bug <<

^[38] Una página excelente para información sobre la física de los copos de nieve es http://www.its.caltech.edu/-atomic/snowcrystals/. <<

^[39] C. A. Rogers, «The packing of equal spheres», Proceedings of the London Mathematical Society, n.º 8 (1958), pp. 609-620. <<

^[40] Puesto que el espacio es infinito, hay infinitas esferas, de modo que el espacio y las esferas tienen un volumen total infinito. No podemos definir la densidad como ∞/∞, porque eso no tiene un valor numérico bien definido. En su lugar consideramos regiones de espacio cada vez más grandes y tomamos el valor límite de la fracción de dichas regiones que llenan las esferas. <<

^[41] http://hydra.nat.uni-magdeburg.de/packing/csq/csq49.html. <<

^[42] C. Song, P. Wang y H. A. Makse, A phase diagram for jammed matter, Nature, n.º 453 (29 de mayo de 2008), pp. 629-632. <<

^[43] Hai-Chau Chang y Lih-Chung Wang, «A simple proof of Thue’s theoreme on circle packing», arXiv:1009.4322v1 (2010). <<

^[44] J. H. Lindsey, «Sphere packing in R³», Mathematika, n.º 33 (1986), pp. 137-147. <<

^[45] Hales utilizó varias nociones diferentes para lo que yo estoy llamando un jaula. La última es «estrella en descomposición». Mi descripción omite algunas distinciones cruciales para hacer comprensible la idea básica. <<

^[46] Supongamos que la región es un polígono, como en la Figura 55. Dado cualquier punto que no está en el polígono, existe una línea recta desde dicho punto que sale fuera de un gran círculo que contiene al polígono y no pasa por ningún vértice del polígono. (Existe un número finito de vértices pero infinitas líneas rectas para escoger). Esta línea corta al polígono un número finito de veces, y este número es par o impar. Definimos el interior como lo que consiste en todos los puntos para los cuales el número es impar, y el exterior como lo que consiste en todos los puntos para los que es par. Es entonces sencillo demostrar que cada una de estas regiones es conexa y el polígono las separa.

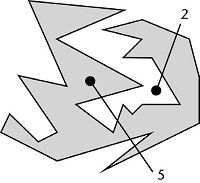
FIGURA 55. Demostrando el teorema de la curva de Jordan para un polígono. Un número impar de intersecciones ocurre para puntos en la región sombreada (interior), y un número par de intersecciones ocurre para puntos en la región blanca (exterior). <<

^[47] http://code.google.com/p/flyspeck/. <<

^[48] Andrew Granville y Thomas Tucker, «It’s as easy as abc», Notices of the American Mathematical Society, n.º 49 (2002), pp. 1224-1231. <<

^[49] Para desarrollar este críptico comentario: la fórmula es

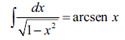
donde arcsen (a menudo escrito sen^-1) es la función inversa del seno. Es decir, si y = sen χ, entonces χ = arcsen y. <<

^[50] Por ejemplo, sea k un número complejo cualquiera y consideremos la integral

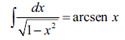
Esta es la función inversa de una función elíptica denotada por sn. Existe una función semejante para cada valor de k. La situación es como la de la nota 49, pero más elaborada. <<

^[51] Véase Ian Stewart, Seventeen Equations that Changad the World, Profile, 2012, capítulo 8. <<

^[52] La demostración puede encontrase en muchos textos sobre teoría de números, por ejemplo Gareth A. Jones y J. Mary Jones, Elementary Number Theory, Springer, 1998, p. 227. En la web, véase http://en.wikipedia.org/wiki/infinite_descentXNon-solvability_og_r2_.2B_s4_.3D_t4. <<

^[53] Una raíz p-ésima de la unidad es el número complejo

ζ = cos 2π/p + i sen 2π/p

y las otras son sus potencias ζ², ζ³… ζ^{p - 1}. Para ver por qué, recordemos que las funciones trigonométricas seno y coseno se definen utilizando un triángulo rectángulo (véase Figura 56, izquierda). Para el ángulo A, utilizando las tradicionales a, b, c para los tres lados, definimos el seno (sen) y el coseno (cos) de A por

sen A = a/c cos A = b/c

Si hacemos c = 1 y situamos el triángulo en el plano complejo, como en la Figura 56 (derecha), el vértice en el que se encuentran c y a es el punto

cos A + i sen A

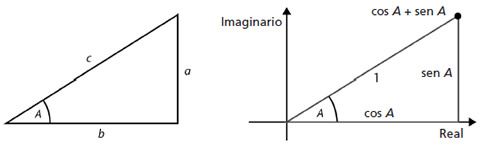
FIGURA 56. Izquierda: Definiendo el seno y el coseno. Derecha: Interpretación en el plano complejo.

Es ahora sencillo demostrar que para cualesquiera ángulos A y B,

(cos A + i sen A) (cos B + i sen B) = cos (A + B) + i sen (A + B)

y esto lleva directamente a la fórmula de De Moivre

(cos A + i sen A)ⁿ = (cos nA + i sen nA)

para cualquier entero positivo n. Por lo tanto

ζ^p = (cos 2π/p + i sen 2π/p)^p = cos 2π + i sen 2π = 1

de modo que cada potencia 1, ζ, ζ², ζ³…, ζ^{p - 1} es una raíz p-ésima de la unidad. Nos detenemos aquí porque ζ^p = 1, de modo que no aparecen números nuevos si tomamos potencias más altas. <<

^[54] Introduzcamos la norma

N(a + b√15) = a² - 15b²

que tiene la bonita propiedad

N(xy) = N(χ)N(y)

Entonces

N(2) = 4 N(5) = 25 N(5 + √15) = 10 N(5 - √15) = 10

Cualquier divisor propio de uno de estos cuatro números debe tener norma 2 o 5 (los divisores propios de sus normas). Pero las ecuaciones a² - 15b² = 2 y a² - 15b² = 5 no tienen soluciones enteras.

Por consiguiente, no existen divisores propios. <<

^[55] Simon Singh, Fermat’s Last Theorem, Fourth Estate, 1997. <<

^[56] O quizá no. Vladimir Krivchenkov ha señalado que la energía del estado fundamental y los primeros estados excitados para el problema de los tres cuerpos cuántico pueden calcularse a mano. Pero en mecánica clásica, el problema análogo es menos tratable debido al caos. <<

^[57] Citado en Arthur Koestler, The Sleepwalkers, Penguin Books, 1990, p. 338. <<

^[58] Puede encontrarse una animación y más información en:

http://www.scholarpedia.org/article/N-body_choreographies <<

^[59] Debe su nombre al Barón de Orrey, a quien se le regaló uno en 1704. <<

^[60] Más formalmente, esto se denomina tiempo de Liapunov. <<

^[61] Existe una variante que integra 1/log t de 2 a χ, y no de 0 a χ. Esto evita una dificultad técnica en t = 0, donde log t no está definido. A veces se utiliza la notación Li(χ) para esta variante, y a la función definida en el texto se le llama li(χ). <<

^[62] El nombre «Pafnuty» no es habitual. Llevó a Philip Davis a escribir un libro peculiar pero absorbente: The Thread: a Mathematical Yarn, Harvester Press, 1983. <<

^[63] Esto se sigue de la curiosa formula de Riemann:

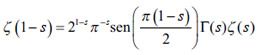
donde Γ(s) es una función clásica llamada función gamma, definida para todo complejo s. El segundo miembro está definido cuando la parte real de s es mayor que 1. <<

^[64] Bernhard Riemann, «Über die Anzahl der Primzahlen unter einer gegebenen Grösse», Monatsberichte der Königlich Preußischen Akademie der Wissenchaften zu Berlin, noviembre 1859. <<

^[65] Riemann definió una función íntimamente relacionada.

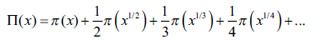
que cuenta potencias primas en lugar de primos. A partir de esta podemos recuperar π(χ). Luego demostró una fórmula exacta para esta función modificada en términos de integrales logarítmicas y una integral relacionada:

Aquí ∑ indica una suma sobre todos los números ρ para los que ζ(ρ) es cero, excluidos los enteros pares negativos. <<

^[66] Por ejemplo, χ + √χ es asintótica a χ: la razón es

(χ + √χ) / χ = 1 + 1 / √χ

Cuando χ aumenta, también lo hace √χ, de modo que 1/√χ tiende a 0 y la razón tiende a 1. Pero la diferencia es √χ, y eso se hace cada vez mayor a medida que χ aumenta. Por ejemplo, cuando χ es 1 billón, √χ es 1 millón. <<

^[67] La constante de Euler es el límite, cuando n tiende a infinito, de

<<

^[68] Douglas A. Stoll y Patrick Demichel, «The impact of ζ(s) complex zeros on π(χ) for 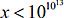», Mathematics of Computation, n.º 276 (2011), pp. 2381-2394. <<

^[69] http://empslocal.ex.ac.uk/people/staff/mnwatkin/zeta/RHproofs.htm. <<

^[70] J. Brian Conrey y Xian-Jin Li, «A note on some positivity conditions related to zeta- and L-functions»:

http://arxiv.org/abs/math.NT/9812166 <<

^[71] La 3-esfera unidad comprende todos los puntos con coordenadas (x, y, z, w) tales que χ² + y² + z² + w² = 1. Hay varias maneras de hacer la 3-esfera más intuitiva. Todas pueden entenderse por analogía con una 2-esfera y comprobarse utilizando geometría de coordenadas. Una descripción semejante («bola sólida con todos los puntos de la superficie identificados») se da en el texto, y la Figura 57 muestra otra. Para establecer la analogía, observemos que si cortamos una 2-esfera a lo largo de su ecuador obtenemos dos semiesferas. Cada una de ellas se aplana hasta dar un disco, y esto es una deformación continua. Para reconstruir la 2-esfera, simplemente identificamos puntos correspondientes en las fronteras de estos dos discos. En cierto sentido hemos hecho un mapa de la 2-esfera utilizando dos discos planos, de forma parecida a como los cartógrafos crean una proyección plana de nuestro planeta redondo. Podemos construir una 3-esfera utilizando un procedimiento análogo. Tomamos dos bolas sólidas e identificamos puntos correspondientes en sus superficies. Ahora ambos tienen la misma superficie (porque identificamos las dos superficies), y es una 2-esfera. Forma el «ecuador» de la 3-esfera.

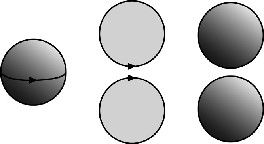
FIGURA 57. Cómo hacer una 3-esfera. Izquierda: Cortar una 2-esfera en semiesferas. Centro: Reconstruir la 2-esfera a partir de las dos mitades uniendo los bordes. Derecha: Por analogía, unir idealmente las superficies de dos bolas de modo que puntos correspondientes se consideran idénticos. Esto da una 3-esfera. <<

^[72] El convenio usual es hablar de suma y utilizar la notación a + b cuando la ley de conmutación es válida, pero hablar de multiplicación y utilizar la notación ab cuando podría no serlo. He ignorado aquí este convenio porque no es un libro de texto sobre teoría de grupos, y «suma» parece más natural. <<

^[73] Empecemos la cuenta en cero. Cada vez que pasamos por la parada del autobús en sentido contrario a las agujas del reloj, incrementamos la cuenta en 1; cada vez que pasamos en el sentido de las agujas, disminuimos la cuenta en 1. Al final del viaje sumamos 1 si llegamos en sentido contrario a las agujas, y restamos 1 si llegamos en el sentido de las agujas. La cuenta final es el número total de veces que dimos vueltas al círculo, medidas en el sentido contrario a las agujas del reloj. <<

^[74] La fórmula de Stirling afirma que n! es aproximadamente

<<

^[75] William J. Cook, In Pursuit of the Travelling Salesman, Princeton University Press, Princeton, 2012. Para información actual, véase http:// www.tsp.gatech.edu/index.html. <<

^[76] Richard M. Karp, «Reducibility among combinatorial problems», en R. F. Miller y J. W. Thatcher (eds.), Complexity of Computer Computations, Plenum, 1972, pp. 8-103. <<

^[77] Z. Xia, «The existence of noncollision singularities in Newtonian systems», Annals of Mathematics, n.º 135 (1992), pp. 411-468. <<

^[78] http://www.claymath.org/millennium/Navier-Stokes_Equations/. <<

^[79] Véase Ian Stewart, Seventeen Equations that Changed the World, Profile, 2012, capítulo 14. <<

^[80] Leonardo Pisano Fibonacci, The Book of Squares, anotado y traducido por L. E. Sigler, Academia Press, 1987. <<

^[81] Leonardo encontró una familia de soluciones.

donde m y n son impares. El papel de d lo desarrolla aquí el número mn(m² - n²), y χ es (m² + n²)/2. Escogiendo m = 5, n = 4 se llega a mn(m² - n²) = 180. Además, 720 = 5 × 6². Dividiendo χ por 6 se obtiene la respuesta. <<

^[82] Si x - n, x y x + n son cuadrados, entonces también lo es su producto, que es x³ - n²χ. Por consiguiente la ecuación y² = χ³ - n²χ tiene una solución racional. Además, y no es cero, de lo contrario χ = n de modo que χ y 2χ son cuadrados, lo que es imposible puesto que √2 es irracional.

Recíprocamente, si χ e y satisfacen la ecuación cúbica e y no es 0, entonces a = (χ² - n²)/y, b = 2nx/y, y c = (χ² + n²)/y satisfacen las ecuaciones a² + b² = c² y ab/2 = n. <<

^[83] Esto es,

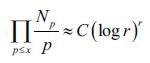
donde r es el rango, C es una constante y ≈ significa que la razón de los dos miembros tiende a 1 cuando χ tiende a infinito. <<

^[84] La razón más probable es que estas son las traducciones naturales de las lenguas utilizadas por los matemáticos más importantes en las dos áreas. <<

^[85] No estoy seguro de por qué b no era el número de bananas. ¿Quizá porque en la Gran Bretaña de la posguerra las bananas eran artículos exóticos que apenas se veían en las tiendas? <<

^[86] Este es un chiste matemático estándar: un biólogo, un estadístico y un matemático están sentados en la terraza de un café observando a la gente que pasa. Un hombre y una mujer entran en un edificio al otro lado de la calle. Diez minutos más tarde salen acompañados de un niño. «Ellos se han reproducido», dice el biólogo. «No —dice el estadístico—, es un error observacional. En promedio, dos personas y media fueron en cada dirección». «No, no, no —dice el matemático—. Es perfectamente obvio. Si alguien entra ahora, el edificio estará vacío». <<

^[87] Bohr puede haber puesto el dedo en la llaga. Las teorías científicas se ponen a prueba por sus predicciones, pero pocas de estas predicen el futuro. La mayoría son enunciados si/entonces: si se hace pasar luz a través de un prisma, se descompondrá en colores. La «predicción» no dice cuándo sucederá esto. Por ello, paradójicamente, podemos hacer predicciones sobre el tiempo sin predecir el tiempo. «Si el aire caliente procedente de un ciclón se junta con aire frío, entonces nevará» es una predicción científica, pero no un pronóstico. <<

^[88] La cita o una variante parecida ha sido atribuida a unas treinta fuentes diferentes, incluidos Sam Goldwyn, Woody Allen, Winston Churchill y Confucio. Véase http://www.larry.denenberg.com/predictions.html. <<

^[89] Para la información más reciente, véase «The Prime Pages»: http:// primes.utm.edu. <<

^[90] Ilia Krasikov y Jeffrey C. Lagarias, «Bounds for the 3x + 1 problemas using difference inequalities», Acta Arithmetica, n.º 109 (2003), pp. 237-258. <<

^[91] Jorge F. Sawyer y Clifford A. Reiter, «Perfect parallelepipeds exist». arXiv:0907.0220 (2009). <<

^[92] R. Fulek y J. Pach, «A computational approach to Conway’s thrackle conjecture», Computational Geometry, n.º 44 (2011), pp. 345-355. <<

^[93] http://en.wikipedia.org/wiki/Langton9627_ant. <<

^[94] La conjetura abc afirma: Para cualquier ε > 0 existe una constante kε > 0 tal que si a, b y c son enteros positivos que no tienen ningún factor común mayor que 1, y a + b =c, entonces c ≤ k_ε P^{1 + ε}, done P es el producto de todos los primos distintos que dividen abc. <<

^[95] Andrew Granville y Thomas J. Tucker, «It’s as easy as abc», Notices of the American Mathematical Society, n.º 49 (2002), pp. 1224-1231.

En septiembre de 2012 Shinichi Mochizuki anunció que había demostrado la conjetura ABC utilizando una aproximación radicalmente nueva a los fundamentos de la geometría algebraica. Los expertos están ahora comprobando su demostración de quinientas páginas, pero esto puede llevar mucho tiempo. <<

^[*] Se trataba del cálculo de la estructura del grupo de Lie E₈». (N. del t.). <<

^[*] Este congreso tuvo lugar en Madrid. (N. del t.). <<

^[*] A veces se traduce «gauge» por calibre o aforo. Un término castellano similar es galga. No obstante, el término «gauge» ya está asentado en el lenguaje científico. (N. del t.). <<

^[*] En castellano no existe esta distinción. La misma palabra «variedad» traduce los términos ingleses «variety» y «manifold». (N. del t.). <<

^[*] En el caso del alfabeto español, de 27 letras, el número de maneras es:

27! =293.999.475.161.295.508.340.736.000.000 <<

^[*] Este es también el epitafio sobre la tumba de Hilbert en Gotinga. (N. del t.). <<

^[**] Hay traducción en castellano: Baúl de tesoros matemáticos, Crítica, Barcelona, 2010. <<