15
Ciclos complejos
La conjetura de Hodge

Algunas áreas de las matemáticas pueden estar relacionadas, de forma bastante directa, con sucesos e intereses cotidianos. No encontramos la ecuación de Navier-Stokes en nuestra cocina, pero todos entendemos lo que son los fluidos y tenemos una idea de cómo fluyen. Otras áreas pueden estar relacionadas con cuestiones esotéricas en la frontera de la ciencia: puede necesitarse un doctorado en física matemática para entender la teoría cuántica de campos, pero las analogías con la electricidad y el magnetismo, o imágenes intuitivas como «onda de probabilidad», llegan muy lejos. Algunas ideas pueden explicarse utilizando imágenes: la conjetura de Poincaré es un buen ejemplo. Pero otras desafían todos estos métodos de hacer accesibles conceptos abstractos difíciles.

La conjetura de Hodge, enunciada por el geómetra escocés William Hodge en 1950, es una de ellas. No es la demostración lo que plantea problemas, porque no la hay. Lo que causa problemas es el enunciado. He aquí el que figura en la página web del Instituto Clay, en una forma ligeramente modificada:

Sobre cualquier variedad algebraica compleja proyectiva y no singular, cualquier clase de Hodge es una combinación lineal racional de clases de ciclos algebraicos.

Evidentemente tenemos trabajo por hacer. Las únicas palabras que tienen un sentido inmediato son «sobre, cualquiera, es, una» y «de». Otras son familiares: «variedad, clase, racional, ciclo». Pero las imágenes que evocan —elección en el supermercado, un aula con niños en la escuela, pensamiento no visceral, un dispositivo con ruedas y manillar— no son obviamente los significados que el Instituto Clay tiene en mente. El resto es, sin duda, propio de una jerga. Pero no es una jerga gratuita, con nombres complicados para cosas sencillas. Son nombres sencillos para cosas complicadas. No hay nombres ya disponibles para tales conceptos en el lenguaje ordinario, de modo que tomamos prestados algunos e inventamos otros.

Mirando el lado positivo, tenemos aquí una oportunidad real (como en «muchacho, tenemos oportunidades»). La conjetura de Hodge es presumiblemente más representativa de las matemáticas reales, las que hacen los matemáticos de los siglos XX y XXI, que cualquier otro tema en este libro. Enfocándola de la manera correcta obtenemos ideas valiosas sobre lo conceptualmente avanzada que es en realidad la frontera de las matemáticas. Comparada con las matemáticas de la escuela, es como el monte Everest frente a un grano de arena.

Entonces, ¿es simplemente un absurdo vano y pretencioso que se lleva a cabo en torres de marfil? Si ninguna persona ordinaria puede entender de qué se trata, ¿por qué alguien debería dedicar dinero de los impuestos a emplear a las personas que piensan en estas cosas? Permítame darle la vuelta. Supongamos que cualquier persona pudiera entender todo en lo que piensan los matemáticos. ¿Sería usted feliz entonces pagando impuestos? ¿Hay que pagarles por sus conocimientos? Si todo fuera tan fácil y comprensible que tuviera un sentido inmediato para cualquier persona a la que preguntáramos al azar en la calle, ¿para qué tener matemáticos? Si todo el mundo supiera cómo manejar un soplete y soldar una juntura, ¿para qué tener fontaneros?

Yo no puedo mostrarle ninguna aplicación espectacular que se base en la conjetura de Hodge, pero puedo explicar su importancia dentro de las matemáticas. Las matemáticas modernas son un todo unificado, de modo que cualquier avance importante, en cualquier área nuclear, mostrará con el tiempo su valor en términos de euros y céntimos. Quizá no la encontremos hoy en nuestra cocina, pero mañana ¿quién sabe? Conceptos matemáticos íntimamente relacionados ya están mostrando su valor en varias áreas de la ciencia, que van desde la física cuántica y la teoría de cuerdas hasta los robots.

A veces las aplicaciones prácticas de nuevas matemáticas aparecen casi al instante. Otras veces tardan siglos. En este último caso, podría parecer más rentable esperar hasta que surja la necesidad de tales resultados y luego instaurar un programa de choque para desarrollarlos. Todos los problemas matemáticos que no tienen usos obvios e inmediatos deberían ser relegados a segundo plano hasta que los tengan. Sin embargo, si así lo hiciéramos iríamos siempre a remolque, pues las matemáticas pasaron algunos cientos de años persiguiendo las necesidades de la ciencia aplicada. Y podría no estar nada claro qué idea necesitamos. ¿Estaría usted contento si nadie empezara a pensar en cómo hacer ladrillos hasta que usted contratara a un constructor para empezar a trabajar en una casa? Cuanto más original es un concepto matemático, menos probable es que saliera de un programa de choque.

Una mejor estrategia es dejar que algunas partes de las matemáticas se desarrollen según sus propias líneas y no esperar un rendimiento inmediato. No tratemos de seleccionar; permitamos que el edificio matemático crezca de forma orgánica. Los matemáticos son baratos: no necesitan un equipamiento costoso como los físicos de partículas (Gran Colisionador de Hadrones: 7500 millones de euros y contando). Se ganan la vida enseñando a estudiantes. Permitir que algunos de ellos dediquen parte de su tiempo a la conjetura de Hodge, si eso es lo que les gusta, es bastante razonable.

Voy a desmenuzar el enunciado de la conjetura de Hodge, palabra por palabra. El concepto más fácil es «variedad algebraica». Una consecuencia natural del uso de coordenadas por parte de Descartes es vincular la geometría y el álgebra (véase capítulo 3). Con su ayuda, el minúsculo juego de herramientas introducido por Euclides y sus sucesores —línea recta, círculo, elipse, parábola, hipérbola— se convirtió en un baúl sin fondo. Una línea recta, la base de la geometría euclídea, es el conjunto de puntos que satisfacen una ecuación algebraica apropiada, por ejemplo y = 3χ + 1. Cambiemos 3 y 1 por otros números, y obtenemos otras rectas. Los círculos necesitan ecuaciones cuadráticas, como lo hacen las elipses, parábolas e hipérbolas. En principio, cualquier cosa que se pueda enunciar geométricamente puede reformularse de manera algebraica, y al revés. Entonces, ¿las coordenadas hacen obsoleta la geometría? ¿Por qué utilizar dos herramientas cuando cada una de ellas hace el mismo trabajo que la otra?

En mi caja de herramientas en el garaje tengo un martillo y unas tenazas grandes. El trabajo del martillo es clavar clavos en la madera, el trabajo de las tenazas es volverlos a sacar. En principio, sin embargo, yo podría golpear los clavos utilizando las tenazas, y el martillo tiene una garra específicamente diseñada para extraer clavos. Entonces, ¿para que necesito las dos herramientas? Porque el martillo es mejor para algunas cosas y las tenazas son mejores para otras. Lo mismo pasa con la geometría y el álgebra: algunas maneras de pensar son más naturales utilizando la geometría, otras son más naturales utilizando el álgebra. Es el vínculo entre ellas lo que importa. Si el pensamiento geométrico se atasca, se pasa al álgebra. Si el pensamiento algebraico se atasca, se pasa a la geometría.

La geometría de coordenadas proporciona una nueva libertad para inventar curvas. Simplemente se escribe una ecuación y se miran sus soluciones. A menos que hayamos escogido una ecuación estúpida como x = x, deberíamos obtener una curva. (La ecuación x = x tiene todo el plano como solución). Por ejemplo, yo podría escribir χ³ + y³ = 3xy, cuyas soluciones están dibujadas en la Figura 45. Esta curva es el folio de Descartes, y no la encontraremos en Euclides. El abanico de nuevas curvas que cualquiera puede inventar es literalmente infinito.

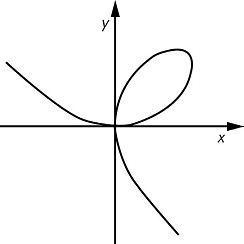
FIGURA 45. El folio de Descartes.

Un comportamiento reflejo entre matemáticos es generalizar. Una vez que alguien ha encontrado una idea interesante, podemos preguntar si sucede algo similar en un contexto más general. La idea de Descartes tiene al menos tres generalizaciones o modificaciones importantes, todas las cuales son necesarias para dar sentido a la conjetura de Hodge.

Primero, ¿qué sucede si trabajamos con espacios distintos del plano? El espacio euclídeo tridimensional tiene tres coordenadas (x, y, z) en lugar de dos. En el espacio, una ecuación define normalmente una superficie. Dos ecuaciones definen una curva, en donde se cruzan las correspondientes superficies. Tres ecuaciones determinan normalmente un punto. (Por «normalmente» quiero decir que a veces puede haber excepciones, pero estas son muy poco habituales y satisfacen condiciones especiales. Vimos algo similar en el plano con la tonta ecuación x = x).

Una vez más, podemos definir nuevas superficies o curvas, que no se encuentran en Euclides, escribiendo nuevas ecuaciones. En el siglo XIX se puso de moda hacer eso. Uno podía hacer pública una nueva superficie si decía algo verdaderamente interesante sobre ella. Un ejemplo típico es el de una superficie introducida por Kummer en 1864, con la ecuación

χ⁴ + y⁴ + z⁴ - y²z² - z²χ² - χ²y² - χ² - y² - z² + 1 = 0

La Figura 46 muestra una imagen. Las propiedades de mayor interés son los 16 «puntos dobles» en donde la forma es como dos conos unidos punta con punta. Este es el máximo número posible para una superficie cuártica, cuya ecuación es de grado 4, y eso era suficientemente interesante para merecer su publicación.

FIGURA 46. Superficie cuártica de Kummer con sus 16 puntos dobles. © University College, Cork, Irlanda.

Para el siglo XIX los matemáticos habían experimentado los embriagadores deleites de los espacios de dimensiones más altas. No hay necesidad de pararse en tres coordenadas; ¿por qué no ensayar cuatro, cinco, seis…, un millón? Esto no es especulación ociosa. Es el álgebra de montones de ecuaciones en montones de variables, y esas se manifiestan en todo el paisaje matemático; por ejemplo, en el capítulo 5 sobre la conjetura de Kepler, y en el capítulo 8 sobre mecánica celeste. Tampoco era generalización ociosa: ser capaces de pensar estas cosas geométricamente, tanto como algebraicamente, es una herramienta poderosa que no debería estar restringida a espacios de dos o tres dimensiones, solo porque es en ellos donde se pueden dibujar imágenes y hacer modelos.

La palabra «dimensión» puede sonar impresionante y mística, pero en este contexto tiene un significado directo: cuántas coordenadas se necesitan. Por ejemplo, el espacio 4-dimensional tiene cuatro coordenadas (x, y, z, w), y por lo que concierne a las matemáticas, eso lo define. En cuatro dimensiones una sola ecuación define normalmente una «hipersuperficie» tridimensional, dos ecuaciones definen una superficie (dos dimensiones), tres ecuaciones definen una curva (una dimensión) y cuatro ecuaciones definen un punto (cero dimensiones). Cada nueva ecuación elimina una dimensión (una variable). Por eso podemos predecir que en el espacio de 17 dimensiones, once ecuaciones definen un objeto 6-dimensional, excepto en los raros (y detectables) casos en donde algunas de las ecuaciones son superfluas.

Un objeto definido de esta manera se llama variedad algebraica. La palabra «variedad» aparece en lenguas como el francés y el español, y tiene un significado similar a «manifold» en inglés: básicamente, la palabra «many» (muchos). Por razones perdidas en las nieblas de la historia, «manifold» se asoció con la topología y la geometría diferencial —topología combinada con cálculo infinitesimal— mientras que «variedad» quedó asociada a la geometría algebraica^[84]. Utilizar nombres diferentes evita la confusión, de modo que ambos cuajaron. Una variedad algebraica podría haberse llamado un «espacio multidimensional definido por un sistema de ecuaciones algebraicas», pero es fácil ver por qué nadie lo hizo^[*].

Una segunda manera atractiva de generalizar las nociones de geometría de coordenadas es permitir que las coordenadas sean números complejos. Recordemos que el sistema de los números complejos incluye un nuevo tipo de número, i, cuyo cuadrado es -1. ¿Por qué complicarlo todo de esa manera? Porque las ecuaciones algebraicas se comportan mucho mejor en el campo complejo. En el campo real una ecuación cuadrática puede tener dos soluciones o ninguna. (También puede tener solo una, pero en cierto sentido es la misma solución que aparece dos veces). En el campo complejo una ecuación cuadrática tiene siempre dos soluciones (de nuevo contando las multiplicidades correctamente). Para algunos fines, esta es una propiedad mucho más agradable. Podemos decir «resolver la ecuación para la séptima variable» y tener la seguridad de que tal solución existe realmente.

Por agradable que pueda ser a este respecto, la geometría algebraica compleja tiene características que hacen necesario un tiempo para habituarse a ella. Con variables reales, una recta puede cortar a un círculo, o ser tangente al mismo, o no cortarlo en absoluto. Con variables complejas, la tercera opción desaparece. No obstante, una vez que uno se ha acostumbrado a estos cambios, las variedades algebraicas complejas se comportan mucho mejor que las reales. A veces las variables reales son esenciales, pero para la mayoría de los fines el campo complejo es una mejor elección. En cualquier caso, ahora sabemos qué es una variedad algebraica compleja.

¿Qué pasa con «proyectiva»? Esta es la tercera generalización y requiere una noción de espacio ligeramente diferente. La geometría proyectiva surgió del interés en la perspectiva por parte de los pintores del Renacimiento y elimina el comportamiento excepcional de las rectas paralelas. En la geometría de Euclides dos rectas o bien se cortan o bien son paralelas: no se encuentran por mucho que se prolonguen. Imagínese ahora situado en un plano infinito, pincel en mano, caballete montado, caja de pinturas preparada, con un par de rectas paralelas que apuntan hacia la lejana puesta de sol como vías de tren infinitamente largas. ¿Qué es lo que usted ve, y qué dibujaría? No dos líneas que no se encuentran. En su lugar, las líneas parecen converger para encontrarse en el horizonte.

¿A qué parte del plano corresponde el horizonte? Es la parte en donde se encuentran las paralelas. Pero no hay tal cosa. El horizonte es la frontera, en su cuadro, de la imagen del plano. Si todo va bien, eso debería ser sin duda la imagen de la frontera del plano. Pero un plano no tiene frontera; continúa indefinidamente. Todo esto es un poco lioso. Es como si faltara una parte del plano euclídeo. Si se «proyecta» un plano (el plano con las vías de tren) sobre otro plano (el lienzo en el caballete) se obtiene una línea en la imagen, el horizonte, que no es la proyección de ninguna línea en el plano.

Hay una manera de deshacerse de esta intrigante anomalía: añadir al plano euclídeo una denominada recta en el infinito que representa el horizonte que falta. Ahora todo se hace mucho más sencillo. Dos líneas siempre se cortan en un punto; la vieja noción de líneas paralelas corresponde al caso en que las dos líneas se encuentran en el infinito. Esta idea, adecuadamente interpretada, puede convertirse en matemáticas perfectamente razonables. El resultado se llama geometría proyectiva. Es una disciplina muy elegante, y los matemáticos de los siglos XVIII y XIX la amaban. Con el tiempo agotó lo que tenía que decir, hasta que los matemáticos del siglo XX decidieron generalizar la geometría algebraica a espacios multidimensionales y utilizar números complejos. En ese momento se hizo claro que también podríamos tirar la casa por la ventana y estudiar soluciones complejas de ecuaciones algebraicas en el espacio proyectivo antes que soluciones reales en el espacio euclídeo.

Permítame resumir. Una variedad algebraica compleja proyectiva es como una curva, definida por una ecuación algebraica, pero:

• El número de ecuaciones y variables puede ser cualquiera que queramos (variedad algebraica).
• Las variables pueden ser complejas en lugar de reales (compleja).
• Las variables pueden tomar valores infinitos en una forma razonable (proyectiva).

Para concluir con esto, hay otro término con el que se puede tratar fácilmente: no singular. Significa que la variedad es suave, sin cordilleras abruptas o lugares donde la forma es más complicada que una región suave de espacio. La superficie de Kummer es singular en esos 16 puntos dobles. Por supuesto, tenemos que explicar qué significa «suave» cuando las variables son complejas y algunas pueden valer infinito, pero eso es una técnica rutinaria.

Estamos casi a mitad de camino en el enunciado de la conjetura de Hodge. Sabemos de qué estamos hablando, pero no sabemos cómo pensaba Hodge que debía de comportarse. Ahora tenemos que abordar los aspectos más profundos y más técnicos: ciclos algebraicos, clases, y (especialmente) clases de Hodge. Sin embargo, puedo revelar su esencia en pocas palabras. Son artificios técnicos que proporcionan una respuesta parcial a una pregunta muy básica sobre nuestra superficie generalizada: ¿qué forma tiene? Los únicos términos restantes, «combinación lineal racional», proporcionan lo que todo el mundo espera que sea la respuesta correcta a esa pregunta.

Veamos hasta dónde hemos llegado. Ya entendemos qué tipo de enunciado es la conjetura de Hodge. Nos dice que dada una superficie generalizada definida por ciertas ecuaciones, se puede calcular qué forma tiene haciendo algo de álgebra con cosas llamadas ciclos. Yo podría haberlo dicho en la primera página de este capítulo, pero en esa etapa no habría tenido más sentido que el enunciado formal. Ahora que sabemos lo que es una variedad, todo empieza a encajar.

También empieza a sonar a topología. «Encontrar la forma haciendo cálculos algebraicos» recuerda sorprendentemente las ideas de Poincaré sobre invariantes algebraicos para espacios topológicos. Así que el último paso requiere una discusión de la topología algebraica. Entre los descubrimientos de Poincaré había tres tipos importantes de invariantes, definidos en términos de tres conceptos: homotopía, homología y cohomología. El que nos interesa es la cohomología, que, por supuesto, por si no lo supiera, es el más difícil de explicar.

Pienso que simplemente tenemos que saltarlo.

En el espacio tridimensional con coordenadas reales, una esfera y un plano se cortan (si es que lo hacen) en un círculo. La esfera es una variedad (omitiré el adjetivo «algebraica» cuando hablemos de variedades), el círculo es una variedad, y el círculo está contenido en la esfera. Le llamamos una subvariedad. Con más generalidad, si tomamos las ecuaciones (muchas variables, complejas, proyectivas) que definen una variedad, y añadimos otras ecuaciones, entonces normalmente perdemos algunas de las soluciones: aquellas que no satisfacen las nuevas ecuaciones. Cuantas más ecuaciones tengamos, menor se hace la variedad. El sistema de ecuaciones ampliado define alguna parte de la variedad original, y esta parte es una variedad por sí misma: una subvariedad.

Cuando contamos el número de soluciones de una ecuación polinómica puede ser conveniente contar el mismo punto más de una vez. Desde esta perspectiva, el conjunto de soluciones consiste en un número de puntos a cada uno de los cuales «asociamos» un número, su multiplicidad. Podríamos, por ejemplo, tener las soluciones 0, 1 y 2 con multiplicidades 3, 7 y 4, respectivamente. El polinomio sería entonces χ³(x - 1)⁷ (x - 2)⁴, si quiere saberlo. Cada uno de los tres puntos χ = 0, 1 o 2 es una subvariedad (bastante trivial) de los números complejos. De modo que las soluciones de este polinomio pueden describirse como una lista de tres subvariedades, con un número entero asociado a cada una como una etiqueta.

Un ciclo algebraico es similar. En lugar de puntos simples utilizamos cualquier lista finita de subvariedades. A cada una de ellas podemos asignar una etiqueta numérica que no tiene por qué ser un número natural. Podría ser un entero negativo, podría ser un número racional, podría ser real e incluso un número complejo. Por varias razones, la conjetura de Hodge utiliza números racionales como etiquetas. A esto es a lo que se refiere «combinación lineal racional». Así, por ejemplo, nuestra variedad original podría ser la esfera unidad en un espacio 11-dimensional, y esta lista podría tener este aspecto:

No trate de representarlo, o si lo hace, piense como un dibujante de comics: tres globos garabateados con pequeñas etiquetas. Cada uno de estos dibujos, cada lista, constituye un ciclo algebraico.

¿Por qué tanto revuelo y molestia para inventar algo tan abstracto? Porque capta aspectos esenciales de la variedad algebraica original. Los geómetras algebraicos están tomando prestado un truco de los topólogos.

En el capítulo 10 sobre la conjetura de Poincaré consideramos una hormiga cuyo universo es una superficie. ¿Cómo puede la hormiga calcular qué forma tiene su universo cuando no puede salir fuera y echar una mirada? En particular, ¿cómo puede distinguir una esfera de un toro? La solución presentada allí implicaba lazos cerrados, trayectos de autobús topológicos. La hormiga sigue estos lazos, descubre lo que sucede cuando se unen y calcula un invariante algebraico del espacio llamado grupo fundamental. «Invariante» significa que espacios topológicamente equivalentes tienen el mismo grupo fundamental. Si los grupos son diferentes, también lo son los espacios. Este es el invariante que llevó a Poincaré a su conjetura. Sin embargo, no es fácil para la pobre hormiga examinar todos los lazos posibles en su universo, y este comentario refleja genuinas sutilezas matemáticas en el cálculo del grupo fundamental. Existe un invariante más práctico, y Poincaré también lo investigó. Deambular por lazos se llama homotopía. Esta alternativa tiene un nombre parecido: homología.

Voy a mostrarle la versión más simple y más concreta de homología. Los topólogos mejoraron rápidamente esta versión, la agilizaron, la generalizaron y la transformaron en una enorme máquina matemática llamada álgebra homológica. Esta versión simple da una idea más escueta de cómo es el tema, pero es todo lo que necesitamos.

La hormiga empieza inspeccionando su universo para hacer un mapa. Como un topógrafo humano, cubre su universo con una red de triángulos. La condición crucial es que ningún triángulo debería rodear a un agujero en la superficie, y la manera de asegurarlo es crear los triángulos pegando parches de goma en la superficie, como alguien que repara un pinchazo en una rueda de bicicleta. Entonces cada triángulo tiene un interior bien definido que es topológicamente igual al interior de un triángulo ordinario en el plano. Los topólogos llaman a un parche semejante un disco topológico, porque también es equivalente a un círculo y su interior. Para ver por qué, examinemos la Figura 36 del capítulo 10, donde un triángulo es deformado de forma continua hasta que se hace un círculo. No es posible ajustar un parche de este tipo a un triángulo que rodea a un agujero, porque el agujero crea un túnel que enlaza el interior del triángulo con su exterior. El parche tendría que dejar la superficie, y a la hormiga no se le permite hacer eso.

Ahora la hormiga ha creado una triangulación de su universo. La condición sobre los parches asegura que la topología de la superficie —su forma, en el sentido de equivalencia topológica— puede reconstruirse si todo lo que se conoce es la lista de triángulos, junto con qué triángulos son adyacentes a cuáles otros. Si fuéramos a Ikea y compráramos un Universo de Hormiga ensamblable con triángulos adecuadamente etiquetados y luego uniéramos el borde A con el borde AA, el borde B con el borde BB, y así sucesivamente, podríamos construir la superficie. La hormiga está confinada en la superficie, de modo que no puede hacer un modelo, pero puede estar segura de que en principio su mapa contiene la información que necesita. Para extraer dicha información tiene que realizar un cálculo. Cuando lo hace, la hormiga ya no tiene que contemplar la infinitud de todos los lazos posibles, pero tiene que contemplar una gran cantidad de ellos: todos los lazos cerrados que recorren los bordes de su red elegida.

En homotopía preguntamos si un lazo dado puede contraerse de forma continua hasta un punto. En homología hacemos una pregunta diferente: ¿forma el lazo la frontera de un disco topológico? Es decir, ¿se pueden ajustar uno o más parches triangulares de modo que el resultado sea una región sin agujeros y la frontera de dicha región sea el lazo concernido?

La Figura 47 (izquierda) muestra parte de una triangulación de una esfera, un lazo cerrado y el disco topológico del cual es frontera. Con las técnicas correctas puede demostrarse que cualquier lazo en una triangulación de una esfera es una frontera: los parches triangulares y, más en general, los discos topológicos, son detectores de agujeros, e intuitivamente una esfera no tiene agujeros. Sin embargo, un toro sí tiene un agujero, y de hecho algunos lazos en un toro no son fronteras. La Figura 47 (derecha) muestra un lazo semejante, que atraviesa el agujero central. En otras palabras: recorriendo una lista de lazos y descubriendo cuáles de ellos son fronteras, la hormiga puede distinguir un universo esférico de un universo toroidal.

Si la hormiga es tan inteligente como Poincaré y los demás topólogos de su tiempo, puede transformar esta idea en un elegante invariante topológico, el grupo de homología de su superficie. La idea básica es «sumar» dos lazos dibujando ambos. Sin embargo, eso no es un lazo, de modo que tenemos que volver al principio y empezar de nuevo. Al mismo principio, de hecho; vuelta a los días en que nos introdujimos por primera vez en el álgebra. Mi profesor de matemáticas empezaba señalando que se puede sumar un número de manzanas a un número de manzanas y obtener un número total de manzanas. Pero no se pueden sumar manzanas y naranjas a menos que se cuente todo como una fruta.

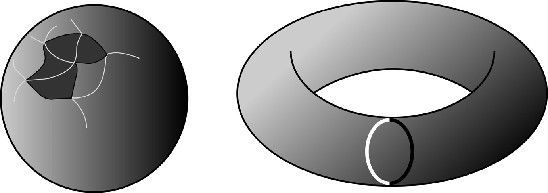
FIGURA 47. Izquierda: Parte de una triangulación de una esfera, un lazo cerrado (líneas negras), y el disco del que es frontera (sombreado oscuro). Derecha: Lazo en un toro que no es la frontera de un disco (la parte más clara está detrás).

Esto es cierto en aritmética, incluso si allí hay que tener cuidado en no utilizar la misma manzana dos veces, pero no es cierto en álgebra. Allí se pueden sumar manzanas con naranjas, aunque se mantengan distintas. De hecho, en matemáticas avanzadas es un tópico sumar cosas que cabría pensar que nadie en su sano juicio hubiera inventado, y mucho menos quisiera sumar. La libertad para hacer cosas de este tipo resulta ser sorprendentemente útil e importante, y los matemáticos que lo hacían no estaban locos después de todo; al menos, no en ese aspecto.

Para entender algunas de las ideas que reúne la conjetura de Hodge tenemos que poder sumar manzanas y naranjas sin amontonarlas como simples frutas. La manera de sumarlas no es realmente muy difícil. Lo que es difícil es aceptar que hay un sentido en hacerlo. Muchos de nosotros ya hemos encontrado una versión de este potencial obstáculo conceptual. Mi profesor contaba a la clase que las letras representaban números desconocidos, con diferentes letras para diferentes incógnitas. Si tuviéramos a manzanas y otras a manzanas, el número total de manzanas sería a + a = 2a. Y eso funcionaba cualquiera que pudiera ser el número de manzanas. Si tuviéramos 3a manzanas y sumáramos 2a manzanas, el resultado sería 5a, cualquiera que pudiera ser el número de manzanas. El símbolo, y lo que representaba, no importaba: si tuviéramos 3b naranjas y sumáramos 2b naranjas, el resultado sería 5b^[85]. Pero ¿qué sucedía cuando teníamos 3a manzanas y 2b naranjas? ¿Qué era 3a + 2b?

3a + 2b

Eso era. No podíamos simplificar la suma y hacerla 5 algos —al menos no sin algunas manipulaciones que incluían una nueva categoría, fruta, y algunas nuevas ecuaciones. Eso era lo más que podíamos hacer: vivir con ello. Sin embargo, una vez que se daba ese paso, se podían hacer sumas como:

(3a + 2b) + (5a - b) = 8a + 4b

sin introducir ninguna idea nueva. O nuevos tipos de fruta.

Había algunas reservas. Ya he advertido que si se suma una manzana a una manzana, solo obtenemos dos manzanas si la segunda manzana es diferente de la primera. Lo mismo sucede con combinaciones más complicadas de manzanas y naranjas. El álgebra supone que con el fin de hacer las sumas, todas las manzanas implicadas son diferentes. De hecho, suele ser razonable hacer esta hipótesis, incluso en casos donde dos manzanas —o cualquier otra cosa que estemos sumando— podrían ser en realidad la misma. Una manzana más la misma manzana es una manzana con multiplicidad dos.

Una vez que nos acostumbramos a esta idea, podemos utilizarla para cualquier cosa. Un cerdo más el mismo cerdo es ese cerdo con multiplicidad dos: cerdo + cerdo = 2 cerdo, cualquier cosa que sea cerdo. Un cerdo más una vaca es cerdo + vaca. Un triángulo más tres círculos es triángulo + 3 círculo. Una superduperesfera más tres quasimontones hiperelípticos es

superduperesfera + 3 cuasimontonhiperelíptico

cualquier cosa que esa jerga signifique (que, aquí, es nada).

Incluso podemos permitir números negativos y hablar de tres cerdos menos once vacas: 3 cerdo - 11 vaca. No tengo la menor idea de lo que sean menos once vacas, pero puedo confiar en que si a eso le sumo seis vacas, he obtenido -5 vacas^[86]. Es un juego formal que se juega con símbolos, y no se necesita ninguna interpretación más realista, útil o —a menudo— posible. Podríamos admitir números reales: π cerdos menos √2 vacas. O números complejos. O cualquier tipo de número fantástico que haya inventado o invente en el futuro cualquier matemático. La idea puede hacerse algo más respetable si consideramos los números como etiquetas unidas a los cerdos y las vacas. Ahora π cerdos menos √2 vacas pueden considerarse como un cerdo etiquetado π junto con una vaca etiquetada √-2. La aritmética se aplica a las etiquetas, no a los animales.

La conjetura de Hodge implica una construcción de este tipo, con algunos detalles extra. En lugar de animales, utiliza curvas, superficies y sus análogas en más altas dimensiones. Por extraño que pueda parecer, el resultado no es un absurdo abstracto sino una conexión profunda entre topología, álgebra, geometría y análisis.

Para establecer el formalismo de homología queremos sumar lazos, pero no de la manera en que lo hicimos en el caso del grupo fundamental. En su lugar, lo hacemos de la manera que me contaba mi profesor. Simplemente escribimos los lazos y ponemos un signo + entre ellos. Para darle sentido trabajamos no con lazos únicos sino con conjuntos finitos de ellos. Etiquetamos cada lazo con un entero que cuenta cuántas veces ocurre. Llamamos un ciclo a dicho conjunto etiquetado. Ahora la hormiga puede sumar dos ciclos cualesquiera agrupándolos y sumando las etiquetas correspondientes, y el resultado es otro ciclo. Quizá debería haber utilizado bicicletas, no autobuses, en mi imagen para los viajes de la hormiga en el capítulo 10.

Cuando estábamos construyendo el grupo fundamental, donde la «suma» une lazos extremo con extremo, había una pega técnica. Sumar el lazo trivial a un lazo no daba exactamente el mismo lazo, de modo que el lazo cero se comportaba mal. Sumar un lazo a su inverso no daba exactamente el lazo trivial, de modo que los inversos no se comportaban correctamente. La vía de escape era considerar que los lazos son el mismo si uno pudiera deformarse hasta el otro.

En el caso de la homología, este no es el problema. Hay un ciclo cero (todas las etiquetas cero), y todo ciclo tiene un inverso (convierte toda etiqueta en su negativo), de modo que obtenemos un grupo. El problema es que se trata del grupo equivocado. No nos dice nada sobre la topología del espacio. Para solucionarlo utilizamos un truco similar, y adoptamos una visión más laxa sobre qué ciclos deberían contar como cero. La hormiga divide el espacio en parches triangulares, y la frontera de cada parche es topológicamente bastante trivial: podemos contraerla hasta un punto empujándola hacia el centro de su parche. De modo que exigimos que estos ciclos frontera sean equivalentes al ciclo cero. Es un poco como convertir números ordinarios en aritmética de reloj fingiendo que el número 12 es irrelevante, de modo que puede hacerse cero. Aquí convertimos ciclos en homología fingiendo que cualquier ciclo frontera es irrelevante.

Las consecuencias de este fingimiento son espectaculares. Ahora el álgebra de ciclos está afectada por la topología del espacio. El grupo de ciclos módulo fronteras es un útil invariante topológico, el grupo de homología de la superficie. A primera vista depende de qué triangulación escoja la hormiga, pero como en el caso de la característica de Euler, diferentes triangulaciones de la misma superficie llevan al mismo grupo de homología. Así que la hormiga ha inventado un invariante algebraico que puede distinguir superficies diferentes. Es un poco enrevesado, pero nunca se obtienen buenos invariantes sin hacer un trabajo duro en alguna parte del camino. Este es tan efectivo que puede distinguir no solo la esfera del toro sino también un toro 2-agujereado de un toro de 5-agujereado, y lo mismo para cualquier otro número de agujeros.

La homología puede parecer un trabalenguas, pero abrió una rica vena de invariantes topológicos y se basa en simples ideas geométricas: lazos, fronteras, agrupar conjuntos, hacer aritmética con etiquetas. Considerando que la pobre hormiga está confinada en su superficie, es sorprendente que la criatura pueda descubrir algo importante sobre la forma de su universo solo con pegar parches triangulares, hacer un mapa y utilizar un poco de álgebra.

Hay una manera natural de extender la homología a dimensiones más altas. El análogo 3-dimensional de un triángulo es un tetraedro; tiene 4 vértices, 6 aristas, 4 caras triangulares y una única «cara» 3-dimensional, su interior. En general, en n dimensiones podemos definir un n-simplex con n + 1 vértices, unidos en pares por todas las aristas posibles, que a su vez forman triángulos que se ensamblan para crear tetraedros, y así sucesivamente. Ahora es fácil definir ciclos, fronteras y homología, y de nuevo podemos construir un grupo sumando (clases de homología de) ciclos. De hecho, ahora obtenemos toda una serie de grupos: uno para ciclos 0-dimensionales (puntos), otro para ciclos 1-dimensionales (líneas), otro para ciclos 2-dimensionales (triángulos), y así sucesivamente, hasta la dimensión del propio espacio. Estos son el 0-ésimo, primero, segundo, y así sucesivamente, grupos de homología del espacio. Hablando en términos generales, hacen precisa la noción de agujeros, de varias dimensiones, en el espacio: ¿existen, cuántos hay y cómo se relacionan entre sí?

Eso, entonces, es la homología, y es casi lo que necesitamos para entender lo que dice la conjetura de Hodge. Sin embargo, lo que necesitamos en realidad es un concepto íntimamente relacionado llamado cohomología. En 1893 Poincaré advirtió una curiosa coincidencia en la homología de cualquier variedad: la lista de grupos de homología se lee igual al revés. Para una variedad de dimensión 5, pongamos por caso, el 0-ésimo grupo de homología es el mismo que el 5.º, el 1.^er grupo de homología es el mismo que el 4.º, y el 2.º grupo de homología es el mismo que el 3.º. Él se dio cuenta de que esto no podía ser solo una coincidencia y la explicó en términos del dual de una triangulación, que encontramos en el capítulo 4 en conexión con los mapas. Este es una segunda triangulación en la que cada triángulo se reemplaza por un vértice, cada arista entre dos triángulos por una arista que enlaza los correspondientes nuevos vértices, y cada punto por un triángulo, como en la Figura 9 del capítulo 4. Nótese cómo la dimensión aparece en orden inverso: triángulos 2-dimensionales se convierten en puntos 0-dimensionales, y recíprocamente; aristas 1-dimensionales siguen siendo aristas 1-dimensionales porque 1 está en el centro.

Resulta útil distinguir las dos listas, incluso si dan los mismos invariantes. Cuando se generaliza el sistema entero y se formula en términos abstractos, las triangulaciones desaparecen y la triangulación dual ya no tiene sentido. Lo que sobrevive son dos series de invariantes topológicos, llamados grupos de homología y grupos de cohomología. Todo concepto en homología tiene un dual, cuyo nombre se forma normalmente añadiendo «co» delante. Así, en lugar de ciclos tenemos cociclos, y en lugar de que dos ciclos sean homólogos tenemos dos cociclos que son cohomólogos. Las clases mencionadas en la conjetura de Hodge son clases de cohomología, y estas son colecciones de cociclos que son cohomólogos entre sí.

Homología y cohomología no nos dicen todo lo que nos gustaría saber sobre la forma de un espacio topológico —distintos espacios pueden tener la misma homología y cohomología— pero proporcionan mucha información útil y un marco sistemático en el que calcularla y utilizarla.

Una variedad algebraica, ya sea real, compleja, proyectiva o no, es un espacio topológico. Por consiguiente tiene una forma. Para descubrir cosas útiles sobre la forma, pensamos como topólogos y calculamos los grupos de homología y cohomología. Pero los ingredientes naturales en geometría algebraica no son objetos geométricos como triangulaciones y ciclos. Son los objetos que más fácilmente podemos describir por ecuaciones algebraicas. Volvamos atrás y examinemos la ecuación para la superficie de Kummer. ¿Cómo se relacionaría con una triangulación? No hay nada en la fórmula que sugiera triángulos.

Quizá necesitemos empezar de nuevo. En lugar de triángulos deberíamos utilizar los bloques constituyentes básicos de las variedades, que son subvariedades definidas imponiendo ecuaciones extra. Ahora tenemos que redefinir los ciclos: en lugar de conjuntos de triángulos con etiquetas enteras, utilizamos conjuntos de subvariedades con cualesquiera etiquetas que mejor sirvan. Por diversas razones —sobre todo porque la conjetura de Hodge es falsa si utilizamos etiquetas enteras— los números racionales son la elección razonable. La pregunta de Hodge se reduce a esto: ¿recoge esta nueva definición de homología y cohomología todo lo que recoge la definición topológica? Si su conjetura es cierta, entonces la herramienta del ciclo algebraico es suficientemente aguda para igualar al cincel cohomológico de la topología. Si es falsa, entonces el ciclo algebraico es un instrumento romo.

Excepto… lo siento, he puesto demasiados huevos en el pudin. La conjetura dice que basta con utilizar un tipo particular de ciclo algebraico, uno que vive en una clase de Hodge. Para explicarlo necesitamos otro ingrediente en una ya rica mezcla: el análisis. Uno de los conceptos más importantes en el análisis es el de una ecuación diferencial, que es una condición sobre los ritmos a que cambian las variables (véase capítulo 8). Casi toda la física matemática de los siglos XVIII, XIX y XX modela la naturaleza utilizando ecuaciones diferenciales, e incluso en el siglo XXI la mayor parte lo hace. En la década de 1930 esta idea llevó a Hodge a un nuevo cuerpo de técnica, ahora llamado teoría de Hodge. Se relaciona de forma natural con muchos otros métodos potentes en el área general del análisis y la topología.

La idea de Hodge era utilizar una ecuación diferencial para organizar las clases de cohomología en tipos característicos. Cada pieza tiene estructura extra, que puede utilizarse con ventaja en problemas topológicos. Las piezas se definen utilizando una ecuación diferencial que apareció a finales del siglo XVIII, en especial en el trabajo de Pierre-Simon de Laplace. En consecuencia, se le llama ecuación de Laplace. La investigación más importante de Laplace era en mecánica celeste, el movimiento y la forma de los planetas, lunas, cometas y estrellas. En 1783 estaba trabajando sobre la forma detallada de la Tierra. Para entonces se sabía que la Tierra no es una esfera perfecta sino que está achatada por los polos para formar un esferoide oblato, como un balón de playa en el que alguien está sentado. Pero incluso esa descripción deja escapar algo del detalle fino. Laplace encontró un método para calcular la forma con cualquier precisión requerida basado en una magnitud física que representa el campo gravitatorio de la Tierra: no el campo propiamente dicho sino su potencial gravitatorio. Este es una medida de la energía contenida en la gravitación, una magnitud numérica definida en cada punto del espacio. La fuerza de la gravedad actúa en la dirección que hace que el potencial disminuya al ritmo más rápido, y la magnitud de la fuerza es el ritmo de disminución.

El potencial satisface la ecuación de Laplace: a grandes rasgos, esto dice que en ausencia de materia —es decir, en el vacío— el valor medio del potencial sobre una esfera muy pequeña es igual a su valor en el centro de la esfera. Es una especie de democracia: el valor de uno es el promedio de los valores de sus vecinos. Cualquier solución de la ecuación de Laplace se llama una función armónica. Tipos especiales de Hodge de clases de cohomología son aquellos que guardan una relación particular con las funciones armónicas. La teoría de Hodge, el estudio de estos tipos, abrió una profunda y maravillosa área de las matemáticas: relaciones entre la topología de un espacio y una ecuación diferencial especial en dicho espacio.

Así que ahora lo tenemos. La conjetura de Hodge postula una conexión profunda y poderosa entre tres de los pilares de las modernas matemáticas: álgebra, topología y análisis. Tomar cualquier variedad. Para entender su forma (topología, que lleva a clases de Hodge por vía de ecuaciones diferenciales) escoger ejemplos especiales de estas (análisis, que lleva a clases de Hodge por vía de ecuaciones diferenciales). Estos tipos especiales de clases de cohomología pueden realizarse utilizando subvariedades (álgebra: introducir algunas ecuaciones extra y examinar ciclos algebraicos). Es decir, para resolver el problema de topología «¿qué forma tiene esto?» para una variedad, se convierte la pregunta en análisis y luego se resuelve utilizando álgebra.

¿Por qué eso es importante? La conjetura de Hodge es una propuesta de añadir dos nuevas herramientas a la caja de herramientas de la geometría algebraica: invariantes topológicos y ecuación de Laplace. No es en realidad una conjetura sobre un teorema matemático: es una conjetura sobre nuevos tipos de herramientas. Si la conjetura es cierta, esas herramientas adquieren al momento nueva importancia y potencialmente pueden ser utilizadas para responder a una cadena sin fin de preguntas. Por supuesto, podría resultar que sea falsa. Eso sería desagradable, pero es mejor entender las limitaciones de una herramienta que seguir dándose en los dedos con ella.

Ahora que apreciamos la naturaleza de la conjetura de Hodge, podemos examinar las pruebas a su favor. ¿Qué sabemos? Bien poco.

En 1924, antes de que Hodge hiciera su conjetura, Solomon Lefschetz demostró un teorema que se reduce a la conjetura de Hodge para la cohomoloía en dimensión 2 de cualquier variedad. Con algo de topología algebraica rutinaria esto implica la conjetura de Hodge para variedades de dimensión 1, 2 y 3. Para variedades de dimensiones más altas solo se conocen unos pocos casos especiales de la conjetura de Hodge.

Hodge enunció originalmente su conjetura en términos de etiquetas enteras. En 1961 Michael Atiyah y Friedrich Hirzebruch demostraron que en dimensiones más altas esta versión de su conjetura es falsa. Por eso hoy interpretamos la conjetura de Hodge utilizando etiquetas racionales. A favor de esta versión hay alguna evidencia alentadora. La prueba más fuerte a su favor es que, sin dar por hecha la conjetura, se ha demostrado una de sus consecuencias más profundas, un teorema todavía más técnico conocido como «algebraicidad de lugares geométricos de Hodge». Eduardo Cattani, Pierre Deligne y Aroldo Kaplan encontraron dicha demostración en 1995.

Para finalizar, hay una conjetura atractiva en teoría de números que es análoga a la conjetura de Hodge. Se denomina conjetura de Tate, por John Tate, y vincula la geometría algebraica con la teoría de Galois, el círculo de ideas que demostraban que no hay fórmula algebraica para resolver ecuaciones polinómicas de grado 5. Su formulación es técnica, e incluye otra versión más de cohomología. Hay razones independientes para esperar que la conjetura de Tate pueda ser cierta, pero su estatus está abierto por el momento. Pero al menos hay un pariente razonable de la conjetura de Hodge, incluso si de momento parece igualmente intratable.

La conjetura de Hodge es una de esas enojosas afirmaciones matemáticas para las que las pruebas a favor o en contra no son muy amplias ni especialmente convincentes. Sin duda, hay peligro de que la conjetura pueda ser falsa. Quizá haya una variedad con un millón de dimensiones que refute la conjetura de Hodge, por razones que se reducen a series de cálculos desestructurados, tan complicados que nadie podría realizarlos jamás. Si es así, la conjetura de Hodge podría ser falsa por razones que en realidad carecen de interés —sencillamente resulta no ser cierta— pero que en la práctica resultan imposibles de refutar. Conozco a algunos geómetras algebraicos que lo sospechan. Si es así, ese millón de dólares estará a salvo en un futuro previsible.