Las leyes de movimiento captan la relación entre las fuerzas que actúan en un cuerpo y cómo se mueve en respuesta a estas fuerzas. El cálculo proporciona técnicas matemáticas para resolver las ecuaciones resultantes. Se necesita un ingrediente más para aplicar las leyes: especificar las fuerzas. El aspecto más ambicioso del Principia de Newton era hacer precisamente eso para los cuerpos del Sistema Solar: el Sol, los planetas, satélites, asteroides y cometas. La ley de gravitación universal de Newton sintetiza, en una sencilla fórmula matemática, milenios de observaciones astronómicas y teorías. Explica muchas características misteriosas del movimiento planetario e hizo posible predecir los movimientos futuros del Sistema Solar con gran precisión. La teoría de la relatividad general de Einstein finalmente suplanta la teoría newtoniana de la gravedad, en lo que a física fundamental se refiere, pero para casi todos los propósitos prácticos la aproximación newtoniana más simple todavía impera. En la actualidad, las agencias espaciales mundiales, como NASA y ESA, todavía usan las leyes de movimiento y gravitación de Newton para averiguar las trayectorias más efectivas para las naves espaciales.

Fue la ley de gravitación universal, sobre todas las demás, la que justificó su subtítulo: El sistema del mundo. Esta ley demostraba el enorme poder de las matemáticas para encontrar patrones escondidos en la naturaleza y revelar simplicidades escondidas tras las complejidades del mundo. Y con el tiempo, a medida que los matemáticos y astrónomos preguntaban cuestiones más difíciles, revelar las complejidades escondidas implícitas en la sencilla ley de Newton. Para apreciar lo que Newton logró, debemos primero remontarnos en el tiempo, para ver cómo culturas anteriores veían las estrellas y los planetas.

Los humanos han estado observando el cielo nocturno desde el amanecer de la historia. Sus impresiones iniciales habrían sido una dispersión aleatoria de puntos de luz brillantes, pero se darían cuenta pronto de que a través de este fondo el brillante orbe de la Luna trazaba un recorrido regular, cambiando de forma a medida que lo hacía. También habrían visto que la mayoría de esos minúsculos destellos brillantes de luz permanecían en los mismos modelos relativos, los cuales ahora llamamos constelaciones. Las estrellas se mueven a través del cielo nocturno, pero se mueven como una única unidad rígida, como si las constelaciones estuviesen pintadas en un bol gigante que rota.^[17] Sin embargo, un pequeño número de estrellas se comportan de un modo bastante diferente, parece que deambulan alrededor del cielo. Sus recorridos son bastante complicados y algunas parece que regresan sobre sí mismas de tanto en tanto. Estos son los planetas, una palabra que viene del término griego para «vagabundos». En la Antigüedad reconocieron 5 de ellos, ahora llamados Mercurio, Venus, Marte, Júpiter y Saturno. Se mueven en relación con las estrellas fijas a diferentes velocidades, y Saturno es el más lento.

Otros fenómenos celestes eran incluso más enigmáticos. De tanto en tanto un cometa aparecía, como si viniese de la nada, siguiendo una estela larga y curva. «Estrellas fugaces» parecerían caer del cielo, como si se hubiesen despegado del bol en el que estaban. No es de extrañar que los primeros humanos atribuyesen estas irregularidades en los cielos a los caprichos de seres sobrenaturales.

Las regularidades podrían resumirse en términos tan obvios que pocos habrían alguna vez soñado con discutirlas. El Sol, las estrellas y los planetas giran alrededor de una Tierra inmóvil. Esto es lo que parece, así es como se siente, así que así es como debe de ser. En la Antigüedad, el cosmos era geocéntrico, la Tierra era el centro. Una solitaria voz cuestionó lo obvio: Aristarco de Samos. Usando principios geométricos y observaciones, Aristarco calculó los tamaños de la Tierra, el Sol y la Luna. Alrededor del año 270 a. C., expuso la primera teoría heliocéntrica: la Tierra y los planetas giran alrededor del Sol. Su teoría rápidamente cayó en desgracia y no resurgió durante casi 2.000 años.

En la época de Ptolomeo, un romano que vivió en Egipto alrededor del 120 d. C., los planteas habían sido domesticados. Sus movimientos no eran caprichosos, sino predecibles. El Almagesto (El gran tratado) de Ptolomeo proponía que vivimos en un universo geocéntrico en el cual todo literalmente gira alrededor de la humanidad en combinaciones complejas de círculos llamadas epiciclos, apoyados en esferas de cristal gigantes. Su teoría era errónea, pero los movimientos que predijo eran lo suficientemente precisos para que los errores no se detectasen durante siglos. El sistema de Ptolomeo tenía una atracción filosófica adicional: representaba el cosmos en términos de figuras geométricas perfectas: esferas y círculos. Continuaba la tradición pitagórica. En Europa, la teoría de Ptolomeo permaneció sin cambios durante 1.400 años.

Mientras Europa perdía el tiempo, nuevos avances científicos se llevaban a cabo en otros lugares, especialmente en el mundo árabe, China e India. En el 499, el astrónomo hindú Aryabhata expuso un modelo matemático para el Sistema Solar en el cual la Tierra giraba sobre su eje y los períodos de órbitas planetarias se establecían en relación con el Sol. En el mundo islámico, Alhazen escribió una crítica punzante a la teoría ptolemaica, aunque esta probablemente no se centraba en su naturaleza geocéntrica. Alrededor del año 1000, Abu Rayhan Biruni aportó reflexiones serias sobre la posibilidad de un Sistema Solar heliocéntrico, con la Tierra girando sobre su eje, pero finalmente optó por la ortodoxia de la época, una Tierra fija. Alrededor del 1300, Najm al-Din al-Qazwini al-Katibi propuso una teoría heliocéntrica, pero pronto cambió de opinión.

El gran paso adelante llegó con el trabajo de Nicolás Copérnico, publicado en 1543 como De Revolutionibus Orbium Coelestium (Sobre las revoluciones de las esferas celestes). Hay evidencias, en particular el hecho de diagramas casi idénticos etiquetados con las mismas letras, que sugieren que Copérnico estaba, como mínimo, influenciado por al-Kabiti, pero fue mucho más lejos. Propuso un sistema explícitamente heliocéntrico, argumentó que encajaba mejor y más económicamente con las observaciones que la teoría geocéntrica de Ptolomeo y expuso algunas de sus implicaciones filosóficas. Primordial entre ellas era el pensamiento novedoso de que los humanos no eran el centro de las cosas. La Iglesia cristiana vio sus sugerencias como contrarias a la doctrina e hizo lo que pudo para disuadirlo. El heliocentrismo explícito era una herejía.

A pesar de todo prevaleció, porque las evidencias eran muy fuertes. Aparecieron teorías heliocéntricas nuevas y mejores. Luego las esferas se descartaron totalmente en favor de una forma diferente de la geometría clásica: la elipse. Las elipses son formas ovaladas y pruebas indirectas sugieren que se estudiaron por primera vez en la geometría griega por Menecmo alrededor del 350 a. C., junto con las hipérbolas y las parábolas, como secciones de un cono (figura 13). Se dice que Euclides habría escrito cuatro libros sobre las secciones cónicas, aunque nada ha sobrevivido si lo hizo, y Arquímedes investigó algunas de sus propiedades. La investigación hecha por los griegos sobre el tema alcanzó su clímax alrededor del 240 a. C. con los ocho volúmenes de Secciones cónicas de Apolonio de Perga, quien encontró un modo de definir estas curvas simplemente en el plano, evitando la tercera dimensión. Sin embargo, la visión pitagórica de que los círculos y las esferas alcanzaban un grado mayor de perfección que las elipses y otras curvas más complejas persistía.

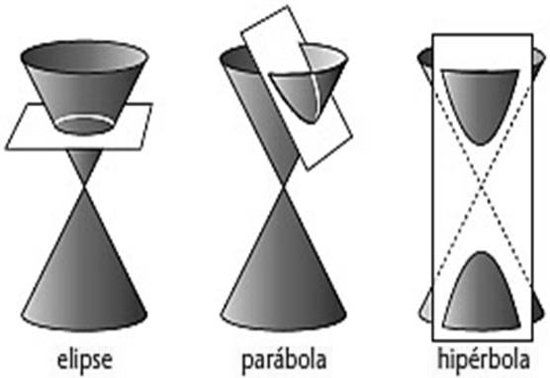
FIGURA 13. Secciones cónicas.

Las elipses consolidaron su papel en la astronomía alrededor del 1600, con el trabajo de Kepler. Sus intereses astronómicos empezaron en la infancia, con seis años fue testigo del gran cometa de 1577,^[18] y tres años más tarde vio un eclipse de la Luna. En la Universidad de Tubinga, Kepler demostró un gran talento para las matemáticas y le sacó un uso rentable haciendo horóscopos. En esa época matemáticas, astronomía y astrología con frecuencia iban juntas. Combinó un embriagador nivel de misticismo con una atención sensata al detalle matemático. Un ejemplo típico es su Mysterium Cosmographicum (El misterio cosmográfico), una defensa vehemente del sistema heliocéntrico publicada en 1569. Combina unos conocimientos claros de la teoría de Copérnico con lo que a ojos actuales es una especulación muy extraña que relaciona las distancias de los planetas conocidos a partir del Sol con los sólidos regulares. Durante mucho tiempo Kepler consideró este descubrimiento como uno de los más importantes, revelando los planes del Creador para el universo. Vio sus investigaciones posteriores, las cuales en la actualidad consideramos mucho más importantes, como meras elaboraciones de este plan básico. En la época, una ventaja de la teoría era que explicaba por qué había justamente seis planetas (de Mercurio a Saturno). Entre estas seis órbitas hay cinco huecos, uno por cada sólido regular. Con el descubrimiento de Urano y, más tarde, Neptuno y Plutón (hasta su reciente degradación de su estatus como planeta) esta característica rápidamente se convirtió en un fallo nefasto.

La duradera contribución de Kepler tiene sus raíces en su empleo con Tycho Brahe. Se encontraron por primera vez en 1600. Después de una estancia de dos meses y una discusión acalorada, Kepler negoció un salario aceptable. Después de una racha de problemas en su ciudad natal, Graz, se mudó a Praga, asistiendo a Tycho en el análisis de sus observaciones planetarias, especialmente de Marte. Cuando Tycho inesperadamente falleció en 1601, Kepler asumió su trabajo como matemático imperial para Rodolfo II. Su papel principal era hacer los horóscopos del imperio, pero también tenía tiempo para continuar su análisis de la órbita de Marte. Siguiendo principios epicíclicos tradicionales refinó su modelo hasta el punto en el que sus errores, comparados con la observación, eran normalmente unos escasos dos minutos de arco, el típico error en las propias observaciones. Sin embargo, no se detuvo ahí porque a veces los errores eran mayores, hasta ocho minutos de arco.

Su búsqueda finalmente lo llevó a dos leyes del movimiento de los planetas, publicadas en Astronomia Nova (Una nueva astronomía). Durante muchos años, había intentado encajar la órbita de Marte en un ovoide —una curva con forma de huevo, más fina en un extremo que en otro— sin éxito. Quizá esperaba que la órbita fuese más curvada cuando estuviese más cerca del Sol. En 1605, a Kepler se le ocurrió intentarlo con una elipse, redondeada por igual en ambos extremos, y cuál fue su sorpresa al ver que encajaba mucho mejor. Concluyó que todas las órbitas planetarias eran elipses, su primera ley. Su segunda ley describía cómo el planeta se mueve a lo largo de su órbita, afirmando que los planetas barren áreas iguales en tiempos iguales. El libro se publicó en 1609. Kepler dedicó entonces mucho de su esfuerzo a preparar varias tablas astronómicas, pero volvió a las regularidades de las órbitas planetarias en 1619 en su Harmonices Mundi (La armonía del mundo). Este libro tenía algunas ideas que ahora encontramos extrañas, por ejemplo que los planetas emitían sonidos musicales a medida que rotaban alrededor del Sol. Pero también incluye su tercera ley: los cuadrados de los períodos orbitales son proporcionales a los cubos de sus distancias al Sol.

Las tres leyes de Kepler fueron prácticamente sepultadas entre una masa de misticismo, simbolismo religioso y especulaciones filosóficas. Pero representaron un salto hacia delante gigantesco, llevando a Newton a uno de los más grandes descubrimientos científicos de todos los tiempos.

Newton obtuvo su ley de la gravedad a partir de las tres leyes del movimiento de los planetas de Kepler. Afirma que toda partícula en el universo atrae a todas las otras partículas con una fuerza que es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia entre ellas. En símbolos:

Aquí F es la fuerza de atracción, d es la distancia, las m son las dos masas y G es un número concreto, la constante de gravitación.^[19]

¿Quién descubrió la ley de gravitación de Newton? Suena como una de esas preguntas que contienen la respuesta, como «¿de qué color es el caballo blanco de Santiago?». Pero una respuesta sensata es el comisario de experimentos en la Royal Society, Robert Hooke. Cuando Newton publicó la ley en 1687, en su Principia, Hooke le acusó de plagio. Sin embargo, Newton proporcionaba la primera derivada matemática de órbitas elípticas a partir de la ley, lo cual era vital para establecer su corrección, y Hooke reconoció esto. Además, Newton había citado a Hooke, entre otros, en el libro. Presumiblemente Hooke sentía que merecía más crédito, había sufrido problemas parecidos varias veces antes y era un asunto delicado.

La idea de que los cuerpos se atraían unos a otros había estado merodeando por un tiempo, y también su probable expresión matemática. En 1645 el astrónomo francés Ismaël Boulliau (Bullialdus) escribió su Astronomia Philolaica (Astronomía filolaica; Filolao de Crotona era un filósofo griego que pensaba que un fuego central, no la Tierra, era el centro del universo). En él escribió:

Con respecto a la fuerza por la cual el Sol agarra o sostiene a los planetas, y la cual, al ser corpórea, funciona de la misma manera que las manos; se emite en líneas rectas por toda la extensión del mundo y, como especies del Sol, gira con el cuerpo del Sol; ahora, viendo que es corpóreo, se hace más débil y atenúa a distancias o intervalos mayores, y la razón de su descenso según la longitud es la misma que en el caso de la luz, a saber, la proporción duplicada, pero inversamente, de las distancias.

Esta es la famosa dependencia del «cuadrado de la inversa» de la fuerza sobre la distancia. Hay razones simples, aunque inocentes, para esperar dicha fórmula, porque el área de la superficie de una esfera varía según el cuadrado de su radio. Si la misma cantidad de «material» gravitacional se extiende por una esfera cada vez mayor a medida que se separa del Sol, entonces la cantidad recibida en cualquier punto debe variar en proporción inversa al área. Exactamente esto sucede con la luz, y Boulliau asumió, sin muchas pruebas, que la gravedad debía ser análoga. También pensó que los planetas se mueven a lo largo de sus órbitas bajo su propia fuerza, por así decirlo: «Ningún tipo de movimiento presiona sobre los planetas restantes, los cuales son conducidos alrededor por formas individuales con las cuales fueron provistos».

Las contribuciones de Hooke datan de 1666, cuando presentó un artículo a la Royal Society con el título «On gravity» (Sobre la gravedad). Aquí ponía en orden lo que Boulliau había hecho erróneamente, argumentando que una fuerza de atracción proveniente del Sol podía interferir con una tendencia natural de los planetas a moverse en línea recta (como especificaba la tercera ley de movimiento de Newton) y por causa de eso se obtenía una curva. También afirmó que «estas fuerzas de atracción son mucho más potentes funcionando, cuanto más cercano está el cuerpo a sus propios centros», mostrando que pensaba que la fuerza decaía con la distancia. Pero no le dijo a nadie más la forma matemática para este decrecimiento hasta 1679, cuando escribió a Newton: «la atracción siempre está en una proporción duplicada de la distancia desde el centro recíproca». En la misma carta dijo que esto implica que la velocidad de un planeta varía como el recíproco de su distancia desde el Sol. Lo cual es erróneo.

Cuando Hooke se quejó de que Newton le había robado su ley, Newton no estaba cogiendo nada de ella, e indicó que había discutido la idea con Christopher Wren antes de que Hooke le hubiese enviado su carta. Para demostrar conocimientos previos, citó a Boulliau, y también a Giovanni Borelli, un psicólogo y físico matemático italiano. Borelli había sugerido que tres fuerzas se combinan para crear movimiento planetario: una fuerza interior causada por el deseo de los planetas de aproximarse al Sol, una fuerza lateral causada por la luz del Sol, y una fuerza exterior causada por la rotación del Sol. Acertó una de tres, y eso siendo generoso.

El principal punto de Newton, generalmente considerado decisivo, es que fuera lo que fuera que Hooke había hecho, no había deducido la forma exacta de las órbitas a partir de la atracción de la ley del cuadrado de la inversa. Newton lo había hecho. De hecho, había deducido las tres leyes del movimiento planetario de Kepler: órbitas elípticas, barrido de áreas iguales en intervalos de tiempo iguales, con el cuadrado del período siendo proporcional al cubo de la distancia. «Sin mis demostraciones», insistía Newton, la ley del cuadrado de la inversa, «un filósofo sensato no podría creer que fuese ni mucho menos correcta». Pero también aceptaba que «el señor Hooke es todavía un extraño» a esta prueba. Una característica clave de la argumentación de Newton es que no se aplica tan solo a un punto, sino a una esfera. Esta extensión, la cual es crucial para el movimiento de los planetas, había supuesto un considerable esfuerzo para Newton. Su prueba geométrica es una aplicación del cálculo integral disfrazada, y estaba, con razón, orgulloso de ella. Hay también evidencias de que Newton había estado pensando sobre dicha cuestión durante bastante tiempo.

De cualquier forma, es frecuente referirse a ella como ley de gravitación universal de Newton, y esto hace justicia a la importancia de su contribución.

El aspecto más importante de la ley de gravitación universal no es la ley del cuadrado de la inversa como tal. Es la afirmación de que la gravedad actúa universalmente. Dos cuerpos cualquiera, en cualquier lugar del universo, se atraen el uno al otro. Por supuesto se necesita una ley de fuerzas precisa (el cuadrado de la inversa) para obtener resultados precisos, pero sin la universalidad, no sabes cómo escribir las ecuaciones para cualquier sistema con más de dos cuerpos. Casi todos los sistemas interesantes, como el propio Sistema Solar, o la sutil estructura del movimiento de la Luna bajo la influencia de (al menos) el Sol y la Tierra, implica más de dos cuerpos, así que la ley de Newton habría sido casi inútil si solo se hubiese aplicado al contexto en el cual la dedujo inicialmente.

¿Qué motivó esta visión de universalidad? En sus Memoirs of Sir Isaac Newton’s Life (Memorias de la vida de Sir Isaac Newton) de 1752, William Stukeley cuenta una historia que Newton le había contado a él en 1726:

La noción de gravedad… era ocasionada por la caída de una manzana, mientras que estaba sentado con un humor contemplativo. ¿Por qué debería esa manzana siempre descender perpendicularmente a la tierra?, pensó. ¿Por qué no va hacia los lados o hacia arriba, sino constantemente al centro de la Tierra? Ciertamente la razón es que la Tierra tira de ella. Debe haber una fuerza tiradora en la materia. Y la suma de la potencia tiradora en la materia de la Tierra debe estar en el centro de la Tierra, no en cualquier lado de la Tierra. Por lo tanto, ¿cae la manzana perpendicularmente o hacia el centro? Si la materia tira de este modo de la materia, debe estar en proporción a su cantidad. Por lo tanto la manzana tira de la Tierra, del mismo modo en que la Tierra tira de la manzana.

Si la historia es la verdad literal o una invención oportuna que Newton se inventó para ayudar a explicar sus ideas más adelante, no está totalmente claro, pero parece razonable tomar el cuento en serio porque la idea no acaba con manzanas. La manzana era importante para Newton porque le hizo darse cuenta de que la misma ley de fuerza puede explicar tanto el movimiento de la manzana como el movimiento de la Luna. La única diferencia es que la Luna también se mueve hacia los lados, esta es la razón por la cual se sostiene. Realmente, está siempre cayendo hacia la Tierra, pero el movimiento lateral causa que la superficie de la Tierra se caiga también. Newton, siendo Newton, no podía detenerse con este argumento cualitativo. Hizo las cuentas, las comparó con las observaciones y se quedó satisfecho creyendo que su idea debía ser correcta.

Si la gravedad actúa en la manzana, la Luna y la Tierra, como una característica inherente de la materia, entonces probablemente actúa sobre todo.

No es posible verificar la universalidad de las fuerzas de gravedad directamente, tendrías que estudiar todos los pares de cuerpos del universo entero, y encontrar el modo de eliminar la influencia de los otros cuerpos. Pero así no es como funciona la ciencia. En su lugar, emplea una mezcla de inferencia y observaciones. La universalidad es una hipótesis, capaz de ser falsificada cada vez que se aplica. Cada vez que sobrevive a una falsificación, un modo extravagante de decir que da buenos resultados, la justificación para usarla se hace un poco más fuerte. Si (como en este caso) sobrevive a miles de dichas pruebas, la justificación se hace realmente fuerte. Sin embargo, la hipótesis nunca se puede verificar; hasta donde sabemos, el próximo experimento podría producir un resultado incompatible. Quizá en algún punto de una galaxia lejana, muy lejos hay una pizca de materia, un átomo, que no es atraído por todo lo demás. Si es así, nunca lo encontraríamos, por lo tanto no alteraría nuestros cálculos. La propia ley del cuadrado de la inversa es extremadamente difícil de verificar directamente, esto es, midiendo realmente la fuerza de atracción. En su lugar, aplicamos la ley a un sistema que podemos medir, usándolo para predecir órbitas y luego comprobar si las predicciones coinciden con las observaciones.

Incluso concediendo la universalidad, no es suficiente para escribir una ley de atracción precisa. Esto solo produce una ecuación para describir el movimiento. Para encontrar el propio movimiento, hay que resolver la ecuación. Incluso para dos cuerpos, esto no es directo y sencillo, e incluso teniendo en mente que sabía por adelantado qué respuesta esperaba, la deducción de Newton de órbitas elípticas es una hazaña. Explica por qué las tres leyes de Kepler proporcionan una descripción muy precisa de la órbita de cada planeta. También explica por qué esa descripción no es exacta: otros cuerpos del Sistema Solar, otros diferentes del Sol y el propio planeta afectan al movimiento. Para explicar estas alteraciones, tienes que resolver las ecuaciones de movimiento para tres o más cuerpos. En particular, si quieres predecir el movimiento de la Luna con una precisión alta, tienes que incluir el Sol y la Tierra en tus ecuaciones. Los efectos de los otros planetas, especialmente Júpiter, tampoco son totalmente desdeñables, pero solo aparecen a largo plazo. Así, fuertes por el éxito de Newton con el movimiento de dos cuerpos bajo la gravedad, los matemáticos y físicos pasaron al siguiente caso: tres cuerpos. Su optimismo inicial se disipó rápidamente: el caso de tres cuerpos resultó ser muy diferente del caso de dos cuerpos. De hecho, se resiste a una solución.

Era posible con frecuencia calcular buenas aproximaciones al movimiento (las cuales a menudo solucionaban el problema para propósitos prácticos), pero ya no parecía ser una fórmula exacta. Este problema aquejaba incluso a versiones simplificadas, tales como el problema de tres cuerpos restringido. Supongamos que un planeta describe una órbita alrededor de una estrella en un círculo perfecto; ¿cómo se moverá una mota de polvo de masa insignificante?

Calculando órbitas aproximadas para tres o más cuerpos, a mano, usando lápiz y papel, era más o menos factible, pero muy laborioso. Los matemáticos diseñaron innumerables trucos y atajos, que llevaban a un entendimiento razonable de varios fenómenos astronómicos. Solo a finales del siglo XIX la verdadera complejidad del problema de tres cuerpos se hizo evidente, cuando Henri Poincaré se dio cuenta de que la geometría que implicaba era, por fuerza, extraordinariamente complicada. Y solo a finales del siglo XX la llegada de ordenadores potentes redujo la labor de los cálculos a mano, permitiendo predicciones precisas de movimiento del Sistema Solar a largo plazo.

El gran avance de Poincaré —si puede llamarse así, ya que en la época parece que decía a todos que el problema era imposible y no tenía sentido buscar una solución— sucedió porque compitió para un premio matemático. Óscar II, rey de Suecia y Noruega, anunció una competición para celebrar su sesenta cumpleaños en 1889. Teniendo en cuenta el consejo del matemático Gösta Mittag-Leffler, el rey escogió el problema general de muchos cuerpos moviéndose arbitrariamente bajo la gravedad newtoniana. Ya que se tenía claro que una fórmula explícita semejante a la elipse para los dos cuerpos era un objetivo poco realista, el requisito era laxo: el premio se concedería por un método de aproximación de un tipo muy específico. Concretamente, el movimiento debía determinarse como una serie infinita, dando resultados tan precisos como quisiéramos si se incluían los términos suficientes.

Poincaré no respondió a esta cuestión. En su lugar, su memoria sobre el tema, publicada en 1890, proporcionaba pruebas de que no podría tenerse ese tipo de respuesta, ni siquiera para tres cuerpos: estrella, planeta y una partícula de polvo. Pensando en la geometría de soluciones hipotéticas, Poincaré descubrió que en algunos casos la órbita de la partícula de polvo debía ser extremadamente compleja y enrevesada. Entonces prácticamente se echó las manos a la cabeza con horror e hizo la pesimista afirmación de que «cuando uno trata de describir la figura formada por estas dos curvas y su infinidad de intersecciones, cada una de las cuales corresponde a una solución doblemente asintótica, estas intersecciones forman un tipo de red, maraña o malla infinitamente ceñida… Uno se da de bruces con la complejidad de esta figura que no me atrevo siquiera a dibujar».

Ahora vemos el trabajo de Poincaré como un gran avance, y pasamos por alto su pesimismo, porque la geometría complicada que le desalentó de resolver alguna vez el problema realmente proporciona una comprensión poderosa si se desarrolla e interpreta adecuadamente. La geometría compleja de la dinámica asociada resultó ser uno de los primeros ejemplos del caos: la existencia, en ecuaciones no aleatorias, de soluciones tan complicadas que de algún modo parecen ser aleatorias (véase el capítulo 16).

Hay varias ironías en la historia. La historiadora matemática June Barrow-Green descubrió que la versión publicada de la memoria ganadora de Poincaré del premio no era la que ganó el premio.^[20] Esta versión anterior contenía un error importante, pasando por alto las soluciones caóticas. El trabajo estaba en una etapa de prueba cuando un avergonzado Poincaré se dio cuenta de su metedura de pata, y pagó por una nueva impresión de una versión correcta. Casi todas las copias de la original fueron destruidas, pero una permaneció guardada en los archivos del Instituto de Mittag-Leffler en Suecia, donde Barrow-Green la encontró.

También resultó que la presencia del caos de hecho no excluía las series como soluciones, sino que estas eran válidas casi siempre en vez de serlo siempre. Karl Frithiof Sundman, un matemático finés, descubrió esto en 1912 para el problema de tres cuerpos, usando series formadas a partir de potencias de la raíz cúbica del tiempo. (Las potencias del tiempo no lo resolverán). Las series convergen —tienen una suma perceptible— a menos que el estado inicial tenga un momento angular igual a cero, pero dichos estados son tremendamente raros, en el sentido de que una elección aleatoria del momento angular es casi siempre distinta de cero. En 1991, el matemático chino Qiudong Wang amplió estos resultados para cualquier número de cuerpos, pero no clasificó las excepciones raras cuando las series no convergen. Dicha clasificación es probable que sea muy complicada, debe incluir soluciones donde los cuerpos escapan al infinito en un tiempo finito, u oscilan incluso más rápido, ambos casos pueden darse para cinco o más cuerpos.

La ley de gravitación universal se aplica rutinariamente al diseño de órbitas para misiones espaciales. Aquí incluso la dinámica de dos cuerpos es útil por sí misma. En sus inicios, la exploración del Sistema Solar principalmente usaba órbitas de dos cuerpos, segmentos de elipses. Quemando combustible, la nave espacial podía pasar de una elipse a otra diferente. Pero a medida que los objetivos de los programas espaciales se hacían más ambiciosos, se necesitaban métodos más eficientes. Vinieron gracias a la dinámica de muchos cuerpos, normalmente tres cuerpos, pero ocasionalmente pueden llegar a ser cinco. Los nuevos métodos de caos y dinámica topológica se convirtieron en las bases de las soluciones prácticas a los problemas de ingeniería.

Todo empezó con una pregunta simple: ¿cuál es la ruta más eficiente para ir de la Tierra a la Luna o los planetas? La respuesta clásica, conocida como una órbita de transferencia de Hohmann (figura 14) empieza con una órbita circular alrededor de la Tierra, y luego sigue con parte de una elipse larga y fina para unir con una segunda órbita circular alrededor del destino. Este método fue empleado durante las misiones espaciales Apolo de las décadas sesenta y setenta del siglo XX, pero para muchos tipos de misión tenía un inconveniente. La nave espacial debe lanzarse fuera de la órbita terrestre y luego reducir la velocidad al entrar en la órbita lunar; esto malgasta combustible. Hay alternativas que implican muchos bucles alrededor de la Tierra, una transición por el punto entre la Tierra y la Luna donde sus campos de gravitación se anulan y muchos bucles alrededor de la Luna. Pero trayectorias como esta llevan mucho más tiempo que las elipses de Hohmann, de modo que no se usaron en las misiones tripuladas Apolo donde la comida y el oxígeno, y por consiguiente el tiempo, eran oro. Para misiones no tripuladas, sin embargo, el tiempo es relativamente barato, mientras que cualquier cosa que añade peso al total de la nave espacial, incluyendo el combustible, cuesta dinero.

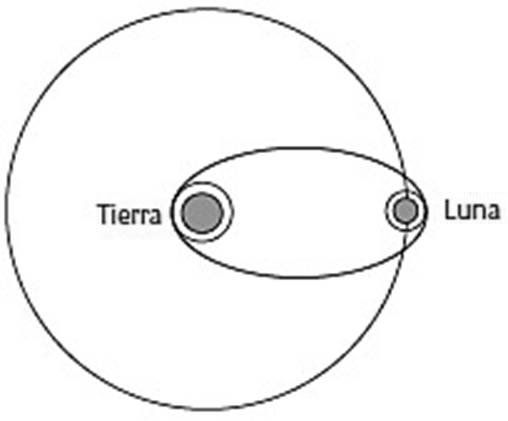
FIGURA 14. Órbita de transferencia de Hohmann de una órbita terrestre baja a la órbita lunar.

Considerando una nueva perspectiva de la ley de gravitación universal y la segunda ley de movimiento de Newton, los matemáticos e ingenieros espaciales han descubierto recientemente una nueva y destacable aproximación a los viajes interplanetarios para que sean eficientes en lo que respecta al combustible.

Viajar en tubo.

Es una idea sacada directamente de la ciencia ficción. En La estrella de Pandora de 2004, Peter Hamilton describe un futuro donde la gente viaja a los planetas rodeando estrellas distantes en tren, donde las vías del tren van a través de un agujero de gusano, un atajo a través del espacio-tiempo. En sus series de El hombre lente de 1934 a 1948, Edward Elmer «Doc» Smith se inventaba un metro hiperespacial, el cual alienígenas malvados usaban para invadir mundos humanos desde la cuarta dimensión.

Aunque todavía no tenemos agujeros de gusano o alienígenas de la cuarta dimensión, se ha descubierto que los planetas y satélites del Sistema Solar están conectados unos a otros por una red de túneles, cuya definición matemática requiere muchas más dimensiones que cuatro. Los tubos proporcionan rutas que son energético-eficientes de un mundo a otro. Solo pueden verse a través de ojos matemáticos, porque no están hechos de materia, sus paredes son niveles de energía. Si pudiésemos visualizar el paisaje siempre cambiante de los campos de gravitación que controlan cómo los planetas se mueven, seríamos capaces de ver los tubos, haciendo remolinos, junto con los planetas a medida que se mueven en su órbita alrededor del Sol.

Los tubos explican algunas dinámicas orbitales misteriosas. Considera, por ejemplo, el cometa llamado Oterma. Hace un siglo, la órbita de Oterma estaba fuera de la de Júpiter. Pero después de un encuentro cercano con el planeta gigante, la órbita del cometa se cambió a la de Júpiter. Después de otro encuentro cercano, se volvió a salir. Podemos predecir con seguridad que Oterma continuará cambiando su órbita de este modo cada pocas décadas, no porque rompa la ley de Newton, sino porque la obedece.

Esto no tiene nada que ver con elipses ordenadas. Las órbitas que predecía la gravedad newtoniana son elípticas solo cuando no hay otros cuerpos que ejerzan una atracción gravitacional significativa. Pero el Sistema Solar está lleno de otros cuerpos y pueden suponer una diferencia enorme, y sorprendente. Es aquí cuando los tubos entran en la historia. La órbita de Oterma está dentro de dos tubos, los cuales se cruzan cerca de Júpiter. Un tubo está ubicado dentro de la órbita de Júpiter y el otro fuera. Encierran órbitas especiales en resonancia 3:2 y 2:3 con Júpiter, esto quiere decir que un cuerpo con dicha órbita girará alrededor del Sol tres veces por cada dos revoluciones de Júpiter, o dos veces por cada tres. En la confluencia de tubos cerca de Júpiter, el cometa puede cambiarse de tubo, o no, dependiendo de efectos bastante sutiles de la gravedad joviana y solar. Pero una vez dentro del tubo, Oterma se queda ahí hasta que el tubo vuelve al punto de cruce. Como un tren que tiene que quedarse en la vía, pero puede cambiar de ruta a otra vía si alguien cambia los puntos, Oterma tiene alguna libertad de cambio de su itinerario, pero no mucha (figura 15).

FIGURA 15. A la izquierda: dos órbitas periódicas en resonancia 2:3 y 3:2 con Júpiter, conectadas por puntos de Lagrange. A la derecha: órbita real del cometa Oterma, 1910-1980.

Los tubos y sus confluencias podrían parecer extraños, pero son características naturales e importantes de la geografía gravitacional del Sistema Solar. Los constructores de las vías de tren de la época victoriana entendieron la necesidad de explotar características naturales del terreno, llevando las vías del tren por valles y a lo largo de curvas de nivel, y excavando túneles a través de colinas en vez de llevar el tren sobre la cima. Una razón era que los trenes tienden a resbalar en pendientes pronunciadas, pero la principal era la energía. Subir una colina, en contra de la fuerza de la gravedad, cuesta energía, la cual se manifiesta como un incremento del consumo de combustible, lo cual cuesta dinero.

Es muy parecido a los viajes interplanetarios. Imagina una nave moviéndose por el espacio. Su siguiente destino no depende solamente de donde está ahora, también depende de lo rápido que se mueva y en qué dirección. Se necesitan tres números para especificar la posición de la nave espacial, por ejemplo, su dirección desde la Tierra, la cual requiere dos números (los astrónomos usan ascensión recta y declinación, que son las análogas a la longitud y la latitud para la esfera celestial, la supuesta esfera formada por el cielo nocturno) y su distancia desde la Tierra. Se necesitan más de tres números para especificar su velocidad en estas tres direcciones. De modo que la nave viaja a través de un terreno matemático que tiene seis dimensiones en lugar de dos.

Un terreno natural no es llano, tiene colinas y valles. Se necesita energía para escalar una colina, pero un tren puede ganar energía deslizándose cuesta abajo hacia un valle. De hecho, entran en juego dos tipos de energía. La altura sobre el nivel del mar determina la energía potencial del tren, la cual representa el trabajo hecho contra la fuerza de gravedad. Cuanto más alto vaya, mayor será la energía potencial que se debe crear. El segundo tipo es la energía cinética, la cual se corresponde con la celeridad. Cuanto más rápido vaya, mayor se hace la energía cinética. Cuando el tren está bajando la colina y acelera, intercambia energía potencial por energía cinética. Cuando sube una colina y baja su velocidad, el intercambio es a la inversa. La energía total es constante, de modo que la trayectoria del tren es análoga a una curva de nivel en la superficie de energía potencial. Sin embargo, los trenes tienen una tercera fuente de energía: carbón, gasoil o electricidad. Gastando combustible, un tren puede subir una pendiente o acelerar, liberándose de su trayectoria natural que se mueve libremente. La energía total todavía no puede cambiar, pero todo lo demás es negociable.

Es muy parecido con la nave espacial. Los campos de gravitación combinados del Sol, los planetas y otros cuerpos del Sistema Solar proporcionan energía potencial. La velocidad de la nave se corresponde con la energía cinética. Y su fuerza motriz, ya sea propergol, iones o presión luminosa, añade una fuente de energía extra, la cual puede apagarse o encenderse según se quiera. La ruta seguida por la nave espacial es un tipo de curva de nivel en la superficie de energía potencial correspondiente y a lo largo de esa ruta la energía total permanece constante. Y algunos tipos de curvas de nivel están rodeadas por tubos, que se corresponden con sus niveles de energía cercanos.

Los ingenieros de trenes victorianos eran también conscientes de que la superficie terrestre tenía características especiales: picos, valles, puertos de montaña; los cuales tiene un gran efecto en rutas eficientes para las vías del tren, porque constituyen un tipo de esqueleto para la geometría global de las curvas de nivel. Por ejemplo, cerca de un pico o en el fondo de un valle, las curvas de nivel están muy cerca unas de otras. En los picos la energía potencial está localmente en un máximo, en un valle, está en un mínimo local. Los puertos combinan características de ambos, siendo un máximo en una dirección, pero un mínimo en otra. De manera similar, las superficies de energía potencial del Sistema Solar tienen características especiales. Las más obvias son los propios planetas y lunas, que se encuentran en el fondo de los pozos gravitacionales, como los valles. Igualmente importantes, pero menos visibles, son los picos y los puertos de las superficies de energía potencial. Todas estas características organizan la geometría global y, con ello, los tubos.

Las superficies de energía potencial tienen otras características atractivas para los turistas, en particular, los puntos de Lagrange. Imagina un sistema formado solo por la Tierra y la Luna. En 1772 Joseph-Louis Lagrange descubrió que en cualquier instante hay precisamente cinco lugares donde los campos gravitacionales de dos cuerpos, junto con la fuerza centrífuga, se anulan totalmente. Tres están alineados con la Tierra y la Luna: L1 está entre ellos, L2 está en la cara más alejada de la Luna y L3 está en la cara alejada de la Tierra. El matemático suizo Leonhard Euler ya había descubierto esto alrededor de 1750. Pero también estaban L4 y L5, conocidos como puntos troyanos, los cuales están en la misma órbita que la Luna pero 60 grados por delante o por detrás de ella. A medida que la Luna rota alrededor de la Tierra, los puntos de Lagrange rotan con ella. Otros pares de cuerpos también tienen puntos de Lagrange: Tierra/Sol, Júpiter/Sol, Titán/Saturno.

La antigua transferencia de órbita de Hohmann está construida a partir de piezas de círculos y elipses, que son las trayectorias naturales para sistemas de dos cuerpos. La nuevas rutas basadas en tubos están construidas a partir de piezas de las trayectorias naturales de los sistemas de tres cuerpos, tales como Sol/Tierra/nave espacial. Los puntos de Lagrange juegan un papel especial, justo como los picos y los puertos lo hacían para las vías del tren, son los cruces donde los tubos se encuentran. L1 es un gran lugar para hacer pequeños cambios de recorrido, porque la dinámica natural de la nave espacial cerca de L1 es caótica (figura 16). El caos tiene una característica útil (véase el capítulo 16): cambios muy pequeños en la posición o velocidad pueden crean grandes cambios en la trayectoria. De modo que es fácil redireccionar a la nave en una manera combustible-eficiente, aunque posiblemente lenta.

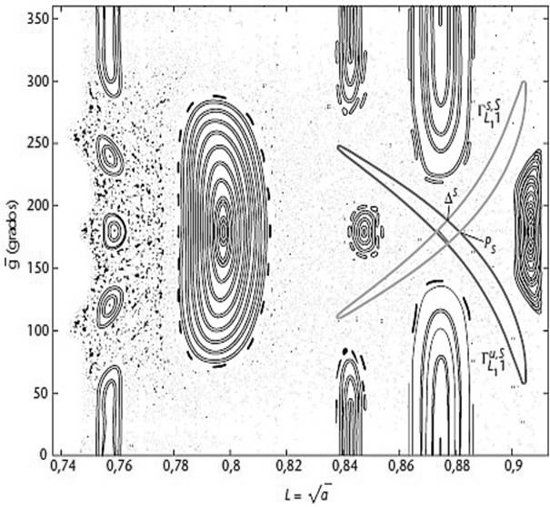
FIGURA 16. Caos cerca de Júpiter. El diagrama muestra una sección de órbitas. Los bucles anidados son órbitas cuasiperiódicas y la restante región punteada es una órbita caótica. Los dos bucles finos que se cruzan en la derecha son secciones de tubos.

La primera persona que se tomó esta idea en serio fue el matemático nacido en Alemania Edward Belbruno, un analista de órbitas en el Jet Propulsion Laboratory (Laboratorio de propulsión a chorro) desde 1985 hasta 1990. Se dio cuenta de que las dinámicas caóticas en sistemas de muchos cuerpos proporcionan una oportunidad para órbitas de transferencia de baja energía novedosas, llamando a la teoría técnica de límites borrosos. En 1991, puso sus ideas en práctica. Hiten, una sonda espacial japonesa, había estado inspeccionando la Luna y había completado la misión planeada, volviendo a la órbita de la Tierra. Belbruno diseñó una nueva órbita que la llevaría de vuelta a la Luna a pesar de estar quedándose sin combustible. Después de aproximarse a la Luna como se pretendía, Hiten visitó sus puntos L4 y L5 para buscar polvo cósmico que quizá se había quedado atrapado ahí.

Un truco similar se usó en 1985 para redireccionar la casi muerta International Sun-Earth Explorer ISEE-3 para encontrarse con el cometa Giacobini-Zinner, y fue usado de nuevo por la misión Génesis de la NASA para traer muestras de viento solar. Los matemáticos e ingenieros querían repetir el truco, y encontrar otros del mismo tipo, lo que significa averiguar qué es lo que realmente lo hace funcionar. Resultó que eran tubos.

La idea subyacente es simple pero inteligente. Esos lugares especiales en las superficies de energía potencial que recuerdan a los puertos de montaña crean cuellos de botella que aspirantes a viajeros no pueden evitar fácilmente. En la Antigüedad descubrieron, a fuerza de palos, que incluso aunque consuma energía subir un puerto, consume más energía seguir cualquier otra ruta, a menos que puedas rodear la montaña en una dirección totalmente diferente. El puerto es la mejor de las opciones.

En las superficies de energía potencial, los análogos a los puertos incluyen puntos de Lagrange. Asociadas a ellos hay rutas entrantes muy específicas, que son el modo más eficiente de subir el puerto. Hay también rutas salientes igualmente específicas, análogas a las rutas naturales de bajada del puerto. Para seguir estas rutas de entrada y salida exactamente, tienes que viajar justo a la velocidad correcta, aunque si tu velocidad es ligeramente diferente puedes todavía permanecer cerca de estas rutas. A finales de la década de los sesenta del siglo XX, los matemáticos americanos Charles Conley y Richard McGehee pusieron en práctica el trabajo pionero de Belbruno, señalando que cada una de dichas rutas está rodeada por un conjunto anidado de tubos, uno dentro de otro. Cada tubo se corresponde con una elección concreta de velocidad; cuanto más lejos está de la velocidad óptima, más ancho es el tubo. En la superficie de un tubo dado cualquiera, la energía total es constante, pero las constantes difieren de un tubo a otro. Algo así como una curva de nivel que está a una altura constante pero la altura es diferente para cada curva de nivel.

Entonces, el modo de planear un perfil eficiente de la misión es calcular qué tubos son relevantes para el destino elegido. Luego haces la ruta para la nave a lo largo del interior del primer tubo entrante y cuando llega al punto de Lagrange asociado provocas un rápido arranque en los motores para redirigirlo a lo largo del tubo saliente más apropiado (figura 17). Ese tubo fluye de modo natural al correspondiente tubo entrante del siguiente punto de cambio… y allá va.

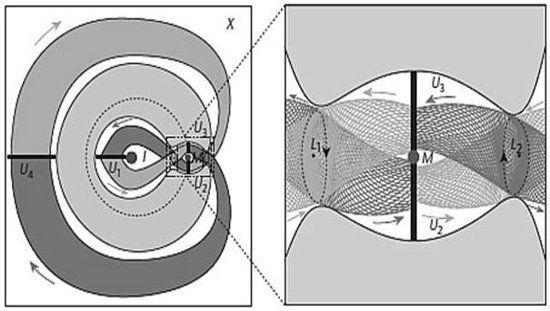
FIGURA 17. A la izquierda: tubos cruzándose cerca de Júpiter. A la derecha: primer plano de la región donde los tubos se cruzan.

Planos para futuras misiones tubulares ya se están preparando. En el año 2000 Wang Sang Koon, Martin Lo, Jerrold Marsfen y Shane Ross usaron la técnica de los tubos para encontrar un «Petit Grand Tour» de las lunas de Júpiter, acabando con una órbita de captura alrededor de Europa, la cual había sido muy escurridiza con métodos anteriores. La ruta supone un empuje gravitacional cerca de Ganímedes seguido por un viaje en tubo a Europa. Una ruta más compleja, que requiere incluso menos energía, incluye también a Calisto. Hace uso de otra característica de la superficie de energía potencial: resonancias. Estas se dan cuando, por ejemplo, dos satélites repetidamente vuelven a las mismas posiciones relativas, pero uno da dos vueltas a Júpiter mientras que el otro da tres vueltas. Cualquier número pequeño puede remplazar a 2 y 3. Esta ruta usa dinámica de cinco cuerpos: Júpiter, las tres lunas y la nave espacial.

En 2005, Michael Dellnitz, Oliver Junge, Marcus Post y Bianca Thiere usaron tubos para planear una misión energético-eficiente de la Tierra a Venus. El principal tubo aquí une el punto L1 del sistema Tierra/Sol con el punto L2 del sistema Sol/Venus. En comparación, esta ruta usa solo un tercio del combustible necesario por la misión Venus Express de la Agencia Espacial Europea, porque puede usar motores de bajo empuje; el precio pagado es una prolongación del tiempo de tránsito de 150 días a alrededor de 650 días.

La influencia de los tubos quizá vaya más lejos. En un trabajo no publicado, Dellnitz ha descubierto pruebas de un sistema natural de tubos que conectan Júpiter a cada uno de los planetas interiores. Esta estructura notable, ahora llamada la Superautopista interplanetaria, insinúa que Júpiter, durante mucho tiempo conocido por ser el planeta dominante del Sistema Solar, también desempeña el papel de una gran estación central celestial. Sus tubos podrían haber organizado la formación de todo el Sistema Solar, determinando los espacios de los planetas interiores.

¿Por qué los tubos no se descubrieron antes? Hasta hace muy poco, se carecía de dos cosas vitales. Una era ordenadores potentes, capaces de llevar a cabo los cálculos necesarios para muchos cuerpos. Son demasiado engorrosos para hacerlos a mano. La otra, incluso más importante, era un entendimiento matemático profundo de la geografía de una superficie de energía potencial. Sin este triunfo imaginativo de los métodos matemáticos modernos, los ordenadores no tendrían nada que calcular. Y sin la ley de gravitación universal, los métodos matemáticos nunca se habrían concebido.