Los números se originaron en problemas prácticos: registro de la propiedad, como animales o tierras; y transacciones financieras, como impuestos y llevar las cuentas. La primera notación numérica conocida, aparte de las marcas simples de contar como IIII, se encuentra en el exterior de envolturas de arcilla. En el 8000 a. C., los contables de Mesopotamia llevaban los registros usando pequeñas piezas de formas diversas. El arqueólogo Denise Schmandt-Besserat se dio cuenta de que cada forma representaba un producto básico: una esfera para el grano, un huevo para una tinaja de aceite, etcétera. Por seguridad, las piezas se encerraban en envoltorios de arcilla. Pero era molesto romper la envoltura de arcilla para abrirla y averiguar cuántas piezas había dentro, de modo que los contables de la época grababan los símbolos en el exterior para indicar lo que había dentro. Finalmente se dieron cuenta de que una vez que tenían estos símbolos, podían deshacerse de las piezas. El resultado fue una serie de símbolos escritos para los números, el origen de todos los símbolos numéricos posteriores y quizá, también, de la escritura.

Junto con los números llegó la aritmética: métodos para sumar, restar, multiplicar y dividir números. Instrumentos como el ábaco se usaban para hacer las sumas, luego los resultados se podían registrar con los símbolos. Con el tiempo, se encontraron formas de usar los símbolos para realizar los cálculos sin asistencia mecánica, y aunque el ábaco todavía se usa en muchas partes del mundo, las calculadoras electrónicas han suplantado los cálculos con lápiz y papel en la mayoría de los países.

La aritmética también resultó ser esencial en otros aspectos, especialmente en astronomía y topografía. Mientras los perfiles básicos de las ciencias físicas empezaban a emerger, los científicos novatos necesitaban realizar cálculos cada vez más elaborados manualmente. Con frecuencia esto consumía mucho de su tiempo, a veces meses o años, lo que se interponía en el camino de actividades más creativas. Finalmente se hizo esencial acelerar el proceso. Se inventaron innumerables instrumentos mecánicos, pero el avance más importante fue uno conceptual: pensar primero, calcular después. Usando las matemáticas de modo inteligente, se podían hacer cálculos difíciles mucho más fáciles.

Las nuevas matemáticas pronto desarrollaron una vida por sí mismas, resultando tener profundas implicaciones teóricas además de las prácticas. Hoy en día, esas ideas tempranas se han convertido en una herramienta indispensable para toda la ciencia, alcanzando incluso la psicología y las humanidades. Se usaban extensamente hasta la década de los ochenta del siglo pasado, cuando los ordenadores las volvieron obsoletas para propósitos prácticos, pero, a pesar de eso, su importancia en las matemáticas y la ciencia ha continuado creciendo.

La idea central es una técnica matemática llamada logaritmo. Su inventor fue un terrateniente escocés, pero fue un profesor de geometría con un gran interés en navegación y astronomía quien remplazó la idea brillante pero defectuosa del terrateniente por una mucho mejor.

En marzo de 1615, Henry Briggs escribió una carta a James Ussher, en la que se registra un suceso crucial en la historia de la ciencia:

Napper, Lord de Markinston, ha puesto mi mente y manos a trabajar con sus nuevos y admirables logaritmos. Espero verlo este verano, si Dios lo permite, porque yo jamás vi un libro que me agradase e hiciese pensar más.

Briggs era el primer catedrático de geometría del Gresham College en Londres, y «Napper, Lord de Markinston» era John Napier, octavo terrateniente de Merchiston, ahora parte de la ciudad de Edimburgo, en Escocia. Napier parece haber sido un poco místico, tenía intereses teológicos fuertes, pero la mayoría se centraban en el Apocalipsis. Desde su punto de vista, su obra más importante era Descubrimientos de todos los secretos del Apocalipsis de San Juan, la cual le llevó a predecir que el mundo se acabaría o en 1688 o en 1700. Se creía que se había dedicado tanto a la alquimia como a la nigromancia, y sus intereses en las ciencias ocultas le crearon una reputación como mago. Según los rumores, llevaba consigo a todas partes una araña negra en una caja y poseía un «espíritu familiar» o compañía mágica: un gallito negro. Según uno de sus descendientes, Mark Napier, John empleaba a su espíritu familiar para pillar a los sirvientes que estaban robando. Encerraba al sospechoso en una habitación con el gallito y le mandaba acariciarlo, diciéndole que su pájaro mágico detectaría, de modo infalible, su culpa. Pero el misticismo de Napier tenía un corazón racional, el cual, en este ejemplo en particular, suponía cubrir al gallo con una fina capa de hollín. Un sirviente inocente tendría la confianza suficiente para acariciar al pájaro tal y como le había indicado, y se quedaría con hollín en sus manos. Uno culpable, temeroso por que se lo pillase, evitaría acariciar al pájaro. Así, irónicamente, las manos limpias probaban que se era culpable.

Napier dedicó mucho de su tiempo a las matemáticas, especialmente a métodos para acelerar los complicados cálculos aritméticos. Una invención, el ábaco neperiano, era un conjunto de diez varillas, marcadas con números, las cuales simplificaban el proceso para una multiplicación larga. La invención que creó su reputación y generó una revolución científica fue todavía mejor; no fue su libro del Apocalipsis, como él habría esperado, sino que fue su Mirifici Logarithmorum Canonis Descriptio (Descripción del maravilloso canon de logaritmos) de 1614. El prefacio muestra que Napier sabía exactamente lo que él había aportado y para qué era bueno:^[6]

Puesto que nada es más aburrido, compañeros matemáticos, en la práctica de las artes matemáticas, que el gran retraso sufrido en el tedio de las multiplicaciones y divisiones largas y pesadas, el hallazgo de proporciones y en la extracción de raíces cuadradas y cúbicas, y… los muchos errores escurridizos que pueden surgir; yo he estado dándole vueltas a mi cabeza de cómo podría ser capaz de solventar las dificultades mencionadas para que sea un arte segura y rápida. Al final, después de pensar mucho, finalmente he encontrado un modo asombroso de acortar los procedimientos… es una tarea agradable exponer el método para el uso público de los matemáticos.

En el momento en que Briggs oyó hablar de los logaritmos se quedó encantado. Como muchos matemáticos de su época, pasaba mucho tiempo realizando cálculos astronómicos. Sabemos esto porque otra carta de Briggs a Ussher, que data de 1610, menciona los cálculos de eclipses y porque Briggs había publicado con anterioridad dos libros de tablas numéricas, uno relacionado con el Polo Norte y otro para la navegación. Todos estos trabajos habían requerido vastas cantidades de aritmética y trigonometría complicada. La invención de Napier ahorraría una gran cantidad de labor tediosa. Pero cuanto más estudiaba Briggs el libro, más convencido estaba de que, aunque la estrategia de Napier era maravillosa, sus tácticas estaban equivocadas. Briggs dio con una mejora simple pero efectiva, e hizo el largo viaje a Escocia. Cuando se encontraron, «casi un cuarto de hora se pasó cada uno contemplando con admiración al otro, antes de que una palabra fuese dicha».^[7]

¿Qué era eso tan emocionante que despertaba tanta admiración? La observación vital, obvio para cualquiera que aprendiera aritmética, era que la suma de números es relativamente fácil, pero multiplicarlos no lo es. La multiplicación requiere muchas más operaciones aritméticas que una suma. Por ejemplo, sumar dos números con una longitud de diez dígitos supone diez pasos simples, pero la multiplicación necesita 200. Con los ordenadores actuales este tema es todavía importante, aunque está escondido tras los algoritmos usados para la multiplicación.

Pero en la época de Napier, todavía tenía que hacerse a mano. ¿No sería fantástico si hubiese algún truco matemático que convirtiese las molestas multiplicaciones en sumas rápidas y agradables? Suena demasiado bien para ser cierto, pero Napier se dio cuenta de que era posible. El truco era trabajar con potencias de un número fijo.

En álgebra, las potencias de un x desconocido se indican con un número pequeño puesto algo más alto. Es decir, xx = x², xxx = x³, xxxx = x⁴, etcétera, donde, como es habitual en álgebra, una letra puesta junto a otra indica que se están multiplicando. De modo que, por ejemplo, 10⁴ = 10 × 10 × 10 × 10 = 10.000. No necesitas juguetear con estas expresiones durante mucho rato antes de descubrir un modo fácil de resolver, digamos, 10⁴ × 10³. Tan solo escríbelo:

El número de ceros en la respuesta es 7, que es igual a 4 + 3. El primer paso del cálculo muestra por qué es 4 + 3, ponemos cuatro 10 y tres 10 seguidos. En resumen:

10⁴ × 10³ = 10^{4 + 3} = 10⁷

Del mismo modo, cualquiera que sea el valor de x, si multiplicamos su a-ésima potencia por su b-ésima potencia, siendo a y b números enteros, entonces obtenemos su (a + b)-ésima potencia:

x^a x^b = x^{a + b}

Esta podría parecer una fórmula inocua, pero en la parte izquierda multiplicamos dos cantidades, mientras que en la derecha el paso principal es sumar a y b, lo cual es mucho más simple.

Supongamos que queremos multiplicar, por ejemplo, 2,67 y 3,51. Haciendo una multiplicación, que es larga, se obtiene 9,3717, que redondeando a dos cifras decimales es 9,37. ¿Qué pasa si intentamos usar la fórmula anterior? El truco recae en la elección de x. Si consideramos x como 1,001, entonces un poco de aritmética revela que (con el redondeo a dos decimales):

Entonces, la fórmula nos dice que 2,87 × 3,41 es:

1,001^{983 + 1.256} = 1,001^2.239

que, redondeando a dos decimales, es 9,37.

El núcleo del cálculo es una suma fácil: 983 + 1.256 = 2.239. Sin embargo, si tratas de comprobar mi aritmética te darás cuenta rápidamente de que si he hecho algo, lo que he hecho ha sido el problema más difícil, no más fácil. Para resolver 1,001⁹⁸³ tienes que multiplicar 1,001 por sí mismo 983 veces. Y para descubrir que la potencia que hay que usar es 983, tienes que llevar a cabo más trabajo. Así que a primera vista esto parece una idea bastante poco útil.

Pero la gran perspicacia de Napier fue considerar esta objeción como errónea. Para vencerla, algún alma resistente tiene que calcular un montón de potencias de 1,001, empezando en 1,001² y siguiendo hasta por ejemplo 1,001^10.000. Entonces se puede publicar una tabla con estas potencias. Después de eso, la mayoría del trabajo está hecho. Tan solo tienes que arrastrar tu dedo a través de las potencias sucesivas hasta que veas 2,67 seguido de 983, y de manera similar localizas 3,51 al lado de 1.256. Entonces sumas estos dos números para obtener 2.239. La fila correspondiente de la tabla te dice que esta potencia de 1,001 es 9,37. Trabajo hecho.

Resultados muy precisos necesitan potencias de algo mucho más próximo a 1, algo como 1,000001. Esto hace la tabla mucho más grande, con más o menos un millón de potencias. Hacer los cálculos para esa tabla es una tarea enorme. Pero solo tiene que hacerse una vez. Si algún benefactor se autosacrifica y hace el esfuerzo, generaciones futuras se ahorrarán una cantidad gigantesca de aritmética.

En el contexto de este ejemplo, podemos decir que las potencias 983 y 1.256 son los logaritmos de los números que queremos multiplicar, 2,67 y 3,51. De modo similar, 2.239 es el logaritmo de su producto, 9,38. Escribimos log como la abreviatura, y lo que hemos hecho equivale a la ecuación:

log ab = log a + log b

que se cumple para cualesquiera números a y b. La elección algo arbitraria de 1,001 se llama la base. Si usamos una base diferente, los logaritmos que calculamos también son diferentes, pero para cualquiera que sea la base fijada, todo funciona del mismo modo.

Esto es lo que Napier debería haber hecho. Pero por razones que solo podemos adivinar, hizo algo ligeramente diferente. Briggs, que se acercó a la técnica desde una perspectiva fresca, descubrió dos modos de mejorar la idea de Napier.

Cuando Napier empezó a pensar en las potencias de números, a finales del siglo XVI, la idea de reducir la multiplicación a la suma circulaba ya entre los matemáticos. En Dinamarca, se usaba un método bastante más complicado conocido como «prostaféresis», basado en una fórmula con funciones trigonométricas.^[8] Napier, intrigado, fue lo suficiente listo para darse cuenta de que las potencias de un número fijo podían hacer el mismo trabajo de manera más simple. Las tablas necesarias no existían, pero eso se remedió fácilmente. Algunas almas patrióticas debían de llevar a cabo el trabajo. El propio Napier se presentó voluntario para la tarea, pero cometió un error estratégico. En vez de usar una base que fuese ligeramente mayor que 1, usó una base ligeramente menor que 1. En consecuencia la secuencia de potencias empezaba con números grandes, que sucesivamente se iban haciendo más pequeños. Esto hizo los cálculos un poco más toscos.

Briggs descubrió este problema, y vio cómo lidiar con él: usó una base ligeramente mayor que 1. También se dio cuenta de un error más sutil, y también lo abordó. Si el método de Napier se modificase para trabajar con potencias de algo como 1,0000000001, no habría relación directa entre los logaritmos de, por ejemplo, 12,3456 y 1,23456. De modo que no estaba totalmente claro cuándo la tabla podía acabarse. La fuente del problema era el valor del log 10, porque:

log 10x = log 10 + log x

Desafortunadamente log 10 no era fácil, con la base 1,0000000001 el logaritmo de 10 era 23.025.850.929. Briggs pensó que sería mucho mejor si la base se pudiese escoger para que log 10 = 1. Entonces log 10x = 1 + log x, de modo que cualquiera que fuese log 1,23456, solo se necesitase sumar 1 para obtener log 12,3456. En este caso, las tablas de logaritmos solo necesitarían ir de 1 a 10. Si se tenían números más grandes, bastaba añadir el número entero apropiado.

Para conseguir log 10 = 1, haces lo mismo que Napier, usando una base de 1,0000000001, pero entonces divides cada logaritmo por el curioso número de 23.025.850.929. La tabla resultante consiste en logaritmos de base 10, lo cual escribiré como log₁₀ x. Satisfacen:

log₁₀ xy = log₁₀ x + log₁₀ y

como antes, pero también:

log₁₀ 10x = log₁₀ x + 1

Dos años después de la muerte de Napier, Briggs empezó a trabajar en una tabla de logaritmos de base 10. En 1617 publicó Logarithmorum Chilias Prima (Logaritmos del primer millar), los logaritmos de enteros del 1 al 1.000 aproximados a 14 cifras decimales. En 1624, continuó con Arithmetic Logarithmica (Aritmética de logaritmos), una tabla de logaritmos de base 10 de números del 1 al 20.000 y del 90.000 al 100.000, con la misma precisión. Rápidamente otros siguieron el ejemplo de Briggs, rellenando el gran hueco y desarrollando tablas auxiliares, tales como logaritmos de funciones trigonométricas como log sen x.

Las mismas ideas que inspiraron los logaritmos nos permiten definir las potencias x^a de una variable positiva x para valores de a que no son números enteros positivos. Todo lo que tenemos que hacer es insistir en que nuestras definiciones sean consistentes con la ecuación x^a x^b = x^{a + b}, y dejarse guiar por la intuición. Para evitar complicaciones molestas, es mejor asumir que x es positiva y definir x^a también como positivo. (Para x negativo, es mejor introducir números complejos, como se ve en el capítulo 5).

Por ejemplo, ¿qué quiere decir x⁰? Teniendo en mente que x¹ = x, la fórmula dice que x⁰ debe satisfacer x⁰ x = x^{0 + 1} = x. Dividiendo por x, tenemos que x⁰ = 1. ¿Qué pasa ahora con x⁻¹? Bien, la fórmula dice que x⁻¹ x = x^{−1 + 1} = x⁰ = 1. Dividiendo por x, tenemos que x⁻¹ = 1/x. De manera similar, x⁻² = 1/x², x⁻³ = 1/x³, etcétera.

Empieza a ponerse más interesante, y potencialmente muy útil, cuando pensamos en x^1/2. Esto tiene que satisfacer que x^1/2 x^1/2 = x^{1/2 + 1/2} = x¹ = x. De modo que x^1/2 multiplicado por sí mismo es x. El único número con esta propiedad es la raíz cuadrada de x. Así que x^1/2 = √x. De manera similar, x^1/3 = ³√x, la raíz cúbica. Si continuamos de este modo, podemos definir x^p/q para cualquier fracción p/q. Entonces, usando fracciones para aproximar números reales, podemos definir x^a para cualquier número real a. Y la ecuación x^a x^b = x^{a + b} todavía se cumple.

También se deduce que log √x = 1/2 log x y que log ∛x = 1/3 log x, así que podemos calcular raíces cuadradas y cúbicas fácilmente usando una tabla de logaritmos. Por ejemplo, para encontrar la raíz cuadrada de un número, consideramos el logaritmo del número y lo dividimos entre 2, y luego averiguamos qué número tiene ese resultado como su logaritmo. Para raíces cúbicas lo mismo pero dividimos entre 3. Los métodos tradicionales para estos problemas eran aburridos y complicados. Puedes ver por qué Napier saca a relucir raíces cuadradas y cúbicas en el prefacio de su libro.

Tan pronto como las tablas completas de logaritmos estuvieron disponibles, se hicieron indispensables para los científicos, ingenieros, topógrafos y navegantes. Se ahorraron tiempo, esfuerzo e incrementaron la probabilidad de que la respuesta fuese correcta. En un primer momento, la astronomía fue una beneficiaria importante, porque los astrónomos necesitaban de modo rutinario realizar cálculos largos y difíciles. El matemático y astrónomo francés Pierre Simon de Laplace dijo que la invención de logaritmos «reduce a unos pocos días la labor de muchos meses, dobla la vida del astrónomo y le ahorra errores y disgustos». A medida que el uso de la maquinaria en la industria crecía, los ingenieros empezaron a hacer más y más uso de las matemáticas: diseñar herramientas complejas, analizar la estabilidad de puentes y edificios, construir coches, camiones, barcos y aviones. Los logaritmos fueron una parte fuerte del currículum escolar de matemáticas hace unas pocas décadas. Y los ingenieros llevaban lo que en realidad era una calculadora analógica para logaritmos en sus bolsillos, una representación física de las ecuaciones básicas para logaritmos para su uso inmediato. Le llamaron una regla de cálculo, y la usaban rutinariamente en aplicaciones que iban desde la arquitectura hasta el diseño de aviones.

La primera regla de cálculo la construyó un matemático inglés, William Oughtred, en 1630, usando escalas circulares. Modificó el diseño en 1632, haciendo las dos reglas rectas. Esta fue la primera regla de cálculo. La idea es simple; cuando colocas dos varillas en fila, sus longitudes se suman. Si las varillas están marcadas usando una escala logarítmica, en la cual los números están separados según sus logaritmos, entonces los números correspondientes se multiplican. Por ejemplo, se coloca el 1 en una varilla frente al 2 de otra. Entonces, frente a cualquier número x de la primera varilla, tenemos 2x en la segunda. De modo que opuesto a 3 encontramos 6, etcétera (véase la figura 11). Si los números son más complicados, digamos que 2,67 y 3,51, colocamos 1 frente a 2,67 y leemos lo que haya enfrentando a 3,59, a saber, 9,37. Es así de fácil.

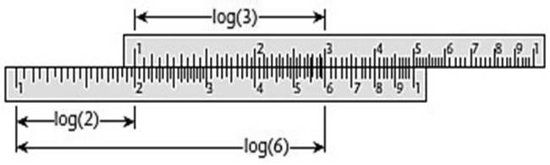
FIGURA 11. Multiplicación de 2 por 3 en una regla de cálculo.

Los ingenieros rápidamente desarrollaron reglas de cálculo elaboradas con funciones trigonométricas, raíces cuadradas, escalas log-log (logaritmos de logaritmos) para calcular potencias, etcétera. Finalmente los logaritmos se relegaron a un segundo término con los ordenadores digitales, pero incluso ahora los logaritmos todavía juegan un papel importante en la ciencia y la tecnología, junto con su inseparable compañera, la función exponencial. Para logaritmos de base 10, esta es la función 10^x; para logaritmos neperianos, la función e^x, donde e = 2,71828, aproximadamente. En cada par, las dos funciones son la inversa una de la otra. Si tomas un número, formas su logaritmo y luego haces el exponencial de ese, obtienes el número con el que empezaste.

¿Por qué necesitamos logaritmos ahora que tenemos ordenadores?

En 2011 un terremoto de magnitud 9.0 en la costa este de Japón causó un tsunami gigantesco, el cual destrozó una gran área poblada y mató alrededor de 25.000 personas. En la costa había una planta de energía nuclear, Fukushima Daiichi (Planta de energía nuclear número 1 de Fukushima, para distinguirla de una segunda situada cerca). Constaba de seis reactores nucleares separados: tres estaban operativos cuando el tsunami la alcanzó; los otros tres se habían detenido temporalmente y su combustible había sido transferido a piscinas de agua fuera de los reactores pero dentro de los edificios de los reactores.

El tsunami arrolló las defensas de la planta, cortando el suministro de la corriente eléctrica. Los tres reactores en uso (números 1, 2 y 3) se apagaron como medida de seguridad, pero sus sistemas de refrigeración todavía se necesitaban para impedir que el combustible se fundiese. No obstante, el tsunami también destrozó los generadores de emergencia, los cuales estaban destinados a alimentar el sistema de refrigeración y otros sistemas de seguridad críticos. El siguiente nivel de seguridad, las baterías, se quedó rápidamente sin energía. El sistema de refrigeración se paró y el combustible nuclear en varios reactores empezó a sobrecalentarse. Improvisando, los operadores usaron coches de bomberos para bombear agua del mar a los tres reactores operativos, pero esta reaccionó con el revestimiento de circonio en las varillas del combustible para producir hidrógeno. La acumulación de hidrógeno causó una explosión en el edificio que albergaba el reactor 1. Los reactores 2 y 3 pronto sufrieron la misma suerte. El agua en la piscina del reactor 4 se fue por el desagüe, dejando su combustible expuesto. Para cuando los operarios recobraron alguna apariencia de control, al menos un recipiente de contención del reactor se había fracturado y la radiación se estaba filtrando al entorno local. Las autoridades japonesas evacuaron a 200.000 personas del área de los alrededores porque la radiación estaba bastante por encima de los límites de seguridad normales. Seis meses más tarde, la compañía operaria de los reactores, TEPCO, afirmó que la situación permanecía siendo crítica y que se necesitaba mucho más trabajo antes de que se pudiese considerar que los reactores estaban totalmente bajo control, pero indicaba que la fuga había sido detenida.

No quiero analizar los méritos o no de la energía nuclear aquí, pero quiero mostrar cómo el logaritmo responde una pregunta vital: si sabes cuánto material radiactivo se ha liberado y de qué tipo, ¿cuánto tiempo permanecerá en un ambiente donde podría ser peligroso?

Los elementos radiactivos se descomponen, esto es, se convierten en otros elementos a través de procesos nucleares, emitiendo partículas nucleares mientras lo hacen. Son estas partículas las que constituyen la radiación. El nivel de radiactividad disminuye con el tiempo del mismo modo que la temperatura de un cuerpo caliente disminuye cuando se enfría: exponencialmente. Así, en las unidades apropiadas, las cuales no discutiremos aquí, el nivel de radiactividad N(t) con el tiempo t, cumple la ecuación:

N(t) = N₀e^−kt

Donde N₀ es el nivel inicial y k es una constante que depende del elemento que nos concierna. Más exactamente, depende de la forma, o isótopo, del elemento que estemos considerando.

Una medida conveniente del tiempo que perdura la radiactividad es el período de semidesintegración, un concepto que se introdujo por primera vez en 1907. Esto es el tiempo que tarda un nivel inicial N₀ en reducirse a la mitad de su tamaño. Para calcular el período de semidesintegración, solucionamos la ecuación:

1/2 N₀ = N₀e^−kt

Tomando logaritmos en ambas partes. El resultado es:

y podemos resolver esto porque de la experimentación sabemos el valor de k.

El período de semidesintegración es un modo práctico de calcular cuánto durará la radiación. Supongamos que el período de semidesintegración es, por ejemplo, una semana. Entonces la velocidad original a la cual el material emite la radiación es la mitad después de 1 semana, habrá bajado a un cuarto después de 2 semanas, un octavo tras 3 semanas, etcétera. Tarda 10 semanas en reducirse a una milésima de su nivel original (realmente 1/1024) y 20 semanas en bajar a una millónesima.

En accidentes con reactores nucleares convencionales, los productos radiactivos más importantes son yodo-131 (un isótopo radiactivo del yodo) y cesio-137 (un isótopo radiactivo del cesio). El primero puede causar cáncer de tiroides, porque la glándula tiroides concentra yodo. El período de semidesintegración del yodo-131 es solo 8 días, por lo tanto, causa daños pequeños si la medicación correcta está disponible, y sus peligros decrecen bastante rápidamente a menos que continue la fuga. El tratamiento estándar es dar a la gente pastillas de yodo, las cuales reducen la candidad de la forma radiactiva que es absorbida por el cuerpo, pero el remedio más efectivo es dejar de beber leche contaminada.

El cesio-137 es muy diferente, tiene un período de semidesintegración de 30 años. Tarda sobre 200 años en alcanzar un nivel de radiactividad que baje a una centésima el valor inicial, por lo que permanece como un peligro durante mucho tiempo. El principal asunto práctico en un accidente de un reactor es la contaminación del suelo y edificios. La descontaminación es hasta cierto punto factible, pero cara. Por ejemplo, el suelo puede quitarse, deshacerse, y almacenarse en un lugar seguro. Pero esto crea cantidades enormes de residuos radiactivos de baja actividad.

La descomposición radiactiva es tan solo una de las áreas de las muchas en las que los logaritmos de Napier y Briggs continúan sirviendo a la ciencia y a la humanidad. Si ojeas capítulos posteriores, los encontrarás en termodinámica y teoría de la información, por ejemplo. Aunque los rápidos ordenadores han hecho ahora los logaritmos redundantes para su propósito original, cálculos rápidos, siguen siendo fundamentales para la ciencia por razones más conceptuales que computacionales.

Otra aplicación de los logaritmos se da en los estudios de la percepción humana: cómo sentimos el mundo alrededor nuestro. Los primeros pioneros de la psicofísica de la percepción hicieron estudios exhaustivos de la vista, el oído y el tacto, y revelaron algunas regularidades matemáticas fascinantes.

En la década de los cuarenta del siglo XIX, un doctor alemán, Ernst Weber, llevó a cabo experimentos para determinar cómo de sensible es la percepción humana. Les daba a los sujetos pesos para soportar en sus manos y les preguntaba cuándo podían percibir que uno era más pesado que otro. Quizá sorprendentemente, esta diferencia (para un sujeto experimental dado) no fuese una cantidad fija. Dependía de cómo de pesados fuesen los pesos que se comparaban. La gente no percibía una diferencia mínima absoluta de, por ejemplo, 50 gramos. Lo que sentían era una diferencia mínima relativa, por ejemplo, un 1% de los pesos que se comparaban. Esto es, la diferencia más pequeña que el sentido humano puede detectar es proporcional a los estímulos, la cantidad física real.

A mediados del siglo XIX, Gustav Fechner redescubrió la misma ley y la reformuló matemáticamente. Esto le llevó a una ecuación, la cual llamó ley de Weber, pero en la actualidad normalmente se hace referencia a ella como la ley de Fechner (o la ley de Weber-Fechner si eres un purista). Afirma que la sensación percibida es proporcional al logaritmo de los estímulos. Los experimentos sugieren que esta ley se aplica no solo a nuestra sensación del peso, sino también a la visión y al oído. Si miramos una luz, el brillo que percibimos varía igual que el logaritmo de la potencia de energía real. Si una fuente es diez veces más brillante que otra, entonces la diferencia que percibimos es constante, comoquiera que realmente sea el brillo de las dos fuentes. Lo mismo aplica para el volumen de los sonidos: una explosión con diez veces más energía suena una cantidad fija más fuerte.

La ley de Weber-Fechner no es totalmente exacta, pero es una buena aproximación. La evolución más o menos tuvo que definirse con algo como una escala logarítmica, porque el mundo externo plantea a nuestros sentidos unos estímulos de una gran variedad de tamaños. Un ruido podría ser tan solo un ratón escabulléndose en un seto, o podría ser un trueno; necesitamos ser capaces de oír ambos. Pero el rango de niveles de sonido es tan vasto que ningún instrumento sensorial biológico puede responder en proporción a la energía generada por el sonido. Si una oreja pudiese oír al ratón escabullirse, entonces el trueno la destrozaría. Si sintoniza a la baja los niveles de sonido, de modo que el trueno produzca una señal confortable, entonces no sería capaz de oír al ratón. La solución es comprimir los niveles de energía a un rango cómodo y los logaritmos hacen exactamente eso. Siendo sensibles a proporciones más que a valores absolutos tiene un excelente sentido y da lugar a sentidos excelentes.

Nuestra unidad estándar de ruido, el decibelio, condensa la ley de Weber-Fechner en una definición. No mide el ruido absoluto, sino el ruido relativo. Un ratón en la hierba produce unos 10 decibelios. Una conversación normal entre personas a un metro de distancia tiene lugar a 40-60 decibelios. Una batidora dirige unos 60 decibelios a la persona que la está usando. El ruido en un coche, causado por el motor y los neumáticos, es 60-80 decibelios. Un avión reactor a una distancia de 100 metros produce 110-140 decibelios, que se incrementa a 150 al estar a treinta metros. Una vuvuzela (el molesto instrumento de plástico parecido a una trompeta que se escuchó mucho durante el Mundial de fútbol de 2010 y llevado a casa como recuerdo por fans insensatos) genera 120 decibelios a un metro; una granada detonadora militar produce hasta 180 decibelios.

Se encuentran escalas como esta sin problema porque tienen una vertiente relacionada con la seguridad. El nivel al cual el sonido puede potencialmente dañar el oído es de alrededor de 120 decibelios. Por favor, tira a la basura tu vuvuzela.