Exploración del tiempo[146]
1
Es un honor para mí la oportunidad de pronunciar esta conferencia, y habría deseado que fuera un tributo adecuado a la memoria de este gran científico, pero soy consciente de que no estaré a su altura. Aharon fue un hombre de múltiples talentos cuya inquietud científica abarcaba una amplia gama de saberes. Fue para todos nosotros maestro y amigo. Un rasgo innegable de su personalidad era su anhelo por elaborar una síntesis entre las ciencias físicas y humanísticas. La ciencia era para él parte integral del esfuerzo humano, y esto creo que explica su profundo interés por el concepto tiempo. La actividad humana, sea a nivel del sujeto cognitivo o al nivel de la sociedad, sólo puede entenderse en términos de evoluciones temporales, en términos de historia. Era su profunda convicción.
Es un hecho que, tres siglos después de Newton, la ciencia experimenta un cambio radical de perspectiva. Los grandes fundadores de la ciencia occidental hicieron hincapié en la universalidad y el carácter eterno de las leyes de la naturaleza. Formularon esquemas generales que coincidieran con la definición de racionalidad más absoluta. Como decía concisamente Isaiah Berlin, «buscaron esquemas globales, marcos unificadores universales en los que todo lo existente apareciera interrelacionado sistemáticamente, es decir, lógica o causalmente, en los que cupieran las vastas estructuras sin dejar fisura alguna por la que se introdujera lo espontáneo, los episodios inesperados; marcos en los que cualquier cosa que ocurriera fuera absolutamente explicable, al menos en principio, en términos de leyes generales inmutables». Actualmente estamos muy lejos de haber logrado estos propósitos. Nuestro interés se orienta cada vez más hacia sistemas complejos, hacia su dinámica y su evolución temporal.
Hoy en día, el concepto de evolución guarda claramente una estrecha relación con el concepto de irreversibilidad. Si el futuro fuera idéntico al pasado, no habría propiamente evolución. Esto fue en esencia el punto de vista que adoptó la física clásica. El universo se nos presenta como una especie de autómata; una vez dadas las condiciones iniciales, el futuro está determinado. En la imagen clásica del universo, el futuro está contenido en el pasado. Esto no sólo es cierto en la descriptiva clásica del mundo en términos de trayectorias, sino que continúa siendo un principio en mecánica cuántica. También en ella la ecuación de Schrödinger no establece distinción fundamental entre pasado y futuro, y el tiempo es un simple parámetro. Este conflicto entre universo estático y evolucionista queda bien ilustrado en la correspondencia de Einstein con su gran amigo de juventud en Zürich, Michele Besso.[147]
Creo que hoy en día la situación ha cambiado. El papel del tiempo, de la irreversibilidad, se perfila con mayor claridad que unos años atrás. No puedo hacer ahora un detallado resumen de la historia de este cambio de perspectiva, pero citaré al menos dos experimentos básicos que cobran enorme significación en este contexto.
2
Hablaré brevemente de dos experimentos que me vienen a la mente. El primero es el descubrimiento de un reloj químico obtenido a través de la reacción de Belousov-Zhabotinski.[148] El asombroso resultado de Zhabotinski se logró a finales de la década de los sesenta, y recuerdo muy vívidamente el entusiasmo con que Aharon y yo hablamos de su importancia. Actualmente, la descripción de estos relojes químicos figura en muchos textos y artículos de divulgación, por lo que limitaré mis explicaciones al mínimo.
Idealmente tenemos una reacción química, cuyo estado controlamos mediante la adecuada inyección de productos químicos y la eliminación de productos de desecho. Supongamos que dos de los componentes intermedios están formados por moléculas rojas y azules respectivamente en cantidades equivalentes. Lo lógico es que se produzca una mezcla confusa quizá con algún retazo de manchas rojas o azules. Sin embargo, no sucede así. En condiciones idóneas, vemos que todo el recipiente se torna sucesivamente rojo, azul y rojo otra vez. Esto es un reloj químico.
En cierto sentido, esto viola nuestro concepto sobre reacciones químicas. Estamos habituados a pensar que éstas son el resultado del movimiento desordenado de unas moléculas que colisionan al azar. Sin embargo, la existencia de un reloj químico demuestra que, en vez de ser caótico, el comportamiento de las especies intermedias es altamente coherente. En cierto sentido, estas moléculas tienen que ser capaces de «comunicarse» para sincronizar su cambio periódico de color. En otras palabras, nos encontramos ante nuevas escalas supramoleculares, tanto temporales como espaciales, producidas por su actividad química, lo que no deja de ser inesperado.
Parece ser que los experimentos de reacciones químicas periódicas se remontan posiblemente a un siglo atrás, pero fueron «suprimidos» porque parecían contravenir todas las teorías sobre la naturaleza de las reacciones químicas. Y, efectivamente, observamos en estos procesos la intervención de un elemento nuevo, y el ejemplo demuestra que los procesos de no equilibrio pueden ser origen de orden.
El segundo experimento básico a que quiero referirme es el descubrimiento de la radiación residual del cuerpo negro que tuvo lugar en 1965. Sabemos que el universo está lleno de fotones que corresponden a temperaturas de 3 °K.
Y lo extraordinario de este descubrimiento es que el tiempo interviene en la descripción de la materia. La tesis tradicional postulaba que el tiempo era fundamental para entender los sistemas vivos, incluidas las sociedades, pero la existencia de una historia de la materia a escala cósmica, que de una forma u otra ha hecho que prevalezca la materia sobre la antimateria, es una característica nueva y sorprendente. También este descubrimiento podría haber acaecido mucho antes; en realidad, ya en 1947 mis amigos Ralph Alpher y Robert Hermán predijeron la existencia de esta radiación, pero nadie estaba entonces en condiciones de realizar el experimento.[149]
No es sorprendente que hoy los procesos irreversibles constituyan el centro de interés de gran parte de la comunidad científica. Las ideas de no linealidad, inestabilidad y fluctuaciones, se difunden a un amplio campo del pensamiento científico y hasta social. El estudio de los procesos irreversibles se efectúa a nivel de la investigación en tres direcciones principales: 1) en la termodinámica fenomenológica que enuncia y estudia las ecuaciones macroscópicas, especialmente cuando nos situamos lejos de las condiciones de equilibrio; 2) a nivel de las fluctuaciones, en el que se estudia el desarrollo de pequeñas perturbaciones de origen interno o externo; y 3) al nivel «básico», en el que se intenta identificar los mecanismos microscópicos de la irreversibilidad. Éste es quizás el aspecto de mayor incentivo, ya que la irreversibilidad parece ser, en cierto modo, un límite a la validez de los conceptos básicos sobre los que se fundamentan la mecánica clásica y la cuántica. Cada uno de estos niveles nos ha dado sorpresas singulares, pero la historia aún no está conclusa y subsisten no pocas lagunas, aunque es muy posible que en años sucesivos se produzcan hallazgos inesperados.
3
Consideremos, en primer lugar, el nivel termodinámico. La característica nueva de mayor relieve es que, cuando nos apartamos mucho de las condiciones de no equilibrio, se originan nuevos estados en la materia. Llamo a estos casos «estructuras disipativas», porque presentan estructura y coherencia, y su mantenimiento implica una disipación de energía. Es curioso que los mismos procesos que, en situaciones próximas al equilibrio, causan la destrucción de estructuras, en situaciones lejanas al equilibrio generan la aparición de una estructura. Las estructuras disipativas generan transiciones de fase hacia el no equilibrio, algo parecido a las conocidas transiciones de fase hacia el equilibrio.
Concretando el problema, recordemos la segunda ley de la termodinámica. Como todos sabemos, la segunda ley se basa en la distinción entre procesos reversibles e irreversibles. En breve: los procesos irreversibles corresponden a evoluciones temporales en las que pasado y futuro desempeñan distinto papel, como sucede en la conducción térmica, la difusión y las reacciones químicas. La segunda ley postula la existencia de una entropía funcional S, cuya evolución temporal podemos dividir en dos fases: una, el flujo de entropía deS y la otra, la producción de entropía diS. De lo que obtenemos:
(3.1)dS = deS + diS
La característica importante es que la producción de entropía está determinada por los procesos irreversibles que se producen dentro del sistema. Es positiva cuando hay procesos irreversibles y desaparece en el equilibrio.
(3.1')diS ≥ 0
Gran parte de los trabajos modernos, llevados a cabo en termodinámica se basan en la simple expresión de la producción de entropía por unidad de tiempo.[150]
(3.2)
En ella, los Jρ son los flujos o índices de los procesos irreversibles, y las Xρ las fuerzas correspondientes, tales como gradiente de temperatura, gradiente de concentración y diferencia de potencial químico.
Ahora podemos distinguir tres fases en el desarrollo de la termodinámica. Primero, la fase de equilibrio en la que tanto fuerzas como flujos desaparecen. En esta escala se obtienen los habituales diagramas de fase que implican la transición de sólido a líquido, líquido a vapor y así sucesivamente. La interpretación de sus correspondientes estructuras no es nada equívoca, y podemos representarla convenientemente en términos de la bien conocida energía libre:
F = E - TS[151]
Las estructuras de equilibrio corresponden a la competitividad entre energía y entropía. A continuación, está el régimen de «cuasi» equilibrio en el que los flujos son proporcionales a las fuerzas. Es la región en la que son aplicables las famosas relaciones de reciprocidad de Onsager. Lo que caracteriza estas dos regiones es la estabilidad del equilibrio, o los estados estacionarios de no equilibrio; las pequeñas fluctuaciones siempre se desvanecen. Con ello, tenemos una descripción del mundo físico fundamentalmente homeostático. La nueva característica es que, en la situación alejada del equilibrio, o tercera región, ya no sucede lo mismo, y en ella las fluctuaciones se amplifican y finalmente modifican el patrón microscópico del sistema.
Hay dos conceptos fundamentales a considerar en las situaciones alejadas del equilibrio: la posibilidad de bifurcaciones y el papel de las fluctuaciones. En los últimos años se han dedicado innumerables trabajos al arquetipo reacción-difusión. Las ecuaciones diferenciales típicas que se han estudiado se ajustan a la forma siguiente:
(3.3)
En ella X es un conjunto de sustancias químicas y λ una serie de parámetros de control, algunos de los cuales pueden ser concentraciones impuestas de sustancias químicas, y jx es el flujo de difusión, que, en el caso más sencillo, puede considerarse igual al descrito en una difusión de Fick. Podemos escribir la ecuación en la forma condensada siguiente:
(3.4)
Esta ecuación admite soluciones estacionarias:
(3.5)F(XS, λ) = 0
El modo más sencillo de poner a prueba la estabilidad del estado estacionario es escribir:
(3.6)X = Xs + x
y buscar la evolución temporal de la «pequeña» perturbación x. Si el sistema es estable (más precisamente, asintóticamente estable), x tiende a cero. Esto es precisamente el caso en las situaciones de equilibrio y en las próximas a él. En condiciones alejadas del equilibrio, por el contrario, tendremos inestabilidad y la aparición de nuevos tipos de soluciones. En la fig. 1, se ilustra un típico diagrama de bifurcación.

FIG. 1. Diagrama de bifurcación típica (v. texto).
La solución «termodinámica» permanece estable hasta λc. Para valores mayores de λc, aparecen dos nuevas «ramas», (b1) y (b2), cada una de las cuales es estable, mientras que la extrapolación de la rama termodinámica (a’) es inestable. Los matemáticos han desarrollado métodos sofisticados para obtener soluciones de ramificación, con frecuencia en términos de expansiones potenciales de un pequeño parámetro como λ − λc. Pero dejemos esto. Lo que sí quiero subrayar son los dos puntos siguientes. Primero, que existe una gran variedad de bifurcaciones, algunas de las cuales conducen a múltiples estados, otras a relojes químicos, ondas químicas o estructuras disipativas, que rompen la simetría espacial. Por ejemplo, las dos ramas b1 y b2 de la fig. 1 corresponden a la distribución de la concentración X en un medio unidimensional (suponiendo condiciones en los límites de flujo cero), representado en la fig. 2. Vemos que se llega a una «estructura» izquierda o derecha. La opción entre ambas posibilidades conlleva un elemento básicamente aleatorio. Ninguna información adicional, sea cual fuere su precisión, nos sirve para predecir cuál de las dos bifurcaciones se originará, al menos mientras sigamos la rama termodinámica en la que progresivamente aumenta el valor de λ. La aparición de una de las ramas corresponde a un episodio singular que ulteriormente resulta amplificado por un comportamiento autocatalítico (muchas veces se ha hecho referencia a esta clase de mecanismo para explicar el predominio de una forma determinada de actividad óptica en los biopolímeros contemporáneos). Sin embargo, si repetimos el experimento, muy posiblemente se restablezca la simetría. Volveremos después al problema de la selección de patrón.
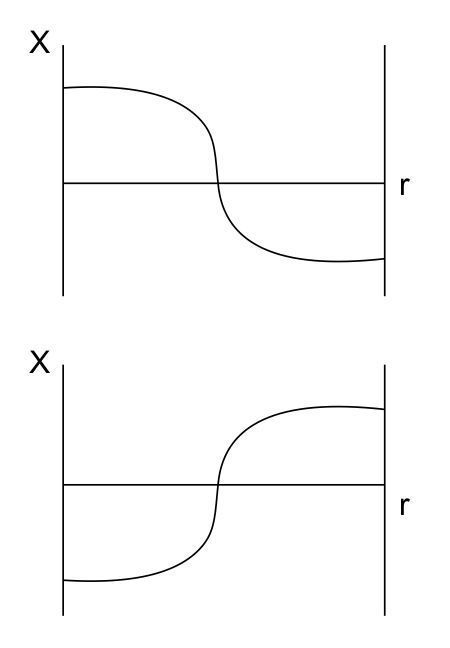
FIG. 2. Estructuras «izquierdas» o «derechas» correspondientes al diagrama de bifurcación de la fig. 1.
Pondremos de relieve que la aplicación de la teoría de la bifurcación a las reacciones químicas es poco habitual. Podría argüirse que, de cualquier modo, la difusión desvanecería las bifurcaciones provocando constantes transiciones. Es una perspectiva apasionante a la que me referiré brevemente más adelante.
Sigamos ahora con la descripción de las bifurcaciones.
La primera bifurcación introduce un parámetro simple o espacial que ya es susceptible de romper la simetría temporal o espacial del sistema. Pero no queda ahí todo: podemos observar bifurcaciones secundarias, o de orden más alto. En la fig. 3. se representan las bifurcaciones sucesivas que se inician en la ramificación termodinámica. No es difícil demostrar que todas las bifurcaciones sucesivas, salvo la primera, se originan en ramas inestables, pero pueden estabilizarse a una distancia suficiente de la rama termodinámica. Esto sucede, por ejemplo, en los sistemas cuya primera bifurcación corresponde a un reloj químico. La siguiente, corresponde a ondas químicas rotatorias. De nuevo, en una geometría simple, como la anular, podemos observar unas ondas químicas que siguen el movimiento de las agujas del reloj y otras en sentido contrario. Se han observado en la reacción de Zhabotinski. Al aumentar la distancia respecto al equilibrio, son posibles muchos tipos de comportamiento.

FIG. 3. Bifurcaciones primarias sucesivas (v. texto).
En la fig. 4, se ilustran algunos de ellos sobre un modelo de la reacción abierta de Belousov-Zhabotinski.[152] Contrastemos este comportamiento con la «tranquila» descripción de los diagramas de equilibrio. En este caso, por el contrario, pequeños cambios del mundo externo modifican radicalmente el comportamiento espacio-temporal del sistema. El orden, la coherencia, parecen ser un estado intermedio entre el caos molecular, que se observa en el equilibrio, y el caos microscópico obtenido en condiciones muy alejadas del equilibrio, en las que múltiples bifurcaciones contribuyen al comportamiento espacio-temporal.
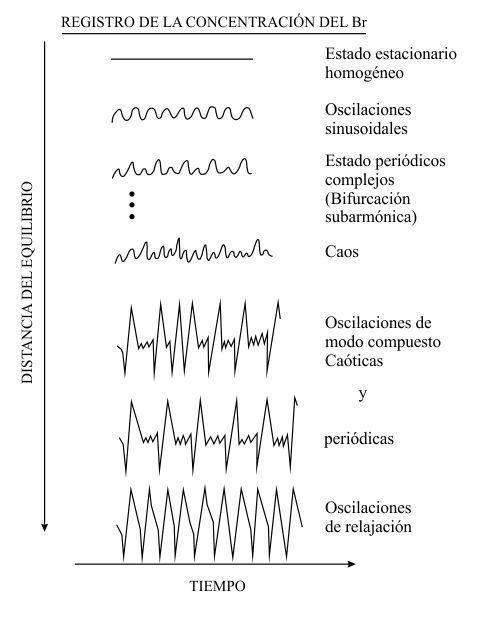
FIG. 4. Bifurcaciones sobre un modelo de la reacción abierta de Belousov-Zhabotinski.
La materia, en condiciones alejadas del equilibrio, adquiere básicamente nuevas propiedades: la posibilidad de comunicación en tiempos y distancias macroscópicos, ya mencionada, la posibilidad de «percibir» pequeños efectos que conducen a una selección de patrón y, finalmente, la posibilidad de memoria correspondiente también a una sucesión temporal de diversas bifurcaciones. Es interesante que estas clases de propiedades siempre se hayan atribuido en el pasado a sistemas «vivos», pero vemos que hasta cierto punto son atribuibles incluso a sistemas «no vivos». Pero, antes de proseguir con el tema de la bifurcación, juzgo de interés mencionar algunos sistemas biológicos simples en los que bifurcaciones y fluctuaciones desempeñan un papel esencial.
Entre los numerosos ejemplos que se han estudiado desde este punto de vista, citaremos en primer lugar la agregación de amebas acrasiales (Dictyostelium discoideum). Este proceso es un caso limítrofe interesante entre la biología unicelular y pluricelular. Cuando el medio en que viven y se reproducen se empobrece en nutrientes, las amebas experimentan una transformación espectacular, y de una población de células individuales pasan a formar una masa compuesta por varias decenas de millar. A continuación, este «pseudoplasmodio» experimenta una diferenciación y cambia de forma continuamente. Se forma un pedúnculo, constituido por un tercio aproximadamente de las células, que contiene celulosa en abundancia. Este pie aguanta una masa esférica de esporas que se separan y dispersan, multiplicándose en cuanto entran en contacto con un medio de alimentación, volviendo a formar una nueva colonia de amebas. Es un ejemplo muy espectacular de adaptación al medio, de nomadismo de una población que ocupa un nicho hasta que agota sus recursos, seguido de metamorfosis, gracias a la cual adquiere una movilidad que le permite invadir otro hábitat.
La investigación de la primera fase de la agregación nos revela que se inicia con la aparición en la población de amebas de ondas de desplazamiento, de un movimiento impulsor de convergencia de las amebas hacia un «centro de atracción», que parece espontáneo. Las investigaciones experimentales y la modelización han demostrado que esta migración es la respuesta de las células a la existencia en el medio de una concentración de gradiente en una sustancia clave, el AMP cíclico, producido periódicamente por el centro atractor y, más tarde, también por otras células merced a un mecanismo de conexión. Vemos aquí, de nuevo, el papel esencial que desempeñan los relojes químicos sobre las ondas químicas, ya que aportan, como hemos señalado, nuevos medios de comunicación. En el caso que nos ocupa, el mecanismo de autoorganización desemboca en la comunicación intercelular.
Hay otro aspecto que quiero poner de relieve. La agregación de las amebas es un ejemplo típico de lo que podemos denominar «orden por fluctuaciones»; la formación de un centro de atracción que segrega el AMP es indicativo del hecho de que el régimen metabólico correspondiente a un medio nutritivo normal se ha hecho inestable, es decir, del agotamiento del entorno alimenticio. El hecho de que, en estas condiciones de escasez de alimento, cualquier ameba sea la primera en emitir el AMP cíclico, convirtiéndose con ello en el centro de atracción, corresponde al comportamiento aleatorio de las fluctuaciones. Después, esta fluctuación se amplifica y organiza el medio.
Otro ejemplo que citaré, aunque a grandes rasgos, es el comportamiento constructivo de las termitas.[153] Un termitero se caracteriza por una complejidad y una escala muy distinta a la de una simple termita. Los termiteros pueden albergar millones de insectos. El comportamiento constructivo parece aportar un comportamiento coherente en el que el papel de las moléculas lo desempeñan las termitas. Hace años ya que Grassé presentó una teoría basada en su observación del comportamiento constructivo, a la que denominó theory of stigmergy.[154] Lo que observó fue la existencia de dos fases en dicho comportamiento. Primero, una fase de actividad descoordinada, durante la cual las obreras exploran el recipiente en que se hallan y, al cabo de cierto tiempo, empiezan a depositar piedrecitas. Cuando, en determinado lugar, el material depositado alcanza un valor crítico, actúa a modo de atractor y se produce una fase coordinada en la que los puntos en que se ha acumulado el material se convierten en columnas. Si hay dos columnas muy próximas, construyen un arco.
En cierto modo, la descripción de Grassé corresponde a la evolución de un estado inestable homogéneo hacia un estado no homogéneo. El mecanismo de atracción es la incorporación a las piedrecitas de sustancias químicas características, las feromonas. La teoría de Grassé se ha difundido mucho en los últimos años, fundamentalmente gracias a Brunsma, y se empieza a entender cómo se efectúa esta complicada actividad sin que exista un cerebro rector y con una información mínima a nivel del insecto como unidad.
Un ejemplo aún más sencillo, en el que puede seguirse admirablemente la formación de bifurcaciones, es el problema de la formación de las rutas que abren las hormigas. El experimento básico, realizado recientemente por Pasteels, junto con mi colega Deneuburg y otros, se representa esquemáticamente en la fig. 5.[155] La hormiga fue colocada a la izquierda y la fuente de alimentación a la derecha. Con dos agujeros dispuestos simétricamente, se posibilita la formación de dos rutas distintas. Cada hormiga que avanza por una ruta va dejando una señal química, una feromona de vida limitada. Si tenemos en cuenta la posibilidad de que se utilice una ruta u otra, en función del número de la población de hormigas, vemos que, curiosamente, se llega a un diagrama de bifurcación típica (fig. 6). Para poblaciones pequeñas, la probabilidad de que empleen una u otra ruta es equivalente; es la rama termodinámica. Si nos aproximamos al valor crítico, se producen amplias fluctuaciones y utilizan prevalentemente una ruta sobre otra. Más allá del valor crítico, eligen una sola, y el noventa por ciento de las hormigas, por ejemplo, utilizan esta ruta preferente. Tenemos en ello un excelente ejemplo biológico sobre la formación de una bifurcación mediante interacciones mediadas por una sustancia química específica. Pero volvamos a la teoría de las bifurcaciones y, en particular, a la cuestión de la selección de patrón.

FIG. 5. Experimento sobre la formación de rutas (v. texto).
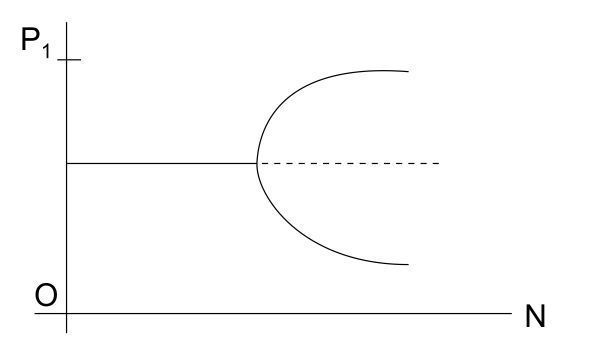
FIG. 6. Bifurcación correspondiente a la probabilidad de utilización de una sola ruta; en las ordenadas, probabilidad, en las abcisas, población de la colonia de hormigas.
4
Consideremos dos ejemplos característicos estudiados recientemente. Uno corresponde a la influencia de la gravitación en una selección de patrón, y el otro a la influencia de las ondas electromagnéticas.
La gravitación modifica evidentemente el flujo de difusión en la ecuación de reacción-difusión (3.3). Los cálculos detallados demuestran que este efecto puede ser muy espectacular próximo a un punto de bifurcación del sistema no perturbado. Vamos a considerar de nuevo un sistema unidimensional con condiciones limítrofes de flujo cero, y supongamos que tenemos un diagrama de bifurcaciones como el representado en la fig. 1. Se supone que, en estado exento de gravitación, g = 0, tenemos, como en la fig. 1. un patrón simétrico «arriba/abajo», así como su imagen especular «abajo/arriba». Ambos son igualmente probables, pero, para g = 0, las ecuaciones de bifurcación se modifican porque el flujo de difusión contiene un término proporcional a g. Como consecuencia, se obtiene un nuevo diagrama de bifurcaciones representado en la fig. 7. En él, la rama bifurcadora superior correspondiente, por ejemplo, al patrón «arriba/abajo» es la preferida. Por lo tanto, podemos afirmar que existe un medio para seleccionar formas «arriba» y «abajo».
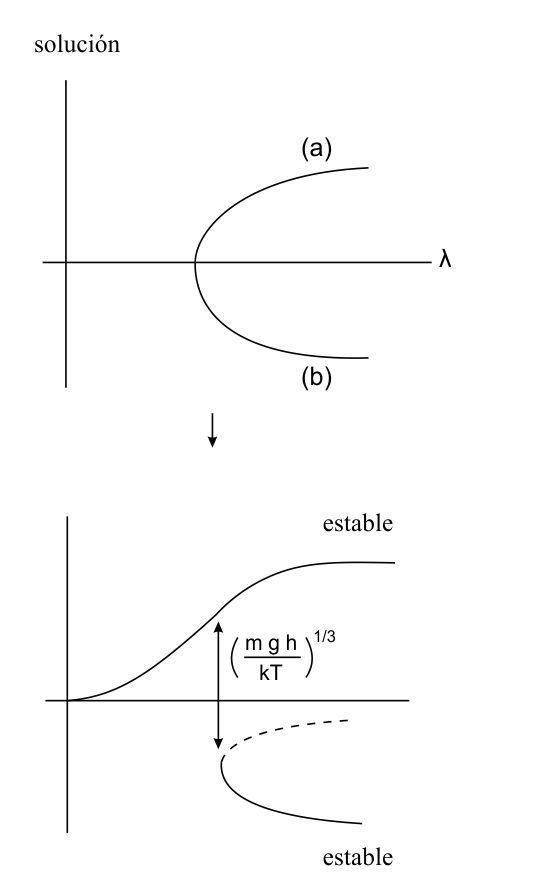
FIG. 7. Influencia de la gravitación en la bifurcación (v. texto).
En realidad, lo interesante es que incluso campos gravitatorios muy pequeños pueden provocar la selección de patrón. En ejemplos simples, el parámetro dimensional característico es:
en lugar del parámetro de equilibrio
Como esta razón suele ser muy pequeña, la adopción de la raíz 1/3 amplifica enormemente el efecto. En cierto modo, el hecho de que los efectos gravitatorios resulten amplificados por las condiciones de no equilibrio ya está implícito en el clásico experimento de Bénard en el que se calienta por abajo un estrato líquido y se produce la convección a determinado valor crítico del gradiente adverso de temperatura. El experimento de Bénard puede efectuarse con un estrato de pocos milímetros de espesor. El efecto de la gravitación sobre un estrato tan fino es negligible en situación de equilibrio. Hay que escalar una montaña para sentir la diferencia de presión atmosférica, pero, debido al no equilibrio inducido por la diferencia de temperatura, los efectos macroscópicos se hacen visibles (a causa de la gravitación), incluso en este estrato. El no equilibrio amplifica el efecto de la gravitación.
Naturalmente, podemos hacer similares consideraciones a propósito de los campos eléctricos. Por ejemplo, en sistemas bidimensionales, se produce una nueva posibilidad de notable interés cuando el campo eléctrico E lo produce un campo electromagnético polarizado. La geometría más sencilla es el anillo (condiciones periódicas en los límites) sometido a iluminación polarizada circular que se propaga en dirección perpendicular al plano anular. En semejante anillo podemos tener dos tipos de ondas, unas en sentido de las agujas del reloj, las otras en dirección contraria. Si el momento angular que imprime la onda actúa sobre el eje positivo (polarización en sentido contrario a las agujas del reloj), se induce una selección preferencial de una onda química en sentido contrario a las agujas del reloj. Se llega así a la selección de un tipo de ondas, por ejemplo, las que van en sentido contrario a las agujas del reloj.
El Dr. Herschkowitz ha realizado recientemente experimentos numéricos en nuestro laboratorio de Bruselas,[156] con los que se ha confirmado esta selección preferencial de una bifurcación. De este modo, podemos inducir una estructuración preferente en un medio o, en otras palabras, disponemos de un mecanismo generador de un medio asimétrico. En un medio de esta clase, la reacción química procede del modo al que estamos acostumbrados y que verosímilmente conduce a la síntesis preferencial de moléculas asimétricas.
Todo esto demuestra que las situaciones químicas lejanas al equilibrio conducen a una posible «adaptación» de los mecanismos químicos a las condiciones externas. Esto contrasta con las situaciones de equilibrio, en las que esencialmente existe un tipo de estructura y son necesarios efectos amplios para que dicha estructura se modifique. Esta descripción esquemática se refiere al nivel fenomenológico macroscópico, pero los resultados del análisis estocástico y microscópico de la irreversibilidad han sido igualmente muy fructíferos, y voy a tratar de ello en la última parte de esta charla.
5
La descripción de las fluctuaciones presenta una evidente importancia. Después de todo, son la causa de la elección de una rama específica en la bifurcación, y determinan las escalas temporales pertinentes para alcanzar un estado final asintóticamente estable. Las fluctuaciones de equilibrio se estudian desde la época de los trabajos clásicos de Gibbs y Einstein. Einstein demostró que la probabilidad de una variable estocástica correspondiente, por ejemplo, al número de partículas de un componente X próximo al equilibrio, puede expresarse en términos de cantidades macroscópicas. De este modo, obtuvo la distribución de Poisson para la probabilidad P(X):
(5.1)
En la que δ2 S es el camino de entropía relacionado con desviaciones del valor del equilibrio y de la constante k de Boltzmann. Una propiedad característica de la distribución de Poisson es que la fluctuación cuadrática media es igual al valor medio.
(5.2)<δX2> = <X>
Esta relación es característica en todos los sistemas que satisfagan la ley de los grandes números y demuestra que el valor relativo de las fluctuaciones, medido en función del cociente
en donde V es el volumen, puede despreciarse perfectamente en grandes sistemas.
Es muy interesante estudiar el significado de las fluctuaciones en sistemas no lineales alejados del equilibrio. Nosotros iniciamos este trabajo hace unos diez años y recientemente mis colegas Nicolis y Malek-Mansur han obtenido unos resultados bastante notables a los que sobre todo me referiré.[157] De una primera observación, se desprende que la amplitud de las fluctuaciones en condiciones de no equilibrio puede resultar anormalmente elevada. Veamos el diagrama de bifurcación en la fig. 1. Más allá de la bifurcación, se observan dos estados estables microscópicos de peso estadístico equivalente. Como consecuencia, el promedio estadístico <X> se sitúa próximo a la rama inestable (a'), pero los estados más probables se hallarán próximos a (b1) y (b2). Por lo tanto, la dispersión en torno al promedio cobra tanta importancia como el propio promedio. En otras palabras, al cruzar un punto de bifurcación, cabe esperar un cambio del orden de magnitud de las fluctuaciones, de manera que, en vez de
(5.3)<δX2> ~ O(V)[158]
tengamos
(5.4)<δX2> ~ O(V2)
En realidad, la propia distinción entre valores promedios y fluctuaciones desaparece.
Podemos considerar las bifurcaciones como fluctuaciones gigantes alimentadas por flujos adecuados de materia y energía. ¿Cuál es el comportamiento de <δX2> en proximidad a la bifurcación λ = λc? Tendremos un comportamiento intermedio expresado por la fórmula:
(5.5)
Naturalmente, para hallar el valor del parámetro a, necesitamos un cálculo que rebasa la descripción microscópica. Para ello, tenemos que modelizar las fluctuaciones mediante un proceso aleatorio apropiado. En nuestro cálculo, hemos asumido que el número de moléculas de las diversas sustancias químicas que fluctúan, define un proceso de Markov en un espacio de estado apropiado. De este modo, puede demostrarse que, en situaciones simples, este parámetro asume un valor de 3/4. Las fluctuaciones en el punto de bifurcación se hacen de gran magnitud, ya que el sistema «duda» entre las diversas posibilidades que se le presentan.
Pero hay otro aspecto que es el alcance de las fluctuaciones. Un ejemplo investigado minuciosamente por Nicolis y Malek Mansur, y que puede resolverse con exactitud, corresponde al conjunto de ecuaciones:
(5.6)
Supongamos que impedimos la aproximación al equilibrio introduciendo A en cantidad excesiva y eliminando constantemente B. El esquema de reacción (5.6) se sustituye por:
(5.7)
Ya no hay reversibilidad microscópica, y tenemos un índice medio ΦAB de una transferencia global de A a B. Mediante una modelación siguiendo los procesos de Markov, vemos que podemos obtener la correlación entre la concentración de X en dos puntos distintos r y r', que es la que se da en el estado estacionario de la forma
(5.8)
Aquí, hemos supuesto un medio tridimensional. Por lo tanto, tenemos un declive exponencial de la correlación con una longitud de correlación dada por
(5.9)
en la que D es el coeficiente de difusión de X. Vemos que ambas cinéticas de la reacción de difusión intervienen en la determinación de la longitud de correlación. Se entiende fácilmente, porque, cuando, a través de la reacción química, se forman dos partículas de X, están correlacionadas, y esta correlación se extiende a toda la difusión.
Lo que interesa poner de relieve es el hecho de que las correlaciones de no equilibrio tienen un origen y un significado totalmente distinto a las correlaciones de equilibrio. En lugar de estar relacionadas con las constantes de las fuerzas o con potenciales intermoleculares, se expresan en términos de constantes cinéticas y de coeficientes de transferencia. Esta competitividad entre difusión y reacciones químicas en la formación de correlaciones de largo alcance da lugar a predicciones muy interesantes que me gustaría explicar brevemente en términos cualitativos.
Introduzcamos primero un tiempo característico para la difusión en un volumen V. Los argumentos dimensionales demuestran fácilmente que este tiempo característico está relacionado con la dimensionalidad d del sistema mediante una relación de forma
(5.10)
Nicolis y Malek Mansur han calculado el tiempo característico para una reacción química, cuyo comportamiento medio, próximo a un punto de bifurcación, puede expresarse mediante la ecuación
(5.11)
en la que x es una constante macroscópica y k un exponente característico que, en el caso más sencillo, toma el valor 3, aunque también puede adoptar valores más altos como 5, etc. Estudiando el espectro del proceso de Markov, han demostrado que el tiempo característico en tal caso es de la forma
(5.12)
k es una constante química típica.
Modifiquemos ahora una dimensionalidad crítica para la cual los tiempos característicos reacción-difusión sean los mismos. Si examinamos las ecuaciones (5.11) y (5.12), vemos que esta dimensionalidad crítica se expresa
(5.13)
Por ejemplo, para k = 3, tenemos dc = 4; para k = 5, dc = 3. El significado físico de esta dimensionalidad es el siguiente. Para mayores dimensionalidades, d más elevado que dc, la difusión será eficaz y las teorías del campo medio son exactas; por el contrario, para d más pequeño que dc, hay que esperar una creciente importancia de la difusión, ya que el sistema no se halla mezclado adecuadamente. Todo esto recuerda mucho la recientemente denominada «teoría del grupo de renormalización» para el punto crítico de equilibrio.
Empezamos a entender que, para lograr un reloj químico, hay que impedir el efecto de la difusión en nuestro espacio tridimensional. Generalmente, se logra agitando el medio, pues, si no lo hacemos, el reloj químico se desfasa. Sin embargo, no es absolutamente necesario. Si la no linealidad es lo bastante alta, k = 5, la difusión puede hacerse dominante y no habrá que agitar. En medios bidimensionales, el efecto de difusión es aún mayor y, en realidad, no se han observado relojes químicos bidimensionales. En medios unidimensionales, las bifurcaciones quedan totalmente destruidas por los efectos de difusión, y sólo se producen dos suaves transiciones, igualmente muy parecidas a las del clásico problema de las transiciones de fase.
Creo que estas reflexiones demuestran la complejidad de la situación en la vecindad de una bifurcación, desde el punto de vista molecular, y aún queda mucho trabajo por desarrollar en este fascinante terreno.
6
Examinemos ahora el tercer aspecto de los procesos irreversibles: la relación con el nivel básico descrito por las leyes de la mecánica clásica o de la cuántica. Es un antiguo problema pendiente. Todos conocemos la fundamental contribución de Boltzmann. Sin embargo, actualmente suele admitirse que el enfoque cinético de Boltzmann está basado en presupuestos fenomenológicos adicionales. Para obtener procesos irreversibles, Boltzmann introdujo el concepto de probabilidad. Pero ¿cómo justificar su intervención en el marco de la teoría dinámica? Para subsanar esta dificultad, Gibbs y Einstein desarrollaron la teoría de colectividades. Pero no podía establecerse una relación entre la función de distribución en el espacio de las fases y la existencia de cantidades monotónicamente crecientes, como es el caso de la entropía. Por este motivo, la opinión predominante es que la irreversibilidad procede de aproximaciones suplementarias que introducimos en la descripción física mediante técnicas tipo coarse graining[159] u otro tipo de modificación de las ecuaciones exactas. Somos nosotros quienes introducimos la irreversibilidad en un mundo estático, dominado por ecuaciones temporales reversibles.
Es difícil dar crédito a este concepto en un momento en que la irreversibilidad desempeña tan relevante papel en una amplia gama de disciplinas desde las partículas elementales hasta la biología, y quisiera volver a referirme al problema desde otro punto de vista. Un tema recurrente en la historia de la física del siglo XX es el análisis de las condiciones en que podemos actuar respecto al mundo que nos rodea. Como se sabe, la existencia de la velocidad de la luz limita nuestras posibilidades de transmitir información y nos obliga a replanteamos el significado del espacio y del tiempo según lo percibirían observadores móviles. También es sabido que la constante de Planck limita las posibilidades de medición simultánea de variables dinámicas, tales como coordenadas y momentos. Incluso antes de esta gran revolución del pensamiento científico, la segunda ley de la termodinámica expresaba ya cierta limitación en relación con los sistemas complejos.
Si cogemos un cuerpo macroscópico, un líquido, pongamos por caso, lo sometemos a diversas manipulaciones experimentales y luego lo aislamos, no podemos evitar que el sistema, al cabo de cierto tiempo, alcance el equilibrio termodinámico. Independientemente de la preparación inicial, el calor específico del líquido será el mismo. Podemos decir que es una limitación a las posibles manipulaciones, en el sentido de que, hagamos lo que hagamos, el sistema, independientemente de nuestra acción, tiende al mismo estado final. Podemos entender la irreversibilidad a escala molecular en términos muy semejantes.
Tanto la mecánica clásica como la cuántica presentan un aspecto bivalente, en relación con las condiciones iniciales que se suponen arbitrarias en una muestra determinada de espacio y a las que se da un valor empírico, y en relación con las leyes del movimiento. ¿Se trata de dos elementos realmente independientes? ¿Podemos realmente prescribir siempre condiciones iniciales arbitrarias? Como veremos, no siempre es posible y, de hecho, la irreversibilidad aparece cuando, como consecuencia de esta imposibilidad, el concepto de trayectoria o de función de onda corresponde a una descripción idealizada.
Consideremos en primer lugar un ejemplo simple del terreno de la mecánica clásica. Consideremos la secuencia de operaciones indicadas en la fig. 5 del capítulo anterior. Empezamos con una unidad cuadrada que transformamos en rectángulo. Luego, superponemos la segunda mitad a la primera y obtenemos el resultado final. Puede verificarse inmediatamente en la figura que, si el cuadrado inicial está medio lleno, la aplicación de la transformación del panadero causa una distribución que incluye dos rectángulos llenos. Por repetición, obtenemos una distribución cada vez más fragmentada. Este cambio suele denominarse «transformación del panadero». Es un ejemplo un tanto simplificado que ilustra las características a que me refiero.
En la transformación del panadero, tenemos una modificación punto a punto perfectamente determinista expresada por la fórmula
(6.1)
Cada punto p, q se transforma en otro punto bien definido.
Sin embargo, supongamos que, en lugar de un punto, consideramos una pequeña región. Entonces, se demuestra que esta región, tras cierto número de transformaciones, se escinde en dos regiones que, a su vez, se escinden y así sucesivamente hasta que queda cubierta toda la superficie del cuadrado.
Es importante comparar estos dos comportamientos. Sin embargo, cada región, por pequeña que sea, contiene varios tipos de trayectorias, y únicamente pueden hacerse predicciones estadísticas sobre el «destino» de esta región. Entonces, ¿cuál es la descripción «correcta»? Es evidente que la descripción de trayectoria corresponde a un conocimiento «infinitamente» preciso de las condiciones iniciales que nunca pueden alcanzarse en la práctica. Esto es de suma importancia si, al incrementar la precisión de las condiciones iniciales, llegásemos cerca del comportamiento de la trayectoria; pero no sucede así. Sea cual fuere la precisión, tenemos una región, y esta región se difunde por todo el cuadrado. Desde luego, no siempre sucede así. Es necesaria la inestabilidad dinámica, en el sentido de que dos puntos cercanos se comporten de forma distinta con el tiempo. En terminología técnica, se dice que la transformación del panadero es un ejemplo de las denominadas «transformaciones de Bemoulli». Esta nomenclatura nos recuerda que, incluso aunque conozcamos el pasado de semejante sistema, su futuro es tan indeterminado como el resultado del movimiento de una ruleta.
El objeto de la física es tratar situaciones que puedan comprobarse experimentalmente, estudiando cómo evolucionan estas situaciones con el tiempo. Este punto de vista, que tan importante fue tanto en la relatividad como en la mecánica cuántica, es perfectamente aplicable en este caso y fundamentalmente nos hallamos ante un nuevo tipo de descripción, en la que el objeto de la dinámica no es la trayectoria individual, sino la función de distribución en el espacio de las fases. La evolución temporal de esta distribución se caracteriza, en cierto modo como en mecánica cuántica, por operadores que actúan sobre dicha función de distribución, y no hay dificultad en introducir en este marco, como han demostrado Misra, Courbage y yo mismo, cantidades que son una analogía microscópica de la entropía.[160] Hay que poner de relieve que en modo alguno existe un coarse graining, o pérdida de información. La irreversibilidad es consecuencia del hecho de que, en este tipo de sistema, la trayectoria es un concepto irreal.
En mecánica cuántica se da una situación más complicada, aunque en igual sentido. No obstante, en mecánica cuántica el problema de la irreversibilidad es más complejo, porque todos los sistemas mecánicos cuánticos de valor finito poseen un comportamiento casi periódico. Sólo en el límite de los grandes sistemas aparece la irreversibilidad, pero la consideración de grandes sistemas mecánicos es bastante natural. Por el contrario, los sistemas mecánicos cuánticos finitos pueden considerarse aproximaciones de los grandes. Por ejemplo, sólo en los grandes sistemas se dan fenómenos como la emisión espontánea de Einstein. Pero vemos este fenómeno, vemos la influencia de números infinitos de grados de libertad, en el comportamiento de la materia a través de diversos efectos, tales como la emisión espontánea de Einstein o el famoso desplazamiento de Lamb.
Por lo tanto, llegamos a la pregunta: ¿hay una limitación a las posibles condiciones iniciales de los sistemas infinitos? Para simplificar el problema, piénsese en un estanque al que arrojamos una piedra. Observamos ondas centrífugas. Probablemente, un buen ingeniero lograría que las ondas convergieran en la piedra y haría que ésta saltara fuera del agua. Un ingeniero más hábil lo lograría, desde una distancia mayor, pero no hay ingeniero capaz de hacerlo desde distancias infinitas. En otras palabras, para tiempos lo bastante largos, sólo observamos ondas centrífugas. Esto demuestra también un límite a nuestras posibilidades de manipular estos sistemas e implica una limitación de las condiciones iniciales. Se dice a menudo que el problema de las ondas centrífugas y centrípetas es que son simétricas, y se añade que las ondas centrípetas asintóticas son de probabilidad cero. Sin embargo, esto encubre el auténtico problema: para sustituir la premisa de condiciones iniciales arbitrarias por afirmaciones probabilistas, necesitaríamos una teoría adicional que nos diera alguna información que la dinámica no nos facilita. Actualmente, no existe semejante teoría. La misma conclusión es aplicable a muchas situaciones, como sucede con la dispersión en mecánica cuántica. También en este caso, únicamente son posibles ondas centrífugas asintóticas. La solución de inversión temporal que corresponde a ondas centrípetas asintóticas requeriría correlaciones entre acontecimientos infinitamente distantes.
Es muy interesante que podamos entender la irreversibilidad y formular una teoría detallada, basándonos en la percepción de que, tanto a nivel macroscópico como microscópico, existe un límite a las manipulaciones. No podemos producir constantemente trabajo a partir de un simple baño de calor. No podemos evitar que la transformación panadero cubra todo el plano. No podemos evitar que las ondas centrífugas sean asintóticamente las únicas posibles de verificar. En resumen: no podemos manipular la naturaleza a voluntad. Existe una flecha temporal, y no pueden crearse situaciones que conduzcan a resultados contradictorios debidos a la presencia simultánea de dos flechas en conflicto. El propósito de esta conferencia no me permite desarrollar en extensión este enfoque.[161] Quizás uno de los conceptos más interesantes que de él se derivan es el de tiempo interno, producto de la evolución del sistema, por oposición al tiempo externo de la física tradicional.
7
Para concluir, diremos que, en condiciones alejadas del equilibrio, la materia adquiere nuevas propiedades, tales como «comunicación», «percepción» y «memoria», propiedades que hasta ahora sólo se atribuían a los sistemas vivos.
Como consecuencia, muchas de las distinciones tradicionales, como es la dualidad azar-necesidad, se hacen mucho más sutiles. Los pequeños efectos permiten pasar de un tipo de comportamiento a otro, mediante el mecanismo de bifurcaciones secundarias. El tiempo cobra nuevo significado. Ya no es un parámetro introducido para la comunicación entre diversos observadores, sino que también se relaciona con la evolución interna del sistema.
Siguiendo el ideario humanístico de Aharon Katzir-Katchalsky, me permitirán que llegue incluso a afirmar que nos lleva quizás a un nuevo concepto de realidad. La concepción tradicional establece una especie de identidad entre lo racional y lo real. Por ejemplo, una trayectoria entre dos puntos, A y B, cumple el mínimo de acción posible. Podemos construir prácticamente trayectorias «imaginarias» en torno a la única trayectoria real posible. En el mundo de las bifurcaciones, ya no es tan sencilla la situación. Si un sistema se halla en un estado correspondiente a una bifurcación determinada, es debido a su desarrollo histórico. También son «racionales» otras posibilidades. En cierto sentido, lo real no es más que una parte de lo posible.
La renovación de la ciencia es en gran medida la historia del redescubrimiento del tiempo. Tras nosotros queda la concepción de la realidad objetiva que reclamaba que la novedad y la diversidad fueran negadas en nombre de leyes inmutables y universales. Ya no nos fascina la racionalidad que describe el universo y el saber como algo que se va haciendo. El futuro ya no está determinado; no está implícito en el presente. Esto significa el fin del ideal clásico de omnipotencia. El mundo de los procesos en que vivimos y que forma parte de nosotros mismos ya no puede rechazarse como si lo constituyeran apariencias o ilusiones determinadas por nuestro modo de observación.
Este mundo, que aparentemente ha renunciado a la seguridad de las reglas estables y permanentes, es, sin lugar a dudas, un mundo de riesgo y aventura. No puede inspirar confianza ciega, a lo sumo, quizás, el mismo sentimiento de discreta esperanza que ciertos textos talmúdicos parecen atribuir al Dios del Génesis.[162]