Tiempo, vida y entropía^[115]

1

En mis anteriores conferencias dentro de este ciclo, me he referido al papel constructivo de los procesos irreversibles. Podemos comprobar numerosos ejemplos de autoorganización en sistemas alejados del equilibrio en las interesantes comunicaciones de Lefever, Babloyantz y otros conferenciantes. Por ello, no entraré en más detalles sobre autoorganización y su relación con los sistemas biológicos, pero abordaré un tema distinto. Jacques Monod ha calificado a los sistemas vivos como extraños, y es cierto que ya son bastante peculiares por el hecho de ser autónomos, aparte de su interacción activa con el medio. Es evidente que uno de los objetivos finales de la actual reconceptualización de la física es entender la generación de la vida en el universo, hombre incluido. Desde esta perspectiva, el relieve de la irreversibilidad, del azar, es ciertamente algo importante a tener en cuenta. Pero existe una característica adicional. La vida no es meramente el resultado pasivo de la evolución cosmológica, ya que introduce un proceso de retroalimentación (feed-back) suplementario. En otras palabras, la vida es el resultado de procesos irreversibles, pero a su vez puede inducir nuevos procesos irreversibles. Cierto que el viejo axioma predica: la vida sólo se origina en la vida. Pero, en términos más generales, podemos decir que la irreversibilidad genera irreversibilidad. Y éste es el problema que voy a abordar.

En primer lugar, hay que aclarar un poco lo que entendemos por irreversibilidad. Actualmente, sabemos que hay muchas «flechas temporales»: el tiempo cosmológico relacionado con la expansión del universo, uno microscópico relacionado con la denominada violación de la invariancia T, y podríamos ampliar la lista, ya que cada vez que se dan clases de acontecimientos asimétricos, podemos hablar de una flecha. Sin embargo, no es éste el sentido de la irreversibilidad termodinámica. En ella, el concepto de entropía desempeña un papel primordial. Los procesos irreversibles pueden encauzarse por un aumento monotónico de entropía, al menos mientras consideremos sistemas cerrados. Desde el punto de vista macroscópico, el significado de la segunda ley es muy sencillo: con él se introduce una especie de principio selectivo que complementa la información que nos aportan otras leyes termodinámicas, como las de la conservación de la energía o de la masa. Desde el punto de vista de la conservación de la energía, el calor y el trabajo desempeñan un papel idéntico. Sin embargo, y como todos sabemos, es fácil transformar trabajo en calor, pero lo contrario no es tan sencillo. Los denominados móviles perpetuos de segunda especie, en los que utilizamos la energía térmica contenida en el mar para mover un barco, quedan explícitamente excluidos de la segunda ley de la termodinámica. Por lo tanto, podemos afirmar que la segunda ley limita nuestra acción sobre la materia, y aún limita los tipos de procesos observables en la naturaleza. Sólo permite los procesos que conducen a una producción positiva de entropía.

Respecto a estas concepciones macroscópicas no existe gran controversia. Pero la pregunta fundamental que se plantea es: «¿Podemos extrapolar el concepto de entropía al mundo microscópico y podemos atribuir un significado a los procesos irreversibles a nivel de la dinámica, ya sea clásica, ya sea cuántica?».

2

Incluso hoy, después de un siglo, nos remitimos para contestar a esta pregunta a los trabajos de Boltzmann. Como se sabe. Boltzmann demostró que la entropía se define en términos de la evolución de una población de moléculas. Hay que señalar que el propio Boltzmann estaba convencido de que su obra en física era, en cierto modo, paralela a la de Darwin en el campo de la biología. La idea verdaderamente importante de la evolución biológica es que la selección natural enunciada en la teoría de Darwin no puede definirse para un solo individuo, sino para una población numerosa. Es, por lo tanto, un concepto estadístico. Siguiendo este criterio conceptual y recurriendo a un modelo de gases diluidos, Boltzmann enunció su transcendental fórmula

S = k log P

que relaciona la entropía con la probabilidad. El aumento de entropía queda así descrito en términos de un proceso probabilístico que expresa que la probabilidad tiende a su valor máximo con el tiempo. Es un hallazgo fundamental, y Boltzmann ha establecido un vínculo definitivo entre entropía y probabilidad.

Sin embargo, quedaban pendientes muchas cuestiones. En el siglo transcurrido desde que Boltzmann desarrolló sus ideas, la literatura sobre el tema es muy abundante y no procede ahora hacer un resumen. Existen textos con la información pertinente. No obstante, quiero poner de relieve dos puntos: en primer lugar, el fracaso de Boltzmann en definir una flecha del tiempo.

Boltzmann pensó al principio que sería capaz de demostrar que la flecha del tiempo estaba determinada por la evolución de los sistemas dinámicos hacia estados de mayor probabilidad, pero, como consecuencia de las objeciones que le plantearan Poincaré, Zermelo y Loschmidt, cambió de parecer y desistió de su proyecto de demostrar que existía una flecha objetiva de tiempo y, en lugar de ello, introdujo un punto de vista subjetivista que, en cierto modo, reducía la ley de la entropía a una pura tautología. La flecha del tiempo sólo sería una especie de convenio que nosotros (o quizá todos los seres vivos) introducimos en un mundo en el que no existe distinción objetiva entre pasado y futuro. En nuestros días, es difícil aceptar esta opinión, ya que no sólo la física, sino la historia, parecen indicar la importancia del cambio unidireccional. Como ha dicho Popper:^[116] «La idea de Boltzmann es insostenible, al menos para un realista. Moteja de ilusión el cambio unidireccional, lo que convierte en ilusión el desastre de Hiroshima. Y, con ello, son ilusión nuestro mundo y nuestros esfuerzos por ampliar nuestros conocimientos sobre el mismo».

Hay un segundo punto, relacionado con la limitación del experimento de Boltzmann en la dilución de gases. Es cierto que, si comprimimos las moléculas de un gas en una pequeña porción de un recipiente, hallamos que, con el transcurso del tiempo, deben estar uniformemente distribuidas. Esto corresponde a la idea de desorden progresivo postulada por Boltzmann. Pero la situación no es siempre tan sencilla. Podemos realizar un experimento con un ordenador, haciendo que unos centenares de moléculas interactúen en un sistema bidimensional mediante los potenciales habituales de atracción y repulsión. En el momento inicial, situamos las moléculas en posiciones al azar con velocidades al azar. En condiciones adecuadas, vemos que se produce una cristalización, que las partículas se ordenan. Incluso podemos observar la aparición de núcleos de cristales y las dislocaciones en la red final. Desde el punto de vista dinámico, el sistema evoluciona hacia el orden, pero la segunda ley requiere una evolución hacia el desorden. ¿Cómo se soluciona este enigma?

3

Comenzamos a disponer de algunas respuestas a este interrogante gracias a los esfuerzos que se llevan a cabo hace algunos años en Bruselas y en Austin. En una comunicación reciente, «Tiempo, probabilidad y dinámica», Misra y el autor llegaban a la siguiente conclusión:

Hay que decir que se trata de una conclusión un tanto abstracta, y voy a hacer unos comentarios. La dinámica clásica o la cuántica pueden transformarse, para ciertos sistemas, en procesos probabilísticos. Esta transformación conlleva siempre una ruptura de simetría. Un proceso probabilístico es unidireccional. Conduce al estado más probable, en el futuro o en el pasado. Por el contrario, el proceso dinámico inicial es invariable respecto a la inversión temporal. Y es precisamente en este punto donde surge la flecha del tiempo. Tenemos que entender por qué sólo uno de los procesos probabilísticos se verifican en la naturaleza. En el siguiente apartado, daremos un ejemplo. Además, la transformación de descripción dinámica en descripción probabilística implica un cambio de representación. En la descriptiva dinámica, la cantidad básica es la función de densidad descrita en los conjuntos de Gibbs (o la matriz de densidad en mecánica cuántica). En el proceso probabilístico, es una nueva función de distribución que satisface el tipo de ecuación de Markov y que denota nuevas entidades. Por ello, los procesos dinámicos pueden conducir al orden en términos de las unidades consideradas, mientras que los procesos probabilísticos conducen a un creciente desorden.

Orden y desorden no son necesariamente conceptos mutuamente excluyentes. Pueden corresponder a distintas descripciones. Voy a ilustrar estas conclusiones generales en términos de un modelo más físico. Muchos sistemas dinámicos pueden describirse en términos de «colisiones» y «correlaciones». Consideremos una nube de partículas que se dirige hacia un blanco (una gruesa partícula inmóvil). En la fig. 1, se describe esta situación. En un pasado lejano, no existían correlaciones entre las partículas. Ahora, la dispersión produce sus efectos. Esparce las partículas (haciendo más simétrica la distribución de velocidad) y, además, produce correlaciones entre las partículas dispersadas y el dispersor. La aparición de correlaciones puede esclarecerse más, aplicando una inversión de velocidad (por ejemplo, colocando un espejo esférico). Vemos esta situación en la fig. 2 (las líneas onduladas representan las correlaciones). Por lo tanto, el papel de la dispersión es el siguiente: en el proceso directo, hace más simétrica la velocidad de distribución y crea correlaciones; en el proceso inverso, la velocidad de distribución se hace menos simétrica y desaparecen las correlaciones. Por lo tanto, con la consideración de las correlaciones, introducimos una distinción fundamental entre procesos directos e inversos.

FIG. 1. Dispersión de partículas. Tras la colisión las dispersiones permanecen correlacionadas con el dispersor (líneas onduladas).

FIG. 2. Inversión de velocidad tras una colisión. Las correlaciones se destruyen tras el impacto con el dispersor.

Apliquemos estas conclusiones a los sistemas de muchos cuerpos. También en este caso, consideraremos dos tipos de situación: en una, llegan partículas sin correlación, se dispersan y se producen partículas correlacionadas (fig. 3). En la situación contraria, llegan partículas correlacionadas, se destruyen las correlaciones por efecto de colisiones y surgen partículas sin correlación (fig. 4).

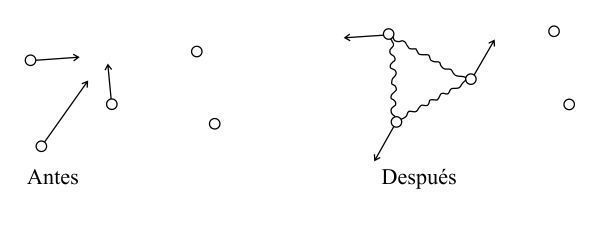
FIG. 3. Origen de correlaciones post-colisionales.

FIG. 4. Destrucción de correlaciones pre-colisionales.

Ambas situaciones se diferencian a través del orden temporal entre colisiones y correlaciones. En el primer caso, tenemos correlaciones «post-colisionales» y, en el otro, correlaciones «pre-colisionales» (no siempre es posible establecer una clara distinción entre estos dos casos: para hacerla más fácil conviene considerar sistemas grandes, «infinitos»).

Para sistemas cuya evolución puede describirse en términos de estas correlaciones dinámicas, podemos atribuir un significado simple a la ruptura de simetría introducida por la segunda ley de la termodinámica y la elección del semigrupo pertinente. Supongamos que preparamos una función de distribución (de la velocidad de una partícula, por ejemplo) a un tiempo dado t₀. Podemos aplicar las ecuaciones dinámicas para observar la desviación del equilibrio que se producirá en el futuro lejano o en el pasado lejano. Es evidente que pueden darse los cuatro tipos de situaciones representadas en la fig. 5. En la situación A, la distribución de velocidad no alcanzará el equilibrio ni para t → +∞ ni para t → −∞ Por el contrario, en la situación B, se alcanza el equilibrio en ambas direcciones del tiempo. En la situación C. se alcanza el equilibrio para t → +∞, pero no para t → −∞; finalmente, en la situación D, se alcanza para −∞ y no para +∞. El tipo de situación verificable depende de las condiciones iniciales. Ahora podemos demostrar, y es un punto importante, que los casos A y D sólo pueden producirse si, en el momento inicial, tenernos entre las partículas correlaciones persistentes de largo alcance que impidan que el sistema alcance el equilibrio mediante sucesivas colisiones. En B y C, también pueden existir correlaciones, pero son correlaciones post-colisión que no impiden que el sistema vaya hacia el equilibrio. En A y en D, tenemos partículas que vienen del infinito y que están correlacionadas antes de colisionar. En B y en C, tenemos correlaciones únicamente después de las colisiones (fig. 5).

FIG. 5. Evolución de la desviación del equilibrio. Con arreglo a las condiciones iniciales pueden darse cuatro casos (V. texto).

Ahora formularemos una ley de selección microscópica que es el fundamento de la segunda ley de la termodinámica. No pueden prepararse ni comprobarse en los sistemas físicos correlaciones pre-colisión persistentes de largo alcance. Las correlaciones son siempre consecuencia de interacciones dinámicas previas. Obsérvese que este principio de selección rompe la simetría temporal y nos permite elegir concretamente el semigrupo adecuado a la flecha tiempo que observamos. Una vez formulado este principio de selección, es cuestión de medios técnicos —que no voy a describir— para pasar del proceso dinámico inicial al proceso probabilístico y reconciliar la evolución dinámica con una probabilidad de aumento incesante en los sistemas aislados.

4

Volvamos a la relación entre tiempo y vida. Primero, quiero señalar que la segunda ley de la termodinámica expresa tal vez la ruptura de simetría más fundamental en el mundo físico que a su vez posibilita otras rupturas de simetría, incluida la de materia y antemateria. En principio, podemos imaginar el mundo poblado por dos tipos de seres, unos que viven hacia el futuro y otros hacia el pasado. Algunas divertidas consecuencias de esta situación se exponen en el maravilloso libro de Martin Gardner El universo ambidiestro. Podemos reconocer tales sistemas físicos o biológicos porque para nosotros su evolución sería la opuesta a la que estamos acostumbrados. El análisis microscópico nos mostraría que estos sistemas transforman las correlaciones en colisiones, mientras que los sistemas que conocemos proceden en sentido contrario.

La segunda ley es una afirmación de la unidad del mundo físico. Sólo existe una flecha del tiempo. Ahora, en esta perspectiva, hablaremos de la relación entre tiempo y vida. La vida es ciertamente una de las manifestaciones más sorprendentes de esta flecha universal del tiempo. Desde este punto de vista, podemos considerarla como una consecuencia de la existencia de procesos irreversibles, pero lo que quiero poner de relieve es que la vida transmite, a su vez, esta situación propia, intrínseca de ruptura de simetría, a objetos del mundo físico que, sin su intervención, tendrían un comportamiento temporal simétrico. Si volvemos a la situación B de la fig. 5, interpretaremos tal situación como la que da origen a una aproximación al equilibrio en nuestro futuro. Los seres que vivan en la dirección opuesta interpretarían, por el contrario, esta situación como la generadora de una aproximación al equilibrio en su futuro, que es nuestro pasado. En cierto sentido, transformamos una situación fundamentalmente simétrica en una situación temporalmente asimétrica por la utilización de nuestra propia asimetría temporal. Como he señalado, suele decirse que la vida produce vida, pero nosotros vemos la vida como transmisora de irreversibilidad; la duración originando duración.

Actualmente se especula mucho sobre cosmología. Es evidente que algunos de los conceptos que hemos expuesto coinciden con lo que suele denominarse cosmología estándar. En sus primeros tiempos, el universo estaba desvinculado de la causalidad. Desde el horizonte de cada observador, sólo podían verse elementos sin correlación. El decurso del tiempo en la interacción de estos elementos introduce correlaciones suplementarias. La evolución general del mundo físico, en esta perspectiva, empieza a interpretarse como una progresiva ampliación de correlaciones a través de la materia, que entra en contacto directo o indirecto, o a través de campos intermedios. Pero la historia a gran escala de nuestro universo sigue en gran parte inexplicada. Aunque hay que tener en cuenta dos características primordiales: la gravitación y la entropía. Nos hallamos aún muy lejos de una concepción sintética que englobe estos dos conceptos, por consiguiente aún existen muchas posibilidades.^[119] De mis estudios sobre sistemas complejos a una escala mucho más modesta, he sacado la impresión firme de que es difícil siquiera llegar a imaginar o enumerar todas las posibilidades que presentan los sistemas no lineales alejados del equilibrio. Y esto me resulta aún más evidente si consideramos el universo como un todo con las sorprendentes no linealidades descritas por la ecuación de Einstein y con las enormes desviaciones del equilibrio que debieron predominar en su fase pretérita de formación. Por consiguiente, finalizaré con una apostilla optimista: la historia no tiene final.

Bibliografía