Diez consejos para sacar mejor nota en los exámenes

En este capítulo
 Organizar bien los conocimientos
Organizar bien los conocimientos
 Desarrollar estrategias inteligentes
Desarrollar estrategias inteligentes
 Evitar errores tontos
Evitar errores tontos

En todos los años que llevo de profesora (no intentes adivinar cuántos, ¡eso es de mala educación!) he dado clase a más de 40.000 alumnos, y cada uno de ellos ha hecho conmigo un mínimo de tres exámenes. Eso hace un total de 120.000 exámenes que he corregido o ayudado a corregir, y puedes creerme si te digo que he visto de todo. He visto respuestas excelentes, respuestas desastrosas y todas las posibilidades intermedias. Un alumno incluso me escribió una nota en un margen pidiéndome que no fuera muy estricta con él porque se le había escapado el perro y no había tenido tiempo de estudiar. Me he encontrado con respuestas que ni siquiera yo he logrado entender. Me he reído, he llorado y me he sentido orgullosa de cómo han respondido mis alumnos en los exámenes.
En este capítulo he puesto una lista de las diez estrategias más utilizadas por los alumnos que suelen sacar buenas notas. Esos alumnos no son necesariamente más inteligentes que los demás (aunque deben conocer la materia, naturalmente), pero sí están mucho mejor preparados. Como resultado, son capaces de enfrentarse a nuevos problemas y situaciones sin venirse abajo, no suelen cometer esos pequeños errores que acaban bajándote la nota final, y es menos probable que un problema los desconcierte de tal modo que no sepan ni por dónde empezar. Es más probable que sepan resolver el problema (o al menos den una respuesta parcial) porque saben etiquetar la información y organizar el trabajo. De esto no hay duda: la clave para bordar un examen de estadística es la preparación.
Tú también puedes aprobar la asignatura de estadística con buena nota (o con mejor nota todavía, si ya se te da bien la materia) aplicando las sencillas estrategias que explico en este capítulo. Recuerda que todo suma, ¡y empieza hoy mismo a mejorar tu nota de examen!
Averiguar qué es lo que no sabes, y ponerle remedio
Cuando se trata de estadística, distinguir entre lo que sabes y lo que no sabes puede resultar bastante complicado. Lees el libro y entiendes todos los ejemplos de los apuntes, pero no consigues resolver los problemas que te mandan de deberes. Sabes responder a todas las preguntas de estadística que te plantea tu compañero de clase, pero no puedes responder a tus propias dudas. Sales del examen pensando que te ha ido bien, pero luego te dicen la nota y te quedas sorprendido.
¿Qué está ocurriendo? Lo que quiero que entiendas es que, para sacar buena nota, debes ser consciente de lo que sabes y de lo que no sabes. Este conocimiento no es fácil de adquirir, pero merece mucho la pena. Lo habitual es que los alumnos descubran lo que no saben de la peor manera posible: metiendo la pata en un examen. Los errores no son malos de por sí, todo el mundo los comete; lo que importa es cuándo los cometes. Si cometes un error antes del examen, cuando todavía estás a tiempo de descubrir qué es lo que estás haciendo mal, no te costará nada. Si cometes ese mismo error en un examen, te costará puntos.

Una estrategia para descubrir lo que sabes y lo que no sabes consiste en leer detenidamente los apuntes de clase y marcar con un asterisco todo lo que no entiendas. También puedes “examinarte” a ti mismo, como explico más adelante en el apartado “Trampa ‘Ya me lo sé’ n.° 2”, y hacer una lista de problemas que te hayan parecido especialmente difíciles. Luego acude a tu profesor con tus apuntes y tu lista y pídele que repase contigo esas dificultades. Como tus preguntas serán lo suficientemente específicas, tu profesor podrá ir directamente al grano, te dará información y ejemplos concretos y se asegurará de que entiendes un concepto antes de pasar al siguiente. Una reunión de este tipo con tu profesor no tiene por qué durar mucho; a veces te responden una pregunta y se produce una especie de efecto dominó, de manera que de golpe se solucionan varias dudas que también tenías apuntadas.

En lo que respecta a comprender todos los conceptos, ejemplos, fórmulas, notaciones y problemas de deberes antes de hacer el examen, no dejes piedra sin remover. Yo siempre les digo a mis alumnos que treinta
minutos conmigo pueden hacer que su nota mejore el 10%, porque se me da de maravilla explicar cosas y responder preguntas (probablemente mejor que a cualquier compañero, cuñado o amigo que hiciera esta asignatura hace cuatro años con otro profesor). Merece la pena que hagas una visita rápida a tu profesor en su despacho, sobre todo si vas con una lista detallada de preguntas. Si, por alguna razón, tu profesor no está disponible, pídele ayuda a un tutor.
Consejos universales para sacar buena nota
Aquí tienes algunos consejos de carácter general que mis alumnos han considerado útiles:
 Ya sé que habrás oído esto
antes, pero es cierto que tienes mucho ganado si vas a clase todos
los días y coges apuntes para luego poder revisarlos. De este modo
también te aseguras de que no te has perdido la explicación de
algún concepto menos destacado que luego pueda salir en alguna
pregunta del examen.
Ya sé que habrás oído esto
antes, pero es cierto que tienes mucho ganado si vas a clase todos
los días y coges apuntes para luego poder revisarlos. De este modo
también te aseguras de que no te has perdido la explicación de
algún concepto menos destacado que luego pueda salir en alguna
pregunta del examen.
 No te limites a escribir en
el cuaderno lo mismo que ponga el profesor en la pizarra, eso es de
aficionados. Los profesionales también apuntan cualquier otra cosa
que el profesor destaque especialmente en su explicación, aunque no
la escriba en la pizarra. Ésa es la diferencia entre un
sobresaliente y un notable.
No te limites a escribir en
el cuaderno lo mismo que ponga el profesor en la pizarra, eso es de
aficionados. Los profesionales también apuntan cualquier otra cosa
que el profesor destaque especialmente en su explicación, aunque no
la escriba en la pizarra. Ésa es la diferencia entre un
sobresaliente y un notable.
 Procura llevarlo todo al día
y s erorganizado; así no tendrás que correr cuando se acerque la
fecha de entrega. El día que invertí 5 dólares en un buen
portaminas, una buena goma, una perforadora de papel y una pequeña
grapadora fue uno de lo smejores días de mi época de estudiante.
Sí, ya sé que ahora todos esos artículos te costarán 10 dólares o
más, pero créeme: merece la pena.
Procura llevarlo todo al día
y s erorganizado; así no tendrás que correr cuando se acerque la
fecha de entrega. El día que invertí 5 dólares en un buen
portaminas, una buena goma, una perforadora de papel y una pequeña
grapadora fue uno de lo smejores días de mi época de estudiante.
Sí, ya sé que ahora todos esos artículos te costarán 10 dólares o
más, pero créeme: merece la pena.
 Conoce a tu profesor y deja
que él o ella te conozca a ti. Si te presentas el primer día le
causarás muy buena impresión, y para que se acuerde de tu cara
puedes plantearle una duda al terminar la clase (si la tienes,
claro) o hacerle alguna visita en horario de atención a los
alumnos. No te preocupes por si tus preguntas son tontas; lo que
importa no es el nivel donde estás ahora, sino tu voluntad de pasar
al siguiente nivel y sacar buena nota en la asignatura. Eso es lo
que tu profesor quiere ver.
Conoce a tu profesor y deja
que él o ella te conozca a ti. Si te presentas el primer día le
causarás muy buena impresión, y para que se acuerde de tu cara
puedes plantearle una duda al terminar la clase (si la tienes,
claro) o hacerle alguna visita en horario de atención a los
alumnos. No te preocupes por si tus preguntas son tontas; lo que
importa no es el nivel donde estás ahora, sino tu voluntad de pasar
al siguiente nivel y sacar buena nota en la asignatura. Eso es lo
que tu profesor quiere ver.
Evitar las trampas “Ya me lo sé”
¿Qué es una trampa “Ya me lo sé”? Es un término que yo utilizo para esa situación en que dices “Bueno, esto ya me lo sé perfectamente, lo tengo más que controlado”, pero luego llega el examen y ¡zas!, resulta que no te lo sabías tan bien como pensabas y no lo tenías controlado en absoluto. Las trampas “Ya me lo sé” son un peligro porque te hacen pensar que no tienes ninguna duda y que vas a sacar un 10 en el examen, cuando la verdad es que todavía hay cosas que no dominas. Aunque existen varios tipos de trampas “Ya me lo sé”, en este apartado describo las dos más frecuentes y te enseño a evitarlas. Las he llamado “trampa ‘Ya me lo sé’ n.° 1” y “trampa ‘Ya me lo sé’ n.° 2” (muy original, ¿verdad?). Las dos trampas son sutiles y en ellas pueden caer incluso los estudiantes más concienzudos, de manera que no te sientas mal si te ves retratado en este apartado. Simplemente piensa en cuántos puntos te ahorrarás cuando salgas del modo “Ya me lo sé” y entres en el modo “Espera un momento, aquí hay algo que no termino de entender bien”.
Trampa “Ya me lo sé” n.° 1
La trampa “Ya me lo sé” n.° 1 ocurre cuando repasas los apuntes de arriba abajo mientras dices: “Vale, esto ya me lo sé”, “Esto lo tengo claro”, “Está chupado”, pero no intentas hacer los problemas desde cero por ti mismo. Si entiendes un problema que ha hecho otra persona, sólo significa que entiendes lo que hizo esa persona cuando resolvió el problema. No quiere decir que tú puedas resolverlo por ti mismo en un examen, cuando estás bajo presión y tienes los ojos clavados en un espacio en blanco donde se supone que va tu respuesta. ¡Hay una gran diferencia!
Yo también caigo a veces en la trampa “Ya me lo sé” n.° 1. Hace poco me leí de cabo a rabo el manual del grabador de vídeo digital y lo tenía todo clarísimo, pero una semana más tarde quise grabar una película y no supe ni por dónde empezar. ¿Por qué no? Había comprendido todo lo que decía el manual pero no había intentado ponerlo en práctica, y cuando llegó el momento no conseguí recordar cómo se hacía.
Los alumnos siempre me dicen que, si ven un problema resuelto, luego ya lo entienden. La pega es que casi todo el mundo es capaz de entender un problema que alguien ya ha resuelto antes. De hecho, la clave está en saberlo razonar y resolverlo sin ayuda, como ocurre en un examen.

Para evitar la trampa “Ya me lo sé” n.° 1, busca en tus apuntes algunos ejemplos que utilizara tu profesor y escríbelos en hojas aparte (sólo el problema, no la solución). A continuación, mezcla todas las hojas y conviértelas en un examen. Para cada problema, empieza escribiendo tan sólo el primer paso. No te preocupes por terminar los problemas; simplemente empiézalos. Una vez hayas hecho esto con todos los problemas, vuelve a mirar los apuntes para ver si los has empezado correctamente (en el reverso de cada hoja, anota de qué parte de los apuntes proviene, para luego tardar menos en comprobar las respuestas).
Trampa “Ya me lo sé” n.° 2
La trampa “Ya me lo sé” n.° 2 es incluso más sutil que la trampa n.° 1. Un alumno entra en mi despacho después del examen y me dice: “Repasé todos los problemas de los apuntes, volví a hacer los problemas de los deberes e incluso hice los exámenes que puso usted de ejemplo, y no cometí apenas errores. Pero a pesar de toda esa preparación, el examen me ha ido de pena”.
¿Qué ha ocurrido? Nueve de cada diez veces, los alumnos que caen en la trampa “Ya me lo sé” n.° 2 hacen de verdad todos esos problemas y se pasan horas y horas estudiando. Lo que pasa es que, cuando se quedan atascados con un problema, echan un vistazo a la solución (que tienen justo al lado, bien a la vista), averiguan en qué se han equivocado, se dicen a sí mismos: “Ah, claro, qué error más tonto, eso ya lo sabía” y continúan. Al final creen que han hecho todos los problemas bien ellos solos, pero el día del examen pierden algunos puntos, o muchos, en función de dónde se quedaran atascados cuando estaban estudiando.
Entonces, ¿cómo se puede evitar la trampa “Ya me lo sé” n.° 2? Haciendo un examen de prueba en condiciones “reales”, con toda la presión. Te explico cómo:
1. Estudia tanto como te haga falta, de la manera que te parezca más adecuada, hasta que te sientas preparado para poner a prueba tus conocimientos.
2. Siéntate a la mesa con un examen de práctica. Si no te lo proporciona el profesor, hazte uno tú mismo eligiendo unos cuantos problemas de los deberes, de los apuntes o del libro de texto.
Igual que en un examen de verdad, necesitarás un lápiz, una calculadora y los materiales que te permitan llevar (¡y nada más!). El hecho de no poder consultar el libro ni los apuntes quizá te ponga un poco nervioso o te haga sentir desprotegido, pero es imprescindible que averigües lo que puedes hacer por ti mismo antes de que llegue la hora de la verdad.

Algunos profesores dejan llevar al examen una hoja-resumen (también llamada chuleta) en la que puedes escribir cualquier información que consideres útil, dentro de unos límites. Si te dejan llevar hojas-resumen a los exámenes, utiliza una también en el examen de práctica.
3. Pon en marcha el cronómetro (o el contador del horno) con el mismo tiempo que te vayan a dar para el examen real y ponte manos a la obra.
4. Resuelve todos los problemas que puedas lo mejor que sepas y, cuando termines (o se te acabe el tiempo), deja el lápiz sobre la mesa.
5. Cuando hayas terminado el “examen”, ponte en la posición del loto, inspira profundamente, aguanta el aire unos instantes y expúlsalo en tres veces. A continuación mira las soluciones y corrige la prueba igual que lo haría tu profesor.
Si ha habido algún problema que no hayas sabido empezar siquiera (aunque sea por alguna tontería y luego, al ver las soluciones, recuerdes de inmediato lo que habías olvidado), entonces no puedes decir: “Ah, sí, esto lo sabía; en un examen de verdad no cometería este fallo”; tienes que decir: “No he sabido empezar el problema sin ayuda. En un examen de verdad me lo habrían contado mal. Tengo que repasarlo bien para que no me vuelva a ocurrir”.

En un examen de verdad no tienes una segunda oportunidad. Por lo tanto, cuando estés estudiando no tengas miedo de admitir que no sabes hacer un problema por ti mismo; simplemente alégrate de haberte dado cuenta a tiempo, y ponle remedio. Repasa los apuntes, mira en el libro de texto, pregunta a tu profesor, haz otros problemas del mismo tipo o pide a un compañero de clase que te pregunte. Además, intenta encontrar una pauta en el tipo de problemas que te hayan resultado más complicados o no hayas sabido resolver. Averigua por qué fallaste donde fallaste. ¿Leíste las preguntas demasiado rápido y por eso te equivocaste en las respuestas? ¿Fue un problema de vocabulario o de notación? ¿Te habías estudiado todas las preguntas del examen?...

Cuesta mucho ser crítico con uno mismo y admitir que no sabías algo que pensabas que sí sabías. Pero si coges el toro por los cuernos y descubres tus errores antes de que te cuesten puntos, podrás centrarte en tus puntos débiles y convertirlos en puntos fuertes, llegarás a dominar de verdad la materia y conseguirás una nota más alta en el examen.
Hacerse amigo de las fórmulas
Muchos alumnos se sienten incómodos con las fórmulas (a menos que estén chiflados por las matemáticas, en cuyo caso las ven como una fuente de diversión constante). Este malestar es comprensible —a mí también solían intimidarme (me refiero a las fórmulas, no a los chiflados por las matemáticas)—. El problema es que en una clase de estadística no se puede sobrevivir mucho tiempo sin utilizar fórmulas, de manera que es importante acostumbrarse a ellas desde el principio. Una fórmula te dice mucho más que la forma de calcular algo. Muestra el razonamiento que subyace a los cálculos. Por ejemplo, puedes obtener una visión general de la desviación estándar analizando su fórmula:

Si a un valor del conjunto de datos, xi, le restas la
media,  ,
sabrás a qué distancia se encuentra ese número por encima o por
debajo de la media. Como no quieres que las diferencias positivas y
negativas se cancelen entre sí, elevas todas al cuadrado para
hacerlas positivas (pero recuerda que con esto obtienes unidades al
cuadrado). A continuación las sumas todas y divides por n–1, que es parecido a encontrar una media, y sacas
la raíz cuadrada para regresar a las unidades originales. En un
sentido general, estás encontrando algo parecido a la distancia
media respecto de la media.
,
sabrás a qué distancia se encuentra ese número por encima o por
debajo de la media. Como no quieres que las diferencias positivas y
negativas se cancelen entre sí, elevas todas al cuadrado para
hacerlas positivas (pero recuerda que con esto obtienes unidades al
cuadrado). A continuación las sumas todas y divides por n–1, que es parecido a encontrar una media, y sacas
la raíz cuadrada para regresar a las unidades originales. En un
sentido general, estás encontrando algo parecido a la distancia
media respecto de la media.
Si retrocedes más aún, a partir de la fórmula sabes que la desviación estándar no puede ser negativa, porque todo está elevado al cuadrado. También sabes que el valor más pequeño que puede adoptar es cero, cosa que ocurre cuando todos los datos son el mismo (es decir, todos son iguales a la media). Asimismo, puedes ver que los datos que están alejados de la media aumentan el valor de la desviación estándar, y viceversa.
Todo este análisis tiene una utilidad concreta. Como ahora entiendes la fórmula de la desviación estándar, sabes lo que está midiendo en realidad: la dispersión de los datos en torno a la media. Así pues, cuando en una pregunta de examen te pidan la dispersión en torno a la media, sabrás exactamente qué hacer. ¡Toma ya!

Para sentirte cómodo con las fórmulas, sigue los siguientes consejos:
 Ten la actitud
mental correcta. Piensa que las fórmulas no son más que
una forma de sintetizar los cálculos matemáticos. Sólo tienes que
saber descifrarlas. Muchos profesores te dejarán llevar una
hojaresumen al examen o directamente te proporcionarán una hoja de
fórmulas, así que a lo mejor no tienes siquiera que aprendértelas
de memoria.
Ten la actitud
mental correcta. Piensa que las fórmulas no son más que
una forma de sintetizar los cálculos matemáticos. Sólo tienes que
saber descifrarlas. Muchos profesores te dejarán llevar una
hojaresumen al examen o directamente te proporcionarán una hoja de
fórmulas, así que a lo mejor no tienes siquiera que aprendértelas
de memoria.
 Entiende todos los
detalles de todas las fórmulas. Para que una fórmula te
sea de utilidad, es importante que entiendas todos sus componentes.
Por ejemplo, antes de utilizar la fórmula de la desviación estándar
debes saber qué son xi y
Entiende todos los
detalles de todas las fórmulas. Para que una fórmula te
sea de utilidad, es importante que entiendas todos sus componentes.
Por ejemplo, antes de utilizar la fórmula de la desviación estándar
debes saber qué son xi y  , y cuál es el significado de
, y cuál es el significado de  . De lo contrario, la
fórmula no sirve de nada.
. De lo contrario, la
fórmula no sirve de nada.
 Practica con las
fórmulas desde el primer día. Utilízalas para comprobar
los cálculos hechos en clase o en el libro de texto. Si te sale una
respuesta diferente de la que pone, averigua qué has hecho mal. No
pasa nada por equivocarte ahora; has detectado el problema a tiempo
y eso es lo que cuenta.
Practica con las
fórmulas desde el primer día. Utilízalas para comprobar
los cálculos hechos en clase o en el libro de texto. Si te sale una
respuesta diferente de la que pone, averigua qué has hecho mal. No
pasa nada por equivocarte ahora; has detectado el problema a tiempo
y eso es lo que cuenta.
 Cuando apliques
una fórmula para resolver un problema, primero escríbela y luego
sustituye las letras y símbolos por números. Cuantas más
veces escribas una fórmula, más cómodo te sentirás cuando tengas
que usarla en un examen. Y si, esperemos que no, escribes mal la
fórmula, el profesor podrá ver cuál ha sido tu error y posiblemente
te cuente algo por esa pregunta.
Cuando apliques
una fórmula para resolver un problema, primero escríbela y luego
sustituye las letras y símbolos por números. Cuantas más
veces escribas una fórmula, más cómodo te sentirás cuando tengas
que usarla en un examen. Y si, esperemos que no, escribes mal la
fórmula, el profesor podrá ver cuál ha sido tu error y posiblemente
te cuente algo por esa pregunta.

Si en clase has aprendido algunas fórmulas, lo más seguro es que luego tengas que utilizarlas en el examen. No esperes poder utilizar esas fórmulas con plena confianza en el examen si no has practicado antes con ellas y las has escrito muchas, muchas veces. Empieza con problemas fáciles, así cuando la cosa se complique no tendrás que preocuparte tanto.
Elaborar una tabla procedimental
En el fútbol americano, los quarterbacks siempre dicen que intentan ver el juego como si todo ocurriera a cámara lenta, para así tener más tiempo de pensar y reaccionar. En un examen de estadística ocurre exactamente lo mismo (ya ves, tienes algo en común con las estrellas de la Super Bowl). El quarterback empieza a ver las cosas a “cámara lenta” cuando empieza a distinguir pautas en la formación defensiva del equipo contrario, en lugar de ver todas las jugadas diferentes. De forma similar, en un examen tú también entras a cámara lenta cuando clasificas los problemas en categorías a medida que los vas leyendo, en lugar de pensar que no se parecen a nada de lo que hayas visto antes.
Para lograr esto, a muchos de mis alumnos les ayuda elaborar una tabla procedimental. Una tabla procedimental sirve para clasificar los tipos de problemas que probablemente te encuentres según las estrategias para resolverlos, con ejemplos que puedas consultar rápidamente. La idea básica es organizar lo que sabes siguiendo el hilo de pensamiento siguiente: “Si el problema me pide X, lo resuelvo haciendo Y, de esta manera”. Una tabla procedimental tiene tres columnas:
 Pregunta.
En esta columna tienes que escribir una breve descripción de lo que
te piden que hagas. Por ejemplo, si el problema te pide que
contrastes una afirmación referida a la media poblacional (en el
capítulo 14 encontrarás más información al respecto), escribe
“Contrastar una afirmaciónmedia poblacional”. Si te pide una
estimación de la media poblacional (más información en el capítulo
13), escribe “Estimar media poblacional”.
Pregunta.
En esta columna tienes que escribir una breve descripción de lo que
te piden que hagas. Por ejemplo, si el problema te pide que
contrastes una afirmación referida a la media poblacional (en el
capítulo 14 encontrarás más información al respecto), escribe
“Contrastar una afirmaciónmedia poblacional”. Si te pide una
estimación de la media poblacional (más información en el capítulo
13), escribe “Estimar media poblacional”.

Los problemas pueden enunciarse de distintas formas, porque así es cómo funciona el mundo real. Si te encuentras con enunciados diferentes para un mismo problema, debes ponerlos todos en la misma celda, puesto que piden la misma cosa. Por ejemplo, puede que un problema te pregunte directamente una estimación de la media poblacional, mientras que otro diga: “Indica un rango de valores probables para la media poblacional”. Ambas preguntas piden lo mismo, de manera que tienes que incluirlas en la misma celda.
 Estrategia. En esta columna tienes que poner el
procedimiento estadístico, fórmula o técnica concreta que necesitas
para resolver cada tipo de problema. Para ello, utiliza la jerga
técnica. Por ejemplo, si en la primera columna has escrito
“Contrastar una afirmaciónmedia poblacional”, en esta segunda
columna deberías poner “Contraste de hipótesis para μ”. Si en la primera columna has escrito “Estimar
una media poblacional”, en la segunda columna debes poner
“Intervalo de confianza para μ”.
Estrategia. En esta columna tienes que poner el
procedimiento estadístico, fórmula o técnica concreta que necesitas
para resolver cada tipo de problema. Para ello, utiliza la jerga
técnica. Por ejemplo, si en la primera columna has escrito
“Contrastar una afirmaciónmedia poblacional”, en esta segunda
columna deberías poner “Contraste de hipótesis para μ”. Si en la primera columna has escrito “Estimar
una media poblacional”, en la segunda columna debes poner
“Intervalo de confianza para μ”.

A la hora de asignar estrategias a las distintas preguntas, guíate por los ejemplos incluidos en tus apuntes de clase y en el libro de texto.
 Procedimiento. En la tercera columna escribe un
ejemplo, una fórmula o una nota breve que te oriente en la
dirección correcta. Escribe cualquier cosa con la que te sientas
cómodo (no va a verlo nadie más que tú, así que hazlo a tu manera).
Por ejemplo, si en la primera columna has escrito “Estimar la media
poblacional” y en la segunda columna has escrito “Intervalo de
confianzamedia poblacional”. En la tercera columna puedes poner la
fórmula.
Procedimiento. En la tercera columna escribe un
ejemplo, una fórmula o una nota breve que te oriente en la
dirección correcta. Escribe cualquier cosa con la que te sientas
cómodo (no va a verlo nadie más que tú, así que hazlo a tu manera).
Por ejemplo, si en la primera columna has escrito “Estimar la media
poblacional” y en la segunda columna has escrito “Intervalo de
confianzamedia poblacional”. En la tercera columna puedes poner la
fórmula.
Aunque acabo de darte una explicación muy larga y detallada, en realidad hacer una tabla procedimental es la mar de sencillo. A continuación, a modo de ejemplo, puedes ver cómo se introduciría en una tabla procedimental el problema del intervalo de confianza que acabo de mencionar.

Utilizando estas tres columnas, continúa introduciendo en tu tabla procedimental los distintos tipos de problemas que te hayan explicado en clase. No hace falta que escribas hasta el último ejemplo; busca modelos recurrentes y reduce la lista de problemas a un número razonable.

Personaliza la tabla procedimental según tus necesidades particulares, porque sólo te servirá de algo si la haces tú mismo. Cada persona es un mundo, y lo que le sirve a tu amigo quizá no te sirva a ti. No obstante, a lo mejor te viene bien comparar tu tabla con la de un compañero de clase para ver si te has dejado algo.

Si te dejan hacer el examen con una hojaresumen, te sugiero que en una cara pongas tu tabla procedimental. En la otra cara, anota las pequeñas perlas de información que el profesor os dio en clase pero no escribió en la pizarra. Y aunque no te dejen llevar una hojaresumen, yo te aconsejo que igualmente prepares una y la utilices para estudiar. Te ayudará a tener las ideas claras, y así te costará menos ver qué te piden en los problemas y cómo tienes que resolverlos. Si sales del examen sin haber mirado siquiera la hojaresumen, significa que has hecho bien las cosas: mientras escribías la hoja fuiste interiorizando todos los contenidos.
Entender qué te están preguntando
Mis alumnos me dicen a menudo que no entienden lo que pide el problema. Ésa es la pregunta del millón de dólares, ¿verdad? Y no es un asunto en absoluto trivial. La pregunta suele estar oculta en el enunciado del problema; generalmente no es directa como “Encuentra la media de este conjunto de datos”.

Por ejemplo, es posible que te pidan que “interpretes” un resultado estadístico. Pero ¿qué significa “interpretar”? Para la mayoría de los profesores, “interpretar” significa explicar algo con palabras que pueda entender cualquier persona sin conocimientos de estadística.
Supongamos que te dan un informe donde se analizan los datos sobre el número de delitos y el número de policías de una determinada ciudad, y te piden que interpretes la correlación existente entre esas dos variables. En primer lugar, encuentras la cifra que corresponde a la correlación (supongamos que es –0,85) y a continuación hablas de sus características más importantes con un lenguaje que sea fácil de entender. La respuesta que yo querría ver en un examen sería algo parecido a lo siguiente: “La correlación entre el número de policías y el número de delitos es –0,85, lo cual indica un relación lineal negativa muy marcada. Cuando el número de policías aumenta, el número de delitos disminuye”.

Si entiendes qué te está pidiendo el problema, es más probable que sepas resolverlo. Cuando sabes lo que tienes que hacer, te sientes más seguro. Por el contrario, si no entiendes lo que pide el problema, incluso comenzarlo te parecerá muy difícil. Eso hará que te pongas más nervioso, lo cual, a su vez, puede influir en tu capacidad de resolver el resto de los problemas. Entonces, ¿qué hay que hacer para interpretar correctamente un enunciado? Aquí tienes algunos consejos:
 Lee despacio la
última frase del problema. Ahí es donde suele estar la
pregunta. En lugar de leer todo el enunciado una segunda
(y tercera, y cuarta) vez y ponerte más nervioso todavía, léelo una
sola vez y concéntrate en la parte final.
Lee despacio la
última frase del problema. Ahí es donde suele estar la
pregunta. En lugar de leer todo el enunciado una segunda
(y tercera, y cuarta) vez y ponerte más nervioso todavía, léelo una
sola vez y concéntrate en la parte final.
 Practica antes del
examen. Repasa todos los ejemplos de los apuntes, los
deberes y los problemas del libro de texto, e intenta dilucidar qué
es lo que se pregunta en cada caso. Al final empezarás a distinguir
pautas en la redacción de los problemas, y cada vez te costará
menos ver lo que te piden en realidad.
Practica antes del
examen. Repasa todos los ejemplos de los apuntes, los
deberes y los problemas del libro de texto, e intenta dilucidar qué
es lo que se pregunta en cada caso. Al final empezarás a distinguir
pautas en la redacción de los problemas, y cada vez te costará
menos ver lo que te piden en realidad.
 Pregúntale al
profesor qué pistas tienes que buscar y llévale algunos problemas
de ejemplo. Cuando vea que intentas obtener una visión más
amplia, lo dejarás impresionado (eso es algo que a los profesores
nos encanta). Luego puedes incorporar esos ejemplos a tu tabla
procedimental. (Releer el apartado “Elaborar una tabla
procedimental”.)
Pregúntale al
profesor qué pistas tienes que buscar y llévale algunos problemas
de ejemplo. Cuando vea que intentas obtener una visión más
amplia, lo dejarás impresionado (eso es algo que a los profesores
nos encanta). Luego puedes incorporar esos ejemplos a tu tabla
procedimental. (Releer el apartado “Elaborar una tabla
procedimental”.)
 Traduce el
enunciado del problema a un enunciado estadístico. Para
eso tienes que etiquetar la información que te dan (como explico en
el siguiente apartado) y también la que quieres encontrar.
Traduce el
enunciado del problema a un enunciado estadístico. Para
eso tienes que etiquetar la información que te dan (como explico en
el siguiente apartado) y también la que quieres encontrar.
Por ejemplo, el profesor Lucio quiere ponerle un sobresaliente al 20% de sus alumnos en el examen de estadística, y tú tienes que averiguar cuál es la nota de corte para sacar un sobresaliente, lo cual es lo mismo que decir: “Encuentra la nota que corresponde al percentil 80”.
Etiquetar la información que te dan

Muchos alumnos intentan resolver los problemas lanzándose directamente a hacer cálculos con los números que les dan. Este sistema puede funcionar con los problemas más sencillos, pero llega un momento en que deja de valer, y entonces necesitas un método más estructurado. En este sentido, el hábito de etiquetarlo todo correctamente te será muy útil, ya que la etiqueta es lo que permite establecer la conexión crítica entre la primera y la segunda columna de la tabla procedimental (descrita anteriormente en este mismo capítulo). Puede que leas un problema y sepas lo que tienes que hacer, pero si no sabes cómo utilizar la información que te dan, no podrás resolverlo correctamente. Para entender de verdad los números que te da el problema, escribe junto a cada uno lo que significa.
Supongamos que te ponen el siguiente problema: “Tienes un piso en una determinada ciudad y quieres predecir su precio (en miles de euros) a partir de su superficie útil (en metros cuadrados). Recopilas datos sobre 100 casas seleccionadas al azar que se han vendido recientemente. Compruebas que el precio medio es de 219.100 euros, con una desviación estándar de 60.100 euros, y sabes que la superficie media es de 92 metros cuadrados, con una desviación estándar de 16 metros cuadrados. Calculas que la correlación entre superficie y precio para estas casas es de +0,9. Encuentra la recta de regresión de mejor ajuste para predecir el precio de la casa a partir de su superficie”.
El primer paso es etiquetarlo todo. Como te
basas en la superficie para predecir el precio, la superficie debe
ser la variable x y el precio debe ser la
variable y. Las medias son  = 92 (metros
cuadrados) e
= 92 (metros
cuadrados) e  = 219,1 (miles de dólares); las
desviaciones estándares son sx = 16,61 (metros cuadrados) y sy = 2,85 (euros), y
la correlación es r = 0,90. El tamaño
muestral es n = 100. Ahora ya puedes
poner los números en las fórmulas que corresponda. (En el capítulo
18 tienes la información sobre la correlación y la regresión.)
= 219,1 (miles de dólares); las
desviaciones estándares son sx = 16,61 (metros cuadrados) y sy = 2,85 (euros), y
la correlación es r = 0,90. El tamaño
muestral es n = 100. Ahora ya puedes
poner los números en las fórmulas que corresponda. (En el capítulo
18 tienes la información sobre la correlación y la regresión.)
Si sabes que vas a trabajar con una recta de regresión y que vas a utilizar fórmulas, resulta muy útil tener toda la información perfectamente organizada y etiquetada. Así tienes una cosa menos en que pensar. (Este problema en concreto está resuelto en el apartado “Establecer la conexión y resolver el problema”.) Si este ejemplo no te convence, aquí tienes otras seis razones para etiquetar toda la información que te den en un problema:
 Las etiquetas
facilitan el repaso. Cuando repases el problema (como te
aconsejo en el apartado “Haz las cuentas... dos veces”), te
resultará muy sencillo ver el hilo del razonamiento que seguiste
para resolverlo.
Las etiquetas
facilitan el repaso. Cuando repases el problema (como te
aconsejo en el apartado “Haz las cuentas... dos veces”), te
resultará muy sencillo ver el hilo del razonamiento que seguiste
para resolverlo.
 Tu profesor
quedará impresionado. Verá las etiquetas y sabrá que al
menos entiendes lo que significa la información que te han dado. De
este modo, aunque te equivoques en los cálculos puede que te den
algún punto por esa pregunta.
Tu profesor
quedará impresionado. Verá las etiquetas y sabrá que al
menos entiendes lo que significa la información que te han dado. De
este modo, aunque te equivoques en los cálculos puede que te den
algún punto por esa pregunta.
 Las etiquetas
ahorran tiempo. Ya sé que escribir más información parece
una extraña manera de ahorrar tiempo, pero las etiquetas permiten
identificar la información necesaria en un santiamén.
Las etiquetas
ahorran tiempo. Ya sé que escribir más información parece
una extraña manera de ahorrar tiempo, pero las etiquetas permiten
identificar la información necesaria en un santiamén.
Por ejemplo, supongamos que tienes que
calcular un intervalo de confianza del 95% para la media
poblacional (del modo descrito en el capítulo 13) y te dicen que la
media muestral es 60, la desviación estándar de la población es 10,
y el tamaño muestral es 200. Sabes que en la fórmula deben aparecer
 , σ y
n, y conoces una que los incluye a
todos:
, σ y
n, y conoces una que los incluye a
todos:
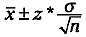
Como ya lo tienes todo etiquetado, simplemente coges lo que necesitas, lo metes en la fórmula, utilizas un valor z* de 1,96 (el valor crítico correspondiente a un nivel de confianza del 95%) y haces los cálculos para obtener la respuesta:

 Las etiquetas
ayudan a organizar la mente. Si trabajas con símbolos, y
no sólo con números, es menos probable que te pierdas en los
cálculos y olvides lo que estás haciendo. Si clasificas toda la
información que te dan, no tendrás que leer el problema una y otra
vez, y no te pondrás tan nervioso.
Las etiquetas
ayudan a organizar la mente. Si trabajas con símbolos, y
no sólo con números, es menos probable que te pierdas en los
cálculos y olvides lo que estás haciendo. Si clasificas toda la
información que te dan, no tendrás que leer el problema una y otra
vez, y no te pondrás tan nervioso.
 Las etiquetas
ayudan a decidir qué fórmula o técnica vas a utilizar para resolver
el problema. Por ejemplo, si crees que debes hacer un
contraste de hipótesis pero no te dan una afirmación sobre la media
poblacional, significa que no vas bien encaminado. Posiblemente
tengas que calcular un intervalo de confianza. Darte cuenta de esto
te ahorra un tiempo precioso, ya que no avanzas en la dirección
equivocada. Las etiquetas ayudan a reducir rápidamente el abanico
de opciones.
Las etiquetas
ayudan a decidir qué fórmula o técnica vas a utilizar para resolver
el problema. Por ejemplo, si crees que debes hacer un
contraste de hipótesis pero no te dan una afirmación sobre la media
poblacional, significa que no vas bien encaminado. Posiblemente
tengas que calcular un intervalo de confianza. Darte cuenta de esto
te ahorra un tiempo precioso, ya que no avanzas en la dirección
equivocada. Las etiquetas ayudan a reducir rápidamente el abanico
de opciones.
 Las etiquetas
ayudan a resistir el impulso de llenarlo todo de números sin
más. Si te lanzas a hacer cálculos, es más probable que
acabes dando una respuesta incorrecta y no te cuenten ningún punto
por el problema. Quizá tu profesor no pueda seguir tu razonamiento,
o sencillamente no esté dispuesto a invertir todo el tiempo que
necesitaría para ello (lo siento, pero esto ocurre a veces).
Las etiquetas
ayudan a resistir el impulso de llenarlo todo de números sin
más. Si te lanzas a hacer cálculos, es más probable que
acabes dando una respuesta incorrecta y no te cuenten ningún punto
por el problema. Quizá tu profesor no pueda seguir tu razonamiento,
o sencillamente no esté dispuesto a invertir todo el tiempo que
necesitaría para ello (lo siento, pero esto ocurre a veces).

Poner etiquetas te ahorrará nervios, tiempo y puntos cuando hagas un examen. Sin embargo, la clave está en practicar desde el principio, cuando los problemas todavía son fáciles. Si nunca te has puesto a clasificar la información de un problema, no esperes que el día del examen sepas hacerlo por ciencia infusa. Conviértelo en hábito y así no te entrará el pánico cuando veas un problema nuevo. Por lo menos sabrás dividirlo en partes más pequeñas, lo cual siempre ayuda.
Hacer un dibujo
Seguro que has oído el dicho “Una imagen vale más que mil palabras”. Como profesora de estadística, yo siempre digo que una imagen vale más que mil puntos (o al menos la mitad de los puntos del problema). Si la información que te dan o la pregunta planteada pueden expresarse de forma gráfica, debes hacerlo. Éstas son las razones:
 Un dibujo puede
ayudarte a entender de qué va el problema. Por ejemplo, si
sabes que las notas de examen tienen una distribución normal con
una media de 75 y una desviación estándar de 5 (en el capítulo 9
encontrarás más información sobre la distribución normal), dibujas
una campana de Gauss y marcas la media en el centro y tres
desviaciones estándares por cada lado. Ahora puedes visualizar la
situación planteada.
Un dibujo puede
ayudarte a entender de qué va el problema. Por ejemplo, si
sabes que las notas de examen tienen una distribución normal con
una media de 75 y una desviación estándar de 5 (en el capítulo 9
encontrarás más información sobre la distribución normal), dibujas
una campana de Gauss y marcas la media en el centro y tres
desviaciones estándares por cada lado. Ahora puedes visualizar la
situación planteada.
 Un dibujo puede
ayudarte a saber lo que debes encontrar. Por ejemplo, si
tienes que averiguar la probabilidad de que Roberto haya obtenido
más de 70 puntos en el examen, sombreas el área que queda a la
derecha del 70 en tu dibujo y ya puedes ponerte manos a la
obra.
Un dibujo puede
ayudarte a saber lo que debes encontrar. Por ejemplo, si
tienes que averiguar la probabilidad de que Roberto haya obtenido
más de 70 puntos en el examen, sombreas el área que queda a la
derecha del 70 en tu dibujo y ya puedes ponerte manos a la
obra.
 Tu profesor puede
ver que entiendes el planteamiento básico del problema, con lo que
es más probable que te cuente al menos una parte de los puntos
aunque lo hagas mal. Por otro lado, si te equivocas en la
respuesta y el profesor sabe que podrías haberlo evitado haciendo
un simple dibujo, no esperes que sea comprensivo contigo.
Tu profesor puede
ver que entiendes el planteamiento básico del problema, con lo que
es más probable que te cuente al menos una parte de los puntos
aunque lo hagas mal. Por otro lado, si te equivocas en la
respuesta y el profesor sabe que podrías haberlo evitado haciendo
un simple dibujo, no esperes que sea comprensivo contigo.
 Los alumnos que
hacen dibujos generalmente resuelven los problemas de manera
correcta. Sin un dibujo es fácil que se te vaya de la
cabeza lo que te están pidiendo y cometas errores como calcular
P(X<70) en lugar de P(X>70), por ejemplo. Además, si tienes dibujos
que mirar resulta más fácil revisar los problemas y corregir
posibles errores antes de entregar el examen.
Los alumnos que
hacen dibujos generalmente resuelven los problemas de manera
correcta. Sin un dibujo es fácil que se te vaya de la
cabeza lo que te están pidiendo y cometas errores como calcular
P(X<70) en lugar de P(X>70), por ejemplo. Además, si tienes dibujos
que mirar resulta más fácil revisar los problemas y corregir
posibles errores antes de entregar el examen.

A lo mejor te parece que hacer un dibujo es una pérdida de tiempo en mitad de un examen, pero lo cierto es que ahorra tiempo porque te encauza en la dirección correcta, te mantiene centrado en tus razonamientos y te ayuda a comprobar si realmente estás respondiendo a lo que te preguntan. Además, puede ayudarte a analizar la respuesta numérica final y confirmar que es correcta, o bien a detectar y corregir rápidamente un error que podría suponerte algunos puntos menos. (Te aconsejo que hagas dibujos cuando estudies, para que luego en el examen te salgan de forma natural.)
Establecer la conexión y resolver el problema

Una vez que tengas claro lo que te piden, hayas etiquetado toda la información y hayas hecho un dibujo, es hora de resolver el problema. Después del trabajo de preparación, nueve veces de cada diez recordarás un método aprendido en clase, una fórmula que contenga los elementos etiquetados o un ejemplo que hayas estudiado. Utiliza o recuerda la tabla procedimental y ponte manos a la obra. (Más información en “Elaborar una tabla procedimental”.)

Dividir un problema en partes significa tener menos que pensar en cada uno de los pasos, lo cual es una gran ventaja en una situación tan estresante como un examen, en la que puedes olvidar hasta cómo te llamas (esta estrategia me recuerda un viejo chiste: “¿Cómo te comerías un elefante? Mordisco a mordisco”).
En el ejemplo anterior en que nos basábamos en la superficie de una casa para predecir su precio (relee el apartado “Etiquetar la información que te dan”), conoces la media y la desviación estándar de la superficie, la media y la desviación estándar del precio, y la correlación entre ambos, y además lo tienes todo etiquetado. Te piden que encuentres la ecuación de la recta de regresión para predecir el precio de la casa a partir de su superficie, y sabes que para eso hay que resolver la ecuación y = a + bx, en la que x = superficie (pies cuadrados), y = precio (miles de euros), b es la pendiente de la recta de regresión, y a es la ordenada en el origen.
Ahora ya sabes lo que tienes que hacer:
encontrar a y b. Como recordarás (y si no, puedes consultarlo),
las fórmulas son  . Coges los números que has etiquetado
(
. Coges los números que has etiquetado
( = 92;
sx = 16,61;
= 92;
sx = 16,61;
 = 219,1;
sy = 2,85; y
r = 0,9), los metes en las fórmulas y
resuelves (casi parece una receta de cocina, ¿verdad?). La
pendiente es
= 219,1;
sy = 2,85; y
r = 0,9), los metes en las fórmulas y
resuelves (casi parece una receta de cocina, ¿verdad?). La
pendiente es 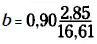 = 0,154 y la ordenada en el origen es
a=219,1 – 0,154 (92) = –204,93, de manera
que la ecuación de la recta de regresión es y = –204,93 + 0,154x. (En
el capítulo 18 explico la regresión con todo detalle.)
= 0,154 y la ordenada en el origen es
a=219,1 – 0,154 (92) = –204,93, de manera
que la ecuación de la recta de regresión es y = –204,93 + 0,154x. (En
el capítulo 18 explico la regresión con todo detalle.)
Haz las cuentas... dos veces
Todavía recuerdo los problemas que tuve con el álgebra en mi época de instituto. Para mí, durante mucho tiempo, 3×2 era igual a 5. Este error, y otros similares, me hicieron perder un montón de puntos en los exámenes, y no había manera de arreglarlo. Un día decidí que ya no iba a perder más puntos por algo tan absurdo. A partir de aquel momento escribí todos los pasos y resistí la tentación de hacer cálculos de cabeza. Cuando llegaba a un resultado final, en lugar de pasar al siguiente problema, volvía al principio y lo repasaba todo paso por paso, convencida de que probablemente habría un error en algún sitio y tenía que encontrarlo antes que el profe.
Esta estrategia me obligaba a revisar cada paso sin dar nada por sentado, como si estuviera calificando el examen de otra persona. Encontraba más errores porque nunca me saltaba un paso sin comprobarlo. De tantas veces que me corregí a mí misma, al final dejé de pensar que 3×2 eran 5. Comencé a sacar mejores notas en los exámenes, simplemente porque empecé a revisarlo todo con más atención. Eso me recuerda un viejo dicho: “El buen carpintero mide dos veces y corta una”. De este modo se desperdicia mucha menos madera.

Cada vez que detectas y corriges un error antes de entregar el examen, estás ganando un montón de puntos. Encuentra tus fallos antes de que lo haga el profesor y te sorprenderás de cuánto mejorarán tus notas. No obstante, ten presente que en los exámenes tienes un tiempo limitado, de manera que conviene hacer los problemas bien al primer intento. Etiquetar toda la información, hacer dibujos y escribir las fórmulas son cosas que ayudan, y mucho.
Analizar tus respuestas
Un estadístico muy destacado que conozco tiene un papel enmarcado en su despacho. Es una página de un examen que hizo cuando estaba en el instituto. Una de las respuestas, que es un número dos, está marcada con un gran círculo rojo. ¿Por qué estaba tan mal poner un dos como respuesta? Porque el problema le pedía que encontrara una probabilidad, y las probabilidades siempre están entre 0 y 1. En consecuencia, no le contaron ningún punto por ese problema. De hecho, estoy segura de que su profesor incluso hubiera querido restarle puntos por haber cometido ese fallo (molesta mucho ver errores tan garrafales).

Comprueba siempre si tu respuesta final tiene sentido. Una desviación estándar negativa, una probabilidad mayor que 1 o una correlación de –121,23 son cosas que no van a sentar nada bien a tu profesor, y no las verá como simples errores matemáticos. Pensará que no sabes (o quizá no te importa) cómo debe ser el resultado final y que tienes enormes lagunas en los conocimientos básicos.

Si sabes que tu respuesta no puede estar bien de ninguna manera pero tampoco tienes idea de dónde te has equivocado, no pierdas más tiempo. Simplemente escribe una nota al margen diciendo que eres consciente de que la respuesta es incorrecta, pero no sabes dónde está el fallo. Así te distingues de ese otro alumno que encuentra una probabilidad de 10.524,31 (sí, he sido testigo) y se queda tan ancho.
Por cierto, quizá te estés preguntando por qué ese estadístico de talla mundial conserva esa hoja de examen enmarcada en una pared de su despacho. Dice que es para no perder la humildad. Aprende de su ejemplo y nunca pases al siguiente problema sin preguntarte antes: “¿Tiene sentido esta respuesta?”.