Herramientas del oficio

En este capítulo

Ver la estadística como un proceso, no sólo como números

Familiarizarse con los términos más importantes de la estadística

Hoy en día la palabra de moda es datos, como cuando uno dice: “¿Puedes aportar datos que respalden tu afirmación?”, “¿Qué datos tenemos sobre esto?”, “Los datos confirmaron la hipótesis original según la cual...”, “Los datos estadísticos demuestran que...” o “Los datos me avalan”. Pero la estadística es algo más que datos.

La estadística es todo el proceso de recopilación de pruebas para dar respuesta a preguntas sobre el mundo, en los casos en que esas pruebas resultan ser datos.

En este capítulo verás que la estadística funciona como un proceso y que los números tienen su propio papel. También te daré a conocer los términos técnicos más utilizados en estadística y te mostraré cómo esas definiciones y conceptos se enmarcan en este proceso. Así pues, la próxima vez que oigas decir que una encuesta tiene un margen de error de más/menos tres puntos porcentuales, tendrás al menos una noción básica de lo que eso significa.

Estadística: algo más que números

Los estadísticos no sólo “hacen estadísticas”. Aunque el resto del mundo los considere unos tipos raros que trabajan con números, ellos se ven a sí mismos como los guardianes del método científico. Naturalmente, los estadísticos colaboran con expertos de otros campos para satisfacer su demanda de información, pero procesar los datos de otro es tan sólo una pequeña parte del trabajo de un estadístico (de hecho, si no hiciéramos otra cosa en todo el día dejaríamos nuestros empleos y nos haríamos asesores de los casinos). En realidad, la estadística interviene en todos los aspectos del método científico: formular preguntas idóneas, diseñar estudios, recopilar datos válidos, analizar esos datos correctamente y extraer conclusiones apropiadas. Pero, aparte de analizar los datos correctamente, ¿qué tienen que ver todos estos aspectos con la estadística? Eso es lo que explico en este capítulo.

Toda investigación comienza con una pregunta, por ejemplo:

Ninguna de estas preguntas habla directamente de cifras. Sin embargo, todas ellas requieren el uso de datos y procesos estadísticos para llegar a una respuesta.

Imagina que un investigador quiere saber quién ganará las próximas elecciones presidenciales en Estados Unidos. Para responder con conocimiento de causa, el investigador debe seguir varios pasos:

1. Determinar la población objeto de estudio.

En este caso el investigador pretende estudiar a los ciudadanos mayores de edad que tengan previsto votar en las siguientes elecciones.

2. Recopilar los datos.

Este paso es todo un desafío, porque no puedes salir a la calle y preguntar a todos y cada uno de los ciudadanos estadounidenses si tienen previsto votar y, en tal caso, por quién. Pero dejando eso de lado, pongamos que alguien dice: “Sí, tengo pensado ir a votar”. ¿Sabes a ciencia cierta que esa persona acudirá a las urnas el día de las elecciones? ¿Y seguro que esa persona te dirá por quién va a votar? ¿Y qué pasa si esa persona cambia de opinión y vota por otro candidato?

3. Organizar, resumir y analizar los datos.

Una vez el investigador ha recopilado todos los datos que necesita, organizarlos, resumirlos y analizarlos le ayuda a responder la pregunta planteada. Este paso es el que la mayoría de la gente asocia con la estadística.

4. Examinar todos los resúmenes de datos, gráficos, diagramas y análisis y extraer conclusiones de ellos para intentar responder la pregunta original.

Por supuesto, el investigador no estará seguro al 100% de que su respuesta sea correcta, ya que no habrá preguntado a todos y cada uno de los ciudadanos estadounidenses. No obstante, sí puede obtener una respuesta de la que esté seguro casi al 100%. De hecho, con una muestra de 2.500 personas seleccionadas de manera no sesgada (es decir, cuando todas las muestras posibles de 2.500 personas tienen la misma probabilidad de ser elegidas), el investigador puede obtener resultados exactos con un error de más/menos un 2,5% (si todos los pasos del proceso de investigación se llevan a cabo correctamente).

A la hora de extraer conclusiones, el investigador debe ser consciente de que todos los estudios tienen sus limitaciones y que, al existir siempre la posibilidad de cometer errores, los resultados podrían ser incorrectos. A este respecto, se puede proporcionar un valor numérico que indique a los demás cuánto confía el investigador en sus resultados y qué grado de exactitud se espera de ellos. (En el capítulo 12 encontrarás más información sobre el margen de error.)

Una vez ha concluido la investigación y se ha contestado la pregunta, es habitual que los resultados den pie a otras preguntas e investigaciones. Por ejemplo, si se observa que los hombres parecen favorecer a un candidato y las mujeres a otro, las siguientes preguntas podrían ser: “¿Quién responde a los sondeos más a menudo el día de las elecciones, los hombres o las mujeres? ¿Y qué factores determinan si acudirán a las urnas?”.

En resumidas cuentas, la estadística consiste en aplicar el método científico para responder preguntas de investigación sobre el mundo. Los métodos estadísticos se utilizan en todos los pasos de un estudio, desde la fase de diseño hasta que se recopilan los datos, se organiza y resume la información, se lleva a cabo el análisis, se extraen conclusiones, se valoran las limitaciones y, por último, se diseña el siguiente estudio para responder las nuevas preguntas surgidas. La estadística es algo más que números: es un proceso.

Terminología básica de estadística

Todos los campos del saber tienen su propia jerga, y la estadística no es ninguna excepción. Si ves el proceso estadístico como una serie de etapas que atraviesas en el camino que va desde la pregunta hasta la respuesta, ya puedes suponer que en cada etapa te encontrarás con varias herramientas y términos técnicos (o jerga) con los que seguir adelante. Si se te están empezando a erizar los pelos de la nuca, tranquilízate. Nadie va a exigir que te conviertas en un experto en estadística ni que utilices esos términos a todas horas. Ni siquiera hace falta que vayas por ahí con una calculadora y un protector para el bolsillo de la camisa (los estadísticos no son así en realidad, es sólo una leyenda urbana). De todos modos, a medida que el mundo entero toma conciencia de la importancia de los números, los términos propios de la estadística se utilizan cada vez más en los medios de comunicación y en el lugar de trabajo, de manera que conocer su verdadero significado puede echarte un cable en muchas ocasiones. Además, si estás leyendo este libro porque quieres aprender a calcular algunas estadísticas, entender la terminología es el primer paso. Por eso en este apartado te doy a conocer algunos términos básicos del campo de la estadística. Para una explicación más detallada, sigue las referencias a los capítulos correspondientes de este libro.

Datos

Los datos son los elementos de información que recopilas durante el estudio. Por ejemplo, les pregunto a cinco amigos míos cuántas mascotas tienen y me dan los siguientes datos: 0, 2, 1, 4, 18 (el quinto amigo cuenta como mascotas todos los peces de su acuario). Pero no todos los datos son números; también tomo nota del sexo de todos mis amigos y obtengo lo siguiente: varón, varón, mujer, varón, mujer.

Existen dos grandes grupos de datos: los numéricos y los categóricos (a continuación comento a grandes rasgos las características de estas variables; en el capítulo 5 encontrarás una explicación más detallada).

Los datos ordinales combinan los datos numéricos y los categóricos. Los datos entran en dos categorías, pero los números asignados a esas categorías tienen significado. Por ejemplo, al valorar un restaurante en una escala de 0 a 5 se obtienen datos ordinales. Los datos ordinales generalmente se consideran categóricos, de manera que los grupos se ordenan al elaborar los gráficos y diagramas. Yo no me referiré a ellos de manera separada en este libro.

Conjunto de datos

Un conjunto de datos es la totalidad de los datos obtenidos de la muestra. Por ejemplo, si has pesado cinco envases y los pesos obtenidos son 6, 8, 11, 34 y 2 kilos, esos cinco números (6, 8, 11, 34, 2) forman tu conjunto de datos. Si únicamente anotas el tamaño del envase (por ejemplo pequeño, mediano o grande), el conjunto de datos podría ser el siguiente: mediano, mediano, mediano, grande, pequeño.

Variable

Una variable es una característica o un valor numérico que varía para cada individuo. Una variable puede representar el resultado de un recuento (por ejemplo, el número de mascotas que tienes) o una medición (el tiempo que tardas en levantarte por la mañana). O bien la variable puede ser categórica, de manera que cada persona se incluye en un grupo (o categoría) según unos criterios determinados (por ejemplo, filiación política, raza o estado civil). Los elementos de información registrados sobre unidades de análisis en relación con una variable son los datos.

Población

Para responder prácticamente a cualquier pregunta que se te ocurra investigar, debes enfocar tu atención a un grupo concreto de unidades de análisis (por ejemplo un grupo de personas, ciudades, animales, especímenes de roca, puntuaciones de examen, etc.). Por ejemplo:

En cada uno de estos ejemplos se plantea una pregunta. Y en cada caso puedes identificar un grupo concreto de unidades de análisis: los ciudadanos españoles, todos los campos plantados de Wisconsin, todas las enfermas de cáncer de mama y todas las cajas de cereales, respectivamente. El grupo de elementos o unidades que quieres estudiar para responder a la pregunta que da pie a la investigación es lo que denominamos población. Sin embargo, a veces cuesta mucho definir una población. En un buen estudio, los investigadores definen la población de forma muy clara, mientras que en uno malo la población no está bien definida.

La pregunta de si los bebés duermen mejor con música es un buen ejemplo de lo difícil que puede ser definir la población. ¿Cómo definirías exactamente a un bebé? ¿Un niño de menos de tres meses? ¿De menos de un año? ¿Y quieres estudiar sólo a los bebes de un determinado país o a los bebés de todo el mundo? Los resultados pueden variar entre bebés de distintas edades, entre bebés españoles y japoneses, etc.

Muchas veces los investigadores quieren estudiar una población muy grande, pero al final (para ahorrar tiempo o dinero o porque no saben hacerlo mejor) acaban estudiando una muy pequeña. Este atajo puede suponer un gran problema a la hora de extraer conclusiones. Por ejemplo, pongamos que un profesor de universidad quiere estudiar el modo en que los anuncios de televisión persuaden a los consumidores para que compren productos. Su estudio está basado en un grupo de sus propios alumnos que participaron para que les subiera medio punto la nota final de la asignatura. Este grupo experimental puede ser adecuado, pero los resultados no pueden extrapolarse a una población distinta de sus alumnos, ya que en el estudio no está representada más que la reducida población del aula.

Muestras y aleatoriedad

¿Qué haces cuando pruebas un cocido? Remueves la olla con la cuchara, coges un poquito y lo pruebas. A continuación extraes una conclusión sobre el contenido de la olla entera, aunque no lo hayas probado todo. Si tomas la muestra de forma imparcial (por ejemplo, no te limitas a probar sólo los ingredientes más sabrosos), puedes hacerte una idea clara del sabor del cocido sin tener que comértelo todo. En estadística las muestras se toman exactamente igual. Los investigadores quieren averiguar algo sobre una población pero no tienen suficiente tiempo o dinero para estudiar a todos los elementos de esa población, de manera que eligen un subconjunto de elementos, los estudian y utilizan la información obtenida para extraer conclusiones sobre toda la población. Este subconjunto de la población es lo que se denomina muestra.

Aunque seleccionar una muestra parece algo muy sencillo, en realidad no lo es. La manera de seleccionar una muestra de la población puede marcar la diferencia entre obtener resultados correctos y acabar con un montón de basura. Un ejemplo: pongamos que quieres una muestra de lo que opinan los adolescentes sobre el tiempo que pasan en Internet. Si envías una encuesta con un mensaje de texto, los resultados no representarán las opiniones de todos los adolescentes, que es la población que quieres estudiar. Únicamente representarán a los adolescentes que tengan acceso a mensajes de texto. ¿Ocurre a menudo este desajuste estadístico? No te quepa duda.

Las encuestas a través de Internet son un claro ejemplo de tergiversación estadística por culpa de una mala selección de la muestra. En la red hay miles de encuestas de opinión en las que se puede participar visitando un determinado sitio web. Pero incluso si contestaran una encuesta en Internet 50.000 españoles, esa muestra no sería representativa de toda la población de España; tan sólo representaría a las personas que tuvieran acceso a Internet, visitaran ese sitio web en particular y estuvieran suficientemente interesadas en el tema como para participar en la encuesta (lo cual generalmente significa que tienen opiniones tajantes al respecto). El resultado de todos estos problemas es el sesgo, el favoritismo sistemático de determinadas personas o determinados resultados del estudio.

¿Cómo debe seleccionarse una muestra de forma que se evite el sesgo? La palabra clave es aleatoriedad. Una muestra aleatoria es aquella que se selecciona con igualdad de oportunidades, es decir, cada muestra posible del mismo tamaño que la tuya tiene la misma probabilidad de ser seleccionada de la población. El significado real de aleatorio es que ningún grupo de población se ve favorecido ni excluido del proceso de selección.

Las muestras no aleatorias (o sea, mal hechas) son las que se seleccionan con algún tipo de preferencia o de exclusión automática de una parte de la población. Un ejemplo típico de muestra no aleatoria es la generada por las encuestas de llamada voluntaria (call-in), en las que es la gente quien llama por teléfono y da su opinión sobre un tema en particular en respuesta a un llamamiento de una cadena de televisión. Las personas que deciden participar en este tipo de encuestas no representan a la población en general porque necesariamente estaban viendo el programa y, además, el tema les interesaba lo suficiente como para llamar. Técnicamente no representan una muestra, en el sentido estadístico de la palabra, porque nadie las ha seleccionado, sino que se han elegido a sí mismas para participar, creando así una muestra de respuesta voluntaria o muestra autoseleccionada. Los resultados presentarán un sesgo hacia las personas que tengan opiniones tajantes sobre esa cuestión.

Para tomar una muestra auténticamente aleatoria necesitas un mecanismo de aleatorización para elegir a los participantes. Por ejemplo, la organización Gallup empieza con una lista informatizada de todas las centralitas telefónicas de Estados Unidos, junto con estimaciones del número de viviendas que tienen conexión telefónica. El ordenador utiliza un procedimiento llamado marcación aleatoria de dígitos (RDD por sus siglas en inglés) para generar al azar una relación exhaustiva de los números de teléfono de las centralitas, y a continuación selecciona muestras de esos números. Es decir, el ordenador crea una lista de todos los números de teléfono posibles de Estados Unidos y luego selecciona un subconjunto de números de esa lista para que Gallup llame.

Otro ejemplo de muestreo aleatorio es el empleo de generadores de números aleatorios. En este proceso, los elementos de la muestra se eligen utilizando una lista de números aleatorios generados por ordenador; de manera que cada muestra de elementos tiene la misma probabilidad de ser seleccionada. Los investigadores pueden utilizar este método de aleatorización para asignar enfermos al grupo experimental y al grupo de control en un experimento. Este proceso es el equivalente a extraer nombres de un sombrero o extraer los números del bombo de la lotería.

Por muy grande que sea una muestra, si está basada en métodos no aleatorios los resultados no serán representativos de la población sobre la cual el investigador quiere extraer conclusiones. No te dejes impresionar por el tamaño de una muestra: primero comprueba cómo la han seleccionado. Busca el término muestra aleatoria. Si ese término aparece, lee la letra pequeña para saber exactamente qué método utilizaron y aplica la definición anterior para cerciorarte de que esa muestra realmente se eligió de forma aleatoria. Una muestra aleatoria pequeña es mejor que una muestra no aleatoria grande.

Estadístico

Un estadístico es un número que resume los datos recopilados de una muestra. Existen muchos estadísticos diferentes para resumir datos. Por ejemplo, los datos se pueden resumir como porcentaje (el 60% de las unidades familiares de la muestra tienen más de dos coches), promedio (el precio medio de una vivienda en esta muestra es de...), mediana (el sueldo mediano de los 1.000 ingenieros informáticos que componen la muestra es de...) o percentil (este mes tu bebé está en el percentil 90 de peso según datos recopilados de más de 10.000 bebés).

El tipo de estadístico que se calcule depende del tipo de datos. Por ejemplo, los porcentajes se utilizan para resumir datos categóricos y las medias se utilizan para resumir datos numéricos. El precio de una casa es una variable numérica, de manera que puedes calcular su media o su desviación estándar. Por el contrario, el color de una casa es una variable categórica; no tiene sentido buscar la desviación estándar ni la media de color. En este caso los estadísticos importantes son los porcentajes de casas de cada color.

No todas las estadísticas son correctas ni ecuánimes, por supuesto. Sólo porque alguien te dé una estadística, no tienes la garantía de que esa estadística sea científica o legítima. A lo mejor has oído alguna vez el siguiente dicho: “Los números no mienten, pero los mentirosos también usan números”.

Parámetro

Los estadísticos se basan en datos de una muestra, no en datos de la población. Si recopilas datos de la población entera, estás haciendo un censo. Si a continuación resumes toda la información del censo en un único número procedente de una variable, ese número es un parámetro, no un estadístico. Las más de las veces, los investigadores intentan estimar los parámetros utilizando estadísticos. El Instituto Nacional de Estadística español quiere dar a conocer el número total de habitantes del país, así que lleva a cabo un censo. Sin embargo, debido a los problemas logísticos que entraña una tarea tan ardua (por ejemplo ponerse en contacto con las personas sin hogar), a la postre las cifras del censo sólo pueden llamarse estimaciones, y se corrigen al alza para dar cuenta de las personas no incluidas en el censo.

Sesgo

La palabra sesgo se utiliza bastante a menudo, y probablemente ya sepas que significa algo malo. Pero ¿qué es el sesgo exactamente? El sesgo es una inclinación sistemática que está presente en el proceso de recopilación de datos y que da lugar a resultados desviados y engañosos. El sesgo puede aparecer por varias razones:

Otras cosas que provocan sesgo son el momento de hacer la encuesta, la longitud y la dificultad de las preguntas, y la forma de ponerse en contacto con las personas de la muestra (por teléfono, por correo postal, de puerta en puerta, etc.). En el capítulo 16 encontrarás más información sobre la manera correcta de diseñar y evaluar encuestas y sondeos.

Cuando analices los resultados de una encuesta que sea importante para ti o en la que tengas un interés especial, antes de extraer conclusiones sobre los resultados entérate de qué preguntas plantearon y cómo las formularon exactamente.

Media (Promedio)

La media, también llamada promedio, es el estadístico más utilizado para medir el centro de un conjunto de datos numérico. La media es la suma de todos los números dividida por la cantidad total de números. La media de la población entera se denomina media poblacional, y la media de una muestra se denomina, lógicamente, media muestral. (En el capítulo 5 hablo de la media con más detalle.)

La media puede no ser una representación ecuánime de los datos, ya que se ve influenciada fácilmente por los valores atípicos (valores muy grandes o muy pequeños que se alejan mucho de otros valores del conjunto de datos).

Mediana

La mediana es otra manera de medir el centro de un conjunto de datos numéricos. La mediana estadística viene a ser como la mediana de una autopista. En la mayoría de las autopistas la mediana es el centro, de manera que en ambos lados de ella hay el mismo número de carriles. En un conjunto de datos numéricos, la mediana es el valor que divide dicho conjunto en dos partes iguales, una con valores superiores y otra con valores inferiores al valor de la mediana. Así pues, la mediana es el centro auténtico del conjunto de datos. En el capítulo 5 encontrarás más información sobre la mediana.

La próxima vez que te den la cifra correspondiente a una media, mira a ver si también te dicen cuál es la mediana. Si no es así, ¡pide que te la den! La media y la mediana son dos representaciones distintas del centro de un conjunto de datos y a menudo cuentan historias muy diferentes sobre los datos, sobre todo cuando el conjunto de datos contiene valores atípicos (cifras muy grandes o muy pequeñas que se salen de lo normal).

Desviación estándar (o típica)

¿Alguna vez has oído a alguien decir que un resultado en particular presenta “dos desviaciones estándares por encima de la media”? Cada vez más, la gente quiere comunicar la importancia de los resultados que han obtenido, y una manera de hacerlo es diciendo el número de desviaciones estándares por encima o por debajo de la media. Pero ¿qué es exactamente una desviación estándar?

La desviación estándar es una medida utilizada por los estadísticos para referirse al grado de variabilidad (o dispersión) de los números de un conjunto de datos. Como el propio término indica, la desviación estándar es el grado estándar (o típico) de desviación (o divergencia) respecto del promedio (o la media, como prefieren llamarla los estadísticos). Así pues, dicho de manera muy burda, la desviación estándar es la divergencia media respecto de la media.

La fórmula de la desviación estándar (representada por la letra s) es la siguiente, donde n es el número de valores del conjunto de datos, cada una de las x representa a un número del conjunto de datos, y es la media de todos los datos:

En el capítulo 5 encontrarás instrucciones detalladas para calcular la desviación estándar.

La desviación estándar también se utiliza para describir la zona donde deberían estar la mayoría de los datos, en relación con la media. Por ejemplo, si los datos siguen una curva con forma de campana (lo que se llama distribución normal), aproximadamente el 95% de los valores se encuentran a no más de dos desviaciones estándares de la media (este resultado es lo que se llama regla empírica, o regla 68-95-99,7; tienes más información sobre ella en el capítulo 5).

La desviación estándar es un estadístico importante, pero a menudo se omite al comunicar resultados estadísticos. Si no te la dan, te están contando sólo una parte de la verdad. A los estadísticos les gusta contar la anécdota de un hombre que tenía un pie metido en un cubo de agua helada y el otro pie en un cubo de agua hirviendo. En promedio estaba la mar de a gusto, pero piensa en la variabilidad de las dos temperaturas de los pies. Si buscamos ejemplos más próximos, el precio medio de una vivienda no te dice nada sobre el abanico de precios que puedes encontrar en el mercado, y el sueldo medio quizá no represente del todo la situación real de tu empresa en el supuesto de que los sueldos sean muy dispares.

No te conformes con saber la media. Asegúrate de preguntar también cuál es la desviación estándar. Sin la desviación estándar no tienes manera de conocer el grado de dispersión de los valores (si estás hablando de sueldos iniciales, por ejemplo, esto podría ser muy importante).

Percentil

Probablemente hayas oído hablar antes de los percentiles. Si alguna vez has hecho alguna prueba normalizada, junto con la puntuación obtenida debieron de darte una medida de tu resultado en comparación con el resto de las personas que hicieron la prueba. Esta medida comparativa probablemente te fue comunicada en forma de percentil. El percentil para un dato concreto es el porcentaje de valores de la muestra que están por debajo de ese dato concreto. Por ejemplo, si te dicen que tu puntuación está en el percentil 90, significa que el 90% de las personas que hicieron la misma prueba obtuvieron una puntuación inferior a la tuya (y el 10% de los que se examinaron obtuvieron una puntuación más alta que tú). La mediana está justo en el centro de un conjunto de datos, de manera que representa el percentil 50. En el capítulo 5 encontrarás más información sobre percentiles.

Los percentiles se utilizan de varias formas con fines de comparación y para determinar la posición relativa (es decir, la situación de un valor en concreto en comparación con el resto de los valores). El peso de los bebés suele indicarse como percentil, por ejemplo. Las empresas también utilizan los percentiles para saber en qué situación se encuentran, en comparación con otras empresas, en cuanto a ventas, beneficios, satisfacción del cliente, etc.

Puntuación estándar (o típica)

La puntuación estándar es una manera hábil de poner en perspectiva unos resultados sin tener que dar un montón de detalles (algo que a los medios de comunicación les encanta hacer). La puntuación estándar representa el número de desviaciones estándares por encima o por debajo de la media (sin preocuparse de cuál es la desviación estándar ni la media).

Por ejemplo, imagina que Roberto ha obtenido una puntuación de 400 en una prueba de acceso a la universidad. ¿Qué significa eso? Pues no mucho, porque no puedes poner ese 400 en perspectiva. Pero si te dicen que la puntuación estándar de Roberto en la prueba es +2, ya lo sabes todo. Sabes que su puntuación está dos desviaciones estándares por encima de la media (¡bien hecho, Roberto!). Ahora imagina que la puntuación estándar de Isabel es –2. En este caso el resultado no es bueno (para Isabel), ya que su nota está dos desviaciones estándares por debajo de la media.

El proceso de convertir un número en una puntuación estándar se llama normalización o estandarización. En el capítulo 9 explico la manera de calcular e interpretar puntuaciones estándares cuando la distribución es normal (con forma de campana).

Distribución y distribución normal

La distribución de un conjunto de datos (o de una población) es una lista o función que muestra todos los valores posibles (o intervalos) de los datos y la frecuencia con la que aparecen. Cuando se organiza una distribución de datos categóricos, ves el número o porcentaje de elementos que hay en cada grupo. Cuando se organiza una distribución de datos numéricos, generalmente se ordenan del más pequeño al más grande, se dividen en grupos de tamaño razonable (si conviene) y luego se pasan a gráficos y diagramas para ver la forma, el centro y el grado de variabilidad de los datos.

Existen muchas distribuciones distintas para datos categóricos y numéricos, y las más comunes tienen sus propios nombres. Una de las distribuciones más conocidas es la distribución normal, cuya representación gráfica es la popular campana de Gauss (también llamada curva gaussiana o curva de campana). La distribución normal se basa en datos numéricos continuos, cuyos valores posibles se encuentran en la recta numérica real. Cuando los datos se organizan a manera de gráfico, esta distribución tiene forma de campana simétrica. Dicho de otro modo, la mayoría (el 68%) de los datos están centrados en torno a la media (la parte central de la campana), y a medida que te alejas de la media hacia los lados encuentras cada vez menos valores (las curvas descendentes de ambos lados de la campana).

La media (y, por tanto, la mediana) está justo en el centro de la distribución normal debido a la simetría, y la desviación estándar se mide por la distancia desde la media hasta el punto de inflexión (el punto donde la curva cambia de ser convexa a ser cóncava). La figura 4-1 muestra un gráfico de una distribución normal en la que la media es 0 y la desviación estándar es 1 (esta distribución tiene un nombre especial, la distribución normal estándar o distribución Z). La curva tiene forma acampanada.

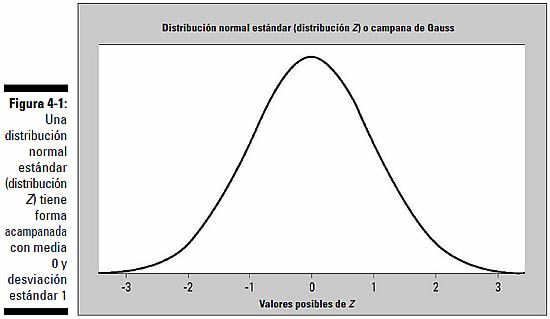
Puesto que cada población de datos tiene su propia media y su propia desviación estándar, existe un número infinito de distribuciones normales, cada una con una media y una desviación estándar que la caracterizan. En el capítulo 9 encontrarás muchísima más información sobre la distribución normal y la normal estándar.

Teorema del límite central

La distribución normal también se utiliza para medir la exactitud de muchos estadísticos, incluida la media, por medio de un importante resultado llamado teorema del límite central. Este teorema permite medir cuánto variará la media muestral sin tener que compararla con otras medias muestrales (¡menos mal!). Teniendo en cuenta esta variabilidad podemos utilizar los datos para responder a preguntas sobre la población, por ejemplo, “¿Cuáles son los ingresos medios por unidad familiar en España?” o “este informe dice que el 75% de las tarjetas regalo no llegan a utilizarse nunca, ¿es eso cierto?”. (Estos dos análisis en particular, posibles gracias al teorema del límite central, se llaman intervalos de confianza y contrastes de hipótesis, respectivamente, y se describen en los capítulos 13 y 14, respectivamente.)

El teorema del límite central (abreviado TLC) dice básicamente que, para datos no normales, la media muestral presenta una distribución aproximadamente normal con independencia de cómo sea la distribución de los datos originales (siempre que la muestra sea suficientemente grande). Y esto no se aplica sólo a la media muestral; el TLC también se cumple para otros estadísticos como, por ejemplo, la proporción muestral (ver capítulos 13 y 14). Como los estadísticos conocen a la perfección la distribución normal (tratada en el apartado anterior), estos análisis son mucho más sencillos. En el capítulo 11 explico mejor el teorema del límite central, conocido en el mundillo como “la joya de la Corona en el campo de la estadística” (estos estadísticos son unos tíos raros de verdad).

Valores z

Si un conjunto de datos tiene una distribución normal y tú normalizas todos los datos para obtener puntuaciones estándares, esas puntuaciones estándares se llaman valores z. Todos los valores z presentan lo que se conoce como distribución normal estándar (o distribución Z). La distribución normal estándar es una distribución normal especial donde la media es igual a 0 y la desviación estándar es igual a 1.

La distribución normal estándar resulta útil para analizar los datos y determinar estadísticos como percentiles, o el porcentaje de datos que se encuentra entre dos valores. Así pues, si los investigadores determinan que los datos poseen una distribución normal, generalmente empiezan por normalizar los datos (convirtiendo cada punto de datos en un valor z) y luego utilizan la distribución normal estándar para analizar los datos más a fondo. En el capítulo 9 encontrarás más información sobre los valores z.

Experimentos

Un experimento es un estudio que impone un tratamiento (o control) a los sujetos (participantes), controla su entorno (por ejemplo limitando su alimentación, administrándoles cierta dosis de un fármaco o placebo o pidiéndoles que permanezcan despiertos durante un tiempo determinado) y registra las respuestas. El propósito de la mayoría de los experimentos es encontrar una relación causa-efecto entre dos factores (por ejemplo el consumo de alcohol y la vista defectuosa, o la dosis de un fármaco y la intensidad de sus efectos secundarios). Aquí tienes algunas preguntas típicas que los experimentos intentan responder:

En este apartado comento otras varias definiciones de palabras que quizá oigas cuando alguien hable sobre experimentos. El capítulo 17 trata exclusivamente sobre esta cuestión. Por ahora, céntrate sólo en la terminología básica de los experimentos.

Grupo experimental y grupo de control

La mayoría de los experimentos intentan dilucidar si un determinado tratamiento experimental (o factor importante) tiene un efecto significativo en un resultado. Por ejemplo, ¿el zinc ayuda a reducir la duración de un resfriado? Los sujetos que participan en el experimento suelen dividirse en dos grupos: un grupo experimental y un grupo de control (también puede haber más de un grupo experimental).

Al final, las respuestas de los integrantes del grupo experimental se comparan con las respuestas del grupo de control para buscar diferencias estadísticamente significativas (diferencias que difícilmente puedan deberse al azar).

Placebo

Un placebo es un tratamiento ficticio, por ejemplo una pastilla de azúcar. Los placebos se administran al grupo de control para producir un fenómeno psicológico llamado efecto placebo, que consiste en que algunas personas presentan una respuesta como si se tratara de un tratamiento real. Por ejemplo, después de tomar una pastilla de azúcar, una persona que experimente el efecto placebo puede decir: “Sí, ya me siento mejor”, o “Vaya, estoy empezando a marearme un poco”. Midiendo el efecto placebo en el grupo de control puedes averiguar qué informes del grupo experimental son reales y cuáles se deben probablemente al efecto placebo (los experimentadores dan por sentado que el efecto placebo afecta tanto al grupo experimental como al grupo de control).

Enmascarado y doblemente enmascarado

Un experimento enmascarado (a veces se llama “a ciegas” o “ciego”) es un estudio clínico en el que los sujetos participantes no saben si están en el grupo experimental (el que recibe el tratamiento) o en el de control. Siguiendo con el ejemplo del zinc, los investigadores se asegurarían de que los comprimidos de vitamina C y los comprimidos de zinc tuvieran exactamente el mismo aspecto, y no dirían a los pacientes cuál de los dos tipos les estarían administrando. Un experimento enmascarado intenta controlar el sesgo por parte de los participantes.

Un experimento doblemente enmascarado, o con doble enmascaramiento, controla el sesgo potencial por parte de los pacientes y de los investigadores. Ni los pacientes ni los investigadores que recopilan los datos saben qué sujetos han recibido el tratamiento y cuáles no. Entonces, ¿quién está enterado? Generalmente es un tercero (alguien que no participa en el experimento de ninguna otra forma) quien se encarga de juntar las piezas. Un estudio con doble enmascaramiento es mejor porque, aunque los investigadores aseguren actuar de forma no sesgada, a menudo tienen un interés especial en los resultados (¡de lo contrario no estarían haciendo el estudio!).

Encuestas (sondeos)

Una encuesta (a veces llamada sondeo) es un cuestionario; generalmente se utiliza para obtener las opiniones de la gente junto con algunos datos demográficos relevantes. Al haber tantos responsables políticos, expertos en marketing y otras personas que quieren “tomar el pulso a la población” y averiguar lo que el ciudadano medio piensa y siente, mucha gente tiene la sensación de no poder escapar a esa persecución. Probablemente tú mismo hayas recibido muchas solicitudes de participación en encuestas, y puede que hasta te hayas vuelto inmune a ellas y te limites a tirar a la basura los cuestionarios que te llegan por correo o a negarte cuando te piden que participes en una encuesta telefónica.

Si se hace como es debido, una encuesta puede ser muy informativa. Las encuestas se utilizan para averiguar qué programas de televisión gustan más, qué piensan los consumidores sobre las compras por Internet y si en Estados Unidos deberían permitir que alguien menor de treinta y cinco años llegue a ser presidente, por ejemplo. Las empresas se sirven de las encuestas para valorar el grado de satisfacción de sus clientes, para averiguar qué productos quiere la gente y para determinar quién compra sus artículos. Las cadenas de televisión utilizan las encuestas para conocer las reacciones inmediatas a noticias que acaban de salir en antena, y los productores cinematográficos las usan para decidir cómo debería terminar una película.

Sin embargo, si tuviera que elegir una palabra para valorar el estado general de las encuestas en los medios de comunicación, creo que sería “cantidad”, y no “calidad”. Dicho de otro modo: hay montones de encuestas mal hechas. Por suerte para ti, en este libro encontrarás montones de buenos consejos e información para analizar, criticar y comprender los resultados de las encuestas, y también para diseñar tus propias encuestas y hacer las cosas bien. (Si quieres meterte ya en materia, pasa al capítulo 16.)

Margen de error

Posiblemente hayas visto u oído resultados como el siguiente: “Esta encuesta tiene un margen de error de más/menos tres puntos porcentuales”. ¿Qué significa eso? La mayoría de las encuestas (salvo los censos) se basan en información recopilada de una muestra de personas, no de la población entera. Forzosamente existirá cierto grado de error, y no me refiero a un error de cálculo (aunque también puede haberlo), sino a un error de muestreo (también llamado error muestral), que ocurre simplemente porque los investigadores no están preguntando a todo el mundo. El margen de error mide la diferencia máxima que puede haber entre los resultados de la muestra y los resultados de la población real. Puesto que los resultados de la mayoría de las preguntas pueden expresarse como porcentajes, el margen de error casi siempre se indica también como porcentaje. ¿Cómo se interpreta un margen de error? Pongamos que sabes que el 51% de las personas de la muestra han dicho que piensan votar por la señora Cálculo en las próximas elecciones. Si quisieras extrapolar esos resultados a todos los votantes, tendrías que sumar y restar el margen de error y proporcionar un intervalo de resultados posibles para estar suficientemente seguro de que salvas la distancia existente entre la muestra y la población entera. Suponiendo que el margen de error es de más/menos tres puntos porcentuales, estarías bastante seguro de que entre el 48% (51–3) y el 54% (51+3) de la población votará por la señora Cálculo en las elecciones, basándote en los resultados muestrales. En este caso la señora Cálculo podría obtener un poco más o un poco menos de la mayoría de los votos, de manera que podría ganar o perder las elecciones. Esta situación se ha repetido en varias noches electorales, cuando los medios de comunicación han querido adelantar quién era el ganador pero, según las encuestas a pie de urna, el resultado estaba “muy reñido”. En el capítulo 12 encontrarás más información sobre el margen de error.

El margen de error mide la exactitud; no mide la cantidad de sesgo que pueda haber (me he referido al sesgo anteriormente en este mismo capítulo). Unos resultados que sean numéricamente exactos no significan nada en absoluto si se han recopilado de forma sesgada.

Intervalo de confianza

Una de las aplicaciones más importantes de la estadística consiste en estimar un parámetro poblacional utilizando un valor muestral. O dicho de otro modo: utilizar un número que resume una muestra para ayudarte a estimar el número correspondiente que resume a toda la población (anteriormente en este mismo capítulo he puesto las definiciones de parámetro y estadístico). En cada una de las siguientes preguntas estás buscando un parámetro poblacional:

Es imposible conocer esos parámetros con exactitud; cada uno de ellos requiere una estimación basada en una muestra. Primero se toma una muestra aleatoria de una población (pongamos una muestra de 1.000 unidades familiares de Azerbaiyán) y a continuación se encuentra el estadístico muestral correspondiente (los ingresos medios por unidad familiar de la muestra). Como sabes que los resultados varían para cada muestra, tienes que añadir un “más/menos algo” a los resultados de la muestra si quieres extraer conclusiones sobre toda la población (todas las unidades familiares de Azerbaiyán). Este “más/menos” que añades al estadístico muestral para estimar un parámetro es el margen de error.

Cuando coges un estadístico de la muestra (por ejemplo la media muestral o un porcentaje muestral) y sumas/restas un margen de error, obtienes lo que en estadística se llama intervalo de confianza. Un intervalo de confianza representa un intervalo de valores probables para el parámetro poblacional, a partir del estadístico muestral. Por ejemplo, pongamos que todos los días tardas una media de treinta y cinco minutos en ir de casa al trabajo, con un margen de error de más/menos cinco minutos. Puedes estimar que el tiempo medio que tardas en llegar al trabajo está comprendido entre treinta y cuarenta minutos. Esta estimación es un intervalo de confianza.

Algunos intervalos de confianza son mayores que otros (y cuanto mayor sea, peor, porque la precisión será menor). Existen varios factores que influyen en la amplitud de un intervalo de confianza, por ejemplo el tamaño de la muestra, el grado de variabilidad de la población estudiada y la confianza que quieres tener en los resultados (la mayoría de los investigadores se contentan con tener un 95% de confianza en sus resultados). En el capítulo 13 encontrarás más factores que influyen en los intervalos de confianza, así como instrucciones para calcular e interpretar intervalos de confianza.

Contrastes de hipótesis

Es probable que en tu devenir diario con números y estadísticas no te hayas tropezado nunca con el término contraste de hipótesis. Sin embargo, puedo asegurarte que los contrastes de hipótesis tienen una gran influencia en tu vida personal y profesional, simplemente por el papel tan importante que desempeñan en la industria, la medicina, la agricultura, el gobierno y muchos otros ámbitos. Cada vez que oyes a alguien decir que su estudio presenta un resultado “estadísticamente significativo” te tropiezas con un contraste de hipótesis (un resultado estadísticamente significativo es uno que difícilmente puede haber ocurrido por casualidad; tienes más información sobre este asunto en el capítulo 14).

Básicamente, un contraste de hipótesis es un procedimiento estadístico mediante el cual se recopilan datos de una muestra y se cotejan con una afirmación referida a un parámetro poblacional. Por ejemplo, si una cadena de pizzerías asegura que entrega todas las pizzas en un tiempo máximo de treinta minutos tras recibir el pedido, como media, podrías comprobar si esa afirmación es cierta recopilando una muestra de tiempos de entrega durante un determinado período y determinando el tiempo medio de entrega para esa muestra. Para tomar una decisión también debes tener en cuenta cuánto pueden variar tus resultados de una muestra a otra (lo cual está relacionado con el margen de error).

Puesto que tu decisión se basa en una muestra y no en la población entera, el contraste de hipótesis puede conducirte a veces a una conclusión errónea. Sin embargo, la estadística es todo lo que tienes, y si la utilizas en la forma debida tendrás muchas posibilidades de acertar. En el capítulo 14 encontrarás más información sobre contrastes de hipótesis.

En los estudios científicos se realizan muchos contrastes de hipótesis, incluidas pruebas t (comparan dos medias poblacionales), pruebas t para datos apareados (se examinan las diferencias entre el antes y el después) y pruebas de afirmaciones referidas a proporciones o medias de una o más poblaciones. En el capítulo 15 encontrarás información más concreta sobre estos contrastes de hipótesis.

Valores p

Los contrastes de hipótesis sirven para verificar la validez de una afirmación referida a una población. Esa afirmación que se somete a juicio se llama hipótesis nula. La hipótesis alternativa es la que creerías si concluyeras que la hipótesis nula está equivocada. Las pruebas de este juicio son los datos y los estadísticos que los acompañan. Todos los contrastes de hipótesis utilizan un valor p para ponderar la solidez de las pruebas (lo que los datos te están diciendo sobre la población). El valor p es un número comprendido entre 0 y 1 que se interpreta de la manera siguiente:

Por ejemplo, imagina que una pizzería dice que entrega las pizzas en treinta minutos o menos, en promedio, pero tú crees que tardan más. Realizas un contraste de hipótesis porque crees que la hipótesis nula H₀ (según la cual el tiempo medio de entrega es de treinta minutos como máximo) es incorrecta. Tu hipótesis alternativa (H_a) es que el tiempo medio de entrega es superior a treinta minutos. Tomas una muestra aleatoria de varios tiempos de entrega y sometes los datos al contraste de hipótesis, y el valor p resulta ser 0,001, muy por debajo de 0,05. Concluyes que la pizzería está equivocada; el tiempo de entrega de las pizzas supera los treinta minutos en promedio y quieres saber qué piensan hacer al respecto (naturalmente, también podrías haberte equivocado por haber incluido en tu muestra por puro azar un número inusualmente alto de pizzas entregadas con retraso, pero eso no se lo creen ni los de la pizzería). En el capítulo 14 encontrarás más información sobre los valores p.

Significación estadística

Cuando se recopilan datos para realizar un contraste de hipótesis, el investigador generalmente busca algo que se salga de lo normal (por desgracia, las investigaciones que se limitan a confirmar algo que ya era conocido no generan titulares). Los estadísticos utilizan los contrastes de hipótesis (ver el capítulo 14) para medir cuánto se sale de lo normal un determinado resultado. Para ello, consideran que un resultado es estadísticamente significativo cuando existe una probabilidad muy pequeña de que haya ocurrido por mero azar, y proporcionan un número llamado valor p para reflejar dicha probabilidad. (Los valores p se tratan en el apartado anterior.)

Por ejemplo, si se comprueba que un fármaco es más eficaz que el tratamiento actual para el cáncer de mama, los investigadores dicen que el nuevo fármaco supone una mejora estadísticamente significativa en la tasa de supervivencia de las pacientes con cáncer de mama. Esto significa que, a partir de los datos obtenidos, la diferencia entre los resultados generales de las pacientes que tomaron el nuevo fármaco y los resultados de las que tomaron el tratamiento anterior es tan grande que sería muy difícil decir que obedece a una simple coincidencia. De todos modos, ándate con cuidado: no puedes decir que esos resultados sean aplicables a todas las personas ni de igual modo a todas las personas. En el capítulo 14 trato más a fondo la cuestión de la significación estadística.

Cuando oigas decir que los resultados de un estudio son estadísticamente significativos, no des por sentado que esos resultados son importantes. Estadísticamente significativo significa que los resultados se salen de lo normal, pero eso no siempre significa que sean importantes. Por ejemplo, ¿te emocionaría mucho descubrir que los gatos mueven la cola más a

menudo cuando están tumbados al sol que cuando están a la sombra, y que esos resultados son estadísticamente significativos? ¡Ese resultado no le importa siquiera al gato, y mucho menos a ti!

A veces los estadísticos llegan a la conclusión equivocada sobre la hipótesis nula porque la muestra no representa a la población (aunque eso ocurra por casualidad). Por ejemplo, un efecto positivo experimentado por una muestra de personas que hayan tomado un nuevo tratamiento puede haberse debido a un golpe de suerte; o siguiendo el ejemplo del apartado anterior, es posible que la pizzería sí entregue las pizzas a tiempo y tú, por mala suerte, hayas elegido una muestra de pizzas entregadas con retraso. No obstante, lo bonito de la investigación es que, en cuanto alguien lanza un comunicado de prensa diciendo que ha descubierto algo significativo, todo el mundo intenta reproducir esos resultados, y, si no es posible reproducirlos, probablemente sea porque los resultados originales eran incorrectos por alguna razón (puede incluso que por puro azar). Por desgracia, los comunicados de prensa que anuncian “avances revolucionarios” tienen mucha repercusión en los medios, mientras que los estudios posteriores que refutan esos resultados casi nunca aparecen en portada.

No te apresures a tomar decisiones por haber obtenido un resultado estadísticamente significativo. En ciencia, un estudio aislado, por extraordinario que sea, generalmente no tiene tanto valor como un conjunto de pruebas acumuladas a lo largo de mucho tiempo, junto con varios estudios de seguimiento bien diseñados. Cuando te hablen de algún logro extraordinario, acéptalo con reservas y espera a que salgan a la luz nuevas investigaciones antes de utilizar la información de un único estudio para tomar decisiones importantes que afecten a tu vida. Puede que los resultados no puedan reproducirse o que, incluso en tal caso, no puedas saber si son aplicables a todo el mundo.

Correlación y causalidad

De todos los equívocos que pueden ocurrir en el campo de la estadística, el que quizá resulta más problemático es el mal uso de los conceptos de correlación y causalidad.

La correlación, como término estadístico, es la medida en que dos variables numéricas presentan una relación lineal (es decir, una relación que aumenta o disminuye a un ritmo constante). Aquí tienes tres ejemplos de variables correlacionadas:

Pero la correlación como estadístico no puede explicar por qué existe una relación entre dos variables x e y; tan sólo nos dice que existe.

La causalidad va un paso más allá que la correlación y significa que un cambio en el valor de la variable x causará un cambio en el valor de la variable y. Este paso adelante se da más veces de las debidas en las investigaciones, en los medios de comunicación y en el consumo público de resultados estadísticos. Por ejemplo, no puedes decir que el consumo de helado causa un incremento en la tasa de homicidios sólo porque ambas cosas estén correlacionadas. De hecho, el estudio mostraba que la temperatura presenta una correlación positiva con las ventas de helado y también con los homicidios. (En el capítulo 18 profundizo sobre la correlación y la causalidad.) ¿Cuándo puedes decir que existe una relación de causalidad? El caso más claro es cuando se lleva a cabo un experimento bien diseñado que descarta otros factores que podrían estar relacionados con los resultados. (En el capítulo 17 encontrarás información sobre experimentos que revelan una relación causa-efecto.)

Es posible que al observar una correlación sientas el deseo de anunciar una relación causa-efecto; los investigadores, los medios y el público en general lo hacen continuamente. Sin embargo, antes de extraer ninguna conclusión averigua cómo se han recopilado los datos y espera a ver si otros investigadores logran reproducir los resultados (es lo primero que intentan cuando ven que un resultado “revolucionario” de un colega se convierte en noticia de portada).