Representación gráfica de datos categóricos

En este capítulo

Representar visualmente datos categóricos

Interpretar y valorar diagramas y gráficos

Las presentaciones visuales de datos, en particular los diagramas y los gráficos, están por todas partes y se utilizan para presentar información de todo tipo de cosas, desde los resultados de unas elecciones (desglosados hasta la característica más nimia) hasta la evolución de un índice bursátil a lo largo de los últimos años (meses, semanas, días, minutos). Vivimos en una sociedad donde prima la gratificación instantánea y la información rápida; todo el mundo quiere llegar en seguida al meollo de las cosas y que le ahorren los detalles.

La abundancia de diagramas y gráficos no es necesariamente algo malo, pero hay que andarse con ojo: algunos son incorrectos o incluso inducen a error (a veces queriendo y otras veces sin querer), y es importante saber lo que debes buscar.

Este capítulo trata de los gráficos hechos con datos categóricos (datos que sitúan a las personas en grupos o categorías, por ejemplo el sexo, la opinión o si un enfermo toma medicación todos los días). En las próximas páginas te enseñaré a interpretar estas presentaciones visuales y te daré algunos consejos para valorarlas críticamente y detectar posibles problemas. (Nota: las presentaciones visuales de datos numéricos, por ejemplo el peso, la nota de un examen o el número de pastillas que un enfermo se toma cada día, se explican en el capítulo 7.)

Los datos categóricos suelen presentarse visualmente mediante gráficos de sectores y gráficos de barras. En este capítulo encontrarás ejemplos de cada tipo de presentación junto con algunas reflexiones sobre su interpretación y consejos para realizar una valoración crítica.

Coge otro trocito de tarta

Los gráficos de sectores separan los datos categóricos por grupos y muestran el porcentaje de personas o elementos que pertenecen a cada grupo. Como los gráficos de sectores tienen forma de tarta, es muy sencillo comparar las “porciones” que representan a los distintos grupos.

Puesto que cada elemento del estudio pertenece a una categoría (y sólo a una), la suma de todas las porciones de la tarta debería ser el 100% o casi el 100% (puede haber un poco de redondeo). De todos modos, ten los ojos bien abiertos por si alguna vez los porcentajes no cuadran.

Contabilidad de gastos personales

Cuando gastas dinero, ¿en qué te lo gastas? ¿Cuáles son tus tres principales fuentes de gasto? Según una encuesta de consumo realizada en 2008 por la Oficina Estadounidense de Estadísticas Laborales, las seis partidas de gasto más importantes en ese país eran la vivienda (33,9%), el transporte (17,0%), la alimentación (12,8%), los seguros y pensiones (11,1%), la sanidad (5,9%) y el ocio (5,6%). Estas seis categorías representan más del 85% de los gastos de un consumidor medio (aunque los porcentajes exactos cambian cada año, las seis partidas principales son siempre las mismas).

La figura 6-1 resume el gasto de los consumidores estadounidenses en 2008 por medio de un gráfico de sectores. Como puedes ver, la categoría “Otros gastos” es bastante grande (13,7%). Lo que ocurre es que, con tantos otros gastos posibles (incluido este libro), a cada uno le correspondería una porción minúscula de la tarta, con lo que el resultado final sería un auténtico embrollo. En este caso resulta demasiado complicado desglosar aún más la categoría “Otros gastos” (pero en muchos otros casos sí se puede).

Lo ideal es que un gráfico de sectores no tenga demasiadas categorías, porque eso distrae al lector de la idea o ideas principales que el gráfico pretende comunicar. Sin embargo, juntar el resto de las categorías en una sola que pasa a ser una de las más grandes del gráfico hace que los lectores se pregunten qué incluye esa categoría. En lo tocante a gráficos y diagramas, hacer bien las cosas obliga a encontrar un delicado equilibrio.

Los ingresos del juego

En Estados Unidos, los organismos estatales de loterías y apuestas generan muchos ingresos y también devuelven gran parte del dinero recaudado (una parte de los beneficios se destina a premios y otra parte a programas estatales, por ejemplo educación). ¿De dónde proceden los ingresos de estos organismos de loterías y apuestas? La figura 6-2 es un gráfico de sectores que muestra los distintos juegos y el porcentaje de ingresos que representa cada uno, según un informe reciente del Organismo de Loterías y Apuestas del estado de Ohio (si te fijas bien, verás que los porcentajes no suman 100 debido al pequeño error de redondeo).

Tal y como puedes ver en el gráfico de la figura 6-2, el 49,3% de los ingresos proceden de juegos instantáneos (rasca y gana). El resto procede de diversos juegos de azar en que los jugadores eligen una serie de números y ganan un premio si varios de esos números coinciden con los elegidos en el sorteo. Es el modelo que en España sigue la BonoLoto, por ejemplo.

Este gráfico de sectores no te dice cuánto dinero se recauda, sino tan sólo el porcentaje de dinero que se recauda con cada juego. Aproximadamente la mitad de los ingresos (49,3%) proviene de juegos de rasca y gana, pero no sabemos si esa cantidad asciende a 1 millón de dólares, 2 millones, 10 millones o incluso más. Es imposible saberlo sin conocer la cantidad total de dinero recaudado.

No obstante, consultando otro gráfico en el sitio web del organismo conseguí enterarme de ese dato: la recaudación total (en un período de diez años) fue de “1.983,1 millones de dólares” (unos 1.513 millones de euros). Puesto que el 49,3% de las ventas procedían de juegos instantáneos, esta modalidad representa unos ingresos de 977.668.300 dólares en un período de diez años (745.800 euros). Desde luego, eso es mucho rascar.

Comida para llevar

Cuando miras el gráfico de sectores de una encuesta, también es importante fijarse en los totales. El otro día leía una noticia con los últimos resultados de una encuesta popular. La pregunta era: “¿Qué día de la semana prefieres cenar comida para llevar?”. Los resultados se muestran en un gráfico de sectores que tienes en la figura 6-3.

Se ve claramente que la noche de los viernes es la más popular entre los consumidores de comida para llevar (lo cual me parece lógico), y luego la demanda va bajando de sábado a lunes. En realidad, los porcentajes indicados en la figura 6-3 sólo son válidos para las personas encuestadas. La medida en que esos resultados reflejen a la población entera dependerá de muchos factores, uno de los cuales es el tamaño de la muestra. Por desgracia, en el gráfico no se menciona el tamaño de la muestra (por ejemplo, estaría bien que debajo del título hubieran puesto “n=XXX”; donde n debería ser el tamaño de la muestra).

Sin conocer el tamaño de la muestra, no puedes saber hasta qué punto la información es exacta. ¿Qué resultados te parecen más exactos, los que se basan en 25 personas, 250 personas o 2.500 personas? Cuando te dan el 10%, no sabes si son 10 de cada 100, 100 de cada 1.000 o incluso 1 de cada 10. Para los estadísticos, 1 de cada 10 no es lo mismo que 100 de 1.000, por mucho que en ambos casos se trate del 10% (no se lo digas a un matemático porque te dirá que estás como una cabra).

Los gráficos de sectores generalmente no mencionan el tamaño total de la muestra. Debes comprobar siempre este dato, sobre todo si los resultados son importantes para ti. ¡No des por sentado que es un número muy grande! Si no te dicen el tamaño de la muestra, ponte en contacto con la fuente de los datos y pídeselo.

Proyección de tendencias de edad

La Oficina del Censo de Estados Unidos proporciona una cantidad ingente de datos, estadísticas y gráficos sobre la población de ese país, incluidas proyecciones de futuro. A menudo se establecen comparaciones entre años al objeto de encontrar variaciones y tendencias.

Un informe reciente de la Oficina del Censo se refería a lo que se ha dado en llamar “las personas mayores” (según la definición del gobierno de Estados Unidos, las personas que tienen sesenta y cinco años o más). Las edades se dividieron en los siguientes grupos: 65-69 años, 70-74 años, 75-79 años, 80-84 años, y 85 años y más. La Oficina calculó y comunicó el porcentaje representado por cada grupo de edad en 2010 y realizó sendas proyecciones para el año 2050.

Yo elaboré gráficos de sectores para los años 2010 y 2050 (proyecciones) con fines de comparación. Puedes ver los resultados en la figura 6-4. Un gráfico de sectores muestra el porcentaje correspondiente a cada grupo de edad en el año 2010, y al lado hay otro gráfico con los porcentajes previstos para 2050 (proyecciones a partir de la edad actual de la población entera de Estados Unidos, las tasas de natalidad y mortalidad, y otras variables).

Si comparas los tamaños de los sectores entre los dos gráficos de la figura 6-4, verás que los sectores de los grupos de edad correspondientes son más grandes en las proyecciones de 2050 (en comparación con 2010) cuanto más viejas son las personas, mientras que los sectores son más pequeños en las proyecciones de 2050 (en comparación con 2010) cuanto menos viejas son las personas. Por ejemplo, el grupo de 65-69 años pasa del 30% en 2010 al 25% previsto para 2050 (es decir, disminuye); mientras que el grupo de 85 años o más pasa del 14% en 2010 al 19% previsto para 2050 (es decir, aumenta).

Los resultados de la figura 6-4 indican que la población estadounidense de personas mayores va a envejecer todavía más. A partir de estos datos, los médicos y los investigadores sociales pueden analizar las implicaciones en cuanto a sanidad, cuidado de ancianos, seguridad social, etc.

La clave aquí está en saber si la tendencia va a continuar. Como sabes, el tamaño de la población depende de muchas variables que debes tener en cuenta a la hora de interpretar estas proyecciones de futuro. El gobierno de Estados Unidos siempre incluye advertencias de este tipo en sus informes, lo cual es una prueba de diligencia por su parte.

Los gráficos de sectores de la figura 6-4 resultan útiles para comparar grupos porque están uno al lado del otro, utilizan la misma codificación para las distintas categorías y además los sectores están en el mismo orden (si estuvieran todos desordenados en cada gráfico, tendrías que buscar un grupo de edad determinado en cada gráfico por separado).

Barra libre de gráficos de barras

Los gráficos de barras (también llamados diagramas de barras) son quizá la forma de presentación visual más utilizada por los medios de comunicación. Igual que un gráfico de sectores, un gráfico de barras divide los datos categóricos en grupos. Sin embargo, a diferencia de un gráfico de sectores, las cantidades se representan utilizando barras de distintas longitudes. Además, mientras que el gráfico de sectores suele indicar las distintas cantidades por medio de porcentajes, el gráfico de barras puede utilizar el número de elementos de cada grupo (la frecuencia) o el porcentaje de elementos que hay en cada grupo (la frecuencia relativa).

Gasto en transporte

¿Qué parte de sus ingresos gastan los ciudadanos estadounidenses en desplazarse de casa al trabajo y del trabajo a casa? Depende del dinero que ganan. La Oficina de Estadísticas sobre Transportes (es sorprendente que exista tal cosa, ¿verdad?) realizó un extenso estudio sobre el transporte en Estados Unidos, y gran parte de los datos recopilados se presentaron en forma de gráficos de barras como el de la figura 6-5.

Este gráfico en concreto muestra cuánto dinero gastan en transporte las personas pertenecientes a distintos grupos de ingresos familiares. Según parece, a medida que aumentan los ingresos de la unidad familiar, aumenta también el gasto total en transporte. Esto tiene lógica, ya que cuanto más dinero gana uno, más tiene para gastar.

Pero ¿cambiaría el gráfico de barras si, en lugar de referirnos a cantidades totales de dólares, analizáramos el gasto en transporte como porcentaje de los ingresos de la unidad familiar? Las familias del primer grupo ganan menos de 5.000 dólares al año y tienen que gastar 2.500 dólares en transporte. (Nota: pone “2,5,” pero como las unidades están en miles de dólares, son 2.500 dólares.)

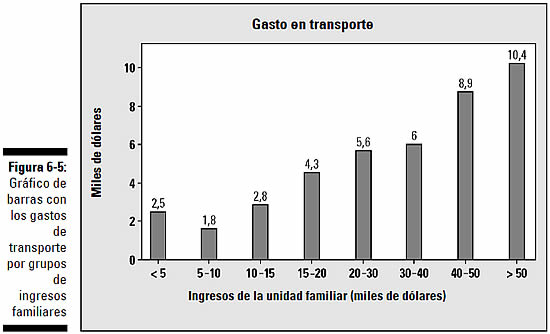
Estos 2.500 dólares representan el 50% de los ingresos anuales de las familias que ganan 5.000 dólares al año, y el porcentaje es incluso más alto para quienes ganan menos de esta cantidad. Las familias que ganan entre 30.000 y 40.000 dólares al año gastan 6.000 dólares en transporte, lo que representa entre el 15 y el 20% de los ingresos. Por tanto, aunque las personas que ganan más dinero también gastan más dólares en transporte, este gasto no es mayor si tenemos en cuenta el porcentaje de sus ingresos totales. Según cómo se considere el gasto, el gráfico de barras dará dos lecturas totalmente diferentes.

Por otro lado, también hay que tener en cuenta las categorías utilizadas en el gráfico. Los grupos de ingresos familiares mostrados no son equivalentes. Por ejemplo, las cuatro primeras barras representan ingresos familiares en intervalos de 5.000 dólares, mientras que los tres grupos siguientes muestran incrementos de 10.000 dólares cada uno, y el último grupo incluye a todas las familias que ganan más de 50.000 dólares al año. Los gráficos de barras que utilizan intervalos de distintos tamaños para representar valores numéricos (como ocurre en la figura 6-5) dificultan la labor de comparar los datos (no obstante, estoy segura de que el gobierno tendrá sus razones para presentar las cifras de esta forma; por ejemplo, puede que sea así como desglosan los ingresos en los tramos de los impuestos).

Una última cosa: las categorías de la figura 6-5 se solapan en los límites. Por ejemplo, la cantidad de 30.000 dólares aparece en la quinta y en la sexta barra del gráfico. Entonces, si tus ingresos familiares son de 30.000 dólares, ¿en qué grupo estás? (mirando la figura 6-5 no lo puedes saber, pero seguro que las instrucciones están enterradas en un informe extensísimo que han guardado en el sótano de algún edificio de Washington). Este tipo de solapamientos aparecen con bastante frecuencia en los gráficos, pero es necesario saber qué hacer con los valores límite. Por ejemplo, podría aplicarse la regla siguiente: “Los datos que coincidan exactamente con un valor límite se incluirán en la barra situada inmediatamente a la derecha” (en la figura 6-5, una familia que gane 30.000 dólares deberá estar en la sexta barra, y no en la quinta). Mientras se siga siempre el mismo criterio para todos los límites, no hay ningún problema. La alternativa, que sería describir los límites de ingresos de la quinta barra como “de 20.000 a 29.999,99 dólares”, no supone ninguna mejora. En este orden de ideas, los datos sobre ingresos también pueden presentarse con un histograma (lo explico en el capítulo 7), que tiene un aspecto ligeramente distinto.

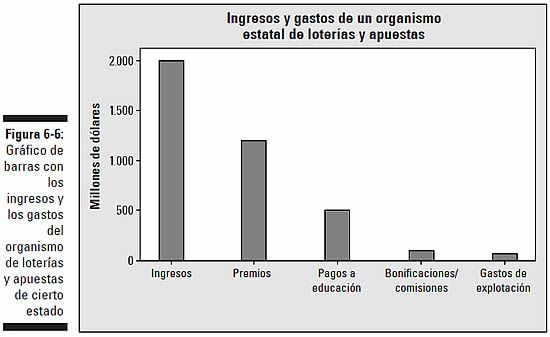
Los beneficios del juego

Que los organismos de loterías y apuestas ingresan dinero a espuertas es algo de sobras conocido, pero es justo decir que también gastan lo suyo. Entonces, ¿qué beneficios tienen? La figura 6-6 muestra los ingresos y los gastos recientes de cierto organismo estatal de loterías y apuestas de Estados Unidos.

En mi opinión, este gráfico de barras necesita más información para que resulte más comprensible. Las barras de la figura 6-6 no representan conceptos del mismo tipo. La primera barra representa los ingresos, y las demás representan gastos. El gráfico sería mucho más claro si la primera barra no estuviera incluida; por ejemplo, los ingresos totales podrían mencionarse en una nota al pie.

Escalas y gráficos de barras

Un gráfico también puede inducir a error según la escala utilizada en el eje de frecuencia/frecuencia relativa (es decir, el eje donde se encuentran las cantidades de cada grupo) o el valor inicial de dicha escala.

Si “estiras” la escala (por ejemplo, que cada centímetro de una barra represente 10 unidades en lugar de 50 unidades), puedes distorsionar la verdad, hacer que las diferencias parezcan mayores o exagerar los valores. Esta distorsión de la verdad también puede ocurrir si el eje de frecuencia comienza en un número que esté muy próximo al punto donde comienzan las diferencias en las alturas de las barras; de este modo básicamente eliminas la parte de abajo de las barras (la menos emocionante) y tan sólo muestras la parte superior, haciendo hincapié (de manera engañosa) en donde está la acción. No todos los ejes de frecuencia tienen que empezar en cero, pero debes estar atento a las situaciones que magnifiquen las diferencias.

Un buen ejemplo de gráfico con la escala estirada aparece en el capítulo 3, en relación con los resultados de los números extraídos en el sorteo Pick 3 (eliges tres números de un solo dígito, y si todos coinciden con los extraídos en el sorteo, te llevas el premio). En el capítulo 3, el porcentaje de veces que se ha extraído cada número (del 0 al 9) se indica en la tabla 3-2, y los resultados se muestran en un gráfico de barras en la figura 3-1a. La escala del gráfico está estirada y comienza en 465, de manera que las diferencias en los resultados parecen mayores de lo que son en realidad; por ejemplo, parece que el número 1 es extraído muchas menos veces, y el número 2 muchas más veces, cuando en realidad no existe diferencia estadística entre el porcentaje de veces que se ha extraído cada número (lo he comprobado).

Entonces, ¿por qué hicieron así el gráfico de la figura 3-1a? La gente podría pensar que tiene información privilegiada y que debería elegir el número 2 porque está en mitad de una buena racha, o el número 1 porque ya le toca subir. Ambas suposiciones son incorrectas, por cierto. Como los números se eligen al azar, lo ocurrido en el pasado no influye en absoluto. La figura 3-1b muestra un gráfico bien hecho. (Para más ejemplos de cómo puede equivocarse la intuición en cuestiones de probabilidad, te recomiendo otro de mis libros, Probability For Dummies, también publicado por Wiley, pero no disponible en español.)

Por otro lado, si “acortas” la escala (por ejemplo, que cada centímetro de una barra represente 50 unidades en lugar de 10 unidades), puedes restar importancia a las diferencias y hacer que los resultados parezcan menos significativos de lo que son en realidad. Por ejemplo, puede que un político no quiera llamar la atención sobre un fuerte incremento de la delincuencia a lo largo de su mandato, de manera que, en el gráfico que muestra el número de delitos de cada tipo, hace que cada barra represente 500 delitos en lugar de 100 delitos. De este modo los números están más juntos y las diferencias son menos apreciables. Su oponente para las próximas elecciones hará justo lo contrario: utilizar una escala estirada para resaltar más el aumento de la delincuencia. (Ahora ya sabes cómo es posible que dos personas manejen los mismos datos y sin embargo lleguen a conclusiones totalmente opuestas. Bienvenido al mundo de la política.)

En el caso de los gráficos de sectores, en cambio, no es posible alterar la escala para poner un énfasis excesivo en los resultados (o para quitarles importancia). Da igual cómo dividas un gráfico de sectores: siempre estarás cortando en porciones una tarta y la proporción correspondiente a cada trozo no cambiará, ni siquiera si dibujas la tarta más grande o más pequeña.

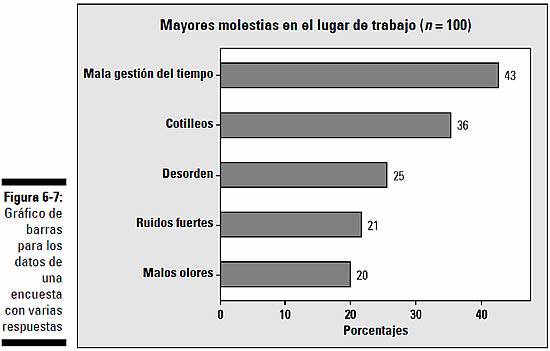
Fastidios cotidianos

En una encuesta reciente se preguntó a 100 oficinistas cuáles eran las cosas que más les molestaban en su lugar de trabajo (antes de continuar leyendo quizá quieras pensar tu respuesta, aunque sólo sea para echarte unas risas). La figura 6-7 muestra un gráfico de barras con los resultados de esa encuesta. Al parecer, la mala gestión del tiempo es lo que más fastidia a esos empleados (espero que no contestaran la encuesta en horario laboral).

Si miras los porcentajes mostrados para cada una de las molestias mencionadas, verás que no suman uno. Por tanto, se deduce que cada una de las personas encuestadas podía mencionar más de una molestia (no es que les costara mucho, seguro); a lo mejor les pidieron que dijeran las tres cosas que más les molestaban, por ejemplo. Con este conjunto de datos, y otros similares que permitan varias respuestas, no es posible utilizar un gráfico de sectores (a menos que hicieras uno para cada una de las molestias indicadas).

Observa que la figura 6-7 es un gráfico de barras horizontal (las barras van de lado a lado), mientras que la figura 6-6 es un gráfico de barras vertical (las barras están dispuestas verticalmente). Ambas orientaciones son igualmente válidas; puedes utilizar la que más te guste. No obstante, asegúrate de que identificas los ejes correctamente y utilizas las unidades apropiadas (por ejemplo sexo, opinión o día de la semana) en cada caso.