Grafische misleiding voor dummies

Laten we simpel beginnen met enkele tweedimensionale lijngrafieken. Tijdens een verblijf in Singapore scheurde ik onderstaand grafiekje uit een locale krant. Geen idee bij welke krant, datum of tekst het plaatje hoorde, maar het is een dankbaar voorbeeld van hoe het niet moet. Wat kun je uit onderstaande grafiek aflezen? Liever gezegd: wat kun je er niet uit aflezen?

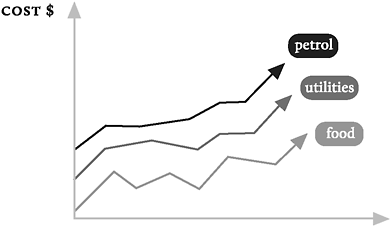
Figuur 11: Voorbeeld van een nutteloze grafiek. Bron: onbekend.

De kosten voor petrol zijn hoger dan die van utilities, die op hun beurt weer hoger zijn dan die van food. Dat is de enige conclusie die ik op basis van figuur 11 kan trekken. Omdat het niet duidelijk is of de x-as de tijd weergeeft, kun je niet eens concluderen dat de kosten in de loop der tijd zijn gestegen. Het kunnen net zo goed de rijlengtes van kassa’s zijn of het aantal klanten dat tegelijkertijd online is. Dit voorbeeld illustreert de belangrijkste truc in grafiekenland, namelijk informatie weglaten. Hoe minder informatie een maker of gebruiker geeft, des te makkelijker is een grafiek te manipuleren. Of je nou in Singapore bent of hier.

De volgende twee voorbeelden laten zien dat misleiding door middel van grafieken ook op iets subtielere wijze kan plaatsvinden.

Figuur 12: Fictieve grafiek die marginale verschillen laat zien.

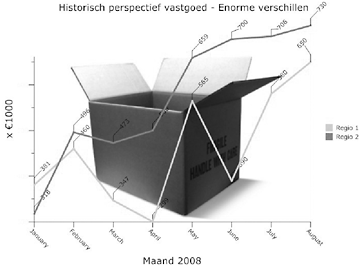
Figuur 13: Fictieve grafiek die grote verschillen laat zien.

Nota bene, de achterliggende data voor beide zelfgemaakte grafieken zijn gelijk. Deze twee figuren bevatten samen de meest voorkomende trucs die makers van grafieken kunnen uithalen. Meerdere manipulaties versterken elkaar onderling en leiden tot een grote mate van gekonkel.

Grafiektruc 1: De start van de verticale as

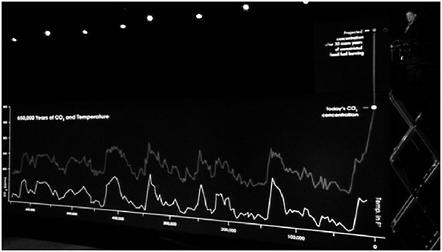
Als je goed kijkt kun je in figuur 13 zien dat de verticale as in de onderste grafiek niet bij nul begint. In figuur 12 is dat wel het geval. Daardoor lijken de schommelingen in de onderste grafiek groter. Om het dramatische effect te vergroten, kun je de verticale as eerder laten ophouden terwijl de grafieklijn nog even doorloopt. Het effect van een grafieklijn die verder loopt dan de hoogste grafiekwaarde, is dat die grafieklijn out-of-scale raakt. De lijn knalt als het ware de grafiek uit. Een dergelijke presentatie versterkt het extreme aspect van de waarde, maar gaat nog verder. De meeste lezers krijgen het gevoel dat een dergelijke hoge grafiekwaarde buitenproportioneel en dus onacceptabel is. Van precies dit effect maakt bijvoorbeeld Al Gore slim en suggestief gebruik in zijn film An Inconvenient Truth. Om het dramatische effect van de door hem gepresenteerde cijfers te vergroten, klimt hij halverwege zijn verhaal op een hoogwerker. Hij ‘toont’ hiermee automatisch aan hoe onacceptabel hoog de stijging van gemeten CO₂ is. Een dergelijke act speelt – los van de discussie of het verhaal inhoudelijk klopt - in op gevoelens van verontwaardiging bij het publiek.

Figuur 14: Al Gore op een hoogwerker. Bron: An Invonvenient Truth van Al Gore uit 2006.

Grafiektruc 2: De schaalverdeling van de verticale as

Niet alleen het startpunt, maar ook de schaalverdeling op de verticale as van figuren 12 en 13 is anders. Hoe ruimer de schaal, des te kleiner lijken de fluctuaties in de lijn. Dit is goed te zien in figuur 12.

Grafiektruc 3: Titels

De titels van beide grafieken zijn suggestief. De titel van figuur 12 suggereert geen verschil, terwijl de titel in figuur 13 de verschillen juist benadrukt. Mijns inziens is elke suggestieve duiding in de titel van een grafiek een belediging voor de kijker. Die mag zelf bepalen of een effect groot of klein is.

Grafiektruc 4: Labels

In figuur 12 is de informatie naast beide assen onvolledig. Het getal duizend kan voor alles staan. Gaat het om dollars, euro’s, vierkante of kubieke meters? Wie het weet, mag het zeggen. Hoe zit het met het label maand in figuur 12? Het is onduidelijk uit welk jaar deze cijfers zijn.

Grafiektruc 5: Chart Junk

Edward Tufte, auteur van het eerder in dit hoofdstuk genoemde standaardwerk over grafieken, introduceerde de term chart junk. Hieronder valt alle informatie die niet ter zake doet. Informatie die niet nodig is voor de interpretatie van een bepaalde grafiek. Voorbeelden van chart junk in figuren 12 en 13 zijn de dozen op de achtergrond. De plaatjes zijn overbodig en leiden af van de grafiek zelf. Je hoeft tegenwoordig geen computerexpert meer te zijn om een simpele grafiek te pimpen.

“Wat Al Gore kan, kan ik ook”, moet Geert Wilders hebben gedacht toen hij in 2008 de film Fitna maakte. De eerste vier staven in figuur 15 staan voor het aantal moslims in Nederland. Het is onduidelijk waarom de jaartallen onregelmatig verspringen: van 1909 via 1960 en 1990 naar 2004. Misschien heeft de keuze daarvoor te maken met momenten waarop volkstellingen werden gehouden, of waarop het onderwerp immigratie prominent op de politieke agenda prijkte. De kijker komt er niet achter. Wilders licht zijn keuze niet toe en noemt geen bronnen.

Figuur 15: Staafgrafiek. Bron: Fitna van Geert Wilders uit 2008.

Het betreffende stukje uit de film toont achter elkaar deze eerste vier balken. Die verkleinen vervolgens. Dat wekt de suggestie dat het ergste nog moet komen. Inderdaad, ze maken als het ware plaats voor een vijfde en buitenproportioneel grote kolom. Deze hoogste staaf schiet letterlijk het scherm uit. Die staat echter niet voor het meest recente aantal moslims in Nederland, maar in Europa. Europese cijfers worden dus opeens naast Nederlandse cijfers gezet en waar komt die 54 miljoen vandaan? Misschien telde Wilders ook aantallen moslims uit Rusland en Turkije mee. Met dat soort noodzakelijke informatie wordt de kijker van Fitna echter niet vermoeid. De grafiek ziet er spectaculair uit, maar is niet minder manipulerend dan die van Al Gore.

Dezelfde truc met de horizontale as die Geert Wilders toepast, wordt ook gebruikt door Danone in een reclame voor Danoontje. In het tijdschrift Kinderen stond eens een advertentie voor dit kindertoetje. Daarin werd beweerd dat Danoontje door de jaren heen steeds minder suikers was gaan bevatten. Om één en ander te onderbouwen, wees een wijsneusje op een schoolbord met een aanwijsstok een grafiek aan. Dezelfde grafiek was ook te vinden op de website Danoontje.nl.

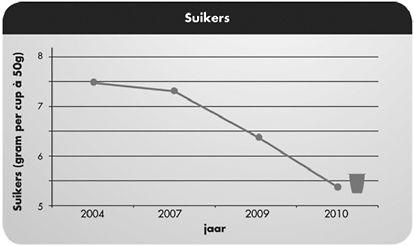
Figuur 16: Lijngrafiek die de suikerafname in een Danoontje toetje laat zien. Bron: www.danoontje.nl, november 2010

Het ziet er indrukwekkend uit, maar de inhoud valt uiteraard weer eens tegen. Kijk maar naar de jaartallen. Die verspringen eerst met drie jaar. Tussen 2009 en 2010 zit er opeens maar één jaar tussen, waardoor een sterke daling lijkt op te treden. Dit wordt nog eens versterkt door de as die niet bij nul te laten beginnen. Alsof dat allemaal niet genoeg is, gooit Danoontje er nog wat chart junk bij. Het punt uit 2010 krijgt er een kuipje bij.

Onderstaande grafiek is een correcte weergave van dezelfde gegevens. Het valt dus tegen met die suikerafname.

Figuur 17: Fictieve, correcte weergave van suikerafname in Danoontje.

Dezelfde gegevens, andere conclusie

Een klassiek voorbeeld van hoe dezelfde gegevens tot tegenovergestelde conclusies kunnen leiden, komt uit het standaardwerk How to lie with statistics van Darrel Huff. Stel, je wilt weten of de prijzen sinds de introductie van de Euro zijn gestegen of gedaald. Daar kun je achter komen door naar de prijzen van een aantal basisproducten te kijken. Laten we voor het gemak uitgaan van een prijs van 1 voor zowel een brood als een liter melk in het jaar 2002. Vervolgens kijken we naar de prijs van deze producten in 2010. We stellen in dit voorbeeld de prijs voor brood even op 2,00 en voor melk op 0,50. Figuur 18 laat de ontwikkeling in prijs van beide producten zien. Het vertrekpunt in tijd is het jaar 2002. De bedragen die de producten in dat jaar kosten, zetten we op honderd procent. In de grafiek zie je dat de prijs van brood is gestegen met honderd procent. De lijn komt daarmee uit op tweehonderd procent, een verdubbeling van de prijs dus. De prijs van melk is gehalveerd en komt uit op vijftig procent. Wat is nu de gemiddelde stijging of daling van de prijzen sinds de introductie van de euro in 2002? Dat kun je goed zien in de grafiek. Het gemiddelde van de tweehonderd procent waarop de broodprijs staat, plus de vijftig procent van de nieuwe melkprijs is 125 % (namelijk 200 + 50 = 250 ÷ 2 = 125). Ten opzichte van het startpunt van 100 % is er dus sprake van een gemiddelde prijsstijging van 25 %.

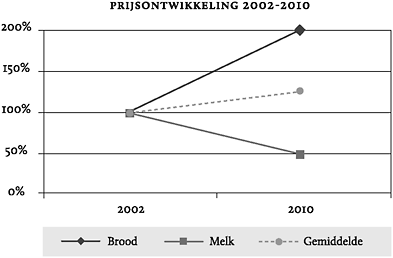
Figuur 18: Fictieve grafiek die de prijsstijging weergeeft.

Nu maken we met dezelfde gegevens een grafiek die precies het tegenovergestelde aantoont. Daarvoor nemen we dezelfde prijzen voor beide jaren maar stellen we 2010 als uitgangspunt. De prijzen in dat jaar staat nu op honderd procent, zoals figuur 19 laat zien.

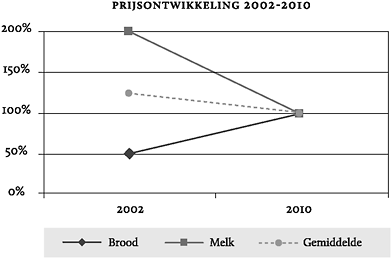
Figuur 19: Fictieve grafiek die de prijsdaling weergeeft.

We kijken in figuur 19 dus terug in de tijd. Volg je de ‘melklijn’ in figuur 19, dan zie je dat de melkprijs in 2002 maar liefst tweehonderd procent duurder was, namelijk 1,00 in plaats van de huidige vijftig cent. De ‘broodlijn’ laat zien dat brood vijftig procent goedkoper is, namelijk één euro in plaats van de huidige twee euro. We kunnen dezelfde som als hierboven toepassen om de gemiddelde prijsstijging te berekenen. Het gemiddelde komt opnieuw uit op 25 %. Figuur 19 laat zien dat het nu echter om een prijsdaling gaat. In 2002 waren de prijzen gemiddeld 25 % hoger dan in 2010. Met andere woorden, kijk je vanuit 2002 vooruit dan trekt de prijsstijging van brood het gemiddelde voor 2010 omhoog. Kijk je vanuit 2010 terug dan trekt de prijsdaling van melk het gemiddelde voor 2010 juist omlaag. In dit voorbeeld kenden wij de prijzen. Mensen die alleen de grafieken in figuur 18 en 19 zien, weten van niets. Je kunt hen alles wijsmaken. Het is de maker van een grafiek die kiest op welke manier hij de cijfers presenteert. Dat is een subjectief proces. Daarom is het des te belangrijker dat, zoals al bleek in hoofdstuk vijf over het percentage, we de cijfers achter een percentage kunnen leren kennen. Alleen dan wordt duidelijk of het gaat om een daadwerkelijke stijging of daling.

Van as tot as zullen wij (ver)gaan - lijndiagrammen

In de vorige paragrafen heb ik enkele basistrucs besproken waarmee een grafiek vrij eenvoudig kan worden gemanipuleerd. Eén van de gemakkelijkste manieren is nog niet genoemd. Met behulp van een lijndiagram kan de maker of gebruiker de boodschap nog sterker manipuleren. In een lijndiagram staan tegelijkertijd twee verschillende verticale Y-assen, zoals is te zien in zelfgemaakte onderstaande figuren 20 en 21. Dit is een veelgebruikte diagramtechniek. Op die manier kan je verschillende gegevens in één grafiek krijgen. In figuren 20 en 21 zijn dat cijfers en aantallen leerlingen. Met één as zijn de getallen voor aantallen leerlingen te hoog ten opzichte van de rapportcijfers. De eerste getallen lopen in de honderden, terwijl de laatste getallen niet boven de tien uitkomen. De rapportcijfers zouden niet te zien zijn bij het gebruik van één as. Door twee Y-assen te gebruiken, los je dat probleem op.

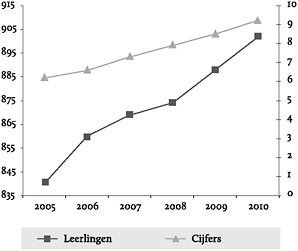
Figuur 20: Toename aantal leerlingen heeft nauwelijks effect op het gemiddelde cijfer. Fictieve lijndiagram.

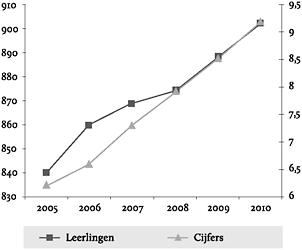
Figuur 21: Toename leerlingen is zeer positief voor het gemiddelde cijfer. Fictieve lijndiagram.

Een aantal van de eerder genoemde foefjes omt hier terug. De verticale assen hebben verschillende startpunten en schaalverdelingen. Ook kun je stellen dat de onderschriften bij de plaatjes suggestief zijn. De conclusie wordt voor de lezer getrokken. Het is daarbij wederom opvallend dat op basis van gelijke data tegengestelde conclusies kunnen worden getrokken. Bij een lijndiagram kun je namelijk de as kiezen die het beste jouw punt ondersteunt. Je kunt een dubbel effect scoren door twee verschillende ontwikkelingen naast elkaar te laten zien. In figuur 20 lijkt het alsof de toename in het aantal leerlingen nauwelijks een effect heeft op het gemiddelde cijfer van de school. De lijnen staan nogal ver uit elkaar. Ze lijken weinig met elkaar te maken te hebben. In figuur 21 is het omgekeerde aan de hand. Daar lijkt sprake van een toenemend positief effect op het gemiddelde cijfer. Beide lijnen lopen immers vrijwel gelijk met elkaar op.

Het volgende niet-fictieve voorbeeld van een lijndiagram is ook de moeite waard. In november 2009 hekelt onafhakelijk econoom en auteur Hans Labohm in een weblog op NOS.nl alle commotie rondom het klimaat. Hij stelt: “De gemiddelde wereldtemperatuur is de laatste tien jaar namelijk gedaald, terwijl de CO₂–concentratie in de atmosfeer nog steeds stijgt”. Deze stelling onderbouwt hij met een grafiek. Die grafiek is handig gekozen. Door het gebruik van twee assen, ontstaat de indruk dat de CO₂-concentratie boven de temperatuur uitstijgt terwijl dit geen effect heeft op de temperatuur. De temperatuur blijft zo ongeveer gelijk. KNMI weerman en NOS journaal weerpresentator Gerrit Hiemstra vroeg zich in een reactie af, waarom Labohm slechts tien jaar liet zien. Hiemstra presenteerde een gelijke grafiek over een langere periode.

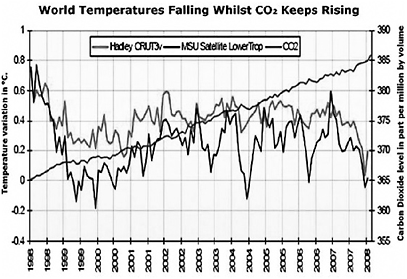
Figuur 22: Door Hans Labohm gebruikte grafiek in een zijn blog op NOS.nl

In figuur 23 is duidelijk te zien, dat in de periode die Hans Labohm uitlicht de CO₂-concentraties gelijk oplopen met de temperatuur. Je ziet ook dat dit niet altijd het geval was. Een vergelijk tussen beide grafieken maakt daarnaast duidelijk dat dit effect lijkt te zijn verdwenen zodra de assen op gelijke hoogte beginnen. Laat ik mij niet in de discussie mengen wie van deze twee heren gelijk heeft, maar slechts concluderen dat Hans Labohm, net zoals Al Gore, de grafiek koos die zijn standpunt het best ondersteunde. Met dubbele assen is het dus uitkijken geblazen. De gebruikte trucs kunnen dubbel zo verraderlijk zijn.

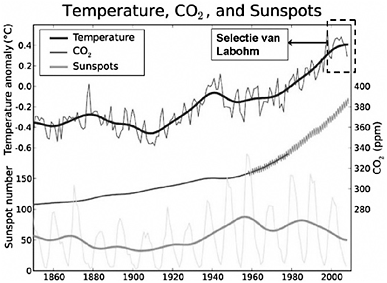
Figuur 23: De grafiek die Gerrit Hiemstra gebruikte in een reactie.

Het venijn zit hem in de taart - taartdiagrammen

Een grafisch middel dat misschien nog populairder is dan het lijndiagram, is het taartdiagram. Dit diagram dankt zijn populariteit aan Excel. Dankzij dat programma kunnen hele volksstammen tegenwoordig in een paar seconden een taart uit hun mouw schudden. De presentatie is prettig, omdat een taartdiagram in verschillende parten kan worden verdeeld en men naar hartenlust kan experimenteren met kleuren en andere geintjes. Vanzelfsprekend luidt mijn zure boodschap dat consumenten taarten met argwaan moeten bekijken. Makers en gebruikers passen de kunst van het weglaten tijdens het taartbakken met verve toe. In onderstaande fictieve taartdiagram zitten meerdere, veelgebruikte handigheidjes die de consument op het verkeerde been kunnen zetten.

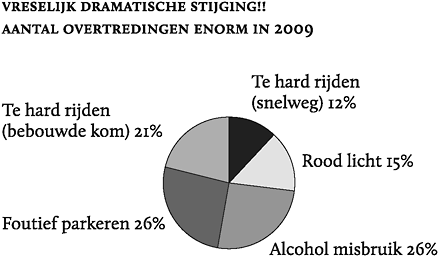
Figuur 24: Fictief voorbeeld van een incorrecte taartdiagram.

Taarttruc 1: het wegtoveren van waarden

Veel makers van taartdiagrammen laten bewust of onbewust wat categorieën weg. Denk aan “Overig”, “Geen mening” of “Weet niet”. Die categorieën horen echter bij de taart, zeker als ze ook nog eens een aanzienlijk grote taartpunt vormen. Tel je de percentages in figuur 24 op, dan kom je uit op honderd procent. Zo op het eerste gezicht lijkt er dus niets mis met de weergave van de totale waarde in verschillende partjes. Omdat we echter niet weten of het in bovenstaand diagram gaat om in totaal twaalf of 1200 overtredingen, is de grafiek waardeloos. Het gaat bij een taartdiagram dus niet om de zo mooi zichtbaar gemaakte verhoudingen, maar om de relatieve verhoudingen ten opzichte van het totaal. Zonder die informatie zegt een taartdiagram de consument niets.

Taarttruc 2: een betoverende titel

De titels in het diagram van figuur 24 zijn met opzet groter dan het diagram zelf. De titel leidt de aandacht af van de onderlinge verhoudingen. Zoals al aan de orde kwam bij het lijndiagram, vormt een titel de eerste hint waarmee de kijker de gebruikte grafiek kan duiden. Over het algemeen geldt dat de betrouwbaarheid van een grafiek groter is als er meer informatie in de titel en eventueel subtitel staat. Geen grote, schreeuwerige en suggestieve teksten of termen maar duidelijke, inhoudelijke informatie die daadwerkelijk is terug te vinden in de grafiek. Wordt er bijvoorbeeld gesproken over een stijging dan is het beter om ook de voorgaande jaren te laten zien.

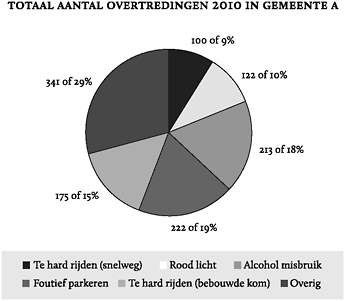
Figuur 25: Fictief voorbeeld van een correcte taartdiagram.

Figuur 25 laat dezelfde grafiek zien, maar dan met een correcte titel, de juiste achtergrondinformatie en normale verhoudingen tussen grafiek en tekst.

Taarttruc 3: percentages omtoveren in andere waarden

Hierboven, bij taarttruc 1, werd al gesteld dat een taartdiagram is bedoeld om de relatieve verhoudingen weer te geven. Relatief ten opzichte van het grote geheel of het totaal. Dat is wat je suggereert als je een taartdiagram gebruikt. Je laat immers alle cijfers, of partjes, deel uitmaken van één en dezelfde cirkel. Relatieve verhoudingen kunnen het best worden weergegeven in percentages. Als een consument in een taartdiagram dus waarden ziet staan die niet zijn uitgedrukt in percentages, mag de alarmbel gaan rinkelen.

Het diagram uit figuur 26 komt uit een presentatie over een onderzoek naar tijdsbesteding door de Stichting tot Promotie en Optimalisatie van Televisiereclame (SPOT) uit 2008. Het figuur laat zien waar wij Nederlanders gedurende één dag zoal onze tijd aan besteden.

Dit taartdiagram laat echter geen percentages zien maar het aantal uren per activiteit per etmaal. Tel je die uren bij elkaar op, dan kom je uit op 28,1. Dat is best verrassend. In een etmaal zitten toch echt maar 24 uur. Het totaal is dus een ander totaal dan wat de consument mag verwachten. In dit voorbeeld zijn de uren gemiddelden. Gemiddeld spendeert een Nederlander per dag dus 4,3 uur aan vrije tijd. In sommige gevallen zal het wat meer zijn, in andere minder.

Figuur 26: Onze dagbesteding volgens onderzoek SPOT, 10 juni 2008.

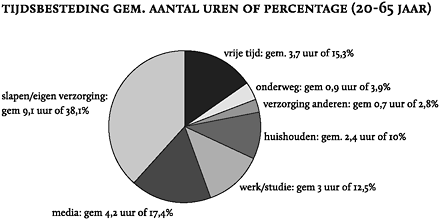
Figuur 27: Dezelfde gegevens als in figuur 26 maar nu correct weergegeven.

Vandaar dat elk van de partjes als onafhanelijk deel moet worden gezien. Ze staan los van elkaar en geven helemaal geen verhoudingen weer, ook al wordt dit door het gebruik van het taartdiagram wel gesuggereerd. Kortom, een taartdiagram zonder percentages is een misbaksel.

Zet je bovenstaande uren af tegen één en hetzelfde totaal, bijvoorbeeld een etmaal van 24 uur, dan kun je wel iets zeggen over de onderlinge verhoudingen. Onderstaand diagram geeft op correcte wijze de verhoudingen weer, namelijk met percentages.

Van 2 naar 3D - de driedimensionale grafiek

Ere wie ere toekomt. Dankzij Excel kregen we ook toegang tot de inmiddels immens populair geworden driedimensionale grafiek. Met een extra dimensie erbij wordt een grafiek pas echt spannend, niet in de laatste plaats voor de consument. Hoe meer effecten, hoe meer kans op gekonkel en gestuntel. Dat is voor een 3D grafiek al niet anders. De volgende twee voorbeelden laten dat zien.

In het bovenste voorbeeld staan de leeftijden van zes kinderen weergegeven. Niels lijkt ouder dan Floor maar nee, ze zijn beiden vier jaar oud. Julia is zes jaar, maar lijkt veel ouder dankzij de kloeke punt van haar feestmuts die zelfs boven de verticale as lijkt uit te stijgen.

In het onderste voorbeeld maakt het driedimensionale effect de zaken ook al niet duidelijker. De percentuele bijdrage per filiaal is misleidend. Alle bijdrages lijken hoger dan ze in werkelijkheid zijn. Daarnaast valt het effect voor Filiaal E bijna in het niet. Filiaal C zit op 36 % maar lijkt ver boven de veertig procent uit te stijgen.

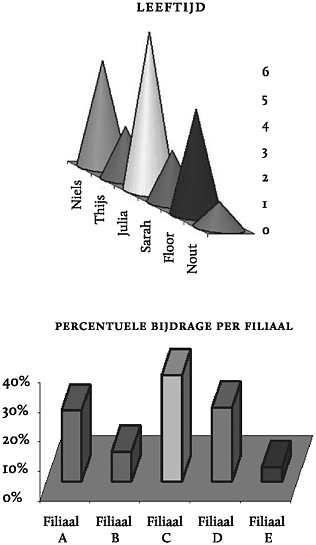
Figuur 28: Twee fictieve voorbeelden van driedimensionale grafieken

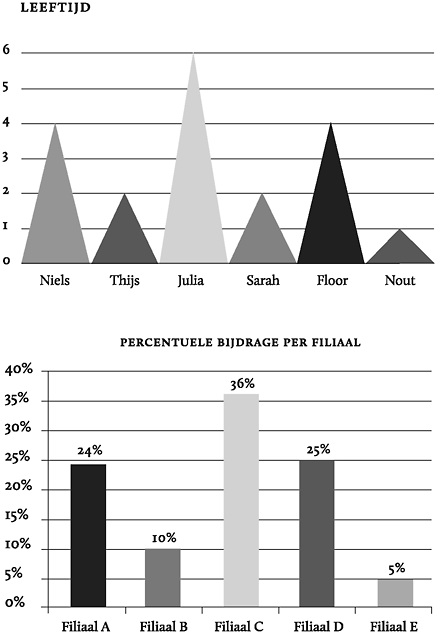
Figuur 29: Twee fictieve voorbeelden van wat niet langer driedimensionale grafieken zijn.

De leeftijden en bijdragen staan duidelijk weergegeven in onderstaande grafieken. Zoals je ziet, zijn de werkelijke waarden bijna niet terug te vinden in de 3D grafieken.

Je kunt met een paar muisklikken extra ook een 3D taart bakken. Dat levert een prachtig gekleurde damschijf op met als driedimensionaal effect een variabele hellingshoek. Zie bijvoorbeeld figuur 30.

De categorie Alcoholmisbruik lijkt door de dikke rand groter dan Foutief Parkeren, maar is in werkelijkheid even groot. Alcoholmisbruik lijkt zelfs groter dan Te hard rijden (snelweg) en Rood licht bij elkaar.

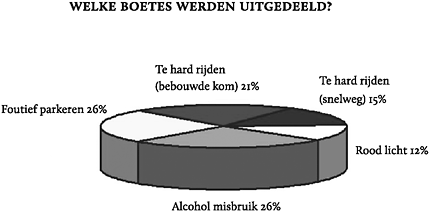
Figuur 30: Fictief voorbeeld van een 3D taartdiagram

Reclamemakers maken dankbaar gebruik van taartdiagrammen. Een prachtig exemplaar kwam ik tegen op de website van Medical Measurement Systems (MMS). Om een medisch meetinstrument aan te prijzen, de zogenaamde Proton Pump Inhibitor (PPI), gebruikte MMS onderstaand diagram.

Figuur 31: Een 3D taartdiagram zoals weergeven op mmsonline.nl

Het diagram zou iets moeten zeggen over de typische symptomen bij patiënten die gebruik maken van het instrument. Het 3D effect verstoort echter de verhoudingen tussen de partjes. Het helpt natuurlijk ook niet dat er geen enkel percentage of cijfer bij vermeld staat.

In plaats van saaie staven of taarten kun je ook 3D plaatjes gebruiken. Dat spreekt meer tot de verbeelding dan droge cijfers en daarin zit ‘m meteen de crux. Als we naar een driedimensionale afbeelding kijen, schat ons brein de grootte van de objecten op basis van lengte, hoogte en diepte. Met andere woorden, we zetten de verhoudingen tussen de gepresenteerde objecten sterker aan. Dit is goed te zien in figuur 32. De flesjes zijn wat hun lengte betreft correct gepresenteerd. Neem het verschil tussen de flessen uit 1995 en 2010. Zoals het hoort, is de lengte 3,5 keer zo groot. In onze verbeelding van de cijfers is de fles uit 2010 echter veel groter.

Figuur 32: Fictief voorbeeld van het gebruik van 3D objecten in een grafiek.

De keuze voor het lange, rondbuikige flesje in een 3D afbeel ding is hier debet aan. Die factoren zorgen ervoor dat de breedte en de diepte vier keer zo groot worden. Gevoelsmatig is de waterconsumptie dus niet 3,5 keer groter geworden, maar 3,5 × 4 × 4 = 56 keer groter.

Blijf scherp! - de visuele effecten

Door te spelen met kleuren en arceringen kan ons brein danig op het verkeerde been worden gezet. We kennen waarschijnlijk allemaal de plaatjes in figuur 33.

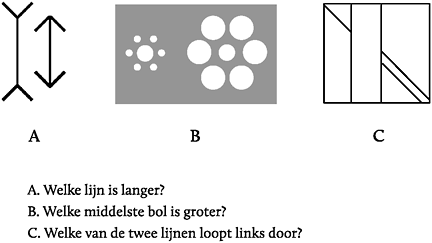
Figuur 33: Drie voorbeelden van optische illusies.

Zoals je ziet, hebben onze hersenen het knap lastig met sommige vragen. Figuur 34 laat bijvoorbeeld zien dat het effect van vraag B in figuur 33 gemakkelijk is toe te passen in een grafiek. De bollen lijken soms groter en soms kleiner, maar de waarde die ze voorstellen is dezelfde.

Een andere mogelijkheid is het gebruik van vloei-effecten en contrast. In figuur 35 is goed te zien dat de vloeiende achtergrond de waarde van Product A oprekt. Product A is in nevelen gehuld en lijkt daarom hoog boven de wolken uit te stijgen, terwijl de waarde van Product B zeer sterk afgebakend en laag bij de grond oogt. Daarmee wordt het verschil tussen beide producten benadrukt.

Figuur 34: Vergelijkende tabel met gegevens over geboorte en seks bij tieners in rijke landen. Bron: Gegevens uit Innocenti Report nummer 3 van Unicef, juli 2001. De tabel komt uit de New York Times van 6 september 2008 uit een artikel van Charles M. Blow “Let’s talk about sex”.

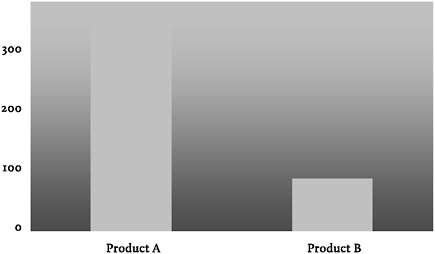
Figuur 35: Fictieve grafiek met kleureffecten

Ook het gebruik van de achtergrond levert een scala aan manipulerende effecten op. Zie bijvoorbeeld figuur 36. De verkoopaantallen voor Product A lijken hoger dan die van Product E. Toch zijn beide staven even lang. Daarnaast lijkt Product B weer minder goed verkocht dan Product D, maar ook dit is gezichtsbedrog. Beide producten werden evenveel verkocht in 2010.

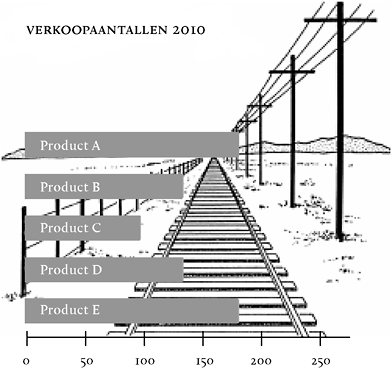
Figuur 36: Fictief voorbeeld met achtergrond en diepte.