VII Az első századmásodperc
Az első három percről szóló beszámolónkat az V. fejezetben nem kezdtük a kezdet kezdetén. Ehelyett egy „első felvételtől” indultunk, amelynek időpontjáig a kozmikus hőmérséklet már 100 milliárd kelvin alá csökkent, nagy számban csupán fotonok, elektronok, pozitronok, neutrínók és antineutrínók voltak jelen. Ha a természetben csak ezek a részecskék léteznének, akkor időben talán visszafelé extrapolálhatnánk az Univerzum tágulását, és arra következtethetnénk, hogy lennie kellett egy igazi kezdőpillanatnak, ami első felvételünket körülbelül 0,0108 másodperccel előzte meg.
A modern fizika azonban még sok más részecskét ismer a felsoroltak mellett: müonokat, pi-mezonokat, protonokat, neutronokat és így tovább. Ahogy egyre koraibb és koraibb időpontokra tekintünk vissza, előbb-utóbb olyan magas hőmérsékletekkel és sűrűségekkel találjuk szemben magunkat, amelyek mellett már mindezek a részecskék is nagy számban lehettek jelen, szüntelen kölcsönhatásban, tehát egymással hőmérsékleti egyensúlyban. Bizonyos okokból – amiket majd később kívánok megvilágítani – ma még egyszerűen nem elegendő a részecskefizikai tudásunk ahhoz, hogy ilyen keverék tulajdonságait kiszámíthassuk. így a mikrofizikában való tudatlanságunk, mint egy fátyol, elhomályosítja látásunkat, ha a kezdet kezdetéig próbálunk visszatekinteni.
Természetesen nehéz ellenállni a csábításnak, hogy megkíséreljünk e fátyol mögé tekinteni. Ez a kísértés különösen erőssé válhat egy olyan elméleti fizikus esetében, mint én, aki sokkal többet munkálkodtam a részecskefizikában, mint az asztrofizikában. Hiszen a mai részecskefizika igen sok érdekes elképzelésének vannak olyan finom következtetései, amelyeket jelenleg rendkívül nehéz lenne laboratóriumi kísérletekkel ellenőrizni, de drámai következményekre vezetnek, ha a korai Univerzumra alkalmazzuk őket.
100 milliárd kelvinnél magasabb hőmérsékletekre visszatekintve, az első komoly problémát a részecskék „erős kölcsönhatása” jelenti. Az erős kölcsönhatás lényegében azokat az erőket jelenti, amelyek az atommagban a protonokat és a neutronokat együtt tartják. A mindennapi életben ezek nem olyan megszokottak, mint az elektromágneses vagy a gravitációs erők, mivel hatótávolságuk rendkívül rövid, mintegy tízbilliomod (10-13) centiméter. Még a molekulákban is, ahol az atommagok átlagos távolsága néhány százmilliomod (10-8) centiméter, elhanyagolható az atommagok erős kölcsönhatása. Pedig – mint azt nevük is jelzi – ezek az erők nagyon erősek. Ha például két proton elég közel kerül egymáshoz, erős kölcsönhatásuk százszorta erősebbé válik az elektromos taszításnál; ezért az erős kölcsönhatás akár 100 proton taszítóereje ellenére is képes együtt tartani az atommagot. A hidrogénbomba robbanását a neutronok és protonok olyan átrendeződése okozza, amely lehetővé teszi, hogy az erős kölcsönhatás az eredeti kötésnél erősebben tartsa össze a magrészecskéket. A bomba energiáját épp az átrendeződés révén felszabadult többletenergia adja.
Nos, épp az erős kölcsönhatások erőssége az oka annak, hogy matematikailag sokkal nehezebb leírni őket, mint az elektromágneses kölcsönhatásokat. Amikor például kiszámítjuk két elektron egymáson való szóródásának valószínűségét, a köztük fellépő elektromos taszítás következtében végtelen számú járulékot kell összeadnunk, amelyek mindegyike olyan folyamatoknak felel meg, amik fotonok, illetve elektron-pozitron párok kibocsátásával vagy elnyelésével mehetnek végbe. Egy-egy ilyen folyamat a 10. ábrán bemutatottakhoz hasonló „Feynman-gráfok”-kal szimbolizálható. (Azt a számítási módszert, amely ezeken a gráfokon alapul, Richard P. Feynman dolgozta ki a negyvenes évek végén Cornellben. Ebben a formalizmusban minden gráf egy járulékot ad, és a szórásfolyamat valószínűségét az egyes járulékok összegének a négyzete adja meg.) Ha bármely diagramban eggyel növeljük a belső vonalak számát, a diagram járuléka számértékben egy olyan tényezővel csökken, amely hozzávetőleg egyenlő egy alapvető természeti állandóval: a „finomszerkezeti állandóival. Ez az állandó elég kicsi, számértéke körülbelül 1/137,036. Éppen ezért a bonyolultabb gráfok egyre kisebb és kisebb járulékot adnak. A szórási folyamat valószínűsége megfelelő pontossággal kiszámítható, ha csupán kevés egyszerű gráf járulékát adjuk össze. (Ezért vagyunk biztosak abban, hogy az atomi színképeket csaknem korlátlan pontossággal ki tudjuk számítani.) De az erős kölcsönhatások esetében az az állandó, amely a finomszerkezeti állandó szerepét játszaná, nem 1/137, hanem közel 1, és ezért a bonyolultabb gráfok csaknem ugyanakkora járulékot adnak, mint az egyszerűbbek. Az elmúlt negyedszázad során ez a probléma – az erős kölcsönhatásokat tartalmazó folyamatok valószínűségének számítási nehézségei – volt a részecskefizika fejlődésének legnagyobb akadálya.

10. ábra. Néhány Feynman-gráf. Az ábrán az elektron-elektron szórás néhány egyszerűbb Feynman-gráfját tüntettük fel. Az egyenes vonalak elektronokat vagy pozitronokat, a hullámvonalak fotonokat jelölnek. Minden gráfnak megfelel egy meghatározott számérték, amely a kimenő és bejövő elektronok lendületétől (impulzusától) és perdületétől (spinjétől) függ. A szórási folyamat valószínűsége e mennyiségek összegének négyzete (számításba véve az összes lehetséges Feynman-gráfot). Minden egyes gráf járuléka ehhez az összeghez az 1/137 finomszerkezeti állandó annyiadik hatványával arányos, amennyi a gráfban levő fotonvonalak száma. Az (a) gráf egyetlen foton cseréjének felel meg, ez adja a fő – 1/137-tel arányos – járulékot. A (b), (c), (d), és (e) bemutatja azoknak a gráfoknak az összes típusát, amelyek (a)-hoz a fő „sugárzási" korrekciókat adják. Ezek mind 1/l372-nel arányosak. Végül (f) egy még ezeknél is kisebb, 1/1373-nel arányos járulékot ad.
Erős kölcsönhatás nem minden folyamatban lép fel. Csupán a részecskék egy meghatározott osztálya, a „hadronok” vesznek részt benne. Ez az osztály magában foglalja a magrészecskéket (protonokat, neutronokat), a pi-mezonokat és más instabil részecskéket, amelyek K-mezon, éta-mezon, lambda-hiperon, szigma-hiperon stb. neveken ismertek. A hadronok általában a leptonoknál nehezebbek (a lepton elnevezés a görög „könnyű” szóból ered), ám nem ez a lényeges különbség közöttük, hanem az, hogy a hadronok részt vesznek az erős kölcsönhatásokban, míg a leptonok – elektronok, neutrínók, müonok – nem. Az a tény, hogy az elektronok nem érzékelik a magerőket, döntő fontosságú: az elektron kis tömegével párosulva ez felelős azért, hogy az elektronfelhő egy atomban vagy egy molekulában 100 000-szer nagyobb kiterjedésű az atommagnál, és azért is, hogy az atomokat a molekulákban együtt tartó kémiai erők milliószorta gyengébbek az atommagokat összetartó magerőknél. Ha az atomokban és a molekulákban az elektronok a magerőket is éreznék, nem lenne se kémia, se kristálytan, se biológia – csak egyedül magfizika.
A 100 milliárd kelvines hőmérsékletet, amivel az V. fejezetben indultunk, gondosan úgy választottuk meg, hogy az kisebb legyen valamennyi hadron küszöbhőmérsékleténél. (A 135. oldalon levő I. táblázat szerint a legkönnyebb hadron, a pi-mezon küszöbhőmérséklete 1,6 billió kelvin.) így az Univerzum történetének az V. fejezetben leírt szakaszában nagy számban csak a fotonok és a leptonok voltak jelen, és a magas hőmérséklet miatt bízvást elhanyagolhatók voltak a köztük fellépő kölcsönhatások.
Ám mi a helyzet akkor, amikor a Világegyetem már olyan forró, hogy benne a hadronok és antihadronok száma is jelentékennyé válik? Erre két – lényegileg eltérő – választ is lehet adni, amik a hadronok természetével foglalkozó két nagyon különböző gondolkodási iskola nézeteit tükrözik.
Az egyik nézet szerint „elemi” hadronok valójában nem is léteznek. Minden hadron éppen annyira alapvető, mint bármely másik, ebbe nem csupán a stabil vagy csaknem stabil hadronokat értve bele, mint például a proton és a neutron, és nem is csak a mérsékelten instabil részecskéket, mint a pi-mezonok, K-mezonok, éta-mezonok és hiperonok, amelyek elég hosszú életűek ahhoz, hogy mérhető nyomot hagyjanak a fotoemulzióban vagy a buborékkamrában; de még a teljesen instabil „részecskék”-et is, mint a rhó-mezonok, amelyek épp csak annyi ideig élnek, hogy csaknem fénysebességgel haladva átszelhessék az atommagot. Ezt a gyakran „nukleáris demokrácia” néven emlegetett elméletet az ötvenes évek végén és a hatvanas évek elején fejlesztette ki Geoffrey Chew és még több más kutató.
Ha a hadronokat ilyen liberálisan definiáljuk, több száz olyan ismert hadron van, amelyeknek a küszöbhőmérséklete 100 billió kelvinnél kisebb, és feltehetőleg további százak, amelyek még fölfedezésre várnak. Némelyik elméletben a számuk végtelen; a részecske-típusok száma így egyre gyorsabban és gyorsabban nő, ahogy egyre nagyobb és nagyobb tömegeket vizsgálunk. Egy ilyenfajta világban reménytelennek tűnhet eligazodni, de szerencsénkre épp a részecskespektrum nagymérvű bonyolultsága végül is valamiféle egyszerűsítésre vezet. Például a rhó-mezon olyan hadron, amely két pi-mezonból összetett instabil képződményként képzelhető el; amikor a rhó-mezonokat számításainkban explicit módon figyelembe vesszük, bizonyos mértékig már a pi-mezonok kölcsönhatásait is figyelembe vettük. így elképzelhető, hogy ha valamennyi hadront expliciten bevesszük termodinamikai számításainkba, akkor elhanyagolhatjuk az erős kölcsönhatások összes más hatását.
Ha továbbá a hadronoknak valóban korlátlan számú fajtája létezik, amikor egy adott térfogatrészbe egyre több és több energiát pumpálunk, a befektetett energia nem a részecskék rendezetlen mozgásainak sebességét fogja növelni, hanem inkább a térfogatelemben jelenlevő részecskefajták számát. A hőmérséklet ezért nem növekszik olyan gyorsan a növekvő energia függvényében, mint tenné akkor, ha a hadronfajták száma véges lenne. S valóban, az efféle elméletekben létezik egy maximális hőmérséklet, vagyis egy olyan véges hőmérsékletérték, amely mellett az energiasűrűség végtelenné válik. Ez éppolyan legyőzhetetlen felső korlátja volna a hőmérsékletnek, mint amilyen alsó korlátja az abszolút nulla fok. A hadronfizikában a maximális hőmérséklet létezésének gondolata eredetileg a genfi CERN Laboratóriumban dolgozó R. Hagedorntól származik. Ezt a gondolatot később más elméleti fizikusok továbbfejlesztették, így például Kerson Huang az MIT-ból és jómagam. Van egy meglehetősen pontos becslés arra, hogy mekkora lehet ez a maximális hőmérséklet. Kiderül, hogy annak számértéke meglepően kicsi, mindössze 2 billió kelvin (2 • 1012 K). Ahogy egyre közeledünk a kezdethez, a hőmérséklet egyre közelebb és közelebb kerül ehhez a maximumhoz, és a hadrontípusok egyre gazdagabb és gazdagabb változatokban tűnnek fel. Ám még ilyen egzotikus feltételek mellett is létezne egy kezdet, egy végtelen energiasűrűségű időpont, mintegy egy századmásodperccel előzve meg az V. fejezet első felvételének időpontját.
Létezik egy másik iskola is, amely jóval konvencionálisabb, jóval közelebb áll a szokásos elképzelésekhez, mint a „nukleáris demokrácia”, és – véleményem szerint – jóval közelebb áll az igazsághoz is. Eszerint nem minden részecske egyenrangú; némelyek valóban elemiek, az összes többi pedig valamiképpen ezekből az elemi részecskékből tevődik össze. E nézet szerint az elemi részecskék közé tartozik a foton, valamennyi ismert lepton, de nem tartozik ide egyetlen ismert hadron sem. A hadronok ebben az elméletben más, elemibb alkotórészecskékből, az úgynevezett „kvarkok”-ból épülnek fel.
A kvarkelmélet eredeti változata a Cal Techen dolgozó Murray Gell-Manntól és (tőle függetlenül) az ugyanitt dolgozó George Zweigtől származik. Az elméleti fizikusok költői képzelete meglehetősen vad nevekkel ruházta fel a kvarkok különféle fajtáit. A kvarkok különböző típusainak – vagy „ízei”-nek – a következő neveket adták: „felső”, „alsó”, „ritka”, „bájos” stb. Ezenfelül mindegyik „kvark-íz” háromféle „szín”-ben fordulhat elő. Az Egyesült Államokban általában a vörös, fehér és kék színeket használják. Pekingi elméleti fizikusok egy kis csoportja már ezt megelőzően kidolgozta a kvarkelmélet egy lehetséges változatát, de ők kvarkok helyett „sztraton”-oknak nevezték ezeket az alapvető részecskéket, mivel a valóság egy mélyebb rétegét (stratum = réteg) fejezik ki, mint a hadronok.
Ha a kvarkelképzelés helyes, akkor az Univerzum kezdeti időszakának fizikája jóval egyszerűbb lehet, mint azt gondoltuk. A magrészecskékben megfigyelhető kvarkeloszlás alapján következtethetünk a kvarkok között ható erőkre, ezek az eloszlások pedig (ha a kvarkmodell igaz) meghatározhatók az elektronok és magrészecskék nagyenergiájú ütközéseiből. Ezen az úton az MIT és a Stanford Lineáris Gyorsító Centrum együttműködésében részt vevő kutatók néhány évvel ezelőtt arra az eredményre jutottak, hogy a kvarkok között ható erők eltűnni látszanak akkor, ha a kvarkok nagyon közel kerülnek egymáshoz. Ez azt sugallja, hogy egy bizonyos hőmérsékleten, ami néhány billió kelvin körül van, a hadronok egyszerűen az őket felépítő kvarkokra foszlanak szét, éppen úgy, ahogy néhány ezer fokon az atomok atommagra és elektronokra, néhány millió fokon pedig az atommagok protonokra és neutronokra esnek szét. E képnek megfelelően elképzelhető, hogy a nagyon korai Univerzum fotonokat, leptonokat és antileptonokat, továbbá kvarkokat és antikvarkokat tartalmazott, amelyek mindegyike lényegében szabad részecskeként viselkedett, és emiatt mindegyik részecskefajta a feketetest sugárzás egy további járulékát adta. Ebben az esetben könnyen kiszámítható, hogy léteznie kellett egy igazi kezdetnek, amely egy végtelen sűrűségű és végtelen hőmérsékletű állapot volt.
Ezeket a meglehetősen intuitív elképzeléseket a hetvenes években sikerült szilárdabb matematikai alapokra fektetni. 1973-ban három fiatal elméleti fizikus (Hugh David Politzer a Harvardról, valamint Dávid Gross és Franck Wilczek Princetonból) megmutatta, hogy a kvantumtérelméletek egy bizonyos speciális osztályában a kvarkok között ható erők valóban gyengülnek, ha a kvarkokat közelítjük egymáshoz. (Az elméleteknek ezt a típusát – itt nem részletezhető technikai okok miatt – „nem-abeli mértékelméletek”-nek nevezik.) Ezeknek az elméleteknek egy figyelemre méltó közös tulajdonsága az úgynevezett „aszimptotikus szabadság”: aszimptotikusan kis távolságok, vagy ami ugyanezt jelenti: nagy energiák esetén a kvarkok szabad részecskékként viselkednek. J. C. Collins és M. J. Perry, a Cambridge-i Egyetem kutatói azt is megmutatták, hogy bármely aszimptotikusan szabad elméletben az anyag tulajdonságai – megfelelően magas hőmérséklet és sűrűség esetén – lényegében ugyanolyanok, mintha az illető közeg tisztán szabad részecskékből állna, így a nem-abeli mértékelméletek aszimptotikus szabadsága szilárd matematikai megalapozását adja az első századmásodpercről felvázolt nagyon egyszerű képnek – vagyis annak, hogy akkor a Világegyetem csupa szabad elemi részből épült fel.
A kvarkmodell egyébként jól működik az alkalmazások igen széles körében. A protonok és a neutronok valóban úgy viselkednek, mintha három kvarkból épülnének fel, a mezonok mintha egy kvarkból és antikvarkból állnának stb. Ám e sikerek ellenére a kvarkmodell egy nagy rejtéllyel is szolgál: a létező gyorsítók legnagyobb energiáival sem sikerült eddig egyik hadront sem alkotó kvarkjaira bontani.
Ugyanígy nem lehet szabad kvarkokat izolálni a kozmológiában sem. Ha a korai Univerzumban uralkodó magas hőmérsékleteken a hadronok valóban szabad kvarkokra estek szét, arra lehetne számítani, hogy néhány szabad kvark mind a mai napig fennmaradt. Ja. B. Zeldovics szovjet asztrofizikus megbecsülte, hogy a visszamaradt szabad kvarkoknak hozzávetőleg az aranyatomokkal azonos gyakoriságban kellene előfordulniuk a mai Világegyetemben. És bár az arany nem túl gyakori, mégis jóval egyszerűbb egy gramm aranyat összegyűjteni, mint akár egyetlen szabad kvarkot is „elcsípni”. (Az utóbbi ugyanis eddig még nem sikerült.)
Az, hogy mindeddig nem sikerült szabad kvarkokat találni, a mai elméleti fizika egyik legfontosabb problémája. Mint azt Gross, Wilczek és én sugalmaztuk, épp az „aszimptotikus szabadság” kínál egy lehetséges magyarázatot. Ha a két kvarkot közelítve egymáshoz, a köztük levő kölcsönhatás erőssége csökken, akkor távolítva őket egymástól, a kölcsönhatás erősödni fog. Ezért a közönséges hadronokban a kvarkok távolságának a növelésével nőni fog az az energia is, ami ahhoz szükséges, hogy egy kvarkot a többitől elszakítsunk, és olyan naggyá is válhat, hogy a vákuumból új kvark-antikvark párokat kelthet. így végül is nem néhány szabad kvarkot, hanem több közönséges hadront kapunk. Ez nagyon hasonlít ahhoz, mintha megpróbálnánk egy húr egyik végét különválasztani: ha nagyon erősen feszítjük, a húr végül is elszakad, ám amit végeredményül kapunk, az két húr, két-két véggel! Az Univerzum korai szakaszában a kvarkok elég közel kerültek egymáshoz ahhoz, hogy ne érezzék ezeket az erőket, így szabad részecskeként viselkedhettek. De ahogy az Univerzum tágulni és hűlni kezdett, valamennyi – a kezdeti szakaszban meglevő – kvark vagy szétsugárzódott egy antikvarkkal, vagy beépült egy proton vagy neutron belsejébe.
Ennyit az erős kölcsönhatásokról. Bár még sok kérdés nyitva maradt, várnak ránk egyéb problémák is, ha az idő kerekét a kezdet kezdetéig próbáljuk visszaforgatni.
A részecskék modern elméletének egyik valóban megragadó következménye az, hogy jó okunk van feltételezni, hogy valamikor a régmúltban az Univerzum egy olyasfajta fázisátalakuláson mehetett keresztül, mint a fagyó víz, amikor 273 kelvin (0 °C) alá hűl. Ez a fázisátalakulás azonban nem az erős kölcsönhatással, hanem a részecskék másik rövid hatótávolságú kölcsönhatásával, a gyenge kölcsönhatásokkal áll kapcsolatban.
Bizonyos radioaktív bomlási folyamatokért, így például a szabad neutron bomlásáért a gyenge kölcsönhatások a felelősek. Mint azt nevük is mutatja, ezek a kölcsönhatások mind az erős, mind pedig az elektromágneses kölcsönhatásoknál jóval gyengébbek. Például egy 1 millió elektronvolt energiával ütköző elektron és neutrínó között fellépő gyenge erő csupán tízmilliomod (10-7) része annak az elektromágneses erőnek, amely az ugyanekkora energiával ütköző elektronok között fellép.
Ám annak ellenére, hogy e két kölcsönhatás erősségében ilyen szembeszökő különbség mutatkozik, régóta fölvetődött az a gondolat, hogy mélyebb kapcsolat is lehet a gyenge és az elektromágneses erők között. 1967-ben kidolgoztam egy olyan térelméletet, amely ezt a két erőt egyesíti, majd 1968-ban – tőlem teljesen függetlenül -Abdus Salam is kiépített egy hasonló modellt. Ez az elmélet többek között a gyenge kölcsönhatások egy újabb formáját jósolta meg, az úgynevezett „semleges áramok”-nak a létezését, amit 1973-ban sikerült kísérletileg is kimutatni. Majd 1974-ben a modell újabb megerősítést kapott a hadronok merőben új típusú családjának fölfedezése révén. Az elméletben kulcsszerepet tölt be az az elképzelés, hogy a természet számos szimmetriatulajdonsággal bír, amelyek a különféle erőkhöz és részecskékhez kapcsolódnak, ám az egyes fizikai folyamatokban ez már nem mutatható ki; a szimmetriák sérülnek. Matematikailag ugyanilyen szerkezetűek azok a térelméletek is, amelyeket 1973 óta az erős kölcsönhatások leírására próbálnak kidolgozni (nem-abeli mértékelméletek). Ma igen sok fizikus úgy véli, hogy a mértékelméletek egy egységes alapot adhatnak a természet valamennyi kölcsönhatásának – a gyenge, az elektromágneses, az erős és talán a gravitációs erőknek – a leírására. Ezt a meggyőződést támasztja alá az egyesített mértékelméletek egyik tulajdonsága, amit Salam és én sejtettünk meg, és Gerard ’t Hooft és Benjamin Lee bizonyított be 1971-ben: a bonyolult Feynman-gráfok járuléka – bár látszólag végtelen – felösszegezhető, és minden fizikai folyamat valószínűségére véges eredmény adódik.
Ami a korai Univerzum vizsgálatát illeti, a mértékelméletek egy lényeges tulajdonsága – mint az D. A. Kirzsnyics és A. D. Linde, a moszkvai Lebegyev Intézet kutatói kimutatták –, hogy ezekben az elméletekben fellép egy fázisátalakulás, egyfajta kikristályosodás vagy „fagyás”, ami mintegy 3000 billió kelvines hőmérsékleten (3 • 1015 K) megy végbe. A kritikus hőmérséklet alatt az Univerzum már sok szempontból nagyon hasonlít a maira; például a gyenge kölcsönhatások valóban gyengék és rövid hatótávolságúak. Ám a kritikus hőmérséklet fölött megmutatkozik a gyenge és elektromágneses erők lényegi egysége: a gyenge kölcsönhatások az elektromágneses erőkkel egyforma erősségűvé válnak, és hatásuk is a távolság négyzetével fordított arányban csökken.
Nagyon tanulságos ezt a folyamatot a víz megfagyásával összehasonlítani. A fagyáspont fölött a víz nagyfokú homogenitást mutat: annak valószínűsége, hogy egy vízmolekulát a pohár belsejének valamelyik adott pontjában találjunk, ugyanakkora bármely pontra. Ám amikor a víz megfagy, elvész a különböző térbeli pontoknak ez az egyenrangúsága, szimmetriája: a jég kristályrácsot képez, amelyben a vízmolekulák bizonyos rendszer szerint helyezkednek el, míg más helyeken az előfordulásuk valószínűsége csaknem nulla. Ehhez hasonlóan, amikor a Világegyetem „megfagyott” – vagyis hőmérséklete 3000 billió kelvin alá csökkent –, egy szimmetria elveszett; nem a térbeli homogenitás, mint a pohár jég esetében, hanem a gyenge és az elektromágneses kölcsönhatások közti szimmetria.
A hasonlatot még tovább is lehetne vinni. Mindenki tudja, hogy amikor a víz megfagy, általában nem képez tökéletes jégkristályt, hanem annál bonyolultabb szerkezet alakul ki: különböző kristálydomének, amelyeket egymástól különféle kristályhibák választanak el. Lehetséges, hogy az Univerzum is doménekben kristályosodott ki? Lehet, hogy egy olyan doménben élünk, amelyen belül sajátos módon sérül a gyenge és az elektromágneses kölcsönhatások eredeti szimmetriája? Fel fogunk-e fedezni más doméneket is a Világegyetemben?
Képzeletünk egészen a 3000 billió fokos hőmérsékletekig vitt vissza, miközben az erős, gyenge és elektromágneses kölcsönhatásokkal foglalkoztunk. De mi a helyzet a fizikában ismert kölcsönhatások negyedik nagy osztályával, a gravitációval? Történetünkben természetesen fontos szerepet játszott a gravitáció is, hiszen az szabályozta a kapcsolatot az Univerzum sűrűsége és a tágulás üteme között. Ám mindeddig nem találtuk semmi jelét sem annak, hogy a gravitáció a korai Univerzum bármely részének belső tulajdonságaira is hatást gyakorolt volna. Ennek oka a gravitációs erők rendkívüli gyöngeségében keresendő: például a hidrogénatomban a proton és az elektron közt ható gravitációs erő mindössze 1039-ed része az elektromos vonzóerőnek!
(Jól szemlélteti a gravitáció gyengeségét a részecskekeltés gravitációs térben. Mint azt Leonard Parker, a Wisconsini Egyetem kutatója megmutatta, a Világegyetem gravitációs terének „árapály”-hatása a kezdet után 10-24 másodperccel elég nagy lehetett ahhoz, hogy az üres térben rész-antirész párokat keltsen. Ám ezen a hőmérsékleten ez a hatás olyan gyenge, hogy az ily módon keltett részecskék száma csaknem elhanyagolható a hőmérsékleti egyensúlyban levő többi részecskéhez képest.)
Mindennek ellenére el tudunk képzelni egy olyan időpontot, amikor a gravitációs erők olyan erősek lehettek, mint az erős kölcsönhatás. Gravitációs tereket ugyanis nem csupán a részecskék tömege, de az energia minden más fajtája is kelt. (A Föld egy kicsit gyorsabban kering a Nap körül, mint ahogy keringene akkor, ha a Nap nem volna olyan forró, mert a Nap magasabb hőmérsékletéből adódó többlet belső energia egy kicsiny járulékot ad annak gravitációs erejéhez.) Szupermagas hőmérsékleteken a hőmérsékleti egyensúlyban levő részecskék energiája olyan nagy lehet, hogy a gravitációs erő nagysága bármely más erőével egyenlővé válhat. Ki is számíthatjuk, hogy ez mikor következett be. Eredményül az adódik, hogy akkor, amikor a hőmérséklet 100 milliószor milliószor milliószor milliószor millió fok (1032 K) volt.
Ezen az elképzelhetetlenül magas hőmérsékleten aztán mindenféle furcsa dolog történt. A gravitációs erők olyan erőssé váltak, hogy a gravitációs tér bőségesen keltette a részecskéket. Egy idő után azonban már az egész „részecske”-elképzelés is érvényét vesztette. Az „eseményhorizont” – vagyis az a távolság, amelyen belülről már semmiféle jelet sem lehet kapni – kisebbé vált, mint a hőmérsékleti egyensúlyban levő részecskék tipikus hullámhossza. Egy kicsit leegyszerűsítve a dolgokat ez annyit jelent, hogy mindegyik részecske olyan nagy volt, mint az egész Világegyetem.
A gravitáció kvantumelméletéről annyira keveset tudunk, hogy még hozzávetőleges képet sem rajzolhatunk az Univerzum történetének ezen időpontot megelőző szakaszáról. Adhatunk ugyan egy hozzávetőleges becslést, mely szerint ez a 1032 kelvines hőmérséklet a kezdőpillanat után 10-43 másodperccel alakult ki, de egyáltalán nem lehetünk biztosak abban, hogy ennek a becslésnek valóban van-e valami értelme. Még ha sikerül is a többi fátyol mögé betekintenünk, ez az utolsó akadály 1032 kelvinnél akkor is megmarad, és elhomályosítja látásunkat, ha a Világegyetem kialakulásának időpontjáig akarnánk visszatekinteni.
Szerencsére ezek a bizonytalanságok alig érintik a jelen csillagászati kutatásait. A lényeg az, hogy az egész első másodpercben az Univerzum feltehetőleg olyan hőmérsékleti egyensúlyi állapotban volt, amelyben valamennyi részecske számát és eloszlását a statisztikus fizika törvényei határozták meg, nem pedig addigi történetük részletei. Amikor ma a hélium gyakoriságát, vagy a mikrohullámú háttérsugárzást, vagy a neutrínók előfordulását mérjük, akkor annak a hőmérsékleti egyensúlynak az emlékeit vizsgáljuk, amely visszamenőleg az első másodperc végével zárult. Amennyire tudjuk, az Univerzum ezt megelőző történetétől semmi olyan jelenség nem függ, amit ma meg is tudnánk mérni. (Főleg, semmilyen ma megfigyelhető mennyiség nem függ attól, hogy az első másodpercet megelőzően a Világegyetem homogén és izotrop volt-e, kivéve talán magát a foton-magrészecske számarányt.) Kicsit olyan ez, mintha nagy műgonddal előkészítenénk egy vacsorát – kiválogatva a legfrissebb hozzávalókat, a leghozzáillőbb fűszereket és a legfinomabb borokat – és aztán az egészet összeöntenénk egy nagy fazékba, és néhány órán keresztül forralnánk. A legkifinomultabb ízlésű vendég is csak nehezen tudná megmondani, hogy valójában mit is szolgáltak fel neki.
Feltehetőleg van egy kivétel: a gravitáció jelensége, amely csakúgy, mint az elektromágnesség, nem csupán statikus távolhatásként, de hullámok formájában is testet ölthet. Két nyugvó elektron a köztük levő távolságtól függő nagyságú statikus erővel taszítja egymást, ám ha az egyik elektront elkezdjük előre-hátra mozgatni, a másik semmiféle erőváltozást nem fog érezni mindaddig, míg nem telik el elegendő idő ahhoz, hogy a távolság megváltoztatásának „hírét” az egyik részecskétől egy elektromágneses hullám eljuttassa a másikig. Aligha kell hangsúlyoznom, hogy e hullámok a fény sebességével terjednek – fényhullámok, még akkor is, ha hullámhosszuk nem esik a spektrum látható részébe. Hasonló módon, ha valamilyen bolondos kedvű óriásnak az az ötlete támadna, hogy a Napot előre-hátra rángassa, ennek hatását a Földön csupán nyolc perc múlva érzékelnénk – ennyi idő kell ugyanis ahhoz, hogy egy fénysebességgel haladó hullám a Napból indulva elérje a Földet. Ám ez nem egy fényhullám – tehát oszcilláló elektromos és mágneses terek keltette hullám – lenne, hanem egy gravitációs hullám, amelyben a gravitációs tér oszcillál. Akárcsak az elektromágneses hullámok esetében, a különböző hullámhosszúságú gravitációs hullámok összességét is „gravitációs sugárzás"-nak nevezik.
A gravitációs sugárzás jóval gyengébb kölcsönhatásban áll az anyaggal, mint az elektromágneses sugárzás, vagyis akár a neutrínók. (Ez lehet az oka annak, hogy bár elméleti alapon meglehetősen biztosak vagyunk a létezésükben, eddig a legbuzgóbb erőfeszítésekkel sem sikerült őket kimutatni.) így a gravitációs sugárzás nagyon hamar kizökken az Univerzum többi anyagával kialakult hőmérsékleti egyensúlyából, éppen akkor, amikor a hőmérséklet eléri a 1032 kelvin körüli értéket. Azóta a gravitációs sugárzás effektív hőmérséklete egyszerűen a Világegyetem méretével fordított arányban csökken. Ugyanígy csökken az Univerzum többi anyagának a hőmérséklete is, azzal a különbséggel, hogy a kvark-antikvark és a lepton-antilepton párok szétsugárzásakor felszabaduló hőmennyiség a gravitációs sugárzást nem melegítette, míg a többi anyagot igen. Ezért a mai Univerzumban létezhet egy olyan gravitációs háttérsugárzás, amelynek a hőmérséklete alig valamivel kisebb, mint a foton- vagy a neutrínóháttéré – feltehetőleg 1 kelvin körüli érték. E sugárzás kimutatása az Univerzum egy olyan korai szakaszának közvetlen megfigyelését jelentené, amiről a mai elméleti fizika nem tud számot adni. Sajnos, a közeli jövőben aligha várható, hogy sikerülhet egy ilyen 1 kelvines gravitációs háttérsugárzás kimutatása.
Egy jórészt erősen spekulatív elmélet segítségével sikerült a Világegyetem történetét egy olyan időpillanatig visszaforgatni, amikor a sűrűség már végtelen volt. Ám még ez sem elégít ki minket. Természetszerűen azt is tudni akarjuk, hogy mi előzte meg azt a pillanatot, amikor a Világegyetem tágulni és hűlni kezdett.
Az egyik lehetőség az, hogy valójában soha nem is létezett végtelen sűrűségű állapot. Az Univerzum mai tágulása elkezdődhetett egy megelőző összehúzódási folyamat végén, amikor a Világegyetem sűrűsége egy igen nagy, de véges értéket vett fel. Erről a lehetőségről egy kicsit bővebben a következő fejezetben szólok majd.
De ha még nem is tudjuk biztosan, logikailag lehetséges, hogy volt egy valódi kezdőpillanat, amit megelőzően magának az időnek sincs jelentése. Ez a gondolat csak első pillantásra látszik meghökkentőnek. Gondoljunk ugyanis az abszolút hőmérsékleti skálára. Ugye, megszokott számunkra az abszolút nulla fok fogalma? Tudjuk, hogy semmit sem lehet -273,16 Celsius-fok alá hűteni, éspedig nem azért, mert ez túlságosan nehéz lenne, hanem azért, mert az abszolút nullánál alacsonyabb hőmérsékletnek nincs értelme – a semminél kevesebb meleg nem lehet. Ehhez hasonlóan hozzászokhatnánk az abszolút nulla időpont gondolatához is – egy olyan múltbeli időpillanatot jelölve ezzel, amelynél régebbre elvben lehetetlen visszakövetni bármely ok-okozat láncot vagy hatást. A kérdés egyelőre nyitott, és lehet, hogy mindig is az marad.
Számomra a korai Világegyetemre vonatkozó elmélkedések legfőbb tanulsága az, hogy a Világegyetem története és annak logikai szerkezete egymással párhuzamba állítható. A Természet ma a részecskefajták és kölcsönhatási típusok nagy változatosságát kínálja. Ám megtanultunk e sokszínűség mögé látni, és megpróbáltuk a különféle részecskéket és kölcsönhatásokat egy egyszerű egyesített mértékelmélet különböző megnyilvánulási formáiként leírni. A mai Univerzum olyan hideg, hogy egyfajta „kikristályosodás” már megtörte a különféle részecskék és kölcsönhatások közt valaha létezett szimmetriát, az többé nem mutatkozik meg a közönséges jelenségekben, de mérték-térelméleteinkben matematikailag még megnyilvánul. És azt, amit mi ma meg tudunk tenni a matematikában, a korai Univerzumban ténylegesen a forróság valósította meg – a fizikai jelenségek akkor közvetlenül is kifejezték a Természet lényegi egyszerűségét. Sajnos, nem volt jelen senki, hogy láthassa ezt.
VIII Epilógus: Pillantás a jövőbe
Az Univerzum bizonyára még jó ideig folytatja tágulását. Hogy ezután mi lesz a sorsa, arra a standard modell kétértelmű jóslatot ad: minden attól függ, hogy a kozmikus tömegsűrűség egy bizonyos kritikus értéknél kisebb vagy nagyobb.
Mint azt a II. fejezetben láttuk, ha a kozmikus sűrűség a kritikus értéknél kisebb, akkor a Világegyetem méretei végtelenek, és a tágulás a végtelenségig folytatódik majd. Távoli utódaink – ha ugyan élnek még akkor – látni fogják, hogy a termonukleáris reakciók lassan valamennyi csillagban leállnak, különféle salaktermékeket hagyva hátra: fekete törpecsillagokat, neutroncsillagokat és talán fekete lyukakat. A bolygók folytathatják keringésüket; kicsit lassulnak ugyan, mivel gravitációs hullámokat sugároznak, de semmilyen véges időn belül nem fognak leállni. A mikrohullámú háttérsugárzás és a neutrínóháttér hőmérséklete pedig tovább csökken, az Univerzum méretével fordított arányban.
A másik esetben, ha az Univerzum sűrűsége a kritikus értéknél nagyobb, akkor a Világegyetem véges, és tágulása előbb-utóbb abbamarad, hogy utat adjon egy egyre gyorsabb ütemű összehúzódásnak. Ha például a kozmikus sűrűség a kritikus értéknek éppen a kétszerese, és a Hubble-állandó ma elfogadott értéke (15 kilométer/másodperc • millió fényév) helyes, akkor a Világegyetem ma 10 milliárd éves; még további 50 milliárd évig tágulni fog, aztán elkezd összehúzódni. (L. a 4. ábrát a 43. oldalon.) Az összehúzódás épp a tágulás fordítottja: újabb 50 milliárd év után az Univerzum visszanyeri jelenlegi méretét, és további 10 milliárd év múlva egy végtelen sűrűségű szinguláris pont felé közeledik.
Az összehúzódás kezdetén a csillagászok – ha ugyan még lesznek – örömüket lelhetik majd abban, hogy egyszerre figyelhetik meg a vörös- és a kékeltolódást. A közeli galaxisokból jövő fény ugyanis olyan időpontokból származik, amikor az Univerzum nagyobb volt, mint a megfigyelés időpontjában, ezért a megfigyelő számára a fény hullámhossza a színkép rövidebb hullámhosszai, vagyis a kék irányába tolódik el. Ezzel szemben a nagyon távoli galaxisokról érkező fény akkor bocsátódott ki, amikor a Világegyetem a régmúltban a tágulás szakaszában volt, s így kisebb is volt, mint a megfigyelés idején: ezért a fény hullámhossza a megfigyelő számára a színkép hosszabb hullámhosszai, vagyis a vörös felé tolódik el.
A kozmikus foton- és neutrínóháttér hőmérséklete először csökken, majd újból nőni kezd, ahogy a Világegyetem előbb tágul, majd összehúzódik: a hőmérséklet mindig az Univerzum méretével fordított arányban változik. Ha a kozmikus sűrűség ma a kritikus érték kétszerese, akkor kiszámítható, hogy a Világegyetem legnagyobb mérete éppen mai kiterjedésének kétszerese lesz. Ekkor a mikrohullámú sugárzási háttér hőmérséklete a mai 3 kelvines értéknek épp a fele, vagyis 1,5 kelvin lesz majd. Később pedig, amint a Világegyetem elkezd összehúzódni, ez a hőmérséklet ismét emelkedni fog.
Ma még nem kell aggódnunk – milliárd éveken keresztül olyan hideg lesz a sugárzási háttér, hogy még a kimutatása is jelentős erőfeszítéseket követel. Ám amikor majd az összehúzódás során az Univerzum eléri jelenlegi méretének századrészét, az égboltot már a sugárzási háttér fogja uralni: az éjszakai égbolt olyan meleg lesz (300 kelvin), mint ma a nappali. Hetvenmillió évvel később a Világegyetem mérete további tizedrészére csökken, és ha még mindig lesznek utódaink, már elviselhetetlenül forrónak fogják találni az égboltot. A bolygók és a csillagok légkörében hamarosan atomokra hullanak szét a molekulák. Nem sokkal ezt követően az atomok is atommagokra és elektronokra töredeznek. Újabb hétszázezer év múlva a Világegyetem hőmérséklete eléri a 10 millió fokot, ekkorra már a csillagok és a bolygók egy sűrű kozmikus „leves”-sé főnek össze, amely túlnyomórészt fotonokat, elektronokat és atommagokat tartalmaz majd. További 22 nap alatt a hőmérséklet 10 milliárd fokra nő. Már az atommagok is alkotóelemeikre – protonokra és neutronokra – kezdenek bomlani, semmissé téve ezzel a kozmikus fejlődés korai szakaszában és a csillagokban végbement atommagszintézis minden eredményét. Nem sokkal ezután, nagyszámú elektron-pozitron pár keletkezik a foton-foton ütközésekben, és a kozmikus neutrínóháttér újra termikus egyensúlyba kerül a Világegyetem többi részecskéjével.
Valóban végig tudjuk követni ezt a szomorú történetet egészen a befejezésig, egy végtelen hőmérsékletű és sűrűségű állapotig? Valóban „megáll az idő” három perccel azután, hogy a hőmérséklet eléri a milliárd fokot? Nyilvánvaló, hogy nem lehetünk biztosak ebben. Amikor az utolsó századmásodperchez közeledünk, visszatér mindaz a bizonytalanság, amivel az előző fejezetben találkoztunk, amikor az első századmásodperc történetét próbáltuk fölkutatni. Csak annyi bizonyos, hogy 1032 kelvin fölött az egész Univerzumot a kvantummechnika nyelvén kell leírnunk, ám egyelőre senki sem tudja megmondani, hogy mi is történhet ekkor. Ha ráadásul az Univerzum nem igazán homogén és izotrop (l. az V. fejezet végét), akkor egész történetünk érvényét veszti már jóval azelőtt, hogy a kvantumkozmológia problémájával szembekerülnénk.
E bizonytalanságokból néhány kozmológus bizonyos fajta reményt merít. Lehetségesnek tartják, hogy a Világegyetem bizonyos értelemben „oszcillál”, vagyis az összehúzódás után ismét tágulni kezd. Mint az Eddában, ahol az istenek és az óriások ragnoraki végső csatája után a Föld a tűz és a víz martalékává válik, ám lassan a víz visszahúzódik, és Thor fiai feljönnek a mélységekből, magukkal hozva apjuk kalapácsát, és az egész világ újra kezdődik. De ha az Univerzum újra tágulni kezd, akkor egy idő után ismét lelassul majd és megáll, amit aztán újabb összehúzódás követ majd, az Univerzum egy újabb kozmikus Ragnorakban leli pusztulását, s így tovább, örökkön-örökké.
Ám ha ilyen a jövőnk, akkor feltehetőleg ilyen a múltunk is. Lehetséges tehát, hogy a mai táguló Univerzum egy előző összehúzódást követő fázis. (A mikrohullámú háttérsugárzásról írott 1965-ös cikkükben Dicke, Peebles, Roll és Wilkinson éppenséggel azt feltételezik, hogy a mai tágulást egy teljes tágulási és összehúzódási ciklus előzte meg, melynek végén a Világegyetem elérte a 10 milliárd kelvines hőmérsékletet, ami ahhoz szükséges, hogy az előző tágulási szakaszban létrejött kémiai elemeket szétrombolja.) Ha még messzebbre tekintünk vissza, elképzelhetjük egymást váltó tágulások és összehúzódások végtelen időkig visszanyúló végtelen láncolatát, amelyeknek sosem volt kezdete.
Néhány kozmológus filozófiailag nagyon vonzónak tartja az oszcilláló modell gondolatát, elsősorban azért, mert – csakúgy, mint az állandó állapotú modell – szépen megkerüli a Genezis problémáját.
De ezzel szemben is felmerülhet egy komoly ellenérv. Ugyanis egyfajta súrlódás (az úgynevezett tömegviszkozitás) következtében minden ciklus végén jelentősen megnő a fotonok és a magrészecskék aránya (helyesebben az egy magrészecskére jutó entrópia). Ezért a Világegyetem minden újabb ciklust a fotonok és magrészecskék arányának határozottan nagyobb értékével kezd el. Ma ez az arány meglehetősen nagy, de nem végtelen, és ezért nehéz elképzelni, hogy az Univerzum már végtelen számú cikluson ment volna keresztül.
Mindezek a problémák talán megoldódhatnak, de bármelyik kozmológiai modell bizonyul is majd helyesnek, nem sok vigaszt lelhetünk benne. Az emberiség szeretné azt hinni, hogy valami kitüntetett helyzetet tölt be a Világegyetemben, és az emberi élet létrejötte nem csupán többé-kevésbé ostoba véletlenek első három percre visszanyúló sorozatának eredménye, hanem az emberiség csírájában már a kezdet kezdetén bennefoglaltatott a korai Univerzumban. Amikor ezeket a sorokat írom, éppen egy 10 000 méter magasan szálló repülőgépen ülök, úton hazafelé San Franciscóból Bostonba. Alattam a Föld nagyon puhának és kényelmesnek tűnik; pelyhes vattafelhők itt és ott, a hegycsúcsok hava rózsaszínbe fordul a lenyugvó Nap fényében, s lent az utak keresztül-kasul szelik a tájat, összekötve egyik várost a másikkal. Nehéz elfogadni, hogy mindez csak parányi csücske egy nyomasztóan ellenséges Univerzumnak. És még nehezebb felfogni azt, hogy ez a mai Világegyetem elképzelhetetlenül szokatlan kezdeti feltételekből fejlődött ki, és vagy dermesztő hideg, vagy elviselhetetlen forróság vet majd véget neki. Minél jobban megértjük az Univerzum történetét, annál értelmetlenebbnek és céltalanabbnak találhatjuk.
Ám ha már kutatásunk gyümölcseiben nem is találhatunk vigaszt, legalább a kutatás maga ad némi vigasztalást. Vannak emberek – nők és férfiak –, akik nem elégszenek meg az istenekről és óriásokról szóló regékkel, s nem kötik le gondolataikat a hétköznapi élet problémái sem: távcsöveket építenek, mesterséges holdakat bocsátanak fel, gyorsítókat terveznek, és vég nélküli órákat töltenek íróasztalaik mellett, hogy az összegyűjtött adatok tömegéből kihámozzák azok értelmét. Az Univerzum megértését célzó kutatás egyike azon kevés dolgoknak, amelyek az emberi létet egy kevéssel a komédia fölé emelik, s valamit kölcsönöznek neki a tragédia méltóságából.
TÁBLÁZATOK
I. A gyakoribb elemi részecskék tulajdonságai

A gyakoribb elemi részecskék tulajdonságai. A nyugalmi energia az az energiamennyiség, amely akkor szabadulna fel, ha a részecske tömege teljes egészében energiává alakulna. A küszöbhőmérséklet egyenlő a nyugalmi energia és a Boltzmann-állandó hányadosával; e hőmérséklet felett a részecske a sugárzásból szabadon keletkezhet. Az effektív állapotszám megadja az egyes részecskefajták hozzájárulásának relatív mértékét a teljes energiához, a nyomáshoz és az entrópiához a küszöbhőmérsékletnél jóval magasabb hőmérsékleteken. Ezt a számot három tényező szorzataként írtuk fel: az első 1 vagy 2 attól függően, hogy részecskének van vagy nincs saját magától különböző antirészecskéje; a második a részecske lehetséges spinállapotainak számát adja meg; a harmadik pedig 7/8 vagy 1 attól függően, hogy a részecskére vonatkozik-e a Pauli-féle kizárási elv vagy sem. A „közepes élettartam” azt az átlagos időtartamot jelöli, amíg a részecske fennmarad, mielőtt radioaktív bomlással más részecskékké alakulna át.
II. A különféle elektromágneses sugárzások tulajdonsága

A különféle elektromágneses sugárzások néhány tulajdonsága. A sugárzások valamennyi fajtája jellemezhető az által kitöltött hullámhossztartománnyal, amit itt centiméterekben adtunk meg. Az egyes hullámhossztartományoknak megfelel a fotonenergiák egy-egy tartománya: ezt elektronvoltokban fejeztük ki. A feketetest-hőmérséklet annak a fekete testnek a hőmérsékletét adja meg, amelynek sugárzása az adott hullámhosszértéknél lenne maximális erősségű: ezt kelvinben adtuk meg, (Például: Penzias és Wilson a kozmikus háttérsugárzást 7,35 centiméteres hullámhossznál figyelte meg: ez tehát mikrohullámú sugárzás. A magrészecskék radioaktív bomlása során tipikusan millió elektronvolt nagyságrendű fotonenergiák szabadulnak fel: ezek tehát gamma-sugarak. A Nap felszíne 5800 kelvin hőmérsékletű, tehát a Nap felszíne látható fényt sugároz.) Meg kell még jegyeznünk, hogy a sugárzások különféle fajtái között nem éles az átmenet, és nincs egyetemes megegyezés a különböző hullámhossztartományok pontos határait illetően.
Szójegyzék
ABSZOLÚT LUMINOZITÁS: Valamely égi objektum által időegység alatt kibocsátott teljes energia.
ÁLLANDÓ ÁLLAPOTÚ MODELL: Bondi, Gold és Hoyle által kidolgozott kozmológiai elmélet, amelyben a Világegyetem átlagos tulajdonságai időben nem változnak. Ahhoz, hogy az Univerzum tágulása során a sűrűség állandó maradhasson, folytonosan új részecskéknek kell keletkezniük.
ÁLTALÁNOS RELATIVITÁSELMÉLET: A gravitáció elmélete, melyet Albert Einstein az 1906-1916 közti évtizedben dolgozott ki. Einstein megfogalmazásában az általános relativitáselmélet alapgondolata az, hogy a gravitáció a téridő-kontinuum görbületének megnyilvánulása.
ANDROMEDA-KÖD: A miénkhez legközelebb eső nagy galaxis. Spirális szerkezetű, mintegy 3 • 1011 naptömeget tesz ki. A Messier-katalógusban M 31 néven szerepel, míg az Új Általános Katalógusban (New General Catalog) NGC 224 a jele.
ANGSTRÖM: A centiméter százmilliomod része (10-8 cm). Jele: Å. Az atomok jellemző méretei angström nagyságrendűek, míg a látható fény hullámhossza néhány ezer angström.
ANTIRÉSZECSKE: Egy másik részecskével megegyező tömegű és perdületű (spinű) részecske, amelynek azonban az elektromos töltése, barionszáma, leptonszáma a részecskével azonos nagyságú, de ellentétes előjelű. Minden részecskének létezik antirészecskéje, kivéve néhány semleges részecskét, mint például a fotont és a π° mezont, amelyek önmaguk antirészecskéi. Az antineutrínó a neutrínó antirészecskéje, az antiproton a protoné, s így tovább. Az antianyag antiprotonokból, antineutronokból és antielektronokból (pozitronokból) áll.
ASZIMPTOTIKUS SZABADSÁG: Az erős kölcsönhatások bizonyos elméleteinek az a tulajdonsága, hogy kis távolságokra az erők egyre gyengébbé válnak.
ATOMMAG-RÉSZECSKÉK: A szokásos atomok atommagjának építőelemei: protonok és neutronok. Szokásos elnevezésük: nukleonok.
ÁTLAGOS SZABAD ÚTHOSSZ: Az az átlagos távolság, amit egy bizonyos közegben mozgó részecske két ütközés között megtesz. Az ütközési idő az ütközések között átlagosan eltelt idő.
BARIONOK: Az erősen kölcsönható részecskék egy osztálya, amely magába foglalja a neutronokat, protonokat és a hiperon néven ismert instabil hadronokat. A barionszám a rendszerben levő barionok számának és az antibarionok teljes számának különbsége.
BOLTZMANN-ÁLLANDÓ: A statisztikus mechnika alapvető állandója, amely a hőmérsékleti skála és az energia közti kapcsolatot adja meg. Jele: k vagy kB. Értéke: 1,3806 • 10-16 erg/K, vagy 0,00008617 elektronvolt/kelvin.
CEPHEIDA-VÁLTOZÓK: Fényes változócsillagok, amelyeknek színe, változási periódusa és abszolút luminozitása jól meghatározott kapcsolatban áll egymással. Nevüket a Cepheus csillagképben fekvő δ Cephei csillagról kapták. Felhasználják őket a viszonylag közeli galaxisok távolságának meghatározására.
CIÁN: Szén és nitrogén kémiai vegyülete: CN. A csillagközi térben a látható fény elnyelése révén találták meg.
DEUTÉRIUM: A hidrogén egyik nehéz izotópja: 2H. A deutérium atommagja a deuteron: egy protont és egy neutront tartalmaz.
DOPPLER-JELENSÉG: Bármely jel frekvenciájának olyan megváltozása, amit a forrás és a megfigyelő relatív mozgása okoz.
ELEKTRON: A legkönnyebb tömeggel bíró elemi részecske. Az atomok és molekulák kémiai tulajdonságait az elektronok egymással és az atommaggal való elektromos kölcsönhatásai határozzák meg.
ELEKTRONVOLT: Az atomfizikában használatos energiaegység, amely megfelel annak az energiának, amire egy elektron 1 volt feszültségkülönbség révén tesz szert. Értéke: 1,60219 • 10-12 erg.
ENTRÓPIA: A statisztikus mechanika egyik alapmennyisége, amely egy fizikai rendszer rendezetlenségét jellemzi. Minden olyan folyamatban, amelyben mindvégig hőmérsékleti egyensúly áll fenn, megmarad az entrópia. A termodinamika második főtétele szerint az entrópia semmilyen folyamatban sem csökkenhet.
ERG: Az energia egysége a CGS-mértékrendszerben. Egy 1 gramm tömegű, 1 cm/s sebességgel mozgó tárgy mozgási energiája 1/2 erg.
ERŐS KÖLCSÖNHATÁSOK: Az elemi részecskék négy kölcsönhatása közül a legerősebb. Ez felelős a protonokat és a neutronokat az atommagban együtt-tartó magerőért. Az erős kölcsönhatásban a fotonok és a leptonok nem vesznek részt, csak a hadronok.
FÁZISÁTALAKULÁS: Éles átmenet a rendszer egyik állapotából egy másikba. Általában szimmetriaváltozással jár. Például az olvadás, a forrás, vagy a közönséges vezetőállapotból a szupravezető-állapotba való átmenet.
FEKETETEST-SUGÁRZÁS: Olyan sugárzás, amelynek energiasűrűsége minden hullámhosszon megegyezik egy teljesen elnyelő anyagú melegített test sugárzásával. Bármely hőmérsékleti egyensúlyi állapotban a sugárzás feketetest-sugárzás.
FÉNYÉV: Az a távolság, amit a fény egy év alatt megtesz, számszerűleg 94 605 millió kilométer.
FÉNYSEBESSÉG: A speciális relativitáselmélet alapvető állandója, 299 729 kilométer/másodperc. Jele: c. Minden zérus nyugalmi tömegű részecske – mint például a foton, a neutrínók vagy a graviton – fénysebességgel mozog. A tömeges részecskék akkor közelítik meg a fénysebességet, amikor energiájuk messze felülmúlja a nyugalmi tömegükbe foglalt mc2 energiát.
FEYNMAN-GRÁF: Olyan gráfok, amelyek egy elemirész-reakció valószínűségének kiszámításakor tekintetbe veendő különféle járulékokat jelképezik.
FINOMSZERKEZETI ÁLLANDÓ: Az atomfizika és kvantumelektrodinamika alapvető állandója, definíció szerint az elektrontöltés négyzete osztva a Planck-állandó és a fénysebesség szorzatával. Jele: α. Értéke: 1/137,036.
FOTON: A sugárzás kvantumelméletében a fényhullámokhoz tartozó elemi kvantum. Jele: γ.
FREKVENCIA: Annak mértéke, hogy valamely hullámmozgás hullámhegyei milyen ütemben haladnak át egy adott ponton. Egyenlő a hullám sebességének és a hullámhossznak a hányadosával: Mértékegysége a hertz (ciklus/s).
FRIEDMANN-MODELL: Az Univerzum téridő-szerkezetének olyan matematikai modellje, amely a (kozmológiai állandót nem tartalmazó) általános relativitáselméleten és a Kozmológiai Elven alapul.
GALAXIS: Nagy – mintegy 1012 naptömeget tartalmazó – gravitációsan kötött csillaghalmaz. A mi galaxisunkat gyakran Galaktikának nevezzük. A galaxisokat általában alakjuk szerint osztályozzák, eszerint elliptikus, spirális, orsós spirális és szabálytalan galaxisokról beszélhetünk.
GRAVITÁCIÓS HULLÁMOK: Az elektromágneses térben fellépő fényhullámok megfelelői gravitációs térben. A gravitációs hullámok terjedési sebessége a fényével egyező, 299 792 km/s. Általánosan elfogadott kísérleti bizonyítéka egyelőre nincsen, de az általános relativitáselmélet megköveteli létezésüket, és azt jobbára nem is vonják kétségbe. A gravitációs sugárzás (fotonnal analóg) elemi kvantumát gravitonnak nevezzük.
GYENGE KÖLCSÖNHATÁSOK: Az elemi részecskék négy általános kölcsönhatásának egyike. Átlagos energiákon a gyenge kölcsönhatások jóval gyengébbek, mint az elektromágneses vagy az erős kölcsönhatás, de jóval erősebbek, mint a gravitáció. Bizonyos részecskék (például a neutron és müon) viszonylag lassú bomlásáért a gyenge kölcsönhatások felelősek, s ugyancsak ezek játszanak szerepet minden neutrínót tartalmazó folyamatban is. Mostanában igen sokan úgy vélik, hogy a gyenge, az elektromágneses és talán az erős kölcsönhatások is egy egyszerű, egyesített mértékelmélet különféle megnyilvánulásai.
HADRON: Az erős kölcsönhatásban részt vevő részecskék közös neve. A hadronokat két csoportba soroljuk: barionok (például a proton és a neutron) és a mezonok csoportjába. A barionok eleget tesznek a Pauli-féle kizárási elvnek, a mezonok viszont nem.
HÉLIUM: A második legkönnyebb, és a második leggyakoribb kémiai elem. A héliumnak két stabil izotópja létezik. A 4He atommag két protont és két neutront tartalmaz, míg a 3He két protont és egy neutront. A héliumatomok az atommagon kívül két elektront tartalmaznak.
HIDROGÉN: A legkönnyebb és leggyakoribb kémiai elem. A közönséges hidrogén atommagja egyetlen protont tartalmaz. Ismeretes még a hidrogén két nehéz izotópja, a deutérium és a trícium. Mindhárom fajta hidrogénatom egy-egy atommagot és egy elektront tartalmaz. A pozitív hidrogénionokból hiányzik az elektron.
HIDROXILION: Az OH- ion, amely egy oxigénatomból, egy hidrogénatomból és egy további elektronból áll.
HOMOGENITÁS: Az Univerzumnak az a feltételezett tulajdonsága, amely szerint a Világegyetem egy adott időpontban minden megfigyelő számára ugyanolyannak tűnik, függetlenül a megfigyelő helyzetétől.
HORIZONT: A kozmológiában használatos fogalom: az a távolság, amelynél messzebbről jövő fényjeleknek még nem volt idejük elérni hozzánk. Ha a Világegyetem életkora véges, akkor a horizont távolsága nagyságrendileg az Univerzum életkora, szorozva a fény sebességével.
HŐMÉRSÉKLETI EGYENSÚLY: Olyan állapot, amelyben bármely sebességtartományba belépő részecskék száma megegyezik az onnan távozó részecskék számával. Bármely fizikai rendszerben, ha megfelelően hosszú ideig magára hagyjuk, kialakul a hőmérsékleti egyensúly.
HUBBLE-TÖRVÉNY: A nem túl távoli galaxisok távolodási sebessége és távolsága közötti arányt megadó összefüggés. Az ebben szereplő arányossági tényező – a sebesség és a távolság hányadosa – a Hubble-állandó, amit H-val vagy H0-val jelölnek.
HULLÁMHOSSZ: Bármely hullámra vonatkozik; az egymást követő hullámhegyek távolsága. Az elektronmágneses hullámokra a hullámhossz úgy definiálható, mint azon pontok távolsága, amelyekben az elektromos vagy mágneses térerőssség vektorának valamely komponense maximális értéket vesz fel. Jele: λ
IBOLYÁNTÚLI SUGÁRZÁS: 10 és 2 000 angström (10-7 cm és 2 • 10-5 cm) hullámhosszak közötti tartományba eső elektromágneses hullámok, amelyek tehát az elektromágneses spektrum röntgenfény és látható fény közti tartományába tartoznak.
INFRAVÖRÖS SUGÁRZÁS: Olyan elektromágneses hullámok, amelyeknek a hullámhossza 0,0001 cm és 0,01 cm (10 000 és 1 millió angström) közé esik. Ez a sugárzás tehát a látható fény és a mikrohullámú sugárzás közti tartományt foglalja el. A szobahőmérsékletű testek túlnyomórészt infravörös sugárzást bocsátanak ki.
IZOTRÓPIA: A Világegyetemnek az a feltételezett tulajdonsága, amely szerint egy tipikus megfigyelő a Világegyetemet minden irányban ugyanolyannak látja.
JEANS-TÖMEG: Az a minimális tömegérték, amelynél a gravitációs vonzás felülmúlhatja a belső nyomást, és így egy gravitációsan kötött rendszer jöhet létre. Jele: Mj
KARAKTERISZTIKUS TÁGULÁSI IDŐ: A Hubble-állandó reciproka. Nagyjából százszorosa annak az időtartamnak, amely alatt az Univerzum 1%-nyit tágulna.
KÉKELTOLÓDÁS: A spektrumvonalak eltolódása a rövidebb hullámhosszak felé, amit egy közeledő forrás Doppler-eltolódása okoz.
KELVIN: A Celsius-skálához hasonló hőmérsékleti skála, amelyben azonban a zéropontot a jég olvadáspontja helyett az abszolút nullapont adja. E skála szerint a jég olvadáspontja 1 atmoszféra (normál légköri) nyomáson 273,15 kelvin.
KOZMIKUS sugárzás: A Föld légkörébe a külső térből érkező nagy energiájú töltött részecskék.
KOZMOLÓGIAI Állandó: Einstein ezzel a járulékkal egészítette ki 1917-ben gravitációs téregyenleteit. Egy ilyen tag nagyon nagy távolságokra taszítást hozna létre, és egy statikus Univerzumban ez egyensúlyozná a gravitációs vonzás hatását. Ma nincs okunk ilyen kozmológiai állandó létezését feltételezni.
KÖDÖK: Felhőszerű megjelenésű, kiterjedt csillagászati objektumok. Némelyikük galaxis, míg mások galaktikánkban fekvő kiterjedt gáz- és porfelhők.
KRITIKUS SŰRŰSÉG: Az a minimális tömegsűrűség, amely ahhoz szükséges, hogy az Univerzum tágulása valamikor megálljon, majd ezt követően összehúzódásba menjen át. Ha a kozmikus sűrűség a kritikus értéket meghaladja, a Világegyetem térben véges.
KRITIKUS HŐMÉRSÉKLET: Olyan hőmérséklet, amelyen fázisátalakulás megy végbe.
KÜSZÖBHŐMÉRSÉKLET: Az a hőmérséklet, amely fölött az adott típusú részecskét bőségesen termeli a feketetest-sugárzás. Egyenlő a részecske tömege és a fénysebesség négyzete szorzatának a Boltzmann-állandóval vett hányadosával.
KVANTUMMECHANIKA: A klasszikus mechanika helyettesítésére az 1920-as években kidolgozott alapvető fizikai elmélet. A kvantummechanikában a részecske és a hullám ugyanazon alapobjektum két megnyilvánulási formája. Egy adott hullámhoz tartozó elemi részecske az adott sugárzás kvantuma. Az olyan kötött rendszerek állapotai, mint például az atomok és molekulák, csak bizonyos különálló energiaszinteket foglalhatnak el, ezt úgy fejezzük ki, hogy az energia kvantált.
KVARKOK: Olyan feltételezett alaprészecskék, amelyekből valamennyi hadron felépíthető. Különálló (szabad) kvarkokat mindeddig még nem figyeltek meg, és elméletileg feltételezik, hogy a kvarkok – mint izolált részecskék – soha nem is lesznek megfigyelhetők.
KVÁZI-CSILLAGOK: Olyan csillagászati objektumok, amelyek csillagszerű megjelenésűek; kis szögkiterjedésűek, de nagy vöröseltolódást mutatnak. Néha kvazároknak is nevezzük őket, vagy – ha erős rádiósugárzást bocsátanak ki – kvázicsillag-forrásoknak. Valódi természetük még nem ismert.
LASSULÁSI PARAMÉTER: Az a szám, amely jellemzi, hogy a távoli galaxisok távolodása milyen ütemben csökken.
LÁTSZÓ LUMINOZITÁS: Valamely égi objektumból a mérőműszer egységnyi felületére időegység alatt beérkező teljes energia.
LEPTON: A részecskéknek olyan osztálya, melynek tagjaira nem hat az erős kölcsönhatás. Ilyen például az elektron, a müon és a neutrínó. A leptonszám a rendszerben levő leptonok teljes száma, levonva ebből az antileptonok számát.
MAXIMÁLIS HŐMÉRSÉKLET: A hőmérséklet felső korlátja, amelynek elérését az erős kölcsönhatások bizonyos elméletei jósolják. Értékét ezekben az elméletekben 2 milliószor millió kelvinre becsülik.
MEGMARADÁSI TÖRVÉNY: Olyan törvény, amely szerint egy bizonyos mennyiség összértéke bármely változás során állandó marad.
MÉRTÉKELMÉLETEK: A térelméletek egy osztálya, amelyet jelenleg erőteljesen tanulmányoznak, mint a gyenge elektromágneses és erős kölcsönhatások lehetséges elméletét. Ezek az elméletek bizonyos – téridőben pontról pontra változó – szimmetria-transzformációkra nézve invariánsak.
MEZONOK: Az erősen kölcsönható részecskék egyik osztálya, ide tartoznak a π-mezonok, K-mezonok, ρ-mezonok és így tovább, valamennyi zérus barionszámú hadron.
MESSIER-SZÁMOK: A különböző csillaghalmazok és ködök sorszáma Charles Messier katalógusában.
MIKROHULLÁMÚ SUGÁRZÁS: A nagyfrekvenciájú rádiósugárzás és az infravörös sugárzás közé eső, 0,01 cm és 10 cm hullámhossz-tartományban levő elektromágneses hullámok. A néhány kelvines testek sugárzása túlnyomórészt mikrohullám-sugárzás.
MÜON: Az elektronhoz hasonló negatív töltésű, de 207-szer nehezebb elemi részecske. Jele: μ. Néha μ-mezonnak is nevezik; az igazi mezonoktól eltérően nem lép erős kölcsönhatásba.
„NAGY BUMM”-KOZMOLÓGIA: Az az elmélet, amely szerint a Világegyetem tágulása egy véges időtartammal ezelőtt kezdődött meg, egy roppant sűrűségű és nyomású állapotból kiindulva.
NEUTRÍNÓ: Zérus tömegű, elektromosan semleges részecske, amely csak a gyenge és a gravitációs kölcsönhatásban vesz részt. Jele: ν. A neutrínóknak több fajtája létezik, így az elektron típusú νe, a müon típusú νμ és a T nehéz leptonhoz tartozó νT neutrínók.
NEUTRON: A proton mellett az atommagok másik, elektromosan semleges alkotóeleme. Jele: n.
NEWTON-ÁLLANDÓ: A gravitáció Newton- és Einstein-féle térelméletének alapállandója. Jele: G. A gravitáció Newton-féle elméletében a két test között fellépő gravitációs erőhatás G-szerese a tömegek szorzata és a köztük levő távolságnégyzet hányadosának. Értéke: 6,67 • 10-8 cm3/g • s2.
NUKLEÁRIS demokrácia: Az az elv, amely szerint valamennyi hadron alapvető.
NYUGALMI ENERGIA: Egy nyugvó részecske energiája, ami akkor szabadulna fel, ha a részecske szétsugárzódna. Nagyságát az Einstein-féle formula adja meg: E = mc.2
PARSZEK: Csillagászati távolságegység. Meghatározása szerint egy olyan objektum távolsága, amelynek parallaxisa (vagyis a Föld Nap körüli mozgása miatti éves elmozdulása az égbolton) egy ívmásodperc. Jelölése: pc. Értéke: 3,0856 • 1013 kilométer vagy 3,2615 fényév. A csillagászati irodalomban szívesebben használják mint a fényévet. A kozmológiában a millió parszek vagy megaparszek egység használatos, melynek jele: Mpc. A Hubble-állandót általában km/s • Mpc egységben adják meg.
PAULI-FÉLE KIZÁRÁSI ELV: Az az elv, amely szerint két azonos típusú részecske nem foglalhatja el ugyanazt a kvantumállapotot. A leptonok és barionok eleget tesznek ennek az elvnek, míg a fotonok és a mezonok nem.
PERDÜLET (SPIN): Az elemi részecskék egyik alaptulajdonsága; a részecske forgásállapotát írja le. A kvantummechanika szabályainak megfelelően a spin is csak bizonyos meghatározott értékeket vehet fel, amelyek nagysága egész vagy félegész számszor a Planck-állandó.
PI-MEZON: A legkönnyebb tömegű hadron. Három formájában fordul elő: a pozitívan töltött π+, annak negatív töltésű antirészecskéje a π-, és az ezeknél könnyebb semleges π°. Néha pionoknak is nevezzük őket.
PLANCK-ÁLLANDÓ: A kvantummechnika alapvető állandója. Jele: h, értéke 6,625 • 1027 erg • s. A Planck-állandót először Planck vezette be, a feketetest-sugárzás elméletében, 1900-ban. Majd újra megjelent Einstein 1905-ös fotonelméletében: a foton energiája eszerint a Planck-állandószor a fénysebesség, osztva a hullámhosszal. Ma inkább a h állandót használják, amely egyenlő a Planck-állandó, osztva 2π-vel.
PLANCK-ELOSZLÁS: Egy hőmérsékleti egyensúlyban levő sugárzás (pl. feketetest-sugárzás) energiaeloszlása különböző hullámhosszakon.
POZITRON: Az elektron pozitív töltésű antirészecskéje: e+.
PROTON: Az atommagok pozitív töltésű részecskéi. Jelük: p. A hidrogén atommagja egyetlen protont tartalmaz.
RAYLEIGH-JEANS-TÖRVÉNY: A Planck-eloszlás hosszúhullámú tartományában érvényes egyszerű összefüggés, amely az egységnyi hullámhossztartományra eső enerigasűrűség és a hullámhossz kapcsolatát fejezi ki. Ebben a határértékben az energiasűrűség a hullámhossz negyedik hatványának inverzével arányos.
REKOMBINÁCIÓ: Az atommagok és az elektronok atomokká való kapcsolódása. A kozmológiában gyakran ezt a kifejezést használják a hélium- és hidrogénatomok kialakulására, ami 3000 kelvin körüli hőmérsékleten ment végbe.
RHÓ-MEZON: Az instabil hadronok egyike. Két π-mezonra bomlik, közepes élettartama 4,4 • 10-24s.
SAJÁTMOZGÁS: Az égitestek helyzetének eltolódása az égbolton, amit a látósugár irányára merőleges mozgásuk okoz. Általában ívmásodperc/év egységekben mérik.
SPECIÁLIS RELATIVITÁSELMÉLET: A tér és az idő új szemlélete, amit Albert Einstein vezetett be, 1905-ben. Csakúgy, mint a newtoni mechanikában, itt is fellép egy sor matematikai transzformáció, amelyek a különféle megfigyelők által használt téridő-koordinátákat viszonyítják egymáshoz, oly módon, hogy a természet törvényei valamennyi megfigyelő számára azonosaknak tűnjenek. De a speciális relativitáselméletben a transzformációk lényegi tulajdonsága, hogy a fény terjedési sebességét a megfigyelő sebességétől függetlenül állandónak hagyják. Minden olyan rendszert, amelyben a részecskék sebessége a fényét megközelíti, a newtoni mechanika törvényei helyett a speciális relativitáselmélet törvényeivel kell leírni.
STEFAN-BOLTZMANN-TÖRVÉNY: A feketetest-sugárzás energiasűrűsége és a hőmérséklet negyedik hatványa közti arányosságot kifejező összefüggés.
SŰRŰSÉG: Valamely mennyiség térfogategységre jutó hányada. A tömegsűrűség a térfogategységre jutó tömeg, ezt gyakran csak sűrűségnek nevezzük. Az energiasűrűség a térfogategységre jutó energia, a részecskesűrűség a térfogategységre jutó részecskék száma.
SZUPERNÓVÁK: Óriási csillagrobbanások, amelyek még a csillagok belső magját is szétszórják a csillagközi térben. Egy szupernóva néhány nap alatt annyi energiát termel, mint amennyit a Nap egymilliárd év alatt sugároz ki. Galaktikánkban szupernóva-robbanást legutóbb Kepler észlelt (és vele együtt még koreai és kínai csillagászok) 1604-ben, az Ophiuchus csillagképben, de feltételezik, hogy a Cas A rádióforrás egy ennél jóval későbbi szupernóva-robbanás maradványa.
SZŰZ GALAXISHALMAZ: Egy nagy, több mint 1000 galaxist tartalmazó halmaz a Szűz csillagképben. E halmaz mintegy 1000 km/s sebességgel távolodik tőlünk, és a távolságát 60 millió fényévre becsülik.
TEJÚT: A galaxisunk síkjába eső csillagok fényes zónájának régi elnevezése. Gyakran ezzel a névvel illetik Galaktikánkat is.
TIPIKUS GALAXISOK: E könyvben olyan galaxisok megnevezésére használjuk, amelyeknek semmiféle különleges, saját sebességük nincs, és ezért teljes mértékben együtt mozognak a Világegyetem tágulásával járó általános anyagáramlással. Ugyanez a jelentése a tipikus részecske vagy a tipikus megfigyelő elnevezésnek.
TRÍCIUM: A hidrogén instabil 3H nehéz izotópja. A trícium atommagja egy protont és két neutront tartalmaz.
VÖRÖSELTOLÓDÁS: A színképvonalak hosszabb hullámhosszak irányába való eltolódása, amelynek oka a távolodó forrás Doppler-jelensége. A kozmológiában a csillagászati objektumok színképvonalainak a hosszabb hullámhosszak irányába való eltolódására használt kifejezés. A vöröseltolódást mint a hullámhossz relatív megnövekedését z-vel jelölik.
Matematikai jegyzetek
Ez a matematikai kiegészítés azon olvasók számára íródott, akik szeretnék közelebbről is megismerni a könyvben leírt jelenségek matematikai hátterét. Mindazonáltal a könyv gondolatmenetének végigkövetéséhez nem szükséges e jegyzetek áttanulmányozása.
1. jegyzet. A Doppler-jelenség
Tegyük fel, hogy az egymást követő hullámhegyek T periódusú időkülönbséggel hagyják el a hullámforrást. Ha a forrás V sebességgel távolodik a megfigyelőtől, akkor az egymást követő hullámhegyek kibocsátása között eltelt idő alatt a forrás VT távolságra jut. Ezért a később kibocsátott hullámhegy a megfigyelőt VT/c időkéséssel éri el (ahol c a fény terjedési sebessége). Így a megfigyelő az egymást követő hullámhegyeket

időkülönbséggel látja beérkezni. A kibocsátott hullám hullámhossza a forrásnál

míg a megfigyelő számára a beérkező fény hullámhossza

A hullámhosszak aránya ezért
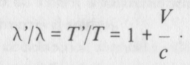
Ugyanez a gondolatmenet alkalmazható, ha a forrás közeledik a megfigyelőhöz, csupán ekkor V-t (-V)-vel kell helyettesíteni. (És természetesen igaz ez az érvelés bármilyen hullámra, nem csak a fény esetében.)
Például az Szűz galaxishalmaz galaxisai mintegy 1000 kilométer/másodperc sebességgel távolodnak a mi galaxisunktól. Ezért a Szűz galaxishalmazból eredő valamennyi színképvonal λ' hullámhossza a normál λ értéket

arányban haladja meg.
2. jegyzet. A kritikus sűrűség
Tekintsünk a Világegyetemben egy R sugarú gömböt! (Számításaink céljának R akkor felel meg, ha nagyobb, mint a galaxishalmazok közötti átlagos távolság, de kisebb, mint az Univerzum egészét jellemző bármely távolság.) E gömb tömege egyenlő a gömb térfogatának és a ρ kozmikus tömegsűrűségnek a szorzatával:
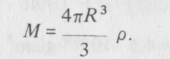
A gravitáció newtoni elmélete szerint e gömb felületén bármely tipikus galaxis helyzeti (potenciális) energiája

ahol m a galaxis tömege és G a Newton-féle gravitációs állandó:
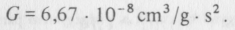
E galaxis sebessége a Hubble-törvény szerint
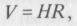
ahol H a Hubble-állandó. Ezért a galaxis mozgási (kinetikus) energiája
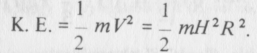
A galaxis teljes energiája a helyzeti és a mozgási energia összege:
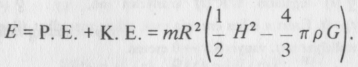
E mennyiségnek az Univerzum tágulása során állandónak kell maradnia.
Ha E negatív, a galaxis sohasem szökhet el a végtelenbe, mivel nagy távolságokra a potenciális energia elhanyagolhatóvá válik, s így a teljes energiát a mozgási energia adná, ami mindig pozitív. Ha azonban E pozitív, a galaxis kiszökhet a végtelenbe, és még némi mozgási energiája is marad. így annak feltétele, hogy a galaxis éppen elérje a szökési sebességet, az, hogy E eltűnjön. Innen
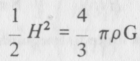
adódik. Másképp kifejezve, ez akkor következik be, ha a sűrűség eléri a
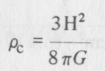
értéket. Ez a kritikus sűrűség. (Bár ezt az eredményt itt a newtoni fizika alapelveinek felhasználásával kaptuk, a végkövetkeztetés érvényes marad akkor is, ha a Világegyetem erősen relativisztikus, feltéve, hogy ρ-t úgy értelmezzük, mint a c2-tel osztott teljes energiasűrűséget.)
Ha például H-ra a jelenleg elfogadott 15 km/s • millió fényév értéket vesszük, akkor figyelembe véve, hogy 1 fényév = 9,46 • 1012 kilométer.
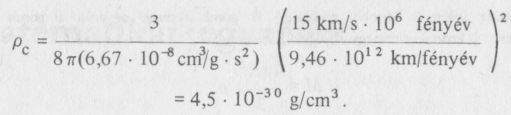
1 grammban 6,02•1023 magrészecske van, így ez a kritikus sűrűség 2,7 • 10-6 részecske/cm3, illetve 0,0027 részecske /dm3 részecskesűrűségnek felel meg.
3. jegyzet. Tágulási időtartományok
Most vizsgáljuk meg azt, hogyan változnak a Világegyetem paraméterei az idő múlásával. Tételezzük fel, hogy egy t időpillanatban egy m tömegű tipikus galaxis egy tetszőlegesen választott központi galaxistól – ez legyen mondjuk a miénk – R(t) távolságra van. Az előző jegyzetben láttuk, hogy e galaxis teljes (helyzeti és mozgási) energiája:
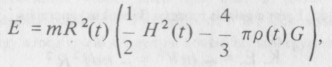
ahol H(t) és ρ(t) a Hubble-féle „állandó”, ill. a kozmikus tömegsűrűség értéke a t időpillanatban. A fenti kifejezésnek valódi állandónak kell lennie. Amint azonban később látni fogjuk, R(t)->0 esetén ρ(t) legalább 1/R3(t) arányban nő, így ρ(t) • R2(t) legalább l/R(t)-vel nő, ha R(t)->0. Ezért a teljes energia csak akkor maradhat állandó, ha a zárójelek közti kifejezés ekkor nullához tart, vagyis R(t)->0 esetén.
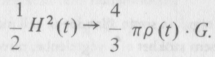
A karakterisztikus tágulási idő éppen a Hubble-állandó reciproka, vagyis

így például az V. fejezet 1. felvételének idején a tömegsűrűség 3,8 milliárd g/cm3, s ezért a tágulási idő:

Lássuk most, hogyan változik ρ (t) az R(t) függvényében. Ha a tömegsűrűséget a magrészecskék tömege szabja meg (atomos anyag dominálta korszak), akkor az R(t) sugarú együtt mozgó gömbben levő teljes tömeg éppen a gömbben levő részecskék számával arányos, és így állandónak kell maradnia:
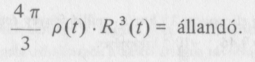
Innen következik, hogy ρ(t) fordítottan arányos R3(t)-vel:
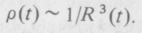
Másrészt, ha a tömegsűrűséget a mozgási energiával ekvivalens tömeg dominálja (sugárzási korszak), akkor ρ (t) a hőmérséklet negyedik hatványával arányos. De mivel a hőmérséklet 1/R(t) szerint változik, ρ (/) fordítva arányos R4(t)-vel:

Abból a céltól, hogy egyidejűleg tárgyalhassuk mind az atomos anyag, mind a sugárzás dominálta korszakot, írjuk ezt az eredményt

alakba, ahol

Egyúttal vegyük észre azt is, hogy ρ(t) legalább l/R3 (t) -vel nő, ha R(t)->0, mint azt már az előbbiekben említettük.
A Hubble-állandó √ρ-val arányos, és ezért
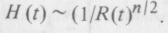
Ám ekkor egy tipikus galaxis sebessége
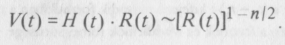
A differenciálszámítás egy elemi eredménye szerint ha a sebesség a távolság valamely hatványával arányos, akkor az az idő, ami ahhoz szükséges, hogy a mozgó test az egyik ponttól a másikba eljusson, a távolság és a sebesség arányának megváltozásával arányos. Esetünkben V arányos r1-n/2-nel, tehát

Vagy
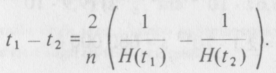
H(t)-t kifejezhetjük ρ(t)-vel, és így azt kapjuk, hogy

így n értékétől függetlenül, a két pont közti távolság megtételéhez szükséges idő a sűrűség reciprok négyzetgyökének megváltozásával arányos.
Például a teljes sugárzási korszakban, az elektron-pozitron-szétsugárzás után az energiasűrűség:

volt (l. a 6. jegyzetet a 152. oldalon). Ekkor n = 4, s így az az idő, ami ahhoz szükséges, hogy a Világegyetem 100 millió fokról 10 millió fokra hűljön le,

Eredményünk jóval egyszerűbben is kifejezhető, ha mondjuk azt a t időt kérdezzük, ami ahhoz szükséges, hogy a sűrűség egy ρ-nál sokkal nagyobb értékről éppen ρ-ra csökkenjen. Ekkor

(Ha ρ(t2) » ρ(t1), akkor a (t1-t2)-t kifejező második formulában a második tag elhanyagolható.) Például 3000 kelvinen a fotonok és a neutrínók tömegsűrűsége

Ez jóval kisebb, mint a 108 kelvinhez (vagy 107 vagy 106 kelvinhez) tartozó sűrűség, s így az az idő, ami ahhoz szükséges, hogy az Univerzum a nagyon magas kezdeti hőmérsékletről 3000 kelvinre hűljön le, egyszerűen így számítható ki (beírva n=4-et):

Megmutattuk, hogy az ahhoz szükséges idő, hogy a Világegyetem sűrűsége egy jóval nagyobb kezdeti értékről ρ-ra csökkenjen, l/√ρ-val, míg ρ maga l/Rn-nel arányos. Ezért ez az idő Rn/2-vel, vagyis másképpen kifejezve:

Ez mindaddig érvényes marad, míg csak a helyzeti és mozgási energia olyan mértékben nem csökken, hogy értékük összemérhetővé válik az összegükkel, a teljes energiával.
Mint azt a II. fejezetben megjegyeztük, a kezdetet követő bármely t időpontban létezik egy nagyságrendileg ct távolságban levő horizont, amelynek külsejéből semmiféle információ sem juthatott még el hozzánk. Most látjuk, hogy t -> 0-ra R(t) lassabban tart nullához, mint a horizonttól mért távolság, ezért elegendően korai időpontokban bármely „tipikus” galaxis a horizonton kívül tartózkodik.
4. jegyzet. A feketetest-sugárzás
A Planck-eloszlás megadja a feketetest-sugárzás du energiasűrűségét a λ és λ + d λ hullámhosszértékek közé eső keskeny sávban:

ahol T a hőmérséklet, k a Boltzmann-állandó (1,38 • 10 16 erg/K), c a fénysebesség (299 729 km/s), e a természetes logaritmus alapszáma (2,718...) és h a Planck-állandó (6,625 • 10-27 erg • s).
Nagy hullámhosszakra a Planck-eloszlás nevezője a következő kifejezéssel közelíthető:

s így ebben a hullámhossz-tartományban a Planck-eloszlás a
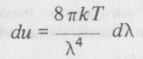
alakot ölti. Ez a Rayleigh-Jeans-formula. Ha ezt tetszőlegesen rövid hullámhosszakra is érvényesnek tekintjük, akkor du/dλ végtelenhez tart λ->0 esetén és a feketetest-sugárzás teljes energiája végtelenné válik.
Szerencsére a Planck-eloszlás a

hullámhossznál elért maximális érték után a kisebb hullámhosszakra fokozatosan csökkenő energiasűrűséget ad. A feketetest-sugárzás teljes energiáját az
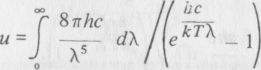
integrál adja meg. Az ilyen típusú integrálok értéke kikereshető a határozott integrálok táblázatából; az eredmény:

Ez a Stefan-Boltzmann-törvény.
A fénykvantumok vagy fotonok fogalmának segítségével könnyen értelmezhetjük a Planck-eloszlást. Minden foton

energiával rendelkezik. így a feketetest-sugárzás egységnyi térfogatában a λ és λ + d λ közé eső hullámhosszsávra jutó fotonok száma
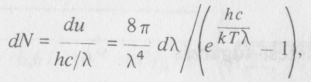
az egységnyi térfogatra jutó fotonok teljes száma ezért
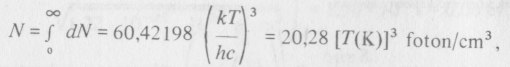
míg az átlagos fotonenergia
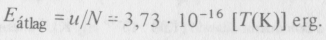
Most vizsgáljuk meg, mi történik a feketetest-sugárzással egy táguló Világegyetemben. Tegyük fel, hogy az Univerzum mérete f-szeresére változik; ha például megkétszerezi a méretét, akkor f= 2. Mint azt a II. fejezetben láttuk, a hullámhosszak ugyanilyen arányban nőnek, az új érték:
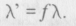
A tágulás után a du' energiasűrűség a λ' és λ' + d λ' hullámhosszsávban két okból is kisebb lesz, mint az eredeti energiasűrűség a λ + d λ közti sávban:
1. Mivel a Világegyetem térfogata f3 arányban nőtt, mindaddig, amíg fotonok nem keletkeznek vagy nem semmisülnek meg, a fotonok száma térfogategységenként l/f3-szörösre csökken.
2. Minden egyes foton energiája a hullámhossz reciprokával arányos, s így l/f-szeresre csökken. Ebből következik, hogy az energiasűrűség l/f3-ször 1/f-szerese, vagyis 1/f4-szeresre csökken:
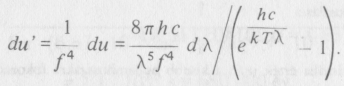
Ha ezt az összefüggést az új λ’ hullámhosszal fejezzük ki, akkor
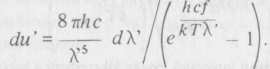
Ez a formula azonban pontosan megegyezik du-nak λ-val és d λ-val kifejezett alakjával, ha egyszer T-t is az új értékével, a

értékkel helyettesítjük. Vagyis egy szabadon táguló feketetest-sugárzás energiasűrűségét továbbra is a Planck-formula írja le, csak benne a hőmérsékletet a tágulás mértékével fordított arányban csökkenteni kell.
5. jegyzet. A Jeans-tömeg
Ahhoz, hogy egy anyagcsomó gravitációsan kötött rendszerré váljék, az szükséges, hogy a gravitációs helyzeti energia a belső termikus energiáját meghaladja. Egy r sugarú és M tömegű anyagcsomó potenciális energiája nagyságrendileg

Az egységnyi térfogatra jutó belső energia a nyomással arányos, így a teljes belső energia nagyságrendileg
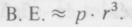
Ezért a gravitációs kötés akkor jön létre, ha

Adott ρ sűrűség mellett azonban r kifejezhető M-mel:

s így a gravitációs kötés kialakulásának feltétele a következő alakban írható:

vagy másképpen

ahol Mj (lényegtelen számtényezőktől eltekintve) a Jeans-tömeg:
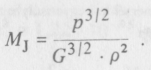
így például a hidrogén rekombinációját megelőzően a tömegsűrűség 9,9 • 10 -22 g/cm3 volt (l. a 3. jegyzet a 146. oldalon), és a nyomás
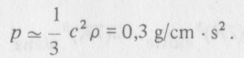
Ezért a Jeans-tömeg:
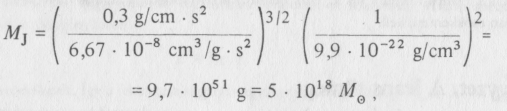
ahol Mθ a Nap tömege (összehasonlításként: a mi galaxisunk tömege 1011 Mθ .) Rekombináció után a nyomás 109 részére csökken, így a Jeans-tömeg
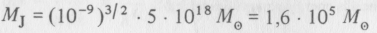
értékre csökken le.
Érdekes, hogy ez nagyságrendileg megegyezik a Galaktikánkban levő nagy gömbhalmazok tömegével.
6. jegyzet. Neutrínóhőmérséklet és -sűrűség
Mindaddig, míg a hőmérsékleti egyensúly fennállt, az „entrópia” néven ismert mennyiség teljes értéke állandó maradt. A térfogategységre jutó S entrópia T hőmérsékleten jó közelítéssel

ahol NT a hőmérsékleti egyensúlyban levő azon részecskék effektív állapotszáma, amelyeknek küszöbhőmérséklete T-nél kisebb. A teljes entrópia akkor marad állandó, ha S az univerzum méretének köbével fordított arányban áll. Vagyis ha R két tipikus részecske közötti távolság, akkor

Az elektron-pozitron-szétsugárzás küszöbén (5 • 109 kelvin körül) a neutrínók és az antineutrínók már kiléptek a termikus egyensúlyból, úgyhogy ekkor az egyensúlyban számottevő mértékben csak az elektronok, a pozitronok és a fotonok játszottak szerepet. Az I. táblázatban (135. oldal) láthatjuk, hogy a szétsugárzás előtt a teljes effektív állapotszám:

volt. Másrészt a szétsugárzás utáni hőmérsékleti egyensúlyban már csak a fotonok maradtak. Ekkor az effektív állapotszám egyszerűen

Az entrópia megmaradásából következik, hogy
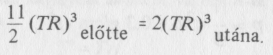
Vagyis az elektron-pozitron-szétsugárzásból eredő hő a TR mennyiséget a
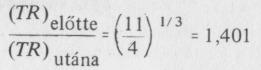
tényezővel növelte meg.
Az elektron-pozitron-szétsugárzást megelőzően a Tν neutrínóhőmérséklet megegyezett a fotonok T hőmérsékletével. Ám ettől kezdve Tν egyszerűen 1/R szerint csökkent, vagyis minden ezt követő időpontra TνR megegyezett a szétsugárzás előtti TR értékkel:

Vagyis amikor a szétsugárzás befejeződött, a fotonok hőmérséklete a neutrínókét
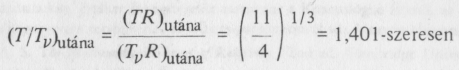
haladja meg.
Jóllehet a neutrínók és az antineutrínók kiváltak már a termikus egyensúlyból, a kozmikus energiasűrűséghez továbbra is jelentős járulékot adtak. A neutrínók és az antineutrínók effektív állapotszáma 7/2, míg a fotonoké (két spinállapot) 7/4. Másrészt azonban a neutrínóhőmérséklet negyedik hatványa (4/1 l)4/3-szorosa a fotonhőmérséklet negyedik hatványának. Ezért a neutrínók és az antineutrínók energiasűrűsége a fotonokéra vonatkoztatva:
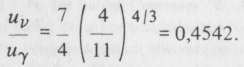
A Stefan-Boltzmann-törvény (l. a III. fejezetet) szerint T hőmérsékleten a fotonok energiasűrűsége:
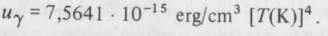
így a teljes energiasűrűség az elektron-pozitron-szétsugárzás után:
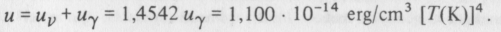
Innen kiszámíthatjuk a megfelelő tömegsűrűséget, elosztva e kifejezést a fénysebesség négyzetével:

Ajánlott irodalom
A. Kozmológia és általános relativitáselmélet
A felsorolt művek bevezetést adnak a kozmológia különböző fejezeteibe és az általános relativitáselmélet kozmológiában fontos részeibe. Legtöbbjük csak szakembereknek ajánlható.
Bondi, H. Cosmology. (Cambridge University Press, Cambridge, England, 1960.) Bár ma már kissé túlhaladott, értékre fejtegetéseket tartalmaz a Kozmológiai Elvről, az állandó állapotú Világegyetem modelljéről, az Olbers-paradoxonról stb. Nagyon olvasmányos.
Eddington, A. S. The Mathematical Theory of Relativity. (2nd ed. Cambridge University Press, Cambridge, England, 1924.) Évek óta a relativitáselmélet irodalmának egyik legfontosabb könyve. Történetileg is érdekes például a vöröseltolódás vagy a de Sitter-modell korabeli leírása.
Einstein, A. és tsai. The Principle of Relativity. (Methuen and Co. Ltd., London, 1923.) Einstein, Minkowski és Weyl speciális és általános relativitáselméletéről szóló felbecsülhetetlen értékű eredeti cikkeinek gyűjteménye, angol fordításban. Tartalmazza Einstein 1917-es cikkét is a kozmológiáról.
Field, G. B., Arp, H., Bahcall, J. N. The Redshift Controversy. (W. A. Benjámin, Inc., Reading, Mass, 1973.) Figyelemre méltó vita a vöröseltolódás kozmológiai értelmezéséről. Hasznos kiegészítése a témára vonatkozó eredeti közleményekből készült. Cikkgyűjtemény.
Hawking, S. W., Eli is, G. F. R. The Large Scale Structure of Space-Time (Cambridge University Press, Cambridge, England, 1973.) A kozmológiai szingularitások és a gravitációs kollapszus szigorú matematikai tárgyalása.
Hoyle, Fred. Astronomy and Cosmology. (W. H. Freeman and Co., San Francisco, 1975.) Elemi csillagászati kézikönyv, amelyben azonban a szokásosnál nagyobb teret kap a kozmológia. Nagyon kevés matematikával.
Misner, C. W., Thome, K. S., Wheeler, J. A. G ram tation. (W. H. Freeman and Co., San Francisco
1973.) Három nagy tekintélyű szakember érthető, modem bevezetője az általános relativitáselméletbe. Érinti a kozmológiát is.
O’Hanian, Hans C. Gravitation and Space Time. (Norton and Co., New York, 1976.) Kézikönyv a relativitásról és a kozmológiáról egyetemistáknak.
Peebles, P. J. E. Physical Cosmology. (Princeton University Press, Cambridge, England, 1971.) Tekintélyes általános bevezetés a kozmológiába, amelyben nagy hangsúlyt kap a kísérleti háttér.
Sciama, D. W., Modern Cosmology. (Cambridge University Press, Cambridge, England, 1971.) Nagyon olvasmányos bevezető a kozmológiába és az asztrofizika más területeire. Viszonylag kevés matematikai és fizikai előképzettséget tételez fel, a képletek száma minimális.
Segal, I. E., Mathematical Cosmology and Extragalactical Astronomy. (Academic Press, New York, 1976.) A modern kozmológia szokatlan, de gondolatébresztő megközelítése.
Tolman, R. C. Relativity, Thermodynamics and Cosmology. (Clarendon Press, Oxford, 1934.) Évek óta tartja helyét mint a standard kozmológia kézikönyve.
Weinberg, Steven. Gravitation and Cosmology. (John Wiley and Sons, Inc., New York, 1972.) Általános bevezetés az általános relativitáselmélet be. A könyvnek mintegy egyharmad része foglalkozik kozmológiával. A további véleménynyilvánítást szerénységem tiltja.
B. A modern kozmológia története
Az alábbiakban felsorolt művek a modern kozmológia történetének első kézből származó beszámolói vagy másodlagos forrásai. E könyvek túlnyomórészt kevés matematikát használnak, de némelyikük azért a fizika és a csillagászat alaposabb ismeretét tételezi fel.
Baade, W. Evolution of Stars and Galaxies. (Harvard University Press, Cambridge, Mass. 1968.) Baade 1958-ban tartott előadásait tartalmazza a könyv, amelyeket magnófelvételek alapiján C. Payne-Gapioschkin rendezett sajtó alá. Meglehetősen személyes hangvételű beszámoló századunk csillagászatának fejlődéséről, beleértve az extragalaktikus távolság-skála kifejlődését.
Dickson, F. P. The Bowl of Night. (M. I. T Press, Cambridge, Mass. 1968.) Kozmológia Thalésztől Gamowig. Tartalmazza de Cheseaux és Olbers – az éjszakai égbolt sötétségéről szóló – cikkeinek hasonmásait.
Gamow, George. The Creation of the Untverse. (Viking Press, New York, 1952.) Ma már túlhaladott, de nagyon értékes, mint Gamow 1950 körüli nézeteinek összefoglalása. A nagyközönségnek íródott, a Gamowtól megszokott ellenállhatatlan stílusban.
Hubble, E. Realm of the Nebulae. (Yale University Press, New Haven, új kiadás: Dover Publica-tions, Inc., New York, 1958.) Hubble klasszikus értékű beszámolója a galaxisok felfedezéséről, beleértve a vöröseltolódás és a távolság közti összefüggés felismerését is.
Jones, Kenneth Glyn. Messier Nebulae and Star Clusters. (American-Elsevier Publisching Co., New York, 1969.) Történeti megjegyzések a Messier-katalógusról és a benne foglalt objektumok megfigyeléséről.
Kant, Immánuel. Universal Natural History and the Theory of Heavens. (University of Michigan Press, Ann Arbor, 1969.) Kant nevezetes munkája arról a feltételezésről, hogy a távoli ködök a mi galaxisunkhoz hasonló csillaghalmazok. Tartalmaz még egy hasznos bevezetőt, amit M. K. Munitz írt, továbbá egy korabeli beszámolót Thomas Wright Tejút-elméletéről.
Koyré, Alexandre. From the Closed World to the Infinite Universe. (John Hopkins Press, Baltimore, 1957.) Kozmológia Nicolaus Cusamustól Newtonig. Érdekes beszámolót tartalmaz Newton és Bentley levelezésének az abszolút térről és a csillagok eredetéről szóló részleteiről.
North, J. D. The Measure of the Universe. (Clarendon Press, Oxford, 1965.) Kozmológia a XIX. századtól 1940-ig. Nagyon részletesen számol be a relativisztikus kozmológia kezdeteiről.
Reines, F. Cosmology, Fusion and Other Matters. (George Gamow Memórial Volume, Colorado Associated University Press, 1972.) Értékes, első kézből származó beszámoló Penziastól, a mikrohullámú sugárzási háttér felfedezéséről; Alphertől és Hermantól az atommagszintézis ősrobbanás-modelljének kidolgozásáról.
Schlipp, P. A. Albert Einstein: Philosopher-Scientist. (Library of Living Philosophers, Inc., 1951.) A második kötet cikkeket tartalmaz Lemaitre-től a kozmológiai állandó Einstein-féle bevezetéséről, és Infeldtől a relativisztikus kozmológiáról.
Shapley, H. Source book in Astronomy 1900–1950. (Harvard University Press, Cambridge, Mass. 1960.) Eredeti cikkek utánnyomása a kozmológia és a csillagászat különféle területeiről, sokszor szerencsétlen rövidítéssel.
C. Részecskefizika
Egyelőre nincs olyan könyv, amely matematika alkalmazása nélkül írná le a részecskefizika VII. fejezetben tárgyalt újabb eredményeit. A témába talán a következő cikk nyújthat némi betekintést:
Weinberg, Steven. Unified Tbeories of Elementary Partiele Interaetions. (Scientific American, July,
1974. 50-59 old.)
Ennél alaposabb betekintést ad a következő könyv:
Feinberg, C. Wbat is tbe World Made ofí (The Achievents of Twentieth Century Physics.) (Garden City, Anchor Press/Doubleday, 1977.)
Szakembereknek – további eredeti irodalomjegyzékkel – az alábbi cikkek valamelyike javasolható:
Taylor, J. C. Gauge Tbeories of Weak Interaetions. (Cambridge University Press, Cambridge, England, 1976.)
Wemberg, S. Recent Progress m Gauge Tbeories of tbe Weak, Electromagnetic, and Strong Interaetions. Reviews of Modern Physics, Vol. 46. 255-277. old. (1974)
D. Vegyes művek
Allen, C. W. Astrophysical Quantities, 3rd ed. (The Athlone Press, London, 1973.) Asztrofizikai adatok és képletek kézikönyve.
Sandage, A. Tbe Hubble Atlas of Galaxies. (Carnegie Institute of Washington, Washington D. C., 1961.) A Hubble-féle osztályozási rendszert számos gyönyörű galaxisfelvétel szemlélteti.
Sturleson, Snorri, Tbe Younger Edda. (Scott, Foresman and Co., Chicago, 1901.) Az északgermán mítoszok gyűjteménye. A Világegyetem kezdetének és végének – könyvünkétől merőben eltérő – elképzelése.
Név- és tárgymutató
abszolút hőmérsékleti skála 129
– luminozitás 28, 137
– nulla időpont 129
Adams, W. S. 65
állandó állapotú modell 19-20, 36, 137
Allen, C. W. 156
Alpher, Ralph A. 12, 53, 108-109, 111, 113-115
Alpher-Herman-féle jóslat 109
al-Szufi, Abdurrahman 26
általános relativitáselmélet 137
Androméda-köd 137
angström 61, 137
antirészecske 137
Arp, Halton 35, 154
Asimov, Isaac 12
aszimptotikus szabadság 122-123, 137
átlagos szabad úthossz 137
atommagrészecskék 137
atommagszintézis 98
– ,,Nagy Bumm” modellje 108
atomos anyag korszaka 70-71
Baade, Walter 28, 155
Bahcall, J. N. 154
barionok 83, 137
barionszám 83-84, 137
Bell, Daniel 9
Bentley, Richard 38
Bethe, Hans 112
Birkhoff, G. D. 41
Birkhoff tétele 41-42
Boltzmann, Ludwig 75
Boltzmann-állandó 149
Bondi, Herman 19, 137, 154
Burbidge, Geoffrey 112
Burbidge, Margaret 112
Burke, Bemard 12, 51, 54
Calder, Nick 12
Cepheida-változók 28, 137
Chew, Geoffrev 120
cián 138
Clerke, Agnes Mary 27
Cohen, I. Bemard 12
Collins, J. C. 122
Damoklész 105
de Sitter, W. II, 39
de Sitter-modell 39
deutérium 18, 138
– a korai Univerzumban 96-98, 101-103
deutériummag keletkezése 96-97
Dicke, Robert H. 12, 53-54, 110-111, 132
Dickson, F. P. 155
Dirac, Paul Adrien Maurice 76
Doppler, Johann Christian 23
Doppler-eltolódáson alapuló sebesség-mérés 24
Doppler-jelenség (Doppler-eltolódás) 22-25, 28, 31, 138, 144
Eddington, Arthur 39, 154
effektív állapotszám 152
egy fotonra jutó barionszám 85-87
– – - leptonszám 85, 88-89
– – - töltés 85-86
egyensúlyi állapot 55-56
egyesített mértékelmélet 124
Einstein, Albert 11, 38, 58, 60, 70, 76, 115, 137, 140, 142, 154-156
Einstein-féle modell 39
– tömeg-energia összefüggés 70
ekvivalens hőmérséklet 50-53, 110
– sugárzási hőmérséklet irányfüggése 67
elektromos töltés megmaradása 83
elektron 17, 135, 138
elektron-pozitron pár 75-76
– szétsugárzás 152-153
elektronvolt 60, 138
elemi részecskék effektív állapotszáma 135
– – közepes élettartama 135
– – küszöbhőmérséklete 135
– – nyugalmi energiája 135
elliptikus köd 27
Ellis, G. F. R. 154
entrópia 138
erg 138
erős kölcsönhatás 117-123, 138
eseményhorizont 46-47, 126, 139
fázisátalakulás 138
Feinberg, Gary 12, 157
feketetest-sugárzás 57-62, 138, 149-151
– teljes energiája 149
fényév 138
fénysebesség 138, 149
Fermi, Enrico 112
Feynman, Richard P. 117
Feynman-gráfok 117-118, 138
Field, George 12, 65, 154
finomszerkezeti állandó 117-119, 138
Follin 109, 111
forró Világegyetem receptje 72-90
foton 17, 54-55, 58, 72, 74, 135, 138
fotonenergia 54
Fowler, William 12, 100-101, 112
Fraunhofer, Joseph 23-24
frekvencia 138
Friedmann, Alekszandr Alekszandrovics 11, 40
Friedmann-modellek 40-41, 43, 138
Galaktika 25
galaktikus sugárzás 59
galaxis 139
– mozgási energiája 145
– teljes energiája 145-146
galaxisok fejlődése 45
– kialakulása 69-70
– szökési sebessége 41-42
Gamow, George 53, 108-109, 111, 113, 115, 155
Gell-Mann, George 121
Gibbs, Willard 75
Glikes, Erwin 9, 12
Gold, Thomas 19, 137
gravitáció 125-128
– háttérsugárzás 128
– hullám 129, 139
– sugárzás 128
graviton 139
Gross, Dávid 122-123
gyenge kölcsönhatások 123-125, 139
hadronok 118-119
Hagedorn, R. 120
Hawking, S. W. 154
hélium 18, 139
hélium-hidrogén arány a mai Univerzumban 107
héliummagok keletkezése 96-97
Herman, Robert 12, 53, 108-109, 111, 113-115
hidrogén 139
hidroxilion 139
homogenitás 31, 105, 139
– elve 30
horizont, lásd eseményhorizont
Hoyle, Fred 12, 19, 53, 100-101, 109, 112-113, 137, 154
hőmérsékleti egyensúly 56-57, 77, 139
Hubble, Edwin 27-30, 32-34, 39, 44, 155
Hubble-állandó 33-36, 42, 44, 130, 145
Hubble-program 44-45
Hubble-törvény 30, 33, 35, 139
Huggins, Sir William 24
hullámhossz 139-140
Humason, Milton 33
ibolyántúli sugárzás 140
ifjabb Edda 15
infravörös sugárzás 140
izotrópia 31, 105, 140
Jeans, Sir James 64, 69
Jeans-tömeg 69, 140, 151
jégkristály 125
Jones, Kenneth 155
Kant, Immánuel 26, 155
karakterisztikus fotonenergia 75
– tágulási idő 35, 93, 140
kékeltolódás 130-131, 140
kelvin 140
kétrészecske-reakciók 93-96
Kirzsnyec, D. A. 124
korai Univerzum, lásd Univerzum kozmikus fotonháttér 131
– héliumgyakoriság 113-115
– neutrínóháttér 131
kozmológiai állandó 39, 105-106, 140
– elv 29-32, 39
Koyré, Alexandre 155
ködök 26-27, 140
kritikus hőmérséklet 140
– sűrűség 40-43, 140, 144-146
küszöbhőmérséklet 140
kvantummechanika 140
kvantumok 58, 60
kvarkelmélet 121-122
kvarkmodell 121-122
kvarkok 121-123, 140
kvázi-csillagok 36, 141
lassulási paraméter 141
látóhatár, lásd eseményhorizont
látszó fényesség 28, 141
Leavitt, Henrietta Swan 28
Lemaítre 11
leptonok 84, 141
leptonszám 84-85, 104
Liller, Martha 12
Linde, D. A. 124
Lockyer, J. Norman 101
Mather, John 68
maximális hőmérséklet 121, 141
McKellar, A. 65
megmaradási törvények 81-84, 141
megmaradó mennyiségek 81-85
Messier, Charles 26, 141
Mesier-katalógus 26, 32
Messier-számok 141
mértékelméletek 141
mezonok 119-121, 141
mikrohullámú háttérsugárzás 48-71, 141
– – irányfüggése 67
Milne, Edward Arthur 29
Misner, Charles W. 106, 154
„mixmaster” modell 106
Morrison, Philip 12
müon 135, 141
„Nagy Bumm”-elmélet 15, 37, 108-109, 111-113, 141
nanométer 61
nehézelemek kialakulása 112
nem-abeli mértékelméletek 122
neutrínó 17, 88-89, 135, 141
neutrínóháttér 104-105
neutrínóhőmérséklet 104, 152
neutrínósűrűség 152
neutron 18, 135, 141
neutron-proton mérleg alakulása 99
New General Catalog (NGC) 137
Newton, Isaac 69, 115
Newton-féle gravitációs állandó 141, 145
North, J. D. 155
„nukleáris demokrácia”-elmélet 119-120, 141
nyugalmi energia 74, 141
O’Hanian, Hans C. 154
Ohm , E. A. 114
Ostriker, J. P. 45
oszcilláló modell 132-133
parszek 142
Pauli, Wolfgang 89
Pauli-féle kizárási elv 78, 142
Peebles, Jim 12, 51-54, 100, 109, 113, 132, 154
Penzias, Arno 12, 48-51, 53-54, 59-60, 62-63, 100, 109, 114
perdület (spin) 142
Perry, M. J. 122
Phillips, Farrel 12
pi-mezonok 135, 142
Planck, Max 57-58, 142
Planck-állandó 142, 149
Planck-eloszlás 58-60, 64, 142, 149
Planck-törvény 58
pozitron 17, 142
Press, Bill 12
proton 18, 135, 142
Pulitzer, Hugh David 122
Rayleigh, Lord 64
Rayleigh-Jeans-eloszlás 59
– tartomány 64
– törvény 142, 149
rekombináció 62, 142
részecske-antirészecske pár 76-77
részecskekeltés 74-77
– gravitációs térben 126
rezgő állapot 65
rhó-mezon 142
Roll, P. G. 53-54, 63, 131
rotáló állapot 65-66
Rutherford, Ernest 36
sajátmozgás 21, 142
Salam, Abdus 124
Salpeter, E. E. 113
Sandage, Alan 34, 44, 156
Schlipp, P. A. 155
Schmidt, Maarten 35
Sciama, D. W. 154
sebesség-összeadási törvény 32
Segal, I. E. 154
„semleges áramok” 124
Shapley, Harlow 28, 155
Sklovszkij, I. Sz. 65
Slipher, Vesto Melvin 28
speciális relativitáselmélet 142
spirális köd 27
standard modell 16, 18-20, 105-106
Stefan-Boltzmann-törvény 62, 143, 149-150
Sturleson, Suorri 156
sugárzási korszak 70-73
sűrűség 143
sztratonok, lásd kvarkok
szupernóva 27, 143
Szűz galaxishalmaz 33
tágulási időtartományok 146-149
Tayler, R. J. 53, 109, 113
Taylor, J. C. 156
Tejút 25, 143
tipikus galaxis 29, 143
Thorne, K. S. 154
Tolman, R. C. 154
Tremaine, S. D. 45
trícium 143
tríciummag keletkezése 96-97
Turkevich, Anthonv 112
Turner, Ken 51
Univerzum az első századmásodpercben 116-129
– 0,01 másodperc elteltével 92-94
– 0,11 másodperc elteltével 94-95
– 1,09 másodperc elteltével 95-96
– 13,82 másodperc elteltével 96-97
– 3 perc és 2 másodperc elteltével 96-97
– egy kicsit később 97-98
– 34 perc 40 másodperc elteltével 98-100
– 700 000 év elteltével 100
– energiasűrűsége 79
– hőmérséklete 80
– inhomogenitása és anizotrópiája 106
– jövője 20, 130-132
–, korai 16, 22
– mérete 43
– oszcilláló modellje 53
– összehúzódása 131
– tágulása 21-47
– téridő-geometriája 38-39
–, véges 16, 43, 130
–, végtelen 16, 43, 130
véges Univerzum, lásd Univerzum
végtelen Univerzum, lásd Univerzum
vöröseltolódás 29, 35-36, 130-131, 143
vöröseltolódás mint a távolság függvénye 44
Wagoner, Purcell 12
Wagoner, Robert 12, 100-101
Weinberg, Steven 12, 155
Wheeler, J. A. 154
Wilczech, Franck 122-123
Wilkinson, D. T. 53-54, 63
Wilson, Robert W. 48-51, 53-54, 59-60, 62-63, 100, 109, 114, 132
Wolleston, William Flyde 23
Woolf, N. J. 65
Wright, Thomas 25-26
Zeldovics, Ja. B. 53, 109, 114, 123
Zweig, George 122