III A kozmikus mikrohullámú háttérsugárzás

 

Az előző fejezetben elbeszélt történet a régi idők csillagászainak fülében is ismerősen csengene. Még a környezet is ismerős: Kalifornia vagy Peru hegycsúcsain hatalmas távcsövek kutatják az éjszakai eget, máshol szabad szemmel figyelik a Göncölszekeret. Az Előszóban már említettem, hogy ez olyan történet, amelyet sokan elmondtak már, gyakran sokkal részletesebben is, mint én itt.

Most viszont egy másfajta csillagászatról lesz szó, olyan dolgokról, amelyeket még egy-két évtizeddel ezelőtt sem mondhattam volna el. Nem a fényt figyeljük majd, amelyet az elmúlt néhány százmillió évben a miénkhez hasonló galaxisok bocsátottak ki, hanem a rádió-háttérzajt, amely egészen az Univerzum keletkezése körüli időkből maradt vissza. A díszlet is változik: egyetemi fizikatanszékek teteje, léggömbök, rakéták messze a Föld légköre felett és New Jersey mezői lesznek történetünk színhelyei.

1964-ben Holmdelben (New Jersey), Crawford Hillen épült fel a Bell Telefon Laboratórium egy szokatlan rádióantennája. Az antenna eredetileg azért készült, hogy az Echo műholddal létesítsen kapcsolatot, de konstrukciója – 6 méteres kürtő alakú antennája és különlegesen kis zaja – sokat ígért a rádiócsillagászat számára is. Két rádiócsillagász, Arno A. Penzias és Robert W. Wilson nekilátott, hogy az antennával a Galaktika síkjára merőleges irányból érkező rádióhullámokat észlelje.

Az ilyen mérések nagyon nehezek. A Galaktikánk által kibocsátott rádióhullámok, akárcsak az egyéb csillagászati objektumok által kibocsátottak, leginkább valamilyen zajra hasonlítanak, mint például amilyen vihar alkalmával a rádiókban hallható. Ezt a rádiózajt nagyon nehéz megkülönböztetni attól az elkerülhetetlen elektromos zajtól, amelyet az antenna és az erősítő elektronjainak véletlen mozgása vagy a Föld légkörében keletkező zavarok okoznak. A feladat nem annyira súlyos, ha egy viszonylag „kicsi” rádióforrást (például egy csillagot vagy egy távoli galaxist) vizsgálunk. Ilyenkor az antennát kapcsolgatni lehet, oda és vissza a forrás és az ég egy közeli üres darabkája között; minden hamis zaj, amely akár az antennából, akár az erősítő áramkörökből, akár a földi légkörből jön, ugyanaz lesz, függetlenül attól, hogy az antenna a rádióforrásra néz vagy csupán az üres égboltra, ezért a két mérés összehasonlításából kiesik. Penzias és Wilson a mi Galaktikánkból jövő rádióhullámokat akarta megmérni, tehát az üres égbolt rádiósugárzását. Ezért alapvetően fontos volt, hogy azonosítani tudjanak mindez zajt, ami vevőrendszerükben keletkezett.

A berendezés előzetes ellenőrzése egy kicsit több zajt mutatott, mint amire eredetileg számítottak, de valószínűnek látszott, hogy ez a kis eltérés az erősítő áramkörökben keletkezik. Hogy ezt is megszüntessék, Penzias és Wilson az antennából jövő jelet összehasonlította egy cseppfolyós héliummal 4 Kelvin-fokra hűtött mesterséges forrás jelével. Az erősítő áramkörökben keletkező zaj mindkét esetben megjelenik, és a két mérést összehasonlítva kiesik, így meghatározható az antennából jövő jel, amely már csak az antenna saját zaját, valamint a földi atmoszférából jövő és a csillagászati eredetű rádióhullámokat tartalmazza.

Penzias és Wilson azt várta, hogy az antenna zaja nagyon kicsi lesz. Ezt akarták ellenőrizni, amikor viszonylag rövid, 7,35 centiméteres hullámhosszon kezdték el méréseiket, ahol a Galaktika saját rádiósugárzása a várakozás szerint elhanyagolhatóan kicsi. Egy kevés zajra a földi légkör miatt is lehetett számítani, de ez könnyen megkülönböztethető jellegzetes irányfüggése miatt: ez a zaj arányos az antenna irányába eső levegőréteg vastagságával, tehát kisebb a zenit és nagyobb a horizont irányában. Azt várták, hogy ha az irányfüggésből meghatározott légköri járulékot levonják, gyakorlatilag nem marad vissza semmi, és ez azt bizonyítaná, hogy az antenna zaja tényleg elhanyagolható. Ezek után a berendezés ismeretében már nyugodtan elkezdhetik a Galaktika rádiósugárzásának vizsgálatát a hosszabb hullámhosszokon, 21 centiméter környékén, ahol a galaktikus rádiósugárzás lényegesen nagyobbnak várható.

(Azokat a rádióhullámokat, amelyek hullámhossza néhány század centiméter és 1 méter közé esik, „mikrohullámú sugárzásnak” nevezzük.)

Legnagyobb meglepetésükre, Penzias és Wilson 1964 tavaszán a 7,35 centiméteres hullámhosszon jelentős mikrohullámú zajt mértek, amely teljesen független volt az antenna irányításától. Azt is megállapították, hogy ez a zaj nem változott néhány nap, de még néhány hónap leforgása alatt sem. Úgy tűnt, mintha a sugárzás nem a mi Galaktikánkból jönne; ha ugyanis így lenne, akkor a nagy M 31 galaxis az Andromedában – amely a legtöbb szempontból a miénkhez hasonló – is erősen sugározna 7,35 centiméteren, és ezt a mikrohullámú sugárzást már régebben észlelték volna. Mindazonáltal, az észlelt zaj intenzitása az iránytól teljesen függetlennek mutatkozott, ami azt sugallta, hogy ezek a hullámok – ha valóban azok -nem a Tejútrendszerből, hanem az Univerzum egy sokkalta nagyobb tartományából származnak.

Természetesen először meg kellett vizsgálni, nem az antenna zajosabb-e, mint ahogyan eredetileg gondolták. Először az antennatorokban fészkelő galambpárra gyanakodtak. Megfogták a galambokat, és postázták a Bell Laboratórium whippanybeli telepére, majd ott szabadon eresztették őket. Néhány nap múlva a galambpár ismét megjelent Holmdelben, az antenna belsejében, ahonnan ezután már határozottabb eszközökkel távolították el őket. A galambok ottlétük alatt az antennatorkot Penzias által finoman „fehér dielektrikum”-nak nevezett anyaggal borították, amely szobahőmérsékleten hozzájárulhatott az antennazajhoz. 1965 elején leszerelték az antennatorkot és kitisztították, de ez és még sok más erőfeszítés alig csökkentette a megfigyelt zajszintet. A rejtély megmaradt: honnan származik a mikrohullámú zaj?

Az egyetlen számszerű adat, ami Penzias és Wilson rendelkezésére állt, a megfigyelt zaj intenzitása volt. Ezt az intenzitást a rádiótechnikában szokásos nyelven írták le, amely ráadásul ebben az esetben különös jelentőséget is kapott. Abszolút nulla foknál magasabb hőmérsékleten mindig minden test sugároz rádiózajt, amelyet a test elektronjainak hőmozgása okoz. Egy átlátszatlan falú doboz belsejében a rádiósugárzás intenzitása egy adott frekvencián csak a falak hőmérsékletétől függ: minél magasabb a hőmérséklet, annál erősebb a zaj. Ezért a megfigyelt rádiózaj intenzitását egy adott hullámhosszon az úgynevezett „ekvivalens hőmérséklettel” is le lehet írni – egy olyan doboz falának hőmérsékletével, amelyen belül a rádiózaj intenzitása megegyezik a megfigyelttel. A rádiótávcső persze nem hőmérő, a rádióhullámok erősségét az antenna szerkezetében a hullámok miatt keletkező parányi elektromos áramok méréséből kapjuk. Amikor egy rádiócsillagász azt mondja, hogy ilyen és ilyen ekvivalens hőmérsékletű rádiózajt észlel, annak az átlátszatlan falú doboznak a hőmérsékletére gondol, amelynek belsejében az antenna éppen a mért intenzitást adná. Az persze, hogy az antenna ilyen dobozban van-e vagy sem, más kérdés.

(Hogy a szakértők kifogásainak elébevágjak, itt említem meg, hogy a rádiómérnökök gyakran használják az antenna-hőmérséklet fogalmát is, ami az ekvivalens hőmérséklettől némileg különbözik. A Penzias és Wilson által használt hullámhosszokon és intenzitásokon azonban a két definíció gyakorlatilag azonos.)

Penzias és Wilson azt találta, hogy a mért rádiózaj ekvivalens hőmérséklete körülbelül 3,5 fokkal volt az abszolút nulla felett (pontosabban 2,5 és 4,5 között). Ha a Celsius-skála egységeiben mérünk, de nem a jég olvadáspontjánál, hanem az abszolút nulla pontnál kezdődik a skála, a hőmérsékletet úgynevezett Kelvin-fokban kapjuk. Azaz a Penzias és Wilson által megfigyelt rádiózajt úgy is leírhatjuk, hogy ekvivalens hőmérséklete 3,5 Kelvin-fok, vagy röviden 3,5 K volt. Ez sokkal magasabb volt a vártnál, de abszolút értelemben mégis nagyon kicsiny, ezért nem meglepő, hogy Penzias és Wilson jó darabig töprengett, mielőtt az eredményt közzétette volna. Természetesen nem ismerték föl azonnal, hogy a vöröseltolódás óta ez volt a legfontosabb kozmológiai felfedezés.

A rejtélyes mikrohullámú zaj jelentése rövidesen tisztább lett az asztrofizikusok „láthatatlan kollégiuma” segítségével. Penzias, más, egyéb ügyek miatt, felhívta telefonon egy rádiócsillagász kollégáját, Bemard Burke-öt a Massachusetts Institute of Technologyban. Burke éppen akkor hallott egy Carnegie Institution-beli kollégájától, Ken Turnertől egy előadásról, amelyet Turner a Johns Hopkins Egyetemen hallgatott meg. Az előadást egy fiatal elméleti fizikus, J. E. Peebles tartotta Princetonból. Az előadás során Peebles arról beszélt, hogy jelenleg is kell egy rádiózaj háttérnek léteznie, körülbelül 10 kelvin ekvivalens hőmérséklettel, amely még az Univerzum korai szakaszából maradt vissza. Burke már tudta, hogy Penzias rádiózajhőmérsékletet mér a Bell Laboratórium antennájával, és így megragadta az alkalmat, hogy a beszélgetés során érdeklődjön a mérések akkori állásáról. Penzias elmesélte, hogy minden jól megy, csak az eredmények körül van valami, amit nem értenek. Burke javasolta Penziasnak, érdeklődjön, hátha a princetoni fizikusoknak van valami érdekes elképzelésük arról, hogy mit is észlel az antenna.

Előadásában és egy 1965 márciusában megírt előzetes közleményében is Peebles a korai Univerzumban esetleg jelenlevő sugárzással foglalkozott. A „sugárzás” persze elég általános fogalom, magába foglalja az összes elektromágneses hullámot – nemcsak a rádióhullámokat, de az infravörös fényt, a látható fényt, az ultraibolya sugarakat, a röntgensugarakat, és az egészen rövid hullámhosszú sugárzást is, amelyet gamma-sugárzásnak hívunk. (L. a 136. oldalon levő táblázatot). Ezek nem válnak el élesen: ahogy a hullámhossz változik, úgy mennek át fokozatosan egymásba a különböző fajta sugárzások. Peebles észrevette, hogy ha az Univerzum korai szakaszában nem lett volna egy nagyon erős háttérsugárzás, a magreakciók olyan gyorsan játszódtak volna le, hogy a jelenlevő hidrogén legnagyobb része nehezebb elemekké „főtt” volna össze, és ez ellentétben állna azzal a ténnyel, hogy a mai Univerzum háromnegyede hidrogénből áll. A gyors atommag-felépülést csak az akadályozhatta volna meg, ha az Univerzum nagyon magas ekvivalens hőmérsékletű, igen rövid hullámhosszú sugárzással lett volna tele, amely az atommagokat gyorsabbat; szét tudja szakítani, mint ahogyan új atommagok kialakulhatnának.

Látni fogjuk, hogy ez a sugárzás túléli az Univerzum tágulását, de ahogyan az Univerzum tágul, ekvivalens hőmérséklete az Univerzum méretével fordított arányban csökken. (Tulajdonképpen ez az oka a vöröseltolódásnak is, amelyről a II. fejezetben esett szó.) Eszerint a mai Univerzum szintén sugárzással van tele, de az ekvivalens hőmérséklet sokkalta alacsonyabb, mint az első néhány percben volt. Peebles becslése szerint az a sugárzás, amely a hélium és a többi nehéz elem kialakulását az ismert határokon belül tudta tartani, ma legfeljebb 10 kelvin hőmérsékletű lehet.

Mint később kiderült, a 10 kelvinnel kicsit túlbecsülték a sugárzás hőmérsékletét. Az eredeti munkát rövidesen sokkal részletesebb és pontosabb számítások követték, amelyeket Peebles és mások végeztek el, ezeket majd az V. fejezetben tárgyaljuk. Peebles cikke végül is sohasem jelent meg eredeti formájában. Mégis, a konklúziója alapvetően helyes volt: a hidrogén megfigyelt mennyiségéből arra következtethetünk, hogy az Univerzum az első percekben olyan hatalmas mennyiségű sugárzást tartalmazott, amely megakadályozta, hogy a nehezebb elemekből túl sok keletkezzen. Azóta az Univerzum tágulása az ekvivalens hőmérsékletet néhány kelvinre csökkentette, ez ma rádiózaj háttérként észlelhető, amely minden irányból egyforma erősséggel jelentkezik. Ez azonnal természetes magyarázatot szolgáltatott Penzias és Wilson méréseire. Valóban azt mondhatjuk, hogy a holmdeli antenna egy dobozban van: ez a doboz az Univerzum. Az antenna végső soron nem a mai, hanem a korai Univerzum hőmérsékletét méri, azonban az azóta végbement hatalmas arányú tágulás miatt redukált értékben.

Peebles munkája akkor a legújabb volt több hasonló kozmológiai „spekuláció” közül. Az 1940-es években George Gamow és munkatársai, Ralph Alpher és Robert Herman kidolgozták az elemek kialakulásának „Nagy Bumm” elméletét, és ebből 1948-ban Alpher és Herman egy körülbelül 5 kelvin hőmérsékletű sugárzási hátteret jósoltak. 1964-ben hasonló számításokat végzett Ja. B. Zeldovics a Szovjetunióban, Fred Hoyle és R. J. Taylor pedig Angliában. Ezeket a korábbi munkákat sem a princetoni csoport, sem a Bell-csoport nem ismerte, és nem befolyásolták a háttérsugárzás felfedezésének tényét, ezért egészen a VI. fejezetig várhatunk, hogy ezeket részleteiben is tárgyaljuk. A VI. fejezetben arra a furcsa történeti kérdésre is kitérünk, hogy a korábbi elméleti jóslatok miért nem vezettek a háttérsugárzás keresésére irányuló kutatásokhoz.

Peebles 1965-ös számításait egy idősebb princetoni kísérleti fizikus, Robert H. Dicke inspirálta. (Többek között Dicketől származik az alapvető mikrohullámú észlelési technika is, amit ma a rádiócsillagászok használnak.) Valamikor 1964-ben Dickének támadt az az ötlete, hogy esetleg a kozmikus történelem korai, forró szakaszából visszamaradt sugárzás megfigyelhető. Dicke elképzeléseit az Univerzum úgynevezett „oszcilláló” modelljére alapozta, amelyre majd a könyv utolsó fejezetében még visszatérünk. Ő nem adott semmilyen számszerű becslést a sugárzás várható hőmérsékletére, de észrevette a lényeget, tudniillik azt, hogy itt van valami, amit érdemes keresni. Dicke javasolta P. G. Rollnak és D. T Wilkinsonnak, hogy kezdjenek kutatni a mikrohullámú háttér után. Ők ezek után egy kis méretű, alacsony zajú antennát építettek a princentoni Palmer Fizikai Laboratórium tetején. (Ehhez a méréshez nem szükséges nagy rádiótávcsövet használni, mert a sugárzás úgyis minden irányból jön, ezért nem nyerünk semmit azzal, ha az antenna irányérzékenysége nagyobb.)

Mielőtt Dicke, Roll és Wilkinson befejezhették volna méréseiket, Dicket felhívta Penzias, aki éppen akkor hallott Burke-től Peebles előadásáról. Elhatározták, hogy egy időben jelentetnek meg két cikket az Astrophysical Journalben, ahol Penzias és Wilson bejelentik észlelésüket, Dicke, Peebles, Roll és Wilkinson pedig megadják a kozmológiai magyarázatot. Penzias és Wilson, még mindig nagyon óvatosan, a cikknek az „Antennahőmérséklet-többlet mérése 4080 MHz frekvencián” címet adta. Az antenna a 4080 megahertz frekvenciára, azaz másodpercenkénti 4080 millió rezgésre volt hangolva, amely éppen 7,35 centiméteres hullámhossznak felel meg. Egyszerűen csak annyit írtak, hogy „a zenit effektív rádiózajának mérése... a vártnál 3,5 kelvinnel magasabb értéket szolgáltatott”, és elkerülték a kozmológiának még az említését is, egyetlen mondatot kivéve: „Az észlelt többlethőmérséklet egy lehetséges magyarázata Dicke, Peebles, Roll és Wilkinson cikkében található, ugyanezen számban.”

Tényleg az Univerzum kezdetétől maradt vissza a Penzias és Wilson által felfedezett mikrohullámú sugárzás? Mielőtt áttekintenénk az 1965 óta elvégzett többi kísérletet, először talán tegyük fel a kérdést, mit várunk, milyen lesz az a sugárzás, amelynek be kell töltenie az Univerzumot, ha helyesek a jelenlegi kozmológiai elképzelések. A válaszhoz nézzük meg, mi történik a sugárzással, miközben az Univerzum tágul – nemcsak a nukleoszintézis, az elemek keletkezése idején, vagy az első három perc végén, hanem az azóta eltelt évmilliárdok alatt is.

Nagy segítségünkre lesz, ha most egy időre feladjuk a sugárzásról alkotott klasszikus elektromágneseshullám-képünket, és helyette a sokkal modernebb „kvantumos” képet használjuk, amely szerint a sugárzás részecskékből, fotonokból áll. Egy közönséges fényhullám rengeteg fotonból jön létre, amelyek együtt mozognak, de ha a hullám energiáját egészen pontosan megmérnénk, kiderülne, hogy az mindig egy bizonyos mennyiség egész számú többszöröse. Ez a bizonyos mennyiség mondható egy foton energiájának. Látni fogjuk, hogy a fotonok energiája általában nagyon kicsi, ezért a legtöbb esetben úgy tűnik, hogy egy elektromágneses hullám energiája akármekkora értéket felvehet. Mégis, a sugárzásnak atomokkal vagy atommagokkal történő kölcsönhatásánál általában csak egy foton szerepel; ha tehát ezeket a folyamatokat vizsgáljuk, akkor a hullámkép helyett a fotonleírást kell használnunk. A fotonok nyugalmi tömege nulla, és elektromosan semlegesek, mégis valódi részecskék, mindegyikük határozott energiával, lendülettel (impulzussal), sőt a haladási irányuk körül még perdülettel (spinnel) is rendelkeznek.

Mi történik egy fotonnal, amikor átszeli az Univerzumot? Ha csak a mai Univerzumot nézzük, nem túl sok. Még a 10 milliárd fényévre levő objektumok fénye is háborítatlanul ér el hozzánk. Akármi is van a galaxisok közötti térben, elég átlátszónak kell lennie, ha a fotonok az Univerzum életének jelentős részében szóródás és elnyelődés nélkül haladhatnak felénk.

A távoli galaxisok vöröseltolódásából tudjuk, hogy az Univerzum tágul, így a benne levő anyag valamikor sokkal sűrűbb volt, mint ma. Egy folyadék hőmérséklete összenyomáskor emelkedik, ezért feltételezhetjük, hogy a múltban az Univerzum anyaga is sokkal forróbb volt. Jelenlegi elképzeléseink szerint az első 700 000 évben az Univerzum anyaga olyan sűrű és forró volt, hogy még nem csomósodott össze csillagokká vagy galaxisokká, sőt még az atomok sem voltak állandóak, mert már kialakulásuk pillanatában újra atommagokra és elektronokra szakadtak szét.

Ilyen „kellemetlen” körülmények között persze a fotonok sem tudtak olyan nagy távolságokat megtenni zavartalanul, mint amire a mai Univerzumban képesek. A fotonok útközben szabad elektronokkal találkoztak, amelyek jórészt szétszórták vagy elnyelték őket. Ha egy foton elektronon szóródik, akkor vagy elnyel, vagy átad egy kis energiát az elektronnak, attól függően, melyikük rendelkezett kezdetben nagyobb energiával. Az az átlagos idő, ameddig egy foton elnyelődés vagy lényeges energiaváltozás nélkül haladhatott, nagyon rövid volt, sokkal rövidebb, mint az Univerzum akkori életkora. A megfelelő átlagos ütközési idő a többi részecske – az elektronok és az atommagok – esetében még sokkal kisebb. így az Univerzum tágulásának első szakasza hiába ment nagyon gyorsan végbe, minden egyes foton, elektron vagy atommag számára bőven volt idő, hogy nagyon sokszor szóródjon, elnyelődjön vagy újra kisugárzódjék.

Minden anyagi rendszerben, ahol a részecskék sokszor ütköznek egymással, egyensúlyi állapot áll be. Az egyes részecskék száma az állapotukat jellemző adatok (hely, energia, sebesség, spin stb.) egy bizonyos tartományában olyan értéket vesz fel, hogy egy másodperc alatt ugyanannyi részecske lép be ebbe a tartományba, mint amennyi az ütközések révén kikerül onnan (dinamikus egyensúly). Az ilyen rendszer tulajdonságait nem a kezdeti feltételek határozzák meg, hanem az a tény, hogy az egyensúly fennáll-e vagy sem. Természetesen itt az „egyensúly” kifejezés nem azt jelenti, hogy az egyes részecskék „befagytak”, hiszen nincsenek statikus egyensúlyban, mert mindegyikük állandóan ütközik a szomszédaival. Az egyensúly statisztikus: a részecskék hely, sebesség, energia stb. szerinti eloszlása egyáltalán nem változik, vagy csak nagyon lassan.

Az ilyen statisztikus állapotot „hőmérsékleti egyensúly”-nak nevezzük, mert ez mindig jól meghatározott hőmérséklettel jellemezhető, amely az egész rendszeren belül állandó. Ha pontosabban fogalmazunk, hőmérsékletről csak hőmérsékleti egyensúly esetén beszélhetünk. Az elméleti fizika egyik igen hatékony ága, a „statisztikus fizika” szolgáltatja a matematikai apparátust a hőmérsékleti egyensúlyban levő rendszerek vizsgálatához.

A hőmérsékleti egyensúly egy kicsit a klasszikus közgazdaságtan árszabályozási mechanizmusához hasonlóan működik. Ha a kereslet meghaladja a kínálatot, az árak emelkednek, ezzel csökkentik a keresletet és növelik a termelést. Ha a kínálat nagyobb, mint a kereslet, az árak leesnek, növekszik a kereslet és csökken a termelés. Mindkét esetben a kereslet és a kínálat a kiegyenlítődés felé közelít. Hasonlóan, ha túl sok vagy túl kevés részecske van egy bizonyos energiatartományon belül, akkor az ütközések révén több, illetve kevesebb részecske hagyja el ezt a tartományt, mint amennyi oda belép, egészen addig, amíg be nem áll az egyensúly.

Persze, az ármechanizmus nem mindig működik olyan szépen, mint ahogyan a klasszikus közgazdaságtan feltételezi, de az analógia ebben a vonatkozásban is fennáll: a legtöbb fizikai rendszer a természetben meglehetősen távol van a hőmérsékleti egyensúlytól. A csillagok belsejében majdnem tökéletes az egyensúly, így elég pontosan meg tudjuk jósolni, milyen viszonyok uralkodnak ott, de például a Föld felszíne távolról sincsen egyensúlyban, ezért nem is tudjuk biztosan megmondani, lesz-e eső holnap vagy sem. Az Univerzum sem volt soha tökéletes egyensúlyban, hiszen tágulóban van! Mégis, a fejlődés korai szakaszában, amikor az egyes részecskék sokkal gyakrabban szóródtak és nyelődtek el egymáson, mint amilyen ütemben az Univerzum tágul, a Világegyetem folyamatosan ment át az egyik – csaknem tökéletes – hőmérsékleti egyensúlyból a másikba.

Az egész könyv gondolatmenete tulajdonképpen azon a feltételezésen alapul, hogy az Univerzum valamikor hőmérsékleti egyensúlyban volt. A statisztikus mechanika szerint egy hőmérsékleti egyensúlyban levő tetszőleges rendszer minden tulajdonsága meghatározott, ha megadjuk a rendszer hőmérsékletét, továbbá néhány megmaradó mennyiség értékét. (Erről majd a következő fejezetben többet tudunk meg.) így az Univerzum a kezdőfeltételekből csak nagyon kevésre „emlékszik”. Ez nagy kár, ha bennünket elsősorban a dolgok kezdete érdekel, viszont kárpótlást is nyújt, mert így viszonylag kevés feltevéssel majdnem az elejétől végig tudjuk követni az Univerzum történetét.

A Penzias és Wilson által felfedezett mikrohullámú háttérsugárzást az Univerzum hőmérsékleti egyensúlyának maradványaként értelmezzük. Ha tehát meg akarjuk jósolni a háttérsugárzás tulajdonságait, először fel kell tennünk a kérdést: milyen tulajdonságai vannak az anyaggal hőmérsékleti egyensúlyban levő sugárzásnak?

Történetesen éppen ez az a kérdés, amelyből a sugárzás fotonokként való értelmezése, és általában a kvantumelmélet kiindult. Az 1890-es években már ismert volt, hogy az anyaggal hőmérsékleti egyensúlyban levő sugárzás valamennyi tulajdonsága csak a hőmérséklettől függ. Pontosabban: az egységnyi térfogatra jutó sugárzási energiát egy bizonyos hullámhossztartományon belül egy általános képlet adja meg, amelyben csak a hullámhossz és a hőmérséklet szerepel. Ugyanez a képlet adja meg az átlátszatlan falú dobozban levő sugárzás mennyiségét is, így a rádiócsillagász is ezt használja, ha a megfigyelt rádiózajt „ekvivalens hőmérsékleteként akarja értelmezni. Ráadásul ugyanez a kifejezés adja meg egy teljesen elnyelő felület által másodpercenként és négyzetméterenként valamilyen hullámhosszon kisugárzott energiát is, ezért az ilyen sugárzást általában „feketetest-sugárzás”-nak nevezzük. Másképpen fogalmazva, a feketetest-sugárzást a kisugárzott energiának a hullámhossztól függő meghatározott eloszlása jellemzi, amelyet egy – csak a hőmérséklettől függő – általános képlet ír le. Az 1890-es években az elméleti fizika egyik legégetőbb kérdése ennek a képletnek a megkeresése volt.

A feketetest-sugárzás helyes képletét a XIX. század utolsó heteiben Max Karl Ludwig Planck találta meg. Planck eredményének pontos alakja a 7. ábrán látható: a hőmérséklet az ábrán 3 kelvin, ami a kozmikus háttérsugárzás hőmérséklete. A Planck-törvényt röviden összefoglalva: egy feketetest-sugárzással teli dobozban az energia a hullámhossz függvényében a növekvő hullámhosszal gyorsan nő, elér egy maximumot, azután meredeken csökken. Ez a Planck-eloszlás univerzális: nem függ a sugárzással kölcsönható anyag tulajdonságaitól, csak a hőmérsékletétől. A mai értelmezés szerint minden olyan sugárzást „feketetest-sugárzás”-nak nevezünk, ahol az energiának a hullámhossz szerinti eloszlása megegyezik a Planck-eloszlással, függetlenül attól, hogy az illető sugárzást tényleg egy fekete test bocsátotta-e ki vagy sem. így az első egymillió évben, amikor az anyag és a sugárzás egyensúlyban volt, az Univerzumot olyan feketetest-sugárzás töltötte be, amelynek hőmérséklete megegyezett az Univerzum anyagának hőmérsékletével.

Planck számításának fontossága messze túlment a feketetest-sugárzás problémáján, mert egy alapvetően új gondolatot vezetett be, azt, hogy az energia elemi adagokban, „kvantumokéban létezik. Planck eredetileg csak a sugárzással egyensúlyban levő anyag energiáját akarta kvantálni, de Einstein néhány év múlva feltételezte, hogy a sugárzás maga is kvantumokban létezik, s ezeket a kvantumokat később fotonoknak nevezték el. Ezek a lépések vezettek végül az 1920-as években a tudomány történetének egyik legnagyobb forradalmához, amikor a klasszikus mechanika helyébe egy merőben más leírásmód, a kvantummechanika lépett.

Ebben a könyvben nem merülhetünk el mélyen a kvantummechanika részleteiben, mégis ahhoz, hogy megértsük, hogyan viselkedik a sugárzás a táguló Univerzumban, segítségünkre lesz, ha látjuk, hogyan vezetett a sugárzásnak fotonokkal történő leírása a Planck-eloszláshoz.

Azt viszonylag egyszerű megmagyarázni, miért csökken le a feketetest-sugárzás energiasűrűsége a nagyobb hullámhosszaknál: nehéz sugárzást hullámhosszánál kisebb méretű tartományban elhelyezni. Ezt még a klasszikus hullámelmélet alapján is meg lehetett érteni, ehhez nem kellett kvantumelmélet.

Az energiasűrűség csökkenése a rövidebb hullámhosszak felé viszont értelmezhetetlen a kvantumkép nélkül. A statisztikus mechanika egyik jól ismert tétele szerint bármilyen hőmérsékleten nehéz olyan részecskéket, hullámokat vagy akármilyen más gerjesztéseket előállítani, amelyek energiája magasabb, mint egy bizonyos hőmérséklettel arányos érték. Ha a sugárzás egyes hullámai tetszőlegesen kis energiával rendelkezhetnének, nem lenne semmi, ami a rövid hullámhosszakon korlátozná a fekete test sugárzásának mennyiségét.

 

 

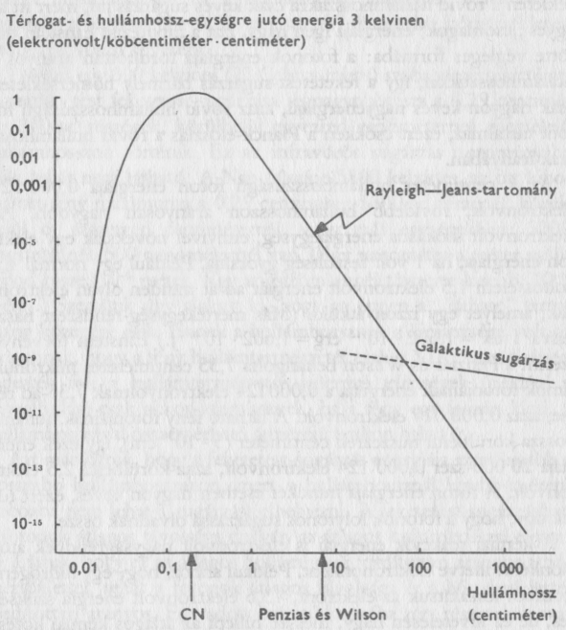
7. ábra. A Planck-eloszlás. Az ábrán az egységnyi hullámhossztartományra jutó energiasűrűséget tüntettük fel a hullámhossz függvényében, egy 3 kelvin hőmérsékletű feketetest-sugárzás esetén. (A 3 kelvinnél f faktorral nagyobb hőmérsékletekre a hullámhosszakat 1/f  arányban kell csökkenteni, az energiasűrűséget pedig f⁵-nel kell szorozni.) A görbe jobb oldali – egyenes – szakaszát közelítőleg jól megadja a jóval egyszerűbb Rayleigh-Jeans-eloszlás; ilyen eloszlás egyébként nemcsak a feketetest-sugárzásnál, de sok más esetben is várható. A bal oldali – meredek esésű – szakasz a sugárzás kvantumos természetéből adódik, és a feketetest-sugárzás jellegzetessége. A „galaktikus sugárzás” feliratú görbe a Galaktikánkból eredő rádiózaj intenzitását mutatja. (Nyilak jelzik az eredeti Penzias-Wilson-féle mérés hullámhosszát, és azt a hullámhosszat, amelynél a sugárzási hőmérséklet a csillagközi CN-molekulák első rotációs gerjesztéséből meghatározható.)

 

Ez nemcsak a kísérlettel volt ellentétben, de arra a katasztrofális eredményre is vezetne, hogy a feketetest-sugárzás teljes energiája végtelen! Az egyetlen kiút az volt, hogy az energia diszkrét csomagokban, kvantumokban érkezik, ahol a csökkenő hullámhosszal minden egyes „csomag” energiája növekszik. Ezért bármely hőmérsékleten a rövid hullámhosszakra csak kevés sugárzás jut, mert itt az egyes „csomagok” energiája igen nagy. Ezt a hipotézist Einstein öntötte végleges formába: a fotonok energiája fordítottan arányos a hullámhosszukkal, így a feketetest-sugárzás bármely hőmérsékleten csak nagyon kevés nagyenergiájú, azaz rövid hullámhosszúságú fotont tartalmaz, ezért csökken a Planck-eloszlás a rövid hullámhosszak irányában.

Az 1 centiméter hullámhosszúságú foton energiája 0,000 124 elektronvolt, rövidebb hullámhosszon arányosan nagyobb. Az elektronvolt szokásos energiaegység, ennyivel növekszik egy elektron energiája, ha 1 volt feszültség gyorsítja. Például egy normál 1,5 voltos elem 1,5 elektronvolt energiát ad át minden olyan elektronnak, amelyet egy izzón átküld. (Más mértékegység-rendszert használva 1 eV = 1,602 • 10^-12 erg = 1,602 • 10^-19 J.) Einstein törvénye szerint a Penzias és Wilson behangolta 7,35 centiméteres mikrohullámok fotonjainak energiája a 0,000124 elektronvoltnak 7,35-ad része, azaz 0,000 017 elektronvolt. A látható fény fotonjainak hullámhossza körülbelül húszezred centiméter (5 • 10^-5 cm), így ezek energiája 20 000-szer 0,000 124 elektronvolt, azaz körülbelül 2,5 elektronvolt. A foton energiája mindkét esetben nagyon kevés, ezért tűnik úgy, hogy a fotonok folytonos sugárzássá olvadnak össze.

A kémiai reakciók energiái is elektronvolt nagyságrendűek atomonként, illetve elektrononként. Például ahhoz, hogy egy hidrogén-atomból leszakítsuk az elektront, 13,6 elektronvolt energia szükséges, de ez kivételesen nagy, messze túllépi az átlagos kémiai kötési energiákat. Számunkra nagyon fontos az a tény, hogy a Nap fotonjainak átlagos energiája is elektronvolt nagyságrendű, ezért tudják ezek a fotonok az élethez szükséges kémiai reakciókat (például a fotoszintézist) létrehozni. Az atommag-reakciók energiája átlagosan millió elektronvolt atommagonként, ezért képes 1 kilogramm plutónium ugyanakkora robbanást létrehozni, mint 1 millió kilogramm TNT.

A fotonkép segítségével könnyen megérthetjük a feketetest-sugárzás néhány fő tulajdonságát. Először is a statisztikus mechanika szerint az átlagos fotonenergia a hőmérséklettel arányos, viszont az Einstein-törvény szerint minden foton hullámhossza az energiájával fordítottan arányos. Ezt a két törvényt összekapcsolva azt kapjuk, hogy a feketetest-sugárzásban a fotonok átlagos hullámhossza a hőmérséklettel fordítottan arányos. Konkrét példához nyúlva: 1 kelvin hőmérsékleten az a hullámhossz, amelynél a feketetest-sugárzás a legerősebb: 0,29 centiméter, magasabb hőmérsékleten pedig arányosan kevesebb.

Például egy 300 kelvines (27 Celsius-fokos) szobahőmérsékletű átlátszatlan test feketetest-sugárzása legnagyobbrészt a 0,29 centiméter 300-ad részének, körülbelül egyezred centiméternek megfelelő hullámhosszon történik. Ez az infravörös sugárzás tartományába esik, tehát nem látható. A Nap felszíne 5800 kelvines, az ott kibocsátott fény maximuma a 0,29 centiméter 5800-ad részénél, körülbelül öt százezred centiméternél, vagy más egységekben: 5000 angströmnél, 500 nanométernél van. (Egy nanométer a méter milliárdod része, 10^-9 méter. Egy angström ennél tízszerte kisebb, 10-10 méter.) Szemünk úgy alakult ki, hogy az éppen a „látható” tartomány közepére esik. Ennek a hullámhossznak a kicsinysége volt az oka annak, hogy a fény hullámtermészetét csak a XIX. század elején fedezték fel; a hullámtermészetre jellemző jelenségek (például a fényelhajlás) csak akkor jelentkeznek, ha a fény egy igazán kicsi, a hullámhosszával összemérhető átmérőjű lyukon halad át.

Azt már láttuk, hogy a feketetest-sugárzás energiája azért kisebb a hosszabb hullámhosszakon, mert a hullámhossznál kisebb méretű dobozba nem lehet a sugárzást elhelyezni. A feketetest-sugárzásban a fotonok átlagos távolsága durván az átlagos hullámhosszal egyenlő. Láttuk, hogy ez az átlagos hullámhossz fordítottan arányos a hőmérséklettel, tehát a fotonok átlagos távolsága is a hőmérséklettel fordítottan arányos. Egy adott méretű kockába zárt részecskék száma az átlagos távolság köbével fordítottan arányos, tehát a feketetest-sugárzás fotonjainak száma egy adott térfogatban a hőmérséklet köbével lesz arányos.

Ebből további információkat kaphatunk a feketetest-sugárzás energiatartalmára. Az energiasűrűség, azaz 1 liternyi térfogatba zárt energia nem más, mint a fotonok száma literenként szorozva egy foton átlagos energiájával. Mint fent már láttuk, a fotonok száma 1 literben a hőmérséklet köbével, átlagos energiájuk pedig magával a hőmérséklettel arányos. így a feketetest-sugárzás energiasűrűsége a hőmérséklet köbének és a hőmérsékletnek a szorzatával, azaz másképp: a hőmérséklet negyedik hatványával arányos. Számszerűen a feketetest-sugárzás energiasűrűsége 1 kelvin hőmérsékleten 4,72 elektronvolt literenként, 10 kelvinen 47 200 elektronvolt literenként stb. (Ezt az összefüggést hívják Stefan-Boltzmann-törvénynek.) Ha a Penzias és Wilson által felfedezett mikrohullámú zaj valóban 3 kelvin hőmérsékletű feketetest-sugárzás, akkor energiasűrűsége 4,72 elektronvoltszor 3-nak negyedik hatványa literenként, vagyis körülbelül 380 elektronvolt literenként. Amikor a hőmérséklet ezerszer nagyobb volt, az energiasűrűség milliószor milliószorosa (billiószorosa) volt ennek az értéknek.

Most visszatérhetünk a mikrohullámú háttérsugárzás eredetéhez. Láttuk, hogy valamikor az Univerzumnak olyan forrónak kellett lennie, hogy az atomok elektronokra és atommagokra bomlottak, a fotonok és elektronok ütközései pedig hőmérsékleti egyensúlyban tartották a töltött anyagot és a sugárzást. Közben az Univerzum tágult és hűlt, idővel így elérte a 3000 kelvin hőmérsékletet, ami már elég hűvös volt ahhoz, hogy az elektronok és az atommagok végre atomokká egyesülhettek. (Az asztrofizikában ezt „rekombinációnak”, újraalakulásnak nevezik, ami rossz kifejezés, hiszen az Univerzum keletkezése óta mindeddig az elektronok és az atommagok sohasem alkottak atomokat!) A szabad elektronok hirtelen eltűnése megszünteti a sugárzás és az atomok kapcsolatát, ettől kezdve a sugárzás szabadon tágul.

Amikor ez bekövetkezett, a sugárzás hőmérsékleti egyensúlyban volt, így az energiaeloszlást a Planck-törvény írta le, a töltött részecskékével egyező 3000 kelvin hőmérsékleten. A fotonok átlagos hullámhossza egy mikron körül volt (ez egymilliomod méter, avagy 10 000 angström), és a fotonok átlagos távolsága is ezzel a hullámhosszal volt egyenlő.

Mi történt azóta a fotonokkal? Újabb fotonok nem keletkeztek és nem is nyelődtek el, ezért a fotonok átlagos távolsága egyszerűen az Univerzum méretével, a galaxisok közti átlagos távolsággal arányosan növekszik. De mint ezt már az előző fejezetben láttuk, a kozmológiai vöröseltolódás a fényre úgy hat, hogy a fény hullámhosszát az Univerzum tágulásával arányosan nyújtja, ezért minden egyes foton hullámhossza is az Univerzum méretével arányosan változik. A fotonok átlagos távolsága változatlanul az átlagos hullámhossz lesz, akárcsak a feketetest-sugárzás esetén. Ezt a gondolatmenetet részletes számításokkal végigkövetve megmutathatjuk, hogy az Univerzumot megtöltő sugárzást továbbra is a Planck-féle feketetest-sugárzási képlet írja le, pedig a fény már nincs is egyensúlyban az atomokkal. (L. a Matematikai jegyzetek 4. pontját a 149. oldalon.) A tágulás egyetlen hatása az, hogy az átlagos fotonhullámhossz az Univerzum sugarával arányosan nő. A feketetest-sugárzás hőmérséklete fordítottan arányos az átlagos hullámhosszal, így a sugárzás hőmérséklete csökken, ahogy az Univerzum tágul.

A Penzias és Wilson által mért mikrohullámú zaj intenzitása például 3 kelvin hőmérsékletnek felel meg. Éppen ezt várnánk, ha az Univerzum a sugárzás és a töltött részecskék hőmérsékleti egyensúlyának megszűnése (3000 kelvin) óta ezerszeresre tágult volna. Ha ez az értelmezés helyes, akkor ez a 3 kelvines rádióháttér messze a legősibb jel, amit valaha csillagászok észleltek; sokkal régebben keletkezett, mint a legtávolabbi galaxisok fénye.

De Penzias és Wilson a kozmikus rádiózaj intenzitását csak egy hullámhosszon: 7,35 centiméteren mérte meg. Azonnal nagyon izgalmassá vált, hogy a sugárzási energia valóban a Planck-törvény szerint oszlik-e el, ahogyan ezt az Univerzum korai szakaszából, a sugárzás és anyag hőmérsékleti egyensúlyából visszamaradt sugárzás esetén várnánk. Ha ez valóban teljesül, úgy a Planck-eloszlással való összehasonlításból más hullámhosszokon is ugyanazt az ekvivalens hőmérsékletet kell kapnunk, mint 7,35 centiméteren.

Mint már láttuk, Penzias és Wilson felfedezése idején egy másik berendezés is majdnem elkészült New Jerseyben a kozmikus rádióháttér tanulmányozására. Nem sokkal az eredeti két cikk után Roll és Wilkinson bejelentették saját eredményüket is: a sugárzási háttér ekvivalens hőmérséklete 3,2 centiméteres hullámhosszon 2,5 és 3,5 kelvin közé esett. Vagyis, a mérési hibán belül a sugárzási háttér intenzitása éppen annyival volt nagyobb a 7,35 centiméteren mértnél, mint amennyit a Planck-törvény jósolt!

1965 óta a mikrohullámú háttérsugárzás intenzitását több mint egy tucat hullámhosszon megmérték, 73,5 centimétertől egészen 0,33 centiméterig. Mindegyik mérés összefér egy 2,7 és 3 kelvin közötti hőmérsékletű Planck-eloszlással.

Mielőtt arra a következtetésre jutnánk, hogy ez valóban Planck-eloszlás, emlékezzünk vissza, hogy a jellemző hullámhossz, amelyen a Planck eloszlás maximális: 0,29 centiméter osztva a kelvinben mért hőmérséklettel. Ez a hullámhossz 3 kelvin esetén 0,1 centiméternél is kevesebb. Ezért az összes mikrohullámú mérés a Planck-eloszlás hosszú hullámhosszú tartományán történt. Ezen a tartományon az energiasűrűség azért csökken, mert kis térfogatba nem férnek bele a hosszú hullámhosszak. Az itt mért energiasűrűségből még nem következik egyértelműen, hogy az eloszlás valóban egyensúlyi. (A rádiócsillagászok a spektrum ezen részét Rayleigh-Jeans-tartománynak nevezik, mert az eloszlás tulajdonságaival először Lord Rayleigh és Sir James Jeans foglalkozott.) Ha be akarjuk bizonyítani, hogy valóban feketetest-sugárzást látunk, úgy a Planck-eloszlás maximuma alatt, a rövid hullámhosszak tartományában kell mérnünk; ezzel bebizonyíthatjuk, hogy az energiasűrűség tényleg lecsökken a csökkenő hullámhosszal, ahogyan ezt a kvantumelmélet alapján várjuk. A 0,1 centiméternél rövidebb hullámhosszakon viszont már kívül vagyunk a rádiócsillagászok számára elérhető mikrohullámú tartományon, és a még frissebb infravörös csillagászat módszereire van szükségünk.

Sajnos, bolygónk légköre, amely a 0,3 centiméteresnél nagyobb hullámhosszakra átlátszó, a rövidebb hullámhosszúságú sugárzásokat szinte teljesen elnyeli. Nem valószínű, hogy akármilyen földi rádiótávcsővel – legyen az akár egy magas hegycsúcson is – meg lehetne mérni a kozmikus háttérsugárzást a 0,3 centiméternél rövidebb hullámhosszakon.

Furcsa módon a háttérsugárzást már megmérték rövidebb hullámhosszakon, méghozzá az itt említett mérések bármelyikénél sokkal korábban, és ráadásul optikai módszerek használatával! Az Ophiuchus (Kígyótartó) csillagképben észleltek egy intersztelláris felhőt, amely a Föld és egy forró, de egyébként eléggé érdektelen csillag, a ζ Oph között található. Amikor a ζ Oph spektrumát meghatározták, sok szokatlan fekete vonalat találtak a spektrumban, melyek jelenléte arra utalt, hogy az intersztelláris gáz néhány meghatározott hullámhosszon élesen elnyeli a fényt. Ezek azok a hullámhosszak, amelyeken a fotonok energiája éppen képes arra, hogy a gázfelhő molekuláit gerjessze, alacsonyabb energiájú állapotból magasabb energiájúba juttassa őket. (A molekulák energiája, akárcsak az atomoké, csak bizonyos „kvantált” értékeket vehet fel.) így ha megmérjük azokat a hullámhosszakat, ahol ezek a sötét vonalak fellépnek, megtudhatjuk, hogy milyen molekulák alkotják a gázfelhőt, és hogy ezek a molekulák milyen állapotban vannak.

A ζ Oph spektrumában az egyik abszorpciós vonal a 387,5 nanométer = 3875 angström hullámhosszon található; ez cián (CN) jelenlétét jelzi a gázban. (Tulajdonképpen a C szén- és N nitrogénatomból álló CN ciánt helyesen cianidgyöknek kellene hívnunk, mert normál körülmények között gyorsan egyesül más atomokkal, és ezáltal sokkal stabilabb molekulát alkot, például HCN hidrogéncianidot. A csillagközi térben viszont a CN elég stabil.) 1941-ben W. S. Adams és A. McKellar felfedezte, hogy ez az abszorpciós vonal felhasad három komponensre, amelyek hullámhossza 3874,608, 3875,763 és 3873,998 angström. Az első hullámhossz egy olyan átmenetnek felel meg, amelyben a CN-molekula a legalacsonyabb energiájú állapotából (az úgynevezett „alapállapotából) egy rezgő („vibráló”) állapotba kerül át. Ezt a vonalat akkor is várnánk, ha a CN-gáz hőmérséklete abszolút zérus lenne. A másik két vonal viszont csak olyan átmenetekben jöhetett létre, ahol a molekula egy – közvetlenül az alapállapot fölött elhelyezkedő – rotáló állapotból egy vibráló állapotba került. Eszerint az intersztelláris felhő CN-molekuláinak jó része rotáló állapotban van. A rotáló állapot energiájának és a megfelelő abszorpciós vonalak intenzitásának ismeretében McKellar arra a következtetésre jutott, hogy a CN-molekulákat valamilyen külső zavar gerjeszti a rotáló állapotba, és a zavar effektív hőmérséklete körülbelül 2,3 kelvin.

Ebben az időben semmi ok nem volt arra, hogy ezt a rejtélyes zavart kapcsolatba hozzák az Univerzum keletkezésével, és nemigen figyeltek fel rá. 1965-ben, a mikrohullámú háttérsugárzás felfedezése után többen (George Field, I. Sz. Sklovszkij és N. J. Woolf) rájöttek, hogy az Ophiuchus-felhőben ez okozza a CN-molekulák rotációját. A rotáció gerjesztéséhez szükséges fotonhullámhossz 0,263 centiméter, ez rövidebb, mint a földi rádiócsillagászat számára elérhető legkisebb hullámhossz, de még mindig nem elég rövid ahhoz, hogy a Planck-eloszlás 0,1 centiméter alatt várt csökkenését észlelni tudjuk.

Azóta rendszeres kutatás folyt a CN- és más molekulák rotációja által okozott egyéb abszorpciós vonalak után. 1974-ben megfigyelték a CN második rotáló állapotának abszorpcióját, ebből meghatározták a sugárzás intenzitását a megfelelő 0,132 centiméteres hullámhosszon, ez is körülbelül 3 kelvines hőmérsékletnek felelt meg. A 0,1 centiméternél rövidebb hullámhosszakon az ilyen mérések eddig csak felső korlátot tudtak adni. Az eredmények mindenesetre biztatóak, mert látszik, hogy az energiasűrűség 0,1 centiméter körüli hullámhossz alatt rohamosan csökkenni kezd, éppen úgy, ahogyan azt a feketetest-sugárzás esetében várjuk. Ezek a felső korlátok azonban nem adnak pontos hőmérsékletet.

Ezeket a problémákat csak úgy lehetett kikerülni, hogy léggömbök vagy rakéták segítségével infravörös vevőkészülékeket juttattak a Föld légköre fölé. Ezek a kísérletek elég bonyolultak voltak, és először ellentmondó eredményeket adtak, amelyek egyszer a Nagy Bumm-elméletet elfogadó, máskor az azt ellenző tudósokat támogatták. A Cornell Egyetem egy csoportja rakétát használt, ők sokkal több sugárzást találtak, mint amit a Planck-eloszlás alapján várni lehetett, egy MIT-s csoport léggömbös kísérlete viszont a feketetest-sugárzással megegyező eredményeket hozott. Mindkét csoport folytatta a munkát, és 1972-re megegyeztek, hogy a kozmikus háttér feketetest-sugárzás, melynek hőmérséklete közel 3 kelvin. 1976-ban egy léggömbös kísérlet a Berkeley Egyetemről megerősítette, hogy a 0,06 és a 0,25 centiméter közötti hullámhossztartományban úgy változik az energiasűrűség, ahogyan azt egy 0,1 és 3 kelvin közötti hőmérsékletű sugárzástól várjuk. Ma már tehát bizonyított tény, hogy a kozmikus háttérsugárzás egy 3 kelvinhez közeli hőmérsékletű feketetest-sugárzás.

E ponton az olvasó föltehetné a kérdést: miért nem kerülték meg ezt a problémát egyszerűen azzal, hogy az infravörösészlelő berendezést egy mesterséges holddal a légkör fölé emeljék, és így végezzék el a mérést. Magam sem tudom, miért lenne ez lehetetlen. Azt szokták ugyan mondani, hogy a 3 kelvines hőmérséklet olyan alacsony, hogy az azt mérő berendezést folyékony héliummal kell hűteni, és a hűtőberendezés mesterséges holdon való szállításának még nincs meg a kialakult technológiája. Én mégis úgy vélem hogy itt inkább pénzkérdésről van szó, és bizony az űrkutatás költségvetéséből nagyobb összegeket is áldozhatnának a kozmológiai kutatásokra.

Még nagyobbnak tűnik a Föld légköre fölött végzett megfigyelések jelentősége akkor, ha a kozmológiai eredetű sugárzási háttérnek nemcsak a hullámhossztól, de az iránytól való függését is tanulmányozni kívánjuk. Ez idáig minden megfigyelés összefér azzal a feltételezéssel, hogy a sugárzási háttér teljesen izotrop, azaz iránytól független. Mint azt már az előző fejezetben is említettem, éppen ez az egyik legnyomósabb érv a Kozmológiai Elv érvényessége mellett. Mindazonáltal, nagyon nehéz lenne megkülönböztetni a kozmikus sugárzási háttér esetleges irányfüggését a Föld légkörétől eredő irányfüggő hatásoktól. Sőt, amikor a sugárzási háttér hőmérsékletét mérik, azt éppen úgy választják el a légköri sugárzásoktól, hogy feltételezik a sugárzási háttér izotrop eloszlását.

A mikrohullámú sugárzási háttér irányfüggésének tanulmányozása azért is nagyon izgalmas, mert sokan feltételezik, hogy annak intenzitása nem teljesen izotrop, hanem lehetnek benne kisebb irányfüggő fluktuációk, amelyeket a Világegyetem tömegeloszlásának egyenetlenségei okozhattak a sugárzás kibocsátásakor vagy az azóta eltelt idők során. Például a galaxisok kiformálódásuk idején olyan meleg foltokként jelenhettek meg az égen, melyeknek kiterjedése meghaladhatta a fél szögpercet, és sugárzásuk is az átlagosnál jóval magasabb hőmérsékletű feketetest-sugárzással lehetett ekvivalens. Ehhez hozzájárulhat még a sugárzási intenzitásnak egy kisebb mérvű folytonos változása is, amit a Föld mozgása okoz. A Föld 30 kilométer/másodperc sebességgel kering a Nap körül, míg maga a Naprendszer a Galaktika középpontja körül 250 kilométer/másodperc sebességgel forog. Azt senki sem tudja pontosan, hogy mekkora lehet Galaktikánknak a tipikus galaxisok eloszlásához viszonyított sebessége, de feltehetőleg az is eléri a néhány száz kilométer/másodpercet valamely irányban. Ha például feltételezzük, hogy a Föld 300 kilométer/másodperc sebességgel mozog az Univerzum anyagához – s így a sugárzási háttérhez – képest, akkor a Föld mozgásirányához képest elölről, illetve hátulról érkező sugárzás hullámhossza a 300 kilométer/másodperc és a fénysebesség arányában, vagyis 0,1 százalékkal lecsökken vagy megnő. így a sugárzási hőmérséklet is gyengén változhat az iránnyal: a Föld mozgásirányában 0,1 százalékkal nagyobb, az ellenkező irányban pedig 0,1 százalékkal kisebb az átlagosnál. Az elmúlt néhány évben az ekvivalens sugárzási hőmérséklet irányfüggésére kapott legjobb felső korlát is éppen 0,1 százalék, vagyis éppen a határán vagyunk annak, hogy mérni tudjuk a Föld mozgásának sebességét az Univerzumon keresztül. Ez a kérdés azonban nem oldható meg mindaddig, amíg nem tudjuk a méréseket a Föld körül keringő műholdakról is elvégezni. [E könyv utolsó korrektúrájának olvasása közben kaptam meg John Mathertől (NASA) a Kozmikus hátteret kutató műholdak című kiadványt. Ebben bejelentik egy hatfős kutatócsoport felállítását Rainer Weiss (MIT) vezetésével, amelynek feladata az, hogy megállapítsa, milyen lehetőségei vannak az infravörös és a mikrohullámú háttérsugárzás űrbéli tanulmányozásának. Jó munkát!]

Láttuk, hogy a kozmikus mikrohullámú háttérsugárzás létezése erőteljesen alátámasztja azt a feltételezést, hogy az Univerzum töltött részecskéi és sugárzása egymással valamikor hőmérsékleti egyensúlyban álltak. Ám mindeddig nem sok kozmológiai következtetést vontunk le az ekvivalens sugárzási hőmérséklet konkrét, 3 kelvines értékéből. Pedig ennek ismerete lehetővé teszi, hogy meghatározzuk azt az egyetlen, döntően fontos számadatot, amire szükségünk lesz ahhoz, hogy az első három perc történetét végigkövessük.

Láttuk, hogy bármely adott hőmérsékleten az egységnyi térfogatban levő fotonok száma egy tipikus hullámhosszérték köbével fordítottan arányos, s ezért a hőmérséklet köbével egyenes arányban áll. 1 kelvinen 1 literre 20 282,9 foton jut, így tehát a 3 kelvines sugárzási háttér literenként körülbelül 550 000 fotont tartalmaz. Ugyanakkor a nukleonok (neutronok és protonok) sűrűsége a mai Univerzumban 6 és 0,03 részecske közé esik ezer literenként. (A felső határ a II. fejezetben tárgyalt kritikus sűrűség kétszerese; az alsó határ pedig a látható galaxisok megfigyelt sűrűségének alsó korlátja.) így a részecskesűrűség jelenlegi értékétől függően a mai Univerzumban az egy nukleonra jutó fotonok száma 100 millió és 20 milliárd közé esik.

Ráadásul a fotonoknak ilyen túlsúlya a nukleonokhoz képest hosszú ideje gyakorlatilag állandónak tekinthető. A sugárzás szabad tágulásának időszaka alatt (vagyis amióta a hőmérséklet 3000 kelvin alá esett) sem háttérfotonok, sem magrészecskék nem keletkeztek, és nem is nyelődtek el, így természetesen arányuk is változatlan maradt. A következő fejezetben látni fogjuk, hogy ez az arány már jóval ezt megelőzően is gyakorlatilag állandó volt, akkor is, amikor még a fotonok keletkezése és elnyelődése nagy gyakorisággal fordult elő.

A legfontosabb mennyiségi következtetés tehát, ami a mikrohullámok sugárzásiháttér-méréséből levonható: amilyen messzire csak vissza tudunk tekinteni, az Univerzum történetének korai szakaszaiban a fotonok és magrészecskék aránya mindig 100 millió és 20 milliárd közé esett. A továbbiakban, hogy a szükségtelen kétértelműséget elkerüljem, ezt a számot szemléltetési célokra 1 milliárdnak fogom tekinteni, vagyis feltételezem, hogy a fotonok és a magrészecskék aránya mind most, mind a múltban 1 milliárd volt.

E következtetésnek nagyon fontos következménye az, hogy az atomos anyag csillagokba és galaxisokba való tömörülése mindaddig nem kezdődhetett meg, amíg a hőmérséklet nem csökkent le annyira, hogy az elektronok befogódhassanak az atomokba. Ahhoz, hogy a gravitáció csomókba gyűjthesse az anyagot – mint azt Newton elképzelte –, az szükséges, hogy a gravitáció fölülmúlja a sugárzás és a többi részecske együttes nyomását. Minden születő anyagcsomóban a csomó méretével együtt nő a gravitációs erő, a nyomás azonban nem függ a mérettől; ezért minden sűrűség- és nyomásértékhez létezik egy olyan minimális tömeg, amely a gravitációs csomósodás megindulásához szükséges. Ezt „Jeans-tömeg” néven ismerik, mivel Sir James Jeans használta először 1902-ben, a csillagok kialakulására vonatkozó elméletében. Később kiderült, hogy a Jeans-tömeg a nyomás kétharmadik hatványával arányos. (L. a Matematikai jegyzetek 5. pontját a 151. oldalon.) Nem sokkal azelőtt, hogy az elektronok számára lehetővé vált, hogy az atommagokhoz kapcsolódva atomokat építsenek fel, mintegy 3000 kelvines hőmérsékleten a sugárzási nyomás még mértéktelenül nagy volt, így ennek megfelelően nagy volt a Jeans-tömeg is: mintegy milliószorosa egy nagy galaxis tömegének. A mai galaxisok, de még a galaxishalmazok is túlságosan kicsik ahhoz, hogy akkoriban formálódhattak volna. Ám nem sokkal később az elektronok és atommagok atomokká kezdtek egyesülni, s ezzel egyidejűleg eltűntek a szabad elektronok: az Univerzum a sugárzás számára átlátszóvá vált, s így a sugárzási nyomás hatástalan lett. Adott hőmérsékleten és sűrűség mellett az atomos anyag, illetőleg a sugárzás nyomása egyszerűen a részecskék (például sugárzásnál a fotonok) számával arányos; így amikor a sugárnyomás megszűnt, a hatásos nyomás mintegy egymilliárdod részére csökkent. A Jeans-féle tömeg ennek 3/2-ik hatványa szerint változott, s így egy galaxis minimális méretének mintegy egymilliomod részére csökkent. Ettől kezdve pedig az anyag nyomása már túlságosan kicsi volt ahhoz, hogy megakadályozza a gravitációt abban, hogy az égen ma látható galaxisok őseit jelentő anyagcsomókat megteremtse.

Nem akarom persze azt a hitet kelteni, hogy ma már pontosan tudjuk, hogyan alakultak ki a galaxisok. A galaxisok kialakulásának elmélete az asztrofizika egyik legnagyobb megoldatlan problémája, olyan kérdés, amelynek megválaszolásától ma még nagyon messze vagyunk. Ám ez más lapra tartozik. Számunkra itt most csak az a fontos, hogy az Univerzum kezdeti szakaszában, amikor a hőmérséklet alig valamivel haladta meg a 3000 kelvint, az Univerzum nem csillagokból és galaxisokból állt, ahogy azt ma látjuk az égen, hanem az ionizált anyag (plazma) és a sugárzás ekkor egy differenciálatlan, sűrű őslevessé olvadt össze.

A fotonok óriási túlsúlya a magrészecskékkel szemben még egy figyelemre méltó következménnyel jár: emiatt ugyanis lennie kellett egy olyan időszaknak – viszonylag nem is olyan nagyon régen –, amikor a sugárzás energiája felülmúlta az Univerzum atomos anyagában fölhalmozott energiát. Az egy magrészecske nyugalmi tömegének megfelelő energia Einstein képlete szerint E–mc², ami mintegy 939 millió elektronvolt. A 3 kelvines feketetest-sugárzás fotonjainak átlagos energiája ennél jóval kisebb, körülbelül 0,0007 elektronvolt, tehát még ha a fotonok és a magrészecskék számaránya 1 milliárd körül is van, ma az Univerzum energiájának túlnyomó része az anyagban összpontosul. Ám régebben, amikor még a hőmérséklet magasabb volt – s ennek megfelelően nagyobb volt az egyes fotonok energiája –, a sugárzás energiája fölülmúlhatta az ionizált atomos anyagét (mivel ez utóbbi mindig ugyanakkora maradt). így az egymilliárdos arányt elfogadva, ahhoz, hogy a sugárzási energia felülmúlja az atomos anyagban tárolt energiát, az szükséges, hogy a feketetest-sugárzás fotonjainak átlagos energiája a nukleontömeg milliárdod részénél nagyobb legyen, vagyis elérje az 1 elektronvoltot. Ez akkor következett be, amikor a hőmérséklet mintegy 1300-szorosa volt a mainak, vagyis mintegy 4000 kelvin volt. Ennél a hőmérsékletnél következett be az átmenet az úgynevezett „sugárzási korszak"-ból – amikor az Univerzum energiájának túlnyomó részét a sugárzás adta – a mai, „atomos anyag korszak”-ba, amelyben az energia túlnyomó része a nukleonok tömegében testesül meg.

Szembeötlő, hogy a sugárzási korszakból az atomos korszakba vezető átmenet csaknem ugyanakkor következett be, amikor az Univerzum a sugárzás számára átlátszóvá vált: mintegy 3000 kelvinen. Azt igazából senki sem tudja, hogy miért van ez így, bár vannak érdekes föltevések. Igazából még azt sem tudjuk pontosan, hogy melyik átmenet ment végbe előbb: ha ma a fotonok száma 10 milliárdszor akkora, mint a nukleonoké, akkor a sugárzás mintegy 400 kelvinig dominál az atomos anyag fölött, vagyis jóval tovább annál az időpontnál, amikor az Univerzum a sugárzás számára átlátszóvá vált.

Ám mindezek a bizonytalanságok nem akadályozzák meg azt, hogy a Világegyetem történetének korai szakaszát tanulmányozhassuk. Számunkra most csupán annyi fontos, hogy bármely olyan időpontban, amely jóval megelőzi az Univerzum átlátszóvá válását, a Világegyetem úgy tekinthető, mint ami túlnyomórészt sugárzásból áll, s benne az atomos anyag mennyisége elenyésző szennyeződés csupán. A korai Univerzum sugárzásának roppant energiasűrűsége aztán az Univerzum tágulása során a fotonhullámhosszak vöröseltolódásának következtében nagymértékben csökkent, utat nyitva így a magrészecskéknek és elektronoknak ahhoz, hogy létrehozzák a mai Világegyetem csillagait és galaxisait.

 

IV A forró Világegyetem receptje

 

Az előző két fejezetben leírt megfigyelések feltárták, hogy az Univerzum egyre tágul, és egy olyan egyetemes háttérsugárzás tölti be, amelynek hőmérséklete ma 3 kelvin körül van. Úgy tűnik, ez a sugárzás olyan időkből maradt fenn, amikor a Világegyetem gyakorlatilag átlátszatlan volt, és mintegy ezerszer kisebb és forróbb, mint ma. (Mint eddig is, amikor azt mondjuk, hogy az Univerzum ezerszer kisebb volt, mint ma, az egyszerűen azt jelenti, hogy bármely két tipikus galaxis közti távolság a mai érték ezredrésze volt.) Ahhoz, hogy az első három perc történetéről beszámolhassunk, még egy utolsó előkészületet kell tennünk. Olyan – még korábbi – időszakokra kell visszatekintenünk, amikor a Világegyetem még az előbb említettnél is jóval kisebb és forróbb volt. Ehhez a visszatekintéshez azonban már sem a szemünket, sem az optikai vagy rádiótávcsöveket nem használhatjuk; az elméletet kell segítségül hívnunk, hogy az ekkor érvényesülő fizikai körülményeket megvizsgálhassuk.

A III. fejezet végén említettük, hogy akkor, amikor az Univerzum jelenlegi méreténél ezerszerte kisebb volt, és anyagtartalma épp azon a határon járt, hogy a sugárzás számára átlátszóvá váljék, a Világ-egyetem még egy döntő változáson ment keresztül: a sugárzási korszakból a jelenlegi, anyagdominált korszakba lépett át. A sugárzási korszakban – csakúgy, mint ma – a fotonok száma messze meghaladta a magrészecskék számát, de ezen túlmenően még az egyes fotonok energiája is elég nagy volt ahhoz, hogy a Világegyetem energiájának túlnyomó része a sugárzásban – s nem a nehéz magrészecskékben – testesüljön meg. (Emlékeztetőül: a fotonok nyugalmi tömeg nélküli részecskék vagy „kvantumok”, a kvantumelmélet szerint belőlük tevődik össze a fény.) Ezért, jó közelítéssel úgy tekinthetjük, mintha ebben a korszakban a Világegyetemet tisztán sugárzás töltené ki, s nehéz részecskékből adódó atomalkotó anyag gyakorlatilag nem lenne benne.

Ám ehhez a következtetéshez egy lényeges módosítást kell még hozzátennünk. Ebben a fejezetben látni fogjuk majd, hogy a tiszta sugárzási korszak csak az első néhány perc eltelte után kezdődött meg, amikor a hőmérséklet már néhány milliárd fok alá esett. Ennél korábbi időszakokban a nehéz részecskékből adódó anyag fontos volt, bár formája nagyon különbözött attól, amit a mai Világegyetem atomjaiban megszoktunk. De mielőtt ilyen messzire visszatekintenénk, tekintsük át röviden az igazi sugárzási korszakot, az első néhány perc eltelte után egészen addig az időpontig, amíg – néhány százezer évvel később – az atomos anyag vette át az uralkodó szerepet.

Ahhoz, hogy a Világegyetem történetének e korszakát végigkövethessük, mindössze a mindenkori hőmérsékletet kell ismernünk. Vagy – más oldalról közelítve a kérdést – azt kell tudnunk, miként viszonylik az Univerzum hőmérséklete annak méretéhez a tágulás során?

Ez utóbbi kérdésre könnyen válaszolhatnánk, ha a sugárzást szabadon tágulónak tekinthetnénk. Akkor ugyanis minden egyes foton hullámhossza az Univerzum tágulásának arányában nyúlna (vöröseltolódás). Másrészt az előző fejezetben láttuk, hogy a feketetest-sugárzás átlagos hullámhossza a hőmérséklettel fordítottan arányos. Következésképp a hőmérséklet az Univerzum méretével fordított arányban csökkenne, csakúgy, mint ma.

Az elméleti kozmológusok szerencséjére, ugyanez az egyszerű összefüggés érvényesül akkor is, ha tekintetbe vesszük, hogy a sugárzás valójában nem szabadon tágult – ugyanis a fotonok szaporán ütköztek a viszonylag kisszámú elektronnal és magrészecskével, amelyek a sugárzási korban a Világegyetemet átlátszatlanná tették. Amíg egy-egy foton az ütközések között szabadon röpült, addig hullámhossza az Univerzum méreteivel arányosan változott; a fotonok száma pedig annyira meghaladta az egyéb részecskék számát, hogy az ütközések a sugárzás hőmérsékletét kényszerítették rá a nehéz részecskék anyagára is, nem pedig megfordítva. így amikor a Világegyetem például mai méreteinél tízezerszerte kisebb volt, ugyanilyen arányban melegebb volt a mainál, tehát hőmérséklete 30 000 kelvin volt.

Ám ahogy egyre visszább és visszább tekintünk az Univerzum múltjában, végül is elérünk egy olyan időpillanatot, amikor a hőmérséklet már olyan magassá vált, hogy a fotonok egymással való ütközései a tiszta sugárzásból nehezebb részecskéket teremthettek. Ki fog derülni, hogy a sugárzásból keletkezett nehezebb részecskék az első néhány percben ugyanolyan fontosak voltak, mint maga a sugárzás; döntő szerepet játszottak mind a különféle magreakciók mértékének, mind az Univerzum tágulási ütemének a meghatározásában. így ahhoz, hogy valóban korai időpontokra követni tudjuk az események lefolyását, először is tudnunk kell azt, hogy milyen forrónak kellett lennie a Világegyetemnek ahhoz, hogy a sugárzási energia rovására nehezebb részecske keletkezhessék, és azt is, hogy ily módon mennyi nehezebb részecske keletkezhetett.

Az a folyamat, melynek révén a sugárzásból nehezebb részecskék keletkezhetnek, a kvantumelmélet alapján érthető meg. Két fénykvantum (foton) ütközhet és eltűnhet oly módon, hogy energiájuk és lendületük (impulzusuk) két vagy több anyagi részecske keltésére fordítódik. (Ezt a folyamatot meg is figyelik a mai nagyenergiájú részecskefizikai laboratóriumokban.) Azonban Einstein speciális relativitáselmélete szerint még nyugvó atomi részecskének is van egy bizonyos „nyugalmi energiája”, amelynek nagyságát a nevezetes E = mc² összefüggés adja meg. (c a fénysebesség. Ez a nyugalmi energia a forrása a magreakciókban fölszabaduló energiának; e folyamatokban elvész az atommagok nyugalmi tömegének egy része.) Ezért ahhoz, hogy két szembeütköző foton m nyugalmi tömegű részecskét kelthessen, mindkét foton energiája legalábbis egyenlő kell legyen a részecskék mc² nyugalmi energiájával. Természetesen a reakció akkor is végbemegy, ha az ütköző fotonok mc²-nél nagyobb energiájúak: ekkor az energiatöbblet arra fordítódik, hogy az atomi részecskék sebességét növelje. Viszont, ha a fotonok energiája mc²-nél kisebb, akkor ez még ahhoz sem elegendő, hogy a részecskék m nyugalmi tömegét fedezze, így ilyen részecskék e két foton ütközéséből nem keletkezhetnek.

Nyilvánvaló tehát, hogy csak akkor tudjuk megítélni, hogy a sugárzás milyen hatékonyan kelthet más részecskéket, ha ismerjük a sugárzás egyedi fotonjainak jellemző energiáját. Ezt pedig – céljainkhoz elegendő pontossággal – egy egyszerű becsléssel kaphatjuk meg: az átlagos fotonenergia egyenlő a hőmérsékletnek és a statisztikus fizika alapvető állandójának, az úgynevezett Boltzmann-állandónak a szorzatával. (Az amerikai Willard Gibbs mellett az osztrák Ludwig Boltzmann volt a statisztikus fizika egyik megalkotója. Úgy mondják, 1906-ban elkövetett öngyilkosságát nagyrészt a munkájával szembeni filozófiai támadások okozták.) A Boltzmann-állandó értéke 0,000 086 17 elektronvolt/kelvin. így például 3000 kelvin hőmérsékleten, ahol a Világegyetem anyaga a fény számára épp átlátszóvá válik, a fotonok karakterisztikus energiája 3000 kelvin és a Boltzmann-állandó szorzata, vagyis 0,26 elektronvolt. (Emlékeztetőül: 1 elektronvolt az az energia, amelyre egy elektron 1 volt feszültség befutása során szert tesz. A kémiai reakciók energiája nagyságrendileg atomonként 1 elektronvolt, és ez az oka annak, hogy 3000 kelvin felett a sugárzás az elektronok jelentékeny részét képes visszatartani attól, hogy az atomokba beépüljön.)

Láttuk, hogy a fotonok ütközéseiben csak akkor keltődhetnek más részecskék, ha a karakterisztikus fotonenergia legalább az mc² értéket eléri. Mivel pedig a karakterisztikus fotonenergia egyenlő a Boltzmann-állandó és a hőmérséklet szorzatával, ebből az következik, hogy a sugárzás hőmérsékletének legalább akkorának kell lennie, mint a kérdéses részecske mc² nyugalmi energiája, osztva a Boltzmann-állandóval. Vagyis, a különféle anyagi részecskéknek van egy úgynevezett „küszöbhőmérséklet”-ük: a megfelelő típusú részecskék csak e hőmérséklet fölött keletkezhetnek sugárzásból. A küszöbhőmérsékletet úgy számíthatjuk ki, hogy az mc² nyugalmi energiát osztjuk a Boltzmann-állandóval.

A fotonnál nehezebb részecskék közül az elektron (e^-) és a pozitron (e⁺) a legkönnyebbek. A pozitron az elektron antirészecskéje – vagyis elektromos töltése ellentétes (negatív helyett pozitív), de a tömege és a perdülete (spinje) megegyezik az elektronéval. Amikor egy pozitron egy elektronnal ütközik, töltéseik semlegesítik egymást, és a két részecske nyugalmi tömegében rejlő energia tiszta sugárzássá olvad össze. Ez az oka annak, hogy a pozitronok oly ritkák környezetünkben – nagyon hamar találkoznak elektronnal, és szétsugárzódnak. (A pozitronokat a kozmikus sugárzásban találták meg 1932-ben.) Ez a sugárzási folyamat fordítva is lejátszódhat. Ha két alkalmas energiájú foton ütközik, elektron-pozitron pár keletkezhet, a fotonok energiája az elektron és pozitron nyugalmi energiájává alakul.

A szembeütköző fotonok csak akkor kelthetnek elektron-pozitron párt, ha mindkét foton energiája meghaladja az elektron és a pozitron mc² nyugalmi energiáját. Ez az energia 0,511 0003 millió elektronvolt. Ahhoz, hogy megkapjuk azt a küszöbhőmérsékletet, amelynél a fotonok már nagy valószínűséggel rendelkeznek ekkora energiával, a nyugalmi energiát el kell osztani a Boltzmann-állandóval. Ennél magasabb hőmérsékleteken a fotonok egymással való ütközései már számos elektron-pozitron párt kelthetnek – amik így nagy számban keletkeznek is. (Egyébként ez a küszöbhőmérséklet 6 milliárd fok, ami jóval magasabb a mai Világegyetemben előforduló legmagasabb hőmérsékleteknél. Még a Nap középpontja is csupán mintegy 15 millió fokos. Ez az oka annak, hogy manapság nemigen találkozunk azzal a jelenséggel, hogy fény hatására az üres térben elektron-pozitron párok keletkeznek.)

Hasonló megjegyzések érvényesek más típusú részecskékre is. A modern fizika egyik alaptörvénye, hogy minden részecskének létezik a megfelelő antirészecskéje a természetben, amelynek pontosan azonos a nyugalmi tömege és a spinje, de ellentétes az elektromos töltése. E szabály alól kivételt csak az elektromosan semleges részecskék képezhetnek, mint például a foton, amelyet úgy lehet tekinteni, mint önmaga antirészecskéjét. A részecske és antirészecske kapcsolata kölcsönös és megfordítható: a pozitron az elektronnak az antirészecskéje, az elektron pedig a pozitroné. Ha az energia elegendő hozzá, fotonok ütközésében bármilyen részecske-antirészecske pár keletkezhet.

(Az antirészecskék létezése közvetlen matematikai következménye a kvantummechanikának és Einstein speciális relativitáselméletének. Az antielektron létezését elméletileg először Paul Adrien Maurice Dirac jósolta meg 1930-ban. Mivel elméletébe nem akart ismeretlen részecskét bevezetni, az antielektront az akkor ismert egyetlen pozitív töltésű részecskével – a protonnal – próbálta azonosítani. Az antirészecskék elméletét a pozitron 1932-es fölfedezése igazolta, és egyúttal azt is megmutatta, hogy nem a proton az elektron antirészecskéje. Később, 1950-ben a proton antirészecskéjét, az antiprotont is sikerült előállítani Berkeleyben.)

Az elektron és a pozitron után a legkönnyebb részecske a müon, jele: μ^- Ez egy instabil nehéz elektron; antirészecskéje a m⁺ – Csakúgy, mint az elektron és a pozitron esetében, a kétféle müon elektromos töltése ellenkező előjelű, de tömegük és spinjük egyenlő, és szintén keletkezhetnek fotonok ütközéseiben. A müonok nyugalmi energiája mc² = 105,6596 megaelektronvolt; ezt elosztva a Boltzmann-állandóval, a küszöbhőmérséklet 1,2 milliószor millió foknak (1,2 billió foknak, 1,2 • 10¹² kelvinnek) adódik. Más részecskékre a megfelelő küszöbhőmérsékletet az I. táblázatban (135. oldal) adtuk meg. Megvizsgálva ezt a táblázatot, meg tudjuk mondani, hogy az Univerzum történetének különböző időszakaiban mely részecskék lehettek jelen nagy számban: azok ugyanis, amelyeknek a küszöbhőmérséklete kisebb volt, mint az Univerzum akkori hőmérséklete.

De ezek az anyagi részecskék milyen mennyiségben voltak ténylegesen jelen a küszöbhőmérséklet fölött? – Ezt az Univerzum korai szakaszában uralkodó magas hőmérséklet és sűrűség viszonyai között a hőmérsékleti egyensúly alapfeltétele szabja meg: a részecskék számának elegendő nagynak kell lennie ahhoz, hogy minden másodpercben ugyanannyi részecske sugárzódjék szét, mint amennyi keletkezett. (Azaz, legyen megfelelő készlet.) Annak valószínűsége, hogy egy adott részecske-antirészecske pár fotonokká sugárzódjék szét, megegyezik annak valószínűségével, hogy egy ugyanilyen energiájú fotonpár részecske-antirészecske párt keltsen. Ebből következik, hogy a hőmérsékleti egyensúly csak akkor állhat fenn, ha azon részecskék száma, amelyeknek a küszöbhőmérséklete az Univerzum pillanatnyi hőmérsékleténél kisebb, egyenlő a fotonok számával. Ha ugyanis e részecskék száma kisebb, mint a fotonoké, akkor gyorsabban keletkeznek, mint amilyen gyorsan szétsugárzódnak, és így számuk növekedni fog; ha pedig több részecske van, mint amennyi foton, akkor gyorsabban sugárzódnak szét, mint amilyen gyorsan keletkeznek, és ekkor számuk csökkenni fog. Például 6 millió fokos hőmérséklet fölött az elektronok és pozitronok számának meg kell egyeznie a fotonok számával: az Univerzum ebben az időszakban úgy tekinthető, mint ami túlnyomórészt fotonokat, elektronokat és pozitronokat tartalmaz.

Ám a küszöbhőmérséklet fölötti hőmérsékleteken a nehezebb részecskék is a fotonokhoz hasonlóan viselkednek. Átlagos energiájuk hozzávetőlegesen a Boltzmann-állandószor a hőmérséklet, ami – jóval a küszöbhőmérséklet felett – messze meghaladja a nyugalmi energiát, s ezért a részecskék nyugalmi energiája, s így nyugalmi tömege is elhanyagolhatóvá válik. Ilyen feltételek mellett az adott típusú anyagi részecskék nyomása és energiasűrűsége egyszerűen a hőmérséklet negyedik hatványával arányos, akárcsak a fotonok esetében. így bármely adott időpillanatban úgy tekinthetjük az Univerzumot, mint ami különböző fajta „sugárzások”-ból áll, minden sugárzástípusnak megfelel egy bizonyos fajta részecske, amelynek a küszöbhőmérséklete alacsonyabb a Világegyetem adott pillanatbeli hőmérsékleténél. Ilyen fizikai feltételek – vagyis olyan magas hőmérséklet, amelyen a részecske-antirészecske párok gyakorisága a fotonokéval megegyezik – a mai Univerzumban nem léteznek (kivéve talán az éppen szétrobbanó csillagok magját). Mégis bízunk annyira a statisztikus mechanika elméletében, hogy arra alapozva megpróbáljunk visszakövetkeztetni, mi is történhetett ilyen egzotikus feltételek között.

A Világegyetem energiasűrűségének meghatározásához még néhány szabályt kell ismernünk. Először is azt, hogy a részecskefajták összeszámlálásánál az antirészecskék (mint például a pozitron) külön fajtának számítandók. Továbbá az olyan részecskéket, amelyek két különböző spinállapotban létezhetnek – mint például a foton vagy az elektron –, a különböző állapotok száma szerint kell számba venni. Végül, az elektronhoz hasonló részecskék egy speciális szabálynak, a „Pauli-elv”-nek engedelmeskednek, amely megtiltja, hogy két azonos fajta részecske minden tekintetben azonos kvantumállapotban legyen. Ez a kizárási elv lényegében egy 7/8-os tényezővel csökkenti az ilyen részecskék járulékát a teljes energiasűrűséghez. (A Pauli-féle kizárási elv teszi lehetetlenné azt, hogy az atomok valamennyi elektronja ugyanabba a legmélyebb energiájú állapotba essen, s így végső soron ennek köszönhető az elemek periódusos rendszerébe foglalt atomok bonyolult héjszerkezete.) Az I. táblázatban (135. oldal) felsoroltuk a különböző részecskék effektív állapotszámát és a küszöbhőmérsékleteket. Az Univerzum energiasűrűsége adott hőmérsékleten a hőmérséklet negyedik hatványával és azon részecskék effektív állapotszámával arányos, amelyek küszöbhőmérséklete a Világegyetem adott pillanatbeli hőmérsékleténél kisebb.

Most már csak az a kérdés, hogy valójában mikor érte el az Univerzum ezeket a hihetetlenül magas hőmérsékleteket. Az Univerzum tágulásának ütemét a gravitációs tér és az anyagáramlás kifelé mutató lendületének (impulzusának) egyensúlya szabja meg. Az Univerzum korai szakaszában a gravitációs tér forrása a fotonok, elektronok, pozitronok stb. teljes energiasűrűsége volt. Mivel a Világegyetem energiasűrűsége lényegében a hőmérséklettől függ, ezért a kozmikus hőmérséklet egyfajta „óramutató”-ként használható, az idő múlását nem egy óra ketyegése, hanem az anyag hűlése jelzi. Pontosabban: kimutatható, hogy az az idő, ami ahhoz szükséges, hogy az Univerzum energiasűrűsége egy megadott értékről egy másik meghatározott értékre csökkenjen, arányos az energiasűrűségek reciprok négyzetgyökének különbségével. (L. a Matematikai jegyzetek 3. pontját, a 146. oldalon.) Másrészt azonban láttuk, hogy maga az energiasűrűség a hőmérséklet negyedik hatványával és azon részecskék effektív állapotszámával arányos, amelyeknek küszöbhőmérséklete az Univerzum hőmérsékleténél kisebb. így mindaddig, amíg a hőmérséklet nem keresztezi egyik küszöbértéket sem, az az idő, ami ahhoz szükséges, hogy a Világegyetem egy meghatározott hőmérsékletértékről egy másik adott hőmérsékletre hűljön le, arányos e hőmérsékletek reciprok négyzetgyökeinek különbségével. Például, ha 100 millió fokos hőmérsékletről indulunk (ami az elektronok küszöbhőmérsékleténél jóval kisebb), akkor azt kapjuk, hogy 0,06 év (vagyis 22 nap) szükséges ahhoz, hogy a hőmérséklet 10 millió fokra csökkenjen, majd további 6 év alatt a Világegyetem hőmérséklete 1 millió fokra csökken, újabb 600 év alatt 100 000 fokra és így tovább. Ahhoz hogy az Univerzum 100 millió fokról 3000 kelvinre hűljön (vagyis addig a hőmérsékletig, amikor az Univerzum anyaga a sugárzás számára átlátszóvá vált), összesen 700 000 évre volt szükség. (L. a 8. ábrát.) Amikor én itt „éveket” említek, akkor persze egy bizonyos számú abszolút időegységet értek ezen, amit például a hidrogénatomban keringő elektron periódusidejével definiálhatunk – jóllehet ekkor még sem hidrogén, sem a Föld vagy a Nap nem létezett.

Ha az első néhány percben a Világegyetem pontosan egyenlő számban tartalmazott volna részecskéket és antirészecskéket, akkor – amint a hőmérséklet 1 milliárd fok alá csökkent – ezek mind szétsugárzódtak volna, nem hagyván mást hátra, mint tiszta sugárzást. Cáfolhatatlan bizonyítékunk van e lehetőség kizárására – saját létezésünk! Ahhoz ugyanis, hogy a részecskék és antirészecskék szétsugárzása után valami is megmaradjon, ami aztán a jelenlegi Világ-egyetem anyagát szolgáltathatja, a pozitronoknál egy kicsit több elektronnak, az antiprotonoknál több protonnak, és az antineutronoknál több neutronnak kellett lennie. E fejezetben mindeddig elhanyagoltam e fennmaradó anyag viszonylag kis hányadát. Ez jó közelítés akkor, ha csupán a korai Univerzum energiasűrűségét vagy tágulásának mértékét akarjuk meghatározni: az előző fejezetben láttuk, hogy mindaddig, amíg az Univerzum 4000 kelvin alá nem hűl, az atomi részecskék energiasűrűsége elhanyagolható a sugárzás energiasűrűségéhez képest. Mindazonáltal az elektronok és a magrészecskék e visszamaradó hányada megkülönböztetett figyelmet érdemel, hiszen döntő szerepet játszik a jelenlegi Univerzum felépítésében, és – ez sem lényegtelen szempont! – ebből adódnak a szerző és az olvasó fő alkotóelemei is.

 

 

8. ábra. A sugárzás által dominált korszak. Az ábrán az Univerzum hőmérsékletét tüntettük fel az idő függvényében arra az időszakra, amely az atommagok szintézisének befejeztétől az atommagok és elektronok atommá történő kapcsolódásáig terjed.

 

Amint elfogadjuk annak lehetőségét, hogy az első néhány percben a közönséges anyag mennyisége felülmúlhatta az antianyagét, máris fölvetődik az az újabb probléma, hogy meg kell határoznunk az Univerzum alkotóelemeinek részletes listáját. A Lawrance Laboratórium (Berkeley) félévenként kiadott táblázatában több száz úgynevezett elemi részecske szerepel. Vajon e részecskék összes fajtájának a részarányát meg kell állapítanunk? És miért állnánk meg e részecskéknél? Talán meg kell határoznunk a belőlük összetett különféle atomok és molekulák, a só és a bors arányát is? Ebben az esetben joggal jelenthetnénk ki, hogy a Világegyetem túlságosan bonyolult ahhoz, semhogy érdemes lenne megismernünk.

Szerencsére az Univerzum korántsem ilyen bonyolult. Hogy összetételének „receptjét” megadhassuk, a hőmérsékleti egyensúly feltételeit kell kicsit alaposabban ismernünk. Már korábban is hangsúlyoztam, hogy mennyire fontos az a körülmény, hogy az Univerzum hőmérsékleti egyensúlyi állapotokon keresztül fejlődött – ez teszi lehetővé, hogy az Univerzum összetételét bármely időpillanatban kellő biztonsággal megadhassuk. Már eddigi fejtegetéseink során is felhasználtuk a hőmérsékleti egyensúlyban levő részecskék és a sugárzás néhány ismert tulajdonságát.

Amikor az ütközések vagy más folyamatok egy anyagi rendszerben termodinamikai egyensúlyt hoznak létre, mindig van a rendszernek néhány olyan tulajdonsága, amelyek e folyamatok során nem változnak. E „megmaradó mennyiségek” egyike a teljes energia: jóllehet egyes ütközésekben egyik részecske energiát ad át a másiknak, az ütközésekben részt vevő valamennyi részecske összes energiája változatlan marad. Nyilvánvalóan következik ebből, hogy mivel e mennyiségek értéke a termikus egyensúlyban levő rendszerben nem változik, nem is lehet őket az egyensúly feltételeiből meghatározni, hanem értéküket előre meg kell adni. Vagyis minden megmaradási törvényhez tartozik egy olyan megmaradó mennyiség, amelynek értékét előre meg kell szabni. Ám ha már egyszer valamennyi megmaradó mennyiség értékét rögzítettük, akkor a hőmérsékleti egyensúlyban levő rendszer összes tulajdonsága egyértelműen meghatározottá válik. Mivel a Világegyetem hőmérsékleti egyensúlyi állapotokon keresztül fejlődött, így ahhoz, hogy a korai Univerzum összetételét megadhassuk, azt kell tudnunk, hogy mely fizikai mennyiségek maradtak meg a tágulás során, és mekkora volt ezek kezdeti értéke.

A hőmérsékleti egyensúlyban levő rendszer teljes energiatartalmát szokásosan a hőmérsékletével adjuk meg. Az olyan fajta rendszerek esetén, mint amilyenekkel mostanáig foglalkoztunk – amik csak sugárzásból, valamint egyenlő számú közönséges részecskéből és antirészecskéből állnak a hőmérséklet az egyetlen olyan adat, amit meg kell adnunk ahhoz, hogy a rendszer egyensúlyi tulajdonságait meghatározzuk. Általában azonban az energia mellett még más megmaradó mennyiségek is vannak, és ezek mindegyikét előre meg kell adnunk.

Például egy pohár szobahőmérsékletű vízben folytonosan olyan reakciók mennek végbe, melyek során egy vízmolekula elbomlik hidrogénionra (ez egy proton; az elektron leszakadt a hidrogén magjáról) és egy hidroxilionra (egy hidrogénatomhoz kötött oxigénatom, meg még egy elektron); illetve a hidrogén- és hidroxilionok ismét vízmolekulákká egyesülnek. E reakciók során egy vízmolekula eltűnését mindig egy hidrogénion megjelenése kíséri, míg a hidrogén- és hidroxilionok mindig együtt keletkeznek, illetve tűnnek el. így a megmaradó mennyiségek: a vízmolekulák és a hidrogénionok teljes száma, és a hidrogénionok mínusz a hidroxilionok száma! (Természetesen más megmaradó mennyiségek is vannak, például a vízmolekulák és a hidroxilionok számának összege, de ezek már csak e két alapvető megmaradó mennyiség kombinációi.) E pohár víz tulajdonságai teljes mértékben meghatározhatók, ha megszabjuk, hogy a hőmérséklete például 300 kelvin legyen (ez szobahőmérsékletnek felel meg), a vízmolekulák és hidrogénionok együttes sűrűsége 3,3 • 10²² molekula vagy ion köbcentiméterenként (ez durván a víz sűrűsége a tengerszinten uralkodó légnyomás mellett), és végül: a hidrogénionok és hidroxilionok számának különbsége (vagyis az eredő töltés) legyen nulla. E feltételek mellett például kiszámítható, hogy minden 500 millió vízmolekulára jut 1 hidrogénion. Ezt a számot nem kell előre megadnunk: a hidrogénionok részarányát megkapjuk a termikus egyensúly feltételeiből. Ezzel szemben a megmaradó mennyiségek sűrűsége nem határozható meg a hőmérsékleti egyensúly fennállásából – hiszen például a nyomás emelésével vagy csökkentésével a vízmolekulák és hidrogénionok együttes számát 3,3 • 10²² molekula/köbcentiméternél nagyobbra vagy kisebbre változtathatjuk –, vagyis csak akkor tudjuk részleteiben megállapítani, mi is van a poharunkban, ha ezeket az értékeket előre megadjuk.

Ez a példa segít megérteni az úgynevezett „megmaradó mennyiségek” változó jelentését is. Például ha a víz egymillió fokos hőmérsékletű környezetbe kerül – mondjuk egy csillag belsejébe –, akkor a molekulák vagy ionok nagyon könnyen disszociálnak, az atomok pedig elvesztik elektronjaikat. Ekkor a megmaradó mennyiségek is mások lesznek: az elektronok száma, a hidrogénatommagok száma és az oxigénatommagok száma. A vízmolekulák plusz hidroxilionok számát e körülmények között ki kell számítani a statisztikus fizika törvényei szerint, nem pedig előre megadni; természetesen ez a szám igen kicsinek adódik majd. (A pokol füzében ritkán képződnek hólabdák.) Ilyen feltételek mellett valójában magreakciók is végbemennek, tehát még a különféle atommagok száma sem állandó, de szerencsére ezek a számok olyan lassan változnak, hogy a csillag úgy tekinthető, mint ami lépésről lépésre egyensúlyi állapotokon keresztül fejlődik.

Végül több milliárd fokos hőmérsékleteken – amik az Univerzum korai szakaszát jellemzik – maguk az atommagok is alkotóelemeikre, protonokra és neutronokra esnek szét. A reakciók olyan gyorsan mennek végbe, hogy tiszta sugárzásból könnyen keletkezhetnek nehezebb részecskék és antirészecskék, amik azután újra szétsugárzódhatnak. Ilyen feltételek mellett a lényeges megmaradási törvények száma olyan kicsire csökken, hogy a még ekkor is érvényes megmaradási tételek – legalábbis mai tudásunk szerint – minden lehetséges körülmény között fennállnak. Ekkor mindössze három olyan megmaradó mennyiség van, amit a korai Univerzum leírásához meg kell adnunk:

1. Elektromos töltés. Kelthetünk vagy szétsugároztathatunk olyan részecskepárokat, amelyekben a részecskék töltése egyenlő nagyságú, de ellentétes előjelű; de a teljes elektromos töltés sosem változhat meg, az feltétlenül állandó. (E megmaradási törvényben biztosabbak lehetünk, mint bármely másikban; ha ugyanis az elektromos töltés nem maradna meg, az elektromágnesség egész Maxwell-féle elmélete érvényét vesztené!)

2. Barionszám. A „barion” gyűjtőnév magába foglalja a magrészecskéket (protonokat és neutronokat), valamint más, nehezebb instabil részecskéket, az úgynevezett hiperonokat. A barionok és antibarionok párokban keletkezhetnek vagy szétsugárzódhatnak, bomlásaikban egy barion másik barionra bomlik, például a radioaktív atommagok béta-bomlása során, ahol egy neutron protonná válik vagy fordítva. Mindezen folyamatok lényeges közös tulajdonsága, hogy bennük a barionok és antibarionok (antiprotonok, antineutronok, antihiperonok) számának különbsége változatlan marad. Ha a protonnak, neutronnak és a hiperonoknak +1 „barionszám”-ot tulajdonítunk, és a megfelelő antirészeknek -1 barionszámot, akkor a fenti szabály úgy fogalmazható meg, hogy a teljes barionszám állandó. A barionszámnak nincs olyan szembetűnő dinamikai jelentése, mint az elektromos töltésnek – legalábbis mai tudásunk szerint a bariontöltés nem kelt maga körül az elektromos vagy mágneses mezőkhöz hasonló mezőt. így a barionszám inkább csak egy „könyvelési segédeszköz” – jelentősége kimerül abban a tényben, hogy értéke minden körülmények között megőrződik.

3. Leptonszám. A „leptonok” könnyű, negatív töltésű részecskék: az elektron és a müon, az elektromosan semleges neutrínó, továbbá ezek antirészecskéi, a pozitron, antimüon és antineutrínó sorolhatók ide. A neutrínók és antineutrínók, nulla nyugalmi tömegük és töltésük ellenére, semmivel sem elképzelhetetlenebb részecskék, mint a fotonok; éppúgy energiát és lendületet (impulzust) hordoznak, mint bármely más részecske. A leptonszám megmaradása egy újabb „könyvelési szabály”: a leptonok és antileptonok számának különbsége a folyamatokban megőrződik, állandó. (1962-es neutrínókísérletek során kiderült, hogy valójában kétféle neutrínó létezik, egy „elektrontípusú” és egy „müontípusú”, és kétféle leptonszám: az elektron-leptonszám az elektronok és elektrontípusú neutrínók teljes száma, mínusz a megfelelő antirészek száma, míg a müon-leptonszám a müonok és müonneutrínók teljes száma, mínusz a megfelelő antirészek száma. Ma úgy tűnik, mindkettő teljes mértékben megmarad, ám ez még nem tekinthető eléggé bizonyítottnak.)

Hogy miként lehet e szabályokat alkalmazni, arra jó példával szolgál a neutron (n) radioaktív bomlása, melynek során proton (p), elektron (e^-) és egy elektron-antineutrínó (ν_e) keletkezik. A folyamatban részt vevő részecskék elektromos töltése, barionszáma és leptonszáma a következő:

 

 

Az olvasó könnyen ellenőrizheti, hogy a végállapotbeli részecskéknél a megmaradó mennyiségek összege megegyezik a kezdeti neutronéval. Ezt jelenti az, hogy ezek a mennyiségek a folyamatban megmaradnak. Valójában ezek a megmaradási törvények egyáltalán nem semmitmondóak: megmondják ugyanis, hogy milyen folyamatok nem mehetnek végbe, így például tiltott az olyan bomlás, amelynek során a neutronból proton, elektron és egynél több antineutrínó keletkezne.

Hogy tehát az Univerzum összetételének teljes „recept”-jét megírhassuk, ahhoz – az adott pillanatban uralkodó hőmérséklet mellett – meg kell adnunk a térfogategységre jutó elektromos töltést, barionszámot és leptonszámot is. A megmaradási törvények szerint a továbbiak során ezek a mennyiségek bármely – az Univerzummal együtt táguló – térfogatban állandók maradnak, megőrzik kezdeti értéküket. Vagyis: a töltés, a barionszám és a leptonszám sűrűsége egyszerűen a Világegyetem lineáris méretének harmadik hatványával fordítottan arányos. Ám ugyanilyen szabály szerint változik a térfogategységre eső fotonok száma is. (A III. fejezetben láttuk, hogy a fotonok sűrűsége a hőmérséklet harmadik hatványával arányos, maga a hőmérséklet pedig – mint azt e fejezet elején említettük – az Univerzum méretének inverze szerint változik.) így az egy fotonra. jutó töltés, barionszám és leptonszám az Univerzum tágulása során állandó marad; „recept”-ünk egyszer s mindenkorra érvényes lesz, ha a megmaradó mennyiségeket a fotonok számához viszonyítva adjuk meg.

[Szigorúan véve, az a mennyiség, amely a Világegyetem méretének köbével fordítottan arányos, nem az egységnyi térfogatra jutó fotonok száma, hanem az entrópiasűrűség. Maga az entrópia a statisztikus fizika egyik alapmennyisége, amely a fizikai rendszer rendezetlenségének mértékével kapcsolatos. Egy konvencionális számtényezőtől eltekintve, az entrópiát jó közelítéssel a hőmérsékleti egyensúlyban levő részecskék (fotonok, neutrínók és nehezebb részecskék) teljes száma adja meg, ahol is a különféle részecskéket az I. táblázatban (l. a 135. oldalt) megadott súllyal kell számba venni. Valójában az Univerzum jellemzésére a töltésnek, a barionszámnak és a leptonszámnak az entrópiához viszonyított arányát kellene megadnunk. De a nehezebb részecskék száma még egészen magas hőmérsékleteken is legfeljebb olyan nagyságrendű, mint a fotonoké, ezért nem követünk el nagy hibát, ha összehasonlítási alapként entrópia helyett a fotonok számát vesszük.]

Az Univerzumban egy fotonra jutó elektromos töltést könnyű megbecsülni. Mai tudásunk szerint a Világegyetem átlagos elektromos töltéssűrűsége nulla. Ha ugyanis például a Föld-Nap rendszerben csak egy picit is túlsúlyba jutna a pozitív (esetleg a negatív) töltés – mondjuk minden milliószor milliószor milliószor milliószor milliószor millió (10³⁶) töltésből csak egy is kiegyenlítetlen maradna –, a Föld és a Nap között olyan erős elektromos taszítás lépne fel, ami messze meghaladná a köztük ható gravitációs vonzást. Ha a Világegyetem zárt és véges, akkor ezt az észrevételt törvénnyé léptethetjük elő: az Univerzum eredő össztöltésének nullának kell lennie, máskülönben az elektromos tér erővonalai mintegy körbetekercselnék az Univerzumot, ezáltal végtelen intenzitású erőteret hozva létre. Ám attól függetlenül is, hogy az Univerzum valójában zárt-e vagy nyitott, alapos okunk van annak feltételezésére, hogy az egy fotonra jutó elektromos töltés mindenképpen elhanyagolható.

Az egy fotonra eső barionszámot is könnyű megbecsülni. A barionok közül csupán a magrészecskék (a proton, a neutron és ezek antirészecskéi, az antiproton és az antineutron) stabilak. A szabad neutron valójában elbomlik, átlagos élettartama 15,3 perc, de az atommagokban levő neutront a magkötés abszolút stabillá teheti. Továbbá, amennyire ma tudjuk, a Világegyetemben nincs jelen jelentősebb mennyiségű antianyag. (Erről később még részletesebben is szólunk.) így a mai Világegyetem tetszőleges részében a barionszám lényegében a magrészecskék számával egyezik meg. Az előző fejezetben említettük, hogy körülbelül egy magrészecske jut a mikrohullámú háttérsugárzás minden 1 milliárd fotonjára. (A pontos érték bizonytalan.) így az egy fotonra jutó barionszám hozzávetőleg 1/1 milliárd (10^-9).

Ez valóban fontos következtetés. Hogy lássuk, mire jutunk ebből, tekintsük a múltnak azt az időszakát, amikor a hőmérséklet 10 billió foknál (10¹³ K) – vagyis a magrészecskék küszöbhőmérsékleténél – magasabb volt. Ebben a korszakban az Univerzum nagyon sok magrészecskét és antirészecskét tartalmazott, körülbelül ugyanolyan sokat, mint amennyi fotont. Ám a barionszám a magrészecskék és antirészecskék számának különbségével egyenlő. Ha ez a különbség a fotonok számának egymilliárdod része volt – vagyis mintegy egy-milliárdod része a magrészecskék teljes számának –, akkor minden 1 milliárd mag-antirészecskére 1 milliárd plusz egy magrészecske jutott. Amikor később az Univerzum hőmérséklete a magrészecskék küszöbhőmérséklete alá csökkent, és a magrészecskék megfelelő antirészeikkel rendre szétsugárzódtak, csupán e parányi többlet maradt meg, s ez alakította ki mai világunkat!

Egy ilyen parányi szám – 1/1 milliárd – fölbukkanása a kozmológiában számos elméleti kutatót arra a föltevésre késztetett, hogy ez a szám valójában nulla: vagyis az Univerzum egyenlő mértékben tartalmaz közönséges anyagot és antianyagot. így azt a megfigyelést, hogy az egy fotonra jutó barionszám 1/1 milliárdnak tűnik, azzal lehetne megmagyarázni, hogy valamikor régen – még mielőtt a hőmérséklet a magrészecskék küszöbhőmérséklete alá csökkent volna – az Univerzum olyan tartományokra vált szét, hogy némelyekben az antianyag, másokban pedig az anyag volt túlsúlyban. (Egymilliárd rész-antirész párra jutott néhány többletrészecske, máshol pedig néhány többlet-antirészecske.) Amint a hőmérséklet a küszöbérték alá csökkent, valamennyi részecske-antirészecske pár szétsugárzódott, csupán a kompenzálatlan részecskéket, illetve antirészecskéket hagyva vissza. így az Univerzum különálló közönséges anyag-, illetve különálló antianyagszigetekre bomlott. Ennek az elképzelésnek csupáncsak annyi a szépséghibája, hogy mindeddig semmi jelét sem tapasztaltuk annak, hogy a Világegyetemben bárhol is nagyobb mennyiségű antianyag lenne található. A Földünk légkörének felső rétegeibe érkező kozmikus sugárzás Galaktikánk távoli részeiből, részben talán még a Galaktikán is túlról származik. És ez a sugárzás túlnyomórészt csak közönséges anyagot tartalmaz, antianyagot alig. Sőt mindeddig egyetlen antiprotont vagy antinukleont sem találtak benne. De nem sikerült eddig olyan fotonokat sem megfigyelni, amelyekről feltételezhető volna, hogy találkozó kozmikus méretű közönséges anyag- és antianyagfelhők szétsugárzásából származnak.

Egy másik lehetőség az lenne, ha a fotonok (vagy pontosabban: az entrópia) sűrűsége nem fordított arányban változna az Univerzum méretével. Ez akkor történhetne meg, ha a hőmérsékleti egyensúlytól eltérések adódnának, például fellépne valamiféle súrlódás vagy viszkozitás, ami felmelegítené az Univerzumot, és közben extra fotonokat keltene. Ebben az esetben megtörténhet, hogy kezdetben az egy fotonra jutó barionszám valami ésszerű (mondjuk egység körüli) érték volt, és ez csupán a fotonok számának növekedése révén csökkent a mai parányi arányszámra. Sajnos, ennek az elképzelésnek is meg van a maga szépséghibája, ugyanis senki sem tud egy elfogadható mechanizmust kitalálni, ami alkalmas volna afféle „extra” fotonok keltetésére. Néhány évvel ezelőtt magam is megpróbáltam ezt a problémát megoldani, de munkám sajnos a legcsekélyebb eredménnyel sem járt.

A továbbiak során ezeket a „rendhagyó” elképzeléseken nem fogom figyelembe venni, hanem egyszerűen azt fogom feltételezni, hogy az egy fotonra jutó barionszám valóban akkora, amekkorának látszik: vagyis 1/1 milliárd.

És végül, mit mondhatunk az Univerzum leptonszámsűrűségéről? – Az a tény, hogy a Világegyetemnek nincs elektromos töltése, egyből arra a következtetésre vezet, hogy ma minden egyes pozitív töltésű protonra egyetlen negatív töltésű elektron jut. A mai Univerzumban a magrészecskék mintegy 87 százaléka proton, vagyis az elektronok teljes száma megközelíti a magrészecskék számát. Ha az elektronok volnának az egyedüli leptonok, akkor rögtön levonhatnánk azt a következtetést, hogy az egy fotonra jutó leptonszám nagyjából megegyezik az egy fotonra jutó barionszámmal.

Azonban az elektronon és pozitronon kívül még más olyan stabil részecskék is vannak, amelyek leptonszámot hordoznak. A neutrínó és antirészecskéje, az antineutrínó, a fotonhoz hasonlóan elektromosan semlegesek, de leptonszámuk +1, illetve -1. Hogy a mai Univerzum leptonszámsűrűségét meghatározzuk, valamit tudnunk kell a neutrínók és antineutrínók populációjáról is.

Sajnos ezt az információt rendkívül nehéz megszerezni. A neutrínó annyiban hasonlít az elektronhoz, hogy szintén nem érzékeli az erős magerőket, amelyek a magrészecskéket együtt tartják az atommagban. (Néha egyszerűen a „neutrínó” elnevezést fogom használni akkor is, amikor neutrínókról és/vagy antineutrínókról beszélek.) De a neutrínó elektromosan is semleges, ezért nem érzékeli azokat az elektromos és mágneses erőket, amelyek az elektront az atomban kötve tartják. Valójában a neutrínókra jelentősebb mértékben semmiféle erő nem hat. Mint valamennyi részecske, ők is részt vesznek a gravitációs kölcsönhatásban, és érzékelik azokat a „gyenge” erőket is, amelyek a neutron bomlásához hasonló radioaktív folyamatokat hoztak létre, ám ezek az erők a közönséges anyaggal csak nagyon csekély kölcsönhatásra vezetnek. Hogy érzékeltessük, milyen gyenge ez a kölcsönhatás, a következő példát említhetjük: ahhoz, hogy számottevő esélyünk legyen egy radioaktív folyamatban keletkezett neutrínó szóródására, több fényév vastagságú ólomréteget kellene annak útjába helyeznünk. A Nap például állandóan sugároz neutrínókat, amelyek a Nap belsejében végbemenő magreakciók során keletkeznek: ezek a neutrínók levilágítanak hozzánk nappal, amikor ránk süt a Nap, és felvilágítanak” éjjel, amikor a Nap a Föld túlsó oldalán van, mivel számukra a Föld gyakorlatilag átlátszó. A neutrínók létezését – jóval a fölfedezésük előtt – Wolfgang Pauli jósolta meg, mint olyan hipotetikus részecskéket, amelyek a neutronbomláshoz hasonló folyamatokban helyreállítják az energiaegyensúlyt. Csupán az ötvenes évek végétől vált lehetővé a neutrínók és antineutrínók közvetlen kimutatása oly módon, hogy magreakciók vagy részecskegyorsítók révén olyan nagyszámú neutrínót hozunk létre, hogy azokból néhány száz a detektorban kölcsönhasson, és így észlelhető legyen.

Látva e kölcsönhatások rendkívül gyenge voltát, könnyű elképzelni, hogy a neutrínók és antineutrínók hatalmas számban népesíthetik be az Univerzumot anélkül, hogy jelenlétüknek bármiféle jelét adnák. A neutrínók és antineutrínók sűrűségére így csupán egy nagyon szegényes felső korlátot adhatunk. Ha ezek a részecskék túlságosan nagy számban lennének jelen, akkor jelenlétükkel számottevően befolyásolnának bizonyos gyenge bomlásfolyamatokat, és a kozmikus tágulás is a megfigyeltnél gyorsabb ütemben lassulna. Mindazonáltal ezek a felső korlátok nem zárják ki annak lehetőségét, hogy a fotonokéval közel azonos számú és energiájú neutrínó és/vagy antineutrínó legyen az Univerzumban.

E megjegyzések ellenére a kozmológusok körében az a feltevés terjedt el, hogy a leptonszám (vagyis az elektronok, müonok és neutrínók száma, mínusz a megfelelő antirészecskék száma) osztva a fotonok számával kicsi, jóval kisebb egynél. E feltételezés alapja jórészt csak analógia: az egy fotonra eső barionszám kicsi, miért ne lenne akkor az egy fotonra eső leptonszám is az? – Nos, ez az egyik legvitathatóbb föltételezés, amit el kell fogadnunk a modellben. Ám e feltevés megdőlése szerencsére csak keveset változtatna a modellből levont általános következtetéseken.

Természetesen az elektronok küszöbhőmérséklete fölött nagy számban volnának jelen leptonok és antileptonok; közel annyi elektron és pozitron, mint amennyi foton. És ilyen körülmények között az Univerzum annyira sűrű és forró lenne, hogy még a „szellemszerű” neutrínók is hőmérsékleti egyensúlyba kerülnének; ezek száma egyébként szintén elérné a fotonokét. Ez lehetséges, hiszen a modellben csupán azt tételeztük fel, hogy a leptonok és antileptonok számának különbsége volt és maradt sokkal kisebb a fotonok számánál. A korai Univerzumban a leptonok száma egy kevéssel fölülmúlhatta az antileptonokét – csakúgy, mint a barionoké az antibarionokét –, és ez a kis túlsúly az, ami az Univerzum atomos anyaga képében a mai napig fönnmaradt. Tekintettel továbbá arra, hogy a neutrínók és antineutrínók gyenge kölcsönhatásban állnak, kézenfekvő az a föltételezés, hogy közülük nagyon sok elkerülhette a szét-sugárzást, vagyis ma közel annyi neutrínó van, mint antineutrínó, és számuk összemérhető a fotonok számával. A következő fejezetben megmutatjuk majd, hogy nyomós okunk van azt hinni, hogy valóban ez a helyzet, bár egyelőre nincs komoly esélyünk arra, hogy megfigyelhessük a neutrínók e hatalmas, mindent betöltő tengerét.

Röviden összefoglalva, a korai Univerzum „recept”-je a következő: Vedd az egy fotonra jutó elektromos töltést nullának, az egy fotonra eső barionszámot 1/1 milliárdnak, az egy fotonra eső leptonszámot pedig határozatlannak, ám mindenesetre jó kicsinek. A háttérsugárzás jelenlegi 3 kelvin hőmérsékleténél magasabb hőmérsékletekre vedd a hőmérséklet értékét az Univerzum akkori és jelenlegi méretének arányában magasabbnak. Keverd meg az anyagot alaposan, hogy a különböző részecskék eloszlását a hőmérsékleti egyensúly feltételei szabják meg. Helyezd el az egészet egy táguló Univerzumban, ahol a tágulás ütemét a benne levő anyag keltette gravitációs tér határozza meg. Ha elegendően sokáig vársz, ebből a kotyvalékból kifő a mai Világegyetem.

 

V Az első három perc

 

Most már minden szükséges előkészületet megtettünk ahhoz, hogy az Univerzum fejlődésének első három percét végigkövethessük. Mint azt már a bevezetőben is említettük, e történetet mintegy egy filmből kivetített állóképekkel fogjuk felidézni. Az események kezdetben jóval sűrűbben követték egymást, mint később, ezért nem volna célszerű egyenlő időközönként vizsgálni a filmkockákat, mint a szokásos filmeknél. Ehelyett a vetítőgép sebességét az Univerzum csökkenő hőmérsékletéhez fogjuk igazítani, megállítva azt minden olyan időpillanatban, amikor a hőmérséklet az előző érték egyharmadára csökken.

Sajnos, nem indíthatom a filmet a nulla időpillanatban, végtelen hőmérsékleten. 1500 milliárd kelvines (1,5 • 10¹² K) küszöbhőmérséklet fölött az Univerzum nagyszámú pi-mezont tartalmaz, melyeknek a tömege a nukleonokénak mintegy hetede. (1. az I. táblázatot, 135. oldal.) Az elektronokkal, pozitronokkal, müonokkal és neutrínókkal szemben a pi-mezonok egymással és a nukleonokkal igen erős kölcsönhatásban állnak – valójában a nukleonok állandó pi-mezoncseréje adja az atommagot összetartó vonzerő jelentős részét. Nagyszámú erősen kölcsönható részecske jelenléte ilyen szupermagas hőmérsékleteken nagyon megnehezíti az anyag viselkedésének leírását, így – e matematikai nehézségeket kikerülendő – ebben a fejezetben a történetet csupán az első századmásodperctől kezdem. Ekkor a hőmérséklet már néhány százmilliárd fokra csökkent, ami jóval alatta van a pi-mezonok, a müonok és a náluk nagyobb tömegű részecskék küszöbhőmérsékletének. A VII. fejezetben röviden majd arról is szólok, hogy az elméleti fizikusoknak milyen elképzeléseik vannak az ennél korábbi időszakok eseményeiről.

E bevezető megjegyzések után lássuk a filmet!

 

ELSŐ KÉP. Az Univerzum hőmérséklete most 100 milliárd kelvin (10¹¹ K). A Világegyetem egyszerűbb, leírása is könnyebb, mint a későbbiekben bármikor is lesz. Anyag és sugárzás szétválaszthatatlan elegye tölti be, amelynek minden egyes részecskéje nagyon gyakran ütközik más részecskékkel. így – a gyors tágulás ellenére – az Univerzum csaknem tökéletes hőmérsékleti egyensúlyban van. Fejlődését tehát megszabják a statisztikus fizika törvényei, függetlenül attól, hogy az első kép felvétele előtt mi ment végbe benne. Csupán annyit kell tudnunk, hogy a hőmérséklet 10¹¹ kelvin, és a megmaradó mennyiségek – elektromos töltés, barionszám, leptonszám – vagy nagyon kicsik, vagy nullával egyenlők.

Nagy számban azok a részecskék vannak jelen, amelyeknek a küszöbhőmérséklete 10¹¹ kelvinnél kisebb. Ezek: az elektron és antirészecskéje, a pozitron, és természetesen a nulla tömegű részecskék, nevezetesen: a foton, a neutrínók és az antineutrínók. Az Univerzum olyan sűrű, hogy még a neutrínók is – amelyek fényéveket tehetnének meg ólomban ütközés nélkül –, gyakori ütközéseik révén, hőmérsékleti egyensúlyba kerülnek az elektronokkal, a pozitronokkal és a fotonokkal.

Az események leírását nagyon megkönnyíti az, hogy a 10¹¹ kelvines hőmérséklet jóval magasabb az elektronok és pozitronok küszöbhőmérsékleténél, s ezért ezek a részecskék – csakúgy, mint a fotonok és a neutrínók – sugárzásként viselkednek. Mekkora az energiasűrűsége ezeknek a sugárzásoknak? A 135. oldalon levő I. táblázatnak megfelelően az elektronok és pozitronok együtt a fotonok energiájának 7/4-szeresét, a neutrínók és az antineutrínók pedig még egyszer ugyanennyi energiát adnak, vagyis a teljes energiasűrűség egy

 

 

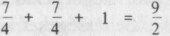
tényezővel nagyobb lesz, mint a tiszta elektromágneses sugárzás energiasűrűsége ezen a hőmérsékleten. A Stefan-Boltzmann-törvény szerint (l. a III. fejezetet) az elektromágneses sugárzás energiasűrűsége ezen a hőmérsékleten 4,72 • 10⁴⁴ elektronvolt/liter, vagyis az Univerzum teljes energiasűrűsége, ami ennek 9/2-szerese, 21 • 10⁴⁴ elektronvolt/liter. Ez – tömegsűrűségre átszámítva – 3,8 milliárd kilogramm/liter sűrűségnek felel meg, ami a normál földi körülmények között levő víz sűrűségének 3,8 milliárdszorosa. (Az energiát tömegre az Einstein-féle E = mc² összefüggés alapján számítottam át.) Ez olyan óriási sűrűséget jelent, hogy ha a Mount Everest ilyen sűrű anyagból lenne, gravitációs vonzása szétrombolná a Földet.

Az első kép felvételekor az Univerzum nagyon gyorsan tágul és hűl. A tágulás ütemét az a feltétel szabja meg, hogy a Világegyetem bármely darabkája épp a szökési sebességgel távolodik bármely középponttól. Az első felvétel idején uralkodó óriási sűrűség mellett a szökési sebesség is megfelelően magas – az Univerzum karakterisztikus tágulási ideje körülbelül 0,02 másodperc. (L. a Matematikai jegyzetek 3. pontját a 146. oldalon. A „karakterisztikus tágulási idő” hozzávetőlegesen annak az időtartamnak a százszorosa, ami alatt a Világegyetem mérete 1 százalékkal nő. Pontosabb meghatározása: a karakterisztikus tágulási idő bármely időszakban a Hubble-állandó akkori értékének a reciprokával egyenlő. Mint azt már a II. fejezetben megjegyeztük, az Univerzum életkora a karakterisztikus tágulási időnél mindig kisebb, mivel a gravitáció folyamatosan csökkenti a tágulás ütemét.)

Ebben az időszakban egy kevés magrészecske is jelen van: minden egymilliárd fotonra (illetve elektronra vagy neutrínóra) jut egy proton vagy neutron. Ahhoz, hogy az Univerzum e korai szakaszában keletkező kémiai elemek gyakoriságát megjósolhassuk, a protonok és neutronok relatív arányát is ismernünk kell. A neutron a protonnál nehezebb, a tömegkülönbség 1,293 millió elektronvolt energiával egyenértékű. Ám e magas, 10¹¹ kelvines hőmérsékleten az elektronok, pozitronok és egyéb részecskék karakterisztikus energiája ennél jóval nagyobb, átlagosan mintegy 10 millió elektronvolt (Boltzmann-állandószor hőmérséklet). így a neutronok és protonok gyakori ütközései a náluk jóval nagyobb számban jelenlevő elektronokkal, pozitronokkal, és egyéb részecskékkel a protonokat neutronokká, a neutronokat viszont protonokká alakítják át. A legfontosabb reakciók a következők:

 

Antineutrínó és proton pozitront és neutront kelt (és viszont).

 

Neutrínó és neutron elektront és protont kelt (és viszont).

 

Mivel feltevéseink szerint az egy fotonra eső leptonszám és elektromos töltés nagyon kicsi, csaknem ugyanannyi neutrínó van, mint amennyi antineutrínó, és ugyanannyi pozitron, mint amennyi elektron; ezért mindkét folyamat ugyanolyan gyakorisággal megy végbe. (A neutronok radioaktív bomlása most elhanyagolható, mivel az mintegy 15 percet venne igénybe, míg itt olyan folyamatokról van szó, amelyek századmásodpercek alatt mennek végbe.) így egyensúly akkor állhat fenn, ha a protonok és neutronok száma csaknem teljesen egyenlő. A magrészecskék ekkor még nem állnak össze atommagokká, ugyanis a 10¹¹ kelvinhez tartozó karakterisztikus hő-mérsékleti energia jóval nagyobb, mint a tipikus atommagok szétha-sításához szükséges energia – ami nukleononként 6-8 millió elektronvolt. így ha létre is jönnének összetett atommagok, azok nyomban szét is hullanának.

Természetesen fölvetődik a kérdés, hogy mekkora volt az Univerzum ebben az időben. Sajnos, ezt nem tudjuk, sőt még abban sem lehetünk biztosak, hogy a kérdésnek egyáltalán van-e értelme. Mint a II. fejezetben már említettük, a Világegyetem ma végtelen is lehet, ám ebben az esetben persze végtelen volt már az első felvétel idején is, mint ahogy mindig is végtelen lesz. Ám az is lehetséges, hogy az Univerzum ma véges kiterjedésű, a kerületét ebben az esetben 125 milliárd fényévre szokták becsülni. (A kerületet úgy értelmezik, mint azt a távolságot, amit meg kell tenni ahhoz, hogy egy pontból kiindulva és mindig egyenesen haladva ugyanoda visszaérjünk. Ez a becslés a Hubble-állandó mai értékén alapul, továbbá azon a feltételezésen, hogy a Világegyetem sűrűsége a kritikus érték kétszerese.) Mivel az Univerzum hőmérséklete a mérettel fordított arányban csökken, az Univerzum kerülete az első felvétel idején úgy aránylik a mai értékhez, mint a mai hőmérséklet (3 kelvin) az akkori 10¹¹ kelvinhez, s eszerint a Világegyetem kerülete az első felvétel időpontjában mintegy 4 fényévnyi lehetett. Szerencsénkre a kozmikus fejlődés első néhány percének egyetlen részlete sem függ attól, hogy az Univerzum kerülete végtelen volt-e vagy csupán néhány fényévnyi.

 

MÁSODIK KÉP. A Világegyetem hőmérséklete most 30 milliárd kelvin (3 • l0¹⁰ K). Az első felvétel óta 0,11 másodperc telt el. Minőségileg semmi sem változott: az Univerzum összetételét még mindig az elektronok, pozitronok, neutrínók, antineutrínók és fotonok uralják, valamennyien hőmérsékleti egyensúlyban vannak egymással, jóval a küszöbhőmérsékletük fölött. így az energiasűrűség egyszerűen a hőmérséklet negyedik hatványa szerint csökkent; értéke most a közönséges víz nyugalmi tömegében tárolt energia 30 milliószorosával egyenlő. A tágulás üteme a hőmérséklet négyzete szerint csökkent, így az Univerzum karakterisztikus tágulási ideje e pillanatra már mintegy 0,2 másodpercre nőtt. A jelenlevő kevés magrészecske még mindig nem csomósodott atommagokká, ám az alacsonyabb hőmérséklet miatt a nehezebb neutronok most már nagyobb gyakorisággal keltenek protonokat, mint fordítva. Ezért megváltozik a nukleonok részaránya: az Univerzum már csak 38 százalék neutront tartalmaz és 62 százalék protont.

 

HARMADIK KÉP. A Világegyetem hőmérséklete 10 milliárd kelvin (10¹⁰ K). Az első felvétel óta 1,09 másodperc telt el. A csökkenő hőmérséklet és sűrűség annyira megnöveli a neutrínók és antineutrínók átlagos kölcsönhatási idejét, hogy azok most már kezdenek olyan szabad részecskékként viselkedni, amik nem állnak hőmérsékleti egyensúlyban az elektronokkal, a pozitronokkal és a fotonokkal. Ettől kezdve a neutrínók már nem játszanak aktív szerepet történetünkben, eltekintve attól, hogy energiájuk révén továbbra is a gravitáció egyik fő forrásai maradnak a Világegyetemben. Egyébként a neutrínók kiválása a hőmérsékleti egyensúlyból nem okoz nagyobb változásokat. (E „lecsatolódást” megelőzően a tipikus neutrínóhullámhosszak fordítottan arányosak voltak a hőmérséklettel, és mivel maga a hőmérséklet az Univerzum méretének reciprokával volt arányos, a neutrínó-hullámhossz az Univerzum méretével egyenes arányban nőtt. A neutrínó-lecsatolódás után a neutrínók szabadon tágulnak, de a vöröseltolódás az Univerzum méretével arányosan nyújtja a hullámhosszat. Ez is mutatja, hogy nem túlságosan fontos a neutrínó-lecsatolódás pontos időpontjának meghatározása, ami azért szerencse, mert az a neutrínó-kölcsönhatások elméletének nem teljesen kidolgozott részleteitől függ.)

A teljes energiasűrűség az előző felvétel időpontjához képest olyan arányban kisebb, mint a hőmérsékletek hányadosának negyedik hatványa, így az most a víz sűrűségének mintegy 380 ezerszerese. Az Univerzum karakterisztikus tágulási ideje pedig 2 másodpercre nőtt. Mivel a hőmérséklet most már csupán kétszerese az elektronok és pozitronok küszöbhőmérsékletének, a szétsugárzás gyakorisága kezdi felülmúlni a párképződését.

A neutronokból és protonokból még mindig nem képződhetnek hosszabb ideig fennmaradó atommagok. De arányuk a csökkenő hőmérséklet következtében tovább változik, és végül 24 százalék neutron és 76 százalék proton összetételnél állapodik meg.

 

NEGYEDIK KÉP. Az Univerzum hőmérséklete most 3 milliárd kelvin (3 • 10⁹ K). Az első felvétel óta 13,82 másodperc telt el. Most már az elektronok és pozitronok küszöbhőmérsékleténél alacsonyabb hőmérsékleten vagyunk, így azok hamarosan fölemésztik egymást, és kiesnek az Univerzum alapösszetevőinek sorából. A szétsugárzás közben fölszabaduló energia lelassítja az Univerzum hűlésének ütemét. Ezért a neutrínók, amik ebből az extra hőmennyiségből lecsa-tolódásuk miatt már nem részesedhetnek, 8 százalékkal hidegebbek, mint az elektronok, pozitronok és fotonok. Ha mostantól kezdve a Világegyetem hőmérsékletéről beszélünk, mindig a fotonok hőmérsékletére gondolunk majd. Az elektronok és pozitronok gyors eltűnésével az Univerzum energiasűrűsége is egy kicsit kisebb lesz, mintha egyszerűen a hőmérséklet negyedik hatványa szerint csökkent volna.

Most már elég hideg van ahhoz, hogy különféle stabil atommagok – például hélium (⁴He) – képződjenek, ám ez nem megy végbe azonnal. Ennek az az oka, hogy a Világegyetem még mindig olyan gyorsan tágul, hogy atommagok csak a gyors kétrészecske-reakciók során keletkezhetnek. Például egy proton és egy neutron nehézhidrogén (más néven deutérium)-magot hozhat létre, a többletenergiát pedig egy foton viszi el. A deutériummag aztán egy protonnal vagy neutronnal ütközve vagy a hélium könnyű izotópjának (³He) a magját hozza létre, vagy a hidrogén legnehezebb izotópját, a tríciumot (³H), ami két neutront és egy protont tartalmaz. Végül, a hélium-3 egy neutronnal, a trícium pedig egy protonnal ütközve létrehozhatja a közönséges héliumatommagot (⁴He), amely két protonból és két neutronból áll. Ám ez a folyamatlánc csak akkor mehet végbe, ha megtörtént az első lépés, a deutérium keletkezése.

Mármost a rendes héliumban az atommagot erős kötelék tartja együtt, olyan erős, ami – mint azt már említettük – már a harmadik kép idején is képes lenne a magot együtt tartani. Ám a tríciumban és a hélium-3-ban ez a kötés gyengébb, a deutérium pedig még ezeknél is gyengébben kötött. (A deutériummag széthasításához kilencedannyi energia elég, mint a héliummagból egy nukleon kiszakításához.) A negyedik felvétel idején uralkodó 3 • 10⁹ kelvines hőmérsékleten a deutériummagok, amilyen gyorsan keletkeztek, ugyanolyan gyorsan szét is esnek, és így a nehezebb magok keletkezésére nincs számottevő esély. A neutronok – bár lassabban, mint eddig – még mindig protonokká alakulnak. Arányuk most már 17 százalék neutron és 83 százalék proton.

 

ÖTÖDIK KÉP. Az Univerzum hőmérséklete ekkor 1 milliárd kelvin (10⁹ K), mindössze hetvenszerese a Nap mai középponti hőmérsékletének. Az első felvétel óta 3 perc és 2 másodperc telt el. Az elektronok és a pozitronok már túlnyomórészt eltűntek, az Univerzum fő alkotóelemei most már csak a neutrínók, az antineutrínók és a fotonok. Az elektron-pozitron-szétsugárzáskor fölszabaduló energia a fotonok hőmérsékletét 35 százalékkal megemelte a neutrínókéhoz képest.

Az Univerzum most már elég hideg ahhoz, hogy a trícium, a hélium-3 és a közönséges hélium magja egyaránt együtt maradhasson, ám a deutérium gyengén kötött voltának gátló hatása még mindig érvényesül: a deutériummagok nem maradnak fenn elég ideig ahhoz, hogy belőlük észrevehető mennyiségben nehezebb magok keletkezzenek. A neutronok és protonok elektronokkal, neutronokkal, illetve ezek antirészecskéivel való ütközései elhanyagolható mértékűvé válnak, ám ehelyett fontossá lesz a szabad neutron bomlása: minden 100 másodpercben a megmaradó neutronok 10 százaléka bomlik el. így a neutronok és protonok aránya tovább csökken, értéke ekkor 14 százalék neutron és 86 százalék proton.

 

EGY KICSIT KÉSŐBB. Alig valamivel az ötödik felvételt követően, drámai események játszódnak le: a hőmérséklet az alá az érték alá csökken, amely mellett a deutériummagok együtt maradnak. Ha pedig ez a gátló tényező megszűnik, a nehezebb magok már igen gyorsan létrejönnek a negyedik felvételnél leírt kétrészecske-reakciólánc során. Ám a héliumnál nehezebb elemek egyéb – hasonló – akadályok miatt még mindig nem keletkezhetnek nagyobb mennyiségben: nem jönnek létre 5 vagy 6 nukleont tartalmazó stabil magok. így amint a hőmérséklet eléri a deutériumképződés hőmérsékletét, az összes meglevő neutron azonnal a héliummagokba épül be. Hogy ez pontosan mekkora hőmérsékleten következik be, az jórészt a magrészecskék egy fotonra jutó számától függ, mivel a magrészecskék nagyobb sűrűsége megkönnyíti az atommagok képződését. (Ezért írtam határozatlanul azt, hogy „egy kicsit később”...) Ha egy magrészecskére egymilliárd foton jut, akkor az atommagok szintézise 900 millió kelvinnél (0,9 • 10⁹ K) kezdődik meg. Ekkorra 3 perc és 46 másodperc telt el az első felvétel óta. (Az olvasó bizonyára megbocsátja nekem, hogy könyvemnek Az első három perc címet adtam. Ez jobban csengett, mintha Az első három és háromnegyed perc címet választottam volna – bár az igazságnak ez jobban megfelelne.) Amikor az atommagszintézis megkezdődik, a magrészecskék aránya 13 százalék neutron és 87 százalék proton. Az atommagszintézis után a hélium súlyaránya ugyanakkora, mint az őt alkotó magrészecskék részaránya volt. E magrészecskék fele neutron, és valamennyi neutron a héliumban van kötve, ezért a hélium részaránya éppen kétszer akkora, mint amekkora a neutronoké volt a magrészecskék között, vagyis mintegy 26 százalék. Ha a magrészecskék sűrűsége nagyobb az Univerzumban, az atommagszintézis egy kicsit korábban kezdődik, amikor még kevesebb neutron bomlott el, ebben az esetben egy kicsivel több hélium keletkezhet – ám a hélium részaránya valószínűleg ekkor sem lesz nagyobb 28 százaléknál. (l. a 9. ábrát.)

Elértük – sőt, túl is léptük! – a könyvünk címében kijelölt időpontot. Ám hogy kicsit jobban lássuk, mit is végeztünk, vessünk még egy pillantást az Univerzumra egy kicsit későbbi időpillanatban.

 

HATODIK KÉP. Az Univerzum hőmérséklete most 300 millió kelvin (3 • 10⁸ K). Az első felvétel óta 34 perc és 40 másodperc telt el. Az elektronok és pozitronok jórészt szétsugárzódtak, eltekintve egy parányi, egymilliárdod résznyi elektrontöbblettől, ami a protonok töltésének kiegyensúlyozásához szükséges. A szétsugárzás során felszabadult energia a fotonok hőmérsékletét a neutrínókéhoz képest 40,1 százalékkal emelte meg. (L. a Matematikai jegyzetek 6. pontját a 152. oldalon.) Az Univerzum energiasűrűsége most a víz anyagsűrűségének 9,9 százaléka, ennek 31 százalékát adják a neutrínók és antineut-rínók, 69 százalékát pedig a fotonok. Ez az energiasűrűség a Világegyetem karakterisztikus tágulási idejét egy és egynegyed órában szabja meg. A magfolyamatok leálltak, a magrészecskék nagyrészt héliumatommagokban vagy szabad protonokként (mint hidrogénatommagok) találhatók; a hélium aránya 22 és 28 százalék között van. Minden szabad vagy kötött protonra egy elektron jut, de a stabil atomok kialakulásához az Univerzum még mindig túlságosan forró.

 

 

9. ábra. A neutron-proton mérleg alakulása. A hőmérséklet függvényében a neutronoknak a részarányát tüntettük fel a magrészecskék közt. A görbe „hőmérsékleti egyensúly” feliratú része annak az időszaknak felel meg, amikor a tömegsűrűség és a hőmérséklet egyaránt olyan nagy volt, hogy valamennyi részecske hőmérsékleti egyensúlyban volt egymással; ekkor a statisztikus fizika törvényei szerint a neutronok részaránya kiszámítható a neutron-proton tömegkülönbségből. A görbe „neutronbomlás”-sal jelölt része azt az időszakot ábrázolja, amikor a szabad neutron radioaktív bomlásától eltekintve már valamennyi proton-neutron-átmenet (oda vagy vissza egyaránt) leállt. A görbének e két időszak közé eső része a gyenge kölcsönhatások átmeneti valószínűségeinek számítási részleteitől függ. A szaggatott vonallal jelölt rész azt mutatja, mi történt volna akkor, ha az atommagok képződése valamilyen okból tiltott. Valamikor az „atommagszintézis korá”-n belül valójában a neutronok gyorsan beépültek a héliummagokba, és a neutron-proton arány befagyott az ennek az időpontnak megfelelő értéknél. E görbe alapján a kozmológiailag létrejött héliumkoncentrációt is megbecsülhetjük: bármely hőmérséklet vagy időpont esetén, az atommagszintézis időszakában, a hélium részaránya a neutronok akkori számának épp kétszerese.

 

A továbbiakban az Univerzum tovább hűl és tágul, ám jó 700 000 évig semmi lényegesebb esemény nem történik. Ekkorra azután a hőmérséklet már annyira lecsökken, hogy az elektronok az atommagokkal stabil atomokat alkothatnak; a szabad elektronok eltűnésével pedig a Világegyetem átlátszóvá válik a sugárzás számára. Az anyag és a sugárzás szétcsatolódása megnyitja az utat az anyag előtt ahhoz, hogy csillagokat és galaxisokat képezhessen. És további mintegy 10 milliárd év múlva bizonyos élőlények megkezdik e történet rekonstruálását...

A korai Univerzum e leírásának van egy olyan következtetése, amely azonnal szembesíthető a tapasztalattal: az első három perc után fennmaradó anyag – amelyből később a csillagok formálódtak – 22-28 százaléknyi héliumot tartalmazott, a fennmaradó rész pedig jórészt hidrogén volt. Mint láttuk, ez az eredmény abból a föltevésből következett, hogy a fotonok száma messze meghaladja a magrészecskéket, ez a becslés pedig a mikrohullámú háttérsugárzás kísérletileg mért 3 kelvines hőmérsékletéből adódott. A héliumképződésre vonatkozó első kozmológiai számításokat a princetoni P. J. E. Peebles végezte el 1965-ben, röviddel azután, hogy Penzias és Wilson kimutatta a mikrohullámú háttérsugárzást. Tőle függetlenül – s vele csaknem egy időben – hasonló eredményre jutott Robert Wagoner, William Fowler és Fred Hoyle. Ezek az eredmények a standard modell nagy sikerét hozták, mivel ekkoriban már más becslések arra mutattak, hogy a Nap és a többi csillag kialakulásukkor túlnyomórészt hidrogénből álltak, bennük a hélium részaránya 20–30 százalék lehetett!

A Földön persze nagyon kevés hélium van, ám ennek az az oka, hogy a héliumatomok nagyon könnyűek és kémiailag közömbösek, ezért nagy részük már rég elszökött a Földről. Az Univerzum kezdeti héliumtartalmára vonatkozó becslések a csillagfejlődést leíró számításoknak és a megfigyelt csillagtulajdonságok statisztikus elemzésének az összehasonlításán alapulnak, továbbá felhasználják a forró csillagok és a csillagközi anyag héliumvonalainak közvetlen megfigyelését is. Egyébként – mint azt neve is jelzi – a héliumot a Nap légkörének színképében fedezte fel J. Norman Lockyer 1868-ban.

Az 1960-as évek elején néhány csillagász megfigyelte, hogy a hélium nemcsak nagy mennyiségben van jelen a galaxisokban, de gyakorisága is sokkal kevésbé változik helyről helyre, mint a nehezebb elemeké. Ez persze várható is, ha a nehéz elemek a csillagokban keletkeztek, a hélium pedig az Univerzum korai szakaszában, még mielőtt a csillagok működni kezdtek volna. Az atommagok gyakoriságának becslésében még ma is elég sok a bizonytalanság, de a kezdeti 20-30 százalékos héliumarányt épp elég bizonyíték támasztja alá ahhoz, hogy ez felbátoríthassa a standard modell híveit.

Az első három perc végén keletkező nagy mennyiségű hélium mellett más könnyű magok is keletkeztek: főképpen deutérium (hidrogén egy többletneutronnal) és a hélium könnyű izotópja (³He), ami nem alakult tovább normál héliummá. (Arányukat először Wagoner, Fowler és Hoyle számította ki 1967-ben.) A héliumtól eltérően a deutérium mennyisége erősen függ a magrészecskék térbeli sűrűségétől az atommagszintézis idején: nagyobb sűrűségek esetén a magreakciók gyorsabban mennek végbe, és több deutérium alakul át héliummá. Az alábbi táblázatban – Wagoner nyomán – összefoglaltuk a korai Univerzumból fennmaradt deutérium mennyiségét a foton-nukleon arány három lehetséges értéke mellett:

 

 

Nyilvánvaló ebből, hogy ha meg tudjuk határozni a deutérium kezdeti – a csillagok kialakulása előtti – mennyiségét, akkor pontosan meghatározhatjuk a foton-magrészecske-arányt; és ismerve a sugárzási háttér jelenlegi 3 kelvines hőmérsékletét, meghatározhatjuk a Világegyetem jelenlegi magrészecske-sűrűségét, s eldönthetjük azt a kérdést, hogy az Univerzum zárt-e vagy nyitott.

Sajnos, a kezdeti deutérium mennyiségének meghatározása egyáltalán nem könnyű feladat. A Föld vizeiben a deutérium részaránya 150 milliomodrész. (Ha a termonukleáris reakciók valaha is szabályozhatóvá válnak, ez a deutérium használható majd a termonukleáris reaktorok fűtőanyagaként.) Ám ez valószínűleg túlzó becslés: mivel a deutériumatomok kétszer olyan nehezek, mint a hidrogén, kicsit valószínűbb, hogy nehézvíz (HDO)-molekulákat képezzenek, s így a Föld gravitációs teréből nagyobb mennyiségű hidrogén tudott elszökni, mint deutérium. Másrészt viszont a spektroszkópiai megfigyelések szerint a Nap felszínén nagyon kevés deutérium található – kevesebb, mint 4 milliomodrész. Ez viszont valószínűleg alulbecsüli a tényleges értéket, mivel a Nap külső rétegeiben a deutérium arányát csökkenti a hidrogénnel való egyesülés, amelynek során könnyű héliumizotóp, ³He keletkezik.

A kozmikus deutériumgyakoriságra vonatkozó tudásunk megbízhatóbb forrásául szolgálnak a Copernicus műhold 1973-ban végzett ultraibolya megfigyelései. A deutériumatomok – csakúgy, mint a hidrogén – az ibolyántúli sugárzást meghatározott hullámhosszakon nyelik el, amelyek az atom alacsonyabb energiájú állapotaiból a magasabban gerjesztett állapotokba vezető átmeneteknek felelnek meg. Ezek a hullámhosszak egy kicsit az atommag tömegétől is függnek, így egy csillag ibolyántúli színképe – ami hozzánk hidrogént és deutériumot tartalmazó csillagközi keveréken át érkezik – olyan sötét elnyelési vonalakat tartalmaz, amelyek mindegyike két komponensre bontható: egyik a hidrogéntől, a másik pedig a deutériumtól származik. így bármely abszorpciós vonalpár relatív intenzitása azonnal megadja a hidrogén és a deutérium relatív gyakoriságát a csillagközi felhőben. Sajnos, a Föld felszínéről végzett ibolyántúli csillagászati megfigyeléseket nagyon megnehezíti a Föld légköre. A műholdakkal ez a nehézség kiküszöbölhető. A Copernicus műholdat egy olyan ibolyántúli spektrométerrel szerelték föl, amely a forró β Centauri csillag színképének elnyelési vonalait tanulmányozta. Ezek relatív intenzitásából azt a következtetést vonták le, hogy a β Centauri és a köztünk levő csillagközi anyag 20 milliomodrész deutériumot tartalmaz (ez tömegarányt jelent). Más csillagok ibolyántúli abszorpciós vonalainak a tanulmányozása hasonló eredményeket ad.

Ha ez a 20 milliomodrész deutérium valóban az Univerzum korai szakaszában keletkezett, akkor a fotonok és nukleonok arányának 1,1 milliárdnak kellett (és kell) lennie. (L. az előbbi táblázatot!) A jelenlegi 3 kelvines kozmikus sugárzási hőmérsékleten a fotonok sűrűsége 550 000 foton literenként, vagyis ma az Univerzum millió literenként 500 nukleont tartalmaz. Ez jóval kisebb a Világegyetem bezárulásához szükséges minimális sűrűségnél, ami – mint azt a II. fejezetben láttuk – millió literenként 3000 nukleon lenne. Ebből azt a következtetést lehetne levonni, hogy az Univerzum nyitott – vagyis a galaxisok a szökési sebességnél gyorsabban mozognak, és az Univerzum tágulása a végtelenségig folytatódni fog. Ha pedig a csillagközi anyag egy része csillagokban dolgozódott fel, amelyek a deutériumot – akárcsak a Nap – szétrombolják, akkor a kezdetben létrejött deutérium mennyisége még nagyobb lehetett, mint a Copernicus műhold megfigyelte 20 milliomodrész. Ekkor pedig a magrészecskék sűrűsége még a millió literenkénti 500 részecskénél is kisebb lehet, ami csak megerősíti azt a következtetést, hogy egy nyílt, a végtelenségig táguló Világegyetemben élünk.

Be kell vallanom, hogy ezt az érvelést nem tartom túlságosan meggyőzőnek. A deutérium nem olyan, mint a hélium – a deutérium abszolút értelemben is nagyon ritka, még akkor is, ha gyakorisága nagyobbnak tűnik, mint azt egy viszonylag sűrű, zárt Világegyetem esetében elvárnánk. Elképzelhető, hogy ez a sok deutérium viszonylag „frissebb” asztrofizikai jelenségek – szupernóvák, kozmikus sugárzás, csillagszerű objektumok – révén képződött. A hélium esetében ez a lehetőség nem áll fenn: elképzelhetetlen, hogy 20-30 százaléknyi hélium képződött volna mostanában, de az ennek során fölszabaduló óriási mennyiségű sugárzást ne figyeltük volna meg. Mások viszont azt mondják, hogy a Copernicus megfigyelte 20 milliomodrész deutérium semmiféle asztrofizikai folyamatban sem jöhetett létre anélkül, hogy eközben ne keletkezett volna nagy mennyiségű más könnyű elem: lítium, berillium és bór. Mindazonáltal egyelőre nem tudom elképzelni, hogy miképp győződhetnénk meg arról, hogy ezt a deutériumot nem valami olyan asztrofizikai mechanizmus hozta létre, amit ma még nem ismerünk.

A korai Univerzumnak van még egy másik olyan maradványa is, ami körülöttünk mindenütt jelen van, kimutatása mégis lehetetlennek tűnik. A harmadik felvételnél láttuk: attól kezdve, hogy a hőmérséklet 10 milliárd kelvin alá csökkent, a neutrínók szabad részecskékként viselkednek. Eközben a neutrínók hullámhossza egyszerűen a Világegyetem méretével arányosan nő, így a neutrínók száma és energiaeloszlása olyan marad, mintha még mindig hőmérsékleti egyensúlyban lennének, de olyan hőmérsékleten, ami a Világegyetem méretével fordított arányban csökken. Ugyanez érvényes a fotonokra is, azzal a különbséggel, hogy azok jóval tovább maradtak hőmérsékleti egyensúlyban a többi részecskével. Ezért a neutrínók jelenlegi hőmérséklete megközelítőleg ugyanakkora, mint a fotonoké. Az Univerzumban tehát minden magrészecskére mintegy egymilliárd neutrínó és antineutrínó jut.

De ennél pontosabb számítást is végezhetünk. Nem sokkal azután, hogy a Világegyetem a neutrínók számára átlátszóvá vált, megkezdődött az elektronok és a pozitronok szétsugárzása. A közben felszabaduló energia felmelegítette a fotonokat, de a neutrínókat – mivel azok már kiléptek a hőmérsékleti egyensúlyból – nem. Ennek következtében a neutrínók jelenlegi hőmérsékletének egy kicsivel alacsonyabbnak, kell lennie, mint amekkora a fotonoké. Könnyen kiszámítható, hogy a jelenlegi neutrínó-hőmérséklet egy ³√4/11 nagyságú tényezővel kisebb a fotonokénál, vagyis annak 71,38 százaléka. Tehát a neutrínók és antineutrínók a Univerzum energiájához a fotonjáruléknak mintegy 45,42 százalékát adják. (L. a Matematikai jegyzetek 6. pontját, a 152. oldalon!) Bár külön nem említettem, de amikor a kozmikus tágulási időket kiszámítottam, ezt az extra neutrínósűrűséget is számításba vettem.

A korai Univerzum standard modelljének legdrámaibb megerősítését e neutrínóháttér kimutatása adná. A háttér hőmérsékletére határozott jóslatunk van; ez a fotonháttér hőmérsékletének 71,38 százaléka, vagyis mintegy 2 kelvin. A neutrínók számára és energiasűrűségére vonatkozó becslésben elméletileg az jelenti az egyetlen bizonytalanságot, hogy vajon a leptonszám valóban olyan kicsi-e, mint azt föltételeztük. (Emlékeztetőül: a leptonszám a neutrínók és a többi leptonok számának, valamint az antineutrínók és az antileptonok számának különbsége.) Ha a leptonszámsűrűség ugyanolyan kicsi, mint a barionszám-sűrűség, akkor a leptonok és antileptonok száma közel egyenlő. Ha ellenben a leptonszámsűrűség a fotonok sűrűségével lenne összemérhető, akkor egy olyan „elfajult állapot” jönne létre, amelyben a neutrínók (vagy antineutrínók) jelentős többlettel, az antineutrínók (neutrínók) pedig jelentős hiánnyal vesznek részt. Egy ilyen elfajulás az első három percben jelentékenyen befolyásolná a neutron-proton-mérleg alakulását, így megváltoztatná a kozmológiailag kialakult hélium és deutérium mennyiségét is. A 2 kelvines kozmikus neutrínó- és antineutrínó-háttér kimutatása eldönthetné azt a kérdést, hogy vajon az Univerzum leptonszáma valóban kicsi-e. Ennél sokkal fontosabb azonban, hogy a Világegyetem standard modelljének újabb fontos igazolását is adhatná.

Sajnos, a neutrínók olyan gyenge kölcsönhatásban vannak az atomos anyaggal, hogy eddig senki sem tudott olyan mérési eljárást javasolni, amivel ez a 2 kelvines kozmikus neutrínóháttér kimutatható lenne. Ez aztán a tantaloszi probléma: minden magrészecskére 1 milliárd neutrínó és antineutrínó jut, és mégsem tudja senki, hogy miként is lehetne kimutatni őket! Reméljük, nemsokára akad majd valaki, aki tudni fogja.

Az első három perc e beszámolóját végigkövetve az olvasó talán úgy érzi, hogy nagyon is vakon bízunk modellünk helyességében. Lehet, hogy igaza van. Mindazonáltal, én nem hiszem azt, hogy a tudományok fejlődését mindig a minden irányba nyitott, sokoldalú kritikára kész elmék vitték előre. Gyakran szükség van arra is, hogy az ember félretegye kétségeit, és végigkövesse, milyen következtetésekre vezetnek a föltevései. Mert nem az a nagy dolog, ha valaki előítéletektől mentes, hanem az, ha az elméleti előítéleteit jól választja meg! Mindig csak az lehet minden elméleti föltevés próbája, hogy végül is hová vezet. A korai Univerzum standard modellje már elkönyvelhet néhány nagy sikert, és a jövő kísérleti programjai számára egy összefüggő elméleti keretet ad. Ez ugyan még nem jelenti azt, hogy feltétlenül igaz, de annyit igen, hogy komoly figyelmet érdemel.

Mindazonáltal meg kell vallanunk, hogy van egy olyan bizonytalan tényező, ami Damoklész kardjaként függ a standard modell fölött. E fejezetben minden leírt számítás mögött az a föltételezés húzódik, hogy a Világegyetemben érvényes a Kozmológiai Elv, vagyis az a föltevés, hogy az Univerzum homogén és izotrop. (A „homogenitás” azt jelenti, hogy az Univerzum ugyanolyannak tűnik minden olyan megfigyelő számára, aki a Világegyetem általános tágulásával együtt mozog, bárhol legyen is egyébként; az „izotrop” kifejezés pedig arra utal, hogy egy ilyen megfigyelő az Univerzumot minden irányba egyformának látja.) Közvetlen megfigyelésekből tudjuk, hogy a kozmikus mikrohullámú háttérsugárzás izotrop körülöttünk. Ebből arra következtetünk, hogy az Univerzum mindig ilyen izotrop volt, amióta csak a sugárzás kilépett az anyaggal való hőmérsékleti egyensúlyból, mintegy 3000 kelvines hőmérsékleten. Arra azonban nincs bizonyítékunk, hogy a Kozmológiai Elv korábban is érvényes lett volna.

Lehetséges, hogy kezdetben az Univerzum nagyon is inhomogén és anizotrop volt, és az egyenetlenségeket csak később simították ki a táguló Világegyetem részeinek egymással való súrlódásai. Ilyen „mixmaster” (mixelő) modellt alkotott a marylandi Charles Misner. Az is lehetséges, hogy az Univerzum homogenizálódását és izotroppá válását létrehozó súrlódás keltette hő a felelős a fotonok és a nukleonok jelenlegi óriási – 1 milliárd az 1-hez – számarányáért. Mindazonáltal – legalábbis amennyire én tudom – senki sem tudja igazán megindokolni, miért is lett volna a Világegyetem kezdetben inhomogén és anizotrop, mint ahogy a kisimulás során fölszabaduló hőmennyiséget sem tudja senki kiszámítani.

Ha a személyes véleményemre kíváncsiak, azt gondolom, hogy az efféle bizonytalanságokra nem az a helyénvaló válasz, hogy elvetjük a standard modellt, hanem inkább az, hogy nagyon is komolyan vesszük, és gondosan kiszámítjuk minden következtetését, még ha valaki annak szurkol is, hogy így majd a megfigyelésekkel ellentmondásra juthat. Még az sincs bebizonyítva, hogy ilyen kezdeti inhomogenitás és anizotrópia jelentősen befolyásolná az ebben a fejezetben elmondott történetet. Lehetséges, hogy az Univerzum már az első másodpercekben kisimult. Ha pedig így történt, akkor a deutérium és a hélium keletkezése ugyanúgy számítható ki, mintha a Kozmológiai Elv mindvégig érvényben lett volna. De ha az Univerzum inhomogenitása és anizotropitása még a héliumszintézis idején is fennállt, még akkor is a hélium és a deutérium képződése minden egyenletesen táguló csomóban csupán e csomó tágulásának az ütemétől függene, és nem különbözne lényegesen attól, amit a standard modellben kiszámítottunk. így még az is lehetséges, hogy az egész általunk belátható Világegyetem csupán egy homogén és izotrop szigete egy nagyobb, inhomogén és anizotrop Világegyetemnek.

A Kozmológiai Elv körüli bizonytalanság főképp akkor válik valóban fontossá, amikor a Világegyetem fejlődésének nagyon korai szakaszát vagy végső szakaszát tekintjük. Az utolsó két fejezet túlnyomó részében továbbra is a Kozmológiai Elvre fogunk támaszkodni. Mindazonáltal el kell ismernünk: lehetséges, hogy egyszerű kozmológiai modellünk csupán az Univerzum egy kicsiny részletét, esetleg történetének csak egy korlátozott időszakát írja le.

 

VI Történeti kitérő

 

Egy rövid időre függesszük föl a korai Univerzum történetének vizsgálatát, s térjünk vissza az elmúlt három évtized kozmológiai kutatásainak történetéhez. Olyan történeti problémával kívánok itt foglalkozni, amely legalább olyan rejtélyes, mint amilyen izgalmas. A kozmikus mikrohullámú háttérsugárzás 1965-beli kimutatása a XX. század egyik legfontosabb tudományos fölfedezése. Kérdés: miért történt ez a fölfedezés szinte véletlenül? Vagy – másképpen fogalmazva – miért nem keresték ezt a sugárzást módszeresen már jóval 1965 előtt?

Mint az előző fejezetben láttuk, a kozmikus sugárzási háttér jelenlegi hőmérsékletének és az Univerzum tömegsűrűségének mért értékei a könnyű elemek olyan előfordulási gyakoriságát jósolják, ami jó egyezésben áll a tapasztalattal. Ezeket a számításokat azonban már jóval 1965 előtt el lehetett volna végezni „fordítva”; s így meg lehetett volna jósolni a kozmikus mikrohullámú háttérsugárzás létezését, s el lehetett volna kezdeni annak keresését is. A hélium és a hidrogén jelenleg megfigyelhető 20-30 százalékos, illetve 70-80 százalékos arányából következtetni lehetett volna arra, hogy az atommagok szintézise akkor kezdődött el, amikor a neutronok száma lecsökkent a magrészecskék számának 10-15 százalékára. (Mivel a hélium jelenlegi részaránya éppen kétszerese a neutronok részarányának az atommagok szintézise idején.) A neutronok száma pedig akkor volt ekkora, amikor az Univerzum hőmérséklete közel 1 milliárd kelvinre (10⁹ K) csökkent. Az a feltétel, hogy az atommagok szintézise ekkor kezdődött meg, lehetővé teszi, hogy 1 milliárd kelvinen megbecsüljük a magrészecskék sűrűségét, míg az e hőmérséklethez tartozó fotonsűrűség a feketetest-sugárzás ismert tulajdonságaiból számítható ki. így erre az időpontra a fotonok és a magrészecskék számaránya is meghatározható. De ez az arány nem változott az Univerzum fejlődése során, így értéke ma is ugyanekkora. A magrészecskék mai sűrűségéből tehát kiszámítható a jelenlegi fotonsűrűség, s így megjósolható egy olyan mikrohullámú kozmikus háttérsugárzás létezése, amelynek a hőmérséklete hozzávetőleg 1 és 10 kelvin közé esik. Ha a tudományok története is olyan egyszerű és töretlen vonalú volna, mint az Univerzumé, akkor e gondolatmenet révén valaki már a negyvenes-ötvenes években megjósolhatta volna a mikrohullámú háttérsugárzás létezését, és e jóslat a sugárzási háttér kimutatására ösztönözhette volna a csillagászokat. Ámde nem egészen így történt.

Tény, hogy 1948-ban már létezett egy ilyen – az előbb ismertetett gondolatmeneten alapuló – jóslat, ám ez sem akkor, sem később nem vezetett a sugárzás módszeres kereséséhez. A negyvenes évek végén ugyanis George Gamow és munkatársai, Ralph A. Alpher és Robert Herman kidolgozták a Nagy Bumm kozmológiai elméletét. Föltételezésük szerint az Univerzumban eredetileg csak neutronok voltak, majd ezek a jól ismert radioaktív bomlással spontán módon protonokra, elektronokra és antineutrínókra bomlottak el. Valamikor a tágulás során az Univerzum elérte azt a hőmérsékletet, amely már elég alacsony volt ahhoz, hogy a neutronok gyors befogadása révén a neutronokból és a protonokból nehéz elemek épüljenek föl. Alpher és Herman azt találta, hogy a könnyű elemek jelenleg megfigyelhető gyakoriságáról akkor lehet számot adni, ha a fotonok és a magrészecskék számaránya nagyságrendileg 1 milliárd. Felhasználva a magrészecskék mai kozmikus sűrűségére vonatkozó becsléseket, meg tudták jósolni a korai Univerzumból visszamaradt sugárzási háttér létezését, amelynek a hőmérsékletét 5 kelvinre becsülték!

Alpher, Herman és Gamow eredeti számításai nem voltak minden részletükben helyesek. Mint az előző fejezetben láttuk, az Univerzum kezdetben valószínűleg csaknem azonos számú protont és neutront tartalmazott – nem pedig csupán neutronokat. Másrészt a neutronok átalakulása protonokká (és viszont) elsősorban az elektronokkal, pozitronokkal, neutrínókkal és antineutrínókkal való ütközések révén történt, nem pedig radioaktív bomlással. E tévedésekre már 1950-ben rámutatott C. Hayashi, és 1953-ra Alpher és Herman (az ifjabb J. W. Follinnal együtt) már ki is dolgozta a módosított modellt, s ebben lényegében helyesen számították ki a proton-neutron-mérleg alakulását. Ez volt a korai Univerzum történetének első valóban mélyreható, modern elemzése.

Mindennek ellenére sem 1948-ban, sem 1953-ban nem kezdtek hozzá a megjósolt mikrohullámú sugárzás kereséséhez. Az igazság ugyanis az, hogy 1965 előtt az asztrofizikusok körében egyáltalán nem volt közismert, hogy a Nagy Bumm-elméletekben a hidrogén és a hélium aránya kikényszeríti egy olyan kozmikus sugárzási háttér létezését, ami a jelenlegi Univerzumban kísérletileg is kimutatható lenne. És ebben valójában nem az a furcsa, hogy az asztrofizikusok nagy többsége nem ismerte Alpher és Herman számításait, hiszen a tudományos közlemények tengerében egy vagy két cikk könnyen szem elől téveszthető. Jóval rejtélyesebb azonban az, hogy mintegy egy évtizeden keresztül miért nem jutott senki más erre az elméleti következtetésre. Hiszen minden elméleti ismeret rendelkezésre állt már. Az első számításokat követően, csupán 1964-ben vetődött fel ismét az a gondolat, hogy a Nagy Bumm modelljében az atommagok szintézisére vonatkozó számításokat végezzenek; ekkor azonban egyszerre többen is nekiláttak, egymástól függetlenül: a Szovjetunióban Ja. B. Zeldovics, Angliában Fred Hoyle és R. J. Tayler, az Egyesült Államokban pedig Peebles. Ám ugyanekkor már Penzias és Wilson is megkezdték megfigyeléseiket Holmdelben – s így végül is a mikrohullámú háttérsugárzás fölfedezését egyáltalán nem az elméleti kozmológusok ösztönözték.

Az is zavarba ejtő, hogy azok, akik pedig tudtak az Alpher-Herman-féle jóslatról, nem tulajdonítottak annak nagyobb fontosságot. Még maga Alpher, Follin, és Herman is azzal zárta 1953-as cikkét, hogy a nukleoszintézis problémája még „további tanulmányozás”-t igényel – vagyis nem voltak abban a helyzetben, hogy javított modelljükben is kiszámítsák a mikrohullámú sugárzási háttér várható hőmérsékletét. (Még csak meg sem említik korábbi becslésüket, amelynek alapján ez a hőmérséklet 5 kelvinnek adódott. Az Amerikai Fizikai Társulat 1953. évi közgyűlésén beszámoltak ugyan az atommagok szintézisére vonatkozó számításaikról, de – talán mert különböző laboratóriumokban dolgoztak – munkájukat sohasem közölték le végleges formában.) Évekkel később – már a mikrohullámú sugárzási háttér fölfedezése után – George Gamow egy Penziashoz intézett levelében rámutatott arra, hogy egy 1953-as cikkében, amely a Proceedings of the Royal Danish Academy című tudományos folyóiratban jelent meg, ő már megjósolta egy 7 kelvines sugárzási háttér létezését. Ez hozzávetőleg ugyanolyan nagyságrend, mint a mért sugárzás. Azonban ha egy kicsit alaposabban megvizsgáljuk az idézett cikket, azonnal kiderül, hogy Gamow jóslata matematikailag hibás érvelésen alapult, ami a Világegyetem korával kapcsolatos, és nem sok köze van az atommagok szintézisének általa kidolgozott elméletéhez.

Lehetne persze azzal is érvelni, hogy az ötvenes években és a hatvanas évek elején a könnyű elemek előfordulásának gyakoriságát még nem ismerték elég jól ahhoz, hogy bármiféle határozott következtetést vonhattak volna le a sugárzási háttér hőmérsékletéről. Tény, hogy még ma sem vagyunk igazán biztosak abban, hogy a hélium részaránya univerzálisan is 20-30 százalék. Ám a lényeg mégis az, hogy már jóval a hatvanas évek előtt is azt hitték, hogy az Univerzum tömegének túlnyomó részét a hidrogén adja. (Például 1956-ban Hans Suess és Harold Urey egy összefoglaló munkája a hidrogén arányát 75 tömegszázalékban adta meg.) Márpedig a hidrogén nem a csillagokban keletkezik – hiszen ő maga az az egyszerű fűtőanyag, amiből a csillagok, a nehezebb elemek fölépítésével, energiájukat nyerik. Már ennek a ténynek is elégnek kellene lennie ahhoz a megállapításhoz, hogy a fotonok és magrészecskék aránya szükségszerűen nagy, mert csak így képzelhető el, hogy az Univerzum korai szakaszában a hidrogén ne süljön össze héliummá és más nehezebb elemekké.

Természetesen fölvetődik a kérdés: valójában mikor is vált technikailag lehetségessé egy 3 kelvines izotrop sugárzási háttér kísérleti kimutatása? Nos, ezt elég nehéz pontosan megmondani, de kísérleti fizikus kollégáim szerint ezt a mérést már jóval 1965 előtt – az ötvenes években, de talán már a negyvenes évek közepén is! – el lehetett volna végezni. 1964-ben az MIT Sugárzási Laboratóriumának egyik csoportja, Robert Dicke vezetésével, egy felső korlátot tudott fölállítani bármiféle Földön kívüli eredetű, izotrop sugárzási háttér hőmérsékletére. Eszerint egy ilyen sugárzási ekvivalens hőmérséklete 1,00, 1,25 és 1,50 centiméteres hullámhosszakon csak 20 kelvinnél kisebb lehet. Ez az eredmény a légköri abszorpcióra vonatkozó vizsgálatsorozatnak csupán a mellékterméke volt, és nem volt valamiféle kozmológiai megfigyelőprogram része. Sőt, maga Dicke említette nekem, hogy amikor gondolkozni kezdett egy kozmikus mikrohullámú sugárzási háttér létezésének a lehetőségén, ő maga is elfeledkezett a saját 20 kelvines felső korlátjáról, amit két évtizeddel korábban kapott e háttér hőmérsékletére!

Ám azt hiszem, nem is az a fontos, hogy pontosan mikor vált lehetségessé a 3 kelvines izotrop mikrohullámú háttér kimutatása. A lényeg nem ez, hanem sokkal inkább az, hogy a rádiócsillagászok nem is tudtak arról, hogy ilyesmit kellene keresniük! Az így kialakult helyzet szöges ellentéte annak, ami a neutrínók fölfedezése körül kialakult. Amikor Pauli 1932-ben megjósolta a neutrínó létezését, teljesen nyilvánvaló volt, hogy a legcsekélyebb esély sincs arra, hogy ennek létezését bármely – akkor elvégezhető – kísérletben kimutassák. Ám ennek ellenére a neutrínók kimutatása állandó kihívásként élt a fizikusok tudatában, és amikor az ötvenes években az atomreaktorok kísérleti célokra hozzáférhetőkké váltak, azonnal elkezdték a neutrínókat keresni, és hamarosan sikerült is elcsípni őket! Még szembeszökőbben látszik ez az ellentét az antiproton esetében. Miután 1932-ben a kozmikus sugárzásban fölfedezték a pozitront, az elméleti fizikusokban megerősödött az a hit, hogy csakúgy, mint az elektronnak, a protonnak is létezik antirészecskéje. A harmincas évek kezdetleges ciklotronjainál nem volt számottevő esély arra, hogy antiprotont hozzanak létre, de a fizikusok számon tartották a problémát, és amikor az ötvenes években Berkeleyben megépítették a Bevatron gyorsítót, azt éppen akkora energiára tervezték, hogy általa majd antiprotonokat is előállíthassanak. A mikrohullámú sugárzási háttér esetében azonban semmi ilyesmi nem történt mindaddig, amíg Dicke és társai el nem kezdték méréseiket 1964-ben. És még ekkor is, a princetoni csoport semmit sem tudott Alpher, Herman és Gamow jó évtizeddel korábbi elméleti számításairól!

De hát hol volt a hiba? Véleményem szerint azt a tényt, hogy a 3 kelvines sugárzási háttér kutatásának jelentőségét nem ismerték fel az ötvenes években, legalábbis három érdekes okra lehet visszavezetni.

Először, tudni kell azt, hogy Alpher, Herman, Gamow és Follin egy tágabb érvényű kozmológiai elmélet keretei között dolgoztak. „Nagy Bumm”-modelljükben lényegében föltételezték, hogy nemcsak a hélium, de valamennyi nehezebb atommag az Univerzum korai szakaszában jött létre, a neutronok gyors elnyelődése révén. Bár ez az elmélet helyesen jósolja meg néhány nehezebb elem gyakoriságát, bajba kerül annak a megmagyarázásánál, hogy egyáltalán miért is léteznek nehéz elemek! Mint már korábban említettük, nincs 5 vagy 8 nukleont tartalmazó stabil atommag, s így nem lehetséges a héliumnál nehezebb elemek felépítése sem azáltal, hogy hélium (⁴He)-maghoz protonokat vagy neutronokat adunk, sem pedig héliummagok egyesítése révén. (Ezt az akadályt először Enrico Fermi és Anthony Turkevich vette észre.) És mivel a modell ebből a szempontból legalábbis megbízhatatlan volt, érthető, hogy nem vették komolyan a héliumgyakoriságra vonatkozó következtetéseit sem.

Az elemek gyakoriságának kozmológiai elmélete még inkább talaját vesztette akkor, amikor sikerült finomítani az alternatív elméletet, amely szerint az elemek a csillagokban szintetizálódtak. 1952-ben E. E. Salpeter megmutatta, hogy a sűrű, héliumban gazdag csillagok magjában az 5 és 8 nukleont tartalmazó magok képződésének előbb említett gátja áthidalható: két héliummag ütközése instabil berillium (⁸Be)-magot hoz létre, s ha ez még elbomlása előtt egy újabb héliummaggal ütközik, stabil szénatommag (¹²C) keletkezik. (Az Univerzum sűrűsége az atommag szintézise idején túlságosan kicsi ahhoz, hogy ez a folyamat végbemehessen.) 1957-ben jelent meg Geoffrey és Margaret Burbridge, Fowler és Hoyle nevezetes cikke, amelyben megmutatták, hogy a nehéz elemek a csillagokban keletkezhettek, olyan időszakokban, amikor a neutronfluxus meglehetősen nagy volt, elsősorban szupernóva-robbanások során. De az asztrofizikusok már az ötvenes évek előtt is erősen hajlottak arra a nézetre, hogy a hidrogéntől eltekintve valamennyi elem a csillagokban keletkezett. Mint Hoyle megjegyezte, ez annak a küzdelemnek a hatása lehetett, amit a csillagászok a század első évtizedeiben folytattak azért, hogy felkutassák a csillagok energiatermelésének forrását. 1940-re azután Hans Bethe és mások munkássága nyomán nyilvánvalóvá vált, hogy az energiatermelés kulcsa négy hidrogénmag fúziója héliumatommaggá, és ez a kép a negyvenes-ötvenes években nagy előrehaladásra vezetett a csillagok fejlődésének megértésében. Mint Hoyle mondja, e nagy sikerek után sok asztrofizikus elképzelhetetlennek tartotta azt a gondolatot, hogy az elemek keletkezése nem a csillagokban ment volna végbe.

De az atommagok csillagokban történő szintézisének elméleténél is problémák adódtak. Nehéz megérteni, miképp hozhattak létre a csillagok 25–30 százaléknyi héliumot – ugyanis a fúzió közben fölszabaduló energia nagyobb annál, mint amit a csillagok egész életük során kibocsátanak. A kozmológiai elmélet nagyon elegánsan szabadul meg ettől a problémától – ez az energia egyszerűen „elvész” a vöröseltolódás révén. 1964-ben Hoyle és R. J. Tayler kimutatta, hogy a jelenlegi Univerzumban levő hatalmas héliummennyiség nem keletkezhetett a csillagokban, és kiszámították, hogy a Nagy Bumm korai szakaszában viszont mintegy 36 tömegszázaléknyi hélium jöhetett létre. Meglehetősen furcsa módon, azt a hőmérsékletet, amin a héliumszintézis végbement, többé-kevésbé önkényesen 5 milliárd kelvinben szabták meg, jóllehet ez a föltevés egy ismeretlen paraméternek – a fotonok és nukleonok arányának – értékétől függ. Számításukat arra használták föl, hogy a meglevő, megfigyelt héliumgyakoriságból becsüljék meg ezt az arányt, és így tudták megjósolni egy hozzávetőleg jó nagyságrendbe eső hőmérsékletű mikrohullámú háttérsugárzás létezését. Mindazonáltal meglepő, hogy Hoyle, az állandó állapotú Világegyetem modelljének egyik kidolgozója hajlandó volt egy ilyenfajta gondolatmenet végigkövetésére, és elismerte azt, hogy ez bizonyítékául szolgálhat a „Nagy Bumm” típusú elméleteknek.

Ma az a nézet terjedt el, hogy az atommagok szintézise részben kozmológiailag, részben a csillagokban ment végbe: a hélium és talán még néhány más könnyű elem a korai Univerzumban keletkezett, míg minden más a csillagokban jött létre. Az atommagszintézis „Nagy Bumm”-modellje, amikor túl sokat akart megmagyarázni, elvesztette hitelét még azon a téren is, ahol pedig igazán illetékes volt: a héliumszintézis magyarázatánál.

Másodszor, ez a történet a kommunikáció megszakadásának klasszikus példája az elméleti és kísérleti szakemberek közt. Az elméleti fizikusok túlnyomó többsége nem ismerte föl, hogy a 3 kelvines sugárzási háttér valaha is detektálható lesz. Egy Peebleshez intézett levelében – amelynek dátuma 1967. június 23. – Gamow kifejtette, hogy sem ő, sem Alpher vagy Herman nem vizsgálta a Nagy Bummból visszamaradt sugárzás kimutatásának lehetőségét, mivel e kozmológiai számítások idején a rádiócsillagászat még gyerekcipőben járt. (Ezzel szemben Alpher és Herman azt mondták nekem, hogy ők megvizsgálták, kimutatható-e a kozmikus sugárzási háttér a John Hopkins Egyetem, a Tengerészeti Kutató Laboratórium és a Nemzeti Szabványügyi Hivatal akkori radarberendezéseivel, ám mindenütt azt a választ kapták, hogy egy 5 vagy 10 kelvines hőmérsékleti sugárzás az akkori technikával nem mutatható ki.) Másrészt úgy tűnik, hogy néhány szovjet asztrofizikus fölismerte a mikrohullámú háttér kimutathatóságát, de az amerikai műszaki folyóiratokban használt szakmai zsargon félrevezette őket. Egy 1964-es cikkében Ja. B. Zeldovics helyesen számította ki a kozmikus héliumgyakoriságot a jelenlegi sugárzási hőmérséklet két lehetséges értékére, és azt is helyesen ismerte fel, hogy ezek a mennyiségek kapcsolatban állnak egymással, mivel a fotonok száma osztva a magrészecskék számával (illetve az egy magrészecskére jutó entrópia) időben állandó. Úgy tűnik azonban, őt az „ég hőmérséklete” kifejezésnek a használata vezette félre E. A. Ohm 1961-es cikkében, amely a Bell System Technical ]ournal-ben jelent meg, s így azt a következtetést vonta le, hogy az említett mérések a sugárzási háttér hőmérsékletére egy 1 kelvines felső korlátot adtak. (Egyébként Ohm ugyanazt a 6 méter magasságú kürtő alakú antennát használta méréséhez, amivel később Penzias és Wilson fölfedezték a mikrohullámú hátteret!) Ez a kozmikus héliumgyakoriságra adódó meglehetősen alacsony becslésekkel párosulva Zeldovicsot a forró korai Univerzum gondolatának feladására késztette.

Természetesen azzal egy időben, amikor a kísérleti fizikusoktól csak gyéren folydogált az információ az elméletiekhez, ugyanez a helyzet állt fenn fordítva is. így Penzias és Wilson, amikor 1964-ben hozzákezdtek antennájuk kipróbálásához, nem ismerte Alpher és Herman elméleti jóslatát.

Harmadszor – és szerintem talán ez a legfontosabb –, a Nagy Bumm elmélete azért nem ösztönzött a 3 kelvines mikrohullámú háttér keresésére, mert a fizikusok számára rendkívül nehéznek tűnt a korai Univerzum bármiféle modelljének vagy elméletének elfogadása. (Ezzel kapcsolatban visszaemlékszem itt részben a saját, 1965 előtti attitűdömre is.) Az előbbiekben felsorolt nehézségek bármelyike leküzdhető lett volna egy kis erőfeszítéssel. De az első három perc időben olyan távol esik tőlünk, a hőmérsékleti és sűrűségviszonyok pedig annyira szokatlanok, hogy senki sem merte volna biztosan állítani, hogy a magfizika és a statisztikus fizika szokásos elméletei alkalmazhatóak ebben az esetben.

Ez is gyakran előfordul a fizikában – nem ott tévedünk, hogy túlságosan komolyan vesszük elméleteinket, hanem inkább abban, hogy nem vesszük eléggé komolyan őket. Szemléletileg gyakran nagyon nehéz tudomásul venni azt, hogy mindazoknak a számoknak és egyenleteknek, amelyekkel az íróasztalunk mellett eljátszogatunk, közük van a valódi világhoz. S ami még rosszabb, gyakran általános egyetértés alakul ki a tekintetben, hogy bizonyos jelenségek megközelítésére tett elméleti és kísérleti erőfeszítések komolytalanok, s nem érdemelnek figyelmet. Éppen ezért Gamow, Alpher és Herman különös elismerést érdemelnek, hogy mindezek ellenére megpróbálták komolyan venni a korai Univerzum modelljét, és kiszámították, hogy az ismert fizikai törvények alapján mit mondhatunk az első három percről. Még akkor is, ha az utolsó, döntő lépést nem tették meg: nem győzték meg a rádiócsillagászokat arról, hogy keresniük kell a mikrohullámú sugárzási hátteret. így a 3 kelvines sugárzási háttér 1965-ös fölfedezésének legfontosabb eredménye szerintem az volt, hogy rákényszerített minket arra, hogy komolyan vegyük azt az elképzelést, hogy valóban volt az Univerzumnak egy ilyen kezdeti szakasza.

Sokáig elidőztem ennél az elmulasztott lehetőségnél, mert számomra ez világítja meg leginkább a tudományok fejlődésének mikéntjét. Érthető, hogy a tudománytörténészek inkább a sikerekkel, a szenzációs fölfedezésekkel, briliáns levezetésekkel. Newton és Einstein géniuszának káprázatos elmeszökkenéseivel foglalkoznak. Ám úgy gondolom, a tudomány sikereinek megértése nem lehetséges anélkül, hogy látnánk, milyen nehézségek is vannak, milyen könnyen tévedhetünk, s gyakran milyen nehéz fölismerni, hogy mi legyen a legközelebbi teendőnk.