LOS HUMANOS SIEMPRE HEMOS QUERIDO CONTROLAR EL FUTURO O, al menos, predecir lo que va a ocurrir. Por esto la astrología es tan popular. Según ella, lo que pasa en la Tierra está relacionado con los movimientos de los planetas en el firmamento. Esto es una hipótesis que puede ser sometida a prueba científicamente, o lo sería si los astrólogos se comprometieran y formularan predicciones definidas que pudieran ser comprobadas. Sin embargo, con considerable astucia, expresan siempre sus predicciones en términos tan vagos que pueden ser aplicados a cualquier cosa que ocurra. Nunca se puede demostrar que predicciones como «sus relaciones personales pueden intensificarse» o «se le presentará una oportunidad financieramente interesante» sean erróneas.
Este mes Marte ocupa Sagitario y para usted será tiempo de intentar conocerse mejor. Marte le pide que viva su vida de acuerdo con lo que usted considera correcto, sin plegarse a lo que los demás consideren adecuado. Y esto ocurrirá.
El día 20, Saturno llega a la zona de su carta solar relacionada con sus obligaciones y su carrera, y aprenderá a asumir responsabilidades y a tratar relaciones difíciles.
Sin embargo, en el plenilunio, gozará de una perspectiva tan maravillosa de la globalidad de su vida que le transformará.
Pero el motivo real por el que la mayoría de científicos no cree en la astrología no es la presencia o la ausencia de evidencias científicas acerca de ella, sino que no resulta consistente con otras teorías que han sido comprobadas experimentalmente. Cuando Copérnico y Galileo descubrieron que los planetas giran alrededor del Sol y no de la Tierra, y Newton formuló las leyes que rigen sus movimientos, la astrología devino extremadamente implausible. ¿Por qué deberían las posiciones de los planetas en el firmamento vistas desde la Tierra, tener correlación alguna con las macromoléculas de un planeta menor que se autodenominan vida inteligente? (Fig. 4.1) Es esto lo que la astrología nos quisiera hacer creer. Para algunas de las teorías descritas en este libro no hay más evidencia experimental que para la astrología, pero creemos en ellas porque son consistentes con teorías que han superado numerosas pruebas experimentales.

(FIG. 4.1) Un observador en la Tierra (azul), que gira alrededor del Sol, observa Marte (rojo) sobre un fondo de constelaciones lejanas.
El complejo movimiento aparente de los planetas en el firmamento puede ser explicado mediante las leyes de Newton y no ejerce ninguna influencia sobre la suerte de las personas.
El éxito de las leyes de Newton y de otras teorías físicas condujo a la idea del determinismo científico, que fue expresada por primera vez a comienzos del siglo XIX por un científico francés, el marqués de Laplace. Laplace sugirió que si conociéramos las posiciones y las velocidades de todas las partículas del universo en un instante, las leyes de la física nos deberían permitir la predicción de cuál será el estado del universo en cualquier otro instante del pasado o del futuro (Fig. 4.2).

(FIG. 4.2) Si sabemos desde dónde y con qué velocidad es lanzada una pelota, podremos predecir adónde irá a parar.

(FIG. 4.3)
En otras palabras, si se cumple el determinismo científico, deberíamos poder, en principio, predecir el futuro y no necesitaríamos la astrología. Naturalmente, en la práctica, incluso algo tan simple como la teoría de la gravitación de Newton conduce a ecuaciones que no podemos resolver exactamente para más de dos partículas. Además, las ecuaciones presentan a menudo una propiedad conocida como caos, según la cual un pequeño cambio en la posición o la velocidad en un instante dado puede conducir a un comportamiento completamente diferente en instantes posteriores. Como bien saben los que han visto la película Parque Jurásico, una perturbación diminuta en un lugar puede provocar un cambio importante en otro. El aleteo de una mariposa en Tokio puede hacer que llueva en Central Park de Nueva York (Fig. 4.3). El problema radica en que la secuencia de acontecimientos no es repetible. La siguiente vez que la mariposa aletea, un cúmulo de otros factores que también influirán en el clima serán diferentes. Esta es la razón de que las predicciones del tiempo resulten tan poco fiables.
Así pues, aunque en principio las leyes de la electrodinámica cuántica nos deberían permitir calcular cualquier cosa de la química y la biología, no hemos logrado mucho éxito en la predicción del comportamiento humano a partir de ecuaciones matemáticas. Pero a pesar de estas dificultades prácticas, la mayoría de científicos se han hecho a la idea de que, de nuevo en principio, el futuro es predecible.

A primera vista, el determinismo también parece amenazado por el principio de incertidumbre, que establece que no podemos medir con precisión la posición y la velocidad de una partícula simultáneamente. Cuanto mayor es la precisión con que medimos la posición, menor será la precisión con que podamos determinar la velocidad, y viceversa. La versión de Laplace del determinismo científico sostenía que si conociéramos las posiciones y las velocidades de las partículas en un instante dado, podríamos determinar sus posiciones y velocidades en cualquier otro instante del pasado y del futuro. Pero ¿cómo podríamos ni siquiera empezar si el principio de incertidumbre nos impide conocer con precisión las posiciones y las velocidades en un instante? Por buenos que sean nuestros ordenadores, si les introducimos datos imprecisos, obtendremos predicciones también imprecisas.
Sin embargo, el determinismo fue restablecido en una forma modificada en una nueva teoría denominada mecánica cuántica, que incorporaba el principio de incertidumbre. Hablando con cierta impropiedad, diríamos que en la mecánica cuántica podemos predecir con precisión la mitad de lo que podríamos esperar predecir en la perspectiva clásica de Laplace. En la mecánica cuántica, una partícula no tiene una posición o una velocidad bien definidas, pero su estado puede ser representado mediante lo que se llama la función de onda (Fig. 4.4).
- Función de onda Ψ con un pico muy acusado.

- Distribución de probabilidad de la velocidad de
la partícula.

- Función de onda Ψ en forma de tren de
ondas.

- Distribución de probabilidad de la velocidad de
la partícula.
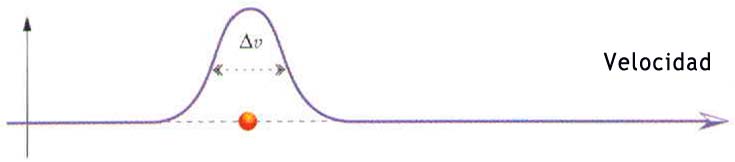
(FIG. 4.4) La función de onda determina las probabilidades de que la particula se halle en diferentes posiciones y tenga diferentes velocidades, de forma que Δx y Δv obedezcan el principio de incertidumbre.
Una función de onda es un número en cada punto del espacio que indica la probabilidad de hallar la partícula en dicha posición. La tasa de variación de la función de onda con la posición indica la probabilidad de diferentes velocidades de la partícula. Algunas funciones de onda tienen un pico muy agudo en un punto particular del espacio. En estos casos, la incertidumbre en la posición de la partícula es pequeña. Pero también podemos ver en el diagrama que, en estos casos, la función de onda cambia muy rápidamente en las proximidades del punto, hacia arriba en un lado y hacia abajo en el otro. Ello significa que la distribución de probabilidad de la velocidad se esparce en un dominio amplio de valores posibles. En otras palabras, la incertidumbre en la velocidad es elevada. Consideremos, en cambio, un tren continuo de ondas. Ahora hay una gran incertidumbre en la posición, pero la incertidumbre en la velocidad es pequeña. Por ello, la descripción de una partícula mediante la función de onda no supone una posición ni una velocidad bien definidas, sino que satisface el principio de incertidumbre. Sabemos ahora que la función de onda es todo cuanto puede ser bien definido. Ni siquiera podemos suponer que la partícula tiene una posición y una velocidad que Dios conoce pero que nos permanecen ocultas. Las teorías de «variables ocultas» predicen resultados que discrepan de las observaciones. Incluso Dios está limitado por el principio de incertidumbre y no puede saber la posición y la velocidad, sino sólo la función de onda.
La tasa con que la función de onda cambia con el tiempo viene dada por lo que se llama la ecuación de Schrödinger (Fig. 4.5). Si conocemos la función de onda en un instante, podemos utilizar dicha ecuación para calcularla en cualquier otro instante, pasado o futuro. Por lo tanto, en la teoría cuántica todavía hay determinismo, aunque a una escala reducida. En vez de poder predecir las posiciones y las velocidades, sólo podemos predecir la función de onda. Ésta nos permite predecir o las posiciones o las velocidades, pero no ambas con precisión. Por lo tanto, en la teoría cuántica la capacidad de efectuar predicciones precisas es justo la mitad que en la visión clásica de Laplace. Sin embargo, en este sentido restringido, todavía es posible sostener que hay determinismo.

(FIG. 4.5) LA ECUACIÓN DE SCHRÖDINGER
La evolución de la función de onda Ψ queda determinada por el operador Hamiltoniano H, relacionado con la energía del sistema físico considerado.
Sin embargo, el uso de la ecuación de Schrödinger para estudiar la evolución de la función de onda hacia adelante en el tiempo (es decir, para predecir lo que pasará en instantes futuros) supone implícitamente que el tiempo fluye con suavidad e indefinidamente. Ciertamente es así en la física newtoniana, en la cual el tiempo se supone absoluto, lo que significa que cada acontecimiento de la historia del universo está etiquetado con un número llamado tiempo, y que la serie de etiquetas temporales se extiende suavemente desde el pasado infinito al futuro infinito. Esto es lo que podríamos llamar la visión del tiempo según el sentido común, y es la visión que, en el fondo de su mente, tiene del tiempo la mayoría de la gente e incluso la mayoría de los físicos. Sin embargo, en 1905, como hemos visto, el concepto de tiempo absoluto fue destronado por la teoría especial de la relatividad, en que el tiempo no es ya una magnitud independiente, sino sólo una dirección más en un continuo cuadridimensional llamado espacio-tiempo. En la relatividad especial, diferentes observadores que se muevan con diferentes velocidades seguirán caminos diferentes en el espacio-tiempo. Cada observador tiene su propia medida del tiempo a lo largo de su camino, y diferentes observadores medirán diferentes intervalos temporales entre sucesos (Fig. 4.6).

(FIG. 4.6) En el espacio-tiempo plano de la relatividad especial, observadores que se muevan con diferentes velocidades medidas del tiempo, pero podemos utilizar la ecuación de Schrödinger con cualquiera de estos tiempos para predecir la función de onda del futuro.
Así pues, en la relatividad especial no hay un único tiempo absoluto que pueda ser utilizado para etiquetar los acontecimientos. Sin embargo, el espacio-tiempo de la relatividad especial es plano, lo que significa que en esta teoría el tiempo medido por cualquier observador que se mueva libremente aumenta suavemente en el espacio-tiempo desde menos infinito en el infinito pasado hasta más infinito en el futuro infinito. Podemos utilizar en la ecuación de Schrödinger cualquiera de estas medidas del tiempo para estudiar cómo evoluciona la función de onda. En la relatividad especial, por lo tanto, todavía tenemos la versión cuántica del determinismo.
La situación es diferente en la teoría general de la relatividad, en la cual el espacio-tiempo no es plano sino curvado y distorsionado por su contenido en materia y energía. En nuestro sistema solar, la curvatura del espacio-tiempo es tan ligera, al menos a escala macroscópica, que no interfiere con nuestra idea usual del tiempo. En esta situación, todavía podríamos utilizar este tiempo en la ecuación de Schrödinger para obtener la evolución determinista de la función de onda. Sin embargo, una vez permitimos que el espacio-tiempo esté curvado, queda abierta la puerta a la posibilidad de que tenga una estructura que no admita un tiempo que aumente continuamente para todos los observadores, como esperaríamos para una medida temporal razonable. Por ejemplo, supongamos que el espacio-tiempo fuera como un cilindro vertical (Fig. 4.7).
(FIG. 4.7) EL TIEMPO SE DETIENE
Las medidas del tiempo se presentarían necesariamente puntos de estancamiento donde el asa toca el cilindro principal; puntos en que el tiempo se detiene. En ellos, no pasaría el tiempo. Por lo tanto, no sería posible utilizar la ecuación de Schrödinger para predecir cómo será la función de onda en el futuro.
La altura en el cilindro constituiría una medida del tiempo que aumentaría para cada observador y transcurriría desde menos infinito a más infinito. Imaginemos, en cambio, que el espacio-tiempo fuera como un cilindro con un asa (o «agujero de gusano») que se ramificara y después volviera a juntarse con el cilindro. En este caso, cualquier medida del tiempo presentaría necesariamente puntos de estancamiento donde el asa toca el cilindro: puntos en que el tiempo se detiene. En ellos, el tiempo no aumentaría para ningún observador. En este espacio-tiempo, no podríamos utilizar la ecuación de Schrödinger para obtener una evolución determinista de la función de onda. Tengan cuidado con los agujeros de gusano: nunca se sabe qué puede salir de ellos.

(FIG. 4.8)

Los agujeros negros son el motivo que nos lleva a creer que el tiempo no aumentará para cada observador. El primer tratado sobre agujeros negros apareció en 1783. Un antiguo catedrático de Cambridge, John Michell, presentó el siguiente argumento. Si disparamos una partícula, como por ejemplo una bala de cañón, verticalmente hacia arriba, su ascenso será frenado por la gravedad y al fin la partícula dejará de subir y empezará a caer de nuevo (Fig. 4.8). Sin embargo, si la velocidad inicial hacia arriba supera un cierto valor crítico llamado velocidad de escape, la gravedad no será suficientemente intensa para detener la partícula, y ésta se escapará. La velocidad de escape vale unos 12 kilómetros por segundo para la Tierra y unos 618 kilómetros por segundo para el Sol.
Estas dos velocidades de escape son mucho mayores que la velocidad de las balas de cañón reales, pero resultan pequeñas en comparación con la velocidad de la luz, que vale 300.000 kilómetros por segundo. Por lo tanto, la luz puede escapar sin dificultad de la Tierra y del Sol. Michell arguyó, sin embargo, que podría haber estrellas cuya masa fuera mucho mayor que la del Sol y tuvieran velocidades de escape mayores que la velocidad de la luz (Fig. 4.9). No las podríamos ver, porque la luz que emitieran sería frenada y arrastrada hacia atrás por la gravedad de la estrella. Serían lo que Michell llamó estrellas negras y hoy denominamos agujeros negros.

(FIG. 4.9)
EL AGUJERO NEGRO DE SCHWARZSCHILD
En 1916, el astrónomo alemán Karl Schwarzschild
obtuvo una solución de la teoría general de la relatividad de
Einstein que representa un agujero negro esférico. El trabajo de
Schwarzschild reveló una consecuencia sorprendente de la
relatividad general. Demostró que si la masa de una estrella se
concentra en una región suficientemente pequeña, el campo
gravitatorio en su superficie deviene tan intenso que ni siquiera
la luz podría escapar de ella. Esto es lo que actualmente llamamos
un agujero negro, una región del espacio-tiempo limitada por un
denominado horizonte de sucesos allende el cual es imposible que
nada, ni siquiera la luz, llegue a un observador distante.
Durante mucho tiempo, la mayoría de los físicos, incluido Einstein,
se mostraron escépticos sobre la posibilidad de que tales
configuraciones extremas de la materia pudieran darse en el
universo real. Sin embargo, ahora comprendemos que cuando alguna
estrella suficientemente pesada y que no gire sobre su eje agota su
combustible nuclear, se colapsará necesariamente hasta formar un
agujero negro de Schwarzschild perfectamente esférico. El radio (R)
del horizonte de sucesos del agujero negro sólo depende de su masa,
y viene dado por la fórmula
R = 2GM/c2
En esta fórmula el símbolo (c) significa la velocidad de la luz, (G) la constante de Newton, y (M) la masa del agujero negro. ¡Un agujero negro que tuviera la misma masa que el Sol, por ejemplo, tendría un radio de tan sólo unos cuatro kilómetros!
La idea de Michell de las estrellas negras estaba basada en la física newtoniana, en la cual el tiempo es absoluto y sigue fluyendo pase lo que pase. Por lo tanto, no afectaba la capacidad de predecir el futuro en la imagen clásica newtoniana. Pero la situación es muy diferente en la teoría general de la relatividad, en que los cuerpos con masa curvan el espacio-tiempo.
En 1916, poco después de la primera formulación de la teoría, Karl Schwarzschild (que murió poco después como consecuencia de una enfermedad contraída en el frente ruso en la primera guerra mundial) obtuvo una solución de las ecuaciones de campo de la relatividad general que representaba un agujero negro. Durante muchos años, el descubrimiento de Schwarzschild no fue comprendido ni valorado en lo que merecía. El mismo Einstein nunca creyó en los agujeros negros, y su actitud fue compartida por la mayor parte de la vieja guardia de la relatividad general. Recuerdo mi visita a París para dar un seminario sobre mi descubrimiento de que la teoría cuántica implica que los agujeros negros no son completamente negros. Mi seminario no tuvo mucho eco porque en aquel tiempo casi nadie en París creía en los agujeros negros. Los franceses opinaban, además, que el nombre, tal como lo traducían, trou noir, tenía dudosas connotaciones sexuales, y debería ser sustituido por astre occlu, o «estrella oculta». Sin embargo, ni éste ni otros nombres que han sido sugeridos han logrado cautivar la imaginación del público como el término agujero negro, que fue acuñado por John Archibald Wheeler, el físico americano que inspiró muchos de los trabajos modernos en este campo.
JOHN WELLER
John Archibald Wheeler nació en 1911 en Jacksonville, Florida. En 1933 se doctoró en la universidad John Hopkins con un trabajo sobre el esparcimiento de la luz por los átomos de helio. En 1938, trabajó con el físico danés Niels Bohr para desarrollar la teoría de la fisión nuclear. Posteriormente, Wheeler trabajó durante un tiempo con su estudiante de doctorado Richard Feynman, dedicado al estudio de la electrodinámica, pero poco después de que los Estados Unidos entraran en la segunda guerra mundial, ambos participaron en el Proyecto Manhattan.
A comienzos de los cincuenta, inspirado por el trabajo de Robert Oppenheimer de 1939 sobre el colapso gravitatorio de una estrella masiva, Wheeler dirigió su atención a la teoría de la relatividad general de Einstein. En aquella época, la mayoría de los físicos estaban inmersos en el estudio de la física nuclear, y la relatividad general no era considerada realmente relevante para el mundo físico. Pero, casi en solitario, Wheeler transformó el campo mediante su investigación y su enseñanza en Princeton del primer curso de relatividad general.
Mucho después, en 1969, acuñó el término agujero negro para el estado colapsado de la materia, en cuya realidad pocos habían creído. Inspirado por el trabajo de Werner Israel, conjeturó que los agujeros negros no tienen pelos, lo que significa que el estado colapsado de cualquier estrella masiva no rotante podría ser descrito de hecho por la solución de Schwarzschild.

(FIG. 4.11) Las estrellas se forman en nubes de gas y polvo, como la nebulosa de Orión.
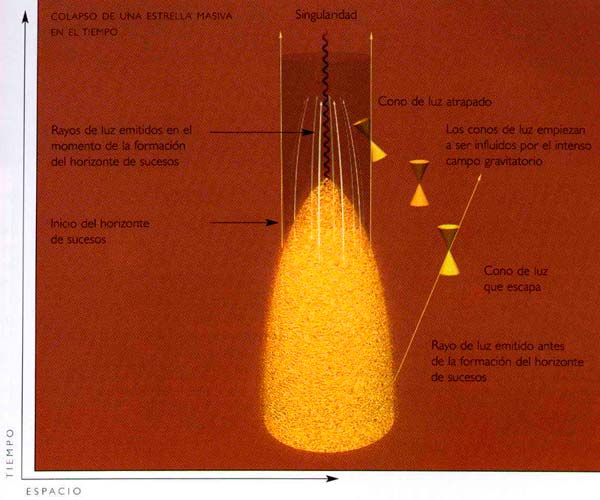
El descubrimiento de los quásares en 1963 conllevó una explosión de trabajos teóricos sobre agujeros negros y de intentos observacionales para detectarlos (Fig. 4.10). He aquí la imagen que emergió de todo ello. Consideremos lo que creemos que sería la historia de una estrella con una masa veinte veces la del Sol. Tales estrellas se forman a partir de nubes de gas, como las de la nebulosa de Orión (Fig. 4.11). A medida que dichas nubes se contraen bajo la acción de su propia gravedad, el gas se calienta y al final llega a temperatura suficientemente elevada para iniciar la reacción de fusión nuclear que convierte hidrógeno en helio. El calor generado en este proceso produce una presión que sostiene la estrella contra su propia gravedad y detiene su contracción. Una estrella permanecerá en este estado durante un largo tiempo, quemando hidrógeno y radiando luz al espacio.

(FIG. 4.10) El quásar 3C273, la primera fuente cuasiestelar de radiofrecuencia que fue descubierta, produce una inmensa potencia de una pequeña región. Parece que el único mecanismo que podria dar razón de esta altisima luminosidad sería la caída de la materia a un agujero negro.
El campo gravitatorio de la estrella afectará las trayectorias de los rayos de luz procedentes de ella. Podemos trazar un diagrama con el tiempo en el eje vertical y la distancia al centro de la estrella en el eje horizontal (Fig. 4.12). En este diagrama, la superficie de la estrella está representada por dos líneas verticales, una a cada lado del eje. Podemos expresar el tiempo en segundos y la distancia en segundos-luz, la distancia que recorre la luz en un segundo. Cuando utilizamos estas unidades, la velocidad de la luz es 1, es decir, la velocidad de la luz es un segundo-luz por segundo. Ello significa que lejos de la estrella y de su campo gravitatorio, la trayectoria de un rayo de luz en este diagrama queda representada por una recta que forma un ángulo de 45 grados con la vertical. Sin embargo, más cerca de la estrella, la curvatura del espacio-tiempo producida por su masa modificará las trayectorias de los rayos luminosos y hará que formen con la vertical un ángulo más pequeño.

(FIG. 4.12) Espacio-tiempo en las proximidades de una estrella que no se colapsa. Los rayos de luz escapan de la superficie de la estrella (líneas verticales rojas). Lejos de ella, los rayos de luz forman un ángulo de 45 grados con la vertical, pero cerca de la estrella la deformación del espacio-tiempo por la masa de ésta hace que los rayos formen con la vertical un ángulo más pequeño.
Las estrellas muy pesadas queman el hidrógeno para formar helio mucho más rápidamente que el Sol, hasta el punto que pueden agotar el hidrógeno en tan sólo unos pocos centenares de millones de años. Tras ello, las estrellas se enfrentan a una crisis. Pueden quemar helio y formar elementos más pesados, como por ejemplo carbono y oxígeno, pero estas reacciones nucleares no liberan mucha energía, de manera que las estrellas pierden calor y disminuye la presión térmica que las sostiene contra la gravedad. Por lo tanto, empiezan a contraerse. Si su masa es mayor que unas dos veces la masa solar, la presión nunca será suficiente para detener la contracción. Se colapsarán a tamaño cero y a densidad infinita para formar lo que llamamos una singularidad (Fig. 4.13). En el diagrama del tiempo en función de la distancia al centro, a medida que la estrella se encoge, las trayectorias de los rayos luminosos procedentes de la superficie emergerán con ángulos cada vez menores respecto de la vertical. Cuando la estrella alcanza un cierto radio crítico, la trayectoria será vertical en el diagrama, lo que significa que la luz se mantendrá suspendida a una distancia constante del centro de la estrella, sin escapar de ella. Esta trayectoria crítica de la luz barre una superficie denominada horizonte de sucesos, que separa la región del espacio-tiempo cuya luz puede escapar y la región de la cual no puede escapar. La luz emitida por la estrella después de atravesar el horizonte de sucesos será devuelta hacia adentro por la curvatura del espacio-tiempo. La estrella se habrá convertido en una de las estrellas negras de Michell o, en términos actuales, en un agujero negro.
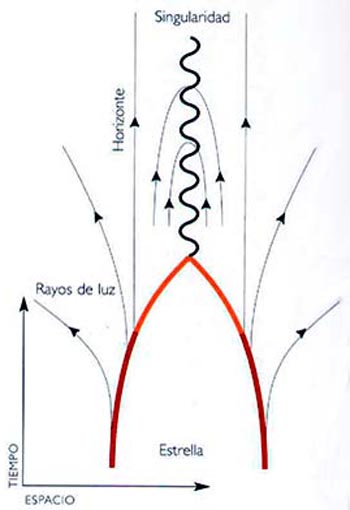
(Fig. 4.13) Si la estrella se colapsa (líneas rojas que se cortan en un punto) la deformación deviene tan grande que los rayos de luz de las proximidades de la estrella se mueven hacia adentro. Se ha formado un agujero negro, una región del espacio-tiempo de la cual la luz no puede escapar
El horizonte, la frontera exterior de un agujero negro, está formado por los rayos de luz que están justo a punto de escapar del agujero negro, pero que permanecen sobrevolándolo a una distancia constante del centro.
¿Cómo podemos detectar un agujero negro si de él no puede escapar ninguna luz? La respuesta es que un agujero negro sigue ejerciendo sobre los objetos circundantes la misma fuerza gravitatoria que ejercía el cuerpo que se colapsó. Si el Sol fuera un agujero negro y se hubiera convertido en tal sin perder masa alguna, los planetas seguirían girando a su alrededor como lo hacen en la actualidad.
Una manera de localizar agujeros negros es por lo tanto buscar materia que gire alrededor de lo que parece un objeto compacto e invisible de gran masa. Se ha observado un cierto número de tales sistemas. Quizás los más impresionantes son los agujeros negros gigantes que hay en el centro de las galaxias y los quásares (Fig. 4.15).
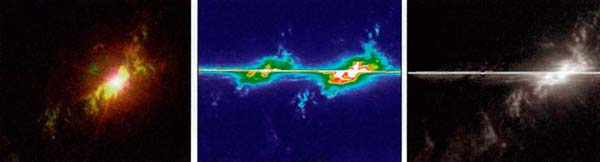
(FIG. 4.15) UN AGUJERO NEGRO EN EL CENTRO DE UNA GALAXIA
Izquierda: La galaxia NGC4151 vista por la cámara
planetaria de campo ancho.
Centro: La línea horizontal que atraviesa la imagen
corresponde a la luz generada por el agujero negro que se halla en
el centro de 4151.
Derecha: Imagen que muestra la velocidad de las emisiones de
oxígeno. Todas las evidencias indican que NGC 4151 contiene un
agujero negro de cien millones de veces la masa del Sol.
Las propiedades de los agujeros negros explicadas hasta aquí no suscitan grandes problemas con el determinismo. El tiempo terminaría para un astronauta que cayera a un agujero negro y chocara con la singularidad. Sin embargo, en la relatividad general tenemos la libertad de medir el tiempo con diferentes ritmos en diferentes lugares. Por lo tanto, podríamos acelerar el reloj del astronauta a medida que se aproxima a la singularidad, de manera que todavía registrara un intervalo infinito de tiempo. En el diagrama del tiempo en función de la distancia, las superficies de valor constante de este nuevo tiempo se acumularían cerca del centro, por debajo del punto donde apareció la singularidad. Pero en el espacio-tiempo aproximadamente plano a gran distancia del agujero negro coincidirían con la medida habitual del tiempo (Fig. 4.14).

(FIG. 4.14)
Podríamos utilizar este tiempo en la ecuación de Schrödinger y calcular la función de onda en tiempos posteriores si la conociéramos inicialmente. Así pues, todavía tendríamos determinismo. Conviene subrayar, sin embargo, que en instantes posteriores una parte de la función de onda se halla en el interior del agujero negro, donde no puede ser observada por nadie del exterior. Por lo tanto, un observador que tome precauciones para no caer en el agujero negro no puede retrotraer la ecuación de Schrödinger hacia atrás y calcular la función de onda en momentos anteriores. Para ello, precisaría conocer la parte de ella que hay en el interior del agujero negro. Ésta contiene la información de lo que cayó en el interior de éste. La cantidad de información puede ser grande, porque un agujero negro de masa y velocidad de rotación determinadas puede ser formado a partir de un número muy elevado de diferentes conjuntos de partículas. Un agujero negro no depende de la naturaleza del cuerpo cuyo colapso lo ha formado. John Wheeler llamó a este resultado «los agujeros negros no tienen pelos». Ello confirmó las sospechas de los franceses.

La ilustración muestra un astronauta que, a las 11:59.57, aterriza sobre una estrella que se está colapsando y se mantiene sobre ella a medida que se encoge por debajo del radio crítico en que la gravedad se hace tan intensa que ninguna señal puede escapar. Envía señales de su reloj a una nave espacial que gira alrededor de la estrella en intervalos regulares.
Alguien que observe la estrella a distancia nunca verá que el astronauta cruce el horizonte de sucesos y entre en el agujero negro, sino que le parecerá que la estrella permanece inmóvil justo encima del radio crítico, y un reloj en su superficie parecerá frenarse hasta detenerse.
El resultado, sin pelo
La dificultad con el determinismo surgió cuando descubrí que los agujeros negros no son completamente negros. Tal como vimos en el Capítulo 2, la teoría cuántica implica que los campos no pueden ser exactamente nulos ni siquiera en lo que llamamos el vacío. Si lo fueran, tendrían tanto un valor exacto de la posición, en el cero, y una tasa de cambio o velocidad que también valdría exactamente cero. Ello violaría el principio de incertidumbre, que exige que la posición y la velocidad no pueden estar bien definidas simultáneamente. Por ello, debe haber un cierto grado de lo que se denomina fluctuaciones del vacío (tal como el péndulo del Capítulo 2 tenía que tener fluctuaciones del punto cero). Las fluctuaciones del vacío pueden ser interpretadas de diversas maneras que parecen diferentes pero que de hecho son matemáticamente equivalentes. Desde una perspectiva positivista, tenemos la libertad de utilizar la imagen que nos resulte más útil para el problema en cuestión. En este caso, resulta conveniente interpretar las fluctuaciones del vacío como pares de partículas virtuales que aparecen conjuntamente en algún punto del espacio-tiempo, se separan y después vuelven a encontrarse y se aniquilan de nuevo la una con la otra. «Virtual» significa que estas partículas no pueden ser observadas directamente, pero sus efectos indirectos pueden ser medidos, y concuerdan con las predicciones teóricas con un alto grado de precisión (Fig. 4.16).

(FIG. 4.16) En el espacio vacío aparecen pares de partículas; tras una breve existencia se aniquilan mutuamente.
TEMPERATURA DEL AGUJERO NEGRO
Los agujeros negros emiten radiación como si fueran cuerpos calientes con una temperatura (T) que sólo depende de su masa. En términos más precisos, la temperatura viene dada por la siguiente fórmula:
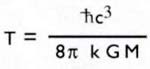
En esta fórmula, el símbolo (c) representa la velocidad de la luz, (ħ) la constante de Planck, (G) la constante de Newton de la gravitación y (k) la constante de Boltzmann.
Finalmente, (M) representa la masa del agujero negro, de manera que cuanto menor sea el agujero, más elevada será su temperatura. Esta fórmula nos indica que la temperatura de un agujero negro de unas pocas veces la masa solar está sólo una millonésima de grado por encima del cero absoluto.
En presencia de un agujero negro, un miembro de un par de partículas puede caer al mismo, dejando libre al otro miembro, que puede escapar al infinito (Fig. 4.17). A un observador lejano le parecerá que las partículas que escapan del agujero negro han sido radiadas por él. El espectro del agujero negro es exactamente el que esperaríamos de un cuerpo caliente, con una temperatura proporcional al campo gravitatorio en el horizonte —la frontera— del agujero negro. En otras palabras, la temperatura del agujero negro depende de su tamaño.

(FIG. 4.17) Partículas virtuales que aparecen y se aniquilan mutuamente en las proximidades del horizonte de sucesos de un agujero negro.
Una de las partículas del par cae al agujero negro, en tanto que su gemela queda libre para escapar. Desde el exterior del horizonte de sucesos, parece que el agujero negro haya radiado las partículas que escapaban.
La temperatura de un agujero negro de unas pocas masas solares valdría aproximadamente una millonésima de grado sobre el cero absoluto, y la de un agujero negro mayor sería todavía más baja. Así pues, cualquier radiación cuántica de dichos agujeros negros quedaría completamente ahogada por la radiación de 2,7 K remanente de la gran explosión caliente: la radiación cósmica de fondo de que hablamos en el Capítulo 2. Sería posible detectar esta radiación para agujeros negros más pequeños y más calientes, pero no parece que haya muchos a nuestro alrededor. Es una lástima, ya que si encontraran uno me darían un premio Nobel. Sin embargo, hay evidencias observacionales indirectas de esta radiación, que provienen del universo primitivo. Como dijimos en el Capítulo 3, se cree que en épocas muy tempranas de su historia el universo pasó por una etapa inflacionaria durante la cual se expandió con ritmo cada vez más rápido. La expansión durante esta etapa habría sido tan rápida que algunos objetos se hallarían demasiado lejos de nosotros para que su luz nos pueda alcanzar, el universo se habría expandido demasiado y demasiado rápidamente mientras la luz estaba viajando hacia nosotros. Por lo tanto, habría en el universo un horizonte como el de los agujeros negros, que separaría la región cuya luz nos puede llegar de aquélla cuya luz no nos puede alcanzar (Fig. 4.18).

(FIG. 4.18) La solución de Sitter de las ecuaciones de campo de la relatividad general representa un universo que se expande de forma inflacionaria. En el diagrama, el tiempo se representa en el eje vertical y el tamaño del universo en el eje horizontal. Las distancias espaciales aumentan tan rápidamente que la luz de las galaxias distantes nunca nos llegará, y hay un horizonte de sucesos, una frontera de la región que no podemos observar, como en los agujeros negros.
Argumentos muy parecidos indican que este horizonte debería emitir radiación térmica, tal como ocurre con el horizonte de los agujeros negros. Hemos aprendido a esperar un espectro característico de las fluctuaciones de densidad en la radiación térmica. En el caso que estamos considerando, tales fluctuaciones de densidad se habrían expandido con el universo. Cuando su escala de longitud hubiera superado el tamaño del horizonte de sucesos se congelarían, de manera que en la actualidad las podemos observar como pequeñas variaciones en la temperatura de la radiación cósmica de fondo remanente del universo primitivo. Lo que hemos podido observar de estas variaciones concuerda con las predicciones de las fluctuaciones térmicas con una notable precisión.
Aunque la evidencia observacional de la radiación de los agujeros negros es bastante indirecta, todos los que han estudiado el problema aceptan que debe producirse, por consistencia con otras teorías comprobadas experimentalmente. Ello tiene consecuencias importantes para el determinismo. La radiación de un agujero negro se llevará energía, lo cual significa que éste deberá perder masa y encogerse. De ello se sigue que su temperatura aumentará y su tasa de radiación crecerá. Al final, la masa del agujero negro se aproximará a cero. No sabemos calcular qué pasa en este punto, pero la única respuesta natural y razonable parece que el agujero negro acabe por desaparecer por completo. Si es así, ¿qué ocurre con la parte de la función de onda y de la información que ésta contiene sobre lo que había caído al agujero negro? Una primera conjetura podría ser que esta parte de la función de onda, y la información que transporta, emergería cuando el agujero negro terminara por desaparecer. Sin embargo, la información no puede ser transportada gratuitamente, como advertimos cuando recibimos la factura telefónica.
La información necesita energía que la transporte, y en las etapas finales de un agujero negro queda muy poca energía. La única manera plausible en que la información interior podría salir sería emerger continuamente con la radiación, en lugar de esperar a la etapa final. Sin embargo, en la descripción en que un miembro de un par de partículas virtuales cae al agujero negro y el otro miembro se escapa, no esperaríamos que la partícula que escapa esté relacionada con la que cayó en el interior, ni lleve información sobre ella. Por lo tanto, parecería que la única respuesta es que la información contenida en la parte de la función de onda del interior del agujero negro desaparece (Fig. 4.19).

(FIG. 4.19) La energía positiva que se lleva la radiación térmica de su horizonte reduce la masa del agujero negro. A medida que pierde masa, su temperatura y su tasa de radiación aumentan, de manera que pierde masa aún más rápidamente. No sabemos qué ocurre cuando la masa deviene extremadamente pequeña, pero lo más probable es que el agujero negro termine por desaparecer completamente.
Esta pérdida de información tendría consecuencias importantes para el determinismo. Para empezar, hemos observado que incluso si conociéramos la función de onda tras la desaparición del agujero negro, no podríamos retrotraer la ecuación de Schrödinger para calcular la función de onda antes de la formación del agujero negro. Lo que ésta era dependería en parte del fragmento de la función de onda que se perdió en el agujero negro. Estamos acostumbrados a pensar que podemos conocer el pasado con exactitud, pero en realidad, si se pierde información en los agujeros negros, podría haber pasado cualquier cosa.
En general, sin embargo, la gente como los astrólogos y los que los consultan están más interesados en predecir el futuro que en retro-decir el pasado. A primera vista, podría parecer que la pérdida de una parte de la función de onda en el agujero negro no impediría predecir la función de onda en el exterior de éste. Pero resulta que esta pérdida sí interfiere con tales predicciones, tal como podemos ver si consideramos un experimento mental propuesto por Einstein, Boris Podolsky y Nathan Rosen en los años 1930.
Imaginemos que un átomo radiactivo decae y emite dos partículas en direcciones opuestas y con espines opuestos. Un observador que sólo mire una partícula no puede predecir si estará girando hacia la derecha o hacia la izquierda. Pero si al efectuar la medición observa que está girando hacia la derecha, puede predecir a ciencia cierta que la otra partícula estará girando hacia la izquierda, y viceversa (Fig. 4.20). Einstein pensó que esto demostraba que la teoría cuántica era ridícula, ya que en este momento la otra partícula se podría hallar en el confín de la galaxia, pero aun así sabríamos instantáneamente cómo está girando. Sin embargo, la mayoría de los otros científicos creen que era Einstein quien se confundía, y no la teoría cuántica. El experimento mental de Einstein-Podolsky-Rosen no demuestra que podamos enviar información con velocidad mayor que la de la luz. Ello sería ridículo. No podemos escoger que la partícula que mediremos nosotros esté girando hacia la derecha, por lo cual no podemos prescribir que la partícula del observador distante esté girando hacia la izquierda.

(FIG. 4.20) En el experimento mental de Einstein-Podolsky-Rosen, el observador que ha medido el espín de una partícula sabrá la dirección del espín de la segunda partícula.
De hecho, este experimento mental describe exactamente lo que ocurre con la radiación del agujero negro. El par de partículas virtuales tendrá una función de onda que predice que los dos miembros tienen espines exactamente opuestos (Fig. 4.21). Lo que nos gustaría es predecir el espín y la función de onda de la partícula saliente, cosa que lograríamos si pudiéramos observar la partícula que ha caído al interior. Pero ahora dicha partícula se halla dentro del agujero negro, donde su espín y su función de onda no pueden ser medidas. Por ello, no es posible predecir el espín ni la función de onda de la partícula que escapa. Puede tener diferentes espines o diferentes funciones de onda, con varias probabilidades, pero no tiene un único espín o una única función de onda. Por lo tanto, parecería que nuestro poder de predecir el futuro quedaría aún más reducido. La idea clásica de Laplace, de que podríamos predecir las posiciones y las velocidades de las partículas, tuvo que ser modificada cuando el principio de incertidumbre demostró que no se podía medir con precisión posiciones y velocidades a la vez. Sin embargo, todavía resultaba posible medir la función de onda y utilizar la ecuación de Schrödinger para calcular su evolución en el futuro. Ello nos permitiría predecir con certeza algunas combinaciones de posición y velocidad, que es la mitad de lo que podríamos predecir según las ideas de Laplace. Podemos afirmar con certeza que las partículas tendrán espines opuestos, pero si una partícula cae al agujero negro, no podemos efectuar ninguna predicción segura sobre la partícula restante. Ello significa que en el exterior del agujero negro ninguna medida puede ser predicha con certeza: nuestra capacidad de formular predicciones definidas quedaría reducida a cero. Quizás, después de todo, la astrología no sea peor que las leyes de la ciencia en la predicción del futuro.

(FIG. 4.21) Un par de partículas virtuales tiene una función de onda que predice que ambas partículas tendrán espines opuestos. Pero si una de ellas cae en el agujero negro, es imposible predecir a ciencia cierta el espín de la particula restante.
Esta reducción del determinismo desagradó a muchos físicos y sugirieron, por lo tanto, que la información de lo que hay en el interior de un agujero negro podría salir de alguna manera. Durante años, hubo tan sólo la esperanza piadosa de que se hallaría alguna manera de salvar la información. Pero en 1996, Andrew Strominger y Cumrum Vafa realizaron un progreso importante. Decidieron considerar el agujero negro como si estuviera formado por un cierto número de bloques constituyentes, denominados p-branas.
Recordemos que una de las maneras de considerar las p-branas es como hojas que se desplazan en las tres dimensiones del espacio y en las siete dimensiones adicionales que no podemos observar (Fig. 4.22). En algunos casos, es posible demostrar que el número de ondas en las p-branas es igual a la cantidad de información que esperaríamos que contuviera el agujero negro. Si las partículas chocan con las p-branas, excitan en ellas ondas adicionales. Análogamente, si ondas que se mueven en diferentes direcciones en las p-branas confluyen en algún punto, pueden producir un pico tan grande que se desgarraría un fragmento de la p-brana y se marcharía en forma de partícula. Por lo tanto, las p-branas pueden absorber y emitir partículas, como lo hacen los agujeros negros (Fig. 4.23).

(FIG. 4.22) Los agujeros negros pueden ser considerados como la intersección de p-branas en las dimensiones adicionales del espacio-tiempo. La información sobre los estados internos de los agujeros negros quedaría almacenada como ondas en las p-branas.

(FIG. 4.23) Una partícula que cae en un agujero negro puede ser considerada como un bucle cerrado de una cuerda que golpea una p-brana (izquierda) y excita ondas en ella (centro). Las ondas pueden confluir y desgajar una parte de la p-brana para formar una cuenta cerrada (derecha). Ésta sería una particula emitida por el agujero negro.
Podemos considerar las p-branas como una teoría efectiva, es decir, aunque no necesitamos creer que hay realmente pequeñas hojas que se desplazan en un espacio-tiempo plano, los agujeros negros podrían comportarse como si estuvieran formados por dichas hojas. La situación es parecida a lo que ocurre con el agua: está formada por miles de millones de moléculas de H2O con interacciones complicadas, pero un fluido continuo proporciona un modelo efectivo muy bueno. El modelo matemático de los agujeros negros formados por p-branas conduce a resultados análogos a los de la descripción basada en pares de partículas virtuales, de la que hemos hablado anteriormente. Desde una perspectiva positivista, son modelos igualmente buenos, al menos para ciertas clases de agujeros negros. Para ellas, el modelo de p-branas predice exactamente la misma tasa de emisión que el de pares de partículas virtuales. Sin embargo, hay una diferencia importante: en el modelo de p-branas, la información de lo que cae en el agujero negro queda almacenada en la función de onda de las ondas de las p-branas. Estas son consideras como hojas en un espacio-tiempo plano y, por ello, el tiempo fluirá continuamente hacia adelante, las trayectorias de los rayos de luz no se curvarán y la información en las ondas no se perderá, sino que acabará por salir del agujero negro en la radiación de las p-branas. Así, según el modelo de las p-branas, podemos utilizar la ecuación de Schrödinger para calcular la función de onda en instantes posteriores. No se perderá nada, y el tiempo transcurrirá suavemente. Tendremos determinismo completo en el sentido cuántico.

Pero ¿cuál de estas descripciones es correcta? ¿Se pierde una parte de la función de onda en los agujeros negros, o toda la información vuelve a salir, como sugiere el modelo de las p-branas? Ésta es una de las grandes preguntas de la física teórica actual. Muchos investigadores creen que trabajos recientes demuestran que la información no se pierde. El mundo es seguro y predecible, y no ocurrirá nada inesperado. Pero no resulta claro que sea así. Si se considera seriamente la teoría de la relatividad general de Einstein, se debe permitir la posibilidad de que el espacio-tiempo forme nudos y se pierda información en los pliegues. Cuando la nave espacial Enterprise pasó por un agujero de gusano, ocurrió algo inesperado. Lo sé porque me hallaba a bordo, jugando a póker con Newton, Einstein y Data. Tuve una gran sorpresa. ¡Ved qué apareció sobre mis rodillas!

Por cortesía de Paramount Pictures,
STAR TREK: THE NEXT GENERATION
Copyright © 2001 por Paramount Pictures.
Todos los derechos reservados
