
FIG. 2.1 MODELO DEL TIEMPO COMO LÍNEA FERROVIARIA
¿Hay una línea principal que sólo funciona en un sentido —hacia el futuro— o puede describir un bucle que vuelva a unirse con la via principal en un enclave anterior?
¿QUÉ ES EL TIEMPO? ¿ES UNA CORRIENTE QUE FLUYE SIN PARAR Y se lleva nuestros sueños, como dice una vieja canción? ¿O es como una vía de ferrocarril? Quizás tenga bucles y ramificaciones, y se pueda seguir avanzando y, aun así, regresar a alguna estación anterior de la línea (Fig. 2.1).
Un autor del siglo XIX, Charles Lamb, escribió: «Nada me produce tanta perplejidad como el tiempo y el espacio. Y sin embargo, nada me preocupa menos que el tiempo y el espacio, ya que nunca pienso en ellos». La mayoría de nosotros no acostumbramos a preocuparnos por el tiempo y el espacio, sean lo que sean, pero todos nos preguntamos en alguna ocasión qué es el tiempo, cómo comenzó y adónde nos lleva.
Cualquier teoría científica seria, sobre el tiempo o cualquier otro concepto, debería en mi opinión estar basada en la forma más operativa de filosofía de la ciencia: la perspectiva positivista propuesta por Karl Popper y otros. Según esta forma de pensar, una teoría científica es un modelo matemático que describe y codifica las observaciones que realizamos. Una buena teoría describirá un amplio dominio de fenómenos a partir de unos pocos postulados sencillos, y efectuará predicciones definidas que podrán ser sometidas a prueba. Si las predicciones concuerdan con las observaciones, la teoría sobrevive a la prueba, aunque nunca se pueda demostrar que sea correcta. En cambio, si las observaciones difieren de las predicciones, debemos descartar o modificar la teoría. (Como mínimo, esto es lo que se supone que ocurre. En la práctica, la gente cuestiona a menudo la precisión de las observaciones y la fiabilidad y el talante moral de los que las han realizado). Si adoptamos la perspectiva positivista, como yo hago, no podemos decir qué es realmente el tiempo. Todo lo que podemos hacer es describir lo que hemos visto que constituye un excelente modelo matemático del tiempo y decir a qué predicciones conduce.

Isaac Newton publicó su modelo matemático del tiempo y el espacio hace unos 300 años.
Isaac Newton nos proporcionó el primer modelo matemático para el tiempo y el espacio en sus Principia Mathematica, publicados en 1687. Newton ocupó la cátedra Lucasiana de Cambridge que yo ocupo en la actualidad, aunque en aquella época no funcionaba eléctricamente. En el modelo de Newton, el tiempo y el espacio constituían un fondo sobre el cual se producían los sucesos, pero que no era afectado por ellos. El tiempo estaba separado del espacio y era considerado como una línea recta, o una vía de tren, infinita en ambas direcciones (Fig. 2.2). El propio tiempo era considerado eterno, en el sentido de que siempre había existido y seguiría existiendo siempre. En cambio, mucha gente creía que el universo físico había sido creado más o menos en el estado presente hace tan sólo unos pocos miles de años. Ello desconcertaba a algunos filósofos, como el pensador alemán Immanuel Kant. Si en efecto el universo había sido creado, ¿por qué se había tenido que esperar infinitamente hasta la creación? Por otro lado, si el universo había existido siempre, ¿por qué no había ocurrido ya todo lo que tenía que ocurrir, es decir, por qué la historia no había terminado ya? En particular, ¿por qué el universo no había alcanzado el equilibrio térmico, con todas sus partes a la misma temperatura?
(FIG. 2.2) El tiempo newtoniano estaba separado del espacio, como una vía de tren que se extendiera al infinito en ambas direcciones.
Kant denominó este problema «antinomia de la razón pura», porque parecía constituir una contradicción lógica, no tenía solución. Pero resultaba una contradicción sólo dentro del contexto del modelo matemático newtoniano, en que el tiempo era una línea infinita, independiente de lo que estuviera ocurriendo en el universo. Sin embargo, como vimos en el Capítulo 1, en 1915 Einstein propuso un modelo matemático completamente nuevo: la teoría general de la relatividad. En los años transcurridos desde su artículo, hemos añadido algunos refinamientos ornamentales, pero nuestro modelo de tiempo y de espacio sigue estando basado en las propuestas de Einstein. Este capítulo y los siguientes describirán cómo han evolucionado nuestras ideas desde el artículo revolucionario de Einstein. Se trata de la historia del éxito del trabajo de un gran número de personas, y me siento orgulloso de haber podido aportar una pequeña contribución a ella.

San Agustín, el pensador del siglo V que dijo que el tiempo no existía antes del comienzo del universo.
Página de De Civitate Dei, siglo XII. Biblioteca Laurenziana, Florencia.
La relatividad general combina la dimensión temporal con las tres dimensiones espaciales para formar lo que se llama espacio-tiempo (Fig. 2.3). La teoría incorpora los efectos de la gravedad, afirmando que la distribución de materia y energía en el universo deforma y distorsiona el espacio-tiempo, de manera que ya no es plano. Los objetos intentan moverse en trayectorias rectilíneas en el espacio-tiempo, pero como éste está deformado, sus trayectorias parecen curvadas: se mueven como si estuvieran afectados por un campo gravitatorio.
Una tosca analogía de la situación, que no debemos tomar demasiado al pie de la letra, consiste en imaginar una lámina de goma. Podemos depositar sobre ella una bola grande que represente el Sol. El peso de la bola hundirá ligeramente la lámina y hará que esté curvada en las proximidades del Sol. Si ahora hacemos rodar pequeñas bolitas sobre la lámina, no la recorrerán en línea recta, sino que girarán alrededor del objeto pesado, como los planetas orbitan alrededor del Sol (Fig. 2.4).


(FIG. 2.3) FORMA Y DIRECCIÓN DEL TIEMPO
La teoría de Einstein de la Relatividad, avalada por su concordancia con un gran número de experimentos, muestra que el tiempo y el espacio están inextricablemente conectados.
No es posible curvar el espacio sin curvar también el tiempo. Así pues, el tiempo tiene una forma. Sin embargo, parece tener tan sólo una dirección, como las locomotoras de la figura.

(FIG. 2.4) ANALOGÍA DE LA LÁMINA DE GOMA
La bola grande central representa un cuerpo de gran masa, como por ejemplo una estrella.
Su peso curva la lámina en su proximidad. La trayectoria de las bolas pequeñas que se desplazan sobre la lámina son desviadas por esta curvatura y giran alrededor de la bola grande, de la misma manera como los planetas en el campo gravitatorio de una estrella orbitan alrededor de ésta.
La analogía es incompleta porque en ella tan sólo está curvada una sección bidimensional del espacio (la superficie de la lámina de goma), pero el tiempo queda sin perturbar, como en la teoría newtoniana. Pero en la teoría de la relatividad, que concuerda con un gran número de experimentos, el tiempo y el espacio están inextricablemente entrelazados. No podemos curvar el espacio sin involucrar asimismo al tiempo. Por lo tanto, el tiempo adquiere una forma. Al curvar el tiempo y el espacio, la relatividad general los convierte en participantes dinámicos de lo que ocurre en el universo, en lugar de considerarlos como un mero escenario pasivo en que se suceden los acontecimientos. En la teoría newtoniana, en que el tiempo existía independientemente de todo lo demás, se podía preguntar: ¿qué hacía Dios antes de crear el universo? Como dijo San Agustín, no deberíamos bromear con estas cuestiones, como el hombre que dijo «estaba preparando el infierno para los que pusieran preguntas demasiado complicadas». Es una pregunta seria que la gente se ha planteado a lo largo de todas las épocas. Según San Agustín, antes de que Dios hiciera el cielo y la Tierra no hacía nada en absoluto. De hecho, esta visión resulta muy próxima a las ideas actuales.
En la relatividad general, el tiempo y el espacio no existen independientemente del universo o separadamente el uno del otro. Están definidos por medidas efectuadas dentro del universo, como el número de vibraciones de un cristal de cuarzo de un reloj o la longitud de una cinta métrica. Es fácilmente concebible que un tiempo definido de este modo, en el interior del universo, debe haber tenido un valor mínimo o un valor máximo —en otras palabras, un comienzo o un final—. No tendría sentido preguntar qué ocurrió antes del comienzo o después del fin, porque tales tiempos no estarían definidos.
Claramente, resultaba importante decidir si el modelo matemático de la relatividad general predecía que el universo, y el propio tiempo, hubieran debido tener un comienzo o un final. El prejuicio general entre los físicos teóricos, incluido el mismo Einstein, era que el tiempo debería ser infinito en ambas direcciones. Si no, se planteaban cuestiones embarazosas sobre la creación del universo, que parecían hallarse más allá del dominio de la ciencia. Se conocían soluciones de las ecuaciones de Einstein en que el tiempo tenía un comienzo o un final, pero todas ellas eran muy especiales, con un grado muy elevado de simetría. Se creía que en los objetos reales que se colapsaran bajo la acción de su propia gravedad, la presión o los efectos de las velocidades laterales impedirían que toda la materia cayera al mismo punto y la densidad se hiciera infinita. Análogamente, si se retrotrajera la expansión del universo, se encontraría que no toda la materia del universo emergería de un punto de densidad infinita. Tal punto de densidad infinita se denomina una singularidad y constituiría un comienzo o un final del tiempo.
En 1963, dos científicos rusos, Evgenii Lifshitz e Isaac Khalatnikov, afirmaron haber demostrado que todas las soluciones de las ecuaciones de Einstein que poseen una singularidad deberían tener una distribución muy especial de materia y de velocidades. La probabilidad de que la solución que representa el universo tuviera esta disposición especial era prácticamente nula. Casi ninguna de las soluciones que podrían representar el universo poseería una singularidad con una densidad infinita. Antes de la etapa de expansión del universo, debería haber habido una fase de contracción durante la cual toda la materia se fue acumulando pero sin llegar a chocar consigo misma, separándose de nuevo en la fase actual de expansión. Si éste fuera el caso, el tiempo seguiría para siempre, desde un pasado infinito a un futuro infinito.
No todos quedaron convencidos por los argumentos de Lifshitz y Khalatnikov. Roger Penrose y yo adoptamos una perspectiva diferente, basada no en el estudio de soluciones detalladas, sino en la estructura global del espacio-tiempo. En la relatividad general, el espacio-tiempo es curvado no sólo por los objetos con masa, sino también por el contenido en energía. Esta siempre es positiva, por lo cual confiere al espacio-tiempo una curvatura que desvía los rayos de luz los unos hacia los otros.
Consideremos ahora el cono de luz (Fig. 2.5) correspondiente a nuestro pasado, es decir, las trayectorias, en el espacio-tiempo, de los rayos de luz de galaxias distantes que nos están llegando en el presente. En un diagrama en que el tiempo corresponda al eje vertical y el espacio a los ejes perpendiculares a éste, tales trayectorias se hallan en el interior de un cono cuyo vértice, o punta, se halla en nosotros. A medida que vamos hacia el pasado, bajando desde el vértice del cono, vemos galaxias de tiempos cada vez más anteriores. Como el universo se ha estado expandiendo y todo estaba mucho más próximo entre sí, a medida que miramos un futuro más distante contemplamos regiones de densidad de materia cada vez mayor. Observamos un tenue fondo de radiación de microondas que se propaga hacia nosotros por el cono de luz del pasado y que procede de un tiempo muy anterior, cuando el universo era mucho más denso y caliente que en la actualidad. Sintonizando receptores a las diferentes frecuencias de las microondas, podemos medir su espectro (la distribución de la potencia en función de la frecuencia) de esta radiación. Hallamos un espectro que es característico de la radiación de un cuerpo con una temperatura de 2,7 grados sobre el cero absoluto. Esta radiación de microondas no resulta muy adecuada para descongelar una pizza, pero el hecho de que su espectro concuerde tan exactamente con el de la radiación de un cuerpo a 2,7 grados nos indica que la radiación debe proceder de regiones opacas a las microondas (Fig. 2.6).
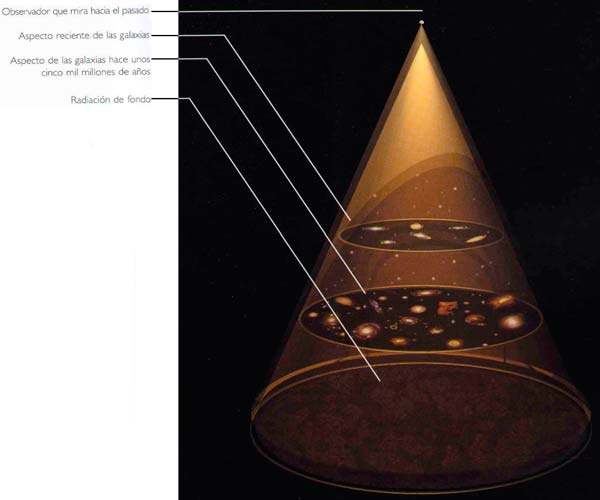

(FIG. 2.5) CONO DE LUZ DEL PASADO
Cuando obervamos las galaxias distantes, vemos el universo en tiempos anteriores, ya que la luz se desplaza con velocidad finita. Si representamos el tiempo en el eje vertical y dos de las tres direcciones espaciales en los ejes horizontales, la luz que nos llega actualmente en el vértice ha viajado hacia nosotros dentro de una región limitada por un cono.
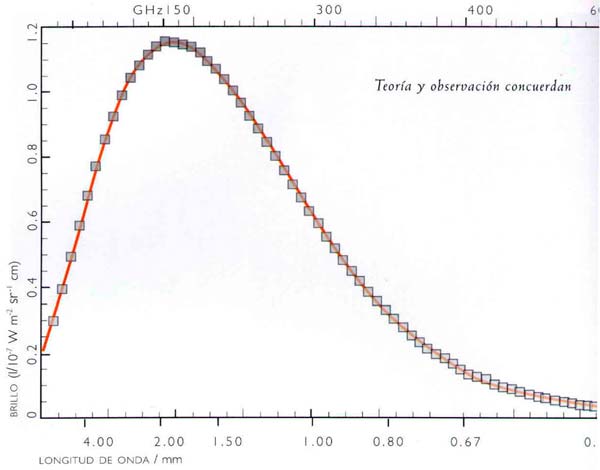
(FIG. 2.6) MEDICIÓN DEL ESPECTRO DEL FONDO DE MICROONDAS
El espectro —la distribución de la intensidad en función de la frecuencia— de la radiación cósmica del fondo de microondas es el característico de un cuerpo caliente. Para que la radiación se halle en equilibrio térmico, la materia debe haberla esparcido muchas veces. Ello indica que en nuestro cono de luz del pasado debe haber habido suficiente materia para que éste esté curvado.
Así pues, podemos concluir que el cono de luz de nuestro pasado debe atravesar una cierta cantidad de materia al ir retrocediendo en el tiempo. Esta cantidad de materia es suficiente para curvar el espacio-tiempo de manera que los rayos de luz de dicho cono del pasado estén curvados los unos hacia los otros (Fig. 2.7).

(FIG. 2.7) DEFORMANDO EL ESPACIO-TIEMPO
Como la gravedad es atractiva, la materia siempre deforma es espacio-tiempo de tal manera que los rayos de luz se curvan los unos hacia los otros.
A medida que retrocedemos en el tiempo, las secciones transversales del cono de luz de nuestro pasado alcanzan un tamaño máximo y empiezan a disminuir de nuevo. Nuestro pasado tiene forma de pera (Fig. 2.8).
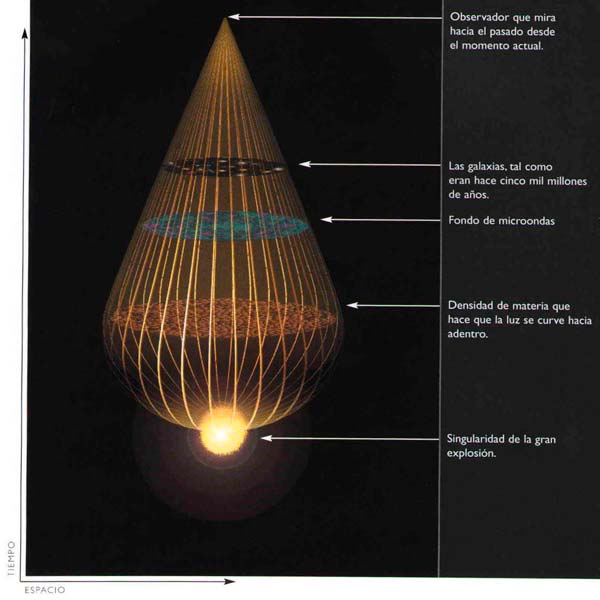
(FIG. 2.8) EL TIEMPO TIENE FORMA DE PERA
Si seguimos nuestro cono de luz hacia el pasado, se curva debido a la atracción de la materia del universo primitivo. Todo el universo que observamos está contenido en una región cuya frontera se encoge hasta hacerse nula en la gran explosión. Ésta constituiría una singularidad, un punto en que la densidad de materia sería infinita y la relatividad general clásica dejaria de ser válida.
Cuando retrocedemos todavía más hacia el pasado, la densidad de energía positiva de la materia hace que los rayos de luz se curven los unos hacia los otros más fuertemente. La sección transversal del cono de luz se reducirá a tamaño cero en un tiempo finito. Ello significa que toda la materia del interior de nuestro cono de luz del pasado está atrapada en una región cuya frontera tiende a cero. Por lo tanto, no resulta demasiado sorprendente que Penrose y yo lográramos demostrar que en el modelo matemático de la relatividad general, el tiempo debe haber tenido un comienzo en lo que denominamos gran explosión inicial (o big bang). Argumentos análogos demuestran que el tiempo tendría un final, cuando las estrellas o las galaxias se colapsaran bajo la acción de su propia gravedad y formaran un agujero negro. Habíamos esquivado la antinomia de la razón pura de Kant eliminando su hipótesis implícita de que el tiempo tenía sentido independientemente del universo. El artículo en que demostrábamos que el tiempo tuvo un comienzo ganó el segundo premio de un concurso patrocinado por la Gravity Research Foundation en 1968, y Roger y yo compartimos la principesca suma de 300 dólares. No creo que los otros ensayos premiados aquel año hayan tenido un interés demasiado duradero.
Nuestro trabajo suscitó reacciones diversas: molestó a muchos físicos pero entusiasmó a los dirigentes religiosos que creían en un acto de creación, para el cual veían aquí una demostración científica. Entre tanto, Lifshitz y Khalatnikov habían quedado en una posición bastante embarazosa. No podían hallar argumentos contra los teoremas matemáticos que habíamos demostrado, pero en el sistema soviético no podían admitir que se habían equivocado y que la ciencia occidental tenía razón. Sin embargo, salvaron la situación al hallar una familia más general de soluciones con singularidad, que no eran especiales en el sentido en que lo eran sus soluciones anteriores. Ello les permitió afirmar que las singularidades, y el comienzo o el final del tiempo, eran un descubrimiento soviético.
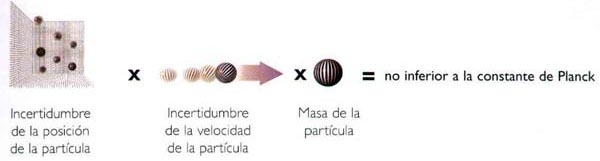
PRINCIPIO DE INCERTIDUMBRE

Izquierda: Las longitudes de onda de baja frecuencia perturban menos la velocidad de la partícula.
Derecha: Las longitudes de onda de frecuencia elevada perturban más la velocidad de la partícula.

Izquierda: Cuanto más larga es la longitud de onda utilizada para observar una partícula, mayor es la incertidumbre en su posición.
Derecha: Cuanto más corta es la longitud de onda utilizada para observar una partícula, menor es la incertidumbre en su posición.
Un hito importante en el descubrimiento de la teoría cuántica fue la propuesta de Max Planck, en 1900, de que la luz siempre va en pequeños paquetes, llamados quanto. Pese a que la hipótesis cuántica de Planck explicaba claramente las observaciones sobre la tasa de emisión de radiación por cuerpos calientes, el calado completo de sus implicaciones no fue advertido hasta mediados de los 1920, cuando el físico alemán Werner Heisenberg formuló su famoso principio de incertidumbre.
Heisenberg observó que la hipótesis de Planck implica que cuanto mayor es la precisión con que intentamos medir la posición de una partícula, menor es la precisión con que podemos medir su velocidad, y viceversa.
En términos más precisos, demostró que la incertidumbre en la posición de una partícula multiplicada por la incertidumbre en su cantidad de movimiento (masa por velocidad) siempre debe ser mayor que la constante de Planck, que es una magnitud estrechamente relacionada con el contenido de energía de un cuanto de luz.
ECUACIÓN DE INCERTIDUMBRE DE HEISENBERG
Muchos físicos seguían rechazando instintivamente la idea de que el tiempo tuviera un comienzo o un final. Por ello, subrayaron que no se podía esperar que el modelo matemático constituyera una buena descripción del espacio-tiempo cerca de una singularidad. La razón es que la relatividad general, que describe la fuerza gravitatoria, es una teoría clásica, como hemos dicho en el Capítulo 1, que no incorpora la incertidumbre de la teoría cuántica que rige todas las otras fuerzas que conocemos. Esta inconsistencia no tiene importancia en la mayor parte del universo ni durante la mayor parte del tiempo, porque la escala correspondiente a la curvatura del espacio-tiempo es muy grande y la escala en que los efectos cuánticos empiezan a resultar relevantes es muy pequeña. Pero cerca de una singularidad ambas escalas serían comparables y los efectos gravitatorios cuánticos serían importantes. Por ello, lo que los teoremas de singularidad de Penrose y mío establecían realmente era que nuestra región clásica de espacio-tiempo está limitada en el pasado, y probablemente en el futuro, por regiones en que la gravedad cuántica es relevante. Para comprender el origen y el destino del universo, necesitamos una teoría cuántica de la gravitación, que será el tema de la mayor parte de este libro.
LOS CAMPOS DE MAXWELL
En 1865, el físico británico James Clerk Maxwell sintetizó todas las leyes conocidas de la electricidad y el magnetismo. La teoría de Maxwell descansa en la existencia de campos que transmiten las acciones de las fuerzas de un lugar a otro del espacio. Maxwell advirtió que los campos que transmiten las perturbaciones eléctricas y magnéticas son entidades dinámicas que pueden oscilar y propagarse por el espacio.
La síntesis de Maxwell del electromagnetismo puede ser condensada en dos ecuaciones que describen la dinámica de estos campos. Él mismo dedujo la primera gran conclusión que se desprende de ellas, a saber, que las ondas electromagnéticas de cualquier frecuencia se propagan en el espacio con la misma velocidad —la velocidad de la luz.
Las teorías cuánticas de sistemas como los átomos, con un número finito de partículas, fueron formuladas en los años 1920 por Heisenberg, Schrödinger y Dirac. (Dirac fue otro de mis antecesores en la cátedra de Cambridge, cuando todavía no estaba motorizada). Sin embargo, se topaba con dificultades cuando se intentaba extender las ideas cuánticas a los campos de Maxwell, que describen la electricidad, el magnetismo y la luz.
Podemos imaginar los campos de Maxwell como constituidos por ondas de diferentes longitudes de onda (la distancia entre dos crestas consecutivas de la onda). En una onda, los campos oscilan de un valor a otro como un péndulo (Fig. 2.9).

(FIG. 2.9) ONDA DE PROPAGACIÓN CON PÉNDULO OSCILANTE
La radiación electromagnética se propaga en el espacio como una onda, de manera que sus campos eléctrico y magnético oscilan, como un péndulo, en direcciones transversales a la del movimiento. La radiación puede estar formada por campos de diferentes longitudes de onda.
Según la teoría cuántica, el estado fundamental o estado de energía más baja de un péndulo no es aquél en que está en reposo hacia abajo. Este estado tendría simultáneamente una posición y una velocidad bien definidas, ambas de valor nulo. Ello constituiría una violación del principio de incertidumbre, que prohíbe la medición precisa simultánea de la posición y la velocidad. La incertidumbre en la posición, multiplicada por la incertidumbre en el ímpetu (velocidad por masa) debe ser mayor que una cierta cantidad, conocida como constante de Planck —un número cuya escritura resulta demasiado larga, por lo cual utilizaremos para él un símbolo: h
Así pues, el estado fundamental o estado de energía más baja de un péndulo no tiene energía nula, como se podría haber esperado, sino que incluso en su estado fundamental un péndulo o cualquier sistema oscilante debe tener una cierta cantidad mínima de lo que se denomina fluctuaciones del punto cero. Estas implican que el péndulo no apuntará necesariamente hacia abajo sino que habrá una cierta probabilidad de hallarlo formando un pequeño ángulo con la vertical (Fig. 2.10). Análogamente, incluso en el vacío o estado de energía más baja, las ondas de los campos de Maxwell no serán exactamente nulas, sino que tendrán un tamaño pequeño. Cuanto mayor sea la frecuencia (número de oscilaciones por minuto) del péndulo o de la onda, mayor será la energía de su estado fundamental.

(FIG. 2.10) PÉNDULO CON UNA DISTRIBUCIÓN DE PROBABILIDAD
Según el principio de Heisenberg, es imposible que un péndulo esté apuntando exactamente hacia abajo, con velocidad nula. En vez de ello, la teoría cuántica predice que, incluso en su estado de energía mínima, el péndulo debe tener una cierta cantidad mínima de fluctuaciones.
Ello significa que la posición del péndulo vendrá dada por una distribución de probabilidad. En su estado fundamental, la posición más probable es la que apunta hacia abajo, pero también hay una cierta probabilidad de hallarlo formando un pequeño ángulo con la vertical.
Cálculos de las fluctuaciones del estado fundamental de los campos de Maxwell y de los electrones pusieron de manifiesto que la masa y la carga aparentes del electrón serían infinitas, en contra de lo que indican las observaciones. Sin embargo, en los años 1940, los físicos Richard Feynman, Julián Schwinger y Shin’ichiro Tomonaga desarrollaron un método consistente de eliminación o «sustracción» de estos infinitos para quedarse sólo con los valores finitos observados de la masa y la carga. Aun así, las fluctuaciones en el estado fundamental seguían causando pequeños efectos que podían ser medidos y concordaban con las predicciones. Unos esquemas de sustracción parecidos conseguían eliminar los infinitos en el caso de los campos de Yang-Mills, en la teoría propuesta por Chen Ning Yang y Robert Mills. Dicha teoría es una extensión de la teoría de Maxwell para describir las interacciones de otras dos fuerzas llamadas fuerza nuclear fuerte y nuclear débil. Sin embargo, las fluctuaciones del estado fundamental tienen efectos mucho más serios en una teoría cuántica de la gravedad. De nuevo, cada longitud de onda tendría una cierta energía en el estado fundamental. Como no hay límite inferior al valor de las longitudes de onda de los campos de Maxwell, en cualquier región del espacio-tiempo habrá un número infinito de longitudes de onda y la energía del estado fundamental será infinita. Puesto que la densidad de energía es, tal como la materia, una fuente de gravitación, esta densidad infinita de energía implicaría que en el universo hay suficiente atracción gravitacional para curvar el espacio-tiempo en un solo punto, lo que evidentemente no ha sucedido.
Podríamos esperar resolver el problema de esta contradicción aparente entre la observación y la teoría diciendo que las fluctuaciones del estado fundamental no tienen efectos gravitatorios, pero ello no funciona. Podemos detectar la energía de las fluctuaciones del estado fundamental en el efecto Casimir. Si tenemos un par de placas metálicas paralelas y muy próximas entre sí, su efecto es reducir ligeramente el número de longitudes de onda que pueden caber entre las placas con respecto al número de longitudes de onda en el exterior. Ello significa que la densidad de energía de las fluctuaciones del estado fundamental entre las placas, aunque sigue siendo infinita, es inferior a la densidad de energía en el exterior de las mismas, en una pequeña cantidad (Fig. 2.11). Esta diferencia de densidad de energía da lugar a una fuerza atractiva entre las placas, que ha sido observada experimentalmente. Como en la relatividad general las fuerzas constituyen una fuente de gravitación, tal como lo es la materia, sería inconsistente ignorar los efectos gravitatorios de esta diferencia de energías.


(FIG. 2.11) EFECTO CASIMIR
La existencia de fluctuaciones en el estado fundamental ha sido confirmada experimentalmente po el efecto Casimir, una diminuta fuerza entre placa metálicas paralelas.

NÚMEROS ORDINARIOS
A x B = B x A
NÚMEROS GRASSMANN
A x B = –B x A
Otra posible solución del problema consistiría en suponer que hay una constante cosmológica, como la introducida por Einstein en su intento de obtener un modelo estático del universo. Si esta constante tuviera un valor infinito negativo, podría cancelar exactamente el valor infinito positivo de la energía del estado fundamental en el espacio libre, pero esta constante cosmológica parece muy ad hoc y tendría que ser ajustada con un grado extraordinario de precisión.
Afortunadamente, en los años 1970 se descubrió un tipo totalmente nuevo de simetría que proporciona un mecanismo físico natural para cancelar los infinitos que surgen de las fluctuaciones del estado fundamental. La supersimetría constituye una característica de los modelos matemáticos modernos, que puede ser descrita de diferentes maneras. Una de ellas consiste en decir que el espacio-tiempo tiene otras dimensiones adicionales además de las que percibimos. Se llaman dimensiones de Grassmann, porque son expresadas en números llamados variables de Grassmann en vez de en números ordinarios. Los números ordinarios conmutan, es decir, tanto da el orden en que los multipliquemos: 6 por 4 es lo mismo que 4 por 6, pero las variables de Grassmann anticonmutan: x por y es lo mismo que –y por x.
La supersimetría fue utilizada por primera vez para eliminar los infinitos de los campos de materia y de Yang-Mills en un espacio-tiempo en que tanto las dimensiones ordinarias como las de Grassmann eran planas, en vez de curvadas. Pero resultaba natural extenderla a situaciones en que ambos tipos de dimensiones fueran curvadas. Ello condujo a diversas teorías denominadas supergravedad, con diferentes grados de supersimetría. Una consecuencia de la supersimetría es que cada campo o partícula debería tener un «supersocio» con un espín superior o inferior en 1/2 a su propio espín (Fig. 2.12).
Las energías del estado fundamental de los bosones, campos cuyo espín es un número entero (0, 1, 2, etc.) son positivas. En cambio, las energías del estado fundamental de los fermiones, campos cuyo espín es un número semientero (1/2, 3/2, etc.), son negativas. Como en las teorías de supergravedad hay el mismo número de bosones que de fermiones, los infinitos de orden superior se cancelan (Fig. 2.13).

(FIG. 2.12) ESPÍN
Todas las partículas presentan una propiedad llamada espín, relacionada con el aspecto que presentan al ser observadas en diferentes direcciones. Lo podemos ilustrar con las cartas de una baraja. Consideremos, en primer lugar, el as de picas. Sólo presenta el mismo aspecto si le damos una vuelta completa, es decir de 360°. Se dice, así, que tiene espín 1.
En cambio, la reina de corazones tiene dos cabezas y por lo tanto ya tiene el mismo aspecto si se le hace dar media vuelta. Se dice que tiene espín 2. Análogamente, podríamos imaginar objetos con espín 3 o superior, que tendrían el mismo aspecto bajo fracciones cada vez menores de una vuelta.
Cuanto mayor es el espín, menor es la fracción de vuelta completa que debe girarse la partícula para que presente el mismo aspecto. Lo más notable es que hay partículas que sólo tienen el mismo aspecto si se les hace dar dos vueltas completas. Se dice que tales partículas tienen espín 1/2.
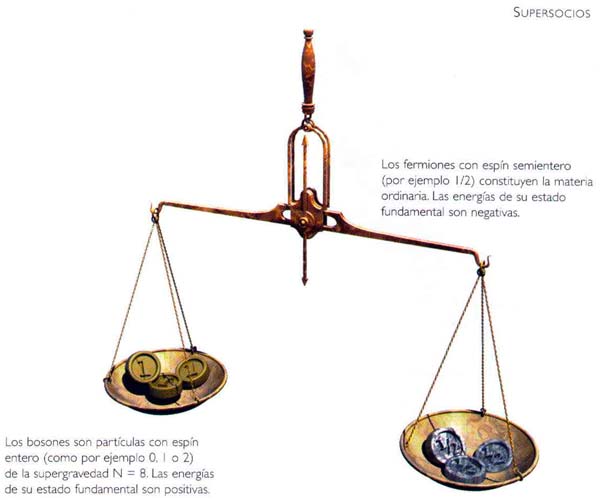
(FIG. 2.13) Todas las partículas conocidas del universo pertenecen a uno de dos grupos, fermiones o bosones. Los fermiones son partículas con espín semientero (como por ejemplo 1/2), y constituyen la materia ordinaria. Las energías de su estado fundamental son negativas.
Los bosones son partículas con espín entero (como 0, 1, 2) y dan lugar a las fuerzas entre los fermiones, tales como la fuerza gravitatoria y la luz. Las energías de su estado fundamental son positivas. La teoría de la supergravedad supone que cada fermión y cada bosón tienen un supersocio con un espín que vale 1/2 más o 1/2 menos que su propio espín. Por ejemplo, un fotón (que es un bosón) tiene espín 1. La energía de su estado fundamental es positiva. El supersocio del fotón, el fotino, tiene espín 1/2, por lo cual es un fermión. Por consiguiente, la energía de su estado fundamental es negativa.
En este esquema de la supergravedad tenemos el mismo número de bosones que de fermiones. La energía positiva del estado fundamental de los primeros cancela la energía negativa del estado fundamental de los segundos, lo cual elimina los infinitos de orden superior.
| MODELOS DE COMPORTAMIENTO DE PARTÍCULAS | |
| 1. Si existieran realmente partículas puntuales discretas, como bolitas, cuando chocaran sus trayectorias serían desviadas en dos nuevas trayectorias. | 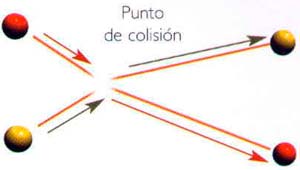 |
| 2. Esto es lo que parece ocurrir cuando dos partículas interactúan, aunque el proceso es mucho más complicado. | 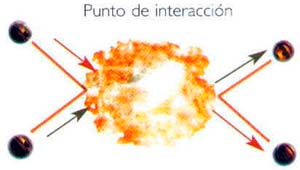 |
| 3. La teoría cuántica de campos estudia la colisión de dos partículas, como un electrón y su antipartícula, el positrón. Al chocar, se aniquilan brevemente en una fantástica explosión de energía y crean un fotón. A continuación, éste cede su energía, produciendo otro par electrón-positrón. Aun así, parece como si se hubieran desviado en nuevas trayectorias. | 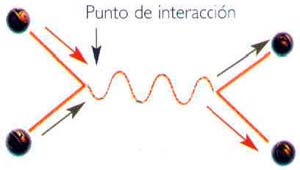 |
| 4. Si las partículas no son puntos de dimensión cero sino cuerdas unidimensionales cuyos bucles vibrantes oscilan como un electrón y un positrón, al chocar y aniquilarse mutuamente crean una nueva cuerda con un patrón de vibración diferente. Al liberar energía, se divide en dos nuevas cuerdas que siguen nuevas trayectorias. | 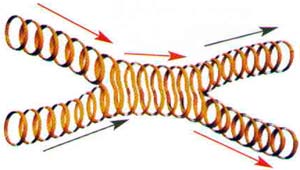 |
| 5. Si las cuerdas originales se consideran como una historia temporal ininterrumpida, y no como instantes discretos, las cuerdas resultantes son vistas como la hoja de universo de una cuerda. | 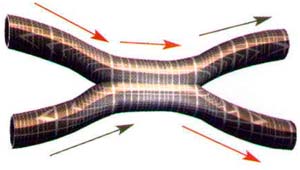 |
Quedaba la posibilidad de que pudieran subsistir sin cancelarse algunos infinitos de órdenes inferiores. Nadie tuvo la paciencia necesaria para calcular si estas teorías eran en verdad completamente finitas. Se bromeaba que un buen estudiante tardaría unos doscientos años en comprobarlo y, ¿cómo podríamos estar seguros de que no había cometido ningún error en la segunda página de los cálculos? Aun así, hacia 1985 la mayoría de los especialistas creían que casi todas las teorías de supergravedad estarían libres de infinitos.
Entonces, de repente, la moda cambió. La gente empezó a decir que no había motivos para esperar que las teorías de supergravedad no contuvieran infinitos, lo cual significaba que podrían resultar fatalmente erróneas como teorías. En su lugar, se proclamó que la única manera de combinar la gravedad con la teoría cuántica era una teoría llamada teoría supersimétrica de cuerdas. Las cuerdas, como sus homologas en la vida cotidiana, son objetos unidimensionales extensos: sólo tienen longitud. Las cuerdas de esta teoría se mueven en el espacio-tiempo de fondo, y sus vibraciones son interpretadas como partículas (Fig. 2.14).
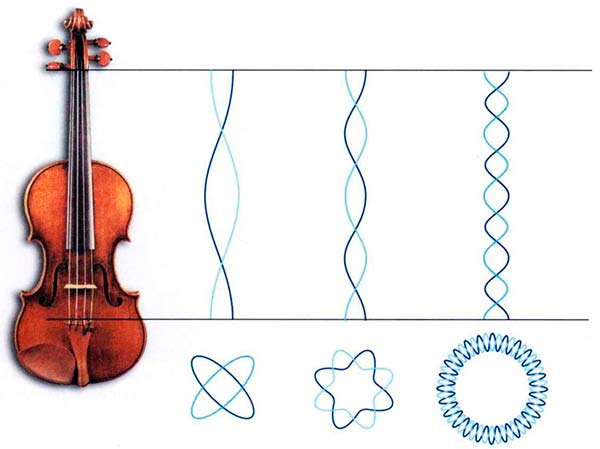
(FIG. 2.14) OSCILACIONES DE CUERDAS
En la teoría de cuerdas, los objetos básicos no son partículas que ocupan un solo punto en el espacio, sino cuerdas unidimensionales. Sus cabos pueden estar sueltos o unidos, formando bucles cerrados.
Tal como las cuerdas de un violín, las de la teoría de cuerdas presentan ciertas figuras de vibración, o frecuencias resonantes, cuyas longitudes de onda se adaptan de forma precisa entre ambos extremos.
Pero así como las diferentes frecuencias resonantes de las cuerdas de un violín dan origen a diferentes notas musicales, las diferentes oscilaciones de una cuerda dan lugar a diferentes masas y cargas de fuerzas, que son interpretadas como partículas fundamentales. En grandes líneas, cuanto menor es la longitud de onda de la oscilación, mayor es la masa de la partícula correspondiente.
Los futuros historiadores de la ciencia encontrarán interesante explorar el cambio de marea de opinión entre los físicos teóricos. Durante algunos años, las cuerdas reinaron sin rival y la supergravedad fue menospreciada como una simple teoría aproximada, válida tan sólo a bajas energías. El calificativo de «bajas energías» era considerado particularmente ominoso, aunque en este contexto bajas energías significaba que las partículas tendrían energías de al menos un millón de billones la de las partículas en una explosión de TNT. Si la supergravedad era tan sólo una aproximación de baja energía, no podía pretender ser la teoría fundamental del universo. En su lugar, se suponía que la teoría subyacente era una de las cinco posibles teorías de supercuerdas. Pero ¿cuál de estas cinco teorías describía nuestro universo? Y, ¿cómo podría formularse la teoría de cuerdas más allá de la aproximación en que éstas son representadas como superficies con una dimensión espacial y otra temporal, desplazándose en un espacio-tiempo plano? ¿No curvarían dichas cuerdas el espacio-tiempo de fondo?
En los años siguientes a 1985, fue haciéndose cada vez más evidente que la teoría de cuerdas no era la descripción completa. Para empezar, se advirtió que las cuerdas son tan sólo un miembro de una amplia clase de objetos que pueden extenderse en más de una dimensión. Paul Townsend, que, como yo, es miembro del Departamento de Matemáticas Aplicadas y Física Teórica de Cambridge, y a quien debemos muchos de los trabajos fundamentales sobre estos objetos, les dio el nombre de «p-branas». Una p-brana tiene longitud en p dimensiones. Así pues, una p = 1 brana es una cuerda, una p = 2 brana es una superficie o membrana, y así sucesivamente (Fig. 2.15). No parece haber motivo alguno para favorecer el caso de las cuerdas, con p = 1, sobre los otros posibles valores de p, sino que deberíamos adoptar el principio de la democracia de las p-branas: todas las p-branas son iguales.

Tomamos por cierta esta afirmación: Todas las p-branas con creadas iguales.

Paul Townsend, el cerebro de las p-branas

(FIG. 2.15) P-BRANAS
Las p-branas son objetos que se extienden en p dimensiones. Casos especiales son las cuerdas, con p = 1, y las membranas, con p = 2, pero también son posibles valores superiores de p en espacio-tiempos de diez u once dimensiones. A menudo, algunas o todas las p dimensiones están enrolladas como un toro.
Todas las p-branas podían ser obtenidas como soluciones de las ecuaciones de las teorías de supergravedad en 10 o 11 dimensiones. Aunque 10 o 11 dimensiones no parecen tener nada que ver con el espacio-tiempo de nuestra experiencia, la idea era que las otras 6 o 7 dimensiones están enrolladas con un radio de curvatura tan pequeño que no las observamos, sólo somos conscientes de las cuatro dimensiones restantes, grandes y casi planas.
Debo decir que, personalmente, me he resistido a creer en dimensiones adicionales. Pero como soy un positivista, la pregunta «¿existen realmente dimensiones adicionales?» no tiene ningún significado para mí. Todo lo que podemos preguntar es si los modelos matemáticos con dimensiones adicionales proporcionan una buena descripción del universo. Todavía no contamos con ninguna observación que requiera dimensiones adicionales para ser explicada. Sin embargo, hay la posibilidad de que podamos observarlas en el Gran Colisionador de Hadrones LHC (Large Hadron Collider), de Ginebra. Pero lo que ha convencido a mucha gente, incluido yo, de que deberíamos tomarnos seriamente los modelos con dimensiones adicionales es la existencia de una red de relaciones inesperadas, llamadas dualidades, entre dichos modelos. Estas dualidades demuestran que todos los modelos son esencialmente equivalentes, es decir, son tan sólo aspectos diferentes de una misma teoría subyacente que ha sido llamada teoría M. No considerar esta red de dualidades como una señal de que estamos en buen camino sería como creer que Dios puso los fósiles en las rocas para engañar a Darwin sobre la evolución de la vida.
Estas dualidades demuestran que las cinco teorías de supercuerdas describen la misma física, y que también son físicamente equivalentes a la supergravedad (Fig. 2.16). No podemos decir que las supercuerdas sean más fundamentales que la supergravedad, o viceversa, sino que son expresiones diferentes de la misma teoría de fondo, cada una de las cuales resulta útil para cálculos en diferentes tipos de situaciones. Como las teorías de cuerdas no tienen infinitos resultan adecuadas para calcular lo que ocurre cuando unas pocas partículas de altas energías colisionan entre sí y se esparcen. Sin embargo, no resultan muy útiles para describir cómo la energía de un gran número de partículas curva el universo o forma un estado ligado, como un agujero negro. Para estas situaciones es necesaria la supergravedad, que es básicamente la teoría de Einstein de los espacio-tiempos curvados con algunos tipos adicionales de materia. Ésta es la imagen que utilizaré principalmente en lo que sigue.
Para describir cómo la teoría cuántica configura el tiempo y el espacio, resulta útil introducir la idea de un tiempo imaginario. Tiempo imaginario suena a ciencia ficción, pero es un concepto matemáticamente bien definido: el tiempo expresado en lo que llamamos números imaginarios. Podemos considerar los números reales, por ejemplo 1, 2, –3,5 y otros, como la expresión de posiciones en una recta que se extiende de izquierda a derecha: el cero en el centro, los números reales positivos a la derecha y los números reales negativos a la izquierda (Fig. 2.17).
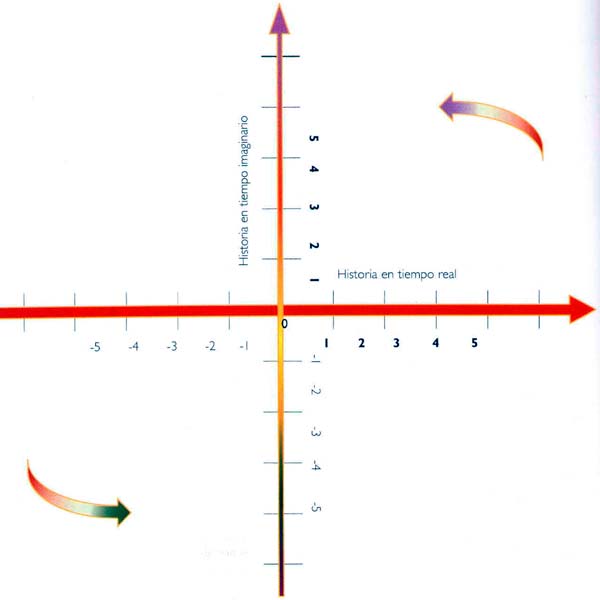
(FIG. 2.17) Es posible construir un modelo matemático en que hay una dirección de tiempo imaginario perpendicular a la del tiempo real ordinario. El modelo establece reglas que determinan la historia en tiempo imaginario en función de la historia en tiempo real, y viceversa.
Los números imaginarios pueden representarse entonces como si correspondieran a las posiciones en una línea vertical: el cero seguiría estando en el centro, los números imaginarios positivos estarían en la parte superior y los imaginarios negativos en la inferior. Así pues, los números imaginarios pueden ser considerados como un nuevo tipo de números perpendiculares en cierto modo a los números reales ordinarios. Como son una construcción matemática no necesitan una realización física: no podemos tener un número imaginario de naranjas ni una tarjeta de crédito con un saldo imaginario (Fig. 2.18).
(FIG. 2.18) Los números imaginarios son una construcción matemática. No podemos tener una tarjeta de crédito con un saldo imaginario.
Podríamos pensar que ello significa que los números imaginarios son tan sólo un juego matemático que nada tiene que ver con el mundo real. Desde la perspectiva positivista, sin embargo, no podemos determinar qué es real. Todo lo que podemos hacer es hallar qué modelos matemáticos describen el universo en que vivimos. Resulta que un modelo matemático en que intervenga un tiempo imaginario predice no sólo efectos que ya hemos observado, sino también otros efectos que aún no hemos podido observar pero en los cuales creemos por algunos otros motivos. Por lo tanto, ¿qué es real y qué es imaginario? ¿Está la diferencia tan sólo en nuestras mentes?
La teoría clásica (es decir, no cuántica) de la relatividad general de Einstein combinaba el tiempo real y las tres dimensiones del espacio en un espacio-tiempo cuadridimensional. Pero la dirección del tiempo real se distinguía de las tres direcciones espaciales, la línea de universo o historia de un observador siempre transcurría en la dirección creciente del tiempo real (es decir, el tiempo siempre transcurría del pasado al futuro), pero podía aumentar o disminuir en cualquiera de las tres direcciones espaciales. En otras palabras, se podía invertir la dirección en el espacio, pero no en el tiempo (Fig. 2.19).

(FIG. 2.19) En el espacio-tiempo con tiempo real de la relatividad general clásica, el tiempo se distingue de las direcciones espaciales porque a lo largo de la historia de un observador sólo crece, a diferencia de las direcciones espaciales que pueden aumentar o disminuir. La dirección del tiempo imaginario de la teoría cuántica, en cambio, es como otra dirección espacial, de modo que tanto puede aumentar como disminuir.

La fórmula del área para la entropía (o número de estados internos) de un agujero negro sugiere que la información sobre lo que cae en el mismo puede almacenarse como en un disco, y ser recuperada o vuelta a tocar cuando el agujero negro se evapora.
En cambio, como el tiempo imaginario es perpendicular al tiempo real, se comporta como una cuarta dimensión espacial. Por lo tanto, puede exhibir un dominio de posibilidades mucho más rico que la vía de tren del tiempo real ordinario, que sólo puede tener un comienzo o un fin o ir en círculos. Es en este sentido imaginario que el tiempo tiene una forma.
Para contemplar algunas de las posibilidades, consideremos un espacio-tiempo con tiempo imaginario que tenga forma de esfera, como la superficie de la Tierra. Supongamos que el tiempo imaginario corresponda a los grados de latitud (Fig. 2.20). Entonces, la historia del universo en tiempo imaginario empezaría en el polo Sur. No tendría sentido preguntar: «¿qué ocurrió antes del comienzo?». Tales tiempos simplemente no están definidos, como no lo están los puntos más al sur del polo Sur. El polo Sur es un punto perfectamente regular de la superficie de la Tierra, y en él se cumplen las mismas leyes que en todos los demás puntos. Ello sugiere que, en el tiempo imaginario, el comienzo del tiempo puede ser un punto regular del espacio-tiempo, y que en él se podrían satisfacer las mismas leyes que en el resto del universo. (El origen y la evolución cuántica del universo serán descritas en el capítulo siguiente.)
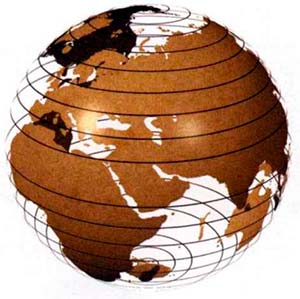 Tiempo imaginario como grados de latitud |
(FIG. 2.20) TIEMPO IMAGINARIO En un espacio-tiempo imaginario que tenga forma de esfera, la dirección del tiempo imaginario podría representar la distancia desde el polo Sur. A medida que nos desplazamos hacia el norte, los paralelos van haciéndose mayores, lo cual correspondería a la expansión del universo en el tiempo imaginario. El universo alcanzaría un tamaño máximo en el ecuador y después se volvería a contraen al seguir aumentando el tiempo imaginario, hasta reducirse a un solo punto en el polo Norte. Aunque en los polos el tamaño del universo sería nulo, estos puntos no serían singularidades sino que, tal como los polos Norte y Sur de la superficie terrestre, serían puntos perfectamente regulares. Ello sugiere que, en el tiempo imaginario, el comienzo del universo podría ser un punto regular del espacio-tiempo. |
 Tiempo imaginario como grados de longitud que coinciden en los polos Norte y Sur |
(FIG. 2.21) En lugar de corresponder a los grados de latitud, la dirección del tiempo imaginario en un espacio-tiempo esférico podría corresponder a los grados de longitud. Como todos los meridianos confluyen en los polos Norte y Sur, en ellos el tiempo se detendría; un incremento de tiempo imaginario nos dejaría exactamente en el mismo lugar, tal como al ir hacia el oeste en el polo Norte terrestre nos quedamos en el mismo polo Norte. |
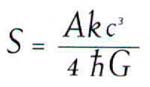
| FÓRMULA DE LA ENTROPÍA DEL AGUJERO NEGRO | |
| A | Área del horizonte de sucesos del agujero negro |
| h | Constante de Planck |
| k | Constante de Boltzmann |
| G | Constante de la gravitación de Newton |
| c | Velocidad de la luz |
| S | Entropía del agujero negro |
Otro posible comportamiento puede ilustrarse suponiendo que el tiempo imaginario corresponde a los grados de longitud en la Tierra. Todos los meridianos (líneas de la misma longitud) se cortan en los polos Norte y Sur (Fig. 2.21). Así pues, en ellos el tiempo se detiene, en el sentido que un incremento del tiempo imaginario, o de los grados de longitud, nos deja en el mismo punto. Esto se parece mucho a la manera en que el tiempo real semeja detenerse en el horizonte de un agujero negro. Hemos caído en la cuenta de que esta detención del tiempo real e imaginario (o los dos se detienen o ninguno de ellos lo hace) significa que el espacio-tiempo tiene una temperatura, como descubrí en los agujeros negros. Los agujeros negros no sólo tienen una temperatura, sino que también se comportan como si tuvieran una magnitud denominada entropía. La entropía es una medida del número de estados internos (maneras como podríamos configurar su interior) que el agujero negro podría poseer sin parecer diferente a un observador exterior, que sólo puede observar su masa, rotación y carga. La entropía del agujero negro viene dada por una fórmula muy sencilla que descubrí en 1974. Es igual al área del horizonte del agujero negro: hay un bit de información sobre el estado interno del agujero negro por cada unidad fundamental de área de su horizonte. Ello indica que hay una conexión profunda entre la gravedad cuántica y la termodinámica, la ciencia del calor (que incluye el estudio de la entropía). También sugiere que la gravedad cuántica puede exhibir la propiedad llamada holografía (Fig. 2.22).

EL PRINCIPIO HOLOGRÁFICO
Haber advertido que el área de la superficie del horizonte que rodea un agujero negro es una medida de la entropía de éste nos hace pensar que la entropía máxima de cualquier región cerrada del espacio no puede sobrepasar un cuarto del área de la superficie que lo circunscribe. Como la entropía no es más que una medida de la información total contenida en un sistema, ello sugiere que la información asociada con todos los fenómenos en el mundo tridimensional puede ser almacenada en su frontera bidimensional, tal como una imagen holográfica. En cierto sentido, el universo sería bidimensional.
La información sobre los estados cuánticos en una región del espacio-tiempo puede ser codificada de algún modo en la frontera de dicha región, que tiene dos dimensiones menos. Algo parecido ocurre con los hologramas, que contienen una imagen tridimensional en una superficie bidimensional. Si la gravedad cuántica incorpora el principio holográfico, significa que podemos seguir la pista de lo que hay dentro de los agujeros negros. Esto es esencial si tenemos que ser capaces de predecir la radiación que sale de ellos. Si no lo podemos hacer, no podremos predecir el futuro en grado tan alto como creíamos. Trataremos esta cuestión en el Capítulo 4. La holografía será tratada de nuevo en el Capítulo 7. Parece que podríamos vivir en una 3-brana —una superficie cuadridimensional (tres dimensiones espaciales más una temporal)— que es la frontera de una región de cinco dimensiones, con las restantes dimensiones enrolladas en una escala muy pequeña. El estado del universo en dicha membrana codificaría lo que está pasando en la región de cinco dimensiones.
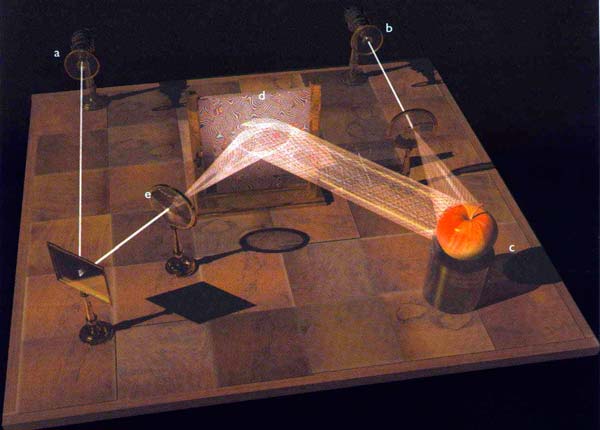
(FIG. 2.22) La holografía es esencialmente un fenómeno de interferencia de figuras ondulatorias. Los hologramas son producidos cuando la luz procedente de un láser es bifurcada en dos rayos separados (a) y (b). Uno de ellos (b) rebota en el objeto (c) e incide sobre una placa fotosensible (d). El otro (a) atraviesa una lente (e) y choca con la luz reflejada de b, produciendo en la placa una figura de interferencia.
Cuando la placa revelada se ilumina con un láser aparece una imagen completamente tridimensional del objeto original. Un observador que se mueva respecto de la imagen holográfica podrá ver las caras ocultas que una fotografía normal no podría mostrar.
La superficie bidimensional de la placa de la izquierda, a diferencia de una fotografía normal, tiene la notable propiedad de que cualquier fragmento diminuto de su superficie contiene toda la información necesaria para la reconstrucción de la imagen completa.
