2. A kvantumfizika rejtelmei

Az első fejezetben hangsúlyoztam, hogy a fizikai világ szerkezetében rendkívül pontosan illeszkedik a matematikához, mintahogyan azt szimbolikusan az 1.3 ábra mutatja. Figyelemre méltó, hogy a fizika legalapvetőbb összefüggéseit milyen rendkívül pontosan leírja a matematika. Egyik híres előadásában 1960-ban Wigner Jenő így utalt erre:

„A matematika szokatlan hatékonysága a fizikai tudományokban.”

A sikerek sora lenyűgöző:

Az euklideszi geometria legalább annyira pontos, mint a hidrogénatom mérete a méterhez képest. Mint azt az első előadásban láttuk, az általános relativitáselméleti eredetű effektusok miatt a pontosság nem tökéletes, mégis a legtöbb gyakorlati alkalmazás szempontjából kielégítő.

A newtoni mechanika pontossága körülbelül egy aránya a 10⁷-hez. Nem teljesen pontos, ismét csak a relativitáselméletre van szükség a pontosság növeléséhez.

Maxwell elektrodinamikája roppant széles tartományban helyesnek bizonyult, a részecskék méreteitől (amennyiben együttesen alkalmazzuk a kvantummechanikával) egészen a távoli galaxisokat jellemző méretekig, ami 10³⁵ vagy ennél is több.

Einstein relativitáselméletének pontossága, mint azt az első fejezetben láttuk, egy a 10¹⁴-hez, hozzávetőleg kétszer olyan pontos, mint a newtoni mechanika. Einstein elmélete magában foglalja a newtoni mechanikát.

A kvantummechanika, jelen fejezetünk tárgya, szintén rendkívül pontos elmélet. A kvantumtérelméletben, mely a kvantummechanikának, Maxwell elektrodinamikájának és Einstein speciális relativitáselméletének kombinációja, vannak olyan effektusok, amelyek pontossága 10 ¹¹. Például, az ún. Dirac-egységekben kifejezve, az elektron mágneses momentumát 1,00115965246-nak jósolja, szemben a kísérletileg meghatározott 1,001159652193-mal.

Lényeges megjegyezni, hogy a matematikának a fizikai világunk leírásában tanúsított hihetetlen hatékonysága és pontossága mellett a kapcsolat gyakran bizonyul a matematika számára is rendkívül termékenynek. Volt már sok példa arra, hogy a matematika legtermékenyebb fogalmai a fizikai elméletekből származtak. Felsorolok néhány olyan matematikai területet, amelynek kialakulását a fizikai elméletek követelményei segítették:

•    valós számok

•    euklideszi geometria

•    differenciál- és integrálszámítás, differenciálegyenletek

•    szimplektikus geometria

•    differenciálformák és parciális differenciálegyenletek

•    Riemann-geometria és Minkowski-geometria

•    komplex számok

•    Hilbert-tér

•    funkcionálanalízis ...stb.

Az egyik legmeglepőbb példa a differenciál- és integrálszámítás felfedezése, amelyet Newton és mások fejlesztettek ki a newtoni mechanika matematikai alapjaként. Amikor az új matematikai eljárásokat elméleti matematikai problémákra kezdték alkalmazni, ott is rendkívül gyümölcsözőnek bizonyultak.

Az első fejezetben a léptékeket vizsgáltuk, kiindulva az idő és a távolság alapegységeitől, a Planck-időtől és Planck-hossztól, át a részecskefizikában előforduló legkisebb méreteken, amelyek a Planck-méreteknél körülbelül 10²⁰-szor nagyobbak; az emberi távolság- és időskálán, melyek azt mutatják, hogy rendkívül stabil struktúrák vagyunk az univerzumban; egészen a fizikai világegyetem életkoráig és sugaráig. Megemlítettem már azt a meglehetősen zavaró tényt, hogy a fizika alapjainál két, egymástól teljesen eltérő szemléletmódot alkalmazunk annak függvényében, hogy nagy- vagy kisléptékű dolgokról van-e szó. A 2.1 ábra (ami az 1.5 ábra megismétlése) tanúsága szerint a kvantummechanikát használjuk, amikor kisléptékű, kvantumos jelenségeket írunk le, a klasszikus fizikát pedig, valahányszor nagyléptékű jelenségeket vizsgálunk.

2.1 ábra

A kétféle tevékenységet a kvantumszinten U-val (unitér), a klasszikus szinten C-vel jelöltem. A nagy léptéken érvényes fizikát az első fejezetben tárgyaltam, és hangsúlyoztam azt is, hogy legjobb tudomásunk szerint nagyléptéken és kisléptéken merőben különböző törvényszerűségek léteznek.

Úgy gondolom, hogy a fizikusok szokásos álláspontja a következő: amennyiben a kvantumfizikát igazán értenénk, képesek lennénk levezetni belőle a klasszikus fizikát. Én azonban másképp érvelnék. A gyakorlatban a kettő együtt nem fordul elő - vagy klasszikus, vagy kvantumos leírást alkalmazunk. Ez megdöbbentően emlékeztet az ókori görögök látásmódjára. Szerintük különböző törvények vonatkoztak a Földre és az Égre. A Galilei-Newton-féle nézőpont erőssége, hogy a két törvényrendszert egybe lehetett kovácsolni, és meg tudta láttatni, hogy mindkettőt ugyanaz a fizika magyarázza. Valamilyen értelemben most visszajutottunk a görög szemlélethez: a törvények egy részét kvantumos szinten, más részüket pedig klasszikus szinten alkalmazzuk.

A 2.1 ábra félreérthető, és ezt most tisztázni szeretném. Newton, Maxwell és Einstein nevét a „klasszikus szint” dobozba helyeztem, a „determinisztikus” jelzővel egyetemben. Azonban ezzel nem azt állítom, hogy ők a világot determinisztikusnak hitték. Feltehetően Newton és Maxwell nem ezt a nézetet képviselte, bár Einstein látszólag igen. A „determinisztikus”, „számítható” jelzők az elméleteiket jellemzik, nem pedig a tudósok hitét a világgal kapcsolatosan. A „kvantumszint” dobozban találjuk a „Schrödinger-egyenletet” és biztos vagyok benne, Schrödinger nem feltételezett olyasmit, hogy a fizika egészét a róla elnevezett egyenlet jellemezné. Később visszatérek erre a megjegyzésre. Másképpen kifejezve, hogy az emberek és a róluk elnevezett elméletek nem azonosak.

Valóban létezik-e a 2.1 ábra két különálló szintje? Bizonyára feltehetjük a kérdést: „Pontosan leírható-e a Világegyetem egyedül a kvantummechanikai törvények segítségével? Megmagyarázhatjuk-e az egész univerzumot kizárólag a kvantummechanikával?” Válaszadás előtt mondanom kell egy-két dolgot a kvantummechanikáról. Kezdeném azzal, hogy felsorolom, mi mindent magyaráz meg.

•    Az atomok stabilitása. A kvantummechanika felfedezése előtt nem értették, miért nem hullnak az elektronok spirális pályán az atommagba, ahogyan azt a klasszikus elmélet jósolná. Stabil klasszikus atomok nem létezhetnek.

•    Spektrálvonalak. Az atomokban létező kvantált energiaszintek lehetővé teszik, hogy a szintek közötti átmenetkor létrejöjjenek a jól meghatározott hullámhosszakon megfigyelhető emissziós vonalak.

•    Kémiai erők. A molekulákat összetartó kémiai erők teljesen kvantummechanikai természetűek.

•    Feketetest-sugárzás. A feketetest-sugárzás spektruma csak a sugárzás kvantált jellegével magyarázható.

•    Az öröklődés megbízhatósága. A DNS molekuláris szintjén a kvantummechanika függvénye.

•    Lézerek. A lézerek működése a molekulák kvantummechanikai állapotai között indukált kvantumátmenetektől és a fény kvantumos (Bose-Einstein) természetétől függ.

•    Szupravezetés és szuperfolyékonyság. Ezek a jelenségek igen alacsony hőmérsékleten lépnek fel, és az elektronok (valamint egyéb részecskék) különböző anyagokban fellépő hosszú távú kvantumkorrelációival kapcsolatosak.

•    stb... stb.

A kvantummechanika tehát igencsak jelen van mindennapi életünkben, a csúcstechnológiák szerves részét képezi, ideértve a számítógépeket is. A kvantumtérelmélet, a kvantummechanika és Einstein speciális relativitáselméletének kombinációja, szintén elengedhetetlen a részecskefizika megértéséhez. Mint már említettük, a kvantumtérelmélet pontossága egy a 10¹¹-hez. Ez a lista jelzi, milyen csodálatos és erőteljes a kvantummechanika.

Hadd ejtsek most néhány szót arról, mi a kvantummechanika. A 2.2 ábra bemutatja az idevágó legtöbbet idézett kísérletet.

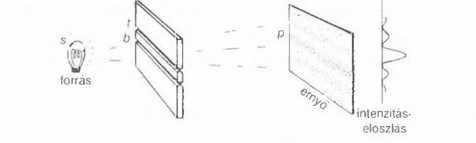
2.2 ábra A kétréses kísérlet, monokromatikus fény egyedi fotonjaival.

A kvantummechanika szerint a fényt fotonoknak nevezett részecskék alkotják. Az ábra olyan fotonforrást mutat, amely egyesével bocsátja ki a fotonokat. Van még két rés, t és b, valamint mögöttük egy ernyő. A fotonok az ernyőre egyesével érkeznek, ott egyesével észlelik őket, akár a közönséges részecskéket. A kvantumos furcsaság a következő. Ha csupán a t rés nyitott, az ernyő különböző pontjaiba érkezhet meg a fény. Bezárva a t rést és kinyitva b-t, a fotonok ismét csak sok helyre becsapódhatnak, akár az előbbi becsapódások helyére is. De ha mindkét rés nyitva áll, és az ernyőn a megfigyelési pontot gondosan megválasztjuk, azt tapasztalhatjuk, hogy a fotonok nem érkeznek meg a kiválasztott pontba, még akkor sem, ha a réseket egyesével megnyitva egyébként odaérkeztek volna. Valamilyen módon a foton által elkövethető két különböző dolog semlegesíti egymást. Ilyen viselkedés nincs a klasszikus fizikában. Vagy az egyik, vagy pedig a másik változat következik be - de olyan nincs, hogy a két lehetőség összebeszél, és közömbösíti egymást.

Ezt a kísérleti eredményt a kvantumelméletben a következőképpen értelmezzük: amikor a foton úton van a forrástól az ernyő felé, az állapota nem az, hogy vagy az egyik résen halad keresztül, vagy pedig a másikon, hanem a kettőnek valamilyen rejtélyes, komplex számokkal súlyozott kombinációja. Vagyis a foton állapotát a

w x (A lehetőség) + z x (B lehetőség)

fejezi ki, ahol w és z komplex számok. (Itt az „A lehetőség” a 2.2 ábrán a foton s-t-p útvonalára vonatkozik, a „B lehetőség” pedig az s-b-p útvonalra.)

Fontos, hogy a két lehetőséget szorzó együtthatók komplexek - a közömbösítés ezért következhet be. Gondolhattuk volna azt, hogy a fotonok viselkedése következhet abból, hogy milyen valószínűséggel következik be az egyik vagy a másik lehetőség. Ekkor w és z valós valószínűségi súlyok lennének. Azonban ez az értelmezés helytelen, mert w és z komplex, és ez rendkívül fontos a kvantummechanikában. A kvantumos részecskék hullámtermészete nem magyarázható a lehetőségek „valószínűségi hullámaként”. Itt a lehetőségek komplex hullámaival szembesülünk! A komplex számok a valós számokon kívül a mínusz egy gyökét is tartalmazzák, azaz i = gyök(-1) -t. Kétdimenziós síkban oly módon ábrázolhatjuk őket, hogy a tisztán valós számokat az x-tengelyen, a tisztán képzeteseket pedig az y-tengelyen sorakoztatjuk fel, mint a 2.3(a) ábrán. Az általános komplex számok a tisztán valós és a tisztán képzetes számok valamilyen kombinációi -például ilyen a 2 + 3xgyök(-1) = 2 + 3i - és a 2.3(a) ábra síkbeli pontjaként ábrázolhatok. Maga a sík Argand-diagramként (vagy Wessel-, illetve Gauss-síkként) ismert.

A komplex számok a 2.3(a) ábra síkbeli pontjainak feleltethetek meg. Meghatározott szabályok szerint adjuk össze, szorozzuk össze stb. őket. Összeadáshoz például egyszerűen a paralelogramma-szabályt alkalmazzuk, ami annyit jelent, hogy a valós és a képzetes részeket külön-külön adjuk össze, mint ahogyan az a 2.3(b) ábrán látható. Ha összeszorozzuk őket, a hasonló háromszögek szabályát alkalmazzuk a 2.3(c) ábrának megfelelően. Ha a 2.3 ábrán bemutatotthoz hasonló diagramokkal megbarátkoztunk, a komplex számok absztrakt fogalomból megfoghatóvá lépnek elő. Mivel a komplex számok már a kvantummechanika alapjaiba beépülnek, az emberekben kialakul az érzés, miszerint a kvantummechanika meglehetősen absztrakt és megismerhetetlen valami.

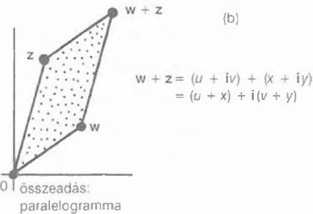
2.3 ábra (a) Egy komplex szám ábrázolása a (Wessel-Argand-Gauss) komplex síkon, (b) A komplex számok összeadásának geometriai ábrázolása, (c) A komplex számok szorzásának geometriai ábrázolása.

Mihelyt megbarátkozunk a komplex számokkal, különösen miután eljátszadozunk velük az Argand-diagramon, megfoghatóvá válnak, eltűnik aggasztó jellegük.

A kvantumelmélet azonban több a komplex számokkal súlyozott állapotok szuperpozíciójánál. Eddig csak a kvantumszintről volt szó, ahol az általam röviden csak U-ként nevezett szabályok érvényesek. Ezen a szinten a rendszer állapotát az összes lehetőség komplex számokkal súlyozott szuperpozíciója adja meg. A kvantumállapot időfejlődését unitér fejlődés (vagy Schrödinger-fejlődés) jellemzi, erre utal az U. Az U fontos tulajdonsága lineáris jellege. Két állapot szuperpozíciója mindig úgy fejlődik, mint a különálló módon fejlődő állapotok időben állandó komplex súlyokkal képezett szuperpozíciója. A lineáris jelleg a Schrödinger-egyenlet egyik alapvető sajátossága. Kvantumszinten a komplex számok által súlyozott szuperpozíció mindig megmarad.

Amikor azonban valamit felnagyítunk klasszikus szintre, a játékszabályok megváltoznak. A klasszikus szintre nagyítás alatt a 2.1 ábrán a felső U szintről az alsó C szintre való átmenetet értem - ez az, ami fizikailag történik, amikor például az ernyőn egy felvillanást megfigyelünk. A kisléptékű kvantumesemény egy nagyobb léptékű, klasszikusan megfigyelhető jelenséget gerjeszt. A standard kvantumelméletben gyakorlatilag valami olyasmit követünk el, amiről az emberek nem szívesen beszélnek. Ez nem más, mint a hullámfüggvény összeomlása, avagy az állapotfüggvény redukciója -a folyamatot a R betűvel jellemzem. Az unitér fejlődéstől gyökeresen különböző eljárásról van szó. A két lehetőség szuperpozíciójában a két komplex szám abszolút értékének négyzetét képezzük -az Argand-síkban a két pont origótól mért távolságainak négyzetét - és ezek megadják a két lehetőség relatív valószínűségét. Mindez azonban csak akkor következik be, amikor „megfigyelést, mérést végzünk”. Így képzelhetjük el a 2.1 ábra U szintjéről a C szintre való nagyítást. Ezzel az eljárással megváltoztatjuk a szabályokat - szó sincs már lineáris szuperpozícióról.

A négyzetre emelt abszolút értékek hirtelen valószínűségekké válnak. De ne feledjük: csupán az U-ról a C-re való átmenet válik nem determinisztikussá. A nem determinisztikus jelleg R-rel jön be. Az U szinten még minden determinisztikus - a kvantummechanika csupán akkor válik nem determinisztikussá, amikor „mérést végzünk”.

Hát, ez a standard kvantummechanikában használt eljárás. Nagyon furcsa eljárás egy alapvető elméletben. Talán, ha csak közelítő leírása volna valamilyen pontosabb elméletnek, könnyebben megbarátkoznánk vele, azonban ezt a hibrid eljárást az összes szakember alapvető elméletnek tekinti!

Hadd meséljek még a komplex számokról. Első pillantásra meglehetősen absztraktnak tűnnek, amíg csak abszolút értéküket négyzetre nem emeljük, hogy valószínűséggé váljanak. Ténylegesen gyakran van határozott geometriai jelentésük. Megadok egy olyan példát, melyből jelentésük tisztábban kiviláglik. Előtte azonban el kell mondanom még néhány dolgot a kvantummechanikáról. Használni fogom a Dirac-zárójelként ismert szellemes jelölést. Ez lényegében a rendszer állapotának rövid jelölése - ha azt írom: | A ), ez azt jelenti: a rendszer az A kvantumállapotban van. A zárójel belseje mindig a rendszer állapotát jellemzi. Gyakran a rendszer kvantum-mechanikai állapotát Ψ jelöli, és ez különböző egyéb állapotok szuperpozíciója. A kétréses kísérletben például:

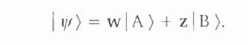
A kvantummechanikában nem a számok nagysága számít, hanem inkább arányuk. A kvantummechanika egyik szabálya szerint a rendszer fizikai állapota nem változik meg, ha állapotfüggvényét valamilyen (nem nulla) komplex számmal megszorozzuk. Másképpen mondva: csak a komplex számok arányának van közvetlen fizikai jelentése. Amikor R bekövetkezik, a valószínűségeket nézzük, ekkor az abszolút értékek négyzeteinek arányaira van szükségünk, a kvantumszinten maradva azonban remélhetjük, hogy maguknak a komplex számoknak az arányait értelmezhetjük, nem csupán az abszolút értékekét.

A Riemann-gömb a komplex számok gömbön való ábrázolásának egy módja (1.10(c) ábra). Mi több, nem csupán a komplex számoknak, de arányaiknak is. Résen kell azonban lennünk az arányokkal, mert a nevező nullává, így az arány végtelenné válhat - ezt is kezelnünk kell valahogyan. A 2.4 ábrán bemutatott egyszerű eljárással az összes komplex számot, a végtelennel egyetemben, nagyon szépen rá tudjuk képezni a gömbre. Most az Argand-sík a gömböt egységnyi sugarú körben metszi, a gömb egyenlítőjének síkjában. Nyilvánvaló, hogy a déli pólusból kiinduló félegyenesek segítségével az egyenlítői sík összes pontját a Riemann-gömbre lehet vetíteni. Mint ahogyan az az ábrán látszik, maga a déli pólus az Argand-sík „végtelenben található pontjának” a vetülete.

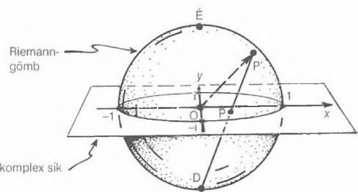
2.4 ábra A Riemann-gömb. A P pontot, mely a komplex síkban u = z/w-t jelképezi, a D déli pólusból a gömb P’ pontjába képezzük. A gömb középpontjából kiinduló OP’ irány két 1/2 spinű részecske szuperponált állapotára jellemző spin iránynak felel meg.

Amikor egy kvantumos rendszernek két lehetséges állapota van, a ketrő kombinációjából előállítható állapotok összességét egy gömb képviseli - egyelőre csupán egy absztrakt gömb amit azonban bizonyos feltételek között akár meg is figyelhetünk. Igazán kedvelem a következő példát. Az 1/2 spinnel rendelkező részecskék - mint az elektron, a proton vagy a neutron - spinállapotainak különböző kombinációi geometriailag is megvalósíthatók. Az 1/2 spinű részecskék kétféle spinállapotban találhatók, az egyikben a forgásvektor felfelé mutat (fel-állapot), a másikban pedig lefelé (le-állapot). A két állapot szuperpozíciója szimbolikusan a következő egyenlettel adható meg.

A kétféle spinállapot különböző kombinációi különféle tengelyek körüli forgásokat eredményeznek. Amennyiben tudni szeretnénk, hol van ez a tengely, képezzük a két komplex együttható arányát, ami egy újabb komplex szám: u = z/w. Helyezzük ezt az új számot a Riemann-gömbre. A keresett forgástengelyt a gömb középpontját a számmal összekötő egyenes adja meg. Látszik tehát, hogy a kvantummechanika komplex számai nem annyira absztraktak, mint első látásra hinnénk. Meglehetősen konkrét értelmük van - amit néha nehéz kihámozni de jelentésük az 1/2 spinű részecskék esetén nyilvánvaló.

Az 1/2 spinű részecskék vizsgálata valami egyebet is elárul. A felfelé és lefelé mutató spinekben semmi különleges nincs. Más tengelyt is választhattam volna, tetszésem szerint: jobbra vagy balra mutatót, előre vagy hátra mutatót - semmi különbséget nem jelent. A kiindulásul választott két állapot nem különlegesebb a többinél, mindössze arra kell vigyázni, hogy egymással ellentétes irányítású legyen. A kvantummechanika törvényei szerint bármely másik spinállapot ugyanolyan jó kiindulási pont, mint amit történetesen kiválasztottunk. Példánk rávilágít erre.

A kvantummechanika szép, jól definiált tudományterület. De rejtélyes is egyben és sok szempontból talányos, ellentmondásos. Hangsúlyozni szeretném, hogy kétféleképpen is rejtélyes. Nevezzük ezeket Z és X rejtélyeknek.

A talányos Z-rejtélyek (Az angol „puZZle” szóból) fizikai világunk részei: megbízható kísérletek hívják fel a figyelmet a kvantummechanika Z-rejtélyes viselkedésére. Bár még nem ellenőriztek teljesen minden Z-rejtélyes effektust, a kvantummechanika helyességében igen kevéssé kételkedhetünk. Ilyen rejtélyek a részecske-hullám kettősség, amiről korábban már beszéltem, a nullmérések, melyekre nyomban rátérek, a spin, amiről most volt szó és a nemlokális hatások, amelyekre szintén hamarosan sor kerül. A felsorolt igazán talányos jelenségek valóságtartalmát kevesen vitatják - bizonyosan a természet részét képezik.

Azonban egyéb gondok is adódnak, az X-rejtélyeknek nevezett paradox rejtélyek. Az én felfogásom szerint ezek jelzik, hogy az elmélet még csonka, hibás vagy valami hasonló - további figyelmet igényel. A leglényegesebb X-rejtély a mérés problémája, amiről beszéltem már - az, hogy a szabályok U-ból R-be mennek át, ha elhagyjuk a kvantumvilágot és belépünk a klasszikusba. Megérthenénk-e, miért jön elő ez az R-folyamat, talán mint kérdés vagy illúzió, ha jobban átlátnánk a kiterjedt és bonyolult kvantumrendszerek viselkedését? Az X-paradoxonok közül a legismertebb Schrödinger macskája. A kísérletben - hangsúlyozom, hogy ez egy elképzelt kísérlet, miután Schrödinger nagyon humánus ember volt - a macska egyszerre található halott és élő állapotban. Nem sok ilyen macska futkározik az utakon. Mindjárt többet mondok erről a problémáról.

Álláspontom szerint meg kell tanulnunk együtt élni a Z-rejtélyekkel, de az X-rejtélyeket fel kell oldanunk, amint erre egy jobb elmélet adódik. Hangsúlyozom, ez az X-rejtélyekkel kapcsolatos saját véleményem. A kvantummechanika (látszólagos) paradoxonait sokan látják más megvilágításban - mondhatnám úgy is: sokféle, egymástól különböző megvilágításban!

Mondanék még valamit a Z-rejtélyekről, mielőtt visszakanyarodom a sokkal komolyabb problémát jelentő X-rejtélyekre. Bemutatom a Z-rejtélyek két talán legmellbevágóbb példáját. Egyikük a kvantumos nemlokalitás, más szóval a kvantumos keveredés. Ez rendkívül figyelemre méltó dolog. Az eredeti ötlet Einsteintől, valamint munkatársaitól, Podolskytól és Rosentől származik és EPR kísérlet néven ismert. A feltehetően legérthetőbb változatát David Bohm dolgozta ki. Vegyünk egy 0 spinű részecskét, ami elbomlik két 1 spinű részecskére, például elektronra és pozitronra, melyek ellentétes irányban haladnak. Később megmérjük az egymástól távoli A és B pontokba kerülő részecskék spinjét. John Bell híres tétele értelmében ellentmondás van az A és a B pontokban végzett mérések eredményeinek csatolt valószínűségeire vonatkozó kvantummechanika elvárása és bármilyen „lokálisan realisztikus” modell között. Utóbbi alatt olyan modellt értek, amelyben az elektron az A pontban, a pozitron egy B pontban van, elkülönítve, és a kettőnek semmi kapcsolata nincs egymással. Ekkor a hipotézis az A és B pontokban végezhető mérések csatolt valószínűségeire olyan végeredményt ad, amely ellentmondásban van a kvantummechanikával, amint azt John Bell világossá tette. Ez rendkívül fontos eredmény, és a későbbi kísérletek, többek között Alain Aspect Párizsban végzett kísérlete a kvantummechanika előrejelzését igazolta. A kísérletet egy központi forrás által ellentétes irányokba kibocsátott fotonpárok polarizációs állapotával foglalkozik, és a 2.5 ábra mutatja be.

Az, hogy melyik irányban mérik meg az egyes fotonok polarizációját, csak akkor dől el, amikor a fotonok már javában távolodnak a forrástól az A és B pontok irányába. A mérések eredményei világosan kimutatták, hogy az A és a B pontokban észlelt fotonok polarizációs állapotainak csatolt valószínűségei a kvantummechanika jóslataival egyeztek, ahogyan a legtöbben várták, beleértve Bellt is, de ellentmondásban azzal a természetes feltevéssel, mely szerint a két foton egymástól különálló, független dolog. Az Aspect-kísérlet a kvantumos keveredés tényét 12 méteres távolságra kiterjedően állapította meg. Hallottam, hogy a kvantum-krisztallográfiával kapcsolatosan léteznek új kísérletek, melyek hasonló jelenségeket mutatnak ki kilométeres léptéken is.

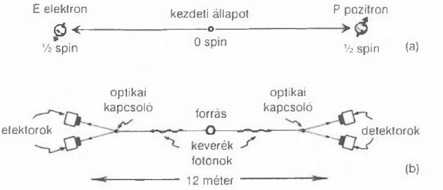
2.5 ábra (a) Egy nulla spinű részecske kér 1/2 spinű részecskére bomlik: pozitronra (P) ás elektronra (E). Valamelyik 1/2 spinű részecske spinjének mérése látszólag rögtön beállítja a másik spin állapotát, (b) Az Alain Aspect és társai által végzett EPR-kísérletben a forrás kevert állapotú fotonpárt bocsát ki. Az egyes fotonok polarizációját két lehetséges irányban mérhetjük meg, de a döntés csak akkor következik be, amikor a fotonok már javában távolodnak egymástól - túl későn ahhoz, hogy üzenet érkezhessen a másik fotonhoz, melyben értesülne a mérési irányról.

Ki kell emelnem, hogy bár a fenti nemlokális jelenségekben különböző A és B pontokban zajló eseményekről van szó, ezek rejtélyes módokon kapcsolódnak egymáshoz. A kapcsolat, vagy keveredés rendkívül kényes kérdés. A keveredés olyan, hogy nem nyújt lehetőséget üzenet küldésére A-ból B-be - ez a kvantummechanikának a relativitáselmélettel való konzisztenciája miatt rendkívül fontos. Ha nem így lenne, a fénysebességénél gyorsabban küldhetnénk üzeneteket a kvantumos keveredés segítségével. A kvantumos keveredés furcsa egy dolog. Különálló dolgok és egymással kommunikáló dolgok között valahol középúton foglal helyet - kimondottan kvantummechanikai jelenség, a klasszikus fizikában nem találni megfelelőjét.

A Z-rejtélyek másik példáját a  nullmérések képezik. Jó illusztráció az Elitzur-Vaidman bombatesztelő feladat. Tegyük fel, hogy terrorista csoport tagjaként nagy bombalerakatra bukkanunk.

Minden egyes bomba orrán szuperérzékeny detonátor van, egyetlen - a látható fény részeként érkező - foton visszaverődése a detonátoron elhelyezett tükrön elegendő impulzust ad át a pusztító robbanás bekövetkeztéhez. A bombák jelentős hányada azonban működés-képtelen, legalábbis egy bizonyos értelemben. Az a gond, hogy a bombák némelyikénél gyártási hiba folytán a tükröt tartó érzékeny lapka beragadt, így hiába éri foton a tükröt, az nem mozgatja meg a lapkát és a robbanás nem következik be (2.6(a) ábra). A lényeges pont az, hogy a selejtes bomba orrán lévő tükör úgy működik, mint egy közönséges rögzített tükör, nem pedig úgy, mint egy mozgatható, amely a detonációs mechanizmus része. Íme a probléma: válasszunk ki egy biztosan működő bombát a számos selejtet is tartalmazó gyűjteményből. A klasszikus fizikában esély sincs erre. Egyetlen lehetőség a kipróbálás: ha jó a bomba, szépet robban.

Egészen rendkívüli, hogy a kvantummechanika lehetőséget ad arra, hogy megvizsgáljuk: megtörténhetett-e volna valami, ami nem történt meg. Kimutatja azt, amit a filozófusok tényellenesnek neveznek. Figyelemre méltó, hogy a kvantummechanika szerint valódi jelenségek következhetnek a meg nem történtekből.

Hadd mutassak rá a megoldásra. A 2.6(b) ábra Elitzur és Vaidman 1993-ban adott eredeti megoldását szemlélteti. Tegyük fel, hogy a bomba hibás. A tükre beragadt, azaz rögzített. Meg sem moccan a foton hatására, és így nem lesz robbanás. Összeállítjuk a 2.6(b) ábrán látható szerkezetet. A kibocsátott foton először egy félig ezüstözött tükörrel találkozik. Az ilyen tükrök a ráeső fény felét engedik át, a másik felét pedig visszaverik. Azt hihetnénk, hogy a fotonok fele átmegy, másik fele visszapattan, de nem ez a helyzet. Kvantum-szinten egészen más történik a fotonokkal. A forrásból kiinduló összes különálló foton a két lehetőség, a visszaverődés és a tükrön való áthaladás kvantumos szuperpozíciójának állapotába kerül. A bomba tükre 45°-os szöget zár be a félig ezüstözött tükrön áthaladó fotonnyaláb pályájával.

A félig ezüstözött tükörről visszavert nyaláb viszont egy másik teljesen ezüstözött tükörrel találkozik, szintén 45 fokos szögben, végül mindkét nyaláb egyesül egy utolsó félig ezüstözött tükörnél. Két helyen találunk detektorokat, az A és a B pontokban.

Kísérjük végig egyetlen foton útját a forrástól kezdve, ha a bomba selejtes. Amikor az első félig ezüstözött tükörrel találkozik, állapota két különálló részre szakad, az egyik a tükrön áteresztett, a selejt irányába tartó fotonnak, a másik pedig a visszaverődött, a teljesen ezüstözört tükör felé igyekvő fotonnak felel meg.

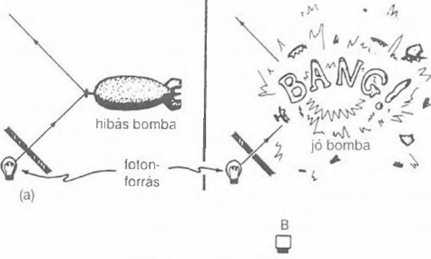
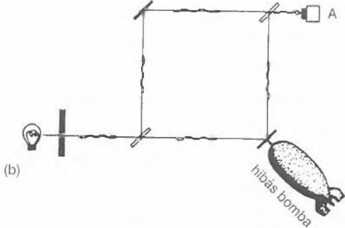
2.6 ábra (a) Az Elitzur-Vaidman bombatesztelő feladat. A bomba hiperérzékeny detonátora már egyetlen látható fényfotonra reagál - feltéve, hogy nem gyári hibás, detonátora nincs beragadva. A feladat: találni egy jó bombát a nagyszámú selejttel tarkított halmazban. (b) A selejtek kiszűrésére készült berendezés vázlata. Jó bomba esetén a jobb oldali alsó tükör mérőkészülékként viselkedik. Amikor azt méri, hogy a foton a másik úton ment végig, a B detektor fotont észlel - ez nem történhet meg, ha a bomba selejt.

(A különböző fotonpályák szuperpozíciója pontosan ugyanaz, mint ami a 2.2 ábrán bemutatott kétréses kísérletben történik. De lényegében a spinek összeadásának jelenségével is megegyezik.) Feltesszük, hogy a kétféle pálya az első és a második féligezüstözött tükör között ugyanolyan hosszú. Ahhoz, hogy megállapíthassuk, milyen állapotban érkezik a foton a detektorokhoz, össze kell hasonlítanunk a két lehetséges - egymással kvantumos szuperpozícióban lévő - útvonalat, melyeken a foton valamelyik detektorhoz érkezhet. Azt látjuk, hogy az utak kioltják egymást a B detektornál, de erősítik egymást az A-nál. Vagyis a jel csupán az A detektort aktiválhatja, a B-t sohasem. Akár a 2.2 ábrán bemutatott interferenciakép esetén, itt is vannak olyan pontok, ahol mindig nulla az intenzitás, mivel a kétféle kvantumállapot kioltja egymást. A selejtes bombáról való visszaverődés esetén az A detektor aktiválódik, sohasem a B.

Más a helyzet egy jó bombával. Az orrán lévő tükör nem rögzített, és elmozdulási képessége mérőeszközzé lépteti elő. A bomba tükre méri a foton egyik vagy másik állapotát, aszerint, hogy a foton a tükörhöz megérkezett vagy sem. Ha a foton keresztülhaladt az első, félig ezüstözött tükrön és a detonátor tükre jelzi, hogy valóban erre vette útját, a bomba, bumm, felrobban. Volt - nincs. Ezután kipróbálhatunk egy másik bombát. Talán az új bomba azt fogja mérni, hogy a foton nem érkezik meg: nem robban fel, így azt méri, hogy a foton a másik úton haladt végig. (Ez egy nullmérés.) Amikor a foton elérkezik a második félig ezüstözött tükörhöz, egyszerre át is megy, vissza is verődik, így megérkezhet B-be. Így egy jó bomba esetén B olykor-olykor észlel egy fotont, ami jelzi, hogy a bomba azt mérte, hogy a foton a másik úton ment. A probléma lényege, hogy a jó bomba egyben mérőeszköz is, azaz annak ellenére, hogy a fotonnal nem lépett kölcsönhatásba, interferál azzal az egzakt kioltással, ami szükséges ahhoz, hogy megakadályozza B-ben a foton észlelését. Nullmérést végzett. Ha a foton nem az egyik pályán érkezett, akkor biztosan a másikon! Ha B fotont észlel, tudjuk, hogy a bomba mérőeszközként működött és így nem selejtes. Mi több jó bomba esetén a B detektor időnként méri a foton megérkezését, és a bomba nem robban. Ez csak akkor történik, ha a bomba jó. Megállapíthatjuk, hogy jó bomba, mert kimutatta, hogy a foton a másik pályán ment végig.

Ez tényleg nagyszerű. 1994-ben Zeilinger Oxfordba látogatott, és elmesélte, hogy végrehajtotta a bomba tesztelésére irányuló kísérletet. Persze, nem bombával, hanem valami hasonlóval. Szeretném hangsúlyozni, hogy Zeilinger nem terrorista. Elmondta, hogy Kwiat, Weinfurter és Kasevich kollégáival kidolgoztak egy olyan megoldást, ami egyáltalán nem pazarolja el a bombákat. Nem mesélem el a részleteket, mert eléggé bonyolult eljárás. Igazából, ha módszerüket alkalmazzuk, van egy elhanyagolhatóan kis mértékű veszteség, de lényegében veszteség nélkül található egy garantáltan jó bomba.

Maradjunk most ennyiben. A bemutatott példák rávilágítanak a kvantummechanika és Z-rejtélyei rendkívüli természetének néhány vonására. A gondok egy része abból származik, hogy egyeseket ez túlságosan elvarázsol. Istenem, milyen bámulatosa kvantummechanika, mondják, és tulajdonképpen igazuk van. A Z-rejtélyeket a valóság részeként elfogadni valóban eléggé bámulatos. Azonban ha ezek után azt gondolják, hogy az X-rejtélyeket is el kell fogadniuk, azt hiszem, ez rossz.

Térjünk vissza Schrödinger macskájához. A 2.7 ábrán bemutatott elképzelt kísérlet nem teljesen Schrödinger eredeti változata, de céljainknak inkább megfelel. Ismét adott egy fotonforrás és egy félig ezüstözött tükör, amely kettéosztja a foton kvantumállapotát két különböző, a visszavert és áteresztett állapot szuperpozíciójába. Az áteresztett foton útjába valamilyen fotondetektáló eszközt helyezünk, ami a foton érkezésekor lelövi a macskát. Azt hihetnénk, a macska a mérés befejezését jelenti; a kvantumos szintről az ellenőrizhető állítások talajára érkezünk, amikor akár élve, akár holtan rátalálunk. A probléma azonban ott kezdődik, ha a kvantummechanikát a macskák világára is érvényesnek fogadjuk el - mert akkor azt kell hinnünk, hogy a macska aktuális állapota az élő és a halott állapotának szuperpozíciója. A foton az egyik vagy a másik irányba haladó állapotok szuperpozíciójában, a detektor a jelez vagy a nem jelez állapotok szuperpozíciójában, a macska pedig az élő és halott macska szuperpozíciójában van. A probléma régóta ismert. Hogyan vélekednek róla különböző emberek? Minden valószínűség szerint a kvantummechanikával kapcsolatos különféle álláspontból több van, minta kvantum-mechanikát művelőkből. Ez még csak nem is ellentmondás, hiszen a kvantumfizikusok bizonyos része több felfogásnak is híve egy időben.

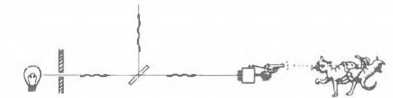
2.7 ábra Schrödinger macskája. A kvantumállapot az átmenő és visszaverődő foton lineáris szuperpozíciója. Az átmenő komponens elsüt egy pisztolyt, ami lelövi a macskát, így az U-fejlődés értelmében a macska az élet és halál állapotainak szuperpozíciójaként létezik.

Bob Wald ebéd közben elejtett remek megjegyzésével szeretném a különböző szemléletmódok osztályozását jellemezni. Ezt mondta:

Amennyiben tényleg hiszel a kvantummechanikában, nem veheted komolyan.

Úgy tűnik nekem, hogy ez egy rendkívül mély és igaz megjegyzés a kvantummechanikáról és az emberek hozzáállásáról a kvantummechanikához. A 2.8 ábrán a kvantumfizikusokat különböző osztályokba soroltam. A felosztás lényege, hogy ki az, aki hisz és ki az, aki komoly. Hogy mit értek komolyság alatt? A komoly emberek a | Ψ> állapotvektor segítségével írják le a világot - az állapotvektor maga a valóság. Azok, akik igazán „hisznek” a kvantummechanikában, nem hiszik, hogy ez lenne a helyes hozzáállás.

Különböző emberek neve szerepel az ábrán. Amennyire meg tudom ítélni, Niels Bohr és a koppenhágai nézőpont követői a hívők táborába tartoznak. Bohr kétségkívül hitt a kvantum-mechanikában, azonban nem tudta az állapotvektort a világ leírásaként komolyan venni. Valamilyen értelemben |Ψ> csupán a gondolatainkban létezik, a mi sajátos módszerünk a világ leírására, de nem maga a világ. Ezt nevezte John Bell FAPP-nak, azaz „minden praktikus célra alkalmasnak”. (For All Practical Purposes) John Bell kedvelte ezt a kifejezést, úgy sejtem, enyhén lekicsinylő hangzása miatt. A FAPP a „dekoherencia-nézőponton” alapul. melyről bővebben szólok majd nemsokára. Gyakran előfordul azonban, amikor alaposan kikérdezzük a FAPP leglelkesebb híveit, mint például Zureket, hogy álláspontjuk visszavezet a 2.8 ábra közepébe. Mit is értek tehát az „ábra közepén”?

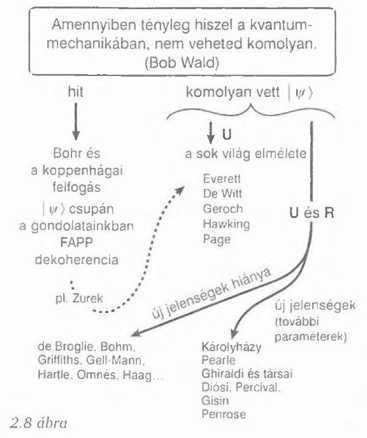
A „komoly” emberek csoportját több részre osztottam. Egyesek hiszik, hogy U-ból áll minden - az unitér fejlődés mindent tartalmaz. Így jutnak el a sok világ nézőpontjához. Ebben a macska tényleg egyszerre élő és holt, de a két macska bizonyos értelemben két különböző univerzumban él. Később még visszatérek erre. Feltüntettem néhányat azok közül, akik magukévá tették ezt az általános nézőpontot, legalábbis gondolkodásuk valamilyen szintjén. A sok világ hívei szerepelnek az ábra közepén.

Nézetem szerint azok az emberek veszik valóban komolyan a |Ψ> állapotfüggvényt - és magamat is ilyennek tartom akik hiszik, hogy U és R egyaránt valós jelenség. Nemcsak unitér fejlődés zajlik a kicsinek tekinthető rendszerekben, de valami más is végbemegy, amit R-nek neveztem - talán nem pontosan R, de valami hasonló. Ezentúl két felfogás közül választhatunk. Vagy azt hisszük, hogy új fizikai jelenségeket már nem kell figyelembe venni, és ideértem de Broglie és Bohm álláspontját, valamint az ettől jelentősen különböző Griffiths, Gell-Mann, Hartle és Omnés által képviselt nézetet. A standard U kvantummechanika mellett R-nek is jut valamelyes szerep, de nem várható új jelenségek felbukkanása. Vannak aztán a második „igazán komoly” nézőpont hívei - magamat közéjük sorolom akik szerint valami újnak kell belépnie, és megváltoztatnia a kvantummechanika szerkezetét, mivel R gyökeresen ellentmond U-nak. Az ábra jobb alsó részén felsoroltam néhány nevet azok közül, akik ezt a felfogást vallják.

Említenék még valami, kissé részletesebbet a matematikáról és arról, miként kezelik Schrödinger macskáját a különböző nézőpontok. Visszatérünk a Schrödinger-macskás ábrához, de ezúttal hozzátesszük a w és z komplex súlyozást (2.9(a) ábra). A foton a két állapot között oszlik meg, és amennyiben komolyan vesszük a kvantummechanikát, hisszük, hogy az állapotvektor valóságos, és hogy a macska valóban az élő és halott állapotok valamilyen szuperpozíciójában van. Az élő és halott állapotokat a Dirac-zárójelek segítségével könnyedén ábrázolhatjuk (2.9(b) ábra). A Dirac-zárójelbe macskákat és más szimbólumokat lehet tenni! Persze, a macska még nem minden, hisz ott a fegyver, a foton és a környező levegőréteg, vagyis a teljes környezet. Az állapot mindkét összetevője valamilyen szorzata az összes hatásnak, de a szuperpozíció még mindig megvan (2.9(b) ábra).

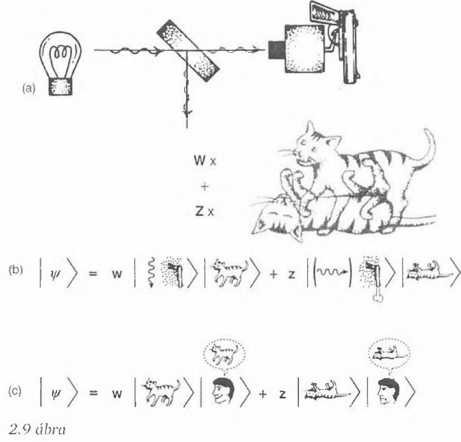
Hogyan egyeztethető össze a sok világ felfogás mindezzel? Ebben a felfogásban valaki jön, ránéz a macskára és mi azt kérdezzük „Vajon ő miért nem a macska kétféle állapotának szuperpozícióját látja?” A sok világ elmélet híve a 2.9(c) ábrán látható módon írná le a helyzetet. Van egy élő macska állapot, melyhez hozzátartozik a szemlélő is, aki mindezt érzékeli; és van egy másik, halott macska állapot egy második szemlélővel. A két lehetőség szuperpozícióban van: a Dirac-zárójelekben a macskát megfigyelő személy lelkiállapotát is feltüntettem - a személy arckifejezése tükrözi a lelkiállapotot.

A sok világ hívői szerint tehát minden rendben - a macska állapotát megfigyelő személyből különböző másolatok léteznek, de ezek „különböző univerzumokban” élnek. Bárki elképzelheti, hogy ő a másolatok egyike, de van belőle még egy másolat egy másik „párhuzamos” univerzumban, aki a másik lehetőséget látja. Természetesen ez nem túl gazdaságos univerzumkép, azonban attól tartok, a helyzet a sok világ leírással valójában még ennél is rosszabb. Nemcsak a gazdaságosság hiánya aggaszt. A fő bajom, hogy nem oldódik meg a probléma. Például miért nem képes a tudatunk makroszkopikus szuperpozíciókat érzékelni? Vegyük azt a speciális esetet, amikor w és z megegyezik. Ezt az állapotot a 2.10 ábrának megfelelően átírhatjuk: az élő macska plusz a holt macska, valamint az élő macskát látó személy plusz a halott macskát látó személy állapot összeadva az élő macska mínusz a holt macska, valamint az élő macskát látó személy mínusz a halott macskát látó személy állapottal.

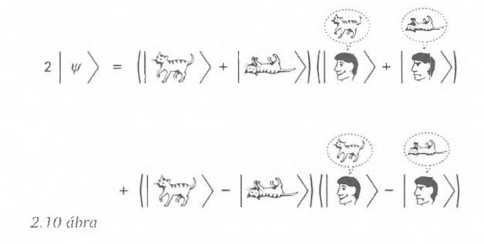
Ez csupán egyszerű algebra. Tiltakozhatunk: „ilyet nem lehet tenni, az érzékelhető állapotok nem ilyenek!” De miért is ne? Nem igazán tudjuk, mi az érzékelés. Honnan tudjuk, hogy egy érzékelt állapot nem állhat az élő és a halott macska egyidejű érzékeléséből? Amíg nem áll rendelkezésünkre az érzékelés megbízható elmélete, mely kizárná a kevert érzékelésű állapotokat - és ez a 3. fejezetben tárgyaltakon jóval túlmutat úgy tűnik számomra, hogy a sok világ felfogás nem jelent megoldást.

Nem magyarázza meg, miért érzékeljük az egyik vagy a másik állapotot, nem pedig a szuperponáltat. Jó elméletté csak az érzékelés elméletével együtt válhatna. Másik gyenge pontja, hogy nem mondja meg: tetszőleges w és z számok esetén a valószínűségek miért pontosan azok, amelyeket a kvantummechanika a négyzetre emelt abszolút értékekkel jósol. A valószínűségeket végül is rendkívül pontosan ellenőrizhetjük.

2. ] 1 ábra

Hadd merüljek kissé mélyebben bele a kvantumos mérések témakörébe. Ehhez részleteznem kell a kvantumos keveredést. A 2.11 ábrán az EPR kísérlet Bohm-féle leírását mutatom be. Emlékezzünk, ez egy Z-rejtély. Hogyan írjuk le az ellentétes irányokba haladó, 1/2 spinű részecskék állapotát? A tel jes spin nulla, így amennyiben az egyik részecske spinje itt felfelé mutat, a másiké ott lefelé kell mutasson. A rendszer kvantumállapota tehát a „fel-itt” és a „le-ott” szorzata lesz. Ha pedig az első részecske spinje lefelé mutat itt, a másiké ott felfelé fog mutatni. (Ezek a lehetőségek merülnek fel. ha a fel-le tengely mentén vizsgáljuk a spint.) A teljes rendszer kvantumállapotát a két lehetőség szuperpozíciója adja. Bármilyen tengelyt választunk is, mindig egy mínuszra lesz szükség ahhoz, hogy a részecskepár teljes spinje nulla legyen.

Tegyük fel, hogy az „itt” lévő detektor felé repülő egyik részecske spinjének meghatározására készülünk, a másik részecske pedig nagyon nagy utat tehet meg, mondjuk, elmehet a Holdig, tehát az „ott” a Holdon van. Most képzeljük azt, hogy valamelyik kutatótársunk a Holdon dolgozik, és meghatározza az odaérkezett részecske spinjét a fel-le tengely mentén. Egyforma valószínűséggel talál majd felfelé és lefelé mutató spineket. Ha felfelé mutató spint talál, a földi detektornak lefelé mutató spint kell érzékelnie, ha pedig lefelé mutató spint mér, a földi detektorban a spin felfelé mutat. Ezért úgy tekintjük, hogy a mérendő részecske állapota a spin-fel és a spin-le állapotok egyenlő valószínűségű keveréke.

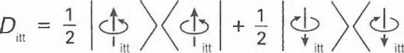
2.12 ábra

A kvantummechanika ismer egy eljárást a fentihez hasonló valószínűségi keverékek kezelésére. Az eljárás a sűrűségmátrix bevezetésén alapszik. A fenti példában az „itt” a Földön használandó sűrűségmátrix a 2.12 ábrán feltüntetett kifejezés lesz. Az egyenlőség jobb oldalán álló első V2 szorzó annak a valószínűsége, hogy a földi mérés felfelé mutató spint érzékel, a második V2 pedig az, hogy lefelé mutatót. Ezek közönséges klasszikus értelemben vett valószínűségek, a mérendő részecske aktuális spinállapotával kapcsolatos bizonytalanságot fejezik ki. A közönséges valószínűségek 0 és 1 közé eső valós számok, a 2.12 ábrán bemutatott kombináció pedig nem kvantum-szuperpozíció - amelyben az együtthatók komplex számok lennének -, hanem egy valószínűségekkel súlyozott kombináció. Megjegyezzük, hogy a két valószínűségi tényező (1) olyan kifejezéseket szoroz, amelyekben az első Dirac-zárójel szögletes zárójele jobbra mutat - neve (Dirac) ket vektor, a másodiké balra - bra vektor. (A bra vektor a ket vektor „komplex konjugáltja”.) A bra és a ket az angol bracket (zárójel) két szótagja.

Nem lenne szerencsés, ha megkísérelnénk a sűrűségmátrixok leírásához szükséges matematika részletes magyarázatát. Számunkra elég annyi, hogy a sűrűségmátrix tartalmaz minden szükséges információt, ami lehetővé teszi a rendszer kvantumállapotának egyik részén végzett mérési eredmények valószínűségeinek kiszámítását - feltéve, hogy az állapot másik részéből származó információ elérhetetlen marad. Példánkban a részecskepár kvantumállapotáról van szó (keverék állapot), és feltesszük, hogy „itt” semmiféle információ nem érhető el az „itt” vizsgált részecske partneréről „ott”, a Holdon elvégezhető mérésekről.

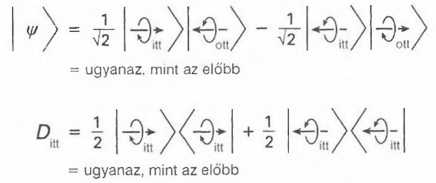
2.13 ábra

Módosítsuk egy kissé a helyzetet, és tegyük fel, hogy holdbéli kollégánk úgy dönt: a részecske spinjét nem a fel-le, hanem a jobb-bal irányban méri. Ehhez kényelmesebb a 2.13 ábrán látható állapotleírás használata. Ez pontosan ugyanaz az állapot, mint a 2.11 ábrán leírt, mint ahogyan az a 2.4 ábrán bemutatott geometriára alapozott kis algebrával kiszámolható, csupán az állapot ábrázolása más. Továbbra sem tudjuk, milyen eredményre vezet kollégám jobb-bal irányú spinmeghatározási kísérlete a Holdon, de azt igen, hogy 1/2 a valószínűsége annak, hogy balra mutató spint talált - ekkor mi jobbra irányítottat mérünk a Földön és ugyancsak 1/2 annak a valószínűsége, hogy jobbra mutatót mért - ekkor mi balra mutatót látunk. A sűrűségmátrix eszerint a 2.13 ábrán látható kell legyen; és ez kötelezően ugyanaz, mint a 2.12 ábrán látható. Ami rendben is van eddig. Holdbéli kollégám arra vonatkozó döntése, hogy miként végzi el mérését, nem befolyásolhatja az általunk mért valószínűségeket. (Ha mégis, az a fénysebességnél gyorsabb üzenetközvetítést jelentene, az üzenet a spin tengelyének a megválasztásába volna kódolva.)

Az algebrát közvetlenül is ellenőrizhetjük, hogy lássuk, a sűrűségmátrixok valóban azonosak. Aki ismeri ezt a fajta algebrát, tudni fogja, miről beszélek, aki pedig nem, az se aggódjék. Ha az állapot bizonyos része elérhetetlen, a sűrűségmátrix a legjobb, amit segítségül hívhatunk. A sűrűségmátrix összekapcsolja a közönséges értelemben vett valószínűségeket a kvantummechanikai leírással, amely implicit módon kvantummechanikai valószínűségeket is tartalmaz. Ha nincs tudomásunk arról, mi történik „ott”, a sűrűség-mátrix az „irt” állapot megadható legjobb leírása.

Mégis, nehéz arra az álláspontra helyezkedni, hogy a sűrűség-mátrix a valóságot írja le. A probléma abból fakad, hogy nem tudhatjuk, vajon később nem érkezik-e üzenet a Holdról, hogy kollégánk ténylegesen megmérte az állapotot, és ezt és ezt az eredményt kapta. Ha igen, akkor bizonyossággal fogjuk ismerni az általunk vizsgált részecske állapotát. A sűrűségmátrix nem mondott el mindent részecskénk állapotáról. A teljességhez ismernünk kellene az összetett rendszer aktuális állapotát. Így a sűrűségmátrix valamilyen ideiglenes leírás, ezért néha FAPP-ként (minden praktikus célra használhatóként) tartják számon.

A sűrűségmátrixot általában nem az ehhez hasonló helyzetek, hanem inkább a 2.14 ábrán bemutatotthoz hasonlók leírására használják. Tizekben nem olyan a kevert állapot, hogy egyik része a számunkra „itt”, a másik a kollégánk számára „ott” a Holdon elérhető, hanem az „itt” állapot egy macska, halott vagy élő, az „ott” állapot (akár ugyanabban a szobában) a teljes környezet állapota, amely a macskával együtt fejlődik. Vagyis az élő macska valamilyen környezettel együtt plusz a halott macska valamilyen más környezettel együtt lehet a teljes kevert állapotvektor. A FAPP hívei szerint sohasem ismerhetjük pontosan a környezetet, így az állapotvektor helyett a sűrűségmátrixot kell használni (2.15 ábra).

A sűrűségmátrix ezt követően valószínűségi keverékként viselkedik, és a FAPP hívei szerint minden gyakorlati alkalmazás szempontjából a macska vagy élő, vagy holt. Lehet, hogy ez rendben is van „minden gyakorlati alkalmazás” szempontjából, de kétségkívül nem fejezi ki a valóságot - nem mondja meg, mi történhet később, ha jön egy nagyon okos ember, és megmondja, hogyan kell kivonni az információt a környezetből. Bizonyos szempontból ideiglenes nézőpontnak fogható fel - ami mindaddig megfelelő, míg senkinek sem sikerül a hiányzó információt pótolni. Azonban a macskára megismételhetjük az EPR-kísérlet kapcsán tett elemzésünket, melyben kimutattuk, hogy a felfelé és lefelé mutató, illetve a jobbra és balra mutató spinállapotok egyformán használhatók. A jobbra és balra állapotokat a fel és le állapotoknak - a kvantummechanika szabályai szerint képezett - kombinációiként állíthatjuk elő. Eredményképpen mindkét esetben ugyanaz a teljes kevert állapotvektor (2.13(a) ábra) és ugyanaz a sűrűségmátrix (2.13(b) ábra) jellemzi a részecskepárt.

A macska és környezete esetén (amikor a w és z amplitúdók azonosak), ugyanazzal a matematikai eljárással a „spin-jobbra” szerepét az „élő macska plusz halott macska”, a „spin-balra” szerepét pedig az „élő macska mínusz halott macska” állapot veszi át. Sem az állapotvektor, sem a sűrűségmátrix nem változik meg (2.14, illetve 2.15 ábra, z = w helyettesítéssel). Igaz lenne az, hogy az „élő macska plusz halott macska" vagy az „élő macska mínusz halott macska” ugyanolyan jó, mint az élő vagy a halott macska? Ugye, ez nem egészen nyilvánvaló. A matematika viszont kézenfekvő, a sűrűségmátrix ugyanaz. A sűrűségmátrix ismerete tehát nem segít annak meghatározásában, hogy a macska ténylegesen élő vagy halott. Másképp kifejezve, a macska élő vagy halott volta nincs benne a sűrűségmátrixban - többre van szükségünk.

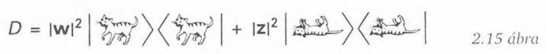
Nemcsak azt nem magyarázza egyik sem, hogy ténylegesen miért élő vagy halott a macska (nem pedig valamilyen kombinációja a kettőnek), hanem azt sem, hogy miért érzékeljük vagy élőnek, vagy pedig halottnak. De még azt sem, hogy tetszőleges w és z esetén a relatív valószínűségek miért |w|² és |z|². Szerintem ez nem elég jó. Visszakanyarodnék most ahhoz a diagramhoz, mely a fizika egészét mutatja, de kiegészítem mindazzal, amit a fizikának véleményem szerint a jövőben tennie kell (2.17 ábra). Az R betűvel jelölt eljárás csupán közelítése valaminek, amit még nem ismerünk. Az ismeretlen eljárást OR-nak, Objektív Redukciónak nevezem. Objektív, mert objektív módon vagy' az egyik, vagy a másik lehetőség valósul meg. Sajnos, ez az elmélet egyelőre hiányzik. (Az OR szép akronimia, ,mert az „or” szót (magyarul: vagy) is jelöli, és éppen ez történik, egyik vagy (or) másik.)

Hogyan zajlik ez a folyamat? Az általam támogatott nézőpont szerint a szuperpozíció elve valahogyan elromlik, amikor lényegesen különböző téridő-geometriákra alkalmazzuk. Téridő-geometriákkal az első fejezetben találkoztunk. A 2.18(a) ábrán bemutatok közülük kettőt, valamint szuperpozíciójukat is, ezt ugyanolyan szabályok szerint írtam fel, mint a fotonok vagy a részecskék esetén. Ha a különböző téridők szuperpozíciója szükségessé válik, a problémák seregével szembesülünk, mivel a két téridőben más irányokba mutathatnak a fénykúpok.

2.17 ábra

Ebbe az alapvető problémába az általános relativitáselméletkvantálására irányuló valamennyi komoly próbálkozás beleütközik. Ilyen különös szuperponált téridőben - véleményem szerint-még senkinek sem sikerült érvényes fizikát kidolgozni.

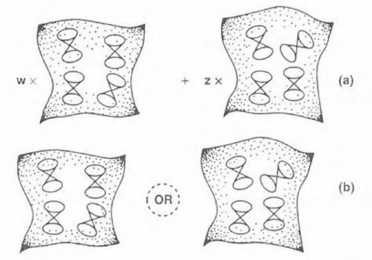
2.18 ábra

Ennek pedig jó oka van - nem ez a követendő eljárás. A szuperpozíció valahogyan az egyik, vagy (OR) másik lehetőséggé válik, és ez a téridő szintjén történik (2.18(b) ábra). Valaki mondhatja: „Elvileg minden rendben van, de amikor a kvantummechanikát és az általános relativitáselméletet próbáljuk összekombinálni, előjönnek ezek a képtelen számok, a Planck-idő és a Planck-hossz, amelyek sok nagyságrenddel kisebbek még a részecskefizikában előforduló időtartamoknál és távolságoknál is. Még annál is távolabb áll a macskák vagy emberek léptékétől. Mi köze lehet így a kvantumgravitációnak ezekhez?” Azt hiszem, elég sok, mert a dolgok alapvető természetéről van szó.

2. 7 9 ábra Mi a jelentősége a 10^-33 cm-es Planck-skálának a kvantumállapot redukciója szempontjából? Az alapelképzelés szerint a redukció akkor jön létre, amikor elégséges tömegkülönbség keletkezik a szuperpozícióban lévő két állapot között, és ennek következtében a két téridő nagyságrendben 10^-33 cm-rel különbözik egymástól.

Mi a jelentősége a Planck-hossznak (10^-33 cm) a kvantumállapot redukciója szempontjából? A 2.19 ábra nagyon vázlatosan mutatja, milyen egy kettéhasadni próbáló téridő. A helyzet két téridő szuperpozíciójához vezet, közülük az egyik a halott macskát, a másik az élő macskát jelképezhetné, és valamilyen oknál fogva a két különböző téridő szuperpozíciója szükségesnek látszik. Meg kell kérdeznünk. „Mikor válik annyira különbözővé a két téridő, hogy aggódni kezdjünk, meg kell-e változtatni a játékszabályokat?” Azt kell figyelni, hogy valamilyen alkalmas értelemben mikor éri el a két geometria különbsége a Planck-hosszt. Ekkor elkezdhetünk töprengeni, hogyan tovább, és ekkor változhatnak a szabályok. Emlékeztetni szeretnék arra, hogy téridőkről beszélünk, és nem terekről. Így „Planek méretű téridő-szeparáció” esetén a kisebb térbeli szeparáció hosszabb, a nagyobb térbeli szeparáció pedig rövidebb időtartamot jelent. Szükségünk van egy olyan kritériumra, mellyel megbecsülhetjük, mikor különbözik jelentősen két téridő, és ez egy időskálát, kapcsol a két lehetőség közötti választáshoz. Tehát e nézőpont szerint a Természet kiválasztja az egyik vagy a másik téridőt, de olyan szabályok szerint, amelyeket még nem ismerünk.

Milyen hosszú ideig tart, amíg a Természet döntést hoz? Kiszámíthatjuk a szükséges időskálát olyan egyszerű esetekben, amikor egyrészt elégséges az einsteini elmélet newtoni közelítését alkalmazni, másrészt a kvantumos szuperpozícióban részt vevő két gravitációs mező közötti különbség jól meghatározható (a két komplex amplitúdó nagysága pedig hozzávetőlegesen azonos nagyságrendű). Az általam javasolt válasz a következő. A macskát most egy görönggyel helyettesítjük - a macska már teljesítette feladatát, megérdemli a pihenést. Mekkora a göröngy, hogyan mozdul el, és milyen időtartam szükséges az állapotvektor összeomlásához? (2.20 ábra). A két állapot szuperpozícióját instabilnak fogom tekinteni -olyasmi ez, mint egy bomló részecske, egy uránium atommag, vagy valami hasonló a bomlásnak többféle végterméke lehet és egy bizonyos időskála kapcsolódik hozzá. Az instabil jelleg egyelőre csak hipotézis, de következnie kell a még felderítendő fizikából.

2.20 ábra A macska helyett a mérés egy gömb alakú göröngy egyszerű mozgásával is történhetne. Milyen nagy és mennyire nehéz kell legyen a göröngy; mennyire kell elmozdulnia; R bekövetkezte előtt mennyi ideig állhat fenn a szuperpozíció?

Az időskála meghatározásához tekintsük azt az E energiát, melynek segítségével a göröngy egyik példányát el tudnánk távolítani a másik gravitációs teréből. A bomlás időskáláját megkapjuk, ha a 2π-vel osztott Planck-állandót, h-t, elosztjuk E-vel:

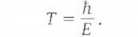
Sok olyan elképzelés létezik, ami ezt az általános érvelést követi - közös vonása ez a gravitációval kapcsolatos elképzeléseknek, bár részleteikben természetesen különbözhetnek.

Más érvek is alátámasztják, hogy egy fentihez hasonló gravitációs séma jó kiindulási pont lehet. Az egyik az, hogy a kvantumos mérés problémáját megoldani szándékozó, új fizikai jelenségeket bevezető összes többi explicit kvantumállapot redukciós sémában sérülnek az energiamegmaradás ismert szabályai. Talán az energia valóban nem marad meg. A gravitációs forgatókönyvekben azonban szerintem jó esély látszik arra, hogy a probléma elkerülhető legyen. Bár a részleteket még nem látom át, elmondom, mire is gondolok.

Az általános relativitáselméletben a tömeg és az energia fölöttébb furcsa dolgok. Először is, a tömeg nem más, mint az energia (elosztva a fénysebesség négyzetével), így a gravitációs potenciális energia hozzájárul a tömeghez (negatív irányban). Vagyis ha két göröngy egymástól távol helyezkedik el, a rendszer tömege kicsivel nagyobb, mint akkor, ha közel vannak (2.21 ábra). Bár a tömegenergia sűrűségek (melyeket az energia-impulzus tenzor mér), kizárólag a göröngyök belsejében különböznek nullától, és a nagyságuk egyikben sem függ lényegesen a másik jelenlététől, a teljes energia a 2.21 ábrán bemutatott két helyzetben különbözik. A teljes energia nem lokális. Az általános relativitáselméletben az energiának valóban van valamilyen alapvetően nem lokális jellege. Biztosan ez a helyzet az első fejezetben ismertetett híres kettős pulzár esetében is: a gravitációs hullámok pozitív energiát és tömeget visznek el a rendszerből, ez az energia viszont nem lokális módon oszlik el a térben. A gravitációs energia nehezen megfogható dolog. Az a benyomásom, hogy az általános relativitáselmélet és a kvantum-mechanika helyes egyesítése jó esélyt adna az állapotvektor redukciója kapcsán felmerülő energiagondok megoldására. A szuperponált állapotban figyelembe kell venni az energiához adódó gravitációs járulékot is. Azonban a gravitáció miatt nemigazán tudunk lokális értelmet adni az energiának, így van egy alapvető bizonytalanság a gravitációs energiában, melynek nagyságrendje a korábban említett E. Ugyanaz a helyzet, mint az instabil részecskékkel. Az instabil részecske tömegenergiájának bizonytalanságát ugyanaz az összefüggés kapcsolja össze az élettartamával.

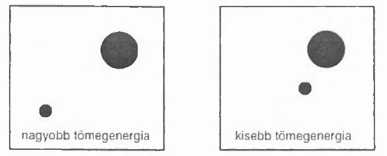
2.2 1 ábra A gravitációsan kölcsönható rendszer teljes tömegenergiája tisztán gravitációs járulékokat is tartalmaz, amelyek nem lokalizálhatok.

Befejezésül az általam támogatott megközelítésben fellépő explicit időtartamokat vizsgálom meg - erre az elképzelésre visszatérek majd a harmadik fejezetben. Milyen bomlási idők jellemzik a valódi rendszereket, melyekben az említett téridő-szuperpozíciók megvalósulnak? A protonra (tekintsük ideiglenesen merev gömbnek) jellemző időtartam néhány millió év. Ez jó, mert a különálló részecskéken végrehajtott interferometriás kísérletekben a jelenség nem tapasztalható. Így ez konzisztens. Egy 10^-5 cm sugarú vízcsepp esetén a bomlási idő néhány óra lenne; ha a sugár egy mikron volna, a bomlási idő a másodperc egyhuszada, ha pedig a sugár a centiméter ezredrésze lenne, akkora másodperc egymilliomoda volna. Ezek a számok érzékeltetik, milyen időtartamok esetén válik jelentőssé a keresett fizika.

Létezik azonban egy lényeges adalék, amelyet muszáj megemlíteni.

Talán kissé ékelődve mutattam be a FAPP-nézőpontot, de van egy olyan eleme, amit nagyon komolyan kell venni - ez a környezet. A környezet ezekben a megfontolásokban rendkívül fontos, én pedig az eddigiekben nem foglalkoztam vele. Komolyabb vizsgálódásra van szükség. Nem elegendő itt az egyik göröngy szuperpozícióját vizsgálni ott a másik görönggyel. Helyesebb, ha a szuperpozícióban az egyik göröngy a környezetével és a másik göröngy, szintén a saját környezetével együtt vesz részt. Figyelmesen meg kell vizsgálni, hogy miben van nagyobb effektus: a göröngy mozgásában vagy a környezet megváltozásában? Ha az utóbbiban, akkor a hatás véletlenszerű. és a standard eljárásokhoz képest semmi újat nem kapunk. Ha azonban a rendszert kellőképpen sikerül elszigetelni ahhoz, hogy a környezetet elhanyagolhassuk, akkor talán a standard kvantummechanikától különböző valamit találhatunk. Igen érdekes lenne tudni, hogy lehetségesek-e olyan meggyőző kísérletek - tudomásom van néhány javaslatról -, melyek eldöntenék, hogy ez a fajta séma igaz-e a természetre, vagy pedig a megszokott kvantummechanika ismét életben marad, és el kell majd fogadnunk, hogy a göröngyök - vagy éppen a macskák - szuperponált állapotokban léteznek.

A 2.22 ábrán összefoglaltam, hogy miben is mesterkedünk. A különböző elméleteket egy síkba rajzolt kocka csúcsaiba helyeztem el a képen. A kocka három tengelye a három legalapvetőbb fizikai állandónak felel meg, ezek a G gravitációs állandó (vízszintes tengely), a fénysebesség reciproka c^-1 (átlós tengely), és a Dirac-Planck-állandó h (függőleges tengely). A szokásos léptékekben mindhárom állandó rendkívül kicsi értéket képvisel, azaz jó közelítésben nullának tekinthető. Ha mindhárom állandót nullának vesszük, akkor azt kapjuk, amit Galilei-féle fizikának nevezünk (bal felső sarok). Nullától különböző gravitációs állandó jobbra visz az ábrán a newtoni gravitációs elmélethez (melynek téridőleírását jóval később dolgozta ki Cartan).

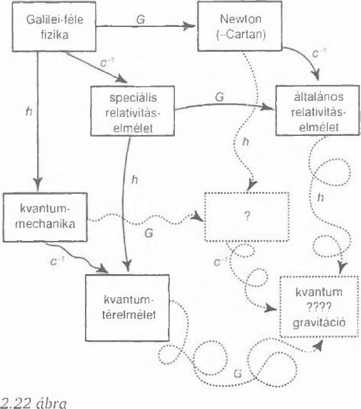
Ha inkább azt engedjük meg, hogy c ^-1 ne legyen nulla, a speciális relativitás Poincaré-Einstein-Minkowski elméletéhez jutunk. Végül kockánk felső lapja teljes, ha a két állandó egyike sem nulla - ekkor Einstein általános relativitáselméletét kapjuk. Ez utóbbi általánosítás azonban távolról sem egyszerű - amit a 2.22 ábrán a felső négyzet torzításával fejeztem ki. A standard kvantummechanikát úgy kapjuk meg, ha megengedjük, hogy h nem nulla, de visszatérünk G = c^-1 = 0 feltevésekhez. Egy nem egészen közvetlen általánosítással c is az elmélet részévé válhat, és előáll a kvantumtérelmélet. Ez kiegészíti a kocka bal oldali lapja is, a kis torzítás jelzi, hogy hiányzik a közvetlenség.

Azt gondolhatnánk, hogy már csak ki kell egészítenünk a kockát, és mindent tudni fogunk. Kiderül azonban, hogy a gravitációs fizika és a kvantummechanika alapelvei összebékíthetetlen ellentmondásban állnak egymással. Ez már a newtoni gravitációelmélet esetében is megmutatkozik (ahol c^-1 = 0), amennyiben a megfelelő Cartan-féle geometriai képben közelítünk a problémához. Erre Joy Christian hívta fel a figyelmemet, akitől a 2.22 ábra megalkotásához is ihletet merítettem. Cartan leírása az Einstein-féle ekvivalenciaelven alapul (e szerint az állandó gravitációs mező megkülönböztethetetlen a gyorsulástól). Jelenleg még nem áll rendelkezésre a kvantummechanikának és a newtoni gravitációnak olyan egyesítése, ami teljességében figyelembe venné Einstein ekvivalenciaelvét, mint ahogyan azt a klasszikus elméletben a Cartan-geometria megteszi. Személyes meggyőződésem szerint az ilyen típusú egyesítés magában kell foglalja a kvantumállapot redukciójának jelenségét - nagyvonalakban követve a fejezet korábbi részében tárgyalt OR elképzeléseket. A kocka hátsó lapját kiegészítő elmélet megalkotása kétségkívül nem lesz egyszerű. A kockát kiegészítő teljes elmélet, mely mindhárom, h, G és c^-1 állandóval számol, várhatóan még ennél is szokatlanabb, matematikailag bonyolultabb lesz. Világos, hogy ez már a jövő zenéje.

3. A fizika és az elme

Az első két fejezet fizikai világunkról és a leírásához használt matematikai szabályokról szólt, arról, hogy ezek milyen figyelemre méltóan pontosak, és néha mennyire furcsák. A harmadik fejezetben a gondolatok világáról beszélek, ezen belül pedig főleg arról, hogy miként kapcsolódik a fizikai világhoz. Feltételezem, Berkeley püspök azt gondolta volna, hogy a fizikai világ bizonyos értelemben a gondolat világunk folyománya; a szokásosabb tudományos felfogás szerint pedig a gondolatvilág valamiféle fizikai struktúra tulajdonsága.

Popper bevezetett egy harmadik világot (3.1 ábra), a kultúra világát. Ezt a gondolatvilág termékének tekintette, és így jutott a világok 3.2 ábrán látható hierarchiájához. Ezen az ábrán a gondolatok világa valamilyen szinten a fizikai világhoz kapcsolódik (belőle ered?), a kultúra pedig a gondolatvilágból jön létre.

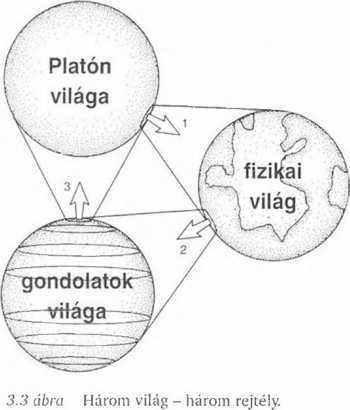
Én azonban kissé másképp látom a dolgokat. Popperrel ellentétben nem hiszem, hogy a kultúra a gondolatvilágunk folyománya, én a világoknak a 3.3 ábrán bemutatott viszonyát részesítem előnyben. Mi több. az én III. világom nem is a kultúra, hanem a platóni abszolútok világa - egész pontosan az abszolút matematikai igazságoké. Az 1.3 ábra elrendezése szerint a fizikai világ mélységesen függ a pontos matematikai törvényektől, ez fontos mondanivalója az ábrának.

3.1 ábra Karl Popper „harmadik világa”.

A jelen fejezet jelentős része e különböző világok kapcsolatával foglalkozik. Nekem úgy tűnik, hogy valami alapvetően sántít azzal az elképzeléssel, miszerint a gondolatok világa a fizikai világból ered - joggal aggodalmaskodnak ezzel kapcsolatosan a filozófusok. A fizikában anyagról, fizikai tárgyakról. nehéz testekről, részecskékről. térről, időről, energiáról és hasonlókról van szó. Hogyan lehetne az érzéseinknek, a vörös szín vagy a boldogság érzékelésének bármi köze a fizikához? Szerintem ez rejtély. A 3.3 ábra világait egymással összekapcsoló nyilak mind rejtélyeknek tekinthetők. Az első két fejezetben a matematika és a fizika kapcsolatát mutattam be (1. számú rejtély). Utaltam Wigner ezzel kapcsolatos megjegyzésére. Ő ezt rendkívülinek tekintette, és én is így vagyok vele. Miért van az, hogy a fizikai világ annyira hihetetlenül pontosan engedelmeskedik a matematika törvényeinek? Ezen túlmenően, a matematika, mely úgy tűnik, hogy fizikai világunk irányítása alatt áll, önmagában, mint matematika is rendkívül termékeny és hatékony. Számomra ez a kapcsolat mélységesen rejtélyes.

A jelen fejezetben a 2-es számú rejtélyt elemzem: a fizikai világ és a gondolatvilág viszonyának rejtélyét. Ehhez kapcsolódóan azonban nem feledkezhetünk meg a 3-as számú rejtélyről sem: mi az alapja annak a képességünknek, hogy megértsük a matematikai igazságot? Amikor a platóni világról beszéltem az első két fejezetben, elsősorban a matematikára és a fizikai világ leírásában felhasznált matematikai fogalmakra gondoltam. Olyan érzése támad az embernek, hogy a fizikai világ leírásához szükséges matematika ott kint van. De az is általános érzés, hogy ezek a matematikai fogalmak a gondolatvilágunk termékei, tehát a matematikát az emberi elme hozta létre. Tekinthetünk a dolgokra így is, bár a [...] tikai igazságra - és én sem. Így bár nyíl kapcsolja össze a gondolatvilágot a platóni világgal, sem ezzel, sem bármely másik nyíllal nem azt fejezem ki, hogy bármelyik világ egyszerű folyománya lenne bármelyik másiknak.

Noha lehet olyan értelmezés, amelyben ez igaz, a nyilak csupán azt ábrázolják, hogy kapcsolat van a különböző világok között.

Fontosabb az a tény, hogy a 3.3 ábra három előítéletemet is megmutatja. Az egyik az, hogy elvben a teljes fizikai világ leírható a matematika segítségével. Nem azt állítom, hogy a matematika egésze használható a fizika leírására. Azt mondom, hogy a matematika megfelelően összeválogatott részei rendkívül pontosan írják le a fizikai világot, így a fizikai világ a matematika szerint viselkedik. A platóni világnak így van egy kicsiny része, amely körülveszi fizikai világunkat. Ugyanakkor azt sem állítom, hogy a fizikai világ minden része kapcsolatban áll a gondolatisággal.

Viszont azt igen, hogy nincsenek önmagukban lebegő gondolati felépítmények, melyek nem a fizikai létezésben gyökereznének. Ez a második előítéletem. Van egy harmadik is, miszerint a matematikai megértésen keresztül, legalábbis elméletben, a platóni világ minden egyes eleme bizonyos értelemben elérhető gondolati világunk által. Biztosan akad, aki kétségbe vonja ez utóbbi előítéletemet - vagy akár mindhármat. Be kell vallanom, csupán az ábra megrajzolása után döbbentem rá, hogy tükrözi a fenti három előítéletemet. A fejezet végén visszatérek még ehhez az ábrához.

Most az emberi tudatosságról ejtenék néhány szót. Olyan kérdés-e ez, amihez tudományos magyarázatot kell fűznünk? Véleményem szerint igenis kell. A fizikai és a gondolatvilágot összekapcsoló nyilat rendkívül komolyan veszem. Másképpen kifejezve: szembe kell néznünk azzal a kihívással, hogy a gondolatvilágot a fizikai világ alapján értsük meg.

A 3.4 ábrán összefoglaltam a fizikai világ és a gondolatvilág néhány sajátosságát. A jobb oldalon a fizikai világ jellemzőit látjuk - e világot olyannak érzékeljük, mint amit pontos matematikai, fizikai törvények uralnak, ahogyan azt az első két fejezetben tárgyaltuk. A bal oldalon a tudatosságán, mely a gondolavilághoz tartozik. Olyan szavak, mint „lélek”, „szellem”, „vallás” stb. gyakran előfordulnak benne. Manapság az emberek előnyben részesítik a tudományos magyarázatokat. Sőt, egyre inkább azt hiszik, hogy bármilyen tudományos leírás felvihető számítógépre, azaz, ha van valamire egy tudományos leírás, azt elvben a számítógép is kezelni tudja. Ez olyan nézet, ami ellen hevesen fogok érvelni, a fizika iránti elfogultságom ellenére.

A 3.4 ábrán a fizikai törvények leírására használt fogalmak: előrejelző. számítható jelleg - azzal kapcsolatosak, hogy a fizikai törvényekben van-e determinizmus vagy sem, és hogy használhatunk-e vagy sem számítógépet e törvények hatásának szimulálására. Az egyik oldalon áll az a nézet, miszerint gondolati fogalmak, mint az érzelem, esztétika, kreativitás, inspiráció és művészet, olyan példák, melyeket nehezen tudnánk elképzelni valamilyen számítás végtermékeként. A másik, „tudományos” szélsőség szerint: „Az emberek csupán számítógépek. Bár nem tudjuk még leírni a fenti fogalmakat, mégis, ha ismernénk a megfelelő számítási eljárásokat, azokkal a 3.4 ábrán felsorolt összes fogalmat ki tudnánk fejezni.” Az utóbbi nézet képviselői e folyamat leírásában gyakran használják a következmény szót. Szerintük a felsorolt minőségek a megfelelő számításból „következnek”.

Mi a tudatosság? Igazság szerint nem tudom, hogyan definiáljam. Nem is gondolom, hogy eljött volna az ideje a tudatosság meghatározásának, mert nem értjük, mi az. Hiszem, hogy fizikailag megközelíthető fogalom; de a meghatározás valószínűleg rossz lenne. Valamilyen fokig mégis le szeretném írni. Nekem úgy tűnik, hogy a tudatosságnak legalább két különböző oldala van. Egyrészt a tudatosságnak léteznek passzív megnyilvánulásai, melyek együtt járnak a tudomással. Gondolok itt a színek észlelésére, a harmóniára, a memória használatára stb. Másrészt vannak aktív megnyilvánulásai is, mint például a szabad akarat és cselekedetek végrehajtása szabad akaratunkból. Az ilyen kifejezések használata a tudatosság különböző oldalait tükrözi.

Most főként valami másra fogok koncentrálni, ami lényeges módon együtt jár a tudatossággal. Különbözik a tudatosságnak mind a passzív, mind az aktív megnyilvánulásaitól, talán valahol a kettő között található. A megértésről, vagy talán a meglátásról van szó, utóbbi gyakran a helyénvalóbb kifejezés. Ezeket a fogalmakat sem definiálom - nem tudom, mit jelentenek. Van még két másik szó is, aminek a jelentésével nem vagyok tisztában. Egyikük a tudomás, tudatában lenni valaminek, a másik az intelligencia. Hogy miért beszélek olyan dolgokról, melyek jelentése számomra sem világos? Valószínűleg azért, mert matematikus vagyok, és a matematikusokat ez nem zavarja annyira. Nincs szükségük azoknak a dolgoknak a pontos definíciójára, amiről beszélnek, mindaddig, amíg mondani tudnak valamit a közöttük lévő összefüggésekről. Az első kulcspont az, hogy szerintem az intelligenciához a megértés elengedhetetlen. Intelligenciáról beszélni úgy, hogy tagadjuk a megértést, szerintem ésszerűtlen. Hasonlóan, megérteni bármit is, aminek nem vagyunk tudatában, szintén nincs értelme. A megértés feltételez bizonyos fokú tudomást. Ez a második kulcspont. Úgy tűnik tehát, hogy az intelligenciához kell a tudomás. Bár a fenti fogalmak egyikét sem definiálom, mégis indokoltnak látom, hogy ragaszkodjam a közöttük fennálló összefüggésekhez.

A tudatos gondolkodás és a számítás közötti viszonnyal kapcsolatban több álláspont létezik. A 3.1 táblázatban összefoglaltam a tudomás négy megközelítését, melyeket A, B, C és D betűkkel címkéztem meg.

Az A felfogás szerint, ami néha az erős mesterséges intelligencia (erős Ml), vagy a (kiszámítható) funkcionalizmus megnevezést kapja, a gondolkodás egésze nem más számítások végrehajtásánál, vagyis a megfelelő számítások eredménye a tudomás.

	3.1 táblázat
A	Minden gondolkodás számítás; a tudatos tudomás érzéseinek előidézéséhez elegendő csupán a megfelelő számítások elvégzése.
B	A tudatosság az agy fizikai működésének sajátossága, és bár minden fizikai tevékenység számítással szimulálható, a számításos szimulálás önmagában nem idézhet elő tudatosságot.
C	Az agy megfelelő fizikai működése tudatosságot idéz elő, de ezt a fizikai tevékenységet mégsem lehet megfelelően szimulálni számítással.
D	A tudatosságot fizikai, számítási vagy más tudományos fogalmakkal nem lehet megmagyarázni.

A második, B nézőpont szerint az agy működését elvben szimulálni lehetne, legalábbis akkor, amikor tulajdonosa valaminek a tudatában van. Az A és a B közötti különbség az, hogy bár ez a tevékenység is szimulálható, a puszta szimuláció a B szerint nem jár együtt érzésekkel vagy tudomással - valami egyéb zajlik, ami talán az objektum fizikai szerkezetével kapcsolatos. Vagyis a neuronokból és egyebekből álló agy lehet tudatos, míg az agy tevékenységének szimulációja nem. Amennyire én értem, ezt a felfogást vallotta John Searle.

Következik a saját nézőpontom, amelyet C-nek nevezek. E nézőpont szerint, hasonlóan B-hez, az agy fizikai működésében van valami, ami kiváltja a tudomást - más szavakkal, valami a fizikában az, amihez fordulnunk kell, de ezt a fizikai cselekvést éppen nem lehet számítással szimulálni. Nincs rá megfelelő szimuláció. Következésképpen, kell, hogy legyen valami az agy fizikai működésében, ami a számításon túl van.

Végül pedig létezik a D vélemény, ami szerint eleve hibás ezeket a fogalmakat a tudomány segítségével magyarázni. Talán nincs tudományos magyarázata a tudomásnak.

A magam részéről a C felfogásban hiszek. Azonban ennek is változatos fajtái léteznek. Nevezhetjük ezeket erős C-nek és gyenge C-nek. A gyenge C szerint az ismert fizikában figyelmesen szemlélődve, találhatunk számítás felett álló cselekménytípusokat. A „számítás felettiség” fogalmát mindjárt pontosabban elmagyarázom. A gyenge C szerint nem kell az ismert fizika határain túllépnünk ahhoz, hogy a megfelelő, nem kiszámítható tevékenységre rábukkanjunk. Az erős C ezzel ellentétben megköveteli, hogy az ismert fizikán túl még létezzen valami; a fizikai megértésünk alkalmatlan a tudomás leírására. Vagyis a fizikai megértés nem teljes. Mint talán a második fejezetből kiderült, én valóban hiszem, hogy fizikai képünk hiányos, mint ahogyan azt a 2.17 ábrán már bemutattam. Az erős C szemszögéből nézve, a jövő tudománya talán magyarázatot ad a tudatosságra, de a ma tudománya biztosan képtelen erre.

A 2.17 ábrán feltüntettem olyan szavakat is, melyekről eddig semmit sem mondtam, ilyen például a számítható. A standard fizikában alapvetően számítható fizikával találkozunk kvantumszinten, és valószínűleg klasszikus szinten is, bár vannak technikai kérdések azzal kapcsolatosan, hogy miként térünk át a számítható diszkrét rendszerekről a folytonos rendszerekre. Ez lényeges pont, de most nem szeretnék ezzel foglalkozni. Úgy gondolom, hogy a gyenge C képviselőinek az itt felmerülő bizonytalanságokban kell valamit találniuk, amit nem lehet számítással megmagyarázni.

A kvantumos szintről a szokásos felfogás szerint az R-nek nevezett eljárás során jutunk el a klasszikus szintre, ami teljes egészében valószínűségi cselekmény. Számíthatósággal és ugyanakkor véletlenszerűséggel állunk tehát szemben. Érvelni fogok, hogy ez nem elég jó - valami másra van szükség, de a két szintet áthidaló új elmélet nem számítható kell legyen. Hamarosan egy kicsit többet mondok arról, mit értek ezalatt.

Tehát az én változatom az erős C-ről: a kvantumos és klasszikus szinteket összekapcsoló fizikában a nem kiszámíthatóság után nyomozunk. Nem könnyű a feladat. Nemcsak, hogy új fizikára van szükség, de ennek olyannak kell lennie, hogy az agy működéséről is mondjon valamit.

3.5 ábra Világos lép és döntetlen - könnyű feladvány az emberek számára, azonban a Deep Thought leütötte a bástyát! (William Hartston feladványa, Jane Seymore és David Norwood cikkéből, New Scientist, 1889-es szám, 23. oldal, 1993.)

Először is tisztázzuk, hogy hihető-e: a megértésnek létezik a számításon túlmutató része. Egy nagyon szép, egyszerű sakkfeladvánnyal szeretnék erre rávilágítani. Napjaink számítógépei igen jól sakkoznak, azonban amikor a 3.5 ábrán látható feladványt a maga idejében legjobb, Deep Thought nevű számítógépnek feladták, elképesztően buta dolgot művelt. A feladványban a sötét jelentős előnnyel rendelkezik: két bástya és egy futó az előnye. Ez tetemes előny lenne, ha a gyalogok sora nem zárná el a sötét tiszteket a világos királytól. Vagyis a világos király egyetlen teendője, hogy a gyalogok által alkotott sorfal mögött bóklásszon, így a világos biztosan nem veszíthet. A Deep Thought azonban tétovázás nélkül leütötte a sötét bástyát, ezzel megnyitotta a gyalgogság sorfalát, reménytelen helyzetbe hozva saját magát. Azért tette, mert programozása szerint lépést lépés után kell elemeznie bizonyos lépésszámig, utána meg összeszámolni a bábokat, vagy valami hasonló. Ebben az esetben a stratégiája nem volt elég jó. Természetesen döntésének következményeit még több lépésre előre számolva, talán rájött volna a helyes lépésre.

3.6 ábra Világos lép és döntetlen - ez a feladvány sem túl nehéz az emberek számára, azonban egy átlagos sakkozó számítógép leüti a bástyát (William Hartston és David Norwood egy Turing-tesztjéből).

Az a helyzet, hogy a sakk kiszámítható játék. Az ember viszont ránéz a gyalogok sorfalára, és megérti, hogy áthatolhatatlan. A számítógép nem volt képes erre a felismerésre -egyszerűen lépést lépés után számolt. Példánk rávilágít a puszta számolás és a megértés magasabb foka közötti különbségre.

A 3.6 ábrán egy másik példát látunk. Nagy a kísértés, hogy a sötét bástyát levegyük a világos futóval. A helyes döntés azonban az, hogy a futóval, mint egy gyaloggal kiegészítsük a gyalogok sorfalát. Ha már megtanítottuk a számítógépet a gyalogok által alkotott sorfalak felismerésére, talán megoldja az első feladványt, de tévedni fog a másodikban, hiszen ahhoz a megértésnek egy magasabb fokára van szükség. Gondolhatnánk, hogy elegendő türelemmel a megértés összes fokozatára beprogramozhatjuk a számítógépet. Talán a sakk esetében így is van. Mivel a sakk kiszámítható játék, végül elegendően nagy teljesítményű számítógéppel lehetséges lenne az összes lehetőség kiértékelése egészen a játszma legvégéig. Jelenlegi számítógépeink lehetőségeit ez messze meghaladja, de elvben lehetséges lenne.

Mégis megmarad az érzés, hogy a „megértés” során valami más megy végbe, mint közvetlen számítás. Kétségkívül másképp közelítjük meg a feladványt mi, emberek, és másképpen a számítógép.

Van-e ennél erősebb érvünk is arra, hogy a megértés több egyszerű számításnál? A helyzet az, hogy van. Nem szeretnék sokáig időzni az ismertetésénél, annak ellenére, hogy ez az egész fejtegetés alapköve. De egy kis időt rá kell szánnom, még akkor is, ha az érvelés kissé technikai jellegűre sikeredhet. Az elme árnyai első 200 oldalán azt próbálom megmutatni, hogy az érvelésnek nincs gyenge pontja.

Hadd mondjak el valamit a számításról. A számítás nem más, mint amit a számítógép végez. A valódi számítógépek tárolási kapacitása véges, azonban én egy idealizált számítógépről fogok beszélni, a Turing-gépről, mely egy valódi, általános célú számítógéptől csak annyiban különbözik, hogy tárolási kapacitása végtelen, valamint hiba és kifáradás nélkül örökké folytathatja számításait. Példa egy ilyen számolásra, mely nem csupán aritmetikát, hanem logikai műveleteket is tartalmaz, a következő:

• Találjunk olyan számot, amely nem összege három négyzetszámnak.

Szám alatt természetes számot értek, például 0, 1, 2, 3, 4, 5,..., négyzetszám alatt pedig a 0², 1², 2², 3², 4², 5²,... számokat. A következő módon járhatunk el - nem túl értelmes eljárás, de megmutatja, hogy mit érthetünk számítás alatt. Kiindulunk a 0-ból, és megvizsgáljuk, vajon három négyzetszám összege-e? Figyelembe vesszük az összes olyan négyzetet, amely kisebb vagy egyenlő 0-nál. Egyetlen ilyen van, ez a 0². Vagyis az egyetlen kipróbálható lehetőség

0 = 0² + 0² + 0²,

ami igaznak bizonyul, tehát a 0 három négyzetszám összege. Ezután megvizsgáljuk az 1-et. Kipróbáljuk az 1-nél kisebb vagy egyenlő négyzetek összes lehetséges kombinációját, és a következő jó megoldást találjuk:

1 = l² + O² + 0².

3.2 táblázat

Folytathatjuk ezt a meglehetősen fárasztó műveletsort, ahogyan azt a 3.2 táblázat mutatja, egészen a 7-es számig. A 0², 1² és 2² számoknak nem létezik olyan kombinációja, mely összegként 7-et adna, a táblázatban felsoroltuk az összes lehetőséget. Vagyis az eredeti kérdésre a válasz a 7 -ez a legkisebb olyan szám, mely nem állítható össze három négyzetszám összegeként. Ez egy példa a számításra.

A példában szerencsések voltunk: a számítás véget ért. Léteznek azonban soha véget nem érő számítások is. Például ha kissé módosítom a feladványt:

• Találjunk olyan számot, amely nem összege négy négyzetszámnak.

Van egy nevezetes tétele a tizennyolcadik században élt híres matematikusnak, Lagrange-nak, aki bebizonyította, hogy minden szám felírható négy négyzetszám összegeként. Ha ész nélkül nekiesnénk a keresésnek, a számítógép egyfolytában csak kattogna és nem találna semmit. Ez illusztrálja a tényt, hogy léteznek véget nem érő számítások is.

Lagrange tételének bizonyítása nem egyszerű, ezért tekintsünk egy másik könnyebbet, melyet remélhetőleg mindenki fog értékelni!

•    Találjunk olyan páratlan számot, amely két páros szám összege.

Elindíthatnánk a számítógépet, hogy keressen ilyet, és az végtelen ideig dolgozna, hiszen tudjuk, hogy két páros szám összege megint csak páros szám lesz.

Vagy vegyünk egy sokkal ravaszabb példát:

•    Találjunk egy 2-nél nagyobb páros számot, amely nem írható fel két prímszám összegeként.

Véget ér-e valaha ez a számolás? Úgy hisszük, nem, de ez csupán sejtés, a Goldbach-sejtés, ami annyira bonyolult, hogy senki sem tudja, igaz-e vagy sem. Láttunk tehát három (valószínűleg) végtelen ideig tartó számítást: egyikük egyszerű, a másik nehéz, a harmadik pedig annyira nehéz, hogy senki sem tudja, véget ér-e valaha vagy sem.

Tegyük most fel a kérdést:

•    Használnak-e a matematikusok valamilyen számítási algoritmust (nevezzük A-nak) annak eldöntésére, hogy bizonyos számítások véget érnek-e valaha?

Például, volt-e Lagrange fejében valamilyen számítógépprogram szerűség, mely elvezette ahhoz a következtetéshez, hogy minden szám négy négyzetszám összege? Nem kell Lagrange-nak lenni, hogy ezt eldöntsük, csupán nyomon kell tudni követni az érvelését. Szeretném hangsúlyozni, hogy most nem az eredetiség, csupán a megértés érdekel. Ezért tettem fel a kérdést a fenti formában. Magunkat meggyőzni valamiről nem más, mint a megértés.

Az olyan állítás technikai megnevezése, amely az előzőhöz hasonló természetű: ∏₁-mondat. Egy ∏₁ -mondat azt állítja, hogy egy megadott számítás nem fejeződik be. A következő érvelés elfogadásához elég lesz ilyen természetű mondatokra gondolni. Arról szeretném meggyőzni az olvasót, hogy nincs ilyen A algoritmus.

A cél érdekében kissé általánosítanom kell. Olyan számításokról kell beszélnem, melyek valamilyen n természetes szám függvényei, íme néhány példa:

•    Találjunk olyan természetes számot, amely nem összege n négyzetszámnak.

Láttuk Lagrange tételéből, hogy amennyiben n = 4 vagy ennél több, a számítás nem ér véget. Azonban ha 3 vagy kevesebb, véget ér. A következő feladat:

•    Találjunk olyan páratlan számot, amely n páros szám összege.

Itt igazán nincs jelentősége n értékének, az nem segít rajtunk. A számítás egyetlen n értékre sem ér véget. A Goldbach-sejtés kiterjesztése pedig a következő:

•    Találjunk olyan 2-nél nagyobb páros számol, amely nem összege n vagy annál kevesebb prímszámnak.

Amennyiben a Goldbach-sejtés igaz, a számítás örökké folytatódik (kivéve a 0 és az 1 esetét). Bizonyos értelemben ez annál egyszerűbb, minél nagyobb n. Úgy tudom, valamilyen nagy n értékre a sejtést igazolták.

Fontos kiemelni, hogy az ilyen típusú számítások az n természetes számtól függenek. Ez rendkívül lényeges Gödel híres érvelése szempontjából. Alan Turing-nak tulajdonított formájában beszélek majd róla, de kissé más értelemben, mint ő. Aki nem kedveli a matematikai érveket, rövid időre most kikapcsolhat. Az eredmény az, ami igazán fontos. Mindenesetre, az érvelés nem túlságosan bonyolult-csak zavarba ejtő.

Fgy n számot felhasználó számítások tulajdonképpen számítógép-programok. Listát készíthetünk a számítógépprogramokról, és mindegyikükhöz számot rendelhetünk, például p-t. Vagyis beadunk az általános célú számítógépünknek valamilyen p számot, és az végrehajtja a „p-edik” számítást a megadott n értékre. A p-t alsó indexként tüntetjük fel. Az n számon végrehajtott programok, avagy számítások tehát sorrendben

C₀(n), C₁(n), C₂(n), C₃(n),..., C_p(n),...

Feltesszük, hogy az összes lehetséges számítást felsoroltuk, és hogy találhatunk valamilyen hatékony módszert sorba rendezésükre, azaz C_p(n) az n természetes számra alkalmazott p-edik program.

Ezután tegyük fel azt, hogy rendelkezésre áll valamilyen számítási vagy algoritmikus A eljárás, mely a (p, n) számpárral dolgozik, és amikor az eljárás véget ér, világosan demonstrálja számunkra, hogy a C_p(n) számítás nem ér véget sohasem. Nem szükségszerű, hogy A mindig működjön; azaz lehetnek olyan végtelen ideig tartó C_p(n) számítások, melyekkel kapcsolatos A(p, n) eljárás sem ér véget sohasem. Ahhoz azonban ragaszkodom, hogy A nem téved, és amennyiben véget ér, tudni fogjuk, hogy C_p(n) örökösen folytatódik. Próbáljuk elképzelni, hogy a matematikusok ilyen A számolási algoritmust követve gondolkodnak, amikor valamilyen szigorú matematikai bizonyítást vagy állítást fogalmaznak meg (például egy ∏₁-mondatot). Tegyük fel, hogy ismerik A-t, és hiszik, hogy az eljárás helytálló. A alatt a matematikusok számára rendelkezésre álló összes olyan eljárást értjük, melyek kétséget felülmúlóan bizonyítják, hogy a számítások nem érnek véget. Az A eljárás először kiválasztja a p-nek megfelelő számítógépprogramot, majd az n alapján kijelöli, hogy milyen számra alkalmazzuk azt. Ha ezután az A eljárás véget ér, abból az következik, hogy C_p(n) nem fog. Vagyis,

ha A(p, n) megáll, C_p(n) nem áll meg.    (1)

A feladata éppen ez: megcáfolhatatlanul győz meg arról, hogy bizonyos számítások nem érnek véget.

Most tegyük fel, hogy p = n. Ez furcsának tűnhet. A Cantor-féle diagonális eljárás néven ismert híres eljárást nyugodtan használhatjuk. Arra a következtetésre jutunk, hogy

ha A(n, n) megáll, C_n(n) nem áll meg.

Azonban most A(n, n) csupán egyetlen szám függvénye, így egyike kell legyen a C_p(n) számítógépprogramoknak, hiszen ez a halmaz az összes n-re ható számítást tartalmazza. Tegyük fel, hogy A(n, n) a halmaz k-adik tagja:

A(n, n) = C_k(n)

Most legyen n = k, így azt kapjuk, hogy

A(k, k) = C_k(k)

Az (1) állítás értelmében pedig ha A(k, k) megáll, C_k (k)nem áll meg.

De A(k, k) ugyanaz, mint C_k(k). Vagyis amennyiben C_k(k) megáll, akkor nem áll meg. Ami azt jelenti, hogy nem ér véget. Ez szép tiszta logika. Itt a csapda - a vizsgált számítás nem ér véget, és ha hiszünk A-ban, akkor azt is el kell hinnünk, hogy C_k(k) nem áll meg.

Azonban A sem áll meg, így nem „tudja”, hogy C_k(k) nem áll meg. Ezért a számítási eljárás nem tartalmazhatja az olyan matematikai meggondolások összességét, melyek eldöntik, hogy bizonyos számítások nem állnak meg-azaz, amelyek a ∏₁-mondatok igaz voltát eldönthetik. Ez a Gödel-Turing érvelés lényege, abban az alakjában, amelyre szükségem lesz.

Természetesen lehet kételkedni a fenti érvelésben. Amit azonban világosan elárul: a matematikai meglátást nem lehet valamilyen számítási formába kódolni, amelyről tudni lehet, hogy helyes. Számomra egyértelmű ez a mások által olykor vitatott tanulság. Érdekes, amit Turing és Gödel mond erről az eredményről. Turing a következőket írta:

Más szavakkal, ha egy gépről várható, hogy csalhatatlan, az nem lehet intelligens is. Több tétel van, amely majdnem pontosan ezt állítja. Ezek a tételek azonban semmit sem árulnak el arról, hogy mennyi intelligenciára számíthatunk, amennyiben a gép nem csalhatatlan.

Vagyis az ő értelmezésében a Gödel-Turing típusú érvelések akkor békíthetők össze azzal az elképzeléssel, miszerint a matematikusok lényegében számítógépek, ha a működésük alapjául szolgáló algoritmusok, melyek a matematikai igazságokat kiderítik, alapvetően hibásak. Megtehetjük, hogy aritmetikai állításokra korlátozzuk vizsgálódásainkat, például ∏₁-mondatokra, melyek az állítások egy igen korlátozott típusát alkotják. Azt hiszem, Turing úgy gondolta, hogy az emberi elme használ algoritmusokat, de ezek valóban rosszak. Szerintem álláspontja egyáltalán nem meggyőző, főként azért nem, mert nem az inspiráció megszületésére keressük a választ, hanem azt firtatjuk, miként lehet követni egy érvelést és megérteni azt. Turing álláspontja engem nem győz meg. Osztályozásom szerint Turing A típusú személy.

És mit állít Gödel? Osztályozásomban ő D típusú lenne. Eszerint Gödel és Turing ugyanazon tények alapján lényegében ellentétes következtetésre jutottak. Bár Gödel hite szerint a matematikai meglátás nem egyszerűsíthető le számításokra, ezt a lehetőséget nem sikerült határozottan kizárnia. Ezzel kapcsolatban Gödel a következőket mondta:

Másrészt, az eddig belátottak alapján létezhet (és talán empirikusan fel is fedezhető) olyan tételbizonyító gép, amely lényegében egyenértékű a matematikai intuícióval. Mindez azonban nem bizonyítható, és az sem, hogy a véges számelméletben kizárólag helyes tételeket lát be.

Véleménye szerint létezik egy „egérút”, így a Gödel-Turing érv nem használható fel közvetlenül a számíthatóság (vagy funkcionalizmus) cáfolatára. Mégpedig azért, mert a matematikusok használhatnak helyes algoritmikus eljárást, de ennek helyességét nem tudhatjuk biztosan. Így a tudható, amit Gödel egérútnak gondolt, és a helyes, amit Turing.

Nézetem szerint valószínűleg egyik értelmezés sem jelenti a kivezető utat. A Gödel-Turing-tétel mondanivalója csupán az, hogy amennyiben bármilyen ∏₁-mondatok megalkotására alkalmas) algoritmikus eljárást helyesnek találunk, rögvest felmutatható valami olyan, ami érvényességi köréből kivezet. Lehetséges, hogy olyan algoritmikus eljárást használunk, amelyről nem vagyunk képesek eldönteni, hogy helyes-e és létezhet olyan tanító eszköz, amellyel kifejleszthetjük ezt a képességet. Ezekről a dolgokról és egyebekről is kimerítően írtam az Az elme árnyai című könyvemben. Nem szeretnék most belemerülni a részletekbe, mindössze két megjegyzést tennék.

Hogyan keletkezhettek ezek az állítólagos algoritmusok? Az emberi lények esetében feltehetően természetes kiválasztódás útján, a robotok esetében pedig MI (mesterséges intelligencia) tudatos megalkotásával. További részletezés helyett a könyvemből kiemelt két rajzzal szeretném ezt szemléltetni.

Az első rajz a természetes kiválasztódással kapcsolatos (3.7 ábra). Láthatjuk a természetes kiválasztódás szemszögéből nemigazán szerencsés helyzetben lévő matematikust, hiszen a háttérben a kard fogú tigris feni rá a fogát.

3.7 ábra Távoli őseink számára a bonyolult matematika művelésére irányuló speciális képesség aligha jelenthetett szelekciós előnyt, azonban a megértés általános képessége bizonyára.

Ellenben a kép másik részén rokonai mamutra vadásznak, házakat építenek, termést gyűjtenek be stb. Ezekben a dolgokban benne van a megértés, de nem sok közük van a matematikához. Vagyis a megértés minősége lehetett az, ami alapján kiválasztódtunk, de különleges algoritmusoknak a matematika művelésére nem sok szerepük lehetett.

A másik rajz a tervezett Ml tudatos megalkotásáról szól. Könyvemben található egy kis történet egy jövőbeli Mi-szakértő és egy robot beszélgetéséről. A teljes érvrendszer a könyvben hosszadalmas és bonyolult - nem érzek késztetést arra, hogy most belemerüljünk. Az általam eredetileg használt Gödel-Turing-érvet mindenféle ember támadta már mindenféle szempontból, és ezekkel mind foglalkozni kellett. Az Árnyakban bemutatott összes új érvet igyekeztem belefoglalni MI és a robot párbeszédébe.

Kanyarodjunk most vissza Gödel érveléséhez, mely különböző, számokkal kapcsolatos állításokat tartalmaz. Gödéi azt mondja, hogy nincs olyan számítási szabályokból álló rendszer, ami a természetes számok tulajdonságait leírja. Annak ellenére, hogy a természetes számok nem jellemezhetőek számításokkal, minden gyermek tudja, mik azok!

3.8 ábra Mester Imperátor megküzd a Matematikailag Védett Kiberrendszerrel. Az elme árnyai első 200 oldala a Gödel-Turing-érvelés használatának kritikájáról szól. Az új érvek lényegét egy MI-s szakértő és robotjának beszélgetése tartalmazza.

Csupán meg kell mutatni a gyermeknek különböző számú tárgyat, mint az a 3.9 ábrán látható, és a néhány példából képes lesz elvonatkoztatni a természetes szám fogalmát. Nem számítási szabályokat adunk a gyermeknek - képessé tesszük arra, hogy „megértse”, mik a természetes számok. Azt mondanám, hogy a gyermek képes valamiféle „kapcsolatot” teremteni a matematika platóni világával. Vannak, akik nem szeretik a matematikai meglátás efféle megközelítését, mégis fenntartom, hogy ilyen természetű felfogásban kell látni azt, ami történik. Valahogyan a természetes számok már „ott” vannak, léteznek valahol a platóni világban, és azon képességünk folytán, hogy a dolgokról tudomást szerzünk, képesek vagyunk csatlakozni ehhez a világhoz. Ha csupán esztelen számítógépek lennénk, nem lenne meg ez a képességünk. Gödel tétele azt mutatja, hogy nem szabályok tesznek képessé a természetes számok természetének megértésére.

3.9 ábra Néhány egyszerű példából a gyermek képes elvonatkoztatni a természetes számok platóni fogalmát.

A természetes számok megértése jó példája a platóni kapcsolatnak.

Általánosabban fogalmazva azt állítom, hogy a matematikai megértés nem kiszámítható dolog, hanem valami egész más. Valami egyéb történik, ami arra a képességünkre támaszkodik, hogy tudomásunk van a dolgokról. Egyesek mondhatnák: „Mindaz, amit bizonyítottál, csupán annyi, hogy a matematikai meglátás nem kiszámítható dolog. Ez azonban nem sokat mond a tudatosság más formáiról.” Nekem azonban úgy tűnik, a matematikai és az egyéb típusú megértés közé vonalat húzni nem ésszerű. Ezt próbáltam az első ábrán is kifejezni (3.7 ábra). A megértés nem a matematika kizárólagos sajátja. Az emberi lényekben kifejlődik az általános megértésnek ez a sajátossága, mely nem számításos tulajdonság, mert a matematikai megértés sem az. Nem választanám szét az emberi megértést és általában a tudatosságot sem. Bár mondtam, hogy nem tudom, mi az emberi tudatosság, úgy tűnik számomra, hogy az emberi megértés egy példája annak, vagy legalábbis valami, ami megköveteli azt. Nem akarok vonalat húzni az emberi és az állati tudatosság közé sem. Itt összeütközésbe kerülhetek különböző emberekkel. Nekem úgy tűnik, az emberek nagyon hasonlóak sok más állatfajhoz, és bár valamivel jobban érthetjük a dolgokat, mint egyes rokonaink, mindamellett nekik is van valamilyen megértésük, és így tudatosságuk is kell legyen.

Összefoglalva, a tudatosság bizonyos vonásaiban, speciálisan a matematikai megértésben jelentkező nem kiszámíthatóság igen erősen utal arra, hogy ez a nem kiszámítható jelleg az egész tudatosságra jellemző. Röviden, ez a javaslatom.

Mit is értek nem kiszámíthatóság alatt? Sokat beszéltem már róla, de ahhoz, hogy jobban rávilágítsak, mondok egy példát. Olyasmit fogok ismertetni, amit gyakran játék univerzummodellként tartanak számon. Ilyesmikkel szórakoznak a fizikusok, amikor semmi jobbat nem tudnak kitalálni. (Ez azonban nem is annyira rossz dolog!) A játék modell általában nem törekszik a valódi univerzum modellezésére. Talán bizonyos tulajdonságait tükrözi, de nem szabad a valóságos univerzum modelljeként kezelni. Az itt ismertetendő modell bizonyosan nem tart erre igényt. Csak azért hozakodom elő vele, hogy szemléltessek egy bizonyos tulajdonságot.

A modellben az idő diszkrét 0, 1, 2, 3, 4 ... értékeket vesz fel, az univerzum állapotait pedig minden időben poliominók halmaza jelképezi. Mit is jelent a poliominókból álló halmaz? Néhány példa a

3.10 ábrán látható. A poliominó olyan síkidom, amelyet különböző élei mentén egymáshoz illesztett négyzetek alkotnak¹. Bennünket a poliominókból álló halmazok érdekelnek. A játék modellben az univerzum állapotát minden időpontban két különálló, véges poliominóhalmaz adja meg. A 3.10 ábrán a poliominók összes lehetséges véges halmazát képzeltem el, melyeket valamilyen megszámolható módon állítottam az S₀, S₁, S₂, ... sorrendbe. Mi lenne ennek a

3.10 ábra  Egy nem kiszámítható játék univerzummodell. A determinisztikus. bár nem kiszámítható jellegű játék univerzum modell különböző állapotait poliominók véges halmazainak párjai jelentik. Mindaddig, míg a pár első halmazának elemeivel parkettázható a sík, az időfejlődés úgy történik, hogy az első tag indexe eggyel növekszik, a második pedig az „időt jelzi". Ha a pár első halmazával nem parkettázható a sík, a pár két tagjának szerepe felcserélődik a fejlődés során. Valahogyan így: (S₀,S₀), (S₀,S₁), (S₁,S₁), (S₂S₁), (S₃,S₁), (S₄S,)..... (S₂₇₈,S₂₅₁,), (S₂₅₁, S₂₇₉).

nevetséges univerzumnak a dinamikája, avagy időfejlődése? A nulla időpontban az (S₀, S₀) párból indulunk ki, majd más poliominópárokkal folytatjuk, bizonyos pontos szabályokat követve. A szabály annak függvénye, hogy a párok első elemeiből álló halmaz lefedi-e vagy sem az egész síkot. A kérdés tehát az, hogy lefedhető-e a teljes sík rések és átfedések nélkül (ezt nevezik parkettázásnak) csak az adott halmaz poliominóit használva? Tegyük fel, hogy a játék univerzum pillanatnyi állapota az (S_q , S_r) pár. Az időfejlődés szabálya eltérő aszerint, hogy az S_q poliominók lefedik-e a síkot vagy sem. Ha igen, a következő, S_q+1 elemmel folytathatjuk, és a következő pillanatban az (S_q+1,S_r) pár az állapot. Ha nem, felcseréljük a sorrendet és az (S_r, S_q+1) párt tekintjük az új állapotnak. Nagyon egyszerű és buta kis univerzum ez - miért is érdekel bennünket? Azért, mert bár a dinamikája kimondottan determinisztikus - fejlődésére rendkívül világos, determinisztikus eljárást adtam meg - mégsem kiszámítható. Robert Berger egyik tételéből következően nem létezik olyan számítógépes eljárás, amely szimulálhatná az ilyen univerzum fejlődését, mert nincs olyan számítógépes eljárás, amely eldöntené, hogy parkettázható-e a sík egy adott poliominóhalmazzal vagy sem.

Együtt azonban képesek rá, ahogyan az a (c) ábrán látható. A (d) példa szintén lefedi a síkot - de egyedül az ábrán látható módszer követésével. Mindez rávilágít, mennyire bonyolulttá válhatnak a lefedések.

A dolgok azonban még tovább bonyolódhatnak. Tekintsük a 3.12 ábra példáját - Robert Berger tétele tulajdonképpen hasonló halmazok létezésén alapszik. Az ábra felső részén bemutatott három alakzat lefedi ugyan a teljes síkot, de ezt nem lehet úgy megvalósítani, hogy a mintázat ismétlődjék. Ahogy folytatjuk a parkettázást, a mintázat állandóan különbözik, és nem olyan könnyű belátni, hogy a lefedés egyáltalán megvalósítható. De végül is belátható, és eljutunk Robert Berger érveléséhez, melyből következik, hogy nem létezik olyan számítógépprogram, amelyik szimulálhatná ezt a játék univerzumot.

És mi a helyzet a valódi univerzummal? A második fejezetben úgy érveltem, hogy a fizikánkból valami alapvető hiányzik. Van-e okunk magából a fizikából kiindulva arra következtetni, hogy a hiányzó részben lehet valami nem kiszámítható? Úgy látom, van ilyen ok, talán a kvantumgravitáció valódi elmélete nem kiszámítható jellegű lesz. Az elképzelés nem teljesen légből kapott. Megmutatom, hogy a nem kiszámíthatójelleg a kvantumgravitáció két különböző megközelítésének is sajátja. A két megközelítésben közös, hogy négydimenziós téridők kvantumos szuperpozíciójával dolgozik. Sok más megközelítés csupán háromdimenziós terek szuperpozícióját tartalmazza.

Az első a kvantumgravitáció Geroch-Hartle sémája, melynek van egy nem kiszámítható eleme, ugyanis felhasználja Markov egyik eredményét, mely szerint a topológiai négyes-sokaságok nem osztályozhatók számíthatóan. Nem merülök bele a technikai részletekbe, de az mindenképpen látszik, hogy a nem kiszámítható jelleg már természetes módon felmerült az általános relativitáselmélet és a kvantummechanika egyesítésének kísérleteiben.

A másik olyan kísérlet a kvantumgravitáció megalkotására, melyben a nem kiszámítható jelleg előjön, David Deutsch egyik munkája. Először egy preprintben adta ki, de furcsa módon, amikor a cikk nyomtatásban is megjelent, már sehol sem volt az eredeti érvelés! Amikor rákérdeztem, biztosított róla, hogy nem azért hagyta ki, mintha hibás lett volna, hanem mert a cikk többi része szempontjából nem játszott szerepet. Véleménye szerint a téridők e mulatságos szuperpozícióiban figyelembe kell venni legalább a lehetőségét annak, hogy ezen lehetséges univerzumok valamelyikében zárt időszerű görbék is előfordulhatnak (3.13 ábra). Ezekben a kauzalitás teljesen fejre áll, jövő és múlt összekeveredik, és a kauzális hatások hurkokban körbejárnak.

3.13 ábra Ma egy téridő elegendően megdöntött fénykúpokat enged meg, zárt időszerű görbék alakulhatnak ki.

Bár az ilyen téridők szerepe csupán a tény-ellenesség, akár a második fejezet bombatesztelő problémájában, mégis befolyásuk van arra, ami ténylegesen történik. Azt nem állítom, hogy az érv világos, de mindenképpen jelzi, hogy a helyes elméletben - ha egyáltalán rábukkanunk valamikor - könnyen lehet valami nem kiszámítható természetű.

Szeretnék egy másik kérdést is felvetni. Hangsúlyoztam, hogy a determinizmus és a számíthatóság különböző dolgok. Ez elvezet a szabad akarat kérdéséhez is. A szabad akarat filozófiai tárgyalásokban mindig a determinizmus keretein belül jelenik meg. Valahogyan így: „Meghatározza-e múltunk a jövőnket?” Úgy tűnik számomra, hogy egyéb hasonló természetű kérdések garmadáját is fel lehetne tenni. Például: „a jövőt a múlt kiszámítható módon határozza-e meg?” - ami nem ugyanaz a kérdés.

Ezek a megfontolások mindenféle más kérdéseket is felvetnek. Felsorolom őket, a válaszadás igénye nélkül. Nagy viták folynak azzal kapcsolatban, hogy cselekedeteinket milyen mértékben határozza meg az öröklődés és a környezet. Amit viszont - eléggé furcsa módon - csak ritkán említenek meg, az a véletlen elemek szerepe.

Bizonyos értelemben mindezek a dolgok nincsenek ellenőrzésünk alatt. Megkérdezhetjük: „Létezik-e bármi más - talán a sajátnak nevezett dolog - ami független a fenti hatásoktól?” A kérdés akár még a törvényesség kapcsán is felmerülhet. Például a jogok és kötelességek kérdései úgy tűnik, valamilyen független „saját” cselekedeteit érintik. Egészen szövevényes probléma lehet. Először is, ott van a determinizmus és a nem determinizmus viszonylag kézenfekvő kérdése. A szokványos nem determinizmus véletlenszerű elemeket tartalmaz, de ezzel nem jutunk messzire. A véletlenszerű elemek nem állnak ellenőrzésünk alatt. Vehetjük helyette a nem kiszámíthatóságot. A nem kiszámíthatóságnak lehetnek magasabb rendű változatai. Különös dolog, hogy a korábban ismertetett Gödel típusú érvek különböző szinteken alkalmazhatók. Azon a szinten is, amit Turing jósgépeknek nevezett - ott az érv sokkalta általánosabb formát ölt, mint amit bemutattam. Meg kell fontolnunk a kérdést, hogy létezhet-e vagy sem egy magasabb rendű típusa a nem kiszámíthatóságnak, amely szerepet játszik az univerzum fejlődésében? Talán a szabad akarathoz fűződő érzéseink állnak valamiképpen kapcsolatban ezzel.

Beszéltem mára platóni világgal való valamiféle kapcsolatról. Mi a természete ennek a „platóni kapcsolatnak”? Vannak szavak, melyek tartalmaznak nem kiszámítható elemeket - mint például ítélet, józan ész, meglátás, esztétikai fogékonyság, együttérzés, erkölcsiség... Ezek számomra olyanoknak tűnnek, hogy nem éppen a számíthatóság jellemzi őket. Ez idáig a platóni világról főként a matematika nyelvén beszéltem, azonban egyebet is ide sorolhatunk. Platón bizonyosan megerősítené, hogy nem csak az igaz, de a szép és a jó is abszolút (platóni) fogalom. Ha valóban létezik valamilyen kapcsolat a platóni abszolúttal, amelyet a tudatunk tesz lehetővé, és amely nem magyarázható a számításos viselkedés fogalmaival, az számomra fontos kérdésnek tűnik.

1

^{Két négyzetből áll az általánosan ismert dominó. - A szerk. megj.}