Most összegezni fogjuk a kísérleteinkből adódó főbb következtetéseket. De az eredményeknek olyan formát adunk, hogy ilyesfajta kísérletekre általánosabban is érvényesek legyenek. Az összegzés egyszerűbb lesz, ha először definiáljuk az „ideális kísérletet”: egy olyan kísérletet, amelyben nincsenek bizonytalan külső hatások, ugrándozás vagy más figyelembe nem vehető dolog. Teljesen pontosak lettünk volna, ha azt mondjuk: „Az ideális kísérlet olyan kísérlet, amelyben teljesen meg vannak határozva a kezdeti és a végfeltételek.
”Itt mindjárt „eseményről” fogunk beszélni; az esemény, általánosságban véve, éppen ilyen kezdeti és végfeltételeknek valamiféle halmaza. (Például: „egy elektron elhagyja az elektronágyút, a detektorba jut, és egyéb semmi nem történik”.) És most lássuk az összegzést.
ÖSSZEFOGLALÁS
(1) Ideális kísérletben valamely esemény valószínűségét egy valószínűségi amplitúdónak nevezett 0 komplex szám abszolút értékének a négyzete adja meg:

(2) Ha egy esemény többféle - egymást kizáró - módon játszódhat le, akkor valószínűségi amplitúdója a valamennyi módra külön kiszámított valószínűségi amplitúdók összegével egyenlő. Ebben interferencia van jelen.
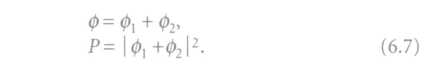
(3) Ha olyan kísérletet végzünk, amellyel megállapítható, hogy a lehetséges módok közül melyik játszódott le a valóságban, akkor az esemény valószínűsége egyenlő a lehetséges módok valószínűségének összegével. Ilyenkor megszűnik az interferencia.
P=P1 + P2. (6.8)
Az ember még most is szeretné tudni, hogy „Mi van emögött? Milyen szerkezet működik emögött a törvény mögött?” De senki nem talált mögötte semmiféle szerkezetet. Senki nem tud annál többet „megmagyarázni”, amennyit az imént „megmagyaráztunk”.
Senki nem fog a helyzet ennél mélyebb ábrázolásával szolgálni. Nem támadt fogalmunk olyasfajta mélyebben rejlő mechanizmusról, amelyből ezek az eredmények kiadódhatnának.
Szeretnénk hangsúlyozni egy igen fontos különbséget a klasszikus mechanika és a kvantummechanika között. Beszéltünk annak valószínűségéről, hogy egy elektron ilyen vagy olyan körülmények közé kerül. Céloztunk arra, hogy kísérleti összeállításunkkal (sőt a lehető legjobbal is) lehetetlen lenne előre pontosan megmondani, hogy mi fog történni. Csak az esélyeket jósolhatjuk meg! Ez úgy hangzik, mintha a fizika letett volna annak a feladatnak a megoldásáról, hogy ilyen és ilyen körülmények között pontosan mi fog majd történni. S le is tett róla, csakugyan! Nem tudjuk, hogyan lehetne megjósolni azt, hogy meghatározott körülmények között mi fog történni, sőt ezt lehetetlennek is tartjuk, és úgy gondoljuk, hogy csupán különböző események valószínűségét lehet megjósolni. Mi tagadás, ez szűkösebb a természet megértésének korábbi eszményénél. Talán visszalépés is ahhoz képest, de senki nem lát lehetőséget az elkerülésére.
Most pedig teszünk néhány észrevételt egy olyan elgondolásról, amelyet néha mégis szembeszegeznek ezekkel a következtetésekkel. „Talán az elektronnak van valamilyen belső szerkezete, valamiféle belső változói, csak még nem tudunk róla. Talán ezért nem tudjuk megjósolni, hogy mi fog történni. Ha közelebbről megvizsgálhatnánk az elektront, akkor megmondhatnánk, hogyan jutott oda, ahová jutott.” Amennyire ma tudjuk, ez lehetetlen. S a bajból ez sem húzna ki bennünket. Tegyük fel, hogy elfogadjuk: az elektron belsejében létezik valamiféle gépezet, s az meghatározza, hogy az elektron hová fog jutni. Ennek a gépezetnek azt is meg kellene határoznia, hogy az elektron innen oda mozogva melyik nyíláson fog majd áthaladni. De ne feledkezzünk meg arról, hogy ami az elektron belsejében van, az nem függhet attól, hogy mi mit teszünk, attól sem tehát, hogy kinyitjuk vagy bezárjuk valamelyik nyílást. Ha tehát egy elektron az indulása előtt már eltökélte, hogy (a) melyik nyílást fogja használni, és (b) hová fog jutni a végén, akkor valószínűségül P1-et kell kapnunk azokra az elektronokra nézve, amelyek az 1. nyílást választották, s P2-t azokra, amelyek a 2. nyílást választották, és szükségszerűen a P1 + P2 összeget kell kapnunk azokra nézve, amelyek a két lyuk valamelyikén át érkeztek. Úgy fest, hogy ez óhatatlanul így van. Csakhogy kísérletileg igazoltuk, hogy még sincs így. És senki nem mutatott még kiutat ebből a rejtélyből. Ezért jelenleg valószínűségek számítására kell korlátozódnunk. Azt mondjuk, hogy „jelenleg”, de erősen gyanítjuk, hogy sohasem fogunk tőle megszabadulni - vagyis ezt a rejtélyt lehetetlen megoldani mert a természet valóban ilyen.
Heisenberg eredetileg a következőképpen fogalmazta meg a határozatlansági elvet: Ha valamely tárgyon mérést végzünk, és lendületének x irányú komponensét Δp bizonytalansággal tudjuk meghatározni, akkor ugyanabban az időpontban a helyzetét legfeljebb Δx = h/Δp pontossággal ismerhetjük. A helyzet és a lendület bizonytalanságának a szorzata bármely időpontban legalább akkora kell hogy legyen, mint a Planck-féle állandó. Ez speciális esete a fentebb már általánosabban kifejtett határozatlansági elvnek. Az általánosabb megfogalmazás ez volt: semmilyen módon nem lehet olyan készüléket tervezni, amely meghatározná, hogy két lehetőség közül melyik válik valóra, egyszersmind ne tenné tönkre az interferenciaképet.
Lássuk egy sajátságos esetben, hogy a Heisenberg által megadott összefüggésnek igaznak kell lennie, mert különben nehézségek támadnának. Képzeljük el, hogy egy kicsit megváltoztatjuk a 6-3. ábrán vázolt kísérletet: a két nyílást kerekeken mozgatható lemezbe ütjük, hogy fel s le mozgathassuk őket az x irányban, ahogyan azt a 6-6. ábra mutatja. Megpróbálhatjuk a lemez mozgásának gondos megfigyelésével megállapítani, hogy ez vagy az az elektron melyik nyíláson megy át. Képzeljük el, hogy mi történik, ha a detektor az x = 0 helyen van. Azt várnánk, hogy egy, az 1. nyíláson áthaladó elektront a lemeznek lefelé kell eltérítenie ahhoz, hogy az a detektorba jusson. Mivel ezenközben megváltozott az elektron lendületének függőleges összetevője, a lemeznek ugyanakkora lendülettel kell visszalökődnie az ellenkező irányba, vagyis a lemez felfelé lódul.
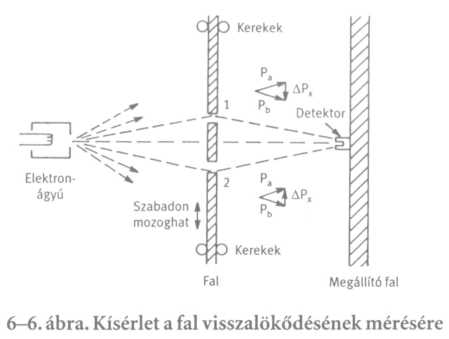
Ha az elektron az alsó nyíláson megy keresztül, akkor a lemeznek lefelé kell lódulnia. Világos, hogy a detektor különböző helyzeteiben a lemez más nagyságú lendületet kap akkor, ha az elektron az 1. nyíláson halad át, mint akkor, ha a 2. nyíláson. Nos hát! Csupán a lemez megfigyelésével, az elektronokat a legkevésbé sem zavarva ilyenformán megállapíthatjuk, hogy az elektron melyik utat választotta.
Ahhoz, hogy ezt megtehessük, tudnunk kell, hogy mekkora a lemez lendülete még azelőtt, hogy az elektron áthalad rajta. Mert ha megint megmérjük a lendületet, már az elektron áthaladása után, akkor megállapíthatjuk, hogy mekkora a lendületváltozás. No de emlékezzünk rá, hogy a határozatlansági elv szerint ugyanebben a pillanatban nem ismerjük akármekkora pontossággal a lemez helyzetét. Ám ha nem tudjuk pontosan, hogy hol van a lemez, akkor azt sem tudjuk pontosan megmondani, hogy hol vannak a nyílások. Minden elektron áthaladásakor más-más helyen lesznek. Ez azt is jelenti, hogy a különböző elektronokhoz tartozó interferenciaképnek más és más lesz a középpontja. Az interferenciakép kiugrásai (maximumai) elkenődnek. A következő fejezetben számszerűen megmutatjuk, hogy ha a lemez lendületét kellő pontossággal meghatározva, a visszalökődésekből megállapíthatjuk, hogy az elektron melyik nyíláson haladt át, akkor a lemez x tengely menti helyzetének bizonytalansága a határozatlansági elv szerint az interferenciaképet már annyival eltolhatja, hogy a detektorra ne maximumhely, hanem egy vele szomszédos minimumhely essék.
Egy ilyen véletlenszerű eltolódás éppen elég a rajzolat szétkenéséhez, és így nem is észlelhető interferencia.
A határozatlansági elv „megvédi” a kvantummechanikát. Heisenberg felismerte, hogy ha a lendületet és a helyet egyszerre nagyobb pontossággal lehetne mérni, akkor a kvantummechanika összeomlana. Feltette tehát, hogy ennél pontosabban nem megy. Ezután az emberek nekiültek, és elkezdtek módszereket keresni ennek a korlátozásnak a kikerülésére, de senki nem talált arra módot, hogy valaminek - egy ernyőnek, egy elektronnak, egy biliárdlabdának vagy bármi egyébnek - a lendületét és a helyzetét nagyobb pontossággal megmérje. A kvantummechanika tartja a pontosság határait és a maga támadott állásait.