Richard P. Feynman
Hat könnyed előadás
„Ha csupán egyetlen könyvet adhatnánk át a tudósok következő nemzedékének, az kétségkívül a Hat könnyed előadás lenne”
John Gribbin, New Scientist
A tudomány egy közkeletű tévhit szerint személytelen, szenvtelen és minden ízében elfogulatlan vállalkozás. Szinte minden más emberi tevékenységet áthat ugyan a divat, a hóbortok, az egyéniségek, de a tudományról feltételezik, hogy az megállapodott szabályoknak, szigorú ellenőrzésnek van alávetve. Az eredmények számítanak benne, s nem azok, akik elérik őket.
Ez persze nyilvánvaló képtelenség. A tudomány éppúgy ember befolyásolta tevékenység, mint bármi más, amit ember művel, és éppúgy alá van rendelve stílusnak és szeszélyeknek. Ebben az esetben a stílust nem is a vizsgálat tárgya szabja meg, hanem sokkal inkább az a mód, ahogyan a tudósok gondolkoznak a világról. Minden korszak a maga jellegzetes módján közelíti meg a tudományos problémákat, s ebben rendszerint hangadókat követ, azokat, akik kijelölik a teendőket, s e teendők elvégzésének legjobb útját-módját is. Időnként a tudósokat színes egyéniségük ismertté teheti a nagy nyilvánosság előtt is, és kiemelkedő tehetségükkel az egész tudományos közösség mintaképeivé válhatnak. A korábbi századokban Isaac Newton volt ilyen mintakép. Ő testesítette meg a tudós férfiút: a jó családból való, vallásos, istenfélő, semmit el nem kapkodó, munkájában módszeres embert. Az, ahogyan a tudományt művelte, kétszáz éven át szolgált mintaképül. A huszadik század első felében a népszerű tudós megtestesítőjeként Albert Einstein lépett Newton helyébe. Az excentrikus, zilált hajú, szórakozott, munkájába mélyen belemerülő Einstein, az elvont gondolkodó eleven őstípusa a fizika sarkfogalmait kérdésessé téve, megváltoztatta a fizika művelésének addigi módját.
Richard Feynman lett a huszadik század végi fizika mintaképe - s az első amerikai e nemben. New Yorkban született, 1918-ban, a keleti parton nevelkedett, s már nem lehetett résztvevője a fizika aranykorának, amely e század első három évtizedében a relativitáselmélet és a kvantummechanika kettős forradalmával átalakította világképünket. Ez a sodró lendületű fejlődés vetette meg annak az épületnek az alapjait, amelyet ma Új Fizikának nevezünk. Feynman ezekkel az alapokkal kezdte, és segített felépíteni az Új Fizika földszintjét. Közreműködése a tárgy szinte minden területére kiterjedt, és mélyrehatóan, tartósan befolyásolta azt a módot, ahogyan a fizikusok a fizikai univerzumról gondolkodnak.
Feynman igazi elméleti fizikus volt. Newton egyaránt volt kísérletező és elméletalkotó. Einstein egyszerűen semmibe vette a kísérleteket, ő inkább a tiszta gondolkodásban bízott. Feynman a természet mély elméleti megértésére törekedett, de mindig közel maradt a kísérleti eredmények valóságos, nemegyszer szurtos világához. Aki látta a korosodó Feynmant, amint a Challenger űrrepülőgép katasztrófáját magyarázza, s ezenközben egy rugalmas szalagot jeges vízbe márt, annak nem lehet kétsége afelől, hogy nagy hatásvadász és igen gyakorlatias gondolkodó volt egy személyben.
Feynman előbb a szubatomi részecskék elméletében - nevezetesen a kvantumelektrodinamikaként ismert témakörben - végzett munkájával szerzett nevet. Valaha éppen ezzel a tárggyal kezdődött a voltaképpeni kvantumelmélet. Max Planck német fizikus 1900-ban azt a gondolatot vetette fel, hogy a fény és más elektromos sugárzások, ha addig hullámnak tekintették is őket, paradox módon kicsiny energiacsomagok, „kvantumok” módjára viselkednek, ha anyaggal kerülnek kölcsönhatásba. Ezek a sajátos kvantumok később foton néven váltak ismertté. Az 1930-as évek kezdetére az új kvantummechanika létrehozói matematikailag leírhatóvá tették az elektromos töltésű részecskék, például elektronok fotonkibocsátását és -elnyelését. Bár a kvantumelektrodinamikának ez a kezdeti megfogalmazása aratott bizonyos sikereket, az elmélet nyilvánvalóan fogyatékos volt. Helyesen feltett fizikai kérdésekre sokszor ellentmondásos, végtelen eredményt adtak a számítások. A fiatal Feynmant az a probléma kezdte érdekelni, hogy hogyan lehetne ellentmondásmentes elméletet alkotni a kvantumelektrodinamikából.
A kvantumelektrodinamikát ehhez a szilárd megalapozáshoz nemcsak a kvantummechanika elveivel kellett összehangolni, hanem a relativitáselmélettel is. Ennek a két elméletnek megvolt a maga külön matematikai eszköztára, sok bonyolult egyenletrendszere, és azokat csakugyan össze lehetett kapcsolni és békíteni úgy, hogy kielégítően írják le a kvantumelektrodinamikát. Csakhogy ez nehéz vállalkozás volt, és nagy matematikai hozzáértés kellett hozzá; Feynman kortársai ezt az utat követték. Feynman azonban gyökeresen más utat választott, olyannyira mást, hogy voltaképpen többé-kevésbé közvetlenül leírhatta a válaszokat, bármi matematika nélkül!
Az intuíciónak ehhez a kivételes vívmányához egy egyszerű diagramrendszer kitalálásával jutott el. Ezek a Feynman-féle diagramok szimbolikus, egyszersmind hatékony heurisztikus módszerrel szolgálnak annak leírására, hogy mi történik az elektronok, fotonok és más részecskék kölcsönhatása közben. Manapság a Feynman-diagramok már mindennapos számítási segédeszközök, az 1950-es évek elején azonban - az elméleti fizika hagyományos műveléséhez képest - elképesztően új utat jelöltek ki.
A kvantummechanika következetes elméletének megalkotása, bár mérföldkő volt a fizika fejlődésében, egyedi probléma volt csupán, s csak a kezdet. Arra volt jó, hogy kijelölje a Feynman-féle jellegzetes stílust: egy sorozatra való fontos eredményre jutni a fizika tudományának széles tartományában. A Feynman-stílusra a tudományos ismeretek iránti tisztelet, egyszersmind tiszteletlenség a legjellemzőbb.
A fizika egzakt tudomány, és a meglevő ismerettömeget, ha nem teljes is, nem lehet egyszerűen félresöpörni. Feynman igen fiatalon roppant sok bevett fizikai elvet szívott magába, és úgy határozott, hogy szinte kizárólag csak hagyományos problémákkal fog foglalkozni. Nem az a fajta lángész volt, aki hód módjára várat épít szaktudományának valamelyik holtágában, hogy ott valami gyökeresen újat találjon. Az volt az ő különleges képessége, hogy jellegzetesen egyéni gondolkodásmóddal közelítsen meg lényeges és nagy horderejű kérdéseket; ebben elkerülte a meglevő formalizmust, és kifejlesztette a maga igen intuitív felfogásmódját. A legtöbb elméleti fizikus gondos matematikai számításokat használt útmutatóul és támaszul, arra az esetre, ha ismeretlen területre jut. Feynman magatartása viszont szinte hetyke, már-már fölényes volt ebben a helyzetben. Az ember azt hihette, hogy úgy olvassa a természetet, mint valami könyvet, és a bonyolult elemzések unalma nélkül, egyszerűen csak elmondja, hogy mit talált benne.
Feynman, való igaz, érdeklődését ily módon követve bizonyos egészséges megvetést mutatott a szigorú formalizmus iránt. Igen nehéz dolog felmérni, hogy a zsenialitásnak mely foka szükséges ehhez a munkamódszerhez. Az elméleti fizika az egyik legnehezebb szellemi gyakorlat: szemléltethetetlen elvont fogalmakat kapcsol össze roppant matematikai bonyolultsággal. A legtöbb fizikus csak a legmagasabb szintű szellemi fegyelem betartásával jut előbbre. Feynman meg mintha keresztülgázolt volna a gyakorlatnak ezen a szigorú törvényén, és úgy jutott az eredményekhez, mint aki érett gyümölcsöt szakít le a Tudás Fájáról.
A Feynman-stílus sok tekintetben Feynman személyiségéből fakad. Tudósként és magánéletében is minden látszat szerint roppant szórakoztató játéknak nézte a világot. A fizikai univerzum - s nemkülönben a társadalmi környezet - mint rejtvények és próbatételek lenyűgöző sorozata mutatkozott meg előtte. Egész életében nagy tréfacsináló volt, a tekintéllyel és a tudományos körökkel éppolyan tiszteletlenül bánt, mint a nagyképűsködő matematikai formalizmussal. Nehezen tűrte az ostobaságot, s áthágta a szabályokat, ha önkényesnek vagy képtelennek tartotta őket. Életrajzi írásaiban szórakoztató történeteket találni arról, hogyan fogott ki a háború idején az atombomba biztonsági szolgálatán, azután arról, hogy páncélszekrényeket nyitoga-tott, és nőket nyűgözött le megbotránkoztató viselkedésével. A kvantumelektrodinamikai munkájáért kapott Nobel-díjat is meglehetős nemtörődömséggel kezelte.
Ki nem állhatta a formalitásokat, a huncutság és a rejtélyesség viszont elbűvölte. Sokan emlékeznek rá, mennyire rögeszméjévé vált Tuva, egy régen elveszett közép-ázsiai ország; erről gyönyörű dokumentumfilm is készült, nem sokkal Feynman halála előtt. Szenvedélye volt a bongódobon való dobolás, a festés, a sztriptízbárok gyakori látogatása, a majául írt szövegek megfejtése.
Maga is sokat tett különös egyénisége ápolásáért. Tollat ugyan nemigen szeretett a kezébe venni, de szívesen beszélgetett, szeretett mesélni gondolatairól és kalandjairól. Ezek az éveken át összegyűlt anekdoták még rejtélyesebbé, sőt, még életében legendás alakká tették. A diákok nagyon kedvelték megnyerő modoráért, a fiatalabbak közül sokan valósággal bálványozták. Amikor 1988-ban rákban meghalt, a Caltechen1 - pályája legnagyobb részét itt töltötte - a hallgatók ezt a rövid feliratot tették ki: Szeretünk, Dick.
Feynmant ez az élet napos oldalát látó életfelfogás nagyon alkalmassá tette bármiféle - különösen a fizikai - ismeretek közlésére. Kevés ideje volt egyetemi előadást tartani vagy PhD-hallgatókat irányítani, de ragyogó előadásokat tartott, ha úgy hozta kedve, s ilyenkor áradt belőle a szikrázó szellemesség, az átható éleselméjűség és az egész kutatói pályáját végigkísérő tiszteletlenség.
Az 1960-as évek elején rávették, hogy első- és másodéves hallgatóknak tartson bevezető fizikai előadás-sorozatot a Caltechen. Meg is tette, a rá jellemző magabiztossággal, a fesztelenségnek, a lendületnek és a helyzet szülte humornak valami utánozhatatlan elegyével. Szerencsére ezek az igen értékes előadások könyv formájában megmaradtak az utókornak. Stílusban és előadásmódban ugyan erősen elrugaszkodtak a hagyományosabb ismeretközléstől, de a Feynman-féle Fizikai előadások2 hatalmas sikert arattak, és diáknemzedékeket lelkesítettek szerte a világon. Ezek a kötetek három évtized múltán mit sem veszítettek csillogásukból és világosságukból. A Hat könnyed előadás közvetlen válogatás ezekből a Fizikai előadásokból. Arra szolgál, hogy e mérföldkőnek tekinthető mű első néhány, a technikai részletekbe még nemigen bocsátkozó fejezetével lényegi benyomást adjon az átlagos olvasónak Feynmanról, az Oktatóról. Ezekből a fejezetekből pompás kötet kerekedett, a fizika alapjaival ismertetve meg a nem szakmabelieket, és bevezetésül szolgálva Feynmanhoz is.
Feynman gondosan felépített előadásában az a leglenyűgözőbb, ahogyan alig néhány fogalommal, a matematikát és a szakmai nyelvet alig-alig használva messze ható fizikai képzeteket alakít ki. Mesteri módon talál párhuzamot vagy hétköznapi hasonlatot ahhoz, hogy kidomborítsa ennek vagy annak a mély elvnek a lényegét, s közben ne homályosítsa el azt esetleges vagy kevésbé lényeges részletekkel.
A témaválogatásnak nem az volt a célja, hogy átfogó képet adjon a modern fizikáról, hanem hogy kíváncsiságot ébresszen Feynman módszere iránt. Hamarosan látni fogjuk, hogyan tudott újszerűen, lényegbevágóan megvilágítani olyan mindennapos dolgokat is, mint az erő meg a mozgás. A hétköznapi életből vagy a régmúltból vett példákkal szemléltet alapfogalmakat; a fizikát folyamatosan összekapcsolja más tudományokkal, de az olvasóban nem hagy kételyt afelől, hogy melyik az alaptudomány.
A Hat könnyed előadásnak már nyomban az elején megtanuljuk, hogyan gyökerezik az egész fizika a törvény fogalmában - abban, hogy létezik egy racionális gondolkodás útján megismerhető, rendezett világegyetem. A fizikai törvényeket azonban nem lehet közvetlenül, a természet megfigyelésével felismerni. Ezek bosszantóan rejtett törvények, ravaszul, finoman vannak belekódolva az általunk vizsgált jelenségekbe. A jelenségekben rejlő törvényszerű valóság felfedéséhez a fizikusok misztikus eljárásaira van szükség: gondosan megtervezett kísérletek és matematikailag megalkotott elméletek elegyére.
A fizikának talán a távolság négyzetével fordítva arányos erőt leíró Newton-féle gravitációs törvény a legismertebb törvénye; ezt a Hat könnyed előadásból az ötödik tárgyalja, kezdetben a Naprendszer és a bolygók mozgásának Kepler-féle törvényei közegében. De a tömegvonzás egyetemes, az egész kozmoszban hat, Feynman tehát a csillagászatból és a kozmológiából vett példákkal fűszerezheti mondanivalóját. A láthatatlan erők által egyben tartott gömbhalmaz képéről szólva Feynman lírai hangot üt meg: „Aki ebben nem látja működni a tömegvonzást, abból hiányzik a lélek.”
Más ismert törvények a természet tömegvonzástól különböző erőit írják le: azt, hogy milyen kölcsönhatás működik az anyag részecskéi között. Nem sok ilyen erő létezik; s Feynman azon kevesek közé tartozik, akik új fizikai törvényt fedeztek fel: ő éppen azt, hogy hogyan hat a gyenge nukleáris erő bizonyos szubatomi részecskék viselkedésére.
A háború utáni tudomány koronájában a nagy energiájú részecskefizika volt az ékkő, egyszerre félelmetes és elbűvölő a maga hatalmas gyorsítóival és az egymás után felfedezett újabb és újabb szubatomi részecskék látszólag végtelen listájával. Feynman kutatómunkája főleg ezeknek az eredményeknek a megértésére irányult. A részecskefizikusok abban egyetértettek, hogy a szimmetria- és megmaradási törvényeknek szerep jut majd a szubatomi „állatkertben” való rendcsinálásban is.
A részecskefizikusok által ismert szimmetriák közül sok történetesen már a klasszikus fizikában sem volt ismeretlen. Legfontosabbak közülük a tér és az idő homogenitásából fakadó szimmetriák. Vegyük az időt: a kozmológiát leszámítva - abban az ősrobbanás megjelöli az idő kezdetét - a fizikában semmi sincs, ami az egyik időpillanatot megkülönböztetné a következőtől. A fizikusok azt állítják, hogy a világ „invariáns az időeltolásra”, s ez annyit tesz, hogy mindegy, mit választunk méréseinkben kiindulópontnak: az éjfélt-e vagy a delet, a fizikai jelenségek leírása ugyanaz marad. A fizikai folyamatok nem függnek az idő abszolút kezdőpontjától. Mint kiderült, ebből az időeltolási szimmetriából közvetlenül következik a fizika legalapvetőbb, egyszersmind leghasznosabb törvénye: az energia megmaradásának törvénye. Ez leszögezi, hogy az energiát ide-oda vihetjük, az alakját is megváltoztathatjuk, de energiát nem állíthatunk elő, és el sem pusztíthatunk. Feynman ezt a törvényt a komisz Dennis kitalált történetével, a mama elől csintalanul elrejtett építőkockák meséjével teszi kristálytisztává (Negyedik előadás).
A kötetben az utolsó előadás - a kvantumfizika bemutatása - a legnagyobb próbatétel. Nem túlzás azt állítani, hogy a huszadik század fizikáján a kvantummechanika uralkodott, s ez a létező legeredményesebb - minden egyébnél jóval eredményesebb — tudományos elmélet. Nélküle nem érthetjük meg a szubatomi részecskéket, az atomokat és az atommagot, a molekulákat és a kémiai kötéseket, a szilárd testek, a szupravezetők és a szuperfolyékony anyagok szerkezetét, a fémek és félvezetők elektromos és termikus vezetőképességét, a csillagok szerkezetét, és még sok minden egyebet sem. Alkalmazásainak köre a lézertől a mikrolapkáig terjed. És mindez egy olyan elméletből következik, amely első pillantásra - sőt a másodikra is - tiszta őrültségnek tűnik. Niels Bohr, a kvantummechanika egyik létrehozója egyszer megjegyezte, hogy aki nem döbben meg ettől az elmélettől, az nem is értette meg.
A kvantummechanikai elgondolások ugyanis lényegileg szembeszegülnek mindazzal, amit a józan ész valóságnak nevez. Egyebek közt az is kérdésessé válik, hogy a fizikai objektumoknak, például az elektronoknak és az atomoknak vajon van-e önálló létük, és megvan-e mindig minden fizikai tulajdonságuk. Például egy elektronnak nem lehet egyszerre térbeli helyzete és jól meghatározott sebessége. Ha azt vizsgáljuk, hogy éppen hol van, akkor valahol meg fogjuk találni, ha meg a sebességét mérjük, akkor is határozott választ kapunk, de ezt a két megfigyelést nem végezhetjük el egy időben. Teljes megfigyelés híján pedig nincs értelme az elektronhoz meghatározott, de ismeretlen helyzet- és sebességértéket kapcsolni.
Az atomi részecskék lényegi természetéből folyó indeterminizmust Heisenberg nevezetes határozatlansági összefüggése foglalja magába. Ez világos határt szab annak, hogy milyen pontosan lehet egyszerre meghatározni az olyan tulajdonságokat, mint a helyzet és a sebesség. Ha a helyzet nagyon pontos, akkor kitágul a lehetséges sebességértékek tartománya, és viszont. Az elektronok, fotonok és más részecskék mozgásának módjában kvantumhatározatlanságok lépnek fel. Bizonyos kísérletek úgy jeleníthetik meg őket, mint amik meghatározott pályán haladnak a térben, olyasformán, ahogyan a lövedék halad pályáján a cél felé. Más kísérletek körülményei között viszont hullámként is viselkedhetnek, hullámjellemzőkkel: elhajlással és interferenciával.
A tudományos tárgyalásmódban ma már klasszikusnak számít a „kétréses” kísérlet Feynman-féle mesteri elemzése; ez a legkihívóbb formában mutatja a megrázó hullám-részecske kettősséget. Feynman néhány igen egyszerű gondolattal a kvantumrejtély kellős közepébe juttat bennünket, majd hagyja, hadd kápráztasson el a feltáruló valóság paradox természete.
Jellemző Feynmanra, hogy noha a kvantummechanika már az 1930-as évek elejétől megjelent a tankönyvekben, ő még fiatal korában teljesen új köntösbe öltöztette a maga használatára. A Feynman-módszernek fontos erénye, hogy eleven képet ad a természet kvantumtrükkjeinek működéséről. Ehhez az a kiindulópont, hogy a részecskének a kvantummechanikában általában nincs jól meghatározott térbeli pályája. Elképzelhetjük például, hogy egy szabadon mozgó elektron nem csupán egyenes vonalban halad A és B között, ahogyan azt a józan ész diktálná, hanem mindenféle ide-oda kanyargó pályán is. Feynman azt mondja: képzeljük el, hogy az elektron valamiképpen kikutatja az összes lehetséges pályát, és mivel nincs tapasztalatunk arról, hogy az elektron melyik pályát választotta, fel kell tennünk, ezek a szóba jöhető pályák mind a valóság részét alkotják. Ilyenformán ha egy elektron eljut egy térbeli pontba, például a képernyőre, akkor ehhez az egyetlen eseményhez sok különböző történetnek kell összegződnie.
Feynman nevezetes útintegrálos, más szóval történetösszegzős kvantummechanika-felfogása matematikai módszernek indult. Sok éven át többé-kevésbé kuriózumnak számított, de amikor a fizikusok a kvantummechanikát teljesítőképességének határáig juttatták - a gravitációra, sőt a kozmológiára is alkalmazták -, akkor kiderült, hogy a kvantum-világegyetem leírásához a Feynman-módszer adja a legjobb számítási eszközt. Talán a történelem egyszer majd úgy ítéli meg, hogy sok kiemelkedő fizikai eredménye közül a kvantummechanikának ez az útintegrálos megfogalmazása a legfontosabb.
A jelen kötetben tárgyalt gondolatok közül sok mélységesen filozófiai. Pedig Feynman rendíthetetlen ellenszenvet táplált a filozófusok iránt. Egyszer volt alkalmam vitatkozni vele a matematika természetéről és a fizika törvényeiről, és arról, hogy vajon független platóni létezőknek tekinthetők-e az absztrakt matematikai törvények. Szellemesen és ügyesen írta le, hogy miért tarthatjuk őket csakugyan ilyen létezőknek, de rögtön visszavonult, mihelyt arra kértem, hogy fejtse ki filozófiai álláspontját. Éppily óvatos lett, amikor a redukcionizmusról faggattam. Visszatekintve mégis azt hiszem, hogy nem érzett megvetést a filozófiai problémák iránt. De ahogyan rendszeres matematika nélkül is kitűnően művelte a matematikai fizikát, éppúgy rendszeres filozófia nélkül is voltak finom filozófiai észrevételei. A formalizmustól idegenkedett, nem a tartalomtól.
A világ aligha fog még egy Richard Feynmant látni. Feynman nagyon is korának gyermeke volt. A Feynman-stílus jól illett a fizika forradalma utáni konszolidációs szakaszhoz, és a messze ágazó következmények felderítésének kezdetéhez. A háború utáni fizikának biztosak voltak az alapjai, érett az elméleti szerkezete, mégis nyitva állt a különc kiaknázok előtt. Feynman az absztrakt fogalmak mesés birodalmába lépett, és sok fogalmon hagyta rajta a maga egyéni gondolkodásmódjának bélyegét. Ez a könyv egyedülálló bepillantást enged egy rendkívüli ember gondolkodásába.
1994 szeptemberében
Paul Davies
Különleges előszó (a Fizikai előadások című kötethez)
Élete vége felé Richard Feynman hírneve túllépett a tudományos körök határain. A Challenger űrrepülőgép katasztrófáját vizsgáló bizottság tagjaként nyújtott kiemelkedő teljesítménye széles körben ismertté tette; egy, a kalandos csínytevéseiről szóló, nagy közönségsikert aratott könyv révén pedig csaknem Albert Einsteinhez hasonló léptékű nemzeti hőssé vált. De már 1961-ben sem csupán a tudományos körök egyik ismert személyisége volt - még azelőtt tehát, hogy a Nobel-díj a nagyközönség előtt ismertté tette volna -, hanem legendás alak. Kétségtelen, hogy rendkívüli oktatói képességei elősegítették a Feynman-legenda terjedését és gyarapodását.
Csakugyan nagy tanító volt, a maga korának és a miénknek is talán legnagyobbika. Feynman számára az előadóterem színházterem volt, az előadó pedig színész, akinek kötelessége drámával és tűzijátékkal szolgálni, éppúgy, mint tényekkel és ábrákkal. Gesztikulálva járkált ide-oda a hallgatóság előtt „az elméleti fizikus és a cirkuszi kikiáltó valami lehetetlen vegyülékeként. Az egész ember csupa testmozgás és hanghatás” -írta róla a New York Times. Akár egyetemistáknak tartott előadást, akár kollégáknak vagy a nagyközönségnek, azoknak a szerencséseknek, akik személyesen részt vehettek rajtuk, a szokásostól elütő, feledhetetlen élmény volt ez, akárcsak maga Feynman.
Mestere volt a drámának; minden hallgatóság figyelmét lekötötte. Sok évvel ezelőtt haladó kvantummechanikai előadás-sorozatot tartott néhány beiratkozott továbbképzősnek és a Caltech fizikus karán oktatók többségének. Az egyik előadáson elkezdte magyarázni, hogyan lehet diagramszerűen ábrázolni bizonyos bonyolult integrálokat: az időt ezen a tengelyen, a teret azon a tengelyen, zegzugos vonal ehelyett az egyenes helyett stb. Leírván azt, amit a fizikusok világa Feynman-diagramként ismer, a hallgatóság felé fordult, és csintalan vigyorral közölte: „És ez a diagram!” Feynman eljutott a végkifejletig, és az előadóterem közönsége spontán tapsviharban tört ki.
Már jó néhány évvel az e könyvben szereplő előadások után alkalmi előadó volt a Caltech elsőéves fizikusainál. Fellépéseit persze titokban kellett tartani, hogy maradjon hely a beiratkozott hallgatóknak is. Egyik ilyen előadásán a görbült téridőről beszélt, és szokása szerint sziporkázott. De az előadás legelején valami feledhetetlen történt. Éppen akkoriban fedezték fel az 1987-es szupernóvát, és Feynmant ez erősen foglalkoztatta. Azt mondta: „Tycho Brahénak megvolt a maga szupernóvája, és Keplernek is megvolt a magáé. Aztán 400 évig egy se volt. És most nekem is megvan a magamé.” A jelenlevők elcsendesedtek, Feynman pedig folytatta. „Galaxisunkban 1011 csillag van. Ezt általában hatalmas számnak veszik, pedig csak százmilliárd, kisebb, mint a költségvetési hiány! Ezeket a számokat csillagászati számoknak szokás nevezni, de most már közgazdasági számoknak kellene.” A hallgatóság nevetésben tört ki, Feynman pedig, miután a terem ismét elcsendesedett, folytatta az előadást.
Az attrakcióktól eltekintve Feynman pedagógiai módszere egyszerű volt. A Caltech irattárában őrzött dokumentumai között van egy 1952-ben, Brazíliában lefirkantott feljegyzés. Ebben így foglalja össze felfogását:
„Először tisztázd, hogy miért akarod a hallgatóknak megtanítani a tárgyat, s hogy szerinted mit kellene belőle tudniuk; a módszer azután már többé-kevésbé adódni fog a józan észből.”
Amit Feynman „józan észnek” hívott, az sokszor a dolog lényegét megragadó, szellemes csavar volt. Egyszer, egy nyilvános előadáson azt igyekezett megmagyarázni, miért nem szabad egy elgondolás igazolására legelőször azokat az adatokat felhasználni, amelyek az elgondolást sugallták. A tárgytól látszólag eltérve, a rendszámtáblákról kezdett beszélni. „Tudják, most este igazán meglepődtem. Ahogy jöttem idefelé az előadásra, átvágtam a parkolón. És nem fogják elhinni, hogy mi történt. Láttam egy ARW 357 rendszámú kocsit. El tudják ezt képzelni?
Mekkora volt az esélye annak, hogy az állam milliónyi rendszámtáblájából pont ezt lássam ma este? Megdöbbentő!” Feynman rendkívüli „józan esze” olyasmit tett világossá, amit még sok tudós sem fog fel.
A Caltechen töltött 35 év alatt (1952-től 1987-ig) a maga 34 előadássorozatával csúcstartó volt az oktatók között. Huszonötöt haladók továbbképzésére tartott, szigorúan véve csak végzetteknek, de külön engedéllyel még nem végzettek is részt vehettek rajtuk (rendszerint megkapták rá az engedélyt). A többi előadás bevezető egyetemi továbbképző előadás volt. Csupán egyszer tanított alsóbb évfolyamokon: ez a nevezetes alkalom az 1961-62-es és az 1962-63-as tanévben volt, meg egy rövid visszatérés 1964-ben; ezekben az években tartotta a később Feynman-féle Fizikai előadások néven ismertté vált előadásait.
Abban az időben általános vélemény volt a Caltechen, hogy a kötelező kétéves fizika inkább elriasztja az első- és másodéves hallgatókat, semmint ösztönözné őket. Hogy javítsanak a helyzeten, felkérték Feynmant, tervezzen egy olyan előadás-sorozatot, amelyet a kétéves előadás-sorozat mellett hallgatnának az egyetemisták, először elsőéves korukban, azután másodévesen. Mihelyt beleegyezett, rögtön elhatározták, hogy az előadásokat publikálásra kész formában is rögzítik. Ez sokkal nehezebbnek bizonyult, mint gondolták volna. Feynman kollégáinak rengeteg munkájába került, hogy kiadható könyvet hozzanak létre, maga Feynman is rengeteg időt fordított rá, hiszen ő volt a kötetek végső szerkesztője.
Közben az előadás-sorozattal kapcsolatos részfeladatokkal is foglalkozni kellett. Bonyolult dolog volt ez, mert Feynmannak csak meglehetősen bizonytalan elképzelései voltak arról, mit fog előadni. Addig tehát, amíg oda nem állt a zsúfolt előadóteremben a diákok elé, senki se tudhatta, miről fog beszélni. A segítségére levő Caltech-professzorok csak ekkor kezdhettek el kapkodni, hogy amennyire lehet, apróbb részletekben - például a házi feladatok megoldásával kapcsolatban - se legyen fennakadás.
Vajon miért szánt Feynman több mint két évet a bevezető fizika tanításának forradalmasítására? Ezen már csak tűnődni lehet, de feltehetőleg három oka volt rá. Az egyik az, hogy szerette, ha van hallgatósága, mert ez tágabb cselekvési teret adott, mint a továbbképző előadások.
A második alighanem az, hogy őszintén törődött a hallgatókkal, és egyszerűen úgy vélte, az elsőévesek oktatása fontos feladat. A harmadik -és talán legfontosabb - indok a fizika újrafogalmazására tett erőfeszítés volt, éspedig úgy, ahogyan azt ő értette: újrafogalmazás a fiatal hallgatóknak előadható formában. Ez volt az ő specialitása: próbaköve annak, hogy valami csakugyan érthető-e. A Caltech oktatói karának egyik tagja egyszer megkérte Feynmant, magyarázza meg, hogy a feles spinű részecskék miért követik a Fermi-Dirac-féle statisztikát, ő végigmérte a hallgatóságot, aztán kijelentette: „Majd kigondolok erről egy elsőéveseknek szóló előadást.” Néhány nappal később visszatért a dologra: „Tudják, nem boldogultam vele. Nem tudtam az elsőévesek szintjére levinni. Ez annyit jelent, hogy valójában nem is értjük.”
A mély gondolatok egyszerű, érthető fogalmakra való jellegzetes visszavezetése végig jelen van a Feynman-féle Fizikai előadásokban-, leginkább a kvantummechanika tárgyalásában. A bennfentesnek világos, hogy mit csinált. Kezdő hallgatóknak adta elő az útintegrál módszerét, azt a maga kiagyalta technikát, amellyel sikerült néhány igen mély fizikai problémát megoldania. Az útintegrálra támaszkodó munkáiért és egyéb eredményeiért kapta 1965-ben a Nobel-díjat, Julian Schwingerrel és Sin-Itero Tomonagával megosztva.
Ezekre az időkre visszaemlékezve sok diák és kari munkatárs hangsúlyozza, hogy ez a kétéves fizika Feynmannal egész életre szóló élményt adott. Akkoriban azonban nem így festett a dolog. A hallgatók közül sokan megrémültek, s az idő előrehaladtával riasztóan csökkent az előadást látogató alsóbb évfolyamos diákok száma, egyre nagyobb számban jöttek viszont a kari munkatársak és a felsőbb évfolyamosok. De a terem végig tele volt, és Feynman talán sosem tudta meg, hogy eredetileg megcélzott hallgatóságának egy részét elvesztette. Pedagógiai próbálkozását ő sem ítélte sikeresnek. Az 1963-ban kiadott Fizikai előadások előszavában így ír: „Nem hinném, hogy a diákok szerint nagyon jól végeztem volna a dolgomat.” Az előadásokat újraolvasva, néha úgy tűnik, mintha Feynman átkacsintana a válla felett, de nem fiatal hallgatóira, hanem közvetlenül a kollégáira: „Látod? Nézd csak, milyen ravaszul fogtam meg ezt a kérdést! Ügyes volt, mi?” De akkor sem azok látták hasznát annak, amit csinált, amikor azt gondolta, hogy világosan kifejtett valamit az első- és másodéveseknek, hanem a vele egyenrangúak: kutatók, fizikusok, professzorok; ők lettek nagyszerű eredményeinek fő haszonélvezői, hiszen Richard Feynman friss, lendületes felfogásában láthatták a fizikát.
Feynman nem csak nagy oktató volt. Képességei az oktatók párját ritkító oktatójává avatták. Ha a Fizikai előadásoknak az volt a céljuk, hogy egy teremre való alsóbb éves diákot fizikai vizsgafeladatok megoldására tanítsanak, akkor nem mondhatni, hogy különösebben sikeresek lettek volna. S ha ezek a könyvek azt a célt tűzték ki, hogy bevezető egyetemi tankönyvként szolgáljanak, akkor még azt sem lehet róluk elmondani, hogy elérték volna céljukat. Mindazonáltal ezeket a könyveket tíz idegen nyelvre fordították le, és négy kétnyelvű kiadásuk is megjelent. Feynman meg volt róla győződve, hogy a fizikában nem a kvantumelektrodinamikával tette a legtöbbet, sem a szuperfolyékony hélium elméletével, s nem is a polaronokkal vagy a partonokkal; egyikkel sem, hanem a Fizikai előadások három vörös kötetével3. Ez tökéletesen megindokolja e híres könyvek jelen emlékkiadását.
1989 áprilisában
DAvid L. Goodstein Gerry Neugebauer Kaliforniai Műegyetem
Feynman előszava (a Fizikai előadásokból)
Ezek azok a fizikai előadások, amelyeket tavaly és tavalyelőtt tartottam a Caltech elsőéves és másodéves hallgatóinak. Volt persze, amit nem szó szerint így mondtam el; ez már szerkesztett, itt-ott megváltoztatott szöveg. Az előadás csak egy része volt a kollégiumnak. A 180 hallgató hetente kétszer jött el egy nagy terembe ezekre az előadásokra; ezután 15-20 fős szemináriumi csoportokban dolgoztak tovább, egy tanársegéd vezetésével. Hetente egyszer laboratóriumi foglalkozásuk is volt.
Ezekkel az előadásokkal azt a sajátos célt igyekeztünk elérni, hogy a középiskolákból a Caltechre jött lelkes és igazán okos hallgatókban megmaradjon az érdeklődés a fizika iránt. A Caltechig jutva már sok mindent hallanak arról, hogy milyen érdekes, izgalmas a fizika - a relativitáselmélet, a kvantummechanika és más modern gondolatok. A korábbi kétéves előadás-sorozat végére sokan elveszthették a kedvüket, mert igen kevés valóban nagy, új és modern gondolattal ismerkedhettek meg benne. Lejtős síkokat, elektrosztatikát és más efféléket tanultattak meg velük, és két év után ez eléggé nevetséges volt. Az volt a kérdés ezek után, hogy sikerül-e elindítanunk egy olyan előadás-sorozatot, amely fenntartja a fizika iránti lelkesedést, s nem hagyja elveszni a gyorsabban haladó, érdeklődőbb diákokat.
Ezek az itteni előadások semmiképpen sem vehetők áttekintő előadásoknak, mégsem könnyűek. Ügy gondoltam, hogy az évfolyamban a legintelligensebbhez mérem őket, éspedig úgy, hogy ha lehet, még a legintelligensebb hallgató se tudja mindazt befogadni, amiről az előadásokban szó esett - felvetettem a szóban forgó gondolatoknak és fogalmaknak a fő csapástól különféle irányban eltérő alkalmazásait. S emiatt igen erősen igyekeztem is állításaimat a lehető legpontosabban megfogalmazni, s mindig tisztáztam, hogy az egyenletek és fogalmak hogyan illeszkednek a fizika egészébe, s hogy mindezek hogyan módosulnak majd a későbbi tanulmányokban. Ügy gondoltam továbbá, hogy az ilyen hallgatóknak meg kell mutatni, mi az, amit - ha elég okosak - az addigiakból következtetés révén maguk is megérthetnek, és mi az, ami már új. A felmerülő új fogalmakat, ha lehet, megkísérlem levezetni, vagy megmagyarázom, hogy az új, a tanultakra nem építhető fogalom, s nem is kell bizonyíthatónak lennie: egyszerűen hozzávesszük az addigiakhoz.
Ezeknek az előadásoknak a kezdetén feltettem, hogy a középiskolából már tudnak egyet-mást, például geometriai optikát, egyszerű kémiai fogalmakat és egyebeket. Arra sem láttam okot, hogy meghatározott sorrendben tartsam az előadásokat, vagyis hogy ne említsek valamit, csak mert részletesen még nem beszéltem róla. Sok olyan dologra volt szükség, amelyet nem lehetett teljesen megtárgyalni, csak később, a kellő előkészületek után. Például az indukció és az energiaszintek először csak kvalitatív módon kerültek szóba, s majd csak később a szükséges részletességgel.
Jóllehet az aktívabb hallgatót céloztam meg, gondoskodni akartam arról a társáról is, akit ezek a külön „tűzijátékok” és mindenféle alkalmazások csak zavarnak, s akiről azt gondolom, hogy az előadás anyagának nagy részét meg sem tanulja majd. Az ilyen hallgatónak az anyag gerincét akartam adni, azt, amit ő is elsajátíthat. Remélem, hogy ha már nem értett meg mindent egy-egy előadáson, legalább nem bosszankodott. Reméltem, hogy ha mindent nem is, legalább a központi, a legközvetlenebb jellegzetességeket felfogja. Persze ahhoz kell valamennyi intelligencia, hogy átlássa, melyek a központi tételek és gondolatok, s melyek azok a haladottabb, de félreesőbb kérdések és alkalmazások, amelyeket a későbbi években érthet majd meg.
Az előadások megtartásával egy nagy baj volt: ez az előadási módszer nem engedett semmilyen visszhangot a hallgatótól a tanárig, s nem lehetett tudni, hogy mennyire jók az előadások. Ez nem kis nehézség, és nem is tudom, hogy voltaképpen mennyire voltak jók. Az egész előadás-sorozat lényegében kísérlet volt. És ha megint megtartanám, nem egészen így csinálnám - bár remélem, hogy nem kell még egyszer megtartanom. Mégis, azt gondolom, hogy az első esztendőben eléggé jól mentek a dolgok, már ami a fizikát illeti.
A második évben nem voltam ennyire elégedett. A kollégium első részében, az elektromosság és a mágnesség tárgyalásában nem tudtam semmilyen tényleg egyedi vagy másféle előadási módot kitalálni, olyat, amely izgalmasabb lett volna a hagyományos előadási módnál. Nem is hiszem tehát, hogy sokra jutottam volna az elektromossággal és a mágnességgel. A második év végén eredetileg tovább akartam menni, és néhány előadást tartani az elektromosság és a mágnesség után az anyagtulajdonságokról, s főleg olyasmiről, mint az alapmódu-sok, a diffúziós egyenlet megoldásai, rezgő rendszerek, ortogonális függvények... s kifejteni az első szakaszait annak, amit „a fizika matematikai módszereinek” neveznek. Most visszatekintve azt gondolom, hogy ha újrakezdeném, akkor visszatérnék ehhez az eredeti ötlethez. De mert nincs szó arról, hogy ezeket az előadásokat megismételném, azért az a gondolat vetődött fel, hogy jó volna egy kvantummechanikai bevezetővel szolgálni; ez van a III. kötetben.
Teljesen világos, hogy azok a hallgatók, akiknek főtanszakjuk a fizika, várhatnak a kvantummechanikával a harmadik évfolyamig. Másfelől meg az előadásokon részt vevők közül soknak csak háttértárgy volt a fizika valami más irányú főtanszakhoz. A kvantummechanika szokásos tárgyalásmódja azonban a hallgatók nagy többségének elérhetetlen lett volna, mert nagyon sok időn át kellett volna tanulniuk. Csakhogy a tényleges alkalmazásokban - különösen a bonyolultabbakban, például a villamosmérnöki és a kémiai alkalmazásokban - a valóságban nem használják a differenciálegyenletes megközelítés teljes kelléktárát. Megpróbáltam tehát olyan módszert választani a kvantummechanika alapelveinek leírására, amelyhez nem kell előzetesen ismerni a parciális differenciálegyenletek matematikáját. Azt hiszem, hogy többféle okból is - az előadásokból talán kiderül, hogy milyen okokból - még fizikusnak is érdekes lehet a kvantummechanikát ilyen fordított módon bemutatni. Mindazonáltal azt hiszem, hogy a kvantummechanikai rész mint kísérlet nem volt teljesen sikeres; jórészt azért, mert a végén tényleg nem maradt elég időm (még kellett volna három vagy négy további előadás, hogy részletesebben foglalkozhassam olyan anyagrészekkel, mint az energiaszintek és az amplitúdók térfüggése). És így még sohasem adtam elő kvantummechanikát, ezért különösen rosszul ért, hogy nincs semmilyen visszhang. Most úgy hiszem, hogy a kvantummechanikát később kell előadni. Lehet, hogy egyszer majd meg is tehetem, s akkor majd jól fogom csinálni.
Problémamegoldással foglalkozó előadások azért nincsenek itt, mert a feladatmegoldás szemináriumi munka volt. Az első évben beiktattam ugyan három előadást a problémamegoldásról, de azok nem kerültek be a kötetekbe. Volt egy előadás a tehetetlenségi vezérlésről is; annak közvetlenül a forgó rendszerekről szóló előadás után kellene következnie, de sajnálatos módon az is kimaradt. Az ötödik és hatodik előadás valójában Matthew Sands előadása; akkor éppen távol voltam.
Kérdés persze, hogy mennyire volt sikeres ez a kísérlet. Magam borúlátó vagyok, a hallgatókkal foglalkozó kollégák többsége azonban nem osztja nézeteimet. Nem hinném, hogy a diákok szerint nagyon jól végeztem volna a dolgomat. Ha azt veszem, hogy a hallgatók többsége hogyan kezelte a problémákat a vizsgákon, akkor azt hiszem, kudarcot vallottunk. Persze, a barátaim hangsúlyozzák, hogy volt egy vagy két tucat olyan hallgató, akik - meglepő módon - szinte mindent megértettek az összes előadáson; ők az anyag feldolgozásában is igen tevékenyek voltak, és sok kérdés foglalkoztatta őket. Azt hiszem, nekik most már elsőrangú alapjuk van a fizikából, s végül is hozzájuk igyekeztem eljutni. Csakhogy: „Az oktatás ritkán nagyon hatékony, kivéve azokat a szerencsés eseteket, amikor már csaknem felesleges.”(Gibbon)
Mindazonáltal egyetlen hallgatót sem akartam teljesen magára hagyni, ha ez talán meg is történt. Azt hiszem, a hallgatókat jobban segítette volna, ha kemény munkával kidolgozunk néhány olyan problémát, amely jobban megvilágítja az előadások egyik-másik gondolatát. A problémák jól kiegészítik az előadások anyagát, valóságosabbá és teljesebbé teszik az előadott gondolatokat, és jobban beleplántálják őket a diákok fejébe.
Akárhogy is van, azt gondolom, az oktatásnak erre a problémájára csak akkor találunk igazán jó megoldást, ha belátjuk, hogy a diáknak közvetlen, személyes kapcsolatban kell lennie egy jó tanárral, s ebben a helyzetben meg kell hánynia-vetnie a gondolatokat, gondolkoznia és beszélnie kell a dolgokról. Az előadásokon ott ülve, sőt még a kijelölt feladatokat megoldva sem lehet túl sok mindent megtanulni. Csakhogy a mi mai világunkban olyan sok hallgatót kell oktatnunk, hogy találnunk kell valamit az ideális helyettesítésére. Előadásaim valamilyen módon talán hozzájárultak ehhez. Talán valami kisebb helyen oktató egyedi tanárok és diákjaik némi ösztönzést meríthetnek belőlük, sőt néhány ötletet is. Talán szórakoztató lesz nekik, ha átgondolják azokat vagy némelyik gondolatot tovább is fejlesztik.
1963 júniusában
Richard R Feynman
ELSŐ ELŐADÁS
Ezen a kétéves tanfolyamon végig abban a meggyőződésben beszélek majd a fizikáról, hogy önök, az olvasók fizikusnak készülnek. Lehetséges persze, hogy nem is ez a szándékuk, mégis mindig minden professzor ebből indul ki, bármi legyen a tárgya. Aki fizikus szeretne lenni, annak sok mindent kell tanulnia, hiszen a leggyorsabban fejlődő ismeretterület legutóbbi kétszáz évének termése vár rá. Ez olyan sok, hogy az olvasó azt gondolhatja: ennyit négy év alatt sem fog tudni megtanulni, és igaza is van, hiszen még további tanulmányokra is szüksége lesz!
Eléggé meglepő, hogy az ez idő alatt elvégzett rengeteg munka roppant sok eredménye nagyrészt összesűríthető: ismereteinket törvényekben lehet összefoglalni. De még a törvényeket is olyan nehéz megragadni, hogy méltánytalanság volna bárkit is valamiféle térkép vagy a tudományterületek egymás közötti kapcsolatát tisztázó vázlat nélkül nekiindítani ennek a hatalmas tárgykörnek. Ezért, hogy könnyebb legyen „megéreznünk”, miről van szó, a bevezető megjegyzések után az első három fejezetben körvonalazzuk majd a fizika és a többi tudomány, valamint a tudományterületek egymás közötti viszonyát, meg azt, hogy mi a tudomány.
Az olvasó joggal kérdezhetné: miért nem úgy tanítjuk a fizikát, hogy az első oldalon megadjuk az alaptörvényeket, s utána megmutatjuk, hogy azok hogyan használhatók az elgondolható összes körülmény között, olyasformán tehát, ahogyan az euklideszi geometriát tanítják: előrebocsátják az axiómákat, majd levonnak belőlük minden lehetséges következtetést? (Szóval nem szeretnék négy évig tanulni a fizikát; jobban tetszenék azt négy perc alatt elsajátítani?) Két okból sem tehetjük ezt. Egyrészt azért, mert még nem ismerjük az összes alaptörvényt: a tudatlanság határai egyre távolabbra nyúlnak. Másrészt azért, mert a fizikai törvények helyes megfogalmazásában támaszkodnunk kell néhány nagyon szokatlan elgondolásra, és azok leírásához magasabb szintű matematika szükséges. Emiatt már ahhoz is sok előkészület kell, hogy megértsük, mit jelentenek a szavak. Nem, ezt a fajta módszert tényleg nem használhatjuk a fizika tanításában. Csak lépésről lépésre, részletről részletre haladhatunk előre.
A természet egészének eme részletei a teljes igazságnak vagy az általunk eddig ismert igazságnak csupán közelítései. Voltaképpen minden, amit ismerünk, csak ilyen vagy olyan közelítés, mert tudjuk, hogy még nem ismerünk minden törvényt. Következésképpen azért tanulunk, hogy a tanultakat elfelejtsük, vagy inkább azért, hogy helyesbítsük őket.
A tudománynak alapelve, már-már meghatározása, hogy minden ismeret próbája a kísérlet. A kísérlet a tudományos „igazság” egyedüli próbaköve. De mi az ismeretek forrása? Honnét valók a próbára teendő törvények? A kísérlet elősegíti ezeknek a törvényeknek a megalkotását, annyiban legalábbis, hogy útbaigazítással szolgál. De képzelő-erőre is szükség van ahhoz, hogy ezekből az utalásokból nagy általánosításokra jussunk - hogy felismerjük a mögöttük rejlő csodálatos, egyszerű, de igen különös jellegzetességeket, majd megint kísérlettel ellenőrizzük, hogy felismerésünk vajon helyes volt-e. Ez a képzelő-erőre támaszkodó folyamat olyannyira nehéz, hogy a fizikában kétfelé válik: vannak elméleti fizikusok - ők képzelik el, vezetik le, találják ki az új törvényeket, de nem kísérleteznek; s vannak kísérleti fizikusok - ők kísérleteznek, elgondolnak valamit, következtetésekre jutnak és találgatnak.
Azt mondtuk, hogy a természettörvények közelítő jellegűek: először a „rosszat” találjuk meg, azután a „jót”. De hogyan lehet „rossz” egy kísérlet? Először is, nyilvánvaló módon: mondjuk, a berendezés valamilyen észrevétlen hibája miatt. De az ilyesmit könnyű kijavítani és oda-vissza ellenőrizni. Hogyan lehet ezek után mégis rossz egy kísérlet eredménye, ha ezektől a kevésbé fontos dolgoktól eltekintünk? Csakis pontatlanság folytán. Például a tárgyak tömege mintha sosem változnék: a pörgő búgócsigának ugyanakkora a súlya, mint a nyugvóé. Ezzel „törvényt” fedeztünk fel: mindegy, hogy mekkora a sebesség, a tömeg állandó. Ma már tudjuk, hogy ez a „törvény” nem állja meg a helyét. Kiderült, hogy a tömeg növekszik a sebességgel, de ez csak akkor válik szembetűnővé, ha a sebesség közel esik a fény sebességéhez. Igaz törvény viszont a következő: ha valamely tárgy másodpercenként 160 kilométeresnél kisebb sebességgel mozog, akkor a tömege egymilliomod résznyi pontossággal állandó. Ebben a közelítő formában ez pontos törvény. A gyakorlatban tehát - gondolhatnánk - ez a törvény nem jár lényeges változással. Holott jár is, meg nem is. Ha a szokásos sebességekről van szó, akkor valóban megfeledkezhetünk róla, s közelítésként használhatjuk a tömeg állandóságának törvényét. De nagy sebességértékeken már hiba állandónak venni a tömeget, és a hiba annál nagyobb, minél nagyobb a sebesség.
Végül, s igen érdekes módon, a közelítő törvény filozófiai szempontból teljesen hibás. Ha a tömeg egy szemernyit is változik, akkor mindenestül meg kell változtatnunk a világképünket. Különös vonása ez a filozófiának, a törvények mögött meghúzódó gondolatoknak. Néha még egy igen kis súlyú jelenség is mélyreható változtatásokat követel eszméinkben, gondolkodásunkban.
Mit tanítsunk tehát először? A pontos, de szokatlan törvényt, furcsa és nehéz fogalmaival, például a relativitáselméletet, a négydimenziós téridőt és egyebeket? Vagy előbb az „állandó tömeg” törvényét, ha csak közelítés is, mert nem jár olyan nehéz fogalmakkal? Az első izgatóbb, csodásabb és szórakoztatóbb, de a másodikat könnyebb első hallásra megérteni, és az az első lépés a második gondolat valódi megértéséhez. Ez a kérdés minduntalan felbukkan a fizika tanításában. Alkalmanként más-más megoldást kell majd találnunk rá, de minden szakaszban meg kell tanulni azt, hogy ma mit tudunk és milyen pontosan, az hogyan illik bele más ismereteinkbe, és hogyan módosulhat, ha majd többet tudunk róla.
S most vázoljuk fel, mit értünk manapság tudományon (legfőképpen fizikán, de a fizika körüli más tudományokon is), hogy ha később valamilyen részletre figyelünk, már legyen valamelyes fogalmunk a hátteréről, arról, hogy az a kérdés vajon miért érdekes, és hogyan illik bele a nagy egészbe. Milyen tehát ez a mi általános világképünk?
Ha egy világfelfordulásban minden tudományos ismeretünk odaveszne, és csak egyetlen mondat maradna örökül a következő nemzedékekre, vajon mely kijelentés adhatná át nekik a legtöbb információt a legkevesebb szóval? Én azt hiszem, hogy az atomhipotézis (vagy az atomosság ténye, ahogy tetszik), az tehát, hogy minden dolog atomokból áll
- olyan apró részekből, amelyek örökös mozgásban vannak, vonzzák egymást, ha kis távolságra vannak egymástól, de taszítás támad köztük, ha valami egymás felé közelítené őket. Ebből a mondatból, mint látni fogják, igen sok információt lehet kihámozni a világról, csak gondolkodás kell hozzá és egy kis képzelőerő.
Az atomhipotézis erejének szemléltetésére tegyük fel, hogy van egy nagyjából 6 milliméter átmérőjű vízcseppünk. Bármily közelről nézzük is, nem látunk mást, csak vizet: folytonos, szakadatlan vizet. Ha a mai legjobb optikai mikroszkópon át - nagyjából kétezerszeres nagyításban - nézzük, akkor ez a vízcsepp már vagy 12 méter átmérőjű lesz, akkora tehát, mint egy jókora szoba; ha most is közelről nézzük, még mindig viszonylag folytonos vizet látunk, de már itt-ott labda formájú, ide-oda úszó valamiket is. Ez igen érdekes látvány: ezek a valamik papucsállatkák. Itt némelyikük talán megáll, mert annyira kíváncsi lesz ezekre az állatkákra, ahogyan ide-oda mozgó csillószőrükkel kígyóznak, hogy nem is akarja a vizet tovább nagyítani, hacsak azért nem, hogy többet lásson a papucsállatkákból, és a belsejüket is megismerhesse. Ez persze a biológia tárgyát képezi, mi azonban most továbbmegyünk, és még közelebbről vizsgáljuk a víz anyagát, további kétezerszeres nagyításban. Ez időre a vízcsepp átmérője már nagyjából 24 kilométer, és ha igen közelről néznénk, valamiféle nyüzsgést látnánk, valami nem folytonosát; mintha nagy távolságból néznénk egy rögbimérkőzés tülekedését, kavargását. Hogy közelebbről lássuk ezt a tolongást, mindent a kétszázötvenszeresére nagyítunk, s akkor valami olyasmi tárul majd a szemünk elé, amit az 1-1. ábrán látni. Ez a víz képe egymilliárdszoros nagyításban, csakhogy több szempontból is idealizált kép. Egyrészt a részecskéket egyszerűen, éles körvonalakkal rajzoltuk fel, holott a valóságban nem ilyenek.

Másrészt a vízrészecskéket az egyszerűség kedvéért szinte sémaszerűen, két dimenzióban ábrázoltuk, holott természetesen három dimenzióban mozognak. Észrevehetik, hogy az oxigénatomokat és a hidrogénatomokat kétféle „folt” vagy kör ábrázolja: az oxigénatomokat fekete, a hidrogénatomokat fehér, s hogy minden oxigénhez két hidrogén kapcsolódik. (Az egy oxigénből és két hidrogénből álló csoportocskákat molekulának nevezzük.) A kép abban is idealizált, hogy a valóságos részecskék a természetben szakadatlanul egymásba ütköznek és visszapattannak egymásról, forognak és kígyóznak egymás körül. Az egészet inkább dinamikus, mintsem statikus jelenségként kell elképzelnünk. A rajzon azt sem lehet szemléltetni, hogy a részecskék „összetapadnak”, vonzzák egymást, ez azt húzza maga felé stb. Az egész csoport úgyszólván „össze van ragadva”. Másfelől, a részecskék nem préselődnek egymásba. Ha megpróbálnánk valamelyik kettőt szorosan egymáshoz préselni, akkor eltaszítanák egymást.
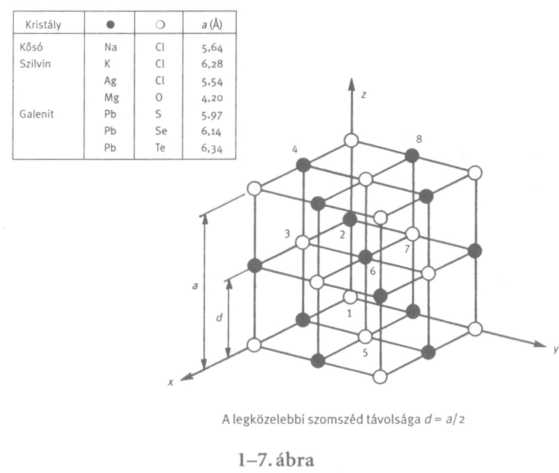
Az atomok sugara 1-szer vagy 2-szer 10-8 cm. A 10-8 centiméteres távolságot angströmnek (Á) nevezik, azt is mondhatjuk tehát, hogy sugaruk 1 vagy 2 angström. Méretüket másképpen is megjegyezhetjük: ha egy almát felnagyítanánk a Föld méretére, akkor az almabeli atomok nagyjából akkorák lennének, mint az alma volt felnagyítása előtt.
Most képzeljük el ezt a hatalmas vízcseppet tömérdek ide-oda mozgó, egymáshoz tapadó, fogócskázó részecskéjével. A víz megtartja térfogatát, nem esik szét, mert a molekulák vonzzák egymást. Ha a csepp egy lejtőn volna, s ott egyik helyről a másikra mozdulhatna, akkor folyni kezdene, de a molekulák vonzása jóvoltából így sem tűnne el - a dolgok nem szoktak szétfolyni.

Ez az ide-oda mozgás pedig a hő: ha növeljük a hőmérsékletet, akkor a mozgás hevesebbé válik. Ha melegítjük a vizet, erőteljesebb lesz az ide-oda mozgás, megnő az atomok közötti térfogat, s ha folytatjuk a melegítést, akkor egyszer csak elérkezik egy olyan pillanat, amelyben a molekulák közötti vonzás már nem elegendő a molekulák összetartására: a molekulák szétrepülnek, elkülönülnek egymástól. Ez a módja a vízgőzfejlesztésnek; a részecskék a hevesebb mozgás következményeképpen szétrepülnek.
Az 1-2. ábrán gőzt láthatunk. Ez a kép azonban bizonyos tekintetben torz: közönséges légköri nyomáson egy egész szobában is csak néhány gőzmolekula van, vagyis az ábrának megfelelő területre bizonyosan nem jutna három. Az ilyen méretű téglalapok legtöbbjére egyetlenegy sem juthatna; ábránkon történetesen kettő és fél van vagy három (csak hogy ne legyen teljesen üres). A gőz jellegzetes molekuláit tisztábban kivehetjük, mint a vízéit. Az egyszerűség kedvéért úgy rajzoltuk őket, hogy a hidrogénatomok 120°-os szöget zárjanak be egymással, de a valóságban ennek a szögnek csak 105° 3' a nagysága. A hidrogénatom és az oxigénatom középpontja között pedig 0,957 Á a távolság, ezt a molekulát tehát igen jól ismerjük.
Lássuk most a gőznek vagy valamely más gáznak néhány tulajdonságát. A molekulák, egymástól elkülönültek lévén, neki fognak ütközni a falaknak. Képzeljünk el egy szobát, és benne mondjuk száz, örökösen mozgó, ide-oda pattogó teniszlabdát. Ahogyan bombázzák a falat, odébb is lökik. (Nekünk persze vissza kell nyomnunk ezt a falat.) Ebből az következik, hogy a gáz szeszélyesen változó nagyságú erővel hat a falra, de annak a mi durva érzékeink (hiszen magunkat nem nagyítottuk fel milliárdszorosra) csak az átlagát észlelik, mint átlagos tolóerőt. A gázt csak nyomással tarthatjuk meg valamilyen véges térfogatban. Az 1-3. ábra egy gázok tárolására szolgáló szokásos edényt ábrázol (ilyet látni az összes tankönyvben): egy dugattyús hengert. Mivel nem fontos, hogy a vízmolekuláknak milyen az alakjuk, az egyszerűség kedvéért teniszlabdáknak vagy kis pontocskáknak rajzoltuk őket. Ezek a pontok örökösen mozgásban vannak, s minden irányban mozoghatnak. Mivel minden pillanatban sok ilyen pont ütközik neki a felső dugattyúnak, azért a dugattyút bizonyos erővel - ezt nyomásnak nevezzük, jóllehet az erő a nyomás és a terület szorzata - szakadatlanul lefelé kell nyomnunk, különben ez az állandó lökdösődés kinyomná a dugattyút a hengerből. Ez az erő nyilván arányos a felülettel, hiszen ha megnöveljük a területet, de a molekulák köbcentiméterenkénti számát változatlanul hagyjuk, akkor a dugattyúba való ütközések száma ugyanakkora arányban fog növekedni, mint a terület.
Most pedig tegyünk kétszer annyi molekulát az edénybe - vagyis duplázzuk meg a gáz sűrűségét -, a sebességüket, vagyis a hőmérsékletüket azonban ne változtassuk meg. Ekkor az ütközések száma jó közelítéssel megkétszereződik, és mivel minden ilyen ütközés éppoly „energikus” lesz, mint korábban, azért a nyomás arányos a sűrűséggel. Ha figyelembe vennénk az atomok közötti erők tényleges természetét, akkor a nyomásban egyfelől némi csökkenésre számíthatnánk az atomok közötti vonzás miatt, másfelől némi növekedésre, az atomok elfoglalta véges nagyságú térfogat miatt. Igen jó közelítéssel mégis igaz, hogy a nyomás arányos a sűrűséggel, ha a sűrűség elég kicsiny, vagyis ha nem túl nagy az atomok száma.
Láthatunk valami mást is: ha változatlanul tartjuk a gáz sűrűségét, a hőmérsékletét azonban megnöveljük - vagyis gyorsabbá tesszük az atomokat -, akkor mi történik vajon a nyomással? Az atomok ilyenkor hevesebben fognak egymásba és a falba ütközni, mivel gyorsabban mozognak, sőt gyakrabban is fognak ütközni, a nyomás tehát megnő. Láthatjuk, hogy milyen egyszerűek az atomelmélet eszmefuttatásai.
Vegyünk egy másik helyzetet. Tegyük fel, hogy a dugattyú befelé mozog, így az atomok lassan kisebb térfogatba szorulnak. Mi történik, ha egy atom nekiütközik a mozgó dugattyúnak? Nyilvánvalóan sebességet nyer az ütközésből. Ezt kipróbálhatjuk például egy mozgó deszkalapról visszapattanó pingponglabdával: nagyobb sebességgel fog visszapattanni, mint amekkorával a deszkának ütközött. (Egy különleges példa: ha a dugattyú meglök egy nyugvó atomot, az bizonyára mozgásba jön.) Az atomok tehát „melegebbek” lesznek a dugattyúról való visszapattanás után, mint voltak előtte. Ezért az edényben levő valamennyi atomnak nagyobb lesz a sebessége. Ez azt jelenti, hogy ha lassan összenyomunk egy gázt, akkor annak emelkedni fog a hőmérséklete. Lassú összenyomáskor tehát növekszik a gáz hőmérséklete, lassú kiterjeszkedéskor pedig csökken.
Térjünk most vissza vízcseppünkhöz, és nézzük másfelől. Tegyük fel, hogy csökkentjük a hőmérsékletét. Tegyük fel azt is, hogy a molekulák ide-oda mozgása a vízben fokról fokra szelídül. Tudjuk, hogy az atomok között vonzóerők hatnak, bizonyos idő után tehát már nem mozoghatnak olyan virgoncan. Az 1-4. ábra mutatja, hogy mi történik, ha a hőmérséklet igen mélyre száll: a molekulák új alakzatba fogódnak be: ez a jég. A jégnek ez a sematikus képe csak kétdimenziós, ennyiben tehát helytelen, minőségileg azonban helyes. Ebben az alakzatban az az érdekes, hogy minden atomnak meghatározott helye van benne, és könnyen átláthatjuk, hogy ha cseppünk egyik végén valamennyi atomot így vagy úgy valamilyen elrendezésben, meghatározott helyen tarthatnánk, akkor a kapcsolódások merev szerkezete folytán a (felnagyított skálán) mérföldekre levő másik végnek is pontosan meg lenne határozva a helye.
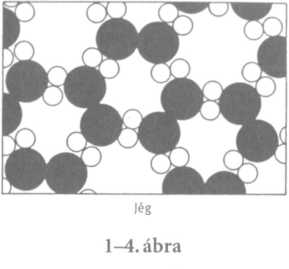
Ha tehát egy jégcsapot megfogunk az egyik végén, akkor a másik vége ellenáll minden félretolásnak, nem úgy, mint a folyékony víz: annak a szerkezete az élénk ide-oda mozgásban felbomlik, és az atomok mind más-más irányban mozognak. A szilárd testek és a folyadékok között tehát az a különbség, hogy a szilárd testben az atomok valamilyen alakzatban - kristályszerkezetben - vannak elrendeződve, és még nagy távolságban sem véletlenszerű a helyzetük: a kristály egyik végén levő atomok helyzete meghatározza a kristály másik végén, milliónyi atommal odább levő atomok helyzetét. Az 1-4. ábra egy kiagyalt kristályszerkezetet mutat be, s bár sokat helyesen ábrázol a jég sajátságai közül, a jégnek nem ez a tényleges szerkezete. Az egyik ilyen helyesen visszaadott vonás a szimmetria: a jég hatszöges (hexagonális) szimmetriája. Látható, hogy ha az ábrát megfelelő tengely körül 120°-kal elforgatjuk, akkor visszakapjuk az eredeti képet. A jégnek ez a szimmetriája magyarázza a hópelyhek hatszögletű formáját is. Az 1-4. ábráról az is leolvasható, hogy miért húzódik össze a jég olvadáskor. Az itt felrajzolt kristályszerkezetben sok a „lyuk”, akárcsak a jég tényleges szerkezetében. Amikor a szervezettség felbomlik, akkor a molekulák ezekbe a lyukakba is beülhetnek. A legtöbb egyszerű anyag, a vizet és betűfémet leszámítva, olvadáskor kitágul, mivel az atomok a szilárd anyag kristályában szorosan töltik ki a teret, s az olvadás után több hely kell nekik az ide-oda mozgáshoz; az üreges szerkezet azonban összeomlik, mint a vízjégé.
A jégnek „merev” kristályformája van ugyan, de a hőmérséklete változhat - a jégben van hő. Ha akarjuk, meg is változtathatjuk ennek a hőnek a mennyiségét. Mit értsünk hőn a jégről szólva? Az atomok nincsenek nyugalomban, hanem ide-oda rezegnek. Ha tehát meghatározott rend - struktúra - van is a kristályszerkezetben, az atomok mind rezegnek a „helyükön”. Ahogyan növeljük a hőmérsékletet, egyre nagyobb és nagyobb kitéréssel rezegnek, egészen addig, amíg ki nem rázódnak a helyükből. Ezt mondjuk olvadásnak. Ha csökkentjük a hőmérsékletet, a rezgés is visszább szorul, mindaddig, amíg - az abszolút zérusponton - ez a rezgés a lehető legkisebb mértékűre szelídül, de akkor sem szűnik meg, nem válik nullává. Az atomoknak ez a lehetséges legkisebb mozgása nem elég ahhoz, hogy olvadt állapotban tartsa az anyagot, az egyetlen hélium kivételével. A héliumban addig enyhül az atomok mozgása, ameddig lehetséges, de még ez az abszolút zérusponti mozgás is hevesebb, semhogy a hélium megfagyhatna. A hélium tehát még az abszolút zérusponton sem fagy meg, hacsak akkorára nem növeljük a nyomást, hogy az atomjai összepréselődjenek. Ha kellően naggyá tesszük a nyomást, akkor megszilárdíthatjuk a héliumot is.
Ennyit a szilárd, folyékony és légnemű testek atomi szempontból való leírásáról. Az atomhipotézis azonban folyamatokat is leír; lássunk tehát most néhány folyamatot atomi szempontból. Az első ilyen folyamat a víz felszínével függ össze. Mi történik a víz felszínén? Ezúttal kissé bonyolítjuk a képet - egyszersmind valószerűbbé tesszük -, éspedig azzal, hogy levegővel érintkező vízfelszínt gondolunk el. Az 1-5. ábrán ilyen vízfelszínt láthatunk. Ezen vannak vízmolekulák, mint az eddigi képeken, de rajta van a vízfelszín is. A felszín felett több minden látszik; először is olyan vízmolekulák, mint a gőzben. Ez a folyékony víz felett mindig ott levő vízpára. (A vízpára és a víz egyensúlyban van egymással; erről később még beszélünk.)
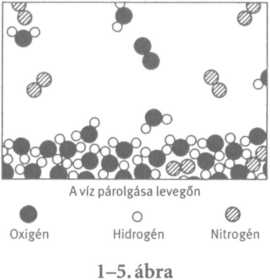
A vízfelszín felett vannak további molekulák is: egy oxigénmolekula - két egymáshoz tapadt oxigénatom - és két nitrogénmolekula - két-két egymáshoz tapadt nitrogénatom. A levegő szinte csak nitrogénből, oxigénből, valamennyi vízgőzből és kisebb mennyiségben szén-dioxidból, argonból meg néhány egyéb anyagból áll. A vízfelszín felett tehát levegő van, vagyis egy némi vízgőzt is tartalmazó gáz. Mi történik ezen az ábrán? A molekulák a vízben állandóan ide-oda mozognak. Időről időre előfordul, hogy a felszín közelében valamelyik kissé erősebb lökést kap a szokásosnál, és kirepül. Ezt persze nemigen lehet látni az ábrán, hiszen az csak állókép. De elképzelhetjük, hogy az egyik molekula a felszín közelében meglökődött és kirepül, sőt egy másik is annyira megütődött, hogy az is kirepül. A víz molekulái tehát egyre fogynak, mígnem a víz eltűnik: elpárolog. De ha az edény száját lezárjuk, akkor egy idő múlva nagyon sok vízmolekulát fogunk találni a levegő molekulái között. Időről időre egy-egy páramolekula lefelé repül, és ismét befogódik a vízbe. Látjuk tehát, hogy ami élettelennek tűnik, az valójában érdekes dolog - egy lezárt szájú üvegben talán már húsz éve álló víz érdekes, dinamikus, soha meg nem szűnő folyamat színtere. Látszatra - tökéletlen emberi szemmel nézve - semmi sem változik, de ha a vizet milliárdszoros nagyításban néznénk, azt látnánk, hogy a vízben bizony szakadatlan a változás: molekulák hagyják el a felszínt, és molekulák térnek vissza a felszín alá.
Mi vajon miért nem látunk semmi változást? Azért, mert ugyanannyi molekula távozik, amennyi visszatér. Hosszú távon „semmi sem történik”.
Ám ha levesszük az edény fedelét, és elfújjuk a nedves levegőt, vagyis száraz levegőt engedünk a helyébe, akkor az elpárolgó molekulák száma ugyanannyi lesz, mint volt, mert az a vízmolekulák mozgásától függ, a visszatérők száma viszont erősen csökkenni fog, mivel sokkal kevesebb vízmolekula marad a vízfelszín felett. Több molekula távozik tehát, mint ahány visszatér, a víz ilyenformán elpárolog. Ha tehát vizet akarunk párologtatni, akkor kapcsoljuk be a ventilátort!
És most megint valami más: mely molekulák távoznak? Csak az a molekula távozhat el, amelyiknek a véletlen jóvoltából valamivel több energia jut annál, amennyi a szomszédos molekulák vonzásából való kiszakadáshoz kell. S mivel ilyenformán a távozóknak az átlagosnál nagyobb az energiájuk, azért a visszamaradok mozgása átlagban kevésbé heves lesz, mint volt. A párolgó folyadék tehát fokozatosan lehűl. Persze ha egy gőzmolekula a levegőből a víz felé tart, nagy vonzóerő hat rá, amint a vízfelszín közelébe kerül. Ez felgyorsítja a vízbe jutó molekulát, és hőtermeléssel jár. Vagyis a molekulák kilépéskor hőt visznek magukkal, visszatéréskor pedig hőt termelnek. Természetesen, ha nincs tényleges párolgás, akkor a víz hőmérséklete nem változik. Ha fújjuk a vizet, hogy folyamatosan túlsúlyban tartsuk a távozó molekulákat, akkor a folyadék hűlni fog. Fújjuk tehát a levest, ha hűteni akarjuk!
Be kell látnunk azonban, hogy az eddig említett folyamatok bonyolultabbak, mint leírtuk őket.
Nemcsak a vízmolekulák lépnek ki a levegőbe; időről időre oxigén- vagy nitrogénmolekulák is leszállnak a vízfelszínre, „belevesznek” a vízmolekulák tömegébe, és utat törnek maguknak közöttük. Más szóval, a levegő feloldódik a vízben; az oxigén-és nitrogénmolekulák utat találnak maguknak, és a vízbe levegő kerül. Ha az edényből hirtelen kiszivattyúzzuk a levegőt, akkor a vízbeli levegőmolekulák gyorsabban távoznak, mint ahogyan a levegőbeliek belépnek a vízbe, s ettől buborékok támadnak. Ez, mint talán tudják, sokat árthat a búvároknak.
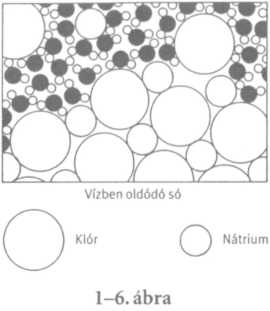
Most egy újabb folyamattal fogunk foglalkozni. Az 1-6. ábrán azt láthatjuk, hogyan fest atomi szempontból egy szilárd test oldódása a vízben. Mi történik, ha vízbe teszünk egy sókristályt? A só szilárd test, kristály, „sóatomok” szabályos elrendeződése. Az 1-7. ábra szemlélteti a konyhasó - a nátrium-klorid - háromdimenziós szerkezetét. Szigorúan véve, ez a kristály nem atomokból épül fel, hanem ionnak nevezett összetevőkből.
Az ion olyan atom, amely szerzett néhány további elektront vagy elvesztett néhányat. A sókristályban kloridionokat találunk (egy fölös elektront szerzett klóratomokat) és nátriumionokat (egy elektronjukat vesztett nátriumatomokat). A szilárd sóban az ionokat összetartja az elektromos vonzóerő, de ha a sót vízbe tesszük, akkor a negatív oxigén és a pozitív hidrogén vonzásának hatására az ionok némelyike kiszabadul. Az 1-6. ábrán éppen egy kloridiont látunk önállósulni, más atomokat pedig már ionokként úszkálni a vízben. Ez az ábra meglehetős gonddal készült. Észrevehetik például, hogy a vízmolekulák hidrogénvégei inkább a klórionok közelében vannak, az oxigénes végük meg inkább a nátriumionok közelében, mivel a nátrium pozitív, a vízmolekula oxigénvége pedig negatív, tehát vonzzák egymást. Vajon az ábrából kiderül-e, hogy a só most éppen oldódik-e vagy átlép a vízből a kristályba? Nem, ezt senki sem tudja megmondani, hiszen némely atom elhagyja a kristályt, mások ez idő alatt visszatérnek a kristályba. Ez is dinamikus folyamat, mint a párolgás, és az iránya attól függ, hogy a vízben több vagy kevesebb só van-e az egyensúlyi állapothoz szükségesnél. Egyensúlyi állapoton azt a helyzetet értjük, amelyben a távozó atomok távozásának üteme megegyezik a visszatérők visszatérésének ütemével. Ha szinte semmi só nincs a vízben, akkor több atom távozik, mint ahány visszatér, a só tehát feloldódik. Ha meg túl sok a „sóatom”, akkor több tér vissza, mint távozik, és a só kikristályosodik.
Mellesleg megemlítjük, hogy a valamely anyag molekulájának a fogalma csak közelítés, és csupán bizonyosfajta anyagokra nézve van értelme. Ami a vizet illeti, világos, hogy a három atom csakugyan összetartozik, de a szilárd nátrium-kloriddal már nem ilyen egyszerű a helyzet. Az csupán nátrium- és kloridionok kocka alakú elrendeződése, s ezeket az ionokat nem lehet semmiféle természetes módon „sómolekulákká” összepárosítani.
Az oldódáshoz és kicsapódáshoz visszatérve, ha növeljük a sóoldat hőmérsékletét, akkor növekszik az atomok távozásának üteme, de növekszik a visszatérésüké is. Általában igen nehéz megjósolni, hogy melyik kerekedik a másik fölébe: hogy több vagy kevesebb szilárd anyag fog-e feloldódni? Magasabb hőmérsékleten a legtöbb anyag jobban oldódik, más anyagok meg kevésbé.
Az eddig tárgyalt folyamatokban az atomok és ionok nem cseréltek partnert, holott természetesen vannak olyan körülmények, amelyek között megváltozik az atomok kombinációja, s új molekulák keletkeznek. Ezt szemlélteti az 1-8. ábra. Az atomi partnerek átrendeződésének folyamatát kémiai reakciónak nevezzük. Az eddig leírt folyamatokat fizikai folyamatoknak mondjuk, bár a kettő között nincs éles különbség. (A természet nem törődik vele, mit hogyan nevezünk, csak teszi a magáét.) Ezzel az ábrával a szén oxigénben való égését igyekeztünk bemutatni. Az oxigénben két-két oxigénatom tapad igen szorosan egymáshoz. (S vajon miért nem három, vagy, mondjuk, négy? Ez igen különös vonásuk az ilyen atomi folyamatoknak. Az atomok rém furcsák: bizonyos partnereket, irányokat stb. jobban kedvelnek, mint a többit. A fizika dolga, hogy kielemezze, miért akarja mindegyik azt, amit akar. Akárhogy s mint, annyi bizonyos, hogy két oxigénatom alkot molekulát - boldogan, mindkét fél megelégedésére.)
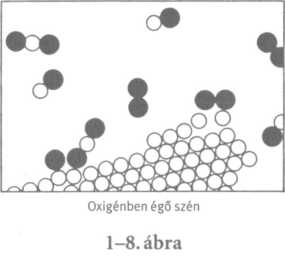
Tegyük fel, hogy a szén szilárd kristályként van jelen (grafit vagy gyémánt formájában4). Mármost például az egyik oxigénmolekula beleütközhet a szénbe, két oxigénatomja felkaphat egy-egy szénatomot, és tovarepül ebben az új „szén-oxigén” kombinációban: a szén-monoxid nevű gáz molekulájában. Ennek CO a kémiai képlete, s ez nagyon egyszerű: a „CO” betűpáros gyakorlatilag a molekula képe. A szén azonban sokkal erősebben vonzza az oxigént, mint az oxigén az oxigént, vagy a szén a szenet. Ezért lehet, hogy az oxigén csak kis energiával lép be ebbe a folyamatba, de olyan hevesen egyesül a szénnel, hogy a közelükben mindennek jut az energiából. Ilyenkor tehát rengeteg mozgási energia, más szóval kinetikus energia fejlődik. Ez a folyamat persze az égés; az oxigén és szén egyesüléséből hőt kapunk. A hő rendszerint molekuláris mozgásként van jelen a forró gázban, de bizonyos körülmények között olyan nagy mennyiségű lehet, hogy fényt kelt. Így lobban a láng.
Tetejébe a szén-monoxid nem túlságosan „elégedett”. Még egy oxigénatom kapcsolódhat ugyanis hozzá, s így végbemehet egy jóval bonyolultabb reakció: abban az oxigén hozzákapcsolódik a szénhez, egyszersmind beleütközhet egy szén-monoxid molekulába. Egy oxigénatom hozzákapcsolódhat a CO-hoz, és végül egy egyetlen szénatomból és két oxigénatomból álló molekulát alkotnak; ennek C02 a képlete és szén-dioxid a neve. Ha a szenet igen gyors reakcióval nagyon kevés oxigénben égetjük el (például egy gépkocsi motorjában; ott olyan rövid idő alatt zajlik le a robbanás, hogy nincs elég idő szén-dioxid keletkezésére), akkor sok szén-monoxid keletkezik. Az ilyen átrendeződések közül jó néhányban nagy mennyiségű energia bocsátódik ki, robbanásban, lángok formájában stb., a reakció milyensége szerint. A vegyészek tanulmányozták az ilyesfajta atomelrendeződéseket, és arra jutottak, hogy minden anyag ilyen vagy olyan atomelrendeződés.
Ennek a gondolatnak a szemléltetésére vegyünk egy másik példát. Ha ibolyákkal teli réten járunk, akkor tudjuk, hogy „mi ez az illat”. Ez valamilyen, az orrunkig elhatolt molekula, vagyis atomcsoport. Először is, hogyan keveredett az orrunkig? Eléggé könnyedén. Ha az illat valamilyen, a levegőben ide-oda mozgó, erre-arra vetődő molekula, akkor alighanem véletlenül jutott az orrunkba. Bizonyára nem külön elhatározással szállt éppen az orrunkba. Ez a molekula tehetetlen részecskéje csupán a molekulák lökdösődő tömegének, és céltalan vándorlása közben éppen ennek az anyagdarabkának sikerült az orrunkig jutnia.

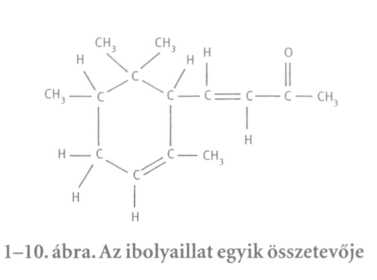
Ma a vegyészek foghatnak egy ilyen sajátságos molekulát, mint az ibolya illata, elemezhetik, és megmondhatják, hogy a molekulát alkotó atomok hogyan helyezkednek el a térben. Tudjuk, hogy a szén-dioxid molekula egyenes és szimmetrikus: O-C-O. (Ezt fizikai módszerekkel is könnyű megállapítani.) De hosszas detektívmunkával még az atomok sokkalta bonyolultabb - s a kémiában nem ritka - elrendezéseiről is kideríthető, hogy mi bennük az atomok rendje. Az 1-9. ábra azt mutatja, hogy milyen a levegő egy ibolya környezetében; ezen is látunk nitrogént és oxigént, meg vízgőzt. (Vízgőzt vajon miért? Azért, mert az ibolya nedves. Minden növény párologtat.) S látni a képen egy „szörnyet” is: szén-, hidrogén- és oxigénatomokat, különös alakzatba rendeződve. Ez jóval bonyolultabb alakzat, mint a szén-dioxidé; voltaképpen igen-igen bonyolult. Sajnos, nem rajzolhatjuk le mindazt, amit tudunk róla a kémiában, mivel ma már tudjuk, hogy pontosan hogyan rendeződnek el a térben az atomjai, de az ábrának csak két dimenziója van. A hat szénatom nem síkbeli, hanem „redős”, térbeli gyűrűt alkot, s ebben a gyűrűben ismerjük az összes távolságot és szöget. A kémiai képlet tehát csupán kép a molekuláról. Ha a vegyész ilyesmit ír fel a táblára, akkor megpróbál két dimenzióban „rajzolni”. Látunk például egy hat szénatomból álló „gyűrűt” és egy, a gyűrűről lelógó „szénláncot”; a lánc utolsó előtti szénatomján egy oxigént, az utolsón három hidrogént, amonnan meg két szenet kiállni, három-három hidrogénnel s más hasonlókat.
Hogyan deríti ki a vegyész az atomok elrendeződését? Összekever üvegekbe öntött anyagokat, és ha azok vörös színűek lesznek, akkor abból már tudja, hogy itt meg itt egy hidrogén és két szén van összekapcsolódva; ha meg kékek lesznek, akkor csak annyit tud, hogy nem. Ez a szerves kémia: az egyik legfantasztikusabb nyomozói munka. A vegyész megfigyeli, mi történik két anyag vegyítésekor, hogy felismerhesse az atomok elrendeződését ezekben a roppant bonyolult alakzatokban. A fizikus soha nem hitte el igazán, hogy a vegyész tudná, miről beszél az atomok elrendeződéséről szólva. Nagyjából húsz éve azonban sikerült fizikai módszerrel is megvizsgálni ilyesfajta molekulákat (igaz, nem ennyire bonyolultakat, de olyanokat, amelyek ennek részét alkották), és ezzel sikerült meghatározni mindegyik atom helyét, nem színek megfigyelésével, hanem az atomok tényleges helyzetének megmérésével És lám, a vegyészeknek szinte mindig igazuk volt!
Mint végül is kiderült, az ibolya illatát három, egymástól valamelyest eltérő molekula alkotja, s a három a hidrogénatomok elhelyezkedésében különbözik egymástól.
A kémiának az anyagok megnevezése az egyik nehézsége: olyan nevet adni az anyagoknak, amelyből tudni lehet, hogy miből állnak. Keressünk nevet erre a molekulaformára! A névnek nemcsak a vegyület formáját kell megadnia, hanem azt is, hogy itt van egy oxigénatom, ott van egy hidrogén: azt tehát, hogy mi hol van. Meg kell tehát értenünk, hogy a teljességre való törekvés miatt a kémiai elnevezések bizony bonyolultak. Az 1-10. ábrán látható vegyület neve, a 4-(2,2,3,6--tetrametil-5-ciklohexil)-3-butén-2-on leírja a molekula szerkezetét is. Átérezhetjük a vegyészek nehézségeit, és megérthetjük, hogy miért adnak ilyen hosszú neveket a vegyületeknek. Nem azért, mert homályba akarnának burkolózni, hanem mert nagyon nehéz feladat szóval leírni a molekula összetételét és szerkezetét!
Honnan tudjuk, hogy léteznek atomok? A korábban említett egyik fogás révén: elfogadjuk azt a hipotézist (feltevést), hogy léteznek, és ebből sorozatos következtetésekre jutunk arról, hogy mit kell tapasztalnunk akkor, ha a dolgok csakugyan atomokból állnak. De van ennél valamivel közvetlenebb bizonyíték is a létezésükre; például a következő. Az atomok olyan kicsinyek, hogy fénymikroszkóppal sem lehet látni őket, sőt elektronmikroszkóppal sem. (A fénymikroszkóppal csak a náluknál jóval nagyobb dolgokat lehet látni.)
Mármost ha az atomok -mondjuk, a vízben - szakadatlanul mozgásban vannak, és valami nagy - az atomoknál jóval nagyobb - labdát teszünk a vízbe, akkor ez a labda ide-oda fog vetődni, éppen úgy, mint a labdalökdöső játékban: amikor sok ember lökdös egy óriási labdát. Az egyik ember erre tolja a labdát, a másik arra, és a labda ettől teljesen szabálytalanul mozog ide-oda a pályán. Éppígy ez a mi „óriáslabdánk” is ide-oda lódul az őt más-más irányokból érő, s pillanatról pillanatra változó egyenetlen ütközésektől. Ha egy kitűnő mikroszkópban vízben lebegő, igen kicsi részecskéket (kolloidokat) figyelünk meg, azt látjuk, hogy ezek a részecskék - az atomoktól állandóan bombázva - szakadatlanul mozgásban vannak. Ezt a mozgást Brown-mozgásnak nevezik.
A kristályok szerkezetében újabb bizonyítékot találhatunk az atomok létezésére. A röntgensugaras elemzéssel kikövetkeztetett struktúrák sok esetben megegyeznek a természetben fellelhető kristályok térbeli „alakjával”. A kristálylapok közötti szögek ívmásodpercnyi pontossággal megegyeznek azokkal a szögértékekkel, amelyeket abból a feltevésből következtettek ki, hogy a kristály igen sok atomrétegből áll.
Minden atomokból épül fel. Ez az alapfeltevésünk. A biológiának például az a legfontosabb feltevése, hogy amit az állatok cselekszenek, az mind az atomok műve. Más szóval: az élőlények nem cselekszenek semmi olyasmit, amit ne lehetne megérteni abból a feltevésből, hogy ők is a fizikai törvényeknek alávetett atomokból állnak. Volt idő, amikor ezt még nem ismerték el; az idáig jutáshoz szükség volt kísérletekre és elméleti munkákra, mára azonban elfogadott elvvé vált, és a biológia területén a leghasznosabb forrás az új eszmék létrejöttéhez.
Ha egy egymással szomszédos atomokból álló acél- vagy sódarabnak ilyen érdekes tulajdonságai lehetnek; ha az ezekből az apró cseppecskékből álló, sok-sok mérföldön át egyforma vízből hullám és hab lehet, s ez a víz robajló hangot hallathat és különös alakot ölthet; ha mindez, ha az áramlatok élete sem más, mint atomok roppant sokasága, akkor mi minden lehetséges még? Ha az atomokat nem valamiféle meghatározott szerkezetbe rendeznénk - újra meg újra ugyanazt ismételve - s nem is olyasfajta kis bonyolult halmazokba, mint az ibolya illata, hanem helyről helyre más, más-más összetételű, sokféleképpen felépülő, folyamatosan változó, sohasem ismétlődő rendszerbe, akkor az mennyivel csodálatosabban viselkedhetne? Lehetséges, hogy ez az önök előtt ide-oda sétáló, önökhöz beszélő „valami” tenger sok atomnak annyira bonyolult elrendeződése, hogy elképzelni sem tudjuk, mi telhet ki tőle? Ha azt mondjuk, hogy egy-egy atomhalmaz vagyunk, azzal nem azt állítjuk, hogy pusztán atomok halmaza lennénk, hiszen nem ismétlődő atomok halmazában jelen lehetnek olyan lehetőségek, amilyeneket az ember a tükörbe nézve láthat.
MÁSODIK ELŐADÁS
Vagyis a Kaliforniai Műegyetemen (California Institute of Technology).
Magyarul Mai fizika címmel adták ki, 9 kötetben (Műszaki Könyvkiadó, 1985)
A Feynman-féle Előadások eredeti kiadása három vörös borítójú kötetben jelent meg.
A gyémántot is el lehet égetni a levegőben.