Írta
ATHENAEUM IRODALMI ÉS NYOMDAI R.-T. KIADÁSA, BUDAPEST
Könyvem megírásánál kétféle olvasóközönségre gondoltam. Egyrészt azokra, akik a középiskola felső évfolyamait még nem végezték el, de érdeklődnek a fizika iránt és az alapfogalmakkal és főbb jelenségekkel tisztába szeretnének jönni. Másrészt azokat tartottam szemem előtt, akiket az élet a fizikától messze sodort, elfeledték már az iskolában tanultakat, de érdeklődésük megmaradt és matematikai segédeszközök nélkül kívánják tudásvágyukat kielégíteni. Hangsúlyozni akarom, hogy nem tankönyvet írtam, az anyag kiválasztásában, elrendezésében és feldolgozásában messze eltértem attól, amit tankönyveink nyújtani szoktak. Mindazt, ami a művelt közönséget a fizikából érdekelheti és aminek tárgyalása nem megy túl a kitűzött célon, felvettem könyvembe. A tárgyalt anyagot pedig igyekeztem úgy elrendezni, hogy az egyes részletek összefüggése kidomborodjék. A fizika ugyanis nem különálló tapasztalatok és törvények halmaza. A fizika tulajdonképpen csak akkor kezdődik, amikor a részek összefüggését keressük, ezért helyeztem súlyt arra, hogy a kapcsolatot mindenütt megér ezt essem. Így a mechanikai kérdések középpontjába a súlyt helyeztem és ezt az egész kört e mindennapi fogalom köré csoportosítottam. Az összes rezgésjelenségeket ugyanebből a célból összefüggően tárgyaltam. Általában könyvemmel népszerűsíteni akartam a fizikát a nélkül, hogy lealacsonyítanám.
A jelenségek szemléltetésére lehetőleg egyszerű kísérleteket választottam. Hiszem, hogy különösen fiatal olvasóim nem egy kísérletet maguk is végre fognak hajtani.
Abban a reményben bocsátom közzé könyvemet, hogy ezen a módon is sikerül hozzájárulnom a fizikai ismeretek terjesztéséhez.
Ha valaki fizikai könyvet kezd olvasni, joggal kérdezheti, milyen kérdésekre kap feleletet. Érzékeink útján a körülöttünk levő testek állandó változásáról szerzünk tudomást. Ha a kezemben levő követ elengedem, ez leesik. Ha fémpálcát melegítek, ez kitágul. A tükörre eső fény visszaverődik. A mágnes a közelében levő vasdarabot magához vonzza. A vas a nedves levegőn megrozsdásodik stb. Az élettelen testek jelenségein a fizika és a kémia osztozik. A fizika körébe olyan jelenségek tartoznak, amelyek nem járnak az anyag minőségének megváltozásával. Ilyen pl. az esés, a pálca kitágulása, a mágneses vonzás s í. t. Ellenben a rozsdásodás kémiai folyamat. De evvel nem vontunk éles határt a természettudományoknak e két nagy ága közt. Így az elektromos áram tulajdonságainak és hatásainak vizsgálata a fizika feladata. De az elektromos áramnak vegyi hatása is van, ennek vizsgálatát egyenlő joggal sorolhatjuk akár a fizika, akár a kémia körébe.
A jelenségek puszta leírásával a fizika feladata korántsem merült ki. Az egyes jelenségeket nem szabad különállóknak tekintenünk, hanem összefüggéseket kell köztük keresnünk. A tudománynak egészen kezdetleges kora volt az, amelyben egyes jelenségek leírásával megelégedtek. Szigorúan véve a fizika csak akkor kezdődött, amikor az összefüggések kéresésének, a rendszerezésnek munkája megindult. Ma az összes természettudományok közül ebben a tekintetben a fizika haladt legmesszebb előre. Ha tehát a fizikának helyes képét akarjuk nyerni, az egyes részek kapcsolatát mindenütt kellően ki kell domborítanunk.
Céljának elérésében a fizika legfőbb eszközei a megfigyelés és kísérletezés. Sok jelenséget csak abban az alakban lehet vizsgálni, ahogyan a természet nyújtja. Ez a megfigyelés, így a csillagász majdnem egyedül erre az eszközre van utalva. De a természeti jelenségek rendesen igen bonyolultak, sokféle oknak hatása egyszerre mutatkozik. Ezért a fizikus egyszerűbb jelenségeket állít elő laboratóriumában, maga szabja meg a feltételeket, amelyek közt a jelenség végbemegy. Az egyes okok hatását elkülöníti és így vizsgálatukat egyszerűsíti. Ez a kísérletezés. Végül a megfigyelő és kísérletező munkáját betetőzi az a feladat, hogy a megismert tényekből következtetéseket vonjunk le, a megismert tényekben rejlő törvényszerűségekét felismerjük.
Elsősorban azokat a jelenségeket akarjuk megismerni, amelyek minden testen egyaránt mutatkoznak.
Támasszunk alá könnyen görbíthető pálcát két végén és helyezzünk rá akármilyen testet, pl. kődarabot vagy könyvet. A pálca többé-kevésbbé lehajlik. Ha gumilabdára vagy szivacsra helyezünk egy testet, ezek összenyomódnak. Ha tenyeremre vasdarabot teszek, közvetlenül érzem a nyomást, amelyet a vas kifejt. Kössünk követ vagy akármilyen testet fonálra és függesszük fel a fonalat, akkor a kő kifeszíti, lefelé húzza a fonalat. Ez az egyszerű eszköz a függőón.
Mindezekben az egyszerű jelenségekben ugyanannak az erőnek hatása nyilvánul meg. Ez az erő a testek súlya. G a l i l e i-nek még külön kísérlettel kellett kimutatnia, hogy a levegőnek is van súlya. Ma már természetesnek találjuk, hogy minden testnek van súlya. Ez okozza, hogy a testek nyomják azt a lapot, amelyen nyugszanak és húzzák lefelé azt a testet (fonalat), amelyen függnek. A függőón kifeszített fonala a súly irányát is megmutatja. Ezt az irányt függőlegesnek nevezzük.
Engedjük el a kezünkben levő testet, akkor ez függőleges irányban esik. Tölcsért, melynek alsó végét ujjunkkal befogtuk, töltsünk meg vízzel. Ha ujjunkat elvesszük, a víz függőleges irányban ömlik ki. Ezekben a példákban a súlynak lefelé húzó hatását az alátámasztó lap vagy felfüggesztő fonal nem akadályozza, a súly mozgathatja a testet és pedig, mint látjuk, saját irányában, vagyis függőlegesen lefelé.
Ha azt látjuk, hogy minden test saját súlyának hatására függőlegesen lefelé esik, ennek okát is kérdezhetjük. A felelet nem nehéz : A Föld maga felé vonzza a testeket. A súly éppen az az erő, amellyel a Föld a testeket vonzza.
Hosszú volt az az út, amely eddig a megismerésig elvezetett. A kiinduló pont a bolygók mozgása volt. Erre nézve Kepler (1571—1630) tapasztalati úton három, a tudomány történetében igen fontos törvényt állított fel. Kepler a prágai csillagvizsgáló intézet vezetője volt. Itt készen kapta azokat az észleléseket, amelyeket előde, Tycho Brahe végzett. Ezekből a feljegyzésekből olvasta ki nevezetes törvényeit.
Kepler észrevette, hogy a bolygók pályája nem kör, hanem olyan ellipszis, melynek egyik gyújtópontjában van a Nap. Az ellipszis a körtől csak kevéssé tér el, vagyis a gyújtópont (1. ábra, N) közel van az ellipszis középpontjához. Aránylag könnyen találta meg Kepler a második törvényt is. Ha valamelyik bolygó középpontját képzeletben a Nap középpontjával összekötjük, a bolygó vezérsugarát kapjuk. S pontban a vezérsugár SN(ζ1), P pontban PN (ζ2). Ez a vezérsugár, mialatt a bolygó a Nap körüli pályáján kering, az ellipszis területét súrolja. Kepler törvénye szerint egyenlő időtartamok alatt a vezérsugár egyenlő területet súrol. E szerint az ANB és CND cikkek területe egyenlő, ha a bolygó az AB és CD íveket egyenlő idő alatt teszi meg.

1. ábra A bolygó pályája a Nap körül.
Kepler, akinek nagy lelkesedésén kívül szárnyaló fantáziája is volt, nem elégedett meg evvel a két törvénynyel, sejtette, hogy még más törvényszerűségnek is kell az észlelések közt rejtőznie. 11 évig tartó kutatás után végre sikerült ezt megtalálnia. Nagy elragadtatásában azt hitte, hogy a teremtés titkát fedezte fel. Ismeretes, hogy a bolygók különböző idő alatt futják be az ellipszist. A Föld 1 év alatt, a Jupiter 50 nap híján 12 év alatt, a Saturnus kereken 29,5 év alatt stb.
Azt is tudjuk, hogy a messzebb levő bolygó keringési ideje nagyobb. De ennél pontosabbak is lehetünk. Emeljük négyzetre a bolygó keringésidejét és köbre távolságát. Osszuk el a keringésidő négyzetét a távolság köbével. Ekkor minden bolygónál jó közelítéssel ugyanazt a számot kapjuk. Ez K e p l e r harmadik törvénye.
Ezeknek a törvényeknek segítségével arra a kérdésre is lehet felelni, milyen erővel vonzza a Nap maga felé a bolygókat. Ez a gondolatmenet egy ideig még a bolygókra korlátozva maradt. Newton (1642—1727) nagy szelleme kellett annak felismeréséhez, hogy az a vonzás, melyet a Nap a bolygókra gyakorol, csak speciális esete egy egész általános, minden testre kiterjedő törvénynek. Newton törvénye szerint bármely két test vonzza egymást és pedig annál nagyobb erővel, mennél nagyobbak a tömegek és annál kevésbé, mennél nagyobb a köztük levő távolság. Pontosabban a vonzóerő a távolság négyzetével fordítva arányos. Ennek értelme a következő. Az 1, 2, 3, 4, . . . számok négyzete l, 4, 9, 16, . . . Ha ugyanazt a két testet 2-szer, 3-szor, 4-szer, . . . nagyobb távolságban helyezzük el egymástól, akkor egymást 4-szer, 9-szer, 16-szor. . . kisebb erővel vonzzák.
A testeknek ez az egymásra gyakorolt vonzása a gravitáció.
Newton törvénye alapján az égitestek pályáját meg lehet határozni és így Newton a modern csillagászatnak is megalapítója. A Royal Society, melynek ülésén gravitációs törvényét előadta, ma is ereklyeként őrzi azt a táblát, melyre Newton törvényét felírta. Másrészt meg kell említenünk azt is, hogy már Kepler Astronomia nova című könyvében azt írja, hogy a gravitáció két test kölcsönös hatása egyesülés végett, sőt egészen helyesen az árapályt is a Hold vonzó hatásának tulajdonítja.
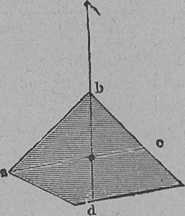
Ha asztalomra teszek két súlyt, a köztük fellépő vonzást aligha veszem észre. Ennek az az oka, hogy a vonzóerő kicsi, nem tudja legyőzni azt a súrlódást, amely a súlyok mozgásával szemben az asztalon fellép. De elég érzékeny berendezéssel a gravitáció szépen kimutatható. Ez az érzékeny eszköz a torziós inga. Vékony, rugalmas fémszálra (2. ábra) erősítsünk pálcát (p) úgy, hogy ez vízszintes legyen. A pálca két végén fémgömbök (aa) vannak. Ez a torziós inga akkor lesz nyugalomban, mikor a rugalmas szálnak semmiféle elcsavarodása (torziója) nincs. Helyezzünk most a gömbök mellé egy-egv nagyobb ólomgömböt (bb) úgy, mint ezt ábránk mutatja. Ezek a gömbök magukhoz vonzzák a torziós ingán levő gömböket, az inga a tömegvonzás folytán előbbi nyugalmi állapotából elcsavarodik.

2. ábra. A tömegvonzás kimutatása torziós ingával.
Az előbbiekben említett vonzás, amelyet a Föld gyakorol a testekre, az általános tömegvonzásnak egyik esete. Ez a gravitáció módot ad a Föld tömegének meghatározására is. A számításokból arra az eredményre jutottak, hogy a Föld tömege 5987xl018 tonna. Olyan szám ez, melyben 5987 után 18 zérus következik, tehát sokkal nagyobb szám, mint amelyet el tudunk képzelni.
A tömegnek ebből az értékéből viszont a Föld sűrűségére lehet következtetést vonni. A Föld, mint ismeretes, a sarkoknál belapult gömb. Sugara az egyenlítő felé 6378,2 km, a sarkok felé 6356,7 km. Ígv térfogatát ki lehet számítani. A Föld sűrűségére nézve pedig azt kapjuk, hogy átlag 1 dm3-nek tömege 5,5 kg. De ha a külső szilárd kéreg különböző helyein a sűrűséget közvetlenül megmérjük, középértékben 2,5-et kapunk, vagyis sokkal kevesebbet, mint az egész földgömb átlagos sűrűsége, 5,5. Ez csak úgy lehet, ha a Föld belső magja jóval sűrűbb anyagból áll. A mag sűrűsége 8,2. Ez a nagy érték valószínűvé teszi, hogy a Föld magja fém, talán vas, mert ennek sűrűsége van legközelebb 8,2-hez.
Báró Eötvös Loránd gravitációs mérései.
a) Tartsunk 20 filléres pénzdarabot két ujjunk közt vízszintesen és helyezzünk rá kis papírszeletet, mely egészen ráfér a pénzdarabra. Ha a pénzt elengedjük, a papírlap együtt esik vele. Ha ellenben a pénzt és a papírt egyszerre ugyan, de egymás mellett ejtjük, a papír visszamarad. A magyarázat egyszerű : A levegő a súrlódás folytán késlelteti minden test mozgását, mégpedig a papírét a kis súly miatt sokkal nagyobb mértékben, mint a pénzét. De mikor a papír a pénzen fekszik, az utóbbi eltolja a levegőt az útból. Ha tehát a papír a pénzzel együtt esik, ebből azt következtetjük, hogy a súly minden testet egyformán mozgat.
A súlynak ez a tulajdonsága ezt az erőt minden más erőtől megkülönbözteti. Ha erős mágnestől ugyanakkora távolságban egyszer 1 grammos vasdarabot, másodszor 2 gr vasat helyezek, a mágnes mind a kettőt magához rántja, de az 1 gr gyorsabban mozog, mint a 2 gramm. Általában, ha ugyanakkora erő két különböző tömegre hat, a nagyobb tömeg lassabban mozog. Egyedül a súly az az erő, amely minden testen egyforma mozgást létesít, a szabad esést.
Ezt a fontos tételt legpontosabban b r. Eötvös Lóránd (1848—1919) igazolta a torziós mérleggel (3. ábra), melynek érzékenységét hihetetlenül tudta fokozni. A esőalakú vízszintes rúd végén gömbök helyett két platinasúly (Pt) van, melyeket a csőbe be lehet dugni. A mérleget a légáramok elkerülése végett kettős falú fémdobozba zárta, amely éppen csak akkora, hogy az inga benne elfér és elfordulhat. Különös gondot igényel a rugalmas fonal helyes megválasztása. Akinek nincs gyakorlata ilyesféle laboratóriumi munkában, az nem is sejti, hogy ez milyen fontos és nehéz feladat. A fonalat még ma is az állami geofizikai intézet szakembereinek támogatásával készítik és a külföldön előállított eszközökbe is jórészt innen szállítják
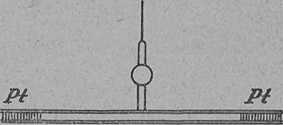
3. ábra. Az Eötvös-féle torziós inga.
Az ólomhengereket E ö t v ö s a torziós mérleg vízszintes rúdja alá helyezte, mert ekkor az elcsavarodást nagyobbítani lehet.
Akármilyen anyagot helyezett a vízszintes rúdra, a tömegvonzás az anyag minőségétől a legpontosabb megfigyelések körében is függetlennek bizonyult.
b) Ezek a megfigyelések, amelyeket E ö t v ö s 1888-tól kezdve évtizedeken át folytatott, mint említettük, tudományos értékükben egyre jelentősebbek. Gyakorlati szempontból viszont azok az eljárások fontosak, amelyekkel E ö t v ö s a nehézségi erőnek nagyságát a tér különböző helyein vizsgálta. Ha ugyanazt a tömeget a Föld különböző helyeire visszük, más-más nehézségi erő hat rá, változik az erő nagysága és iránya. De ez a változás egymáshoz közel levő pontokban rendkívül csekély, csak a legfinomabb módszerekkel mutatható ki. Semmiféle módszer érzékenység tekintetében Eötvös eljárását meg sem közelíti. Az imént megismert torziós inga vízszintes pálcájának két végén egyenlő tömegű platinadarabok vannak. Minthogy a pálca két végén a nehézségi erő szigorúan véve nem egyenlő, az inga megérzi a különbséget, kissé elcsavarodik. Ebből a nehézségi erő irány-változására következtetni lehet.
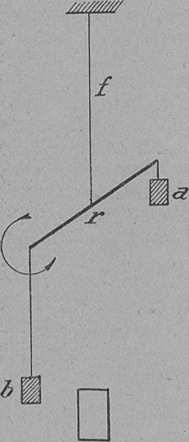
4. ábra. Az Eötvös-féle nehézségi variomotor vázlata.
Sokkal pontosabban lehet a nehézségi erő igen kis változásait az úgynevezett nehézségi variometerrel mérni. Ennek vázát 4. ábránk mutatja. Az f fonál r rudat tartja, melynek egyik végén a súly van, másik végén pedig a fonálra függesztett b súly. Ez utóbbi oldalára helyezzünk pl. 10 kg súlyt. Ez különböző nagyságú erővel vonzza az a és b súlyokat. Ennek folytán a rúd a nyíl irányában kissé elfordul. Ha ezt a súlyt a b súly másik oldalára visszük, az elfordulás éppen fordított irányú. Végül, ha a súly abban a függőleges síkban van, amelyet az r rúdon át fektethetünk, elfordulás nem keletkezik gyakorlati kivitelben a vízszintes pálca két végén egy-egy, platinatömeg van, mégpedig az egyik a csőalakú rúdba van erősítve, a másik pedig dróton függ.
Az egész eszközt függőleges tengely körül el leket forgatni. A vízszintes pálcát először észak-dél irányba kell beállítani, majd pedig öt különböző helyzetbe elforgatni. Mindegyik esetben a rúd helyzetét pontosan le kell olvasni.
Ha a talaj fölött hegy, árok, vízfolyás van, ezeknek tömegvonzó hatását az E ö t v ö s-féle mérleg kimutatja. De a talaj szint alatt is vannak szabálytalanságok, fémes telepek, földgáztartalmú üregek, petróleum stb. A mérleggel végzett észlelésekből ezekre is lehet nagy valószínűséggel következtetni. 5. ábránk Ménes hegyaljai falu alatt mutatja a talaj alatti réteg metszetét nyugat-keleti irányban.
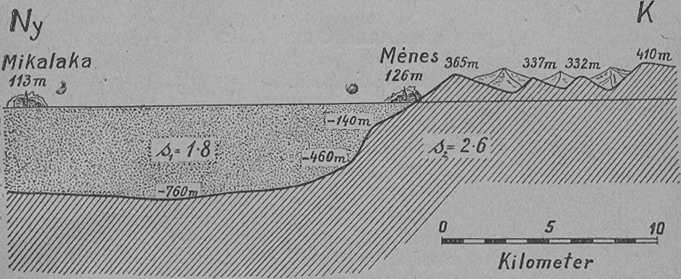
5. ábra. A talaj keresztmetszete Ménes falunál.
A rovátkolt rész sziklás talajt jelent, a pontozott pedig lazább réteget. Látjuk, hogy a Ménes mellett emelkedő sziklás hegy a talaj alatt folytatódik. Ez az altalaj a régi tengerfenék, melyre utóbb laza réteg rakódott. Az s1 = 1,8 a laza réteg sűrűségét jelenti, tehát 1 liter térfogatú talaj súlya 1,8 kg. A sziklás talaj sűrűsége s2 = 2,6. Rajzunkon még a magasságokat is látjuk. A — jel a talaj alatti mélységet jelent.
Budapest környékének felkutatása azt mutatta, hogy a budai hegyek a talaj alatt folytatódnak, mégpedig erős lejtéssel az Alföld felé. Az eredmények megegyeznek azzal, amit a fúrások közvetlenül mutatnak. Eötvös maga idegenkedett attól, hogy eljárását tudományos feladatok megoldásán kívül gyakorlati célokra is alkalmazzák, minden ilyen ajánlatot visszautasított.
De az élet követelményei végül mégis diadalmaskodtak a nagy tudósnak előkelő gondolkodásán. 1917-ben már földgázt kerestek evvel a módszerrel a. Hortobágyon. Az eredmény az volt, hogy elég ezt a vidéket két helyen megfúrni. Ha egyik helyen sem találnak földgázt, akkor az egész vidéken sincs. Az utóbbi években a külföldön is egyre kiterjedtebb mértékben alkalmazzák ezt az eljárást. Mexikóban, Indiában petróleumot keresnek és a mérések elvégzésére a magyar geofizikai intézetnek jól begyakorolt, hozzáértő szakembereit kérték fel, akik eszközeiket is hazulról vitték magukkal.
A gravitáció mint centrális erő.
Az előbbiekben már említettük, hogy a bolygók mozgásának egyik oka az a. vonzóerő, amelyet a Nap a bolygókra kifejt. Amint a bolygó pályáján halad, ennek az erőnek iránya folyton változik, t. i. a bolygótól a Nap felé. A fizikában az olyan erőt, melynek iránya mozgás közben állandóan egy pont felé tart, mint a bolygóra ható erő a Nap középpontja, felé, centrális erőnek nevezzük.
A példáknak egész során beláthatjuk, hogy ilyen erő nélkül körmozgás nem lehetséges. Kössünk fonálra kődarabot, fogjuk meg a fonal szabad végét és lendítsük meg a követ, mint ezt a kis gyerekek szokták tenni. A kő megfeszíti a fonalat és körben mozog. Itt a kőre ismét hat erő, amely a középpont felé húzza és így a középponttól nem engedi, eltávolodni. Ez a fonal szilárdsága, amellyel az elszakításnak ellenáll.
Ezen az egyszerű kis példán többet is tanulhatunk. Ahhoz, hogy a követ körmozgásba hozzuk, meg is kellett lendíteni. Kezünk lökésével a kőnek sebességet adtunk. A körmozgás csak a két mozgató ok együttes következménye. Az egyik az a sebesség, amelyre a kő a meglökés folytán tett szert, a másik a centrális erő, amelyet a fonal fejt ki a kőre.
A hullámvasút példájából ugyanezeket a tanulságokat vezethetjük ki. Ennek egyszerűsített alakját 6. rajzunk mutatja. Hosszú pléhszalagot vagy kettős sínt meggörbítünk úgy, hogy eleinte lejtőalakban haladjon, majd pedig körben görbüljön.
Indítsunk el felülről kis kocsit vagy a sínekre férő golyót, akkor ez végigfut a kör belső oldalán a nélkül, hogy leesnék. Ha a kocsiba golyót teszünk, ez végig benne marad. Amíg a kocsi leért a lejtőn, az esés folytán sebességre tett szert.
Itt tehát ez az esés pótolja azt a lökést, amelyet előbbi példánkban a kőnek adtunk.
A fonal szilárdsága helyett a pléhszalag ellenállása lép fel, ez nem engedi a kocsit a körpálya középpontjától eltávolodni.
Hasonló kísérletet még egyszerűbben is végezhetünk. Üres konzervdobozt, melynek tetejét levágtuk, függesszünk fel fonálra (7. ábra) és öntsünk bele vizet.

6. ábra. A centrális kocsipálya.

7. ábra, Vizet tartalmazó edény körmozgása.
Ha ezt a dobozt körben mozgatjuk, mint előbb a követ, a víz a dobozból nem ömlik ki, mint a golyó som esett ki az előbbi kocsiból.
Előbbi okoskodásunk a testeknek egyik alapvető tulajdonságát, a tehetetlenséget foglalja magában, melynek értelmét egyszerű példákon világíthatjuk meg.
Ha a kocsi, melyben ülünk, hirtelen megindul, akkor arrafelé esünk, ahonnan a kocsi elindult, mert tehetetlenségünknél fogva előbbi nyugalmi helyzetünkben akarunk megmaradni.
Amikor a kocsi hirtelen megáll, az a veszély fenyeget, hogy a menet irányában esünk el, mert most meg akarjuk tartani előbbi sebességünket.
E példák után a tehetetlenséget könnyen megérthetjük : minden test igyekszik nyugalmi állapotát vagy előző sebességét változatlanul megtartani. Magától egy test sem tud nyugalmi helyzetéből elindulni és sebességét sem tudja megváltoztatni. Ehhez erő kell. Ha a testre egyetlen erő hat, akkor a test vagy nyugalmából mozgásba megy át, vagy pedig eddigi sebességét megváltoztatja.
Ha erő nem hat a testre, akkor még nem kell nyugalomban lennie, mozoghat is, de csak úgy, hogy sebességének sem nagysága, sem iránya nem változik. Ez éppen az a pont, amely a Galilei előtti fizikát a mai fizikától elválasztja. Azelőtt azt hitték, hogy minden mozgáshoz erő kell, vagyis az erő a mozgás oka. Galilei óta a fizika azt tanítja, hogy az erő a mozgás sebességének megváltoztatásához kell.
Ezt a fontos elvet már Leonardo da Vinci ismerte, aki nemcsak nagy művész, hanem kiváló fizikus is volt és több önálló fizikai kutatásával vitte előbbre a tudományt. Galilei egész pontosan felfogta a tehetetlenség törvényét, mai megfogalmazása pedig Newton-tól ered.
Eddigi kísérleteink elvezetnek a fizikának fontos alaptörvényéhez, a hatás és visszahatás elvéhez is, amelyet szintén Newton állított fel. Ez a törvény a következőket mondja : Ha két test kölcsönösen hat egymásra, akkor azok az erők, melyeket egymásra gyakorolnak, egyenlő nagyságúak és ellentett irányúak.
Néhány egyszerű példa ezt az elvet is még jobban megvilágít ja. Mindenki tudja, hogy a mágnes a vasat vonzza. De könnyen ki lehet mutatni, hogy a vas is vonzza maga felé a mágnest. Szélesebb edénybe öntsünk vizet, a vízre tegyünk nagyobb parafadugót, erre pedig kis mágnesrúdat vagy patkót. A dugó akkora legyen, hogy a mágnessel megterhelve is ússzék a vízen. Közeledjünk most oldalról közönséges vasdarabbal a mágnes felé, akkor az úszó mágnes a vas felé elmozdul.
Tehát a vas éppen úgy vonzza a mágnest magához, mint a mágnes a vasat. Csak a berendezéstől függ, hogy melyik mozdul el.
Említettük már, hogy a Nap vonzza a Földet. Törvényünk szerint ugyanakkora erővel kell a Földnek is a Napot vonzania. Ez a példa az első pillanatban zavart szokott okozni azoknál, akik ezt a törvényt csak felületesen nézik. Ha a két égitestre ugyanakkora erő hat, ebből még nem következik, hogy a két test egyforma gyorsan mozog. Sőt ez nem is lesz így, mert tömegük lényegesen különböző. Ugyanaz az erő a nagyobb tömeget lassabb mozgásra indítja.
Ugyanezt az okoskodást a fegyverek és ágyúk vissza csapására is szokták alkalmazni. Mikor a lövedék a fegyvert elhagyja, maga a fegyver hátrafelé mozog. Ágyúknál külön rugókkal fékezik a vissza csapást. Egyszerűbb azonban a következő magyarázat. Az elsütésnél gázok fejlődnek, amelyeknek nyomása a lövedéket kirepíti. De a gázok minden irányban fejtenek ki nyomást, így a fegyverre visszafelé is hat gáznyomás, ez okozza a vissza csapást .
Térjünk vissza még egy pillanatra a fonálhoz erősített és körben forgatott kövünkhöz. Már láttuk, hogy a fonal a követ a kör középpontja felé húzza. Ez a centrális erő. Ennek visszahatása az az erő, amellyel a kő a fonalat feszíti. Ez az erő éppen fordított irányú, mint a centrális erő, vagyis a középponttól kifelé irányul. A centrális erőnek ezt a visszahatását centrifugális erőnek nevezzük.
Üveggömböt, melybe kevés festett vizet öntöttünk, hozzunk pl. motor segítségével forgásba. Forgás közben a víz egyre feljebb emelkedik a gömbben, távolodik a függőleges forgástengelytől, végül az egyenlítő mentén mint színes öv helyezkedik el. Ennél távolabb a gömb nem engedi. A magyarázatot könnyen szokták elintézni : a vizet a centrifugális erő a tengelytől eltávolítja. De ehhez a magyarázathoz sok szó fér. A centrifugális erő magában nem működik, csak mint a centrális erőnek visszahatása.. A víz nem is ezért távolodik a tengelytől, hanem egyszerűen tehetetlenségénél fogva.
Ugyanavval az esettel van dolgunk, mint mikor a sár leválik a forgó kerékről. Valóban, ha a víz emelkedését az üveggömbben jobban megfigyeljük, azt látjuk, hogy csavarvonalban emelkedik felfelé. Mindenesetre levonhatjuk azt a következtetést, hogy a forgó test a tengelytől távolodni igyekszik, vagyis úgy viselkedik, mintha centrifugális erő hatna rá.
A centrifugális erő hatását tekintetbe kell venni kocsik és vonatok kanyarodásánál. Ha a kocsi sík pályán nagy sebességgel fordul, akkor könnyen megeshet, hogy a centrifugális erő folytán kifelé felborul. Ezért a kocsiknak ilyen helyen sebességüket csökkentem kell. A kerékpáros úgy segít magán, hogy a kanyarulatnál testét befelé fordítja. A vonat kocsijával is ezt teszik, még pedig úgy, hogy a két párhuzamos sín közül a külsőt kissé felemelik. Ekkor a sínpár befelé lejt.
Ha egy pontra két erő hat, akkor általában az a feladatunk, hogy az együttesen ható erőket egyetlen erővel helyettesítsük, vagy ahogyan mondani szoktuk, a két erőt össze akarjuk tenni. Ennek a feladatnak megoldása végett induljunk ki a következő kísérletből.
Függesszünk AB kötélre (7a. ábra) 20 kg súlyt. Ez a kötelet lefelé feszíti. B ponthoz kössünk másik fonalat, és vessük át oldalt megerősített csigán úgy, hogy ez a fonal pl. vízszintesen húzódjék. A fonalat terheljük meg 16 kg súllyal. A 20 kg erőt úgy szoktuk ábrázolni, hogy B pontból kiindulva az erő irányában, tehát most függőlegesen lefelé, tetszés szerinti 20 egységet mérünk fel és az így kapott távolság végére nyilat rajzolunk. Így kapjuk a Q = 20 kg erő képét. A másik P = 16 kg erőt hasonló módon ábrázoljuk B pontból kiindulva vízszintes irányban. A két erő együttes hatására az AB fonal ferde irányban feszül, amint ezt ábránk is mutatja. Ezt az irányt egyszerűen meg lehet szerkeszteni. Q erő végpontjából húzzunk párhuzamost P erővel és P erő végpontjából Q erővel. (Rajzunkon ezek a párhuzamosok szaggatott vonalak.) Így a P és Q erőket parallelogrammává egészítettük ki.
A fonal AB iránya ennek a parallelogrammának átlója. Tehát az az erő, amely az eredeti P és Q erőket helyettesíti, BC átló irányába esik és nagyságát is ez az átló (R) ábrázolja. A mi példánkban ez az erő R = 25 kg. Az adott két erőt (Q és P) összetevőknek (componens) szoktuk nevezni, a helyettesítő erőt (R) pedig eredőnek (resultans).
Ezt az eljárást akármilyen irányú erők összetételére használhatjuk. Ha A pontra (7b. ábra) olyan két erő (összetevő) hat, amelyeket irány és nagyság szerint az említett értelemben AB és AC távolságok ábrázolnak, akkor ezt a két távolságot most is a BD) és CD párhuzamosak segítségével parallelogrammává (ABDC) egészítjük ki. Ennek AD átlója a keresett eredő.
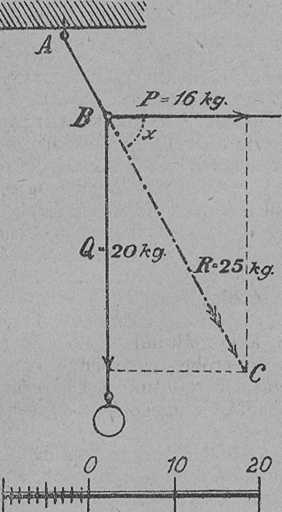
7a. ábra. Erők összetétele.

Ezt az egyszerű szabályt, amelynek alapján adott összetevők eredőjét meg lehet szerkeszteni, parallelogramma-tétel néven szokták idézni.
Ezt az eljárást meg is fordíthatjuk. Az AD erőt helyettesíthetjük AB és AC erőkkel, tehát egy erő helyett a két összetevőt vehetjük. Ilyenkor azt mondjuk, hogy az AD erőt két összetevőre bontottuk fel.
A Föld tengely körüli forgásának bizonyítékai.
Az előbbiekben ismételten hivatkoztunk arra, hogy a Föld egy nap alatt tengelye körül megfordul. Ezért most azokat a bizonyítékokat soroljuk fel, amelyek ezt objektíve igazolják.
a) A Föld lapultsága.
A közvetlen mérések azt mutatják, hogy a Föld a sarkoknál lapult, az egyenlítőnél pedig kidomborodik. Ezt a jelenséget utánozni is lehet. Köralakra görbített rugalmas fémszalagot forgassunk egyik átmérője körül. Ekkor a szalag a tengely mentén belapul, az egyenlítő körül pedig kiszélesedik, mert a forgás folytán a szalag tömege a tengelytől távolodik. A centrifugális erő úgy hat, mintha a szalagot az egyenlítőnél megfogtuk és kifelé húztuk volna.
Ezt az okoskodást visszafelé a Földre is alkalmazhatjuk. A Föld valamikor, sok millió évvel ezelőtt, izzó folyékony állapotban volt, tehát alakja még változhatott. A tengely körüli forgás miatt az egyenlítőnél éppen úgy kidomborodott, mint golyóvázunk szalagjai.
b) A Foucault-féle ingakísérlet.
Foucault (1850) hosszú fémdrótra fémgömböt függesztett. Ezt az ingát észak-dél irányban kilendítette. Már fél óra múlva azt vette észre, hogy a lengés síkja jelentékenyen elfordult. Aki ezt a kísérletet látja, azt a benyomást szerzi, mintha a lengés síkja a nyugvó Föld fölött keletről délen át nyugat felé elfordulna. Valóban az inga a tehetetlenség folytán ezt a síkot megtartja. Erről könnyen meggyőződhetünk, ha állványra (8. ábra) B pontban ingát függesztünk, ezt A pont felé kilendítve lengésbe hozzuk, azután pedig az állványt centrifugális gépen forgatjuk. Az inga a forgás ellenére is abban a síkban marad, amelyben elindítottuk. Ha mi mégis azt látjuk, hogy Foucault ingájának lengsíkja elfordult, ez csak látszólagos lehet.

8. ábra. Az inga lengéssíkja állandó.
Valóban mi fordultunk el a Földön ellenkező irányban, mint ahogyan az ingát elfordulni látjuk, vagyis nyugatról délen át kelet felé. A mozgó vonaton is gyakran megesik, hogy nem tudjuk, mi mozgunk-e, vagy pedig a mellettünk levő vonat ellenkező irányban. Foucault ingájának elfordulásában a Föld forgása tükröződik vissza.
c) A Newton-féle eséskísérlet.
Menjünk fel magas torony tetejére és álljunk a nyugat felé forduló falhoz (9. ábra, AB). Ejtsünk le a torony ablakából követ. Ez a kő nem a fal mellett esik, habár a fal pontosan függőleges, hanem a falba ütődik. Ennek okát ismét a Föld forgásában találjuk.
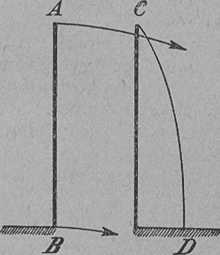
9. ábra A toronyról eső kő mozgása
Ugyanis a kő a tehetetlenség miatt megtartja azt a sebességet, amelyet a Föld forgása a torony tetején adott neki. Ámde itt nagyobb a sebesség, mint a Föld színén, mert A pont, amely messzebb van a Föld középpontjától, nagyobb kört ír le egy nap alatt, mint B. A leejtett kő ennélfogva nagyobb sebességgel mozog kelet felé, mint a torony talppontja (B) és így ehhez a talpponthoz képest a mozgás irányában, vagyis kelet felé előresiet. Tehát a torony falát már közbeeső helyen eléri.
Álljunk most a kelet felé néző oldalra, pl. G ablakhoz, akkor ugyanilyen okoskodással könnyen beláthatjuk, hogy a leejtett kő, amely a torony talppontjához képest most is előresiet, a toronytól nagyobb távolságban éri a földet (1) pontban).
d) Báró Eötvös Lóránt kísérlete.
Eötvös élete vége felé azzal a kérdéssel foglalkozott, hogyan folyásolja be a Föld forgása a nehézségi erőt. Kutatásai közben olyan eszközt szerkesztett, amellyel a Föld forgását lehet igazolni. Készüléke (10. ábra) kis érzékeny mérleg (M), melynek karjain kerek súlyok vannak. A mérleg állványát O hajtószíjjal függőleges tengely körül forgatni lehet. A mérleget a légáramtól ráborított üvegtok védi.
A mérlegen kis tükör (t) van a fizikában gyakran használt, tükrös leolvasás végett. Az I lámpa fénye D nyíláson át t tükörre esik, innen visszaverődve T tükörre jut, innen pedig V vetítőernyőre, amelyen P fényfoltot kelti. A mérleg mellett még vezetékből sodort tekercset (E) találunk. Ha ezen megfelelő erősségű elektromos áramot bocsátunk át, akkor a földmágnesség hatását kiegyenlíthetjük. Forgás közben a mérleg egyensúlya megbomlik, egyik karja lehajlik. Ekkor a visszavert fény az ernyőn eltolódik.
Az előbbiek után a magyarázat nem ütközik nehézségbe. A Földön levő testre nemcsak a nehézségi erő hat, hanem a Föld forgása folytán centrifugális erő is.
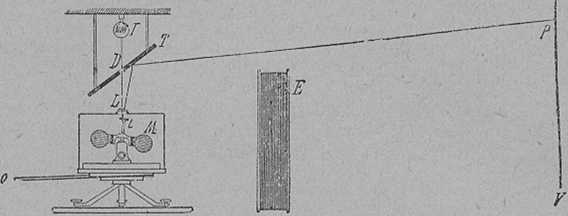
10. ábra. Eötvös kísérlete.
A nehézségi erő iránya a Föld középpontja felé tart. A centrifugális erő, amely kifelé irányul, a tömegvonzást csökkenti. Azt is tudjuk, hogy a centrifugális erő nagyobb, ha a test gyorsabban forog. Ha mi pl. hajón nyugat felé mozgunk, akkor a hajó sebessége hozzájárul a Föld forgásának sebességéhez, mert a Föld is nyugat felé forog. A hajó mozgása tehát növeli a centrifugális erőt, ennélfogva a nehézségi erő kisebb. Ha pedig a hajó kelet felé halad, akkor sebessége éppen ellenkező irányú, mint a Földé, tehát a hajó sebessége csökkenti a Föld sebességét. Ekkor a centrifugális erő kisebbedik, a nehézségi erő nagyobb.
Térjünk most vissza Eötvös kísérletéhez. Forgás közben a mérleg karja váltakozva kelet és nyugat felé mozog. A kelet felé mozgó kar a forgás folytán súlyosabb lesz, a másik kar pedig, amely ugyanakkor nyugat felé mozog, veszít súlyából. Ezért a mérlegkar nem maradhat vízszintes
e) A passzát szél elhajlása.
Az egyenlítőn a levegő erősen felmelegszik, felszáll és a sarkok felé áramlik. Helyét viszont a sarkok felől jövő hidegebb, alul áramló levegő foglalja. Ez az alsó, hidegebb áram a passzát szél. Ha a Föld nyugalomban lenne, akkor mint északi szél lépne fel. A valóságban a passzát szél az északi földgömbön északkeleti, a déli földgömbön pedig délkeleti. Ezt az elhajlást a Föld forgása okozza. A passzát szél a mi félgömbünkön északról jön, tehát olyan helyről, mely kisebb sebességgel forog, mint az egyenlítő tája. A szél megtartja ezt a kisebb sebességét, ezért a nyugatról kelet felé forgó Földdel szemben visszamarad (11. ábra) és így északkeleti, illetőleg a déli félgömbön délkeleti szél lesz belőle.

11. ábra. A passzát szél elhajlása.
Első pillantásra talán meglepőnek látszik, hogy a tengelye körül forgó Föld lényegében ugyanaz, mint az a «búgócsiga», amelyet gyerekkorunkban sima kövezeten pörgettünk. Mind a kettő pörgettyű. A lényeges, hogy a test olyan tengely körül forog, amelyre nézve a tömeg szimmetrikusan oszlik el.
Ha nagyobb érmet élével asztalunkra állítunk, hamar eldől éppen úgy, mint a búgó csiga, ha csúcsára állítjuk és nem pörgetjük meg a szokott módon ostorcsapásokkal. De hozzuk az érmet vagy a búgócsigát gyors forgásba, akkor egyik sem dől el, hanem a függőlegesen maradó tengely körül forog. Ha azután később a súrlódás folytán a forgás lassú lesz, az érem az asztalra dől.
Készítsünk viaszból köralakú korongot vagy szerezzünk ugyanilyen alakú fémlapot. Fúrjuk át korongunkat középen és a furaton dugjunk át vastagabb drótot. Evvel kész is a pörgettyűnk. A drót lesz majd kísérleteink közben a forgástengely. A pörgettyű tömege most is szimmetrikusan oszlik el a tengely körül. Állítsuk kis eszközünket a drót csúcsára, akkor bizony hamar eldől. De hozzuk gyors forgásba, még pedig célszerűen úgy, hogy a tengelyre fonalat sodrunk és a fonalat gyorsan lehúzzuk. Ha forgó pörgettyűnket úgy állítjuk sima alapra, hogy tengelye kezdetben függőleges legyen, akkor ilyen is marad.
Állítsuk ezután a forgó pörgettyűt úgy az asztalra, hogy tengelye ferdén álljon. Ekkor a tengely kúpot ír le, vagyis a tengely felső vége körpályán mozog. Ez azt jelenti, hogy a tengely a forgás közben az asztal síkjával állandóan ugyanakkora szöget zár be.
Bizonyára mindenki tudja hogy a Föld forgástengelye nem merőleges a Nap körüli pálya síkjára, hanem 66° 32' szöggel hajlik hozzá. Mialatt a Föld pályáját befutja, ez a hajlás mindig ugyanaz marad. Pörgettyűnkkel ezt a mozgást utánozhatjuk. Állítsunk asztalunkra lámpát, amely a Napot helyettesíti. Pörgettyűnket függesszük fonalra, hozzuk forgásba és állítsuk tengelyét ferdén. Most vigyük a kezünkben tartott fonálnál fogva a lámpa körül, akkor a pörgettyű egészen a Föld mozgását utánozza.
Sőt még egy lépéssel tovább is mehetünk. Úgy, mint a ferdén álló pörgettyű tengelye, a Föld tengelye is kúpot ír le, a tengely végpontja pedig kört. Most a Föld tengelye közel az égboltnak azon pontja felé mutat, ahol a Kisgöncöl legfényesebb csillaga van. Ezért nevezik ezt a csillagot sarkcsillagnak. De ez nem mindig volt így és nem is lesz így. A földtengely a kúpos mozgás folytán az égboltnak mindig más és más csillaga felé mutat, tehát más csillag lesz a sarkcsillag. Csakhogy ez az úgynevezett precessziós mozgás olyan lassú, hogy néhány emberöltő alatt nem tűnik fel és csak pontos csillagászati eszközökkel mutatható ki. 12.000 évig tart, míg a Föld tengelye egy teljes körforgást befejezett.
Említettük már, hogy a testek súlyuknál fogva függőlegesen lefelé esnek. Ennek a mozgásnak vizsgálata a fizika történetében korszakos jelentőségű volt, evvel alapította meg Galilei a mai fizikát. De a szabad esés igen gyors lefolyású, megfigyelése nehéz és pontatlan lett volna. Galilei-nek egyik zseniális ötlete volt, hogy a szabad esést lassított alakjában vizsgálta : a testet lejtőn engedte esni.
A lejtőn esés.
Simára gyalult, körülbelül 170 cm hosszú deszkában vágjunk formagyaluval a deszka hosszirányában négy párhuzamos csatornát (12. ábra). A csatornák egészen simák legyenek, mert különben a súrlódás túlságosan zavarja a megfigyelést. Négy keresztlécre is szükségünk van, ezeket csavarral akárhol megerősíthetjük.
12. ábra. Lejtő párhuzamos csatornákkal.

Az egyik keresztléc az első csatornáig ér, a második léc a második csatornáig s i. t. A léc oldalára helyezzünk vagy rajzoljunk cm osztályzatot. A deszka egyik végét támasszuk fel úgy, hogy a deszkának kis lejtése legyen. Mindegyik csatornába tegyünk egy-egy golyót és ezeket keresztbe tartott vonalzóval tartsuk vissza (lásd a rajzot). A golyók a cm osztályzat 0 helyéről induljanak. Próbálgatással a lejtő hajlását úgy lehet beállítani, hogy az első golyó
1 mp alatt éppen 10 cm-t tegyen. E végett az első keresztlécet mindjárt 10 cm-hez állítjuk és a hajlást óvatosan változtatjuk. A második keresztlécet oda állítjuk, ahova a második golyó 2 mp múlva ér. Ugyanígy járunk el a harmadik és negyedik golyónál. Ekkor a lécek a lejtőn eső testnek 1, 2, 8, 4 mp alatt megtett útját jelzik. A kísérlet azt mutatja, hogy ezek az utak 10, 40, 90, 160 cm.
Könnyen kiolvashatjuk azt a törvényszerűséget, amely ezekben a megfigyelésekben rejlik. 2 mp alatt a megtett út 4-szer nagyobb, mint 1 mp alatt, 3 mp alatt 9-szer nagyobb, 4 mp alatt 16-szor nagyobb s i. t. Ezt röviden úgy szoktuk összefoglalni, hogy a megtett út az idő négyzetével arányos. Pl. a 8 mp alatt megtett utat úgy kapjuk meg, ha az 1 mp alatt megtett utat 8-nak négyzetével, vagyis 64-gyel szorozzuk. Ez a könnyű kis okoskodás egyúttal egyszerű példája annak, hogyan lehet a kísérleti adatokból a bennük rejlő törvényszerűséget kihámozni.
Kövessük tovább Galilei-t kísérleteiben és okoskodásában. Galilei kimutatta, hogy az út törvényszerűsége a szabad esésnél ugyanaz, mint a lejtőn esésnél, t. i. a befutott út az idő négyzetével arányos. Ha a levegő okozta súrlódást egyelőre figyelembe nem vesszük, akkor a szabad esésnél
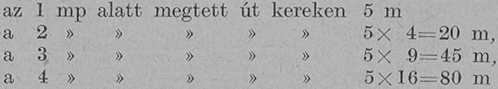
Pontosabban nálunk 5 m helyett 4,91 m-t kell mondani. Minthogy a nehézségi erő a Föld különböző helyein változó, ez az érték is ingadozik. Az egyenlítőn az első mp alatt a test 4,907 m-nyire esik, a sarkon pedig 4,916 m-nyire.
Az inga.
A nehézségi erő tulajdonságainak vizsgálatában ma is fontos szerepe van az ingának.
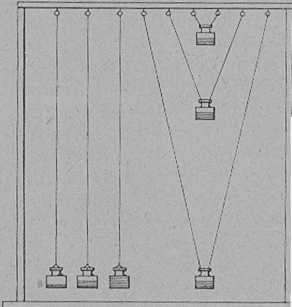
Állványunk (13. ábra) felső lécébe kampós szögeket erősítünk. Persze az állványt egyszerű léccel is pótolhatjuk, melyet vízszintes helyzetben csavarral szekrényünk tetejéhez erősítünk. A kampós szöghöz kössünk fonalat, a fonal alsó végére pedig súlyt (lásd az ábrát). A fonal lágy, könnyű és lehetőleg vékony legyen. A súly akármilyen test lehet, semmiféle szabályos alakjának nem kell lenni. Ez a könnyen előállítható eszköz az egyszerű inga.
13. ábra. Egyszerű ingák.
Emeljük ki ingánkat nyugalmi függőleges helyzetéből. Ha elengedjük, akkor a súly lefelé húzza. A fonal nem engedi a súlyt függőleges irányban esni, hanem a súly köríven mozog. Tartsunk vízszintesen vonalzót a felemelt súly magasságában. Ha az inga leng, akkor a másik oldalon éppen a vonalzó magasságáig emelkedik, vagyis ugyanolyan magasságig, mint amelyből elengedtük.
Szerezzünk még stopper-órát, amilyennel versenyeknél is az időtartamot mérik. Lengessük ingánkat és mérjük le 5, majd 10, végül 15 lengés idejét. 10 lengés kétszer, 15 lengés háromszor annyi ideig tart, mint 5 lengés. Ez azt mutatja, hogy az inga egy-egy lengést ugyanannyi idő alatt végez. Ezért az inga lengésidejéről beszélhetünk. Így nevezzük azt az időt, amely alatt az inga egyik szélső helyzetéből a másikba jut.
Most vizsgáljuk meg, mitől függ az egyszerű inga lengésideje.
Egyelőre megelégszünk egyetlen ingával. Térítsük ki kevéssé ingánkat, hagyjuk lengeni és mérjük meg 10 lengés idejét. Azért nem egy lengését, mert ez nagyon pontatlan lenne, hiszen az indításnál és megállításnál mindenki követ el hibát. Így ez a hiba 10 lengésre oszlik meg. Most térítsük ki ingánkat más szöggel, pl. kissé magasabbra. Ha ismét lemérjük 10 lengés idejét, ugyanazt találjuk, mint előbb. Tehát az inga lengésideje, amíg a kitérítés nem nagy, a kitérítés szögétől nem függ.
Függesszünk fel állványunkra három, teljesen egyforma hosszú ingát (lásd az ábrát), de a súlyok különbözők legyenek, akár különböző anyagúak is (fa, vas, kő stb.). Csak arra ügyeljünk, hogy a fonal jól kifeszüljön. Ha az ingák lengésidejét az előbbi módon lemérjük, ezeket egyenlőknek találjuk. Tehát a lengés ideje az inga anyagától és tömegétől sem függ.
Ha azt akarjuk, hogy az inga a lengés síkját állandóan megtartsa, kettős fonálra függesztjük fel úgy, mint ábránk jobb oldalán látjuk. Ilyenkor a hosszúságot nem a fonal mentén, hanem függőlegesen lefelé kell mérni. Tehát rajzunkon a leghosszabb kettősfonalú inga ugyanolyan hosszúnak számít, mint a baloldali egyfonalú ingák.
Függesszünk fel három ingát, melyek közül a második 4-szer, a harmadik 9-szer hosszabb, mint az első. A rövid inga gyorsan leng, a hosszabbak egyre lassabban. Tehát a hosszúság lényeges a lengésidőre.
Ha az ingák lengésidejét lemérjük, a másodikét 2-szer, a harmadikét 3-szor akkorának találjuk, mint az elsőét. Ha tehát az inga hossza 1:4:9... arány szerint nő, akkor a lengésidő 1:2:3... arányban nagyobbodik.
Még másik körülmény is befolyásolja a lengésidőt. R o g er, francia fizikus észrevette, hogy ingája, amely Párizsban másodpercinga volt, vagyis minden lengését 1 mp alatt végezte, Cayenne-ban az egyenlítő közelében naponként
2 percet és 28 mp-et késett, más szóval lassabban lengett. Ennek az az oka, hogy a nehézségi erő az egyenlítőn, mint már láttuk, kisebb, mint a sarkok felé. Egyszerű kísérlettel valószínűvé tehetjük, hogy a lengésidő a nehézségi erő nagyságától is függ. Kössünk ingánk fonalára vassúlyt és mérjük le a lengésidőt. Tartsunk közvetlenül az inga alá erős mágnest. Ez vonzza magához a vasat, tehát úgy hat, mintha a nehézségi erőt növeltük volna. Most az inga gyorsabban leng, a lengésidőt kisebbnek találjuk. Helyezzünk most a fonaltól jobbra és balra közvetlenül a vasgolyó fölé egy-egy mágnest. Ezek a vasat felfelé húzzák, tehát a nehézségi erőt kisebbítik. Ekkor a lengésidőt nagyobbnak találjuk.
Végezzük Galilei-nek következő egyszerű kísérletét. Egyenlő hosszú fonalakra függesszünk egyenlő átmérőjű parafa- és vasgolyót. Ezt a két ingát hozzuk lengésbe. Lengésidejük, mint már tudjuk, egyenlő lesz. De a parafagolyó, ha kezdetben ugyanannyira térítettük is ki, mint a vasat, csakhamar kisebb kilengéseket végez, vagy amint mondani szoktuk, lengése gyorsabban csillapodik.
Ennek a levegő az oka. Az ingának lengés közben a levegőt útjából el kell tolnia, ezért mozgása egyre lassul. Ezt az akadályt közegellenállásnak nevezzük. Minden mozgásnál fellép, hacsak nem léghíjas térben történik a mozgás. Természetéről jól tájékoztat N e u m a n n következő kísérlete. Vágjunk ki vékony falapból négyszöget .(14. ábra) és erősítsünk mindegyik oldalára kampós szöget. Az egyik kampóhoz kötött fonalnál fogva függesszük lapunkat, a szemben levő kampóra pedig akasszunk kis súlyt, hogy a fonal kifeszüljön. Most sodorjuk meg jó néhányszor a fonalat úgy, hogy a lapot forgatjuk. Ha eszközünket ezután magára hagyjuk, kicsavarodik. A levegő közegellenállása a mozgást többé-kevésbbé lassítja.
Könnyen meggyőződhetünk róla, hogy ha ugyanarra a fonalra nagyobb lapot akasztunk, ennek mozgását a levegő nagyobb mértékben akadályozza. Ezért adnak a hajóknak ékalakot. Ha egész lapjukkal hasítanák a vizet, nehezebben tudnák a vizet útjukból eltolni, nagyobb lenne az ellenállás. Újabb mozdonyok előlapját is kúpalakra formálják. Ugyanezt látjuk egyes autókon is.
Ha lapunkat vízbe merítjük, sokkal lassabban csavarodik vissza, mint levegőben. Tehát vízben nagyobb a közegellenállás, mint levegőben, mert a víz sokkal sűrűbb közeg, mint a levegő.

14. ábra A közegellenállás kimutatása.
A közegellenállást értékesíteni is lehet.
Ennek egyik példája az ejtőernyő. Ha az összehajtott ernyőt magas helyről leejtjük, kinyílik és sokkal lassabban esik lefelé, mint pl. egy kődarab.
A levegő ellenállása az esőcseppek sebességét is lényegesen csökkenti. Nélküle az eső az erős ütés miatt több kárt okozna, mint hasznot.
A mozgásnak más akadálya is van. Ha golyót vízszintes lapon elgurítunk, sebessége egyre csökken, mégpedig annál gyorsabban, mennél érdesebb a lap, amelyen a golyót elgurítottuk. Ez az akadály a súrlódás, amely itt a golyó és a lap közt lép fel.
A súrlódás annál nagyobb, mennél érdesebbek az egymáson mozgó lapok. Az olajozásnak éppen az a célja, hogy az egymáson súrlódó lapok érdességeit kitöltse és így a súrlódást csökkentse. Ha a mozgó testet megterheljük, a súrlódás fokozódik. Tehát megegyező felületeken a súrlódás a mozgó test súlyával nő.
Ha a mozgó test nem csúszik, hanem kereken gördül, a súrlódás lényegesen kisebb, mint a csúszó mozgásnál. Ezért használnak golyós csapágyakat. A közönséges csapágyakban a felületek egymáson csúsznak, itt e helyett a golyók gördülnek.
Vágjunk ki fából tetszés szerinti lapot, azonkívül fektessünk asztalunkra vonalzót úgy, hogy vízszintes legyen (15. ábra). Kevés próbálgatással rá tudjuk állítani az élre falapunkat úgy, hogy le ne essék. Jelöljük meg azt az irányt,
amelyen a lap az élre támaszkodik. Tegyük meg ugyanezt a falapnak más irányú ráfektetésével is. Így a lapon két egyenest kapunk. Ha parafadugóba tűt szúrunk, lapunkat a két egyenes metszőpontjában a tűre helyezzük, a lap nem esik le.
15. ábra. A súlypont meghatározása alátámasztással.
Mit lehet ebből következtetni? A lapot saját súlya lefelé akarja mozgatni. Ha a lap mégis nyugalomban van, akkor a súlyt az alátámasztással kiegyensúlyoztuk. Tehát a súly az egész testre éppen abban a pontban hat, amelyben alátámasztottuk. Ezért hívjuk ezt a pontot súlypontnak.
Éppen ilyen könnyen lehet ezt a pontot felfüggesztéssel kikeresni. Kössünk lapunkhoz (16. ábra) b pontban fonalat.
16. ábra.
A súlypont kikeresése felfüggesztéssel.

17. ábra. A súlypont a legmélyebb helyet foglalja el.
Fonalunk irányának meghosszabbítását (bd) rajzoljuk rá a lapra. Ezen a vonalon kell lenni a súlypontnak, mert a test különben lefelé esnék. Függesszük most fel testünket a pontban és rajzoljuk rá ismét a fonal ac irányát. A két irány metszőpontja a keresett súlypont.
Mint gyermekkorunkban gyakran tettük, vágjunk ki bodzabélből vagy más könnyű anyagból palackalakot (17. ábra) és fenekébe szúrjunk nagyobb, gömbölyű fejű vasszöget vagy gömbölyűre formált ólmot. Ha a palackot lefektetjük, magától felugrik. A magyarázat nagyon egyszerű. A súlypont mindig a nagyobb tömeg felé esik. Pl. a kúp súlypontja közelebb van a kúp alapjához, mert errefelé a kúp kiszélesedik, a tömeg nagyobb része az alap felé esik. A mi előbbi példánkban a bodzabél tömege kicsi a vas vagy ólom tömegéhez képest, ezért a súlypont egészen Jent van a vasban. Ha a palackot lefektetjük, akkor súlypontja még emelkedik. De a nehézségi erő a súlypontot lefelé húzza, ezért a palack felugrik, hogy súlypontja lejjebb kerüljön.
Általában, ha azt akarjuk, hogy a test ne essék le, arról kell gondoskodnunk, hogy súlypontja alá legyen támasztva. A pisai torony ferde ugyan, de ha súlypontján függőlegest bocsátunk át, ez még az alapra esik, tehát súlypontja alá van támasztva, a torony biztosan áll. Csak ha annyira dőlne, hogy súlypontja már nem esnék az alap fölé, akkor kellene a torony ledőlésétől félni.
A súlyveszteség vízben és levegőben.
Szigorúan véve, a súlymérést léghíjas térben kellene végeznünk, mert a levegő csökkenti a testek súlyát. Pontos méréseknél ezt számba is veszik. Ez a súlycsökkenés nemcsak levegőben áll elő, hanem akármilyen anyagba (folyadékba vagy gázba) helyezzük is a testet. Kezdjük a feltűnőbb és ezért könnyebben kimutatható eseten, mikor a test vízbe merül.
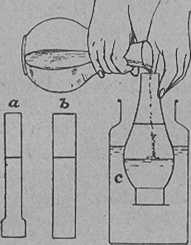
Kétkarú mérleg egyik csészéjére tegyünk kis üres üvegpalackot (18. ábra, a), a csésze alá pedig kötözzünk akármilyen testet, pl. követ (b). Az így megterhelt mérleget a másik csészébe helyezett mérősúlyokkal vagy akár apró seréttel egyensúlyozzuk. Mártsuk a kődarabot vízzel telt pohárba (c), akkor az egyensúly megbomlik, a kő veszít súlyából. De mennyit? Kezdjük a kísérletet elölről. A c edénybe, mielőtt a követ belemártjuk, dugjunk meggörbített gumicsövet (d), melyet kissé megszívunk. Mikor a víz megszűnik folyni, a csőben ugyanaddig van víz, mint az edényben. Vegyük le az üres poharat (a) a mérlegről, mártsuk a kődarabot az edénybe és a kiszorított vizet fogjuk fel az a pohárban.
Ha a poharat a mérlegre visszatesszük, a mérleg egyensúlya megmarad. Tehát a vízbe mártott kő annyit veszít súlyából, mint amennyi az általa kiszorított víz súlya. Ez Archimedes (Kr. e. a 3. században) híres tövénye.
Könnyen kimutathatjuk, hogy ugyanilyen súlyveszteség levegőben is előáll.

18. ábra. Archimedes törvényének kimutatása.

19. ábra. A levegőben előálló súly veszteség igazolása.
Kis mérleg (19. ábra) egyik karjára vasgömböt (f) csavarunk, másik karjára pedig jóval nagyobb térfogatú, de a levegőn ugyanakkora súlyú zárt üveggömböt (l) akasztunk. A mérleg tehát levegőn egyensúlyban van. Állítsuk mérlegünket légszívó burája alá. Amint a levegőt egyre jobban eltávolítjuk, az egyensúly megbomlik, az üveggömb (l) a kart lehúzza. A magyarázaton nem sokat kell fejünket törnünk. A levegőn a vas és az üveg is veszítettek súlyukból, még pedig az üveggömb többet, mert nagyobb térfogatú és így több levegőt szorított ki. A levegőn a két súly a veszteség után volt egyenlő. Léghíjas térben az lesz súlyosabb, amelynek előbb nagyobb vesztesége volt, tehát az üveggömb.
Ne elégedjünk meg a súlyveszteség kimutatásával, keressük ennek a feltűnő jelenségnek okát is.
Ha edénybe vizet öntünk, a víz súlyánál fogva nyomja az edény fenekét. Tekintsünk először hengeralakú palackot, melynek alapja pl. 10 cm2 területű, öntsünk az edénybe 15 cm magasságig tiszta vizet.
A beleöntött víz tehát 150 cm3. Minthogy 1 cm3 víz kereken 1 g súlyú, a hengerben 150 g víz van, ekkora súly nyomja a fenéket. A nyomást rendesen 1 cm2 területre szoktuk vonatkoztatni, ezért azt mondjuk, hogy edényünk alapjára cm2-enként 15 g víznyomás hat. Ha edényünkbe higanyt öntöttünk volna, mely 13,6-szer sűrűbb, mint a víz, a nyomás is 13,6-szer nagyobbodnék.
De hogyan számítsuk ki a nyomást, ha az edény szabálytalan alakú? A következő kísérlet rögtön útba igazít bennünket. Szerezzünk három lámpaüveget, mely különböző alakú ugyan, de ugyanarra a lámpára illik, vagyis alapterületük megegyező (20. ábra, a, b, c).

21. ábra. Az oldalnyomás.
Mind a három üvegen jelöljük meg ugyanazt a magasságot. Szorítsunk hozzá vastagabb papírlapot a cső aljához és így mártsuk be a csövet szélesebb, vízzel telt edénybe éppen a jelig, öntsünk a csőbe színezett vizet. Az elengedett papírlap akármelyik cső aljáról csak akkor esik le, ha a festett víz a csőben a külső víz magasságát elérte.
20. ábra. A felfelé ható nyomás és a hidrosztatikus paradoxon.
Ebből a kísérletből kétféle tanulságot is vonhatunk le. Ha a cső aljához szorított lap a bemártás után nem esik le, ez azt jelenti, hegy a víz a lapot feljelé nyomja. Tehát van felfelé ható nyemás is. A lap csak akkor esett le, mikor a víz a csövön belül és kívül egyenlő magasságba jutott. Ebből azt látjuk, hogy a lapra ugyanakkora nyomás hat felfelé, mint amekkora ezen a helyen a lefelé nyomás.
Most vonjuk le kísérletünkből a második tanulságot. Mindegyik csövet ugyanaddig a magasságig kellett töltenünk, tehát a víznyomás nem függ az edény alakjától. Akármilyen alakú edényben minden 1 cm vízmagasságnak cm2-enként 1 g nyomás felel meg, vagy 10 m magasságnak 1 kg. Ez a úgynevezett hidrosztatikus paradoxon. (A paradoxon látszólagos ellenmondást jelent.) Azért paradoxon, mert a keskeny edénybe öntött kis tömegű víz ugyanakkora nyomást fejt ki, mint a szélesebb edénybe öntött sok víz, hacsak a magasság megegyező.
Egészítsük még ki a víznyomásra vonatkozó ismereteinket az oldalnyomás megfigyelésével. Vegyünk olyan palackot, melynek oldalán is van nyílása (21. ábra). Ezt egyelőre dugaszoljuk el. A palack dugóján keresztül hosszú cső nyúlik ki. Öntsünk vizet különböző magasságig, vegyük ki az oldaldugót, akkor a víz annál messzebbre lövell ki, mennél magasabban van a víz. Tehát a víz oldalt is nyomja az edény falát, mégpedig a nyomás annál nagyobb, mennél mélyebben vagyunk a víz felszínétől. A gátaknak ezt az oldalnyomást kell kitartaniuk.
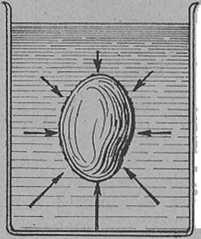
A vízben keletkező súlyveszteség okát most már megtalálhatjuk, még pedig a víznyomásban. Ha egy testet vízbe mártunk, ennek felületére minden irányban hat a nyomás, mint 22. ábránk mutatja. De felül kisebb a lefelé nyomás, mint alul a felfelé nyomás, mert felül kisebb a számba jövő vízmagasság. Az összes nyomásoknak tehát az lesz az eredménye, hogy a testre felfelé erő hat, amelyet felhajtó erőnek nevezünk. Ez a test súlyát csökkenti.
22. ábra. A súlyveszteség magyarázata.
Ha vasdarabot vízbe mártunk, ez az edény fenekéig esik, mert a vas súlya nagyobb, mint a felhajtó erő, amely a kiszorított víz súlyával egyenlő. De mártsunk fadarabot vízbe, akkor a fa súlya kisebb, mint a felhajtó erő, a fa felfelé mozog, míg végül a víz felszínén úszik. A fa addig merül a vízbe, míg annak a víznek súlya, amelyet a vízbe merülő rész kiszorít, ugyanakkora, mint az egész fadarab súlya. Ekkor a felhajtó erő és a fa súlya egymással egyensúlyt tartanak. Könnyen előállíthatjuk azt az esetet is, mikor a test súlya éppen akkora, mint a kiszorított vízé. Kötözzünk vasdarabot parafához, melynek sűrűsége kereken négyszer kisebb, mint a vízé.
Ha a test a vízben még alámerül, akkor vagy kisebb vasdarabot vagy nagyobb parafát kell vennünk. Ha pedig a test a víz felületén úszik, akkor éppen fordítva, a vasat kell nagyobbítani vagy a parafát kisebbíteni. Próbálgatással könnyen elérhetjük, hogy testünk sem alá nem merül, sem a víz felületére nem száll fel, hanem a víz belsejében lebeg, akárhová állítjuk, ott megmarad.
Ennek a lebegésnek még szebb példáját is előállíthatjuk. Mindenki tudja, hogy az olaj a vizen úszik. Az olaj sűrűsége kisebb, mint a vízé. Az alkohol viszont még kisebb sűrűségű, mint az olaj. Ezért ha a vízhez óvatosan alkoholt keverünk, elérhetjük, hogy a keverék sűrűsége éppen akkora, mint a táblaolajé. Ilyenkor az olaj szép gömbalakban lebeg az alkohollal kevert vízben.
A vízben előálló súlyveszteség, mint láttuk, a víznyomát következménye. Ilyen súlyveszteség a levegőben is van, ezért teljesen jogos, ha a víznyomásnak megfelelő jelenséget s levegőben is keressük. Ez a jelenség a légnyomás, melyet először Galilei-nek egyik kiváló tanítványa, Toricelli (1608—1647) mutatott ki és mért meg. Híres kísérlete a következő.
Kb. 1 m hosszú üvegcsövet, melyet egyik végén csappal elzártunk, töltsünk meg higannyal. Fogjuk le ujjunkkal a cső nyílt végét, fordítsuk fel a csövet és állítsuk be higanyt tartalmazó szélesebb edénybe (23. ábra). Ha most ujjunkat elvesszük, a higany a csőben leszáll, de a szélesebb edényben levő higany felszínétől számítva kb. 76 cm magasságban megállapodik. Toricelli a helyes magyarázatot is megadta. A higanyoszlopot az a légnyomás tartja fenn, amely a szélesebb edényben levő higany felületére hat. Tehát a levegő nyomása akkora, mint a csőben levő higanyé. 76 cm magas vízoszlop nyomása cm2-enként 76 g, ennek a higanyoszlopnak nyomása pedig 13,6x76 g, vagyis 1033 g cm2-enként. Ekkora súllyal nyomja a levegő asztalunknak minden cm2-ét.
Okoskodásunk ellenőrzésére nyissuk meg a cső felső csapját rövid időre. Előbb a csőben a higany fölött léghíjas tér (T o r i c e l l i-féle űr) volt, most kevés levegőt engedtünk be.
A csőben a higany leszáll, mert most a külső légnyomással nemcsak a higany nyomása, hanem a csőben levő kevés levegő nyomása is egyensúlyt tart. Ha a csapot egészen kinyitjuk, akkor a higany egészen addig száll le, ahol a szélesebb edényben van.
Nagyon nehézkes lenne ezt a kísérletet mindig elvégezni, valahányszor a légnyomást mérni akarjuk.
A higanyban elnyelt levegőt forralással ki kellene hajtani, a csövet a hozzátapadt levegőtől meg kellene fosztani. Ez pedig nem is egyszerű feladat. Ezért Toricelli berendezését állandó alakban készítik. Ez az eszköz a higanyos barometer (24. ábra). U alakú cső egyik szára hosszú és be van forrasztva, másik szára rövid és széles, nyílt edényben végződik. Ezt éppen úgy megtöltik higannyal, mint előbb mi tettük egyenes csövünkkel. A magasságot a cső mellett levő mm osztályzaton olvassuk le. Ennek az osztályzatnak rendesen csak felső részét készítik el és úgy kell felszerelni, hogy 0 pontja a szélesebb edényben levő higany szintjével essék össze.
Jól tudjuk, hogy a higany állása nagyon ingadozik. A 760 mm higanymagasság, melyet normális légnyomásnak nevezünk, ritkán található.
Ha a déli szél meleg, tehát ritkább levegőt hoz, akkor a barometer higanya esik, ha pedig az északi szél hideg, sűrű levegőt hoz, a barometer emelkedik. Mennyiben lehet ebből az időjárásra következtetni, arról később lesz szó.
A higanyos barometer kényelmetlen és nem hordozható. Ezért szobáinkban inkább a fémes barométert, az aneriod barométert használjuk (25. ábra). Ennek működését az eszköz vázlatos rajzán (26. ábra) könnyen megérthetjük. Belsejében hullámos fedelű fémszelence (D) van, amelyben levegő van elzárva.

23. ábra. Toricelli kísérlete.

24. ábra. Higanyos barometer.
A hullámalak arra való, hogy a felület és evvel együtt a ráható egész légnyomás nagyobb legyen. Ha a külső levegő nyomása nagyobb lesz, akkor a szelence rugalmas falát kissé benyomja. Ha pedig a külső nyomás csökken, akkor a szelencében levő levegő kifelé nyomja a falat. Ezt a kis eltolódást k, k1 és k2 karok, továbbá l fonál segítségével mutatóra (M) visszük át. Az osztályzat úgy készül, hogy a mutató mellé azt a légnyomást írjuk, amelyet ugyanakkor a higanyos barométer mutat.

25. ábra. Aneroid barometer.
A légnyomás alapján méri a repülő, milyen magasra emelkedett.

26. ábra. Az aneroid barometer vázlata.
Ha ugyanis felfelé megyünk, a légnyomás egyre csökken, mert mindig kevesebb levegő van fölöttünk. Az alsó rétegben jó közelítéssel azt mondhatjuk, hogy minden 10 m magasságnak 1 mm-es csökkenés felel meg a légnyomásban. De nagy emelkedésnél ez a számítás már alapos hibára vezethet. A levegő t. i. felfelé egyre ritkul és így folyton nagyobb és nagyobb lesz az a légréteg, amely 1 mm-es esést idéz. Ismerjük azt a törvényt, amely szerint a légnyomás felfelé csökken. Ebből az úgynevezett barométerformulából a légnyomás alapján a magasságot ki lehet számítani. A repülőnek, ha az elért magasságot hitelesíttetni akarja, olyan aneroidot kell vinnie, amely a légnyomást fel is írja (barográf).
A légnyomáson alapuló sokféle eszköz legfontosabbika a légszívó. A legrégibb alakja a köpűs légszívó (27. ábra). Ennek szélesebb csöve (K), a köpű alul keskenyebb csőben folytatódik, amely vízszintes tányérban (T) végződik. A köpüben jól záró dugattyút mozgathatunk fel-alá. A dugattyúban felfelé nyíló szelep (b) van. A tányérra burát (B) teszünk, alája pedig azt az eszközt, amelyet ritkított levegőben akarunk figyelni.

27. ábra. Köpűs légszívó.
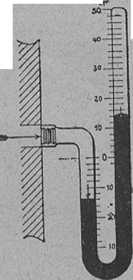
28. ábra. Manometer.
Ha a köpüben a dugattyút felhúzzuk, akkor a dugattyú alatt a köpű levegője megritkul, tehát a (B) bura levegője az (a) szelepen át a köpübe jut. Ha a dugattyút leszorítjuk, az a szelep bezárul, a köpű összenyomott levegője pedig a dugó szelepét (b) kinyitja és a szabadba távozik. Valahányszor ezt a műveletet megismételjük, a bura levegőjének egy részét kiszívtuk. Ha a ritkított levegő nyomását is meg akarjuk mérni, manometerre (U) van szükségünk. A higanyos manometer (28. ábra) egészen ugyanaz, mint a higanyos barometer, csak zárt ága rövidebb. Ezért a higany közönséges légnyomásnál az egész csövet kitölti. Mikor a ritkítás már előrehaladt, a higany a zárt csőben esik. A nyomás a két csőben levő higany felszínének különbségével egyenlő. Rajzunkban a manometer 20 mm nyomást jelez, mert a nyílt szárban a higany felülete 14 mm-rel van az önkényesen elhelyezett mm osztályzat 0 pontja alatt, a zárt szárban 15 mm-rel fölötte.
A légszívónak ezt az alakját Guericke, magdeburgi polgármester (1602—1686) készítette. Légszívója, melyet 1654-ben mutatott be, ma is megvan a müncheni Deutsches Museumban, melyre nagy nyomatékkal hívom fel olvasóim figyelmét. G u e r i c k e légszívója mellett fekszenek az eredeti «magdeburgi félgömbök». Két egymásra illesztett félgömbből kiszívjuk a levegőt. Ekkor a külső levegő a félgömböket összenyomja. Ha a gömbök elég nagyok, akkor a külső nyomás akkora, hogy néhány ló ereje sem elég a széthúzásra.
A köpűs légszívón kívül ma a légszívóknak egész sorát ismerjük. Gaede egymaga négyféle, egészen különböző elveken alapuló légszívót szerkesztett. Ezeknek köszönhetjük, hogy a levegőt annyira tudjuk ritkítani, hogy nyomása csak 1 milliomod mm vagy még ennél is sokkal kisebb marad. A légritkító technikának mai fejlettségét a gyakorlat ki is használja. A rádióban használt elektroncsövek belsejében legalább 1 milliomod mm-ig menő ritkítást kell előállítani.
A léggömb. A levegő felső rétegei.
Az úszásnak szép példája a léggömb. Ha azt akarjuk, hogy a léggömb felemelkedjék, akkor a léggömb teljes súlyának kisebbnek kell lenni, mint a kiszorított levegő súlya. Ezért a gömböt a levegőnél ritkább gázzal kell megtölteni. Montgolfier testvérek, a léggömb első készítői, meleg, tehát ritkább levegőt használtak töltésre. De így a felhajtó erő csak kevéssel múlta felül a léggömb súlyát. Mikor a gömb emelkedett, a magasabb rétegekben a külső levegő is ritkább, ezért hamar vége lett az emelkedésnek. Ezért a legutóbbi ideig hidrogén gázzal töltötték a léggömböt. Ennek viszont más hátránya van. A hidrogén a legjobb burkon is átszivárog és a léggömb mellett a levegővel keveredik. Ez a keverék pedig igen könnyen robban. A felső légrétegben gyakran keletkezik kis villám és akkor máris megvan a baj. Ezért újabban különösen az Amerikai Egyesült Államokban a töltésre héliumot használnak. Itt t. i. gazdag héliumtartalmú forrásokat találtak. A hélium nem robban, nem is ég el. Más országokban nincs annyi hélium, amennyi a léghajózáshoz kellene, az Egyesült Államok pedig katonai okokból a hélium kivitelét nem engedi. Ezért a legtöbb helyen ma is hidrogént kell használni.
A léggömbök ma nem annyira katonai, mint inkább tudományos szempontból fontosak. A léggömböket automatikusan jelző eszközökkel szerelik fel és így a felbocsátott léggömböket a felső légrétegek tanulmányozására használják. Ma a levegőben két réteget különböztetünk meg. Az alsó réteg kb. 10 km magasságig terjed, ez a troposzféra. Ebben a levegő összetétele állandó. Ismeretes, hogy a levegő főleg két gáz keveréke, még pedig térfogatának kereken 4/5 része nitrogén, 1/5 része oxigén. Azonkívül még kisebb mennyiségben több más gáz is van benne, melyek közül elsősorban a széndioxidot említjük, amelyet a növények belélegeznek. A troposzférában a szelek a levegőt állandóan keverik, ezért összetétele mindenüt ugyanaz. Azt is tudjuk, hogy a troposzféra nem mindenütt egyenlő magas. Európa fölött télen 9,5—10 km, nyáron 10,5—11 km. 14 km-en túl sohasem terjed, a legtöbb megfigyelésnél 12 km-en alul marad. Amerika fölött a troposzféra 1 km-rel magasabb.
A troposzféra fölött van a sztratoszféra. Ide a felszálló áramlatok már nem érnek, összetételéről kevés tapasztalatunk van. A levegő egyre gazdagabb lesz könnyű gázokban. Körülbelül 70—80 km magasságban a nitrogénből és oxigénből álló légkört hidrogén légkör váltja fel. Az újabb megfigyelések azonban azt mutatják, hogy a felső rétegekben nehezebb gázok is vannak, mint pl. oxigén.
Ezt az alkalmat fel akarjuk használni arra, hogy mindjárt a felső légrétegek meteorológiai viszonyait is röviden jellemezzük. 4 km-rel a talaj fölött az évi átlagos hőmérséklet —12° és felfelé a sztratoszféráig km-enként 6—7°-kal csökken. A sztratoszféra alsó határán a hőmérséklet kb. —55° és felfelé alig változik, csak néha kissé emelkedik. Ahol a sztratoszféra magasabban kezdődik, ott a hőmérséklet az alsó határán alacsonyabb. — 60°-on is alul lehet.
A troposzféra legfelső részében a szél sebessége jelentékeny. Középeurópa fölött óránként 240 km-t, Észak-Amerika fölött 300 km-t elérhet. A sztratoszférában a szél sebessége lényegesen lecsökken. Viharfelhők a sztratoszférába nem szoktak behatolni, nagyobb elektromos kisülések (villám) szintén nem fordulnak elő.
A sárkány.
Ki nem engedett fel gyermekkorában sárkányt, ezt az ősrégi, valószínűleg Kínából eredő gyermekjátékot? A fizikus már jó ideje komolyabb szemmel nézi. Franklin Benjámin használta először fizikai célokra, mikor 1742-ben a légköri elektromosság tanulmányozására sárkányt bocsátott fel. Bizonyos tekintetben a sárkány a repülőgép előde. Ezért néhány szóval leírjuk a sárkány működését.
Legyen ABCD (29. ábra) a sárkány lapja, amelyet csak egyszerűség kedvéért mutat rajzunk négyszögnek, egyébként akármilyen alakú lehet.
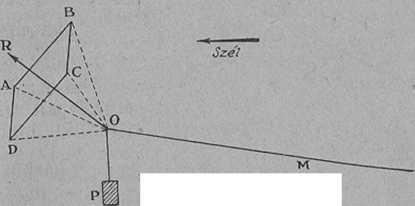
29. ábra. A sárkány.
A lapot fonalak (AO, BO, CO, DO) tartják, melyeknek közös pontjából (0) indul a sárkány kötele (M). A sárkány önműködően jelző eszközöket is hordoz, ezeket P súly ábrázolja. A szél irányát nyíl jelzi. Erre a sárkányra három erő hat. Először is saját súlya, melyhez a megterhelést is hozzászámítjuk. A szél is nyomja a sárkányt a lapra merőleges irányban M erővel. Ezt a két erőt kiegyensúlyozza az a húzás, amelyet a kötélen lefelé kifejtünk. Így a sárkány egyensúlyban marad, a levegőben lebeg. Ha nincs szél vagy csak gyenge szél van, akkor a gyermek kezében a kötéllel futni kezd és evvel szelet csinál.
Egyetlen sárkánnyal 1000 m magasságot sikerült elérni. Avval, hogy négy sárkányt kötöztek egymás fölé, 4000 m-ig jutottak el. Ekkor egyik sárkány a másikat hordozza. Repülésre a sárkányt először Hargrave használta (1894). B a d enpowell, angol tiszt 1896-ban 100 m-re emelkedett sárkányon, Cody, francia kapitány pedig 1906-ban több száz méterig jutott. A háború alatt léggömbökön kívül sárkányokat is használtak légi megfigyelőállomások céljára.
A siklórepülő.
A motoros repülőnek másik előde a siklórepülő, mely nélkül nem tudták volna elvégezni azokat a kísérleteket, amelyek a motoros repülő pontos ismeretéhez szükségesek voltak. A módszeres és kitartó kísérletezés Lilienthal
érdeme, aki vakmerő vállalkozásáért életével fizetett.
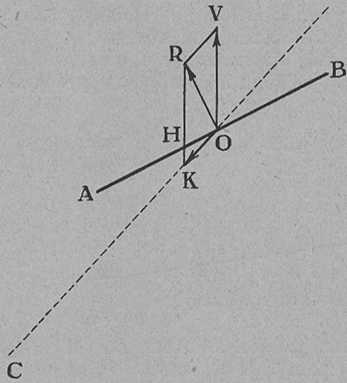
30. ábra. A szélcsendben leszálló siklórepülés magyarázata.
A siklórepülő lényegében nagy kiterjedésű sík felület, melynek kiterjedése legalább 10m2, de eléri az 50 m2-t is. Az egysíkú (monoplán) repülőn kívül használnak két párhuzamos síkból álló (biplán) vagy akár több párhuzamos síkkal szerkesztett (multiplán) siklórepülőt. Ezen a hordfelületen van a pilóta ülőhelye, ennek oldalán pedig a kormányok.
Szélcsendben a siklórepülővel csak leszállni lehet. A madarakon megfigyelték, hogy magas helyről le tudnak szállni úgy, hogy szárnyuk teljesen nyugodt marad. Kis figyelemmel ezt a jelenséget és egyúttal a siklórepülő leszállásának elvét megérthetjük. Legyen AB (30. ábra) a madár szárnyának vagy a siklórepülő szárnylapjának metszete, OC pedig a leszállás iránya. A lap és a leszállás irányát meg lehet választani úgy, hogy a leszállás egyenletes sebességgel menjen végbe.
Tudjuk, hogy minden mozgással szemben közegellenállás lép fel, amely, mint mindig, merőleges a mozgó lapra. Rajzunkban az OR erő jelenti ezt a közegellenállást. Az OR erőt úgy tekintjük, hogy a függőleges OV erő és a menet irányába eső OK erők eredője. Mint már tudjuk, ekkor az OR erőt erre a két összetevőre bontottuk fel.
Más szóval az OR erőt evvel a két erővel helyettesítjük. Ha a sebességet megfelelően választjuk, elérhetjük, hegy OV erő éppen akkora legyen, mint a készüléknek lefelé ható súlya. Ekkor ez a két erő kiegyenlíti egymást. Az OK erő legyőzi azt az ellenállást, amelyet a levegő a menet irányában kifejt. Ha az OK erő erre a célra éppen elég, akkor a lap mozgását erő nem gyorsítja, vagyis a lap egyenletesen siklik. Egyúttal azt is látjuk, hogy ha a siklórepülő szélcsendben leszáll, a hordfelületet (AB) kissé fel kell emelni.
Ha szél van, melynek iránya és erőssége változó, akkor a siklórepülő a vitorlás repüléssel halad tovább. Ennek lényegét a következő magyarázata, egyszerű példából érthetjük meg. Vegyük fel, hogy a szél vízszintes síkban fúj és a repülő a szél ellen halad. Legyen a a szél, b a repülő iránya (31. rajz). Ha a szél iránya kissé elfordul, mégpedig a repülőnek baloldala felé (c), akkor a gép tengelye megmarad az előbbi irányban, csak a lap a tengely körül kevéssé jobbra fordul. Ha pedig a szél kelet felé tér el (d), akkor a lap balra hajlik. A hajlás nagyságát úgy kell választani, hogy a levegő ellenállásának függőleges összetevője (a 30. ábrában OV) a készülék súlyával legyen egyenlő. Ha ugyanakkor a lap kissé előre is hajlik, akkor sebességét növelheti.
30. ábra A vitorlás repülés magyarázata.
Ha a szél gyengül, akkor a repülő lefelé száll, ellenben mikor a szél erősödik, a repülő emelkedik. Az ilyen vitorlázó repüléshez még csak az kell, hogy a szél ingadozásai elég erősek legyenek.