CAPÍTULO 2
Las leyes matemáticas del universo
Durante la revolución científica, muchos estudiosos dirigieron la vista hacia el cielo para estudiar el movimiento de los planetas y descubrir las leyes que regían sus órbitas, que parecían contradictorias en una simple observación. Tal empeño se hizo realidad gracias a Newton, una mente genial que encontró la relación entre la atracción de los planetas y la que experimentaban los cuerpos sobre la Tierra.
Antes del siglo XVII existían muy pocos matemáticos profesionales. Lo habitual era que personas que se ganaban la vida con otros oficios, o que procedían de familias acomodadas, se dedicaran a las matemáticas por vocación y no por necesidad. Así, Copérnico era administrativo, Viète y Fermat trabajaban de juristas, Napier pertenecía a la aristocracia escocesa, Descartes se dedicaba principalmente a la filosofía, etcétera.
Por otra parte, desde el Renacimiento, los nobles europeos se aficionaron a la ciencia y muchos se convirtieron en mecenas de científicos. Suponía un grado de distinción apadrinar a intelectuales de renombre, que acostumbraban a realizar calendarios, pronósticos astrológicos o informes sobre cualquier asunto que les encargaran.
No obstante, durante mucho tiempo los científicos fueron trabajadores solitarios que desconocían lo que se investigaba en otros lugares. Por esta razón, era frecuente que distintos científicos llegasen a las mismas conclusiones de manera independiente. Aun con la invención de la imprenta, los libros de ciencia y, especialmente, los de matemáticas, se difundían poco comparados con otros. Las obras se daban a conocer casi exclusivamente entre los aficionados a la ciencia y sus resultados no obtenían la repercusión deseable. Además, era usual que los libros apareciesen de forma póstuma, ofreciendo resultados que habían sido descubiertos décadas atrás o ya presentados por otros autores. Esta situación desató numerosas polémicas sobre quién había sido él descubridor de una u otra teoría.
Sin embargo, en el siglo XVII, todo cambió con el surgimiento de círculos y sociedades que contaban con un importante medio de difusión; las revistas científicas.
ANNUS MIRABILIS
Tras abandonar Cambridge a causa de la epidemia de peste, Newton regresó a su casa natal en Woolsthorpe. Allí pasó dos años sumergido en una frenética creatividad. También se quedó una temporada en Boothby Pagnell, un pueblo cercano a cargo de cuya rectoría se encontraba su amigo Humphrey Babington. Como el propio científico indicó, fue durante aquella estancia cuando calculó el área de la hipérbola con una precisión nunca antes alcanzada.
Newton regresó a Cambridge en marzo de 1666, pues, al parecer, la plaga había remitido y la universidad abrió de nuevo sus puertas. Sin embargo, un par de meses después, la peste rebrotó y se cerró la universidad hasta la primavera del año siguiente.
El bienio formado por 1665 y 1666 es conocido como «los años maravillosos», pues fueron los más fructíferos en la historia de la ciencia. Newton modificó los cimientos de la matemática y la física e inauguró la era de la ciencia moderna. Él mismo explicó, en una nota escrita cincuenta años después, cómo realizó aquellos cruciales descubrimientos:
A comienzos de 1665 descubrí el método de las series aproximativas y la regla para reducir cualquier dignidad de todo binomio en dichas series. En el mes de mayo del mismo año descubrí el método de las tangentes de Gregory y Slusius, y en noviembre obtenía el de las fluxiones. En enero del año siguiente desarrollé la teoría de los colores y en mayo había empezado a trabajar en el método inverso de las fluxiones. Ese mismo año comencé a pensar en la gravedad extendida a la órbita lunar —habiendo descubierto cómo estimar la fuerza con la cual un globo, que gira dentro de una esfera, presiona la superficie de esta— a partir de la regla de Kepler, según la cual, los tiempos periódicos de los planetas guardan una proporción sesquiáltera de sus distancias con respecto al centro de sus órbitas, deduje que las fuerzas que mantienen a los planetas en sus órbitas deben ser recíprocas a los cuadrados de sus distancias de los centros alrededor de los cuales giran. Por lo cual, comparé la fuerza necesaria para mantener la luna en su órbita con la fuerza e gravedad en la superficie de la Tierra, y descubrí que estas eran muy parecidas. Todo esto corresponde al periodo 1665-1666, los años de epidemia. Porque en aquel tiempo me encontraba en la plenitud de mi ingenio, y las matemáticas y la filosofía me ocupaba más de lo que lo harían nunca después.
Al regresar a la universidad, Newton ya había descubierto las tres teorías que colocarían su nombre en el altar de las divinidades. Con solo veinticuatro años, había cambiado radicalmente la ciencia y ya no volvió a investigar más. El resto de su vida lo dedicó a perfeccionar y corregir sus resultados.
Curiosamente, nunca quiso dar publicidad a sus logros. Aunque era consciente de la importancia de estos, no consideraba que pudieran tener interés para otros. A lo largo de su vida, siempre minusvaloró sus descubrimientos, y solo los defendió cuando otras personas intentaron arrebatárselos. Su afán perfeccionista, por otra parte, le impedía dar a conocer nada que no hubiera trabajado hasta la extenuación. Todo lo que publicó fue siempre por petición de sus amistades y después de muchos ruegos.
Y DE LA MANZANA, ¿QUÉ?
Pero antes del regreso de Newton a la universidad es obligado detenerse en la que es considerada su anécdota más famosa, es decir, la que asegura que descubrió la ley de la gravedad mirando caída de una manzana.
Aunque se desconoce si el episodio es cierto o falso, varios de sus biógrafos lo recogen en sus obras. Así lo relató, por ejemplo, John Conduitt (1688-1737):
[…] Y mientras meditaba en un jardín, le vino al pensamiento la idea —suscitada por la caída al suelo de una manzana— de que el poder de la gravedad no se limitaba a una cierta distancia de la Tierra, sino que este poder debía extenderse mucho más allá de lo que normalmente se creía. «¿Por qué no hasta la luna?» Se dijo a sí mismo. Y si esto era así, ese hecho debería influir en su movimiento y, quizá, retenerla en su órbita; lo que le llevó a calcular cual seria el efecto de esa suposición.
Newton contó esta historia cincuenta años después de haberse producido, lo que hace sospechar que, tal vez, lo hizo para alimentar una imagen de genio que no necesitaba. Ciertamente, no parece propio de su carácter sacar conclusiones tajantes después de una mera observación. Su método de trabajo se basaba en el rigor y la constancia, por lo que parece más probable que, tras observar la Luna durante meses, extrajese la hipótesis y luego la demostrase mediante ecuaciones. Ya en 1664, según comentaba Wickins, su compañero de cuarto, había pasado incontables noches en vela estudiando la aparición de un cometa, actitud que encaja mejor con la idea que tenemos de Newton.
REGRESO A LA UNIVERSIDAD
Al volver a la universidad Newton retomó el mismo ritmo de trabajo que se había impuesto en los meses anteriores a su cierre. Esporádicamente, se ocupaba de varios problemas matemáticos en torno a tangentes y cuadraturas. A pesar de todo, a finales de 1666 dio el trabajo por terminado y pospuso el asunto un par de años.
Durante ese tiempo, centró su mirada en otras materias. En su cuaderno Quaestiones, bajo el epígrafe Sobre el movimiento violento, se adentró en la mecánica planteando el principio de la inercia de los cuerpos en movimiento. Mientras que en el cuaderno baldío se limitaba a apuntar ideas que le surgían durante la lectura, lo que anotaba ahora eran soluciones a los problemas y vías de estudio alternativas. Así, desarrolló la influencia de las fuerzas en los impactos y perfeccionó lo que en el futuro serían las leyes del movimiento.
El estudio sobre los colores fue otro de sus focos de interés. Al parecer, tras estudiar la obra sobre los colores de Robert Boyle y la Micrographia de Robert Hooke, rechazó sus resultados y se lanzó a formular una teoría diferente. Comenzó realizando experimentos con prismas y terminó planteando una teoría del color que revolucionó los conceptos vigentes en la época.
Sus investigaciones no le impidieron proseguir con su trabajo en la universidad. El 2 de octubre de 1667 consiguió el título de minor fellow, nombre que recibían los becarios de investigación con baja especialidad. Ocho meses después alcanzó el nivel de major fellow. Ese mismo año de 1668 obtuvo el título de Master of Arts, que llevaba aparejada la obligación de ordenarse en la Iglesia anglicana en un plazo máximo de siete años. Esta situación le acarreó numerosos problemas, que casi le hicieron abandonar sus estudios.
Al parecer, la relación con los compañeros, salvo con Wickins siguió brillando por su ausencia. Resulta llamativo que, pese a vivir en el Trinity College durante veintiocho años, no dejara apenas recuerdos en sus colegas fellow. Posiblemente, mientras Newton vivía obsesionado con sus investigaciones. Wickins contaba una anécdota que da fe de la entrega de Newton: tenían un gato en la habitación que llegó a engordar varios kilos solo con la comida que el científico dejaba en el plato sin tocar.
EL ALQUIMISTA
Entre las obsesiones que robaban el sueño a Newton se encontraba el estudio de la alquimia. En 1669, en su primera visita a Londres, sus cuentas reflejan una importante adquisición de material de laboratorio relacionado con aspectos químicos: un horno, un mezclador, productos químicos variados y una recopilación de tratados alquímicos.
Es posible que Newton tomara contacto con la alquimia durante su estancia en casa del boticario Clark, ya que en aquella época aparecen es sus cuadernos anotaciones sobre productos y fórmula medicinales. Lo cierto es que alrededor de 1670, según contó el propio Newton, dispuso en su habitación varios hornos para realizar experimentos alquímicos. En una ocasión, a causa de uno de estos experimentos, su cabello se tornó blanco. Wickins, sin embargo, lo atribuía en broma a que pensaba demasiado.
LA ALQUIMIA

Pese a que se considera que la alquimia había nacido en China, fueron los científicos árabes los que potenciaron el trabajo en laboratorio. El principio formulado por Platón según el cual unos elementos se podían convertir en otros fue lo que dotó de fundamento a esta disciplina. Por una parte, la alquimia llevaba a cabo operaciones químicas habituales como evaporaciones, destilaciones o estudios de las propiedades de los elementos, pero por otra, seguía interesada en la transmutación de los metales, la búsqueda del elixir de la vida o la búsqueda de la piedra filosofal, que permitía convertir el plomo en oro. A partir del siglo XIV su carácter esotérico le valió el rechazo de los científicos. Se convirtió en una ciencia oculta, y los alquimistas tuvieron que trabajar en secreto. A pesar de todo, en el siglo XVI la alquimia vivió un cierto resurgir: al aumentar la demanda de productos industriales, creció el estudio de los productos químicos y sus aplicaciones. Contó con figuras de relieve como Paracelso (1495-1541), alquimista y médico suizo que usó conocimientos alquímicos en el mundo de la medicina. Gracias a él, la industria farmacéutica comenzó a trabajar con preparados químicos minerales, convirtiéndose en los primeros medicamentos artificiales producidos en laboratorios. Sin embargo, en el siglo XVIII, los sucesivos avances en el campo de la química, cada vez más rigurosa y racional, acabaron por desterrar definitivamente esta disciplina.
Aunque Newton mantuvo oculta su afición por la alquimia durante toda su vida, sus escritos y los libros de su biblioteca revelan que estaba al corriente de las diversas tendencias en la materia y que se carteaba con otros aficionados.
Uno de ellos fue el inglés Robert Boyle, quien fue un ferviente alquimista, pero que, al mismo tiempo, es considerado el padre de la química moderna. En su opinión, los conocimientos sobre química alcanzados hasta aquel momento carecían de la consistencia suficiente para conformar una ciencia. Por eso, en su obra principal, El químico escéptico, insistía en la experimentación científica para convertir en verdaderas las teoría presentadas. También abogaba por emplear una terminología estándar para explicar los nuevos productos y las reacciones entre ellos.
EL GENIO SE DA A CONOCER
A pesar de que Newton había revolucionado la ciencia, seguía siendo un estudiante desconocido. Solo las personas más cercanas, aun sin saber de sus logros, percibían su valía, especialmente Barrow. Aunque sus primeros contactos no fueron muy prometedores, la relación entre Newton y Barrow fue estrechándose y, en 1669, este último le pidió que revisara un manuscrito sobre lecciones de óptica que deseaba publicar. Newton cumplió con su cometido, a pesar de que las teorías de su colega debieron de parecerle desfasadas. El trabajo satisfizo a Barrow, que, al año siguiente, contó con él para revisar sus lecciones de geometría. Todo indica que su relación debió de ser fluida y que Barrow conocía los descubrimientos de Newton.
Como se ha comentado anteriormente, en 1668 Nikolaus Mercator publicó Logarithmo-technica. En esta obra, además de estudiar los logaritmos, Mercator utilizaba series infinitas para hallar el área de la hipérbola. El matemático inglés John Collins le envió un ejemplar a Barrow, quien le respondió que un amigo suyo ya había hecho lo mismo hacía dos años. En cuanto tuvo noticias, Collins solicitó más información, Barrow, entonces, pidió a Newton que pusiera por escrito sus resultados para enseñárselos a Collins y reclamar su paternidad.
Newton escribió así De analysi per aequationes numero terminorum infinitas (Sobre el análisis por series infinitas). En él demostraba que empleando el desarrollo en series de potencias se podían calcular series armónicas mediante logaritmos. En pocos días se lo envió a Collins, a través de Barrow, sin indicarle quién era el autor y solicitándole, además, que devolviera el manuscrito una vez leído. Collins se entusiasmó al descubrir la genialidad de los métodos que se explicaban en él. Tras la insistencia a Barrow, Collins descubrió que el autor era Newton. Como dio por sentado que Newton estaría deseoso de ver reconocidos sus méritos, Collins copió el manuscrito y empezó a mostrarlo sin permiso. Así, se lo envió a matemáticos con los que mantenía correspondencia, como David Gregory, René Sluse o Giovanni Alfonso Borelli. Luego, escribió a Newton preguntándole si podía leer la obra en una reunión de la Royal Society. Tras recibir la negativa del científico, Collins se dio cuenta de que se había extralimitado y mantuvo en secreto las copias que había realizado.
Tanto Collins como Barrow trataron de convencer a Newton de que publicara su trabajo. Ambos le sugirieron que el texto figurase como apéndice de un libro de Barrow que estaba a punto de ver la luz, pero el genio se mostró inflexible.
La práctica sugerida por Collins y Barrow no era inusual. Cuando un matemático publicaba un libro, solían añadirse apéndices con textos de otros matemáticos que guardasen relación con el asunto de la obra. Esto sucedía así por la dificultad que entrañaba publicar un libro sobre matemáticas en aquella época.
En cualquier caso, los tímidos signos de apertura de Newton fueron aprovechados por sus colegas. Barrow le pidió que revisara y anotara una traducción al latín del Álgebra, de Gerard Kinckhuysen que pretendía publicar Collins. Las observaciones que hizo Newton aumentaron su fama entre los matemáticos. Sin embargo, una vez más, exigió que su nombre no apareciera.
JOHN COLLINS

Entrada de la Royal Society, en la que John Collins fue bibliotecario y nexo de unión entre los matemáticos de la época.
El inglés John Collins (1625-1683) contribuyó a difundir por el continente europeo los descubrimientos matemáticos de la época. Tras la guerra civil inglesa, se dedicó a la navegación durante siete añosos, sin dejar de profundizar en las matemáticas. Posteriormente, ejerció de maestro hasta 1660, año en que aceptó un puesto de administrativo. Fundador de una librería, se dedicó a publicar libros propios y ajenos. Entre los suyos figuran obras sobre aritmética, relojes de sol o trigonometría aplicado a la navegación. Publicó las Lecciones de Barrow y el Álgebra de Wallis, así como ediciones de obras de Apolonio y Arquímedes. Pero la labor por la que ha pasado a la historia es por haber sido el nexo de unión entre los matemáticos del momento. Desde su puesto de bibliotecario en la Royal Society, enviaba libros recién publicados a todo aquel que lo deseaba, acumulando una impresionante correspondencia entre matemáticos como Wallis, Barrow, Leibniz, Gregory o, por supuesto, Newton. En 1712 la Royal Society compiló las misivas y las publicó con el título de Commercium epistolicum. La obra fue utilizada como prueba en la polémica en torno al descubrimiento del cálculo entre Newton y Leibniz. Pero, sobre todo, fue la primera persona que dio a conocer al mundo el genio de Isaac Newton.
ROMPER EL AISLAMIENTO
El aislamiento en que hasta entonces había permanecido Newton no era infrecuente. Durante el Renacimiento, la figura del estudioso matemático era más bien la de un sabio solitario que investigaba y, en ocasiones, divulgaba sus resultados. Eran pocos los investigadores profesionales que pudiesen vivir de las matemáticas. Cuanto mucho, alguno conseguía una cátedra que le permitía desarrollar su labor docente mientras investigaba sus propias teorías, como le sucedió a Newton. Hoy en día, inmersos en la era de información, en la que cualquier hecho que ocurre en un lugar de la Tierra puede ser inmediatamente conocido en la otra punta, puede resultar complicado imaginar el aislamiento de un científico del pasado milenio. En la actualidad, cualquier científico puede trabajar codo con codo con compañeros que se encuentran físicamente muy alejados, pero en el siglo XVI no era así.
Por otra parte, algunos científicos que no ansiaban reconocimiento, como Fermat o Newton, se resistían a publicar sus descubrimientos. No fue el caso de Gilles de Roberval (1602-1675), quien ocultó sus logros por razones más prosaicas. El matemático francés, uno de los precursores del cálculo, ideó el llamado «método de los indivisibles», que servía para calcular la cuadratura de las superficies y el volumen de los sólidos. Sin embargo, no divulgó su hallazgo durante cuatro décadas para no perder la cátedra Ramus en el College Royal. Gracias a ello, cuando debía defender su plaza frente a otros candidatos cada tres años, siempre podía proponer problemas que estaba en disposición de resolver. No obstante, al no publicar apenas nada en vida, la autoría de sus descubrimientos quedó en entredicho.
Esto explica que las teorías pudieran tardar meses o años en ser conocidas por otros científicos. Sin embargo, la situación comenzó a cambiar en ese mismo momento. En primer lugar, empezaron a surgir los círculos, en los que una serie de científicos se reunían para intercambiar información sobre cualquier descubrimiento del que tuvieran noticia, fuese suyo o de otros. Uno de los más conocidos fue el Círculo de Mersenne, un grupo matemático que se reunía en torno al sacerdote francés Marín Mersenne, teólogo, matemático y descubridor de los números primos que llevan su nombre. En su celda del convento de L’Annonciade de París se congregaban de forma periódica una serie de matemáticos para intercambiar ideas y conocimientos. Aunque no todos podían asistir físicamente a las reuniones, al círculo pertenecieron, entre otros, matemáticos como Descartes, Pascal, Roberval, Desargues, Fermat y Gassendi.
El grupo de Mersenne acabó fusionándose con uno similar formado por los bibliotecarios reales Pierre y Jacques Dupuy, cuya unión constituyó el germen de la Academia de las Ciencias de París. Un caso parecido fue el del círculo inglés surgido en torno al diácono alemán Theodore Haak (1605-1690), conocido como Grupo 1645, y que más tarde dio lugar a la Royal Society.
Otro círculo relevante se formó alrededor del filósofo y teólogo francés Nicolás Malebranche (1638-1715), sacerdote de la congregación del Oratorio de San Felipe Neri. Este se reunía en la propia congregación con figuras de la talla de Pierre Varignon, el marqués de L’Hòpital o Johann Bernoulli. Malebranche no solo dio a conocer los descubrimientos de Newton y Leibniz en Europa, sino que editó la obra de L’Hòpital, la primera que se imprimió sobre el cálculo.
LAS SOCIEDADES CIENTÍFICAS
Aunque los círculos científicos ayudaron a expandir el conocimiento, su verdadera difusión llegó con la continuación lógica de estos: las sociedades científicas. La primera de la que se tiene noticia se creó en Roma en 1603 y era conocida como Accademia dei Lincei (Academia de los Linces). Fue auspiciada por el príncipe Federico Cesi y su labor se prolongó hasta la muerte de este en 1630. La figura más prominente de la academia fue Galileo Galilei. En 1623 esta publicó una de las obras mayores de Galilei, El ensayador, que incluía una de sus frases más celebres: «Las matemáticas son el alfabeto con el que Dios ha escrito el universo».
En 1657 el duque de Toscana, Fernando II, y el príncipe Leopoldo crearon en Florencia la Accademia del Cimento (Academia del experimento). A ella pertenecieron dos discípulos de Galileo: Evangelista Torricelli, inventor del barómetro, y el físico y matemático Vincenzo Viviani, a quien se debe el teorema que anuncia que la suma de las distancias desde un punto a cada uno los lados de un triángulo equilátero es igual a la altura del triángulo. Otros integrantes fueron el físico y matemático Giovanni Alfonso Borelli o el médico Marcello Malpiaghi.
En 1666 Jean-Baptiste Colbert, ministro de Luís XIV, creó en París la Académie des Sciences, que llevó a cabo sus actividades hasta la Revolución francesa. Entre los objetivos fundacionales figuraba «Animar y proteger el espíritu de la investigación, y contribuir al progreso de las ciencias y sus aplicaciones». Entre sus fundadores se contaban Descartes, Fermat o Pascal. Como en otras academias, incorporó a miembros extranjeros. Así, en 1669 ingresaron en ella Bernoulli, Viviani y el propio Newton.
A finales del siglo XVI se creó en Berlín la Academia Prusiana de la Ciencias a instancias de Leibniz, su primer presidente. Fue respaldada por el príncipe Federico III, elector de Brandenburgo. A diferencia de las anteriores, esta academia se preocupo tanto de las ciencias como de las humanidades, y a ella llegaron a pertenecer Voltaire, Diderot o Immanuel Kant.
LA ROYAL SOCIETY
Pero, sin duda, la sociedad científica más importante que se creó en esa época, y que sigue vigente en la actualidad, es la Royal Society.
A principios de la década de 1650, había surgido en Oxford un círculo filosófico alrededor del clérigo naturalista inglés John Wilkins (1614-1672), a la sazón director del Wadham College. En sus propias dependencias se reunían una serie de científicos interesados en debatir sobre la nueva ciencia, especialmente sobre el método experimental. A ese círculo pertenecían, entre otros, John Wallis, Robert Boyle, Robert Hooke o el filósofo y teólogo alemán Henry Oldenburg. Mención aparte merece el matemático y arquitecto Christopher Wren, quien diseñó algunos de los mejores edificios londinenses tras el gran incendio de Londres de 1666.
Tras la restauración de los Estuardo (1660), el círculo de Oxford se disolvió y muchos de sus miembras se instalaron en Londres, donde siguieron las reuniones de manera informal. Varios de los científicos entraron como profesores en el Gresham College. Allí fundaron la Royal Society of London for the promotion of natural Knowledge (Real Sociedad de Londres para la promoción del conocimiento natural). Durante los primeros quince años su director fue el matemático aficionado lord Brouncker y la sociedad cosechó éxito rápidamente: solo entre el 20 de mayo y el 22 de junio de 1662 se invitó a 119 miembros.
A diferencia de otras academias, la Royal Society no contaba con el respaldo económico de ningún tipo. Esto les hizo atravesar con frecuencia apuros económicos, sobre todo al principio. En cambio, no les afectó cuando menguaron las fuentes de financiación, como les ocurrió a las academias italianas, lo que contribuyó a su longevidad.
Desde el principio, uno de los intereses de la Royal Society fue el estudio y el desarrollo de las ciencias más experimentales. Su filosofía se resumía en el lema de la sociedad: Nulluis in verba (En palabras de nadie). Esto significaba que, con independencia del prestigio del investigador, solo se aceptaría aquello que pudiera ser demostrado. Se planteó que en cada reunión se presentaran varios experimentos y se creó la figura del curator para planificarlos, cargo que recayó en Robert Hooke. Asimismo, se nombró bibliotecario a John Collins y secretario a Henry Oldenburg. Este último, que ocupó el cargo hasta su muerte, realizó una labor primordial haciendo de nexo de unión entre los científicos de toda Europa. Todas las cartas le llegaban a Oldenburg, quien, tras guardar una copia, las remitía a sus destinatarios. De esta manera, quedaba constancia de quién trataba por primera vez un asunto determinado, evitando disputas posteriores sobre su autoría.
LOS MEDIOS DE DIFUSIÓN
En las reuniones de la Royal Society se realizaban experimentos propuestos por los miembros o por el propio encargado de experimentos, y se leían cartas y manuscritos de los socios que informaban de avances o consultaban dudas. Pero a esas reuniones no podían asistir todos los socios, ya que muchos vivían lejos.
Este escollo lo salvó la aparición de las revistas científicas, con frecuencia vinculadas a las sociedades. La primera revista de divulgación como tal fue el Journal des Sçavans, aparecida en París en enero de 1665 y fundada por el asesor parlamentario Denis de Sallo bajo los auspicios del ministro de Luis XIV Jean-Bapatiste Colbert. En realidad, no era solo científica e incluía legislación y necrológicas de personas influyentes. En ella se publicaron trabajos de Descartes. Huygens, Hooke o Leibniz.
«No hay nada más necesario para promover los avances de los asuntos filosóficos que la comunicación de los mismos».
— HENRY OLDENBURG, EN LA CARTA DE PRESENTACIÓN DE LAS PHILOSOPHICAL TRANSACTIONS.
Un par de meses después, en marzo de 1665, apareció Philosophical Transactions, que fue la cabecera más importante de la época y que sigue editándose en la actualidad. Inicialmente, surgió como un encargo personal del secretario Henry Oldenburg, pero más tarde se convirtió en el órgano oficial de difusión de la sociedad.
Desde el principio, resultó patente la importancia de la revista en la divulgación de la nueva ciencia. Fue el modelo en el que se fijaron las revistas científicas que salieron después. En ella se incluían reseñas de publicaciones, semblanzas de matemáticos fallecidos, cartas de los miembros o requerimientos de otros socios. También fue la primera en que se establecieron unas normas de publicación.
Por último, entre las publicaciones relevantes aparecidas en el siglo XVII, también destacó Acta Eruditorum. Fue fundada por el filósofo y científico alemán Otto Mencke, en 1682, a instancias de Gottfried Wilhelm Leibniz. Se trata de la primera revista que publicó, en 1684, un artículo sobre cálculo infinitesimal, en este caso escrito por el científico y filósofo alemán.
ROBERT HOOKE

Uno de los científicos más completos del siglo XVII es el inglés Robert Hooke (1635-1703), quien abordó disciplinas como la astronomía, la química, la biología, la geología, la anatomía, la cristalografía, la meteorología, la mecánica, la óptica, la arquitectura, etcétera. Diseño multitud de instrumentos científicos, algunos de los cuales se siguen utilizando en la actualidad. Comenzó su carrera científica como ayudante de Robert Boyle, hasta que fue elegido curator de la Royal Society. También fue secretario, pero solo durante un breve período, y trabajó como arquitecto junto a Christopher Wren diseñando edificios para la reconstrucción de Londres tras el incendio de 1666. Lamentablemente, muchas de estas obras se han perdido. Era un científico con una inventiva extraordinaria, pero abarcaba tantos temas que sufría carencias en muchos de ellos, con lo que sus brillantes ideas no siempre llegaban a buen puerto. Debido a ello, se vio envuelto en numerosas polémicas a lo largo de su vida. Si algún científico presentaba una nueva teoría, era frecuente que a él se le hubiera ocurrido antes, aunque no la hubiese formalizado. Eso fue lo que le ocurrió con Newton en sus disputas sobre los colores o la gravitación. También protagonizó sonoras polémicas con Oldenburg y Huygens. La relación de Hooke con Newton recuerda, en ocasiones, a la de Salieri respecto a Mozart. En este caso, sin embargo, Newton, a la muerte de Hooke, se encargo de hacer desaparecer prácticamente todo rastro de los logros de Hooke. En cualquier caso, su valía como científico resulta innegable, y llegó a ser bautizado como El Leonardo de Londres.
DE ESTUDIANTE A PROFESOR
En 1669 Isaac Barrow decidió dejar la cátedra Lucasiana y propuso a Newton para que lo sustituyera. Ciertos historiadores sospechan que Barrow, al conocer la obra De analysi, reconoció que su discípulo era superior a él y prefirió dar un paso atrás. Una segunda hipótesis sostiene que Barrow aspiraba a puestos más elevados, pues al año siguiente fue nombrado capellán real, y tres años más tarde, director del Trinity College. Sin embargo, no parece que fuese obligatorio renunciar a la cátedra para desempeñar esas labores. Westfall, en su biografía de Newton, plantea una tercera posibilidad: esto es, que Barrow se considerara más teólogo que científico y renunciara para dedicarse por entero a la teología. Fuese como fuese, lo cierto es que Barrow designó a Newton para sustituirle en la cátedra y, como entonces no existían oposiciones ni concursos de méritos, la contratación fue directa y sin intermediarios.
El catedrático lucasiano debía impartir una conferencia semanal sobre matemáticas y otras diez al año. Barrow ya se había saltado esta norma limitando las conferencias a un solo trimestre. Lo mismo hizo Newton, que solo entregó cuatro manuscritos. Estos, además, se parecían más a guiones de clase que a conferencias totalmente estructuradas. Esta falta de interés quizá se deba a que estaba enfrascado en el estudio de los colores. Hay constancia de que el año anterior había comprado varios prismas con los que estaba realizando experimentos sobre la luz. De hecho, las primeras clases que impartió fueron sobre óptica. Conviene recordar que por aquel entonces la óptica, así como la astronomía y la estática, se consideraban parte de las matemáticas aplicadas.
Como profesor no se puede decir que Newton cosechara un éxito apoteósico. A pesar de la fama que alcanzó como científico, muy pocas personas recordaban sus clases, que contaban con muy poca asistencia. Es probable que las dedicase a los experimentos o teorías que estaba desarrollando, con lo que casi nadie debía de poder seguir sus razonamientos. El teólogo y matemático William Whiston (1667-1752), discípulo de Newton y su sustituto en la cátedra, comentó que había asistido a algunas de sus conferencias, pero que apenas entendió nada. Por su parte, su ayudante, Humphrey Newton, confirmó su escaso poder de convocatoria: «Cuando Newton impartía sus conferencias, eran tan pocos los que iban a escucharle, y menos aun los que le entendían que, a menudo, a falta de oyentes, leía para las paredes».
No obstante, no parece que Newton se explicara mal, ya que lo mismo le ocurría a la mayoría. El propio Barrow se había quejado de que a sus conferencias acudían muy pocos alumnos, y lo mismo comentaban otros catedráticos. Y es que en la época los alumnos no tenían obligación de asistir a las clases y, cuando la tenían, no se la tomaban muy en serio.
Lo cierto es que la labor de profesor no constituyó una carga para Newton: en época escolar viajaba con frecuencia a Londres para asistir al Parlamento. A pesar de que durante cinco años no residió en Cambridge, mantuvo su plaza hasta 1701.
NEWTON, INVENTOR
Apenas un mes después de que le concedieran la cátedra, Newton pasó en Londres un par de semanas. Allí aprovechó para realizar compras de objetos relacionados con la óptica y la alquimia. Durante la visita tuvo ocasión de reunirse con el bibliotecario de la Royal Society, John Collins, al que comentó que, tras pulir lentes y cristales con un método propio, había construido una suerte de catalejo. Este, a pesar de ser muy pequeño comparado con los de la época, permitía conseguir hasta 150 aumentos. Collins le solicitó que lo mostrase a la Royal Society y Newton accedió.
Ya en su juventud, Newton se había caracterizado por su facilidad para construir objetos con sus propias manos: maquetas, relojes de sol y casas de muñecas para sus amigas, entre otras creaciones. Esta habilidad no le abandonaría nunca, lo que le permitió construir aparatos con los que pulir cristales con una perfección insólita hasta entonces.
Incluso al final de su vida recordaba con orgullo aquella construcción, y así se lo refirió a Conduitt, su biógrafo: «Le pregunté a quién se lo había encargado y me dijo que lo había hecho él mismo. Cuando le pregunté dónde había conseguido las herramientas, me dijo que las había hecho él mismo, y, riendo, añadió que si hubiera tenido que confiar en otras personas para que le hicieran sus herramientas u otras cosas, nunca hubiera hecho nada».
En 1671 Barrow asistió a una reunión de la Royal Society y presentó el telescopio de Newton, que causó asombro entre los asistentes. También se lo mostró al rey Carlos II. Fue tal el revuelo que ocasionó que los socios ausentes no tardaron en pedir información sobre el aparato. La propia Royal Society, a fin de asegurar la paternidad del descubrimiento, elaboró un detallado informe y lo envió a todos sus miembros. También contrataron a una persona para que reprodujera el artefacto, pero fue un desastre: no pudieron conseguir espejos con la perfección alcanzada por Newton.
El telescopio superó tan ampliamente a las herramientas que se tenían hasta el momento que permitió a Newton entrar en la Royal Society por la puerta grande.
LA EVOLUCIÓN DE LOS TELESCOPIOS
Acostumbrados a los avances tecnológicos, parece que algunos nos hayan acompañado siempre. Es el caso de los telescopios. Sin embargo, los primeros de los que se tiene constancia se remontan a principios del siglo XVII, menos de setenta años antes de que Newton revolucionara la observación astronómica.
El primer telescopio del que se tiene noticia se atribuye al óptico alemán Hans Lippershey (1570-1619), que invento un aparato formado por una lente fija y otra móvil, capaz de aumentar el volumen aparente de objetos lejanos. Lippershey trato de patentar su aparato en 1608, pero no lo consiguió.
Pese a ello, la información llegó a oídos de Galileo Galilei. Este dedujo cómo debía de ser el telescopio del alemán y diseñó el suyo propio en una sola noche.
No obstante, el primero en dirigir el telescopio hacia el cielo o fue Thomas Harriot (1560-1621), astrónomo y matemático a quien se atribuye la teoría de la refracción y la creación de numerosos símbolos matemáticos. En 1609, meses antes de hacerlo Galileo, enfocó su telescopio hacia la Luna, lo que le permitió dibujar cráteres y mares de la superficie lunar.
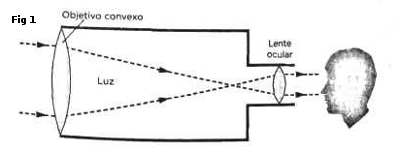
Pero quien mayor rendimiento le sacó al telescopio fue el propio Galileo, quien descubrió cuatro satélites de Júpiter, las montañas de la Luna, estrellas desconocidas en Orión y las Pléyades, y la estructura de la Vía Láctea. El telescopio de Galileo estaba formado por dos lentes: el objetivo, que es la que se dirigía al objeto observado, de forma convergente, y la ocular, donde se colocaba la vista, de forma divergente.
El astrónomo Johannes Kepler diseño otro telescopio similar, aunque utilizando dos lentes convexas. Nunca llegó a construirlo, pero, años más tarde, lo hizo el astrónomo alemán Christopher Scheiner (1575-1650), inventor del pantógrafo. Este tipo de aparatos son conocidos como «telescopios de refracción». La refracción es el cambio de dirección que sufre un rayo de luz cuando pasa de un medio a otro de distinta densidad. Es muy fácil de observar, pues basta colocar un lápiz en un vaso de agua y comprobar cómo este parece quebrado. En el esquema básico del telescopio de refracción la lente ocular puede ser convergente, como en Kepler (figura 1), o divergente, como en Galileo.
Con idea de eliminar la aberración cromática, el astrónomo y científico escocés James Gregory (1638-1675) diseñó un telescopio que sustituía las lentes por espejos parabólicos. Es conocido que, en un espejo parabólico, los rayos paralelos que llegan a él convergen concentrándose en el foco. Este tipo de telescopio se llama «de reflexión». El diseño de Gregory contaba con un espejo agujereado al que llegaban los rayos de luz y, al reflejarse en otro espejo secundario, se dirigían a la lente ocular. El esquema de dicho telescopio es el que puede verse en la figura 2.

Gregory diseñó su telescopio en 1663, pero no encontró a nadie capaz de construirlo hasta diez años después. Quien lo hizo posible fue Hooke, pero por entonces ya se había dado a conocer el de Newton.
El científico inglés tuvo noticias del telescopio diseñado por Gregory y, tras mejorar su diseño, construyó uno con sus propios medios. En el telescopio newtoniano, el espejo parabólico no está agujereado y el segundo espejo, de forma plana, está colocado en diagonal. El esquema podría ser el de la figura 3.

LENTES Y ABERRACIÓN CROMÁTICA
Las lentes, en general, suelen ser de dos tipos: convergente, los rayos convergen hacia el foco de la lente, situado detrás de ella; en la divergente, los rayos divergen como si partieran de un foco virtual colocado delante. Los rayos que atraviesan el centro óptico de la lente no se desvían. Los demás se refractan según la ley de Snell, que indica que es constante el producto del índice de refracción de una lente por el seno del ángulo que forman los rayos con la normal. El gran problema de las lentes es que sufren de aberración cromática. Cuando un rayo de luz incide en un prisma, se descompone en colores primarios. Lo mismo ocurre en los bordes de las lentes. Por eso, es casi imposible volver a unir los colores en un mismo lugar, y las imágenes terminan con una corola difuminada alrededor que empaña su visión. Aunque se intentó ampliar el tamaño o probar con distintos tipos de lentes, como hizo Kepler, la aberración podía reducirse pero no eliminarse.

La ventaja del aparato inventado por Newton es que, además de evitar la aberración cromática, con menos tamaño conseguía más aumento. El primer telescopio que construyó tenía alrededor 15 cm de lago y, sin embargo, aumentaba la imagen cuarenta veces el diámetro. Más de un siglo después, el astrónomo alemán William Herschel (1738-1822), descubridor del planeta Urano, construyó una versión mejorada del telescopio de Newton. En el suyo no había espejo plano, pero sí reflector, por lo que. al reflejare los rayos una sola vez, se perdía mucho menos luz en la observación.
NEWTON EN LA ROYAL SOCIETY
La impresión que causó el telescopio de Newton en la Royal Society se aprecia en la carta que le envió el secretario de la sociedad, Henry Oldenburg:
Habiendo sido examinado y aplaudido por nuestros más eminentes especialistas en la ciencia y la práctica de la óptica, estos consideran necesario poner a salvo esta invención de usurpadoras manos extrajeras. […] dichos especialistas han elaborado un esquema de este primer ejemplar enviado por usted, […] y han enviado dicho esquema y descripción a través del secretario de la Royal Society, en carta solemne, a París, al señor Huygens, con el objeto de prevenir la usurpación de dichos extranjeros, quienes pueden haberlo visto aquí, o tal vez, con usted, en Cambridge, ya que es demasiado frecuente que los nuevos inventos y artefactos sean arrebatados de sus verdaderos creadores por intrusos.
La carta refleja la preocupación por los plagios antes mencionada. Pero, sobre todo, es llamativo el carácter marcadamente nacionalista que recorre la misiva. Al parecer, lo que más les preocupaba era que un extranjero pudiera copiar el diseño.
Lo importante, en cualquier caso, era que en la carta se invitaba a Newton a formar parte de la Royal Society. Ingresó en la sociedad el 11 de enero de 1672 y, más tarde, fue su presidente durante casi cinco lustros.
«A HOMBROS DE GIGANTES»
Un mes después de ser elegido socio de la Royal Society. Newton envió al secretario de la sociedad un tratado sobre los colores, en el que elaboraba un esquema de su teoría apoyándose en tres experimentos. Oldenburg le contestó que la lectura de su tratado había tenido una gran acogida y que seria publicado en Philosophical Transactions. Ese articulo, así como otro sobre su telescopio, dio a conocer a Newton entre los científicos europeos, con los que comenzó a cartearse.
«No he podido aún llegar a deducir de los fenómenos la razón de esas propiedades de la gravedad, y no imagino hipótesis».
— ISAAC NEWTON, EN EL CIERRE DE LOS PRINCIPIA
Los problemas surgieron cuando su teoría empezó a recibir críticas. Una de las primeras provino de Robert Hooke, considerado un experto en óptica. Este, aunque destacó su interés, criticó con dureza el tratado, indicando que las hipótesis de Newton no quedaban suficientemente demostradas. Newton respondió con furia, afirmando que Hooke no había entendido nada su trabajo y que era imposible que en tan pocos días hubiese podido reproducir su experimento. Esto era cierto, y el propio Hooke confeso más adelante que solo había dedicado unas horas a estudiar el artículo.
En esta disputa desempeño un papel importante Oldenburg, que recibía las cartas de ambos. Oldenburg, enemistado con Hooke, solo leyó en público las cartas de Newton lo que levantó las iras del óptico Hooke, entonces, decidió prescindir de Oldenburg y escribir directamente a Newton. En la carta de respuesta figura una de las frases más famosas de Newton: «Si he llegado a ver más lejos, ha sido porque he subido a hombros de gigantes». La sentencia, sin embargo, no es original de Newton, pues ya en el siglo XII había aparecido en la obra Metalogicon, de Juan de Salisbury.
Pero las críticas de Hooke no fueron las únicas. Christiaan Huygens, considerado el mejor científico europeo de la época, alabó su teoría en un primer momento, pero poco a poco fue encontrándole reparos. Quizá la disputa más encendida fue la que sostuvo con el jesuita inglés Francis Hall, que se prolongo con sus discípulos tras la muerte del sacerdote. Las críticas coincidían en tachar de hipótesis las aseveraciones de Newton. Esto le encrespaba y, como reza una de sus máximas. Hyphoteses non fingo, defendía que él no realizaba hipótesis. Lo cual, sin embargo, no siempre era cierto.
La desesperación se apoderó de Newton, que veía que las polémicas inacabables le quitaban tiempo para lo fundamental: sus estudios. Su enfado llegó al punto de que pidió a Oldenburg que le dieran de baja de la Royal Society, pero la petición nunca se hizo efectiva.
DE DESGRACIA EN DESGRACIA
En 1677, las muertes de Barrow y Oldenburg sumieron a Newton en el aislamiento. El primero fue su mentor, y el segundo, el único hilo que lo mantenía unido a la comunidad científica. Por otra parte, con la intención de zanjar la disputa sobre su teoría de los colores, decidió escribir una obra más completa que reuniese sus múltiples experimentos y explicase definitivamente cuál era su teoría óptica. Pero, por desgracia, después de haber terminado el manuscrito, se produjo un incendio en sus habitaciones y perdió todo su trabajo. Newton se quedó tan afectado que tardó meses en recuperarse. Tanto es así que tardó veinticinco años en publicar de nuevo su teoría de la luz.
En 1679 tuvo que regresar a su casa natal de Woolsthorpe, ya que su madre agonizaba. Al parecer, su hermanastro Benjamin había enfermado de unas fiebres malignas y su madre, mientras lo cuidaba, se había contagiado. Durante los últimos días de su madre Newton la cuidó con una entrega inédita en su relación. Según cuenta su biógrafo John Conduitt:
Pasaba noches enteras sentado junto a ella, le daba él mismo las medicinas, curaba sus ampollas con sus propias manos y hacía uso de su extraordinaria destreza manual para aliviar el dolor producido por el terrible remedio que se emplea habitualmente en las curas de esa enfermedad, con mayor entrega de la que nunca había demostrado en sus experimentos más interesantes.
Ver acercarse el final de su progenitora debió de removerle la conciencia y se volcó con ella como nunca había hecho. Y es que, desde que había vuelto a Cambridge tras la peste más de doce años atrás, se podían contar con los dedos de la mano las veces que la había visitado. En Woolsthorpe permaneció varios meses arreglando los papeles de la herencia. Durante ese tiempo, aparco sus estudios y ejerció de terrateniente, poniendo al día sus asuntos y repasando los contratos de arrendamiento. Su objetivo era dejarlo todo en orden para centrarse de nuevo en la investigación.
A su regreso a Cambridge se resquebrajó otro de sus pilares. Su compañero de cuarto, Wickins, con quien había convivido desde su llegada, fue nombrado rector de Stoke Edith y un año más tarde abandonó el college. Aunque no hay constancia de conflicto alguno entre ambos, a partir de entonces su relación fue muy fría e, incomprensiblemente, apenas mantuvieron el contacto.
De pronto, Newton se encontró sin nadie a quien acudir en caso de necesitar consuelo o consejo. Fue por esas fechas cuando mandó traer desde Grantham a Humphrey Newton, el estudiante que le sirvió de secretario y ayudante —labor que, hasta entonces, había realizado Wickins—. Sin embargo, en su vida aparecieron nuevas amistades. Sin duda, la más importante fue la que entabló con Edmund Halley (1656-1742). Y es que, al convencer a Newton de que diese a conocer su concepción del universo, le hizo entrar en la historia de la ciencia.
LA EVOLUCIÓN DEL CONCEPTO DEL UNIVERSO
Copérnico había revolucionado la ciencia al plantear que el centro del universo era el Sol y que los planetas giraban en tomo a él. Sin embargo, las leyes que regían ese movimiento no se habían establecido con solidez hasta que llegó Newton.
Pese a que la teoría heliocéntrica de Copérnico no fue aceptada por todos, sí tuvo seguidores que, incluso, llegaron a perfeccionarla. Por ejemplo, el filósofo y sacerdote italiano Giordano Bruno (1548-1600). El clérigo italiano fue el primero en diseñar una teoría cosmológica opuesta a la aristotélica, partiendo de los principios copernicanos, pero defendiendo que el Sol era solo una estrella más y que el universo era infinito y homogéneo. En su obra La cena de las cenizas, planteó el movimiento de la Tierra con argumentos físicos, que solo fue superado con la llegada de Galileo. Desgraciadamente, no pasó a la historia por sus logros, sino porque la Inquisición lo quemó en la hoguera. Aunque las acusaciones fueron principalmente de índole religiosa, su herética concepción del universo contribuyó a su triste final.
Otra de las figuras imprescindibles de la segunda mitad del siglo XVI fue el danés Tycho Brahe (1546-1601), que realizó las observaciones astronómicas más perfectas hasta el momento. El rey de Dinamarca financió la construcción de lo que se considera como el primer observatorio astronómico de la historia. En la isla de Hven se levantó el palacio conocido como Uraniborg, que albergaba instrumentos astronómicos diseñados por Brahe. Pese a que en la época no existían los telescopios astronómicos, Brahe alcanzó una precisión en sus observaciones nunca igualadas. Era un pésimo teórico, pero un excelente observador, y contribuyó a la destrucción del cosmos aristotélico. Y ello a pesar de no ser copernicano. Brahe oponía al enfoque de Copérnico uno propio según el cual la Tierra permanecía fija rodeada por la Luna y el Sol y los restantes planetas giraban alrededor de este. Sin embargo, desde el punto de vista de las matemáticas, su sistema era similar al de Copérnico. Brahe fue el primero que planteó que las observaciones debían ser sistemáticas, y no reducirse a fenómenos extraordinarios.
Pero la figura más destacada en la astronomía del siglo XVI es, sin duda, el astrónomo alemán Johannes Kepler (1571-1630). Desde su infancia se interesó por los fenómenos del cielo y, con solo cinco años, observó el cometa que cruzó los cielos en 1577. Estudió con el astrónomo y matemático Michael Maestlin, quien lo introdujo en la teoría heliocéntrica. En 1596 publicó un primer libro, El secreto del universo, en el que defendía la teoría copernicana y relacionaba la creación de Dios con los planetas. Creía que solo existían los seis planetas que se conocían en ese momento porque estaban relacionados con los sólidos platónicos. Construyó un sistema en el que cada poliedro regular se encontraba dentro de una esfera y lo explicó de la siguiente manera:
La Tierra es un círculo que es medida de todo. Circunscríbele un dodecaedro. El círculo que lo circunscriba será Marte. Circunscribe a Marte con un tetraedro, el círculo que comprenda a este será Júpiter. Circunscribe a Júpiter con un cubo. El círculo que comprenda a este será Saturno. Ahora inscribe en la Tierra un icosaedro. El círculo inscrito en este será Venus. Inscribe en Venus un octaedro. El círculo inscrito en él será Mercurio. Tienes la razón del número de los planetas.
Kepler poseía una poderosa intuición y creaba excelentes hipótesis de trabajo, pero defendía que cualquier teoría debía ser sometida a la práctica, es decir, a los datos que confirmaran esa teoría. Por otra parte, en astronomía no era raro que se seleccionaran los datos que corroboraban una teoría y que se desechara el resto.
Kepler era un excelente teórico, pero un deficiente observador. De hecho, su obra anterior se basó en datos que, en parte, resultaron erróneos. En este sentido, fue una suerte que entrara en contacto con Tycho Brahe, que era justo lo contrario que él. Kepler estaba ampliando su obra El secreto del universo, pero para corroborar sus teorías, a pesar de llevar veinte años haciendo observaciones, necesitaba más datos. Convertirse en colaborador de Brahe le permitió, tras la muerte de este, acceder a toda la información que acumulaba el danés. De esta manera, por ejemplo, fue como descubrió que las órbitas de los planetas se ajustaban a una elipse en lugar de a un círculo, como se defendía desde la antigua Grecia. También comprobó que los planetas se movían más rápido cuando se hallaban próximos al Sol.
En 1609 publicó su obra Astronomia nova, en la que aparecen sus dos primeras leyes acerca del movimiento planetario. La primera de ellas reza que los planetas se mueven formando elipses alrededor del Sol, el cual se encuentra en uno de los focos de esas órbitas elípticas. En cuanto a la segunda, establece que una línea recta que uniese el Sol con un planeta recorrería áreas equivalentes en tiempos equivalentes.
Según la imagen de la figura 4, el planeta tardaría el mismo tiempo en ir desde A hasta B que desde C hasta D, y las zonas señaladas tendrían la misma área.
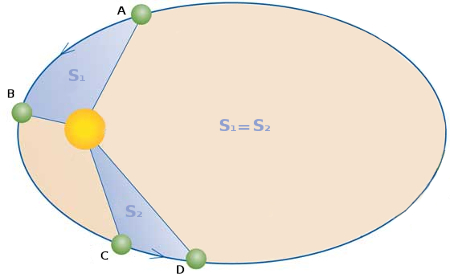
Esquema de la segunda ley del movimiento de Johannes Kepler.
La tercera ley de Kepler no apareció hasta 1619 en La armonía del mundo, su obra magna, que recogía muchos de sus trabajos sobre poliedros, música, astrología y astronomía. Sostenía lo siguiente: «El cuadrado del tiempo empleado por un planeta en recorrer su órbita es proporcional al cubo de la distancia media entre ese planeta y el Sol».
En esta ley se encuentra la fórmula T2 = Kd3 en la que T es el tiempo de rotación medido en años, y d la distancia entre el planeta y el Sol medida en unidades astronómicas (es decir, la distancia entre el Sol y la Tierra). Según esta ley, cuanto más lejos está el planeta del Sol, más lentamente recorre su órbita.
EL COMETA DE 1680
A finales del año 1680, el cielo despertó el interés de numerosos científicos. Sin embargo, esta vez el asunto no tenía nada que ver con la religión, sino con la aparición de un «nuevo» cometa. El primero en observarlo fue el astrónomo alemán Gottfried Kirch (1639-1710), que más tarde fue astrónomo real en el Observatorio de Berlín También fue pionero en descubrir un cometa utilizando el telescopio.
El cometa fue visible durante cuatro meses, por lo que pudo ser observado por muchos científicos. El uso del telescopio se había generalizado entre los investigadores, sobretodo por las mejoras aportadas por Newton, lo que permitió que la evolución del cometa fuese seguida con más precisión. Es conocido que el científico inglés siguió su trayectoria a diario.
Sin embargo, las características de estos cuerpos aún no estaban claras. Muchos científicos seguían considerando que su naturaleza era más atmosférica que celeste, es decir, que guardaban más relación con el entorno de la Tierra que con el propio espacio. Esta opinión era defendida, por ejemplo, por Robert Hooke o por el astrónomo real John Flamsteed (1646-1719). Este último mantuvo una fuerte discusión con Newton sobre el cometa avistado aquel año: mientras que él sostenía que el cometa había girado, dentro de su órbita, antes de llegar al Sol, Newton defendía que lo había rodeado antes de seguir su camino.
Algunas anotaciones hacen pensar que, por esos años, Newton aún no había extendido sus fuerzas gravitatorias a todos los cuerpos celestes. En este sentido, es muy probable que no aplicase aún a los cometas las leyes de los planetas.
Poco antes, en 1679. Robert Hooke, nombrado secretario de la Royal Society tras la muerte de Oldenburg, había escrito a Newton para convencerle de que se carteara con el resto de científicos. En ta misiva, además, planteaba al genio una sugerente cuestión: ¿cómo serian las órbitas de planetas afectados por la inercia y por una atracción hacia el cuerpo que se hallaba en el centro de su giro? Newton planteó una ley de inercia, según la cual los cuerpos se desplazan en linea recta si ninguna fuerza modifica su movimiento. Además, desechó el concepto de fuerza centrifuga y se centró en otra que denominó fuerza «centrípeta», que definió como la que provoca que, en un movimiento circular, el cuerpo sea atraído hacia el centro de revolución.
Newton respondió proponiendo un experimento para estudiar la rotación de la Tierra alrededor de su eje. Tal vez por la rapidez en contestar, cometió la torpeza de suponer que los cuerpos que cayesen hacia el centro de la Tierra lo harían trazando una espiral. Hooke, que detectó el error de inmediato, sugirió que la trayectoria fuera una elipse. Pese a que, en un principio, Newton rechazó la idea, más tarde se sirvió de ella para rehacer sus cálculos.
EL GENIO DESPIERTA
En el siglo XVII se habían puesto de moda en Londres los establecimientos para tomar café, surgidos a mediadas del siglo. En ellos solían formarse tertulias y grupos de discusión sobre cualquier tema, incluida la ciencia. No es de extrañar, pues, que, tras las sesiones de la Royal Society, los miembros que no tenían prisa en volver a casa se reunieran en un café para continuar la conversación.
En enero de 1684 en uno de estos locales tuvo lugar una curiosa reunión. En él se encontraban Robert Hooke, Christopher Wren y Edmund Halley, que solían debatir con frecuencia sobre el movimiento planetario. En aquella ocasión, discutían sobre una propuesta de Hooke, que sostenía que el Sol atraía a los planetas con una fuerza inversamente proporcional al cuadrado de la distancia. Tanto Wren como Halley se mostraban de acuerdo con Hooke. El problema que se les planteaba era cuál podría ser la órbita que siguiera un planeta con la influencia de esa fuerza. Amparándose en las leyes de Kepler, imaginaban que la respuesta seria una elipse, pero carecían de herramientas para demostrarlo.
Siguiendo su costumbre, Hooke se jactó de tener la solución, pero se negaba a revelarla hasta que los otros no se diesen por vencidos. Tanto Halley como Wren, impotentes, reconocieron su fracaso. Sin embargo, pasaban los meses y Hooke no desvelaba el secreto. Halley, entonces, para salir de dudas, se decidió a preguntar a otro de los mayores científicos de Inglaterra, Isaac Newton.
El matemático francés Abraham de Moivre (1667-1754), amigo de Newton y uno de los que mejor guardó sus recuerdos, fue testigo del encuentro: «El doctor Halley le pidió su opinión sobre cómo pensaba que sería la curva descrita por los planetas, suponiendo que la fuerza de atracción hacia el Sol fuese reciproca al cuadrado de su distancia de este. Sir Isaac respondió inmediatamente que seria una elipse». Tras la rápida respuesta, el doctor, sorprendido le preguntó cómo lo había sabido. «Lo he calculado», contestó él. Sin embargo, cuando Halley le pidió ver los cálculos, Newton aseguró que los había perdido. En su biografía del inglés, Richard S. Westfall sostiene que aquella excusa era falsa, ya que en la actualidad se conservan los manuscritos con los citados cálculos. Seguramente Newton, dado su perfeccionismo, no estaba dispuesto a mostrar su trabajo sin haberlo revisado.
«La parte más importante de la revolución científica fue el descubrimiento de la gravitación universal de Isaac Newton».
— BERNARD COHEN, HISTORIADOR DE LA CIENCIA.
En cualquier caso, en noviembre Halley recibió un breve manuscrito de nueve páginas titulado De motu corporum in gyrum (Sobre el movimiento de los cuerpos en una órbita). En él encontró lo que esperaba y mucho más: un esbozo de una ciencia general de la dinámica. Halley recibió permiso de Newton para comentar la obra en la Royal Society. También logró arrancarle el compromiso de revisar el tratado para que fuera registrado en la sociedad. No obstante, aquella revisión tardó más de lo que pensaba Halley, pues Newton paso dos años volcado en cuerpo y alma en la que iba a ser su obra magna: los Principia.
Tras solicitar a Flamsteed los datos que necesitaba para fundamentar sus resultados, se dedicó a ampliar el tratado añadiendo todo lo que había averiguado previamente sobre el mundo celeste. En el verano de 1686, Newton escribió a Halley contándole que, durante el invierno, había terminado el primer libro pero, al alargarse más de lo previsto, había decidido dividirlo en dos partes. Cuando consideró que el primer tomo estaba completo, encargó a su amanuense que lo copiara en limpio y lo envió a la Royal Society. Ni que decir tiene que la acogida fue magnífica, y los miembros cubrieron de elogios su labor.
No obstante, un incidente empañó en parte la alegría de Newton. Mientras se encontraba organizando el material del tercer libro, recibió una carta de Halley para informarle del extraordinario recibimiento obtenido por el primero. De soslayo, también le contentó que Hooke aseguraba que muchas de las ideas que aparecían en la obra eran suyas. Esto era cierto, pero solo en parte: Hooke había entrevisto las posibilidades del movimiento planetario, pero fue Newton quien hizo las demostraciones y les otorgó entidad.
Conociendo el temperamento del genio, es probable que su furia hirviera como uno de sus calderos alquímicos. No en vano su primera reacción fue abandonar ña redacción del tercer libro, que se encontraba ya en proceso de revisión. Afortunadamente, gracias a las tácticas diplomáticas de Halley, aceptó continuar con el trabajo.
A pesar de los problemas de financiación que atravesaba en ese momento la Royal Society, Halley consiguió el respaldo de la sociedad para publicar el libro. La única condición fue que él mismo fuera quien se encargara de la publicación. Halley aceptó, convirtiéndose así en editor de los Principia.
En otoño del 1686 Newton había concluido el libro segundo, en el que atacaba sin piedad las teorías cartesianas, sobre todo su filosofía natural.
Halley tenía prisa en que el libro saliera a la venta porque era consciente de la importante obra que tenía entre las manos. Por este motivo. Por este motivo, entregó el segundo tomo a un editor distinto para que fuera editándose a la vez que el primero, operación que repitió cuando tuvo en su poder el tercer volumen.
Por fin, el 5 de julio de 1687, la obra vio la luz. Su grado de complejidad excedía el de la media universitaria. Se cuenta que un estudiante, al cruzarse en Cambridge con Newton, comentó: «Ahí va el hombre que ha escrito un libro que nadie, ni siquiera él, comprende».
Halley presentó la obra final con una oda dedicada a Newton, en la que destaca esta apasionada estrofa:
A la luz están los íntimos secretos del cielo revelado, no se oculta ya la fuerza que hace girar el orbe más lejano. En su trono ordena el Sol declinar en derredor el curso del universo, permitiendo que el rumbo de los astros, manifiesta su falsa derechura por el inmenso vacío, gire en órbitas certeras sobre su centro. Se reveló ya la órbita curva de los terribles cometas, no nos asustamos ya de estrellas barbadas.
LAS REFLEXIONES SOBRE LA GRAVEDAD
Se supone que, gracias a la anécdota de la manzana anteriormente descrita, a Newton se le ocurrió relacionar las fuerzas que regían los movimientos planetarios con las que movían los objetos en nuestro planeta. Esto le condujo a estudiar las leyes de Kepler y las leyes del movimiento de Galilei.
Mientras se encontraba en Woolsthorpe, desarrolló la idea de que la Luna se veía atraída hacia la Tierra igual que una manzana, pero que la distancia paliaba esa atracción tomándola casi inapreciable. Por la misma razón, esa fuerza de atracción debía de acercar los planetas al Sol.
Estudiando los órbitas de los planetas concluyó también que la fuerza se atenuaba en función del cuadrado de la distancia. Para llegar a ese resultado, partió de la fuerza centrífuga, es decir, la que provoca que un cuerpo en movimiento circular alrededor de un objeto tienda a separarse de ese objeto. De esta forma, si se tiene un cuerpo de masa m que se mueve con velocidad v constante alrededor de un centro, y sobre una circunferencia de radio r, la fuerza centrípeta es a la total (ma) como el perímetro de la circunferencia (2πr) es al radio. Como la aceleración es v/t, la fuerza resultante es
Como el tiempo t es el cociente entre el espacio recorrido y la velocidad,
sustituyendo en la fuerza y simplificando llegamos a la fórmula de la fuerza centrífuga:
Newton alcanzó sus conclusiones sirviéndose de la fórmula anterior y de la tercera ley de Kepler. Y lo hizo de la forma descrita a continuación: si hay dos planetas con velocidades v1 y v2 alrededor del sol, y sus distancias medias con este son r1 y r2 se obtienen las fórmulas siguientes:
Como la velocidad es el cociente entre espacio y tiempo, siendo T el período de revolución del planeta,
aplicándolo a la fórmula anterior se convierte en:
Aplicando ahora la tercera ley de Kepler, si se considera una constante universal de proporcionalidad k, se verifica:
Esto último conduce a la expresión anterior:
De esto se concluye, sin considerar el cociente de las masas ni la constante de proporcionalidad, que las fuerzas son inversamente proporcionales al cuadrado de las distancias medias de los planetas al Sol.
En realidad, Newton había ido gestando su teoría del movimiento planetario a lo largo de los años. Así, en el período de la epidemia de peste comenzó a estudiar la atracción del Sol sobre los planetas. Luego se pasó al estudio de la Luna, pero, con los datos que en ese momento tenía sobre la Tierra, no le salían los cálculos. Cuando en 1675 se publicaron cálculos más exactos de las medidas terrestres, realizadas por el astrónomo francés Jean Picard (1620-1682), pudo retomar sus cálculos y comprobar que sus hipótesis se cumplían. Inicialmente, se encontró con un problema: considerar que la fuerza de atracción de un planeta esférico se puede estimar como si toda la masa estuviera concentrada en su centro. Esto, que es aplicable a las fuerzas que se basan en cuadrados inversos, no es fácil de demostrar. Planteó incluso varios experimentos con péndulos para comprobar cómo la fuerza influía en el movimiento; experimentos que, más tarde, incluyó en el primer libro de los Principia. Estos ensayos, y otros realizados con esferas, le llevaron a desechar el enfoque adoptado por Descartes en los vórtices.
Su visión del movimiento de los cuerpos celestes siguió cambiando y a mediados de la década de 1680, Newton había generalizado la acción a distancia a casi todos los fenómenos de la naturaleza, según plantea Richard S. Westfall en su biografía del científico. Fueron los días en que el científico se encontraba inmerso en la gran obra de su vida.
LOS PRINCIPIA
Considerada una de las obras más importantes de la historia de la ciencia, los Philosophiae naturalis principia mathematica (Principios matemáticos de la filosofía natural) se componen de tres libros y se basan en los principios de la filosofía experimental, seña de identidad de la revolución científica. Así lo expuso Newton en el tomo tercero:
En la filosofía experimental debemos recoger proposiciones verdaderas, o muy aproximadas, inferidas por inducción general a partir de fenómenos, prescindiendo de cualesquiera hipótesis contrarias, hasta que se produzcan otros fenómenos capaces de hacer más precisas esas preposiciones o sujetas a excepciones.
Es decir, se debe siempre corroborar las hipótesis a partir de los datos y la experimentación.
En los Principia Newton fundamentó matemáticamente el movimiento en el universo. Escarmentado de polémicas y de objeciones de científicos que no consideraba a su altura, escribió el libro en latín, de forma que solo pudiese ser leído por los miembros del mundo científico.
Ya en el pequeño manuscrito De motu corporum, germen de los Principia, Newton demostraba que la trayectoria que genera una fuerza de atracción inversamente proporcional al cuadrado de la distancia es una cónica; en concreto, una elipse para velocidades por debajo de cierto límite.
En Los movimientos del cuerpo, el primer tomo de los Principia, Newton desgranó las tres leyes del movimiento. La primera ley afirmaba que todo cuerpo continúa en un estado de reposo, o de movimiento en línea recta, a menos que sea obligado a cambiar ese estado por fuerzas impuestas sobre él. La segunda, que el cambio de movimiento es proporcional a la fuerza motriz impresa, y ocurre según la línea recta en que se imprime dicha fuerza. Por último, la tercera sostenía que a cada acción se opone siempre una reacción igual y opuesta. Es decir, la acción mutua de dos cuerpos, el uno sobre el otro, es siempre igual y dirigida hacia las partes contrarias. Las dos primeras leyes las dedujo de las leyes de Galileo y Kepler, pero la tercera le pertenece por entero. Esta, aplicada a la Tierra y la Luna, demuestra que ambos cuerpos se influyen mutuamente, lo que explica el fenómeno de las mareas condicionadas por el satélite.
Es en este libro donde Newton utilizó por primera vez la palabra «masa» en su significado actual: «La cantidad de materia es aquella que surge por la conjunción de su densidad y magnitud. La cantidad de un cuerpo con el doble de densidad en el doble de espacio es cuatro veces mayor. Designo esta cantidad por el nombre de cuerpo o masa». Es decir, la masa es la cantidad de materia que posee un cuerpo independientemente de su volumen. Además, comprobó que dicha masa era proporcional a su peso. En concreto, la fuerza es igual a masa por aceleración.
También definió la fuerza centrípeta; «Fuerza centrípeta es aquella por la cual los cuerpos son arrastrados o impelidos, o tienden de cualquier modo hacia un punto como hacia un centro». Asimismo, se incluyen en el libro los teoremas sobre la atracción de esferas, experimentos a los que había dedicado gran atención. De ellos dedujo que la fuerza de atracción entre cuerpos esféricos debe producirse desde sus centros. Newton definía la cantidad de movimiento como el producto de la masa por la velocidad. Y, en ese movimiento, incluía dos tipos de fuerzas: la vis insita, proporcional a la masa, que provoca que el cuerpo mantenga su estado de reposo o movimiento rectilíneo, y la vis impressa, encargada de cambiar el estado del cuerpo. Esta última puede ser debido a un choque, una presión o la fuerza centrípeta.
Finalmente, incluyó algunos de sus experimentos con la luz, dedicando una sección al movimiento de las partículas diminutas.
LOS VÓRTICES DE DESCARTES

Detalle de una lámina que representa los vórtices cartesianos, incluida en los Principios de la filosofía.
En 1644, siete años después de haber publicado su Discurso del método, René Descartes sacó a la luz sus Principios de la filosofía, donde planteó su idea sobre como se producen los movimientos de los planetas. El filósofo y científico francés concebía el universo repleto de un fluido invisible que formaba remolinos similares a lo que se podía encontrar en un rio, símil ya empleado en la antigua Grecia. Esos remolinos o vórtices arrastraban a los planetas y eran los que provocaban el movimiento. El propio Descartes lo explica así: «Podemos asumir, en este asunto de los cielos, que los planetas se hallan girando sin cesar, en un vórtice que tiene el Sol en su centro, que los que están más cerca del Sol se mueven más rápidamente que los más alejados; y que así todos los planetas […] siempre permanecerán suspendidos con sus mismas partes en este asunto celestial. Porque solo por ello, sin ningún otro dispositivo, todos los fenómenos son muy fáciles de entender». Él supuso que el Sol estaba en el centro de uno de los vórtices y arrastraba a los planetas, que a su vez eran centro de otros vórtices más pequeños que afectaban a los satélites, como la Luna. Fue su intento de explicar el movimiento en una época en que no se imaginaba que las fuerzas pudieran actuar a distancia. El problema reside en que esta concepción no explicaba cómo se comportaban los cuerpos terrestres. Descartes imaginaba la Tierra como una inmensa centrifugadora, cuyo movimiento constante influía en las partículas de la siguiente forma: «La fuerza con que la materia celeste, más ligera, tiende a alejarse del centro de la Tierra no puede tener su efecto si las partículas de la materia celeste que se alejan no alcanzan el lugar de algunas partes terrestres que descienden, al mismo tiempo, hasta pasar a ocupar el lugar dejado por las partículas de la materia celeste».
En el segundo libro se hallan pasajes que pueden considerarse como una introducción a la hidrodinámica. En él trató la mecánica de los fluidos y la influencia de la fricción en el movimiento de los cuerpos sólidos incluidos en un medio líquido. De ello dedujo que la resistencia variaba con el cuadrado de la velocidad. También estudió la forma que deben tener los cuerpos para ofrecer menor resistencia, el movimiento ondulatorio y una fórmula para la velocidad del sonido en el agua. En alguna proposición, como la XXIII, intuyó una teoría cinética de los gases. Asimismo, dedujo la ley fundamental de la velocidad expresada por la raíz cuadrada de la elasticidad entre la densidad, lo que le permitió distinguir entre tres tipos de fluidos, el comprensible, el incomprensible y el viscoso.
El título del tercer libro es muy descriptivo: El sistema del mundo. El propio Newton explicó lo que pretendía en él:
En el [libro] tercero derivo de los fenómenos celestes las fuerzas de gravedad, por las cuales los cuerpos tienden hacia el Sol y los distintos planetas. Luego, de esas fuerzas, mediante otras proposiciones que son también matemáticas, deduzco los movimientos de los planetas, los cometas, la Luna y el mar.
En cierta forma, Newton aplicó lo que planteaba en el primer libro al movimiento de los cuerpos celestes y al influjo de la Luna en la periodicidad de las mareas.

(1) Portada de la primera edición de los Principia de Newton, publicada en latín (en inglés no apareció hasta décadas más tarde).
(2) Modelo el sistema solar según el libro del astrónomo Johannes Kepler, El secreto del universo (Mysterium cosmographicum).
(3) Representación de Isaac Newton como «geómetra del universo», obra del poeta, pintor y grabador inglés William Blake (1757-1827).
Por otro lado, dedujo que la Tierra estaba achatada por los polos, lo que contradecía a René Descartes, ya que el filósofo francés defendía justo lo contrario. La cuestión se dilucidó un siglo después. En 1733, la Academia de las Ciencias de París envió dos expediciones, una a Laponia y otra a Perú, para medir los dos meridianos. En ellas participaron, entre otros, los españoles Jorge Juan y Antonio de Ulloa, y los franceses Charles Marie de La Condamine y Louis Godin. Después de sufrir un sinfín de penalidades, corroboraron los postulados de Newton. En este sentido, Voltaire le comentó a La Condamine: «Usted lo ha encontrado después de largos ensayos mientras que Newton lo encontró sin salir de su casa».
De hecho, no solo calculó con precisión los equinoccios, sino también el radio entre el eje de la Tierra y su diámetro en el ecuador. Debido a la forma de la Tierra, Newton demostró que la atracción no era constante en su superficie y calculó el movimiento cónico del eje terrestre. Explicó cómo obtener el valor de la masa del Sol y del resto de los planetas en función de la masa de la Tierra.
Además, fue el primero que trabajó el movimiento de los cometas como si fuesen planetas girando alrededor del Sol.
El hallazgo más destacado del tercer libro fue aplicar una fuerza común a todos los fenómenos terrestres y celestes, que denominó «ley de gravitación universal» y que definió así:
Dos cuerpos cualesquiera se atraen con una fuerza que es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia entre ellas.
Su expresión sería
donde G es la constante de gravitación universal. Fue calculada empíricamente por primera vez en 1798 por el físico inglés Henry Cavendish (1731-1810).
En el planteamiento de Newton de fuerza centrípeta, gracias a la cual, recordemos, los planetas no se salen de sus órbitas, no tiene cabida la fuerza centrípeta definida por Huygens, que es una fuerza en dirección contraria del centro de su órbita. Para Newton, dicha fuerza no influye a la hora de que los planetas describan una órbita elíptica, ni tampoco en que los cuerpos caigan en la Tierra.
LAS MATEMÁTICAS EN LOS PRINCIPIA
Definitivamente, los Principia eran una obra difícil de entender. En el último libro, el propio Newton reconocía que ese hermetismo de la obra era deliberado:
Considerando que aquellos que no hubiesen entendido correctamente los principios no podrían fácilmente discernir el alcance de las consecuencias, ni dejar de lado los prejuicios a los que habían estado acostumbrados durante años, y para prevenir las disputas que podrían derivarse de ello, decidí reducir el contenido de este libro en forma de proposiciones de corte matemático, las cuales solo podrán ser leídas por aquellos que previamente hubiesen dominado los principios establecidos en los libros precedentes.
Inicialmente, Newton había previsto que el tercer libro fuera más asequible. Sin embargo, tras las discusiones con Hooke, decidió complicar la parte matemática, quedando así fuera de las capacidades de este último. Aunque en sus descubrimientos empleara el nuevo cálculo, las demostraciones de los Principia las hizo sirviéndose de la geometría clásica, que consideraba más precisa y elegante. De todas formas, el segundo libro también contiene aspectos analíticos.
Por descontado, los Principia albergan en sus páginas mucha matemática. Destaca el estudio de las secciones cónicas, que presenta dos maneras de generarlas por medio de intersecciones de rectas móviles. Esto le conduce a la construcción de una cónica que debe cumplir cinco condiciones: pasar por cinco puntos, ser tangente a cinco rectas, pasar por dos puntos y ser tangente a tres rectas… Para estas aplicaciones utiliza, por ejemplo, un cuadrilátero formado por cuatro rectas cualesquiera: al trazar las cónicas tangentes a esas rectas, sus centros pasan por una recta que, además, atraviesa los puntos medios de las diagonales del cuadrilátero. Esa última recta se conoce como «recta de Newton».
En la proposición XXVII del primer libro, Newton se propone construir una cónica que toque a cinco rectas dadas, y la acompaña con la imagen de la figura 5. En ella aparecen las rectas ABG, BCF, GCD, FDE y EA.

También demostró el conocido como «problema de las cuatro rectas» de Pappus, que ya había demostrado parcialmente Descartes. Newton aclaró que su solución «no consiste en un cálculo analítico, sino en una composición geométrica tal como exigían los antiguos». Este problema lo planteó en el lema XIX, cuya demostración puede verse gráficamente en la figura 6:

Encontrar un punto P desde el cual, si cuatro líneas PQ, PR, PS y PT son trazadas hasta otras tantas rectas AB, CD, AC y BD dadas por posición, cada una a cada una, en ángulos dados, el rectángulo PQ - PR, bajo dos cualesquiera de las líneas trazadas, mantendrá con el rectángulo PS - PT, bajo las otras dos, una razón dada.
Como ejemplo concreto del razonamiento matemático que Newton aplicó en los Principia puede extraerse el presentado por el científico inglés en la primera sección del primer libro, donde expuso su método de las primeras y últimas razones de cantidades aplicándolo en una serie de proposiciones. Este es el lema II con su demostración (figura 7):

Si en cualquier figuraba AaE, delimitada por las líneas rectas Aa, AE y curva acE, se inscribe cualquier número de paralelogramos Ab, Bc, Cd, etcétera, comprendidos bajo bases iguales AB, BC, CD, etcétera, y lodos Bb, Cc, Dd, etcétera, paralelos al lado Aa de la figura, y se completan los paralelogramos aKbl, bLcm, cMdn, etcétera, si la anchura de esos paralelogramos se supone que irá disminuyendo y su número aumentando infinitamente, afirmo que las últimas razones que guardarán entre la figura inscrita AKbLcMdD, la figura circunscrita AalbmcndoE y la figura curva AabcdE son razones de igualdad. Porque la diferencia de las figuras inscritas y circunscritas es la suma de los paralelogramos Kl, Lm, Mn, Do, esto es —por la igualdad de todas sus bases—, el rectángulo bajo una de sus bases Kb y de altura la suma de sus alturas Aa, esto es, el rectángulo ABla. Pero este rectángulo, dado que su anchura AB se supone disminuida infinitamente, se hace menor que cualquier espacio dado. Y por tanto —según el lema I— las figura inscritas y circunscritas se hacen en última instancia iguales entre sí, y mucho más la figura curva intermedia. Quod erat demonstrandum.
Por último, el lema I sostenía que «las cantidades, y las razones de cantidades, que en cualquier tiempo finito tienden continuamente a la igualdad, y antes de terminar ese tiempo se aproximan una a otra más que ninguna diferencia dada, acaban haciéndose en última instancia iguales».
Véase otro ejemplo tomado del tercer libro, en este caso el lema II. En él, se pide lo siguiente:
Cortar tres líneas rectas dadas en posición con una cuarta línea recta que pase por un punto dado en cualquiera de las tres de forma que sus partes interceptadas estén en razón dada entre sí. Sean AB, AC, BC las tres lineas rectas dadas en posición, y supóngase que D es el punto dado en la línea AC. Trácese DG paralela a AB, encontrándose con BC en G; llevando GF a BG en la razón dada, trácese FDE, y FD será a DE como FG a BG.
En este lema, cuya representación gráfica puede verse en la figura 8, también incluye la opción de demostrarlo por la vía trigonométrica: «En el triángulo CGD están dados todos los ángulos y el lado CD, con lo que se determinan los otros lados, y las líneas GF y BE están también dadas por las razones dadas».

Newton tuvo la feliz idea de unir el comportamiento de los cuerpos sobre la Tierra con el movimiento celeste. Estructuró a la perfección el comportamiento de los cuerpos en movimiento. A diferencia de otros que solo lo intuyeron, él se valió de las matemáticas para demostrar que sus leyes eran irrefutables. Su construcción fue tan precisa que, hasta la llegada de Einstein, todo se rigió por las pautas establecidas por Newton. Pero no fue este su único logro. Además, el genio inglés revolucionó el mundo de matemáticas gracias al cálculo infinitesimal y planteó una teoría sobre la luz que fue la prioritaria durante todo el siglo XVIII.